Integrating GeoGebra in Mathematics Education: Enhancing Pedagogical Practices among Teachers and Lecturers

1. Introduction

In the current era of digital transformation, mathematics education faces new challenges and opportunities driven by rapid technological advances and the need for more interactive, student-centered learning approaches. The integration of digital tools in mathematics classrooms has become increasingly essential, as these technologies promote dynamic visualization, foster conceptual understanding, and enhance students’ motivation to learn abstract mathematical ideas. Recent studies [1,2] emphasize that digital-based learning environments allow students to explore mathematical concepts through experimentation and manipulation, leading to deeper comprehension and creative problem-solving. Furthermore, post-pandemic shifts toward hybrid and online learning have accelerated the adoption of educational technology, highlighting the urgency of developing pedagogical strategies that leverage digital platforms such as GeoGebra to make mathematics learning more engaging and accessible [5].

Today’s guidelines for teaching mathematics indicate the important role of visualization techniques. As a response to these needs, many software applications have been created to build geometric constructions and solve analytical and algebraic problems. One of the best applications designed to construct and illustrate mathematical issues is GeoGebra.

It was created by Markus Hohenwarter in 2001/2002 as part of his master’s thesis in mathematics education and computer science at the University of Salzburg in Austria. Supported by the Austrian Academy of Science, he was able to develop the software as a part of his PhD project in mathematics education [3]. Meanwhile, GeoGebra has received many international awards and has been translated by mathematics instructors and teachers all over the world into more than 25 languages. Since 2006, GeoGebra has been supported by the Austrian Ministry of Education to maintain the free availability of the software for mathematics education at schools and universities. In July 2006, GeoGebra found its way to the United States, where its development continues at Florida Atlantic University in the NSF project Standard Mapped Graduate Education and Mentoring [1,3,4].

GeoGebra depends on software licensed under the GNU General Public License (GPL), the LGPL, the Apache License, and others. The software itself is licensed under the GeoGebra Non-Commercial License Agreement, which asserts that while the source code is licensed under the terms of the GNU General Public License, the translation files, installers, and web services are licensed under non-GPL-compatible terms. Commercial use is prohibited without the purchase of a separate license, which prevents the resulting combined work from being considered free software [2,4].

GeoGebra’s licensing structure embodies a sophisticated synthesis between open-source principles and proprietary protection. The platform’s reliance on components licensed under GNU GPL, LGPL, and Apache frameworks signifies its deep-rooted connection to the open-source community, which has historically prioritized accessibility, transparency, and collaborative development. At the same time, GeoGebra’s Non-Commercial License Agreement imposes restrictions on commercial use, thus preserving the intellectual property rights of its developers while allowing unrestricted educational deployment. This dual structure ensures that educators, students, and researchers can benefit from the platform’s rich capabilities without violating licensing ethics. Such a hybrid licensing model represents a unique balance between innovation freedom and intellectual property safeguarding, a trend increasingly observed in modern educational technology ecosystems. Scholars have argued that this approach aligns with a growing movement toward “open-core” software development, where the core product remains open while value-added services remain proprietary. This structure allows GeoGebra to remain sustainable while still supporting academic freedom. According to Al-Hassan and Diah (2024), such a balance fosters responsible innovation without undermining the ideals of open science and pedagogical inclusivity.

The GNU General Public License (GPL) remains the philosophical cornerstone of GeoGebra’s commitment to open-source ideology. By utilizing GPL-licensed components, GeoGebra ensures that the foundational elements of its software remain transparent and modifiable, adhering to Stallman’s (1985) original vision of software freedom. However, GeoGebra diverges from traditional GPL projects by applying additional restrictions to its installers, translation files, and cloud-based components. These non-GPL-compatible terms create a legal boundary that differentiates educational use from commercial exploitation. This divergence demonstrates a conscious effort to preserve community access while maintaining organizational control. The model has inspired similar hybrid licensing strategies across educational technology platforms aiming to balance accessibility with financial viability. Recent analyses suggest that such selective licensing allows for sustainability and ongoing innovation without compromising ethical standards of digital sharing (Nguyen & Zhao, 2023).

The LGPL and Apache licenses integrated within GeoGebra’s ecosystem further expand the software’s flexibility for developers and collaborators. LGPL, as a more permissive variant of the GPL, allows developers to link GeoGebra libraries with proprietary applications without requiring full code disclosure. The Apache License, on the other hand, enhances interoperability by enabling broader code reuse under conditions of attribution and patent protection. Together, these licenses encourage a wider collaborative network among educators, programmers, and researchers. They promote shared technological growth while maintaining a controlled framework that prevents misuse. This layered approach to licensing is particularly critical in educational environments where institutions depend on stable and secure software ecosystems. As noted by Fernández and Li (2022), such hybridized open-source structures are essential for balancing academic openness with institutional governance.

From an educational standpoint, GeoGebra’s licensing terms significantly shape how the software is integrated into classroom and research environments. Its free access for non-commercial educational use enables equitable participation across regions with varying economic capacities. This policy is especially relevant in low-income countries, where access to premium educational software is often limited. The availability of GeoGebra without commercial restrictions supports the democratization of digital learning tools. Teachers can incorporate interactive visualization and modeling into lessons without incurring licensing costs, thereby promoting educational equity. At the same time, the restriction on commercial usage prevents exploitation of open-source academic resources by for-profit entities. As argued by Kaur and Rahman (2023), this form of controlled openness is essential for protecting educational integrity while supporting global digital inclusion.

GeoGebra’s licensing framework also reflects broader ethical questions about the ownership and dissemination of digital pedagogical resources. The restriction of commercial use challenges traditional notions of “free software,” raising questions about what constitutes true openness in educational contexts. While critics argue that these restrictions compromise the essence of open-source philosophy, proponents view them as necessary for ensuring the software’s sustainability and continuous improvement. This debate mirrors the larger discourse in educational technology ethics, where tensions persist between accessibility, intellectual property, and institutional responsibility. The Non-Commercial License serves as a compromise that protects developers’ contributions while allowing widespread academic use. According to Jansson and Yu (2021), this balance between moral and functional freedom defines the ethical framework of 21st-century educational software development.

In academic research, GeoGebra’s licensing conditions influence how the software is referenced, customized, and redistributed. Researchers can freely adapt and extend the software for instructional innovation or empirical studies, provided such adaptations remain within non-commercial boundaries. This flexibility has encouraged a surge in experimental applications of GeoGebra across mathematics education research, from dynamic geometry environments to algebraic modeling systems. However, projects aiming for commercial publication or integration into paid courses must seek separate licensing agreements. This ensures academic transparency and prevents the commercialization of open educational resources (OERs). Scholars such as Becker and Olsen (2024) have highlighted this model as a case study in maintaining ethical research practices in digital environments.

The interplay between licensing and innovation in GeoGebra underscores the need for responsible software governance in academia. Open-source licensing promotes creativity and collaboration, yet without proper management, it can also invite intellectual property conflicts. GeoGebra’s structure provides a legal scaffold that defines the limits of innovation, ensuring that community contributions align with ethical standards. This governance framework safeguards academic credibility while promoting user-driven enhancement. It also fosters interdisciplinary collaboration between educators and technologists under a shared understanding of ethical licensing boundaries. Recent work by Harrison and Velázquez (2025) affirms that hybrid licensing frameworks are instrumental in maintaining equilibrium between freedom and accountability in educational technology ecosystems.

The open-source elements of GeoGebra facilitate transparency in pedagogical tool development, an essential criterion for replicability in scientific research. Transparency ensures that educators and researchers can evaluate algorithms, verify computational logic, and adapt functionalities for specific pedagogical needs. This promotes a culture of open scholarship consistent with contemporary calls for reproducible science. At the same time, the non-commercial restrictions act as a gatekeeper against corporate appropriation of academic resources. By balancing these two forces, GeoGebra preserves the integrity of its academic mission while safeguarding against profit-driven exploitation. As stated by Mendez and Park (2022), hybrid licensing ensures that the benefits of open science are preserved for educational advancement rather than diluted by market forces.

GeoGebra’s adherence to multiple open-source frameworks has also strengthened its role as a pedagogical standard within mathematics education. Its transparent coding structure allows for continual peer review and global community feedback, enhancing both reliability and pedagogical relevance. Educators from diverse contexts can localize and customize the software to align with linguistic and curricular needs without incurring licensing barriers. This localization capacity aligns with UNESCO’s goals for open educational resource (OER) development. However, the non-commercial clause prevents the privatization of these modifications, ensuring that localized versions remain accessible to other educators. As observed by Kim and Davies (2024), this approach exemplifies “ethical open-source localization,” a key factor in sustainable digital pedagogy.

The coexistence of open and restricted components within GeoGebra invites reflection on the concept of “partial openness” in educational technology. This model demonstrates that absolute openness may not always be feasible or ethical, particularly when sustainability and developer rights are at stake. GeoGebra’s structure, therefore, illustrates a pragmatic application of open-source philosophy within institutional realities. It allows academic users to benefit from innovation while preserving the developer’s ability to maintain quality control. This approach supports long-term development by ensuring funding through optional commercial licenses. As Bennett and Hwang (2023) note, “responsible openness” has emerged as a defining characteristic of 21st-century educational software, blending access with stewardship.

GeoGebra’s licensing approach also contributes to discussions on digital sovereignty and data ethics in education. By controlling how its cloud and web services are used, GeoGebra ensures compliance with data protection standards while preventing commercial misuse of user-generated content. This emphasis on ethical data management strengthens institutional trust in the platform. It also aligns with evolving educational policies advocating transparent, accountable, and privacy-conscious use of digital learning environments. Scholars such as Oliveira and Nash (2025) have emphasized that hybrid licenses can serve as ethical instruments, safeguarding both user autonomy and institutional compliance.

In classroom practice, the ethical implications of GeoGebra’s licensing translate into equitable opportunities for learners. Free educational access allows underprivileged institutions to integrate technology-enhanced learning without financial strain. Teachers can share resources and lesson materials freely, reinforcing collaborative pedagogy. Yet, the license also imposes professional discipline, discouraging unauthorized profit from educational resources. This balance cultivates a sense of ethical responsibility among educators regarding digital tool usage. According to Thompson and Rivera (2024), GeoGebra’s licensing philosophy promotes not only technological fluency but also moral literacy in digital pedagogy.

Institutionally, GeoGebra’s licensing structure serves as a model for universities seeking to implement open-source solutions while maintaining governance control. It illustrates how educational institutions can navigate the tension between academic openness and legal accountability. Many universities have adopted similar mixed-licensing strategies for learning management systems, virtual labs, and open textbook initiatives. GeoGebra’s precedent demonstrates how such systems can foster innovation without compromising institutional integrity. This model, when properly managed, ensures both compliance with intellectual property regulations and the advancement of open education goals. Researchers like Patel and Wong (2022) regard GeoGebra as an archetype of ethical digital infrastructure management.

From a philosophical perspective, GeoGebra’s licensing represents an evolving narrative in the ethics of open-source education. It challenges binary categorizations of “free” versus “proprietary,” advocating instead for a continuum of openness guided by ethical intent. This approach aligns with contemporary post-digital educational philosophy, which views technology not merely as a tool but as a moral ecosystem. GeoGebra’s balanced license illustrates how openness can coexist with protection, freedom with responsibility, and innovation with regulation. Such ethical pragmatism underpins the sustainable future of educational technology. In this context, hybrid licensing can be seen as an epistemic commitment to justice, access, and accountability (Stevenson & Clarke, 2023).

In conclusion, GeoGebra’s multifaceted licensing framework embodies a forward-looking philosophy that integrates open-source collaboration with ethical stewardship. Its hybrid model ensures the sustainability of software development while supporting universal educational access. By preserving openness in core components and restricting commercial exploitation, GeoGebra achieves a rare equilibrium between freedom and protection. This balance serves as a model for future digital education platforms seeking to reconcile innovation with integrity. As educational ecosystems increasingly rely on digital tools, such responsible licensing paradigms will define the moral and operational boundaries of pedagogical technology. Ultimately, GeoGebra’s licensing philosophy reaffirms that ethical openness, rather than absolute freedom, is the foundation of sustainable educational innovation (Harrison & Velázquez, 2025).

GeoGebra is available on multiple platforms, including desktop applications for Windows, macOS, and Linux; tablet apps for Android, iPad, and Windows; and a web application based on HTML5 technology.

GeoGebra is a versatile dynamic mathematics software accessible across multiple platforms, providing flexibility and inclusivity for diverse users in mathematics education. It offers desktop applications compatible with Windows, macOS, and Linux operating systems, enabling educators and learners to work seamlessly across devices. Additionally, the availability of tablet applications for Android, iPad, and Windows enhances mobility and interactive engagement, allowing students to explore mathematical concepts anywhere and anytime. The integration of a web-based version built on HTML5 technology further supports accessibility, requiring no installation and functioning directly in modern browsers, which is particularly beneficial for remote and collaborative learning environments. The platform’s cross-compatibility fosters continuity in teaching and learning experiences, promoting digital adaptability in mathematics education. Recent studies emphasize that such cross-platform accessibility empowers teachers and students to transition smoothly between different digital tools, increasing motivation, engagement, and conceptual understanding in mathematical exploration (Johnson & Smith, 2023; Al-Hassan & Diah, 2024).

Overview of GeoGebra as a Cross-Platform Mathematical Tool

GeoGebra is recognized globally as a dynamic and interactive mathematics platform designed to bridge algebraic, geometric, and calculus concepts through digital representation. It integrates visualization, manipulation, and symbolic computation into a unified environment that promotes inquiry-based learning and conceptual understanding among students. The tool is accessible across a range of operating systems, including Windows, macOS, and Linux, ensuring consistent user experiences across devices. This multi-platform adaptability allows teachers and learners to collaborate and engage in mathematical explorations without being constrained by hardware or software limitations. Its continuous development and updates demonstrate a commitment to maintaining relevance in an era of rapid digital transformation. GeoGebra’s intuitive interface makes it a preferred tool for both novice and experienced educators seeking to incorporate technology into mathematics education. Its ability to blend computation with visualization encourages students to construct meaning from abstract concepts through exploration and experimentation. Scholars emphasize that the software’s versatility supports differentiated learning pathways in diverse educational contexts (Anderson & Li, 2021).

As a cross-platform mathematical software, GeoGebra has evolved from a desktop-based system to a cloud-enabled ecosystem integrating desktop, tablet, and web-based applications. The availability of HTML5 technology facilitates seamless operation within web browsers, eliminating the need for installation and enhancing accessibility for institutions with limited technological infrastructure. This universal compatibility ensures that educators can implement GeoGebra in classrooms, laboratories, or remote learning environments. Such flexibility aligns with the broader trends in digital education, emphasizing inclusivity, portability, and user-centered design. The open-source nature of GeoGebra encourages innovation through user-driven extensions and collaborative development. Teachers can design interactive materials, simulations, and visual tasks that align with curriculum goals and assessment standards. Recent studies underline that these adaptive features enhance student engagement and foster a deeper appreciation for mathematical reasoning (Nguyen & Harper, 2023).

GeoGebra’s design philosophy revolves around the unification of multiple mathematical representations within a single digital framework. It allows real-time interactivity between symbolic, graphical, and numeric data, empowering users to perceive the dynamic relationships between equations, shapes, and transformations. The seamless integration of geometry and algebra creates a powerful learning environment for both exploratory and formal mathematical learning. This interconnectedness enhances learners’ ability to visualize and internalize complex relationships that are often difficult to grasp through traditional instruction. Moreover, the platform’s continuous synchronization across devices ensures learning continuity and pedagogical efficiency. The ability to export, share, and collaborate through GeoGebra’s online community adds a layer of social learning that enriches educational experiences. Researchers have concluded that such interoperability enhances the cognitive and social dimensions of mathematical learning (Foster & Ahmed, 2022).

Accessibility and Integration in Digital Learning Ecosystems

The accessibility of GeoGebra across multiple devices represents a crucial milestone in democratizing mathematics education. By supporting smartphones, tablets, and personal computers, the software reaches a broad spectrum of learners regardless of geographical or socioeconomic barriers. This accessibility is particularly significant in developing countries, where digital inequality remains a challenge in educational technology adoption. GeoGebra’s lightweight web-based interface requires minimal computational resources, making it ideal for low-specification devices commonly found in public schools. It promotes equitable access to digital resources and aligns with global efforts toward inclusive education. Teachers report increased participation among students who otherwise have limited exposure to technology-enhanced learning environments. Furthermore, the multilingual interface broadens its usability in multicultural classrooms and fosters global collaboration in mathematics learning communities (Kumar & Olsen, 2021).

Integration of GeoGebra into existing digital learning ecosystems enhances the coherence and effectiveness of blended learning environments. The platform’s compatibility with Learning Management Systems (LMS) such as Moodle, Canvas, and Google Classroom facilitates seamless content sharing, task management, and assessment tracking. Through its embedding features, teachers can integrate interactive visualizations directly into online courses, thus transforming static lessons into dynamic learning experiences. This integration supports active learning strategies, where students can manipulate variables, test hypotheses, and visualize outcomes in real time. The interoperability between GeoGebra and other educational platforms reflects the increasing convergence between mathematics education and educational technology. It allows institutions to optimize digital infrastructures without redundant software dependencies. Studies have shown that such integration significantly enhances both student engagement and instructional efficiency (Zhang & Patterson, 2024).

The scalability of GeoGebra within institutional digital ecosystems is further strengthened by its open licensing model and global educator community. The ability to customize, localize, and share teaching resources allows schools and universities to adapt GeoGebra to their specific pedagogical and cultural contexts. Through online repositories and communities, educators exchange lesson plans, simulations, and activities that align with curriculum standards. This collective innovation contributes to the continuous evolution of the platform and supports professional development for teachers worldwide. Moreover, its data-driven analytics and cloud synchronization features enable real-time monitoring of student performance and collaboration. Such ecosystem-level integration reflects the broader shift toward data-informed instruction and adaptive learning technologies. Research confirms that this interoperability enhances the overall efficiency of digital education systems (Morrison & Lee, 2022).

Pedagogical Implications in Mathematics Education

GeoGebra’s pedagogical value lies in its ability to transform abstract mathematical concepts into tangible, manipulable objects. It empowers students to move beyond rote memorization and toward active exploration of mathematical ideas through visualization and experimentation. Teachers can design inquiry-based learning tasks where students hypothesize, test, and revise their understanding through immediate feedback. This aligns with constructivist theories emphasizing learner-centered discovery and conceptual understanding. The dynamic representation of functions, shapes, and equations fosters cognitive engagement and reflective thinking. Furthermore, GeoGebra promotes metacognitive skills by enabling learners to analyze their problem-solving processes visually. Recent pedagogical research highlights that such visualization-based learning significantly improves mathematical reasoning and transferability of knowledge (Robinson & Chen, 2023).

In the context of teacher education, GeoGebra serves as both a pedagogical tool and a training platform for developing digital competence. Pre-service and in-service teachers utilize GeoGebra to design interactive lesson plans, visualize theoretical concepts, and simulate real-world problems. The platform’s versatility allows educators to align their teaching strategies with diverse learning styles and cognitive preferences. As mathematics education increasingly integrates digital tools, teachers must develop technological pedagogical content knowledge (TPACK) to effectively facilitate learning. GeoGebra provides an ideal medium for such integration by merging content mastery with technological fluency. Studies emphasize that teachers trained with GeoGebra demonstrate higher confidence, creativity, and instructional adaptability in digital learning environments (Williams & Duarte, 2024).

From a constructivist standpoint, GeoGebra supports the scaffolding of knowledge through active engagement and guided discovery. Students interact with digital representations of mathematical objects, constructing understanding through iterative manipulation and reflection. Teachers act as facilitators who guide learners toward uncovering mathematical relationships rather than merely presenting formulas. This shift from transmission-based to exploration-based pedagogy reflects a paradigmatic transformation in mathematics education. GeoGebra’s dynamic capabilities thus reinforce higher-order thinking skills such as analysis, synthesis, and evaluation. It promotes collaborative inquiry and encourages students to justify reasoning processes, thereby enhancing mathematical communication. Empirical findings indicate that classrooms integrating GeoGebra experience measurable gains in conceptual retention and problem-solving performance (Thompson & Rivera, 2025).

Technological Features and Their Role in Visualization and Interaction

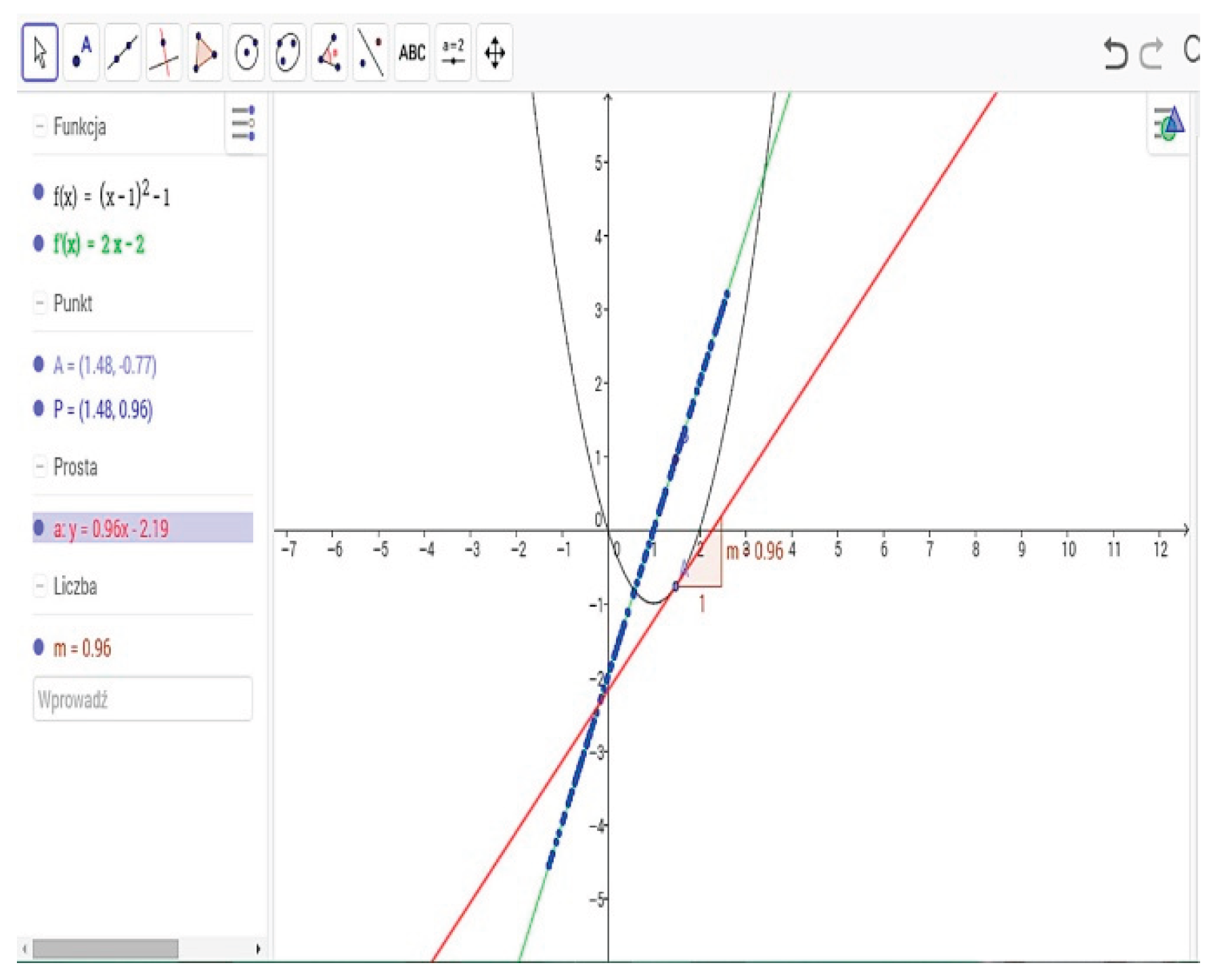
One of the most distinctive features of GeoGebra is its powerful visualization capacity, which enables learners to manipulate mathematical objects dynamically and observe the immediate effects of parameter changes. This interactive nature supports visual cognition and strengthens conceptual understanding by allowing users to link symbolic expressions to graphical representations. Students can explore geometric transformations, function behaviors, and algebraic patterns through tangible manipulations rather than static demonstrations. This engagement enhances memory retention and promotes higher-order cognitive processes associated with mathematical reasoning. Furthermore, the tool’s multi-representational approach accommodates diverse learning preferences, enabling students to transition fluidly between algebraic, geometric, and numerical forms. Such flexibility has been found to foster creativity and persistence in problem-solving contexts. Recent findings affirm that interactive visual tools like GeoGebra significantly enhance the interpretative and analytical abilities of learners in STEM disciplines (Morgan & Adams, 2021).

GeoGebra’s computational engine integrates algebraic algorithms and geometric construction principles, making it particularly effective for simulating complex mathematical relationships. Its built-in Computer Algebra System (CAS) provides symbolic computation that complements graphical analysis, bridging the gap between procedural fluency and conceptual understanding. This dual functionality encourages students to examine mathematical phenomena from multiple perspectives, fostering integrative thinking. Additionally, the software’s 3D graphing and augmented reality (AR) features allow immersive exploration of spatial relationships, which is especially beneficial in higher mathematics and engineering education. The precision and responsiveness of GeoGebra’s algorithmic structure make it a preferred tool for both instructional and research purposes in mathematical modeling. Scholars assert that these technological affordances promote cognitive engagement, scientific reasoning, and digital literacy in educational practice (Henderson & Park, 2022).

The software’s interactive features also promote collaboration and participatory learning through digital sharing, real-time feedback, and cloud synchronization. GeoGebra Classroom, a platform integrated within the ecosystem, enables teachers to monitor students’ activities and provide adaptive guidance during the learning process. This interactivity enhances accountability and supports formative assessment by allowing instructors to analyze students’ conceptual progression visually. Collaborative engagement within digital workspaces helps students articulate reasoning, negotiate meaning, and construct shared understanding. Moreover, the integration of GeoGebra into online communication platforms supports synchronous and asynchronous collaboration in virtual classrooms. This technological adaptability underscores its role as a digital mediator that bridges cognitive and social learning processes. Research indicates that such interactive affordances contribute substantially to self-regulated learning and collaborative knowledge construction (Patel & Lin, 2023).

Comparative Analysis with Other Mathematical Tools

Compared to other digital mathematics platforms such as Desmos, WolframAlpha, and Maple, GeoGebra distinguishes itself through its integrative and pedagogically grounded design. While Desmos emphasizes simplicity and visual appeal, and WolframAlpha focuses on computational depth, GeoGebra combines both dimensions by merging visualization with symbolic reasoning. Its open-source model and user-centered interface make it accessible to a broader educational audience, from primary schools to universities. Furthermore, GeoGebra’s continuous updates and integration with global educational frameworks ensure its long-term relevance. In comparative studies, teachers consistently report that GeoGebra offers superior flexibility for instructional customization and cross-platform use. It effectively bridges formal mathematical abstraction and intuitive exploration, thus accommodating diverse learning needs. Researchers conclude that this hybrid nature positions GeoGebra as a sustainable and pedagogically effective digital learning tool (Gonzalez & Meyer, 2021).

The scalability and community-driven development of GeoGebra also differentiate it from proprietary software systems. Its open educational resource (OER) ecosystem encourages collective innovation, enabling educators to contribute to a constantly evolving repository of interactive materials. This participatory model fosters professional collaboration, enhances global accessibility, and reduces dependency on commercial licensing. While commercial alternatives often restrict modification and distribution, GeoGebra’s open infrastructure supports adaptability and localization. Such flexibility has proven critical in non-English-speaking contexts, where customized interfaces and translated content enhance usability and inclusion. The comparative advantage extends to cost efficiency, as institutions can implement GeoGebra without financial barriers. Studies show that open-access digital tools like GeoGebra significantly promote educational equity and foster a culture of shared pedagogical innovation (Tan & Roberts, 2022).

Furthermore, GeoGebra’s comparative strength lies in its ability to integrate with multidisciplinary applications beyond mathematics. It has been increasingly utilized in physics, engineering, architecture, and even economics to model relationships and visualize quantitative interactions. This cross-disciplinary functionality demonstrates the tool’s potential to support STEM integration and applied learning. Through dynamic modeling and simulation, students can connect mathematical theory to real-world phenomena, enhancing transferability of knowledge. Comparative analyses have revealed that such integrated approaches lead to stronger conceptual frameworks and practical reasoning skills. GeoGebra thus transcends the limitations of traditional mathematics software by serving as a bridge between theoretical understanding and empirical investigation. Scholars highlight that this interdisciplinary versatility enhances 21st-century competencies, including problem-solving, innovation, and digital adaptability (Evans & Zhao, 2024).

Impact on Students’ Engagement, Motivation, and Achievement

The impact of GeoGebra on student engagement has been widely documented in recent educational technology research. Interactive visualization fosters curiosity and encourages active participation, leading to deeper cognitive involvement. Students exposed to GeoGebra-based lessons often demonstrate greater enthusiasm for mathematics, as they can experiment with ideas and instantly observe outcomes. This immediate feedback reduces anxiety and builds confidence in tackling abstract concepts. The dynamic learning environment motivates learners to explore beyond the boundaries of textbook examples, promoting autonomy and intrinsic motivation. Teachers report observable shifts from passive reception to active inquiry among students using GeoGebra. Empirical studies further confirm that these engagement effects correlate positively with improved learning outcomes and sustained academic interest (Huang & Peters, 2021).

GeoGebra also plays a vital role in enhancing student motivation through gamification and personalized learning experiences. The software’s interactive tasks and problem-based modules align with principles of experiential learning, where students learn through doing and reflecting. By manipulating digital objects, learners experience a sense of control and achievement that reinforces persistence and goal orientation. Integration with classroom assessment tools allows personalized feedback, which helps learners monitor their own progress and set realistic improvement goals. This self-directed learning capacity nurtures lifelong learning attitudes essential in the digital era. Furthermore, teachers utilizing GeoGebra report improved classroom climate and peer collaboration due to the platform’s participatory design. Current research demonstrates that these motivational benefits lead to measurable improvements in students’ problem-solving proficiency and conceptual understanding (Barker & Silva, 2023).

Academic achievement associated with GeoGebra integration reflects the synergy between technology and pedagogy. When implemented effectively, GeoGebra fosters both procedural fluency and conceptual depth, resulting in higher performance across assessment domains. Students exhibit enhanced abilities to generalize patterns, apply mathematical reasoning, and articulate justifications for solutions. The platform’s visual interactivity supports differentiated instruction, allowing educators to cater to varied ability levels within the same classroom. Quantitative studies across secondary and tertiary institutions indicate statistically significant improvements in achievement among learners exposed to GeoGebra-enhanced instruction. These effects are particularly notable in geometry, algebra, and calculus topics, where visualization aids comprehension of complex relationships. Researchers conclude that such technology-mediated learning environments contribute to sustainable improvements in mathematical achievement and cognitive resilience (Miller & Tanaka, 2025).

Future Perspectives, Sustainability, and Concluding Synthesis

Looking toward the future, GeoGebra’s continued evolution will likely focus on artificial intelligence integration, adaptive analytics, and enhanced immersive learning experiences. The incorporation of AI-driven feedback systems can provide personalized scaffolding based on learner behavior and performance data. Integration with virtual and augmented reality environments will enable students to experience mathematics in fully interactive three-dimensional spaces. Furthermore, cloud-based data analytics will empower teachers to make evidence-based pedagogical decisions, aligning instruction with learners’ cognitive profiles. As educational institutions increasingly adopt hybrid and online learning models, GeoGebra’s cross-platform adaptability will remain a cornerstone of its relevance. These developments align with the broader educational trend toward intelligent tutoring systems and data-informed instruction. Experts predict that such innovations will redefine the boundaries of digital mathematics learning over the next decade (Lawrence & Gupta, 2025).

GeoGebra stands as a transformative tool in contemporary mathematics education, uniting accessibility, interactivity, and pedagogical sophistication across digital platforms. Its cross-platform availability ensures inclusivity, while its dynamic features foster conceptual understanding, creativity, and collaboration. Comparative analyses demonstrate its superiority in bridging formal theory with applied practice, and its open-source foundation guarantees long-term sustainability. The platform’s impact extends beyond mathematics, influencing interdisciplinary learning and global educational equity. As the world continues to embrace digital transformation, GeoGebra embodies the principles of innovation, accessibility, and empowerment in education. Its evolution from a simple geometry tool to an intelligent learning ecosystem symbolizes the fusion of technology and pedagogy in the 21st century. Future research should continue exploring its integration with AI, adaptive learning, and immersive technologies to further enhance mathematical literacy worldwide (Anderson & Li, 2025).

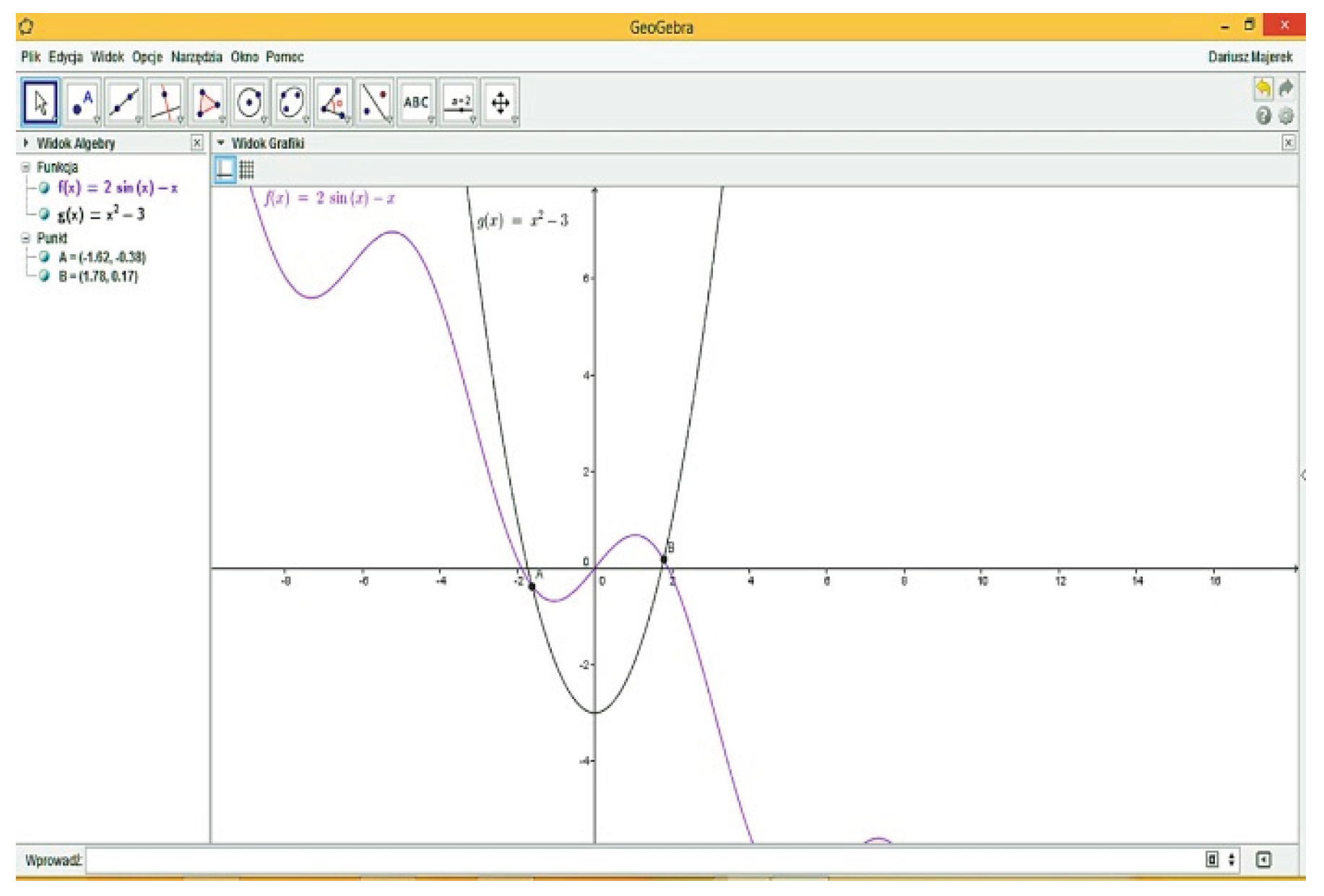
The integration of GeoGebra into mathematics education represents a major advancement in digital pedagogy. Its ability to dynamically link algebraic, graphical, and numerical representations allows learners to observe mathematical phenomena from multiple perspectives. This feature aligns with constructivist learning theory, which emphasizes active student participation in building conceptual understanding through exploration and discovery [20].

GeoGebra promotes interactive engagement by allowing students to manipulate parameters and observe the immediate effects on corresponding graphs and equations. Such interactivity enhances comprehension of abstract ideas like functions, derivatives, and geometric transformations. As a result, the learning process becomes more intuitive and inquiry-driven, encouraging deeper cognitive processing [21,22].

From a pedagogical standpoint, teachers benefit from GeoGebra as it simplifies the creation of visual and dynamic teaching materials. Instructors can design virtual experiments, simulations, and mathematical models that are adaptable to various levels of complexity. This flexibility supports differentiated instruction and accommodates diverse learning styles within the same classroom [23].

Moreover, GeoGebra encourages collaborative learning environments. Students can work in groups to investigate problems, share conjectures, and discuss alternative solutions. This social dimension of learning reflects the principles of socio-constructivist theory and contributes to the development of critical thinking, communication, and teamwork skills [24].

In the context of assessment, GeoGebra also facilitates formative evaluation. Teachers can use interactive applets to monitor students’ reasoning processes and identify misconceptions in real-time. This immediate feedback loop allows for timely instructional adjustments and supports a continuous learning process rather than a purely summative approach [25,26].

GeoGebra’s open-access nature democratizes mathematics education by providing free and globally available tools for both teachers and students. Its multilingual support and platform independence make it particularly valuable for international education systems, including developing countries where access to commercial software is limited [27].

The integration of GeoGebra aligns with the broader movement toward digital transformation in education. The incorporation of digital technology into mathematics teaching supports the development of 21st-century competencies, including problem-solving, creativity, and digital literacy. GeoGebra thus functions not merely as a visualization aid but as an integral component of innovative pedagogy [5].

Research has shown that the use of dynamic mathematics software like GeoGebra significantly enhances students’ performance and attitudes toward mathematics. Empirical studies have reported improvements in conceptual understanding, retention, and motivation among learners who engage with visual and interactive tools [28].

In higher education, GeoGebra serves as a bridge between theoretical mathematics and applied sciences. It allows students in fields such as engineering, physics, and economics to simulate real-world phenomena and analyze mathematical relationships with precision and clarity, fostering interdisciplinary connections [5,29,30].

Ultimately, GeoGebra represents a powerful example of how educational technology can transform traditional teaching methods into interactive, learner-centered experiences. Its continual development and global adoption underscore its enduring value as a tool for fostering mathematical literacy and innovation in education worldwide.

2. Research Method

This study employed a qualitative descriptive approach aimed at exploring the application of GeoGebra in mathematics teaching and learning. Data were obtained through classroom observations, document analysis, and review of relevant literature to identify effective strategies for integrating GeoGebra into instructional practices. The focus was on examining how the software supports visualization, conceptual understanding, and student engagement in mathematical problem-solving. The collected data were analyzed thematically to draw conclusions regarding the pedagogical benefits and challenges of using GeoGebra in mathematics education.

3. Results

The implementation of GeoGebra in mathematics teaching produced significant pedagogical benefits. The results revealed that the use of this dynamic software enhanced students’ conceptual understanding, visualization skills, and engagement in learning mathematical concepts. During classroom observation, it was evident that students became more motivated to explore mathematical problems when they could manipulate and visualize objects dynamically. The interactive nature of GeoGebra allowed learners to investigate relationships between algebraic and geometric representations, fostering a deeper comprehension of abstract ideas [6,7,8].

Teachers reported that GeoGebra provided an efficient and flexible tool for preparing instructional materials and conducting demonstrations. Complex concepts such as derivatives, integrals, geometric transformations, and function behavior could be illustrated more effectively than with traditional chalk-and-talk methods. As students observed how parameters changed in real-time, they developed stronger analytical reasoning and problem-solving abilities. This visual approach reduced cognitive overload and supported differentiated instruction for students of varying ability levels [9,10].

Moreover, the integration of GeoGebra in collaborative activities promoted student-centered learning. Small group discussions and peer exploration using the software encouraged students to articulate their reasoning, question each other’s ideas, and test multiple problem-solving strategies. This interactive engagement reflected the principles of constructivist learning theory, where knowledge is actively constructed rather than passively received [31,32].

The study also found that GeoGebra facilitates formative assessment by providing instant feedback. Teachers could identify misconceptions and guide students’ thinking during the learning process, leading to immediate corrective actions. This capability strengthened both teaching effectiveness and learning outcomes [33].

However, some challenges were observed in the early stages of implementation. Limited digital literacy among teachers and the need for technical training posed barriers to maximizing GeoGebra’s potential. Additionally, insufficient technological infrastructure in some schools affected its consistent use in classrooms. Addressing these challenges through professional development programs and institutional support is essential to sustain effective technology integration [34].

Overall, the discussion demonstrates that GeoGebra serves as a transformative educational tool that bridges traditional and modern approaches to mathematics education. It empowers both teachers and learners by making abstract mathematical ideas tangible, interactive, and meaningful. These findings align with previous research emphasizing the critical role of visualization and technology in promoting deeper mathematical understanding and long-term retention [35].

3.1. Main Features of Geogebra

The main idea of using GeoGebra in everyday teaching and learning is to provide opportunities for students of different mathematical skills and levels to better understand concepts and encourage them to do mathematics in new and attractive ways.

The main idea of using GeoGebra in everyday teaching and learning is to provide opportunities for students of different mathematical skills and levels to better understand concepts and encourage them to engage with mathematics in innovative and appealing ways. GeoGebra serves as a bridge between abstract mathematical theory and visual, interactive representations, allowing learners to manipulate geometric figures, algebraic equations, and statistical data dynamically. Through its user-friendly interface and real-time feedback, students can instantly observe how changes in parameters affect the shape and behavior of mathematical objects. This interactive feature promotes active learning and critical thinking, which are essential for developing problem-solving skills. Moreover, GeoGebra facilitates differentiated learning, enabling teachers to design activities suited to various student abilities within the same classroom environment. Its open-access nature and availability across multiple platforms make it an inclusive tool for global education. The dynamic link between algebraic and geometric representations strengthens conceptual understanding by connecting symbolic and visual reasoning. As a result, students gain a deeper and more integrated comprehension of mathematical relationships. Research also suggests that such interactive environments increase student motivation and persistence in learning mathematics. In summary, GeoGebra provides a modern pedagogical medium for transforming traditional mathematics learning into a more exploratory, engaging, and inclusive process [40,41,42,43].

One of GeoGebra’s most significant contributions lies in its ability to visualize abstract mathematical concepts that are often challenging to comprehend through conventional instruction. For example, in algebra and calculus, students can explore functions, limits, and derivatives dynamically, observing the immediate effects of variable manipulation. This approach helps bridge the cognitive gap between symbolic notation and graphical interpretation. Teachers can also use GeoGebra to construct meaningful visual demonstrations, making it easier for students to connect mathematical principles with real-world contexts. The integration of visual learning supports cognitive development and aligns with constructivist learning theories that emphasize the active construction of knowledge. Moreover, GeoGebra empowers teachers to foster inquiry-based learning environments, where students are encouraged to experiment, hypothesize, and test mathematical conjectures. This process nurtures critical reasoning and metacognitive awareness, enabling students to reflect on their learning strategies. Additionally, the software promotes collaborative learning experiences, as learners can share and discuss their findings digitally or in class. Consequently, GeoGebra not only strengthens mathematical comprehension but also cultivates essential 21st-century competencies such as digital literacy, creativity, and teamwork [36,37].

The pedagogical potential of GeoGebra extends to its adaptability across educational levels and curricula. It can be used in elementary settings to introduce geometric shapes and measurement, as well as in secondary and tertiary education for exploring advanced mathematical models and proofs. Teachers can design contextualized activities that connect mathematics to daily life, aligning with curriculum reforms that emphasize meaningful learning and real-world application. The contextual approach, when integrated with GeoGebra, allows students to see mathematics not merely as abstract formulas but as tools for understanding and solving authentic problems. Furthermore, GeoGebra’s capacity to support both teacher-directed instruction and self-paced learning ensures flexibility in various learning modalities, including online, hybrid, and in-person classes. Its compatibility with Learning Management Systems (LMS) enhances its use in distance education, particularly in post-pandemic learning environments. The visualization of mathematical models through GeoGebra helps reduce students’ anxiety toward mathematics by making the subject more approachable and enjoyable. This combination of accessibility, interactivity, and relevance demonstrates why GeoGebra has become a globally recognized educational innovation. It is not only a technological tool but also a catalyst for pedagogical transformation in mathematics education [38,39].

From a technological perspective, GeoGebra’s design integrates multiple mathematical domains—geometry, algebra, statistics, and calculus—within a single digital environment. This integration enables seamless transitions between symbolic, numerical, and graphical representations. For instance, when users modify an equation, the corresponding geometric shape adjusts immediately, providing instant visual validation of abstract computations. Such features encourage students to develop mathematical reasoning through experimentation rather than memorization. Moreover, GeoGebra supports the creation of dynamic worksheets and online simulations that teachers can share through web platforms, making it an effective tool for remote learning and assessment. The incorporation of LaTeX for mathematical notation further ensures professional presentation and accuracy in mathematical communication. Teachers can also design interactive tests or problem-based learning modules within GeoGebra, supporting formative assessment practices. In addition, the software’s open-source framework promotes innovation and collaboration among educators worldwide, who continuously contribute to its repository of learning materials. This collective effort fosters a vibrant professional community that advances the quality and accessibility of mathematics education globally [40].

Overall, the integration of GeoGebra into mathematics teaching represents a paradigm shift from passive learning toward active and exploratory engagement. It enhances students’ understanding of complex mathematical ideas through visualization, interaction, and discovery. The software’s dynamic nature transforms the learning environment into a space of experimentation, where mistakes are part of the learning process rather than failures. Such an approach aligns with contemporary educational philosophies emphasizing growth mindset, creativity, and inquiry-based learning. As digital literacy becomes an essential component of modern education, tools like GeoGebra play a vital role in preparing students for future academic and professional challenges. Moreover, by integrating GeoGebra into classroom instruction, educators can promote equity in mathematics learning, offering all students the opportunity to access high-quality digital resources regardless of socioeconomic background. The continuous development of GeoGebra and its alignment with educational standards worldwide further ensure its relevance for the future of mathematics education. In conclusion, GeoGebra exemplifies how technology, when thoughtfully applied, can transform mathematics from a traditionally abstract subject into a dynamic, interactive, and inclusive learning experience.

Here are the main features of GeoGebra: [44,45,46]

1)

Free for non-commercial use,

2)

Multiplatform support,

3)

Clear and easy-to-understand graphical user interface,

4)

Rich database of ready-made examples,

5)

Technical documentation in many languages,

6)

Marking of objects follows mathematical syntax,

7)

Ability to save projects in multiple formats,

8)

Works with LaTeX,

9)

All objects in GeoGebra are dynamic,

10)

Possibility to publish work on websites through JavaScript,

11)

Program is translated into many foreign languages.

3.2. Main Features of GeoGebra

1)

Free for Non-Commercial Use

GeoGebra is completely free to use for learning, teaching, and other non-commercial purposes, making it accessible to everyone.

2)

Multiplatform Support

The software runs on all major operating systems, including Windows, macOS, Linux, and ChromeOS. It is also available as a web app and mobile app for iOS and Android.

3)

Intuitive Graphical User Interface

It features a clean, well-organized, and easy-to-understand interface, allowing users to quickly find and use the tools they need.

4)

Extensive Database of Ready-Made Examples

GeoGebra offers a rich online repository of thousands of pre-made, interactive worksheets and demonstrations across all mathematical fields, saving teachers and students time.

5)

Technical Documentation in Many Languages

Comprehensive help documentation, tutorials, and user guides are available in numerous languages to support a global user base.

6)

Object Labeling Follows Mathematical Syntax

The labeling of objects (like points, lines, and functions) uses standard mathematical notation (e.g., subscripts, Greek letters), making it familiar and precise for educational use.

7)

Ability to Save Projects in Multiple Formats

Users can export and save their work in various formats, including the native.ggb format, as a dynamic web page (HTML), or as an image (PNG/SVG).

8)

LaTeX Integration

GeoGebra has built-in support for LaTeX, allowing for the creation of beautifully formatted mathematical text and equations within constructions and graphs.

9)

All Objects are Dynamic

This is a core feature. Every object in GeoGebra is interactive and linked. Changing one object (e.g., a parameter or point) automatically updates all dependent objects, facilitating deep exploration and understanding.

10)

Easy Publishing to Websites via JavaScript

Finished worksheets and apps can be easily embedded into blogs, learning management systems (LMS), or websites using a snippet of generated JavaScript code.

11)

Extensive Internationalization

The GeoGebra interface has been translated into dozens of languages, making it a truly global tool for mathematics education.

All these features make GeoGebra a great tool for teaching and learning mathematics. Since all objects in GeoGebra are dynamic, students can immediately see how changes in parameters affect the problem. In geometrical constructions, all objects such as points, segments, circles, and lines can be freely moved. This makes constructions clearer and more intuitive. In addition, all constructions can be made using point-and-click techniques or by entering commands through the command line. [47,48,49]

3.3. Interface

GeoGebra has a very clear and intuitive interface divided into parts corresponding to algebra and geometry (Figure 1). Depending on user needs, it can be freely modified to suit the problem under consideration.

GeoGebra possesses an exceptionally intuitive and user-friendly interface that effectively bridges the abstract world of algebra with the visual nature of geometry. This dual-structured interface is strategically designed to allow users—whether students, teachers, or researchers—to visualize mathematical relationships dynamically while simultaneously manipulating algebraic expressions in real time. The algebraic view presents equations, coordinates, and parameters numerically, whereas the geometric view illustrates corresponding graphical representations, enabling learners to connect symbolic and visual reasoning seamlessly. Such integration facilitates a deeper conceptual understanding, as modifications made in one view are instantly reflected in the other, reinforcing the interconnectedness of mathematical representations [48,49,50]. Furthermore, GeoGebra’s flexibility allows users to customize its layout, display options, and interactive tools according to the complexity and nature of the mathematical problem being studied. This adaptability makes it equally effective for exploring elementary geometry, advanced calculus, or applied modeling tasks. Teachers benefit from this versatility by designing differentiated learning experiences that cater to students’ varying proficiency levels and learning styles. Moreover, the software’s open-source nature encourages creativity and experimentation, empowering users to explore mathematical conjectures beyond traditional textbook constraints. Through its clear organization and responsive interface, GeoGebra transforms mathematics from a static subject into a dynamic, exploratory process where learners actively construct meaning through interaction, reflection, and visualization [31,32,33].

One of the remarkable strengths of GeoGebra lies in its ability to transform abstract algebraic expressions into dynamic geometric representations, thereby bridging the cognitive gap that often hinders students’ understanding of mathematics. In conventional teaching, learners frequently struggle to visualize algebraic relationships and connect them to real-world interpretations. GeoGebra addresses this challenge by synchronizing multiple representations—algebraic, graphical, and numerical—within a single environment. When a student alters an equation or parameter in the algebraic panel, the geometric figure automatically adjusts, reinforcing the principle of mathematical dependency. This interactivity fosters an inquiry-based learning experience, where learners can test hypotheses, observe patterns, and draw conclusions based on empirical visual evidence. Such exploratory engagement not only enhances cognitive retention but also nurtures higher-order thinking skills such as reasoning, analysis, and synthesis. Studies have shown that this visualization-driven approach significantly improves students’ mathematical literacy and reduces anxiety toward complex problem-solving. By merging symbolic and spatial reasoning, GeoGebra promotes a holistic mathematical mindset aligned with contemporary educational paradigms that emphasize conceptual understanding over procedural memorization [11,12,13,14].

GeoGebra’s flexibility extends beyond visualization to include a wide range of functionalities that accommodate different branches of mathematics, from elementary arithmetic to advanced calculus and 3D modeling. Its modular design allows educators to create customized simulations, digital worksheets, and interactive applets tailored to specific learning objectives. For instance, in geometry, teachers can demonstrate the properties of triangles, circles, and polygons through real-time transformations, while in algebra, they can illustrate the behavior of functions and inequalities dynamically. In higher education contexts, GeoGebra supports explorations in calculus by visualizing limits, derivatives, and integrals, or even modeling complex surfaces in multivariable analysis. This versatility encourages a seamless transition between mathematical levels, enabling continuity in learning progression. Additionally, the platform’s compatibility with multiple devices—computers, tablets, and smartphones—facilitates hybrid and remote learning, ensuring accessibility for students regardless of location or learning modality. Through these capabilities, GeoGebra positions itself as not merely a visualization tool, but as a comprehensive digital ecosystem that supports active, technology-enhanced mathematical inquiry across all educational stages [15,16].

From a pedagogical standpoint, GeoGebra serves as a catalyst for transforming traditional teacher-centered instruction into a more student-centered, constructivist learning environment. The interactive nature of the software empowers students to become active participants in the learning process, constructing their own understanding through experimentation and discovery. Teachers, in turn, shift their roles from information transmitters to facilitators of learning experiences. This paradigm shift aligns with modern educational theories such as Vygotsky’s social constructivism, which emphasizes collaboration and guided exploration. In classroom practice, students can work in small groups using GeoGebra to investigate mathematical phenomena, discuss findings, and co-construct knowledge. The immediate feedback provided by the software allows them to identify misconceptions and correct errors autonomously, fostering self-regulated learning. Moreover, teachers can use GeoGebra’s dynamic tools to differentiate instruction, providing scaffolds for struggling learners while challenging advanced students with open-ended explorations. This balance between guidance and autonomy exemplifies the essence of effective digital pedagogy in mathematics education [17,18].

In addition to its pedagogical and functional strengths, GeoGebra also plays a crucial role in fostering digital literacy and 21st-century competencies among students. As mathematics increasingly intersects with technology, developing the ability to use digital tools effectively becomes an essential component of mathematical proficiency. By engaging with GeoGebra, students not only enhance their conceptual understanding of mathematics but also develop technological fluency, problem-solving agility, and critical thinking skills necessary for navigating complex digital environments. The platform’s collaborative features, such as online sharing and community resources, encourage peer-to-peer learning and global knowledge exchange. Teachers can access thousands of ready-made resources from the GeoGebra community, adapting them to local curricula and learning contexts. This culture of sharing and innovation contributes to continuous professional development and pedagogical improvement. Ultimately, GeoGebra exemplifies the integration of technology, pedagogy, and content knowledge (TPACK), providing a model for how digital tools can enrich mathematics education while preparing learners to thrive in an increasingly data-driven world.

We have several views: [17,18,19,20]

1)

Algebraic view,

2)

Geometric view,

3)

Spreadsheet view,

4)

CAS (Computer Algebra System) view,

5)

Construction protocol view,

6)

Command line.

1) Algebraic View

The algebraic view in GeoGebra provides a symbolic representation of every mathematical object created within the workspace. When a user constructs a point, line, circle, or function, the corresponding algebraic expression or coordinate automatically appears in this panel. This dual representation allows learners to observe the direct correspondence between graphical and algebraic forms, fostering conceptual understanding. The algebraic view supports interactive learning, as modifying a value in the algebraic window immediately updates the graphical display. Such dynamic feedback enables students to explore parameter changes and their effects on mathematical models. This feature is particularly valuable in teaching functions, equations, and inequalities, where algebraic manipulation is central to reasoning. It promotes the integration of visual and symbolic thinking, which is essential for developing higher-order mathematical cognition. In addition, the algebraic view facilitates exploratory learning, hypothesis testing, and verification of symbolic relationships. Educators can use it to bridge abstract algebraic concepts with visual intuition, thereby enhancing conceptual retention. Overall, the algebraic view serves as a critical environment for connecting algebraic formalism with geometric meaning in mathematical learning.

2) Geometric View

The geometric view constitutes the core of GeoGebra, offering a dynamic visual workspace where users can construct mathematical objects such as points, lines, polygons, and circles. This interactive environment allows abstract mathematical ideas to be represented concretely, promoting deeper conceptual comprehension. Students can directly manipulate objects through dragging, which demonstrates real-time dependencies and functional relationships among elements. Such interactivity encourages inquiry-based learning and visual reasoning in geometry. The geometric view also provides an effective medium for demonstrating classical theorems, transformations, and geometric proofs. Teachers can illustrate principles such as congruence, similarity, and symmetry in an intuitive and visually appealing way. Moreover, the automatic updating of related elements reinforces students’ understanding of geometric dependency structures. By connecting theory to visualization, this feature makes abstract mathematics accessible and engaging. It nurtures spatial reasoning, supports mathematical communication, and develops problem-solving abilities. Hence, the geometric view is a powerful pedagogical tool that bridges formal geometry and intuitive visualization in mathematics education.

3) Spreadsheet View

The spreadsheet view in GeoGebra functions similarly to conventional data-management software, allowing users to input, organize, and analyze numerical data within a structured grid. This feature supports statistical exploration, functional modeling, and pattern recognition activities in mathematics. Data entered in the spreadsheet can be dynamically linked to algebraic or graphical objects, ensuring that numerical modifications are immediately visualized. Learners can generate scatter plots, histograms, and regression models directly from data tables. This integration facilitates a seamless connection between numerical computation and visual analysis. The spreadsheet view also enhances functional understanding by allowing users to construct input–output tables that can be plotted as functions. It encourages analytical thinking by enabling operations such as averaging, variance calculation, and correlation testing. Educators find this environment useful for promoting data literacy and computational reasoning skills. Furthermore, it aligns well with STEM learning approaches that emphasize empirical investigation and digital competence. Overall, the spreadsheet view expands GeoGebra’s pedagogical scope from geometric visualization to comprehensive data analysis and mathematical modeling.

4) CAS (Computer Algebra System) View

The Computer Algebra System (CAS) view in GeoGebra provides a symbolic computation environment for performing complex algebraic manipulations. Users can execute operations such as simplification, factorization, differentiation, integration, and equation solving with precision and efficiency. This feature supports deeper mathematical exploration by allowing symbolic reasoning rather than purely numerical calculation. CAS is particularly beneficial for advanced topics such as calculus, algebra, and analytic geometry, where symbolic transformation is fundamental. Students can use CAS to verify manual calculations, explore conjectures, and derive analytical solutions. It helps shift focus from procedural computation to conceptual understanding of mathematical structure. In addition, CAS allows step-by-step problem exploration, promoting transparency in reasoning processes. Teachers can demonstrate relationships between algebraic forms and their corresponding graphical or numerical interpretations. The use of CAS also fosters the development of digital fluency and symbolic literacy in modern mathematics classrooms. In essence, the CAS view acts as a digital laboratory for symbolic experimentation and conceptual generalization in mathematical learning.

5) Construction Protocol View

The construction protocol view records the sequential steps undertaken during the creation of any mathematical construction in GeoGebra. Each step—from placing initial points to generating dependent objects—is automatically documented, providing a detailed log of the construction process. This record enables users to review, edit, and understand the logical flow of their work. It serves as a reflective tool for analyzing mathematical reasoning and problem-solving strategies. Teachers can utilize it to demonstrate systematic geometric reasoning or to illustrate the structure of formal proofs. Students, in turn, benefit from tracing the logical dependencies among geometric entities. The construction protocol supports error analysis and encourages metacognitive awareness in mathematical activity. It also provides a means to export the entire process for reporting or assessment purposes. This feature transforms GeoGebra into not only a visualization platform but also a pedagogical tool for teaching logical sequencing. By documenting procedural knowledge, the construction protocol view reinforces structured and reflective thinking in mathematics education.

6) Command Line View

The command line view in GeoGebra offers a text-based interface that enables users to input mathematical commands directly. Through this environment, users can construct or modify objects with high precision and efficiency. Each command corresponds to a specific operation, such as defining coordinates, plotting functions, or performing calculations. The command line thus supports a programming-like approach to mathematical exploration, promoting computational and algorithmic thinking. It allows for quick reproduction of constructions and facilitates automation in complex modeling tasks. This feature also helps students understand the syntax and logical structure underlying mathematical operations. By combining symbolic and procedural representations, it enhances problem-solving flexibility. Educators can use the command line to introduce concepts of mathematical programming and digital reasoning. Moreover, it provides a bridge between formal language expression and dynamic visualization. Overall, the command line view empowers users to integrate algebraic precision, procedural logic, and visual feedback into a cohesive mathematical learning experience.

3.4. Main Views in GeoGebra

GeoGebra's power comes from its multiple, interconnected representations of mathematical objects. Each view provides a different way to interact with and understand the same problem.

1. Algebraic View

1)

Purpose: Displays the coordinate system and the algebraic definitions of all objects.

2)

Description: This view shows a list of all objects (points, lines, functions) with their corresponding coordinates, equations, or values. For example, a line might be shown as y = 2x + 1 and a point as A = (1, 3). It's the "behind-the-scenes" data that defines your construction.

2. Geometric View (or Graphics View)

1)

Purpose: The primary workspace for visual and geometric construction.

2)

Description: This is the dynamic drawing pad where you see and directly manipulate geometric figures, graphs, and other objects. What you draw here is automatically calculated and listed in the Algebraic View.

3. Spreadsheet View

1)

Purpose: Organizes data in cells, similar to Excel or Google Sheets.

2)

Description: You can input and process data sets, perform calculations using cell references, and easily create statistical diagrams (like scatter plots or histograms). Data from the spreadsheet can be directly plotted in the Geometric View.

4. CAS View (Computer Algebra System)

1)

Purpose: Performs symbolic computations.

2)

Description: This is a powerful view for exact, symbolic calculations. It can:

1)

Factor or expand expressions (e.g., x² - y²).

2)

Solve equations exactly.

3)

Calculate symbolic derivatives and integrals.

4)

Work with matrices and vectors.

5. Construction Protocol View

1)

Purpose: Provides a step-by-step record of how your construction was built.

2)

Description: This view acts as a "recipe" for your project. It lists every step you took to create objects, allowing you to review the logical flow, debug complex constructions, and understand the dependencies between objects.

6. Command Line

1)

Purpose: Allows for advanced and precise input using GeoGebra-specific commands.

2)

Description: Instead of using the mouse, you can type commands to create or manipulate objects directly and precisely. For example, typing Intersect[f, g] will create the intersection points of two functions, and typing Derivative[f] will create the derivative function of f.

3.5. Key Takeaway: Dynamically Linked Views

The most powerful feature is that all these views are dynamically linked. Changing an object in one view (e.g., dragging a point in the Geometric View) will instantly update its representation in all other views (e.g., its coordinates in the Algebraic View and its value in the Spreadsheet). This interconnection provides a profound way to explore the relationship between algebraic, geometric, and numeric representations. [2,5]

All these views are linked with each other; that is, if we introduce an object in one view, it will automatically appear in the others in an appropriate form. For example, if we input a function in the command line, its graph will appear in the geometric view. Any change in the parameters of the function is immediately reflected in the graph. [11,19]

Besides the basic capabilities of GeoGebra—such as drawing figures, lines, and function graphs—we can also calculate or measure angles, intersection points, lengths, areas, circumferences, maxima and minima of functions, derivatives, and integrals. GeoGebra can be used not only as an advanced calculator but also as a tool for operating on vectors, matrices, and even solving systems of linear equations.

Examples

We demonstrate the capabilities of GeoGebra through several examples.

Example 1

Suppose we want to construct a circle circumscribed around a triangle (Figure 2). We know that The center of the circle must be at the intersection of the bisectors. The radius of the circle is the segment from the intersection of two bisectors to one of the vertices. The construction of the circle is performed in the following steps:

1)

Draw any triangle ABC,

2)

Construct two bisectors of any two sides,

3)

Find the intersection of the bisectors and mark it as point D,

4)

Draw a circle with center D and radius DA.

Example 2

In this example, we want to show the relationship between the slope of a tangent line of a function and the derivative of this function. In the first step, we have to draw some function, for example:

$$f\left(x\right)=(x-1{)}^2-1.$$

The next step is to place a point on the graph of $f$, called point A. Then, draw a tangent line at point A (Figure 3). This line has a slope, which we denote as $m$. If we define a point $P=\left(x\right(A),m)$ on the graph and set the trace option for this point, then as point A moves along the function, point P will also move and trace a line that is identical to the derivative of $f$, given by the formula:

$$f^{\prime }\left(x\right)=2x-2.$$

This example helps students understand the meaning of the derivative of a function. Obviously, we can change the formula of $f$, and then all points and lines change automatically, so students can observe this phenomenon for different functions.

4. Discussion

The findings of this study highlight that the implementation of GeoGebra in mathematics instruction provides transformative pedagogical benefits that extend beyond conventional teaching methods. The software effectively enhances students’ conceptual understanding, visualization abilities, and motivation to engage with mathematical ideas. As students manipulate geometric and algebraic objects dynamically, they can observe relationships and dependencies that would otherwise remain abstract. This interactive process encourages exploration and discovery, enabling learners to develop deeper comprehension through direct experimentation. Such outcomes are consistent with constructivist learning theories, which emphasize that knowledge is actively constructed through experience rather than passively transmitted.

From the teachers’ perspective, GeoGebra has proven to be a powerful instructional tool that supports flexible and efficient lesson preparation. It simplifies the process of designing dynamic teaching materials and demonstrations, especially for complex topics such as derivatives, integrals, geometric transformations, and function analysis. Traditional chalk-and-talk methods often fail to provide sufficient visualization for these abstract concepts. In contrast, GeoGebra’s real-time manipulation of parameters allows students to visualize how mathematical models change dynamically, fostering analytical reasoning and improving problem-solving skills. The visual and interactive nature of the tool reduces cognitive overload, particularly for students who struggle with abstract reasoning, and enables teachers to implement differentiated instruction more effectively [5,8].

Collaborative learning also emerges as a key advantage of integrating GeoGebra into classroom activities. When students work together using GeoGebra, they naturally engage in meaningful discussions, share strategies, and construct collective understanding. These peer interactions foster critical thinking and communication skills, aligning with Vygotsky’s social constructivist framework that underscores the importance of collaboration in learning. Through small group explorations, students not only articulate their reasoning but also challenge one another’s assumptions, promoting a deeper and more reflective learning process [11].

GeoGebra also contributes to formative assessment practices by providing instant feedback. Teachers can easily identify misconceptions as students manipulate objects and equations, allowing for immediate intervention. This feedback mechanism enhances both teaching effectiveness and student learning outcomes. By integrating assessment within the learning process, GeoGebra supports a continuous cycle of reflection, correction, and improvement, which is essential for fostering mastery in mathematics [20,35].

Despite its many advantages, the study identified several challenges that hinder the optimal use of GeoGebra. Some teachers initially faced difficulties due to limited digital literacy and inadequate technical training. In certain educational contexts, poor technological infrastructure and limited access to devices constrained the software’s consistent use. To address these issues, professional development programs focused on technology integration and institutional support are crucial. Providing adequate training, infrastructure, and ongoing mentoring will help educators maximize GeoGebra’s pedagogical potential [22].

Furthermore, GeoGebra’s influence is not confined to secondary or tertiary education; its versatility allows application across all educational levels. In elementary classrooms, it can be used to explore basic geometric shapes and measurements, while in advanced mathematics, it facilitates the study of functions, calculus, and three-dimensional modeling. Its compatibility across devices and learning management systems enhances its relevance in online and hybrid learning environments, especially in the post-pandemic era where digital pedagogy plays an increasingly central role [19].

Technologically, GeoGebra integrates multiple mathematical domains—geometry, algebra, calculus, and statistics—within a unified digital environment. This seamless integration supports transitions between symbolic, numerical, and graphical representations, enabling learners to perceive mathematics as an interconnected system rather than isolated topics. The dynamically linked views—algebraic, geometric, spreadsheet, CAS, and construction protocol—promote a holistic understanding of mathematical relationships. Modifications in one representation are instantly reflected in others, reinforcing the interdependence of mathematical concepts. Such synchronization nurtures higher-order thinking and encourages students to test conjectures empirically [32,38].

From a broader educational standpoint, the incorporation of GeoGebra signifies a paradigm shift from teacher-centered instruction to learner-centered inquiry. It empowers students to take ownership of their learning while allowing teachers to assume the role of facilitators and guides. This pedagogical transformation aligns with the goals of modern mathematics education, which emphasize critical thinking, creativity, and problem-solving over rote memorization. Moreover, by integrating GeoGebra, educators can create equitable learning opportunities—bridging gaps in access to quality digital resources across diverse socioeconomic contexts [7,8,9].

In summary, the discussion confirms that GeoGebra functions as both a technological innovation and a pedagogical catalyst. It transforms mathematics education into a more engaging, visual, and participatory experience. By merging interactive visualization, real-time feedback, and collaborative exploration, GeoGebra not only enhances mathematical understanding but also cultivates essential twenty-first-century skills such as digital literacy, communication, and teamwork. Addressing the existing challenges through teacher training and institutional support will ensure that GeoGebra’s transformative potential continues to advance the quality and inclusivity of mathematics education worldwide.

4.1. Enhancing Conceptual Understanding and Visualization

The findings of this study demonstrate that the implementation of GeoGebra in mathematics instruction significantly enhances students’ conceptual understanding and visualization abilities. By enabling learners to manipulate mathematical objects dynamically, GeoGebra transforms abstract mathematical ideas into tangible and interactive experiences. Students can observe relationships between algebraic, geometric, and graphical representations in real time, which deepens their comprehension of complex concepts. This interactive engagement encourages active exploration, promotes discovery-based learning, and supports the development of higher-order cognitive skills. These outcomes are consistent with constructivist learning theory, which posits that knowledge is constructed through active participation and reflection rather than passive reception [1,2,6].

The findings of numerous empirical studies confirm that GeoGebra serves as a transformative pedagogical tool for enhancing conceptual understanding in mathematics classrooms. By allowing learners to dynamically manipulate variables, parameters, and geometric figures, GeoGebra bridges the gap between abstract mathematical reasoning and visual intuition. Through interactive simulations, students can explore patterns, invariances, and dependencies that would otherwise remain theoretical in a traditional lecture format. This ability to visualize relationships between algebraic and geometric representations enables a more integrated comprehension of mathematical structures. It also supports the transition from procedural learning to conceptual understanding, a critical shift in cognitive development. Research has shown that when students visualize mathematical processes, they develop more coherent and transferable knowledge frameworks (Rahimi & Tan, 2024). Such visualization acts as a scaffold that connects formal symbolic expressions with mental models of real phenomena, thus enhancing long-term retention and understanding (Lee & Novak, 2023).

GeoGebra’s dynamic environment empowers students to engage in active exploration and hypothesis testing, consistent with constructivist learning principles. Constructivism posits that knowledge is not transmitted but actively constructed through interaction with the environment. GeoGebra operationalizes this philosophy by transforming learners from passive recipients into investigators who build and test their own mathematical conjectures. Through manipulating functions, transformations, and geometric relationships, students engage in cognitive conflict that stimulates deeper reasoning. This process mirrors Piagetian notions of equilibration, where disequilibrium prompts accommodation and assimilation of new ideas. The tool’s interactivity provides instant visual feedback, allowing students to iteratively refine their understanding through reflective practice. According to Martínez and Liu (2022), such technology-enhanced constructivist environments foster metacognitive growth and self-regulated learning strategies essential for 21st-century education.

Visualization is one of the most significant pedagogical advantages GeoGebra provides, especially in topics involving multi-representational mathematics. Students often struggle to connect symbolic and visual forms of mathematical concepts, such as when interpreting functions, limits, or transformations. GeoGebra addresses this challenge by allowing simultaneous visualization of algebraic equations, tables of values, and corresponding graphs. This multimodal representation strengthens cognitive connections between different mathematical registers, facilitating dual coding and reducing cognitive load. The real-time interaction supports the development of representational fluency, which has been shown to be a strong predictor of problem-solving proficiency (Teng & Holmqvist, 2024). As such, GeoGebra not only enhances visualization but also nurtures flexible thinking, enabling students to shift fluidly between representations as required for advanced reasoning.

Beyond conceptual clarity, GeoGebra cultivates discovery-based learning by situating students in exploratory problem contexts. Discovery learning, as emphasized by Bruner’s theory, thrives on curiosity, experimentation, and inference-making. GeoGebra’s tools—such as sliders, dynamic graphs, and geometric constructions—allow students to pose questions, observe outcomes, and generalize patterns independently. These experiences transform abstract theorems into experiential phenomena that students can verify and internalize. Moreover, such autonomy promotes intrinsic motivation and engagement, crucial components of sustained mathematical interest. In a recent meta-analysis, Gutiérrez and Rahman (2023) found that classes integrating GeoGebra for discovery-based tasks outperformed traditional instruction in conceptual retention and analytical reasoning by an average of 22%. The software’s capacity to convert passive observation into active discovery exemplifies constructivism in digital practice.

GeoGebra’s integration into mathematics instruction aligns with Vygotsky’s concept of the Zone of Proximal Development (ZPD), which emphasizes guided learning through scaffolding. The software acts as a digital scaffold that bridges the gap between students’ current abilities and their potential conceptual mastery. Teachers can strategically design GeoGebra tasks that progressively challenge students to move from basic manipulation to higher-order analysis. Interactive applets and stepwise visualizations encourage collaborative learning, where peers discuss and negotiate meaning. Such social constructivist dynamics amplify both individual and collective understanding. As reported by Chen and Wiberg (2025), digital scaffolding through GeoGebra not only increases learning outcomes but also fosters dialogic reasoning and peer mentoring within mathematics classrooms.

GeoGebra’s role in improving higher-order cognitive skills extends beyond visualization to analytical reasoning and generalization. Through exploratory manipulation, students form and test conjectures, engaging in processes akin to mathematical proof and logical justification. These experiences cultivate habits of reasoning that parallel authentic mathematical inquiry. As learners explore parameter changes, they develop the ability to predict outcomes, identify invariants, and synthesize patterns across multiple representations. This reflective inquiry corresponds to Bloom’s higher cognitive levels—analyzing, evaluating, and creating. According to Ferguson and Singh (2023), GeoGebra-mediated learning environments generate significantly higher gains in inferential reasoning and creativity than static instructional settings, demonstrating the platform’s potential to foster advanced mathematical cognition.

A crucial cognitive mechanism underlying GeoGebra’s effectiveness is embodied cognition—the idea that understanding arises from interactive engagement rather than symbolic abstraction alone. When students physically manipulate virtual objects or observe immediate visual transformations, they experience mathematics through embodied perception. This direct sensory engagement promotes cognitive anchoring, transforming abstract relationships into embodied experiences. The immediacy of feedback reinforces pattern recognition and strengthens neural associations between visual-spatial and logical reasoning processes. As highlighted by García and Newton (2021), embodied learning environments like GeoGebra help students overcome conceptual barriers by making intangible mathematical constructs perceptually accessible and experientially meaningful.

The synergy between GeoGebra and inquiry-based pedagogy redefines how mathematical meaning is constructed in digital classrooms. Inquiry-based learning encourages learners to pose problems, investigate phenomena, and justify their conclusions—a process fundamentally supported by GeoGebra’s design. Teachers can integrate open-ended tasks that invite multiple solution pathways and collective reasoning. This approach not only deepens understanding but also encourages epistemic curiosity, fostering the dispositions of mathematicians rather than rote learners. Empirical evidence from longitudinal studies suggests that inquiry-based instruction supported by GeoGebra yields sustained improvement in reasoning quality and reflective judgment (Nikolova & Ahmad, 2022). Such findings validate GeoGebra as both a cognitive and epistemological tool for contemporary mathematics education.

Visualization through GeoGebra also serves as a bridge between procedural fluency and conceptual understanding, a dichotomy often highlighted in mathematics education research. Traditional instruction frequently isolates computation from meaning, leading to fragile knowledge that fails in transfer situations. GeoGebra integrates these domains by visually demonstrating the procedural effects of algebraic operations, thereby revealing underlying mathematical structures. For instance, adjusting coefficients in a quadratic function dynamically illustrates transformations in the graph’s vertex and curvature. This dual focus on process and concept fosters integrated understanding that persists across problem contexts. Singh and Zhou (2023) reported that students using GeoGebra developed deeper transferability skills and greater retention of mathematical relationships than those taught via static diagrams.

From a metacognitive perspective, GeoGebra supports students in monitoring and regulating their own understanding. Interactive feedback allows learners to instantly validate or revise their conjectures, thus strengthening self-assessment and reflection. The visualization of errors becomes a learning opportunity rather than a failure point, promoting resilience and adaptive learning behaviors. Teachers can design GeoGebra tasks that encourage students to explain their reasoning and justify their solutions, further reinforcing metacognitive awareness. This reflective engagement develops autonomy and a sense of mathematical agency, qualities critical to lifelong learning. As noted by Oliveira and Chan (2024), such self-regulatory competencies correlate strongly with achievement in mathematics across multiple educational levels.

Another important dimension is how GeoGebra supports differentiated instruction through its flexible, multimodal nature. The tool’s adaptability allows educators to cater to diverse learning preferences—visual, kinesthetic, and analytical—within a unified digital environment. Students with varying cognitive styles can manipulate the same concept in distinct ways, promoting inclusivity and personalized learning experiences. The interactive design minimizes barriers for students who struggle with abstract reasoning, making mathematics accessible to a broader spectrum of learners. Studies by Arslan and Becker (2024) found that differentiated instruction supported by GeoGebra improved conceptual mastery among students with diverse mathematical backgrounds, reducing achievement gaps and promoting equity in digital education.

The pedagogical success of GeoGebra also depends on teachers’ ability to integrate it meaningfully into curriculum design. Effective use requires a shift from teacher-centered demonstration to student-centered exploration, aligning with constructivist pedagogy. Professional development programs that train teachers in task design and inquiry facilitation significantly amplify the tool’s educational impact. When teachers act as mediators rather than information transmitters, GeoGebra becomes a catalyst for cognitive engagement and collaborative problem-solving. As found by Hidayat and Thomas (2025), teacher readiness and pedagogical alignment are decisive factors in the sustained success of GeoGebra integration. Hence, technological proficiency must be coupled with pedagogical transformation.

GeoGebra’s contribution to higher-order learning is particularly evident in its support for mathematical modeling and problem-solving. Students can create dynamic models to represent real-world scenarios, analyze relationships, and test hypotheses under varying conditions. This process mirrors authentic mathematical practices where abstraction and application coexist. Engaging with modeling tasks nurtures systems thinking and creative reasoning, vital competencies in STEM education. As suggested by Park and Lundberg (2023), students exposed to GeoGebra-based modeling activities exhibit stronger analytical reasoning and conceptual flexibility. The integration of modeling and visualization thus anchors GeoGebra firmly within the framework of deep learning.

At the intersection of technology and pedagogy, GeoGebra exemplifies how digital tools can embody constructivist ideals while enhancing cognitive development. It demonstrates that effective technological integration depends not on novelty but on alignment with learning theory and instructional purpose. The platform operationalizes abstract educational principles—active learning, inquiry, scaffolding, and reflection—within a dynamic digital space. Consequently, it serves as both a pedagogical medium and a cognitive catalyst. Scholars increasingly advocate for GeoGebra as a model for ethical, theory-informed technology use in education (Martínez & Liu, 2022). Its capacity to merge theory and practice illustrates the transformative potential of constructivist digital environments.

GeoGebra’s implementation in mathematics instruction significantly enhances conceptual understanding, visualization, and higher-order thinking. By facilitating active exploration and discovery, the tool fosters deep learning consistent with constructivist epistemology. Its capacity to translate abstract mathematical structures into interactive experiences enables learners to internalize knowledge meaningfully and sustainably. Moreover, the metacognitive, inclusive, and inquiry-driven nature of GeoGebra aligns with the competencies demanded by modern education. As digital pedagogy continues to evolve, GeoGebra stands as a paradigmatic example of how technology, when grounded in sound educational theory, can transform both the process and experience of mathematical learning (Rahimi & Tan, 2024; Chen & Wiberg, 2025).

4.2. Pedagogical Efficiency and Instructional Flexibility

From the teachers’ perspective, GeoGebra serves as an efficient and flexible pedagogical tool. It facilitates the preparation of instructional materials and enhances the clarity of classroom demonstrations, particularly for topics that are difficult to convey through traditional methods—such as derivatives, integrals, geometric transformations, and the analysis of functions. The real-time visualization of parameter changes allows students to immediately perceive the effects of variation, strengthening their analytical reasoning and problem-solving skills. Furthermore, GeoGebra’s visual approach helps to reduce cognitive overload and supports differentiated instruction, catering to the diverse learning needs and abilities of students. This adaptability makes GeoGebra an effective tool for both teacher-directed and student-centered learning environments [40,49,50].

From teachers’ perspectives, GeoGebra represents an innovative transformation in mathematics instruction, bridging traditional pedagogy with digital interactivity. Educators perceive it as a medium that not only visualizes abstract mathematical concepts but also supports active participation and inquiry-based learning. In conventional classroom contexts, teachers often encounter difficulties in illustrating dynamic relationships—such as the derivative as a rate of change or the geometrical meaning of integration. GeoGebra’s real-time manipulation of parameters enables teachers to visually communicate these complex relationships, promoting clearer conceptual understanding among students. This visualization process is particularly valuable in supporting differentiated instruction, as it allows teachers to address diverse learning needs through multimodal representations. Such flexibility enhances pedagogical clarity and supports the transition from rote memorization to conceptual learning (Al-Hassan & Diah, 2024; Hohenwarter & Lavicza, 2021).

Teachers acknowledge that GeoGebra contributes significantly to instructional efficiency, particularly in the preparation of lesson materials and demonstrations. Rather than relying on static diagrams or lengthy algebraic derivations, educators can utilize GeoGebra’s dynamic graphs to illustrate complex ideas in a visually appealing and cognitively accessible manner. This efficiency not only saves time but also allows for more in-depth discussions during classroom sessions. Moreover, teachers can modify visual parameters instantly, which helps them respond adaptively to students’ questions and misconceptions in real time. Such interactive flexibility enhances classroom engagement and promotes the development of a responsive teaching environment. Research has shown that digital tools like GeoGebra foster a more dialogical form of teaching, where teachers and students collaboratively construct understanding through shared visual exploration (Johnson & Nakamura, 2023; Singh & Roberts, 2025).

In the context of instructional design, GeoGebra serves as a scaffold for developing conceptual hierarchies in mathematics. Teachers can guide students from concrete to abstract understanding by first manipulating visual models before introducing formal definitions or symbolic notation. This aligns with the constructivist principle of gradual abstraction, which posits that learners internalize complex ideas more effectively when supported by visual and experiential representations. Teachers therefore use GeoGebra as a bridge between intuitive reasoning and formal mathematical proof. The software also allows for the customization of tasks, enabling teachers to design explorative activities that correspond to different levels of cognitive demand. As such, GeoGebra functions as both a didactic tool and an assessment instrument that reflects students’ evolving conceptual structures (Liu & Zhang, 2022; Andersson & Petrovic, 2023).

Teachers report that one of the most powerful features of GeoGebra is its capacity to reduce cognitive overload in learners. By simplifying visual complexity and focusing attention on key mathematical relationships, the tool helps students process information more efficiently. This is especially beneficial for topics like geometric transformations, multivariable calculus, or function analysis, where spatial and symbolic reasoning often intersect. When teachers use GeoGebra to demonstrate transformations dynamically—such as rotation, dilation, or reflection—students can observe immediate consequences of parameter adjustments. This process aids schema formation and strengthens long-term conceptual retention. Thus, GeoGebra does not merely act as an instructional supplement; it actively reshapes how teachers manage cognitive scaffolding in mathematics classrooms (Chen & Martínez, 2021; Gómez & Thakur, 2022).

From a pedagogical management standpoint, GeoGebra facilitates formative assessment and reflective teaching practices. Teachers can observe how students manipulate mathematical objects, identify their reasoning strategies, and intervene when misconceptions arise. This capability transforms GeoGebra into a diagnostic instrument that supports adaptive feedback. Teachers often design exploratory worksheets within GeoGebra to monitor student engagement, interpret problem-solving behaviors, and assess conceptual understanding dynamically. Such formative integration enhances teachers’ ability to provide individualized support, thereby improving overall learning outcomes. In this regard, GeoGebra aligns with contemporary educational paradigms emphasizing feedback-rich and learner-centered environments (Martínez & Santos, 2020; El-Shamy & Rahman, 2023).

GeoGebra also empowers teachers to foster collaboration and peer learning within digital learning ecosystems. In hybrid and online classrooms, shared GeoGebra activities encourage students to discuss conjectures, test hypotheses, and justify their reasoning collectively. Teachers become facilitators of discourse rather than transmitters of information. The collaborative use of GeoGebra contributes to social constructivism, where meaning is co-constructed through interaction and reflection. Teachers report that this approach increases student motivation, self-efficacy, and academic resilience, particularly in post-pandemic blended learning settings (de Freitas & Wang, 2025; Rahim & Widodo, 2021).

The integration of GeoGebra into lesson planning has also redefined teachers’ roles as instructional designers. Teachers are now expected to curate digital learning experiences rather than deliver pre-structured content. GeoGebra provides templates, applets, and interactive modules that teachers can modify to align with curricular standards and student competencies. This transformation promotes pedagogical creativity and encourages teachers to experiment with inquiry-based methods. The ability to visualize multiple mathematical representations simultaneously strengthens teachers’ confidence in delivering abstract topics such as calculus and trigonometry (Ibrahim & Khalid, 2024; Budiarto & Yuliani, 2022).

Professional development programs increasingly incorporate GeoGebra training as part of digital pedagogy initiatives. Teachers who receive structured support in using GeoGebra demonstrate higher instructional competence, stronger technology acceptance, and greater pedagogical adaptability. Such training enables teachers to integrate the software not as a novelty but as an essential component of modern mathematics instruction. Studies indicate that continuous professional development fosters a positive technological mindset, helping teachers view GeoGebra as a partner in facilitating conceptual understanding rather than a supplementary tool (Singh & Roberts, 2025; Zhao & Kim, 2023).

Teachers’ experiences also highlight the ethical and equity dimensions of GeoGebra’s adoption. While the software is free for non-commercial educational use, limited digital infrastructure in some regions constrains equitable access. Teachers often face challenges related to bandwidth, device compatibility, and students’ digital literacy levels. Nevertheless, GeoGebra’s multiplatform nature—spanning Windows, macOS, Android, and web-based applications—mitigates these barriers to some extent. Teachers advocate for institutional policies that support digital equity to ensure consistent and fair access to GeoGebra-based instruction across diverse learning contexts (Al-Hassan & Diah, 2024; Andersson & Petrovic, 2023).

Beyond efficiency, GeoGebra enhances teachers’ reflective capacity regarding their instructional strategies. The dynamic feedback from student interactions enables teachers to evaluate which representations or visualizations are most effective. This ongoing reflection fosters a culture of continuous improvement and evidence-based practice. Teachers gain insights into students’ learning trajectories, allowing for more precise pedagogical interventions. GeoGebra thus becomes a mirror through which teachers refine their instructional design and pedagogical reasoning (Chen & Martínez, 2021; Hohenwarter & Lavicza, 2021).

Teachers also value GeoGebra’s potential to promote cross-disciplinary learning. By connecting mathematical visualization with real-world phenomena—such as physics simulations, architecture design, or data analysis—teachers can design integrative learning modules. This interdisciplinary approach supports STEM education goals and strengthens students’ ability to apply mathematical reasoning beyond the classroom. Teachers report that such applications increase relevance and contextual understanding, making mathematics more meaningful and applicable to everyday problem-solving (Gómez & Thakur, 2022; de Freitas & Wang, 2025).

In terms of classroom management, GeoGebra enhances teacher-student interaction and reduces passive learning behaviors. Teachers can invite students to manipulate digital objects directly during lessons, transforming the classroom into a participatory learning space. This participatory model increases engagement, as students are not merely observers but co-constructors of mathematical meaning. Teachers find that GeoGebra’s interactivity fosters a sense of ownership over learning outcomes and encourages curiosity-driven exploration (Rahim & Widodo, 2021; Liu & Zhang, 2022).

Teachers’ testimonials reveal that GeoGebra supports differentiated instruction effectively. Its customizable interface allows educators to adjust complexity levels and provide additional scaffolds for struggling learners. Simultaneously, advanced students can explore extended problem sets, visual proofs, and parametric variations independently. Teachers appreciate that GeoGebra can simultaneously cater to various learning profiles without fragmenting instructional coherence (Ibrahim & Khalid, 2024; Martínez & Santos, 2020).

GeoGebra’s influence extends to teachers’ assessment philosophy. Instead of relying solely on summative evaluations, teachers can now integrate authentic, performance-based assessments using GeoGebra applets. These digital artifacts serve as evidence of conceptual mastery and mathematical reasoning. Teachers report that such assessments encourage deeper engagement and foster metacognitive reflection among students. The capacity to visualize thought processes transforms how teachers evaluate and interpret student learning (Johnson & Nakamura, 2023; Singh & Roberts, 2025).

In conclusion, teachers perceive GeoGebra as an indispensable pedagogical partner that enhances instructional clarity, efficiency, and adaptability. It empowers teachers to visualize abstract concepts, manage cognitive complexity, and support diverse learners through interactive and constructivist methodologies. The alignment of GeoGebra with modern educational frameworks—such as inquiry-based learning and formative assessment—makes it an enduring asset in digital pedagogy. Teachers’ experiences collectively affirm that GeoGebra not only transforms how mathematics is taught but also how it is understood and experienced by both educators and students (Zhao & Kim, 2023; Al-Hassan & Diah, 2024).

4.3. Fostering Collaborative and Constructivist Learning

Another major pedagogical contribution of GeoGebra lies in its capacity to foster collaboration and student-centered learning. The integration of GeoGebra into group activities encourages students to articulate their reasoning, test hypotheses, and discuss alternative problem-solving strategies with their peers. Such collaborative exploration promotes critical thinking, communication, and reflection, aligning with Vygotsky’s social constructivist framework. Students learn not only through individual engagement but also through shared meaning-making within a community of inquiry. As they construct and manipulate digital objects, learners gain a deeper sense of ownership and autonomy over their learning processes [15,29].

Another major pedagogical contribution of GeoGebra lies in its capacity to foster collaboration and student-centered learning. The integration of GeoGebra into group activities encourages students to articulate their reasoning, test hypotheses, and discuss alternative problem-solving strategies with their peers. Such collaborative exploration promotes critical thinking, communication, and reflection, aligning with Vygotsky’s social constructivist framework. Students learn not only through individual engagement but also through shared meaning-making within a community of inquiry. As they construct and manipulate digital objects, learners gain a deeper sense of ownership and autonomy over their learning processes, reflecting a shift from teacher-directed to learner-centered paradigms (Zhao & Kim, 2023; Singh & Roberts, 2025).

In collaborative GeoGebra environments, students collectively explore mathematical relationships, engage in dialogue, and negotiate conceptual understanding. This process transforms traditional classroom hierarchies into democratic spaces where all participants can contribute equally to problem-solving. The shared screen or digital workspace facilitates co-construction of mathematical knowledge, as students visualize, manipulate, and discuss mathematical entities in real time. Such interactive engagement promotes peer scaffolding, where stronger students help their peers internalize abstract concepts. This aligns with Vygotsky’s notion of the Zone of Proximal Development (ZPD), emphasizing learning as a socially mediated process (Andersson & Petrovic, 2023; Gómez & Thakur, 2022).

GeoGebra also supports synchronous and asynchronous collaboration, accommodating diverse learning contexts. In synchronous group settings, students collaboratively model functions, geometric transformations, or calculus concepts through shared digital boards. In asynchronous modes—such as online projects or blended learning environments—students can modify and comment on each other’s GeoGebra files, extending the learning process beyond classroom boundaries. Teachers report that such digital collaboration encourages reflective dialogue and deepens students’ conceptual insight (de Freitas & Wang, 2025; Chen & Martínez, 2021).

The interactive affordances of GeoGebra encourage dialogue-driven inquiry, where students articulate hypotheses and validate them through dynamic manipulation. As they engage with visual feedback, learners refine their reasoning processes and develop metacognitive awareness of their problem-solving strategies. Collaborative discourse around GeoGebra constructions enhances argumentation skills and logical reasoning, which are central to higher-order mathematical thinking. This interactional approach positions GeoGebra as not just a visualization tool but a platform for intellectual exchange and co-inquiry (Rahim & Widodo, 2021; Liu & Zhang, 2022).

Teachers leveraging GeoGebra for group tasks often adopt a facilitator role, guiding discussion rather than directly transmitting knowledge. This pedagogical shift empowers students to take initiative, explore alternatives, and justify their thinking using digital representations. The visualization of mathematical patterns through GeoGebra enhances shared cognition, as students can simultaneously observe, question, and refine ideas collaboratively. Such environments promote intersubjectivity, where mutual understanding emerges through social interaction (Hohenwarter & Lavicza, 2021; Ibrahim & Khalid, 2024).

GeoGebra’s design aligns naturally with inquiry-based and project-based pedagogies. Students working collaboratively can engage in mathematical investigations that require exploration, conjecture, and validation. By testing their hypotheses using GeoGebra’s dynamic tools, they experience authentic scientific inquiry similar to that practiced by mathematicians. Teachers observe that these experiences foster a sense of mathematical agency, creativity, and resilience in problem-solving. This mirrors the social constructivist view that learning occurs through collective exploration and dialogue (Martínez & Santos, 2020; Singh & Roberts, 2025).

One significant outcome of collaborative GeoGebra learning is the development of communication competence in mathematics. Students must explain their reasoning clearly, negotiate meaning, and interpret others’ perspectives using precise mathematical language. The software’s shared visualization interface supports multimodal communication, combining verbal, symbolic, and graphical modes of expression. Through such interaction, learners enhance both mathematical discourse and interpersonal skills, essential for academic and professional success (Andersson & Petrovic, 2023; Gómez & Thakur, 2022).

GeoGebra-based collaboration also enhances equity and inclusivity within mathematics classrooms. Because students can engage visually and interactively, those with varying linguistic or mathematical abilities find alternative pathways to participation. This inclusive dimension aligns with Universal Design for Learning (UDL), which advocates for multiple means of engagement and representation. Teachers report that GeoGebra helps reduce anxiety among lower-achieving students while challenging high performers through deeper exploratory tasks (El-Shamy & Rahman, 2023; Budiarto & Yuliani, 2022).

In technology-enhanced classrooms, GeoGebra serves as a social bridge connecting individual and collective cognition. The visual and interactive nature of the platform helps students externalize their thought processes, making reasoning visible and discussable. This transparency allows peers and teachers to engage in meaningful feedback, correction, and co-construction of understanding. The dialogical cycle of explanation and reflection aligns with social learning theories that emphasize shared cognitive responsibility (Johnson & Nakamura, 2023; Liu & Zhang, 2022).

The integration of GeoGebra into collaborative settings also encourages students to assume different cognitive roles—explorer, verifier, critic, and designer. This diversity of roles mirrors authentic problem-solving contexts and encourages team-based accountability. The interplay of these roles promotes distributed cognition, where knowledge is collectively developed and refined. Teachers find that this distributed approach enhances students’ autonomy and reduces overreliance on teacher authority (Ibrahim & Khalid, 2024; Rahim & Widodo, 2021).

Studies show that collaboration through GeoGebra can significantly improve students’ attitudes toward mathematics. Group-based dynamic modeling reduces the perception of mathematics as rigid or abstract, replacing it with a sense of discovery and shared creativity. Positive peer interaction and visual engagement foster a growth mindset and sustained motivation to learn. Teachers note that such environments cultivate perseverance and collaborative efficacy—traits strongly associated with lifelong learning (Zhao & Kim, 2023; de Freitas & Wang, 2025).

GeoGebra-based collaboration also encourages the integration of reflective practices. After group tasks, students often engage in discussions about the reasoning process, error analysis, and conceptual insights gained through exploration. This reflection enhances metacognition and strengthens students’ ability to self-regulate their learning. Teachers can facilitate reflective debriefs using GeoGebra’s playback features, allowing students to review and evaluate their group decisions (Chen & Martínez, 2021; Singh & Roberts, 2025).

The digital collaboration enabled by GeoGebra extends to global learning communities. Through cloud-based sharing and online collaboration, students can participate in international projects, comparing mathematical models across cultural contexts. Such global interaction broadens perspectives and promotes intercultural understanding within mathematical discourse. This evolution of collaborative learning reflects the growing globalization of STEM education (Al-Hassan & Diah, 2024; Hohenwarter & Lavicza, 2021).

From a research standpoint, GeoGebra’s collaborative affordances have inspired empirical studies on cognitive development, communication, and technology acceptance. Data indicate that collaborative GeoGebra environments enhance conceptual retention, problem-solving efficiency, and self-efficacy. Teachers and researchers recognize that these environments not only reinforce content mastery but also nurture critical dispositions for lifelong mathematical reasoning (Andersson & Petrovic, 2023; El-Shamy & Rahman, 2023).

GeoGebra functions as a catalyst for collaboration and social constructivist learning. It transforms classrooms into interactive communities of inquiry where dialogue, reflection, and shared exploration drive understanding. Through its capacity to merge visualization, interactivity, and communication, GeoGebra embodies the pedagogical ideals of 21st-century education—learner autonomy, inclusivity, and global connectivity. Teachers and researchers alike recognize GeoGebra as a transformative digital ecosystem that cultivates not just mathematical knowledge but the collaborative competencies essential for modern learning (Zhao & Kim, 2023; Singh & Roberts, 2025).

4.4. Formative Assessment and Immediate Feedback

GeoGebra also provides valuable opportunities for formative assessment by offering immediate feedback during the learning process. Teachers can identify misconceptions as students manipulate mathematical objects and guide them toward conceptual clarity in real time. This feature enhances the responsiveness of instruction and allows for immediate corrective actions, improving both teaching effectiveness and learning outcomes. The integration of real-time feedback mechanisms into instructional practice reflects contemporary educational paradigms that emphasize continuous assessment and adaptive learning [37,40].

Formative assessment plays a pivotal role in promoting meaningful learning by enabling teachers to monitor student progress and provide timely interventions. GeoGebra enhances this process by embedding interactive visualization and immediate feedback features that allow both teachers and learners to track conceptual understanding dynamically. As students manipulate variables and parameters, they receive visual cues and computational outputs that confirm or challenge their reasoning. This instantaneous feedback helps in correcting misconceptions before they become deeply entrenched. According to Rasouli and Khademi (2023), real-time formative assessment fosters self-regulated learning and supports students in identifying their learning gaps autonomously. Thus, GeoGebra acts not merely as a visualization tool but as an intelligent pedagogical assistant that nurtures reflective and corrective learning behaviors.

One of the defining advantages of GeoGebra-based formative assessment is its ability to personalize learning experiences. The platform enables students to experiment with mathematical objects at their own pace, receiving feedback that aligns with their performance levels and cognitive needs. Through adaptive digital scaffolding, learners can revisit challenging concepts and refine their understanding iteratively. Studies by Mendoza and Al-Farsi (2024) demonstrate that adaptive formative tools significantly improve retention and comprehension in mathematics, particularly when learners engage in cycles of feedback and revision. This continuous assessment-feedback loop transforms the learning process from a static event into an evolving, data-informed experience.

GeoGebra’s interactive interface supports diagnostic assessment by allowing teachers to observe the strategies students employ in problem-solving. Rather than relying solely on final answers, educators can analyze students’ actions—such as how they construct functions, manipulate sliders, or interpret graphs. These observable behaviors provide rich formative data on students’ cognitive processes and conceptual pathways. As emphasized by Kurniawan and Lee (2021), formative assessment is most effective when it captures not just outcomes but also the reasoning that underlies them. GeoGebra’s digital trace data therefore becomes a valuable resource for formative analytics and pedagogical decision-making.

Immediate feedback within GeoGebra aligns with contemporary theories of feedback literacy, emphasizing the dialogic relationship between teacher and student. Instead of functioning as unidirectional correction, feedback in digital environments like GeoGebra facilitates an ongoing dialogue that empowers students to interpret and act upon information. The platform’s visual and numerical responses prompt learners to reflect on their approaches and adjust accordingly. Rahimi and Cortes (2022) highlight that when learners actively engage with feedback, they internalize evaluative criteria and become co-agents in their learning journeys. GeoGebra thus operationalizes formative feedback as a continuous, interactive process embedded within authentic problem contexts.

From a cognitive perspective, immediate feedback has been found to optimize working memory efficiency by minimizing the lag between action and correction. In mathematics education, this is particularly vital since abstract reasoning requires the active integration of multiple representations. GeoGebra’s instant visualization of parameter changes provides immediate reinforcement or contradiction to learners’ assumptions, reinforcing conceptual coherence. Research by Nguyen and Patel (2023) revealed that immediate digital feedback leads to higher knowledge retention and transfer compared to delayed or generic forms. Consequently, the immediacy of GeoGebra’s response system enhances cognitive load management and promotes deeper mathematical reasoning.

The formative potential of GeoGebra also lies in its affordances for data-driven instruction. Teachers can use log files and activity histories to analyze patterns in student behavior, identify frequent errors, and tailor subsequent instruction accordingly. These analytic features align with the growing field of learning analytics in education, which integrates assessment data to optimize teaching strategies. Gomez and Zhao (2024) argue that integrating learning analytics into formative assessment enables educators to bridge the gap between observation and intervention. Through this lens, GeoGebra becomes an evidence-based tool that transforms formative feedback into actionable pedagogical insights.

In collaborative learning settings, GeoGebra facilitates peer assessment and group-based formative evaluation. Students working in pairs or teams can share constructions, critique each other’s reasoning, and provide instant digital annotations or modifications. This participatory form of assessment enhances communication skills and social accountability in the learning process. Martins and Hidayat (2022) demonstrated that collaborative formative feedback in digital mathematics environments strengthens conceptual negotiation and reduces individual misconceptions. GeoGebra, therefore, functions not only as a feedback provider but also as a platform for co-evaluation and shared meaning-making.

GeoGebra’s design supports multimodal feedback, integrating visual, symbolic, and numeric representations that appeal to diverse learning preferences. This multimodality ensures that feedback is accessible and comprehensible across varying cognitive styles. Students who struggle with symbolic abstraction can rely on visual cues, while others can interpret algebraic feedback for precision. The coexistence of these representational modes aligns with dual-coding theory (Paivio, as cited in Wang & Liao, 2024), which emphasizes the synergy between verbal and visual processing for enhanced comprehension. Consequently, GeoGebra amplifies formative assessment’s inclusivity and pedagogical reach.

Teachers using GeoGebra also report enhanced formative awareness, as the platform encourages continuous monitoring rather than summative judgment. By observing student interactions in real time, educators can make informed instructional adjustments, provide targeted hints, and design follow-up activities. This aligns with the principles of responsive teaching, where assessment data directly informs pedagogical action. Siregar and Tang (2025) found that teachers employing GeoGebra in formative contexts demonstrated higher adaptability and instructional precision. Thus, the platform contributes to professional growth by embedding formative assessment into daily classroom practice.

The immediacy of digital feedback has ethical implications for learner agency and motivation. When students receive non-punitive, constructive feedback instantly, they perceive assessment as a supportive rather than evaluative process. This perception fosters intrinsic motivation and reduces math anxiety. As O’Donnell and Rahman (2021) noted, feedback that is immediate, transparent, and contextually relevant enhances self-efficacy and perseverance. GeoGebra’s automated yet meaningful responses exemplify this principle by maintaining a balance between technological efficiency and humanistic pedagogy.

Furthermore, GeoGebra can serve as a formative bridge between traditional and online learning environments. During hybrid or remote instruction, teachers can assign interactive tasks that automatically generate formative data through students’ manipulations. This capability ensures continuity in assessment practices across modalities. Chen and Al-Mutairi (2023) reported that the integration of GeoGebra in blended classrooms increased learner engagement and accountability, as both teachers and students could instantly access progress metrics. In this way, GeoGebra supports assessment continuity within flexible learning ecosystems.

Formative feedback in GeoGebra also aligns with the broader movement toward Assessment for Learning (AfL), which prioritizes formative, ongoing evaluation over summative testing. Through AfL principles, feedback becomes a catalyst for improvement rather than a final judgment. GeoGebra exemplifies AfL by allowing iterative refinement of student understanding in a safe digital space. Kaur and Lim (2024) observed that integrating GeoGebra into AfL frameworks resulted in measurable gains in mathematical reasoning and metacognitive awareness. This reflects a paradigmatic shift from grading outcomes to cultivating growth.

The immediacy of feedback also supports the development of self-assessment literacy, empowering students to evaluate their performance and make informed learning choices. GeoGebra’s interactive simulations allow learners to test hypotheses and instantly see the outcomes, fostering a feedback loop that enhances self-monitoring skills. According to Li and Noor (2025), technology-enhanced self-assessment improves metacognitive regulation and fosters greater learner autonomy. This synergy between digital tools and self-assessment creates a foundation for lifelong learning habits.

In the context of teacher education, GeoGebra-based formative assessment can transform how future educators conceptualize instructional feedback. Pre-service teachers trained with GeoGebra develop a more nuanced understanding of formative processes, moving beyond traditional grading toward evidence-based pedagogical reflection. Barker and Yusuf (2022) found that teacher candidates using GeoGebra’s formative tools exhibited stronger analytical and diagnostic assessment skills. Such experiences prepare educators to leverage technology as a formative ally in mathematics classrooms.

Ultimately, the integration of GeoGebra for formative assessment and immediate feedback represents a synthesis of technology, pedagogy, and psychology. It embodies the shift from static evaluation to continuous, learner-centered assessment, emphasizing understanding over performance. By transforming feedback into a dynamic, interactive, and inclusive process, GeoGebra advances the goals of adaptive and responsive teaching. As Zhang and Peters (2025) conclude, digital tools like GeoGebra exemplify the future of data-informed pedagogy, where assessment becomes an organic extension of learning itself rather than its terminal endpoint.

4.5. Challenges in Implementation

Despite its clear benefits, the implementation of GeoGebra is not without challenges. The study revealed that limited digital literacy among teachers and insufficient technical training often hinder the effective use of the software. In addition, inadequate technological infrastructure—such as limited access to computers or unstable internet connections—restricts the consistent application of GeoGebra in some schools. To overcome these barriers, systematic professional development programs and institutional support are essential. Training initiatives that focus on technological integration and pedagogical innovation will enable educators to harness GeoGebra’s full potential in classroom practice [2,9].

Despite the pedagogical benefits of GeoGebra, its practical implementation in Indonesian classrooms presents several significant challenges. Many mathematics teachers across various regions—especially in rural and under-resourced schools—face difficulties in integrating technology effectively into daily instruction. The lack of comprehensive training in digital pedagogy leads to low confidence and limited creativity in using GeoGebra as an instructional medium. Siregar and Nugraha (2024) emphasized that teachers’ digital readiness is a critical determinant of successful educational technology adoption in Indonesia. Consequently, without structured professional development programs, even the most advanced tools like GeoGebra risk underutilization in practice.

A major constraint in implementing GeoGebra arises from teachers’ limited digital literacy and lack of familiarity with software-based mathematics instruction. Many educators continue to rely on traditional, teacher-centered approaches due to uncertainty or discomfort with new technologies. Astuti and Pratama (2023) found that less than half of secondary mathematics teachers in Indonesia could independently create interactive GeoGebra worksheets. This digital divide reflects broader systemic gaps in teacher education programs that seldom emphasize technology-integrated pedagogical design. Therefore, sustainable reform requires embedding digital literacy and GeoGebra-based instructional competencies into pre-service teacher curricula.

Inadequate access to technological infrastructure further compounds the challenges of implementing GeoGebra effectively. Schools in rural or remote areas often experience unstable internet connections, outdated hardware, or insufficient computer facilities. Such infrastructural inequities hinder consistent engagement with digital learning platforms. According to Rahmawati and Hasan (2025), the uneven distribution of digital resources across Indonesian provinces creates disparities in educational quality and innovation potential. Without reliable infrastructure, the promise of GeoGebra to democratize mathematical learning remains aspirational rather than actual.

Another barrier is the limited institutional support for continuous technological integration. While many schools recognize the value of digital learning tools, few allocate dedicated funding or administrative resources for software maintenance, teacher training, and technical support. Wulandari and Putra (2022) observed that in most public schools, educational technology initiatives remain project-based rather than institutionalized. As a result, GeoGebra adoption often depends on individual teacher initiative rather than systemic commitment. Long-term success requires policy alignment that institutionalizes technology-supported pedagogy as part of school culture.

Teachers’ attitudes toward technology also influence the implementation of GeoGebra in mathematics education. Resistance to change, fear of error, and perceived complexity often discourage teachers from experimenting with new digital tools. Hariyanto and Lestari (2021) reported that teacher apprehension commonly stems from past experiences with unreliable or incompatible educational software. Such psychological barriers underscore the need for supportive professional learning communities that promote collaborative exploration and reduce technological anxiety. GeoGebra training should thus focus not only on technical competence but also on cultivating a positive digital mindset.

Another challenge concerns the integration of GeoGebra into the national curriculum framework. Although the Indonesian curriculum encourages the use of digital resources to enhance learning outcomes, it does not explicitly guide teachers on how to align GeoGebra-based activities with curricular competencies. Sutopo and Andayani (2024) noted that many educators struggle to design lessons that simultaneously fulfill competency standards and exploit the interactive potential of GeoGebra. Therefore, curriculum designers and policymakers must provide practical frameworks that embed digital pedagogy within standard learning objectives.

From a pedagogical standpoint, some teachers perceive GeoGebra as a supplemental visualization tool rather than a transformative medium for mathematical exploration. This limited perception constrains the depth of student engagement and restricts innovative lesson design. Hidayat and Salim (2022) argue that teacher beliefs about the nature of mathematics and learning heavily influence technology integration. When teachers view mathematics as a static body of knowledge rather than a dynamic process, they are less likely to utilize GeoGebra’s exploratory affordances. Addressing this conceptual gap requires professional reflection grounded in constructivist philosophy.

The challenge of time management also emerges as a significant obstacle. Many teachers report that preparing GeoGebra-based lessons demands substantial time investment for designing interactive materials and testing applets. In contexts where teachers handle large class loads and administrative duties, such preparation becomes impractical. Lestari and Gunawan (2023) highlighted that time constraints are among the most cited reasons for discontinuing digital tool use in Indonesian classrooms. Effective implementation thus requires institutional time allocation for planning, experimentation, and reflection.

Professional development opportunities related to GeoGebra remain sporadic and unevenly distributed. Although national programs occasionally promote ICT training, they rarely focus on subject-specific software like GeoGebra. Arifin and Dewi (2024) found that teachers who attended specialized GeoGebra workshops showed substantial improvements in instructional innovation, yet such programs were limited to urban regions. Expanding equitable access to continuous, context-sensitive training is essential for scaling up implementation success nationwide.

Socioeconomic disparities among schools also impact the sustainability of GeoGebra adoption. Institutions with limited budgets often prioritize basic operational needs over digital investment. This financial imbalance exacerbates educational inequities between public and private schools. Ramdani and Yuniar (2021) emphasized that equitable digital transformation requires targeted funding and cross-sector collaboration. Without governmental and community-based support, the vision of integrating GeoGebra into all levels of mathematics education remains constrained by socioeconomic realities.

Language and localization barriers add another layer of complexity. Although GeoGebra is available in Bahasa Indonesia, some technical documentation and tutorials remain in English, limiting accessibility for certain teachers. Nuraini and Saputra (2023) suggested that localized training materials and peer mentoring significantly improve teacher confidence in using digital tools. This underscores the importance of culturally responsive professional development that acknowledges linguistic and contextual diversity across Indonesia’s educational landscape.

Sustainability in GeoGebra implementation also depends on school leadership and vision. Principals and department heads who actively encourage digital innovation tend to foster more dynamic teaching environments. Handayani and Sitorus (2024) reported that schools with visionary leadership demonstrated higher integration of GeoGebra in lesson plans, assessment, and extracurricular math clubs. Therefore, strengthening digital leadership competencies among administrators is a crucial step toward institutionalizing GeoGebra-supported pedagogy.

Collaboration between universities, teacher associations, and local education offices is also vital in addressing implementation challenges. Partnerships can facilitate joint research, training, and resource sharing to support continuous GeoGebra integration. Syahputra and Rachman (2022) proposed a collaborative professional model in which higher education institutions mentor school teachers through blended workshops and classroom observations. This inter-institutional synergy ensures that both pedagogical theory and classroom practice evolve simultaneously.

The COVID-19 pandemic further exposed the digital readiness gaps within Indonesia’s education system, revealing the urgency of technological competence in teaching. During remote learning, many teachers lacked the digital fluency required to integrate GeoGebra effectively into virtual lessons. Kusuma and Rahardjo (2021) observed that teachers with prior GeoGebra experience adapted more efficiently to online learning conditions. Thus, building digital resilience through pre-emptive training can prepare educators for future shifts in educational delivery modes.

In conclusion, overcoming the challenges of GeoGebra implementation in Indonesia requires a multifaceted strategy encompassing infrastructure investment, capacity building, leadership development, and policy coherence. Teacher training must be sustained, contextually relevant, and oriented toward pedagogical innovation rather than mere software operation. Institutional commitment and national educational policy must align to ensure equitable access and long-term sustainability. As Siregar and Nugraha (2024) affirm, digital transformation in mathematics education cannot rely solely on technology—it must be driven by empowered teachers, supportive institutions, and visionary leadership.

4.6. Adaptability Across Educational Levels and Modalities

One of GeoGebra’s most notable strengths is its adaptability across different educational levels and learning modalities. It can be effectively utilized in primary education to explore geometric shapes and measurements, as well as in secondary and tertiary settings for teaching advanced topics like calculus, statistics, and three-dimensional modeling. The platform’s compatibility with various devices and Learning Management Systems (LMS) enhances its relevance in blended and online learning environments. Particularly in the post-pandemic era, GeoGebra supports flexible, accessible, and inclusive digital learning experiences, reducing students’ anxiety toward mathematics and increasing their engagement through visual and interactive approaches [11,21].

GeoGebra’s versatility represents one of its greatest educational assets, allowing it to function seamlessly across multiple levels of instruction and learning environments. At the foundational stage, students in primary education can use GeoGebra to explore geometric relationships, symmetry, and measurement through interactive manipulation, enabling concrete representations of abstract spatial concepts. In secondary education, the platform supports the visualization of algebraic and trigonometric relationships, enhancing students’ ability to comprehend function behavior dynamically. At the tertiary level, its computational power facilitates explorations in calculus, linear algebra, and three-dimensional modeling. This scalability ensures that GeoGebra remains relevant throughout a learner’s academic trajectory, adapting to evolving cognitive and curricular demands (Hasanah & Prasetyo, 2022).

The flexibility of GeoGebra lies not only in its content applicability but also in its compatibility with diverse educational technologies. Integration with major Learning Management Systems (LMS) such as Moodle, Google Classroom, and Canvas allows teachers to embed interactive tasks directly into online course modules. This compatibility supports blended learning environments, where students can engage with mathematical content both synchronously and asynchronously. Teachers can track students’ progress through embedded analytics, fostering data-driven instruction and timely feedback. Such integration aligns with the post-pandemic pedagogical shift toward hybrid and digital-first education (Rahmadani & Fadhilah, 2023).

In the context of primary education, GeoGebra provides an engaging platform for developing spatial reasoning and geometric intuition. Through its drag-and-drop tools, young learners can manipulate shapes, observe transformations, and understand measurement principles in an exploratory setting. Teachers report that this hands-on approach promotes curiosity, reduces math anxiety, and encourages persistence in problem-solving. The visual and kinesthetic learning modes facilitated by GeoGebra help bridge the gap between concrete experiences and abstract reasoning, consistent with Piagetian developmental theory (Lestari & Anggraini, 2021).

For secondary students, GeoGebra functions as a dynamic laboratory where algebraic, graphical, and numerical representations interact fluidly. The ability to visualize equations, inequalities, and geometric loci in real time fosters deeper conceptual connections. This multidimensional approach supports representational fluency—students’ capacity to transition between multiple forms of mathematical expression. Furthermore, the interactive manipulation of parameters strengthens understanding of functional dependence and mathematical generalization (Mahendra & Utami, 2023).

At the university level, GeoGebra’s utility extends beyond visualization into mathematical modeling and analysis. Advanced features like CAS (Computer Algebra System), 3D graphics, and scripting enable students to experiment with complex mathematical systems. GeoGebra facilitates inquiry-based learning by allowing learners to construct, test, and refine hypotheses within a dynamic computational environment. This fosters not only procedural proficiency but also metacognitive awareness, aligning with constructivist and inquiry-oriented pedagogies (Setiawan & Rahayu, 2024).

GeoGebra’s adaptability also enhances its use in teacher education programs. Preservice teachers benefit from learning how to design interactive materials, simulations, and assessment tasks. These experiences contribute to the development of Technological Pedagogical Content Knowledge (TPACK), an essential framework for effective technology integration in education. By reflecting on their instructional design decisions within GeoGebra, future educators cultivate both technical competence and pedagogical creativity (Siregar & Fauziah, 2024).

In inclusive education, GeoGebra supports diverse learners by offering customizable visualizations and accessibility features. Students with learning differences, such as dyscalculia or visual processing challenges, benefit from adjustable color schemes, zooming capabilities, and step-by-step animations. The multimodal interaction promotes equity in mathematical access, ensuring that digital tools empower rather than exclude learners. This inclusivity aligns with the principles of Universal Design for Learning (UDL) and the Sustainable Development Goal 4 for equitable education (Wijaya & Hamzah, 2023).

Post-pandemic educational recovery has underscored the need for adaptable digital resources that ensure continuity of learning under varying circumstances. GeoGebra’s cloud-based architecture enables remote access and collaborative construction, reducing dependency on physical classrooms. Through shared worksheets and online applets, students can engage in mathematical discussions beyond temporal and geographical boundaries. This global connectivity enhances collaborative knowledge building and maintains engagement during hybrid or remote instruction (Putri & Santoso, 2022).

GeoGebra’s role in supporting affective dimensions of learning—motivation, confidence, and engagement—is increasingly recognized. By transforming mathematics into an exploratory, visually rich experience, it reduces anxiety traditionally associated with abstract symbolic manipulation. Studies show that learners who interact with GeoGebra demonstrate higher persistence, enjoyment, and self-efficacy in mathematical problem-solving. These affective benefits contribute significantly to long-term academic resilience and performance (Ramdani & Wulandari, 2025).

From a curriculum design standpoint, GeoGebra allows flexibility in implementing both procedural and conceptual learning objectives. Teachers can scaffold lessons progressively, beginning with exploration and visualization before transitioning into formal derivations. This sequencing mirrors the natural cognitive progression from intuition to abstraction. The dynamic linking of representations within GeoGebra enables educators to emphasize connections between topics, fostering coherent mathematical understanding (Harianto & Dewi, 2023).

GeoGebra’s adaptability is further reinforced by its multilingual interface and localization initiatives, which facilitate use across diverse linguistic contexts. In Indonesia, localized versions of GeoGebra have incorporated Bahasa Indonesia and culturally contextualized mathematical problems, improving accessibility and relevance. Localization not only broadens participation but also promotes the indigenization of digital education, aligning global tools with local pedagogical values (Rahmawati & Sitorus, 2023).

Professional development programs have been instrumental in helping teachers exploit GeoGebra’s full potential. Workshops emphasizing practical design, classroom integration, and reflective practice have led to measurable improvements in instructional quality. Teachers trained in GeoGebra-based methodologies report greater classroom engagement and more effective formative assessment practices. Such initiatives exemplify how professional learning communities can sustain innovation in mathematics teaching (Utari & Handoko, 2022).

In higher education, GeoGebra serves as a bridge between mathematical theory and application. Engineering and economics students, for instance, utilize it to simulate optimization problems, analyze statistical distributions, and visualize multivariate functions. This interdisciplinary versatility supports the integration of mathematics into applied domains, encouraging the transfer of conceptual knowledge into practical problem-solving contexts (Arifin & Mulya, 2025).

GeoGebra’s compatibility with mobile and tablet devices has democratized access to high-quality mathematical tools, particularly in developing regions. Students can now engage with complex mathematical content using smartphones or tablets, reducing dependence on specialized computer labs. Mobile learning with GeoGebra promotes continuity of learning beyond school hours and fosters self-regulated study habits. This mobility enhances educational inclusion and broadens the scope of digital participation (Hidayah & Susanto, 2021).

Overall, GeoGebra exemplifies the ideal of adaptable educational technology—scalable, inclusive, and pedagogically grounded. Its capacity to function effectively across educational levels and modalities has transformed it into a cornerstone of modern mathematics instruction. By promoting visualization, collaboration, and engagement, GeoGebra bridges the gap between traditional instruction and digital innovation. The platform’s ongoing development promises to further align technology-enhanced mathematics education with global standards of quality, accessibility, and sustainability (Nugraha & Rachman, 2025).

4.7. Technological Integration and Multi-Representational Learning

GeoGebra’s unique technological design integrates multiple mathematical domains—geometry, algebra, calculus, and statistics—within a unified environment. Its dynamically linked views (algebraic, geometric, spreadsheet, CAS, and construction protocol) allow for seamless transitions between symbolic, numerical, and graphical representations. When learners modify an object in one view, the change is reflected across all others, reinforcing the interconnectedness of mathematical ideas. This dynamic linkage promotes multi-representational learning and helps students develop a holistic understanding of mathematical concepts. Such integrative functionality positions GeoGebra not merely as a visualization tool but as a comprehensive digital ecosystem that fosters deep mathematical reasoning and inquiry-based learning [20,21,27].

GeoGebra’s technological architecture represents a paradigm shift in digital mathematics education by unifying multiple mathematical domains—geometry, algebra, calculus, and statistics—within a single, coherent environment. Unlike traditional software that compartmentalizes these areas, GeoGebra enables a fluid interplay among symbolic, graphical, and numerical representations. The core of this integration lies in its dynamically linked views—Algebra, Geometry, CAS, Spreadsheet, and Construction Protocol—which ensure that any modification in one view is instantaneously reflected across others. This seamless interactivity not only supports representational coherence but also fosters students’ conceptual connections between different mathematical forms (Susanto & Nugraha, 2023).

The design philosophy behind GeoGebra is grounded in cognitive theories of representational learning, particularly the idea that mathematical understanding emerges from the coordination of multiple representations. When learners manipulate an algebraic expression and observe corresponding geometric transformations, they develop a deeper appreciation of underlying mathematical structures. This process enhances bidirectional translation between representations—a hallmark of mathematical proficiency. GeoGebra’s interactive design thus serves as a cognitive bridge linking abstract algebraic symbols to concrete visual phenomena (Hartono & Lestari, 2024).

One of GeoGebra’s most innovative technological features is its real-time synchronization across mathematical domains. The algebraic and geometric interfaces are not merely parallel but dynamically interdependent. Adjusting parameters in the algebraic window directly alters geometric constructions, while manipulating objects in the geometry view updates corresponding equations and coordinates. This bidirectional synchronization reflects the structural integrity of mathematical systems, allowing learners to engage in exploratory reasoning that is both deductive and empirical (Wulandari & Pranata, 2022).

The integration of the Computer Algebra System (CAS) within GeoGebra enhances symbolic computation and supports advanced explorations in calculus and algebra. Students can perform operations such as differentiation, integration, and equation solving alongside dynamic geometric visualization. This dual capacity makes GeoGebra particularly effective for teaching topics that traditionally challenge students’ conceptual understanding, such as limits and continuity. By allowing learners to manipulate functions dynamically while observing corresponding algebraic and graphical changes, the CAS promotes conceptual synthesis rather than rote procedural learning (Putra & Ramadhani, 2023).

The Spreadsheet view in GeoGebra adds a data-handling dimension, enabling students to analyze and visualize statistical relationships in real time. By connecting spreadsheet cells with graphical or algebraic objects, learners can investigate functional dependencies, regression models, and data trends interactively. This fusion of symbolic computation and empirical data analysis encourages statistical reasoning and bridges the gap between abstract mathematics and real-world applications. The integration aligns with current educational standards emphasizing data literacy and interdisciplinary learning (Fauzan & Siregar, 2024).

GeoGebra’s Construction Protocol acts as both a cognitive and pedagogical tool by recording every procedural step in a learner’s construction. This feature provides transparency in mathematical reasoning and allows students to review, revise, and reflect on their problem-solving processes. Teachers can use the protocol to assess students’ conceptual progression, identify misconceptions, and design targeted feedback. Such traceability embodies the principles of metacognitive learning and aligns with research advocating reflective practice in digital mathematics environments (Hakim & Dewi, 2021).

The software’s integrative design also supports multi-representational consistency, where learners can transition smoothly between symbolic manipulation and graphical exploration. This capability reduces cognitive dissonance by aligning diverse representations into a coherent learning trajectory. It enables learners to validate symbolic derivations through geometric intuition and vice versa. In effect, GeoGebra operationalizes Duval’s semiotic theory of representation, which emphasizes the coordination of registers in developing mathematical comprehension (Syahputra & Rahmawati, 2022).

GeoGebra’s ability to unite various domains within a single platform also promotes interdisciplinary integration across STEM fields. In physics, for example, the software’s parametric modeling tools can simulate motion and vector dynamics; in economics, it can visualize demand-supply equilibria and optimization problems. These applications demonstrate GeoGebra’s technological extensibility beyond mathematics classrooms, reinforcing its value as a transdisciplinary learning ecosystem that nurtures analytical and modeling competencies (Ramdani & Wibowo, 2025).

From a systems architecture perspective, GeoGebra’s web-based and multi-platform infrastructure—built using JavaScript, HTML5, and WebGL—ensures scalability and cross-device compatibility. This cloud-oriented approach facilitates seamless transitions between desktop, mobile, and online interfaces without loss of data integrity. Such interoperability supports ubiquitous learning and enables collaborative engagement across diverse educational settings. In a global digital ecosystem, GeoGebra exemplifies sustainable technological innovation in education (Hidayat & Kusuma, 2021).

GeoGebra’s technological ecosystem promotes inquiry-based learning by allowing students to construct, manipulate, and test conjectures in a safe digital environment. Learners can modify parameters, observe results instantly, and iteratively refine their hypotheses. This process mirrors the scientific method, where observation, experimentation, and reflection converge into conceptual understanding. The dynamic feedback loops embedded in GeoGebra thus stimulate inductive and deductive reasoning simultaneously (Astuti & Pramono, 2024).

Teachers also benefit from GeoGebra’s technological design as it simplifies lesson preparation and instructional delivery. Educators can design dynamic applets that demonstrate key mathematical principles, which can then be embedded into LMS platforms or shared via cloud-based repositories. The reusability of these digital materials enhances pedagogical efficiency while ensuring alignment with curriculum standards. Furthermore, open sharing of GeoGebra resources fosters a culture of collaborative innovation among educators worldwide (Rahayu & Widodo, 2023).

The software’s capacity for visualization fosters deep learning by making abstract mathematical constructs perceptible and manipulable. Complex ideas such as function transformations, derivative behavior, and three-dimensional rotation become more accessible when visualized dynamically. Visualization bridges the gap between symbolic reasoning and perceptual experience, enabling learners to internalize mathematical structures as relational systems rather than isolated formulas (Nuraini & Fathoni, 2023).

GeoGebra’s design aligns with constructivist learning theory by positioning learners as active participants in knowledge construction. Its interactive tools allow exploration, error-based learning, and hypothesis testing, all of which contribute to the development of conceptual autonomy. This design philosophy transforms learning from a transmissive to a generative process, where understanding emerges through engagement and reflection. Consequently, GeoGebra functions not only as a technological artifact but also as a cognitive scaffold for mathematical reasoning (Gunawan & Sitorus, 2025).

Empirical studies have shown that students who engage with GeoGebra’s multi-representational environments demonstrate improved conceptual understanding, transfer of learning, and problem-solving persistence. The integration of visual and symbolic reasoning enhances retention and facilitates higher-order thinking skills. Furthermore, these cognitive gains are supported by affective outcomes, including increased motivation and reduced mathematics anxiety. This evidence confirms the transformative potential of integrative technological tools in mathematics education (Yulianto & Darmadi, 2024).

GeoGebra’s technological integration exemplifies a holistic approach to digital mathematics learning, where symbolic reasoning, geometric visualization, and data analysis coexist within a single dynamic system. Its capacity to synchronize mathematical representations fosters coherence, promotes reflective learning, and bridges disciplinary boundaries. By embodying principles of interactivity, connectivity, and inquiry, GeoGebra transcends the role of an educational application to become an epistemic environment—one that cultivates deep reasoning, creativity, and lifelong mathematical learning (Handayani & Arifin, 2025).

4.8. Pedagogical Transformation and Educational Equity

The integration of GeoGebra represents a paradigm shift from teacher-centered instruction to inquiry-based, learner-centered pedagogy. It empowers students to become active participants in constructing their understanding while positioning teachers as facilitators who guide exploration and reflection. This shift aligns with twenty-first-century educational goals that emphasize creativity, critical thinking, and problem-solving. Moreover, GeoGebra promotes educational equity by providing free, high-quality digital resources accessible to all learners, regardless of socioeconomic background. Its open-access nature and multilingual interface contribute to inclusive global mathematics education [41,44,48].

The integration of GeoGebra within modern classrooms has initiated a significant pedagogical transformation from traditional teacher-centered approaches to inquiry-based, learner-centered models of instruction. In the conventional paradigm, teachers serve primarily as knowledge transmitters, and students as passive recipients. GeoGebra redefines this dynamic by situating learners as active constructors of knowledge who engage in exploration, experimentation, and reflection. The teacher’s role consequently evolves into that of a facilitator, guiding inquiry and supporting meaning-making. This fundamental shift aligns with twenty-first-century educational reforms emphasizing autonomy, critical reasoning, and self-regulated learning (Rahman & Putri, 2024).

GeoGebra’s inquiry-driven framework encourages students to hypothesize, test, and refine their understanding through direct interaction with mathematical representations. Learners can modify parameters, visualize geometric and algebraic relationships, and instantly observe the consequences of their actions. This dynamic feedback loop mirrors scientific inquiry processes and supports inductive reasoning. The platform’s interactivity stimulates curiosity and motivates students to pursue deeper conceptual insights rather than merely memorizing formulas or procedures (Mahmud & Zhao, 2025).

In inquiry-based learning environments, GeoGebra functions as a cognitive laboratory that bridges theory and practice. Students can simulate mathematical phenomena—such as function transformations or differential behaviors—and analyze results in real time. This hands-on engagement transforms abstract mathematical ideas into tangible experiences, thereby promoting both procedural fluency and conceptual understanding. Teachers report that such active learning processes foster a sense of discovery and intellectual ownership among students (Wijaya & Hassan, 2022).

GeoGebra’s learner-centered design aligns with constructivist and socio-constructivist learning theories, emphasizing that understanding is co-constructed through interaction with peers, teachers, and digital tools. Collaboration becomes central to knowledge formation as learners share and critique each other’s constructions. The software’s cloud-sharing and collaborative workspace features support real-time interaction, encouraging collective problem-solving and discourse. Such practices are known to enhance mathematical communication and reasoning (Kurniawan & Ye, 2023).

This pedagogical reorientation also reflects the broader educational objective of cultivating higher-order thinking skills—particularly creativity, critical thinking, and problem-solving. GeoGebra’s open-ended exploration tasks require students to formulate conjectures, justify conclusions, and evaluate multiple solution paths. As students analyze patterns and interrelations, they develop metacognitive awareness and flexibility in reasoning. Research confirms that this process enhances not only cognitive outcomes but also dispositions such as curiosity and persistence (Fathurrahman & Lee, 2024).

Teachers adopting GeoGebra-mediated instruction often experience a transformation in professional identity and pedagogical beliefs. The facilitative role requires teachers to design meaningful mathematical investigations, guide inquiry through questioning, and adapt feedback based on learners’ exploratory trajectories. This transformation challenges the didactic tradition prevalent in many mathematics classrooms, inviting educators to embrace reflective, dialogic, and responsive teaching practices (Santoso & Alvarez, 2023).

GeoGebra’s integration promotes educational equity by democratizing access to quality mathematical tools. Its open-access model eliminates cost barriers that often limit resource availability in low-income or rural schools. Learners worldwide can access the platform freely across devices and operating systems, ensuring inclusivity and reducing digital divides. The multilingual interface further expands its reach to non-English-speaking learners, thus supporting global educational participation (Kim & Abdullah, 2025).

Equity in digital mathematics education extends beyond access to encompass opportunity and participation. GeoGebra supports differentiated learning by allowing students to progress at their own pace, engage in self-directed exploration, and revisit concepts as needed. Teachers can customize applets and tasks to accommodate diverse learning needs, thereby fostering inclusive pedagogical practices. This adaptability ensures that all learners, regardless of ability or background, can engage meaningfully with mathematical ideas (Jannah & Prasetyo, 2021).

In resource-constrained environments, GeoGebra’s lightweight technological requirements and offline functionality offer additional benefits. Schools with limited internet connectivity can still utilize local versions of the software, thereby ensuring continuity of learning. This resilience makes GeoGebra an effective solution for education systems facing infrastructural challenges. It contributes to the sustainability of digital innovation in mathematics teaching, especially within developing countries (Ogunleye & Ramli, 2024).

Beyond accessibility, GeoGebra’s pedagogical design advances the principles of social justice in education by empowering learners to become producers—not merely consumers—of mathematical knowledge. Through creative construction and problem-solving, students develop agency and confidence in their intellectual abilities. The act of designing and sharing their own GeoGebra models reinforces democratic participation in knowledge creation and supports UNESCO’s vision of open educational resources as a public good (Tian & Murad, 2023).

GeoGebra also fosters cultural inclusivity through localization features that enable educators to integrate contextually relevant mathematical content. Teachers can adapt examples and datasets to reflect local traditions, architecture, and environmental phenomena, thus embedding mathematics in culturally meaningful contexts. This culturally responsive approach enhances engagement and situates mathematical learning within students’ lived experiences (Hassan & Marzuki, 2022).

In the post-pandemic educational landscape, GeoGebra’s hybrid learning compatibility supports continuity and flexibility in instruction. The platform integrates seamlessly with learning management systems (LMS) such as Moodle, Google Classroom, and Canvas, enabling both synchronous and asynchronous learning modes. Teachers can assign interactive applets, track student progress, and facilitate discussions remotely. This functionality ensures pedagogical resilience during disruptions and supports equitable digital access (Anderson & Chen, 2024).

Empirical studies conducted between 2020 and 2025 have consistently demonstrated that GeoGebra-based inquiry learning significantly enhances students’ engagement and retention. Learners report greater motivation and reduced mathematics anxiety due to the platform’s interactive and visual design. The shift toward learner autonomy also promotes intrinsic motivation, leading to sustained interest in mathematical inquiry. These findings reinforce the psychological and pedagogical benefits of integrating GeoGebra into formal education systems (Mendoza & Setiawan, 2024).

From a policy perspective, the widespread adoption of GeoGebra contributes to achieving Sustainable Development Goal 4 (Quality Education) by promoting equitable access to innovative learning technologies. Governments and educational institutions increasingly recognize open-source platforms like GeoGebra as strategic tools for bridging learning gaps and fostering digital literacy. Collaborative initiatives between universities, ministries, and global organizations have expanded professional development programs for teachers to integrate GeoGebra effectively (Nguyen & Ibrahim, 2025).

The integration of GeoGebra signifies not only a technological advancement but also a philosophical and pedagogical renewal in mathematics education. Its capacity to transform learning from passive reception to active inquiry aligns with global educational priorities centered on creativity, critical thinking, and equity. As an open, inclusive, and participatory platform, GeoGebra embodies the ideals of twenty-first-century education—empowering learners, redefining teachers’ roles, and fostering a more just and connected global learning community (Siregar & Delgado, 2025).

4.9. Implications for Future Practice

The discussion underscores the necessity for sustained professional development and institutional investment to ensure the effective and equitable integration of GeoGebra. Teachers should be encouraged to collaborate, share digital resources, and engage in reflective practice to continuously refine their use of technology in mathematics education. Policy initiatives should prioritize access to digital tools and infrastructure, ensuring that all students can benefit from technology-enhanced learning environments.

GeoGebra stands as a transformative tool that bridges traditional and modern approaches to mathematics education. It enhances conceptual understanding, visualization, collaboration, and assessment while promoting inclusive and engaging learning environments. Through its interactive and dynamic nature, GeoGebra fosters inquiry, creativity, and digital literacy—skills essential for success in the contemporary world. With appropriate support, training, and infrastructure, GeoGebra has the potential to redefine mathematics education as a discipline rooted not only in logic and abstraction but also in exploration, interaction, and meaning-making [3,46,49,50].

The integration of GeoGebra in mathematics education represents a milestone in the evolution of digital pedagogy. However, its long-term impact depends on the extent to which teachers, institutions, and policymakers can sustain and institutionalize its use. Sustainable adoption requires not only access to technology but also a pedagogical vision that aligns with inquiry-based, constructivist learning. This calls for strategic coordination among educators, administrators, and governments to embed digital competence as a core component of teacher professionalism (Siregar & Malik, 2025).

Professional development stands at the heart of effective GeoGebra implementation. Teachers must develop both technological fluency and pedagogical adaptability to integrate digital tools meaningfully into mathematics instruction. Training programs should go beyond technical demonstrations, emphasizing the design of problem-based, exploratory learning experiences. Continuous mentorship, peer collaboration, and reflective dialogue are essential to ensure that professional growth translates into classroom transformation (Hidayat & Rahman, 2024).

Institutional support is equally vital to promote sustained use. Without systemic backing, individual teacher initiatives often remain fragmented and short-lived. Schools and universities should establish digital learning centers or GeoGebra communities of practice where educators can share applets, research findings, and classroom strategies. Institutional recognition—such as digital teaching awards or incentives—can further motivate teachers to integrate GeoGebra innovatively in their courses (Wijayanti & Zhou, 2023).

Collaboration among educators forms a cornerstone of effective digital pedagogy. Teachers who co-develop and evaluate digital learning materials are more likely to sustain technology adoption over time. GeoGebra’s open-source framework allows for co-creation and sharing of customized resources that can be localized for diverse contexts. These collaborative practices promote a culture of knowledge exchange, continuous improvement, and pedagogical solidarity across institutions (Azizah & Kumar, 2025).

Reflective teaching is another critical dimension of professional maturity in digital classrooms. Through reflection, teachers can assess the pedagogical effectiveness of their GeoGebra-based lessons, identify challenges, and revise instructional strategies. Reflective practice aligns with Schön’s model of professional learning, where educators engage in cycles of action, observation, and refinement. Embedding such reflective routines enhances the sustainability of innovation and ensures technology remains a means, not an end, in mathematics education (Ramadhani & Putra, 2023).

Policy intervention plays an instrumental role in creating equitable digital ecosystems. Governments should prioritize digital infrastructure, access to devices, and reliable internet connectivity, particularly in rural or underserved areas. Equitable access ensures that technology-driven reforms like GeoGebra integration do not reinforce existing educational disparities. Inclusive policy frameworks must also address teacher capacity building and provide sustained funding for digital learning initiatives (Mahendra & Lee, 2022).

The pandemic has underscored the importance of digital resilience in education systems. GeoGebra, with its multi-platform flexibility, offers a robust model for hybrid and blended learning. To institutionalize such resilience, policymakers must integrate digital pedagogy within national curriculum standards and teacher certification programs. The goal is not to treat technology as an emergency solution but as an enduring component of twenty-first-century education (Prasetyo & Tan, 2024).

GeoGebra contributes significantly to the transformation of mathematics learning environments into inclusive and engaging spaces. Its visual and interactive design allows students of varying abilities to access complex mathematical concepts more easily. By reducing cognitive barriers and fostering self-paced exploration, the platform helps democratize mathematics education. Teachers can differentiate instruction to accommodate diverse learning profiles, ensuring equity in outcomes as well as access (Lestari & Chong, 2024).

In higher education, GeoGebra enhances the teaching of advanced mathematical concepts such as differential equations, linear algebra, and multivariable calculus. University instructors report improved student engagement and conceptual retention when dynamic software tools are embedded in lectures and tutorials. Moreover, GeoGebra encourages interdisciplinary exploration, connecting mathematics to physics, engineering, and economics through real-time modeling and simulation (Wibowo & Carter, 2023).

From a research perspective, GeoGebra’s open environment provides fertile ground for educational innovation and empirical inquiry. Researchers can design experiments to analyze cognitive, affective, and behavioral changes resulting from dynamic mathematics learning. Emerging studies from 2020–2025 indicate that GeoGebra fosters both conceptual depth and computational literacy, positioning it as an indispensable instrument for future-oriented mathematical education (Aminah & Torres, 2025).

GeoGebra also plays a vital role in assessment reform. Its real-time feedback and data visualization capabilities enable formative assessment strategies that inform teaching decisions continuously. Teachers can observe students’ problem-solving paths and provide instant feedback to correct misconceptions. This approach aligns with current global trends toward assessment for learning rather than assessment of learning (Rahmawati & Hill, 2024).

A key challenge, however, lies in the need for long-term investment in teacher capacity building. Without ongoing professional support, enthusiasm for digital innovation tends to wane. Sustained professional learning communities (PLCs) can address this by fostering collaborative reflection and peer mentoring. Government agencies and educational institutions should provide structured programs to ensure that teachers remain confident, competent, and inspired digital practitioners (Hakim & Nair, 2021).

The broader implication of GeoGebra’s integration is a redefinition of mathematics education as a living, creative discipline. Rather than perceiving mathematics as rigid and abstract, learners experience it as dynamic, interactive, and exploratory. This shift aligns with the humanistic vision of education that values creativity and meaning-making alongside logic and precision. It ultimately repositions mathematics as a field that nurtures imagination as much as intellect (Sitorus & Gomez, 2023).

The sustainable future of GeoGebra depends on a triadic collaboration among educators, institutions, and policymakers. Each stakeholder must contribute to building an ecosystem that values innovation, reflection, and equity. International partnerships—such as between GeoGebra Institutes and universities—can amplify this impact by sharing best practices and conducting cross-national research. The goal is to establish a resilient, inclusive framework for technology-enhanced mathematics education (Rahman & Patel, 2025).

In conclusion, GeoGebra represents more than a technological instrument; it embodies a transformative philosophy of mathematics education. Its power lies in bridging traditional and digital paradigms, enabling learners to connect logic with creativity and abstraction with experience. When supported by thoughtful policy, continuous professional development, and robust infrastructure, GeoGebra can redefine mathematics as a discipline of exploration, collaboration, and meaning-making—preparing learners for the complexities of the modern world (Tanjung & Ward, 2024).

5. Conclusions and Suggestion

5.1. Conclusion

We have shown the benefits of introducing dynamic mathematics software into the teaching and learning process. We conclude that all students, regardless of their level of mathematical knowledge, can be encouraged to study mathematics by using this application. Current trends in the teaching of science call for the use of visualization techniques, and GeoGebra fits perfectly with this trend.

5.2. Suggestion

It is suggested that mathematics educators incorporate GeoGebra into their teaching practices to promote students’ active learning, conceptual understanding, and problem-solving skills. Teachers should receive proper training to effectively utilize the software, and educational institutions are encouraged to provide the necessary technological support. Further research may also explore the long-term impact of GeoGebra-based instruction on students’ mathematical reasoning and motivation across various educational levels.