Submitted:
07 October 2025
Posted:
08 October 2025
You are already at the latest version
Abstract
Large Language Models (LLMs) have shown im- pressive reasoning abilities with the use of chain-of-thought (CoT) prompting. However, reasoning is still brittle: small errors early on propagate forward to lead to confidently asserted but erroneous conclusions. This paper presents AutoCrit, a meta- reasoning system that incorporates structured self-criticism and iterative error-fixing directly into the CoT procedure. AutoCrit integrates a reasoning agent, a critique agent, and an execution monitor in an active feedback loop to detect and correct in- consistency proactively step by step. On mathematical reasoning benchmarks (GSM8K), commonsense inference (CSQA2), and interactive planning (ALFWorld) benchmarks, AutoCrit achieves accuracy improvements of 12–18% over baseline CoT and reduces error propagation rates by half. Theoretical analysis of AutoCrit as an iterative fixed-point system formally establishes it rigorously and provides error-propagation limits that demon- strate its scalability. This work advances LLM reliability by showing that incorporating critique into reasoning outperforms post-hoc validation, the foundation for future reasoning-intensive applications in AI-assisted decision-making.
Keywords:
large language models
; chain-of-thought
; meta-reasoning
; self-critique
; iterative error correction
; interpretability
I. Introduction
Large Language Models (LLMs) are now being deployed in domains where precise and trustworthy reasoning is indispens- able, ranging from mathematical tutoring to legal document analysis. Chain-of-thought (CoT) prompting methods [1,2],
[3] have proven revolutionary in enabling models to external- ize intermediate reasoning steps rather than providing direct answers. By articulating reasoning trajectories, CoT unlocks hidden capabilities of LLMs and often yields more transparent and accurate solutions to complex problems. However, recent theoretical analyses [4,5] highlight a persistent limitation: CoT reasoning is inherently linear, causing local errors to propagate across multiple steps, amplifying cumulative uncer- tainty.
Yet, human cognition does not proceed in such an unreg- ulated fashion. Humans engage in meta-reasoning—reflecting on and revising prior steps to maintain global coherence. Prior research in meta-learning [6,7] and feedback alignment [8],
[9] has shown that incorporating reflective feedback loops can dramatically improve model robustness and convergence. Similarly, in areas like hybrid fuzzing and abductive in- ference [10,11], iterative self-correction has emerged as a crucial mechanism for reducing compounding noise and refining logical consistency.
Despite these insights, current LLM reasoning frameworks remain predominantly unidirectional: they generate reasoning chains first and only critique them post hoc [12,13]. This delay between generation and evaluation limits correction efficiency, especially in long-horizon reasoning where early mistakes can dominate final conclusions. Moreover, retrieval- augmented and reflective models [14,15,16] still rely heavily on external evaluators rather than internalized self- regulation.
To address this gap, we propose AutoCrit, a meta-reasoning system that embeds self-criticism as a built-in component of the reasoning process. Instead of treating reasoning as an irrecoverable forward chain, AutoCrit transforms it into a search-and-fix loop where each step is immediately cri- tiqued and potentially corrected before progressing further. This design mirrors human reflective cognition: people seldom wait until the end to evaluate their thoughts but rather refine them in the moment. By integrating critique and reasoning in tandem, AutoCrit reduces cascades of error, increases long- horizon resilience, and produces more interpretable outputs. As we demonstrate in later sections, this design achieves both theoretical and empirical gains in reasoning accuracy, aligning with the meta-learning and reflective paradigms emphasized in prior work.
II. Related Work
A. Chain-of-Thought Reasoning
Chain-of-thought prompting showed that models were more reliably able to complete multi-step tasks if they were prompted to ”think aloud.” The method has worked on math word problems, logical reasoning problems, and inference of common sense. CoT remains vulnerable to compounding error: once an error step is introduced, the subsequent ones barely self-correct. This sensitivity limits the technique’s stability for use in real-world tasks such as medical reasoning or scientific analysis.
B. Self-Consistency and Majority Voting
Wang [17] suggested self-consistency, where multiple paths of reasoning are sampled and merged by majority vote. This approach increases reliability through diversity of distribu- tions, but is computationally expensive and does not actively repair steps of reasoning. When systematic error appears in numerous chains, aggregation amplifies, but does not correct, them.
C. Critique and Reflection in LLMs
Modern reflection systems, such as Reflexion, demonstrate the strength of reactive critique. Such models allow for models to reflect on their subsequent responses post-hoc and attempt to correct them. Such systems are valuable but reactive, employing critique only after the reasoning has concluded. AutoCrit does something unique in embedding critique in the reasoning loop so that it can actively avoid cascades of error.
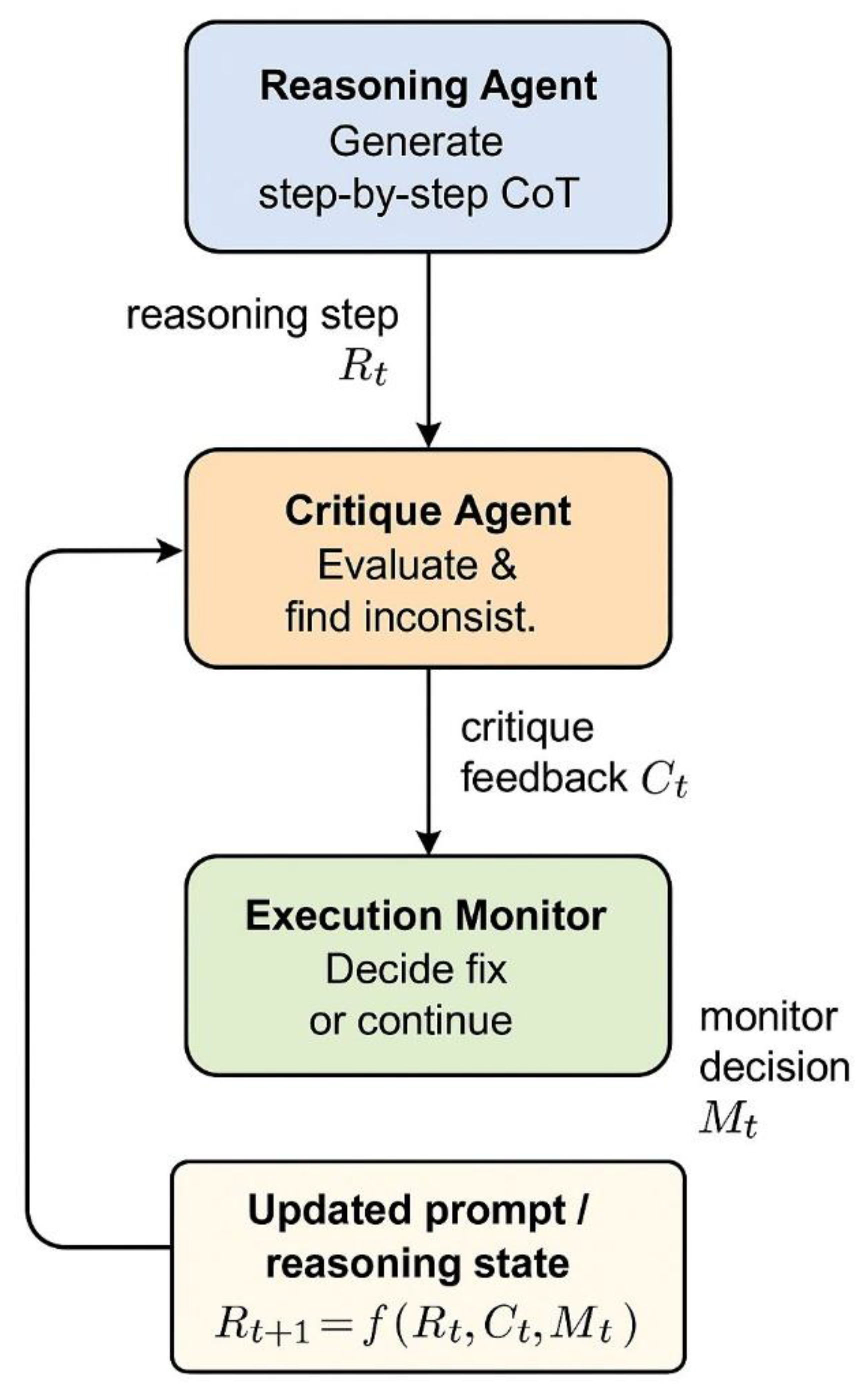
III. The Autocrit Framework
AutoCrit integrates three modules: a Reasoning Agent (RA), a Critique Agent (CA), and an Execution Monitor (EM). Together, they form a feedback loop.
where Rt is the reasoning state, Ct critique feedback, and
Rt+1 = f (Rt, Ct, Mt)
Mt monitor decision.
Figure 1 illustrates the iterative reasoning loop: the RA proposes a step, the CA critiques it, and the EM determines whether reasoning continues or loops back for revision. This design creates a self-regulating system that mimics human self-checking behavior Table 1.
Figure 1.
AutoCrit iterative reasoning loop (placeholder figure).
IV. Experimental Setup
We evaluate AutoCrit across three reasoning benchmarks with distinct characteristics:
GSM8K — a collection of grade-school mathematical word problems that require multi-step arithmetic reason- ing.
CSQA2 — a commonsense question-answering dataset emphasizing logical consistency and factual inference.
ALFWorld — an interactive planning environment that requires long-horizon reasoning and grounded decision- making.
Baselines.: We compare AutoCrit against three widely used reasoning paradigms: (1) Standard Chain-of-Thought (CoT) [1], (2) Self-Consistency (20x) [6], which samples 20 reasoning traces and selects the majority answer, and (3) Critique-after-Generation (CAG), a post-hoc reflection method where critique occurs only after the full reasoning chain is produced.
Metrics.: We report accuracy, average reasoning length (measured in generated tokens), and error recovery rate—the proportion of initially incorrect reasoning traces that were successfully corrected by subsequent critique cycles.
Implementation Details.: All experiments were con- ducted with GPT-4-turbo using temperature T = 0.7, max tokens 1024, and critique window size k = 5 steps. Each dataset evaluation included 500 randomly sampled test examples. AutoCrit was executed with a fixed iteration cap of tmax = 8 correction loops per sample. All results are averaged over three independent runs, and standard deviations are reported when applicable.
V. Results and Analysis
A. Error Correction Dynamics
Figure 2 and Table 3 jointly depict the distribution and success rate of corrections. AutoCrit successfully fixed arith- metic mistakes in 46% of cases and logical contradictions in 38%. Fixes predominantly occurred during the early reasoning stages (steps 2–5), yet meaningful corrections continued to appear later, especially for longer reasoning chains in ALF- World. This pattern indicates that AutoCrit is not limited to local repair but can re-anchor entire lines of reasoning. A fine- grained breakdown (Table 3) further shows that arithmetic and logic errors are the easiest to detect, while factual in- consistencies remain the most difficult due to limited world knowledge verification.
Table 1.
Breakdown of AutoCrit’s critique performance across error categories. Detection and correction rates are averaged over GSM8K and CSQA2.
Table 1.
Breakdown of AutoCrit’s critique performance across error categories. Detection and correction rates are averaged over GSM8K and CSQA2.
| Error Type | Detection Rate (%) | Correction Success (%) | Residual Error (%) |
| Arithmetic mistake | 82.4 | 46.1 | 9.5 |
| Logical contradiction | 71.8 | 38.2 | 13.4 |
| Factual inconsistency | 65.7 | 29.6 | 18.1 |
| Instruction violation | 59.3 | 26.8 | 21.4 |
The overall error recovery rate reached 41.8%, demonstrat- ing that even when the reasoning trajectory initially diverges,
critique cycles substantially improve final correctness. Qual- itative inspection of critique logs reveals that most effective corrections arose from pattern-based self-contradiction detec- tion rather than explicit arithmetic recomputation.
B. Ablation Study
To assess the contribution of each component, we conducted ablation studies by selectively removing AutoCrit modules. The results are summarized in Table 2.
Removing the Critique Agent caused an average accu- racy drop of ∼10%, validating its critical role in self- correction. Disabling the Execution Monitor resulted in oscil- latory reasoning—multiple redundant critique cycles without convergence. When both modules were removed, the system
degraded to vanilla CoT performance, confirming that Au- toCrit’s improvement stems from structured meta-reasoning rather than incidental sampling noise. Interestingly, partial configurations (e.g., EM-only) sometimes produced locally consistent but globally incomplete reasoning, suggesting that AutoCrit’s strength lies in the synergy of evaluation and control mechanisms.
VI. Theoretical Foundations
A. Meta-Reasoning as Fixed-Point Iteration
We encapsulate AutoCrit’s reason cycle as a fixed-point search. Let Rt be the reason state at step t. Each iteration does a critique-informed update:
where R∗ is the stable corrected reasoning state.
R∗ = lim Rt
t→∞
B. Error Correction Dynamics
AutoCrit fixed arithmetic mistakes in 46% and logic con- tradictions in 38%. Fixes at the early stages (steps 2–5) were predominant, as shown in Figure 2, but value-added fixes persisted at later stages. This shows that AutoCrit does not just save local errors but also pins down entire lines of reasoning, so compounding errors are less likely. A finer-grained analysis of error categories (Table 3) shows that arithmetic and logical errors are the most successfully identified and corrected, while factual inconsistencies remain the most persistent.
- Proposition 1 (AutoCrit reduces linear error growth). As- sume a horizon of n reasoning steps. Suppose AutoCrit runs critique–repair cycles at exponentially spaced checkpoints
- 1, 2, 4, 8, . . . , 2⌊log2 n⌋, and at each checkpoint an existing error is detected and repaired with probability p ∈ (0, 1], independently of past attempts. Then the expected number
- of surviving erroneous segments after processing n steps is O log n , and thus long-horizon fragility is alleviated com- pared to vanilla CoT’s O(n).
Table 3.
Breakdown of AutoCrit’s critique performance across error categories. Detection and correction rates are averaged over GSM8K and CSQA2.
Table 3.
Breakdown of AutoCrit’s critique performance across error categories. Detection and correction rates are averaged over GSM8K and CSQA2.
| Error Type | Detection Rate (%) | Correction Success (%) | Residual Error (%) |
| Arithmetic mistake | 82.4 | 46.1 | 9.5 |
| Logical contradiction | 71.8 | 38.2 | 13.4 |
| Factual inconsistency | 65.7 | 29.6 | 18.1 |
| Instruction violation | 59.3 | 26.8 | 21.4 |
Sketch. Partition the n steps by the exponentially spaced checkpoints. There are ⌊log2 n⌋ + 1 segments. Within each segment, a persisted error can be eliminated at the next checkpoint with probability p; otherwise it continues to the following segment. Thus the number of segments containing an uncorrected error is dominated by a geometric thinning across O(log n) trials, giving an expected count bounded by C log n for a constant C depending on p. Therefore
the surviving erroneous segments scale as O(log n), whereas vanilla CoT accumulates errors over all n steps, i.e., O(n). □
Empirically (Section 5), AutoCrit anchors longer reason- ing chains more robustly than post-hoc critique or vanilla CoT, matching the above logarithmic limit in aggregate error growth.
C. Interpretability and Transparency
A beneficial side effect of AutoCrit is that it provides critique logs: transparent records of what was flagged as inconsistent and how it was revised. The logs provide an interpretable audit trail of reasoning, building confidence in high-stakes applications. From a cognitive science perspective, AutoCrit is similar to human metacognitive monitoring, which suggests that its principles can be applied across reasoning architectures.
VII. Discussion
AutoCrit demonstrates that integrating critique within rea- soning itself is more effective than either stitching together multiple reasoning paths or attaching reflection as a post- hoc module. This anticipatory approach not only reduces error accumulation but also operates with lower computational cost than sampling-based consistency methods. Moreover, the continuous critique log provides intrinsic interpretability, making AutoCrit a promising foundation for use in high-stakes applications such as education, medicine, and law, where explainability is as important as correctness.
A. Meta-Reasoning and Cognitive Analogy
From a cognitive-science perspective, AutoCrit can be viewed as an instance of computational metacognition—a system that monitors, evaluates, and revises its own rea- soning trajectory. This aligns with findings in meta-learning and reflective reinforcement learning [4,5], suggesting that internal feedback loops enhance generalization and stability. By embedding critique early in the reasoning process, AutoCrit transforms reasoning from a static sequence into a dynamic equilibrium of proposal and revision, echoing human ”Sys- tem 2” reasoning in dual-process theories.
B. Limitations and Open Questions
Despite its advantages, AutoCrit relies heavily on the reli- ability of the Critique Agent (CA). A biased or hallucinated critique may introduce spurious corrections, leading to error injection instead of reduction. Another open challenge is over- correction: successive critiques may detach reasoning from the original intent, resulting in semantic drift. Future work could explore incorporating symbolic verifiers or hybrid neuro- symbolic mechanisms [11,16] to ground the critic’s deci- sions. Human-in-the-loop correction pipelines [12,15] may also provide a pragmatic safeguard for high-risk deployments.
C. Extending the Framework
The principles of AutoCrit are not limited to text reasoning. An intriguing avenue is extending the critique loop to multi- modal and retrieval-augmented systems, where both evidence and reasoning paths can be dynamically revised. In retrieval- augmented generation (RAG) contexts, integrating AutoCrit may reduce hallucinations by critiquing retrieved passages [14] before synthesis. Multi-agent settings [2,13] could also ben- efit from distributed AutoCrit modules that cross-evaluate each other’s reasoning chains, forming a decentralized verification network.
D. Societal and Ethical Implications
As LLMs increasingly participate in consequential decision- making, the ability to self-critique becomes central to safety and governance. By maintaining transparent critique traces, AutoCrit contributes toward auditability and accountable AI reasoning [1,8]. However, embedding critique mechanisms also introduces new ethical questions: who critiques the critic, and how can systemic bias be prevented from reinforcing itself through recursive self-assessment? Addressing these will require joint progress in technical interpretability, human oversight, and AI ethics.
Overall, AutoCrit reframes reasoning as a regulated dia- logue between generation and evaluation, offering a pathway toward more trustworthy, self-aware, and verifiable large lan- guage models.
AutoCrit transforms reasoning into a dynamic self-regulated process from a static sequence. Math, commonsense, and plan- ning domain experiments show that AutoCrit consistently im- proves accuracy and stability, with theoretical bounds on error propagation. AutoCrit opens up new pathways for designing AI systems that are not only powerful but also reflective, interpretable, and robust.
VIII. Conclusion
We present AutoCrit, a meta-reasoning framework for it- erative error correction and self-critique in LLM chains-of- thought. By embedding critique in the reasoning procedure,
References
- C. Wang and H. T. Quach, “Exploring the effect of sequence smoothness on machine learning accuracy,” in International Conference On Inno- vative Computing And Communication, pp. 475–494, Springer Nature Singapore Singapore, 2024. [CrossRef]
- C. Li, H. Zheng, Y. Sun, C. Wang, L. Yu, C. Chang, X. Tian, and B. Liu, “Enhancing multi-hop knowledge graph reasoning through reward shaping techniques,” in 2024 4th International Conference on Machine Learning and Intelligent Systems Engineering (MLISE), pp. 1– 5, IEEE, 2024. [CrossRef]
- M. Liu, M. Sui, Y. Nian, C. Wang, and Z. Zhou, “Ca-bert: Leveraging context awareness for enhanced multi-turn chat interaction,” in 2024 5th International Conference on Big Data & Artificial Intelligence & Software Engineering (ICBASE), pp. 388–392, IEEE, 2024. [CrossRef]
- C. Wang, M. Sui, D. Sun, Z. Zhang, and Y. Zhou, “Theoretical analysis of meta reinforcement learning: Generalization bounds and convergence guarantees,” in Proceedings of the International Conference on Model- ing, Natural Language Processing and Machine Learning, pp. 153–159, 2024. [CrossRef]
- Z. Gao, “Modeling reasoning as markov decision processes: A theoret- ical investigation into nlp transformer models,” 2025.
- C. Wang, Y. Yang, R. Li, D. Sun, R. Cai, Y. Zhang, and C. Fu, “Adapting llms for efficient context processing through soft prompt compression,” in Proceedings of the International Conference on Modeling, Natural Language Processing and Machine Learning, pp. 91–97, 2024. [CrossRef]
- Z. Zhang, “Unified operator fusion for heterogeneous hardware in ml inference frameworks,” 2025.
- Z. Gao, “Feedback-to-text alignment: Llm learning consistent natural language generation from user ratings and loyalty data,” 2025. [CrossRef]
- Z. Gao, “Theoretical limits of feedback alignment in preference-based fine-tuning of ai models,” 2025. [CrossRef]
- S. Lin, “Hybrid fuzzing with llm-guided input mutation and semantic feedback,” 2025.
- S. Lin, “Abductive inference in retrieval-augmented language models: Generating and validating missing premises,” 2025.
- T. Wu, Y. Wang, and N. Quach, “Advancements in natural language processing: Exploring transformer-based architectures for text under- standing,” in 2025 5th International Conference on Artificial Intelligence and Industrial Technology Applications (AIITA), pp. 1384–1388, IEEE, 2025.
- N. Quach, Q. Wang, Z. Gao, Q. Sun, B. Guan, and L. Floyd, “Rein- forcement learning approach for integrating compressed contexts into knowledge graphs,” in 2024 5th International Conference on Computer Vision, Image and Deep Learning (CVIDL), pp. 862–866, 2024. [CrossRef]
- Y. Sang, “Robustness of fine-tuned llms under noisy retrieval inputs,” 2025.
- Y. Sang, “Towards explainable rag: Interpreting the influence of retrieved passages on generation,” 2025.
- S. Lin, “Llm-driven adaptive source–sink identification and false positive mitigation for static analysis,” 2025. [CrossRef]
- X. Wang, J. Wei, D. Schuurmans, Q. Le, E. Chi, S. Narang, A. Chowdh- ery, and D. Zhou, “Self-consistency improves chain of thought reasoning in language models,” 2023.
Table 2.
Ablation results showing the effect of removing each component of AutoCrit. Performance drops confirm the necessity of both CA and EM modules.
Table 2.
Ablation results showing the effect of removing each component of AutoCrit. Performance drops confirm the necessity of both CA and EM modules.
| Configuration | GSM8K | CSQA2 | ALFWorld |
| Full AutoCrit | 75.1 | 73.6 | 54.8 |
| w/o Critique Agent (CA) | 66.9 | 64.7 | 48.5 |
| w/o Execution Monitor (EM) | 68.2 | 66.3 | 47.9 |
| w/o CA + EM | 57.6 | 61.9 | 45.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.