Toward Efficient and Faithful Reasoning in Large Language Models

1. Introduction

Large Language Models (LLMs), such as GPT, BERT, and their variants, have revolutionized natural language processing (NLP) by demonstrating unprecedented capabilities in a wide array of tasks, including language understanding, generation, summarization, and reasoning. These models, typically based on the Transformer architecture, possess billions of parameters and are pre-trained on massive corpora, enabling them to capture intricate linguistic patterns and world knowledge [1]. However, despite their remarkable performance, LLMs encounter significant challenges when tasked with complex reasoning processes due to their inherent architectural and computational constraints. Reasoning, the ability to draw logical conclusions, infer implicit information, and synthesize knowledge, is central to many advanced NLP applications such as question answering, dialogue systems, code generation, and scientific discovery. While early NLP models primarily relied on symbolic and rule-based approaches for reasoning, LLMs have shifted the paradigm by implicitly encoding reasoning skills within distributed representations [2]. Nonetheless, achieving efficient and reliable reasoning in LLMs remains a formidable challenge, as reasoning often requires multi-step, compositional, and context-dependent inference that can strain the models’ memory, computation, and interpretability. This survey focuses on the development and advancement of efficient reasoning models for LLMs, aiming to bridge the gap between the expressive power of large-scale pre-trained models and the practical demands of reasoning-intensive applications [3]. By "efficient reasoning models," we refer to techniques, architectures, and frameworks that enhance the reasoning abilities of LLMs while optimizing resource consumption such as computational cost, memory footprint, latency, and scalability [4]. The pursuit of efficiency is motivated by the need to deploy reasoning-capable LLMs in real-world scenarios where computational resources are limited, response times are critical, and interpretability is desired [5]. Several key challenges underscore the complexity of designing efficient reasoning models for LLMs:

• Computational Complexity: Large-scale transformers involve quadratic complexity with respect to sequence length, making long-horizon reasoning prohibitively expensive. Efficient models seek to reduce this burden through architectural innovations or approximations.
• Memory Constraints: Reasoning tasks often require maintaining and manipulating large context windows or knowledge bases, which can exceed the memory capacity of standard LLMs. Methods to compress, retrieve, or summarize context play a critical role [6].
• Interpretability and Transparency: Unlike symbolic reasoning systems, neural reasoning models are often black boxes, limiting their explainability. Efficient reasoning models aim to improve interpretability while maintaining performance [7].
• Generalization and Compositionality: Reasoning frequently involves applying learned knowledge in novel combinations and contexts [8]. Efficient models must generalize beyond training distributions without excessive retraining or parameter increase.
• Multi-step and Hierarchical Reasoning: Complex reasoning may require sequential inference steps or hierarchical decomposition of problems. Models must balance reasoning depth with efficiency and error accumulation.

In response to these challenges, the research community has proposed a diverse array of approaches spanning algorithmic innovations, architectural modifications, training paradigms, and auxiliary components. These include sparse attention mechanisms, retrieval-augmented models, modular and compositional architectures, memory-augmented networks, and hybrid neuro-symbolic frameworks. Moreover, advances in efficient fine-tuning, knowledge distillation, and pruning techniques contribute to making reasoning-capable LLMs more practical and accessible. This survey aims to provide a comprehensive and systematic overview of the state-of-the-art in efficient reasoning models for LLMs. We categorize and analyze recent developments, highlighting their principles, advantages, limitations, and potential application domains [9]. We also discuss benchmarking strategies, evaluation metrics, and open research questions that are critical for advancing this vibrant area [10]. The remainder of this paper is structured as follows [11]. Section 2 reviews the background and foundational concepts in LLMs and reasoning [12]. Section 3 delves into architectural approaches for efficiency, including sparse attention and memory enhancements. Section 4 covers algorithmic and training strategies such as retrieval augmentation and multi-step reasoning frameworks. Section 5 explores hybrid models integrating symbolic and neural reasoning paradigms. Section 6 discusses evaluation methodologies and benchmarks. Finally, Section 7 outlines future directions and concluding remarks. By synthesizing the current landscape of efficient reasoning models for LLMs, this survey aims to facilitate informed research and development that push the boundaries of intelligent language understanding and reasoning while maintaining practical feasibility.

2. Background and Foundations

Large Language Models (LLMs) are predominantly built upon the Transformer architecture [? ], which utilizes self-attention mechanisms to capture contextual dependencies across input sequences [13]. Formally, given an input token sequence $\mathbf{x}=(x_1,x_2,\dots ,x_n)$, the self-attention operation computes attention weights ${\alpha }_{ij}$ between tokens $x_i$ and $x_j$ as

$${\alpha }_{ij}={\displaystyle \frac{exp\left(\frac{{\mathbf{q}}_i^{\top }{\mathbf{k}}_j}{\sqrt{d_k}}\right)}{{\sum }_{m=1}^{n}exp\left(\frac{{\mathbf{q}}_i^{\top }{\mathbf{k}}_m}{\sqrt{d_k}}\right)}},$$

where ${\mathbf{q}}_i=W^Q{x}_i$ and ${\mathbf{k}}_j=W^K{x}_j$ are the query and key projections respectively, and $d_k$ is the dimensionality of the key vectors [14]. The output representation at position i is then a weighted sum of the value vectors ${\mathbf{v}}_j=W^V{x}_j$,

$${\mathbf{z}}_i=\sum _{j=1}^n{\alpha }_{ij}{\mathbf{v}}_j\text{[15]}.$$

This mechanism allows the model to dynamically attend to relevant parts of the input, enabling effective capture of long-range dependencies. However, the self-attention’s quadratic complexity in sequence length n, i.e., $O\left(n^2\right)$, poses substantial computational challenges for reasoning tasks that require processing extensive contexts or multi-hop inference chains. Reasoning within LLMs can be characterized by various forms, including deductive, inductive, abductive, and analogical reasoning. These can be abstracted as transformations on knowledge representations, where the model learns to approximate inference functions $f:\mathcal{K}\times \mathcal{Q}\to \mathcal{A}$, mapping a knowledge base $\mathcal{K}$ and query $\mathcal{Q}$ to an answer $\mathcal{A}$ [16]. Efficient reasoning demands models that not only approximate f with high fidelity but also do so within tractable computational budgets and time constraints. Historically, classical symbolic reasoning systems leverage logic programming, theorem proving, or rule-based inference, offering interpretability and soundness guarantees but suffering from brittleness and poor scalability to natural language understanding. Neural approaches, in contrast, embed reasoning implicitly within distributed representations, enabling robust generalization and end-to-end training, but often lacking explicit transparency and efficiency [17]. To bridge these paradigms, several foundations are key [18]. Memory-augmented neural networks introduce external memory modules $\mathcal{M}$ that can be read and written over multiple reasoning steps, extending the model’s capacity to store intermediate conclusions. Formally, the memory state at step t can be described as ${\mathbf{M}}_t\in {\mathbb{R}}^{m\times d}$, updated via

$${\mathbf{M}}_{t+1}=\mathrm{Update}({\mathbf{M}}_t,{\mathbf{h}}_t),$$

where ${\mathbf{h}}_t$ denotes the current hidden state [19]. This facilitates iterative refinement and multi-hop reasoning [20]. Another foundational concept is retrieval-augmented generation, where an external knowledge retriever $\mathcal{R}$ dynamically fetches relevant documents or facts $\mathbf{D}$ based on the query $\mathcal{Q}$. The model then conditions its reasoning on the augmented input $(\mathbf{x},\mathbf{D})$, effectively integrating symbolic knowledge bases with learned representations [21]. The retriever is often trained to optimize

$$\underset{\theta }{max}{\mathbb{E}}_{(\mathcal{Q},\mathcal{A})}log{P}_{\theta }(\mathcal{A}\mid \mathcal{Q},\mathcal{R}\left(\mathcal{Q}\right)),$$

where $\theta$ are the model parameters [22]. In addition, compositionality plays a critical role in reasoning efficiency. Compositional models factorize complex reasoning tasks into sequences of simpler subproblems, leveraging the principle that complex functions can be decomposed as

$$f(\mathcal{K},\mathcal{Q})=f_n\circ f_{n-1}\circ \dots \circ f_1(\mathcal{K},\mathcal{Q}),$$

where each $f_i$ represents a distinct reasoning step or module. This modularity enables focused computation, reuse of sub-solutions, and improved interpretability. In terms of evaluation, reasoning capability is measured through diverse benchmarks encompassing multi-hop question answering (e.g., HotpotQA [? ]), logical inference, commonsense reasoning (e.g., CommonsenseQA [? ]), and code generation challenges. Metrics typically involve accuracy, reasoning step efficiency, and resource consumption [23]. Table 3 summarizes some prominent benchmarks, their reasoning type, and key evaluation metrics [24].

Table 1. Summary of prominent reasoning benchmarks used for evaluating LLM reasoning capabilities.

Benchmark	Reasoning Type	Domain	Input Format	Evaluation Metric
HotpotQA [? ]	Multi-hop QA	Wikipedia Articles	Textual Questions	Exact Match, F1
CommonsenseQA [? ]	Commonsense	General Knowledge	Multiple Choice	Accuracy
CLUTRR [? ]	Relational Reasoning	Synthetic Stories	Textual Stories	Accuracy
ProofWriter [? ]	Logical Deduction	Synthetic Rules	Rule Sets	Accuracy, Stepwise Correctness
GSM8K [? ]	Mathematical Reasoning	Math Problems	Word Problems	Accuracy
CodeXGLUE [? ]	Program Synthesis	Code Repositories	NL-to-Code	BLEU, Exact Match

Table 1. Summary of prominent reasoning benchmarks used for evaluating LLM reasoning capabilities.

Benchmark	Reasoning Type	Domain	Input Format	Evaluation Metric
HotpotQA [? ]	Multi-hop QA	Wikipedia Articles	Textual Questions	Exact Match, F1
CommonsenseQA [? ]	Commonsense	General Knowledge	Multiple Choice	Accuracy
CLUTRR [? ]	Relational Reasoning	Synthetic Stories	Textual Stories	Accuracy
ProofWriter [? ]	Logical Deduction	Synthetic Rules	Rule Sets	Accuracy, Stepwise Correctness
GSM8K [? ]	Mathematical Reasoning	Math Problems	Word Problems	Accuracy
CodeXGLUE [? ]	Program Synthesis	Code Repositories	NL-to-Code	BLEU, Exact Match

The convergence of architectural innovations, training paradigms, and external knowledge integration constitutes the foundation upon which efficient reasoning models for LLMs are built. In subsequent sections, we explore these advances in detail, analyzing how they address the dual objectives of enhancing reasoning performance and optimizing computational efficiency [25].

Figure 1. Comparison of computational complexity as a function of input sequence length n for various attention mechanisms [26]. Full self-attention exhibits quadratic growth, while sparse and linear attention mechanisms approximate this with reduced complexity, enabling more efficient reasoning over longer contexts.

Figure 1. Comparison of computational complexity as a function of input sequence length n for various attention mechanisms [26]. Full self-attention exhibits quadratic growth, while sparse and linear attention mechanisms approximate this with reduced complexity, enabling more efficient reasoning over longer contexts.

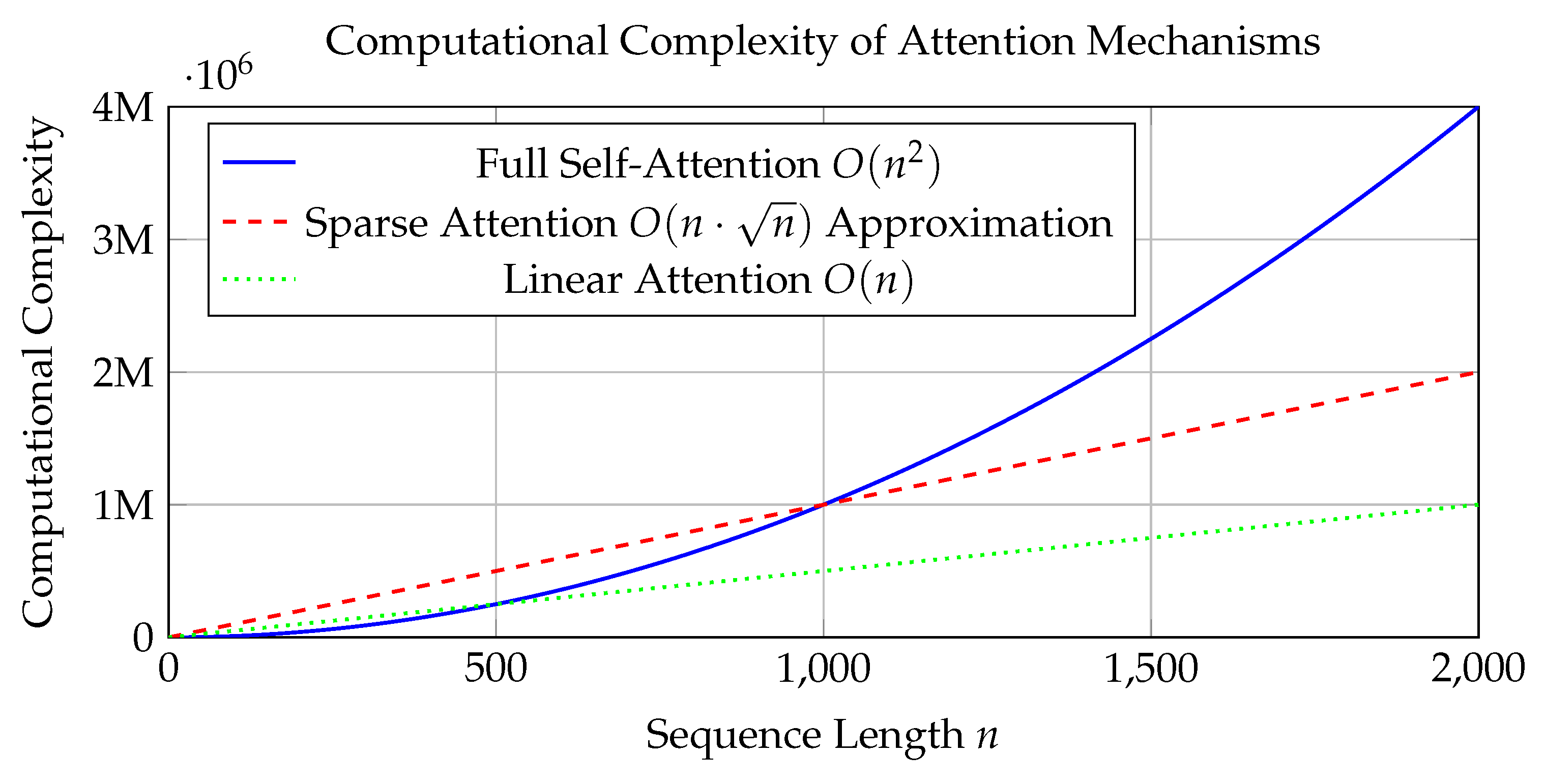
3. Architectural Approaches for Efficient Reasoning

The core computational bottleneck in Large Language Models (LLMs) arises primarily from the self-attention mechanism, which scales quadratically with the input sequence length, thereby limiting the practical applicability of reasoning tasks that involve long contexts or multi-hop inference chains [27]. To mitigate these constraints, numerous architectural innovations have been proposed to enhance reasoning efficiency by reducing complexity, improving memory usage, and enabling hierarchical or modular computation. One prominent class of approaches focuses on sparse attention mechanisms that selectively attend to a subset of tokens rather than the full sequence [28,29], thus lowering the effective complexity from $O\left(n^2\right)$ to near-linear or sub-quadratic scales. Formally, a sparse attention mask $M\in {\{0,1\}}^{n\times n}$ restricts the attention computation such that

$${\alpha }_{ij}={\displaystyle \frac{exp\left(\frac{{\mathbf{q}}_i^{\top }{\mathbf{k}}_j}{\sqrt{d_k}}\right)M_{ij}}{{\sum }_{m=1}^{n}exp\left(\frac{{\mathbf{q}}_i^{\top }{\mathbf{k}}_m}{\sqrt{d_k}}\right)M_{im}}},$$

where $M_{ij}=1$ indicates allowed attention, and zero otherwise. Various sparsity patterns have been explored, including local windows [? ], fixed patterns (strided, block), learnable sparse topologies [? ], and random attention [30]. These designs trade off expressivity and coverage to achieve substantial computational savings without significant performance degradation [31]. Complementing sparse attention, linear attention mechanisms reformulate the attention computation by leveraging kernel feature maps $\varphi \left(\right(·)$ to express attention as

$$\mathrm{Attention}(\mathbf{Q},\mathbf{K},\mathbf{V})=\varphi \left(\mathbf{Q}\right)\left(\varphi {\left(\mathbf{K}\right)}^{\top }\mathbf{V}\right),$$

which can be computed in $O\left(n\right)$ time and space [? ]. Although these approximations enable scaling to very long sequences, they may introduce approximation errors affecting the fidelity of multi-step reasoning chains [32]. Another architectural advancement involves hierarchical and chunk-based processing [33]. Models such as Longformer [? ] and BigBird [? ] partition the input sequence into overlapping or non-overlapping chunks processed at multiple scales [34]. This hierarchical representation allows the model to first extract local features and then aggregate global context via sparse or global tokens, effectively balancing local detail with long-range dependencies crucial for reasoning tasks. Formally, the hierarchical attention can be expressed as

$${\mathbf{Z}}^{\left(l\right)}=\mathrm{Attention}\left({\mathbf{Q}}^{\left(l\right)},{\mathbf{K}}^{\left(l\right)},{\mathbf{V}}^{\left(l\right)}\right),l=1,2,\dots ,L,$$

where each layer l operates at different resolution or chunk granularity. Memory-augmented architectures extend the Transformer paradigm by introducing explicit memory modules that decouple context size from model complexity. Models like Compressive Transformers [? ] and Memory-Enhanced Transformers [? ] maintain external memory buffers $\mathbf{M}\in {\mathbb{R}}^{m\times d}$ updated dynamically to store past computations or intermediate reasoning states [35]. The update mechanism often employs a combination of writing new information and compressing or forgetting obsolete content, defined as

$${\mathbf{M}}_{t+1}=\mathrm{Compress}({\mathbf{M}}_t\cup {\mathbf{h}}_t),$$

where ${\mathbf{h}}_t$ is the current hidden representation. This approach enables effective long-horizon reasoning by preserving salient information over extended sequences while controlling memory size [36]. Modular and compositional architectures decompose reasoning into specialized sub-networks or modules tailored for different reasoning primitives [37]. Such models utilize gating or routing functions $g_i(·)$ to dynamically select relevant modules,

$$\mathbf{z}=\sum _{i=1}^M{g}_i\left(\mathbf{x}\right)f_i\left(\mathbf{x}\right),$$

where each $f_i$ is a module performing a distinct reasoning operation (e.g., arithmetic, logic, retrieval), and M is the number of modules [38]. This design enhances interpretability and allows reusing modules across different tasks, fostering sample efficiency and scalability. To further alleviate memory and computational demands, parameter-efficient fine-tuning techniques such as adapters [? ], LoRA [? ], and prompt tuning [? ] have been integrated with efficient reasoning models [39]. These methods fine-tune a small subset of parameters or learn task-specific prompts to adapt LLMs for reasoning without retraining or storing full model weights, reducing overhead and enabling deployment on resource-constrained devices [40]. Table 2 summarizes representative architectural approaches for efficient reasoning, detailing their core mechanisms, complexity, and typical application scenarios.

In summary, architectural innovations have significantly expanded the feasibility of applying LLMs to reasoning-intensive tasks by reducing computational bottlenecks and extending effective context length [41]. These techniques enable efficient multi-step inference, scalable memory management, and modular composition of reasoning capabilities. The integration of these architectural methods with advanced training strategies and retrieval augmentation further advances the frontier of efficient reasoning models, which we explore in the next section.

4. Training Paradigms and Optimization for Efficient Reasoning

Beyond architectural innovations, the training paradigms employed to teach Large Language Models (LLMs) to reason effectively and efficiently are central to their overall performance. Reasoning, particularly multi-step or compositional reasoning, poses challenges related to supervision, optimization stability, generalization, and computational efficiency. In this section, we explore curriculum learning, supervised vs [42]. self-supervised training, intermediate supervision, step-by-step reasoning supervision, and techniques such as distillation and reinforcement learning that enhance reasoning efficiency. A key strategy for improving reasoning efficiency is curriculum learning, wherein training data is presented in a structured progression from simple to complex examples. This pedagogical approach, inspired by human learning, facilitates more stable convergence and better generalization in LLMs. Formally, let $\mathcal{D}=\{{\mathcal{D}}_1,{\mathcal{D}}_2,\dots ,{\mathcal{D}}_k\}$ be a partitioned dataset where ${\mathcal{D}}_i$ contains tasks of difficulty i, with $i<j\Rightarrow \mathrm{difficulty}\left({\mathcal{D}}_i\right)<\mathrm{difficulty}\left({\mathcal{D}}_j\right)$ [43]. The model is trained iteratively on ${\mathcal{D}}_1$, then ${\mathcal{D}}_2$, etc., to minimize the empirical loss:

$$\mathcal{L}\left(\theta \right)=\sum _{i=1}^k{\mathbb{E}}_{(x,y)\in {\mathcal{D}}_i}\left[\ell (f_{\theta }\left(x\right),y)\right]\text{[44]}.$$

This results in improved reasoning performance on higher-difficulty tasks due to gradual complexity exposure. Supervised learning remains the dominant training method for fine-tuning LLMs for reasoning, particularly when using datasets like GSM8K, HotpotQA, and ProofWriter that contain structured input-output pairs [45]. However, labeled reasoning traces are expensive to obtain. Self-supervised methods, including masked language modeling (MLM), causal language modeling (CLM), and denoising objectives, offer scalability. Yet, they typically lack explicit reasoning supervision [? ]. To compensate, auxiliary objectives have been introduced to enforce structure in the model’s internal computation. For example, chain-of-thought (CoT) prompting and supervision require the model to generate intermediate reasoning steps:

$$\mathrm{Input}:x\Rightarrow \mathrm{Output}:(s_1,s_2,\dots ,s_k,y),$$

where $(s_1,\dots ,s_k)$ are intermediate reasoning steps and y is the final answer [46]. The model is trained with a multi-step cross-entropy loss:

$${\mathcal{L}}_{\mathrm{CoT}}=\sum _{t=1}^{k+1}\mathrm{CE}(f_{\theta }{\left(x\right)}^{\left(t\right)},s_t),$$

where $s_{k+1}=y$ [47]. This promotes decomposition of complex problems into smaller logical steps. Step-by-step supervision has been shown to improve not only the final accuracy but also the interpretability and controllability of model outputs. However, it increases training cost [48]. To mitigate this, a compromise is achieved using intermediate reward-based optimization, where correctness of intermediate steps is rewarded but not strictly enforced. Distillation techniques have also been used to compress complex reasoning into smaller, more efficient student models. Given a teacher model $f_T$ and student model $f_S$, the distillation loss combines standard supervised loss ${\mathcal{L}}_{\mathrm{hard}}$ and soft target loss ${\mathcal{L}}_{\mathrm{soft}}$ as

$${\mathcal{L}}_{\mathrm{distill}}=\lambda {\mathcal{L}}_{\mathrm{soft}}+(1-\lambda ){\mathcal{L}}_{\mathrm{hard}},$$

where ${\mathcal{L}}_{\mathrm{soft}}=\mathrm{KL}(f_S\left(x\right)\parallel f_T\left(x\right))$, and $\lambda$ balances the trade-off. This strategy enables the student model to mimic reasoning behaviors of the teacher while maintaining reduced model size and faster inference [19]. Another paradigm is reinforcement learning (RL), especially Reinforcement Learning with Human Feedback (RLHF) [? ], which aligns model outputs with human preferences. For reasoning, RL can be extended to optimize a sequence of decisions, with rewards defined over correctness, step efficiency, and answer compactness. Let $s_t$ be the model’s reasoning state at step t, and $a_t$ the reasoning action [49]. The objective is to maximize the expected return:

$$J\left(\theta \right)={\mathbb{E}}_{{\pi }_{\theta }}\left[\sum _{t=1}^{T}r(s_t,a_t)\right],$$

where $r(·)$ measures reasoning utility [50]. RL fine-tuning, although unstable and sample inefficient, has been used successfully in models like InstructGPT to produce more coherent and correct reasoning outputs [51]. In addition, contrastive learning has emerged as a promising self-supervised paradigm to refine representations for reasoning [52]. Given a positive pair $(x,x^{+})$ and a set of negatives $\left\{x^{-}\right\}$, the model is trained to maximize the similarity of the positive pair while minimizing similarity to negatives, using a contrastive loss such as NT-Xent:

$${\mathcal{L}}_{\mathrm{contrastive}}=-log{\displaystyle \frac{exp(\mathrm{sim}(x,x^{+})/\tau )}{{\sum }_{x^{\prime }}exp(\mathrm{sim}(x,x^{\prime })/\tau )}},$$

where $\mathrm{sim}(·,·)$ is cosine similarity and $\tau$ is a temperature hyperparameter. This objective improves clustering of semantically related reasoning paths in latent space [53]. Recent works have also explored meta-learning approaches to enable fast adaptation to new reasoning tasks with limited examples. Model-Agnostic Meta-Learning (MAML) trains a model on a distribution of reasoning tasks such that it can adapt quickly to a new task with minimal gradient steps [54]. The inner and outer loop optimization are defined respectively as:

$${\theta }_i^{\prime }=\theta -\alpha {\nabla }_{\theta }{\mathcal{L}}_{{\mathcal{T}}_i}\left(\theta \right),\theta \leftarrow \theta -\beta \sum _i{\nabla }_{\theta }{\mathcal{L}}_{{\mathcal{T}}_i}\left({\theta }_i^{\prime }\right),$$

where ${\mathcal{T}}_i$ is a task sampled from the task distribution. Figure 2 illustrates the conceptual differences between standard supervised learning, CoT supervision, and distillation-based reasoning optimization.

In conclusion, efficient reasoning in LLMs not only relies on architecture but also heavily depends on thoughtful training strategies [55]. Techniques such as stepwise supervision, distillation, RL fine-tuning, and curriculum learning contribute significantly to improving reasoning accuracy, sample efficiency, and inference speed. In the following section, we analyze the role of external retrieval and tool augmentation in enhancing reasoning efficiency.

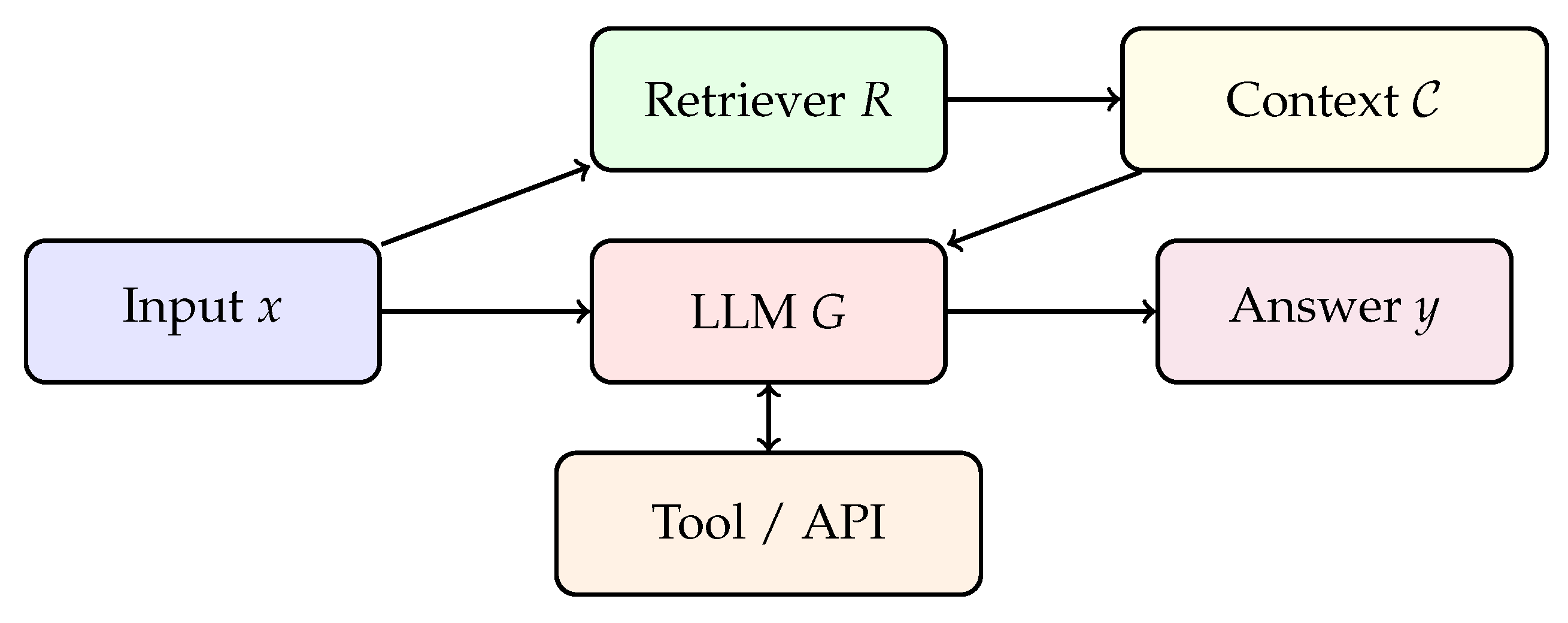
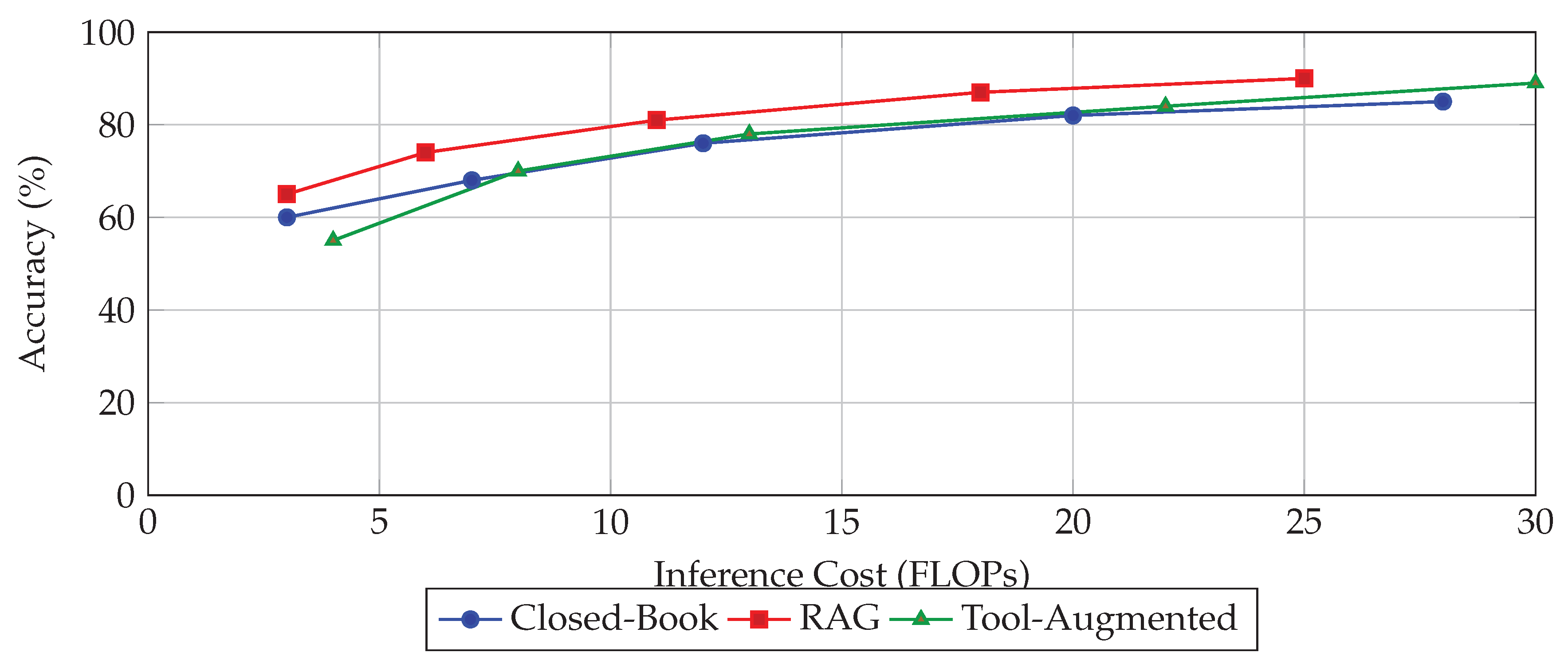
5. Retrieval-Augmented Reasoning and Tool Use

As LLMs scale in size and capability, a persistent limitation remains: the inefficiency of internalizing and processing large quantities of world knowledge within finite context windows and parameters [56]. Retrieval-augmented reasoning (RAR) offers a compelling solution by allowing LLMs to access and incorporate external information dynamically during inference. In parallel, tool-augmented reasoning enables LLMs to delegate complex sub-tasks—such as calculation, symbolic logic, or code execution—to specialized tools [57]. These strategies shift the computational burden away from internal model capacity and toward interaction with structured external systems. The retrieval-augmented framework introduces a modular paradigm comprising three main components: (1) a retriever R, which selects relevant context $\mathcal{C}\subseteq \mathcal{D}$ from a corpus $\mathcal{D}$, (2) a generator G, typically an LLM, that produces output y conditioned on input x and retrieved content $\mathcal{C}$, and (3) a scorer or ranker for refining the context [58]. Formally, the reasoning objective is redefined as:

$$y=G(x,\mathcal{C})\mathrm{where}\mathcal{C}=R(x,\mathcal{D}),$$

and R is trained or heuristically designed to optimize retrieval quality. In this setting, LLMs perform reasoning not purely from internal memory but through compositional use of retrieved facts, thereby enabling few-shot generalization with minimal additional training [34]. A key challenge in RAR is the integration of retrieved passages into the reasoning process [49]. Traditional models concatenate retrieved passages with input text, leading to inefficient use of the attention mechanism and input budget. Recent approaches like Fusion-in-Decoder (FiD) [? ] address this by encoding each retrieved document separately and fusing them at the decoding stage:

$$y=\mathrm{Decoder}(\sum _{i=1}^k\mathrm{Encoder}\left(d_i\right),x),$$

where $d_i\in \mathcal{C}$ [59]. This preserves document granularity while maintaining scalability. Tool-augmented models extend reasoning capabilities by interfacing with external APIs, calculators, code interpreters, databases, or symbolic engines [60]. These models decompose a reasoning task into a series of actions $a_t\in \mathcal{A}$, where each action invokes a tool or emits a reasoning step. Let ${\pi }_{\theta }\left(a_t\right|s_t)$ be the policy over actions given state $s_t$. The model’s goal is to maximize task reward by choosing optimal sequences of actions:

$${\mathbb{E}}_{{\pi }_{\theta }}\left[\sum _{t=1}^{T}r(s_t,a_t)\right],$$

where $r(·)$ encodes correctness, efficiency, or tool usage costs. For example, a mathematical reasoning model might first generate an equation, call a calculator tool to compute a result, and then compare or refine the output. These tool-use pipelines are often modeled as programs, with LLMs trained to generate executable code or symbolic expressions [61]. This is formalized as a program induction task: for input x, the model emits a program $p=f_{\theta }\left(x\right)$ such that

$$y=\mathrm{Exec}\left(p\right),$$

where $\mathrm{Exec}$ is a deterministic interpreter [62]. This method allows the model to offload high-precision computation or symbolic logic to external environments while focusing its capacity on planning and program generation. Hybrid retrieval+tool pipelines integrate these paradigms. For example, in WebGPT [? ], the model first retrieves documents from the web and then generates responses conditioned on those documents, sometimes invoking citation generators or ranking modules as tools [63]. This interaction creates a dynamic reasoning graph rather than a linear text completion task [64]. Similarly, Toolformer [? ] learns to invoke tools in-context during self-supervised training, resulting in implicit planning and execution capabilities embedded into the language model. Figure 3 illustrates a typical retrieval-augmented tool reasoning pipeline [65].

RAR and tool use dramatically improve both reasoning accuracy and efficiency by extending the LLM’s effective capacity beyond its parameters. However, these systems introduce new challenges in latency, tool reliability, external API access, and hallucination control [66]. Current research focuses on improving retrieval relevance through differentiable retrievers, learning tool invocation protocols through self-supervised training, and minimizing dependency chains for fast inference [67]. Overall, these methods represent a fundamental shift from monolithic reasoning toward distributed, modular computation paradigms [68]. In the next section, we discuss benchmark datasets and evaluation protocols that are essential for measuring the effectiveness and efficiency of reasoning in LLMs.

6. Benchmarks and Evaluation Protocols for Reasoning Efficiency

The proliferation of reasoning capabilities in large language models necessitates rigorous and standardized evaluation methodologies [69]. Efficient reasoning is not merely a question of accuracy but also involves considerations such as inference cost, latency, reasoning interpretability, step efficiency, and generalization across diverse domains [70]. This section surveys key benchmark datasets, evaluation metrics, and experimental protocols employed in assessing reasoning efficiency in LLMs. Benchmarks for reasoning are broadly categorized into arithmetic reasoning, symbolic logic, multi-hop question answering, mathematical problem solving, and program synthesis [71]. Table 3 summarizes several widely-used datasets, categorized by domain, complexity, and the nature of reasoning required.

A central challenge in evaluation is defining metrics that go beyond accuracy [72]. For example, in multi-step reasoning, models may produce the correct final answer through incorrect or unfaithful intermediate steps—a phenomenon known as spurious reasoning. Hence, metrics such as step accuracy, reasoning fidelity, and path consistency are introduced. Let $s=(s_1,\dots ,s_T)$ denote the reasoning steps and y the final answer. Define the total reasoning loss as:

$${\mathcal{L}}_{\mathrm{reason}}=\sum _{t=1}^T{\ell }_{\mathrm{step}}(s_t,s_t^{*})+{\ell }_{\mathrm{final}}(y,y^{*}),$$

where ${\ell }_{\mathrm{step}}$ evaluates the semantic correctness of each intermediate step. Efficiency metrics quantify resource use during inference [73]. These include:

• Inference latency (in milliseconds or FLOPs): Time or computation required to reach the answer [74].
• Token economy: Average number of generated tokens per answer, including intermediate steps.
• Step length: Average number of reasoning hops or function calls required.
• Invocation count: Number of external tool or retrieval calls made [75].
• Error locality: Position in the reasoning chain where the first error occurs.

One advanced metric is faithfulness, which measures whether the generated reasoning path truly supports the answer. Faithfulness can be estimated through logical consistency checks or automated theorem provers in symbolic settings. Let $\mathcal{P}\left(s\right)$ be the logical implications of reasoning steps s, then the faithfulness condition is:

$$\mathcal{P}\left(s\right)\vDash y\Rightarrow \mathrm{faithful}\mathrm{reasoning}citewang2025don.$$

Benchmark protocols increasingly employ multi-phase evaluation, where models are tested in both open-book (with access to retrieval or tools) and closed-book (pure internal reasoning) settings. This distinction reveals the model’s reliance on memory vs [77]. external knowledge. Furthermore, adversarial evaluation—using perturbed, counterfactual, or minimally-different inputs—is gaining traction for measuring robustness [78]. In program synthesis, execution-based accuracy is favored over string match:

$$\mathrm{ExecAcc}={\mathbb{E}}_{(x,y)}\left[{\mathbf{1}}_{\mathrm{Exec}\left(f_{\theta }\left(x\right)\right)=y}\right].$$

As shown in Figure 4, tool-augmented and retrieval-augmented models outperform closed-book models in accuracy but incur increased inference cost [80]. Efficient reasoning therefore entails careful tradeoffs across multiple dimensions, best evaluated through comprehensive benchmark suites and diverse metrics. In the next section, we will explore future directions and open challenges in building reasoning-efficient LLMs, including neuro-symbolic hybrids, continual learning, and adaptive inference strategies [81].

7. Future Directions and Open Challenges

Despite significant progress in enabling efficient reasoning in large language models, numerous open challenges remain. These stem from both theoretical and engineering limitations, as well as the growing demand for reliability, interpretability, and generalizability in real-world applications. In this section, we outline key future directions and challenges that must be addressed to realize the full potential of reasoning-augmented LLMs [82].

Neuro-Symbolic Integration

A central avenue of research is the unification of neural and symbolic reasoning [83]. While neural models exhibit impressive generalization across fuzzy and high-dimensional inputs, they often struggle with precision, consistency, and compositionality. Symbolic systems, by contrast, excel at logic, abstraction, and rigorous semantics. The integration of these paradigms seeks to leverage their complementary strengths [84]. This could take the form of:

• Embedding symbolic execution environments inside LLM inference loops [85].
• Training models to emit formal programs or logical statements as intermediate representations.
• Using structured symbolic traces as supervision signals for pretraining and finetuning [86].

The challenge lies in making symbolic interfaces differentiable or aligning them effectively with gradient-based learning objectives. One promising direction is neuro-symbolic scaffolding, where an LLM constructs a structured representation (e.g., abstract syntax tree $\mathcal{T}$), and a symbolic engine verifies or executes it:

$$y=\mathrm{Exec}\left(\mathcal{T}\right),\mathrm{where}\mathcal{T}=f_{\theta }\left(x\right).$$

Continual and Lifelong Learning for Reasoning

Current reasoning models are mostly static; once trained, they retain fixed knowledge and reasoning strategies. Lifelong learning—the ability to incorporate new reasoning patterns or tools over time without catastrophic forgetting—is largely unsolved for LLMs. Efficient lifelong reasoning requires mechanisms for:

• Dynamically updating knowledge and procedural templates.
• Memorizing, abstracting, and generalizing from novel task distributions.
• Adapting inference strategies to user feedback or task drift.

A potential solution is modular meta-learning, where the model maintains a library of reasoning modules $\left\{M_i\right\}$ and learns to reuse or fine-tune them incrementally based on incoming tasks [87]. Formally, let ${\mathcal{T}}_t$ denote task t; the objective becomes:

$$\underset{\theta }{min}\sum _{t=1}^T{\mathcal{L}}_{{\mathcal{T}}_t}(f_{\theta };\left\{M_i\right\}),$$

subject to constraints on storage, latency, and update stability [88].

Interpretable and Faithful Reasoning Chains

Interpretability is critical for high-stakes applications such as scientific discovery, healthcare, and legal reasoning [89]. While chain-of-thought prompting has made progress in exposing intermediate reasoning steps, the generated chains are often not faithful—i.e., they do not causally support the final answer. Improving interpretability requires:

• Training models on datasets with verified logical traces and proofs.
• Developing metrics for semantic faithfulness and causal attribution [90].
• Encouraging consistency between different reasoning paths that yield the same answer [91].

A promising idea is to enforce traceability constraints during decoding. For example, models can be trained to maximize the mutual information between intermediate steps s and the output y, conditioned on input x:

$$maxI(s;y\mid x)\mathrm{s}.\mathrm{t}.\mathrm{valid}(s,y).$$

Adaptive and Budget-Aware Inference

Most existing models perform reasoning using fixed-length generation and uniform computational budgets [45]. However, efficient reasoning must be adaptive—spending more resources only when necessary. This motivates dynamic computation strategies such as early exiting, adaptive sampling, or budget-constrained planning [92]. Let $\mathcal{B}$ be the total allowed budget (e.g., in FLOPs or time), the goal is:

$$\underset{s,y}{max}Pr(y\mid x,s)\mathrm{s}.\mathrm{t}.\mathrm{Cos}\mathrm{t}(s,y)\le \mathcal{B}.$$

Such models require meta-reasoning abilities—i.e., reasoning about the reasoning process—to decide whether to retrieve additional information, call tools, or terminate inference early. Incorporating utility-based decision policies, such as reinforcement learning with budget-sensitive rewards, remains an open research area.

Robustness and Adversarial Reasoning

Finally, the robustness of reasoning is a critical issue [93]. Current models are highly sensitive to input perturbations, adversarial prompts, and misleading intermediate steps [94]. Reasoning chains can be derailed by subtle errors early in the chain [95,96]. Future models must be robust to:

• Semantic paraphrasing or rephrasing of inputs.
• Adversarial distractors introduced in context.
• Noisy or unreliable retrieved or tool-generated content.

Approaches such as ensemble reasoning, redundancy via self-consistency, and verification using auxiliary models may mitigate this brittleness [97]. For example, in self-consistency decoding, a model generates K reasoning paths ${\left\{s^{\left(i\right)}\right\}}_{i=1}^K$, and aggregates the final answers via majority vote:

$$y=\mathrm{mode}\left({\left\{f\left(s^{\left(i\right)}\right)\right\}}_{i=1}^K\right),$$

where $f\left(s^{\left(i\right)}\right)$ maps reasoning chains to final predictions [98].

Toward General-Purpose Reasoning Agents

In the long term, the goal is to build general-purpose reasoning agents—models capable of solving a wide spectrum of cognitive tasks with high efficiency, correctness, and autonomy [26]. Such agents will need to integrate language understanding, formal reasoning, retrieval, tool-use, and interactive planning in a unified architecture [99]. They should be capable of formulating subgoals, using tools strategically, learning new procedures on the fly, and engaging in reflective reasoning. Achieving this vision will require innovations in architecture (e.g., modular reasoning graphs), learning algorithms (e.g., meta-RL for reasoning), training data (e.g., curated symbolic traces), and evaluation frameworks (e.g., simulated agent environments). Despite the challenges, the trajectory of research in efficient reasoning is rapidly accelerating, bringing us closer to LLMs that can not only generate fluent text, but also think with clarity, rigor, and efficiency.

8. Conclusion

The emergence of large language models as general-purpose problem solvers has revitalized interest in machine reasoning—a core component of artificial intelligence that encompasses logical inference, mathematical deduction, strategic planning, and structured decision-making. Yet, scaling reasoning capabilities in LLMs remains a formidable challenge, particularly when considering the dual imperatives of accuracy and efficiency. This survey has aimed to provide a comprehensive overview of recent progress in building efficient reasoning models for LLMs, by examining methodologies, architectural innovations, benchmark ecosystems, and open research frontiers.

We have seen that reasoning in LLMs takes multiple forms—ranging from arithmetic and symbolic logic to tool use and multi-hop natural language inference. Each of these tasks demands different forms of inductive and deductive capabilities, as well as different kinds of internal and external knowledge representations. We categorized the primary approaches to efficient reasoning into three broad classes: prompt-based reasoning (e.g., chain-of-thought and self-consistency), architecture-level enhancements (e.g., modularity, memory, and external tool integration), and training-time strategies (e.g., distillation, imitation learning, and curriculum learning). These approaches are often complementary, and when combined, they can significantly improve the sample-efficiency, latency, and faithfulness of LLM reasoning.

Nonetheless, evaluating reasoning efficiency is nontrivial. We emphasized the importance of going beyond final-answer accuracy, by incorporating step-wise fidelity, interpretability, execution correctness, and cost-aware metrics such as inference time, computation, and invocation budgets. We surveyed a variety of benchmarks—ranging from GSM8K and MATH to DROP and ProofWriter—and illustrated the tradeoffs between reasoning power and computational cost across different configurations, including closed-book inference, retrieval augmentation, and tool use.

Looking ahead, we outlined several promising research directions: neuro-symbolic integration for compositional generalization, lifelong learning frameworks for procedural acquisition, interpretable and faithful reasoning chain supervision, budget-aware dynamic inference, and robustness under adversarial and noisy environments. Perhaps the most ambitious frontier is the construction of general-purpose reasoning agents that can autonomously plan, reason, and interact with complex external environments across extended timescales.

Ultimately, efficient reasoning in LLMs is not only a matter of engineering; it is a deeply cognitive and epistemological endeavor. It requires us to ask: What does it mean for a machine to reason? How can we evaluate and trust its conclusions? And how do we ensure that the process leading to those conclusions is reliable, transparent, and robust? As models grow in size, scope, and responsibility, answering these questions will be central to aligning LLMs with human values and aspirations in science, education, governance, and beyond.