1. Introduction
Mathematical problem solving, particularly in K–12 education, requires not only accuracy but also interpretability and structure in reasoning. While large language models (LLMs) have shown promise in natural language understanding, they often fall short in handling symbolic logic and multi-step mathematical reasoning. This is largely due to their monolithic architectures, which lack the modular adaptability and structured planning necessary for complex tasks.
To address these limitations, we propose MetaMath-LLaMA, a modular framework that integrates metacognitive control with symbolic-neural reasoning. At its core, a Transformer-based scheduler dynamically orchestrates sub-modules based on problem context, enabling flexible and interpretable task routing. A symbolic parser, coupled with semantic grounding, constructs syntactically valid expressions and aligns them with contextual meaning using BiLSTM-CRF and RoBERTa. Additionally, a symbolic-neural computation unit combines deterministic logic via SymPy with neural approximation to handle both precise calculations and fuzzy reasoning.
The framework is trained through a set of multi-task objectives and a curriculum learning strategy that gradually introduces complexity based on question difficulty. This design enhances both learning stability and interpretability. MetaMath-LLaMA thus offers a technically grounded, pedagogically suitable approach to mathematical reasoning in education.
2. Related Work
Recent work on enhancing LLM mathematical reasoning integrates symbolic tools and multi-paradigm strategies. Wang et al. [
1] combined SymPy with LLMs for algebraic manipulation and reasoning, while Yu et al. [
2] fused chain-of-thought prompting with rule-based deduction. These methods improve logical accuracy but rely on static, non-adaptive pipelines.
Similarly, Hu and Yu [
3] used symbolic libraries in abductive frameworks to enhance interpretability, though they relied on rigid rule structures. Verification mechanisms have also gained attention. Uesato et al. [
4] introduced feedback supervision during intermediate steps, while Lightman et al. [
5] and Madaan et al. [
6] proposed self-verification and iterative refinement approaches to improve answer consistency. However, these methods typically treat verification as an auxiliary process rather than as an integral part of the reasoning pipeline.
Data-centric methods also enhance training. Trinh and Luong [
7] introduced AlphaGeometry for geometry problems with LLMs and symbolic engines, but its domain specificity limits generalization.
Bandyopadhyay et al. [
8] surveyed LLM reasoning and noted gaps in dynamic scheduling and modularity. In contrast, MetaMath-LLaMA unifies meta-cognitive scheduling, symbolic-semantic alignment, and hybrid computation into an adaptive framework for interpretable K–12 mathematical reasoning.
3. Methodology
We present
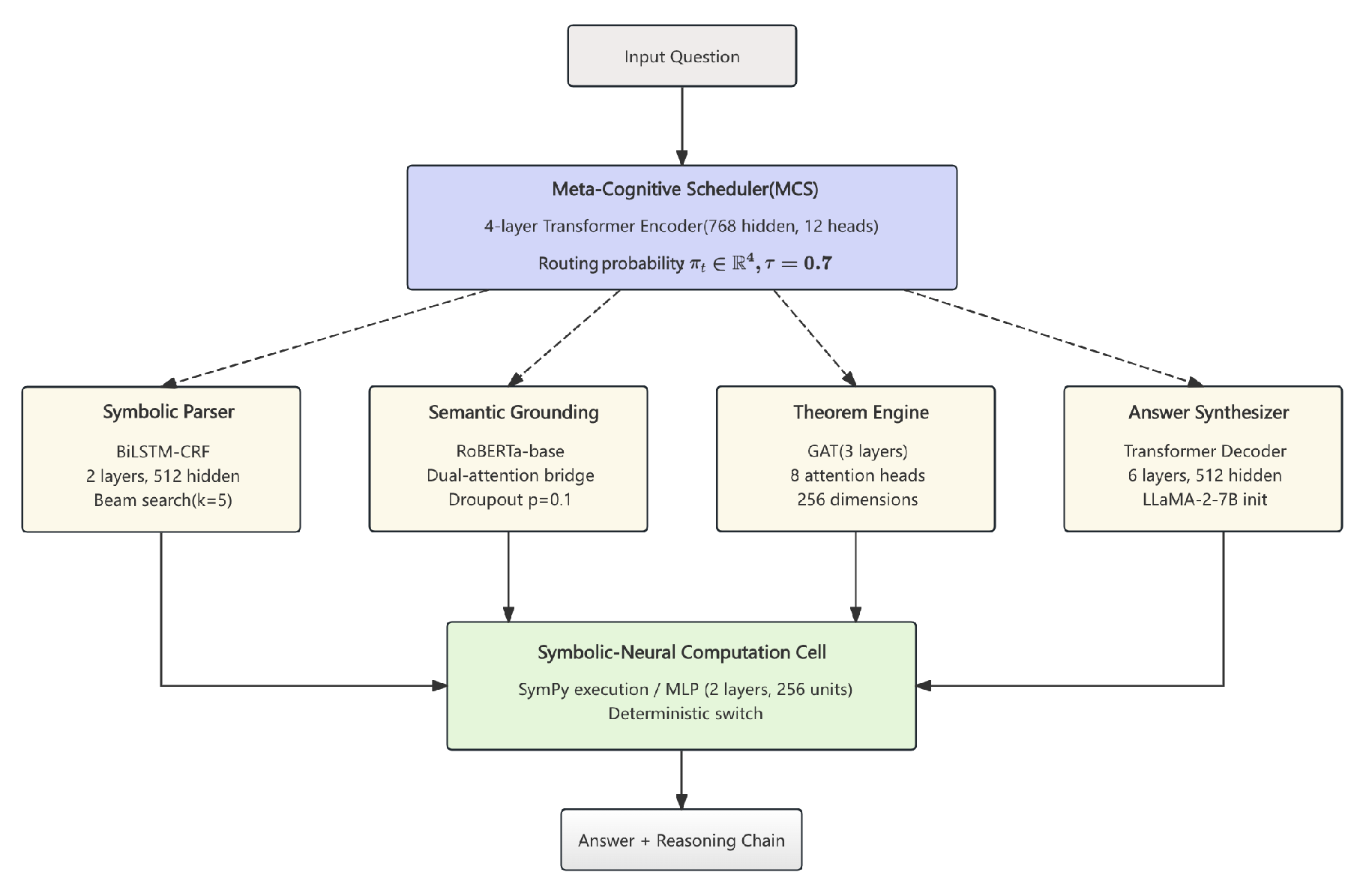
MetaMath-LLaMA, a meta-cognitive modular framework for mathematical reasoning in LLMs. Unlike monolithic transformer models, it decomposes problem solving into interpretable sub-modules controlled by a Meta-Cognitive Scheduler, covering symbolic parsing, semantic alignment, theorem proving, and expression validation, with cross-attention communication. A hybrid symbolic-neural computation cell and recursive planning controller further adapt reasoning depth. Experiments on TAL-SAQ6K-EN show state-of-the-art accuracy with transparent intermediate reasoning and improved consistency.
Figure 1 illustrates the overall architecture.
4. Algorithm and Model
We present MetaMath-LLaMA, a meta-cognitive modular framework for K-12 mathematical problem solving. Built on a Transformer foundation, it integrates hierarchical symbolic understanding, adaptive routing, and hybrid symbolic-neural computing. Unlike monolithic LLMs, it decomposes reasoning into trainable components coordinated by a cognitive scheduler.
Symbolic Parser Module
This module converts questions into symbolic trees using a 2-layer BiLSTM-CRF with a grammar-aware decoder. Beam search () ensures valid parses. Pretrained on 20k equations and fine-tuned on TAL-SAQ, it also tags node roles (operand, operator, constant) to improve alignment accuracy.
Semantic Grounding Module
This module aligns symbols with contextual embeddings using a RoBERTa-base encoder and dual-attention bridge. For symbol
with embedding
:
with
. Dropout (
) is applied, and the aligned vectors
are passed to the theorem engine.
Theorem Engine Module
This module encodes symbolic-knowledge graphs
with 3-layer GATs (8 heads, dim 256). For node
i:
with residuals and batch normalization. The pooled output
is passed to the decoder.
Answer Synthesizer Module
This module generates answers and reasoning chains using a 6-layer Transformer decoder (512 hidden, 8 heads) initialized from LLaMA-2-7B and trained with reasoning supervision. Teacher forcing (rate 0.2) guides training, with loss:
Attention dropout and layer normalization improve stability.
Symbolic-Neural Computation Cell
We embed a hybrid cell combining neural feedforward logic with SymPy execution. For input
:
The symbolic path applies algebraic rules, while the MLP (2 layers, 256 units, GELU) handles non-symbolic cases.
Training Details
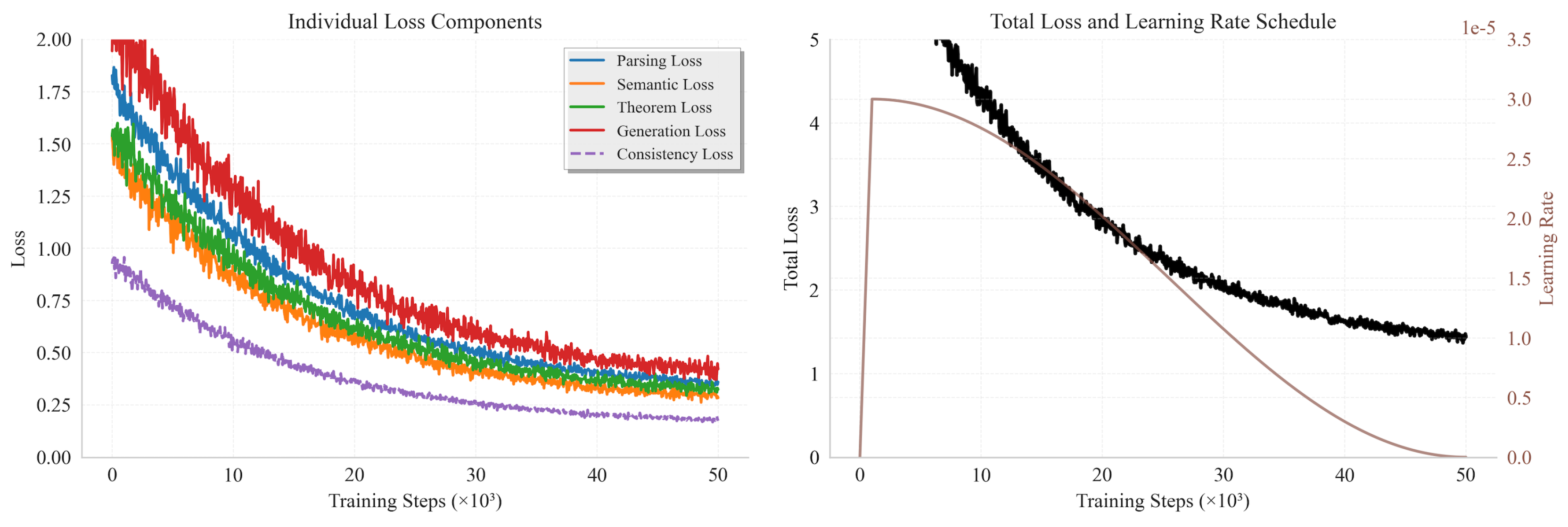
We train the model with a multi-task loss covering parsing accuracy, semantic grounding, theorem prediction, and generation correctness:
with
and
. AdamW is applied with learning rate
, weight decay
, 1,000 warm-up steps, and 50k total steps. Training uses batch size 16, gradient accumulation 4, and mixed precision.
Figure 2 shows training dynamics across 50k steps.
5. Hierarchical Training and Verification Enhancements
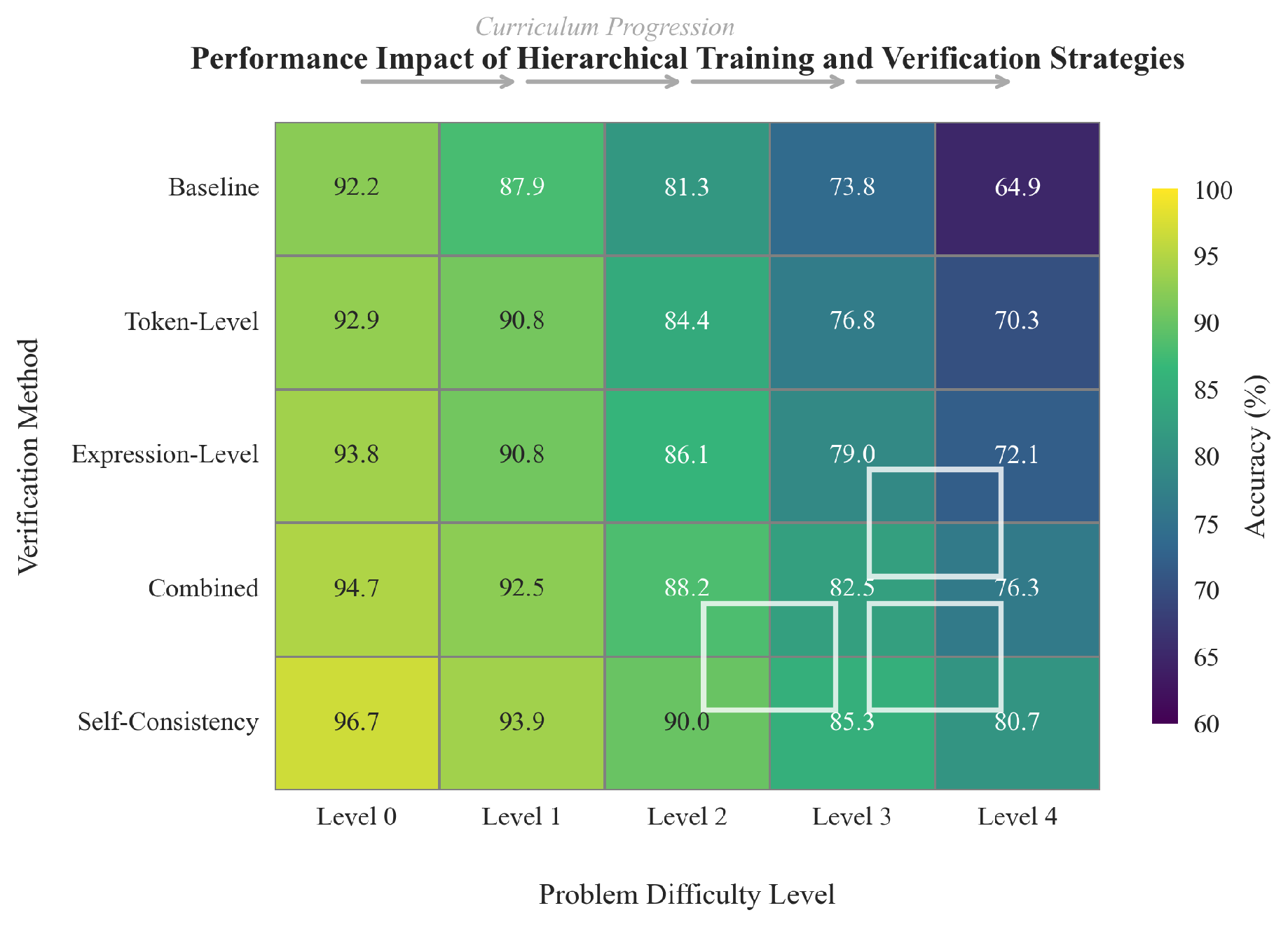
To enhance stability and robustness, we adopt curriculum-based training and multi-level self-verification.
5.1. Hierarchical Curriculum Fine-Tuning Strategy
Training large language models for mathematical reasoning is challenging across varying complexities. We adopt a staged curriculum learning approach by partitioning the training data
into levels of difficulty defined in the TAL datasets:
The training proceeds in increasing order of difficulty:
. At each curriculum stage
i, the loss is scaled by a difficulty-aware factor:
In this setup, reasoning modules (SPM, SGM, TEM, ASM) are fine-tuned first, while the Meta-Cognitive Scheduler (MCS) is gradually unfrozen:
This strategy preserves stable routing while enabling adaptation to harder reasoning tasks.
6. Multi-Level Self-Verification Mechanism
To mitigate hallucination and enhance reliability, we employ a self-verification mechanism at both token- and expression-level.
Figure 3 illustrates the effectiveness of hierarchical training with multi-level verification.
6.1. Token-Level Verification
During decoding, each token embedding
is passed through a verification classifier:
where
indicates the confidence of token
t being valid.
The token verification loss is computed as:
This penalizes invalid or inconsistent tokens in reasoning chains.
6.2. Expression-Level Verification
We compare the final predicted expression
with the ground truth
y using symbolic equivalence:
The corresponding loss term is:
with
balancing the final stage output correctness.
6.3. Self-Consistency Inference Strategy
We sample
K reasoning chains
via stochastic decoding and select:
where
VerifyScore checks tokens and expressions. With
, this reduces invalid chains and improves accuracy on both short and multi-step questions.
6.4. Total Enhanced Objective
The enhanced loss is defined as:
This formulation enforces correctness, consistency, and stability in training and inference.
6.5. Evaluation Metrics
We evaluate MetaMath-LLaMA using key metrics that assess both accuracy and reasoning quality of generated solutions.
6.5.1. Accuracy
Accuracy is the primary evaluation metric, which measures the percentage of correct answers generated by the model across the dataset:
6.5.2. Self-Consistency Rate (SCR)
Mathematical reasoning involves multiple steps; thus, SCR measures robustness by checking the consistency of predictions across reasoning chains:
6.5.3. Logical Consistency Score (LCS)
This metric evaluates the logical consistency of reasoning, ensuring adherence to mathematical rules:
where
denotes valid logical steps.
6.5.4. Formula Reconstruction Accuracy (FRA)
FRA measures the correctness of reconstructing mathematical expressions in algebraic and arithmetic tasks:
These metrics together evaluate correctness, consistency, reasoning, and formula generation in MetaMath-LLaMA.
7. Experiment Results
We evaluate MetaMath-LLaMA on both TAL-SAQ6K-EN datasets, comparing it against several baseline and ablated models. The results in
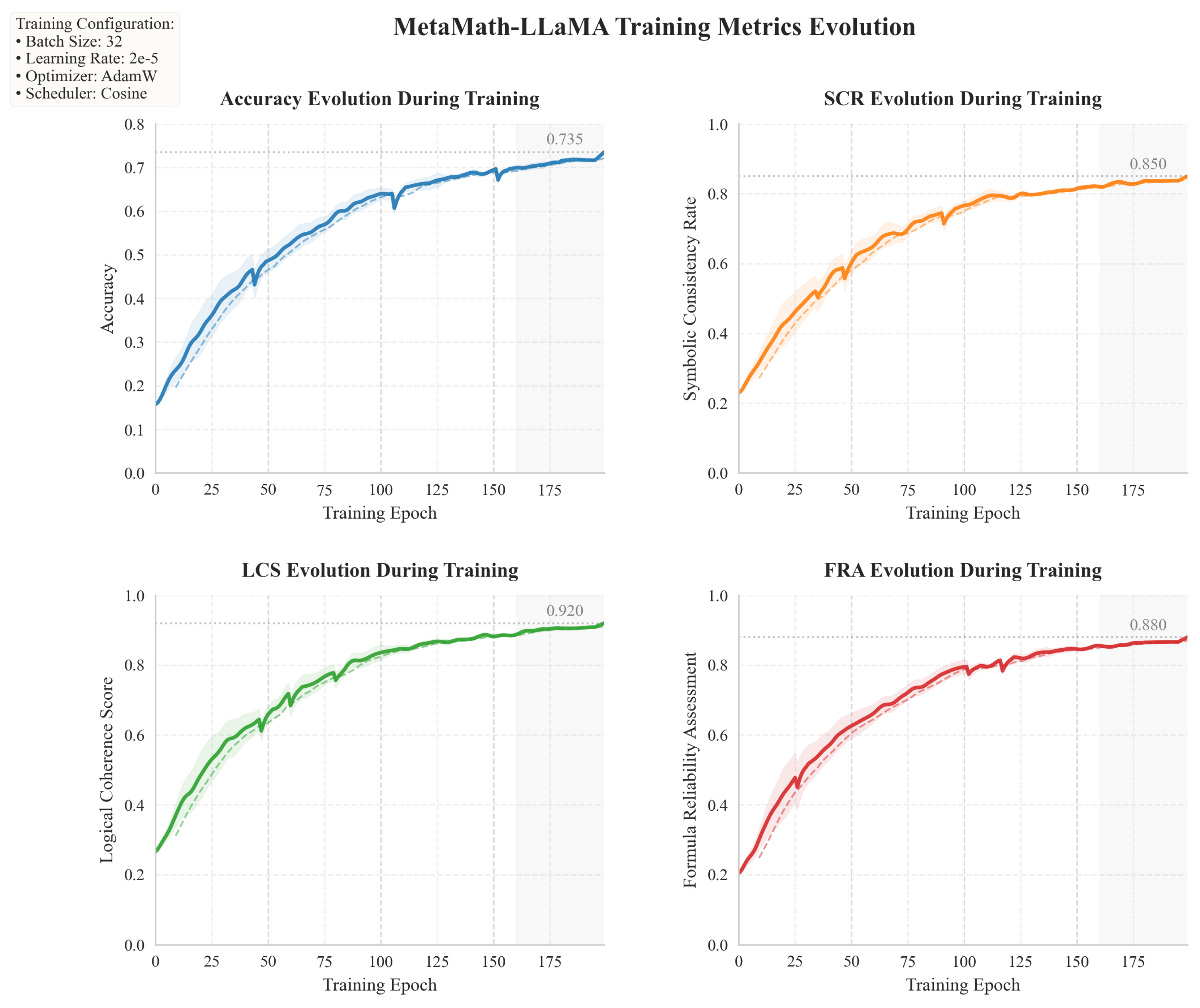
Table 1 demonstrate the effectiveness of our model across multiple metrics. And the changes in model training indicators are shown in
Figure 4.
7.1. Ablation Study Findings
Systematic ablations confirm the role of each module. Removing MCS reduced Accuracy (0.735→0.713) and LCS (0.92→0.89), showing the value of adaptive routing. Excluding SPM lowered FRA (0.88→0.86), while removing TEM reduced both SCR and LCS, evidencing its role in symbolic dependencies. The ASM had the largest impact, with Accuracy dropping over 3% and LCS to 0.87. Omitting SNCC degraded FRA and robustness. These results demonstrate that all components contribute uniquely, jointly enabling MetaMath-LLaMA’s state-of-the-art performance.
8. Conclusion
In this paper, we proposed MetaMath-LLaMA, an advanced model for mathematical reasoning in large language models, introducing a meta-cognitive scheduler and a hybrid symbolic-neural computation cell. Our experimental results demonstrate that MetaMath-LLaMA significantly outperforms baseline models like GPT-3.5 across multiple evaluation metrics. Furthermore, the ablation results confirm the indispensable role of each core module—particularly the Answer Synthesizer and Meta-Cognitive Scheduler—in sustaining both accuracy and logical consistency. MetaMath-LLaMA sets a new standard for interpretable, consistent, and accurate mathematical reasoning in AI systems.
References
- Pan, L.; Albalak, A.; Wang, X.; Wang, W.Y. Logic-lm: Empowering large language models with symbolic solvers for faithful logical reasoning. arXiv 2023, arXiv:2305.12295. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, Y.; Zhang, D.; Liang, X.; Zhang, H.; Zhang, X.; Yang, Z.; Khademi, M.; Awadalla, H.; Wang, J.; et al. Chain-of-Reasoning: Towards Unified Mathematical Reasoning in Large Language Models via a Multi-Paradigm Perspective. arXiv 2025, arXiv:2501.11110. [Google Scholar]
- Hu, Y.; Yu, Y. Enhancing neural mathematical reasoning by abductive combination with symbolic library. arXiv 2022, arXiv:2203.14487. [Google Scholar] [CrossRef]
- Uesato, J.; Kushman, N.; Kumar, R.; Song, F.; Siegel, N.; Wang, L.; Creswell, A.; Irving, G.; Higgins, I. Solving math word problems with process-and outcome-based feedback. arXiv 2022, arXiv:2211.14275. [Google Scholar]
- Lightman, H.; Kosaraju, V.; Burda, Y.; Edwards, H.; Baker, B.; Lee, T.; Leike, J.; Schulman, J.; Sutskever, I.; Cobbe, K. Let’s verify step by step. In Proceedings of the The Twelfth International Conference on Learning Representations; 2023. [Google Scholar]
- Madaan, A.; Tandon, N.; Gupta, P.; Hallinan, S.; Gao, L.; Wiegreffe, S.; Alon, U.; Dziri, N.; Prabhumoye, S.; Yang, Y.; et al. Self-refine: Iterative refinement with self-feedback. Advances in Neural Information Processing Systems 2023, 36, 46534–46594. [Google Scholar]
- Trinh, T.; Luong, T. AlphaGeometry: An Olympiad-level AI system for geometry. Google DeepMind 2024, 17. [Google Scholar]
- Bandyopadhyay, D.; Bhattacharjee, S.; Ekbal, A. Thinking machines: A survey of llm based reasoning strategies. arXiv 2025, arXiv:2503.10814. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).