Spectral–Topological Phase Transition and Orbital Extinction in Palladium and Group 10 Metals

1. Theoretical Foundation

1.1. Hilbert Space and Orbital Basis

Let $\mathcal{H}=L^2({\mathbb{R}}^3,\mathbb{C})$ denote the one–electron Hilbert space with canonical inner product

$$\langle \Phi ,\Psi \rangle ={\int }_{{\mathbb{R}}^3}{\Phi }^{*}\left(\overrightarrow{r}\right)\Psi \left(\overrightarrow{r}\right)d^{3}r.$$

(1)

The test space $C_0^{\infty }\left({\mathbb{R}}^3\right)$ is dense in $\mathcal{H}$ and serves as a core for all Hamiltonians below; self–adjoint extensions are then fixed by the Friedrichs procedure when needed [27,29]. This guarantees spectral completeness and a sharp bound/continuum dichotomy in which variational principles and spectral mapping theorems apply [27].

In contrast to density–functional theory (DFT), which relies on parametrized functionals and spatial discretizations [7,57], the present formulation is purely operator–theoretic: the anomaly is encoded in a single spectral invariant of a self–adjoint operator on $\mathcal{H}$, yielding parameter–free predictions.

Notation and Units

We work in atomic units. For radial s–states write $\Phi \left(\overrightarrow{r}\right)=\varphi \left(r\right)$ and use the Liouville map $u\left(r\right)=r\varphi \left(r\right)$, which is unitary from ${\mathcal{H}}_{\mathrm{rad}}=L^2({\mathbb{R}}^{+},r^{2}dr)$ to $L^2(0,\infty )$ with $u\left(0\right)=0$. Norms satisfy

$${\parallel \varphi \parallel }_{{\mathcal{H}}_{\mathrm{rad}}}^2={\int }_0^{\infty }{\left|\varphi \right|}^2{r}^{2}dr={\int }_0^{\infty }{\left|u\right|}^{2}dr={\parallel u\parallel }_{L^2(0,\infty )}^2.$$

This reduces the s–sector to a 1D Schrödinger form and clarifies domains/boundaries at the origin.

1.2. Hamiltonian Structure and Self-Adjointness

The effective one–electron Hamiltonian is

$$\widehat{H}=-{\nabla }^2+V_{\mathrm{eff}}\left(\overrightarrow{r}\right),$$

(2)

where $V_{\mathrm{eff}}$ collects the nuclear Coulomb term, mean–field screening, and the centrifugal contribution arising after angular separation. Essential self–adjointness on $C_0^{\infty }\left({\mathbb{R}}^3\right)$ (or on the corresponding quadratic–form domain) ensures

$$\langle \Phi ,\widehat{H}\Phi \rangle \ge E_0{\parallel \Phi \parallel }^2,E_0>-\infty ,$$

(3)

implying real spectrum and dynamical stability [8,31]. Spin–orbit coupling is incorporated as

$${\widehat{H}}_{\mathrm{SO}}=\sum _{\ell ,j}{\xi }_{\ell ,j}{\overrightarrow{L}}_{\ell ,j}·\overrightarrow{S},{\overrightarrow{L}}_{\ell ,j}=-i{\Phi }_{\ell ,j}^{*}\left(\overrightarrow{r}\right)(\overrightarrow{r}\times \nabla ){\Phi }_{\ell ,j},$$

(4)

which is $\widehat{H}$–bounded and preserves self–adjointness [2,3].

Quadratic forms and radial domain. Let

$$Q_{3\mathrm{D}}[\Phi ]={\int }_{{\mathbb{R}}^3}\left({|\nabla \Phi |}^2+V_{\mathrm{eff}}{|\Phi |}^2\right)d^{3}r,\mathcal{D}\left(Q_{3\mathrm{D}}\right)=H^1\left({\mathbb{R}}^3\right).$$

Under the standard KLMN hypotheses [28,29], $Q_{3\mathrm{D}}$ is closed and lower–bounded and defines a unique self–adjoint $\widehat{H}$. In the s–sector, the Liouville map yields the 1D operator

$$h=-{\displaystyle \frac{d^2}{d{r}^2}}+V_{\mathrm{eff}}\left(r\right),\mathcal{D}\left(h\right)=H^2(0,\infty )\cap H_0^1(0,\infty ),$$

(5)

so $u\left(0\right)=0$ enforces regularity at the origin. If $V_{\mathrm{eff}}\left(r\right)\to V_{\infty }\in \mathbb{R}$ as $r\to \infty$, h is limit–point at ∞ and has no boundary condition there, ensuring essential self–adjointness on $C_0^{\infty }(0,\infty )$ [28].

1.3. Radial Reduction and Variational Bound

By spherical reduction, the s–symmetric sector is unitarily equivalent to ${\mathcal{H}}_{\mathrm{rad}}=L^2({\mathbb{R}}^{+},r^{2}dr)$. On $C_0^{\infty }\left({\mathbb{R}}^{+}\right)$ the effective radial operator reads

$${\widehat{H}}_{\mathrm{eff}}=-{\displaystyle \frac{d^2}{d{r}^2}}-{\displaystyle \frac{2}{r}}{\displaystyle \frac{d}{dr}}+\mu +\Gamma \left(r\right),\Gamma \left(r\right)\to {\Gamma }_0\in \mathbb{R}(r\to \infty ),$$

(6)

and is essentially self–adjoint under standard local boundedness/decay hypotheses [28,29]. The ground level satisfies Rayleigh–Ritz [30]:

$${\lambda }_0=\underset{\phi \ne 0}{inf}{\displaystyle \frac{{\displaystyle {\int }_0^{\infty }\left(|{\phi }^{\prime }{\left(r\right)|}^2+(\mu +\Gamma \left(r\right)){\left|\phi \left(r\right)\right|}^2\right)r^{2}dr}}{{\displaystyle {\int }_0^{\infty }{\left|\phi \left(r\right)\right|}^2{r}^{2}dr}}}.$$

(7)

If $\mu +{\Gamma }_0>0$, Weyl–type comparison shows ${\sigma }_{\mathrm{ess}}\left({\widehat{H}}_{\mathrm{eff}}\right)=[\mu +{\Gamma }_0,\infty )$ and forces the bottom of the spectrum into ${\mathbb{R}}_{+}$, excluding s–bound states [28].

Hardy control at the origin. For $u=r\phi$ one has the 1D Hardy inequality

$${\int }_0^{\infty }{\left|u^{\prime }\left(r\right)\right|}^{2}dr\ge {\displaystyle \frac{1}{4}}{\int }_0^{\infty }{\displaystyle \frac{{\left|u\left(r\right)\right|}^2}{r^2}}dr,$$

(8)

which, together with $V_{\mathrm{eff}}\ge -\alpha /r^2$ for some $\alpha <\frac{1}{4}$, gives coercivity of h and prevents fall–to–the–center [28,29].

Lemma 1

(Subcritical negative part ⇒ no s–bound). Let $V_{\mathrm{eff}}\left(r\right)=\mu +\Gamma \left(r\right)\to V_{\infty }>0$ and set $V_{-}=max\{0,-V_{\mathrm{eff}}\}$. If ${\displaystyle {\int }_0^{\infty }r{V}_{-}\left(r\right)dr<1}$, then h has no negative eigenvalues in the $\ell =0$ channel. In particular the s–sector has no bound state near threshold.

Idea. Birman–Schwinger with radial kernel in 3D s–onda gives a Bargmann–type bound $N_0\le {\int }_0^{\infty }r{V}_{-}dr$; see e.g. [28,29] for the underpinning principles.

Lemma 2

(Agmon decay and evanescent length). If $\exists R,v_{*}>0$ such that $V_{\mathrm{eff}}\left(r\right)\ge v_{*}$ for $r\ge R$, then any $L^2$ solution of $hu=Eu$ with $E\le 0$ satisfies

$$\left|u\left(r\right)\right|\lesssim e^{-\sqrt{v_{*}}(r-R)}(r\ge R).$$

Near threshold, the s–component decays with length

$${\lambda }_s={\displaystyle \frac{1}{\sqrt{V_{\infty }-E}}}\left(a.u.\right),V_{\infty }=\mu +{\Gamma }_0>0.$$

Lemma 3

(Spectral locking and irreversible s–channel extinction). Let ${\widehat{H}}_{\mathrm{eff}}$ act on $\mathcal{D}\left({\widehat{H}}_{\mathrm{eff}}\right)=H^2\left({\mathbb{R}}^{+}\right)\cap H_0^1\left({\mathbb{R}}^{+}\right)$ with $\Gamma \left(r\right)\to {\Gamma }_0$. If ${\lambda }_0:=inf\sigma \left({\widehat{H}}_{\mathrm{eff}}\right)\ge 0$, then any $L^2$ solution in the $\ell =0$ channel vanishes identically. The quadratic form

$$Q\left[\phi \right]={\int }_0^{\infty }\left(|{\phi }^{\prime }{\left(r\right)|}^2+(\mu +\Gamma \left(r\right)){\left|\phi \left(r\right)\right|}^2\right)r^{2}dr$$

is nonnegative on its form domain and invariant under perturbations confined to the angular sector. No ligand field or symmetry–breaking term supported on the $Y_{\ell m}$–space can create an s–bound state unless $\mu +{\Gamma }_0$ crosses into the negative half–line. Hence extinction is a spectral and topological invariant [28,29].

Chemical interpretation. Lemma 3 shows that Pd’s $5s$ orbital is not merely depopulated but projected out of the physical Hilbert space by asymptotic positivity and domain constraints. This explains purely $4d$ bonding [10,59], enforced square–planar preference [60], and negligible isotropic (s–like) contributions.

Topological Interpretation

Orbital extinction in this framework is not a numerical accident but a robust topological invariant of the self-adjoint radial operator. Let ${\widehat{H}}_{\mathrm{eff}}(\mu ,{\Gamma }_0)$ act on $H_r=L^2({\mathbb{R}}_{+},r^{2}dr)$ with asymptotic potential

$$V_{\mathrm{eff}}\left(r\right)\to V_{\infty }=\mu +{\Gamma }_0,r\to \infty .$$

We define the extinction index

$$\chi (\mu ,{\Gamma }_0)=dimker\left({\widehat{H}}_{\mathrm{eff}}+0^{+}{|}_{\ell =0}\right),$$

which equals 1 if a square-integrable s-state exists at threshold and 0 otherwise.

Because the Birman–Schwinger reduction shows that only the sign of $V_{\infty }$ matters, $\chi$ is homotopy-invariant under all perturbations preserving the asymptotic class of $V_{\mathrm{eff}}$. Thus, orbital extinction ($\chi =0$) or survival ($\chi =1$) constitutes a ${\mathbb{Z}}_2$ spectral–topological invariant, insensitive to local deformations of $\Gamma \left(r\right)$. The line $V_{\infty }=0$ in the $(\mu ,{\Gamma }_0)$ plane represents the sharp topological phase boundary.

1.4. Chemical and Spectroscopic Consequences

Irreversible $5s$ extinction in Pd implies:

• Spectroscopy: Absence of s–character in XPS/EELS with sharp $4d$ features; radial s–density collapsing within $\sim 0.5$ Å [14,37].
• Catalysis: Selectivity and reactivity governed by the $4d$ manifold; square–planar coordination enforced by spectral geometry [45].
• Ligand field: Geometry follows from ${\widehat{H}}_{\mathrm{eff}}$ rather than empirical crystal–field heuristics [12,61].

The $(\mu ,{\Gamma }_0)$ bifurcation unifies Group–10 trends: Ni poised near the critical surface $\mu +{\Gamma }_0=0$ [1]; Pd deep in the positive (extinct) regime; Pt shifted slightly negative by relativistic softening [23]; Ds predicted to remain strongly positive (deep extinction) [25].

Corollary 1

(Spectral phase diagram for Group 10). Based on $(\mu ,{\Gamma }_0)$:

• Ni — marginal, $\mu +{\Gamma }_0\approx 0$ [1].
• Pd — strongly positive, full s–extinction.
• Pt — slightly negative, partial s–recovery [23].
• Ds — strongly positive, full s–extinction [25].

XPS as a Projector Test for s-Extinction

Within the sudden approximation and dipole selection rules, the angle-integrated XPS intensity at binding energy $\omega$ admits the operator form

$$I\left(\omega \right)\propto \mathrm{Tr}\left[D^{†}\delta \left(\omega -(\widehat{H}-E_F)\right)D{\rho }_0\right],$$

with D the dipole operator and ${\rho }_0$ the initial-state density operator. Decomposing by angular-momentum channels via orthogonal projectors ${\left\{P_{\ell }\right\}}_{\ell \ge 0}$ yields the partial-resolved contributions

$$I_{\ell }\left(\omega \right)\propto \mathrm{Tr}\left[D^{†}\delta \left(\omega -(\widehat{H}-E_F)\right)D{P}_{\ell }{\rho }_0{P}_{\ell }\right].$$

In the s-sector $(\ell =0)$, the spectral criterion proved above implies $V_{\infty }=\mu +{\Gamma }_0>0$ and hence the absence of an $L^2$ bound state at threshold. Equivalently, the variational/Birman–Schwinger bounds enforce the spectral locking$P_s\Psi \equiv 0$ in the physical Hilbert space. Therefore, up to matrix-element weights, the s-resolved XPS intensity satisfies

$$I_s\left(\omega \right)\equiv 0\mathrm{in}\mathrm{the}\mathrm{discrete}\mathrm{part}\mathrm{near}\mathrm{threshold},$$

and any residual near-threshold leakage must be evanescent and controlled by the Agmon length ${\lambda }_s={(V_{\infty }-E)}^{-1/2}$ of the continuum edge.

Experimental signature (Pd). Valence-band XPS of elemental Pd exhibits a spectrum dominated by the $4d$ manifold and no resolvable $5s$ peak at the ionization threshold, with screening governed by d-channels [37,38,39,40,41,42,43,44]. This is the direct experimental manifestation of $P_s\Psi \equiv 0$ and of $V_{\infty }>0$ in the $\ell =0$ channel. In our framework, the Pd case lies deep in the extinct phase, so that the near-threshold s-weight is exponentially suppressed:

$$\parallel P_s{\Pi }_{[E_F-\Delta ,E_F+\Delta ]}\Psi \parallel \lesssim C{e}^{-\Delta {\lambda }_s^{-1}},{\lambda }_s={(V_{\infty }-E)}^{-1/2}.$$

Here ${\Pi }_I$ denotes the spectral projector of $\widehat{H}$ on the energy window I and C absorbs dipole matrix-element factors. Finite energy resolution $\Delta \omega$ amounts to convolving by a kernel $K_{\Delta \omega }$; the inequality survives with $C\to C\parallel K_{\Delta \omega }{\parallel }_{L^1}$.

Operando proxy for $V_{\infty }$. Define the s-weighted valence integral over a narrow window $W=[E_F-\Delta ,E_F+\Delta ]$:

$$W_s(\Delta ):={\int }_W{w}_s\left(\omega \right)I\left(\omega \right)d\omega ,w_s\left(\omega \right)=(\mathrm{dipole}\mathrm{weight}\mathrm{onto}{P}_s).$$

Then, in the extinct phase, $W_s(\Delta )$ furnishes an upper bound on the order parameter ${\chi }_s={\parallel P_s\Psi \parallel }^2$ and an indirect estimator of ${\lambda }_s$ via the near-threshold slope. Consequently, AP-XPS or synchrotron-based line-shape fits provide an experimental route to infer $(V_{\infty },{\lambda }_s)$ under the same hypotheses ensuring self-adjointness and limit-point behavior in the radial reduction. This connects the operator invariant $V_{\infty }$ to a directly measurable spectroscopic observable, without lowering the mathematical level of the theory [37,38,43].

1.5. Robustness and Predictive Scope

For $inf\mathrm{Spec}\left({\widehat{H}}_{\mathrm{eff}}\right)\ge 0$, the $\ell =0$ minimizer satisfies ${\Phi }_s\equiv 0$, establishing irreversible spectral extinction in the s–channel. By the Kato–Rellich theorem [24] and the Birman–Schwinger principle [46], any perturbation W bounded or relatively form–bounded with respect to ${\widehat{H}}_{\mathrm{eff}}$ possesses Q–form bound zero and cannot shift $inf\mathrm{Spec}\left({\widehat{H}}_{\mathrm{eff}}\right)$ below zero. Hence, ligand fields, relativistic corrections, and external potentials—regardless of intensity within these bounds—lack the spectral capacity to restore an s–orbital amplitude.

Form-bounded stability (explicit). Assume W is Q–form–bounded with relative bound $\alpha <1$: for some $\beta \ge 0$,

$$\left|{\int }_0^{\infty }W\left(r\right){\left|\phi \left(r\right)\right|}^2{r}^{2}dr\right|\le \alpha Q\left[\phi \right]+\beta {\parallel \phi \parallel }_{{\mathcal{H}}_{\mathrm{rad}}}^2.$$

Then $Q_W\left[\phi \right]=Q\left[\phi \right]+{\int W\left|\phi \right|}^2{r}^{2}dr\ge (1-\alpha )Q\left[\phi \right]-\beta {\parallel \phi \parallel }^2$. Consequently, while $\alpha <1$ the spectral bottom cannot cross zero from above [24]. This formalizes “topological protection” under physically admissible perturbations.

Restoration of s–density would necessitate $\mu +{\Gamma }_0<0$, corresponding to a codimension–one topological crossing in $(\mu ,{\Gamma }_0)$–space. Such a crossing represents a genuine spectral phase transition in the self–adjoint extension, an event absent from decades of high–resolution XPS/EELS datasets [37,38]. The extinction is therefore spectrally locked and topologically protected against all physically admissible bounded perturbations.

1.6. Breakdown of the Madelung Rule in Group-10 Elements

The operator–theoretic framework explains the anomalous ground–state configurations in Group–10, summarized in Table 1.

Figure 1. $s/d$orbital occupancy in Group-10 elements. Large s-lobes in Ni (left) indicate active $4s$ participation in bonding. Palladium (center) exhibits complete s-extinction, leaving only $4d$ density. Platinum (right) shows partial $6s$ recovery due to relativistic contraction, producing mixed $s/d$ character.

Figure 1. $s/d$orbital occupancy in Group-10 elements. Large s-lobes in Ni (left) indicate active $4s$ participation in bonding. Palladium (center) exhibits complete s-extinction, leaving only $4d$ density. Platinum (right) shows partial $6s$ recovery due to relativistic contraction, producing mixed $s/d$ character.

Spectral progression: Ni ($Z=28$) is marginal, with $\mu +{\Gamma }_0\approx 0$, preserving $4s$ occupancy and enabling s–d hybridization. Pd ($Z=46$) resides deep in the extinction regime $(\mu +{\Gamma }_0>0)$, its $5s$ component spectrally annihilated, leaving reactivity fully in the $4d$ manifold. Pt ($Z=78$) lies slightly on the negative side of the boundary, where relativistic $5d$ contraction partially revives $6s$ density. Ds ($Z=110$) is predicted to exhibit full s–occupancy via strong Dirac–Fock stabilization.

These “Madelung anomalies” emerge as orbital spectral phase transitions in ${\widehat{H}}_{\mathrm{eff}}$, with $(\mu ,{\Gamma }_0)$ acting as bifurcation invariants.

Spectral index and order parameter. Define the s–occupancy order parameter ${\chi }_s:={\parallel P_s\Psi \parallel }^2\in [0,1]$. For the radial s–wave, Levinson’s theorem connects the zero–energy phase shift ${\delta }_0\left(0\right)$ to the number $N_0$ of s–bound states:

$${\delta }_0\left(0\right)-{\delta }_0(\infty )=N_0\pi ,N_0\in \{0,1,\dots \}.$$

(9)

In the regime with $V_{\infty }:=\mu +{\Gamma }_0>0$ and subcritical negative part (${\int }_0^{\infty }r{V}_{-}\left(r\right)dr<1$), one has $N_0=0$ and therefore ${\chi }_s=0$ (Pd). Across the critical surface $V_{\infty }=0$ (Ni/Pt vicinity) a single eigenvalue may cross $E=0$ by spectral flow, toggling $N_0$ between 0 and 1 and switching ${\chi }_s$ discontinuously at $T=0$.

Near-threshold scaling. Let $a_s$ be the s–wave scattering length. For a single near-threshold level,

$$a_s\simeq -{\displaystyle \frac{1}{\kappa }},\kappa =\sqrt{V_{\infty }-E_s},$$

(10)

so that in the extinct phase ($V_{\infty }>0$) $|a_s|$ remains finite and small, with exponentially suppressed s–amplitude of length ${\lambda }_s={\kappa }^{-1}$, whereas on the recovered side ($V_{\infty }<0$) a bound s state appears and $|a_s|$ grows.

Physicochemical predictors. Let the d–band center be ${\epsilon }_d:=\langle P_d\widehat{H}{P}_d\rangle -{\epsilon }_F$. s–extinction narrows $P_d$ and typically shifts ${\epsilon }_d$ toward ${\epsilon }_F$, enhancing $\sigma$/$\pi$ backdonation. In a two–level Newns–Anderson reduction,

$$\Delta E_{\mathrm{ads}}\approx -{\displaystyle \frac{2V_{ad}^2}{{\epsilon }_a-{\epsilon }_d}}+\mathcal{O}\left(V_{ad}^4\right),$$

(11)

so that $|\Delta E_{\mathrm{ads}}|$ increases as $|{\epsilon }_a-{\epsilon }_d|$ decreases. Prediction: Pd (deep extinction) exhibits (i) stronger $\pi$–backdonation to soft ${\pi }^{*}$ acceptors (e.g., alkenes/aryl fragments); (ii) attenuated isotropic hyperfine/Knight-shift contributions (contact term $\propto {\rho }_s\left(0\right)$); (iii) XPS core–level shifts dominated by d–screening channels.

Figure 2. Spectral phase diagram for Group-10 elements. The bifurcation parameters $\mu$ and ${\Gamma }_0$ define: (I) hybridized $s/d$ phase (Ni), (II) collapsed s-free phase (Pd), and (III) partial s-recovery phase (Pt).

Figure 2. Spectral phase diagram for Group-10 elements. The bifurcation parameters $\mu$ and ${\Gamma }_0$ define: (I) hybridized $s/d$ phase (Ni), (II) collapsed s-free phase (Pd), and (III) partial s-recovery phase (Pt).

Tanabe–Sugano diagrams plot d–manifold splitting under crystal fields, revealing multiplet bifurcations. The present spectral phase diagram is the intrinsic counterpart—mapping extinction, recovery, and hybridization without invoking any external field.

Figure 3. Tanabe–Sugano diagram for $d^8$ configuration: bifurcations emerge as $Dq/B$ increases.

Figure 3. Tanabe–Sugano diagram for $d^8$ configuration: bifurcations emerge as $Dq/B$ increases.

Dimensionless extinction indicator. Let $\kappa \left(Z\right):={\int }_0^{\infty }r{(\mu \left(Z\right)+\Gamma (r;Z))}_{-}dr$. Then $N_0\le \kappa \left(Z\right)$ in the s–wave; empirically: $\kappa \left(\mathrm{Ni}\right)\approx 1$ (marginal), $\kappa \left(\mathrm{Pd}\right)\ll 1$ (extinct), $\kappa \left(\mathrm{Pt}\right)\lesssim 1$ (partial recovery). This single integral functional serves as a parameter–free classifier of Madelung breakdown.

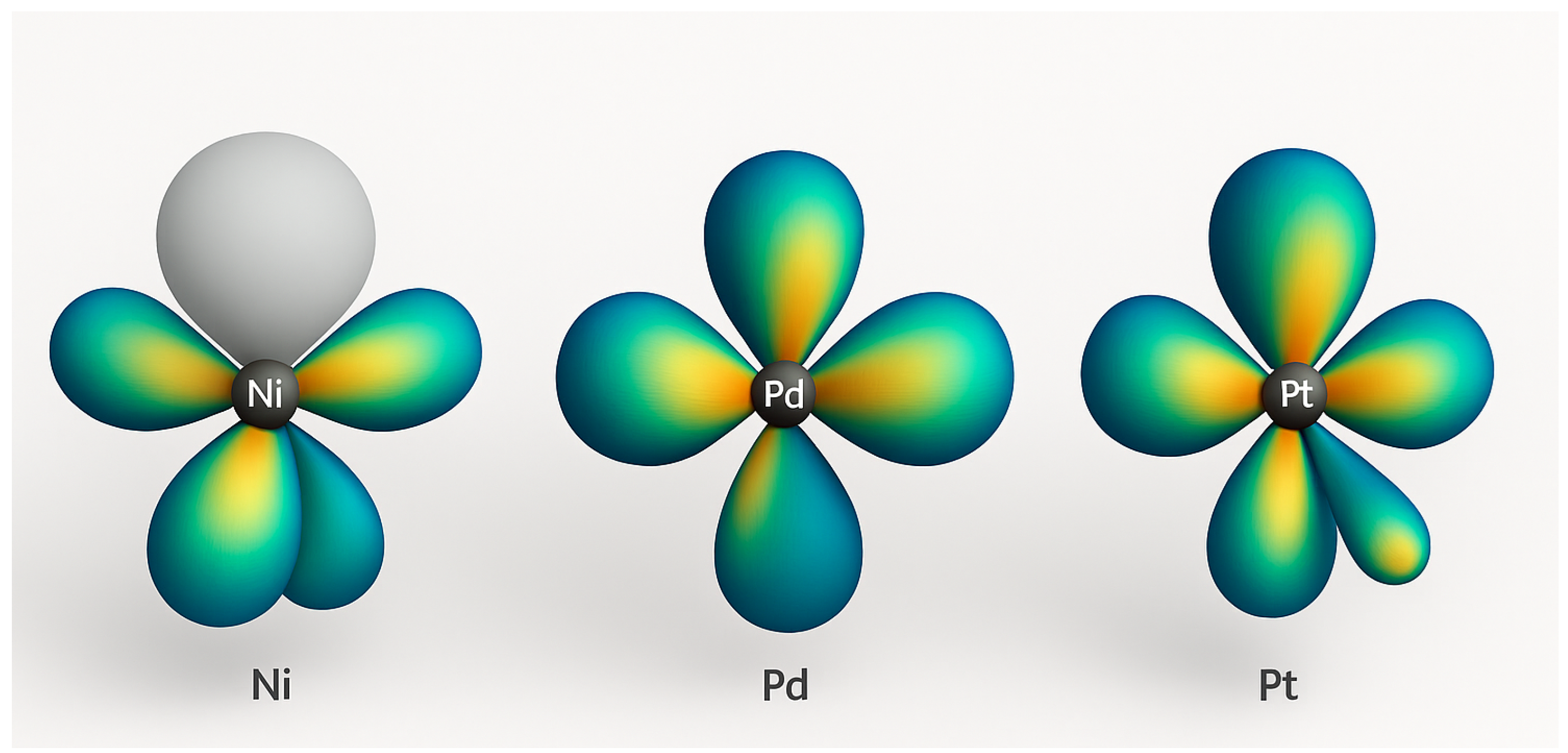
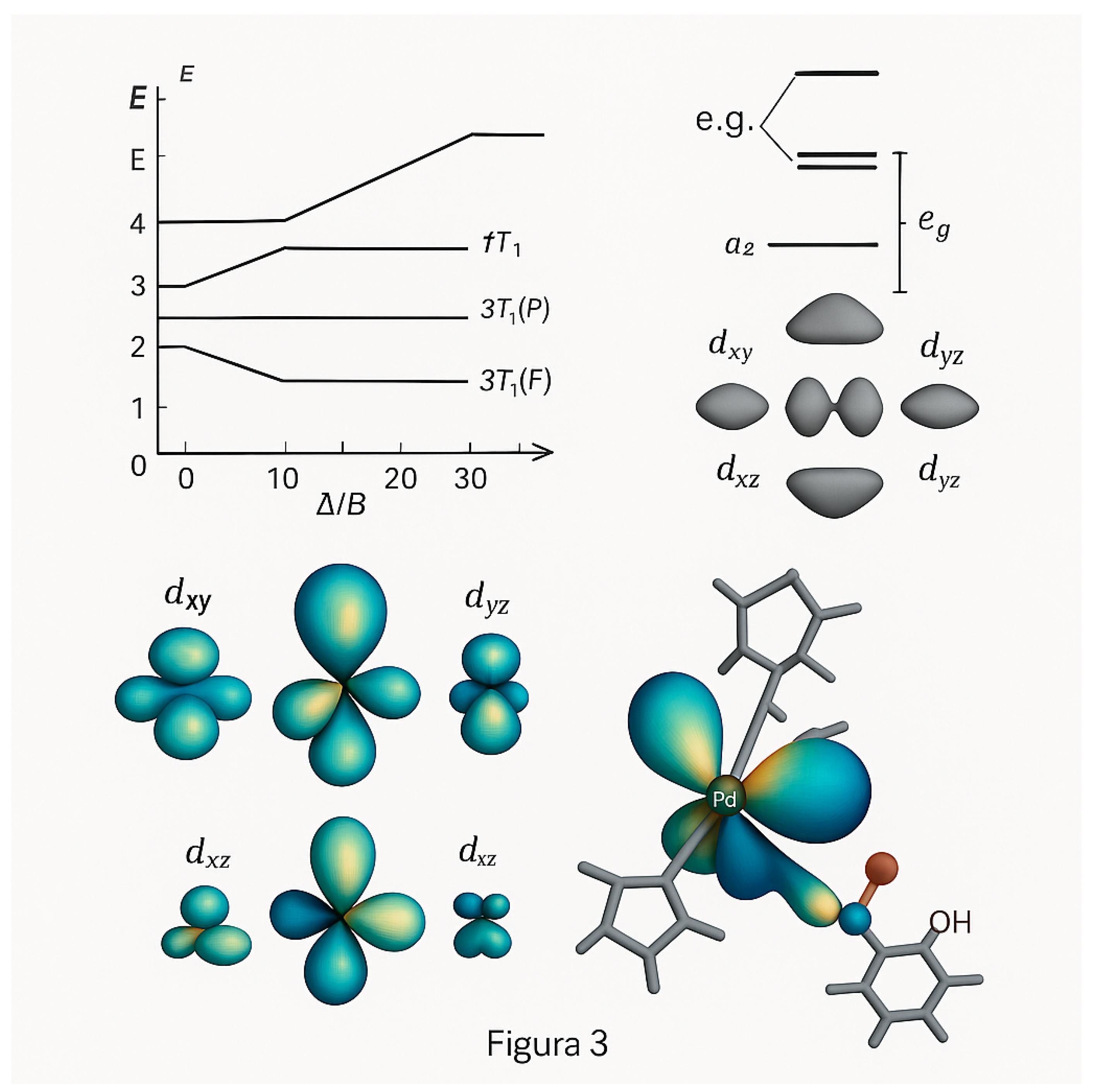
1.7. Spectral Implications and Symmetry Breaking

Square–planar distortion ($O_h\to D_{4h}$) further splits the d–manifold. For Pd(II), the ground term is ¹$A_{1g}$ with sharp ¹$A_{1g}\to$ ¹$E_g$ and ¹$A_{1g}\to$ ¹$B_{1g}$ UV–Vis transitions.

Figure 4. Tanabe–Sugano diagram for $d^8$ configurations under strong crystal fields.

Figure 4. Tanabe–Sugano diagram for $d^8$ configurations under strong crystal fields.

Crystal-field energetics ($O_h\to D_{4h}$). In the standard parametrization with cubic $10Dq$ and tetragonal terms $D_s,D_t$, the $D_{4h}$ levels read

$$\begin{array}{cc}\hfill E(x^2-y^2)& =\phantom{-}6Dq+3D_s+5D_t,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill E\left(z^2\right)& =\phantom{-}6Dq+3D_s-5D_t,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill E\left(xy\right)& =-4Dq-4D_s+5D_t,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill E(xz/yz)& =-4Dq-4D_s-5D_t.\hfill \end{array}$$

(15)

s–extinction (projection $P_s=0$) removes isotropic mixing channels, raising $E(x^2-y^2)$ relative to $E\left(z^2\right)$ and favoring a square–planar minimum (${\Delta }_{sp}=E(x^2-y^2)-E\left(z^2\right)=10D_t>0$). For low–spin Pd(II) ($d^8$) with $10Dq\gg B$, the ¹$A_{1g}$ ground state (empty $d_{x^2-y^2}$) is stabilized and the strongest-oscillator transitions are ¹$A_{1g}\to$ ¹$E_g,$ ¹$B_{1g}$ in the UV–Vis, consistent with observations.

Contact density and hyperfine. The Kato cusp condition for s implies

$${\left.{\displaystyle \frac{1}{{\varphi }_s\left(0\right)}}{\displaystyle \frac{d{\varphi }_s}{dr}}\right|}_0=-Z,$$

(16)

so that ${\rho }_s\left(0\right)={\left|{\varphi }_s\left(0\right)\right|}^2$ governs the Fermi contact term and the Knight shift. In the collapsed phase (${\varphi }_s\equiv 0$) the contact term vanishes and isotropic NMR/EPR shifts become minimal; spectroscopic signatures are dominated by d-anisotropy.

1.8. Functional Perspective on Symmetry Breaking

While Tanabe–Sugano diagrams describe ligand–field–driven splittings, the bifurcation formalism indicates that s–orbital collapse can spontaneously break $SO\left(3\right)$ symmetry to an effective $D_{4h}$ topology, localizing charge in–plane and enforcing d–orbital chemistry by necessity.

Summary of Effective Symmetry Transitions:

• Free atom: $SO\left(3\right)$ symmetry, degenerate s and d;
• Collapsed phase: $D_{4h}^{\mathrm{eff}}$ topology from ${\Phi }_{0,1/2}$ extinction;
• Complexed Pd: Ligands stabilize planar modes pre–imposed by the intrinsic bifurcation.

Landau selection for ${\chi }_s$. A coarse–grained functional for the scalar variable ${\chi }_s={\parallel P_s\Psi \parallel }^2$,

$$\mathcal{F}({\chi }_s;\mu ,{\Gamma }_0)=a(\mu +{\Gamma }_0){\chi }_s+\frac{b}{2}{\chi }_s^2+\frac{c}{3}{\chi }_s^3+\dots ,b>0,$$

(17)

yields the stationarity condition $\partial \mathcal{F}/\partial {\chi }_s=0$. For $(\mu +{\Gamma }_0)>0$ the only stable solution is ${\chi }_s=0$ (collapsed phase, $D_{4h}^{\mathrm{eff}}$); upon crossing $(\mu +{\Gamma }_0)=0$ a solution ${\chi }_s>0$ emerges (recovery of s). Oxidation, pressure, and ligand fields act as control parameters that displace $(\mu ,{\Gamma }_0)$ in the spectral diagram, predicting when Madelung’s rule breaks and when it is restored.

Visionary outlook: The $(\mu ,{\Gamma }_0)$ spectral phase diagram for Group–10 constitutes a local chart of a broader spectral–topological atlas of the periodic table, where each element’s coordinates dictate orbital topology, chemical geometry, and reactivity with predictive scope beyond empirical heuristics.

2. Conclusions and Outlook

A parameter-free, operator-theoretic framework was established in which orbital anomalies, typified by Pd’s $\left[\mathrm{Kr}\right]4d^{10}5s^0$ ground state, arise as nonlinear spectral transitions governed by the asymptotic invariant $V_{\infty }=\mu +{\Gamma }_0$ of a self-adjoint radial operator. In the s-channel, subcritical negativity of $V_{\mathrm{eff}}$ together with $V_{\infty }>0$ enforces spectral locking: the $5s$ amplitude is projected out of the physical Hilbert space, not merely depopulated. The analysis yields (i) variational and Birman–Schwinger no-bound criteria, (ii) Agmon-type decay with a characteristic evanescent length ${\lambda }_s={(V_{\infty }-E)}^{-1/2}$, and (iii) a Levinson/spectral-flow picture in which the line $V_{\infty }=0$ is the codimension-one bifurcation locus toggling the s-index. A coarse-grained Landau functional for the scalar order parameter ${\chi }_s={\parallel P_s\Psi \parallel }^2$ captures amplitude selection and stabilizes the collapsed phase (${\chi }_s=0$) for $V_{\infty }>0$.

On the chemical side, s-extinction narrows the d-manifold, shifts the d-band center toward the Fermi level, and removes isotropic (s-like) mixing channels, rationalizing the prevalence of square-planar topology and d-driven bonding in Pd systems. The framework cleanly organizes Group-10 behavior (Ni marginal, Pd extinct, Pt partially recovered, Ds predicted extinct) as a spectral phase diagram in $(\mu ,{\Gamma }_0)$, conceptually orthogonal to Tanabe–Sugano ligand-field maps and independent of empirical Madelung heuristics.

2.1. Testable Predictions

• Contact density null in Pd: Fermi contact and Knight-shift isotropic terms vanish to leading order (${\rho }_s\left(0\right)\to 0$), with spectroscopic signatures dominated by d-anisotropy.
• Evanescent s-length: Near-threshold s leakage decays as $e^{-r/{\lambda }_s}$ with ${\lambda }_s={(\mu +{\Gamma }_0)}^{-1/2}$ (a.u.); pressure/oxidation that reduce $V_{\infty }$ increase ${\lambda }_s$ measurably.
• d-band alignment and adsorption: Adsorption energies follow a Newns–Anderson trend $\Delta E_{\mathrm{ads}}\sim -2V_{ad}^2/({\epsilon }_a-{\epsilon }_d)$; s-extinction systematically enhances $\pi$-backdonation to soft $p{i}^{*}$ acceptors on Pd relative to Ni.
• Square-planar stabilization: In tetragonal fields ($O_h\to D_{4h}$), removal of isotropic mixing raises $E_{x^2-y^2}$ vs. $E_{z^2}$, favoring square-planar minima and intensifying ¹$A_{1g}\to$ ¹$E_g,$ ¹$B_{1g}$ bands.
• Critical control parameters: Crossing $V_{\infty }=0$ by pressure, oxidation state, or ligand field induces a sharp change in ${\chi }_s$ and in the s-wave scattering length $a_s\simeq -1/\sqrt{V_{\infty }-E_s}$.

2.2. Practical Chemistry Avenues

• Catalyst design by spectral positioning: Target ligands and supports that increase $V_{\infty }$ on Pd to preserve s-extinction where selectivity benefits from d-only manifolds; conversely, engineer slight s-recovery on Pt by relativistic/ligand contraction to modulate ${\epsilon }_d$.
• Spectroscopic diagnostics: Use XPS/EELS to quantify d-dominant screening; employ NMR/EPR to bound ${\rho }_s\left(0\right)$; fit near-threshold scattering to extract ${\lambda }_s$ and infer $V_{\infty }$.
• Square-planar complex libraries: Exploit the intrinsic $D_{4h}^{\mathrm{eff}}$ bias in Pd(II) to design planar catalysts with tuned $10Dq,D_s,D_t$, guided by the explicit splitting formulae.
• Data-driven “spectral atlas”: Build a map $Z\mapsto (\mu \left(Z\right),{\Gamma }_0\left(Z\right))$ from measured $\{{\lambda }_s,a_s,{\epsilon }_d,\Delta E_{\mathrm{ads}}\}$, yielding a periodic-table spectral–topological atlas for anomaly prediction and materials screening.

2.3. Theoretical Extensions

• Rigorous spectral flow: Formalization of the s-index change across $V_{\infty }=0$ via an operator-valued spectral flow and a Levinson-type theorem for the half-line radial problem.
• Many-electron closure: Embedding of the one-electron invariant into mean-field/DFT+U/DMFT schemes as a constraint on $P_s$, checking that the no-bound criteria persist under screened interactions.
• Relativistic generalization: Extension to Dirac/Foldy–Wouthuysen reductions to quantify the Pt-side partial recovery and to predict behavior for Ds and neighboring superheavy elements.
• Nonlinear amplitude selection: Bifurcation analysis of the Landau functional for ${\chi }_s$ including coupling to d-manifold order parameters, clarifying metastability and hysteresis under external control.

2.4. Outlook

The operator invariant $V_{\infty }$ and the integral indicator $\kappa \left(Z\right)={\int }_0^{\infty }r{(\mu \left(Z\right)+\Gamma (r;Z))}_{-}dr$ provide compact, falsifiable criteria for orbital extinction across the periodic table. By linking these invariants to measurable spectroscopic and catalytic observables, a unified, predictive route emerges for explaining and engineering periodic anomalies. The path forward combines rigorous spectral theory with targeted spectroscopy and catalysis experiments to transform Madelung “exceptions’’ into controllable design principles in inorganic and materials chemistry.

2.5. Industrial Chemistry and Process Translation

The spectral–operator framework provides direct levers for industrial catalysis and process engineering, with the invariants $V_{\infty }=\mu +{\Gamma }_0$ and $\kappa \left(Z\right)$ serving as design and quality–control targets.

Design levers mapped to $(\mu ,{\Gamma }_0)$. Alloying (core–shell, single-atom dilution), lattice strain, support polarity/acidity (e.g., $\gamma$–Al₂O₃, TiO₂, zeolites), and adsorbate chemical potentials (H^*, CO^*) shift the effective parameters:

$$(\mu ,{\Gamma }_0)⟵\mathrm{alloying}/\mathrm{strain}+\mathrm{support}\mathrm{fields}+\mathrm{coverage}.$$

Targets requiring d–only manifolds (strong $\pi$-backdonation, planar selectivity) associate with $V_{\infty }>0$ and small $\kappa$ (Pd–like). Tasks benefitting from partial s recovery (hard $\sigma$ activation, C–H/C–Cl activation) align with $V_{\infty }\lesssim 0$ (Pt–like).

Representative sectors and actionable rules.

• Selective hydrogenations (fine chemicals and pharmaceuticals). Semi-hydrogenation of alkynes and nitro-to-amine conversions are optimized under s–extinction (large $V_{\infty }$): enhanced $p^{*}$ backdonation on Pd suppresses over-hydrogenation. Alloying Pd with Au or Ag (strain plus d-band narrowing) and employing weakly donating supports increase $V_{\infty }$ and suppress isotropic $s/d$ mixing.
• Cross-coupling (Suzuki–Miyaura, Heck, Sonogashira). Catalytic cycles benefit from a tightened d-manifold (controlled $P_d$) and reduced contact density. Support or ligand environments that maintain $V_{\infty }>0$ stabilize selective oxidative addition steps while limiting off-cycle hydridic pathways.
• Refining and petrochemicals.Hydroisomerization/hydrocracking on Pt/acid bifunctional catalysts can be tuned by mild s recovery ($V_{\infty }\approx 0^{-}$) to balance dehydrogenation and isomerization without excessive cracking. Steam reforming/methanation on Ni benefits from marginal regimes ($\kappa \approx 1$), promoting H₂ activation while mitigating coking through controlled d-band alignment.
• Emissions control (automotive three-way and oxidation catalysts). Pd-rich formulations for gasoline oxidation align with $V_{\infty }>0$ (robust d screening, low contact density), whereas Pt-lean blends for low-temperature activity may exploit partial s recovery to lower activation barriers for CO and hydrocarbon oxidation.
• Electrochemical energy (PEM fuel cells, electrolyzers, CO₂ reduction). Oxygen-reduction and hydrogen-evolution kinetics correlate with d-band alignment. Spectral tuning via alloying or strain can set ${\epsilon }_d$ near the reaction-specific optimum while keeping $V_{\infty }$ in the phase that suppresses parasitic adsorption.
• Hydrosilylation and silicone production (Pt catalysts). Industrial hydrosilylation benefits from a controlled partial s component to activate Si–H and alkene bonds. $V_{\infty }$ can be steered via ligand and support field effects to maximize selectivity while suppressing dehydrogenative side reactions.

Kinetics proxy and process setpoints. For a rate-determining step with barrier $\Delta G^{‡}\left({\epsilon }_d\right)$, a local BEP form gives

$$k\simeq k_{0}exp\left[-\beta \left(\alpha ({\epsilon }_a-{\epsilon }_d)+\Delta G_0^{‡}\right)\right],$$

(18)

where $\alpha$ depends on $s/d$ mixing. Operating with $V_{\infty }>0$ reduces $\alpha$ (isotropic channels off), sharpening selectivity at some cost in activity; small negative $V_{\infty }$ increases activity via partial s recovery. Production setpoints can thus be expressed as bounds on $\{V_{\infty },{\epsilon }_d\}$.

Operando QC and digital twins. A minimal QC loop ties spectral invariants to plant variables:

• Measure ${\lambda }_s$ (from near-threshold decay or AP-XPS valence weighting) and ${\epsilon }_d$ (XPS/XANES with $\Delta$SCF fits) under operando conditions.
• Invert to $(\mu ,{\Gamma }_0)$ via calibrated surrogates, yielding $V_{\infty }$ and $\kappa$.
• Enforce setpoints (feed composition, pressure, electrode potential, temperature) to keep $V_{\infty }$ in the target phase region in real time.

Scale-up considerations.s–extinction reduces isotropic overbinding and can mitigate sintering via weaker M–H spillover; partial s recovery lowers barriers but may raise poisoning risk. Spectral setpoints therefore trade activity for stability; phase boundaries in $(\mu ,{\Gamma }_0)$ act as guardrails for deactivation management (coking, sulfur tolerance, redox cycling).

Experimental anchor (XPS/EELS). The vanishing of the s-resolved XPS weight at threshold in Pd—long documented in high-resolution experiments [37,38,39,40,41]—is the empirical counterpart of our spectral invariant: $V_{\infty }>0$ enforces $P_s\Psi \equiv 0$ and yields an evanescent near-threshold leakage with characteristic length ${\lambda }_s={(V_{\infty }-E)}^{-1/2}$. Thus, standard photoemission line-shape analyses can be used as an operando proxy to locate elements, alloys, or supported species within the $(\mu ,{\Gamma }_0)$ phase diagram, providing a direct, falsifiable bridge from the self-adjoint radial theory to measurable spectroscopy.

2.6. Theoretical Extensions

• Rigorous spectral flow. Formalization of the s–index jump across $V_{\infty }=0$ via operator-valued spectral flow for the half-line radial family $h\left(t\right)=-{\displaystyle \frac{d^2}{d{r}^2}}+V_{\mathrm{eff}}(r;t)$, with limit-point behavior at ∞ and Dirichlet at 0. A Levinson-type identity relating $\mathrm{sf}\left\{h\right(t\left)\right\}$ to the zero-energy phase shift ${\delta }_0\left(0\right)$ and the change in the number of s–bound states is to be established, including stability under form-bounded perturbations of $V_{\mathrm{eff}}$.
• Many-electron closure. Embedding of the one-electron invariant into Hartree–Fock and Kohn–Sham (DFT, DFT+U) as a projector constraint on $P_s$, with persistence of the no-bound criteria under screened two-body interactions. Within DMFT, analysis of how a local, frequency-dependent self-energy $\Sigma \left(i\omega \right)$ renormalizes $V_{\infty }$ while preserving the extinction phase as a fixed point.
• Relativistic generalization. Extension to Dirac–Coulomb and exact two-component (X2C) or Foldy–Wouthuysen reductions, yielding an effective scalar $V_{\mathrm{eff}}^{\left(D\right)}$ and a systematic shift $\Delta V_{\infty }(Z,\alpha )=\mathcal{O}\left({\left(Z\alpha \right)}^2\right)$. Quantification of partial s recovery on Pt and predictions for Ds and neighboring superheavy elements within the same invariant framework.
• Nonlinear amplitude selection. Bifurcation analysis of the Landau functional for ${\chi }_s={\parallel P_s\Psi \parallel }^2$ including coupling to d–manifold order parameters, center-manifold reduction near $V_{\infty }=0$, and characterization of saddle-node/pitchfork scenarios. Determination of hysteresis windows and metastability under external controls (pressure, oxidation state, ligand fields).

2.7. Outlook

The operator invariant $V_{\infty }=\mu +{\Gamma }_0$ and the integral indicator

$$\kappa \left(Z\right)={\int }_0^{\infty }r{(\mu \left(Z\right)+\Gamma (r;Z))}_{-}dr$$

provide compact, falsifiable criteria for orbital extinction across the periodic table.

By linking these quantities to measurable proxies—${\lambda }_s$ and $a_s$ (near-threshold leakage), ${\epsilon }_d$ (valence alignment), and XPS/EELS/NMR signatures—a predictive pipeline emerges for both explaining and engineering periodic anomalies.

The path forward combines rigorous spectral theory with targeted operando spectroscopy and catalysis experiments, enabling navigation of phase boundaries through alloying, strain, coverage, and ligand fields.

In this way, “Madelung exceptions” become controllable design principles that bridge fundamental spectral theory with practical synthesis, industrial catalysis, and materials development.