2.1. Materials Introduction
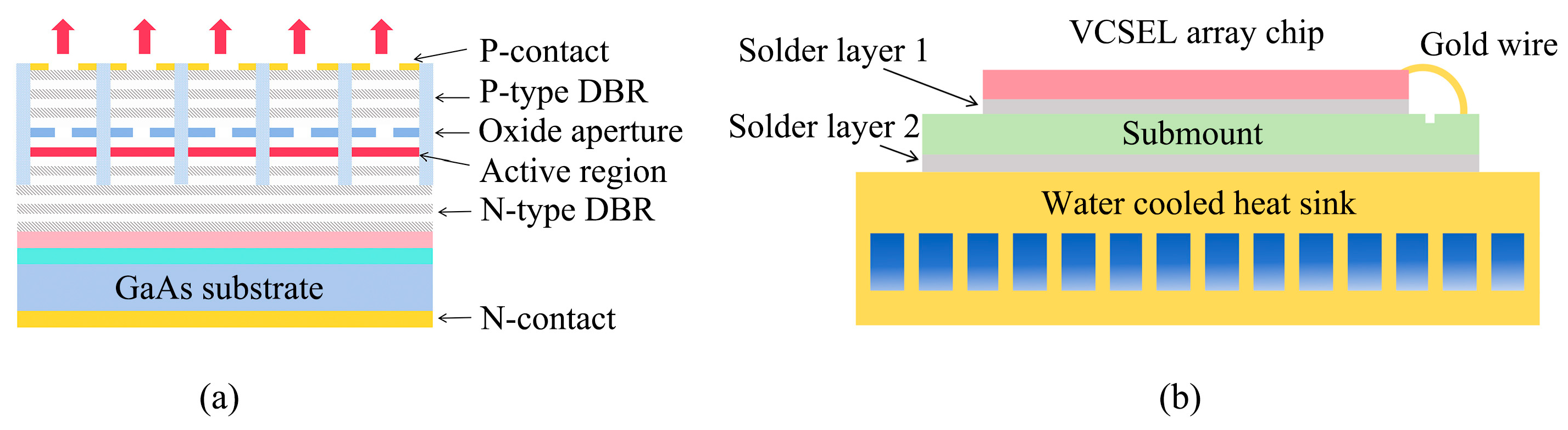
The 808nm, 6 mm×6 mm, AlGaAs/GaAs top-emitting VCSEL array chip’s main schematic is shown in
Figure 1a. The VCSEL array chip is mainly made of P contact electrode layer, P-type distributed Bragg reflector (DBR), oxide aperture, active region, N-type DBR, GaAs substrate, and N contact electrode layer, and so on. The schematic of the VCSEL array module with remote cooling packaging style is shown in
Figure 1b.
The module consists of the single VCSEL array chip, the special solder layer 1, the aluminum nitride heat sink submount, the special solder layer 2, and the water cooled heat sink. The packaging form is usually defined as the remote cooling, which is widely used for high-power VCSEL array modules for a long time. Here, the chip with thousands of luminous points is thined to no more than 100μm and then metallized. Nano silver sintering is used between the VCSEL array chip and the submount to ensure no void inside the whole solder layer, which is extremely important. Because the void will cause excessive thermal resistance, which will result in local burning of the VCSEL array. The thickness of the solder layer 1 is merely less than 5μm which is achieved under the process, 20Mpa, 200℃, 90min. At the same time, the solder layer’s thermal conductivity can reach up to 200W/m•K, which is a satisfactory thermal interface. The submount is made of aluminum nitride material which owns thermal expansion coefficient which is similar to gallium arsenide to relieve packaging stress. Double side welding method with indium is used to connect submount and water cooling heat sink. On the one hand, the method is used to reduce voids in the solder layer 2. On the other hand, it also alleviate packaging stress for that indium is so soft which is usually as suitable solder for laser module. The thickness of the solder 2 is about 10μm. The water-cooled heat sink is made of purple copper, which is processed by wire electrical discharge machining to form multi-channel array. By that, we can enhance the ability of convective heat transfer with water or other coolants to dissipate the heat of the module. The channel width of the water cooling heat sink is about 300μm, and the ratio of channel width to wall thickness is about 1:1 in this water-cooled heat sink.
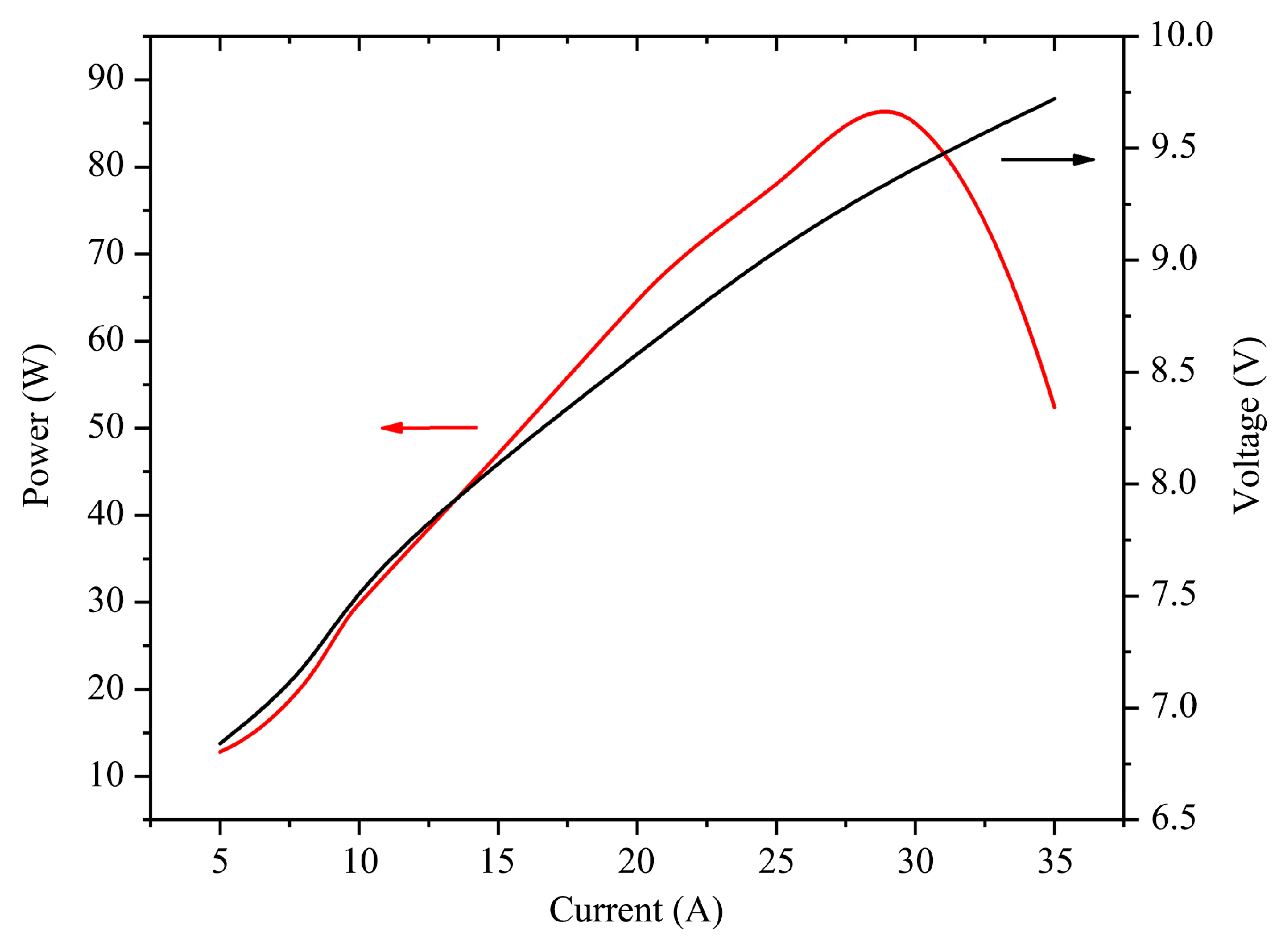
The threshold current of the chip is about 5A. The power/ current/ voltage (PIV) chart is shown in
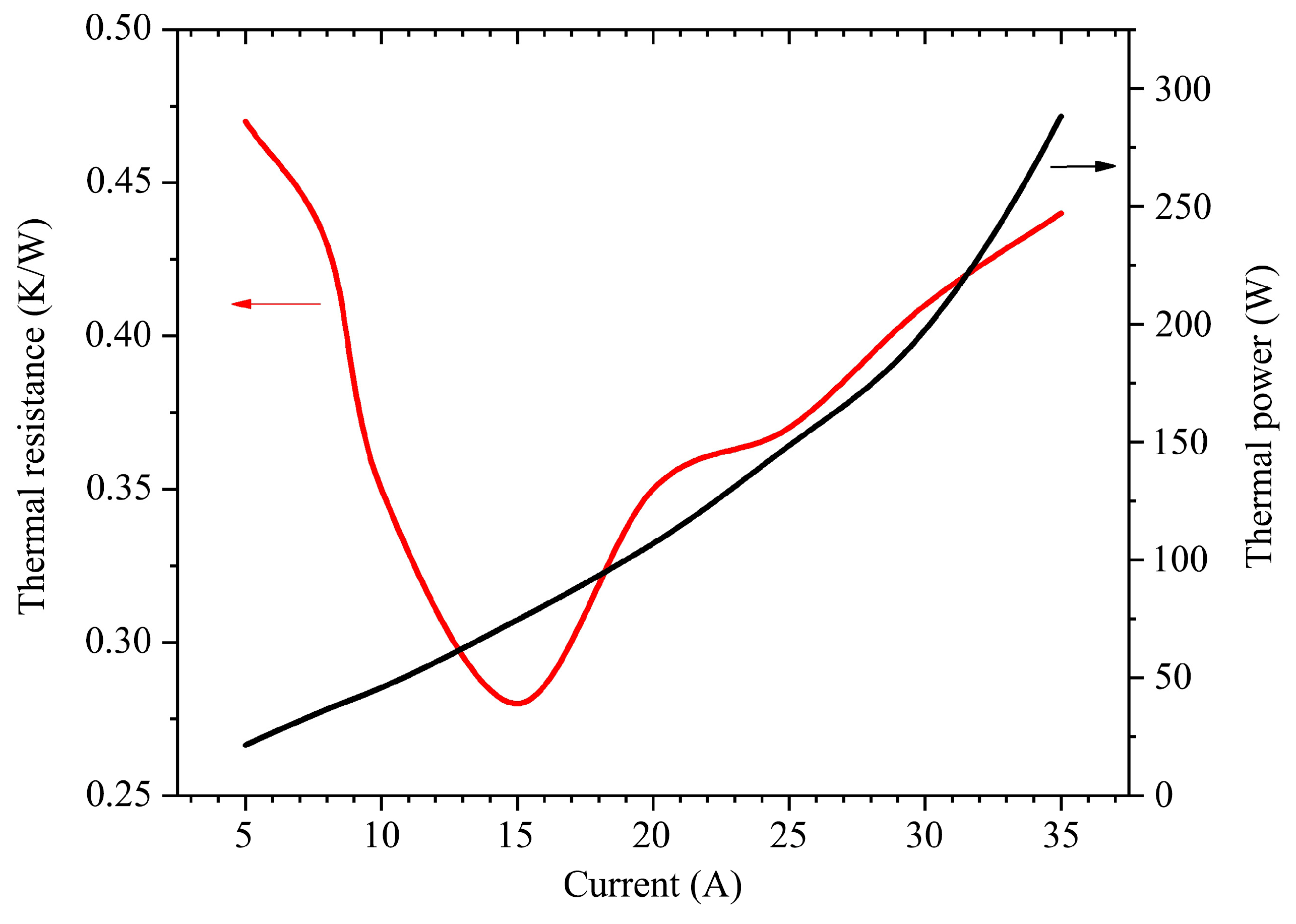
Figure 2, when the module was in continuous wave operation on a water-cooled heat sink, the water temperature was set at around 20℃ and the water flow rate was set at 25L/min to maintain the flow state in turbulence.
The laser power tester was used for laser power detection which is based on the principle of thermo-electric conversion. When the current was set at about 27A, the laser power of the module reached the peak power of about 85W. Then, the output laser power of the module began to decrease due to insufficient heat dissipation of the remote cooling module. To more intuitively reflect the thermal resistance effect of the module, the power conversion efficiency (PCE) curve is shown in
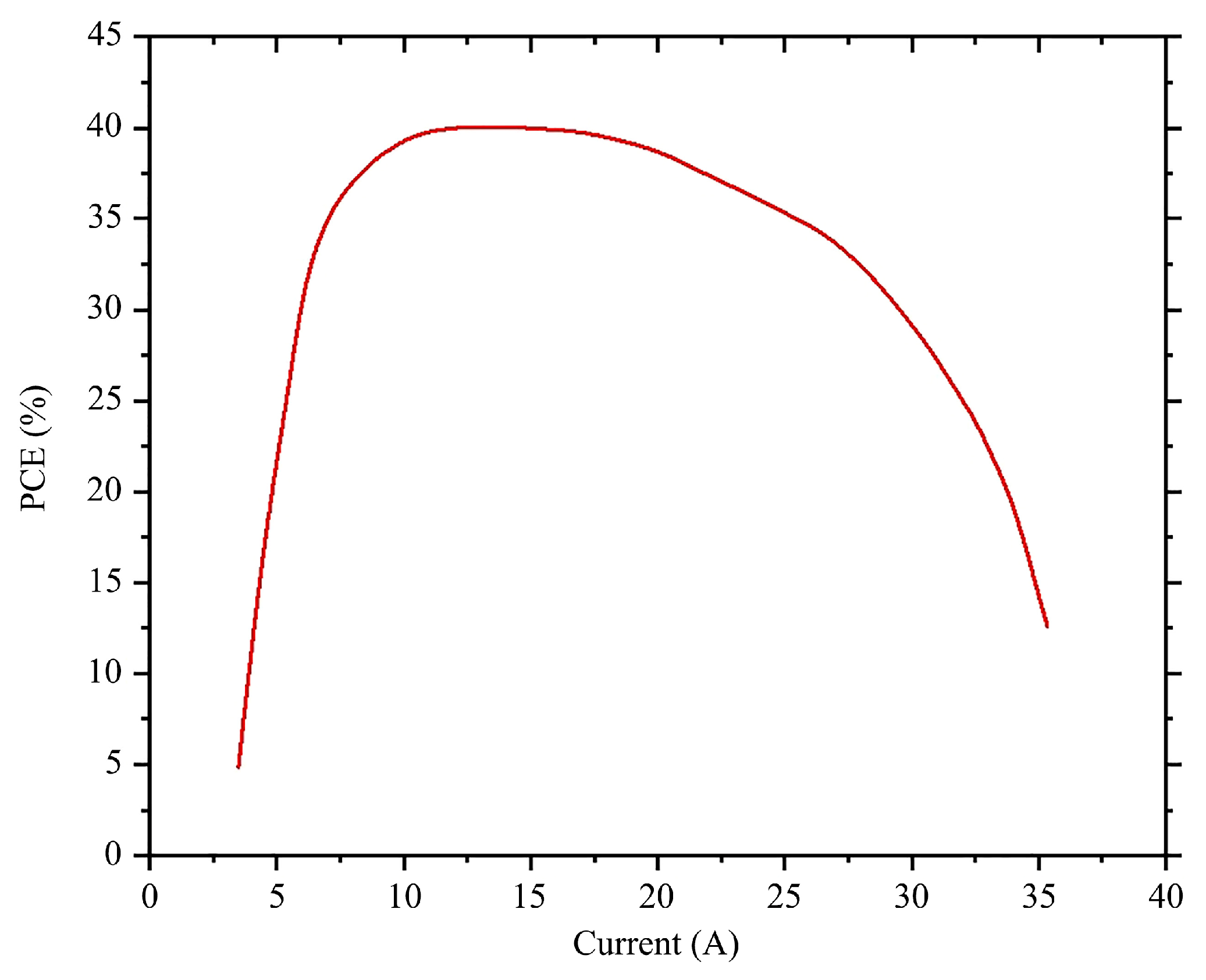
Figure 3.
The maximum electro-optic conversion efficiency approached 40% of the module occurs at a loading currents of about 9A~15A. Thereafter, the efficiency started to rapidly decay as the current was gradually loading. As mentioned above, the thermal resistance effect severely limits the electro-optic conversion efficiency of the module. Therefore, detailed thermal resistance analysis of the VCSEL array module is extremely meaningful.
The thermal resistance is a key indicator of thermal performance in semiconductor lasers. The JEDEC standard No.51-1 defines it as [
18]:
In this equation(1),refers to the heat dissipation power, refers to the junction temperature of the chip, refers to the ambient temperature. When the VCSEL array is loaded with input current, heat will generate inside the chip and packaging structure, which contains joule heating, scattering absorption, spontaneous emission, carrier leakage, band alignment, and so on. Once the loading current exceeds the threshold current (), the VCSEL array chip will emit laser.
2.2. Structural Function Method
The structural function method for measuring thermal resistance refers to utilizing the linear relationship between the voltage and the temperature of the semiconductor junction. During the heating or cooling process of the semiconductor laser, the transient temperature curve can be obtained by rapidly measuring the junction voltage of the device. With the thermal RC network analysis theory, the transient temperature response curve is analyzed into a thermal RC network, and then transformed into a differential structure function curve by mathematical processing. Thus, a detailed analysis for the thermal resistance of each layer in the device packaging can be well done [
19]. Semiconductor devices are generally packaged into multi-layer structures composed of different materials [
20]. Within the thermal conduction path of a device, different materials exhibit varying thermal resistances and thermal capacities, leading to distinct temperature responses. Therefore, semiconductor devices and their packaging structures can be regarded as one-dimensional thermal networks. At t=0, we apply heat power to the device, and then the junction voltage of the device is measured to obtain the curve of temperature variation with time during the temperature rise process, which is called the transient response curve. The curve can be equivalent to the response of a Foster RC network model with n units. The response can be expressed as a linear combination of exponential terms with n different time constants:
In the formula (2),
represents the thermal response curve,
=
×
is the time constant of the No
i RC,
refers to the amplitude coefficient of the exponential term, the time constant spectrum. Real thermal systems exhibit a continuous distribution of time constants expressed in integral form:
Introducing the exponential time variable z=ln t, is expressed as:
For the spectrum of unknown time constants
, formula (4) is a devolution type differential equation. Taking the derivative of both sides with respect to z, we obtain:
In the formula (5), W(z)=exp
,
represents convolution operation. Therefore, after measuring the thermal response curve, it is transformed into an exponential time variable form. Take the derivative of it, then, by performing a deconvolution operation based on equation (5), we can obtain the time constant spectrum of the one-dimensional thermal structure
. So, the thermal resistance R
i and thermal capacity C
i in the Foster network can be extracted. In fact, the point-to- point heat capacity in the Foster network has no practical physical significance. Therefore, it is necessary to transform the Foster network into the Cauer network with point to ground thermal capacity model. The N pieces RC units obtained from the Cauer network can be used to approximately describe the heat transfer structures of the device. The thermal response curve of the junction temperature is determined by the structural function of the device. In addition, the structural function is defined as the ratio of heat capacity per unit length to thermal resistance per unit length, that is:
In the formula, x is the linearity of the one-dimensional thermal conduction path.
Along the heat transfer path, we sum up the thermal resistance and heat capacity of each RC unit to get R
(x) and C
(x). By comparing with them,the distribution of the structural function along the thermal conduction path x can be obtained. In fact, the commonly used structure in thermal resistance test instruments is the differential structure function, which is the function value obtained by differentiating C
(x) with respect to R
(x):
Considering a thin material with a cross-sectional area of A and a thickness of dx. Its heat capacity can be represented as dC
=c
Adx. The thermal resistance can be represented as dR
=dx/eA. In the formula, c
is the volumetric heat capacity. e is the thermal conductivity of the material. Therefore, the differential structure function of equation (7) can be expressed as:
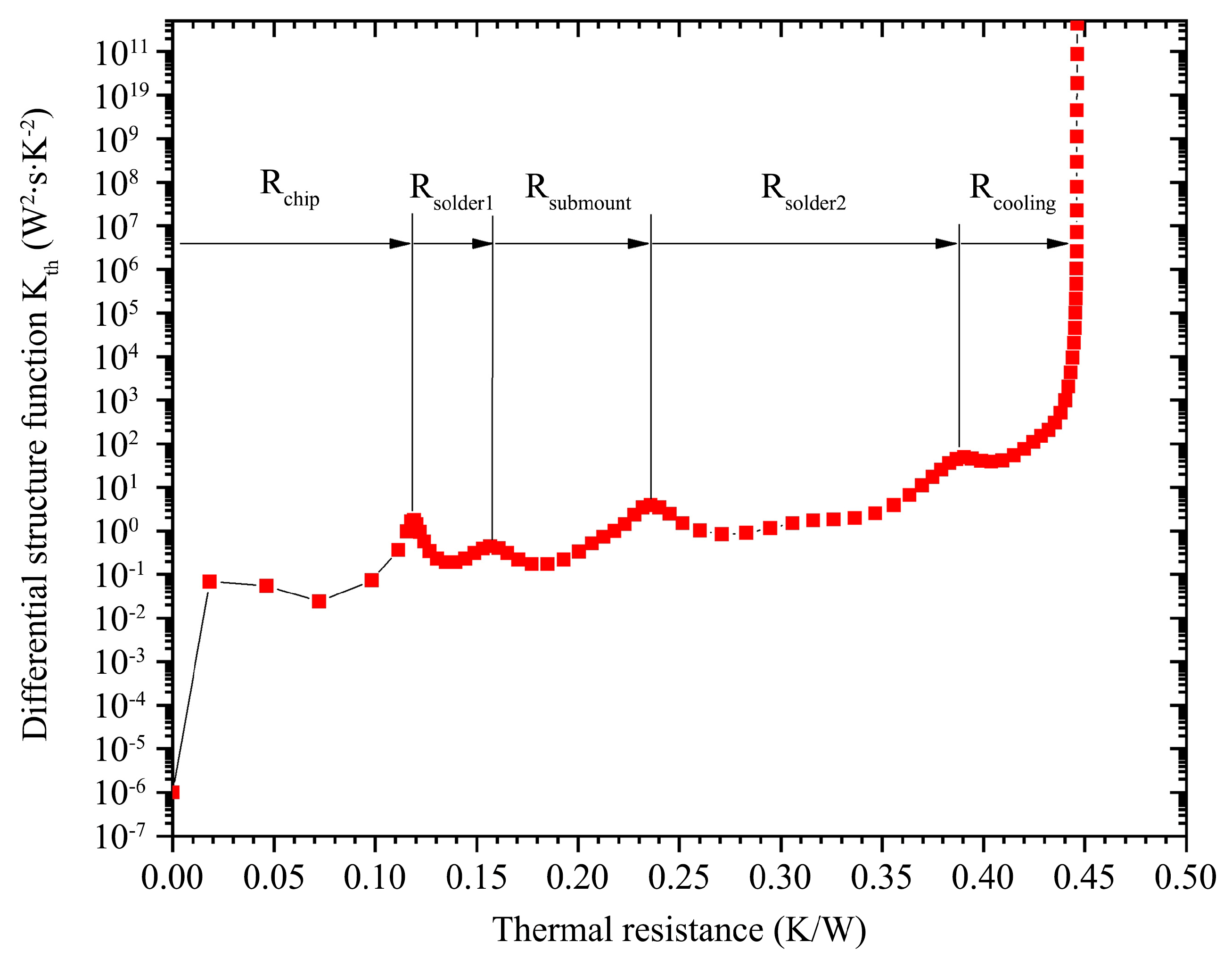
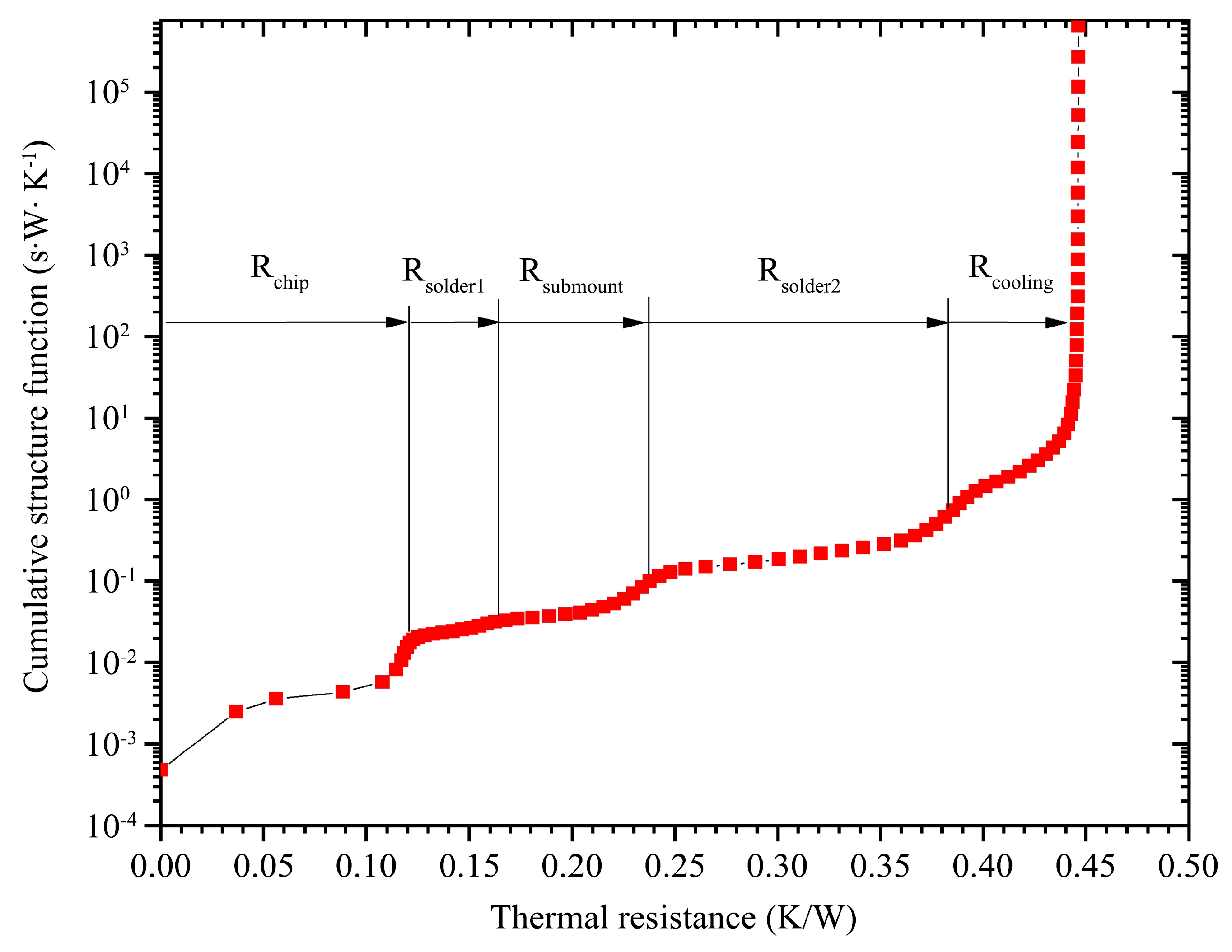
For a certain structure along the heat flow path, both c
and e are constants, while the heat flow cross-sectional area A gradually increases due to thermal diffusion effects. There are local peaks or troughs on the curve of the differential structure function. This is caused by the sudden changes in c
and e, indicating that the heat flow has reached a new material. Therefore, by analyzing the curve of the differential structure function, we can identify and analyze the internal layer structures of the devices and their thermal conductivity characteristics [
20].
The temperature rise and the thermal resistance in the VCSEL array are measured by electrical transient measurement technique. The electrical method is according to the linear relationship between the forward voltage and the junction temperature variation, which is defined as [
21]:
is the forward voltage difference of the VCSEL array between before and during operation.
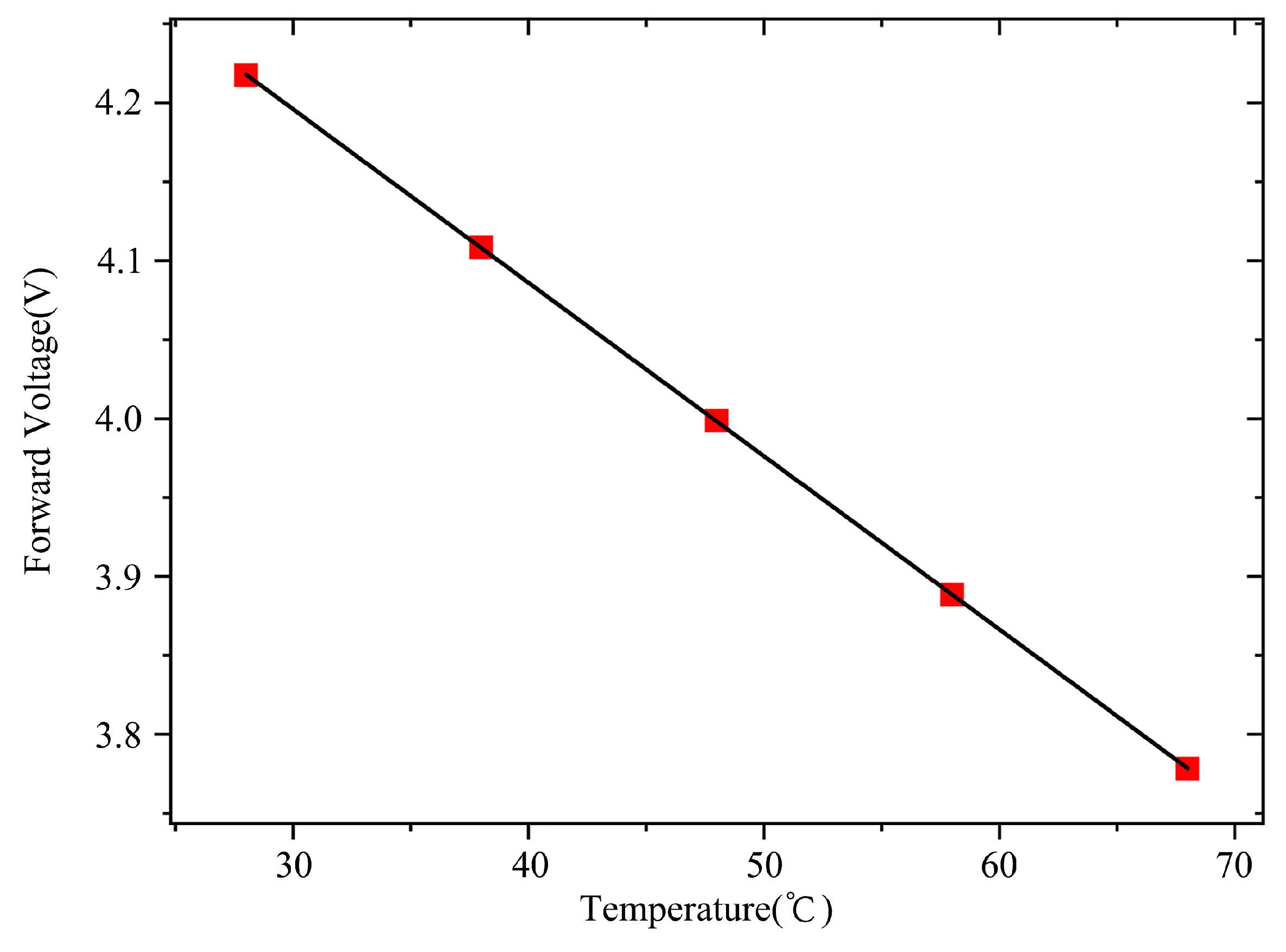
means a temperature coefficient. We measured the forward voltages at a steady diminutive current of 1mA under various temperatures from 28℃ to 68℃, in 10℃ per step. The current was loaded with Keithley 2400 source meter, which can keep the stability of the testing data. The ambient temperature was regulated and kept by a constant temperature bath, the temperature tolerance can be controlled within ±0.05℃. Then, we obtained a clear linear proportionality constant, which is about -11mV/℃ at the tiny current of 1mA, as shown in
Figure 4.
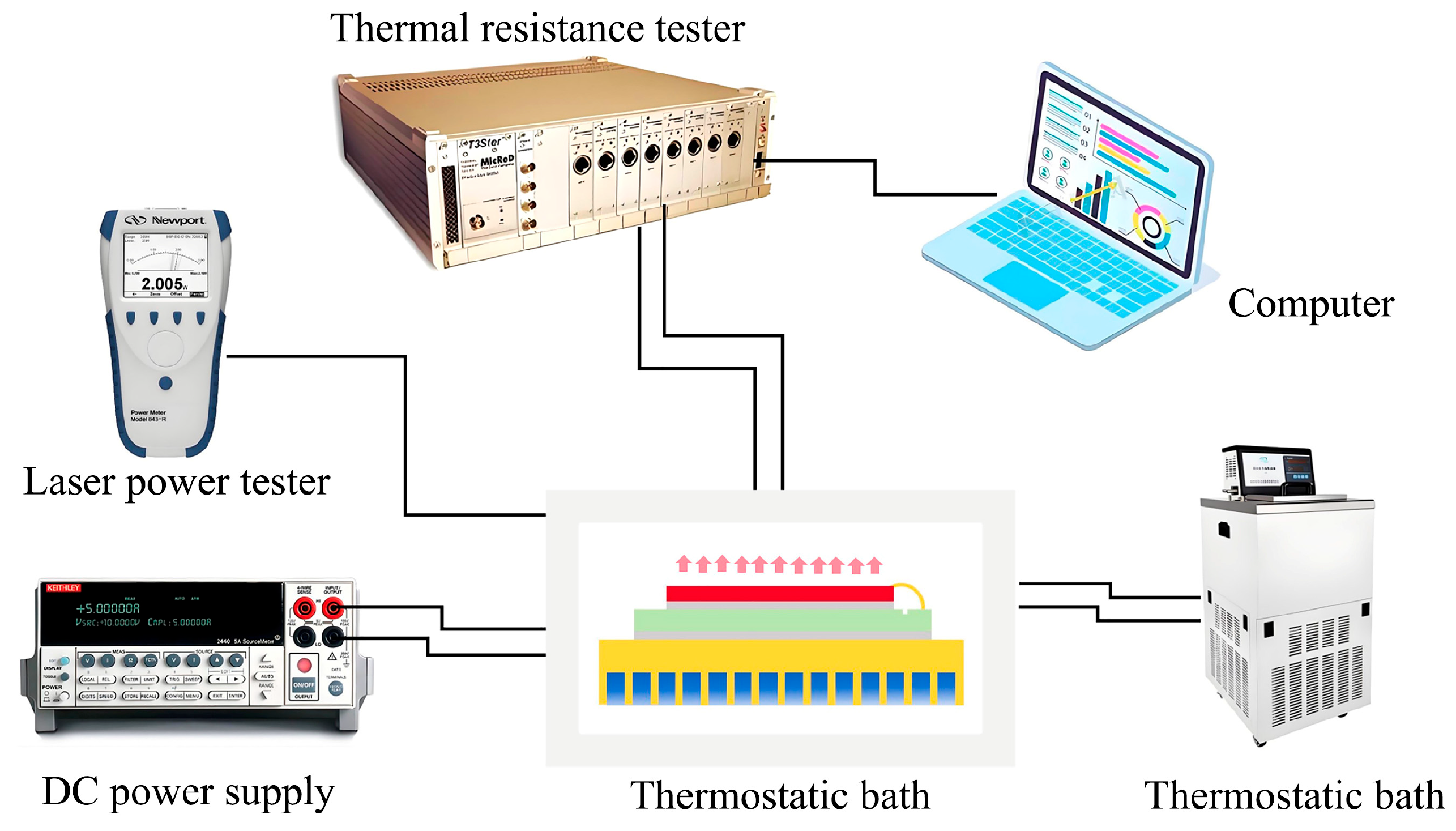
The thermal resistance of the module was tested by a thermal resistance tester at working currents from 2A to 8A with IT6722A DC power supply, in 2A per step, which is around the threshold current of 5A of the top-emitting VCSEL array chip. The module was set at a stabilized temperature of about 25℃during the thermal transient measurement with a thermostatic bath, as shown in
Figure 5.
The laser power was measured by Newport Laser power tester. In addition, the thermal power was acquired by the equation:
means the thermal power. I means the operating current, V means the operating voltage,
means the laser power. The VCSEL array was operated at a set current within only 15 seconds, which is enough to keep the device at a steady state. Then, it was quickly switched from just working state to a measurement state to check the forward voltage under a sensor current of only 1 mA. In addition, Due to the fast cooling of the water-cooled module, the cooling time for testing can be completed within merely 10 seconds. The switching process was quick enough within 1μs. With the equation(1) and (9), we can obtain the thermal resistance curve and the transient cooling curve. The transient cooling curve can be switched to a transient temperature rise curve by a mathematical inversion [
21,
22,
23,
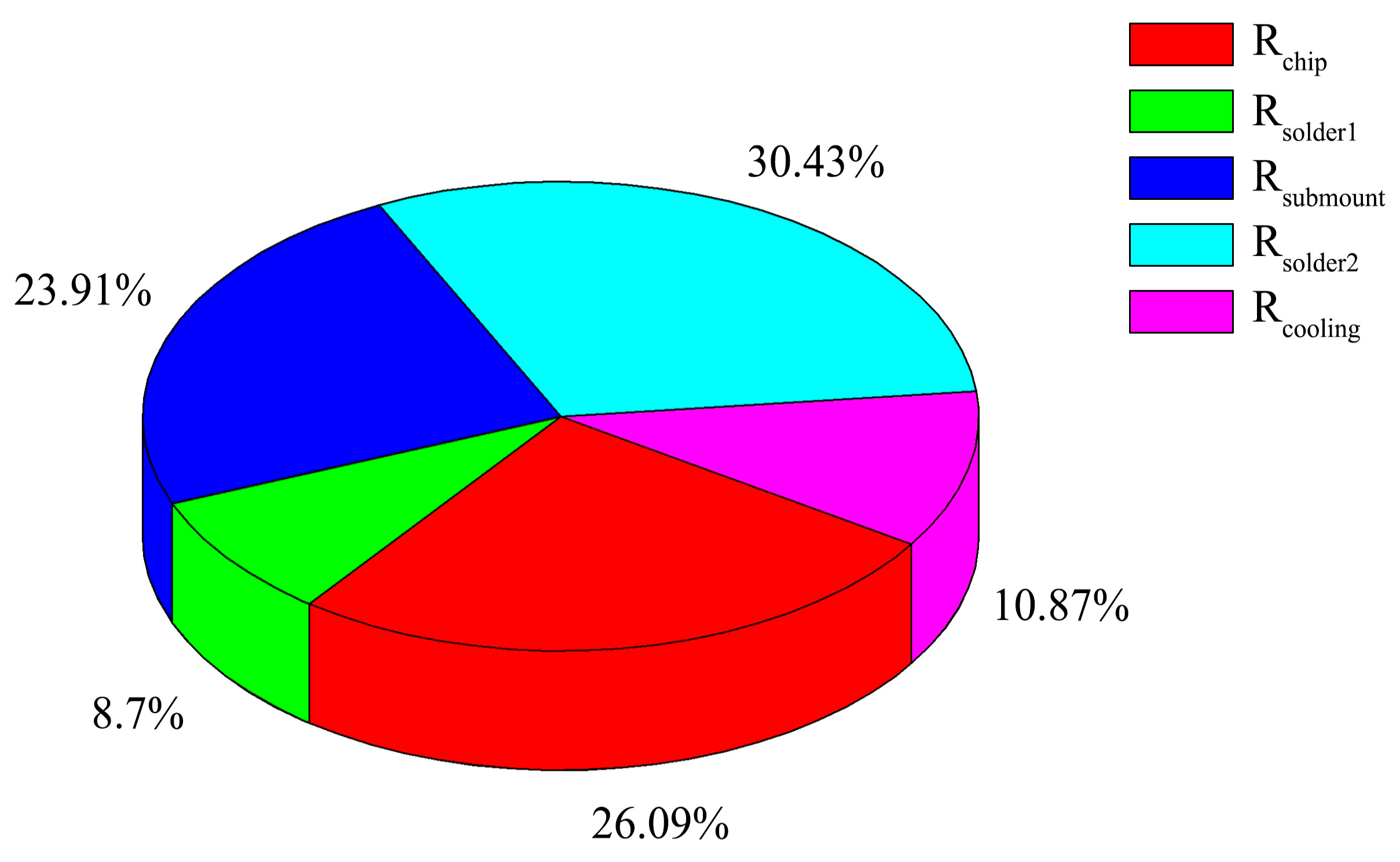
24]. To get clearer detailed information on the heat conduction process of the module, we analyzed its thermal resistance composition using the transient temperature rise curve with structure function algorithm.
2.3. Spectroscopy Method
The structural function method has considerable advantages in detecting the composition of the module thermal resistance. However, the method has a deficiency in accurately detecting the thermal resistance of the overall water cooling laser module. In this regard, the spectroscopy method is more suitable. GaAs semiconductor lasers are made of direct band gap materials: the junction temperature changes linearly with laser wavelength, which is defined as [
25]:
In the above equation,
T means the junction temperature variation of the laser chip.
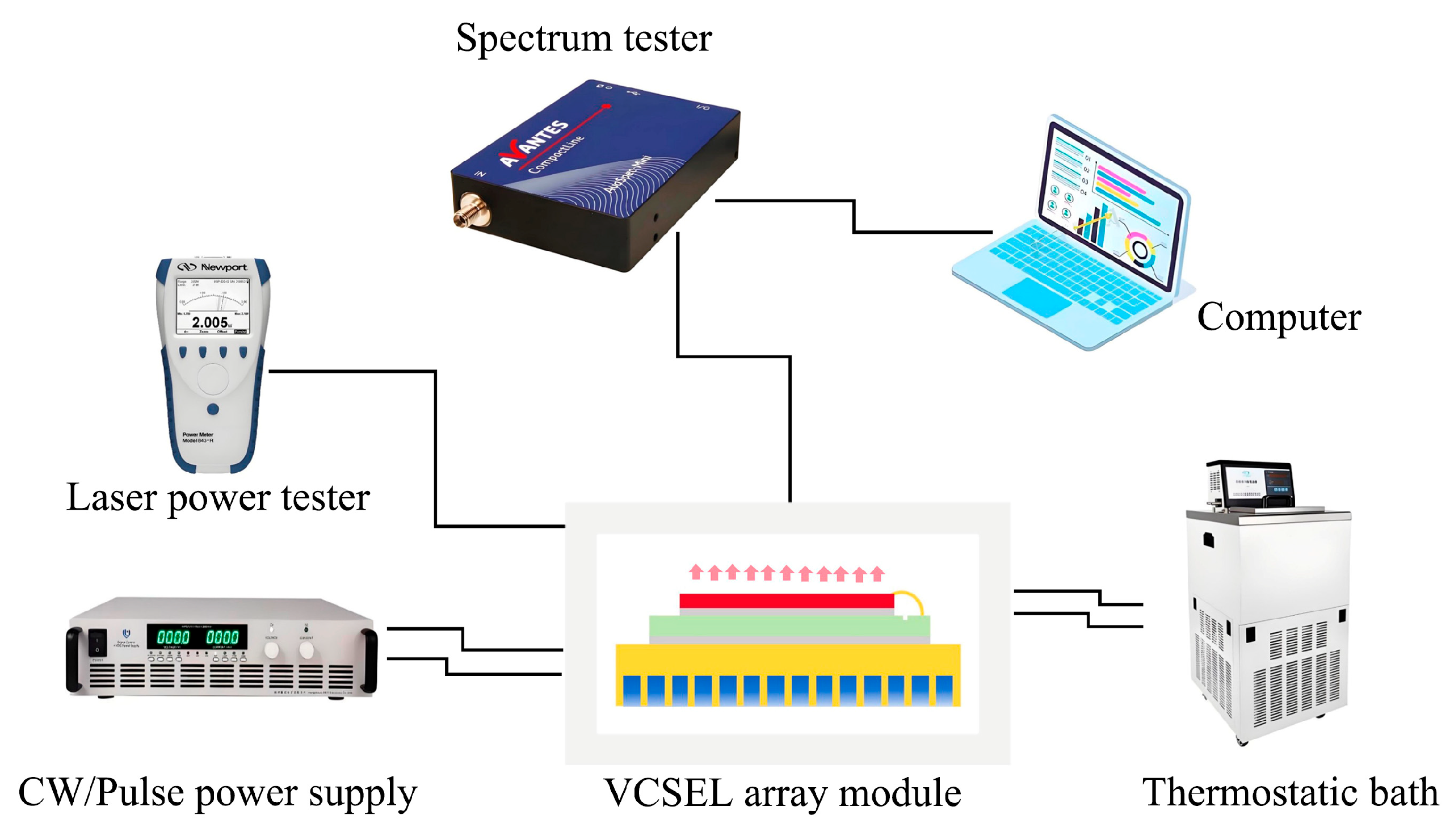
λ means wavelength variation. λ(T) means temperature drift coefficient. Firstly, we obtained the temperature drift coefficient by observing the variation of pulse laser wavelength under 5A, 100μs, 100Hz with a stable junction temperature by gradually changing environmental temperature. The ambient temperature was adjusted and controlled by a thermostatic bath instrument shown in
Figure 6.
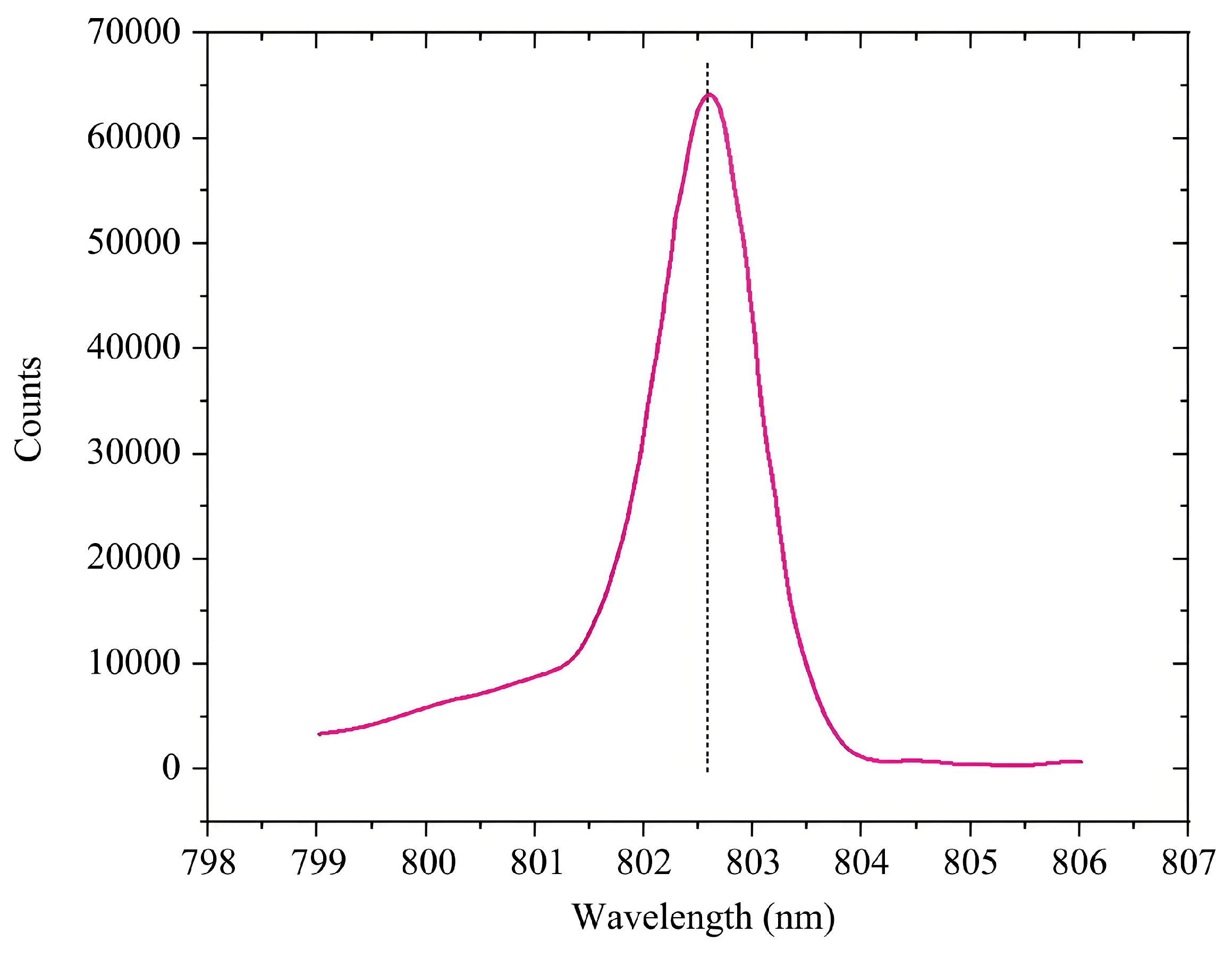
We applied Avantes spectrometer to monitor laser wavelength. Due to the high power of the laser, we used the laser reflection method with a mental plate above to reduce overly intense laser spectral intensity for detection to avoid damaging the instrument. When the temperature was set at constant 25℃, the spectral distribution test is shown in
Figure 7, the center wavelength at the low duty cycle is approximately 802.60nm, which is commonly known as cold temperature wavelength. As depicted in
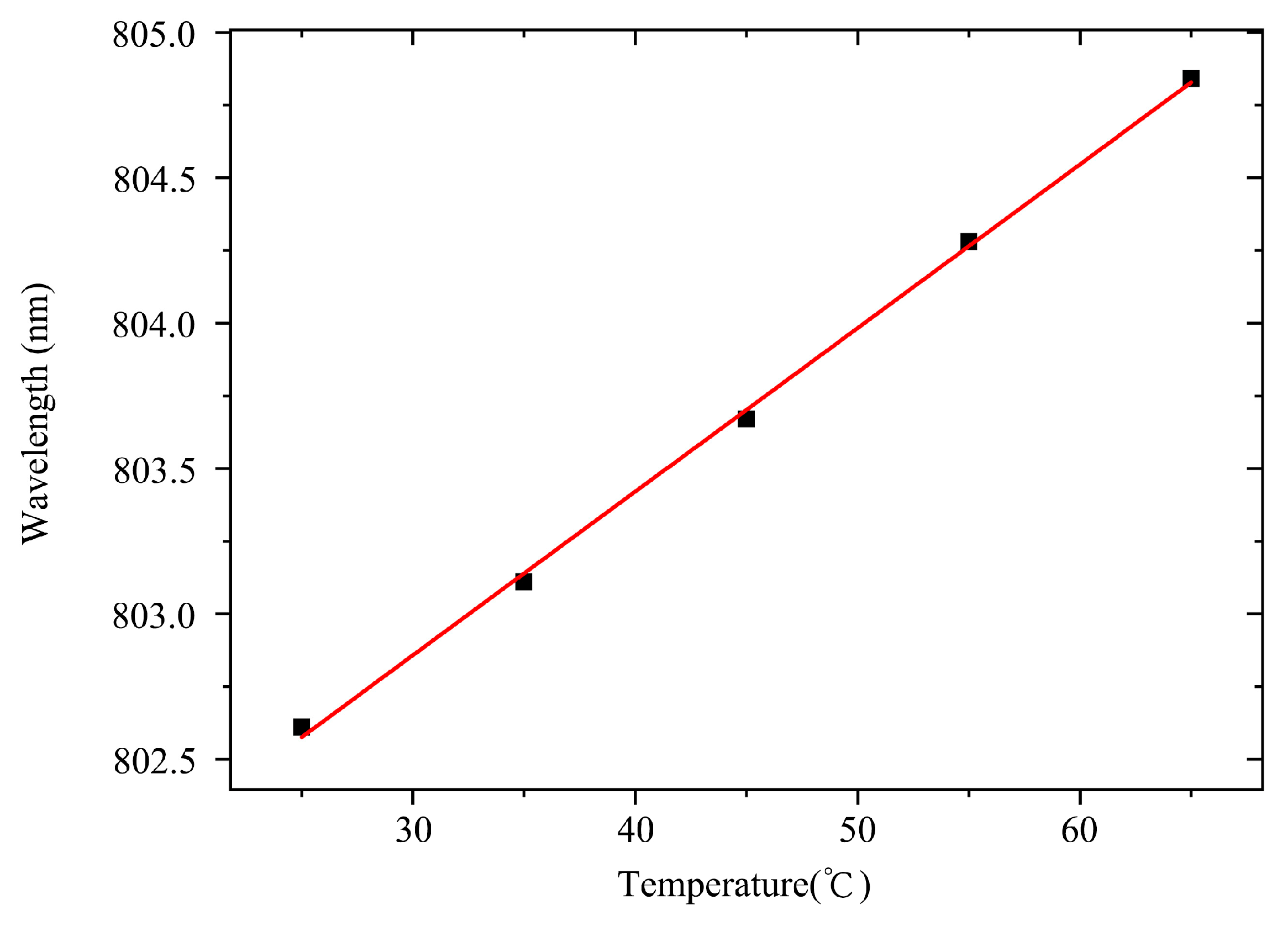
Figure 8, the temperature drift coefficient is about 0.056nm/K.
Then, we employed the wavelength drift method to monitor the laser wavelength variation with various operating currents, thereby inferring the junction temperature rise with thermal power, and subsequently calculating the total thermal resistance of the device. To get convenient detection and calculation for the thermal resistance of the laser module, equation (1) can be transformed into the following form [
26]:
In the above equation,
is the thermal resistance.
means the thermal power. We tested the voltage, the laser power, and the wavelength of the VCSEL array module at several different loading currents: 5A~35A, at continuous working condition. These test parameter data are shown in
Table 1: