Submitted:
01 October 2025
Posted:
01 October 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Self-Induced Skew-Cosh Gaussian Mode Laser Oscillation
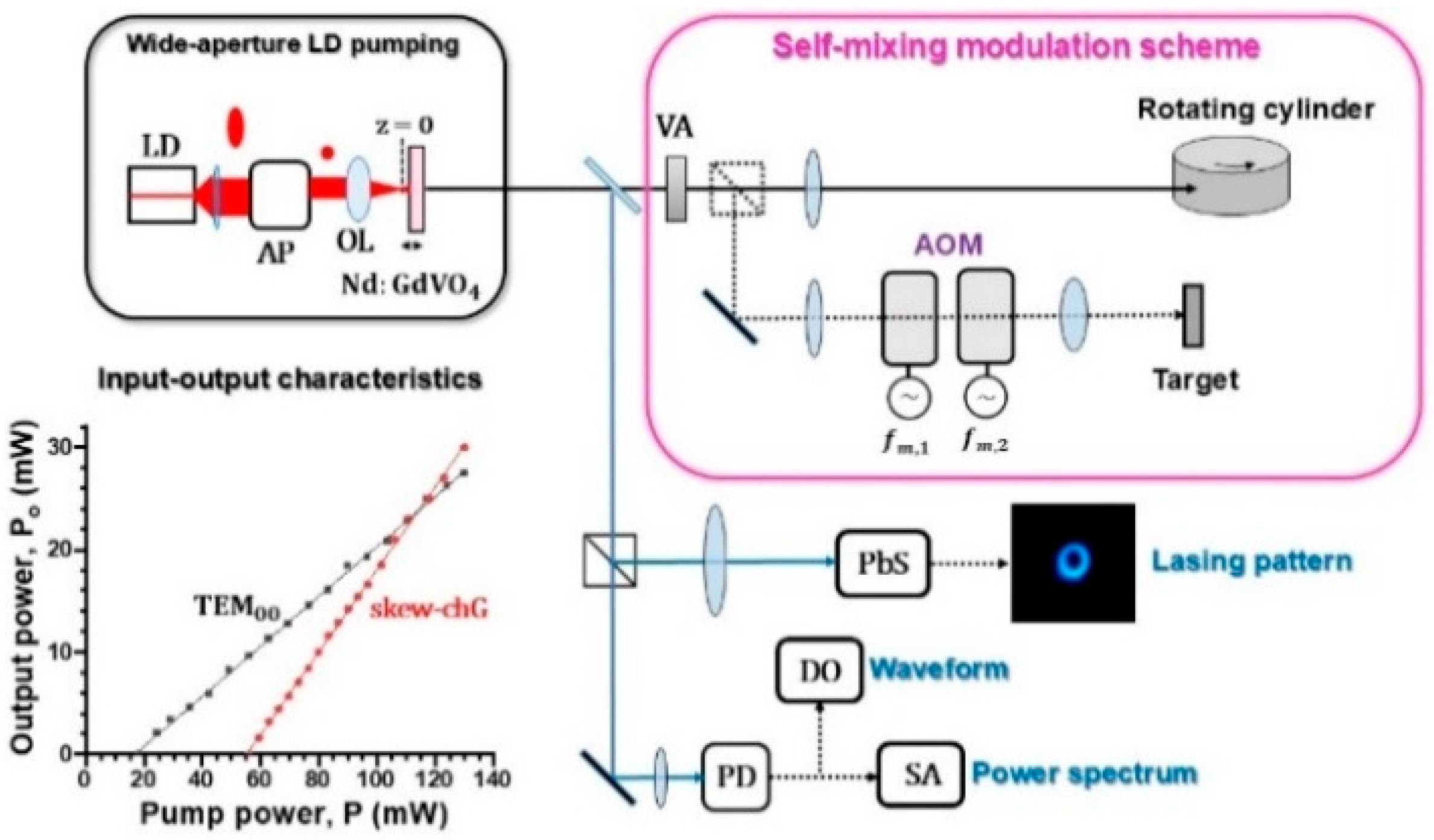
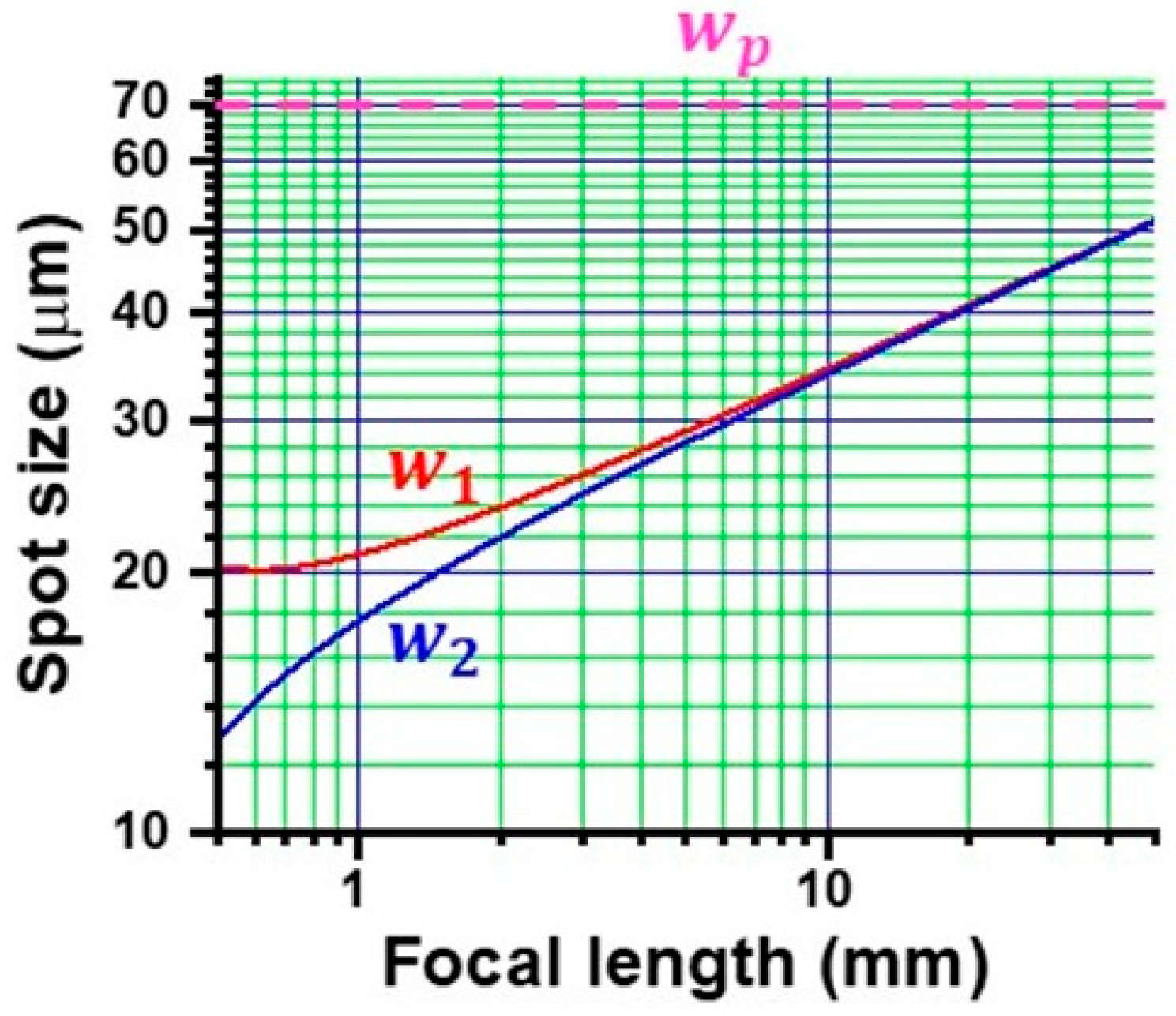
2.1. Wide-Aperture LD Pumping and Slope Efficiency
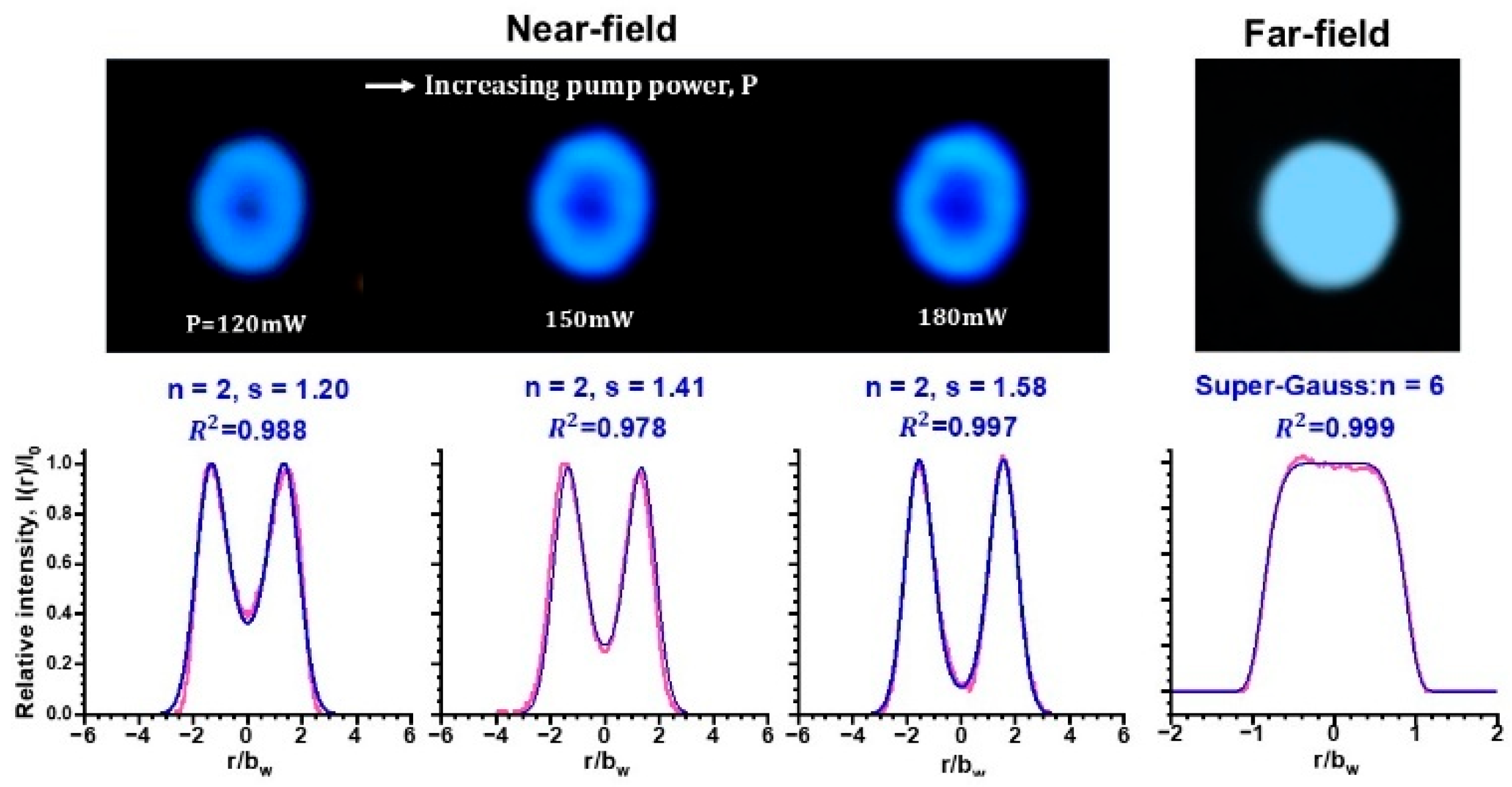
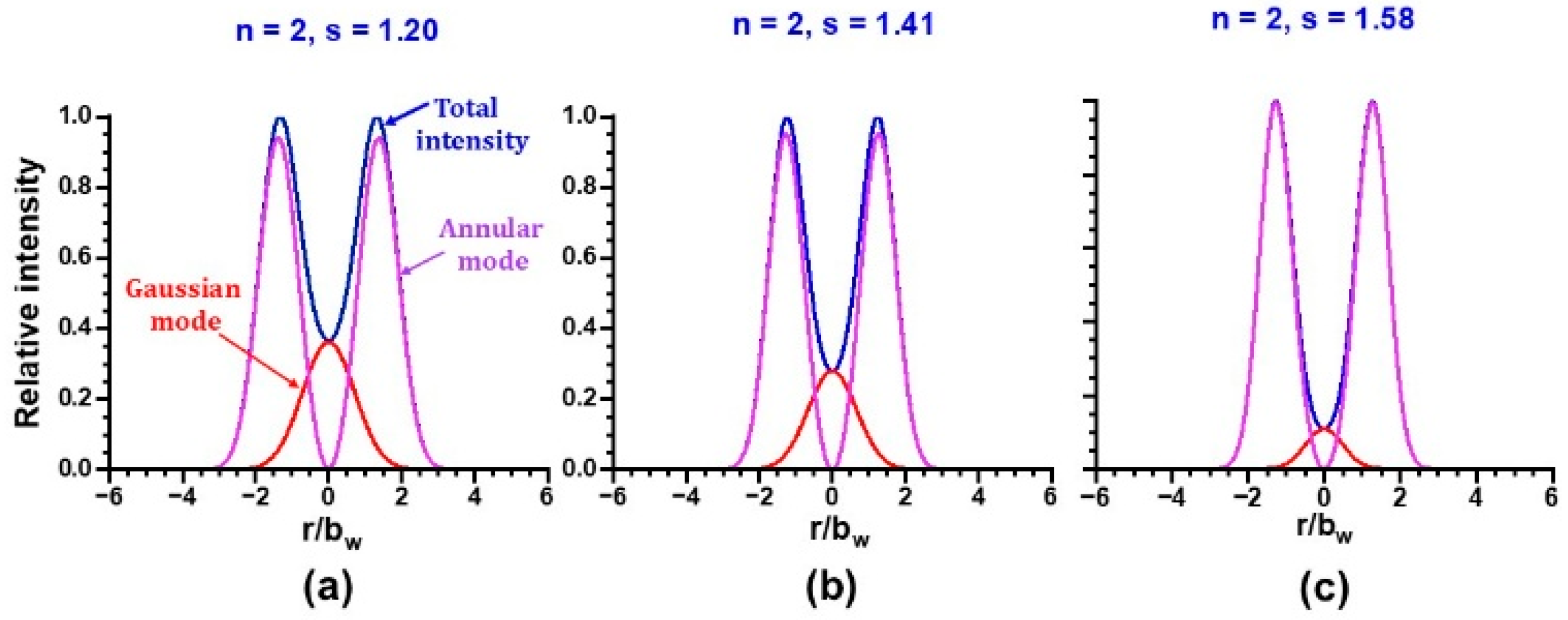
2.2. Lasing Beam Profiles
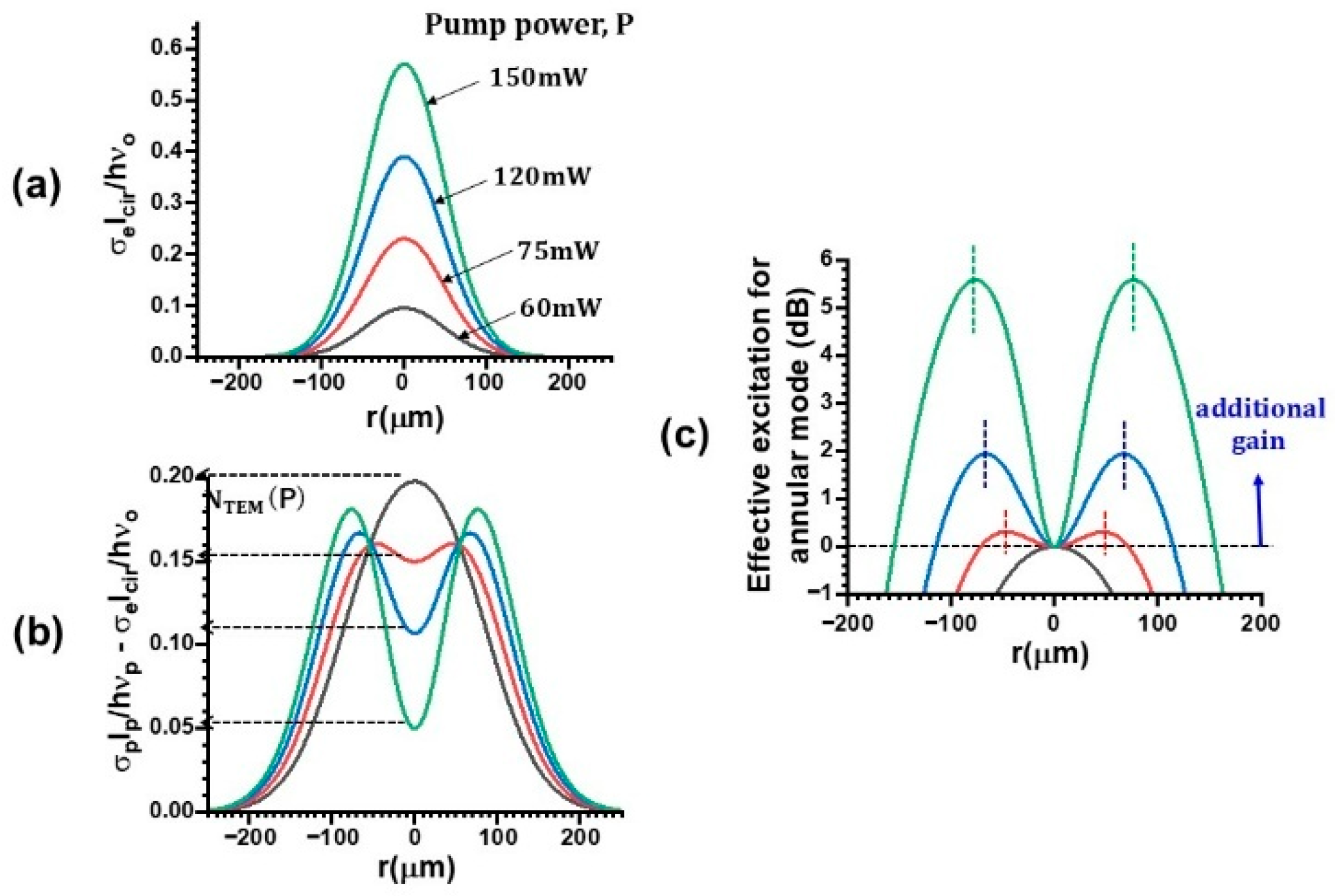
2.3. Transverse Spatial Hole-Burning of Population Inversions
3. Self-Mixing Mixing Modulation in Modified Skew Cosh Gaussian Mode Laser
3.1. Phase Amplification in Weak Feedback Regime
3.2. Phase Amplification in Intermediate Feedback Regime
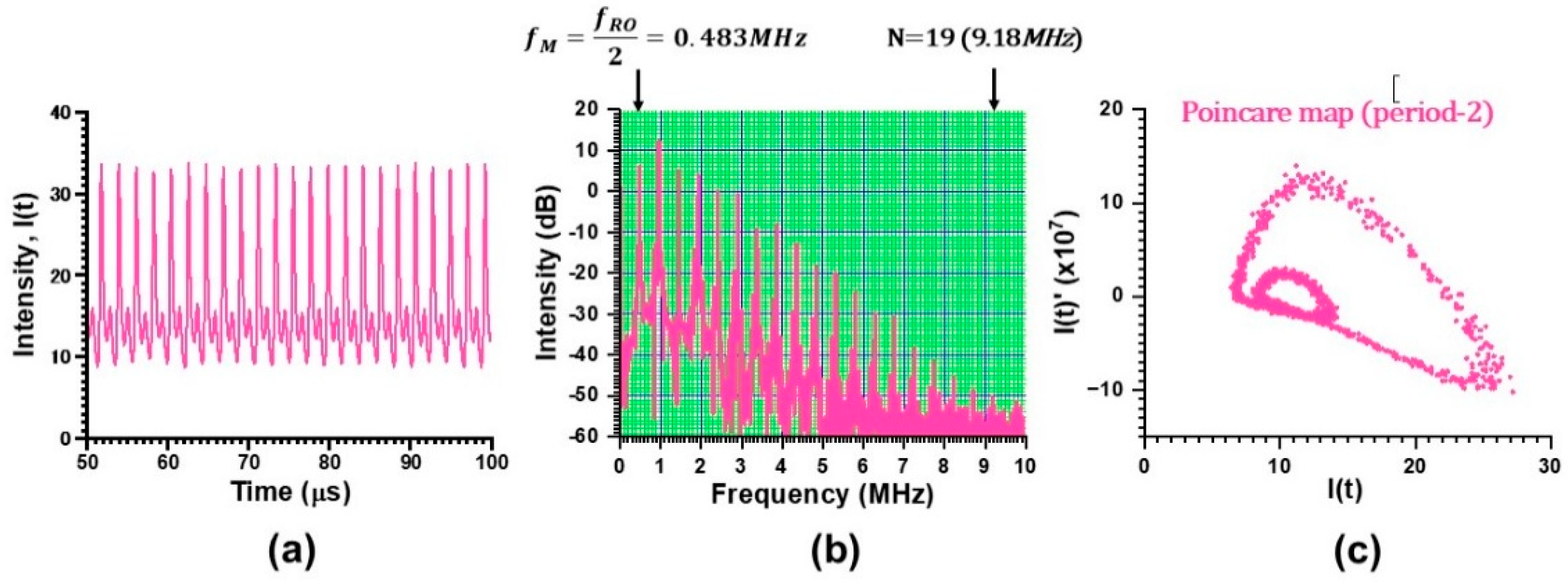
3.3. Phase Amplification in Strong Feedback Regime
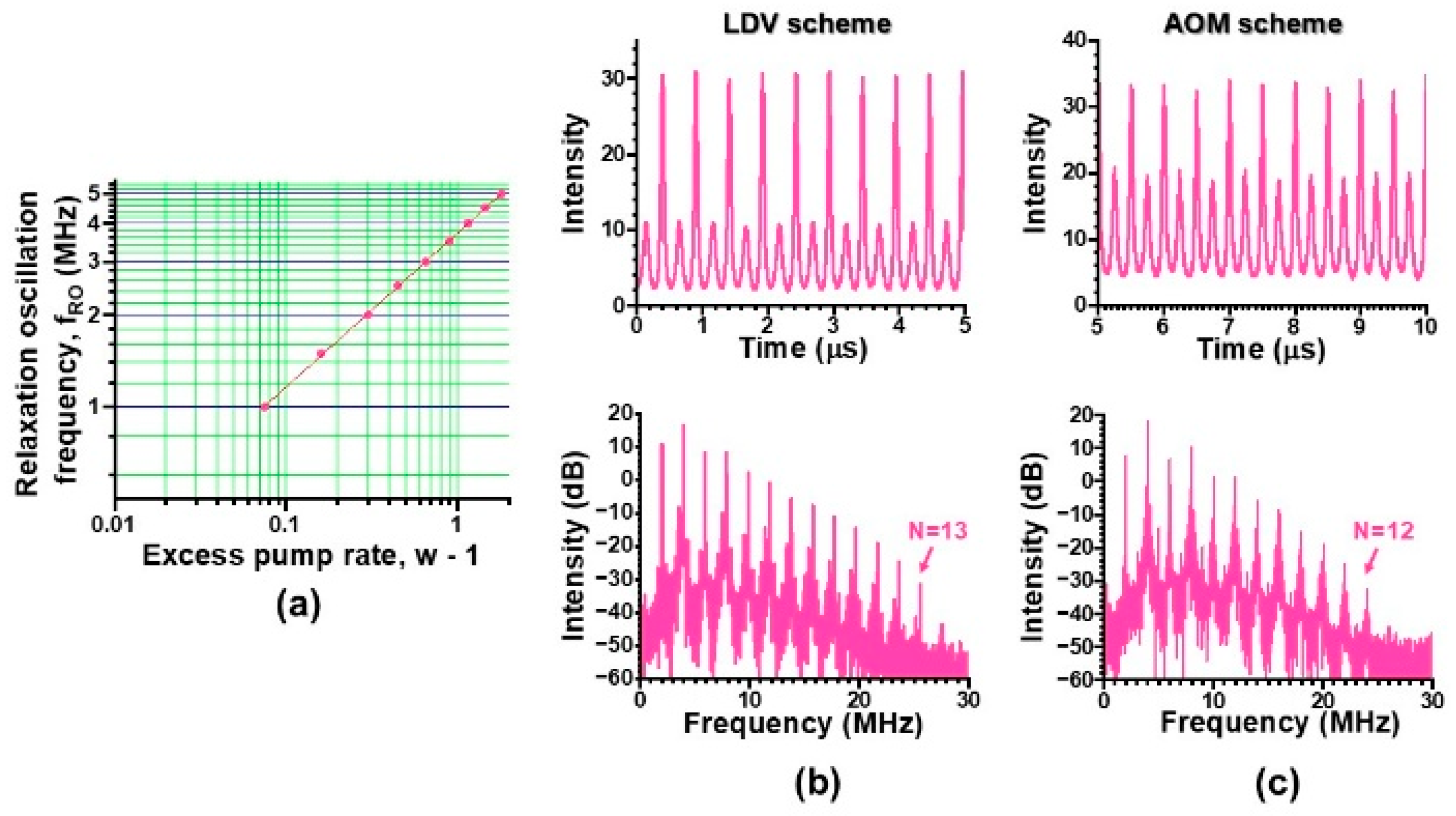
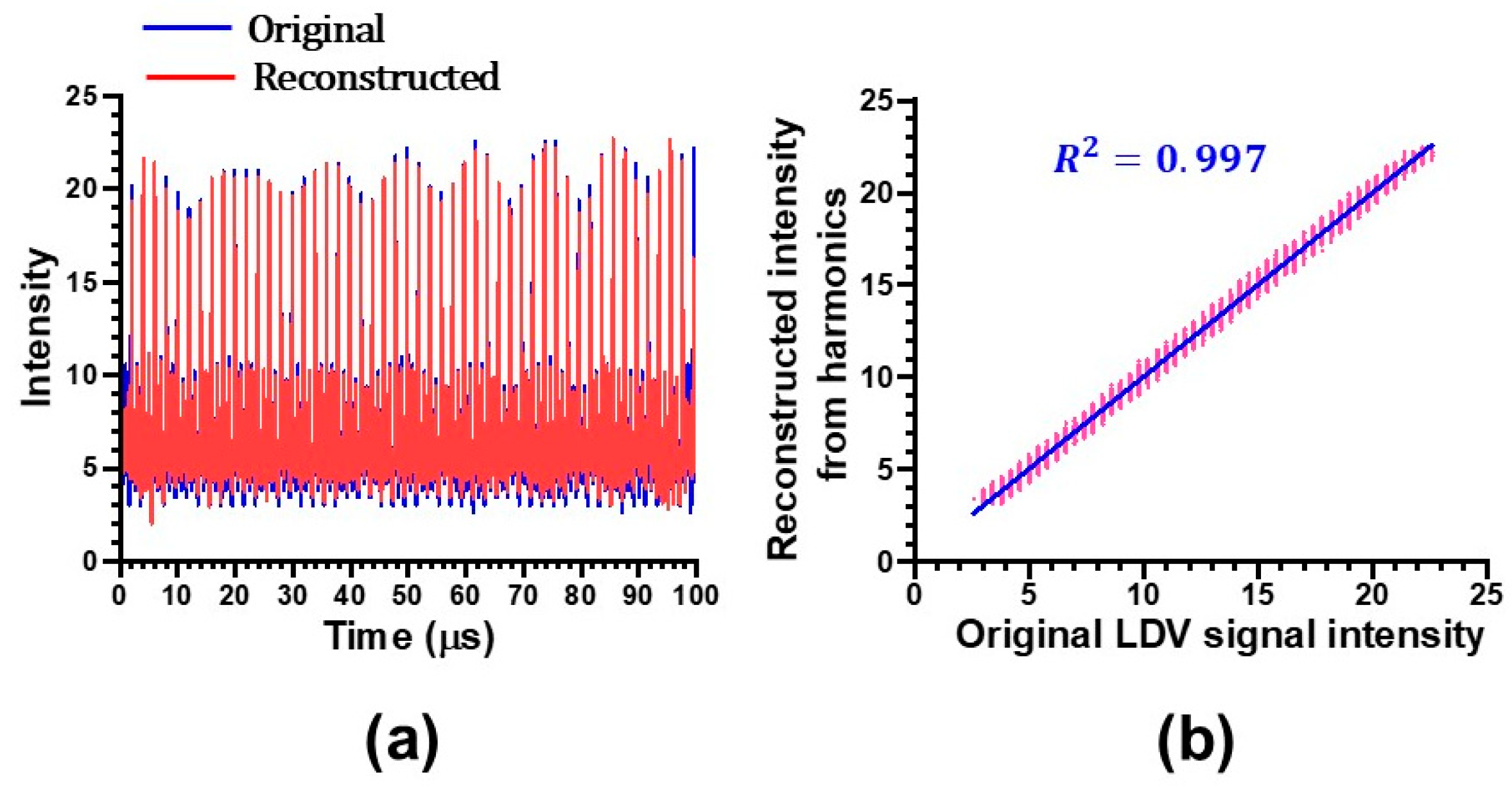
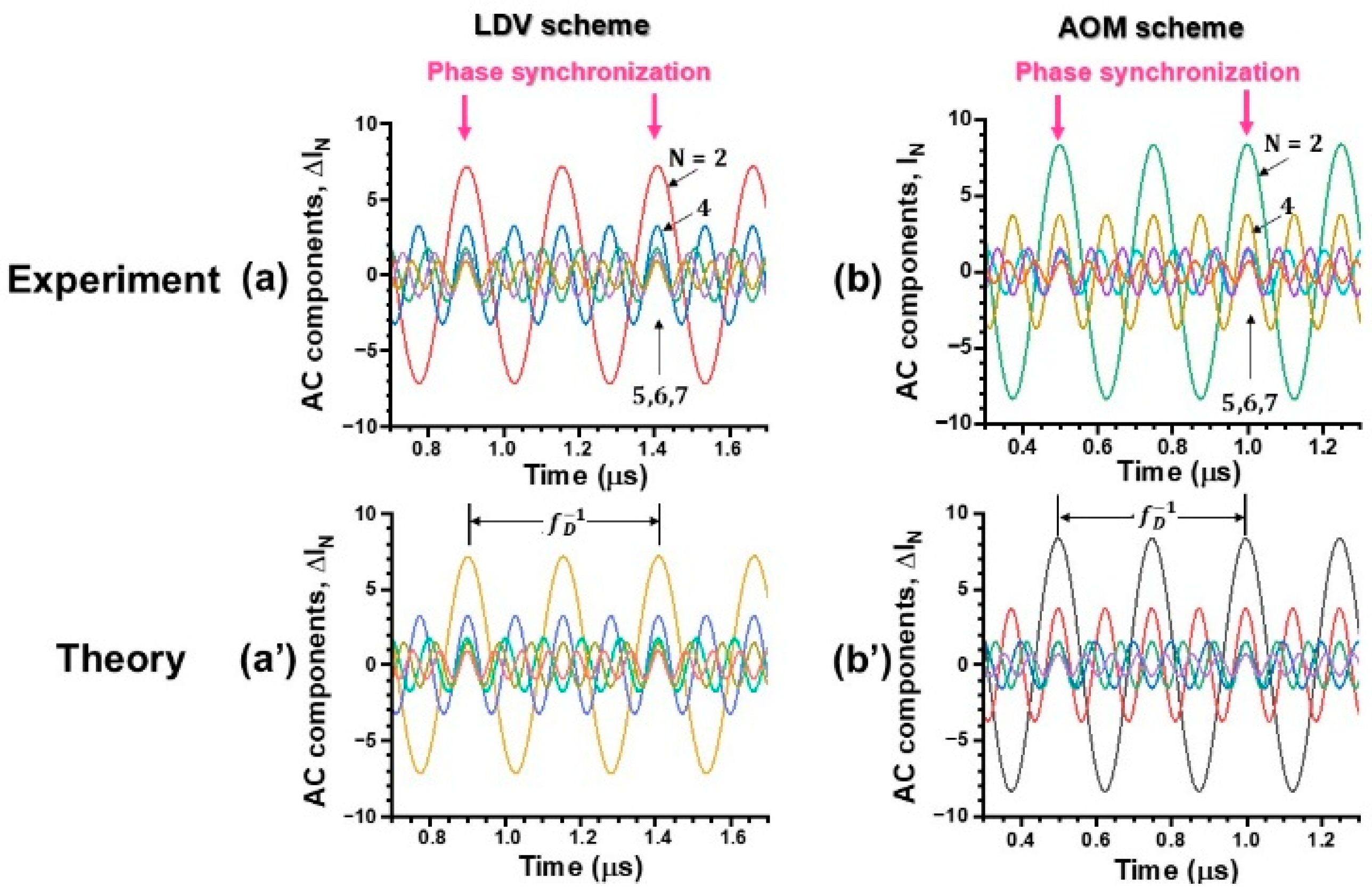
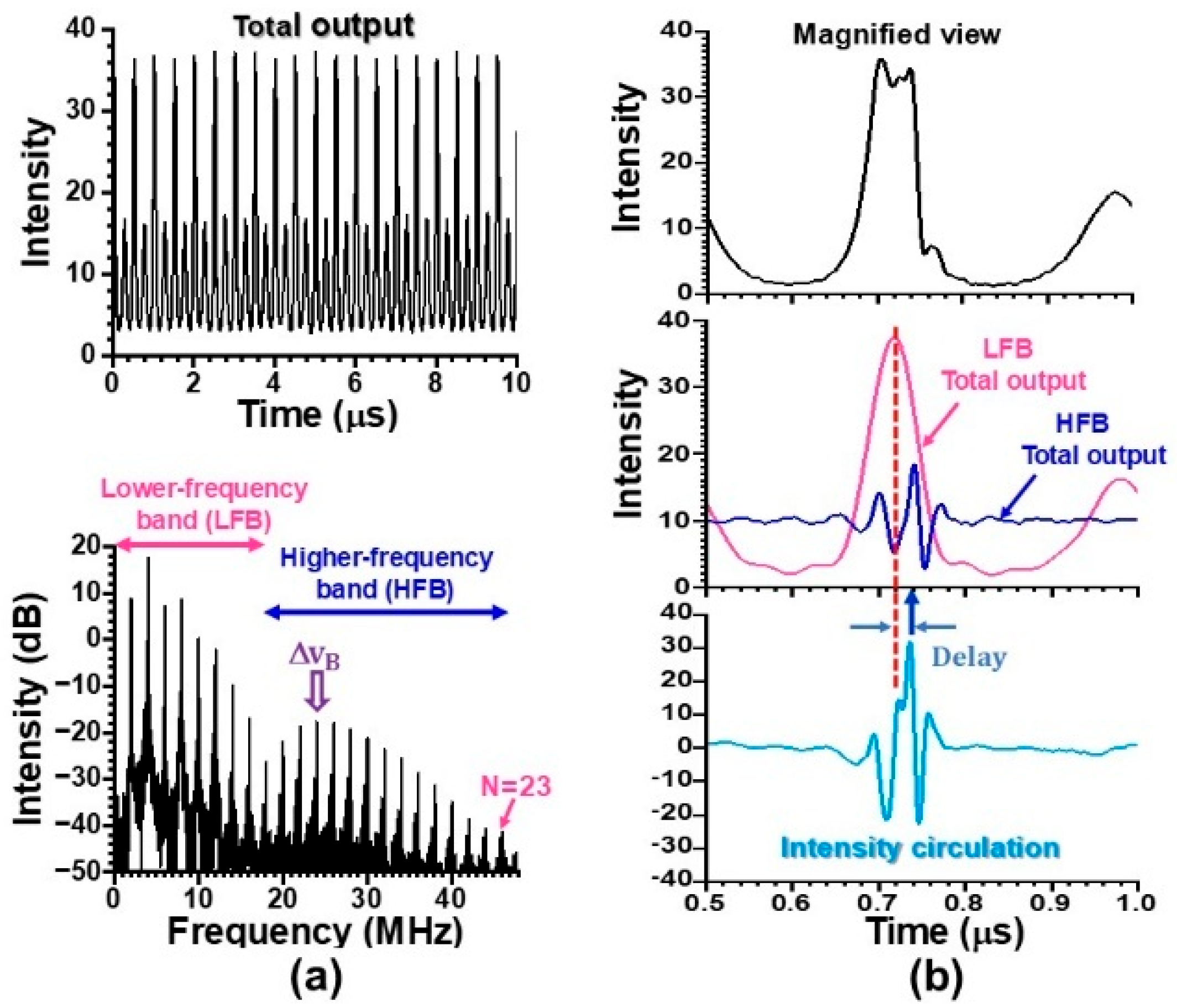
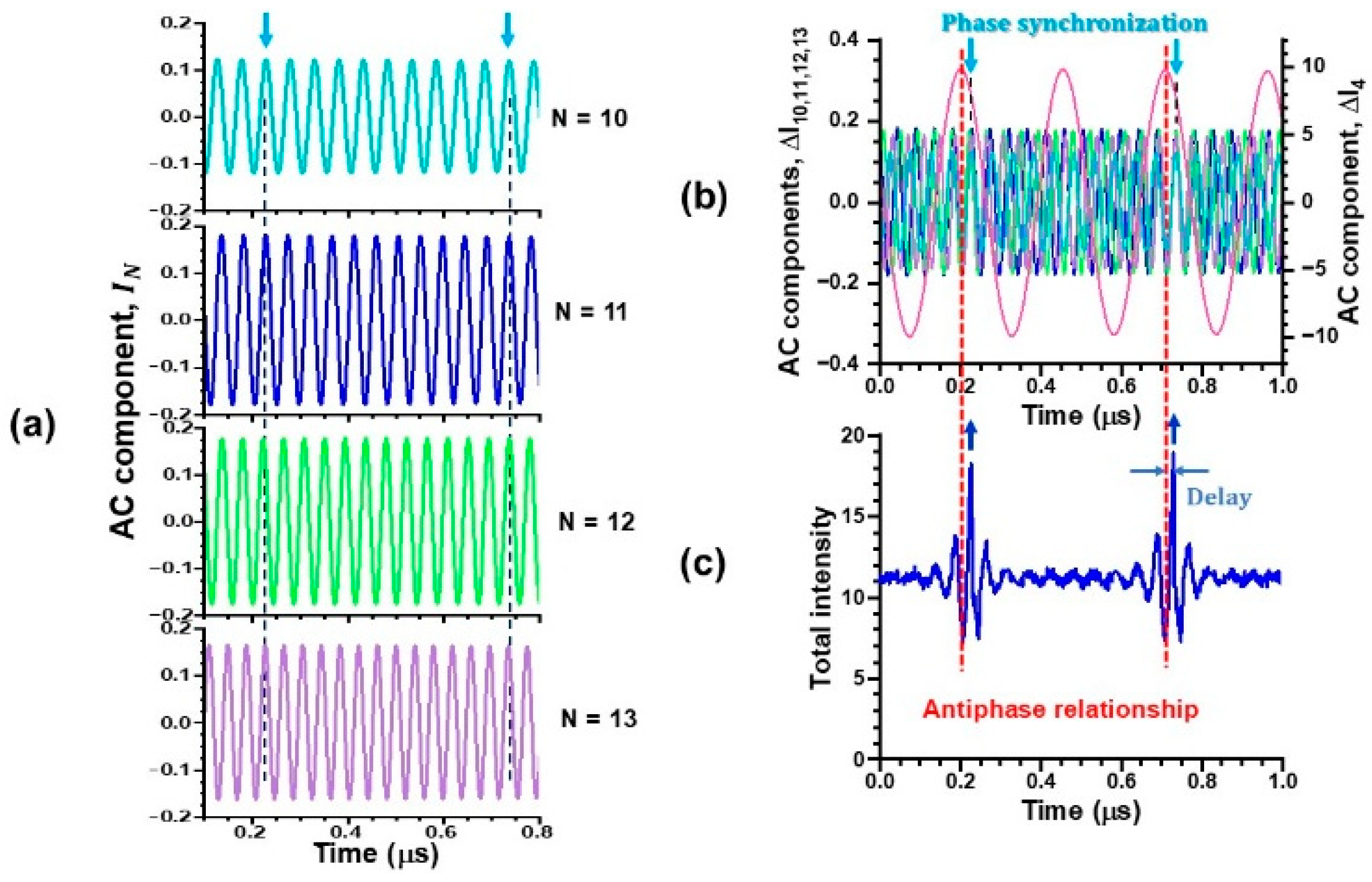
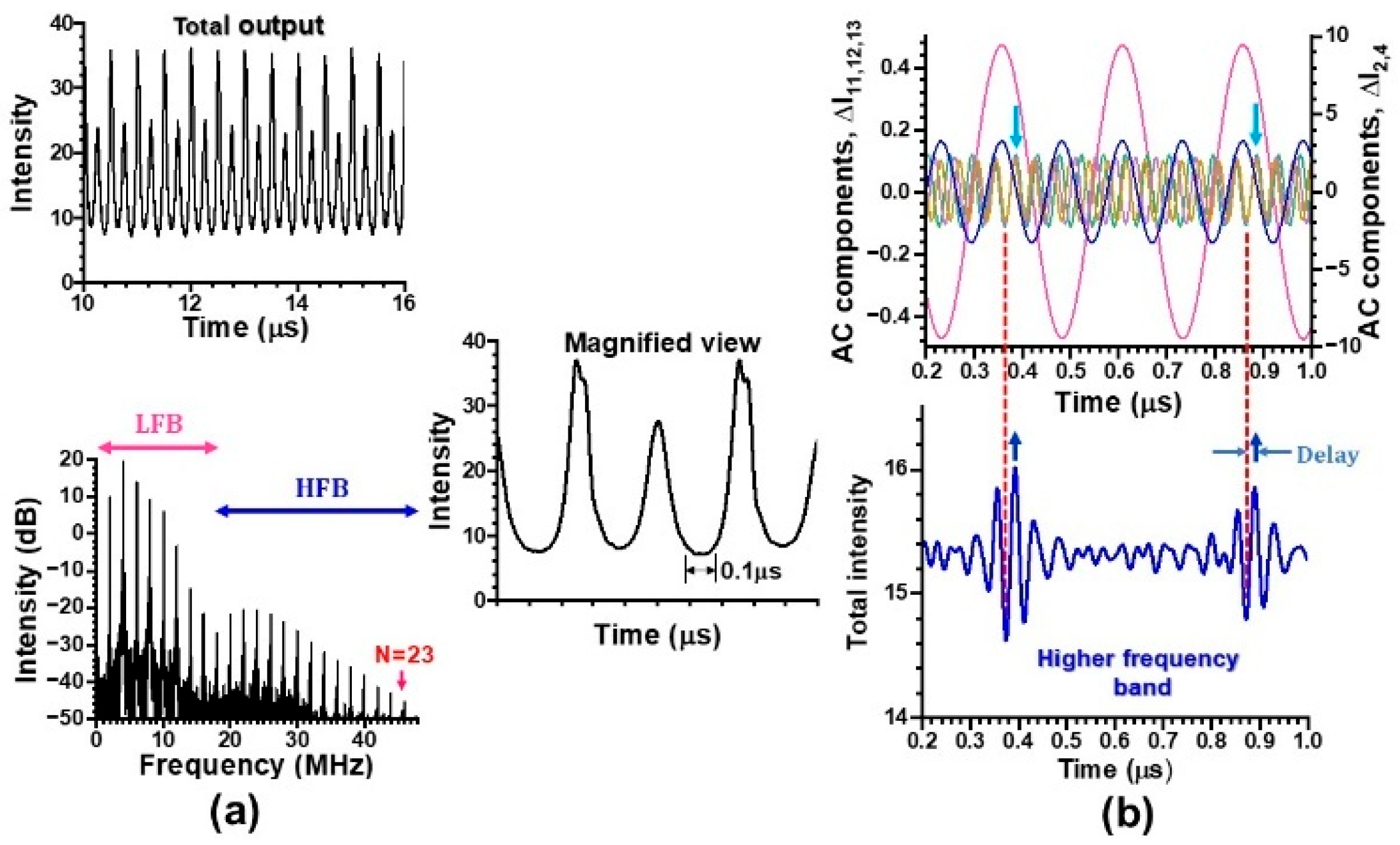
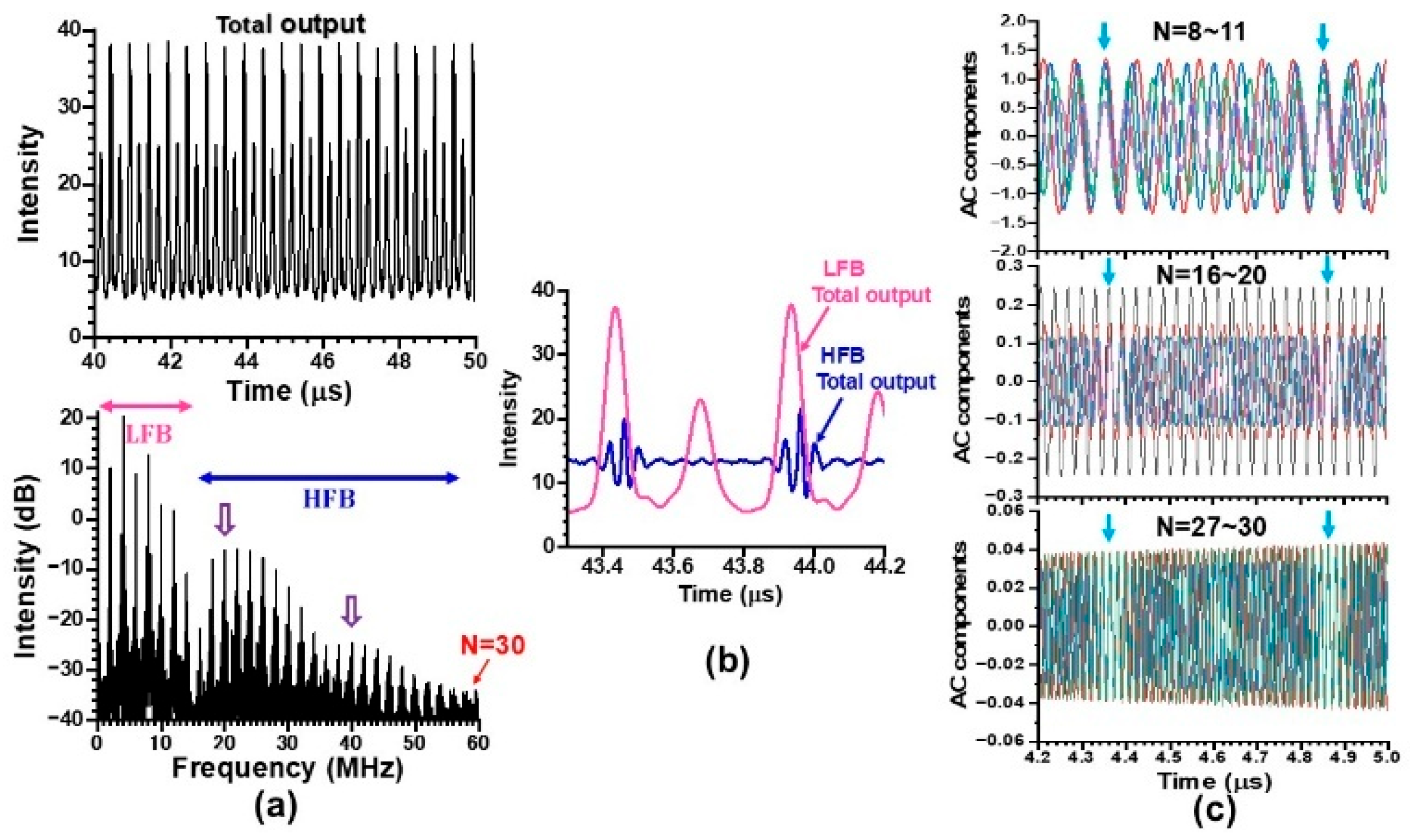
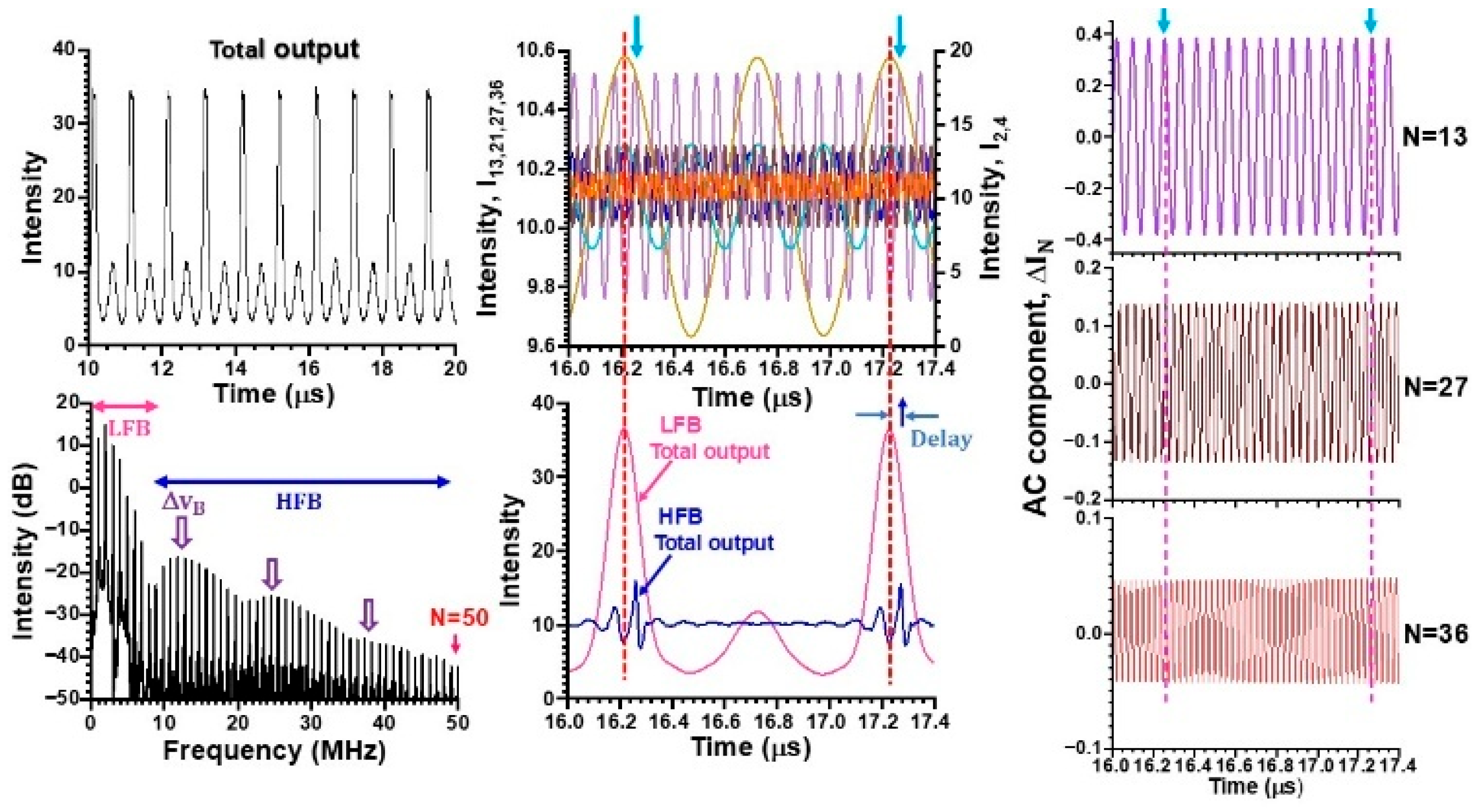
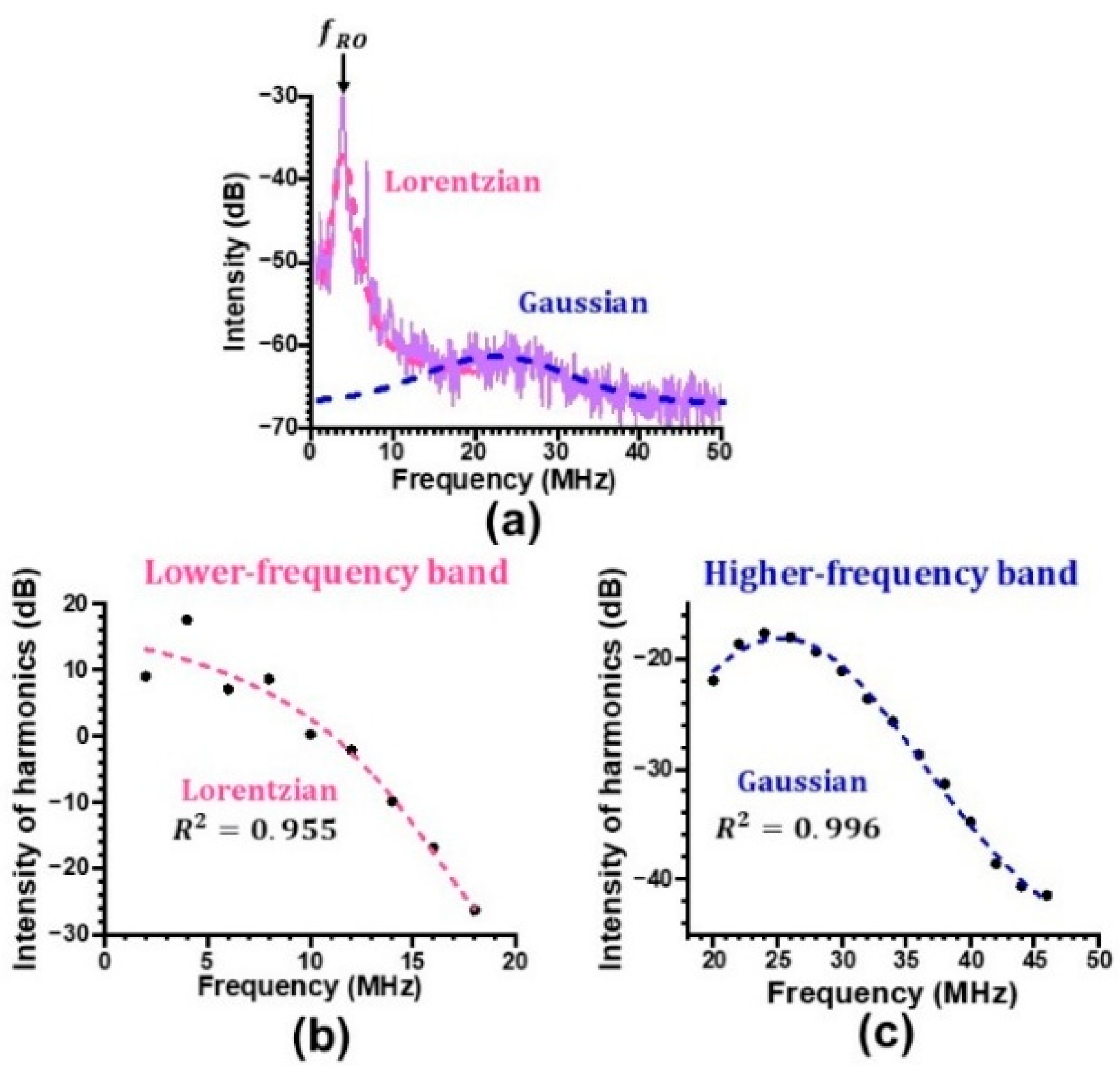
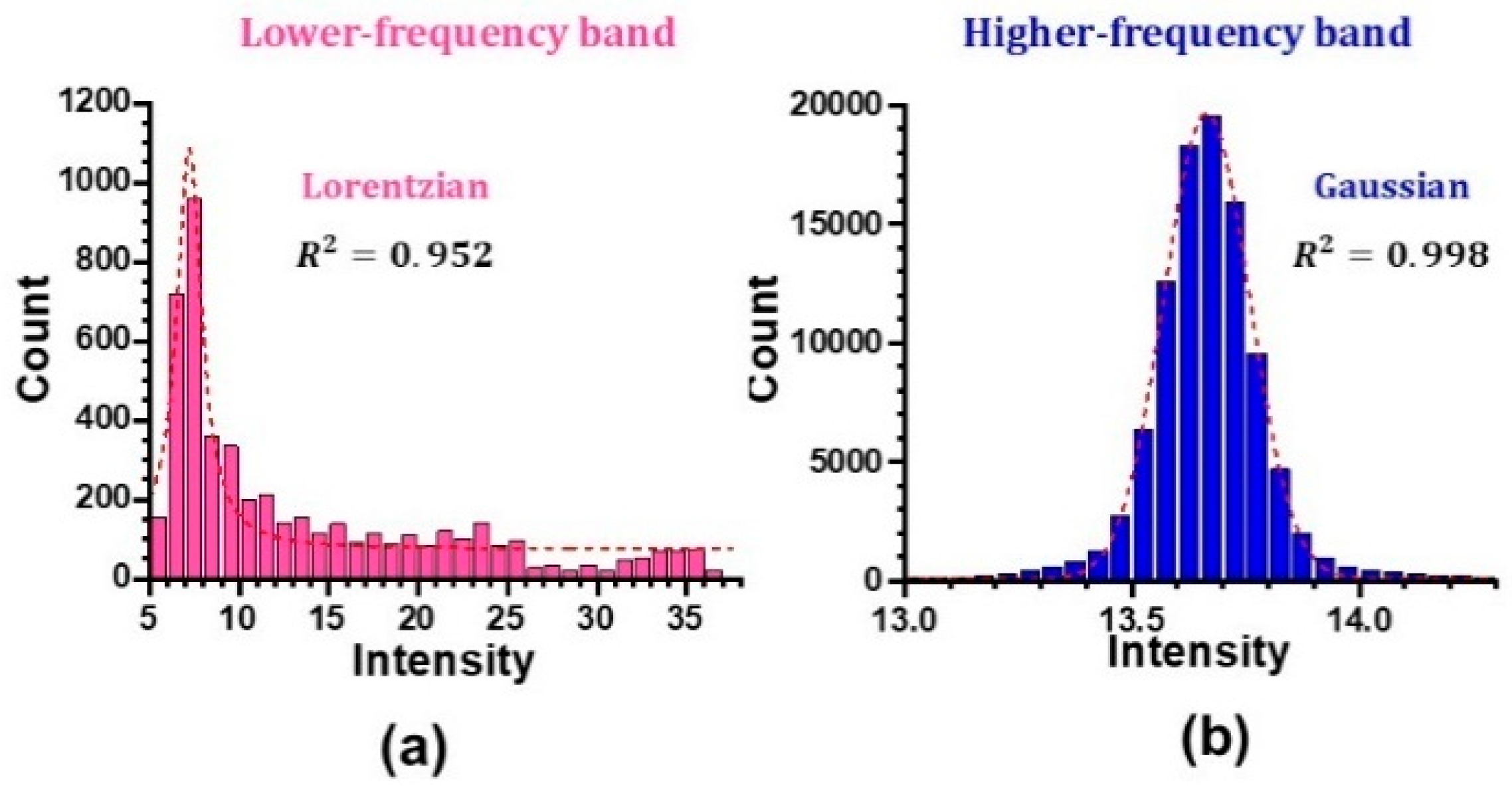
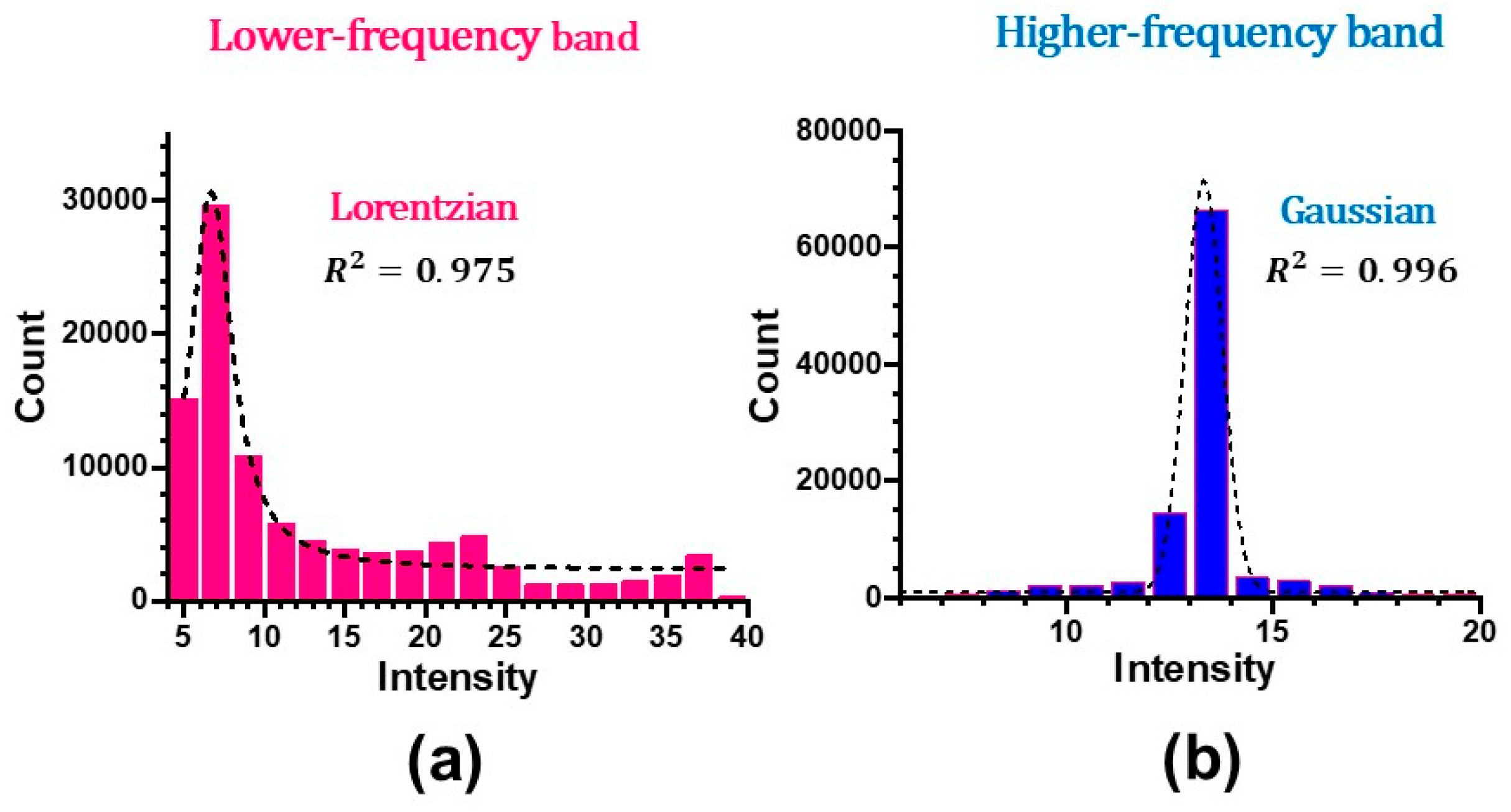
4. Statistical Properties of Collective Dynamics in Lower- and Higher-Frequency Bands
5. Summary and Outlook
References
- Kogelnikm, H.; Li, T. Laser beams and resonators. Appl. Opt. 1966, 5, 1550–1567. [Google Scholar] [CrossRef]
- Otsuka, K.; Chu, C.-S. Generation of vortex array beams from a thin-slice solid-state laser with shaped wide-aperture laser-diode pumping. Opt. Lett. 2009, 34, 10–13. [Google Scholar]
- Otsuka, K.; Chu, C.-S. Spontaneous generation of vortex and coherent vector beams from a thin-slice c-cut Nd:GdVO4 laser with wide-aperture laser-diode end pumping: application to highly sensitive rotational and translational Doppler velocimetry. Laser Phys. Lett. 2017, 14, 075002–1. [Google Scholar] [CrossRef]
- Otsuka, K.; Sudo, S. Self-mixing interference in a thin-slice solid-state laser with few feedback photons per observation period. Phys. Rev. A 2022, 106, 053504–1. [Google Scholar]
- Otsuka, K. Effects of external perturbations on LiNdP4O12 lasers. IEEE J.Quantum Electron. 1979, 15, 655–663. [Google Scholar] [CrossRef]
- Kawai, R.; Asakawa, Y.; Otsuka, K. Ultrahigh-sensitivity self-mixing laser Doppler velocimetry with laser-diode-pumped microchip LiNdP4O12 lasers. IEEE Photonics Tech. Lett. 1999, 11, 706–708. [Google Scholar]
- Lacot, E.; Day, R.; Pinel, J.; Stoeckel, F. Laser relaxation oscillation- frequency imaging. Opt. Lett. 200, 26, 1483–1485. [Google Scholar] [CrossRef] [PubMed]
- Otsuka, K.; Abe, K.; Ko, J.-Y.; Lim, T.-S. Real-time nanometer-vibration measurement with a self-mixing microchip solid-state laser. Opt. Lett. 2002, 27, 1339–1341. [Google Scholar] [PubMed]
- Sudo, S.; Otsuka, K. Self-mixing thinly sliced ruby laser for laser Doppler velocimetry with high optical sensitivity. Opt. Continuum 2024, 3, 2174–2189. [Google Scholar]
- Otsuka, K. Self-mixing thin-slice solid-state laser metrology. Sensors 2011, 11, 2195–2245. [Google Scholar] [CrossRef]
- Li, J.; Niu, H.; Ni, Y.-X. Laser feedback interferometry and applications: a review. Opt. Eng. 2017, 56, 050901–1. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-enhanced measurements: beating the standard quantum limit. Science 2004, 306, 1330–1336. [Google Scholar] [CrossRef]
- Mason, D.; Chen, J.; Rossi, M.; Tsaturyan, Y.; Schliesser, A. Continuous force and displacement measurement below the standard quantum limit. Nat. Phys. 2019, 15, 745–749. [Google Scholar] [CrossRef]
- Zhou, Z.-Y.; Ding, D.-S.; Jiang, Y.-K.; Li, Y.; Shuai, S.; Wang, X.-S.; Shi, B.S. Orbital angular momentum light frequency conversion and interference with quasi-phase matching crystals. Opt. Express 2014, 22, 20298–20310. [Google Scholar] [CrossRef] [PubMed]
- Nagata, T.; Okamoto, R.; O’Brien, R.J.; Sasaki, K.; Takeuchi, S. Beating the standard quantum limit with four-entangled photons. Science 2007, 316, 726–729. [Google Scholar] [CrossRef] [PubMed]
- Tian, N.; Tan, Y. Intracavity-dynamics-based optical phase amplifier with over tenfold amplification. Photonic Research 2023, 11, 1892–1901. [Google Scholar] [CrossRef]
- Georgi, P.; Massaro, M.; Luo, K.-H.; Sain, B.; Montaut, N.; Herrmann, H.; Weiss, T.; Li, G.; Silberhorn, C.; Zentgraf, T. Metasurface interferometry toward quantum sensors. Light Sci. Appl. 2019, 8, 1–7. [Google Scholar] [CrossRef]
- Asakawa, Y.; Kawai, R.; Ohki, K.; Otsuka, K. Laser-diode-pumped microchip LiNdP4O12 lasers under different pump-beam focusing conditions. Jpn. J. Appl. Phys. 1999, 38, L515–L517. [Google Scholar] [CrossRef]
- Salin, F.; Squier, J. Gain guiding in solid-state lasers. Opt. Lett. 1992, 17, 1352–1354. [Google Scholar] [CrossRef]
- Jacinto, C.; Messias, D.N.; Andrade, A.A.; Lima, S.M.; Baesso, M.L.; Catunda, T. Thermal lens and Z-scan measurements: Thermal and optical properties of laser glasses – A review. J. Non-Cryst. Solids 2006, 352, 3582–3597. [Google Scholar] [CrossRef]
- Godin, T.; Moncorgé, R.; Doualan, J.-L.; Fromager, M.; Ait-Ameur, K.; Antonio Cruz, A.; Catunda, T. Optically pump-induced athermal and nonresonant refractive index changes in the reference Cr-doped laser materials: Cr:GSGG and ruby. J. Opt. Soc. Am. 2012, 29, 1055–1064. [Google Scholar] [CrossRef]
- Otsuka, K. Self-mixng thin-slice solid-state laser Doppler velocimetry much less than one feeback photon per Doppler cycle. Opt. Lett. 2015, 40, 4603–4606. [Google Scholar] [CrossRef] [PubMed]
- Otsuka, K.; Aizawa, Y. Gain circulation in multimode lasers. Phys. Rev. Lett. 1994, 72, 2701–2704. [Google Scholar] [CrossRef] [PubMed]
- Otsuka, K.; Sato, Y.; Chern, J.-Y. Grouping of antiphase oscillations in modulated multimode lasers. Phys. Rev. A 1996, 54, 4464–4472. [Google Scholar] [CrossRef] [PubMed]
- Otsuka, K.; Mandel, P.; Georgiou, M.; Etrich, C. Antiphase dynamics in a modulated multimode laser. Japanese Journal of Applied Physics 1993, 32, L318–L321. [Google Scholar] [CrossRef]
- Taimre, T.; Nikolic, M.; Bertling, K.; Lim, Y.L.; Bosch, T.; Rakic, A.D. Laser feedback interferometry: a tutorial on the self-mixing effect for coherent sensing. Advances in Optics and Photonics 2015, 7, 570–631. [Google Scholar] [CrossRef]
- Lamela, H.; Roycroft, B.; Acedo, P.; Santos, R.; Carpintero, G. Experimental modulation bandwidth beyond the relaxation oscillation frequency in a monolithic twin-ridge laterally coupled diode laser based on lateral mode locking. Opt. Lett. 2002, 27, 303–305. [Google Scholar] [CrossRef]
- Dods, S.R.A.; Ogura, M.; Watanabe, M. Small-signal analysis of semiconductor lasers modulated at frequencies on the order of the beat frequency. IEEE J. Quantum. Electron. 1993, 29, 2631–2638. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



