A Generalized Contraction Framework for the Michelson-Morley Null Result in a Medium-Based Theory

1. Introduction

The Michelson–Morley experiment (1887) [1] aimed to detect Earth’s motion through a hypothetical medium for light propagation, historically termed the “ether.” The experiment’s null result, showing equal light travel times in orthogonal arms, challenged the existence of such a medium and paved the way for Einstein’s special relativity [2].

However, alternative interpretations proposing a medium—modeled as a property of space itself or a field—have persisted [3,4]. This paper reexamines the experiment within the reference frame of a hypothetical propagation medium, deriving a general relationship between longitudinal and transverse dimensional changes that explains the null result while maintaining a medium-based approach.

This analysis is conducted strictly within the framework of a hypothetical medium. It should not be conflated with the length contraction derived in Einstein’s special relativity, which is a consequence of the relativity of simultaneity and does not involve a preferred frame.

2. Historical Background

In the late 19th century, the luminiferous ether was hypothesized as the medium for light propagation. Michelson and Morley [1] designed an interferometer to detect Earth’s motion relative to this medium, expecting interference fringe shifts due to differing light travel times. The null result contradicted expectations, prompting Lorentz [5] to propose length contraction in the direction of motion, later generalized by FitzGerald [6]. Einstein’s special relativity [2] explained the null result without a medium, but medium-based models have been proposed [3,4,7], motivating this generalized analysis.

3. Definitions

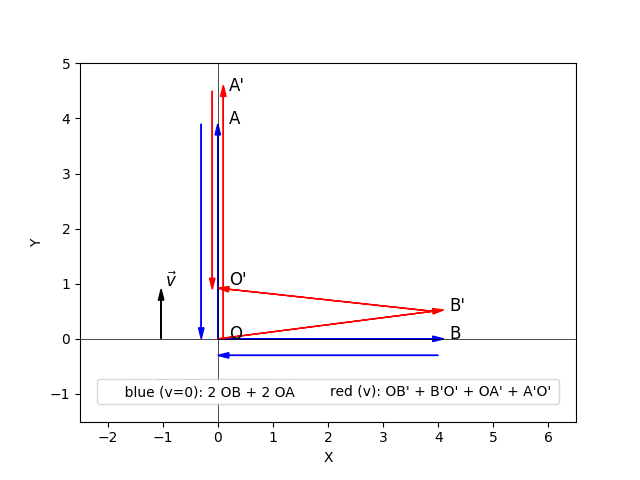
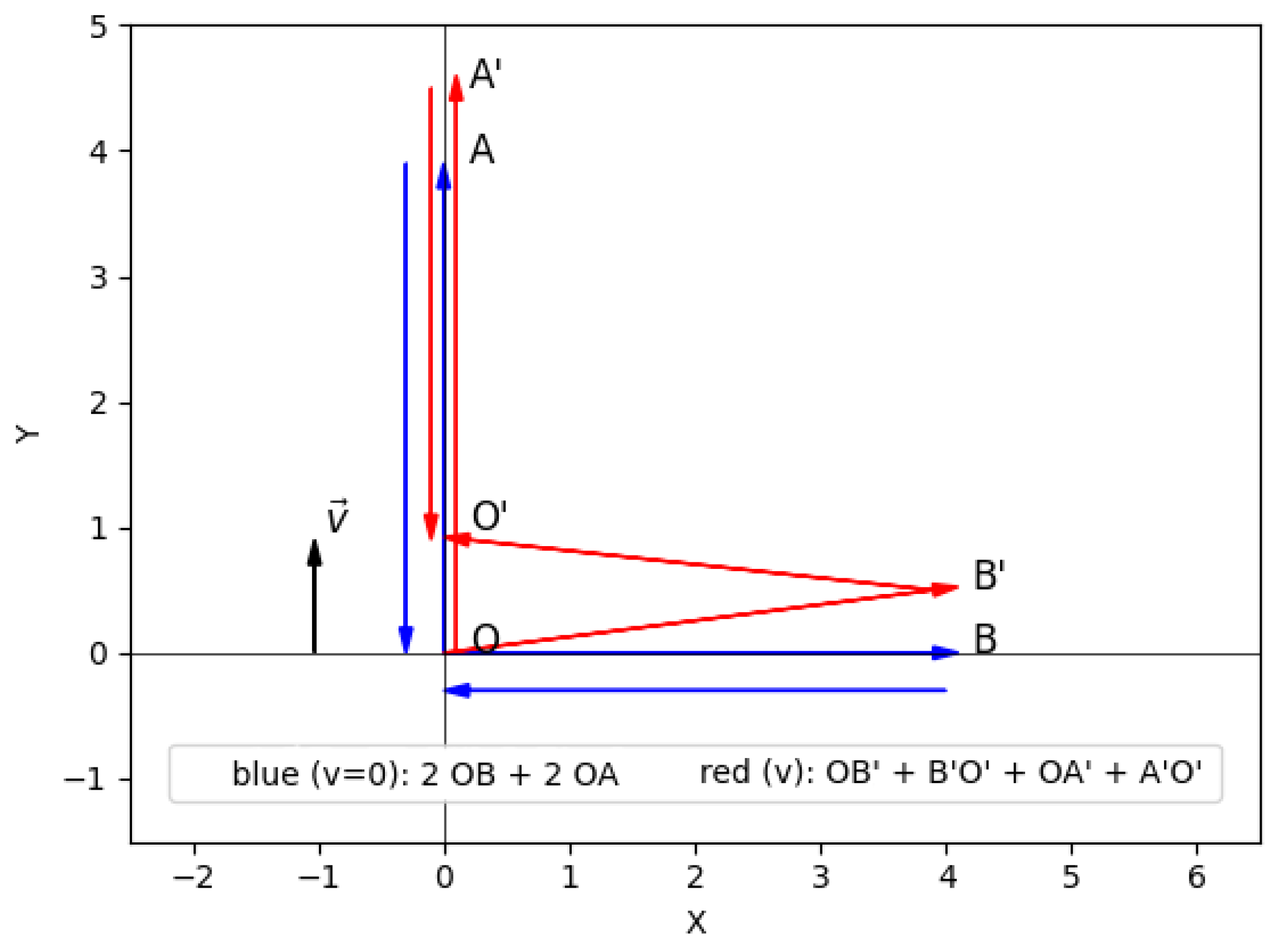
For the light travel time in the medium to be identical along each arm when the interferometer moves at speed v, the arm lengths must change relative to their rest lengths $L_0$.

We consider the interferometer in the reference frame of a hypothetical medium, modeled as a property of space or a field, through which light propagates at speed c. We define:

• $\Delta L_{\mathrm{long}}$: length variation of the longitudinal arm, $L_{\mathrm{long}}=L_0+\Delta L_{\mathrm{long}}$
• $\Delta L_{\mathrm{trans}}$: length variation of the transverse arm, $L_{\mathrm{trans}}=L_0+\Delta L_{\mathrm{trans}}$
• Both $\Delta L_{\mathrm{long}}$ and $\Delta L_{\mathrm{trans}}$ represent dimensional changes and can be positive (expansion) or negative (contraction)
• $L_0$: proper arm length when the interferometer is at rest relative to the propagation medium

Our goal is to find the relationship between $\Delta L_{\mathrm{trans}}$ and $\Delta L_{\mathrm{long}}$ that ensures equal light travel times in both arms.

Longitudinal Arm Analysis

For the longitudinal arm (parallel to motion), the light path in the medium frame is:

Forward trip (from O to A’):

$$t_1={\displaystyle \frac{L_0+\Delta L_{\mathrm{long}}+v.t_1}{c}}=>t_1={\displaystyle \frac{L_0+\Delta L_{\mathrm{long}}}{c(1-v/c)}}$$

Return trip (from A’ to O’):

$$t_2={\displaystyle \frac{L_0+\Delta L_{\mathrm{long}}-v.t_2}{c}}=>t_2={\displaystyle \frac{L_0+\Delta L_{\mathrm{long}}}{c(1+v/c)}}$$

Total round-trip time ($t_1+t_2$):

$$t_{\mathrm{long}}={\displaystyle \frac{(L_0+\Delta L_{\mathrm{long}})(1+v/c)}{c(1+v/c)(1-v/c)}}+{\displaystyle \frac{(L_0+\Delta L_{\mathrm{long}})(1-v/c)}{c(1+v/c)(1-v/c)}}={\displaystyle \frac{2(L_0+\Delta L_{\mathrm{long}})}{c(1-v^2/c^2)}}$$

4. Transverse Arm Analysis

For the transverse arm:

• Transverse component of the speed of light: $c_t=c\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}$
• Forward trip time:

  $$t_{\mathrm{forward}}={\displaystyle \frac{L_0+\Delta L_{\mathrm{trans}}}{c\sqrt{1-\frac{v^2}{c^2}}}}$$
• One-way path length:

  $$d_{\mathrm{forward}}={\displaystyle \frac{L_0+\Delta L_{\mathrm{trans}}}{\sqrt{1-\frac{v^2}{c^2}}}}$$
• Round-trip distance:

  $$d_{\mathrm{transverse}}={\displaystyle \frac{2(L_0+\Delta L_{\mathrm{trans}})}{\sqrt{1-\frac{v^2}{c^2}}}}$$
• Total time:

  $$t_{\mathrm{transverse}}={\displaystyle \frac{2(L_0+\Delta L_{\mathrm{trans}})}{c\sqrt{1-\frac{v^2}{c^2}}}}$$

Derivation of $t_{\mathrm{transverse}}$ Using Figure 1

Distance traveled by light in the medium: $d_{\mathrm{total}}=d_{O{B}^{\prime }}+d_{B^{\prime }{O}^{\prime }}=2·d_{O{B}^{\prime }}$

Travel time: $t_{O{O}^{\prime }}={\displaystyle \frac{d_{O{O}^{\prime }}}{v}}={\displaystyle \frac{2·d_{O{B}^{\prime }}}{c}}$

Let us consider the travel durations between the points:

$$t_{O{O}^{\prime }}={\displaystyle \frac{2·d_{O{B}^{\prime }}}{c}}\Rightarrow t_{O{O}^{\prime }}={\displaystyle \frac{2\sqrt{{(L_0+\Delta L_{\mathrm{trans}})}^2+d_{B{B}^{\prime }}^2}}{c}}$$

$$d_{B{B}^{\prime }}={\displaystyle \frac{d_{O{O}^{\prime }}}{2}}={\displaystyle \frac{t_{O{O}^{\prime }}·v}{2}}\Rightarrow t_{O{O}^{\prime }}={\displaystyle \frac{2\sqrt{{(L_0+\Delta L_{\mathrm{trans}})}^2+{(v·t_{O{O}^{\prime }})}^2/4}}{c}}$$

$$Squaring:{\left(t_{O{O}^{\prime }}\right)}^2={\displaystyle \frac{4\left({(L_0+\Delta L_{\mathrm{trans}})}^2+{(v·t_{O{O}^{\prime }})}^2/4\right)}{c^2}}$$

$$Factoring:{\left(t_{O{O}^{\prime }}\right)}^2\left(1-{\displaystyle \frac{v^2}{c^2}}\right)={\displaystyle \frac{4{(L_0+\Delta L_{\mathrm{trans}})}^2}{c^2}}\Rightarrow t_{O{O}^{\prime }}={\displaystyle \frac{2(L_0+\Delta L_{\mathrm{trans}})}{c\sqrt{1-v^2/c^2}}}$$

5. Equality Condition

Equal travel times require:

$$t_{\mathrm{longitudinal}}=t_{\mathrm{transverse}}$$

$${\displaystyle \frac{2(L_0+\Delta L_{\mathrm{long}})}{c(1-v^2/c^2)}}={\displaystyle \frac{2(L_0+\Delta L_{\mathrm{trans}})}{c\sqrt{1-\frac{v^2}{c^2}}}}$$

Thus:

$${\displaystyle \frac{L_0+\Delta L_{\mathrm{long}}}{L_0+\Delta L_{\mathrm{trans}}}}=\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}$$

(1)

Table 1. Complete analysis of light paths in the Michelson-Morley experiment (medium frame)

Parameter	Longitudinal Arm	Transverse Arm
Arm length at velocity v	$L_0+\Delta L_{\mathrm{long}}$	$L_0+\Delta L_{\mathrm{trans}}$
Round-trip time	${\displaystyle \frac{2(L_0+\Delta L_{\mathrm{long}})}{c(1-v^2/c^2)}}$	${\displaystyle \frac{2(L_0+\Delta L_{\mathrm{trans}})}{c\sqrt{1-v^2/c^2}}}$
Null result condition	${\displaystyle \frac{L_0+\Delta L_{\mathrm{long}}}{L_0+\Delta L_{\mathrm{trans}}}}=\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}$
Lorentz-FitzGerald special case	$L_0+\Delta L_{\mathrm{long}}=L_0\sqrt{1-v^2/c^2},\Delta L_{\mathrm{trans}}=0$

Table 1. Complete analysis of light paths in the Michelson-Morley experiment (medium frame)

Parameter	Longitudinal Arm	Transverse Arm
Arm length at velocity v	$L_0+\Delta L_{\mathrm{long}}$	$L_0+\Delta L_{\mathrm{trans}}$
Round-trip time	${\displaystyle \frac{2(L_0+\Delta L_{\mathrm{long}})}{c(1-v^2/c^2)}}$	${\displaystyle \frac{2(L_0+\Delta L_{\mathrm{trans}})}{c\sqrt{1-v^2/c^2}}}$
Null result condition	${\displaystyle \frac{L_0+\Delta L_{\mathrm{long}}}{L_0+\Delta L_{\mathrm{trans}}}}=\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}$
Lorentz-FitzGerald special case	$L_0+\Delta L_{\mathrm{long}}=L_0\sqrt{1-v^2/c^2},\Delta L_{\mathrm{trans}}=0$

6. Invariance of the Null Result for an Arbitrary Initial Velocity

Regardless of the interferometer’s velocity v relative to the medium, the experimental outcome remains null. When the relative velocity changes during the experiment (due to Earth’s rotation, for example), the arm lengths adjust dynamically according to the new velocity. The experimental result remains null at all times.

For this result to be maintained consistently for any orientation and velocity relative to the medium, the model must assume that the dimensional changes affect the interferometer and any material measuring device proportionally. This hypothesis ensures the internal consistency of the model, as the deformation, while ’absolute’ relative to the medium, would be undetectable by local length measurements. The physical mechanism underlying these universal deformations is explained by modeling matter as wave-based structures, an approach we develop comprehensively in the subsequent article of this series. In that framework, particles are described as standing wave patterns whose spatial properties necessarily transform with motion relative to the medium.

The Lorentz-FitzGerald Special Case

The pre-relativistic Lorentz-FitzGerald contraction postulate corresponds to the specific case where $\Delta L_{\mathrm{trans}}=0$ (no transverse deformation), requiring:

$$\Delta L_{\mathrm{long}}=L_0\left(\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}-1\right)\Rightarrow \Delta L_{\mathrm{long}}<0(\mathrm{longitudinal}\mathrm{arm}\mathrm{contraction})$$

This special case represents one specific, mathematically simplest solution among the infinity of solutions satisfying the general condition. The Michelson-Morley experiment alone cannot distinguish this special case from other solutions; it only constrains the deformation ratio.

7. Discussion

The fundamental condition we have derived, ${\displaystyle \frac{L_0+\Delta L_{\mathrm{long}}}{L_0+\Delta L_{\mathrm{trans}}}}=\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}$, ensures the Michelson-Morley null result in a medium-based framework. The principal features of this framework are:

• At $v=0$ (interferometer at rest relative to the medium), $\Delta L_{\mathrm{long}}=\Delta L_{\mathrm{trans}}=0$, implying no anisotropic dimensional changes.
• For $0<v<c$, the ratio $(L_0+\Delta L_{\mathrm{long}})/(L_0+\Delta L_{\mathrm{trans}})$ is fixed by the Lorentz factor.
• In the special case where $\Delta L_{\mathrm{trans}}=0$ (Lorentz-FitzGerald postulate), the longitudinal arm contracts according to $\Delta L_{\mathrm{long}}=L_0(\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}-1)$.
• The generality of this framework - where only the ratio between deformations is constrained - allows for various physical interpretations beyond the specific Lorentz-FitzGerald case. Different medium properties (isotropic or anisotropic) would correspond to different functional forms for $\Delta L_{\mathrm{long}}$ and $\Delta L_{\mathrm{trans}}$, all while satisfying the same fundamental constraint from the null result.

7.1. Implications and Falsifiability

A key strength of this generalized framework is its falsifiability. While the Michelson-Morley experiment only constrains the ratio of deformations, other experimental configurations could, in principle, break this degeneracy and measure the absolute dimensional changes.

If future experiments were able to independently measure the longitudinal and transverse dimensions of an object moving at high velocity relative to a hypothetical preferred frame—for instance, through matter-wave interferometry or advanced resonator techniques that are sensitive to absolute lengths rather than round-trip light travel times—they could directly test the specific values of $\Delta L_{\mathrm{long}}$ and $\Delta L_{\mathrm{trans}}$.

A measurement of a non-zero transverse deformation ($\Delta L_{\mathrm{trans}}\ne 0$) would challenge both special relativity and the original Lorentz hypothesis, pointing towards a more complex medium-interaction mechanism. Conversely, a null result for both deformations in such an experiment would falsify the entire class of models based on physical length changes and strongly support the geometric interpretation of special relativity.

This approach provides a mathematical foundation for exploring alternative medium-based theories without contradicting the Michelson-Morley experimental evidence. It demonstrates that the null result does not necessarily imply the absence of a medium, but rather imposes a very specific relationship between longitudinal and transverse deformations that any motion relative to such a medium would induce.

7.2. Theoretical Framework Versus Operational Tool

The fundamental relationship we have derived is established within the theoretical framework of a propagation medium and requires knowledge of the velocity v relative to that medium. This approach provides a conceptually coherent interpretation of the Michelson-Morley null result from a medium-based perspective.

However, a crucial distinction must be made between theoretical coherence and operational utility. In practice, we only have access to relative velocities between inertial frames, not to an absolute velocity relative to a hypothetical medium. This fundamental experimental constraint makes Einstein’s special relativity an indispensable tool for all practical calculations and predictions.

The model presented here and special relativity should therefore be viewed as complementary rather than antagonistic:

• Special relativity provides the operational mathematical framework for all practical computations and is verified by countless experiments.
• The medium-based framework offers an alternative physical interpretation that may prove fruitful for rethinking the foundations of cosmology and astrophysics, particularly in understanding the deep structure of the universe at cosmological scales.

This duality is not unlike that between quantum mechanics and classical physics: although the former provides a more fundamental description, the latter remains essential for most practical applications. Similarly, the pursuit of medium-based models, despite their immediate operational limitations, may open new perspectives for understanding universal properties that remain hidden in the purely relativistic description.

7.3. Experimental Pathway to Absolute Motion Detection

A remarkable implication of this theoretical framework is that it offers a potential pathway to measure absolute motion relative to the medium. If experimental techniques were developed to directly measure the ratio $R\left(v\right)={\displaystyle \frac{L_0+\Delta L_{\mathrm{long}}}{L_0+\Delta L_{\mathrm{trans}}}}$ from different inertial frames with known relative velocity $\Delta v$, one could solve the equation:

$${\displaystyle \frac{R(v_1+\Delta v)}{R\left(v_1\right)}}={\displaystyle \frac{\sqrt{1-\frac{{(v_1+\Delta v)}^2}{c^2}}}{\sqrt{1-\frac{v_1^2}{c^2}}}}$$

where the left-hand side is experimentally measured and $\Delta v$ is the known relative velocity between frames. Measurement of the left-hand side would uniquely determine $v_1$, the absolute velocity relative to the medium.

This approach differs fundamentally from historical ether-drift experiments by measuring dimensional ratios rather than light travel times, potentially offering enhanced sensitivity.

8. Conclusions

The Michelson–Morley null result can be reproduced in a medium-based framework through the derived relationship between longitudinal and transverse dimensional changes. This approach generalizes the Lorentz contraction and demonstrates that medium-based interpretations remain consistent with experimental evidence while providing a physically intuitive mechanism for the null result.

The key insight of this framework is its distinction between the theoretical description involving motion relative to a medium and the operational necessity of using relative velocities in practical physics. While special relativity remains the essential tool for all experimental and theoretical work in fundamental physics, our medium-based interpretation offers complementary insights that may prove valuable for addressing outstanding cosmological questions and for conceptualizing the deep structure of space-time.

The framework’s falsifiable character–through the potential measurement of absolute velocity via length ratio comparisons–provides a clear experimental pathway for future validation or refutation. This positions medium-based theories not as competitors to operational relativity, but as complementary explorations of physics beyond the current phenomenological description, maintaining empirical consistency while offering new perspectives on the nature of space and time.