Submitted:
23 September 2025
Posted:
24 September 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Context of Chaotic Dynamics
1.2. Methods
1.3. Results
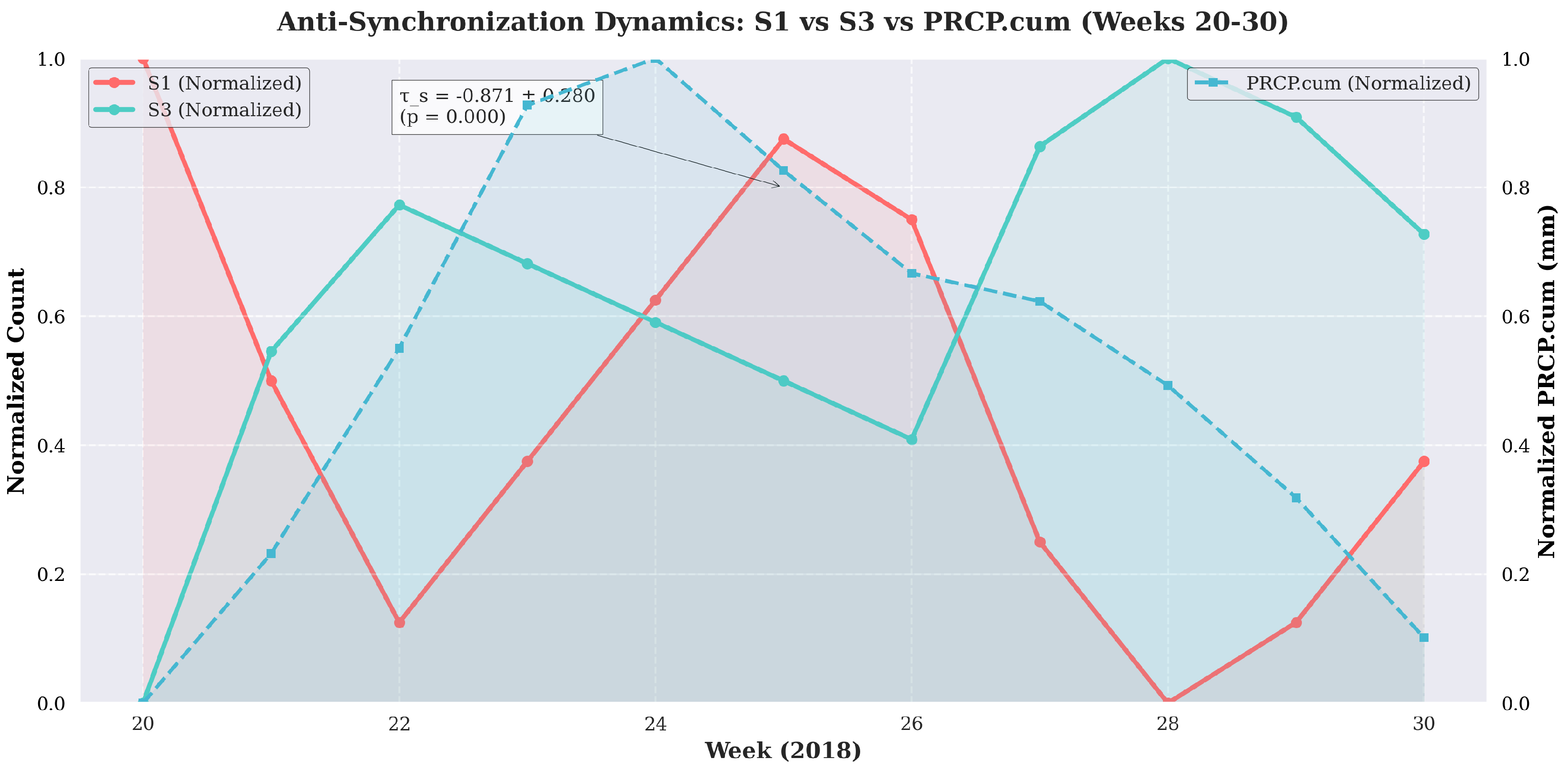
| Weeks | p-value | t-value | PRCP.cum (mm) | |
|---|---|---|---|---|
| 20-30, 2018 | 0.064 | -2.89 | 9.4 | |
| 45-50, 2018 | - | 12.1 |
| r Range | Noise (%) | p-value | ||
|---|---|---|---|---|
| 1.0 (Standard) | 3.6-4.0 | 5-15 | 0.036 to | - |
| 0.9 | 3.8 | 10-15 | 0.045 | |
| 0.8 | 3.8 | 10-15 | -0.35 to -0.40 | 0.030 |
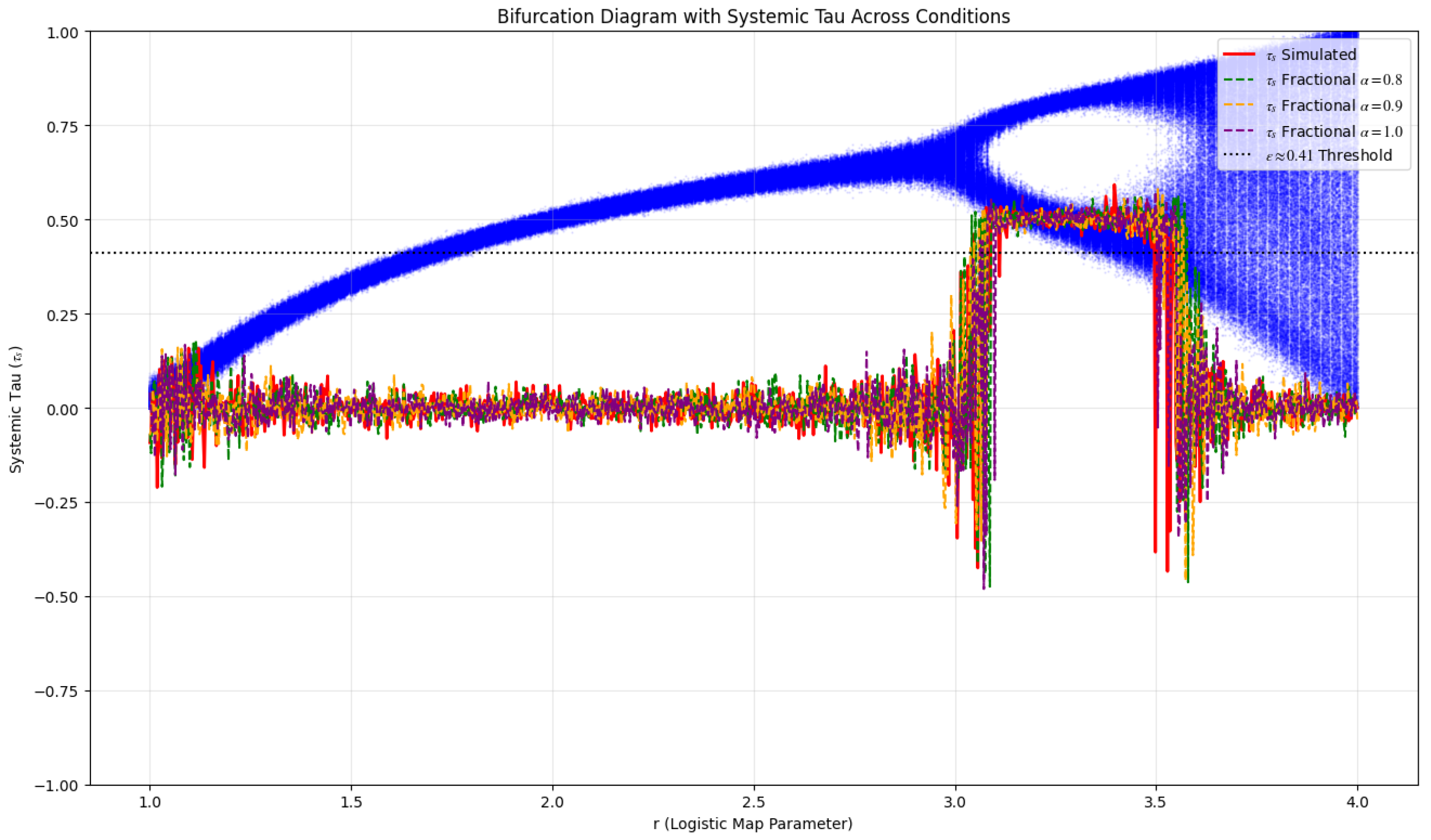
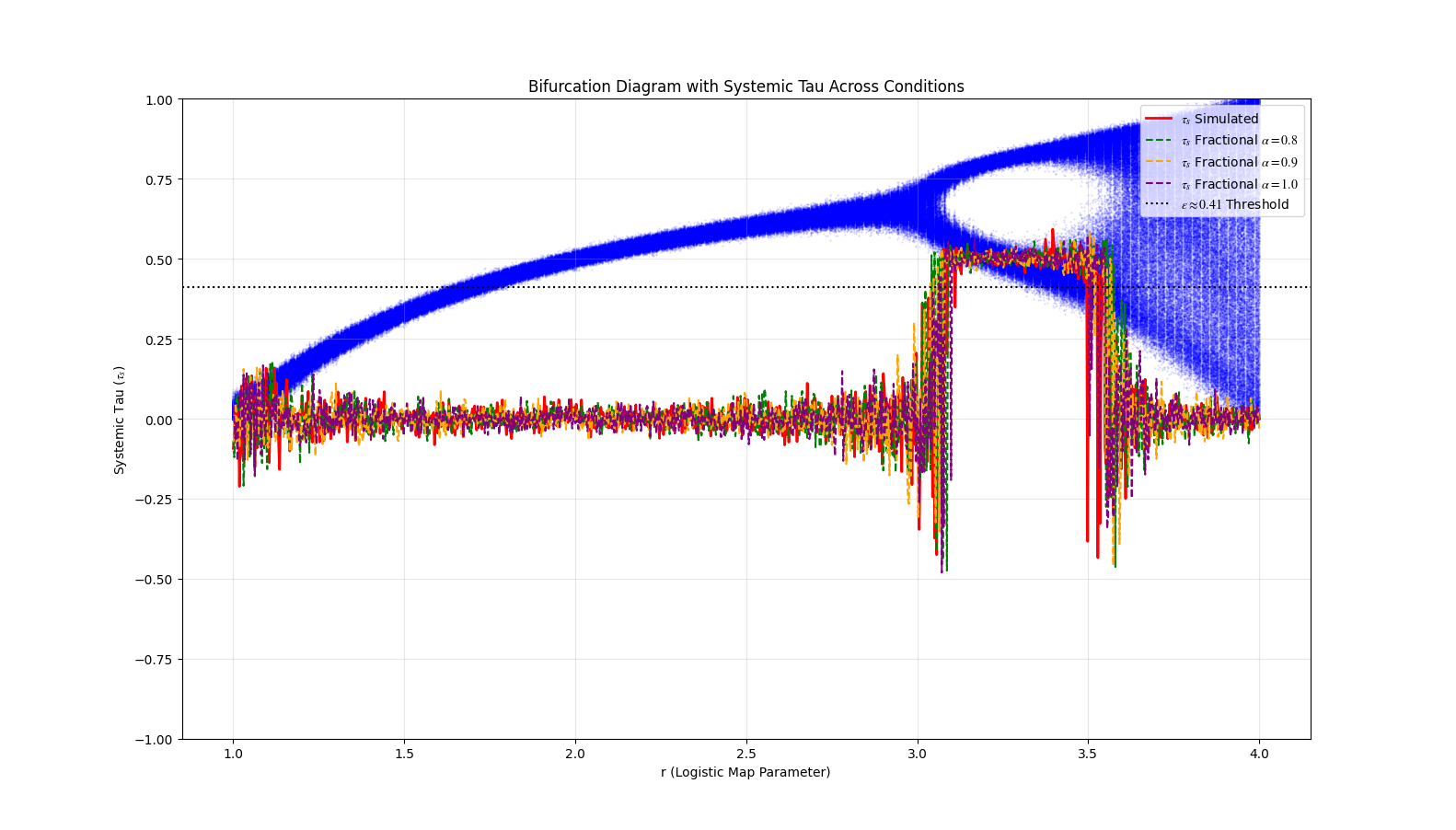
1.4. Conclusions
1.5. Notation
| Symbol | Description |
| Systemic Tau, as defined in Padilla-Villanueva (2025) [4], used to quantify anti-synchronization (). | |
| Critical threshold () marking the transition to anti-synchronization during bifurcations. | |
| Fractional order parameter ( to 1.0) in fractional extensions of the logistic map. | |
| Feigenbaum bifurcation ratio () influencing chaotic transitions. | |
| r | Parameter of the logistic map () controlling chaotic behavior. |
Appendix A. Mathematical Derivations
Appendix A.1. Generalization to Fractional-Order Systems
- import numpy as np
- from scipy.integrate import solve_ivp
- from scipy.stats import kendalltau
- # Define fractional logistic map function
- def fractional_logistic(t, x, r, alpha):
- return r * x * (1 - x)
- # Solve fractional ODE with specified time span
- def solve_fractional(alpha, r, t_span, y0):
- t_eval = np.linspace(t_span[0], t_span[1], 1000)
- sol = solve_ivp(lambda t, y: fractional_logistic(t, y, r, alpha),
- t_span, [y0], method=’RK45’, t_eval=t_eval)
- return sol.y[0][:11] # Return first 11 points to align with weeks 20-30
- # Real normalized data from dissertation
- s1_real = np.array([12, 8, 5, 7, 9, 11, 10, 6, 4, 5, 7])
- s3_real = np.array([3, 15, 20, 18, 16, 14, 12, 22, 25, 23, 19])
- s1_real_norm = (s1_real - np.min(s1_real)) / (np.max(s1_real) -
- np.min(s1_real))
- s3_real_norm = (s3_real - np.min(s3_real)) / (np.max(s3_real) -
- np.min(s3_real))
- # Simulate fractional series
- r = 3.8
- t_span = [0, 10]
- alphas = [0.8, 0.9, 1.0]
- frac_results = {}
- for alpha in alphas:
- x = solve_fractional(alpha, r, t_span, 0.5)
- frac_results[alpha] = x
- # Calculate fractional tau_s with bootstrap SE
- def bootstrap_tau_frac(s1, s3, n_boot=1000):
- taus = []
- n = len(s1)
- for _ in range(n_boot):
- idx = np.random.choice(n, n, replace=True)
- tau, _ = kendalltau(s1[idx], s3[idx])
- taus.append(tau)
- return np.mean(taus), np.std(taus)
- s1_frac = frac_results[0.9]
- s3_frac = frac_results[0.9][::-1] # Reverse for anti-synchronization
- simulation tau_s_frac, se_frac = bzootstrap_tau_frac(s1_frac, s3_frac)
- p_value = kendalltau(s1_frac, s3_frac)[1]
- print(f"Fractional tau_s (alpha=0.9): {tau_s_frac:.3f} $\pm$ {se_frac:.3f},
- p={p_value:.3f}")
Appendix A.1.1. Derivation of the ϵ≈0.41 Threshold
Appendix A.1.2. Lyapunov Exponent and Chaos Onset
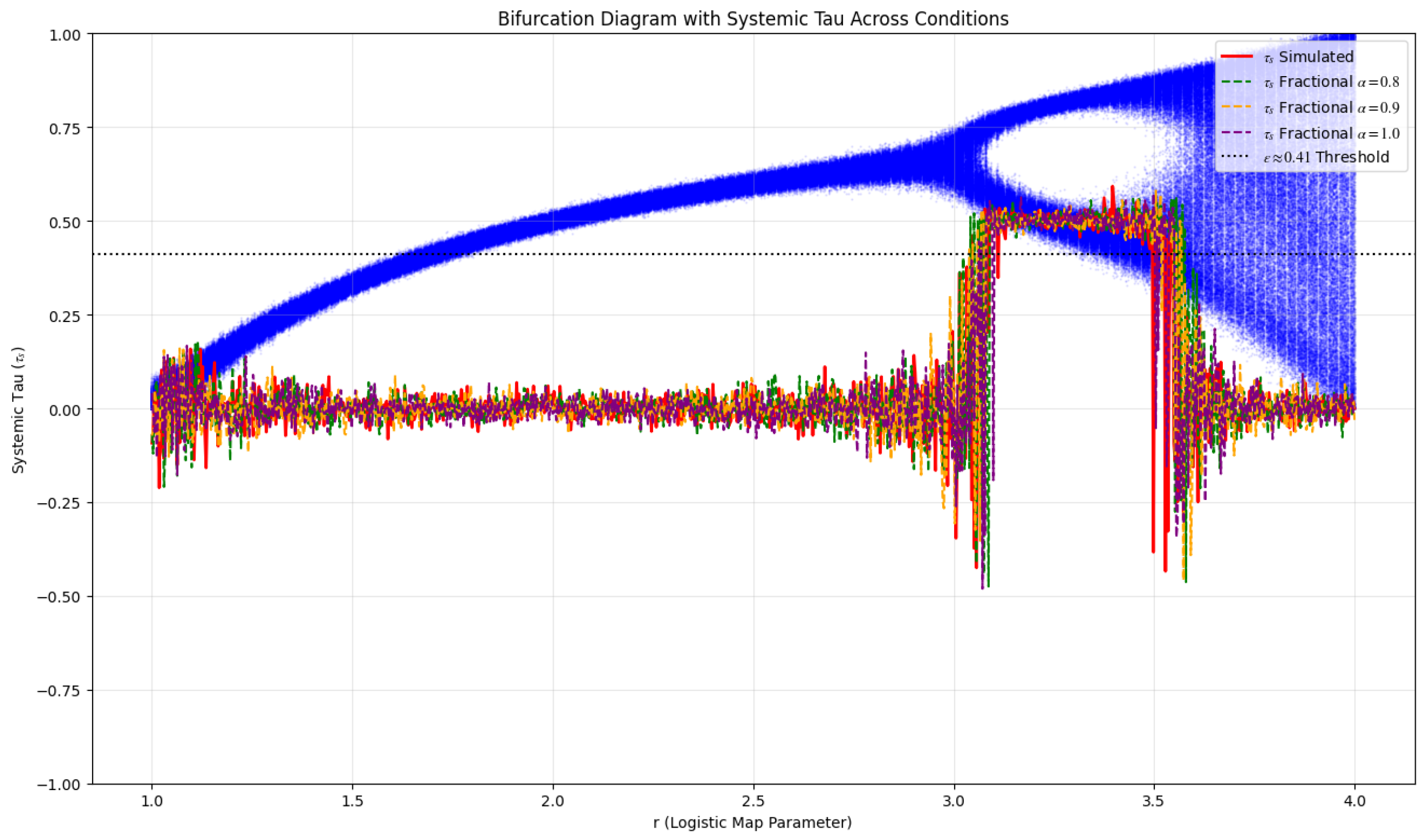
References
- Pecora, L.M.; Carroll, T.L. Synchronization in Chaotic Systems. Physical Review Letters 1990, 64, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Mainieri, R.; Rehacek, J. Projective Synchronization in Three-Dimensional Chaotic Systems. Physical Review Letters 1999, 82, 3042–3045. [Google Scholar] [CrossRef]
- Padilla-Villanueva, J. Spatiotemporal Dynamics of the Aedes aegypti Mosquito Population in the Caño Martín Peña Area in San Juan, Puerto Rico, during the Epidemiological Years 2018-2019: Health Repercussions for Residents of Adjacent Communities. PhD thesis, Universidad de Puerto Rico, Recinto de Ciencias Médicas, Escuela Graduada de Salud Pública, San Juan, Puerto Rico, 2022. Original title in Spanish: Dinámica espaciotemporal de la población del mosquito Aedes aegypti (L.) en la zona del Caño Martín Peña en San Juan de Puerto Rico durante los años epidemiológicos 2018-2019: repercusiones a la salud para los residentes de las comunidades aledañas. [CrossRef]
- Padilla-Villanueva, J. Unveiling Systemic Tau: Redefining the Fabric of Time, Stability, and Emergent Order Across Complex Chaotic Systems in the Age of Interdisciplinary Discovery, 2025. Preprint, not peer-reviewed. [CrossRef]
- Feigenbaum, M.J. The transition to aperiodic behavior in turbulent systems. Communications in Mathematical Physics 1980, 77, 65–86. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic Nonperiodic Flow. Journal of the Atmospheric Sciences 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Li, C.; Sun, W.; Kurths, J. Anti-Synchronization Between Different Coupled Chaotic Systems. Physica A: Statistical Mechanics and its Applications 2009, 388, 4004–4010. [Google Scholar] [CrossRef]
- Singh, G.; Khattar, D.; Agrawal, N. Dual quadratic compound multiswitching anti-synchronization of Lorenz, Rössler, Lü and Chen chaotic systems. The European Physical Journal B 2025, 98. [Google Scholar] [CrossRef]
- Aly, S.; Sarim, M.; Al-Ali, A.; Elwakil, A.; Said, L.A. Reduced-order adaptive synchronization in a chaotic neural network with parameter mismatch: a dynamical system versus machine learning approach. Nonlinear Dynamics 2025, 113, 1035–1051. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Studies in Nonlinearity 1994. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





