Estimation of the Gas in Place for Marcellus Shale Horizontal Wells by Rate Transient Analysis

1. Introduction

To assess the economic viability of a reservoir, it is necessary to estimate the quantities of hydrocarbons in place. This estimate can be obtained by several methods including volumetric, decline curve analysis, and material balance equation (MBE). MBE, which relies on the performance of the reservoir, is the most reliable method and has been used for decades to estimate the hydrocarbons in place and reserves in oil and gas reservoirs. The main drawback for this method is the need for the static average reservoir pressures that must be obtained when the boundary-dominated flow (BDF) has been established in the reservoir. To overcome this obstacle, Mattar and McNeil (1998) proposed utilizing the flowing wellbore pressures and developed the flowing material balance (FMB). The application FMB to unconventional reservoirs, such Marcellus Shale, becomes problematic because of the ultra-low permeability which leads to a very long time for establishing BDF.

Shales are naturally fractured formations that are characterized by very low porosity (typically less than 5%) and extremely low permeability values (in order of nano-darcy). The gas is stored both in the limited pore space of the shale and is also adsorbed into the organic material, or kerogen, in shale due to its large surface area and the affinity for gas. To achieve economic production from the shale reservoirs, two key technologies including horizontal drilling and hydraulic fracturing have been implemented which has led to a dramatic increase in economic gas recovery from the shale gas plays in the United States. Typically, a horizontal well is completed with multiple transverse hydraulic fractures to create a high conductivity fracture network or stimulated reservoir volume (SRV) to allow the gas to flow to the wellbore. Hydraulic fractures are the key component for economic gas production from the shale gas reservoirs. The efficacy of a fracturing treatment is determined by the properties of the induced fracture including conductivity and length. However, the increase in the effective stress during production may lead to shale compaction and reduction in the shale permeability and the hydraulic fracture conductivity which are detrimental to gas recovery. Marcellus shale, due to its low Young's modulus and moderate Poisson's ratio, is more sensitive to the increase in the effective stress.

During the early production period from a horizontal well completed in a shale formation with multiple hydraulic fractures, the linear flow is the predominant and the interference among the hydraulic fracture stages leads to a BDF period within the SRV. Consequently, FMB can be applied to the production data from this early BDF period for estimation of the gas in place. The estimated gas in place is attributed to SRV and would be less than the total gas in place in the reservoir. It should be noted that the gas in SRV is of higher economic interest since the production from reservoir beyond the SRV would occur at very low rates. Our previous investigation (El Sgher et al. 2025) concluded that the adverse impact of the shale compaction is more significant during the early production due to higher gas production rates. It is therefore important to investigate the applicability of FMB as well as the impacts of the adsorbed gas, shale compaction, and completion design on the estimation of the gas in place in SRV.

2. Background

The conventional material balance equation (MBE) for a gas reservoir, which is not subject to water encroachment, is as follows:

$${\displaystyle \frac{p}{z}}={\displaystyle \frac{p_i}{z_i}}\left(1-{\displaystyle \frac{G_p}{G}}\right)$$

(1)

The linear relationship between p/z and G_p can be used to determine the gas in place, G. Assuming the reservoir is producing under constant rate boundary-dominated flow, the gas in place can be estimated the same way by using flowing bottomhole pressures (BHP) since the differences between the values of static and the flowing p/z are constant. In practice, it is difficult to maintain the flow rate constant throughout the entire production period particularly in wells completed in unconventional formations. When the flow rate is variable, the difference between the static and the flowing p/z values depends on the flow rate. To develop analytical procedures for variable flow rate (or BHP) cases, superposition is typically employed based on either the linear superposition time or material balance time. Agarwal et al. (1999) developed the following equation for a variable rate reservoir during BDF:

$${\displaystyle \frac{q}{\Delta p_p}}={\displaystyle \frac{1}{b_{pss}}}-{\displaystyle \frac{1}{b_{pss}G}}{Q}_n$$

(2)

Where:

$${\displaystyle \frac{q_g}{\Delta p_p}}=\mathrm{Normalized} \mathrm{Rate}={\displaystyle \frac{q_g}{\left(p_{p_i}-p_{p_{wf}}\right)}}$$

(3)

$$Q_n=\mathrm{Normalized} \mathrm{Cumulative}={\displaystyle \frac{\left(p_{pi}-p_p\right)}{\left(p_{p_i}-p_{p_{wf}}\right)}}G$$

(4)

$$p_p=psedopressure={\displaystyle \underset{0}{\overset{p}{\int }}\frac{2p^{/}}{{\mu }_{g}z}\hspace{0.17em}}d{p}^{/}$$

(5)

As can be observed from equation 2, the normalized rate changes linearly with the normalized cumulative. For FMB Analysis (or RTA), the normalized rate is plotted against the normalized cumulative, and a line is then drawn through the best fit of the points. The original gas-in-place (G) is the x-intercept of the line. The determination of the normalized cumulative however requires the average pressure. The average reservoir pressure can be estimated from the conventional MBE given in equation 1. The computation of the average reservoir pressure from equation 1 requires the value of the gas in place. The gas in place can be estimated from the volumetric method. However, if the necessary information to determine the gas in place by the volumetric approach is not available, then an iterative procedure using equation 1 must be implemented to determine the initial gas in place.

As was mentioned earlier, the gas is adsorbed into the organic matter in the shale. The adsorption of a given gas on a particular solid is typically represented by an adsorption isotherm. The adsorption of natural gas on shale is commonly assumed to follow Langmuir type isotherm (Langmuir, 1916). Langmuir isotherm is characterized by two constants, Langmuir volume (V_L) and Langmuir pressure (P_L). King (1993) incorporated the Langmuir adsorption model in the gas reservoir MBE and developed a general MBE for unconventional gas reservoirs as follows:

$${\displaystyle \frac{p}{z*}}={\displaystyle \frac{p_i}{z_i*}}\left(1-{\displaystyle \frac{G_p}{G}}\right)$$

(6)

Where:

$$z*={\displaystyle \frac{z}{\left(1-c_f\right)\left(p_i-p\right)\left(1-S_w\right)+\frac{{\rho }_b{B}_g}{\varphi }\left(\frac{V_L\hspace{0.17em}p}{P_L+p}\right)}}$$

(7)

The permeability of the Marcellus shale, as previously mentioned, is sensitive to the effective stress. Thompson et al (2010) introduced the pressure-dependent permeability pseudopressure, as given below, for the application of the FMB techniques to gas reservoirs with pressure-dependent permeability:

$$p_p^{*}={\displaystyle \frac{2}{k_i}}{\displaystyle \underset{0}{\overset{p}{\int }}\frac{k\left(p\right)p^{/}}{{\mu }_{g}z}}\hspace{0.17em}d{p}^{/}$$

(8)

In order to determine pressure-dependent permeability pseudopressure, a correlation between the permeability and pressure is required. A general correlation which represents permeability changes with pressure (or stress) is commonly given as (Yilmaz et al. 1991):

$$k=k_i\hspace{0.17em}{e}^{\gamma \left(p-p_i\right)}$$

(9)

The coefficient, γ, is the permeability modulus which can be determined by matching laboratory permeability measurements as a function of stress.

3. Objective and Methodology

The goal of this study was to apply rate transient analysis (RTA) to estimate the gas in place in the stimulated reservoir volume (SRV) by analyzing the production data from a Marcellus shale horizontal well completed with multiple hydraulic fracture stages. More specifically, the objectives of this study were to investigate:

• the applicability of RTA for estimation of the gas in place in SRV.
• the impact of the compaction on the estimated gas in place in SRV by FMB analysis.
• the impact of the adsorbed gas on the estimated gas in place in SRV by FMB analysis.
• the impact of the fracture spacing on the estimated gas in place in SRV by FMB analysis.
• the impact of fracture half-length on the estimated gas in place in SRV by FMB analysis.

In order to accomplish the objectives of this study, a previously developed numerical reservoir model (El Sgher et al., 2025) which accurately simulates the production profile of a horizontal Marcellus shale well with multiple hydraulic fractures was employed. The model, developed using a reservoir simulation pacakge (CMG-GEM, 2021), can efficiently model the gas production from hydraulic fractures of a horizontal shale well by implementing a dual permeability system with local grid refinement which is the customary approach in numerical simulations (Yu and Sepehrnoori, 2014; Rubin, 2010). Marcellus shale petrophysical and geomechanical properties were estimated from the publicly available and published data acquired from the Marcellus shale energy and environment laboratory (MSEEL). MSEEL is field laboratory which consists of two sites containing several Marcellus shale horizontal wells and vertical wells which were used for collecting subsurface samples as well as microseismic monitoring. The collected data included core plug analysis, well logs, image logs, and desorption tests.

The basic model parameters (model inputs) used in this study are summarized in Table 1. The hydraulic fractures were assumed to have equal lengths and conductivity and are evenly spaced. The wellbore pressure was set as a constraint in the model. The model was then coupled with geomechanics module to account for the shale compaction due to increase in effective stress during the production. The main coupling variables that are directly related to the effective stress include matrix porosity, matrix permeability, fissure (natural fracture) permeability, and the hydraulic fracture conductivity. The matrix porosity is determined by a correlation (Tran et al., 2002) incorporated in the geomechanics module. The correlations for the fissure permeability, matrix permeability, and the hydraulic fracture conductivity as a function of effective stress were obtained by matching the experimental data to equation 9. The correlations were then transformed to correlations in terms of the reservoir pressure (multipliers) and were incorporated in the reservoir model (El Sgher et al., 2025).

4. Estimation of the Gas in Place in SRV

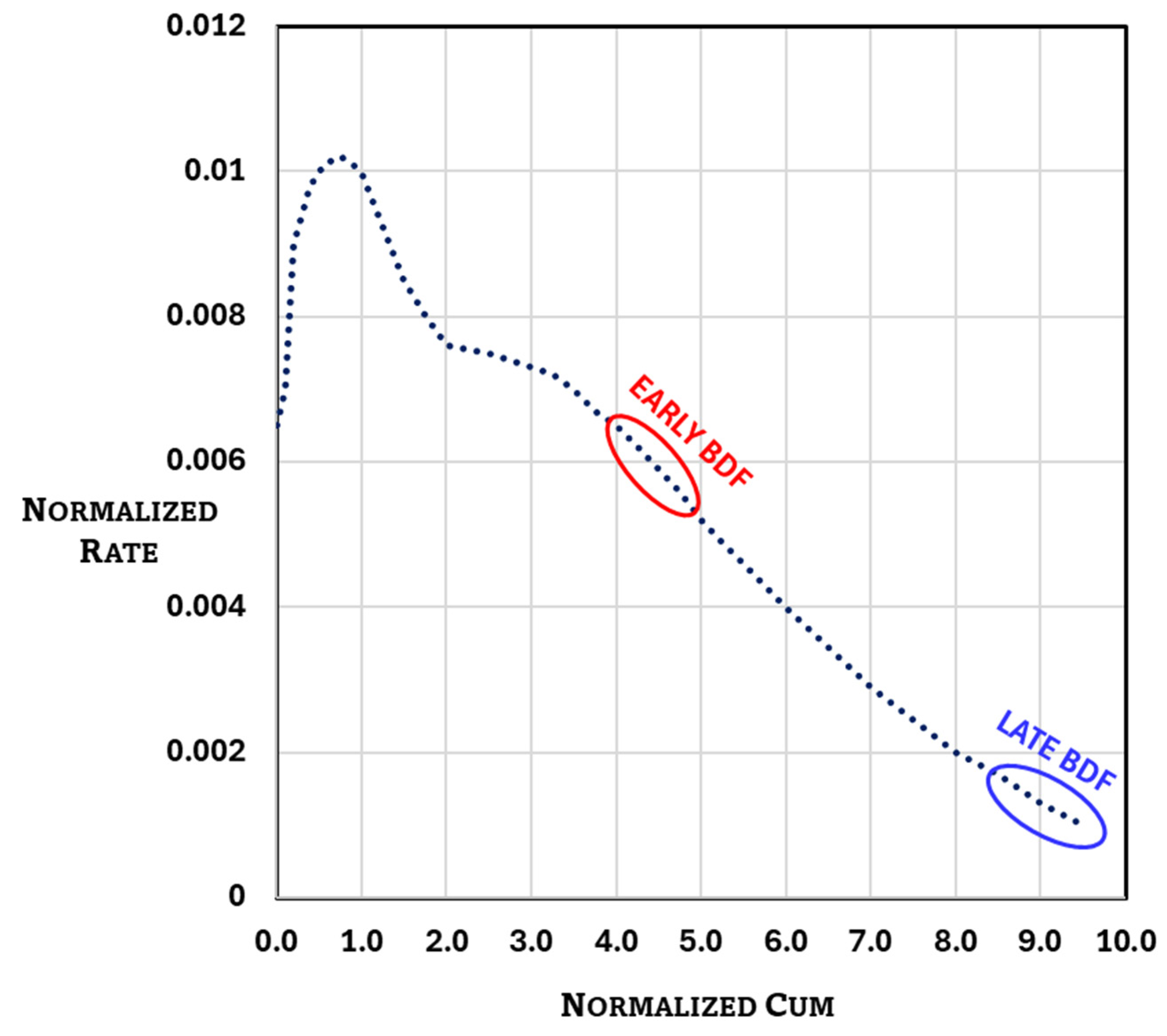
The simulated production profile was utilized to estimate the gas in place in SRV by RTA. The normalized rate and the normalized cumulative were determined according to equations 3-5. In order to calculate the normalized cumulative, the general MBE for unconventional gas reservoirs (equation 6) is used to determine the average reservoir pressure by assuming the gas in place. The normalized rate is then plotted against the normalized cumulative and the gas in place is the horizontal intercept of the line through the early BDF data points. The process is repeated until the assumed and the calculated values of the gas in place converge. Figure 1 illustrates a plot of the normalized rate against the normalized cumulative. As can be observed from Figure 1, an early and a late BDF periods (linear trends) are present. It should be noted that Figure 1 is prepared by using the converged value of the gas in place in SRV (early BDF line) which is provided in Table 2.

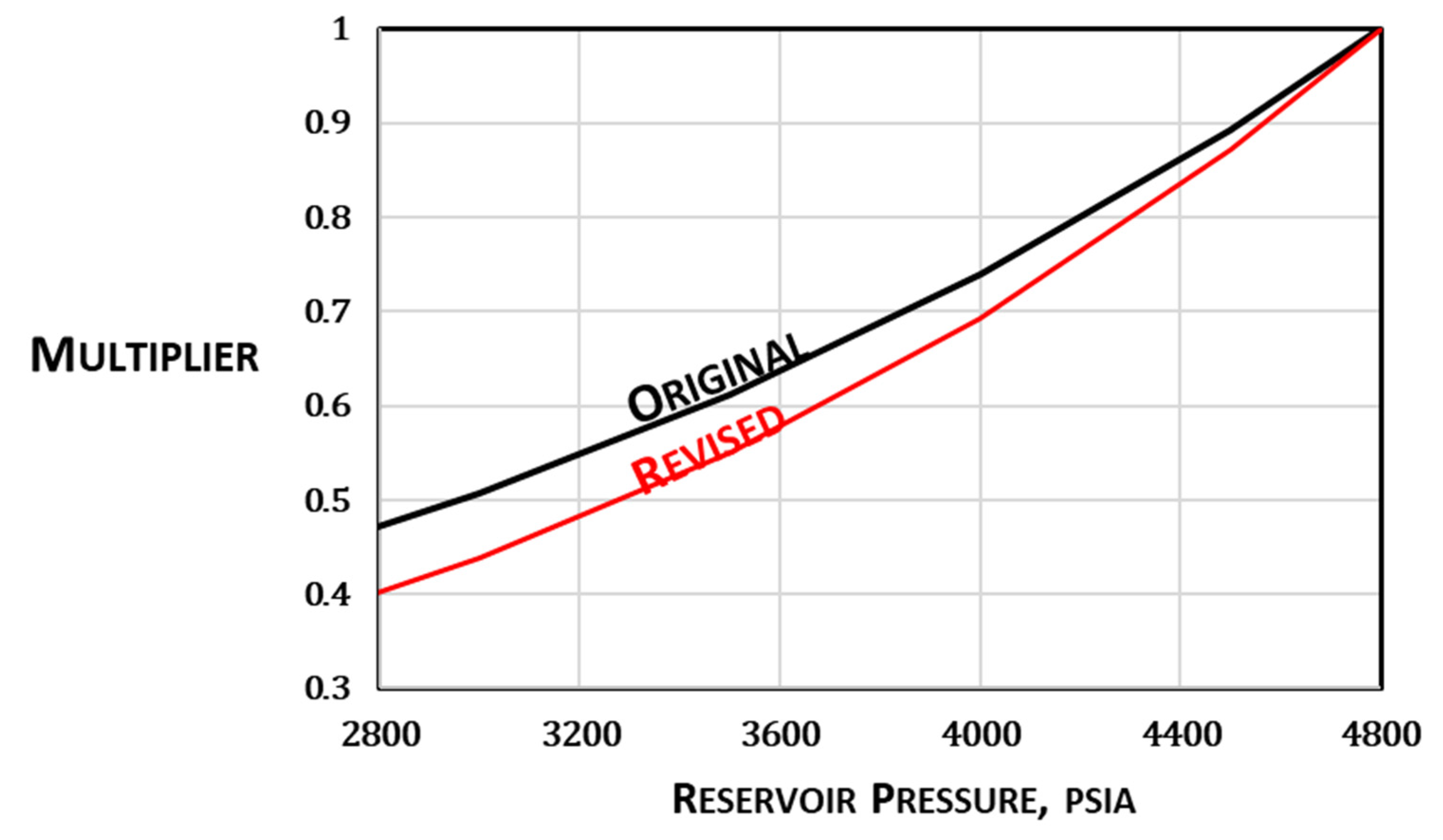
To account for the shale compaction, equation 5 must be replaced with equation 8 when calculating the normalized cumulative. To use equation 8, a correlation between the permeability and pressure according to equation 9 must be developed. The coefficient γ, in equation 9 was estimated by matching laboratory permeability measurements on Marcellus shale core plugs at different net stress values (Elsaig, et al., 2016) with equation 9. The correlation was then transformed to permeability in terms of the reservoir pressure (multiplier) which illustrated as the curve marked “original” in Figure 2. The normalized rate is then plotted against the compaction corrected normalized cumulative and the estimated gas in place in SRV is determined (by iteration) from the early BDF period which is also provided in Table 2. For comparison purposes, the estimated gas in place in SRV from the model is also included in Table 2. It can be observed from the results in Table 2 that ignoring the compaction impact on the production leads to under-estimation of the gas in place.

5. Impact of the Compaction

Previous studies (El Sgher et al., 2025) have revealed that the reduction in the hydraulic fracture conductivity, due to net stress increase, adversely impact the gas recovery from the Marcellus shale particularly during early stage of the production. RTA only accounts for shale compaction and does not take into account the impact of the hydraulic fracture conductivity impairment. Consequently, the gas in place in SRV is under-estimated by RTA. In order to account for the impact of compaction on hydraulic fractur conductivity, a “revised” multiplier for RTA was developed, as illustrated in Figure 2. As can be observed from Figure 2 the revised multiplier treats the shale as more compressible than the original multiplier. The results of RTA using the revised multiplier is also provided in Table 2. The estimated gas in place in SRV when the revised multiplier is used for RTA is in close agreement with the value from the model.

6. Impact of the Adsorbed Gas

To perform the analysis using the general MBE for unconventional gas reservoirs (equation 6), Langmuir constants (P_L and V_L) are necessary to calculate z* (see equation 7). The reliable estimates for the shale Langmuir constants may not be always available. In this study, three different values for Langmuir volume constant (V_L ), as listed in Table 3, were considered for performing RTA. The estimate values of the gas in place in SRV for each case are also provided in Table 3. As can be observed from Table 3, the estimated gas in place in SRV is not significantly impacted by the assumed value of the Langmuir Volume constant (V_L). This is because the pressure depletion during the early production period is not sufficient to results in significant gas desorption.

7. Impact of the Fracture Spacing

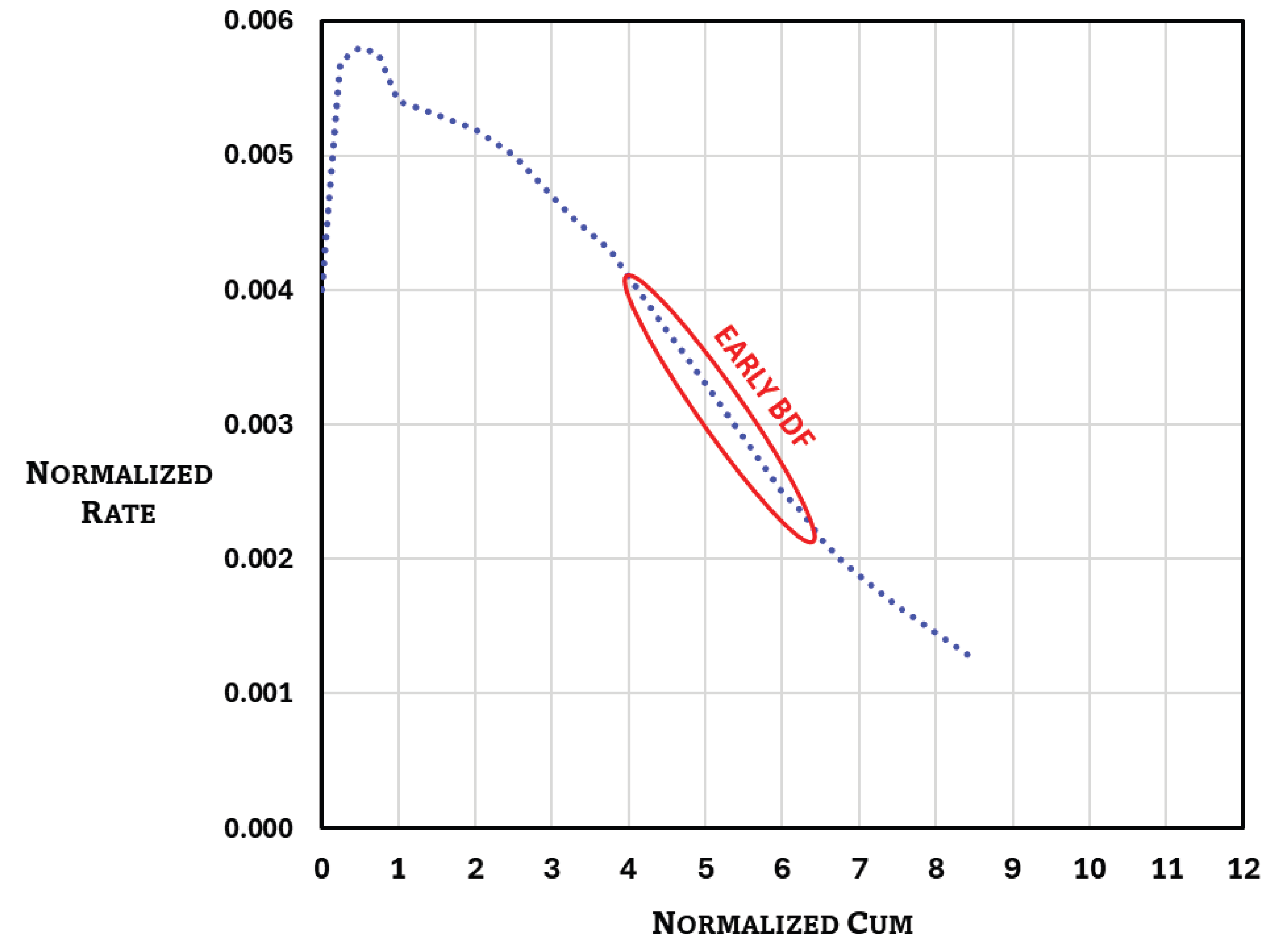
To investigate the impact of the hydraulic fracture spacing on the analysis, three different spacing, as listed in Table 4, were considered. The production profile for each case was simulated and the used to determine the gas in place in SRV by RTA. Table 4 summarizes the results of the analysis for different hydraulic fracture spacings. The revised multiplier was used for compaction correction. Figure 3 illustrates the plot of the normalized rate against the normalized cumulative for 150-ft spacing by using the converged value gas in place in SRV (early BDF line). As can be observed from Figure 3, the early BDF period (linear trend) is longer, as compared to Figure 1, and can be identified readily. As can be observed from the results in Table 4, the hydraulic fracture spacing does not appear to significantly impact the estimation of the gas in place in SRV. This is because the size of SRV depends on the lengths of the fractures which are assumed to be uniform for different cases.

8. Impact of the Fracture Half-length

To investigate the impact of the hydraulic fracture half-length on the analysis, three different fracture half-lengths, as listed in Table 5, were considered. The production profile for each case was simulated and the used to determine the gas in place in SRV by RTA. Table 5 summarizes the results of the analysis for different hydraulic fracture spacings. The revised multiplier was used for compaction correction. As can be observed from the results in Table 5, the fracture half-length have a significant impact in the estimated gas in place in SRV. This is because the size of SRV depends on the lengths of the fractures.

9. Conclusions

The following conclusions were reached in this study:

1. The production data from a horizontal Marcellus shale well with multiple hydraulic fractures exhibits an early boundary-dominated flow (BDF) period which occurs within the stimulated reservoir volume(SRV).

2. The production data from the early BDF period can be analyzed by flowing material balance(FMB) method to estimate the gas in place in SRV.

3. Accurate estimates of gas in place in SRV can be obtained when the compaction impact is included in FMB analysis.

4. Gas desorption has a minor impact on gas production during the early period and consequently does not significantly impact the estimated value gas in place in SRV.

5. The number of fractures does not significantly impact the gas in place in SRV because the size of the SRV does not depend on the number of stages.

6. When the fracture stages are spaced widely, the early BDF period may last for a longer time and can be identified more readily.

7. When the fractures are closely spaced, the early BDF period lasts for a relatively short time. Consequently, the identification of the early BDF period becomes difficult, leading to uncertainty in the estimated of the gas in place in SRV.