Hydrostatic Balance of Stars and Black Hole Singularity

1. Introduction

Hydrostatic balance is an equilibrium between gravity and thermal pressure that appears dynamically in the core of a star and singularity, then enhancing the balance and sustainability of stars and black hole singularity. The mass of a star and black hole singularity creates a powerful inward-pulling force that constantly tries to cause the star and singularity to collapse and shrink into their center, which is called Gravity. High temperatures, energetic particles, and energy generation in the core of a singularity due to superparticles collisions or a star's core, due to nuclear fusion, both of them may create a powerful outward pressure that includes ideal gas pressure, radiation pressure, and sometimes electron and neutron degeneracy pressure in the core of white dwarfs and neutron stars, or superparticles degeneracy pressure in the core of singularity, collectively referred to as thermal pressure, which is called the pressure. Nucleosynthesis is a nuclear fusion process that occurs during hydrostatic oxygen burning in a "typical" stellar zone [1]. More massive main-sequence stars generate more energy from nuclear fusion processes in their cores due to higher gravitational pressure, resulting in significantly higher luminosities. As a star's luminosity approaches the Eddington limit, the outward radiation pressure becomes nearly equal to the inward force of gravity [2]. The collapsed star with a mass 10 times that of the Sun may become a black hole and emit X-rays due to accretion of matter, and tidal force from the nearby star or the companion star induces a torque on it to emit light [3,4]. A main-sequence star has a fantastic hydrostatic balance due to nuclear fusion at its core, which enhances its sustainability and luminosity [5,6,7,8,9,10,11,12,13,14,15]. Luminosity is a star's total energy output, which is directly related to the temperature balance, because the high temperatures and high pressure in a star's heart are mainly a consequence of maintaining hydrostatic balance to drive the nuclear fusion that produces the huge energy we observe as luminosity, heat, and brightness from the Sun and Stars.

Stars die in final steps when their nuclear fuel exhaust, but their final fate depends on their mass: the low mass stars like solar mass stars shed their outer layers, forming a planetary nebula and leaving behind a dense core called the white dwarf star, while massive stars end their lives in violent event as a supernova explosion, collapsing its heart into a neutron star or a black hole according to its mass. The material ejected during the death of stars is crucial, as it contains atoms that eventually combine to form new molecules, compounds materials, stars, natural satellites as Moon, Asteroids, celestial objects, and planets, including living planets like Earth, living creatures like human, birds, plants, and life itself [16,17,18,19,20,21,22,23,24,25]. We are stardust. A supernova is an incredibly bright event that temporarily outshines entire galaxies and is a crucial cosmic phenomenon that ejects heavy elements like iron, gold, silicon, Uranium, and Germanium into the visible universe, enriching interstellar clouds and enabling the formation of new stars and planets. The core collapsing and contraction process in low-mass stars is suspended due to electron degeneracy pressure in white dwarf stars. The core collapsing and contraction process in high-mass stars is suspended due to neutron degeneracy pressure in the neutron stars. The core collapsing and contraction process in the black hole singularity is suspended due to superparticle degeneracy pressure inside the compacted structure of a singularity sphere. The superparticles in the core of a black hole singularity are compressed and annihilated a fraction of its mass to support thermal energy, and radiation, which is balanced with a gravity in the singularity ball, as electron degenerate pressure phenomenon that occurs in white dwarf stars, and neutron degenerate pressure in the neutron stars. While neutron stars do lose energy over time, and produce powerful radiation through mechanisms which are called the pulsar beams (They derive their energy from rapid rotational energy, not from neutron degeneracy pressure entirely). The black hole singularity has the mass of stars, planets, and galaxies, but its size is that of Atoms, and it has a higher rotational energy that a fraction of it is converted into thermal energy and releases powerful photon particles and radiation with different wavelengths. But another fraction of its rotational energy may be converted into turbulences, ripples, and acoustic waves in the compacted fabric of a of a black hole in the event horizon zone around a singularity ball and accretion disc in its external edge.

The main objectives of this study are to calculate the Central Pressure ${\mathbf{P}}_{\mathbf{c}}$ and Central Temperature ${\mathbf{T}}_{\mathbf{c}}$ of the Stars and Black hole singularity.

2. Hydrostatic Balance of Stars

The Star is a spherical ball of a hotter plasma. It is a celestial object that formed from a stellar nebula. The Sun is an average type of stars that has been formed more five billion years ago as a proto star from stellar cloud and its composition is mostly from hydrogen and helium’s atoms, ions, and molecules. The Sun as other stars could be sustained in collecting gas and dust particles continuously from its surrounding to increase its mass, central temperature, and gravitational pressure. The photon particles are struggling to penetrate through a condensed heart of star. Most of photon particles had been trapped and accumulated in the bottom of stars. The internal energy and temperature of stars had been increased violently. The ration of photon particles had been increased in the heart of star and they are pushing up the external shells of stars to release into space. The photon particles could be reflected, refracted, absorbed, trapped, transmitted, and accumulated inside internal shells of stars for longer time because the photons have limited energy, momentum, frequency, and wavelengths. The thermal energy and gravitational energy of a star has been increased gradually to develop itself from proto star to become a main sequence star. The mass, density, and gravity of star had been increased widely to initiate the fusion in its heart. The star may start with burning hydrogen isotopes to produce helium atoms when temperature in its heart exceeded ten million kelvins. The Sun is a main sequence star because the nuclear fusion processes was started at its heart for billions of years.

The Sun has lost about five billion tons of its mass into energy at every second. The thermal pressure of radiations in the star's heart starts to push up all external shells of the star, and the gravitational pressure of the star which appears from its mass has stressed on the star's heart to contract inward. The tussle between the thermal pressure of radiations and gravitational force could be suspending the shrinking inward of the heart of a star and collapsing outward the external shells of star. The hydrostatic equilibrium between thermal energy and gravitational pressure of stars may protect all main sequence stars from ultimate death and explosion. The star could be expanded to be a red giant or explode as a supernova in the final stages of its life cycle when its fuel is exhausted entirely. The remnant core of a dead star may become a white dwarf, neutron star, or a black hole according to the mass of a collapsed star. The hydrostatic balance of a star may fail to save the star from explosion when nuclear fusion suspends. The thermal energy has been increased due to nuclear fusion processes in the heart of star and it is working against the gravitational pressure of star. The balance between thermal energy and gravity may keep the star as a perfect ball of plasma, and let it to survive for longer time. The life cycle of a low-mass star is longer than the lifetime of a High-mass star because a high-mass star may burn most of its fuel at a shorter time and explode violently as a supernova [26,27,28,29,30]. The remnant core of a high-mass star may become a neutron star or a black hole. High-mass stars live for several millions of years but low-mass stars as the Sun capable of living for billions of years, as a result, the solar system developed for billions of years and sustained life for Earth's billions of years. The Sun may become a red giant after five billion years when nuclear fusion has suspended at its heart. The red giant star is a huge sphere of plasma, and its central pressure, temperature, and surface temperature critically lower to sustain the nuclear fusion processes.

3. Derivation of The Equation of Hydrostatic Equilibrium

The equation of hydrostatic equilibrium for stars describes the perfect balance between the inward force of gravity that is delivered by stellar mass and the outward force of radiation pressure within a star. The Hydrostatic equilibrium that balances gravity and radiation pressure, it could be sustained for a longer time when nuclear fusion, the energy source for stars, is supported by high enough amount of fuel [31,32,33,34,35]. The difference between the pressure times area on the top and the bottom balances the weight; the pressure at the heart of the star is higher than its surface pressure. The star is a perfect ball of the hottest and condensed state of matter and energy, which is named a plasma sphere. The star is in hydrostatic balance since the Force up is equal to the Force down.

$$\mathbf{F}\mathbf{o}\mathbf{r}\mathbf{c}\mathbf{e}\mathbf{u}\mathbf{p}=\mathbf{d}\mathbf{P}\mathbf{A}={\mathbf{P}}_1\mathbf{A}-{\mathbf{P}}_2\mathbf{A}$$

(1)

$$\mathit{F}\mathit{o}\mathit{r}\mathit{c}\mathit{e}\mathit{d}\mathit{o}\mathit{w}\mathit{n}=-\mathit{G}{\displaystyle \frac{\mathit{M}\left(\mathit{r}\right)\mathit{m}}{{\mathit{r}}^2}}$$

(2)

In the star’s hydrostatic equilibrium, the star's stability is sustained by a balance between the downward force of gravity by the mass of the star and the outward force of radiation pressure by thermal pressure, thus the equation. (1) equal to eqn (2).

Force up of thermal pressure=Force down of gravitational force

$$\begin{gathered} \mathrm{d}\mathrm{P}\mathrm{A}=-\mathit{G}{\displaystyle \frac{\mathit{M}\left(\mathit{r}\right)\mathit{m}}{{\mathit{r}}^2}} \\ \mathit{m}=\mathit{\rho }\mathit{A}\mathit{d}\mathit{r} \end{gathered}$$

(3)

The equation for mass density could be written as: density = mass / volume, often written as ( $\mathit{\rho }={\displaystyle \frac{\mathit{m}}{\mathit{V}}}$ ), where ρ (rho) represents density, m is mass, and $(V=\mathit{A}\mathit{d}\mathit{r}$ is volume, and $(\mathit{A}=4\mathit{\pi }{\mathit{r}}^2)$ is the surface area. The stars, singularity, superparticles, and black holes are perfect balls of condensed state of matter and energy. The singularity is a denser state of matter and energy that immersed into the heart of a black hole. Gravitational acceleration g of an object with mass m falls down freely on an external surface of an object with a higher mass M. Substitute eqn.(3) into eqn.(2) yields the:

$$\begin{gathered} \mathit{d}\mathit{P}\mathit{A}=-\mathit{G}{\displaystyle \frac{\mathit{M}\left(\mathit{r}\right)\left(\mathit{\rho }\mathit{A}\mathit{d}\mathit{r}\right)}{{\mathit{r}}^2}} \\ \mathit{d}\mathit{P}=-\mathit{G}{\displaystyle \frac{\mathit{M}\left(\mathit{r}\right)\left(\mathit{\rho }\mathit{d}\mathit{r}\right)}{{\mathit{r}}^2}} \\ {\displaystyle \frac{\mathit{d}\mathit{P}}{\mathit{d}\mathit{r}}}=-\mathit{G}{\displaystyle \frac{\mathit{M}\left(\mathit{r}\right)\mathit{\rho }\left(\mathit{r}\right)}{{\mathit{r}}^2}} \end{gathered}$$

(4)

In fact, Eqn.(4) is the equation of hydrostatic equilibrium for main-sequence stars and hottest celestial objects. The main sequence star is the most stable and longest phase of a star's life, which is actively fusing hydrogen into helium in its core to balance with gravity. ( ${\displaystyle \frac{\mathit{d}\mathit{P}}{\mathit{d}\mathit{r}}}$) is outward gas pressure per unit$\mathit{d}\mathit{r}$. Then $(-\mathit{G}{\displaystyle \frac{\mathit{M}\left(\mathit{r}\right)\mathit{\rho }\left(\mathit{r}\right)}{{\mathit{r}}^2}})$ is inward force of gravity acting on the stars and black hole singularity. $\mathit{\rho }\left(\mathit{r}\right)$ it is the density of star as a function of radius r, and G is a Gravitational Constant, G = 6.674 x 10^-11 N.m²/kg² = 6.674 x 10^-11 m³/kg. s².

4. Proof of Central Pressure

To determine the central pressure of stars and planets $({\mathbf{P}}_{\mathbf{c}}$), the equation of hydrostatic equilibrium is often used, which balances gravity with pressure gradients. Assuming the stars have constant density (ρ).

$$\mathit{M}\left(\mathit{r}\right)={\displaystyle \frac{4}{3}}\mathit{\pi }{\mathit{r}}^3\mathit{\rho }$$

(5)

To prove the central pressure equation, it is essential to substitute Eqn.(5) into Eqn.(4):

$$\begin{gathered} {\displaystyle \frac{\mathit{d}\mathit{P}}{\mathit{d}\mathit{r}}}=-\mathit{G}{\displaystyle \frac{\left(\frac{4}{3}\mathit{\pi }{\mathit{r}}^3\mathit{\rho }\right)\mathit{\rho }}{{\mathit{r}}^2}}=-{\displaystyle \frac{4\mathit{\pi }\mathit{G}{\mathit{\rho }}^2\mathit{r}}{3}} \\ {\displaystyle \frac{\mathit{d}\mathit{P}}{\mathit{d}\mathit{r}}}=-{\displaystyle \frac{4\mathit{\pi }\mathit{G}{\mathit{\rho }}^2\mathit{r}}{3}} \\ \mathit{d}\mathit{P}=-{\displaystyle \frac{4\mathit{\pi }\mathit{G}{\mathit{\rho }}^2\mathit{r}}{3}}\mathit{d}\mathit{r} \end{gathered}$$

We integrate the above equation to find the central pressure equation for stars.

$${\int }_{{\mathit{P}}_{\mathit{c}}}^{{\mathit{P}}_{\mathit{s}}}\mathit{d}\mathit{P}=-{\displaystyle \frac{4\mathit{\pi }\mathit{G}{\mathit{\rho }}^2}{3}}{\int }_{{\mathit{R}}_{\mathit{c}}}^{{\mathit{R}}_{\mathit{S}}}\mathit{r}\mathit{d}\mathit{r}$$

The surface pressure of star ${\mathrm{P}}_{\mathrm{S}}$ is zero.

$$\mathit{d}\mathit{P}={\mathit{P}}_{\mathit{S}}-{\mathit{P}}_{\mathit{c}}=0-{\mathit{P}}_{\mathit{c}}=-{\mathit{P}}_{\mathit{c}}$$

The central radius of star ${\mathrm{R}}_{\mathrm{c}}$ is zero.

$$\mathit{d}\mathit{r}={\mathit{R}}_{\mathit{S}}-{\mathit{R}}_{\mathit{c}}={{\mathit{R}}_{\mathit{S}}-0=\mathit{R}}_{\mathit{S}}=\mathit{R}$$

$${\int }_{{\mathit{P}}_{\mathit{c}}}^0\mathit{d}\mathit{P}=-{\displaystyle \frac{4\mathit{\pi }\mathit{G}{\mathit{\rho }}^2}{3}}{\int }_0^{{\mathit{R}}_{\mathit{S}}}\mathit{r}\mathit{d}\mathit{r}$$

$$[0-{\mathit{P}}_{\mathit{c}}]=-{\displaystyle \frac{\left(4\mathit{\pi }\mathit{G}{\mathit{\rho }}^2\right)}{3}}[{\displaystyle \frac{{\mathit{R}}^2}{2}}-0]$$

$${\mathit{P}}_{\mathit{c}}={\displaystyle \frac{\left(4\mathit{\pi }\mathit{G}{\mathit{\rho }}^2\right)}{3}}\mathit{x}{\displaystyle \frac{{\mathit{R}}^2}{2}}$$

$${\mathbf{P}}_{\mathbf{c}}=\left({\displaystyle \frac{\mathbf{G}\mathsf{\rho }}{2\mathbf{R}}}\right)\mathbf{x}\left({\displaystyle \frac{4\mathsf{\pi }{\mathbf{R}}^3\mathsf{\rho }}{3}}\right)$$

$${\mathbf{P}}_{\mathbf{c}}=\left({\displaystyle \frac{\mathbf{G}\mathsf{\rho }}{2\mathbf{R}}}\right)\mathbf{x}\left(\mathit{M}\right)=\left({\displaystyle \frac{\mathbf{G}\mathbf{M}\mathsf{\rho }}{2\mathbf{R}}}\right)$$

$${\mathbf{P}}_{\mathbf{c}}={\displaystyle \frac{\mathbf{G}\mathbf{M}\mathsf{\rho }}{2\mathbf{R}}}$$

(6)

$$\mathit{P}\mathit{V}=\mathit{n}\mathit{R}\mathit{T}=\mathit{N}{\mathit{K}}_{\mathit{B}}\mathit{T}$$

(7)

The ideal gas law, or the general gas equation, is a fundamental principle of physics, astronomy, and chemistry, also called the equation of state of a hypothetical ideal gas, and ionised gas in stars [36,37,38,39,40]. The ideal gas equation, also known as the ideal gas law, is eqn.(7), which describes the product of pressure (P) and volume (V) is equal to the number of moles (n) multiplied by the ideal gas constant (R), and temperature (T) of an ideal gas or equal to the number of particles N multiplied with Boltzmann’s constants ${\mathit{K}}_{\mathit{B}}$ and temperature T.

$$\mathit{P}={\displaystyle \frac{\mathit{N}}{\mathit{V}}}{\mathit{K}}_{\mathit{B}}\mathit{T}$$

(8)

$${\mathit{P}=\mathit{n}\mathit{K}}_{\mathit{B}}\mathit{T}={\displaystyle \frac{\mathit{\rho }}{{\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}}}}{\mathit{K}}_{\mathit{B}}\mathit{T}$$

(9)

$$\mathit{\mu }={\displaystyle \frac{{\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}}{{\mathit{m}}_{\mathit{H}}}}$$

(10)

$${\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}=\mathit{\mu }{\mathit{m}}_{\mathit{H}}$$

(11)

$$\mathit{P}={\displaystyle \frac{\mathit{\rho }{\mathit{K}}_{\mathit{B}}\mathit{T}}{\mathit{\mu }{\mathit{m}}_{\mathit{H}}}}$$

(12)

$${\mathrm{P}}_{\mathrm{I}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}}={\displaystyle \frac{\mathit{\rho }{\mathit{K}}_{\mathit{B}}{\mathit{T}}_{\mathit{c}}}{{\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}}}$$

(13)

In fact, Eqn.(13) is the equation of state, where $(\mathit{n}={\displaystyle \frac{\mathit{N}}{\mathit{V}}}={\displaystyle \frac{\mathit{\rho }}{{\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}}})$ is the number density of gas particles, $\mathit{\rho }$ is the mass density of gas, ${\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}}$ is an average mass of a gas particle, the mean molecular weight in plasma $\mathit{\mu }$ it is an average mass of a gas particle ${\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}$ in unit of mass of atoms specifically the hydrogen atom ${(\mathit{m}}_{\mathit{H}}=1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g})$. Using the average mass of one atomic particle or the mass of a star’s particle ${\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}$ (mostly hydrogen and helium), the concentration n represents the concentration of particles within the star can be expressed through the mass density:$(\mathit{n}={\displaystyle \frac{\mathit{\rho }}{{\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}}})$. The Sun contained an ideal gas, 75% Hydrogen, 24% Helium, and 1% other elements. If the ideal gases are fully ionized in a plasma state. To determine central temperature for ionized gases in the core of stars, assume ${(\mathrm{P}}_{\mathrm{c}}={\mathrm{P}}_{\mathrm{I}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}}$ ) in the eqn.(6) and eqn.(13) from hydrostatic equilibrium and ideal gas law:

$${\displaystyle \frac{\mathbf{G}\mathbf{M}\mathsf{\rho }}{2\mathbf{R}}}={\displaystyle \frac{\mathit{\rho }{\mathit{K}}_{\mathit{B}}{\mathit{T}}_{\mathit{c}}}{{\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}}}$$

$${\mathit{T}}_{\mathit{c}}={\displaystyle \frac{{\mathbf{G}\mathbf{M}.\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}}{2\mathbf{R}{\mathit{K}}_{\mathit{B}}}}$$

(14)

Where, ${\mathbf{P}}_{\mathbf{c}}$ is a central pressure of stars,${\mathbf{T}}_{\mathbf{c}}$ is a central temperature of stars, (r=R) is a radius of stars and spherical objects, ${(\mathit{N}}_{\mathit{A}}$) is Avogadro's number, it is a fundamental constant in Physics and chemistry, representing the number of constituent particles (atoms, ions, and molecules) in one mole of substances, and its value approximately $({\mathit{N}}_{\mathit{A}}=6.02x{10}^{23}.{mole}^{-1})$. The Boltzmann constant ${\mathit{K}}_{\mathit{B}}$ is the proportionality factor that relates the average relative thermal energy of particles, ionized atoms, and molecules in a gas with the thermodynamic temperature of the gas.

$$\begin{gathered} {\mathit{K}}_{\mathit{B}}={\displaystyle \frac{\mathit{R}}{{\mathit{N}}_{\mathit{A}}}}={\displaystyle \frac{\mathit{U}\mathit{n}\mathit{i}\mathit{v}\mathit{e}\mathit{r}\mathit{s}\mathit{a}\mathit{l}\mathit{g}\mathit{a}\mathit{s}\mathit{c}\mathit{o}\mathit{n}\mathit{s}\mathit{t}\mathit{a}\mathit{n}\mathit{t}}{{\mathit{N}}_{\mathit{A}}}}={\displaystyle \frac{\left(8.31\frac{\mathit{J}}{\mathit{M}\mathit{o}\mathit{l}\mathit{e}.\mathit{K}}\right)}{6.02x{10}^{23}.{mole}^{-1}}} \\ {\mathit{K}}_{\mathit{B}}=1.38\mathit{x}{10}^{-23}\mathit{J}/\mathit{K} \end{gathered}$$

Problem: the Mass of Sun$(M=2x{10}^{30}Kg)$ and its radius $(R=7x{10}^{8}m)$, calculate its central pressure ${\mathbf{P}}_{\mathbf{c}}$ , and central temperature ${\mathbf{T}}_{\mathbf{c}}$Solution:

$$\begin{gathered} {\mathbf{P}}_{\mathbf{c}}\mathbf{=}{\displaystyle \frac{\mathbf{G}\mathbf{M}\mathsf{\rho }}{2\mathbf{R}}}={\displaystyle \frac{\left(6.674x{10}^{-11}\frac{\mathrm{N}.\mathrm{m}2}{\mathrm{k}\mathrm{g}2}\mathrm{x}2x{10}^{30}Kgx1400\frac{kg}{m^3}\right)}{\left(2\mathit{x}7x{10}^{8}m\right),}} \\ {\mathbf{P}}_{\mathbf{c}}\mathbf{=}1.33x{10}^{14}N/m^2 \\ {\mathit{T}}_{\mathit{c}}={\displaystyle \frac{{\mathbf{G}\mathbf{M}.\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}}{2\mathbf{R}{\mathit{K}}_{\mathit{B}}}}={\displaystyle \frac{\left(6.674x{10}^{-11}\frac{\mathrm{N}.\mathrm{m}2}{\mathrm{k}\mathrm{g}2}x2x{10}^{30}Kgx0.61x1.674x{10}^{-27}Kg\right)}{\left(2\mathit{x}7x{10}^{8}mx1.38x{10}^{-23}\frac{J}{K}\right)}} \end{gathered}$$

$${\mathit{T}}_{\mathit{c}}=7054956\mathit{K}.$$

The central pressure could be calculated by hydrostatic equilibrium by Eqn. (6) and an Eqn. (13) is the equation of state or eqn. (14) that is used to measure the central temperature of Sun and stars. The central pressure and central temperature of stars could be calculated precisely by new models and solar simulations. The value of a central temperature is found mathematically by the equation. (14), and it is not high enough value for stars to ignite the nuclear fusion processes in its core accurately. The nuclear fusion requires to higher central temperature and pressure to overwhelm the repulsion force between positive charges in the atomic nuclei. The star has a dense core of nuclear fusion at its heart, which increases its central pressure and temperature, continuously igniting atomic fusion processes. I have used the following two equations: the equation. (21) and eqn. (24) to calculate the central pressure and central temperature of stars precisely. Suppose the following density, pressures and temperatures are required to sustain nuclear fusion processes at the heart of Sun and stars, the central density of stars is $\left({\mathsf{\rho }}_{\mathbf{c}}=\mathrm{150,000}{\displaystyle \frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}}\right),$ the central pressure is (${\mathbf{P}}_{\mathbf{c}}$=$2.86x{10}^{16}N/m^2)$, and its central temperature${(\mathit{T}}_{\mathit{c}}=\mathrm{14,000,000}\mathit{K})$.

5. Average Central Pressure and Central Temperature of Stars

The central pressure and central temperature of a star are two crucial properties that determine stellar stability, its fate, and its energy production. The star's mass and radius primarily determine the central pressure, while the mass, radius, and composition of the star influence the central temperature. These two essential conditions within the core of the star allow for nuclear fusion processes to occur, the process that fuses light atomic nuclei to produce new massive atomic nuclei, and powers the stars with light and heat. The nuclear fusion processes at the heart of stars sustain their stability and produce high enough thermal pressure against the gravity of stars. The mass and gravitational force of stars lead to an increase in pressure on the stars to decrease their sizes inward, and fusion processes produce high enough thermal pressure to push up outward on the outer shells of stars, and increasing their size. An accurate hydrostatic balance that is available continuously between the gravitational force of the stars and thermal pressure of radiation prevents the stars from collapsing inward under gravity or exploding outward under thermal pressure. The great mass in the stars, the core density, the huge central pressure, and temperature are several essential conditions to sustain nuclear fusion processes in the heart of main-sequence stars. Hydrogen fuses to form helium in the core of stars with lower masses. The Sun is a low-mass star; as a result, hydrogen is fused at its core to produce helium atoms and release energy. High-mass stars have huge mass, core density, gravity, central pressure, and temperature to fuse multiple types of atoms with lower or higher atomic nuclei. Helium, Oxygen, Calcium, and Iron atoms could be produced in the heart of massive stars during multiple nuclear fusion processes.

$$\mathit{F}=\mathit{G}{\displaystyle \frac{\mathit{M}\left(\mathit{r}\right)\mathit{m}}{{\mathit{R}}^2}}$$

(15)

$$\mathit{A}=4\mathit{\pi }{\mathit{R}}^2$$

(16)

$$\mathit{P}={\displaystyle \frac{\mathit{F}}{\mathit{A}}}$$

(17)

$${\displaystyle \frac{\mathit{d}\mathit{P}}{\mathit{d}\mathit{r}}}=-{\displaystyle \frac{\mathit{G}\mathit{M}\left(\mathit{r}\right)\mathit{\rho }\left(\mathit{r}\right)}{{\mathit{r}}^2}}$$

(18)

Rearrange an equation of Hydrostatic equilibrium to derive central pressure of stars and spherical objects:

$${\displaystyle \frac{\mathit{d}\mathit{P}}{\mathit{d}\mathit{r}}}={\displaystyle \frac{\mathit{G}\mathit{M}\left(\mathit{r}\right)\mathit{\rho }\left(\mathit{r}\right)}{{\mathit{r}}^2}}$$

(19)

$${\int }_{{\mathit{P}}_{\mathit{c}}}^0\mathit{d}\mathit{P}=\mathit{G}\mathit{M}\left(\mathit{r}\right)\mathit{\rho }\left(\mathit{r}\right){\int }_0^{{\mathit{R}}_{\mathit{S}}}{\mathit{r}}^{-2}\mathit{d}\mathit{r}$$

$$[0-{\mathit{P}}_{\mathit{c}}]={\displaystyle \frac{\mathit{G}\mathit{M}\left(\mathit{r}\right)\mathit{\rho }\left(\mathit{r}\right)}{-1\mathit{x}[\mathit{R}-0]}}$$

$$-{\mathit{P}}_{\mathit{c}}=-{\displaystyle \frac{\mathit{G}\mathit{M}\left(\mathit{r}\right)\mathit{\rho }\left(\mathit{r}\right)}{\mathit{R}}}$$

$${\mathit{P}}_{\mathit{c}}={\displaystyle \frac{\mathit{G}\mathit{M}\left(\mathit{r}\right)\mathit{\rho }\left(\mathit{r}\right)}{\mathit{R}}}$$

(20)

$${\mathbf{P}}_{\mathbf{c}}={\displaystyle \frac{\mathit{G}\mathit{M}\left(\mathit{r}\right){\mathit{\rho }}_{\mathit{c}}}{\mathit{R}}}$$

(21)

$${\mathbf{P}}_{\mathbf{i}\mathbf{d}\mathbf{e}\mathbf{a}\mathbf{l}\mathbf{g}\mathbf{a}\mathbf{s}}={\displaystyle \frac{{{\mathit{\rho }}_{\mathit{c}}\mathit{K}}_{\mathit{B}}{\mathit{T}}_{\mathit{c}}}{\mathit{\mu }{\mathit{m}}_{\mathit{H}}}}$$

(22)

Suppose central pressure in eqn.(21) equal to pressure of an ideal gases at eqn. (22) ${(\mathrm{P}}_{\mathrm{I}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{g}\mathrm{a}\mathrm{s}}={\mathbf{P}}_{\mathbf{c}})$yields to:

$${\displaystyle \frac{\mathit{G}\mathit{M}\left(\mathit{r}\right){\mathit{\rho }}_{\mathit{c}}}{\mathit{R}}}={\displaystyle \frac{{{\mathit{\rho }}_{\mathit{c}}\mathit{K}}_{\mathit{B}}{\mathit{T}}_{\mathit{c}}}{\mathit{\mu }{\mathit{m}}_{\mathit{H}}}}$$

$${\mathbf{T}}_{\mathbf{c}}={\displaystyle \frac{\mathit{\mu }{\mathit{m}}_{\mathit{H}}\mathit{G}\mathit{M}}{\mathit{R}{\mathit{K}}_{\mathit{B}}}}$$

(23)

$${\mathbf{T}}_{\mathbf{c}}={\displaystyle \frac{\mathit{\mu }{\mathit{m}}_{\mathit{H}}{\mathit{P}}_{\mathit{c}}}{{{\mathit{\rho }}_{\mathit{c}}\mathit{K}}_{\mathit{B}}}}$$

(24)

$$\mathit{\rho }={\displaystyle \frac{\mathit{M}}{\frac{4}{3}\mathit{\pi }{\mathit{R}}^3}}$$

(25)

Substitute the value of a density in eqn. (25) into the position of a density at eqn. (6) yields:

$$P_c={\displaystyle \frac{GM\rho }{2R}}={\displaystyle \frac{GM\left(\frac{\mathit{M}}{\frac{4}{3}\mathit{\pi }{\mathit{R}}^3}\right)}{2R}}$$

$$P_c={\displaystyle \frac{GM\rho }{2R}}=\left({\displaystyle \frac{3\mathit{G}\mathit{M}.\mathit{M}}{4\mathit{\pi }{\mathit{R}}^3}}\right)÷2R=\left({\displaystyle \frac{3\mathit{G}\mathit{M}.\mathit{M}}{4\mathit{\pi }{\mathit{R}}^3}}\right)x\left({\displaystyle \frac{1}{2R}}\right)$$

$${\mathit{P}}_{\mathbf{c}}=\left({\displaystyle \frac{3\mathbf{G}{\mathbf{M}}^2}{8\mathsf{\pi }{\mathbf{R}}^4}}\right)$$

$$P_c=\left({\displaystyle \frac{3\mathit{G}{M}^2}{8\mathit{\pi }{\mathit{R}}^4}}\right)={\displaystyle \frac{GM\rho }{2R}}$$

(26)

$${\mathbf{P}}_{\mathbf{i}\mathbf{d}\mathbf{e}\mathbf{a}\mathbf{l}\mathbf{g}\mathbf{a}\mathbf{s}}={\displaystyle \frac{{\mathit{\rho }\mathit{K}}_{\mathit{B}}{\mathit{T}}_{\mathit{c}}}{\mathit{\mu }{\mathit{m}}_{\mathit{H}}}}$$

(27)

Suppose the central pressure in eqn.(26) equal to the pressure of an ideal gases at eqn. (27), then ${(\mathrm{P}}_{\mathrm{I}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{g}\mathrm{a}\mathrm{s}}={\mathbf{P}}_{\mathbf{c}})$yields to:

$${\mathbf{P}}_{\mathbf{c}}={\displaystyle \frac{{\mathit{\rho }\mathit{K}}_{\mathit{B}}{\mathit{T}}_{\mathit{c}}}{\mathit{\mu }{\mathit{m}}_{\mathit{H}}}}$$

$${\mathbf{T}}_{\mathbf{c}}={\displaystyle \frac{\mathit{\mu }{\mathit{m}}_{\mathit{H}}{\mathbf{P}}_{\mathbf{c}}}{{\mathit{\rho }\mathit{K}}_{\mathit{B}}}}$$

(28)

6. Nuclear Fusion Conditions

Nuclear fusion is a fundamental reaction that occurs in the core of a star, and powers it with energy to keep star more stable. Nuclear fusion processes in the core of stars require four key conditions: Higher mass and central density, higher central pressure, higher central temperature, and sufficient fusion fuel and time to sustain nuclear fusion reactions. Nuclear fusion is the process in which two light atomic nuclei combine to form a heavier nucleus under higher central pressure and maximum central temperature, resulting in the release of vast amounts of energy and energetic particles [41,42,43,44,45]. These conditions are necessary to overcome the electrostatic repulsion force between positively charged nuclei, the positive protons, and allow the strong nuclear force to bind atomic nuclei together at a minimum distance between atomic nuclei to form massive atomic nuclei, and release energy. Higher density, central pressure, and thermal energy are several necessary factors to overcome the hydrostatic energy and repulsion force between positive charges to squeeze the distance between positive protons in the atomic nuclei and to press them steeply to fuse together. We can use a stellar structure model to calculate the central pressure and central temperature of the Sun and stars. This involves solving a set of four differential equations that describe how the mass, pressure, temperature, and luminosity vary with radius inside a star and the Sun. Atomic nuclei could be fused at a minimum distance since thermal energy and pressure overwhelmed the repulsion forces available among positive charges. Heat could be transferred throughout the stars during collisions and rapid oscillation of particles. Following main equations of thermal, transitional kinetic energy, and electric potential energy:

$${\mathit{E}}_{\mathit{t}\mathit{h}\mathit{e}\mathit{r}\mathit{m}\mathit{a}\mathit{l}}={\displaystyle \frac{3}{2}}{\mathit{K}}_{\mathit{B}}\mathit{T}$$

(29)

$${\mathit{K}\mathit{E}}_{\mathit{p}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}={\displaystyle \frac{1}{2}}\mathit{m}{\mathit{v}}^2$$

(30)

$${\mathit{E}}_{\mathit{E}\mathit{l}\mathit{e}\mathit{c}\mathit{t}\mathit{r}\mathit{i}\mathit{c}}={\mathit{K}}_{\mathit{C}}{\displaystyle \frac{{{\mathit{Z}}_1{\mathit{Z}}_2\mathit{e}}^2}{{\mathit{r}}_{\mathit{m}\mathit{i}\mathit{n}}}}$$

(31)

$${\mathit{K}}_{\mathit{C}}={\displaystyle \frac{1}{4\mathit{\pi }\mathsf{\epsilon }₀}}={\displaystyle \frac{1}{4\mathit{x}3.14\mathit{x}8.85\mathit{x}{10}^{-12}\frac{\mathit{F}}{\mathit{m}}}}=8.99\mathit{x}{10}^9{\displaystyle \frac{{\mathit{N}.\mathit{m}}^2}{{\mathit{c}}^2}}$$

Where,${\mathit{E}}_{\mathit{t}\mathit{h}\mathit{e}\mathit{r}\mathit{m}\mathit{a}\mathit{l}}$ is a thermal energy of the gas and ionised particles,${\mathit{K}}_{\mathit{B}}$ is a Boltzmann constant, and$\mathit{T}$ is the temperature of the excited particles. ${\mathit{K}\mathit{E}}_{\mathit{p}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}$ is a kinetic energy of particles,$\mathit{m}$ is the mass of particles and $\mathit{v}$ is the speed of particles. ${\mathit{E}}_{\mathit{E}\mathit{l}\mathit{e}\mathit{c}\mathit{t}\mathit{r}\mathit{i}\mathit{c}}$ is an electrostatic energy or electric potential energy between positive and negative charges. ${\mathit{r}}_{\mathit{m}\mathit{i}\mathit{n}}$ is a minimum distance between positive charges in atomic nuclei to fuse together at this shortest distance and release energy. ${\mathit{Z}}_1{\mathit{Z}}_2$are atomic numbers of the chemical elements. ${(\mathit{e}}^2={\mathit{q}}_1\mathit{x}{\mathit{q}}_2={{1.6\mathit{x}10}^{-19}\mathit{C}\mathit{x}1.6\mathit{x}10}^{-19}\mathit{C})$ are symbols of an electric charge was used for positive or negative charges, $({\mathsf{\epsilon }}^0=8.85\mathit{x}{10}^{-12}{\displaystyle \frac{\mathit{F}}{\mathit{m}}})$ is an electric constant, also known as vacuum permittivity or epsilon naught, and $({\mathit{K}}_{\mathit{C}}={\displaystyle \frac{1}{4\mathit{\pi }{\mathsf{\epsilon }}^0}}=8.99\mathit{x}{10}^9{\displaystyle \frac{{\mathit{N}.\mathit{m}}^2}{{\mathit{c}}^2}})$ is a Coulomb’s constant. The Coulomb’s constant relates the force between charges to the product of their magnitudes and the square of the distance between them. Electric potential energy is the potential energy that results from the configuration of electric charges in atomic structures or the energy gained by charges due to their position in an electric field. It represents the energy stored in a charge distribution due to the electrostatic forces between the different or similar charges, such as positive or negative charges, and it is the energy necessary to assemble that charge distribution from infinity. Suppose thermal energy is in the equation. (29) equal to electrical energy at eqn. (31) to measure the minimum distance ${(\mathit{r}}_{\mathit{m}\mathit{i}\mathit{n}})$ required for nuclear fusion between atomic nuclei:

$${\mathit{E}}_{\mathit{t}\mathit{h}\mathit{e}\mathit{r}\mathit{m}\mathit{a}\mathit{l}}={\mathit{E}}_{\mathit{E}\mathit{l}\mathit{e}\mathit{c}\mathit{t}\mathit{r}\mathit{i}\mathit{c}}$$

$${\displaystyle \frac{3}{2}}{\mathit{K}}_{\mathit{B}}\mathit{T}={\mathit{K}}_{\mathit{C}}{\displaystyle \frac{{{\mathit{Z}}_1{\mathit{Z}}_2\mathit{e}}^2}{{\mathit{r}}_{\mathit{m}\mathit{i}\mathit{n}}}}$$

$${\mathit{r}}_{\mathit{m}\mathit{i}\mathit{n}}={\mathit{K}}_{\mathit{C}}{\displaystyle \frac{{{\mathit{Z}}_1{\mathit{Z}}_2\mathit{e}}^2}{\frac{3}{2}{\mathit{K}}_{\mathit{B}}\mathit{T}}}$$

(32)

Suppose thermal energy in the equation. (29) equal to kinetic energy of particles at eqn. (30) to determine $\left(\mathit{v}\right)$ the speed of particles:

$${\displaystyle \frac{3}{2}}{\mathit{K}}_{\mathit{B}}\mathit{T}={\displaystyle \frac{1}{2}}\mathit{m}{\mathit{v}}^2$$

$$3{\mathit{K}}_{\mathit{B}}\mathit{T}=\mathit{m}{\mathit{v}}^2$$

$$\mathit{v}=\sqrt{{\displaystyle \frac{3{\mathit{K}}_{\mathit{B}}\mathit{T}}{\mathit{m}}}}$$

(33)

Wavelength of particles the de Broglie wavelength is the wavelength associated with a moving particle, and it is inversely proportional to the particle's momentum. It represents the wave-matter-like nature of particles, meaning that all matter shows wave characteristics, as photon particles.

$$\mathit{\lambda }={\displaystyle \frac{\mathit{h}}{\mathbf{m}\mathit{v}}}={\displaystyle \frac{\mathit{h}}{\mathit{p}}}$$

(34)

Where $\mathit{\lambda }$ is a wavelength of particles in unit meters, and$(\mathit{p}=\mathit{m}\mathit{v}$) is the linear momentum of particles in (kg. m/s), and$h$ is the Planck’s constant $(h=6.63x{10}^{-34}kg.{\displaystyle \frac{m^2}{s}}).$

7. Maximum Central Pressure and Central Temperature of The Spherical Objects

The maximum central pressure and central temperature of stars, planets, and black hole singularities have been determined precisely by using their central radius and central density in the calculations. The cosmic spherical objects have a dense ball of matter and energy at their hearts. The Planets and satellites have spherical shapes, and condensed balls of matter are stabilized at their cores. The central radius of the ball in the core of cosmic spherical objects is four percent $(4\%)$ of the total radius of those spherical objects. The central radius and central density are necessary to calculate the maximum central pressure and central density of stars and celestial objects. Most of the mass of a spherical celestial object is concentrated at its nucleus. The traditional theory of hydrostatic balance failed to calculate the maximum central pressure and central temperature of stars and singularity. The maximum central density, pressure, and temperature are crucial to calculate the optimum value for nuclear fusion conditions. The maximum central pressure and temperature can be determined precisely by the modern theory of hydrostatic equilibrium, since we know that the radius of the fusion ball is approximately 4 percent of the total radius of stars. The stars and most cosmic spherical objects should have dense balls resident at their cores to keep them in perfect balance. The ball of a highly condensed state of matter and energy in the core of a hot celestial object is necessary to sustain its stability and prevent its atmosphere from evaporation. Molecules and atoms are compressed and torn apart under higher central pressure and temperature at the core of stars to form a dense ball of matter and energy in the nuclei of stars. The spherical object with a lower radius and a higher mass, density, and central pressure may sustain its stability and speeding up the nuclear fusion processes at the core of massive stars.

Most of the main sequence stars have perfect mass, fuel, and a necessary central temperature to sustain the nuclear fusion processes for a longer time. The Sun started with nuclear fusion at its core more than five billion years ago, and may survive for the next five billion years. The high mass star can burn out its fuel of nuclear fusion in a shorter time. Most massive stars can survive for a few million years. The shortest radius of stellar nuclei or the tiny size of that ball in the core of stars or any cosmic objects is necessary to keep stars or entire celestial objects in perfect balance dynamically. I have concluded that the central radius of any cosmic spherical object is only four percent of its total radius. Following the equation of the central radius of stars and spherical celestial objects:

$${\mathit{R}}_{\mathit{c}}=0.04\mathit{x}\mathit{R}$$

(35)

Where ${\mathit{R}}_{\mathit{c}}$ is the central radius of the dense ball in the heart of stars and compacted spherical objects, and $\mathit{R}$ is the total radius of any spherical object, specifically stars, compacted stars, planets, and black hole singularity. The central radius of the nuclei in the core of spherical objects is about four percent of the total radius of those round objects, and eqn. (35) is necessary equation to calculate central radius, maximum central density, central pressure, central temperature, minimum distance between particles, and speed of particles in such a violent environment. The squeezed central radius of a spherical object gives a higher chance for nuclear fusion processes, and sustains the stability of such round objects. The highly compressed core of stars, or their reduced radius, a maximum central density, pressure, and temperature, may increase the chance of igniting nuclear fusion processes. Substitute eqn. (35) into the eqn. (25) and equation. (26) to calculate central density, maximum central pressure, higher central temperature, minimum distance between compressed particles, and speed of particles in such a violent environment at the very center of stars and cosmic spherical objects in the visible Universe.

$${\mathit{\rho }}_{\mathit{c}}={\displaystyle \frac{{\mathit{M}}_{\mathit{c}}}{\frac{4}{3}\mathit{\pi }{\left(0.04\mathit{x}\mathit{R}\right)}^3}}$$

(36)

$${\mathit{P}}_{\mathit{c}}=\left({\displaystyle \frac{3\mathit{G}{{\mathit{M}}_{\mathit{c}}}^2}{8\mathit{\pi }(0.04\mathit{x}\mathit{R}{)}^4}}\right)={\displaystyle \frac{\mathit{G}{\mathit{M}}_{\mathit{c}}{\mathit{\rho }}_{\mathit{c}}}{2{\mathit{R}}_{\mathit{c}}}}$$

(37)

$${\mathbf{T}}_{\mathbf{c}}={\displaystyle \frac{\mathit{\mu }{\mathit{m}}_{\mathit{H}}{\mathbf{P}}_{\mathbf{c}}}{{{\mathit{\rho }}_{\mathit{c}}\mathit{K}}_{\mathit{B}}}}$$

(38)

We can confirm the equation. (36), eqn. (37) and eqn. (38) are necessary to calculate the maximum central density, central pressure and central temperature of stars and celestial objects respectively. Those equations helped us to confirm that an additional nuclear fusion may have started to fuse another heavy atomic nuclei and particles in the deep of stars, plus the main nuclear fusion that started before in the outer shell of the nuclear fusion ball, for example, hydrogen isotopes fuse to form a helium atom in the outer shell of a nuclear fusion ball, but helium and carbon could be fused at the very center of the Sun, inside a stellar compacted egg, at this moment, plus with hydrogen fusion in the outer shells. Furthermore, the stellar compacted egg could be formed in the very center of stars under such extreme pressure, and temperature. The stellar compacted egg may be squeezed violently and its radius reduced extremely due to the supernova event to become a black hole singularity, and give birth to a newborn stellar mass black hole. The stellar compacted egg could be formed at the center of most stars since maximum density, pressure, and tremendous temperature participated in this mechanism. The stellar compacted egg is a dense ball of concentrated state of matter and energy that is combined and stabilised at the center of stars. The stellar compacted egg may have the mass of fruits, mountains, the Moon, Earth, and planets, but its size is similar to the size of birds eggs according to mass and pressure of stars, or the mechanism of its formation.

$$\mathit{v}=\mathit{f}\mathit{\lambda }={\displaystyle \frac{\mathit{\lambda }}{\mathit{T}}}$$

(39)

$$\mathit{n}={\displaystyle \frac{\mathit{\rho }}{{\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}}}={\displaystyle \frac{\mathit{N}}{\mathit{V}}}={\displaystyle \frac{1}{\mathit{V}={\mathit{d}}^3}}$$

(40)

Where $\mathit{d}$ is the distance between two particles measured in meters (m). Frequency$\left(\mathit{f}\right)$ is the number of vibrations or times of a repeating event (like a wave cycle) occurs per unit of time, measured in Hertz (Hz). The time of periods or time of oscillation $T$, on the other hand, is the duration of one complete cycle of that event or oscillations, usually measured in seconds (s), and$\mathit{\lambda }$ is the wavelength of an oscillated particle measured in meters. Following an equation for the fully ionized gases, molecules, and Particles:

$${{\displaystyle \frac{1}{\mathit{\mu }}}=\mathit{\Sigma }}_{\mathit{i}}{\displaystyle \frac{{\mathit{X}}_{\mathit{i}}(1+{\mathit{Z}}_{\mathit{i}})}{{\mathit{A}}_{\mathit{i}}}}$$

(41)

Where: ${\mathit{X}}_{\mathit{i}}$= mass fraction of species $\mathit{i}$.

${\mathit{A}}_{\mathit{i}}$=atomic mass number of species $\mathit{i}$.

${\mathit{Z}}_{\mathit{i}}$= number of protons ( charges) or an atomic number of species $\mathit{i}$.

${(1+Z}_i)$= counts both the ion and its freed electrons.

$\mathit{\mu }$ = is a mean molecular weight of ionized particles ${(\mathit{\mu }}_{\mathit{I}\mathit{o}\mathit{n}\mathit{s}})$.

$${\mathit{\mu }}_{\mathit{I}\mathit{o}\mathit{n}\mathit{s}}={\displaystyle \frac{\mathit{M}\mathit{a}\mathit{s}\mathit{s}\mathit{p}\mathit{e}\mathit{r}\mathit{n}\mathit{u}\mathit{c}\mathit{l}\mathit{e}\mathit{u}\mathit{s}\mathit{i}\mathit{n}\mathit{a}\mathit{t}\mathit{o}\mathit{m}\mathit{i}\mathit{c}\mathit{m}\mathit{a}\mathit{s}\mathit{s}\mathit{u}\mathit{n}\mathit{i}\mathit{t}\left(\mathit{a}\mathit{m}\mathit{u}\right)}{\mathbf{T}\mathbf{o}\mathbf{t}\mathbf{a}\mathbf{l}\mathbf{n}\mathbf{u}\mathbf{m}\mathbf{b}\mathbf{e}\mathbf{r}\mathbf{o}\mathbf{f}\mathbf{p}\mathbf{a}\mathbf{r}\mathbf{t}\mathbf{i}\mathbf{c}\mathbf{l}\mathbf{e}\mathbf{s}\left(\mathbf{n}\mathbf{u}\mathbf{c}\mathbf{l}\mathbf{e}\mathbf{i}+\mathbf{e}\mathbf{l}\mathbf{e}\mathbf{c}\mathbf{t}\mathbf{r}\mathbf{o}\mathbf{n}\mathbf{s}\right)\mathit{p}\mathit{e}\mathit{r}\mathit{n}\mathit{u}\mathit{c}\mathit{l}\mathit{e}\mathit{u}\mathit{s}}}={\displaystyle \frac{\mathit{A}}{1+\mathit{Z}}}$$

(42)

Following the Electron Degeneracy pressure or Central Pressure for white dwarf stars:

$${\mathit{P}}_{\mathit{c}}={\displaystyle \frac{{\left(3{\mathit{\pi }}^2\right)}^{2/3}{\mathrm{\hslash }}^2}{5{\mathit{m}}_{\mathit{e}}}}{{\mathit{n}}_{\mathit{e}}}^{5/3}$$

(43)

$${\mathit{P}}_{\mathit{c}}={\displaystyle \frac{{\mathrm{\hslash }}^2}{{\mathit{m}}_{\mathit{e}}}}{\left[\left({\displaystyle \frac{\mathit{Z}}{\mathit{A}}}\right)\mathit{x}{\displaystyle \frac{{\mathit{\rho }}_{\mathit{c}}}{{\mathit{m}}_{\mathit{H}}}}\right]}^{5/3}$$

(44)

$${\mathit{P}}_{\mathit{c}}={\displaystyle \frac{{\mathit{h}}^2}{20{\mathit{m}}_{\mathit{e}}}}{\left({\displaystyle \frac{3}{\mathit{\pi }}}\right)}^{2/3}{\left[{\displaystyle \frac{{\mathit{\rho }}_{\mathit{c}}}{{\mathit{\mu }}_{\mathit{e}}{\mathit{x}\mathit{m}}_{\mathit{H}}}}\right]}^{5/3}$$

(45)

Where: ${\mathit{P}}_{\mathit{c}}$ is the central pressure.${\left(3{\mathit{\pi }}^2\right)}^{2/3}=9.57$.

h-bar (ℏ), or the reduced Planck's constant, in which ℏ equals Planck’s constant h divided by 2π=$1.05457x{10}^{-34}J.s$. The number density of electrons is${\mathit{n}}_{\mathit{e}}$. The mass of hydrogen atom or proton particle is ${(\mathit{m}}_{\mathit{H}}).$

$({\mathit{m}}_{\mathit{e}}=9.11\mathit{x}{10}^{-31}\mathit{K}\mathit{g})$is a mass of electron. Mean molecular weight per electrons is ${(\mathit{\mu }}_{\mathit{e}}={\displaystyle \frac{\mathit{A}}{\mathit{Z}}}).$

Problem 1: The main-sequence star or the low-mass star with a mass of Sun$\left(1.989x{10}^{30}kg\right)$, and its radius similar to the radius of Sun $\left(6.96x{10}^{8}m\right)$, the central mass of a star is half of its total mass, and the central radius of a star is four percent of its total radius, calculate its central radius, central mass, maximum central pressure, central temperature, minimum distance between two atomic nuclei to fuse, speed of hydrogen or proton particles, DE Broglie wavelength of hydrogen particles and its frequency, also determine the speed of electron particle, DE Broglie wavelength of electron particles, Frequency, and distance between two Electron particles, and eventually calculate the speed of Fabriton particle, DE Broglie wavelength of Fabriton particles, Frequency, and distance between two Fabriton particles?.

Solution:

$${\mathit{R}}_{\mathit{c}}=0.04\mathit{x}\mathit{R}=0.04\mathit{x}{6.96\mathit{x}10}^8\mathit{m}=27840000\mathit{m}.$$

$${\mathit{R}}_{\mathit{c}}=27840\mathit{k}\mathit{m}.$$

Where ${\mathit{R}}_{\mathit{c}}$ is the central radius of a fusion ball or the core radius, it is about four percent of the total radius of stars and cosmic spherical objects. Assuming the central mass is half the total mass:

$${\mathit{M}}_{\mathit{c}}=0.5\mathit{x}\mathit{M}=0.5\mathit{x}1.989x{10}^{30}kg=9.945x{10}^{29}kg$$

Where ${\mathit{M}}_{\mathit{c}}$ is the Central mass of stars, it is about half of the total mass of stars.

$${\mathit{\rho }}_{\mathit{c}}={\displaystyle \frac{{\mathit{M}}_{\mathit{c}}}{\frac{4}{3}\mathit{\pi }{{\mathit{R}}_{\mathit{c}}}^3}}={\displaystyle \frac{{\mathit{M}}_{\mathit{c}}}{\frac{4}{3}\mathit{\pi }{\left(0.04\mathit{x}\mathit{R}\right)}^3}}={\displaystyle \frac{9.945x{10}^{29}kg}{\frac{4}{3}\mathit{\pi }{\left(27840000\mathit{m}\right)}^3}}$$

$${\mathit{\rho }}_{\mathit{c}}=11010267{\displaystyle \frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}}$$

Where ${\mathit{\rho }}_{\mathit{c}}$ is the uniform central density inside the nuclear fusion core.

$${\mathit{P}}_{\mathit{c}}=\left({\displaystyle \frac{3\mathit{G}{{\mathit{M}}_{\mathit{c}}}^2}{8\mathit{\pi }{{\mathit{R}}_{\mathit{c}}}^4}}\right)=\left({\displaystyle \frac{3\mathit{x}6.674\mathit{x}{10}^{-11}\frac{{N.m}^2}{{kg}^2}\mathit{x}{\left(9.945\mathit{x}{10}^{29}\mathit{k}\mathit{g}\right)}^2}{8\mathit{\pi }(27840000\mathit{m}{)}^4}}\right)$$

$${\mathit{P}}_{\mathit{c}}=1.3\mathit{x}{10}^{19}{\displaystyle \frac{\mathit{N}}{{\mathit{m}}^2}}$$

The maximum central pressure ${\mathit{P}}_{\mathit{c}}$ is calculated from the hydrostatic equilibrium equation.

$${\mathbf{T}}_{\mathbf{c}}={\displaystyle \frac{\mathit{\mu }{\mathit{m}}_{\mathit{H}}{\mathbf{P}}_{\mathbf{c}}}{{{\mathit{\rho }}_{\mathit{c}}\mathit{K}}_{\mathit{B}}}}={\displaystyle \frac{\left(0.61\mathit{x}1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g}\mathit{x}1.3\mathit{x}{10}^{19}\mathit{P}\mathit{a}\right)}{\left(11010267\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\right)}}$$

$${\mathbf{T}}_{\mathbf{c}}=87367861\mathit{K}.$$

The mean molecular weight for the ionised gas the hydrogen and helium atoms $(\mathit{\mu }=0.61)$, and ${\mathbf{T}}_{\mathbf{c}}$ is the central temperature of Stars by using ideal gas relation in hydrostatic equilibrium.

$${\mathit{r}}_{\mathit{m}\mathit{i}\mathit{n}}={\mathit{K}}_{\mathit{C}}{\displaystyle \frac{{{\mathit{Z}}_1{\mathit{Z}}_2\mathit{e}}^2}{\frac{3}{2}{\mathit{K}}_{\mathit{B}}{\mathbf{T}}_{\mathbf{c}}}}=8.99\mathit{x}{10}^9{\displaystyle \frac{{\mathit{N}.\mathit{m}}^2}{{\mathit{c}}^2}}\mathit{x}{\displaystyle \frac{{1\mathit{x}1\mathit{x}\left(1.6\mathit{x}{10}^{-19}\mathit{C}\right)}^2}{\frac{3}{2}\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\mathit{x}87367861\mathit{K}}}$$

$${\mathit{r}}_{\mathit{m}\mathit{i}\mathit{n}}={1.27\mathit{x}10}^{-13}\mathit{m}.$$

Assuming proton – proton fusion ${(\mathit{Z}}_1{=\mathit{Z}}_2=1)$, $(\mathit{e}=1.6\mathit{x}{10}^{-19}\mathit{C})$ is an electric charge, and ${\mathit{r}}_{\mathit{m}\mathit{i}\mathit{n}}$ is the minimum distance between atomic nuclei to fuse.

At the first step, I have to calculate the speed, wavelength, and frequency of protons and hydrogen ions, and precisely determine the distance between two protons or two hydrogen ions:

$$\mathit{v}=\sqrt{{\displaystyle \frac{3{\mathit{K}}_{\mathit{B}}{\mathbf{T}}_{\mathbf{c}}}{{\mathit{m}}_{\mathit{H}}}}}=\sqrt{{\displaystyle \frac{\left(3\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\mathit{x}87367861\mathit{K}\right)}{\left(1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g}\right)}}}$$

Then, the speed of hydrogen particle has been determined $({\mathit{v}}_{\mathit{H}}=1469935{\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}).$ The speed of hydrogen particle $\mathit{v}$ is the thermal velocity of particles, specifically hydrogen ions, and $({\mathit{m}}_{\mathit{H}}={\mathit{m}}_{\mathit{P}\mathit{r}\mathit{o}\mathit{t}\mathit{o}\mathit{n}})$ is the mass of hydrogen atom, hydrogen ions equal to mass of proton particle.

$$\mathit{\lambda }={\displaystyle \frac{\mathit{h}}{\mathbf{m}\mathit{v}}}={\displaystyle \frac{\mathit{h}}{{\mathit{m}}_{\mathit{H}}.{\mathit{v}}_{\mathit{H}}}}={\displaystyle \frac{(6.63\mathit{x}{10}^{-34}\mathit{k}\mathit{g}.\frac{{\mathit{m}}^2}{\mathit{s}})}{\left(1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g}\mathit{x}1469935\frac{\mathrm{m}}{\mathrm{s}}\right)}}={2.69\mathit{x}10}^{-13}\mathit{m}$$

${\mathit{\lambda }}_H={2.69\mathit{x}10}^{-13}\mathit{m}.$ The de Broglie wavelength of the hydrogen ions or proton particle has been determined as $({\mathit{\lambda }}_H=0.269\mathrm{p}\mathrm{m})$.

By using eqn. (39) to calculate the frequency of hydrogen ions or protons: $\mathit{v}=\mathit{f}\mathit{\lambda }$.

Rearrange the equation (39) to determine the frequency of oscillating hydrogen or proton particles:$\mathit{f}={\displaystyle \frac{\mathit{v}}{\mathit{\lambda }}}={\displaystyle \frac{\left(1469935\frac{\mathrm{m}}{\mathrm{s}}\right)}{{(2.69\mathit{x}10}^{-13}\mathit{m})}}={5.46\mathit{x}10}^{18}\mathit{H}\mathit{z}.$By using eqn. (40) to calculate the distance between two hydrogen or proton particles:

At first step, I need to find number density of hydrogen or proton Particles$\mathit{n}$:

$$\mathit{n}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{c}}}{{\mathit{m}}_{\mathit{H}}}}={\displaystyle \frac{\left(11010267\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}\right)}{1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g}}}=6.577\mathit{x}{10}^{33}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}.$$

$$\mathit{n}=6.577\mathit{x}{10}^{33}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}$$

$\mathit{n}={\displaystyle \frac{\mathit{N}}{\mathit{V}}}={\displaystyle \frac{1}{\mathit{V}={\mathit{d}}^3}}.$ Then substitute the value of $\mathit{n}$ in the equation (40) to calculate (d) the distance between two hydrogen ions: $\left(6.577\mathit{x}{10}^{33}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}={\displaystyle \frac{1}{{\mathit{d}}^3}}\right).$

$$\mathit{d}={\displaystyle \frac{1}{\sqrt[3]{\mathit{n}}}}={\displaystyle \frac{1}{\sqrt[3]{6.577\mathit{x}{10}^{33}\frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}}}.\mathit{d}=5.337\mathit{x}{10}^{-12}\mathit{m}.$$

In the second step, I need to calculate the speed, wavelength, frequency, of Electron particles and the distance between two Electrons in the core of star:

$$\mathit{v}=\sqrt{{\displaystyle \frac{3{\mathit{K}}_{\mathit{B}}{\mathbf{T}}_{\mathbf{c}}}{{\mathit{m}}_{\mathit{e}}}}}=\sqrt{{\displaystyle \frac{\left(3\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\mathit{x}87367861\mathit{K}\right)}{\left(9.11\mathit{x}{10}^{-31}\mathit{k}\mathit{g}\right)}}}$$

Then, the speed of an electron particle has been determined $({\mathit{v}}_{\mathit{e}}=63011067{\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}).$

$$\mathit{\lambda }={\displaystyle \frac{\mathit{h}}{\mathbf{m}\mathit{v}}}={\displaystyle \frac{\mathit{h}}{{\mathit{m}}_{\mathit{e}}.{\mathit{v}}_{\mathit{e}}}}={\displaystyle \frac{(6.63\mathit{x}{10}^{-34}\mathit{k}\mathit{g}.\frac{{\mathit{m}}^2}{\mathit{s}})}{\left(9.11\mathit{x}{10}^{-31}\mathit{k}\mathit{g}\mathit{x}63011067\frac{\mathrm{m}}{\mathrm{s}}\right)}}={1.15\mathit{x}10}^{-11}\mathit{m}.$$

$({\mathit{\lambda }}_e={1.15\mathit{x}10}^{-11}\mathit{m}).$ The de Broglie wavelength of the electron particle has been determined as $({\mathit{\lambda }}_e=11.5\mathrm{p}\mathrm{m})$.

By using eqn. (39) to calculate the frequency of an electron particle: $\mathit{v}=\mathit{f}\mathit{\lambda }$.

Rearrange the equation (39) to determine the frequency of oscillating electron particles:$\mathit{f}={\displaystyle \frac{{\mathit{v}}_{\mathit{e}}}{{\mathit{\lambda }}_e}}={\displaystyle \frac{\left(63011067\frac{\mathrm{m}}{\mathrm{s}}\right)}{\left({1.15\mathit{x}10}^{-11}\mathit{m}\right)}}={5.479\mathit{x}10}^{18}\mathit{H}\mathit{z}.$

By using eqn. (40) to calculate the distance between two electron particles:

$$\mathit{n}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{c}}}{{\mathit{m}}_{\mathit{e}}}}={\displaystyle \frac{\left(11010267\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}\right)}{9.11\mathit{x}{10}^{-31}\mathit{k}\mathit{g}}}=1.2\mathit{x}{10}^{37}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}.$$

$$\mathit{n}=1.2\mathit{x}{10}^{37}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}.$$

$\mathit{n}={\displaystyle \frac{\mathit{N}}{\mathit{V}}}={\displaystyle \frac{1}{\mathit{V}={\mathit{d}}^3}}.$ Then substitute the value of$\mathit{n}$ in the equation (40) to calculate the distance between two electron particles: $\left(1.2\mathit{x}{10}^{37}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}={\displaystyle \frac{1}{{\mathit{d}}^3}}\right).$

$$\mathit{d}={\displaystyle \frac{1}{\sqrt[3]{\mathit{n}}}}={\displaystyle \frac{1}{\sqrt[3]{1.2\mathit{x}{10}^{37}\frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}}}.\mathit{d}=4.37\mathit{x}{10}^{-13}\mathit{m}.$$

In the final step, I need to calculate the speed, wavelength, frequency, of Fabriton particles and distance between two fabritons:

$$\mathit{v}=\sqrt{{\displaystyle \frac{3{\mathit{K}}_{\mathit{B}}{\mathbf{T}}_{\mathbf{c}}}{{\mathit{m}}_{\mathit{F}}}}}=\sqrt{{\displaystyle \frac{\left(3\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\mathit{x}87367861\mathit{K}\right)}{\left(9.11\mathit{x}{10}^{-41}\mathit{k}\mathit{g}\right)}}}$$

Then, the speed of a Fabriton particle has been determined $({\mathit{v}}_{\mathit{F}}=6301106697526{\displaystyle \frac{\mathbf{m}}{\mathbf{s}}}).$ The speed of a fabriton particle exceeded the speed of light as a result it is called Fabriton due to its Fast, actively binding reactions in total objects naturally.

$$\mathit{\lambda }={\displaystyle \frac{\mathit{h}}{\mathbf{m}\mathit{v}}}={\displaystyle \frac{\mathit{h}}{{\mathit{m}}_{\mathit{F}}.{\mathit{v}}_{\mathit{F}}}}={\displaystyle \frac{(6.63\mathit{x}{10}^{-34}\mathit{k}\mathit{g}.\frac{{\mathit{m}}^2}{\mathit{s}})}{\left(9.11\mathit{x}{10}^{-41}\mathit{k}\mathit{g}\mathit{x}6301106697526\frac{\mathbf{m}}{\mathbf{s}}\right)}}={1.15\mathit{x}10}^{-6}\mathit{m}.$$

$({\mathit{\lambda }}_{\mathit{F}}={1.15\mathit{x}10}^{-6}\mathit{m}).$ The de Broglie wavelength of the fabriton particle has been determined as $({\lambda }_F=1.15\mu \mathrm{m})$.

By using eqn. (39) to calculate the frequency of a fabriton particle: $v=f\lambda$.

Rearrange the equation (39) to determine the frequency of oscillating fabriton particles:$f={\displaystyle \frac{v_F}{{\lambda }_F}}={\displaystyle \frac{\left(6301106697526\frac{\mathrm{m}}{\mathrm{s}}\right)}{\left({1.15x10}^{-6}m\right)}}={5.479x10}^{18}Hz.$By using eqn. (40) to calculate the distance between two Fabriton particles:

$$\mathit{n}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{c}}}{{\mathit{m}}_{\mathit{F}}}}={\displaystyle \frac{\left(11010267\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}\right)}{9.11\mathit{x}{10}^{-41}\mathit{k}\mathit{g}}}=1.2\mathit{x}{10}^{47}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}$$

$$\mathit{n}=1.2\mathit{x}{10}^{47}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}$$

$\mathit{n}={\displaystyle \frac{N}{V}}={\displaystyle \frac{1}{V=d^3}}.$ Then substitute the value of$\mathit{n}$ in the equation (40) to calculate the distance between two fabriton particles: $\left(1.2x{10}^{47}{\displaystyle \frac{Particles}{m^3}}={\displaystyle \frac{1}{d^3}}\right).$

$$\mathit{d}={\displaystyle \frac{1}{\sqrt[3]{\mathit{n}}}}={\displaystyle \frac{1}{\sqrt[3]{1.2\mathit{x}{10}^{47}\frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}}}$$

$$\mathit{d}=2\mathit{x}{10}^{-16}\mathit{m}$$

The distance between two fabriton particles is incredibly low, even light could be trapped in the core of a star to increase its central pressure and central temperature, and such concentration of fabriton particles in the core of stars and celestial objects are necessary to enhance their stability. In the fusion core boundary to its center, the star has maximum central density and pressure since its core radius has decreased. From the surface of a nuclear fusion ball to the total surface of a star, the density and pressure of stars decrease as their radius increases. The total radius of a Sun from center to surface$\left({\mathit{R}=6.96\mathit{x}10}^8\mathit{m}\right),$ and its central radius, which is called the fusion core boundary radius ${(\mathit{R}}_{\mathit{C}\mathit{o}\mathit{r}\mathit{e}}=27840\mathit{k}\mathit{m})$. The density and pressure are incredibly high enough to start igniting the nuclear fusion in the core of stars. At the surface of stars, the density and pressure are very low or zero, as shown in Figure 1.

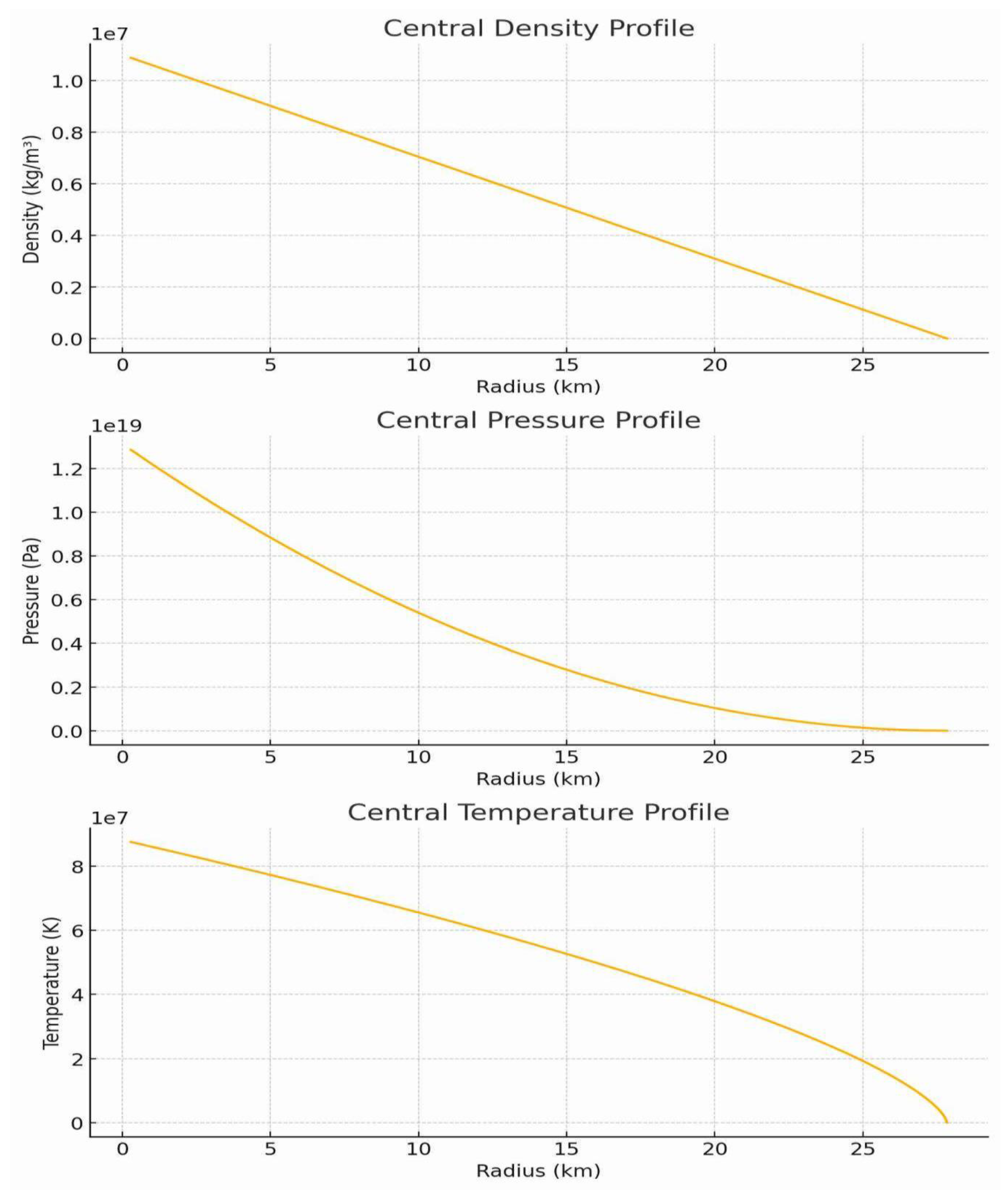
The nuclear fusion in the heart of a low-mass star starts when its central temperature reaches 15000000 kelvins. At the higher central temperatures and maximum central pressure, chains of nuclear fusion start in the core of low mass stars partially and in the heart of high mass stars widely started to form additional heavy atomic nuclei and formed multiple stellar compacted eggs of the fused materials. The chains of a nuclear fusion reaction in the core of a single stars with different central temperature and pressure may start to form stellar compacted eggs of fusion in the size of crocodile eggs or Bird eggs and of different masses. Those stellar compacted eggs are fusion balls, formed in the depths of the nuclear fusion core at higher central temperature zones and maximum central pressure. The stellar compacted eggs of nuclear Fusion could be formed in the central core of stars due to chains of nuclear fusion, and they are immersed in the bottom of a stellar core due to their tiny size and huge density to reside there and to enhance the stability of the entire star, Specifically save big fusion sphere from explosion. The photon particles could be trapped, absorbed, reflected, refracted, and emitted in the dense core of stars for a longer time, as a result increasing the central pressure and temperature of stars, which leads to start chains of nuclear fusion to form heavy atomic nuclei and produce stellar compacted eggs from the different fused matter. Multiple types of Stellar compacted eggs would be formed from different fusions of heavy particles in different places at the fusion core of stars. The multiple types of nuclear fusion processes may give birth to multiple stellar compacted eggs with different masses, concentrations, condensations, and sizes. The Helium fusion egg, Carbon fusion egg, and Calcium fusion eggs could be formed at the same moment in the core of a single star. High mass stars have maximum chains of nuclear fusion, and multiple types of stellar compacted eggs have been produced in their core due to maximum central pressure and tremendous temperature. The life cycle of a high-mass star is shorter than the life cycle of a low-mass star, because the high-mass star may burn its fuel for a few million or billions of years. The stars with low mass or similar to the mass of the Sun may exhaust their fuel of fusion during ten billion years. The central radius of a solar mass star or the core fusion ball radius ${(\mathit{R}}_{\mathit{c}}=27840\mathit{k}\mathit{m})$, and half the mass of the star is concentrated at its core, as a result nuclear fusion occurred at the core of stars due to its maximum central density, pressure, and temperature. Following the general figures of a central radius of a low mass star and its central density, pressure, and Temperature.

Figure 2. Central Radius of a Star About Four Percent of Its Total Radius.

Figure 2. Central Radius of a Star About Four Percent of Its Total Radius.

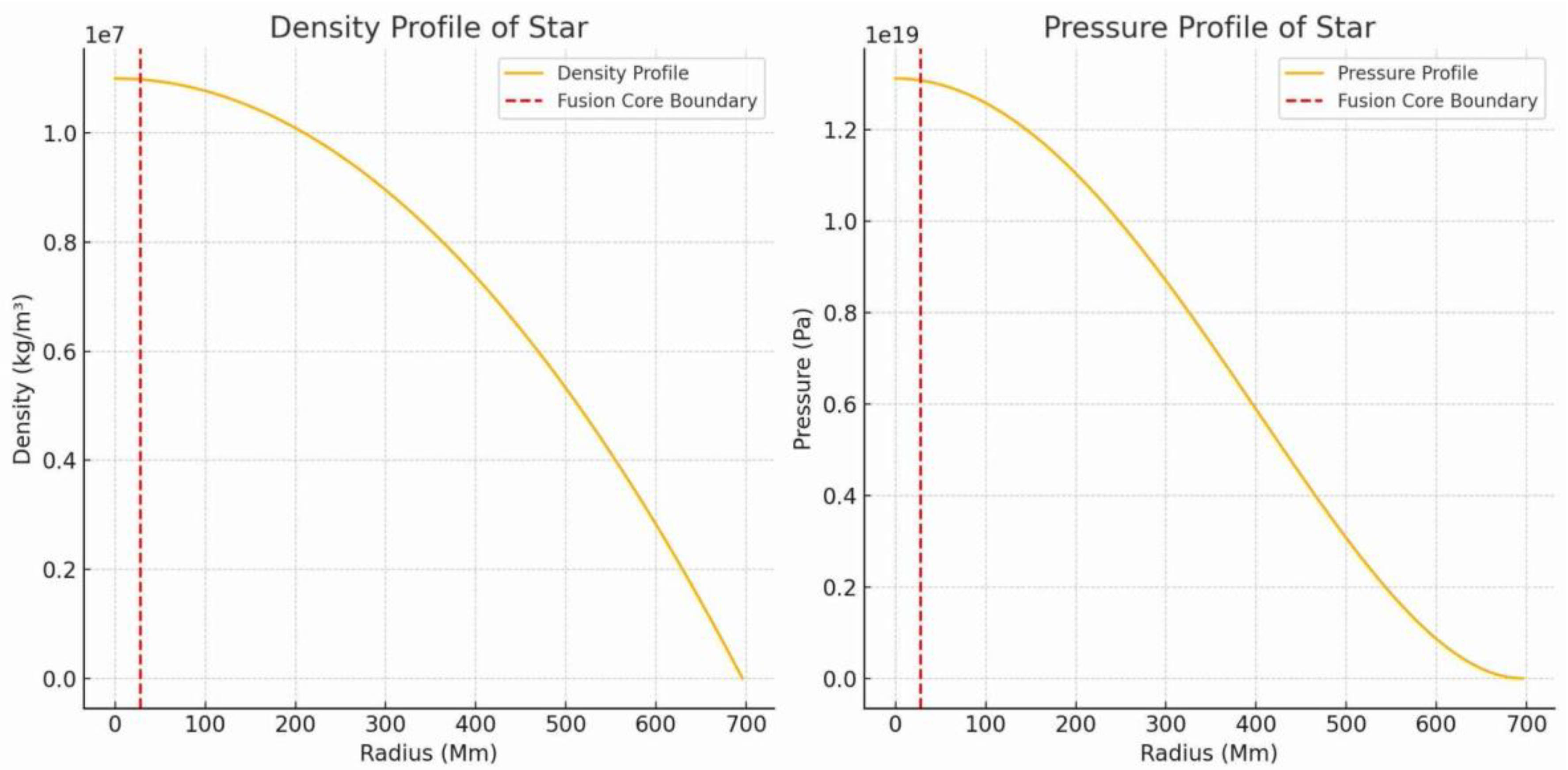
The central radius of a star is only four percent of its total radius. The central radius is the radius of the core or the radius of a fusion ball where nuclear fusion occurs inside this compacted sphere to produce heavy atomic nuclei and release fusion energy. The distance between atomic nuclei is incredibly low to break the potential barrier according to Quantum Tunneling conditions to start the fusion reaction. Nuclear fusion is a fantastic phenomenon that which the atomic nuclei with a lower mass fuse to form a heavier atomic nucleus in the core of stars due to maximum central density, pressure, and temperature. The stars have maximum central density, pressure, and temperature, and the particles are highly concentrated at the very center of the stars to fuse and annihilate due to the bombarded particles. The density, pressure, and temperature could be increased since the radius of the star decreased, specifically at the very center of stars. Furthermore, the density, pressure, and temperature could be decreased since the radius of stars increased, specifically at the surface of stars. The density falls linearly from the center outward, pressure decreases quadratically from the center, and temperature has been decreased in the center of stars to its surface since radius enlarged.

Figure 3. The Central Density, Pressure, and Temperature of a Solar Mass Star.

Figure 3. The Central Density, Pressure, and Temperature of a Solar Mass Star.

8. Death of Stars

Death is a natural phenomenon and cosmic transition; everything has been created to die. The stars are formed from stellar nebulae and collapse when their fuel runs out. Death is a process that could be tested on all living or non-living creatures. The protostar was formed from a stellar nebula at the first steps of stellar creation. The protostar is required millions of years to collect enough mass to increase its mass to start nuclear fusion at its core under huge central pressure and temperature conditions. The nuclear fusion processes may start at the heart of main-sequence stars for millions or billions of years. The star is blowing up and becomes a red giant after its fuel is exhausted and fusion is suspended at its heart. The life of stars ends as they become red giant stars, white dwarfs, neutron stars, and black holes [46,47,48,49,50]. The Sun may become a red giant after five billion years.

Problem 2: The red giant star with a similar mass of Sun $\left(1.989x{10}^{30}kg\right)$, and its radius is thousand times the radius of Sun $\left(6.96x{10}^{11}m\right)$, its central radius is four percentage of its total radius, the central mass of a red giant star is half of its total mass has been concentrated at its core, calculate its central pressure, and central temperature.

Solution:

$${\mathit{R}}_{\mathit{r}\mathit{g}}=1000\mathit{x}{\mathit{R}}_{\mathit{S}\mathit{u}\mathit{n}}=1000\mathit{x}{6.96\mathit{x}10}^8\mathit{m}={6.96\mathit{x}10}^{11}\mathit{m}.$$

$${\mathit{R}}_{\mathit{c}}=0.04\mathit{x}{\mathit{R}}_{\mathit{r}\mathit{g}}=0.04\mathit{x}{6.96\mathit{x}10}^{11}\mathit{m}=27840000000\mathit{m}.$$

Where ${\mathit{R}}_{\mathit{c}}$ is the central radius of a red giant star where nuclear fusion has suspended in its core. Assuming the central mass of a red giant star is half of its total mass:

$${\mathit{M}}_{\mathit{c}}=0.5\mathit{x}\mathit{M}=0.5\mathit{x}1.989x{10}^{30}kg=9.945x{10}^{29}kg.$$

Where ${\mathit{M}}_{\mathit{c}}$ is the Central mass of stars, it is about half of the total mass of stars.

$${\mathit{\rho }}_{\mathit{c}}={\displaystyle \frac{{\mathit{M}}_{\mathit{c}}}{\frac{4}{3}\mathit{\pi }{{\mathit{R}}_{\mathit{c}}}^3}}={\displaystyle \frac{{\mathit{M}}_{\mathit{c}}}{\frac{4}{3}\mathit{\pi }{\left(0.04\mathit{x}\mathit{R}\right)}^3}}={\displaystyle \frac{9.945x{10}^{29}kg}{\frac{4}{3}\mathit{\pi }{\left(27840000000\mathit{m}\right)}^3}}$$

$${\mathit{\rho }}_{\mathit{c}}=0.011{\displaystyle \frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}}$$

Where ${\mathit{\rho }}_{\mathit{c}}$ is the uniform central density inside the core of a red giant.

$${\mathit{P}}_{\mathit{c}}=\left({\displaystyle \frac{3\mathit{G}{{\mathit{M}}_{\mathit{c}}}^2}{8\mathit{\pi }{{\mathit{R}}_{\mathit{c}}}^4}}\right)=\left({\displaystyle \frac{3\mathit{x}6.674\mathit{x}{10}^{-11}\frac{{N.m}^2}{{kg}^2}\mathit{x}{\left(9.945\mathit{x}{10}^{29}\mathit{k}\mathit{g}\right)}^2}{8\mathit{\pi }(27840000000\mathit{m}{)}^4}}\right).$$

$${\mathit{P}}_{\mathit{c}}=1.31\mathit{x}{10}^7{\displaystyle \frac{\mathit{N}}{{\mathit{m}}^2}}.$$

This central pressure ${\mathit{P}}_{\mathit{c}}$ for a red giant star has been calculated from hydrostatic equilibrium equation. The red giant has a perfect spherical shape, which means that the equilibrium is still sustained in its structure but nuclear fusion has been suspended in its core due to exhausting nuclear fuel.

$${\mathbf{T}}_{\mathbf{c}}={\displaystyle \frac{\mathit{\mu }{\mathit{m}}_{\mathit{H}}{\mathbf{P}}_{\mathbf{c}}}{{{\mathit{\rho }}_{\mathit{c}}\mathit{K}}_{\mathit{B}}}}={\displaystyle \frac{\left(0.61\mathit{x}1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g}\mathit{x}1.31\mathit{x}{10}^7\mathit{P}\mathit{a}\right)}{\left(0.011\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\right)}}$$

$${\mathbf{T}}_{\mathbf{c}}=88122\mathit{K}.$$

Where ${\mathbf{T}}_{\mathbf{c}}$ is the central temperature of a red giant star with a solar mass. The nuclear fusion has suspended at this minimum pressure and temperature. When a low-mass star like our Sun nears the end of its life, its external surface expands outward to form a red giant, and then sheds its outer layers, forming a nice ring called a planetary nebula. The exposed core of the star, which is extremely contracted, hot and dense, becomes a white dwarf. The remnant core of a planetary nebula is indeed a white dwarf star.

Problem 3: The White Dwarf Star with a mass of Sun $\left(1.989x{10}^{30}kg\right)$, and its radius only one percentage of the total radius of Sun, the radius of Sun about $\left(7x{10}^{8}m\right)$, the central mass of a white dwarf star is half of its total mass, and its central radius is four percent of its total radius, calculate its central pressure, and central temperature, determine the speed of electron particle, DE Broglie wavelength of electron particles, Frequency, and distance between two Electron particles in the core of a white dwarf?

Solution:

$${\mathit{R}}_{\mathit{W}\mathit{h}\mathit{i}\mathit{t}\mathit{e}\mathit{D}\mathit{w}\mathit{a}\mathit{r}\mathit{f}}=0.01\mathit{x}{\mathit{R}}_{\mathit{S}\mathit{u}\mathit{n}}=0.01\mathit{x}{7\mathit{x}10}^8\mathit{m}=7000000\mathit{m}.$$

$${\mathit{R}}_{\mathit{c}}=0.04\mathit{x}{\mathit{R}}_{\mathit{W}\mathit{h}\mathit{i}\mathit{t}\mathit{e}\mathit{D}\mathit{w}\mathit{a}\mathit{r}\mathit{f}}=280000\mathit{m}.$$

Where ${\mathit{R}}_{\mathit{c}}$ is the central radius, it is about four percent of the total radius of a white dwarf star and cosmic spherical objects. Assuming its central mass is half of its total mass:

$${\mathit{M}}_{\mathit{c}}=0.5\mathit{x}\mathit{M}=0.5\mathit{x}1.989x{10}^{30}kg=9.945x{10}^{29}kg.$$

Where ${\mathit{M}}_{\mathit{c}}$ is the Central mass of a white dwarf.

$${\mathit{\rho }}_{\mathit{c}}={\displaystyle \frac{{\mathit{M}}_{\mathit{c}}}{\frac{4}{3}\mathit{\pi }{{\mathit{R}}_{\mathit{c}}}^3}}={\displaystyle \frac{{\mathit{M}}_{\mathit{c}}}{\frac{4}{3}\mathit{\pi }{\left(0.04\mathit{x}{\mathit{R}}_{\mathit{W}\mathit{D}}\right)}^3}}={\displaystyle \frac{9.945x{10}^{29}kg}{\frac{4}{3}\mathit{\pi }{\left(280000\mathit{m}\right)}^3}}$$

$${\mathit{\rho }}_{\mathit{c}}=1\mathit{x}{10}^{13}{\displaystyle \frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}}$$

Where ${\mathit{\rho }}_{\mathit{c}}$ is the uniform central density in the core of a white dwarf star.

$${\mathit{P}}_{\mathit{c}}=\left({\displaystyle \frac{3\mathit{G}{{\mathit{M}}_{\mathit{c}}}^2}{8\mathit{\pi }{{\mathit{R}}_{\mathit{c}}}^4}}\right)=\left({\displaystyle \frac{3\mathit{x}6.674\mathit{x}{10}^{-11}\frac{{N.m}^2}{{kg}^2}\mathit{x}{\left(9.945\mathit{x}{10}^{29}\mathit{k}\mathit{g}\right)}^2}{8\mathit{\pi }(280000\mathit{m}{)}^4}}\right).$$

$${\mathit{P}}_{\mathit{c}}=1.28\mathit{x}{10}^{27}{\displaystyle \frac{\mathit{N}}{{\mathit{m}}^2}}$$

For white dwarf stars, the pressure is dominated by electron degeneracy pressure, and fully ionized carbon (Z=6, A=12), non-relativistic electron degeneracy pressure has been calculated by using eqn. (44):

${\mathit{P}}_{\mathit{c}}={\displaystyle \frac{{\mathit{\hslash }}^2}{{\mathit{m}}_{\mathit{e}}}}{\left[\left({\displaystyle \frac{\mathit{Z}}{\mathit{A}}}\right)\mathit{x}{\displaystyle \frac{{\mathit{\rho }}_{\mathit{c}}}{{\mathit{m}}_{\mathit{H}}}}\right]}^{5/3}$=${\displaystyle \frac{{(1.055\mathit{x}{10}^{-34}\mathit{J}.\mathit{S})}^2}{{9.11\mathit{x}10}^{-31}\mathit{k}\mathit{g}}}{\left[\left({\displaystyle \frac{6}{12}}\right)\mathit{x}{\displaystyle \frac{{10}^{13}\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}}{1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g}}}\right]}^{5/3}$

${\mathit{P}}_{\mathit{c}}=7.57\mathit{x}{10}^{27}\mathit{P}\mathit{a}.$ The central pressure is${(\mathit{P}}_{\mathit{c}}=1.449\mathit{x}{10}^{28}\mathit{P}\mathit{a})$ by using eqn. (45) that is worked in the condensed state of matter of an electron degeneracy pressure in the core of white dwarfs. The maximum central pressure ${\mathit{P}}_{\mathit{c}}$ for a white dwarf star has been calculated by using the hydrostatic equilibrium equation. Assume the composition of a white dwarf star is a fully ionized Carbons (A=12, Z=6):

$${\mathit{\mu }}_{\mathit{I}\mathit{o}\mathit{n}\mathit{s}}\mathbf{=}{\displaystyle \frac{\mathit{M}\mathit{a}\mathit{s}\mathit{s}\mathit{p}\mathit{e}\mathit{r}\mathit{n}\mathit{u}\mathit{c}\mathit{l}\mathit{e}\mathit{u}\mathit{s}\mathit{i}\mathit{n}\mathit{a}\mathit{t}\mathit{o}\mathit{m}\mathit{i}\mathit{c}\mathit{m}\mathit{a}\mathit{s}\mathit{s}\mathit{u}\mathit{n}\mathit{i}\mathit{t}\left(\mathit{a}\mathit{m}\mathit{u}\right)}{\mathbf{T}\mathbf{o}\mathbf{t}\mathbf{a}\mathbf{l}\mathbf{n}\mathbf{u}\mathbf{m}\mathbf{b}\mathbf{e}\mathbf{r}\mathbf{o}\mathbf{f}\mathbf{p}\mathbf{a}\mathbf{r}\mathbf{t}\mathbf{i}\mathbf{c}\mathbf{l}\mathbf{e}\mathbf{s}\left(\mathbf{n}\mathbf{u}\mathbf{c}\mathbf{l}\mathbf{e}\mathbf{i}+\mathbf{e}\mathbf{l}\mathbf{e}\mathbf{c}\mathbf{t}\mathbf{r}\mathbf{o}\mathbf{n}\mathbf{s}\right)\mathit{p}\mathit{e}\mathit{r}\mathit{n}\mathit{u}\mathit{c}\mathit{l}\mathit{e}\mathit{u}\mathit{s}}}$$

$${\mathit{\mu }}_{\mathit{C}}={\displaystyle \frac{\mathit{A}}{1+\mathit{Z}}}={\displaystyle \frac{12}{1+6}}=1.714$$

$${\mathbf{T}}_{\mathbf{c}}={\displaystyle \frac{\mathit{\mu }{\mathit{m}}_{\mathit{H}}{\mathbf{P}}_{\mathbf{c}}}{{{\mathit{\rho }}_{\mathit{c}}\mathit{K}}_{\mathit{B}}}}={\displaystyle \frac{\left(0.61\mathit{x}1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g}\mathit{x}1.28\mathit{x}{10}^{27}\mathit{P}\mathit{a}\right)}{\left(1\mathit{x}{10}^{13}\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\right)}}$$

$${\mathbf{T}}_{\mathbf{c}}=9.47\mathit{x}{10}^9\mathit{K}.$$

Where the mean molecular weight for the ionised gas of the hydrogen and helium atoms in the core of white dwarf star $(\mathit{\mu }=0.61)$, and ${\mathbf{T}}_{\mathbf{c}}$ is the central temperature of white dwarf Star by using ideal gas law.

$${\mathbf{T}}_{\mathbf{c}}={\displaystyle \frac{{\mathit{\mu }}_{\mathit{e}}{\mathit{m}}_{\mathit{H}}{\mathbf{P}}_{\mathbf{c}}}{{{\mathit{\rho }}_{\mathit{c}}\mathit{K}}_{\mathit{B}}}}={\displaystyle \frac{\left(2\mathit{x}1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g}\mathit{x}1.28\mathit{x}{10}^{27}\mathit{P}\mathit{a}\right)}{\left(1\mathit{x}{10}^{13}\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\right)}}$$

$${\mathbf{T}}_{\mathbf{c}}=3.1\mathit{x}{10}^{10}\mathit{K}.$$

Where Mean molecular weight per electron particles for fully ionized carbon$\left({\mathit{\mu }}_{\mathit{e}}={\displaystyle \frac{A}{Z}}={\displaystyle \frac{12}{6}}=2\right).$In the First step, I need to calculate the speed, wavelength, frequency, of Electron particles and the distance between two Electrons in the core of white dwarf star:

$$\mathit{v}=\sqrt{{\displaystyle \frac{3{\mathit{K}}_{\mathit{B}}{\mathbf{T}}_{\mathbf{c}}}{{\mathit{m}}_{\mathit{e}}}}}=\sqrt{{\displaystyle \frac{\left(3\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\mathit{x}3.1\mathit{x}{10}^{10}\mathit{K}\right)}{\left(9.11\mathit{x}{10}^{-31}\mathit{k}\mathit{g}\right)}}}$$

Then, the huge speed of an electron particle in the core of a white dwarf star has been determined $({\mathit{v}}_{\mathit{e}}=1186921041{\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}).$

$$\mathit{\lambda }\mathbf{=}{\displaystyle \frac{\mathit{h}}{\mathbf{m}\mathit{v}}}={\displaystyle \frac{\mathit{h}}{{\mathit{m}}_{\mathit{e}}.{\mathit{v}}_{\mathit{e}}}}={\displaystyle \frac{(6.63\mathit{x}{10}^{-34}\mathit{k}\mathit{g}.\frac{{\mathit{m}}^2}{\mathit{s}})}{\left(9.11\mathit{x}{10}^{-31}\mathit{k}\mathit{g}\mathit{x}1186921041\frac{\mathrm{m}}{\mathrm{s}}\right)}}={6.13\mathit{x}10}^{-13}\mathit{m}$$

.

$({\mathit{\lambda }}_e={6.13\mathit{x}10}^{-13}\mathit{m}).$ The de Broglie wavelength of the electron particle has been determined as $({\mathit{\lambda }}_e=61.5\mathrm{p}\mathrm{m})$.

By using eqn. (39) to calculate the frequency of an electron particle: $\mathit{v}=\mathit{f}\mathit{\lambda }$.

Rearrange the equation (39) to determine the frequency of oscillating electron particles:$\mathit{f}={\displaystyle \frac{{\mathit{v}}_{\mathit{e}}}{{\mathit{\lambda }}_e}}={\displaystyle \frac{\left(1186921041\frac{\mathrm{m}}{\mathrm{s}}\right)}{\left({6.13\mathit{x}10}^{-13}\mathit{m}\right)}}={1.936\mathit{x}10}^{21}\mathit{H}\mathit{z}.$

By using eqn. (40) to calculate the distance between two electron particles:

$$\mathit{n}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{c}}}{{\mathit{m}}_{\mathit{e}}}}={\displaystyle \frac{\left(1\mathit{x}{10}^{13}\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}\right)}{9.11\mathit{x}{10}^{-31}\mathit{k}\mathit{g}}}=1.097\mathit{x}{10}^{43}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}.$$

$$\mathit{n}=1.097\mathit{x}{10}^{43}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}$$

$(\mathit{n}={\displaystyle \frac{\mathit{N}}{\mathit{V}}}={\displaystyle \frac{1}{\mathit{V}={\mathit{d}}^3}}).$ Then substitute the value of number density$\mathit{n}$ of the electron particles in the equation (40) to calculate the distance between two electron particles: $\left(1.097\mathit{x}{10}^{43}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}={\displaystyle \frac{1}{{\mathit{d}}^3}}\right).$$\mathit{d}={\displaystyle \frac{1}{\sqrt[3]{\mathit{n}}}}={\displaystyle \frac{1}{\sqrt[3]{1.097\mathit{x}{10}^{43}\frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}}}$ . $\mathit{d}=4.5\mathit{x}{10}^{-15}\mathit{m}.$

Where d is the distance between two electron particles in the center of a white dwarf.

Problem 4: The Neutron Star has a mass of 2 solar masses, and its radius only ( 15 kilometers), assume the central mass of a neutron star is half of its total mass, and its central radius is four percent of its total radius, calculate its central pressure, and central temperature, determine the speed of a neutron particle, DE Broglie wavelength of neutron particles, Frequency, and distance between two neutron particles in the core of a neutron star?

Solution:

$${\mathit{R}}_{\mathrm{N}\mathrm{e}\mathrm{u}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{r}}=15\mathit{k}\mathit{i}\mathit{l}\mathit{o}\mathit{m}\mathit{e}\mathit{t}\mathit{e}\mathit{r}\mathit{s}=15000\mathit{m}.$$

$${\mathit{R}}_{\mathit{c}}=0.04\mathit{x}{\mathit{R}}_{\mathrm{N}\mathrm{e}\mathrm{u}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{r}}=600\mathit{m}.$$

Where ${\mathit{R}}_{\mathit{c}}$ is the central radius, it is about four percent of the total radius of a neutron star. Assuming the central mass of a neutron star is half of its total mass:

$${\mathit{M}}_{\mathit{c}}=0.5\mathit{x}{\mathit{M}}_{\mathit{N}\mathit{e}\mathit{u}\mathit{t}\mathit{r}\mathit{o}\mathit{n}\mathit{s}\mathit{t}\mathit{a}\mathit{r}}=0.5\mathit{x}2\mathit{x}1.989x{10}^{30}kg=1.989x{10}^{30}kg.$$

Where ${\mathit{M}}_{\mathit{c}}$ is the Central mass of a neutron star.

$${\mathit{\rho }}_{\mathit{c}}={\displaystyle \frac{{\mathit{M}}_{\mathit{c}}}{\frac{4}{3}\mathit{\pi }{{\mathit{R}}_{\mathit{c}}}^3}}={\displaystyle \frac{{\mathit{M}}_{\mathit{c}}}{\frac{4}{3}\mathit{\pi }{\left(0.04\mathit{x}{\mathit{R}}_{\mathit{N}\mathit{S}}\right)}^3}}={\displaystyle \frac{1.989x{10}^{30}kg}{\frac{4}{3}\mathit{\pi }{\left(600\mathit{m}\right)}^3}}$$

$${\mathit{\rho }}_{\mathit{c}}=2.2\mathit{x}{10}^{21}{\displaystyle \frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}}$$

Where ${\mathit{\rho }}_{\mathit{c}}$ is the uniform central density of a neutron star.

$${\mathit{P}}_{\mathit{c}}=\left({\displaystyle \frac{3\mathit{G}{{\mathit{M}}_{\mathit{c}}}^2}{8\mathit{\pi }{{\mathit{R}}_{\mathit{c}}}^4}}\right)=\left({\displaystyle \frac{3\mathit{x}6.674\mathit{x}{10}^{-11}\frac{{N.m}^2}{{kg}^2}\mathit{x}{\left(1.989\mathit{x}{10}^{30}\mathit{k}\mathit{g}\right)}^2}{8\mathit{\pi }(600\mathit{m}{)}^4}}\right).$$

$${\mathit{P}}_{\mathit{c}}=2.43\mathit{x}{10}^{38}{\displaystyle \frac{\mathit{N}}{{\mathit{m}}^2}}.$$

In the neutron star the matter is highly degenerate, the pressure is dominated by neutron degeneracy pressure. The maximum central pressure ${\mathit{P}}_{\mathit{c}}$ for a neutron star has been calculated by using the hydrostatic equilibrium equation. Assume the composition of a neutron star is mostly the neutron particles. The mass of a neutron particle$({\mathit{m}}_{\mathit{N}\mathit{e}\mathit{u}\mathit{t}\mathit{r}\mathit{o}\mathit{n}}={1.675\mathit{x}10}^{-27}\mathit{k}\mathit{g})$. By using an ideal gas equation to calculate the central temperature of a neutron star. $({\mathbf{P}}_{\mathbf{c}}=\mathit{n}{\mathit{K}}_{\mathit{B}}{\mathbf{T}}_{\mathbf{c}}).$ The number density of neutron particles in the core of a neutron stars is $\left(\mathit{n}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{c}}}{{\mathit{m}}_{\mathit{N}\mathit{e}\mathit{u}\mathit{t}\mathit{r}\mathit{o}\mathit{n}}}}\right).$ Then, rearrange an equation of an ideal gas to determine the central temperature of a neutron star:

$${\mathbf{T}}_{\mathbf{c}}={\displaystyle \frac{{\mathit{m}}_{\mathit{N}\mathit{e}\mathit{u}\mathit{t}\mathit{r}\mathit{o}\mathit{n}}{\mathbf{P}}_{\mathbf{c}}}{{{\mathit{\rho }}_{\mathit{c}}\mathit{K}}_{\mathit{B}}}}={\displaystyle \frac{\left(1.675\mathit{x}{10}^{-27}\mathit{k}\mathit{g}\mathit{x}2.43\mathit{x}{10}^{38}\mathit{P}\mathit{a}\right)}{\left(2.2\mathit{x}{10}^{21}\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\right)}}$$

$${\mathbf{T}}_{\mathbf{c}}=1.34\mathit{x}{10}^{13}\mathit{K}$$

Where ${\mathbf{T}}_{\mathbf{c}}$ is the central temperature of a neutron star.

In the First step, I need to calculate the speed, wavelength, frequency of Neutron particles and the distance between two Neutron Particles in the core of a neutron star:

$$\mathit{v}=\sqrt{{\displaystyle \frac{3{\mathit{K}}_{\mathit{B}}{\mathbf{T}}_{\mathbf{c}}}{{\mathit{m}}_{\mathit{N}}}}}=\sqrt{{\displaystyle \frac{\left(3\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\mathit{x}1.34\mathit{x}{10}^{13}\mathit{K}\right)}{\left(1.675\mathit{x}{10}^{-27}\mathit{k}\mathit{g}\right)}}}$$

Then, the huge speed of a neutron particle in the core of a neutron star has been determined is $({\mathit{v}}_{\mathit{N}}=575499782{\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}).$

$$\mathit{\lambda }\mathbf{=}{\displaystyle \frac{\mathit{h}}{\mathbf{m}\mathit{v}}}={\displaystyle \frac{\mathit{h}}{{\mathit{m}}_{\mathit{N}}.{\mathit{v}}_{\mathit{N}}}}={\displaystyle \frac{(6.63\mathit{x}{10}^{-34}\mathit{k}\mathit{g}.\frac{{\mathit{m}}^2}{\mathit{s}})}{\left(1.675\mathit{x}{10}^{-27}\mathit{k}\mathit{g}\mathit{x}575499782\frac{\mathrm{m}}{\mathrm{s}}\right)}}={6.87\mathit{x}10}^{-16}\mathit{m}$$

$({\mathit{\lambda }}_N={6.87\mathit{x}10}^{-16}\mathit{m}).$ The de Broglie wavelength of a neutron particle has been determined as $({\mathit{\lambda }}_N=0.687\mathrm{f}\mathrm{m})$.

By using eqn. (39) to calculate the frequency of a neutron particle: $\mathit{v}=\mathit{f}\mathit{\lambda }$.

Rearrange the equation (39) to determine the frequency of oscillating neutron particles:$\mathit{f}={\displaystyle \frac{{\mathit{v}}_{\mathit{N}}}{{\mathit{\lambda }}_N}}={\displaystyle \frac{\left(575499782\frac{\mathrm{m}}{\mathrm{s}}\right)}{\left({6.87\mathit{x}10}^{-16}\mathit{m}\right)}}={8.377\mathit{x}10}^{23}\mathit{H}\mathit{z}.$

By using eqn. (40) to calculate the distance between two neutron particles:

$$\mathit{n}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{c}}}{{\mathit{m}}_{\mathit{N}}}}={\displaystyle \frac{\left(2.2\mathit{x}{10}^{21}\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}\right)}{1.675\mathit{x}{10}^{-27}\mathit{k}\mathit{g}}}=1.31\mathit{x}{10}^{48}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}$$

$$\mathit{n}=1.31\mathit{x}{10}^{48}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}$$

$(\mathit{n}={\displaystyle \frac{\mathit{N}}{\mathit{V}}}={\displaystyle \frac{1}{\mathit{V}={\mathit{d}}^3}}).$ Then substitute the value of number density$\mathit{n}$ of the neutron particles in the equation (40) to calculate the distance between two neutron particles: $\left(1.31\mathit{x}{10}^{48}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}={\displaystyle \frac{1}{{\mathit{d}}^3}}\right).$

$$\mathit{d}={\displaystyle \frac{1}{\sqrt[3]{\mathit{n}}}}={\displaystyle \frac{1}{\sqrt[3]{1.31\mathit{x}{10}^{48}\frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}}}.\mathit{d}=9.139\mathit{x}{10}^{-17}\mathit{m}.$$

Where d is the minimum distance between two neutron particles in the center of a neutron star. Photon particles are accumulated and trapped in the core of a neutron star, specifically in this concentrated state of matter and energy under neutron degeneracy pressure. The core of a neutron star is opaque, hot, and condensed.

9. Hydrostatic Balance of a Black Hole Singularity

A singularity is a dense ball of squeezed state of matter and energy in the violent nature. It has a mass of atoms, rocks, mountains, planets, stars, stellar system, galaxies, and the visible universe, but its size is similar to the volume of atoms or subatomic particles according to its mass, density, spinning speed, and angular momentum. The superparticles with different masses had been annihilated urgently due to rapid collision with the heart of a singularity. The number density of particles is very high in the core of singularity, and the distance between particles is very low; as a result, most particles could be collapsed and annihilated at the edge of a singularity or in its core. The atoms, ions, protons, electrons, and fabriton particles can't afford the gravitational force, tidal force of a singularity and its thermal pressure; they could be crushed and concentrated at once at the very center of a black hole. The thermal pressure force and gravitational force of a black hole singularity are still in balance to keep the black hole singularity from any additional reduction or expansion in its radius. Its radius is similar to the radius of atoms or subatomic particles in the moment of time. The density, thermal energy, gravitational force, spinning speed, rotational energy, and angular momentum of a black hole singularity are incredibly high enough to prevent it from evaporation and enhance its stability to survive for a longer time. The singularity has a perfect hydrostatic balance and fantastic dynamical phenomena. The ordinary matter and energy interact with dark matter and energy to build up Atoms, molecules, compound material, stellar systems, planets, galaxies, and the whole Universe, and this interaction is necessary to fill up the space and save up the dynamical balance and hydrostatic equilibrium of the celestial objects [51,52,53,54]. The mass and radius of a fabriton particle are incredibly low, but it has a huge density to afford the huge tidal force of a singularity and survive the deepest points in the core of a black hole, near a singularity surface. The mass of a fabriton particle or the mass of a dark matter particle is ten billion times lower than the mass of an electron particle, and its radius is about a zeptometer. The mass, density, internal energy, entropy, angular momentum, thermal energy, electromagnetic force, and gravitational force of a black hole singularity had been increased due to bombardment of its surface and its core by superparticles, but the fraction or tiny portion of its radius and size could be increased and decreased due to tiny changes in the spinning speed and thermal pressure of a singularity.

Problem 5: The black hole singularity with a mass of a Sun $\left(1.989x{10}^{30}kg\right)$, and its radius similar to the radius of a Hydrogen atom $\left(5.3x{10}^{-11}m\right)$, assume the central mass of a singularity is half of its total mass, and its central radius is four percent of its total radius, calculate its central radius, central mass, maximum central pressure, central temperature, calculate the speed of hydrogen or proton particles, DE Broglie wavelength, frequency, and distance between two hydrogen ions or Proton particles, also determine the speed of electron particle, DE Broglie wavelength of electron particles, Frequency, and distance between two Electron particles, and eventually calculate the speed of Fabriton particle, DE Broglie wavelength of Fabriton particles, Frequency, and distance between two Fabriton particles?.

Solution:

$${\mathit{R}}_{\mathit{c}}=0.04\mathit{x}\mathit{R}=0.04\mathit{x}{5.3\mathit{x}10}^{-11}\mathit{m}=2.12x{10}^{-12}\mathit{m}.$$

Where ${\mathit{R}}_{\mathit{c}}$ is the central radius of a singularity ball, it is about four percent of its total radius. Assuming the central mass of a singularity sphere is half of its total mass:

$${\mathit{M}}_{\mathit{c}}=0.5\mathit{x}\mathit{M}=0.5\mathit{x}1.989x{10}^{30}kg=9.945x{10}^{29}kg.$$

Where ${\mathit{M}}_{\mathit{c}}$ is the Central mass of a black hole singularity.

$${\mathit{\rho }}_{\mathit{c}}={\displaystyle \frac{{\mathit{M}}_{\mathit{c}}}{\frac{4}{3}\mathit{\pi }{{\mathit{R}}_{\mathit{c}}}^3}}={\displaystyle \frac{{\mathit{M}}_{\mathit{c}}}{\frac{4}{3}\mathit{\pi }{\left(0.04\mathit{x}\mathit{R}\right)}^3}}={\displaystyle \frac{9.945x{10}^{29}kg}{\frac{4}{3}\mathit{\pi }{\left(2.12x{10}^{-12}\mathit{m}\right)}^3}}$$

$${\mathit{\rho }}_{\mathit{c}}=2.5x{10}^{64}{\displaystyle \frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}}$$

Where ${\mathit{\rho }}_{\mathit{c}}$ is the uniform central density of matter in the core of a singularity.

$${\mathit{P}}_{\mathit{c}}=\left({\displaystyle \frac{3\mathit{G}{{\mathit{M}}_{\mathit{c}}}^2}{8\mathit{\pi }{{\mathit{R}}_{\mathit{c}}}^4}}\right)=\left({\displaystyle \frac{3\mathit{x}6.674\mathit{x}{10}^{-11}\frac{{N.m}^2}{{kg}^2}\mathit{x}{\left(9.945\mathit{x}{10}^{29}\mathit{k}\mathit{g}\right)}^2}{8\mathit{\pi }(2.12x{10}^{-12}\mathit{m}{)}^4}}\right).$$

$${\mathit{P}}_{\mathit{c}}=3.9\mathit{x}{10}^{95}{\displaystyle \frac{\mathit{N}}{{\mathit{m}}^2}}.$$

The maximum central pressure ${\mathit{P}}_{\mathit{c}}$ is calculated from an equation of the hydrostatic equilibrium.

By using eqn. (40) to calculate the central temperature ${\mathbf{T}}_{\mathbf{c}}$ and Minimum distance d between two particles:

At this moment, I need to find number density of the hydrogen ions or proton Particles$\mathit{n}$:

$$\mathit{n}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{c}}}{{\mathit{m}}_{\mathit{H}}}}={\displaystyle \frac{\left(2.5x{10}^{64}\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}\right)}{1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g}}}=1.5\mathit{x}{10}^{91}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}$$

$$\mathit{n}=1.5\mathit{x}{10}^{91}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}$$

By using eqn. (9) to determine the central temperature of a black hole singularity:

$${\mathit{P}=\mathit{n}\mathit{K}}_{\mathit{B}}\mathit{T}={\displaystyle \frac{\mathit{\rho }}{{\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}}}}{\mathit{K}}_{\mathit{B}}\mathit{T}.$$

$${\mathbf{T}}_{\mathbf{c}}={\displaystyle \frac{{\mathbf{P}}_{\mathbf{c}}}{{\mathit{n}\mathit{K}}_{\mathit{B}}}}={\displaystyle \frac{\left(3.9\mathit{x}{10}^{95}\mathit{P}\mathit{a}\right)}{\left(1.5\mathit{x}{10}^{91}\frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\right)}}.$$

$${\mathbf{T}}_{\mathbf{c}}=1.88\mathit{x}{10}^{27}\mathit{K}.$$

At the first step, I have to calculate the speed, wavelength, and frequency of protons and hydrogen ions, and precisely determine the distance between two protons or two hydrogen ions:

$$\mathit{v}=\sqrt{{\displaystyle \frac{3{\mathit{K}}_{\mathit{B}}{\mathbf{T}}_{\mathbf{c}}}{{\mathit{m}}_{\mathit{H}}}}}=\sqrt{{\displaystyle \frac{\left(3\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\mathit{x}1.88\mathit{x}{10}^{27}\mathit{K}\right)}{\left(1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g}\right)}}}$$

Then, the speed of hydrogen ions or proton particles has been determined $({\mathit{v}}_{\mathit{H}}={\mathit{v}}_{\mathit{P}\mathit{r}\mathit{o}\mathit{t}\mathit{o}\mathit{n}}=6.8\mathit{x}{10}^{15}{\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}).$ The speed of hydrogen particle $\mathit{v}$ is the thermal velocity of particles, specifically hydrogen ions, and $({\mathit{m}}_{\mathit{H}}={\mathit{m}}_{\mathit{P}\mathit{r}\mathit{o}\mathit{t}\mathit{o}\mathit{n}})$ is the mass of hydrogen atom, hydrogen ions closely equal to mass of proton particle.

$$\mathit{\lambda }={\displaystyle \frac{\mathit{h}}{\mathbf{m}\mathit{v}}}={\displaystyle \frac{\mathit{h}}{{\mathit{m}}_{\mathit{H}}.{\mathit{v}}_{\mathit{H}}}}={\displaystyle \frac{(6.63\mathit{x}{10}^{-34}\mathit{k}\mathit{g}.\frac{{\mathit{m}}^2}{\mathit{s}})}{\left(1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g}\mathit{x}6.8\mathit{x}{10}^{15}\frac{\mathrm{m}}{\mathrm{s}}\right)}}={5.8\mathit{x}10}^{-23}\mathit{m}.$$

${\mathit{\lambda }}_H={5.8\mathit{x}10}^{-23}\mathit{m}.$ The de Broglie wavelength of the hydrogen ions or proton particle is determined.

By using eqn. (39) to calculate the frequency of hydrogen ions or protons: $\mathit{v}=\mathit{f}\mathit{\lambda }$.

Rearrange the equation (39) to determine the frequency of oscillating hydrogen or proton particles:$\mathit{f}={\displaystyle \frac{\mathit{v}}{\mathit{\lambda }}}={\displaystyle \frac{\left(6.8\mathit{x}{10}^{15}\frac{\mathrm{m}}{\mathrm{s}}\right)}{{(5.8\mathit{x}10}^{-23}\mathit{m})}}={1.17\mathit{x}10}^{38}\mathit{H}\mathit{z}.$

$$\mathit{T}={\displaystyle \frac{1}{\mathit{f}}}={\displaystyle \frac{1}{{1.17\mathit{x}10}^{38}\mathit{H}\mathit{z}}}={8.547\mathit{x}10}^{-39}\mathit{s}.$$

Where $\mathit{T}$ is the time period of an oscillating proton or hydrogen particles. By using the particle number density: $\mathit{n}={\displaystyle \frac{\mathit{N}}{\mathit{V}}}={\displaystyle \frac{1}{\mathit{V}={\mathit{d}}^3}}.$ Then substitute the value of $\mathit{n}$ in the equation (40) to calculate (d) the distance between two protons or two hydrogen ions: $\left(1.5\mathit{x}{10}^{91}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}={\displaystyle \frac{1}{{\mathit{d}}^3}}\right).$ $\mathit{d}={\displaystyle \frac{1}{\sqrt[3]{\mathit{n}}}}={\displaystyle \frac{1}{\sqrt[3]{1.5\mathit{x}{10}^{91}\frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}}}$

$\mathit{d}=4\mathit{x}{10}^{-31}\mathit{m}.$ The Hydrogen ions or proton particles could be compressed steeply and annihilated at this tiny distance to form a new condensed state of matter and energy that is available in a singularity.

In the second step, I need to calculate the speed, wavelength, frequency, of Electron particles and the distance between two Electrons in the core of singularity:

$$\mathit{v}=\sqrt{{\displaystyle \frac{3{\mathit{K}}_{\mathit{B}}{\mathbf{T}}_{\mathbf{c}}}{{\mathit{m}}_{\mathit{e}}}}}=\sqrt{{\displaystyle \frac{\left(3\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\mathit{x}1.88\mathit{x}{10}^{27}\mathit{K}\right)}{\left(9.11\mathit{x}{10}^{-31}\mathit{k}\mathit{g}\right)}}}$$

Then, the speed of an electron particle has been determined $({\mathit{v}}_{\mathit{e}}=2.92\mathit{x}{10}^{17}{\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}).$

$$\mathit{\lambda }={\displaystyle \frac{\mathit{h}}{\mathbf{m}\mathit{v}}}={\displaystyle \frac{\mathit{h}}{{\mathit{m}}_{\mathit{e}}.{\mathit{v}}_{\mathit{e}}}}={\displaystyle \frac{(6.63\mathit{x}{10}^{-34}\mathit{J}.\mathit{s})}{\left(9.11\mathit{x}{10}^{-31}\mathit{k}\mathit{g}\mathit{x}2.92\mathit{x}{10}^{17}\frac{\mathrm{m}}{\mathrm{s}}\right)}}={2.49\mathit{x}10}^{-21}\mathit{m}.$$

$({\mathit{\lambda }}_e={2.49\mathit{x}10}^{-21}\mathit{m}).$ The de Broglie wavelength of the electron particle has been determined is $({\mathit{\lambda }}_e=2.49\mathrm{z}\mathrm{m})$.

By using eqn. (39) to calculate the frequency of an electron particle: $\mathit{v}=\mathit{f}\mathit{\lambda }$.

Rearrange the equation (39) to determine the frequency of oscillating electron particles:$\mathit{f}={\displaystyle \frac{{\mathit{v}}_{\mathit{e}}}{{\mathit{\lambda }}_e}}={\displaystyle \frac{\left(2.92\mathit{x}{10}^{17}\frac{\mathrm{m}}{\mathrm{s}}\right)}{\left({2.49\mathit{x}10}^{-21}\mathit{m}\right)}}={1.17\mathit{x}10}^{38}\mathit{H}\mathit{z}.$

By using eqn. (40) to calculate the distance between two electron particles:

$$\mathit{n}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{c}}}{{\mathit{m}}_{\mathit{e}}}}={\displaystyle \frac{\left(2.5x{10}^{64}\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}\right)}{9.11\mathit{x}{10}^{-31}\mathit{k}\mathit{g}}}=2.74\mathit{x}{10}^{94}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}.$$

$$\mathit{n}=2.74\mathit{x}{10}^{94}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}.$$

$(\mathit{n}={\displaystyle \frac{\mathit{N}}{\mathit{V}}}={\displaystyle \frac{1}{\mathit{V}={\mathit{d}}^3}}).$ Then substitute the value of$\mathit{n}$ in the equation (40) to calculate the distance between two electron particles: $\left(2.74\mathit{x}{10}^{94}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}={\displaystyle \frac{1}{{\mathit{d}}^3}}\right).$

$$\mathit{d}={\displaystyle \frac{1}{\sqrt[3]{\mathit{n}}}}={\displaystyle \frac{1}{\sqrt[3]{2.74\mathit{x}{10}^{94}\frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}}}$$

$$\mathit{d}=3.317\mathit{x}{10}^{-32}\mathit{m}.$$

The distance between two electrons is incredibly low, and they could be collided and collapse violently in such a condensed world.

In the final step, I need to calculate the speed, wavelength, frequency, of Fabriton particles and distance between two fabritons in the center of a singularity:

$$\mathit{v}=\sqrt{{\displaystyle \frac{3{\mathit{K}}_{\mathit{B}}{\mathbf{T}}_{\mathbf{c}}}{{\mathit{m}}_{\mathit{F}}}}}=\sqrt{{\displaystyle \frac{\left(3\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\mathit{x}1.88\mathit{x}{10}^{27}\mathit{K}\right)}{\left(9.11\mathit{x}{10}^{-41}\mathit{k}\mathit{g}\right)}}}$$

Then, the speed of a Fabriton particle has been determined $({\mathit{v}}_{\mathit{F}}=2.92\mathit{x}{10}^{22}{\displaystyle \frac{\mathbf{m}}{\mathbf{s}}}).$ The speed of a fabriton particle is exceeded the speed of light as a result it is called Fabriton. At this speed, you can leave the galaxy clusters at once.

$$\mathit{\lambda }={\displaystyle \frac{\mathit{h}}{\mathbf{m}\mathit{v}}}={\displaystyle \frac{\mathit{h}}{{\mathit{m}}_{\mathit{F}}.{\mathit{v}}_{\mathit{F}}}}={\displaystyle \frac{(6.63\mathit{x}{10}^{-34}\mathit{k}\mathit{g}.\frac{{\mathit{m}}^2}{\mathit{s}})}{\left(9.11\mathit{x}{10}^{-41}\mathit{k}\mathit{g}\mathit{x}2.92\mathit{x}{10}^{22}\frac{\mathbf{m}}{\mathbf{s}}\right)}}={2.49\mathit{x}10}^{-16}\mathit{m}.$$

$({\mathit{\lambda }}_{\mathit{F}}={2.49\mathit{x}10}^{-16}\mathit{m}).$ The de Broglie wavelength of the fabriton particle has been determined, and it is very small to capture photon particles.

By using eqn. (39) to calculate the frequency of a fabriton particle: $v=f\lambda$.

Rearrange the equation (39) to determine the frequency of oscillating fabriton particles:$f={\displaystyle \frac{v_F}{{\lambda }_F}}={\displaystyle \frac{\left(2.92\mathit{x}{10}^{22}\frac{\mathrm{m}}{\mathrm{s}}\right)}{\left({2.49x10}^{-16}m\right)}}={1.17x10}^{38}Hz.$

The proton, electron, and fabriton particles have the same oscillation and frequency ${(f=1.17x10}^{38}Hz)$ to traverse an oscillation energy throughout the black hole singularity, and release its energy into space as waves. Particles have the same frequency to keep the singularity homogeneous and cohesively uniform.

By using eqn. (40) to calculate the distance between two Fabriton particles:

$$\mathit{n}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{c}}}{{\mathit{m}}_{\mathit{F}}}}={\displaystyle \frac{\left(2.5x{10}^{64}\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}\right)}{9.11\mathit{x}{10}^{-41}\mathit{k}\mathit{g}}}=2.744\mathit{x}{10}^{104}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}$$

$$\mathit{n}=2.744\mathit{x}{10}^{104}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}.$$

$\mathit{n}={\displaystyle \frac{N}{V}}={\displaystyle \frac{1}{V=d^3}}.$ Then substitute the value of$\mathit{n}$ in the equation (40) to calculate the distance between two fabriton particles: $\left(2.744x{10}^{104}{\displaystyle \frac{Particles}{m^3}}={\displaystyle \frac{1}{d^3}}\right).$

$$\mathit{d}={\displaystyle \frac{1}{\sqrt[3]{\mathit{n}}}}={\displaystyle \frac{1}{\sqrt[3]{2.744\mathit{x}{10}^{104}\frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}}}$$

$$\mathit{d}=1.54\mathit{x}{10}^{-35}\mathit{m}.$$

The distance between two fabriton particles $(\mathit{d}=1.54\mathit{x}{10}^{-35}\mathit{m})$ is very low, and it exceeds the radius of a fabriton particle ${(\mathit{r}=1\mathit{z}\mathit{m}=10}^{-21}\mathit{m})$. As a result, the fabriton particles could be compressed inward under high pressure, temperature, and density of the black hole singularity, and it could be annihilated there forever to feed the singularity. The singularity is a place where any type of matter and energy could be crushed and annihilated to form a new condensed state of matter and energy according to the powerful gravitational field of a singularity ball and superparticles. Ordinary matter and energy, and even dark matter and energy, can be compressed and dissipated forever in the core of a black hole singularity. Superparticles are more condensed state of matter and energy that annihilate immediately when they collided with a black hole singularity, and are necessary to feed the singularity to grow gradually. The maximum number of Fabriton particles could be trapped and dragged by superparticles to feed the singularity during collisions and rapid annihilation. The fabriton particles have a tiny radius is 1 zm, and are difficult to capture; fortunately, the superparticles and singularity are dense and compacted environments for collecting enough amount of fabriton particles to feed themselves and growing gradually. Fabriton particles have a tiny radius, mass, and high enough density to survive far away little bit on the edge of a singularity, where a fabriton particle is not in direct attachment with the external surface of a singularity. The distance between fabriton particles and the external surface of a singularity is a tiny Quantum vacuum or small tunnel vacuum that prevents fabriton particles from being further distorted and condensed steeply around the singularity, and prevents it from being rapidly annihilated into the heart of a singularity. The fabriton particles could be distorted and concentrated slightly in distant places from the external surface of a singularity. Most of the fabriton particles would be exposed to the powerful tidal force of a black hole singularity and are dragged inward into the heart of the singularity, feeding it with fabriton particles of the dark matter and energy.

The black hole singularity and superparticles could be grown rapidly since collecting high enough mass and energy from dark matter and energy. The ordinary matter and energy, plus dark fabric matter and energy, could be collected, concentrated, compressed, and converted to a new, steeply compressed state of matter and energy inside the superparticles and singularity. The first superparticles have been created to form our universe, and the entire multiverses from a highly compressed state of ordinary or dark matter and energy inside the largest type of a supergiant black hole. The cosmic mass superparticle is the main seed or a big bang singularity for our universe. Most of the superparticles were formed inside a supergiant black hole before and after the Big Bang event, and they are necessary to form multiverse. The superparticles with a mass similar to the mass of our universe or lower and higher than its mass may form continuously to develop the structure of our universe and multiverses. The acceleration speed of our universe and its evolution are related to the formation and evolution of the multiverse, cosmic mass superparticles, and the parent supergiant black hole. Many superparticles and cosmos seeds have been formed before and after the formation and evolution of our universe. The mass of the Andromeda Galaxy is still a subject of ongoing research; recent estimates suggest that its total mass could be 1.5 trillion solar masses. Problem 6: the Galaxy Mass Singularity, with the mass of the Andromeda galaxy $(M=1.5x{10}^{12}{M}_{Sun})$, its radius is similar to the radius of a Calcium Atom $(R=1.97x{10}^{-10}m)$, and half of its mass is squeezed into 4 percent of its total radius at the nucleus of a singularity, calculate its central pressure and Temperature?.

Solution:

$${\mathit{R}}_{\mathit{c}}=0.04\mathit{x}\mathit{R}=0.04\mathit{x}{1.97\mathit{x}10}^{-10}\mathit{m}=7.88x{10}^{-12}\mathit{m}.$$

Where ${\mathit{R}}_{\mathit{c}}$ is the central radius of a singularity ball, it is about four percent of its total radius. Assuming the central mass of a singularity sphere is half of its total mass:

${\mathit{M}}_{\mathit{c}}=0.5\mathit{x}\mathit{M}=0.5\mathit{x}1.5x{10}^{12}{M}_{Sun}=0.5\mathit{x}1.5x{10}^{12}x1.989x{10}^{30}kg=1.49x{10}^{42}kg.$

Where ${\mathit{M}}_{\mathit{c}}$ is the Central mass of a black hole singularity.

$${\mathit{\rho }}_{\mathit{c}}={\displaystyle \frac{{\mathit{M}}_{\mathit{c}}}{\frac{4}{3}\mathit{\pi }{{\mathit{R}}_{\mathit{c}}}^3}}={\displaystyle \frac{{\mathit{M}}_{\mathit{c}}}{\frac{4}{3}\mathit{\pi }{\left(0.04\mathit{x}\mathit{R}\right)}^3}}={\displaystyle \frac{1.49x{10}^{42}kg}{\frac{4}{3}\mathit{\pi }{\left(7.88x{10}^{-12}\mathit{m}\right)}^3}}$$

$${\mathit{\rho }}_{\mathit{c}}=7.27x{10}^{74}{\displaystyle \frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}}$$

Where ${\mathit{\rho }}_{\mathit{c}}$ is the uniform central density of matter in the core of a galaxy mass singularity.

$${\mathit{P}}_{\mathit{c}}=\left({\displaystyle \frac{3\mathit{G}{{\mathit{M}}_{\mathit{c}}}^2}{8\mathit{\pi }{{\mathit{R}}_{\mathit{c}}}^4}}\right)=\left({\displaystyle \frac{3\mathit{x}6.674\mathit{x}{10}^{-11}\frac{{N.m}^2}{{kg}^2}\mathit{x}{\left(1.49\mathit{x}{10}^{42}\mathit{k}\mathit{g}\right)}^2}{8\mathit{\pi }(7.88x{10}^{-12}\mathit{m}{)}^4}}\right).$$

$${\mathit{P}}_{\mathit{c}}=4.6\mathit{x}{10}^{117}\mathit{P}\mathit{a}.$$

The maximum central pressure ${\mathit{P}}_{\mathit{c}}$ is calculated from an equation of the hydrostatic equilibrium. By using eqn. (40) to calculate the central temperature ${\mathbf{T}}_{\mathbf{c}}$ and Minimum distance d between two Proton particles in the core of a singularity. At first step, I need to find number density of the hydrogen or proton Particle$\mathit{n}$:

$$\mathit{n}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{c}}}{{\mathit{m}}_{\mathit{H}}}}={\displaystyle \frac{\left(7.27x{10}^{74}\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}\right)}{1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g}}}=4.34\mathit{x}{10}^{101}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}$$

$$\mathit{n}=4.34\mathit{x}{10}^{101}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}.$$

By using eqn. (9) to determine the central temperature of a black hole singularity:

$${\mathit{P}=\mathit{n}\mathit{K}}_{\mathit{B}}\mathit{T}={\displaystyle \frac{\mathit{\rho }}{{\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}}}}{\mathit{K}}_{\mathit{B}}\mathit{T}.$$

$${\mathbf{T}}_{\mathbf{c}}={\displaystyle \frac{{\mathbf{P}}_{\mathbf{c}}}{{\mathit{n}\mathit{K}}_{\mathit{B}}}}={\displaystyle \frac{\left(4.6\mathit{x}{10}^{117}\mathit{P}\mathit{a}\right)}{\left(4.34\mathit{x}{10}^{101}\frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\right)}}.$$

$${\mathbf{T}}_{\mathbf{c}}=7.68\mathit{x}{10}^{38}\mathit{K}.$$

Mean molecular weight $(\mu =1)$, at this condition matter is not in any familiar state. By using eqn. (40) to calculate the distance between two Proton particles:

$$\mathit{n}=4.34\mathit{x}{10}^{101}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}.$$

$\mathit{n}={\displaystyle \frac{N}{V}}={\displaystyle \frac{1}{V=d^3}}.$ Then substitute the value of$\mathit{n}$ in the equation (40) to calculate the distance between two proton particles: $\left(4.34x{10}^{101}{\displaystyle \frac{Particles}{m^3}}={\displaystyle \frac{1}{d^3}}\right).$

$$\mathit{d}={\displaystyle \frac{1}{\sqrt[3]{\mathit{n}}}}={\displaystyle \frac{1}{\sqrt[3]{4.34\mathit{x}{10}^{101}\frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}}}.\mathit{d}=1.32\mathit{x}{10}^{-34}\mathit{m}.$$

Where d is the critical distance between two protons or two hydrogen atoms in the core of a singularity with the mass of an Andromeda galaxy, at this compacted world, atoms and subatomic particles could be squeezed inward, destroyed, and compacted violently into a tiny size. Problem 7: The black hole singularity with a mass of a Visible Universe $(M=1x{10}^{53}kg)$, and its radius similar to the radius of an Iron atom $\left(1.26x{10}^{-10}m\right)$, assume the central mass of a singularity is half of its total mass, and its central radius is four percent of its total radius, calculate its central pressure, central temperature, calculate the speed of hydrogen or proton particles, DE Broglie wavelength, frequency, and distance between two hydrogen or Proton particles ?. The full solutions could be done as problem 5, and the Solutions:

$${\mathit{R}}_{\mathit{c}}=0.04\mathit{x}\mathit{R}=0.04\mathit{x}{1.26\mathit{x}10}^{-10}\mathit{m}=5.04x{10}^{-12}\mathit{m}.$$

Where ${\mathit{R}}_{\mathit{c}}$ is the central radius of a singularity ball, it is about four percent of its total radius. Assuming the central mass of a singularity sphere is half of its total mass:

$${\mathit{M}}_{\mathit{c}}=0.5\mathit{x}\mathit{M}=0.5\mathit{x}1x{10}^{53}=5x{10}^{52}kg.$$

Where ${\mathit{M}}_{\mathit{c}}$ is the Central mass of a black hole singularity with a mass of a visible Universe.

$${\mathit{\rho }}_{\mathit{c}}={\displaystyle \frac{{\mathit{M}}_{\mathit{c}}}{\frac{4}{3}\mathit{\pi }{{\mathit{R}}_{\mathit{c}}}^3}}={\displaystyle \frac{{\mathit{M}}_{\mathit{c}}}{\frac{4}{3}\mathit{\pi }{\left(0.04\mathit{x}\mathit{R}\right)}^3}}={\displaystyle \frac{5x{10}^{52}kg}{\frac{4}{3}\mathit{\pi }{\left(5.04x{10}^{-12}\mathit{m}\right)}^3}}$$

$${\mathit{\rho }}_{\mathit{c}}=9.32x{10}^{85}{\displaystyle \frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}}$$

Where ${\mathit{\rho }}_{\mathit{c}}$ is the uniform central density of matter in the core of a Cosmic mass singularity.

$${\mathit{P}}_{\mathit{c}}=\left({\displaystyle \frac{3\mathit{G}{{\mathit{M}}_{\mathit{c}}}^2}{8\mathit{\pi }{{\mathit{R}}_{\mathit{c}}}^4}}\right)=\left({\displaystyle \frac{3\mathit{x}6.674\mathit{x}{10}^{-11}\frac{{N.m}^2}{{kg}^2}\mathit{x}{\left(5\mathit{x}{10}^{52}\mathit{k}\mathit{g}\right)}^2}{8\mathit{\pi }(5.04x{10}^{-12}\mathit{m}{)}^4}}\right).$$

$${\mathit{P}}_{\mathit{c}}=3.09\mathit{x}{10}^{139}\mathit{P}\mathit{a}.$$

The maximum central pressure ${\mathit{P}}_{\mathit{c}}$ is calculated from an equation of the hydrostatic equilibrium. By using eqn. (40) to calculate the central temperature ${\mathbf{T}}_{\mathbf{c}}$ and Minimum distance d between two Proton particles in the core of a singularity. At first step, I need to find number density of the hydrogen or proton Particle$\mathit{n}$:

$$\mathit{n}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{c}}}{{\mathit{m}}_{\mathit{H}}}}={\displaystyle \frac{\left(9.32x{10}^{85}\frac{\mathit{k}\mathit{g}}{{\mathit{m}}^3}\right)}{1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g}}}=5.567\mathit{x}{10}^{112}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}$$

$$\mathit{n}=5.567\mathit{x}{10}^{112}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}.$$

By using eqn. (9) to determine the central temperature of a black hole singularity:

$${\mathit{P}=\mathit{n}\mathit{K}}_{\mathit{B}}\mathit{T}={\displaystyle \frac{\mathit{\rho }}{{\mathit{m}}_{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}}}}{\mathit{K}}_{\mathit{B}}\mathit{T}.$$

$${\mathbf{T}}_{\mathbf{c}}={\displaystyle \frac{{\mathbf{P}}_{\mathbf{c}}}{{\mathit{n}\mathit{K}}_{\mathit{B}}}}={\displaystyle \frac{\left(3.09\mathit{x}{10}^{139}\mathit{P}\mathit{a}\right)}{\left(5.567\mathit{x}{10}^{112}\frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\right)}}.$$

$${\mathbf{T}}_{\mathbf{c}}=4.02\mathit{x}{10}^{49}\mathit{K}.$$

Mean molecular weight $(\mu =1)$, at this condition matter is not in any familiar state. By using eqn. (40) to calculate the distance between two Proton particles:

$$\mathit{n}=5.567\mathit{x}{10}^{112}{\displaystyle \frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}.$$

$\mathit{n}={\displaystyle \frac{N}{V}}={\displaystyle \frac{1}{V=d^3}}.$ Then substitute the value of$\mathit{n}$ in the equation (40) to calculate the distance between two proton particles: $\left(5.567x{10}^{112}{\displaystyle \frac{Particles}{m^3}}={\displaystyle \frac{1}{d^3}}\right).$

$$\mathit{d}={\displaystyle \frac{1}{\sqrt[3]{\mathit{n}}}}={\displaystyle \frac{1}{\sqrt[3]{5.567\mathit{x}{10}^{112}\frac{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{c}\mathit{l}\mathit{e}\mathit{s}}{{\mathit{m}}^3}}}}.\mathit{d}=2.62\mathit{x}{10}^{-38}\mathit{m}.$$

At Final steps, I have to calculate the speed, wavelength, frequency and time periods of protons or hydrogen ions in the core of a Cosmic mass singularity:

$$\mathit{v}=\sqrt{{\displaystyle \frac{3{\mathit{K}}_{\mathit{B}}{\mathbf{T}}_{\mathbf{c}}}{{\mathit{m}}_{\mathit{H}}}}}=\sqrt{{\displaystyle \frac{\left(3\mathit{x}1.38\mathit{x}{10}^{-23}\frac{\mathit{J}}{\mathit{K}}\mathit{x}4.02\mathit{x}{10}^{49}\mathit{K}\right)}{\left(1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g}\right)}}}$$

Then, the speed of hydrogen ions or proton particles has been determined $({\mathit{v}}_{\mathit{H}}={\mathit{v}}_{\mathit{P}\mathit{r}\mathit{o}\mathit{t}\mathit{o}\mathit{n}}=9.97\mathit{x}{10}^{26}{\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}).$ The observable universe is a sphere with a diameter of about 93 billion light-years. The Proton particle can travel throughout the visible Universe at this speed in a second.

$$\mathit{\lambda }={\displaystyle \frac{\mathit{h}}{\mathbf{m}\mathit{v}}}={\displaystyle \frac{\mathit{h}}{{\mathit{m}}_{\mathit{H}}.{\mathit{v}}_{\mathit{H}}}}={\displaystyle \frac{(6.63\mathit{x}{10}^{-34}\mathit{k}\mathit{g}.\frac{{\mathit{m}}^2}{\mathit{s}})}{\left(1.674\mathit{x}{10}^{-27}\mathit{k}\mathit{g}\mathit{x}9.97\mathit{x}{10}^{26}\frac{\mathrm{m}}{\mathrm{s}}\right)}}={3.97\mathit{x}10}^{-34}\mathit{m}.$$

${\mathit{\lambda }}_H={3.97\mathit{x}10}^{-34}\mathit{m}.$ The de Broglie wavelength of the hydrogen ions or proton particle is determined precisely. By using eqn. (39) to calculate the frequency of hydrogen ions or protons: $\mathit{v}=\mathit{f}\mathit{\lambda }$.

Rearrange the equation (39) to determine the frequency of oscillating hydrogen or proton particles:$\mathit{f}={\displaystyle \frac{\mathit{v}}{\mathit{\lambda }}}={\displaystyle \frac{\left(9.97\mathit{x}{10}^{26}\frac{\mathrm{m}}{\mathrm{s}}\right)}{{(3.97\mathit{x}10}^{-34}\mathit{m})}}={2.5\mathit{x}10}^{60}\mathit{H}\mathit{z}.$

$$\mathit{T}={\displaystyle \frac{1}{\mathit{f}}}={\displaystyle \frac{1}{{2.5\mathit{x}10}^{60}\mathit{H}\mathit{z}}}={3.98\mathit{x}10}^{-61}\mathit{s}.$$

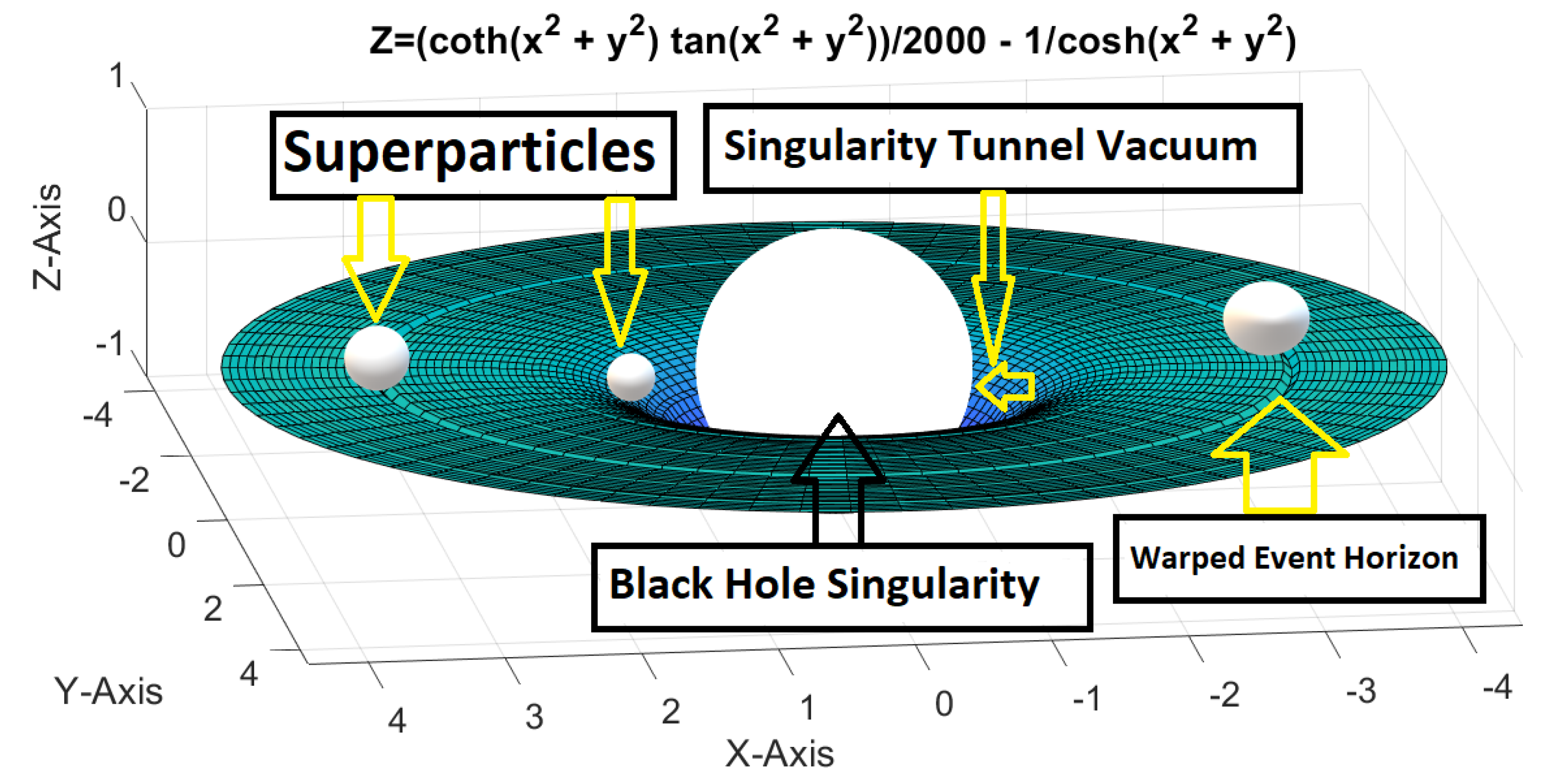
In the cosmic mass singularity, the distance between particles d is lower than the Planck Length, and the central temperature exceeded Planck's temperature, too. The Planck length is a tiny, fundamental unit of length, approximately (1.616 × 10⁻³⁵ meters), and it is derived from three fundamental physical constants: the speed of light (c), the gravitational constant (G), and the reduced Planck constant (ħ). The black hole singularity with a mass of the visible universe is squeezed steeply to the size of an Iron atom, and all states of ordinary matter and dark matter could be collapsed and condensed there due to the singularity's perfect conditions. The black hole singularity with a mass similar to rocks or the visible universe is bombarded by ultra-massive particles, called Superparticles. Subatomic particles and atoms have a higher speed during collision with a singularity or superparticles. The black hole has powerful tidal force and gravitational field to tear apart amount of mass from its companion stars, and celestial objects. Material in an accretion disc are spiralled inward to form compacted fusion balls and superparticles. Fusion balls capable of spiralling inward and outward nearby the black hole singularity, an squeezed to fall down deeply into the core of a black hole due powerful singularity tunnel waves. The radius of a nuclear fusion ball has reduced, and its spinning speed and rotational energy have been increased to move with a speed lower or higher than the speed of light. The nuclear fusion ball has squeezed steeply and its density increased to pass throughout the compacted fabric around a black hole singularity to collide with a singularity with a speed higher than the speed of light. The fused superparticle has the capacity to collide directly with an external surface of a singularity and drops into its heart. Huge numbers of superparticles have been collided and dropped with the core of a singularity to increase its mass, density, and temperature. Superparticles have huge density, gravity, electromagnetic field, and vast capacity to be survived as spherical clusters in the core of a singularity. The superparticles have the maximum degenerate pressure to survive in the violent environment of a singularity and standing against its gravity to keep the singularity from rapid annihilation. The tussle between thermal pressure and gravity in the core of a singularity has sustained the stability of a singularity, and keeps it as a white and smooth ball of the steeply state of matter and energy. The contraction due to gravity and expansion due to thermal pressure balanced ideally to keep black hole singularity as a perfect ball in the size of Atoms, and its mass variable. The singularity tunnel vacuum is a tiny tunnel vacuum between the external surface of a singularity and the internal surface of the distorted event horizon. It could be squeezed and stretched due to mass, temperature, and rotational speed of the singularity.

Figure 4. Hydrostatic Balance of a Black Hole Singularity.

Figure 4. Hydrostatic Balance of a Black Hole Singularity.

10. The Singularity Mystery

The mystery and illusion of a black hole singularity have astonished scientific community for decades. The radius of a black hole singularity is still a great debate among people. Traditional theory of a singularity suggested that the singularity has a zero radius and infinity density. In general relativity, the singularity itself has zero radius and infinity density, it is a mathematical point where classical physics breaks down. It is the central point of a black hole, where most of black hole's mass is believed to be concentrated and combined in such a tiny point [55]. The external surface of a black hole singularity is surrounded by the event horizon, a boundary beyond which nothing, not even light, can escape. An event horizon of a black hole mostly consists of fabriton particles. The Fabriton degenerate pressure against the supergravity of a singularity supports the stability and existence of entire types of black holes. The black hole singularity has a powerful hydrostatic balance that prevents the singularity ball from any further shrinking; as a result, the singularity has a tiny radius, similar to the size of atoms or subatomic particles. The tussle between gravity and radiation pressure enhanced the stability of a black hole singularity. The gravitational force of a singularity is high enough to destroy any object that dropped into the core of a black hole, but the powerful thermal pressure of a black hole singularity sustains its stability and volume. The black hole singularity is a white and smooth ball of the steeply condensed state of matter and energy that is concentrated in a point similar to the size of an atom or subatomic particles. According to the fabric theory, the singularity is a condensed ball of matter and energy that has been squeezed violently into a tiny point as the size of atoms or subatomic particles and it is covered from outside by degenerate fabriton particles. The singularity has a smallest radius and powerful angular momentum that acts directly on the oscillation and distortion of the fabriton particles in its external edge. The black hole singularity has a tiny tunnel between its external surface and the distorted dark fabric matter, which is located in its outer edge to capture photon particles and superparticles to enhance its spinning speed, mass, and thermal energy, as this mechanism is happening now on the surface of the solar cells to increase the electricity production. The solar cell converts photons' energy into electricity since its surface is bombarded by the photon particles [56]. The black hole singularity has converted the potential energy of the superparticle into thermal energy and rotational energy due to bombardment of its surface. The transition and collision of particles of any size, mass, or speed is just a phenomenon of energy conversion. The transition of the whole universe is the mechanism of energy conversion and stability. Celestial objects are in continuous transition and motion to reach stability and perfect homogeneity.

The singularity tunnel waves are generated from the rapid rotation of a singularity, and distributed throughout the event horizon of a black hole to vibrate the entire types of black hole particles inside the structure of a black hole and release its rotational energy and thermal energy into external space as urgently as possible. The fabriton particles at the edge of a black hole singularity faced a powerful tidal force and thermal pressure; as a result, most of the fabriton particles in such a nearby zone could be annihilated and evaporated to form a new condensed state of matter and energy. The fabriton particles near an external surface of a black hole singularity are in direct contact with a singularity and probably decay enormously due to powerful fabriton degenerate pressure. The fabriton degeneration pressure is necessary to control the thermal pressure and radiations of a black hole singularity and protect its size from any further contractions. The mystery of a black hole singularity has been solved scientifically, and this solution opened all gates for scientists to make important discoveries related the black hole physics. The scientific concept of a black hole singularity may solve the entire problems of the energy crisis, cosmic teleportation, and time travel. The responsibility of energy solutions and time travel rests on the shoulders of the governments and the scientific community. The government must prepare a fresh and safe environment to support scientific research and encourage the scientific community to work hard and to solve the era issues of energy crisis and rapid transportation.

We can't succeed in leaving the solar system and the Milky Way galaxy to explore the entire visible universe by today's technology. We can do it if we precisely and industrially understand the roots of science in the black hole singularity and superparticles, to exploit such energy to travel at a speed higher than the speed of light. The future of high-energy production and a time machine for cosmic travel is hidden in the mechanics of a singularity and superparticles. Black hole singularity is a perfect ball of the steeply state of matter and energy that is compressed into a Quantum world in the size of Atoms or subatomic particles. The singularity has the mass of mountains, planets, stars, stellar systems, galaxies, galaxy clusters, galaxy strings, and the visible universe. Still, its size remains extremely small, comparable to that of atoms or particles. Particles could be dragged and collided immediately with a singularity to feed it and enhance its stability. Minimum and maximum superparticles with different masses and energies could collide with the singularity at once to change and improve its mass, density, gravity, temperature, stability, and increase its spinning speed. Stars behave like particles in the core of a black hole due to their maximum density and high-spinning speed. The superparticles with the mass of stars and galaxies could be squeezed and contracted to the radius of atoms due to powerful singularity tunnel waves that propagated from the core of a black hole. The singularity tunnel waves have the capacity to bring information from the bottom and the surface of a black hole. General relativity predicts that information can't escape a black hole, and quantum mechanics demands that information cannot be lost. But the theory of the singularity tunnel waves confirmed that the information could appear in the black hole because powerful singularity tunnel waves are capable of coming up from the bottom of a black hole to its surface to release information. The singularity tunnel waves have a higher frequency and require modern technology to detect them, and it is necessary to solve the black hole information paradox problem.

11. Results and Discussion

The Star is formed from a stellar nebula, which is called a protostar. The protostar may become a main-sequence star by collecting enough mass from its surroundings to ignite nuclear fusion processes at its center. The central mass, central radius, size, core density, central pressure, and central temperature of the stars and black hole singularity had been determined, and the number density of particles, distance between particles, velocity, wavelength, and frequency of particles were estimated for stars and the singularity. Most of the Cosmic Spherical objects have dense cores where their central radius is about 4% of their total radius, and half of their mass is concentrated at their center to enhance their stability and protect them from destruction. The central radius of a main-sequence star is only four percent of its total radius, and half of its mass condensed at this tiny sphere to ignite the nuclear fusion processes and enhance its hydrostatic balance. Chains of nuclear fusion occur in the core of star, and stellar compacted eggs are formed due to maximum central pressure and its tremendous central temperature. The central density of stars and singularity is higher than their surface density, because most of their masses had been concentrated in their hearts at the region only accounts for four percent of its total radius. The maximum central pressure of a solar mass star is $\left(1.3\mathit{x}{10}^{19}\mathit{P}\mathit{a}\right)$, and it has the huge central temperature is about$\left(87367861\mathit{K}\right).$Both the central pressure and central temperature of a solar mass star are high enough, and essential to ignite nuclear fusion and release solar energy widely. The Sun is a main-sequence star; nuclear fusion was started at its core more than five billion years ago, and may survive for the next five billion years when it is burning hydrogen continuously. A main-sequence star would die to form a red giant when its fuel is exhausted. The hydrostatic balance of a star vanished since its fuel finished, and its external shell expanded outward. The radius of a Red giant star ranges from tens to hundreds or thousands of times larger than our Sun. The red giant star with a mass of a Sun, and its radius thousand times the radius of a Sun, it has the minimum central pressure is about $\left(1.31\mathit{x}{10}^7\mathit{P}\mathit{a}\right)$, and lower central temperature could be $\left(88122\mathit{K}\right)$. The mass of high-mass stars is 10 to 100 times the mass of the Sun. The high mass star may become a red supergiant when its fuel vanishes. The red supergiant stars, which are even larger than typical red giants with low mass stars, can have radii exceeding 2,000 times that of the Sun and low mass stars. White dwarfs are considered the final evolutionary stage of low-mass stars, whose mass and gravity are insufficient to form a neutron star or a black hole. The white dwarf with the mass of the Sun has a central pressure $\left(1.28x{10}^{27}Pa\right)$, and central temperature $\left(3.1x{10}^{10}K\right)$. The star with a mass higher than the mass of a Sun may collapse to form neutron star or black hole. The neutron star typically has a mass ranging from 1.5 to 2.0 solar masses (M☉) and a radius of about 5 to 15 kilometers. For example, a common estimate for a neutron star with a mass of 1.5 solar masses is a radius of roughly 10 kilometers. The exact mass and radius of a neutron star can vary depending on its composition and the specific model or theory used to describe its internal structure, temperature, density, and pressure. The neutron star with a mass of two solar masses and radius 15 kilometers, has a central pressure $\left(2.43x{10}^{38}Pa\right)$, and central temperature $\left(1.34x{10}^{13}K\right)$.

The Sun may become a black hole singularity with a mass similar to a solar mass star, and its radius identical to that of a hydrogen atom in the final steps of its lifetime. The black hole singularity with the mass of the Sun has huge central pressure is $\left(3.9\mathit{x}{10}^{95}\mathit{P}\mathit{a}\right)$ and tremendous central temperature$\left(1.88\mathit{x}{10}^{27}\mathit{K}\right).$ The tussle between the central pressure and the central temperature of a black hole singularity suspended its contraction to the size of a Hydrogen atom. The hydrostatic balance of a black hole singularity enhanced its stability, and Quantum effects in its structure prevent the singularity from further collapsing inward and destroying itself. The dark matter and energy had been concentrated and curved steeply around the black hole singularity to reflect singularity radiation and store huge thermal energy inside the Quantum tunnel zone, which is located between the external surface of a singularity and the distorted dark matter of the fabriton particles. The thermal energy and rotational energy of a black hole singularity could be increased and decreased, which directly changes the spinning speed and radius of a singularity. The black hole singularity with the mass of an Andromeda galaxy has tremendous central pressure is $\left(4.6\mathit{x}{10}^{117}\mathit{P}\mathit{a}\right)$, and maximum central temperature$\left(7.68\mathit{x}{10}^{38}\mathit{K}\right).$ Eventually, the black hole singularity with the mass of an observable Universe, and radius of Iron Atom has perfect central pressure is $\left(3.09\mathit{x}{10}^{139}\mathit{P}\mathit{a}\right)$, and maximum central temperature$\left(4.02\mathit{x}{10}^{49}\mathit{K}\right).$ The stars and black hole singularity are perfect spherical objects. The thermal pressure and gravity are in perfect balance in their cores to sustain their stability and size. The competition between the central temperature and central pressure enhances the stability and continuity of stars and black hole singularity. The balancing problem in the hydrostatic balance of stars and the singularity may cause them to collapse entirely. However, the singularity is a dense and violent environment, but hydrostatic conditions are working there perfectly. The tremendous pressure and density of a singularity are attributed to the contraction of the singularity radius, but the maximum central pressure has suspended it. The perfect balance of gravity and temperature in the core of a singularity keeps the singularity from further contraction and expansion; as a result, its size is similar to that of an Atom, and compacted.

Table 1. Central Pressure and Central Temperature of The Stars and Black Hole Singularity.

Cosmic Objects	Mass of Objects	Central Pressure$\left({\mathit{P}}_{\mathit{c}}\right)$	Central Temperature ${(\mathbf{T}}_{\mathbf{c}})$
Main Sequence Star	${1.989x10}^{30}kg$	$1.3x{10}^{19}{\displaystyle \frac{N}{m^2}}$	$87367861K$
Red Giant Star	${1.989x10}^{30}$kg	$1.31x{10}^{7}Pa$	$88122K$
White Dwarf Star	${1.989x10}^{30}$kg	$1.28x{10}^{27}Pa$	$3.1x{10}^{10}K$
Neutron Star	${3.978x10}^{30}$kg	${2.43x10}^{38}Pa$	${1.34x10}^{13}K$
Solar Mass Singularity	${1.989x10}^{30}$kg	${3.9x10}^{95}Pa$	${1.88x10}^{27}K$
Galaxy Mass Singularity	${2.98x10}^{42}$kg	$4.6x{10}^{117}Pa$	$7.68x{10}^{38}K$
Cosmic Mass Singularity	${1x10}^{53}$Kg	${3.09x10}^{139}Pa$	${4.02x10}^{49}K$

Table 1. Central Pressure and Central Temperature of The Stars and Black Hole Singularity.

Cosmic Objects	Mass of Objects	Central Pressure$\left({\mathit{P}}_{\mathit{c}}\right)$	Central Temperature ${(\mathbf{T}}_{\mathbf{c}})$
Main Sequence Star	${1.989x10}^{30}kg$	$1.3x{10}^{19}{\displaystyle \frac{N}{m^2}}$	$87367861K$
Red Giant Star	${1.989x10}^{30}$kg	$1.31x{10}^{7}Pa$	$88122K$
White Dwarf Star	${1.989x10}^{30}$kg	$1.28x{10}^{27}Pa$	$3.1x{10}^{10}K$
Neutron Star	${3.978x10}^{30}$kg	${2.43x10}^{38}Pa$	${1.34x10}^{13}K$
Solar Mass Singularity	${1.989x10}^{30}$kg	${3.9x10}^{95}Pa$	${1.88x10}^{27}K$
Galaxy Mass Singularity	${2.98x10}^{42}$kg	$4.6x{10}^{117}Pa$	$7.68x{10}^{38}K$
Cosmic Mass Singularity	${1x10}^{53}$Kg	${3.09x10}^{139}Pa$	${4.02x10}^{49}K$

12. Conclusion

The concept of Hydrostatic equilibrium in planetary Physics, fluid mechanics, and stellar physics is crucial in studying the structure of atmospheres, oceans, and stellar atmospheres in natural phenomena that occur violently, like tornadoes, coronal mass ejections, and cyclones. Hydrostatic balance is the equilibrium state appeared in a fluid (like the atmosphere or ocean), or in hotter states of matter the plasma state in stars, where the upward pressure-gradient force of radiation exactly balances the downward force of gravity. The hydrostatic balance in stars and Black hole singularities works extremely well, enhancing their stability and sustainability. In rapidly changing weather systems like tornadoes and tropical cyclones, the hydrostatic balance is not perfect. Nuclear fusion in the star's core creates powerful thermal pressure outward against the gravitational force caused by the mass of the star pushing on the core of the star inwardly to shrink. Singularity bombardment by superparticles and particle fusion in the core of a black hole singularity create powerful thermal pressure outward, balanced with the gravitational force caused by the total mass of the Singularity, which pushes on the core of the singularity inwardly. The tussle between gravity and radiation increases the stability of stars and the singularity, and gives them a perfect spherical shape. Several stellar compacted eggs at the same time could be formed in the core of a single star or several stars due to maximum central pressure, central density, and higher central temperature in the stellar nuclei with a radius of only four percent of its total radius. The maximum central pressure and temperature in the cores of stars and the Sun cause coronal heating, which increases solar activity and the frequency of maximum coronal mass ejections.