1. Introduction
The accuracy of mechanical properties of soft tissue obtained by experiments directly affects the accuracy of organ tissue evaluation by doctors[
1]. On the other hand, as an important object of robot assisted virtual surgery simulation, the mechanical response of soft tissue also determine the authenticity of the simulation process[
2]. Mechanical responses of biological tissues are obtained through many experimental methods, such as compression, tension, and impression experiments, etc.[
3]. However, there are many challenges and influencing factors in obtaining the mechanical properties of soft tissue[
4].
Mechanical properties of soft tissue are widely studied. Miller [
5] proposed a more reliable compression test method to obtain the relationship between the total variation of height ( measured value ) and the strain. Some important conclusions have been drawn to improve the accuracy of the mechanical response of soft obtained from compression tests. Gao et al [
6]conducted three experiments on soft tissue samples to obtain mechanical response curves, and proposed a constitutive model that can well reflect the nonlinear stress-strain relationship. Islam et al [
7] proposed an experimental strategy based on nanoindentation to characterize the microscale pore elasticity and viscoelasticity of mouse heart, kidney and liver tissues. Mattei et al [
8] obtained the mechanical response of three soft tissues, and the constitutive model parameters of soft tissues were fitted based on the experiment data. Sandeep et al [
9] considered the variability of the mechanical response obtained by the experiment, and proposed a Bayesian calibration framework to explain the variability. Fu et al [
10] obtained the mechanical properties of soft tissue samples through compression test. Costin et al [
11] studied the tensile mechanical properties of bovine liver at different loading rates and studied the biomechanical properties and failure characteristics of the liver. Sun et al [
12] performed dynamic multidirectional unconfined compression and simple shear loading tests on subcutaneous adipose tissue and obtained mechanical loading responses. Li et al [
13,
14] measured the compression and dynamic viscoelastic properties of brain tissue, and proposed a mathematical model for capturing tissue behavior in frequency domain based on the results of mechanical response.
In the study of biological tissue mechanical response of irregular sample shape, Gervaso et al [
15] considered the geometry and boundary conditions of the samples in the constrained experiment, and established a more realistic finite element model. The reliability evaluation method of soft tissue parameters identified from the test data was established. In Commisso et al [
16] research, the effect of non-uniform thickness of samples on the mechanical response of compression relaxation process was analyzed, and the resulting error was quantified.
2. Problem Statement
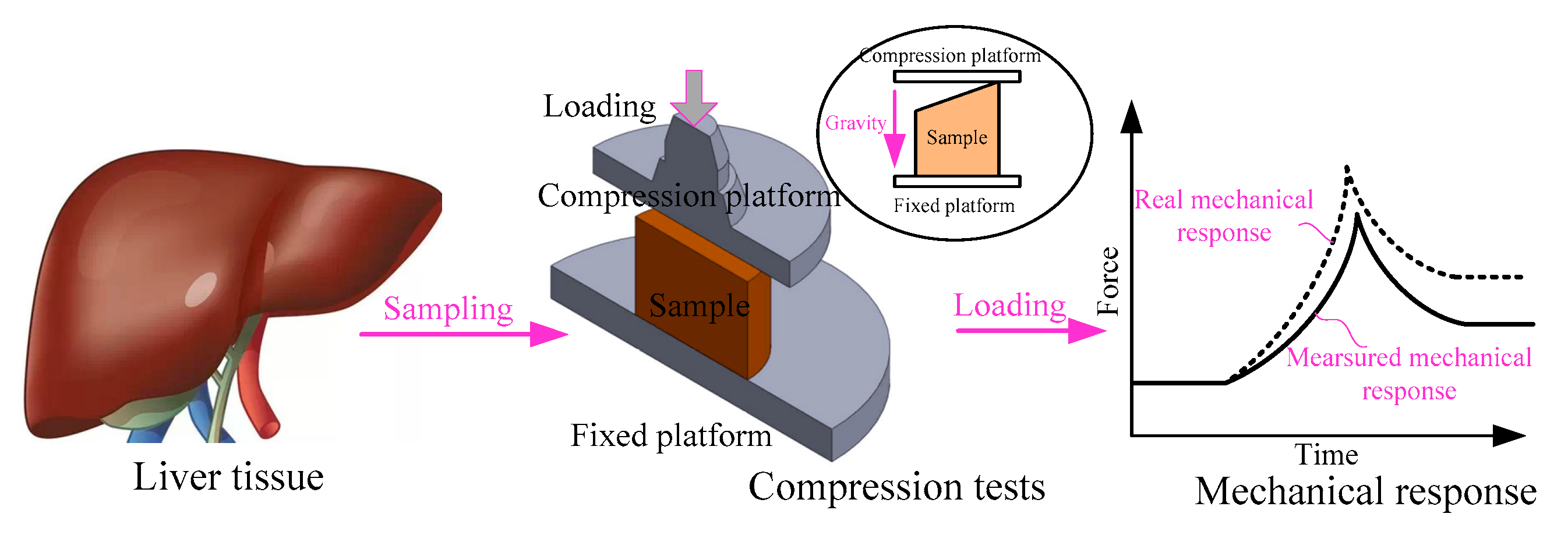
Compression experiment is a common method to study the mechanical properties of soft tissue, and the general process is shown in
Figure 1. Firstly, the samples with regular shapes need to be obtained from the soft tissue. The compression experiment is carried out on the test platform. The test platform is divided into mobile platform and fixed platform. The soft tissue samples are placed on the fixed platform and loaded through the mobile platform. The displacement of the mobile platform is the displacement of the soft tissue sample compression, and the force sensor data is the compression force of the soft tissue sample. The compressed displacement and force of the obtained soft tissue sample are the mechanical response. In this process, soft tissue samples with regular shapes has an important effect on the accuracy of the obtained mechanical response. In the process of sampling soft tissue specimens, the shape of the sample cannot be guaranteed to be regular. Different sample sizes will affect the mechanical properties of soft tissue, resulting in the obtained mechanical response deviating from the true value. At the same time, gravity will also affect the accuracy of mechanical response.
Figure 1.
Acquisition process of mechanical properties of liver tissue.
Figure 1.
Acquisition process of mechanical properties of liver tissue.
In this paper, the sample size parameters were defined, and a finite element model of the sample compression process was established to analyze the influence of sample gravity, diameter and sample angle parameters on the mechanical response. The analysis of these factors will help to obtain more accurate mechanical response of soft tissue.
3. Method
3.1. Constitutive Model and Definition of Sample Dimensional Parameters
Hyperelastic constitutive model has been used to describe the mechanical properties of soft tissue[
17,
18], such as liver, kidney, brain, etc. Considering that Ogden model is suitable for small and medium deformation, and is generally suitable for the strain of about 100%(tensile) and 30%(compressive). In theory, the accurate prediction of experimental curves with multiple deformation modes is realized, which is regarded as an important advance in nonlinear elastic modeling[
19]. In this paper, the first-order hyperelastic Ogden equation is selected as the material model of liver samples, as shown in Equ. 1.
where μ is the shear modulus of the material, α is the material parameter, λ is the stretch of the sample, and σ is the stress in the sample loading process. Referring to previous research results[
20], the material parameters are determined as
,
. In this paper, the stress is in the form of engineering stress, that is, σ=F/A, F is the loading force, A is the cross-sectional area of the sample. The sample density is ρ=1.3 g/cm3.
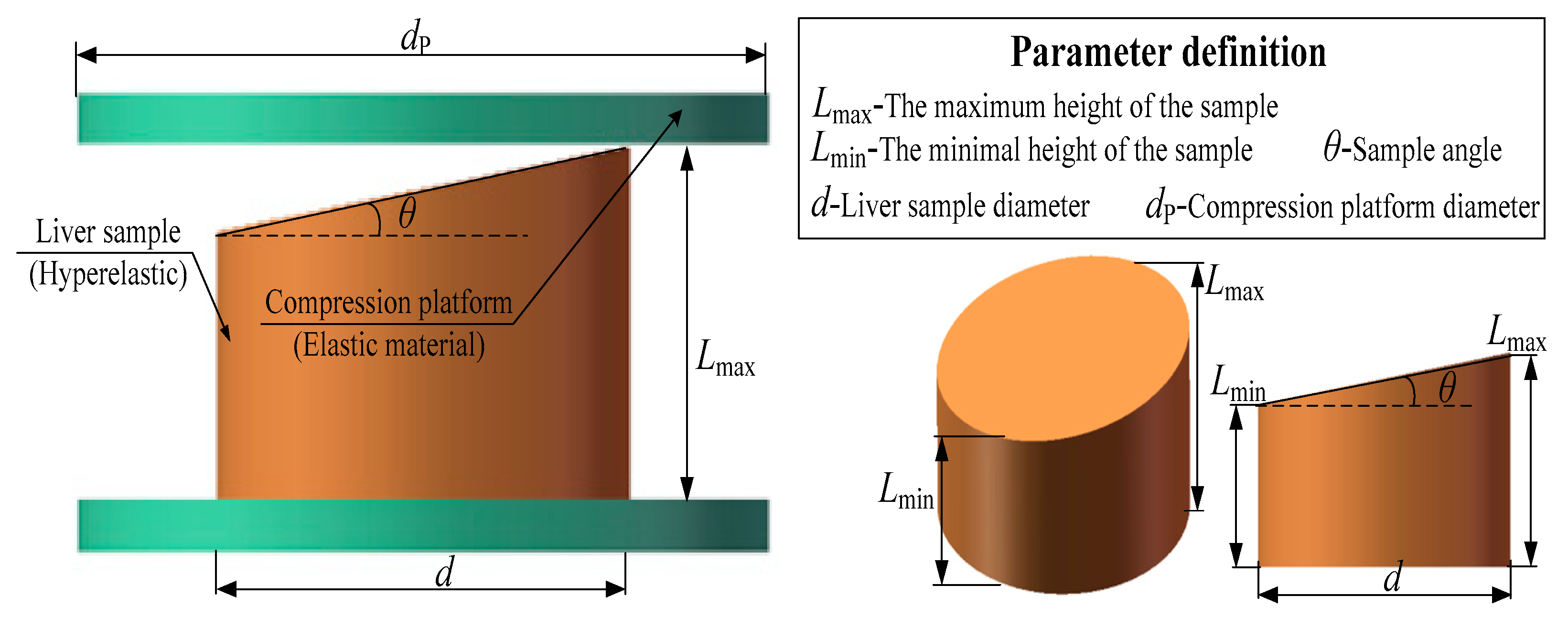
The liver tissue compression test platform was established in Abaqus software, including mobile platform, fixed platform and soft tissue samples, as shown in
Figure 2. The established finite element model refers to previous studies [
21]. The diameter of the compression platform is 50 mm, and the thickness is 3 mm. The sample is a cylinder-like shape with the upper end of the oblique plane. The sample diameter
is the diameter of the bottom surface of the cylinder. In the actual slicing process, the upper end of the cylinder always forms an oblique plane. The minimum distance from the oblique plane to the bottom of the sample is defined as the minimum height of the sample
, and the maximum distance is
. The angle between the circular plane where the minimum height of the sample is located and the oblique plane on the slice is the sample angle
.
Figure 2.
Definition of liver tissue sample parameters.
Figure 2.
Definition of liver tissue sample parameters.
The effects of slice tissue diameter
,sample angle
and gravity
on the mechanical characteristics of soft tissue were considered. The high strain modulus, low strain modulus and stress difference percentage were defined as the analysis indexes [
22]. The strain-stress linear fitting slope in the strain range of 0.25 to 0.3 is defined as the high strain modulus. The slope of strain-stress linear fitting in the range of 0 to 0.05 is defined as the low strain modulus.
3.2. Numerical Tests of Liver Tissue
Based on the established finite element model of the compression process, the numerical tests were performed. In the simulation test, the maximum compression distance was 6 mm (the corresponding stretch is 0.7) and the loading speed v=1 mm/s. With the increasing compression distance, the stress of liver tissue also gradually changes, and the stress-strain diagram of liver tissue under compression can be obtained. In order to analyze the sample parameters on mechanical characteristics of soft tissue, four numerical tests were performed. In Test1, the sample size is d=30 mm, h=20 mm. The sample is s regular shape, namely the sample angle is 0°. In the simulation, the sample mechanical responses under gravity and non-gravity conditions were obtained by setting the density of the sample. In Test 2, three sample diameters were used for simulation under two conditions of gravity and non-gravity, respectively. The test was used to analyze the influence of gravity on the mechanical characteristics under different sample diameter parameters. In Test 3, all tests were performed under the condition of no gravity. Five sample angle parameters were applied to simulate the corresponding mechanical response, and the regular sample shape was compared to analyze the influence of sample angle on the mechanical response. Test 4 is given three sample diameters and simulated under two sample angles to obtain their respective mechanical response curves, and the influences of sample angles under different sample diameters were analyzed.
Table 1.
Different parameters used in each numerical test.
Table 1.
Different parameters used in each numerical test.
| |
Sample diameter d
|
Sample height h
|
Sample angle θ
|
Density ρ
|
Description |
Results |
| Test1 |
d=30 mm |
h=20 mm |
θ=0° |
ρ=1.3 g/cm3
ρ=0 g/cm3
|
Influence of gravity on mechanical response of liver tissue |
See Figure 3
|
| Test2 |
d=20 mm, d=30 mm, d=40 mm |
h=20 mm |
θ=0° |
ρ=1.3 g/cm3
ρ=0 g/cm3
|
Influence of gravity under different sample diameters |
See Figure 4 and Figure 5
|
| Test3 |
d=30 mm |
h=20 mm |
θ=0°,θ=2°,θ=4°,θ=6°,θ=8°,θ=10° |
ρ=0 g/cm3
|
Influence of sample angle on mechanical response of liver tissue |
See Figure 6
|
| Test4 |
d=20 mm, d=30 mm, d=40 mm |
h=20 mm |
θ=0°,θ=4° |
ρ=0 g/cm3
|
Influence of sample angle under different sample diameters |
See Figure 7 and Figure 8
|
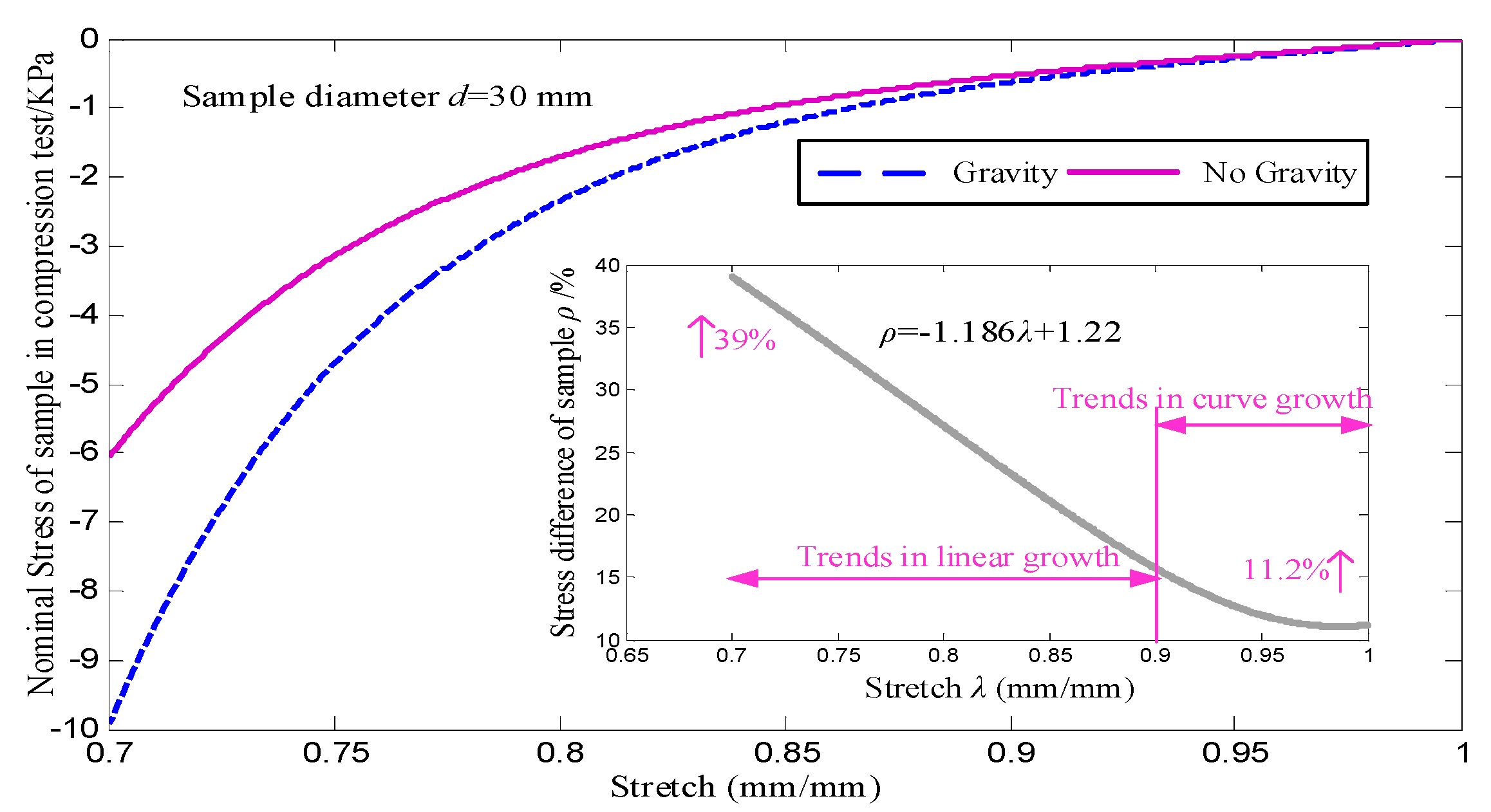
Figure 3.
Comparison of mechanical responses under gravity and without gravity.
Figure 3.
Comparison of mechanical responses under gravity and without gravity.
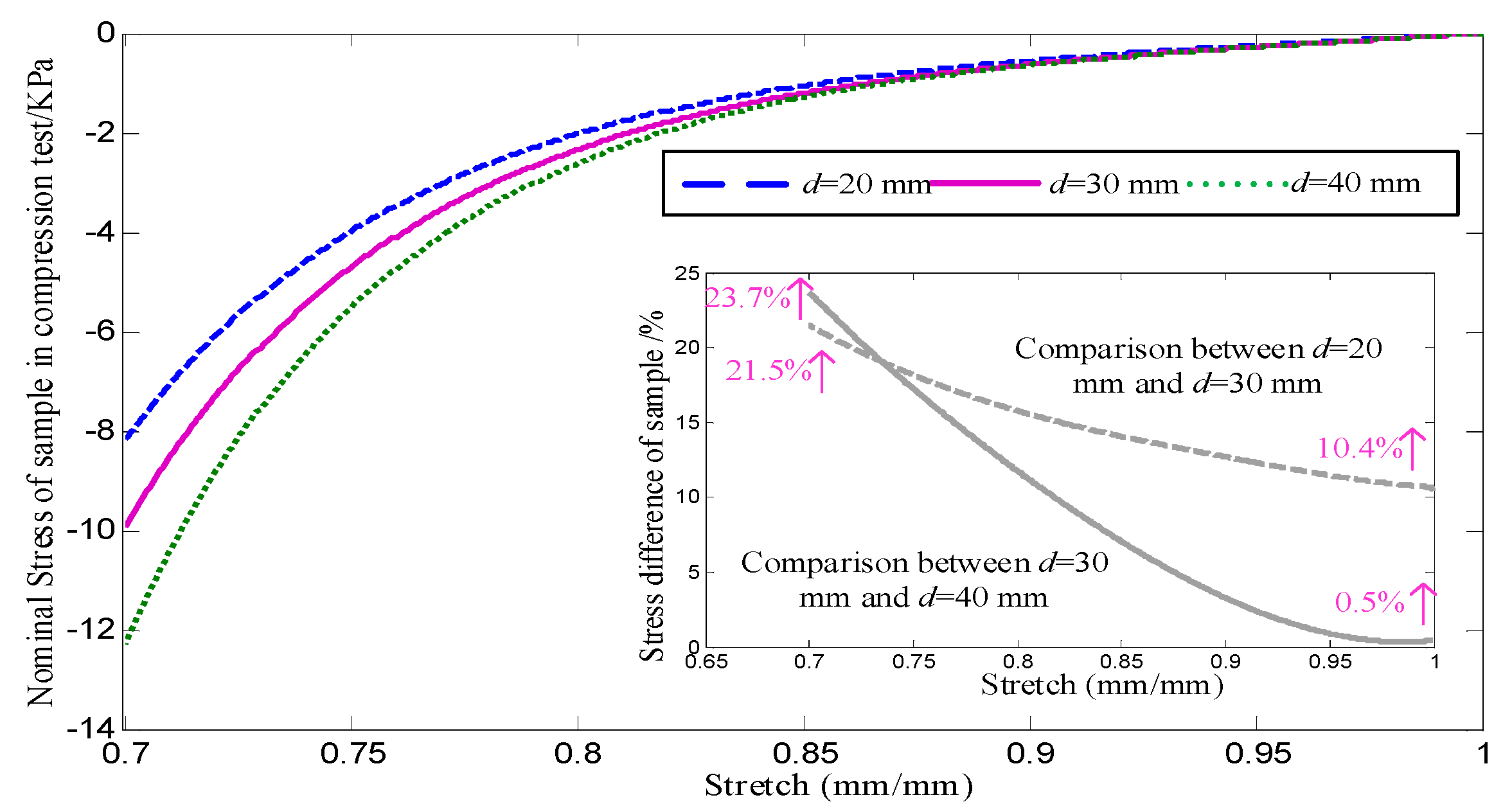
Figure 4.
Gravity effects under different sample diameters.
Figure 4.
Gravity effects under different sample diameters.
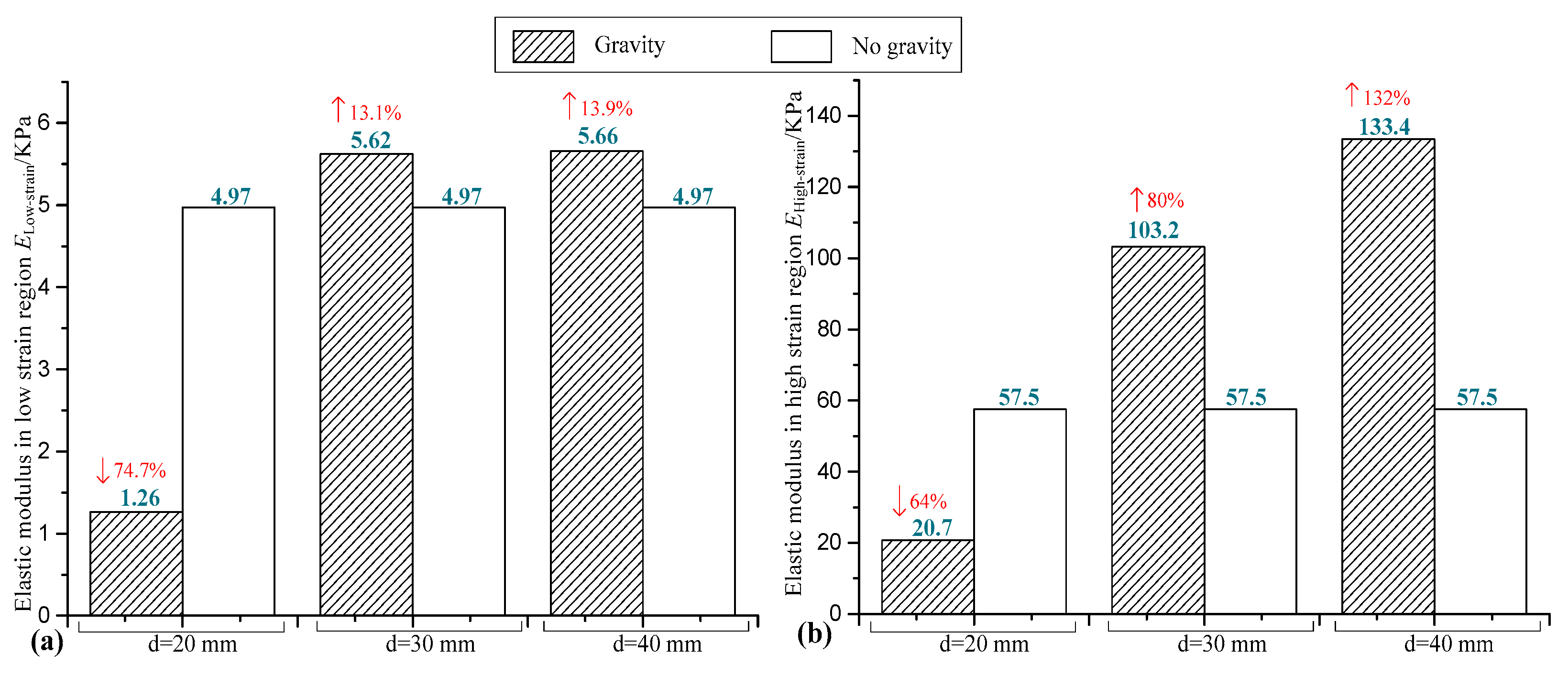
Figure 5.
Effect of gravity on elastic modulus. (a) Effect of gravity on ELow-strain modulus;(b)Effect of gravity on EHigh-strain modulus.
Figure 5.
Effect of gravity on elastic modulus. (a) Effect of gravity on ELow-strain modulus;(b)Effect of gravity on EHigh-strain modulus.
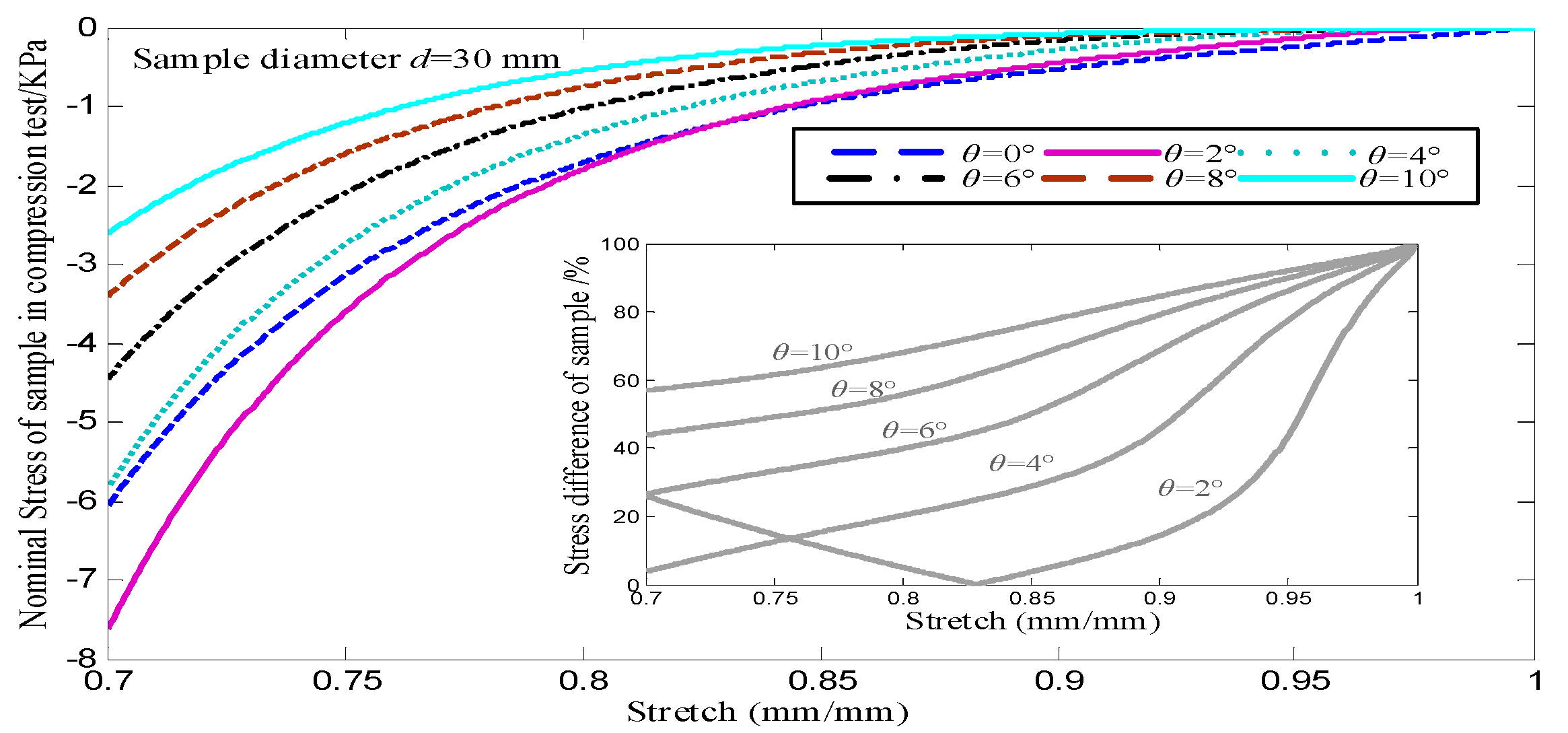
Figure 6.
Comparison of mechanical responses under different sample angle.
Figure 6.
Comparison of mechanical responses under different sample angle.
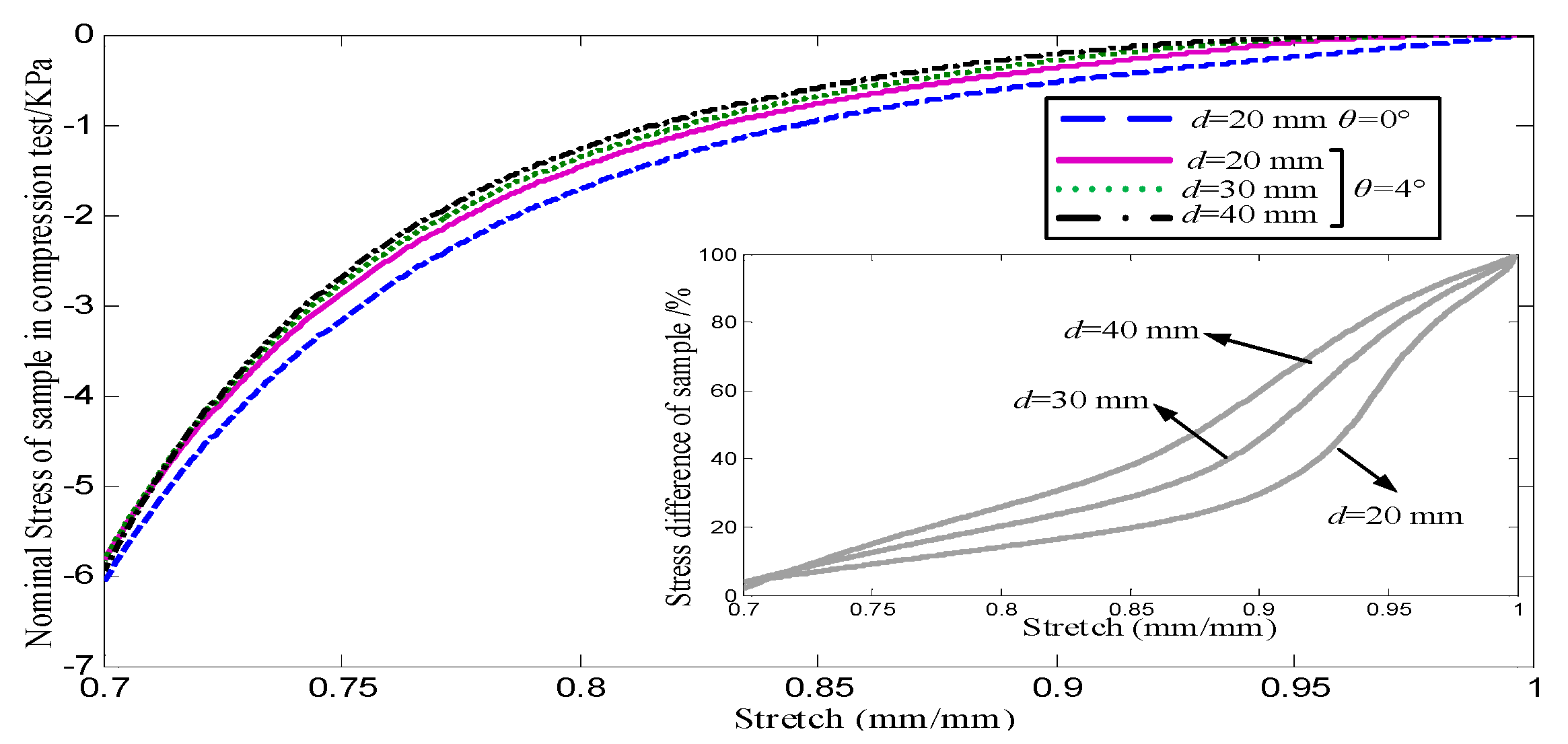
Figure 7.
Sample angle effects under different sample diameters.
Figure 7.
Sample angle effects under different sample diameters.
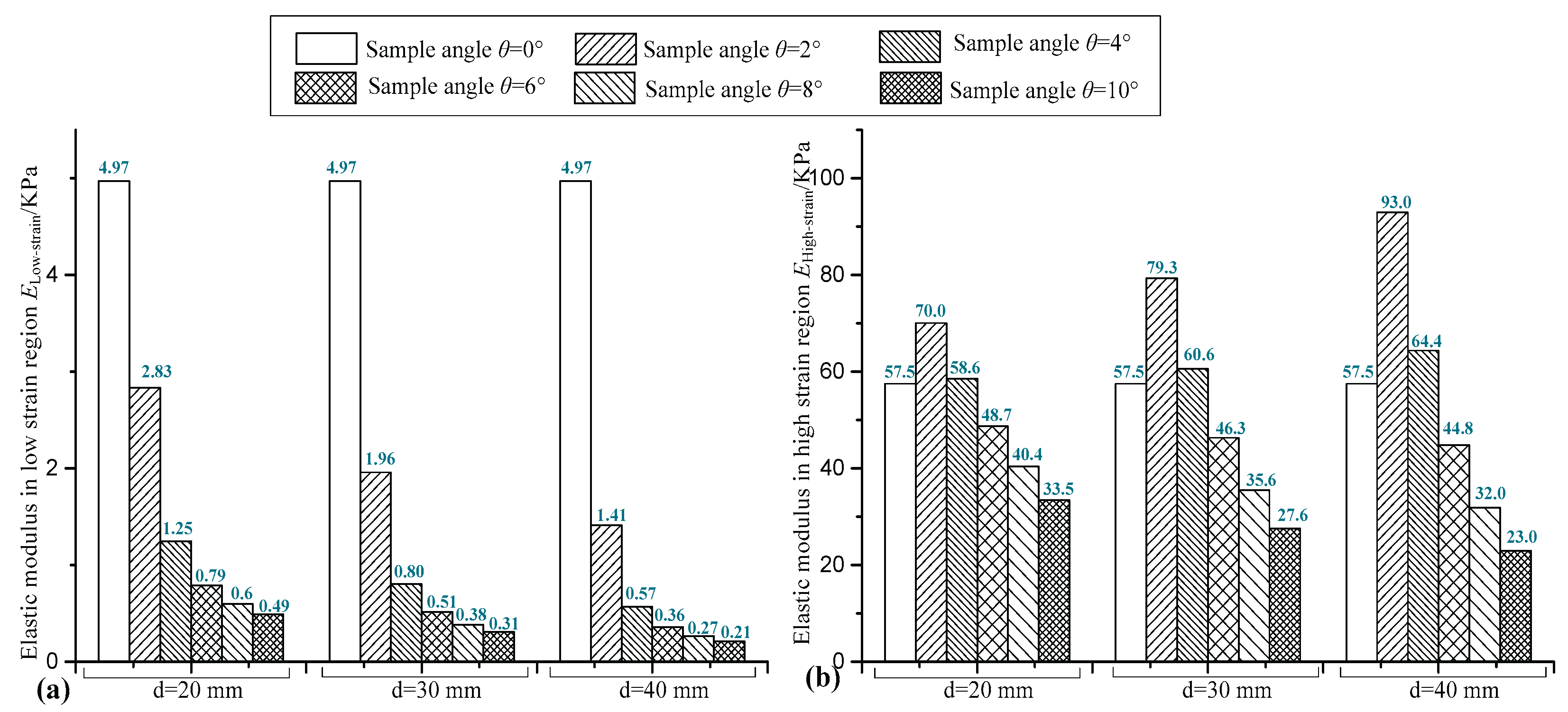
Figure 8.
Effect of sample angle on elastic modulus. (a) Effect of sample angle on ELow-strain modulus. (b)Effect of sample angle on EHigh-strain modulus.
Figure 8.
Effect of sample angle on elastic modulus. (a) Effect of sample angle on ELow-strain modulus. (b)Effect of sample angle on EHigh-strain modulus.
4. Results and Discussion
4.1. The Effect of Gravity on Mechanical Characteristics of Soft Tissue
For test1, the mechanical response of regular shape sample under gravity and without gravity are obtained by simulation, the sample diameter is 30mm and sample height is 20mm, the results were shown in
Figure 3. The results show that when considering the gravity, the stress of soft tissue sample is larger than that when ignoring the gravity. Compared with non-gravity condition, at the initial time of compression, the sample stress considering gravity condition increases by 11.2 %, and at the final stage of compression (λ=0.7), the sample stress considering gravity condition increases by 39 %. When the stretch is between 1.0 and 0.9, the influence of gravity shows a curve growth trend. When the compression continues, the influence of gravity shows a significant linear growth trend, linear relationship expression is ρ=-1.186λ+1.22 (R2=0.9997). The results show that under the same sample diameter, the influence of gravity on the mechanical response is divided into two stages. In the first stage, in the small strain region, the existence of gravity increases the mechanical response of soft tissue samples, and the increasing proportion shows a curve growth trend. In the second stage, in the area outside the small strain, the increase of gravity on the mechanical response is linear.
For test 2, The mechanical response with three sample diameters is shown in
Figure 4. By comparing the mechanical response difference of samples with diameters of 20 mm and 30 mm, and the mechanical response difference of samples with diameters of 30 mm and 40 mm, it can be found that in the region of small strain, the larger the sample diameter with a same height, the smaller the difference in stress caused by gravity. When the compressive strain is large, the sample height and diameter change greatly, and the influence of gravity becomes more and more obvious.
The influence of gravity on elastic modulus is shown in
Figure 5. For the influence of gravity on low-strain modulus ELow-strain, when the sample diameter is small, the existence of gravity will reduce the low-strain modulus of the mechanical response of the sample. As the diameter increases, gravity will increase the low strain modulus. The results show that the influence of gravity on the low strain modulus of small diameter samples is more obvious. The influence of gravity on high strain modulus EHigh-strain is close to that on low strain modulus ELow-strain. When the sample diameter is small, the existence of gravity will reduce the EHigh-strain of the sample mechanical response. As the diameter increases, gravity will continue to increase the high strain modulus. The results show that the influence of gravity on the high strain modulus of the sample is more obvious. When the diameter is larger, the influence of gravity is greater.
4.2. The Influence of Sample Angle on Mechanical Response of Soft Tissue
For test 3, five sample angles were set in numerical tests, and the corresponding mechanical response curves were obtained by simulation, as shown in
Figure 6. The stress difference percentage curves were obtained by comparing the mechanical response of the regular shape sample ( θ=0° ). When the sample angle is 2°, the stress shows a trend of first decreasing and then increasing. The reason may be that the existence of the sample angle at the initial stage of compression reduces the cross-sectional area of the sample, and the compression force of the sample is small. When the compression continues, the internal shear force will be generated on the inclined plane of the sample, leading to an increase in the elastic modulus of the sample and the stress. As the sample angle increases, the stress of the compression process becomes smaller and smaller.
For test4, The mechanical response with three sample diameters is shown in
Figure 7. The stress difference percentage curves were obtained by comparing the mechanical response of the regular shape sample (d=20 mm, θ=0° ). The results show that under the samples with different diameters, the influence of sample angle is mainly concentrated in the intermediate region of compression, and the stress is basically not affected at the beginning and end.
The influence of sample angle on elastic modulus is shown in
Figure 8. For the influence of sample on low-strain modulus ELow-strain, the sample angle will be significantly smaller low strain modulus ELow-strain. The larger the sample angle, the smaller the low strain modulus. The relationship between sample angle and low strain modulus is negative correlation. The influence of sample angle on EHigh-strain is similar to that of low strain modulus, and is negatively correlated. When the sample angle is 2°, the high strain modulus is higher than that of regular shape sample. The high strain modulus decreases with the increase of sample angle. The results show that the influence of sample angle on the ELow-strain and EHigh-strain of the sample is obvious. When the diameter is larger, the influence of sample angle is greater.
5. Conclusions
In this paper, three sample dimension parameters are defined, diameter d, gravity and sample angle θ. Based on the established finite element model, simulations were performed under different parameter settings. The influence of defined parameters on stress difference and modulus is analyzed by the obtained mechanical response of the sample. Gravity has little effect on low strain modulus, but has obvious effect on high strain modulus. Gravity will significantly increase the stress response of the sample. Under the same sample height, the larger the sample diameter, the more obvious the influence of gravity on the sample stress. The sample angle has a significant impact on the sample stress, and the larger the sample angle is, the more obvious the stress reduction is. The high strain modulus and low strain modulus decreased with the increase of sample angle, and the larger the sample diameter is, the more obvious the modulus reduction is.
Author Contributions
Jing Yang conceived the presented idea. Jing Yang, Dandan Liu and Yanjie Yang developed the theory and performed the computations. Yixun Fang and Yiming Huang preformed the simulation compression test in Abaqus Software. All authors discussed the results and contributed to the final manuscript. All authors have read and agreed to the published version of the manuscript.
Data Availability Statement
Not applicable.
Acknowledgments
This work is supported by Zhejiang Provincial Natural Science Foundation under Grant LQ21F020026.
Conflicts of Interest
The authors have no conflicts of interest to declare.
References
- David Anwanwan, Santosh Kumar Singh, Shriti Singh, et al. Challenges in liver cancer and possible treatment approaches. BBA - Reviews on Cancer 2020, 1873, 188314. [Google Scholar]
- Bielsa V, F. Virtual reality simulation in Plastic Surgery training. Literature Review. Journal of Plastic Reconstructive & Aesthetic Surgery 2021, 74, 2372–2378. [Google Scholar]
- Alekya, B. , Sanjay Rao, Hardik J. Pandya. Engineering approaches for characterizing soft tissue mechanical properties: A review. Clinical Biomechanics 2019, 69, 127–140. [Google Scholar]
- Kishev Navindaran, John S. Kang, Kee Moon. Techniques for characterizing mechanical properties of soft tissues. Journal of the Mechanical Behavior of Biomedical Materials 2023, 138, 105575. [Google Scholar]
- Miller, K. Method of testing very soft biological tissues in compression. Journal of Biomechanics 2005, 38, 153–158. [Google Scholar] [CrossRef]
- Gao Z, Lister K, Desai J P. Constitutive Modeling of Liver Tissue: Experiment and Theory. Annals of Biomedical Engineering 2010, 38, 505–516. [Google Scholar] [CrossRef]
- Islam M R, Virag J, Oyen M L. Micromechanical poroelastic and viscoelastic properties of ex-vivo soft tissues. Journal of Biomechanics 2020, 113, 110090. [Google Scholar] [CrossRef]
- Umale Sagar,Decka Caroline, Bourdet Nicolas, et al. Experimental mechanical characterization of abdominal organs: liver, kidney & spleen. Journal of the Mechanical Behavior of Biomedical Materials 2013, 17, 22–33. [Google Scholar] [CrossRef]
- Sandeep Madireddy, Bhargava Sista, Kumar Vemaganti. Bayesian calibration of hyperelastic constitutive models of soft tissue. Journal of the Mechanical Behavior of Biomedical Materials 2016, 59, 108–127. [Google Scholar] [CrossRef]
- Fu, Y.B. , Chui C.K. Modelling and simulation of porcine liver tissue indentation using finite element method and uniaxial stress–strain data. Journal of Biomechanics 2014, 47, 2430–2435. [Google Scholar] [CrossRef]
- Costin, D. Untaroiu, Lu Yuan-Chiao. Material characterization of liver parenchyma using specimen-specific finite element models, Journal of the Mechanical Behavior of Biomedical Materials 2013, 26, 11–22. [Google Scholar]
- Sun Z, Gepner B D, Lee S H, et al. Multidirectional mechanical properties and constitutive modeling of human adipose tissue under dynamic loading. Acta Biomaterialia 2021, 129, 188–198. [Google Scholar] [CrossRef] [PubMed]
- Li W, Shepherd D, Espino D M. Dynamic mechanical characterization and viscoelastic modeling of bovine brain tissue. Journal of the Mechanical Behavior of Biomedical Materials 2020, 114, 104204. [Google Scholar]
- Li W, Shepherd D, Espino D M. Frequency dependent viscoelastic properties of porcine brain tissue. Journal of the Mechanical Behavior of Biomedical Materials 2019, 102, 103460. [Google Scholar]
- Gervaso F, Pennati G, Boschetti F. Effect of geometrical imperfections in confined compression tests on parameter evaluation of hydrated soft tissues. Journal of Biomechanics 2007, 40, 3041–3044. [Google Scholar] [CrossRef]
- Commisso, M.S. , Martínezreina J., et al. Effect of non-uniform thickness of samples in stress relaxation tests under unconfined compression of samples of articular discs. Journal of Biomechanics 2014, 47, 1526–1530. [Google Scholar] [CrossRef]
- Miller, K. Constitutive modelling of abdominal organs. Journal of biomechanics 2000, 33, 367–373. [Google Scholar] [CrossRef]
- Chagnon G, Rebouah M, Favier D. Hyperelastic energy densities for soft biological tissues: a review, Journal of Elasticity 2015, 120, 129–160.
- Peng Xiangfeng, Li Luxian. State of the art of constitutive relations of hyperelastic materials. Chinese Journal of Theoretical and Applied Mechanics 2020, 52, 1221–1232. [Google Scholar]
- Yang Jing, Yu Lingtao, Wang Lan, Wang Wenjie, Cui Jianwei. The estimation method of Friction in unconfined compression tests of soft tissue, Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine 2018, 232, 573–587.
- Yang J, Hu M, Han Z, et al. A novel elimination method of preloading force on the unconfined compression tests of soft tissue. Advances in Mechanical Engineering 2021, 13, 168781402110106. [Google Scholar] [CrossRef]
- Yang Jing, Yang Liuqing, Ma Shanhong, et al. Numerical coupling analysis of the influence of blood flow on the mechanical response for liver. Journal of Mechanics in Medicine and Biology 2021, 21, 2150018. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).