Submitted:
14 September 2025
Posted:
15 September 2025
You are already at the latest version
Abstract
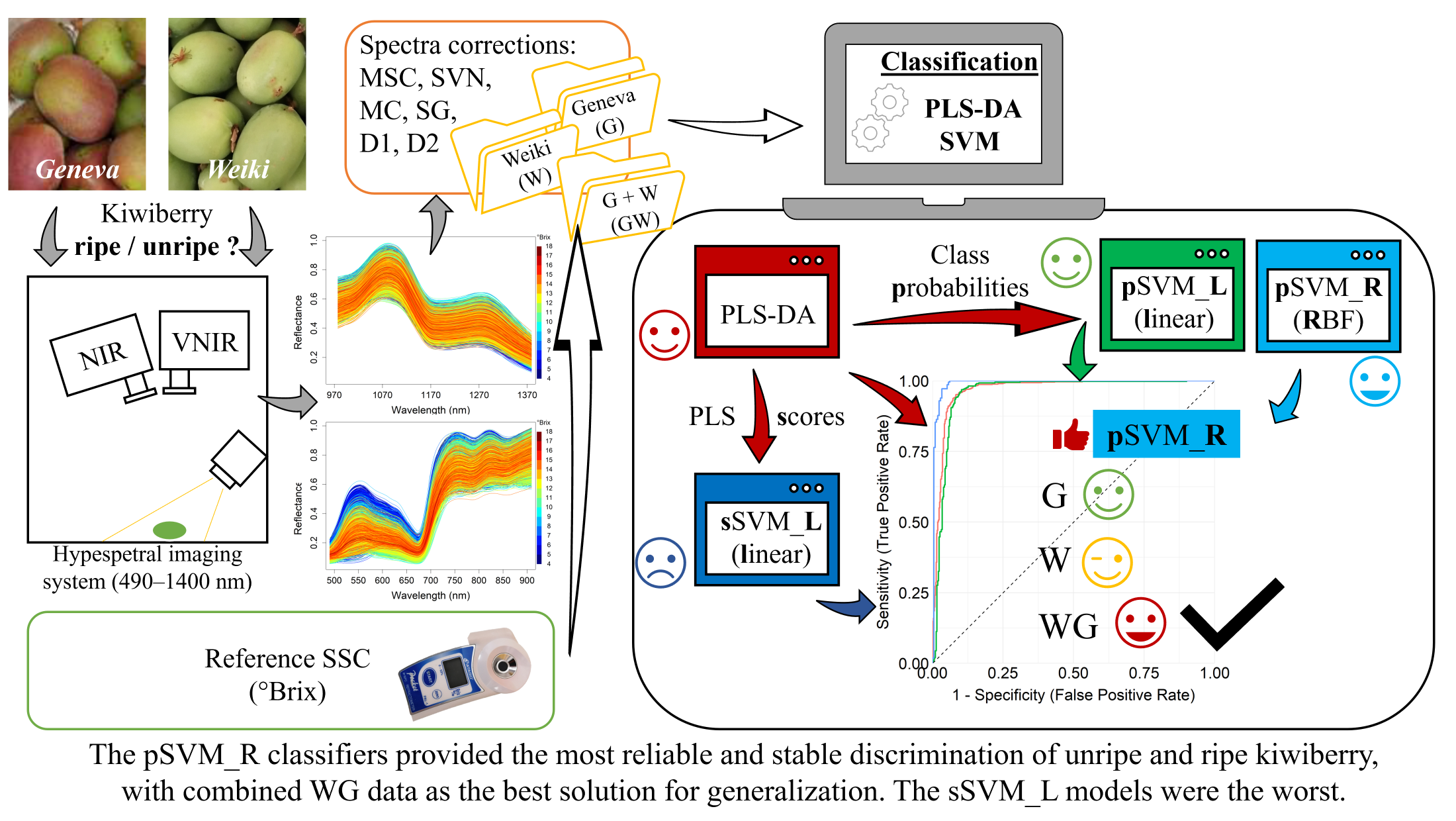
Keywords:
1. Introduction
2. Materials and Methods
2.1. Collection and Preparation of Kiwiberry Samples
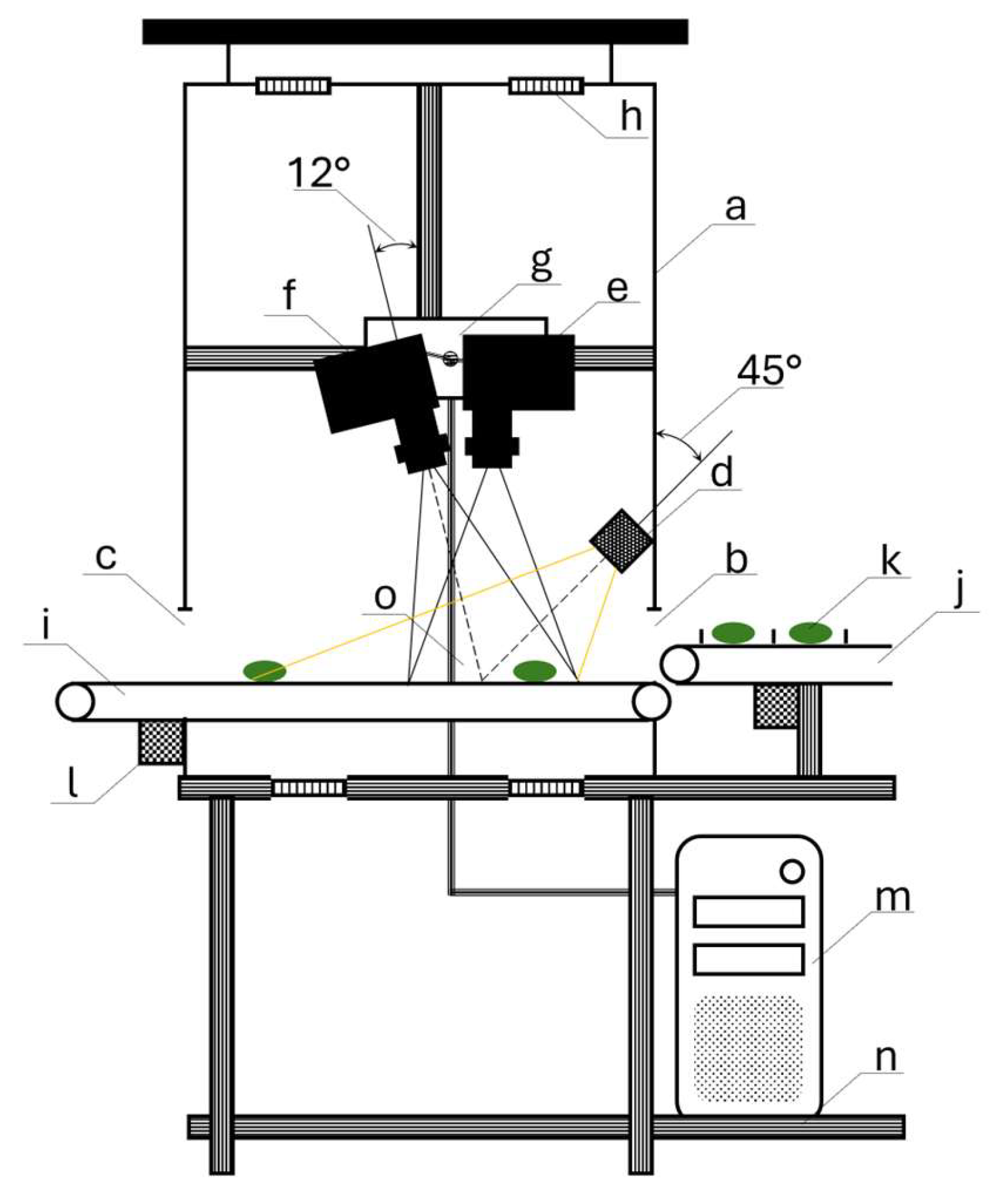
2.2. Hyperspectral Imaging Setup
2.3. Processing Workflow for Hyperspectral Reflectance Data
2.4. Determination of SSC as a Ripeness Index
2.5. Data Preparation
2.6. PLS-DA & SVM Classification
2.7. Evaluation of Classification Performance
3. Results
3.1. Classification Results of ‘Geneva’ Kiwiberry
3.2. Classification Results of ‘Weiki’ Kiwiberry
3.3. Classification Results for the Combined Data of ‘Geneva’ and ‘Weiki’ Kiwiberry
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nishiyama, I.; Yamashita, Y.; Yamanaka, M.; Shimohashi, A.; Fukuda, T.; Oota, T. Varietal Difference in Vitamin C Content in the Fruit of Kiwifruit and Other Actinidia Species. J. Agric. Food Chem. 2004, 52, 5472–5475. [Google Scholar] [CrossRef]
- Latocha, P.; Łata, B.; Stasiak, A. Phenolics, Ascorbate and the Antioxidant Potential of Kiwiberry vs. Common Kiwifruit: The Effect of Cultivar and Tissue Type. J. Funct. Foods 2015, 19, 155–163. [Google Scholar] [CrossRef]
- Latocha, P.; Debersaques, F.; Decorte, J. Varietal differences in the mineral composition of kiwiberry - Actinidia arguta (Siebold et Zucc.) Planch. Ex. Miq. In Proceedings of the Acta Horticulturae; International Society for Horticultural Science (ISHS), Leuven, Belgium, September 21 2015; pp. 479–486. [Google Scholar]
- Latocha, P. The Nutritional and Health Benefits of Kiwiberry (Actinidia Arguta) – a Review. Plant Foods Hum. Nutr. Dordr. Neth. 2017, 72, 325–334. [Google Scholar] [CrossRef] [PubMed]
- Wojdyło, A.; Nowicka, P. Anticholinergic Effects of Actinidia arguta Fruits and Their Polyphenol Content Determined by Liquid Chromatography-Photodiode Array Detector-Quadrupole/Time of Flight-Mass Spectrometry (LC-MS-PDA-Q/TOF). Food Chem. 2019, 271, 216–223. [Google Scholar] [CrossRef] [PubMed]
- Pinto, D.; Delerue-Matos, C.; Rodrigues, F. Bioactivity, Phytochemical Profile and pro-Healthy Properties of Actinidia arguta: A Review. Food Res. Int. Ott. Ont 2020, 136, 109449. [Google Scholar] [CrossRef]
- Latocha, P. Some Morphological and Biological Features of ‘Bingo’ – a New Hardy Kiwifruit Cultivar from Warsaw University of Life Sciences (WULS) in Poland. Rocz. Pol. Tow. Dendrol. 2012, 60.
- Latocha, P.; Krupa, T.; Jankowski, P.; Radzanowska, J. Changes in Postharvest Physicochemical and Sensory Characteristics of Hardy Kiwifruit (Actinidia arguta and Its Hybrid) after Cold Storage under Normal versus Controlled Atmosphere. Postharvest Biol. Technol. 2014, 88, 21–33. [Google Scholar] [CrossRef]
- Stefaniak, J.; Przybył, J.L.; Latocha, P.; Łata, B. Bioactive Compounds, Total Antioxidant Capacity and Yield of Kiwiberry Fruit under Different Nitrogen Regimes in Field Conditions. J. Sci. Food Agric. 2020, 100, 3832–3840. [Google Scholar] [CrossRef]
- Fisk, C.L.; Silver, A.M.; Strik, B.C.; Zhao, Y. Postharvest Quality of Hardy Kiwifruit (Actinidia arguta ‘Ananasnaya’) Associated with Packaging and Storage Conditions. Postharvest Biol. Technol. 2008, 47, 338–345. [Google Scholar] [CrossRef]
- Boyes, S.; Strübi, P.; Marsh, H. Sugar and Organic Acid Analysis of Actinidia arguta and Rootstock–Scion Combinations of Actinidia Arguta. LWT - Food Sci. Technol. 1997, 30, 390–397. [Google Scholar] [CrossRef]
- Nishiyama, I.; Fukuda, T.; Shimohashi, A.; Oota, T. Sugar and Organic Acid Composition in the Fruit Juice of Different Actinidia Varieties. Food Sci. Technol. Res. 2008, 14, 67–73. [Google Scholar] [CrossRef]
- Wojdyło, A.; Nowicka, P.; Oszmiański, J.; Golis, T. Phytochemical Compounds and Biological Effects of Actinidia Fruits. J. Funct. Foods 2017, 30, 194–202. [Google Scholar] [CrossRef]
- Lü, Q.; Tang, M. Detection of Hidden Bruise on Kiwi Fruit Using Hyperspectral Imaging and Parallelepiped Classification. Procedia Environ. Sci. 2012, 12, 1172–1179. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Pourdarbani, R.; Sabzi, S.; Rohban, M.H.; Arribas, J.I. From Harvest to Market: Non-Destructive Bruise Detection in Kiwifruit Using Convolutional Neural Networks and Hyperspectral Imaging. Horticulturae 2023, 9, 936. [Google Scholar] [CrossRef]
- Haghbin, N.; Bakhshipour, A.; Zareiforoush, H.; Mousanejad, S. Non-Destructive Pre-Symptomatic Detection of Gray Mold Infection in Kiwifruit Using Hyperspectral Data and Chemometrics. Plant Methods 2023, 19, 53. [Google Scholar] [CrossRef]
- Chen, X.; Zheng, L.; Kang, Z. Study on Test Method of Kiwifruit Hardness Based on Hyperspectral Technique. J. Phys. Conf. Ser. 2020, 1453, 012143. [Google Scholar] [CrossRef]
- Li, J.; Huang, B.; Wu, C.; Sun, Z.; Xue, L.; Liu, M.; Chen, J. Nondestructive Detection of Kiwifruit Textural Characteristic Based on near Infrared Hyperspectral Imaging Technology. Int. J. Food Prop. 2022, 25, 1697–1713. [Google Scholar] [CrossRef]
- Zhu, H.; Chu, B.; Fan, Y.; Tao, X.; Yin, W.; He, Y. Hyperspectral Imaging for Predicting the Internal Quality of Kiwifruits Based on Variable Selection Algorithms and Chemometric Models. Sci. Rep. 2017, 7, 7845. [Google Scholar] [CrossRef]
- Benelli, A.; Cevoli, C.; Fabbri, A.; Ragni, L. Ripeness Evaluation of Kiwifruit by Hyperspectral Imaging. Biosyst. Eng. 2022, 223, 42–52. [Google Scholar] [CrossRef]
- Bakhshipour, A. A Data Fusion Approach for Nondestructive Tracking of the Ripening Process and Quality Attributes of Green Hayward Kiwifruit Using Artificial Olfaction and Proximal Hyperspectral Imaging Techniques. Food Sci. Nutr. 2023, 11, 6116–6132. [Google Scholar] [CrossRef] [PubMed]
- Qin, L.; Zhang, J.; Stevan, S.; Xing, S.; Zhang, X. Intelligent Flexible Manipulator System Based on Flexible Tactile Sensing (IFMSFTS) for Kiwifruit Ripeness Classification. J. Sci. Food Agric. 2024, 104, 273–285. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Sarkar, S.; Park, Y.; Yang, J.; Kweon, G. Feasibility Study for an Optical Sensing System for Hardy Kiwi (Actinidia arguta) Sugar Content Estimation. J. Agric. Life Sci. 2019, 53, 147–157. [Google Scholar] [CrossRef]
- Xu, L.; Chen, Y.; Wang, X.; Chen, H.; Tang, Z.; Shi, X.; Chen, X.; Wang, Y.; Kang, Z.; Zou, Z.; et al. Non-Destructive Detection of Kiwifruit Soluble Solid Content Based on Hyperspectral and Fluorescence Spectral Imaging. Front. Plant Sci. 2023, 13. [Google Scholar] [CrossRef]
- Mansourialam, A.; Rasekh, M.; Ardabili, S.; Dadkhah, M.; Mosavi, A. Hyperspectral Method Integrated with Machine Learning to Predict the Acidity and Soluble Solid Content Values of Kiwi Fruit During the Storage Period. Acta Technol. Agric. 2024, 27, 187–193. [Google Scholar] [CrossRef]
- Mumford, A.; Abrahamsson, Z.; Hale, I. Predicting Soluble Solids Concentration of ‘Geneva 3’ Kiwiberries Using Near Infrared Spectroscopy. HortTechnology 2024, 34, 172–180. [Google Scholar] [CrossRef]
- Lee, J.-E.; Kim, M.-J.; Lee, B.-Y.; Hwan, L.J.; Yang, H.-E.; Kim, M.S.; Hwang, I.G.; Jeong, C.S.; Mo, C. Evaluating Ripeness in Post-Harvest Stored Kiwifruit Using VIS-NIR Hyperspectral Imaging. Postharvest Biol. Technol. 2025, 225, 113496. [Google Scholar] [CrossRef]
- Ballabio, D.; Consonni, V. Classification Tools in Chemistry. Part 1: Linear Models. PLS-DA. Anal. Methods 2013, 5, 3790–3798. [Google Scholar] [CrossRef]
- Fordellone, M.; Bellincontro, A.; Mencarelli, F. Partial Least Squares Discriminant Analysis: A Dimensionality Reduction Method to Classify Hyperspectral Data. Stat. Appl. - Ital. J. Appl. Stat. 2019, 181–200. [Google Scholar] [CrossRef]
- Wold, H. Path Models with Latent Variables: The NIPALS Approach*. In Quantitative Sociology; International Perspectives on Mathematical and Statistical Modeling; Blalock, H.M., Aganbegian, A., Borodkin, F.M., Boudon, R., Capecchi, V., Eds.; Academic Press, 1975; pp. 307–357. ISBN 978-0-12-103950-9. [Google Scholar]
- Wold, S.; Ruhe, A.; Wold, H.; Dunn, W.J., III. The Collinearity Problem in Linear Regression. The Partial Least Squares (PLS) Approach to Generalized Inverses. SIAM J. Sci. Stat. Comput. 1984, 5, 735–743. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-Regression: A Basic Tool of Chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Barker, M.; Rayens, W. Partial Least Squares for Discrimination. J. Chemom. 2003, 17, 166–173. [Google Scholar] [CrossRef]
- Tian, P.; Meng, Q.; Wu, Z.; Lin, J.; Huang, X.; Zhu, H.; Zhou, X.; Qiu, Z.; Huang, Y.; Li, Y. Detection of Mango Soluble Solid Content Using Hyperspectral Imaging Technology. Infrared Phys. Technol. 2023, 129, 104576. [Google Scholar] [CrossRef]
- Li, X.; Wei, Y.; Xu, J.; Feng, X.; Wu, F.; Zhou, R.; Jin, J.; Xu, K.; Yu, X.; He, Y. SSC and pH for Sweet Assessment and Maturity Classification of Harvested Cherry Fruit Based on NIR Hyperspectral Imaging Technology. Postharvest Biol. Technol. 2018, 143, 112–118. [Google Scholar] [CrossRef]
- Sharma, S.; Sumesh, K.C.; Sirisomboon, P. Rapid Ripening Stage Classification and Dry Matter Prediction of Durian Pulp Using a Pushbroom near Infrared Hyperspectral Imaging System. Measurement 2022, 189, 110464. [Google Scholar] [CrossRef]
- Flach, P. Machine Learning: The Art and Science of Algorithms That Make Sense of Data; Cambridge University Press: Cambridge, 2012; ISBN 978-1-107-09639-4. [Google Scholar]
- Burkov, A. The Hundred-Page Machine Learning Book; Polen, 2019; ISBN 978-1-9995795-0-0. [Google Scholar]
- Baesens, B. Analytics in a Big Data World.
- Mendez, K.M.; Reinke, S.N.; Broadhurst, D.I. A Comparative Evaluation of the Generalised Predictive Ability of Eight Machine Learning Algorithms across Ten Clinical Metabolomics Data Sets for Binary Classification. Metabolomics 2019, 15, 150. [Google Scholar] [CrossRef]
- Sarkar, S.; Basak, J.K.; Moon, B.E.; Kim, H.T. A Comparative Study of PLSR and SVM-R with Various Preprocessing Techniques for the Quantitative Determination of Soluble Solids Content of Hardy Kiwi Fruit by a Portable Vis/NIR Spectrometer. Foods 2020, 9, 1078. [Google Scholar] [CrossRef]
- Janaszek-Mańkowska, M.; Ratajski, A. Hyperspectral Imaging and Predictive Modelling for Automated Control of a Prototype Sorting Device for Kiwiberry (Actinidia arguta). Adv. Sci. Technol. Res. J. 2025, 19, 50–64. [Google Scholar] [CrossRef]
- Xiong, Z.; Xie, A.; Sun, D.-W.; Zeng, X.-A.; Liu, D. Applications of Hyperspectral Imaging in Chicken Meat Safety and Quality Detection and Evaluation: A Review. Crit. Rev. Food Sci. Nutr. 2015, 55, 1287–1301. [Google Scholar] [CrossRef] [PubMed]
- Theodoridis, S.; Koutroumbas, K. Chapter 14 - Clustering Algorithms III: Schemes Based on Function Optimization. In Pattern Recognition (Fourth Edition); Theodoridis, S., Koutroumbas, K., Eds.; Academic Press: Boston, 2009; pp. 701–763. ISBN 978-1-59749-272-0. [Google Scholar]
- Geladi, P.; MacDougall, D.; Martens, H. Linearization and Scatter-Correction for Near-Infrared Reflectance Spectra of Meat. Appl. Spectrosc. 1985, 39, 491–500. [Google Scholar] [CrossRef]
- Maleki, M.R.; Mouazen, A.M.; Ramon, H.; De Baerdemaeker, J. Multiplicative Scatter Correction during On-Line Measurement with Near Infrared Spectroscopy. Biosyst. Eng. 2007, 96, 427–433. [Google Scholar] [CrossRef]
- Barnes, R.J.; Dhanoa, M.S.; Lister, S.J. Standard Normal Variate Transformation and De-Trending of Near-Infrared Diffuse Reflectance Spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Witteveen, M.; Sterenborg, H.J.C.M.; van Leeuwen, T.G.; Aalders, M.C.G.; Ruers, T.J.M.; Post, A.L. Comparison of Preprocessing Techniques to Reduce Nontissue-Related Variations in Hyperspectral Reflectance Imaging. J. Biomed. Opt. 2022, 27, 106003. [Google Scholar] [CrossRef] [PubMed]
- Kucheryavskiy, S. Mdatools – R Package for Chemometrics. Chemom. Intell. Lab. Syst. 2020, 198, 103937. [Google Scholar] [CrossRef]
- R Core Team R: A Language and Environment for Statistical Computing 2025.
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Liland, K.H.; Mevik, B.-H.; Wehrens, R.; Hiemstra, P. Pls: Partial Least Squares and Principal Component Regression 2024.
- Karatzoglou, A.; Smola, A.; Hornik, K.; Zeileis, A. Kernlab - An S4 Package for Kernel Methods in R. J. Stat. Softw. 2004, 11, 1–20. [Google Scholar] [CrossRef]
- Karatzoglou, A.; Smola, A.; Hornik, K.; Australia (NICTA), N.I.; Maniscalco, M.A.; Teo, C.H. Kernlab: Kernel-Based Machine Learning Lab 2024.
- Ting, K.M.; Witten, I.H. Issues in Stacked Generalization. J. Artif. Intell. Res. 1999, 10, 271–289. [Google Scholar] [CrossRef]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Lavazza, L.; Morasca, S. Comparing ϕ and the F-Measure as Performance Metrics for Software-Related Classifications. Empir. Softw. Eng. 2022, 27, 185. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. Support Vector Machines and Flexible Discriminants. In The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer New York: New York, NY, 2009; pp. 417–458. ISBN 978-0-387-84858-7. [Google Scholar]
- Sokolova, M.; Lapalme, G. A Systematic Analysis of Performance Measures for Classification Tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Japkowicz, N.; Shah, M. Evaluating Learning Algorithms: A Classification Perspective; Cambridge University Press: Cambridge, 2011; ISBN 978-0-521-19600-0. [Google Scholar]
- Yang, H.; Chen, Q.; Qian, J.; Li, J.; Lin, X.; Liu, Z.; Fan, N.; Ma, W. Determination of Dry-Matter Content of Kiwifruit before Harvest Based on Hyperspectral Imaging. AgriEngineering 2024, 6, 52–63. [Google Scholar] [CrossRef]
- Mishra, P. Developing Multifruit Global Near-Infrared Model to Predict Dry Matter Based on Just-in-Time Modeling. J. Chemom. 2024, 38, e3540. [Google Scholar] [CrossRef]
| Dataset | Training | Test | ||
| class A | class B | class A | class B | |
| ‘Weiki’ (W) | 1526 | 1524 | 380 | 380 |
| ‘Geneva’ (G) | 852 | 852 | 212 | 212 |
| ‘Weiki’ + ‘Geneva’ (WG) | 2378 | 2376 | 592 | 592 |
| Predicted positive (A) | Predicted Negative (B) | Overall observed | |
| Observed positive (A) | TP – true positive | FN – false negative | OP = TP + FN |
| Observed negative (B) | FP – false positive | TN – true negative | ON = FP + TN |
| Overall predicted | PP = TP + FP | PN = FN + TN | n = TP + FN + FP + TN |
| ACC (%) | κ (%) | F05 (–) | PPV (%) | TPR (%) | TNR (%) | LR+ (–) | LR– (–) | nC 2) (–) | |
| Calibration | |||||||||
| G_PLS-DA (D2) 1) | 89.67 | 79.34 | 87.38 | 85.58 | 95.42 | 83.92 | 5.93 | 0.054 | 20 |
| G_sSVM_L (D2) | 92.37 | 84.74 | 90.53 | 89.15 | 96.48 | 88.26 | 8.22 | 0.040 | 20 |
| G_pSVM_L (D2) | 89.50 | 78.99 | 88.17 | 87.10 | 92.72 | 86.27 | 6.75 | 0.084 | |
| G_pSVM_R (SG) | 93.19 | 86.38 | 91.61 | 90.44 | 96.60 | 89.79 | 9.46 | 0.038 | |
| Prediction | |||||||||
| G_PLS-DA (D2) | 92.22 | 84.43 | 89.84 | 88.09 | 97.64 | 86.79 | 7.39 | 0.027 | 20 |
| G_sSVM_L (D2) | 69.10 | 38.21 | 70.60 | 74.85 | 57.55 | 80.66 | 2.98 | 0.526 | 20 |
| G_pSVM_L (D2) | 92.92 | 85.85 | 91.82 | 90.99 | 95.28 | 90.57 | 10.10 | 0.052 | |
| G_pSVM_R (SG) | 96.93 | 93.87 | 95.32 | 94.22 | 100.00 | 93.87 | 16.31 | 0.000 | |
| ACC (%) | κ (%) | F05 (–) | PPV (%) | TPR (%) | TNR (%) | LR+ (–) | LR– (–) | nC 2) (–) | |
| Calibration | |||||||||
| W_PLS-DA (D2) 1) | 94.39 | 88.79 | 93.44 | 92.74 | 96.33 | 92.45 | 12.78 | 0.040 | 18 |
| W_sSVM_L (D2) | 94.43 | 88.85 | 93.68 | 93.13 | 95.94 | 92.91 | 13.56 | 0.044 | 18 |
| W_pSVM_L (D2) | 94.33 | 88.66 | 93.69 | 93.23 | 95.61 | 93.04 | 13.76 | 0.047 | |
| W_pSVM_R (D2) | 95.51 | 91.02 | 94.75 | 94.21 | 96.99 | 94.03 | 16.26 | 0.032 | |
| Prediction | |||||||||
| W_PLS-DA (D2) | 91.84 | 83.68 | 90.21 | 88.97 | 95.53 | 88.16 | 8.07 | 0.051 | 18 |
| W_sSVM_L (D2) | 68.68 | 37.37 | 68.98 | 69.83 | 65.79 | 71.58 | 2.31 | 0.478 | 18 |
| W_pSVM_L (D2) | 92.24 | 84.47 | 90.75 | 89.63 | 95.53 | 88.95 | 8.64 | 0.050 | |
| W_pSVM_R (D2) | 92.89 | 85.79 | 91.09 | 89.76 | 96.84 | 88.95 | 8.76 | 0.036 | |
| ACC (%) | κ (%) | F05 (–) | PPV (%) | TPR (%) | TNR (%) | LR+ (–) | LR– (–) | nC 2) (–) | |
| Calibration | |||||||||
| WG_PLS-DA (D2) 1) | 90.30 | 80.61 | 89.08 | 88.11 | 93.19 | 87.42 | 7.41 | 0.078 | 20 |
| WG_sSVM_L (D2) | 90.41 | 80.82 | 89.50 | 88.78 | 92.51 | 88.30 | 7.91 | 0.085 | 19 |
| WG_pSVM_L (D2) | 90.18 | 80.35 | 89.32 | 88.64 | 92.18 | 88.17 | 7.80 | 0.089 | |
| WG_pSVM_R (D1) | 93.31 | 86.62 | 92.04 | 91.10 | 96.01 | 90.61 | 10.24 | 0.044 | |
| Prediction | |||||||||
| WG_PLS-DA (D2) | 88.94 | 77.87 | 87.36 | 86.07 | 92.91 | 84.97 | 6.18 | 0.083 | 20 |
| WG_sSVM_L (D2) | 62.16 | 24.32 | 62.15 | 62.54 | 60.64 | 63.68 | 1.67 | 0.618 | 19 |
| WG_pSVM_L (D2) | 89.95 | 79.90 | 88.64 | 87.60 | 93.07 | 86.82 | 7.06 | 0.080 | |
| WG_pSVM_R (D1) | 92.40 | 84.80 | 90.51 | 89.10 | 96.62 | 88.18 | 8.17 | 0.038 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





