1. Introduction
Most scientific endeavours are accomplished by human beings in conscious mental states. These conscious states constitute the subjective experience of the self. Many of these states seem to connect an external entity, the world, with the self, the inner subject who observes the world. One of the central pillars of Western natural philosophy since ancient Greece was precisely to assume the existence of such external world independent of the observer (Schrödinger, 1954). In this way, a third-person objective point of view was adopted in the classical study of nature. And basically, until the development of quantum mechanics this state of affairs was the mainstream in natural sciences.
On the other hand, the study of mind was practically restricted to philosophy from Descartes and his dualistic description of the mind-body problem in the seventeenth century to the introduction of quantum mechanics at the beginning of the twentieth century. However, consciousness entered physics as a possible necessary central piece in the resolution of the measurement problem within several interpretations of quantum mechanics (e.g., Copenhagen interpretation (Faye, 2019; Plotnitsky, 2012), Wigner interpretation (Wigner, 1961) …). In the end, all the information about the outside world reaches the brain of a human being mediated by the senses of their body and therefore the properties of that external world can only be indirectly deduced through these data (see von Helmholtz (1903) and chapter 6 of von Neumann’s book (1955) devoted to quantum measurement theory). Therefore, at a certain level of reduction in the description of this process, it would be reasonable to expect the necessity of studying the properties of consciousness in order to reliably extract the characteristics of the outside world from the representation generated in the mind. A schematic overview of some of the main philosophical descriptions of the problem of consciousness is briefly outlined in
Section 2.
In this paper, a physical model for consciousness is devised in the framework of an approach to study the foundations of quantum mechanics (Baladrón, 2010, 2014, 2017; Baladrón and Khrennikov, 2016, 2017, 2018, 2019, 2023) in which it is assumed that matter possesses the capacity of processing information. In this approach, a fundamental particle is characterized at time t by its position and mass in physical space, and it is supplemented with an information space in which a classical Turing machine (Barker-Plummer, 2012) (basically, a mathematical model of a classical digital computer) and a randomizer (a random number generator) are stored. In physical space, particles follow continuous trajectories and interact by exchanging carriers of momentum, energy and information, satisfying the principle of conservation of momentum and energy. The information conveyed by the carriers impinging on a particle is transferred to its information space and, in turn, after a run of the program, the output determines the momentum and energy of the carrier to be emitted by the particle in physical space.
One of the messages of our work is that information space should be treated on the equal grounds with the physical space. The flows of information are not less real than the flows of matter and fields.
A strong assumption has been made in this approach disregarding in a first-order approximation the contribution of gravitation to the evolution of the structure and interaction mechanisms of the fundamental particles from the Big Bang. As abovementioned, it has been assumed that momentum and energy are conserved in physical space. On the contrary, information is not conserved in the union of all the information spaces associated by definition with the fundamental particles. Specifically, inconsequential information for the dynamics of a particle will be deleted on the information space of the particle, introducing irreversibility in the model and constituting a central element for the characterization of consciousness in this approach, as it will be discussed throughout the article.
Every particle in this approach is governed by a program, a classical algorithm that encodes the quantum mechanical formalism, and an anticipation module that predicts the configuration of the surrounding systems at time
. In this way, as will be analysed in the
Appendix, a fundamental particle would behave quantum mechanically in real time. Given that every particle follows a continuous trajectory, the quantum dynamics resembles a generalized Bohmian mechanics, in particular, the measurement problem is solved in a similar way to Bohmian mechanics (Goldstein, 2021; Hoffman and Vona, 2014).
This information-theoretic model of fundamental particles has been applied in previous articles (Baladrón, 2010, 2014, 2017; Baladrón and Khrennikov, 2016, 2017, 2018, 2019, 2023) to study the relationships between classicality and quantumness and, in particular, to analyse a possible scenario in which quantum behaviour would emerge as a consequence of Darwinian evolution under natural selection acting on populations of these information-theoretic particles.
In the present article, a second way of interaction between the physical and the information space of a particle is postulated in the framework of this Darwinian approach to quantum mechanics (DAQM). When an apparatus measures the property of a particle, at the end of the process, only a branch of the wave function of the particle effectively keeps playing a role in its dynamics. The superfluous branches are then erased on the information space of the particle and it is hypothesized that this erasure of information on the information space induces an elementary event of phenomenological consciousness (or proto-consciousness) on the particle. This event of elementary proto-consciousness consists in the experience of the spatial locations of the surrounding particles as calculated by the program of the particle. Notice that our basic postulate characterizes elementary phenomenological consciousness as the result of the effective collapse of the wave function, just the other way around with respect to the usual assumption in quantum mechanical Wigner-like interpretations, but the same causal-effect order as in the Penrose-Hameroff theory of consciousness (Hameroff and Penrose, 1996), in which the objective collapse of the wave function is induced by a gravitational process (Diósi-Penrose scheme for the objective reduction of the quantum state (Diósi, 1989; Penrose,1996)).
In our model, proto-consciousness, by definition, is a property of matter associated to the erasure of superfluous information for the dynamics of the particle on its information space. This is the core of this model of consciousness that is developed in
Section 3.
In
Section 4, the characterization of measurement and observation in our model for a fundamental particle is formalized, and the implications for the quantum mechanical description of the world are further analysed, in particular, discussing how the model describes elementary Wigner’s friend (Wigner, 1961) scenarios in which the predictions of this model could be compared with possible future experiments.
The assumption of proto-consciousness in fundamental particles leads to the so-called combination problem, i.e., determining the way in which higher-level consciousness appears in a system composed of conscious subsystems, and the extent in which the lower-level consciousness in the constituents is affected by the emergence of consciousness in the composite system. The combination problem and an outline of its natural possible solution in this model by means of the concept of entanglement is addressed in
Section 5. Information-theoretic Darwinian evolution makes room for a possible mechanism through which consciousness might play an active role in the physical space without altering the observed status quo of physics. This mechanism is preliminarily described in
Section 6. The fundamental role that proto-consciousness, as a hypothetical intrinsic property of matter, might play in Darwinian evolution and the manner in which high-level consciousness might be generated through evolution in complex biological systems is schematically discussed in
Section 7. The implications of the model for the possible development of high-level consciousness in a future artificial general intelligence (AGI) are briefly considered. To end
Section 7, the natural implementation of a mechanism bringing about genuine, compatibilist free will for complex biological systems in this DAQM model for consciousness is succinctly described. Some conclusions of the article are drawn in
Section 8. Finally, the Darwinian approach to quantum mechanics (DAQM), the physical framework in which the model of consciousness has been developed, is briefly summarized in the
Appendix.
2. Overview of Some Philosophical Approaches to the Mind-Body Problem
The majority of scientists explicitly or implicitly adopt a materialist perspective as fundamental ontology of the world. Materialism (Stoljar, 2023) (or physicalism in more modern and precise language) assumes that matter is the fundamental stuff from which anything that exists in the world is made. In particular, consciousness also ought to be exclusively describable in terms of matter. Physicalism is a monistic philosophical doctrine, the simplest way of describing the world. However, physicalism is confronted with the so-called “hard problem of consciousness”, as named by Chalmers (1995), that is, the unsurmountable difficulty, in appearance, of describing consciousness, subjective experience, in terms of space, time, mass, charge, spin…the fundamental properties characterizing the physical world. This explanatory gap seems to defeat physicalism and its endeavour of reducing the qualities of the subjective sensations of a conscious system to the structure and function of physical entities. Several philosophical arguments (e.g., the philosophical zombie (Chalmers, 1996; Kirk, 2009), Mary’s room (Jackson, 1982)) have been developed to illustrate and highlight the unparalleled nature of this problem. The “hard problem of consciousness” has fuelled the search for other philosophical frameworks being able to give a satisfactory scientific account of subjective experience.
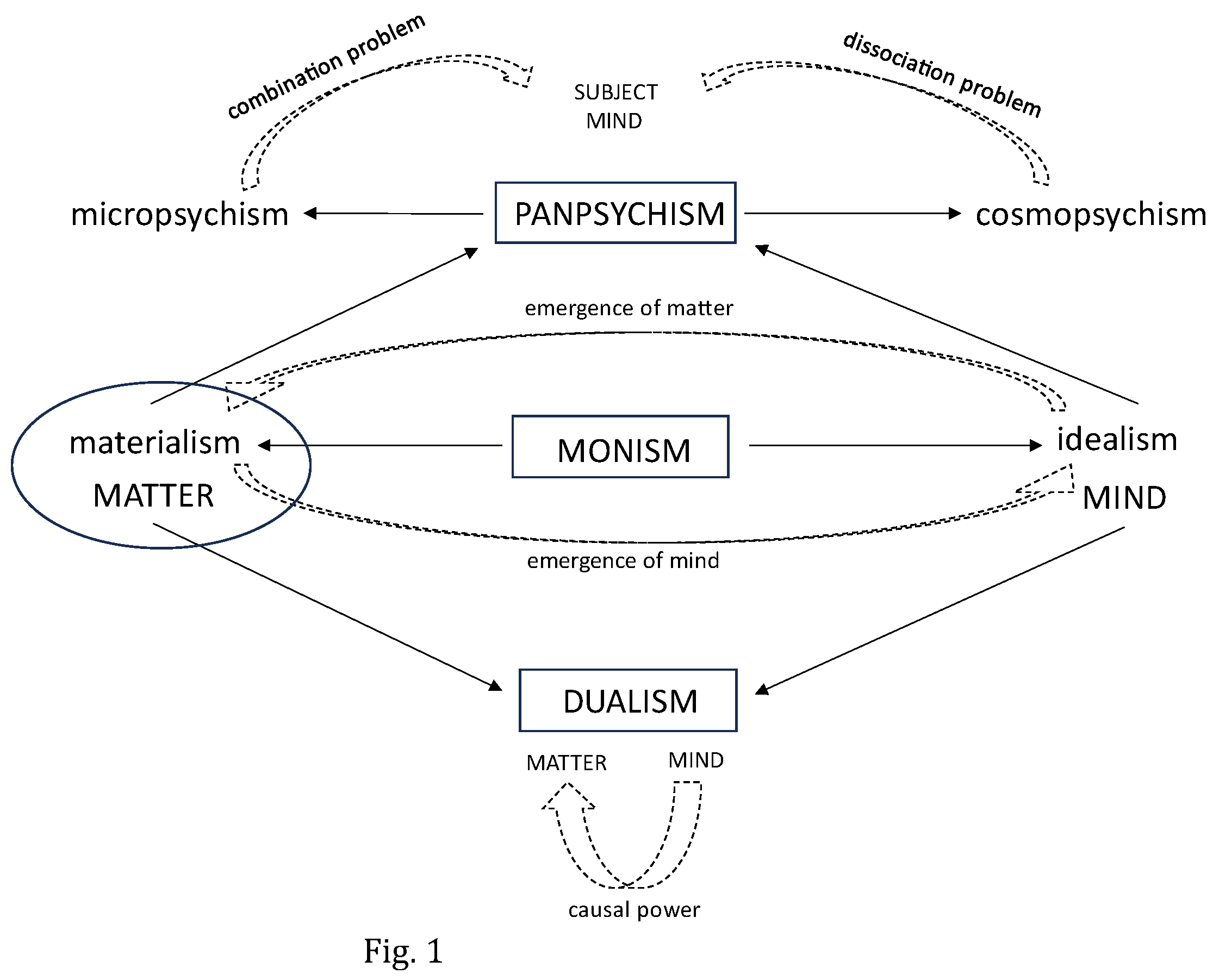
There is another monistic perspective for contemplating the world (see
Figure 1 for an interconnected summary of some of the most relevant philosophical theories facing up to the mind-body problem). This is idealism (Guyer and Horstmann, 2023), namely, the philosophical school in which the foundation of all reality is considered to be something mental (mind, thought, consciousness). Matter would be a derivative entity produced by consciousness. One of the main problems of idealism in its classical formulation is the risk of solipsism, namely, that the only sure thing to exist is the mind of the own thinking subject. Idealism could seem, at first sight, an old-fashioned philosophical scheme from the perspective of the down-to-earth scientist, however, there are some modern and invigorating descriptions of the world (Chalmers, 2022) that can be framed in this school and some of them could connect with certain anti-realist interpretations of quantum mechanics (Chalmers, 2022).
A natural way of avoiding the problems of monistic doctrines is dualism. This philosophical view assumes that the world is constituted by two fundamental elements: matter and mind. The central difficulty of dualism is the seemingly well-established causal closure of matter. The fact that every event in the physical world seems to have a material cause, what would leave no room for the interaction between matter and mind, therefore apparently making superfluous and irrelevant the existence of mind for the physical world.
In Eastern and Western philosophy, panpsychism (Goff, Seager, and Allen-Hermanson, 2022) was another salient option to solve the mind-body problem until the beginning of the twentieth century (Goff, Seager, and Allen-Hermanson, 2022). However, it has attracted a renewed interest as a promising solution in these last decades. In simple terms, panpsychism considers that mind or consciousness (perhaps in an elementary manner that could be named proto-consciousness) is essential and ubiquitous in the physical world. Among the many variants of this philosophy (see Goff, Seager, and Allen-Hermanson (2022) for an extensive discussion), two of them particularly representative are micropsychism, in which fundamental particles would have some kind of elementary subjective experience (i.e., microphysical systems would have mental states (Chalmers, 2021a)) and cosmopsychism, in which the universe as a whole would be a conscious entity (i.e., the universe would have mental states (Chalmers, 2021a)). Panpsychism in its different versions can soften the difficulties of the other philosophical views, but it comes with its own lot of problems: the so-called combination problem (Chalmers, 2021a; Goff, Seager, and Allen-Hermanson, 2022) for micro-panpsychism, namely, how to describe the generation of consciousness for a composite system in terms of the consciousness of the component subsystems, and the dissociation problem (Chalmers, 2021a; Kastrup, 2017) for cosmo-panpsychism, i.e., how and why the consciousness of a system is dissociated from the consciousness of the universe as a whole (Goff, Seager, and Allen-Hermanson, 2022).
A fundamental work of modern philosophy that can be considered as a contribution to panpsychism is Whitehead’s “Process and Reality” (Whitehead, 1929). The concept of proto-mental elements of reality introduced by Whitehead can serve as a base for a quantum-like treatment of panpsychism (see Khrennikov (2003) for a deeper discussion).
The philosophical system developed by Whitehead with its central concept of process as the cornerstone of its structure was mainly thought to answer the crucial questions that the new physics was posing to philosophers and scientists at the beginning of the twentieth century. However, this initial physical perspective would inevitably drive to the mind-body problem revealing a natural panpsychist component in the nucleus of Whitehead’s philosophical endeavour. In spite of the opinion shared by several scholars (McHenry, 1995; Seager, 2004) on the plausible panpsychist adscription of Whitehead’s philosophy, this view is the subject of some controversy. Whitehead himself was reluctant to admit the panpsychist imprint in his philosophy when overtly confronted with the question (McHenry, 1995). His reply to Victor Lowe was an elusive “Yes, and No” (McHenry, 1995).
Although physicalism in principle seems unable of solving satisfactorily the hard problem of consciousness, however, its paramount success in describing the observed universe largely justifies the sustained engagement entertained in modern science in order to find out a scheme that reduces consciousness to sheer material elements. A reflection of this engagement is the ample gallery of proposals ranging from the pure denial of the existence of consciousness, the assertion that consciousness is just an illusion (Frankish, 2016), going through the identity theory (Smart, 2022) that equates mental states to brain states, continuing with theories, like computational functionalism (Smart, 2022), that characterizes consciousness as a complex enough computational process that is independent of the nature of the material support, until reaching the most radical proposals contending that new physics is required for reducing consciousness to the function and structure of physical systems.
The boundary between philosophical views is somehow fuzzy, e.g., Tegmark’s physicalist theory holds that the ontology of the physical world is its mathematical structure (Tegmark, 2008), i. e., the equations describing the universal laws that govern the behaviour of matter. This perspective is not far from a platonist view. This fuzziness of frontiers can also be identified between panpsychism and dualism. The version of dualism named property dualism considers consciousness not as a substance, but as a non-physical property of matter what drastically reduces the differences with panpsychism.
The theoretical model that is going to be introduced in the next section can be classified, as will be discussed below, within the physicalist stream that incorporates new physics. Although, given its structure, some caveats may arise regarding its philosophical adscription, in the end it is claimed that this model can be catalogued as physicalist.
An extensive list of current theories for consciousness can be found in Chalmers (2023). A volume devoted to mathematical and empirical foundations of models of consciousness has been edited by Arsiwalla et al. (2023). Several approaches that propose quantum theory may contribute to understand consciousness have been surveyed by Atmanspacher (2024). Within the same domain, a set of articles studying the possible connections between consciousness and quantum mechanics have been edited by Gao (2022). An encyclopaedic effort for compiling a guide to explore the vast landscape of theories of consciousness has been accomplished by Kuhn (2024).
3. Model for Elementary Consciousness in a Fundamental Particle
A direct implication of quantum mechanics is that matter is more complex than envisaged in classical physics. The simple, classical characterization of the evolution of matter states, giving the temporal trajectory of a particle in its phase space is not adequate to describe the behaviour of matter at the microscopic level, mainly, whose greater complexity is already manifest in the required Hilbert space structure for the space of states of a system in quantum mechanics.
Perhaps the mind-body problem, as pointed out by Chomsky (2022), is not as much on the side of consciousness, as on the nature of matter that is not yet completely understood. The current situation for the problem of consciousness, as remarked by Chalmers (2021b), resembles the impasse at the end of the eighteenth century for describing electric phenomena in the conceptual framework of Newtonian mechanics. That deeply baffling state of affairs came to an end by incorporating a new intrinsic property, the electric charge, for characterizing matter.
Following these thought-provoking ideas, two main new elements are introduced in the model of consciousness that is going to be defined. First, it is assumed that matter has an intrinsic capacity of processing information what is captured in the information-theoretic characterization of a fundamental particle in DAQM (Baladrón, 2010, 2014, 2017; Baladrón and Khrennikov, 2016, 2017, 2018, 2019, 2023). Second, it is considered, as hypothesized by Chalmers (1995), that information might have two aspects: a physical facet and a phenomenal facet. The first aspect would coincide with its usual quantitative character, and the second one with a qualitative character of information that might constitute the basis for describing the emergence of experience from the physical (Chalmers, 1995).
The model is then developed elaborating these two basic assumptions. Accordingly, a fundamental particle
is characterized as a classical-like point mass with coordinates
in physical space, subject to the conservation of momentum and energy, and supplemented with an information space in which a classical Turing machine is included. In addition, a control program
, an anticipation module
, a randomizer
, and an information deleting subroutine
1 are stored on the information space of the particle. Now, if
, which is a classical algorithm, encoded the quantum mechanical formalism, then, as is discussed in the
Appendix2, the fundamental particle might behave as a quantum system in real time. In this way, the first requirement of the model, the fact that the particle has an intrinsic capacity of processing information, is fulfilled. The particle has been characterized as an agent whose behaviour is not determined by universal laws, beyond the conservation principles, but by the program that is stored on its information space. The possibility that a population of particles such as the characterized in this model might emerge under the action of Darwinian evolution from sheer classical-like particles supplemented with an information space and endowed with a classical Turing machine and just a randomizer
is analysed in the
Appendix.
The DAQM particles deeply resemble actual occasions --the elementary entities in Whitehead’s process philosophy (Whitehead, 1929)-- in its characterization as potentialities determined by past occasions. In DAQM, these past occasions would be programs and data stored in the information spaces of the particles, whose actualizations would result from the output generated by the control algorithm in response to the interaction with the environment or the measurement apparatus. The input or external data would condition the output, and therefore would dynamically determine the actual property of a particle, not as an intrinsic parameter of the particle, but as a magnitude that only takes a value when properly prompted by a specific environment or measurement apparatus. Thus, DAQM particles are not classical systems in the sense that they are not characterized by intrinsic properties (excluding the location of the particles) well defined at any moment in time, but, as actual occasions, are better characterized as processes, the combination of information and material processes, whose realization would be jointly determined by the inner state or past occasions and the input data or external state that characterizes the environment.
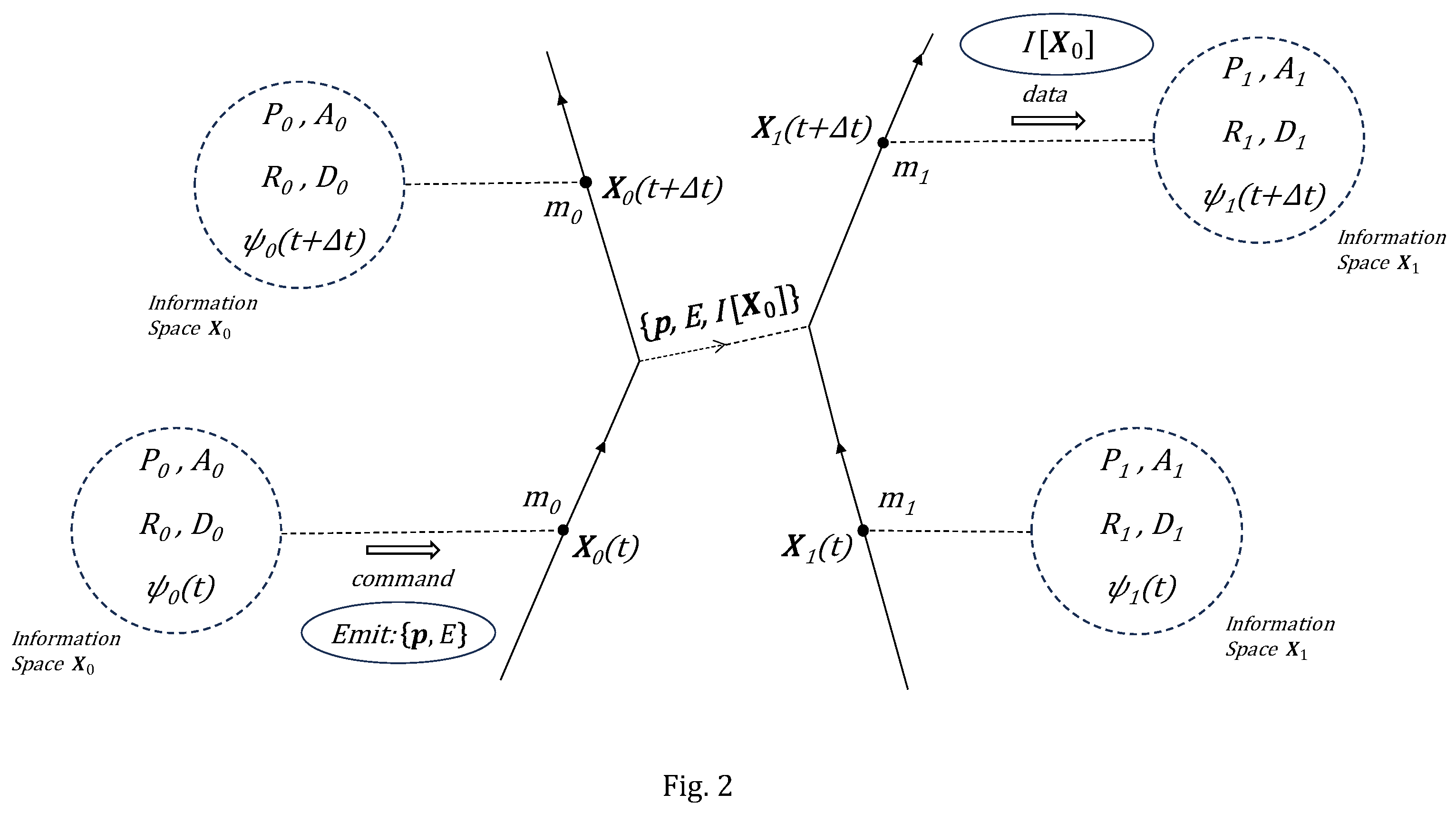
A generic interaction, in the framework of DAQM, between two particles with masses
and
, and space coordinates
and
is depicted in
Figure 2. Both particles are initially represented in physical space at time
. Their respective information spaces are drawn as dotted line circumferences encircling their respective control algorithms,
and
, anticipation modules,
and
, randomizers,
and
, information deleting subroutines,
and
, and wave functions,
and
, at time
t.
After a run of the control program
on the information space of the particle
, a command of emitting an information carrier of momentum
p and energy
E is sent to the particle
. As a consequence, the trajectory of the particle (straight solid line associated with the particle
in
Figure 2) changes according to the conservation of momentum and energy, and the wave function
ψ0(
t +Δ
t) at time
is computed.
When the emitted carrier impinges on the particle , the carrier is absorbed by the particle, the new trajectory of the particle is determined by the conservation of momentum and energy, and the information about the emitting particle that is transported by the carrier arrives at the information space of the particle . The wave function ψ1(t +Δt) at time t +Δt for the particle has been calculated by the algorithms on the information space of the particle .
The current carriers of momentum, energy and information in DAQM would be the field bosons in the Standard Model. In particular, considering for simplicity an ensemble of electrons, these carriers would be photons. Hypothetically, the fundamental particles of the Standard Model should have emerged as the fittest physical species in the Darwinian evolutionary complex dynamics in which quantum mechanical behaviour would encode the optimal strategy for the survival of the populations of information-theoretic fundamental particles. These particles would attain a dynamic stability characterized by an average mass and a set of classical algorithms in their information spaces that were able to emulate quantum behaviour in real time as a consequence of the initial conditions at the Big Bang and Darwinian evolution under natural selection acting on these information-theoretic classical-like particles that at time
were exclusively controlled by the individual randomizers stored on the information spaces of every particle. As mentioned, the feasibility of this scenario is discussed in the
Appendix.
In this DAQM model, like in Bohmian mechanics (Goldstein, 2021; Hoffman and Vona, 2014) and in de Broglie’s theory of the double solution (de Broglie, 1963), position is the realist physical parameter that characterizes the particle at any time. The trajectory of the particle in physical space is a continuous function (straight solid lines in
Figure 2). In this sense, the measurement problem is solved like in Bohmian mechanics. At any time, the positions of all the systems involved in the process are well defined.
The DAQM model might be considered a sort of generalized Bohmian mechanics, but in which nonlocality has been removed thanks to the supplementary information spaces ascribed to every particle and the development of anticipation modules on them. In this Bohmian picture of the DAQM model, the prescribed trajectory of a particle given by the guiding equation would coincide with the trajectory generated by the emission of the photons sequence as computed by the control program on the information space of the particle. In particular, the model considered in this article should be compared with the variant of Bohmian mechanics that defines the wave function as a purely epistemological object, and even in more precise terms, the Bohm-Vigier stochastic version (Bohm and Vigier, 1954) including a random term in the guiding equation would properly match the action of the randomizer on the dynamics of the particle.
The second main element of the model is the central hypothesis characterizing consciousness. It is assumed that the qualitative, phenomenal aspect of information is an intrinsic property of matter that generates an elementary conscious event in any fundamental particle when the branches of the wave function that become, for all practical purposes, irrelevant for the dynamics of the particle are erased on its information space. In other words, this elementary conscious event occurs when the wave function
of the particle effectively collapses. The core of the model is then the assumption that when the superfluous information for the dynamics of the particle is erased on the information space, i.e., when the collapse of the wave function irreversibly
3 happens, then a subjective experience is induced on the particle
corresponding to a representation of the estimated sharp locations {
} of the surrounding systems,
, (that are not necessarily the actual positions {
} of such surrounding systems,
) as calculated by the program stowed on the information space of the particle
.
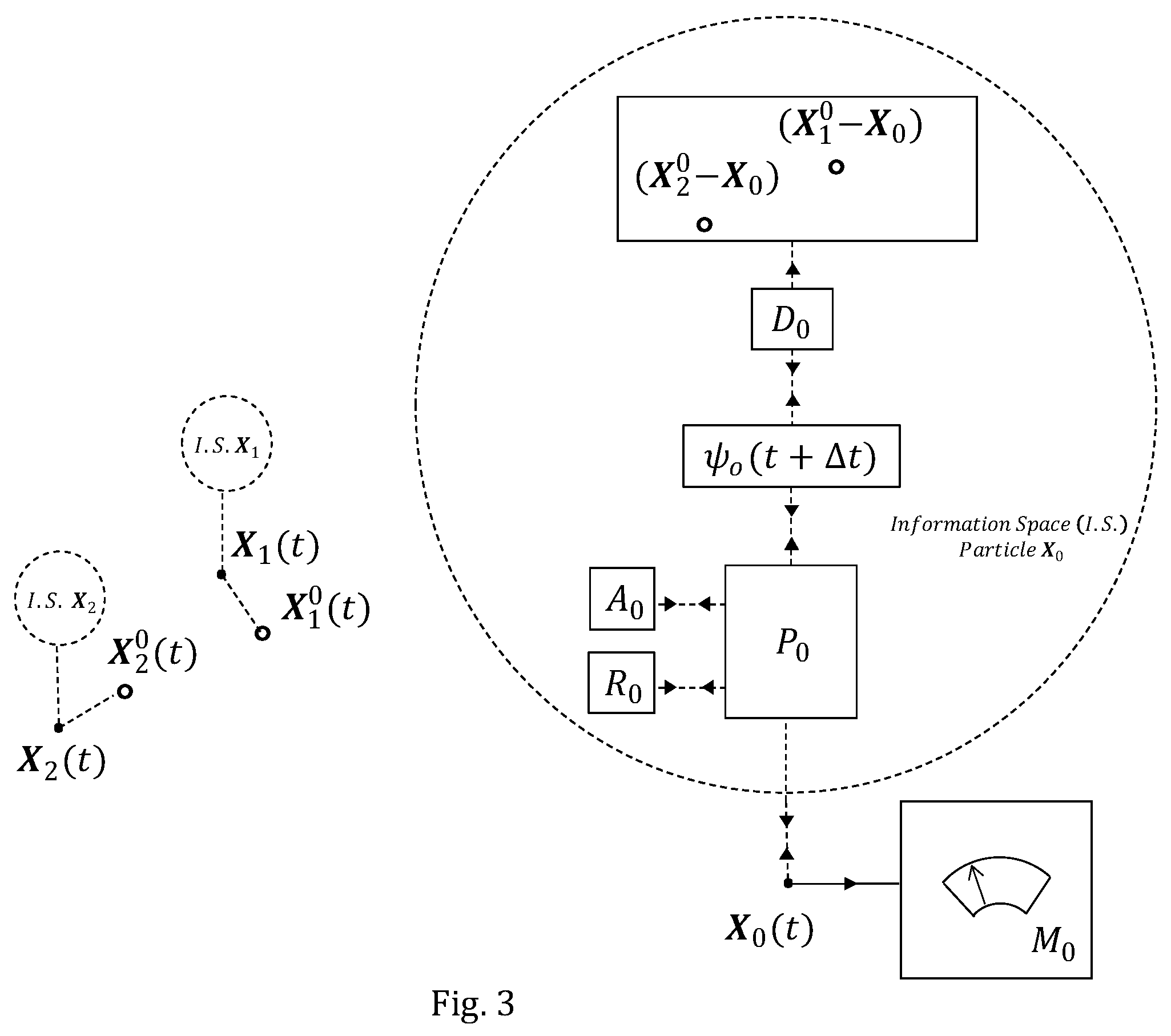
An example of the generation of an elementary conscious event for the particle
surrounded by two particles (
is represented in
Figure 3. The particle
at time
t is surrounded by two other particles located (black dots) at
and
. The information spaces of the particles are represented by dashed line circumferences. At time
t, the particle
is measured by the device
. This implies that only the branch of the wave function
whose support contains the actual location of the particle is meaningful for the dynamics of such particle
. Therefore, the empty branches of the wave function
computed by the control algorithm
are deleted by the subroutine
, and according to the model an elementary conscious event is generated on the particle
, corresponding to the spatial representation of the calculated positions on the information space of particle
of the surrounding systems (
and
). These calculated positions are drawn in
Figure 3 as empty dots, and, in general, they do not coincide with the actual locations (
and
) of the particles. The perspective of the representation (the subjective experience) corresponds with the position occupied by the particle
.
Consciousness, in this model, is considered as part of a process, much in the like of Whitehead’s philosophy of organism (Sulis, 2025; Whitehead, 1929, 1933). A connection can also be established with the concept of mediation, in the sense discussed by Taguchi (2022), considering consciousness, in the present microscopic model, as a kind of mediation between the world and the particle, between the objective property of the world, systems’ locations, and its subjective representation on the information space of the particle.
4. Measurement, Observation, and Wigner’s Friend-like Scenarios
The measurement problem in this model is solved as in the de Broglie-Bohm theory (de Broglie, 1963; Goldstein, 2021; Hoffman and Vona, 2014), given that particles have well-defined positions at any time
4, and that all systems, even macroscopic systems and measuring apparatuses, can be characterized as constituted by quantum particles. Therefore, in this model as in the de Broglie-Bohm theory, a measurement is just a particular kind of interaction that results in the effective collapse of the wave function of a system when interacting with a measurement device, that is defined as a system whose possible configurations after an interaction are macroscopically distinguishable, like different directions for a pointer (Hoffman and Vona, 2014). The interaction between the system and the measurement apparatus reduces, for all practical purposes, the overlap of the different terms of the system’s wave function to negligible values, what implies that only the branch of the wave function whose support in the configuration space contains the actual location of the system retains its dynamical relevance.
When the effective collapse is induced, according to the introduced model, the dynamically superfluous branches of the wave function are deleted on the information space of the system, triggering the computation by the control program of the estimated positions of the surrounding systems, and generating an elementary conscious event that constitutes an elementary observation of its surrounding world by the system. Therefore, if a system is measured at time , this system is an observer at time .
If the observer system is a fundamental particle, then the information that is contained in the observation is stored on the information space of the particle, but this information cannot be shared with or communicated to other systems, unless the particle and such systems become entangled.
Note that in this model measurement and observation are two different processes. A measurement is a specific, well-defined kind of interaction that drives a system to the effective collapse of its wave function, and an elementary observation is a register of estimated information about the locations of the surrounding systems of the observer that is stored on its information space and associated with an elementary subjective experience of the observer caused by the erasure of the dynamically superfluous branches of its wave function that irreversibly completes its effective collapse.
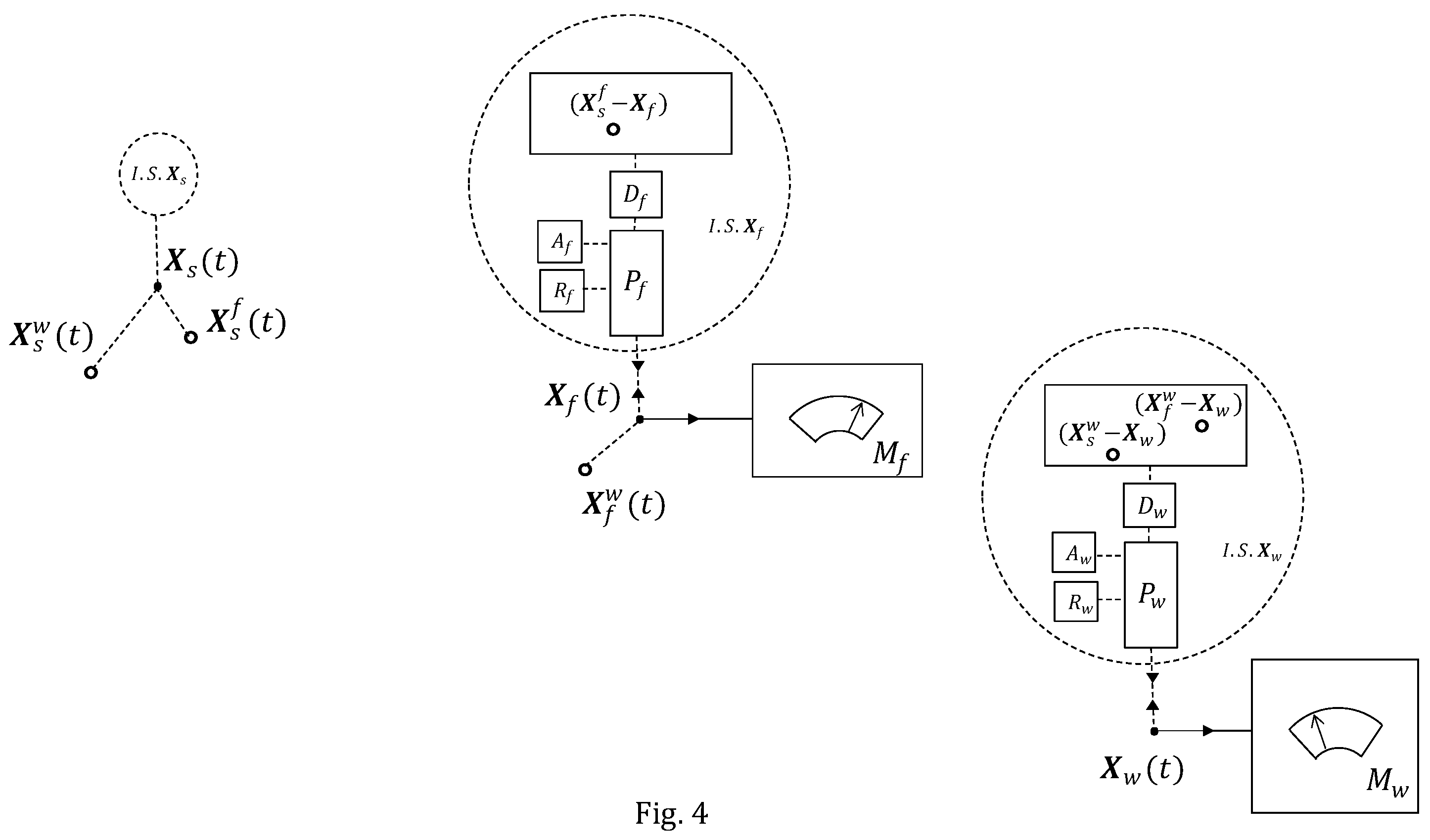
In this model, fundamental particles are qualified as elementary Wigner’s friends (Wigner, 1961) since fundamental particles are characterized as elementary conscious observers. Therefore, an elementary Wigner’s friend-like scenario (see
Figure 4) may be constituted by three particles, the test particle
whose position is going to be observed by the second particle
, the Wigner’s friend, and finally a third particle
that plays the role of Wigner as a system that observes the composite system
5 formed by particle
and particle
. Every fundamental particle in DAQM is supplemented by its information space (dashed-line circles in
Figure 4). In order to be observers and register the observations, the wave functions of particles
and
must be effectively collapsed at the moment of the respective observations. This can be achieved by conveniently disposing measurement apparatuses acting on
and
. The result of the observation of the particle
at time
t performed by the particle
will be
, as calculated by the program
controlling particle
, meanwhile the observation of the particle
by the particle
will be
, as computed by the program
on the information space of
. The actual position of particle
at time
t being
.
The observations are associated with subjective believes (estimations) of every observer about the real, well-defined, objective location of a particle. Consequently, it is natural to expect different assignments of the same observed particle’s position from different observers. Therefore, there is no contradiction in elementary Wigner’s friend-like scenarios within the framework of DAQM, so that the existence of a realist, unique world in which every particle has an objective position is compatible with the observation from different systems of unequal locations at time t (and, accordingly, hypothetical unequal properties) for the same observed particle.
Is this conclusion applicable to usual macroscopic Wigner’s friend scenarios? In order to answer this question, it is necessary to properly describe the process through which consciousness is formed in composite systems whose different parts are in turn individually conscious. This is known as the combination problem and is discussed in the following section.
5. The Combination Problem: Generating Consciousness in a Composite System
Let us consider two initially independent particles characterized in DAQM by their respective average masses, positions, algorithms, and wave functions (see
Figure 5 for a graphical representation). In DAQM, the entanglement of these two particles is defined as the process in which non-classical correlations are established between the particles by mutually copying the algorithms and data stored on their information spaces. This mutual copying enables each particle to compute on their respective information spaces the entangled wave function of the compound system that results from the entanglement process. This definition implies an entirely local characterization of entanglement (Baladrón and Khrennikov, 2019) thanks to supplementing every particle with an information space in which a randomizer and a module of anticipation are stored (see the
Appendix for a deeper discussion).
When a measurement is performed on the composite entangled system as a whole, a conscious event is induced on the entangled system (see
Figure 5). At the moment in which the erasure of the irrelevant information for the dynamics of the compound system happens, the representation of the estimated configuration of the surrounding particles is projected onto the perception screen of each particle that constitutes the entangled system. This representation is identical for both particles and consists in the estimated position of the surrounding particles as calculated by the algorithms and data of both particles that are simultaneously stored on both information spaces. It is postulated that the perspective of the representation (the origin of coordinates) is taken from the mass centre of the system, therefore, playing the role of the proto-experiential point of view of the system (a kind of elementary Cartesian theatre that is located in the set of information spaces of the entangled systems). Notice that the key element of the model is again the postulated assignment of precise information processing capacities to matter, and their role in the dynamics of the particles what endows information with an explicit physical status.
This DAQM model for consciousness seems to solve satisfactorily the combination problem through entanglement. Entanglement, as no other phenomenon, fits in with the generation of the identity of a composite, new system that cannot be reduced to the addition of the individual properties of the parts. The entangled system is described in terms of the correlations between both particles. Every component particle can no longer be characterized separately. In most interpretations of quantum mechanics, both particles, their individual properties, seem to dissolve into the compound entangled system whose state is determined by the correlations between the constituent particles.
In the defined DAQM model of entanglement, the two subjective experiences of two initially independent particles would be transformed into the subjective experience of a new objective system formed by those two particles that are now entangled. The phenomenal experience of the new-formed entangled pair would not be reducible to the addition of the individual experience of the two previously independent parts.
The possibility that entanglement solves the combination problem has already been proposed in previous studies (Chalmers,2017; D’Ariano and Faggin, 2022). The concept of entanglement looks tailored to accommodate the generation of consciousness in a compound system whose constituents were themselves independently conscious prior to the entanglement.
The hard core of the combination problem seems to admit a solution by means of the concept of entanglement. However, an essential problem persists associated with the apparently required isolation of the entangled system in order to preserve the correlations within the system from the perturbation caused by the interaction with the environment. The fragility of entanglement entails a major difficulty in the scaling up of the process when increasing the number of entangled particles within complex macroscopic biological systems. In principle, the usually complex, wet, and hot environment that is generally needed by biological systems to stay out of equilibrium in order to maintain their structures and functions (Marais et al., 2018) seems to imply extremely short decoherence timescales for collective states of ions involved in the firing rate of a neuron. A reported estimation (Tegmark, 2000) of this decoherence timescale ) was many orders of magnitude shorter than the firing timescale (Ritchie, 1995)) of a neuron. A similar conclusion was drawn for estimated decoherence timescales of neuron microtubules processes (Tegmark, 2000)) in relation to the dynamical timescale ( (Satarić, Tuszyński and Žakula, 1993)) of a microtubule excitation (excitation traversing time of a short tubule).
Short decoherence timescales in comparison with typical dynamical timescales for neuronal activity might be considered, in principle, detrimental to the option of grounding a physical description of consciousness in composite systems on quantum entanglement.
However, based on more recent studies (Hameroff and Penrose, 2014) that consider detailed stipulations of the Penrose-Hameroff theory of consciousness (Hameroff and Penrose, 2014) for the calculation of the decoherence timescale of excitations in neuron microtubules, it has been claimed (Hameroff and Penrose, 2014) a drastic increase in the estimated decoherence timescale (, see Hameroff and Penrose (2014) and reference therein). These results, as suggested by Hameroff and Penrose (2014), in addition to the extraordinary advance of quantum biology (Marais et al., 2018), unveiling the relevance of quantum phenomena in explaining fundamental functions of biological systems that cannot be satisfactorily described by classical physics, pave the way for future theoretical and experimental studies that might clarify whether quantum coherence is a central concept for describing consciousness in complex biological systems.
6. Doing-Otherwise Mechanism in DAQM: Consciousness Backaction on Physical Space
Consciousness as defined in the DAQM model until now seems to be an epiphenomenon, i.e., a side effect with no causal role in the physical realm. The apparent causal closure of the physical world suggests that the backaction of consciousness on matter, if any, ought to be an elusive process. In DAQM, a natural extension of the model of consciousness consists in introducing as backaction of a conscious event the transfer of the particle’s control from the original main program
to an alternative second program
that could either directly return the control to the program
or lead to a different self-interaction output when a conscious event has happened (see
Figure 6). This would be associated with a different computational route activated as a consequence of the conscious state. This alternate algorithm
endows the particle with the capacity of doing otherwise, and it constitutes a backreaction on the physical particle from the information space when an elementary event of subjective experience takes place, giving consciousness a definite influence on the material world.
However, the physical action caused by conscious events on a fundamental particle should not be distinguishable from the usual quantum behaviour predicted by the standard quantum formalism and observed in experiments. That is to say, the sequential outputs generated by the particle must be in accordance with the standard quantum behaviour of the particle either conscious events have occurred or not. Therefore, the physical action caused by conscious events on the system should be only distinguishable in the long run, i.e., in the evolutionary trajectory on the fitness landscape of possible control algorithms for a population of fundamental particles, and consequently the backaction of conscious events on matter should be only distinguishable within meaningful evolutionary time scales.
This capacity of doing otherwise might constitute a central mechanism for speeding up evolution. The reasoning is as follows. Having a set of alternative strategies (that are coded in the program
) starting from a common original control algorithm
enables the system to probe different close paths on the landscape of possible algorithms that control the behaviour of the particle. This structure might resemble the ‘regeneration process’ described by Chatterjee et al. (2013) in the framework of a theory for estimating time scales of evolutionary trajectories in biology. As studied by Chatterjee et al. (2013), this ‘regeneration process’ which requires that the starting sequence (whose key variable is its length) that undergoes adaptation –the equivalent entity in DAQM would be the particle’s control algorithm
-- both be close to the target sequence (i.e., the number of different bits, for binary sequences, between the considered two sequences be small) and can be generated repeatedly would allow biological evolution to overcome the exponential barrier and work in polynomial time (see the
Appendix for a more detailed discussion).
Further studies must be accomplished in order to check the validity of the analogy established between the results obtained by Chatterjee et al. (2013) for evolution in biology with the hypothetical doing-otherwise mechanism considered in the DAQM model of consciousness, but it seems a mechanism that is worth exploring given that it enables consciousness to play a causal role in the physical world preserving at the same time the agreement with the predictions of standard quantum mechanics and the observed experimental results.
7. The Road from Elementary Microscopic Proto-Consciousness to Consciousness in Complex Biological Macroscopic Systems
The possible central role played by evolution in the generation of consciousness in complex biological systems, in particular in human beings, has been analysed by several authors (e.g., see Humphrey (2023) and Jablonka and Ginsburg (2022)). The main target of the model of consciousness in DAQM is to study the possibility that Darwinian evolution might generate high-level consciousness in complex biological macroscopic systems starting from elementary proto-consciousness events as characterized in information-theoretic DAQM fundamental particles. A first fundamental difficulty would be to determine if high-level consciousness, with all the variety and richness of phenomenological subjective experience related to sensations and feelings, might be described in terms of elementary proto-consciousness events associated with the subjective experience of the locations of the surrounding systems
6. These problems, however daunting they might be, can be categorized as “weak problems” (à la Chalmers (1995)) in comparison with the “hard problem” of consciousness (Chalmers,1995). Leaving aside the extraordinary scientifical and technological difficulty associated with these endeavours (the “weak problems” of consciousness), an initial discussion of the plausibility of the main target of the model, taking into account its features analysed in the previous sections, can be considered.
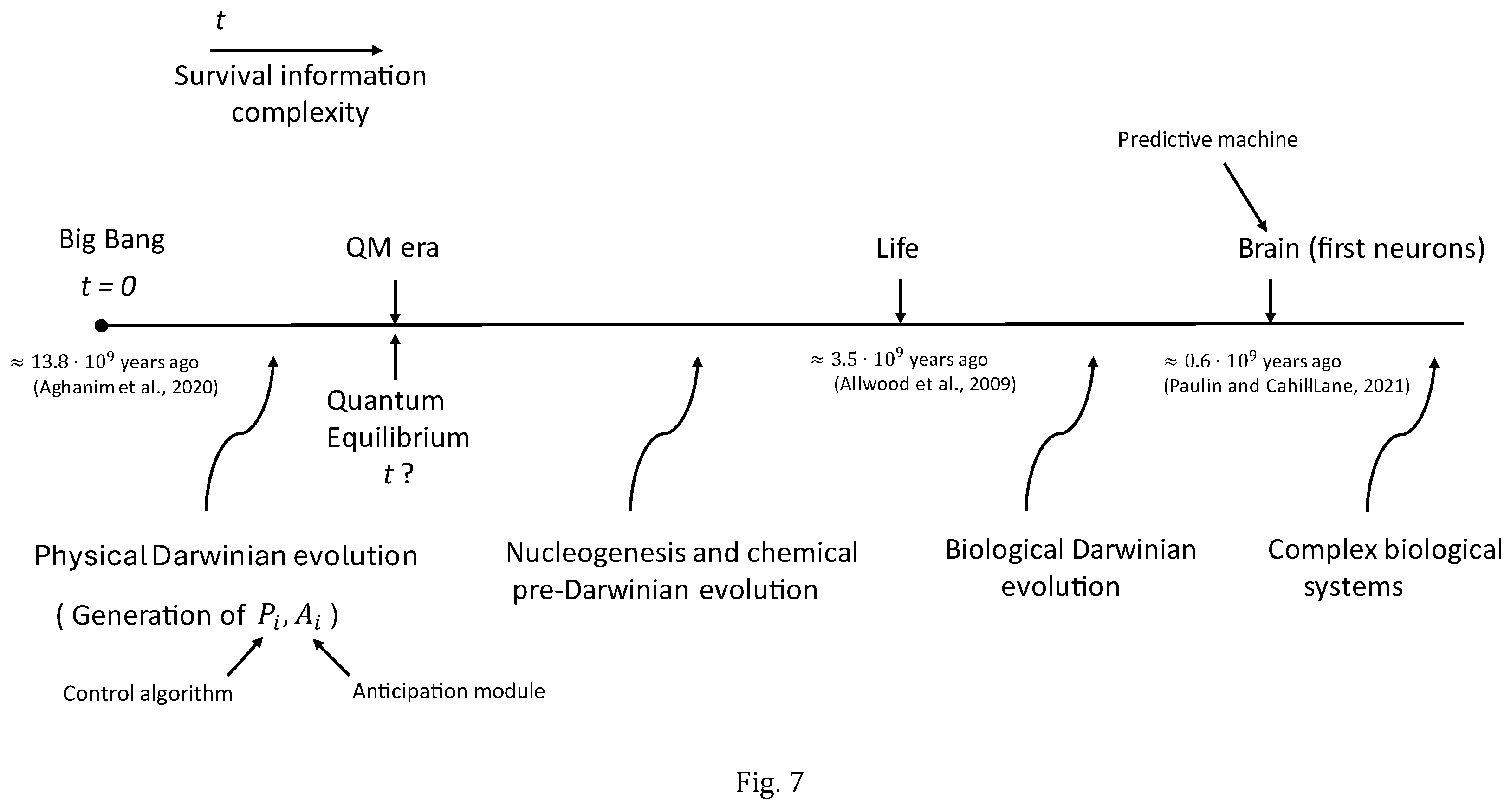
The characterization of fundamental particles in DAQM as systems that can store and process information, which in turn explicitly possesses causal power on the dynamical behaviour of the physical particles, makes these DAQM particles susceptible of Darwinian evolution, transforming the initial random behaviour of the particles (see
Figure 7) that are exclusively controlled at
by the randomizers stowed on their information spaces into quantum behaviour as the classical algorithms (
that progressively take control of the dynamics of the particles are generated by the action of Darwinian evolution under natural selection.
The plausibility of achieving a quantum equilibrium regime in which most particles in the universe were controlled by algorithms coding the rules of quantum mechanics, and generating quantum behaviour of matter in real time according to the Standard Model is further discussed in the
Appendix. However, three remarks are worth highlighting.
First, as mentioned in
Section 3, a fundamental assumption of DAQM (Baladrón and Khrennikov, 2023) is that although evolution in the short time (or microevolution) that is determined by fitness is fundamentally random due to the random mutations in the control algorithms of the particles as fundamental mechanism of variation, however evolution in the long run (or macroevolution) has a direction that is determined by the increase of complexity, in particular by the increase of the so-called survival information complexity (see the
Appendix for a mathematical definition of this magnitude) that measures, on the one hand, the capacity of a system for predicting the locations of the surrounding systems and, on the other hand, the capacity of such system for being stealthy, i.e., for minimizing the accuracy of the surrounding systems when foreseeing the position of the referred system. This function seems to gauge the quality of the information flows against survival, characterizing the fundamental general properties of a strategy for optimizing the possibilities of survival for a system.
Second, the DAQM description of the physical world recovers a rational characterization of matter behaviour even at the microscopic level. The experimentally demonstrated violation of Bell inequalities for certain systems configurations is reconciled in DAQM (Baladrón and Khrennikov, 2019) with the simultaneous existence in nature of the properties of realism (a particle has at any time a well-defined space position), causality (every non-random event has a previous cause, and the persistence in nature of random events is caused by Darwinian evolution), and locality (the speed of light is the limit for the propagation of any physical influence). These points will be further extended in the
Appendix. The weirdness of quantum mechanics is demystified in DAQM (Baladrón, 2010, 2014, 2017; Baladrón and Khrennikov, 2016, 2017, 2018, 2019, 2023) as resulting from two main elements, the in-flight calculation of the properties of a system on the information space, what explains that the result of an experiment can only be asserted when such experiment is actually performed (Peres, 1978), and the anticipation module that is the central element responsible for the non-classical correlations in Bell inequality violation experiments. The conclusion is that the systems that persist in the universe present quantum behaviour and that this behaviour is generated by Darwinian evolution under natural selection acting on populations of information-theoretic classic-like particles.
The third remark on the possible Darwinian evolution of physical systems refers to the hypothetical role played by proto-consciousness, as defined in the DAQM model for a particle, in such evolution. As previously discussed in
Section 6, proto-consciousness might accelerate the pace of evolution becoming a crucial element in explaining the transformation of an exponential problem in time, in terms of computational complexity, into a polynomial problem in time (see the
Appendix).
In DAQM, physical evolution plausibly saturated (see
Figure 7) or nearly stopped when the quantum equilibrium state was attained in the universe
7. After achieving the quantum equilibrium regime, the nucleogenesis and the synthesis of chemical compounds in the universe would be satisfactorily described by the Standard Model. The formation of heavier composite systems that in adequate environments (as presumably the Earth around 3.5 billion years ago (Allwood, 2009)) would plausibly lead to the appearance of macromolecules (chemical pre-evolution as analysed in modern chemistry (Chen and Novak, 2012; Eigen, 1971)) and ultimately life might be satisfactorily described by the increase of survival information complexity in the framework of DAQM. From this perspective a primordial alive entity would be characterized by its capability of storing and processing information (with causal power on matter) on physical parts of a system that would be able to maintain (metabolism) and replicate (inheritance) its structure and functions. The causal capacity of the information stowed on chemical compounds should now be reducible in DAQM to the causal power of the information stored on the information space of all the fundamental particles that constitute the chemical compounds. Thus, the agency of biological organisms would be a direct consequence of the postulated agency of fundamental particles in DAQM, removing one of the main difficulties in explaining the origin of life (Walker and Davies, 2013) and its early arising on Earth. Therefore, life in DAQM would be a natural result of the assumed evolutionary characteristics of matter, representing a phase transition determined by the increase in survival information complexity that drives Darwinian evolution in the long run as hypothesized in DAQM.
Biological Darwinian evolution would then start after the pre-evolutionary chemical epoch and the subsequent emergence of life. Assuming again for biological evolution as previously for physical evolution that the increase of survival information complexity would determine the direction of evolution in the long term, the development in biological systems of an anticipation module (see
Figure 7) now built with physical elements is straightforwardly implied from the definition of survival information complexity (see the
Appendix for its mathematical characterization). But precisely some modern theories (Clark, 2023, Friston et al., 2017; Kuhn, 2024; Seth and Bayne, 2022) characterize the brain as a predictive machine that builds models of the world around and of the self in order to monitor the differences between perceptual expectations and sensory inputs. The brain would work as an anticipation module in physical space for complex biological systems.
There is still a second crucial element involved in the definition of survival information complexity. It is that taking into account the characterization of quantum entanglement in DAQM (see
Section 5 and the
Appendix), the survival information complexity in a collection of particles would be increased by the entanglement of those particles. Therefore, not only the generation of a predictive physical system would favour the increase of survival information complexity, but also the spread of entanglement between the parts of that system, implying the raise of consciousness in the compound system as a whole, as it was discussed in
Section 5 when analysing the solution of the combination problem in the DAQM model of consciousness. It then seems reasonable to ponder the value of the survival information complexity (more precisely, of a term of the survival information complexity -see the
Appendix-) of a system as an adequate index to measure its degree of consciousness. However, there is a serious issue associated with the difficulty of calculating that magnitude beyond some extremely simplified modelled systems.
Summarising, consciousness in a complex biological system might be scaled up as a flow of conscious events on a dynamic quantum network constituted by a changing entangled collection of inter-neuronal components. This would require that brains were entanglement-protecting containers in spite of being wet and hot tissues in order to sustain consciousness. As pointed out in
Section 5, the Penrose-Hameroff theory (Hameroff and Penrose, 2014) proposing that microtubules might hold long range quantum coherence has received an extraordinary support in some recent experiments (Khan et al., 2024), and could explain the mechanism by which quantum coherence might be the basic phenomenon sustaining consciousness in complex biological systems.
The way in which the quantum coherence dynamical network, i.e., complex consciousness, and its interaction with the classical cognitive structure of the brain, plausibly at the interneuron level, are built, in addition to the interplay between the conscious and unconscious processes, are arduous problems to be investigated in the future.
The DAQM model leaves open the possibility that a future artificial general intelligence might be conscious since proto-consciousness is an intrinsic property of matter as hypothesized in DAQM. But the key point, from the present perspective, seems to be connected not only with the enormous difficulty of artificially developing complex enough quantum coherence dynamical networks, presumably necessary to give rise to high-degree consciousness in the framework of DAQM, but, in addition, with the development of adequate environments being able to protect that hypothetically huge quantum networks. These procedures seem to be completely out of reach for the present technological state of the art.
There is still a central question to be considered. How does consciousness act on matter in complex biological systems? As it has been already discussed for microscopic systems, the action of consciousness on matter in complex biological systems might be confined to accelerating the pace of evolution in the long run. However, a possible second crucial manner of action at the macroscopic level is especially interesting. The structure of the DAQM model based on anticipation opens up a new possibility of explaining free will in complex biological systems in a genuine compatibilist line. The main idea is that the free decision making would come from the future
8, more precisely from an anticipated future, but without violating the classical principle of causality, since in the doing-otherwise module (see
Figure 6) a self-referential model of the decision making structure of the system (a self-anticipating subroutine of
that by extension may be named
) might be built through the action of Darwinian evolution under natural selection. The construction of this self-referential subroutine would be equivalent to acquire self-awareness by the system. In this mechanism, the free-will decision event would be determined by asking from the control program
to the self-referential predicting module
what decision will be made by the own system in the immediate future. In this way, free will might constitute a real, definite survival advantage for a complex biological system.
8. Conclusions
A model for proto-consciousness as an intrinsic property of matter has been introduced. The model in turn is based on a characterization of fundamental particles as classic-like systems supplemented with an information space with the capacity of storing and processing information, and interacting with the bare particle in physical space through commanding the emission of carriers of momentum and energy (photons when the considered fundamental particles are electrons) calculated by the particle’s control algorithm. This structure transforms the fundamental particles into information-theoretic Darwinian systems susceptible of evolution under natural selection. In this physical framework, which might plausibly reconstruct the observed quantum properties of fundamental particles as is discussed in the
Appendix, the characterization of proto-consciousness as a microscopic intrinsic property of matter associated with the irreversible erasure of dynamically superfluous information conveyed by a particle on its information space is naturally incorporated.
The model of proto-consciousness that might initially be catalogued as a panpsychist model, given its characterization as a fundamental intrinsic property of matter, however, it might also properly be considered as a physicalist model because of its natural assembly into the physical structure of matter without modifying the predictions of the quantum formalism, and at the same time dissolving most of the difficulties associated with the long-standing conundrums in the foundations of quantum mechanics. In this sense, proto-consciousness might be incorporated as a new property in the list of fundamental entities and intrinsic properties that constitute the set of elements defining the ontology of the physical world.
The DAQM model of consciousness allows for a clear-cut resolution of the process of measurement (one of the deepest problems in the foundations of quantum mechanics) in the line of the de Broglie-Bohm theory and the model also introduces a precise definition of the process of observation by identifying the conditions that qualify a physical system as an observer. Therefore, the DAQM model of consciousness is a reductionist scheme that would describe any kind of physical process (potentially extensible to any kind of biological or cognitive process) in terms of quantum mechanical properties and interactions excluding the necessity of introducing (among other options) classical macroscopic systems (or, in general, systems out of the quantum realm, i.e., non-describable as mere compounds of fundamental physical particles) as fundamental elements in order to characterize a measurement or an observation.
To check the consistency of the DAQM model of consciousness, it has been applied to describe simplified basic Wigner’s friend-like scenarios in which the observers are the most elementary systems being eligible as observers (i.e., fundamental DAQM particles under the defined right conditions). These Wigner’s friend-like scenarios can be tagged as Gedankenexperiments since the considered elementary observers lack the capacity of communicating between them. The model accounts for the compatibility of the existence of one universe in which every fundamental particle has a well-defined position at any time with the possibility of apparently incongruent observations corresponding to different assignments, made by the particle playing the role of Wigner’s friend and the particle in the role of Wigner himself, referring to the position occupied by the observed system.
The model is also able to give a satisfactory solution to the combination problem for the generation of consciousness in a composite system. The set of individual consciousnesses of the constituents is transformed into the high-level consciousness of the compound in which the initial individual identity of the components is dissolved into the resultant collective entity characterized by the correlations among the constituents through the quantum entanglement as modelled in DAQM.
Quantum entanglement gives rise to a cogent description of the consciousness formation process in compound systems, but the question of how this process is implemented in the brain of complex biological systems immersed in hot and usually highly interconnected environments is raised. Recent experiments (Khan et al., 2024) have yielded promising results in which the presence of long-range quantum coherence in neuron microtubules, as was predicted in the Penrose-Hameroff theory (Hameroff and Penrose, 2014), has been detected.
A possible sketchy scenario of the evolution of the universe from the Big Bang, assuming as basic ontological entities information-theoretic fundamental particles, as characterized in DAQM, therefore, susceptible of experiencing Darwinian evolution under natural selection, has been briefly discussed. The plausible emergence of quantum behaviour in matter from the assumption of these initial random-behaved, classic-like, Darwinian fundamental particles is analysed. The picture arising from DAQM would alleviate most of the interpretational problems in the foundations of quantum mechanics by assuming both that matter possesses the intrinsic capacity of storing and processing information, and that information reciprocally has a fundamental causal control on matter. As mentioned, the approach in physical terms resembles in many respects a generalization of the de Broglie-Bohm theory, but with the additional asset of eliminating non-locality through the anticipation capability of systems developed by the action of Darwinian evolution under natural selection. On the biological side, the model might constitute the germ for explaining both the emergence of life in a continuous, natural way and the mechanism for the generation of high-level consciousness in complex biological systems with its elaborated agent attributes.
The mathematical analysis of DAQM is far from being completed, however, the expectations of the model seem to justify continuing its study. In particular, the interest of investigating the possibility of efficiently simulating quantum behaviour on classical Turing machines is supported by the recent stunning advancements in artificial intelligence (AI) exemplified by the computational development of the neural network-based model AlphaFold (Jumper et al., 2021) that is able to efficiently predict the correct folding of proteins within the astronomically large space of possible three-dimensional structural states from its one-dimensional amino acid sequences. Exponentially complex structural problems in quantum chemistry seemed to be the specific domain reserved to the application of the future quantum computer since the quantum advantage was patent in this type of computation. However, AlphaFold has deeply changed the perspectives on the plausibility of developing efficient computational procedures for applying classical Turing machines to the resolution of quantum problems originally considered out of their scope (Hassabis, 2024).
At the price of both assuming information processing capabilities in matter, what presents the positive counterpart of endowing information with an unequivocal physical character, and postulating proto-consciousness as an intrinsic property of fundamental particles, not only might the development of the DAQM model satisfactorily integrate high-level consciousness to the physical world, but also account for the deep conceptual issues of quantum mechanics in a rational, compelling manner, and to a great extent reduce the difficulties in understanding life and its early appearance on Earth.
Appendix A. Overview of the Darwinian Approach to Quantum Mechanics (DAQM)
The first strong hypothesis on which DAQM (Baladrón, 2010, 2014, 2017; Baladrón and Khrennikov, 2016, 2017, 2018, 2019, 2023) is built relies on the assumption that matter has an intrinsic capacity for storing and processing information. This hypothesis is articulated through a model of a fundamental particle that consists in two interacting elements. First, the bare classic-like particle in physical space characterized by its position and mass, and subject to the principles of momentum and energy conservation. And second, an information space attached to the physical particle that stores the information that transport the physical carriers (photons if the particle is an electron) of momentum, energy and information impinging on the physical particle. In addition, it is assumed that the information space has the capability of processing information by means of a classical Turing machine and also incorporates a random number generator. The output of the Turing machine determines the parameters of a carrier of momentum and energy to be emitted by the physical particle. This accounts for self-interaction of the particle what is the indication of its agency, i.e., the causal power ascribed in the DAQM to the information space on matter.
In DAQM, it is further assumed that gravitation, in a first-order approximation, does not play an essential role in the determination of the interactions and inner structures of fundamental particles, basically constituting the backdrop in which the evolution of matter interactions happen. In addition, information is assumed not to be conserved on the information spaces of the particles as it becomes manifest in the characterization of the process of measurement.
Initially, at time , all the particles, whose distribution of masses would reflect the initial conditions at the Big Bang, would be controlled by their randomizers (random number generators stored on their respective information spaces). As information starts to arrive at the particle, it is assumed that errors in the read/write operations on the Turing machine generate algorithms that progressively take over the control on the particle to the detriment of the randomizer. These random read/write errors would constitute the first source of variation for the algorithm that controls the dynamics of the particle. Different mechanisms for variation can be conceived mimicking those encountered in biological Darwinian evolution. In particular, certain processes responsible for duplication or recombination of algorithms respectively resembling biological mitosis or meiosis might have been crucial for the dynamics of particles populations at high-energy stages, but becoming much less frequent at lower-energy levels, even being undetectable at the present, hypothesized, evolutionarily stable physical scenario. These duplication and recombination methods might also have been central for the process of retention or inheritance of algorithmic variation in subsequent populations of physical particles as they are in biological Darwinian evolution. Finally, the mechanism of natural selection would act on particles populations completing the characterization of Darwinian evolution on hypothesized information-theoretic physical systems.
The central idea of DAQM is that then quantum mechanics would emerge as an evolutionarily stable attractor strategy (Rand, Wilson and McGlade, 1994) for physical systems. In addition, ideally, DAQM should predict or at least make plausible the intrinsic parameters of the fundamental particles in the Standard Model from the initial conditions at the Big Bang.
To start the analysis of DAQM, the first fundamental issue to be considered is whether beyond the canonical central role played by fitness in Darwinian evolution, in addition, there also exists a regulatory principle that determines the direction of evolution in the long run. Several schemes (Friston, 2019; Martyushev and Seleznev, 2006; Saunders and Ho, 1976) have been proposed to study this open problem in the general framework of Darwinism (schemes that might also shed light on the origin of life). Among them, those envisaging complexity as a crucial element for predicting evolution in the long term face the difficulty of finding out a satisfactory mathematical characterization that captures the essentials of the concept.
Appendix A.1. Regulating Principle: Increase of Survival Information Complexity
In DAQM, a magnitude named survival information complexity
is defined (Baladrón and Khrennikov, 2023) as a function of time for a fundamental particle
. This magnitude is meant to grasp the fundamentals
9 of an optimal strategy for survival from the perspective of information flows for a generic physical system independently of its environment, structure and functions. Two terms contribute to the survival information complexity:
The first term
evaluates the capacity of the fundamental particle
at time
for predicting the future configuration of the environment at time
and is mathematically defined as follows:
where
is the number of particles surrounding the particle
whose survival information complexity is going to be calculated,
is the real location that will be occupied by particle
(a particle in the vicinity of the studied particle
) at time
,
is the predicted position (according to the estimation of the central particle
) that would hypothetically be occupied by particle
at time
as computed on the information space of particle
at time
by the Turing machine of particle
, and
is the squared distance between the locations that will really be occupied by particle
and its surrounding particle
at time
.
The second term
measures the stealthiness of the particle
, i.e., the performance of such particle
for maximising the unpredictability of its position
for the surrounding systems
by optimising the information that the particle
sends outwards. Therefore, the magnitude is mathematically defined as follows:
where
is again the number of particles surrounding the central particle
whose survival information complexity is going to be calculated,
is the real location that will be occupied by particle
at time
,
is the estimated location of the central particle
at time
as calculated on the information space of particle
at time
by its Turing machine, and, as for equation A-2,
is the squared distance between the locations that will really be occupied by particle
and its surrounding particle
at time
.
Let us consider a system
constituted by
particles. The survival information complexity of such system
is defined as:
Now, in case the system
is being measured by the environment or by an apparatus and, therefore, experiencing a conscious event associated to the erasure of superfluous information, then the degree of consciousness of the system
at time
is determined in the DAQM by the following quantity connected with the first term of the survival information complexity of the system:
This magnitude captures the faithfulness of the representation of the environment that is subjectively experienced by the system taking also into account the structural complexity of such environment through the number of particles surrounding every constituent particle of the system .
Some weakly emergent quantities ought to be defined in future developments in terms of this microscopic quantitative characterization of the degree of consciousness or some adequate extension of it in order to provide a satisfactory quantitative description of high-level properties for human being consciousness.
Once the formalism of DAQM is equipped with a mathematical characterization of the survival information complexity, the goal of the theory is to explore the possibility of plausibly deducing the generation of quantum behaviour for the postulated initially random-behaved information-theoretic classic fundamental particles as a consequence of Darwinian evolution whose direction would be hypothetically determined by the increase of survival information complexity in the long run.
Appendix A.2. Discussion on the Derivation of the Postulates of Quantum Mechanics
A possible starting point to analyse the main properties that characterise quantum versus classical behaviour is the perspective of computation. From this point of view, the kind of problems that a quantum computer can solve is exactly the same that a classical computer can, the only difference being the degree of efficiency for certain types of problems (Timpson, 2008). In particular, optimisation schemes and simulation of quantum systems are two areas for which the quantum advantage
10 might be patent. This perspective suggests to explore quantumness in relation to classicality fundamentally as computational efficiency. Efficiency seems a natural enhancer of survival expectations in a world of limited resources. Those physical systems presenting computational efficient performances would have a substantial survival advantage. Therefore, if survival information complexity drives, as assumed in DAQM, Darwinian evolution in the long run, then it seems plausible to consider that it should propel the computational efficiency of physical systems that possess the capacity of processing information. Might the optimisation of the information flows in information-theoretic particles eventually lead to the arise of quantum behaviour in real time? Two conditions are required, namely, the development of both a classical algorithm
on the information space of the particle that codes the rules of quantum mechanics, and an efficient enough procedure that enables the classical Turing machine of the particle to emulate quantum behaviour in real time. Let us first discuss the possible deduction of the postulates of quantum mechanics (and, therefore, the possible generation of
on the information space of a DAQM particle) assuming that the increase of survival information complexity would determine the direction of Darwinian evolution in the long term.
The dynamics of a DAQM particle, as mentioned in previous sections, can be compared to a generalised Bohmian description in which the pilot wave, whose role can be envisaged in Bohmian mechanics as twofold, containing active information about the surrounding particles and guiding the own particle trajectory, is calculated by the control program stored on the information space of the particle. This particle might be considered as a ship that follows a continuous trajectory and is steered by a computer, borrowing the analogy established by Bohm and Hiley (1993) for describing the dynamics of a particle in the de Broglie-Bohm theory. The problem of determining the trajectory of a particle can then be divided into two parts. The first one is related to the way in which the data about the environment of the particle are collected, stored and analysed on the information space. The second part refers to the way in which these data are processed to compute an output that ultimately shapes the dynamical behaviour of the particle.
Appendix A.2.1. Data Storage: Complex Wave Function
A first step towards computational efficiency would be to store data optimising the computational resources and with a structure that improved the retrieval and processing speed of information. To begin with, as Frieden and Soffer (1995) point out, it is intriguing that Fisher (Fisher and Mather, 1943) himself used probability amplitudes (the square root of probabilities) instead of directly probabilities in his statistical studies of inheritance in populations of living organisms, having no connection to quantum mechanics whatsoever, arguing that it was more convenient for identifying different population classes.
To examine the process of acquiring and storing information, let us assume that a DAQM particle is endowed with a collection of methodological detectors that enable the particle to register the momentum and energy of the photons impinging on it. These detectors can be envisaged as a convenient set of yes/no methodological sensors whose output arrives at the information space of the particle. This characterisation of the particle accommodates to the description that Summhammer (1994, 2001, 2007) adopts for the generic process of acquisition of information from a system in the laboratory by means of a set of click-yielding detectors. Replacing the system in Summhammer’s model by the environment of the DAQM particle and the set of click-yielding detectors in the laboratory in Summhammer’s description by the registering detectors in the DAQM particle, the analysis and conclusions of Summhammer can be applied to the process of information gaining by a DAQM particle about its surrounding systems.
Summhammer (1994, 2001, 2007) starts his study considering that the basic phenomenology in physics is the observation of clicks in detectors, adopting a probabilistic view to interpret the observations, and assuming that the information about the world always increases through observation. The information gathered by these yes/no detectors is discrete and constituted by a finite number of bits. Summhammer’s analysis then drives to the conclusion that storing the information captured by the detectors as a complex probability amplitude vector whose module is the squared root of the relative frequency of click events for every detector maximises the predictive power of the information by ensuring that the gain of information only depends on the number of registered events and not on the nature of the registered physical parameters. The complex character of the probability amplitude, as discussed by Summhammer, is more powerful for predictions than the sheer real representation.
The incorporation of the phase of the wave function is also justified in DAQM as an element required for optimising the flows of information, because it works as a clock associated to the particle that facilitates the projection to the future of the registered information and determines in an efficient way the temporal and spatial correlation between the information captured by the particle from different locations at different times. This possible role of the wave function’s phase as a method of efficiently projecting information into the future is also pointed out in the transactional interpretation of quantum mechanics (Cramer, 1986).
In addition, following the analysis of Summhammer (2001), requiring maximum predictive power when calculating the probability amplitude for an experimental compound configuration encompassing two different elementary component configurations results in the superposition principle for the probability amplitudes of the components and as a consequence in the probability rule of quantum mechanics.
Appendix A.2.2. Data Retrieval and Processing: Hilbert Space Structure
Formal connections have been established among quantum mechanics and several disciplines related to the theory of information, as information retrieval (van Rijsbergen, 2004), network computation (Pavlovic, 2008), and signal theory (Aerts, 2008). The link between these seemingly distant subject matters can be tracked back to the underlying common mathematical structure supplied by the Hilbert space. And the reason from the DAQM perspective is clear, namely, all these theories study the most efficient ways of storing, processing and transmitting information.
From the point of view of DAQM, the Hilbert space structure for the state space of DAQM particles would then be directly implied by the unambiguous survival advantage that a system acquires by organizing its information space under such algebraic structure. Therefore, these systems would plausibly increase their information survival complexity by improving , i.e., their capacity of predicting the future locations of their surrounding systems thanks to their increased efficiency in the storing, retrieval and processing of information.
Appendix A.2.3. Further Data Processing: Schrödinger Equation
Let us consider a DAQM fundamental particle (e.g., an electron) confined to move along a right line under the action of a potential. Its actual location in physical space is well determined at any time, however an observer gathering information about the particle through a set of detectors will at most have access to a probability distribution function
of its position. The Fisher information of this function is given by the following expression (Frieden and Soffer, 1995):
Fisher information is a magnitude well fitted to locally measure the smoothness or sharpness of a function (Frieden, 1989). Low levels of Fisher information are associated to smooth functions. Fisher information is a suitable quantity to characterize the information content of a function when the goal is to establish a differential equation of the phenomenon under analysis.
Following the study of Frieden (Frieden, 1989), the process of capturing information about the particle by the observer, that in the present study is assimilated to the environment, can be considered as a zero-sum game in which the information sent out by the particle is gained by the environment. In these terms, those DAQM systems that minimize the Fisher information conveyed outside by their information carriers will maximize their , the second term of the survival information complexity that measures the stealthiness of a system, i.e., its capacity of maximizing the unpredictability of its location for the surrounding systems. Therefore, in the long term, according to DAQM, information-theoretic Darwinian evolution would select those systems whose dynamics minimizes the Fisher information sent to the environment.
Frieden (1989) has deduced the Schrödinger equation applying the principle of minimum Fisher information or maximum Cramer-Rao bound to the probability distribution function
of the location of a particle in the presence of a potential, adding a constraint that characterizes physically the problem:
where the first term is the Fisher information of
, and the second term is the average kinetic energy of the particle for an unknown total energy
and a potential energy
, being
a fixed negative parameter that determines the weight of every term in the minimization procedure.
The Eq. (A-7) can be recast (Frieden, 1989) in terms of a probability amplitude
that is related to the probability distribution function through the expression
The equation now reads:
being
. The calculus of variations (e.g., see Morse and Feshbach (1953)) reduces this extremum problem to solve the following Euler-Lagrange equation:
where
,
, and
. Taking
, where
is the mass of the particle and
the reduced Planck constant, the Schrödinger equation is obtained as solution of the variational problem:
Reginatto (1998) has derived the time-dependent Schrödinger equation with a complex wave function also from the principle of minimum Fisher information.
Appendix A.2.4. Output Computing: Guiding Equation
In DAQM, from the information that arrives at the particle, a model of how the particle itself may be detected by the environment is constructed on the information space by means of the wave function, that is designed as an efficient epistemological tool, and an optimization procedure is coded in the Schrödinger equation. This equation is then solved on the information space of the particle so that the calculated wave function now represents the strategies for minimizing the outwards flows of information.
However, the ontological parameter of a DAQM particle is its location. Therefore, the control algorithm should include a subroutine that determines the trajectory to be followed by the particle in order to optimize the information sent outside. Specifically, the output of a run of the program should be the command of emission of a photon (in the case of electrons) with the appropriate parameters to follow the informationally optimal trajectory. These particles will present high values of , the second term of the survival information complexity that measures the stealthiness of a system.
Goldstein (2010), in the framework of Bohmian mechanics, points out the similar role played by the logarithm of the wave function in the guiding equation of Bohmian mechanics and the Hamiltonian in classical mechanics, highlighting the plausibility of considering the wave function more as an element of physical law than as a physical real object. This same perspective is adopted in the framework of DAQM.
Therefore, following the analogy, let us consider that the velocity of a particle is proportional to the gradient of the logarithm of the wave function, in order to minimize the information sent outside, plus a Brownian-like term
that incorporates randomness to the dynamics of the particle what, according to game theory (Ross, 2006), would improve the performance of a pure deterministic strategy. Thus, the velocity of the particle would obey the following guiding equation:
being
the phase of the wave function expressed in polar form
.
This expression is similar to the stochastic guiding equation (Baccigaluppi, 1999) in the stochastic variant of Bohmian mechanics (Bohm and Hiley, 1989; Bohm and Vigier, 1954):
where
is the reduced Planck constant,
the mass of the particle, and
is a constant that can take a value between 0 and 1, and that reproduces (Baccigaluppi, 1999) the original guiding equation of de Broglie-Bohm theory for
and Nelson’s stochastic mechanics for
.
In quantum fluid dynamics (Ghosh and Deb, 1982), based on the Madelung’s hydrodynamic analogy of the Schrödinger equation, the complex velocity field defined from the momentum operator has the expression where, therefore, the real part coincides with the first term on the right-hand side of the equation (A-12), and the imaginary part is proportional to the second term.
The stochastic guiding equation, Eq. (A-12), asymptotically ensures the Born rule (Bohm, 1988) independently of the initial distribution of particles thanks to the second term, the so-called osmotic velocity, and the third term, the Brownian-like term.
Finally, as has been discussed in
Section 4, there is no need for the projection postulate in DAQM being, as it is, a realist theory, since every particle has a well-defined position at any time, what solves the measurement problem as in Bohmian mechanics.
Appendix A.3. Computing Quantum Behaviour in Real Time: Simulation of Closed Timelike Curves (CTCs) on Information Spaces
It has been discussed how through the action of natural selection on information-theoretic DAQM fundamental particles a classical algorithm encoding the rules of quantum mechanics might plausibly be generated on the information spaces of such particles. However, a second condition is required so that DAQM particles may mimic quantum behaviour in real time: The implementation of a computing procedure that supplies enough efficiency to the classical Turing machine as for equating the performance of a hypothetical quantum computer simulating the dynamics of any collection of real elementary particles.
This task that seems in principle daunting, since it implies to break the quantum advantage, however, it may be attained through the development of an anticipation module
on the information space of a particle. This module should be able to predict the future configuration of the surrounding systems to the particle. Assuming that this module may be implemented, then, as has been discussed in Baladrón and Khrennikov (2023), a classical circuit equivalent to an informationally simulated closed timelike curve
11 (CTC) can be built on the information space of the particle. Let us summarize the procedure. Following Deutsch (1991), the CTC has been characterized, in terms of the information flows in a physically equivalent quantum circuit that models the interaction. It is then assumed that in the CTC spacetime region nature has to impose a causal consistency condition (Aaronson and Watrous, 2009; Deutsch, 1991), which ensures the absence of logical inconsistencies, as the so-called “grandfather paradox”
12, for any physically realizable initial state. This global causal consistency condition, as established by Deutsch (1991), requires that for the evolution operator,
, of that region, nature has to find a fixed point of such operator (it finds an input
that satisfies the equation
). Deutsch (1991) has shown that in quantum mechanics there always exists at least one fixed point for any quantum operation (i.e., there is always a density matrix
for every quantum operation
such that
. As shown by Tolksdorf and Verch (2021), and also mentioned by Aaronson and Watrous (2009) the result demonstrated by Deutsch (1991) is also valid for classical statistical mixtures. Therefore, the presence of the anticipation module on the information space of a DAQM particle ensures the simulation of the CTC since the anticipation module by definition finds the fixed point of the evolution function for the corresponding classical circuit. Finally, applying the stunning result mathematically demonstrated by Aaronson and Watrous (2009) that a classical computer and a quantum computer both with access to a CTC are computationally equivalent, then the classical Turing machine on the information space of a DAQM particle with access to a simulated CTC might induce quantum behaviour on the particle in real time.
Appendix A.4. Bell Inequality Violations in DAQM
The anticipation module of a DAQM fundamental particle is also a central piece of the theory to satisfactorily describe Bell inequality violations
13 in DAQM. In order to study these violations of the Bell inequality, an EPR-Bohm experiment with electrons
14 can be analysed by means of the DAQM model for entanglement (Baladrón and Khrennikov, 2019) in which two particles are entangled by mutually copying and storing all the algorithms (including the randomizers,
and
, and anticipation modules,
and
, of each particle) and data stowed on their information spaces (see
Figure 5 in the main text for a graphical representation). Therefore, although DAQM is a local and realist theory, since no physical influence travels over the speed of light and every fundamental particle has a well-defined position at any time, it can explain Bell inequality violations thanks to violating the conditions of parameter independence and outcome independence
15, since both entangled particles share the programs,
and
, the entangled singlet state, the randomizers,
and
, the information deleting subroutines,
and
, and the anticipation modules,
and
(Baladrón and Khrennikov, 2019). DAQM circumvents the Bell’s theorem by supplementing the physical space with an information space for every fundamental particle (Baladrón and Khrennikov, 2019). Each particle in an entangled pair stores on its information space its programs and those of its partner what enables every particle to anticipate not only the orientation of the analyser on its own wing, but also the orientation of the analyser on the opposite wing of the setup, and to know as well the particular outcome obtained on the opposite arm of the experimental array. The results accommodate to the predictions of quantum mechanics since both partners are controlled by classical algorithms coding the quantum mechanical rules.
Appendix A.5. Generating Anticipation Modules on Information Spaces
The first term, , in the definition of survival information complexity implies that the development of a reliable anticipation module on the information space of a system directly ensures the increase in survival information complexity for the system. Therefore, it seems plausible that if Darwinian evolution is driven in the long term by the increase of survival information complexity, as it has been assumed, then the construction of anticipation modules would be a ubiquitous process in evolution.
Let us examine the presence of anticipation in biological evolution. As highlighted by Igamberdiev (2015), the role played by anticipation in the theory of the stable non-equilibrium state for the study of the origin of life (Bauer, 1935; Maturana and Varela, 1972) is central. The very idea of self-regulated system is basically connected to an anticipation function.
Recent findings (Chatterjee et al. 2013, 2014; Kaznatcheev, 2021) suggest that Darwinian evolution might identify pathways that would convert certain, in appearance, exponential-time problems (i.e., problems whose time of resolution originally scales exponentially with the length of the defining sequence) into polynomial-time problems (Chatterjee et al. 2013, 2014; Kaznatcheev, 2021). In some theoretical scenarios in which the expected time of evolution is exponential with the sequence length that undergoes adaptation in the model (Chatterjee et al. 2013, 2014), a proposed mechanism can overcome this exponential barrier and enable evolution to proceed in polynomial time, as demonstrated in computer simulations by Chatterjee et al. (2013, 2014). This feature is characteristic of quantum computation and, as has been discussed (see Section A.3 in this Appendix), the kind of potential computational boost that an anticipation module might generate. However, in the study of Chatterjee et al. (2013, 2014), it is not established any direct connection to anticipatory mechanisms.
Another sign that hints to the plausible generation of anticipation modules in Darwinian evolution comes out from the development of brains in complex biological systems. Several theories studying the functions of the brain characterize this organ as a predictive machine that generates a model of the world and aims to minimize the difference between the predictions of the model and the sensory inputs (Friston, 2010; Seth, 2020).
One of the elements that have determined the success of the neural network-based model AlphaFold (Jumper et al., 2021) is the stunning capacity of a classical Turing machine (Hassabis, 2024) to efficiently predict the folding of proteins, a problem that implies to find in polynomial time (i.e., the time needed to solve the problem increases polynomially with the number of amino acids –constituents-- of the protein) the target state within a space of states whose dimension increases astronomically with the number of amino acids –constituents-- of the protein, following a guided, efficient pathway based on a deep learning algorithm that incorporates physical and biological results about protein structure, and benefits from novel machine learning methods
There are certain interesting similarities between the structure of the problem studied with AlphaFold and that one studied in DAQM, namely, developing a classical algorithm to be implemented on a classical Turing machine that efficiently predicts a solution for a specific problem within an astronomically large space of states (i.e., a space of states whose dimension would increase exponentially with the number of constituents). These similarities suggest the following central questions in the framework of DAQM: Might nature or Darwinian evolution through natural selection, for that matter, have followed a similar path to developing an anticipation module on the information spaces of hypothetical information-theoretic fundamental particles? And, if so, might proto-consciousness have played a crucial role in that process (as is preliminarily discussed in
Section 6 and
Section 7 within the main text of this article), supplying a mechanism for speeding up the appearance and improvement of anticipation, and subsequently of quantum mechanics and then of life? These are open questions in the framework of DAQM whose relevance merits further exploration.
Appendix A.6. Conclusions
DAQM, on the one hand, pertains to the kind of approaches that consider information a central concept for clarifying the structure and foundations of quantum mechanics (Brukner and Zeilinger, 2009; Chiribella, D’ Ariano and Perinotti, 2012; D’Ariano, 2007; Fuchs, Mermin and Schack, 2014; Hardy, 2002; Khrennikov, 2019, 2021, 2024; Zeilinger, 1999). On the other hand, DAQM also aligns with those approaches (Casado et al., 2021; Khrennikov, 2024) that intent to eliminate or at least reduce weirdness in the quantum mechanical account of the fundamental processes observed in nature.
The characterization of a fundamental particle in DAQM as an information processing system, which possesses the three following elements, namely, a control algorithm mimicking quantum mechanical properties, a randomizer, and an anticipation module, and whose properties are computed in-flight (giving rise to contextuality) by the control program, would explain most weird long-standing conundrums of quantum mechanics in a rational and self-consistent manner that would be ultimately determined by Darwinian evolution under natural selection.
The model restores a realist (although in a minimalist stance) description of physical systems since every particle has a well-defined position at any time determining a continuous trajectory in physical space. In addition, the model is also local. In DAQM, entangled particles share their programs, randomizers and anticipation modules on their respective supplementary information spaces what allows for sidestepping Bell’s theorem. The classical principle of causality is also recovered admitting the intrinsic presence of the randomizers in every fundamental particle and methodologically incorporating these randomizers into the causal description. The anticipation modules enable physical systems, while complying with the classical principle of causality, to generate outcomes that depend on a possible, computed future.
Finally, the DAQM model, as has been discussed, also crucially opens the door to naturally incorporate proto-consciousness to the physical domain, constituting a promising basis to account for the properties of consciousness in complex biological systems.
| 1 |
This module will play a central role in the characterization of consciousness in the information-theoretic model of a fundamental particle in DAQM as will be mentioned bellow. |
| 2 |
The function of the enumerated elements that are stored on the information space will be further analysed in the Appendix. |
| 3 |
The possible fundamental relationship between irreversibility and consciousness has been highlighted by Aaronson (2014). |
| 4 |
Nevertheless, although the DAQM is then a realist approach as the de Broglie-Bohm theory, in contraposition to the patent nonlocality of the latter, DAQM is a local theory, as will be further discussed in the Appendix. |
| 5 |
Notice that in this elementary Wigner’s friend-like scenario the Wigner’s friend particle f does not measure the test particle s (as it is considered in standard Wigner´s friend scenarios), but it just observes the location occupied by the test particle as a consequence of that the Wigner’s friend particle itself is being measured, and therefore, according to the DAQM model, it becomes an observer. In addition, as has been mentioned, an elementary Wigner´s friend particle f and an elementary Wigner particle w cannot communicate between them. |
| 6 |
Note, however, that, in DAQM, as in Bohmian mechanics, the result of any measurement would be given in terms of positions of particles or positions of pointers in the measurement apparatus. |
| 7 |
The possibility that in certain regions or domains a different equilibrium might have been reached should be contemplated as a possible test for DAQM. |
| 8 |
This mechanism has already been proposed by Penrose (2023) to explain free will, but assuming a real backward in time causation. |
| 9 |
More elaborated definitions of may be considered for a detailed technical analysis (e.g., including elements of anticipation depth or incorporating a minimum value for denominators to avoid singularities, etc.), but the adopted definition seemingly captures the essentials for a conceptual discussion. |
| 10 |
The quantum advantage is the capacity of a quantum computer for solving in polynomial time, when specific appropriate quantum algorithms have been developed, certain exponentially computational complex problems for classical computers. |
| 11 |
Closed timelike curves are possible theoretical solutions of general relativity field equations representing loop paths through spacetime that return to a prior event in the worldline. |
| 12 |
The “grandfather paradox” refers to the illogical situation that the presence of a CTC raises. A time traveller voyaging through a CTC might hypothetically kill his own grandfather precluding his own existence. |
| 13 |
The Bell inequality establishes a mathematical constraint on the correlations of the outcomes of measurements on two spatially separated parts of a system assuming local causality (also named Bell locality condition or factorizability) and certain supplementary assumptions. Bell inequality violations are then the consequence of nonclassical correlations predicted by the quantum mechanical formalism and experimentally observed in specific setups involving spatially separated parts of composite systems for certain states of such systems. See Myrvold, Genovese and Shimony (2024) for a deep theoretical and experimental discussion of Bell inequality violations. |
| 14 |
An EPR-Bohm experiment with electrons consists in a setup in which a source of entangled electron pairs is situated between two analysers respectively located on the left and right wing of the array. The analysers are Stern-Gerlach apparatuses whose characteristic axes are determined by the directions of their magnetic fields that measure the spin component of the impinging electron. The pair of entangled electrons that travel in opposite directions from the source towards the analysers are generated in the spin-singlet state, i. e., the spin components of both electrons in each pair are anticorrelated for any considered direction in space (Baladrón and Khrennikov, 2019; Myrvold, Genovese and Shimony, 2024). |
| 15 |
Parameter independence and outcome independence are the two conditions in which the so-called factorizability or Bell locality condition can be decomposed following Shimony’s terminology (Myrvold, Genovese and Shimony, 2024). This factorizability condition expresses the central explicit hypothesis in the Bell’s theorem (Myrvold, Genovese and Shimony, 2024). The Bell’s theorem contends that those theories satisfying the factorizability condition and certain additional conditions cannot reproduce the predictions of quantum mechanics under all circumstances. Assuming an EPR-Bohm experiment with pairs of entangled electrons in the spin singlet state and that the choice of the orientation of the analyser axis on one arm of the setup is made at spacelike separation from the other arm of the experiment, parameter independence asserts that the probability of obtaining a certain result on one arm of the EPR-Bell experiment for any orientation of the analyser’s axis does not depend on the orientation of the analyser’s axis on the other arm. Outcome independence expresses the condition that, for any couple of fixed orientations of the analysers’ axes on both sides of the setup, the probability of obtaining an outcome on one side of the experiment does not depend on the outcome on the other side. |
References
- Aaronson, S. (2014) ‘Could a Quantum Computer Have Subjective Experience?’, Workshop “Quantum Foundations of a Classical Universe”, Watson Research Center in Yorktown Heights, NY, August 11-14, 2014. Available at: https://scottaaronson.blog/?p=1951 (Accessed: 4 August 2025).
- Aaronson, S.; Watrous, J. Closed timelike curves make quantum and classical computing equivalent. Proceedings of the Royal Society A 2009, 465, 631–647. [Google Scholar] [CrossRef]
- Aerts, S. An operational characterization for optimal observation of potential properties in quantum theory and signal analysis. International Journal of Theoretical Physics 2008, 47, 2–14. [Google Scholar] [CrossRef]
- Aghanim, N.; et al. Planck 2018 results-VI. Cosmological parameters. Astronomy & Astrophysics 2020, 641, A6. [Google Scholar]
- Allwood, A.C.; et al. Controls on development and diversity of Early Archean stromatolites. Proceedings of the National Academy of Sciences of the USA 2009, 106, 9548–9555. [Google Scholar] [CrossRef] [PubMed]
- Arsiwalla, X.D.; et al. Editorial: Mathematical and empirical foundations of models of consciousness. Frontiers in Applied Mathematics and Statistics 2023, 9, 1214939. [Google Scholar] [CrossRef]
- Atmanspacher, H. (2024) ‘Quantum Approaches to Consciousnes’, The Stanford Encyclopedia of Philosophy (Summer Edition), eds. Zalta, E.N. & Nodelman, U. Available at: https://plato.stanford.edu/archives/sum2024/entries/qt-consciousness/.
- Baccigaluppi, G. Nelsonian mechanics revisited. Foundations of Physics Letters 1999, 12, 1–16. [Google Scholar] [CrossRef]
- Baladrón, C. In search of the adaptive foundations of quantum mechanics. Physica E: Low-dimensional Systems and Nanostructures 2010, 42, 335–338. [Google Scholar] [CrossRef]
- Baladrón, C. (2014) ‘Elements for the development of a Darwinian scheme leading to quantum mechanics’. In: Nieuwenhuizen, T.; et al. (eds.) Quantum Foundations and Open Quantum Systems. Singapore: World Scientific, pp. 489–519.
- Baladrón, C. Physical microscopic free-choice model in the framework of a Darwinian approach to quantum mechanics. Fortschritte der Physik 2017, 65, 1600052. [Google Scholar] [CrossRef]
- Baladrón, C.; Khrennikov, A. Quantum formalism as an optimisation procedure of information flows for physical and biological systems. BioSystems 2016, 150, 13–21. [Google Scholar] [CrossRef]
- Baladrón, C.; Khrennikov, A. Outline of a unified Darwinian evolutionary theory for physical and biological systems. Progress in Biophysics & Molecular Biology 2017, 130, 80–87. [Google Scholar]
- Baladrón, C.; Khrennikov, A. (2018) ‘At the Crossroads of Three Seemingly Divergent Approaches to Quantum Mechanics’. In: Quantum Foundations, Probability and Information. Cham: Springer, pp. 13–21.
- Baladrón, C.; Khrennikov, A. Bell inequality violation in the framework of a Darwinian approach to quantum mechanics. European Physical Journal: Special Topics 2019, 227, 2119–2132. [Google Scholar] [CrossRef]
- Baladrón, C.; Khrennikov, A. Simulation of Closed Timelike Curves in a Darwinian Approach to Quantum Mechanics. Universe 2023, 9, 64. [Google Scholar] [CrossRef]
- Barker-Plummer, D. (2012) ‘Turing machines’, The Stanford Encyclopedia of Philosophy (Winter Edition), ed. Zalta, E.N. Available at: http://plato.stanford.edu/archives/win2012/entries/turing-machine/.
- Bauer, E.S. (1935) Theoretical Biology [in Russian]. Moscow and Leningrad: VIEM. (Bauer, E.S. 1982. Theoretical Biology, with English translation. Budapest: Akadémiai Kiadó.).
- Bohm, D. (1988) ‘Non-locality in the stochastic interpretation of the quantum theory’, Annales de l’Inst. Henri Poincaré, section A, tome 49, no 3, pp. 287-296 <http://www.numdam.org/item?id=AIHPA_1988__49_3_287_0>.
- Bohm, D.; Hiley, B.J. Non-Locality and Locality in the Stochastic Interpretation of Quantum Mechanics. Physics Reports 1989, 172, 93–122. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J. (1993) The Undivided Universe: An Ontological Interpretation of Quantum Theory. London: Routledge and Kegan Paul.
- Bohm, D.; Vigier, J.P. Model of the causal interpretation of quantum theory in terms of a fluid with irregular fluctuations. Physical Review 1954, 96, 208. [Google Scholar] [CrossRef]
- Brukner, Č.; Zeilinger, A. Information invariance and quantum probabilities. Foundations of Physics 2009, 39, 677–689. [Google Scholar] [CrossRef]
- Casado, A.; Cetto, A.M.; Hess, K.; Valdés-Hernández, A. (eds.) (2021) Towards a Local Realist View of the Quantum Phenomenon. Lausanne: Frontiers Media SA. [CrossRef]
- Chalmers, D.J. Facing up to the problem of consciousness. Journal of Consciousness Studies 1995, 2, 200–219. [Google Scholar]
- Chalmers, D.J. (1996) The Conscious Mind. New York: Oxford University Press.
- Chalmers, D.J. (2017) ‘The combination problem for panpsychism’. In: Panpsychism: Contemporary Perspectives, pp. 179–214.
- Chalmers, D. (2021a) ‘Idealism and the mind-body problem’. In: The Routledge Handbook of Idealism and Immaterialism, pp. 591–613. London: Routledge.
- Chalmers, D. (2021b) ‘What is Property Dualism?’, The Royal Institute of Philosophy. Available at: https://www.youtube.com/@RoyIntPhilosophy (Accessed: 4 August 2025).
- Chalmers, D. (2022) ‘Dualism and idealism in the foundations of quantum mechanics’, Mind & Agency Conference—Chapman University. Available at: https://www.youtube.com/watch?v=V5TnJmfNiqY (Accessed: 4 August 2025).
- Chalmers, D. (2023) ‘Could a large language model be conscious?’, Science of Consciousness Conference, Taormina, Sicily, May 2023. Available at: https://www.youtube.com/watch?v=Fgm7Ftoq6ME (Accessed: 4 August 2025).
- Chatterjee, K.; Pavlogiannis, A.; Adlam, B.; Nowak, M.A. (2013) ‘The Time Scale of Evolutionary Trajectories’. Hal Science Ouverte. Available at: https://hal.science/hal-00907940/document (Accessed: 17 January 2023).
- Chatterjee, K.; Pavlogiannis, A.; Adlam, B.; Nowak, M.A. The time scale of evolutionary innovation. PLoS Computational Biology 2014, 10, e1003818. [Google Scholar] [CrossRef] [PubMed]
- Chen, I.A.; Nowak, M.A. From prelife to life: how chemical kinetics become evolutionary dynamics. Accounts of Chemical Research 2012, 45, 2088–2096. [Google Scholar] [CrossRef]
- Chiribella, G.; D’ Ariano, G.M.; Perinotti, P. (2012) ‘Informational axioms for quantum theory’. In D’ Ariano, M., Fei, S.M., Haven, E., Hiesmayr, B., Jaeger, G., Khrennikov, A.; Larsson, J.A., (eds.) Foundations of Probability and Physics-6. Melville, NY, USA: AIP, pp. 270–279.
- Chomsky, N. (2022). What is the mind body problem? In Podcast Mind-Body Solution with Tevin Naidu. URL=https://www.youtube.com/watch?v=PSLlW58OZoI (Accessed: : 4 August 2025).
- Clark, A. (2023) The Experience Machine: How Our Minds Predict and Shape Reality. New York: Pantheon.
- Cramer, J.G. The transactional interpretation of quantum mechanics. Reviews of modern physics 1986, 58, 647–687. [Google Scholar] [CrossRef]
- de Broglie, L. (1963) Étude critique des bases de l’interprétation actuelle de la mécanique ondulatoire. Paris: Gauthier-Villars.
- Deutsch, D. Quantum mechanics near closed timelike lines. Physical Review D 1991, 44, 3197–3217. [Google Scholar] [CrossRef]
- D’ Ariano, G.M. (2007) ‘Operational axioms for quantum mechanics’. In Adenier, G., Fuchs, C., Khrennikov, A. (eds.) Foundations of Probability and Physics-4. Melville, NY, USA: AIP, pp. 79–105.
- D’Ariano, G.M.; Faggin, F. (2022) ‘Hard problem and free will: An information-theoretical approach’. In: Artificial Intelligence versus Natural Intelligence, Cham: Springer International Publishing, pp. 145–192.
- Diósi, L. Models for universal reduction of macroscopic quantum fluctuations. Physical Review A 1989, 40, 1165–1174. [Google Scholar] [CrossRef]
- Eigen, M. Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften 1971, 58, 465–523. [Google Scholar] [CrossRef]
- Faye, J. (2019) ‘Copenhagen Interpretation of Quantum Mechanics’, The Stanford Encyclopedia of Philosophy (Winter Edition), ed. Zalta, E.N. Available at: https://plato.stanford.edu/archives/win2019/entries/qm-copenhagen/ (Accessed: 4 August 2025).
- Fisher, R.A.; Mather, K. The inheritance of style length in Lythrum salicaria. Annals of Eugenics 1943, 12, 1–23. [Google Scholar] [CrossRef]
- Frankish, K. Illusionism as a theory of consciousness. Journal of Consciousness Studies 2016, 23, 11–39. [Google Scholar]
- Frieden, B.R. Fisher information as the basis for the Schrödinger wave equation. American Journal of Physics 1989, 57, 1004–1008. [Google Scholar] [CrossRef]
- Frieden, B.R.; Soffer, B.H. Lagrangians of physics and the game of Fisher-information transfer. Physical Review E 1995, 52, 2274. [Google Scholar] [CrossRef]
- Friston, K. The free-energy principle: a unified brain theory? Nature Reviews Neuroscience 2010, 11, 127–138. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. (2019) ‘A free energy principle for a particular physics’. arXiv:1906.10184 [q-bio.NC].
- Friston, K.; et al. Active inference: a process theory. Neural Comput. 2017, 29, 1–49. [Google Scholar] [CrossRef]
- Fuchs, C.A.; Mermin, N.D.; Schack, R. An introduction to QBism with an application to the locality of quantum mechanics. American Journal of Physics 2014, 82, 749–754. [Google Scholar] [CrossRef]
- Gao, S. (ed.) (2022) Consciousness and Quantum Mechanics. Oxford: Oxford University Press.
- Ghosh, S.K.; Deb, B.M. Densities, density-functionals and electron fluids. Physics Reports 1982, 92, 1–44. [Google Scholar] [CrossRef]
- Goldstein, S. Bohmian mechanics and quantum information. Foundations of Physics 2010, 40, 335–355. [Google Scholar] [CrossRef]
- Goldstein, S. (2021) ‘Bohmian Mechanics’, The Stanford Encyclopedia of Philosophy (Fall Edition), ed. Zalta, E.N. Available at: https://plato.stanford.edu/archives/fall2021/entries/qm-bohm/ (Accessed: 4 August 2025).
- Goff, P.; Seager, W.; Allen-Hermanson, S. (2022) ‘Panpsychism’, The Stanford Encyclopedia of Philosophy (Summer Edition), ed. Zalta, E.N. Available at: https://plato.stanford.edu/archives/sum2022/entries/panpsychism/ (Accessed: 4 August 2025).
- Guyer, P.; Horstmann, R.P. (2023) ‘Idealism’, The Stanford Encyclopedia of Philosophy (Spring Edition), eds. Zalta, E.N. & Nodelman, U. Available at: https://plato.stanford.edu/archives/spr2023/entries/idealism/ (Accessed: 4 August 2025).
- Hameroff, S.R.; Penrose, R. Conscious events as orchestrated space–time selections. Journal of Consciousness Studies 1996, 3, 36–53. [Google Scholar] [CrossRef]
- Hameroff, S.; Penrose, R. Consciousness in the universe: A review of the ‘Orch OR’ theory. Physics of Life Reviews 2014, 11, 39–78. [Google Scholar] [CrossRef] [PubMed]
- Hardy, L. (2002) ‘Quantum Theory from Intuitively Reasonable Axioms’. In Khrennikov, A. (ed.) Quantum Theory: Reconsideration of Foundations. Växjö (Sweden): Växjö University Press, Volume 2, pp. 117–130.
- Hassabis, D. (2024) ‘Nobel Prize in Chemistry 2024 Lecture’. Available at: https://www.nobelprize.org/prizes/chemistry/2024/hassabis/lecture/ (Accessed: 4 August 2025).
- Hoffman, F.; Vona, N. (2014) ‘Introductory Lecture on Bohmian Mechanics’. Available at: https://www.mathematik.uni-muenchen.de/~bohmmech/BohmHome/files/Lecture_an_Introduction_to_BM.pdf (Accessed: 4 August 2025).
- Humpfrey, N. (2023) Sentience: The Invention of Consciousness. Cambridge, MA: MIT Press.
- Igamberdiev, A.U. Anticipatory dynamics of biological systems: from molecular quantum states to evolution. International Journal of General Systems 2015, 44, 631–641. [Google Scholar] [CrossRef]
- Jackson, F. Epiphenomenal qualia. Philosophical Quarterly 1982, 32, 127–136. [Google Scholar] [CrossRef]
- Jablonka, E.; Ginsburg, S. Learning and the Evolution of Conscious Agents. Biosemiotics 2022, 15, 401–437. [Google Scholar] [CrossRef]
- Jumper, J.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Kaznatcheev, A. (2021) ‘Evolution is exponentially more powerful with frequency-dependent selection’, bioRxiv.
- Kastrup, B. An ontological solution to the mind–body problem. Philosophies 2017, 2, 2. [Google Scholar] [CrossRef]
- Khan, S.; et al. (2024) ‘Microtubule-stabilizer epothilone B delays anesthetic-induced unconsciousness in rats’, eNeuro, 11(8).
- Khrennikov, A. Quantum-like formalism for cognitive measurements. Biosystems 2003, 70, 211–233. [Google Scholar] [CrossRef]
- Khrennikov, A. Get Rid of Nonlocality from Quantum Physics. Entropy 2019, 21, 806. [Google Scholar] [CrossRef]
- Khrennikov, A. Is the Devil in h? Entropy 2021, 23, 632. [Google Scholar] [CrossRef] [PubMed]
- Khrennikov, A. (2024) Contextual Reinterpretation of Quantum Nonlocality. New York: Cambridge University Press. [CrossRef]
- Kirk, R. (2009) ‘Zombie’, The Stanford Encyclopedia of Philosophy (Summer Edition), ed. Zalta, E.N. Available at: https://plato.stanford.edu/archIves/sum2009/entries/zombies/index.html.
- Kuhn, R.L. A landscape of consciousness: Toward a taxonomy of explanations and implications. Progress in Biophysics & Molecular Biology 2024, 190, 28–169. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Physics Reports 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Marais, A.; et al. The future of quantum biology. Journal of the Royal Society Interface 2018, 15, 20180640. [Google Scholar] [CrossRef]
- Maturana, H.R.; Varela, F.G. (1972) Autopoiesis and Cognition. Dordrecht: Reidel.
- McHenry, L.B. Whitehead’s Pansychism as the Subjectivity of Prehension. Process Studies 1995, 1, 1–14. [Google Scholar] [CrossRef]
- Morse, P.M.; Feshbach, H. (1953) Methods of Theoretical Physics, Part I. New York: McGraw-Hill.
- Myrvold, W.; Genovese, M.; Shimony, A. (2024) ‘Bell’s Theorem’, The Stanford Encyclopedia of Philosophy (Spring Edition), eds. Zalta, E.N. & Nodelman, U. Available at: https://plato.stanford.edu/archives/spr2024/entries/bell-theorem/ (Accessed: 4 August 2025).
- Paulin, M.G.; Cahill-Lane, J. Events in early nervous system evolution. Topics in Cognitive Science 2021, 13, 25–44. [Google Scholar] [CrossRef]
- Pavlovic, D. (2008) ‘On quantum statistics in data analysis’, arXiv:0802.1296 [cs.IR] (Accessed: 4 August 2025).
- Penrose, R. On gravity’s role in quantum state reduction. General Relativity and Gravitation 1996, 28, 581–600. [Google Scholar] [CrossRef]
- Penrose, R. (2023) ‘Effective Quantum Retroactivity in Rapid Conscious Decisions’, The Science of Consciousness Conference, Taormina, Sicily, May 2023. Available at: https://www.youtube.com/watch?v=EAASoTStEMs (Accessed: 4 August 2025).
- Peres, A. Unperformed experiments have no results. American Journal of Physics 1978, 46, 745–747. [Google Scholar] [CrossRef]
- Plotnitsky, A. (2012) Niels Bohr and complementarity: An introduction. Dordrecht: Springer Science & Business Media.
- Rand, D.A.; Wilson, H.B.; McGlade, J.M. Dynamics and evolution: Evolutionarily stable attractors, invasion exponents and phenotype dynamics. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences 1994, 343, 261–283. [Google Scholar] [CrossRef] [PubMed]
- Reginatto, M. Derivation of the equations of nonrelativistic quantum mechanics using the principle of minimum Fisher information. Physical Review A 1998, 58, 1775–1778. [Google Scholar] [CrossRef]
- Ritchie, J.M. (1995) ‘Physiology of axons’, In: Waxman, S.G., Kocsis, J.D., and Stys, P.K. (eds.) The Axon. New York: Oxford University Press, pp. 68–96.
- Ross, D. (2006) ‘Game theory’, The Stanford Encyclopedia of Philosophy (Spring Edition), ed. Zalta, E.N. Available at: http://plato.stanford.edu/archives/spr2006/entries/game-theory/ (Accessed: 4 August 2025).
- Satarić, M.V.; Tuszyński, J.A.; Žakula, R.B. Kinklike excitations as an energy-transfer mechanism in microtubules. Physical Review E 1993, 48, 589. [Google Scholar] [CrossRef]
- Saunders, P.T.; Ho, M.W. On the increase in complexity in evolution. J. Theor. Biol. 1976, 63, 375–384. [Google Scholar] [CrossRef]
- Schrödinger, E. (1954) Nature and the Greeks. Cambridge: Cambridge University Press.
- Seager, W. (2004) ‘Whitehead and the Revival (?) of Panpsychism’. In: Riffert, F.; Weber, M. (eds.) Searching for New Contrasts: Whiteheadian Contributions to Contemporary Challenges in Neurophysiology, Psychology, Psychotherapy and the Philosophy of Mind. New York: Peter Lang.
- Seth, A. (2020) ‘Preface: The brain as a prediction machine’. In: The Philosophy and Science of Predictive Processing. London: Bloomsbury Academic.
- Seth, A.; Bayne, T. Theories of consciousness. Nature Reviews Neuroscience 2022, 23, 439–452. [Google Scholar] [CrossRef]
- Smart, J.J.C. (2022) ‘The mind/brain identity theory’. The Stanford Encyclopedia of Philosophy (Winter Edition), eds. Zalta, E.N.; Nodelman, U. Available at: https://plato.stanford.edu/archives/win2022/entries/mind-identity/ (Accessed: 4 August 2025).
- Stoljar, D. (2023) “Physicalism”, The Stanford Encyclopedia of Philosophy (Summer Edition), Edward N. Zalta & Uri Nodelman (eds.), URL = <https://plato.stanford.edu/archives/sum2023/entries/physicalism/>.
- Sulis, W. (2025) Process and Time. Singapore: World Scientific.
- Summhammer, J. Maximum predictive power and the superposition principle. International Journal of Theoretical Physics 1994, 33, 171–178, arXiv:quant-ph/0008098. [Google Scholar] [CrossRef]
- Summhammer, J. (2001) ‘Invariants of Elementary Observation’, arXiv:quant-ph/0008098.
- Summhammer, J. (2007) ‘Quantum theory as efficient representation of probabilistic information’, arXiv:quant-ph/0701181.
- Taguchi, S. (2022) ‘Mediation and Contextuality: Rethinking the concept of consciousness’, 2022 Apr 8 Consciousness Talks 2: Phenomenology and Quantum Cognition by Bruza and Taguchi. Available at: https://www.youtube.com/watch?v=3HehCZbcF70 (Accessed: 4 August 2025).
- Tegmark, M. Importance of quantum decoherence in brain processes. Physical Review E 2000, 61, 4194. [Google Scholar] [CrossRef]
- Tegmark, M. The mathematical universe. Foundations of Physics 2008, 38, 101–150. [Google Scholar] [CrossRef]
- Timpson, C. (2008) ‘Philosophical aspects of quantum information theory’. In: Rickles, D. (ed.) The Ashgate Companion to the New Philosophy of Physics. Ashgate.
- Tolksdorf, J.; Verch, R. The D-CTC Condition is Generically Fulfilled in Classical (Non-quantum) Statistical Systems. Foundations of Physics 2021, 51, 93. [Google Scholar] [CrossRef]
- Van Rijsbergen, C.J. (2004) The Geometry of Information Retrieval. New York: Cambridge University Press.
- Von Helmholtz, H. (1903) Die Thatsachen in der Wahrnehmung. In Vorträgeund Reden, Funfte Auflage, Zweiter Band (Braunschweig: Friedrich Vieweg und Sohn), pp. 215-247, 387-406; translated as The Facts in Perception. In R. S. Cohen and Y. Elkana (eds), Hermann von Helmholtz Epistemological Writings: The Paul Hertz/Moritz Schlick Centenary Edition of 1921 with Notes and Commentary by the Editors (Dordrecht: D. Reidel, 1977), pp. 115-185.
- Von Neumann, J. (1955) Mathematical Foundations of Quantum Mechanics. Princeton, NJ: Princeton University Press.
- Walker, S.I.; Davies, P.C. The algorithmic origins of life. Journal of the Royal Society Interface 2013, 10, 20120869. [Google Scholar] [CrossRef] [PubMed]
- Whitehead, A.N. (1929) Process and Reality: An Essay in Cosmology. New York: Macmillan.
- Whitehead, A.N. (1933) Adventures of Ideas. New York: Macmillan.
- Wigner, E.P. (1961)’Remarks on the Mind-Body Question’. In Good, I.J. (ed.). The Scientist Speculates: An Anthology of Partly-Baked Ideas. London: Heinemann. Reprinted in Wigner, E.P. (1995) ‘Remarks on the Mind-Body Question’. In: Mehra, J. (ed.) Philosophical Reflections and Syntheses. The Collected Works of Eugene Paul Wigner Vol. B/6. Berlin, Heidelberg: Springer, pp. 247–260. [CrossRef]
- Zeilinger, A. A foundational principle for quantum mechanics. Foundations of Physics 1999, 29, 631–643. [Google Scholar] [CrossRef]
Figure 1.
Fundamental philosophical approaches to the mind-body problem. A sketchy description of every approach and a brief discussion on some elementary relationships between the approaches are included in the main text. Materialism (in modern terms, physicalism) is encircled to highlight the usual starting point for the explicit or implicit philosophical standpoint of most modern scientists. The dotted arrows identify the central drawback associated with every philosophical perspective.
Figure 1.
Fundamental philosophical approaches to the mind-body problem. A sketchy description of every approach and a brief discussion on some elementary relationships between the approaches are included in the main text. Materialism (in modern terms, physicalism) is encircled to highlight the usual starting point for the explicit or implicit philosophical standpoint of most modern scientists. The dotted arrows identify the central drawback associated with every philosophical perspective.
Figure 2.
Elementary interaction process between two fundamental particles in the DAQM model. The particle 0 characterized in physical space by its mass and position , and supplemented with its information space (dotted line circle) emits, as result of a run of its control program, a carrier of momentum, energy and information that is absorbed by particle 1. A detailed description of the interaction process and a precise definition of the symbols are included in the main text.
Figure 2.
Elementary interaction process between two fundamental particles in the DAQM model. The particle 0 characterized in physical space by its mass and position , and supplemented with its information space (dotted line circle) emits, as result of a run of its control program, a carrier of momentum, energy and information that is absorbed by particle 1. A detailed description of the interaction process and a precise definition of the symbols are included in the main text.
Figure 3.
Generation of an elementary conscious event for the particle located at surrounded by two particles, 1 and 2, located (black dots) respectively at and . The dashed line circumferences represent the information spaces of the respective particles. The estimated positions ( and ) occupied at time t by particles 1 and 2 as computed by the Turing machine of particle 0 are represented by empty dots. identifies the measurement device acting on particle 0. The process of generating an elementary conscious event in particle 0 is described within the main text.
Figure 3.
Generation of an elementary conscious event for the particle located at surrounded by two particles, 1 and 2, located (black dots) respectively at and . The dashed line circumferences represent the information spaces of the respective particles. The estimated positions ( and ) occupied at time t by particles 1 and 2 as computed by the Turing machine of particle 0 are represented by empty dots. identifies the measurement device acting on particle 0. The process of generating an elementary conscious event in particle 0 is described within the main text.
Figure 4.
Elementary Wigner’s friend-like scenario constituted by three particles: the test particle , the Wigner’s friend particle , and the Wigner particle . The actual positions of the three particles at time t are represented by black dots. Every fundamental particle in DAQM is supplemented by its information space (dashed-line circles). Empty dots represent the estimated position of the particle identified by the subscript as computed by the Turing machine of the particle referred to by the superscript. The analysis of the scenario is developed in the text.
Figure 4.
Elementary Wigner’s friend-like scenario constituted by three particles: the test particle , the Wigner’s friend particle , and the Wigner particle . The actual positions of the three particles at time t are represented by black dots. Every fundamental particle in DAQM is supplemented by its information space (dashed-line circles). Empty dots represent the estimated position of the particle identified by the subscript as computed by the Turing machine of the particle referred to by the superscript. The analysis of the scenario is developed in the text.
Figure 5.
The process of entanglement in DAQM of two initially independent fundamental particles is described. At time
t (
Figure 5a), the two particles characterized in physical space by their respective masses (
) and positions (
,
), and on their respective information spaces by the control program (
,
), the randomizer (
,
), the anticipation module (
,
), the deleting module (
,
), and the calculated wave function (
,
) start the entanglement process by mutually copying their respective algorithms and data stored on the information spaces. At time
(
Figure 5b), the physical process of entanglement has already finished determining the entangled wave function of the system that has been computed and stored on both information spaces of the particles. On the information space of every particle, both the set of the own algorithms and the set of the algorithms of the entangled partner are stored. In addition, it has been assumed that the entangled system (
e.s.) has been joint measured (by the measurement apparatus
). Therefore, the entangled wave function has effectively collapsed to one of its possible branches (
), and, according to the DAQM model of consciousness, and elementary event of proto-consciousness has been induced on the system. In this case, it has been supposed that there is only a surrounding particle whose actual position at time
is
(black dot). Thus, the conscious event consists in the representation on the perception screen of every particle of the estimated configuration of the surroundings (
) from the perspective of the centre of mass of the system (
).
Figure 5.
The process of entanglement in DAQM of two initially independent fundamental particles is described. At time
t (
Figure 5a), the two particles characterized in physical space by their respective masses (
) and positions (
,
), and on their respective information spaces by the control program (
,
), the randomizer (
,
), the anticipation module (
,
), the deleting module (
,
), and the calculated wave function (
,
) start the entanglement process by mutually copying their respective algorithms and data stored on the information spaces. At time
(
Figure 5b), the physical process of entanglement has already finished determining the entangled wave function of the system that has been computed and stored on both information spaces of the particles. On the information space of every particle, both the set of the own algorithms and the set of the algorithms of the entangled partner are stored. In addition, it has been assumed that the entangled system (
e.s.) has been joint measured (by the measurement apparatus
). Therefore, the entangled wave function has effectively collapsed to one of its possible branches (
), and, according to the DAQM model of consciousness, and elementary event of proto-consciousness has been induced on the system. In this case, it has been supposed that there is only a surrounding particle whose actual position at time
is
(black dot). Thus, the conscious event consists in the representation on the perception screen of every particle of the estimated configuration of the surroundings (
) from the perspective of the centre of mass of the system (
).
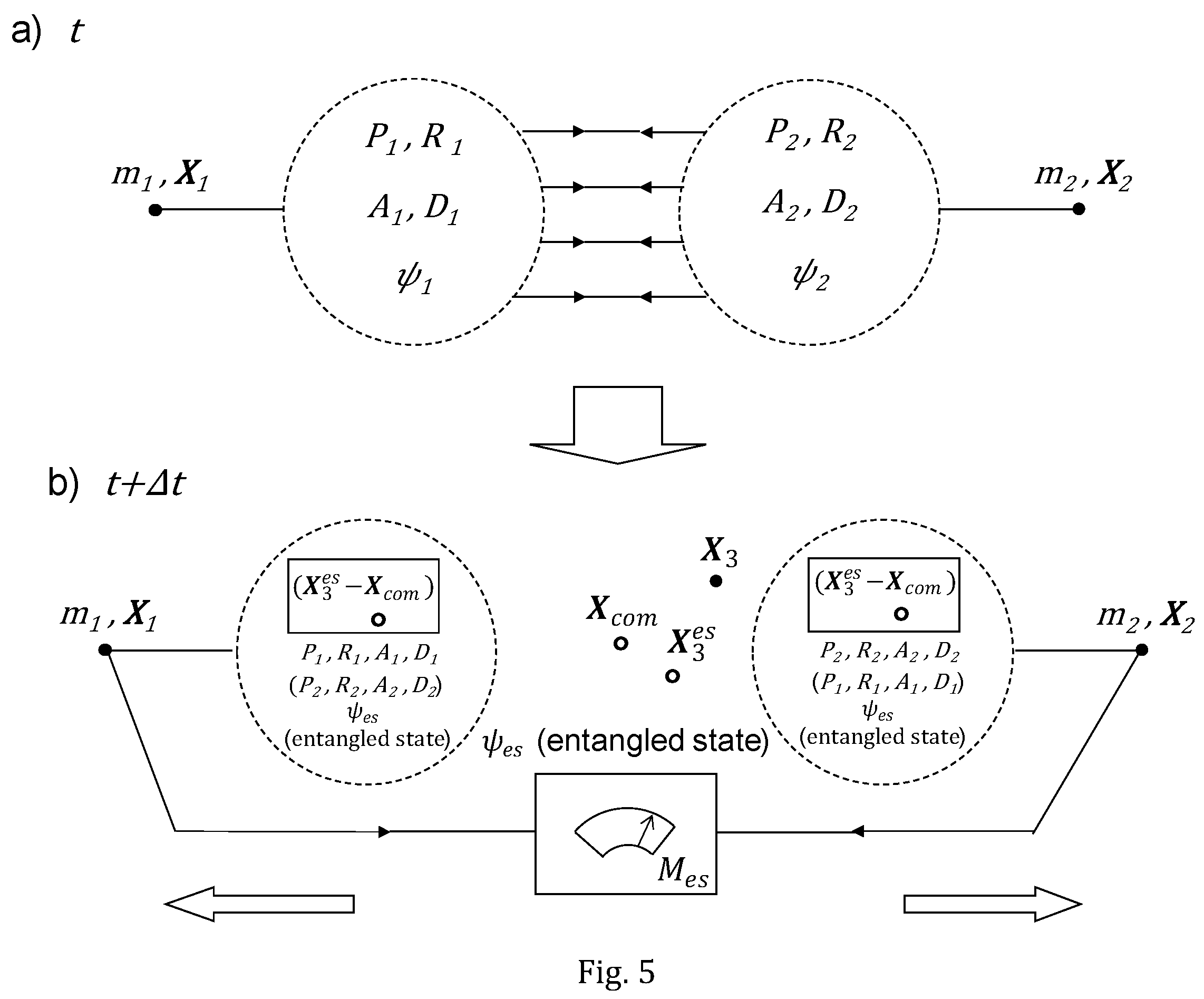
Figure 6.
The doing-otherwise mechanism in an information-theoretic DAQM fundamental particle is schematized. The particle characterized by its position is measured at time t by the apparatus . Two other particles, whose actual locations are and (black dots in the figure), stand at the vicinity of particle . The measurement process on particle restraints the dynamical relevance of the wave function to only one branch (that one whose support contains the actual particle position ). Therefore, the information deleting module erases the dynamically superfluous branches of the wave function generating an elementary conscious event that corresponds to the representation on the perception screen of the particle of the positions ( and , empty dots in the figure) occupied by the surrounding particles at time t as estimated by the program of the particle, being the perspective of the representation from the location occupied by the particle . Immediately after the elementary conscious event occurs, the control of the particle is transferred to an alternative program that can either return the control to the original control program , after updating the wave function to the effectively collapsed expression, or compute an output according to this alternative algorithm . The alternative program has access to the anticipation module, the randomizer, and the stored data on the information space of the particle.
Figure 6.
The doing-otherwise mechanism in an information-theoretic DAQM fundamental particle is schematized. The particle characterized by its position is measured at time t by the apparatus . Two other particles, whose actual locations are and (black dots in the figure), stand at the vicinity of particle . The measurement process on particle restraints the dynamical relevance of the wave function to only one branch (that one whose support contains the actual particle position ). Therefore, the information deleting module erases the dynamically superfluous branches of the wave function generating an elementary conscious event that corresponds to the representation on the perception screen of the particle of the positions ( and , empty dots in the figure) occupied by the surrounding particles at time t as estimated by the program of the particle, being the perspective of the representation from the location occupied by the particle . Immediately after the elementary conscious event occurs, the control of the particle is transferred to an alternative program that can either return the control to the original control program , after updating the wave function to the effectively collapsed expression, or compute an output according to this alternative algorithm . The alternative program has access to the anticipation module, the randomizer, and the stored data on the information space of the particle.
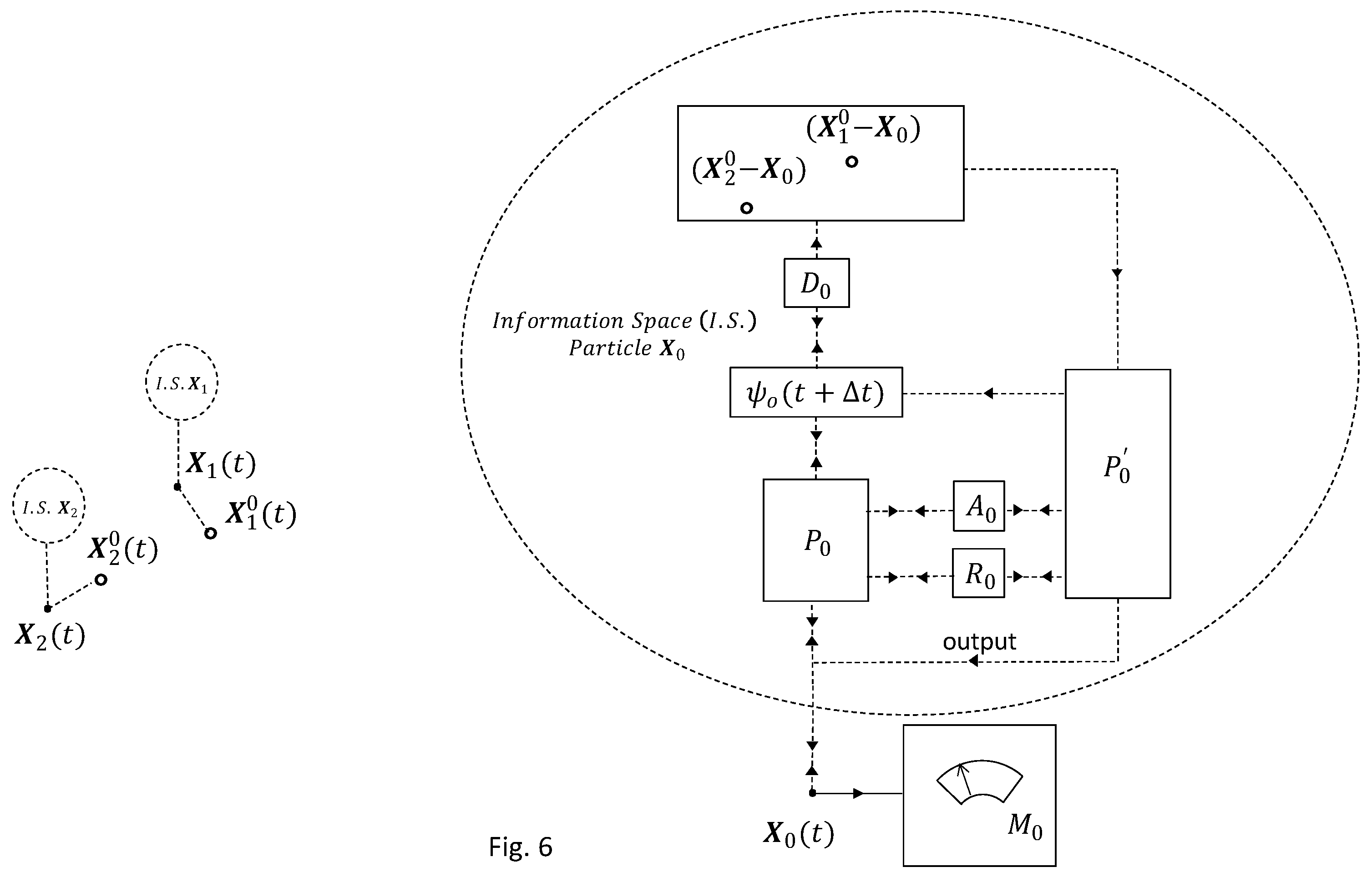
Figure 7.
Temporal line sketching the possible generation of high-level consciousness in complex biological systems from the hypothesized microscopic DAQM model of consciousness in information-theoretic fundamental particles. The main landmarks are identified and some of them approximately dated according to referenced studies (Aghanim et al., 2020; Allwood et al., 2009; Paulin and Cahill-Lane, 2021). The course of the temporal line is explained within the main text.
Figure 7.
Temporal line sketching the possible generation of high-level consciousness in complex biological systems from the hypothesized microscopic DAQM model of consciousness in information-theoretic fundamental particles. The main landmarks are identified and some of them approximately dated according to referenced studies (Aghanim et al., 2020; Allwood et al., 2009; Paulin and Cahill-Lane, 2021). The course of the temporal line is explained within the main text.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).