On the Hughes–Keating–O’Connell Conjecture: Entropy-Sieve Methods for Negative Moments of ζ′(ρ)

1. Introduction

Let $\zeta \left(s\right)$ denote the Riemann zeta function and $\rho =\frac{1}{2}+i\gamma$ denote its nontrivial zeros. The size of the derivative ${\zeta }^{\prime }\left(\rho \right)$ at these zeros plays a central role in analytic number theory, with deep connections to the distribution of zeros, random matrix theory, and the moments of L-functions. For $k\in \mathbb{C}$, we define the discrete moment

$$J_k\left(T\right):=\sum _{0<\gamma \le T}{|{\zeta }^{\prime }\left(\rho \right)|}^{2k},$$

where the sum runs over all nontrivial zeros $\rho$ of $\zeta \left(s\right)$, counted with multiplicity. For $k<0$ this sum is finite only if every zero is simple, since a multiple zero would satisfy ${\zeta }^{\prime }\left(\rho \right)=0$ and force $J_k\left(T\right)=+\infty$. Thus, proving upper bounds for $J_k\left(T\right)$ in the negative range has direct implications for the simplicity of zeros.

1.1. Motivation and Conjectures

Understanding the asymptotic growth of $J_k\left(T\right)$ has been the subject of considerable research. Based on random matrix theory and probabilistic heuristics, Hughes, Keating, and O’Connell ([1],Conjecture 1.7, p. 5) conjectured that for $\Re \left(k\right)>-\frac{3}{2}$,

$$J_k\left(T\right)\sim {\displaystyle \frac{G^2(2+k)}{G(3+2k)}}a\left(k\right){\displaystyle \frac{T}{2\pi }}{\left(\log {\displaystyle \frac{T}{2\pi }}\right)}^{{(k+1)}^2},$$

(1)

where $G(·)$ is the Barnes G-function and $a\left(k\right)$ is an explicit arithmetic factor. In particular, for $k=-1$, conjecture (1) predicts

$$J_{-1}\left(T\right)\asymp T,$$

so the negative second moment is expected to be of the same order as the number of zeros up to height T.

1.2. State of the Art

For positive moments ($k\ge 0$), significant progress has been achieved:

• Gonek ([2], p. 35) initiated the study of discrete moments of ${\zeta }^{\prime }\left(\rho \right)$ and derived asymptotic formulas for $J_1\left(T\right)$ under the Riemann Hypothesis (RH).
• Hejhal ([3], Section 3, pp. 343–370) studied the distribution of $\log |{\zeta }^{\prime }\left(\rho \right)|$ and showed that it behaves approximately like a Gaussian with variance $\asymp \log \log T$, providing the foundation for later probabilistic approaches.
• Kirila ([4], Theorem 1.1, pp. 2–4) obtained sharp upper bounds for positive moments by adapting Harper’s Dirichlet-polynomial techniques to sums over zeros:

  $$J_k\left(T\right){\ll }_{k}N\left(T\right){\left(\log T\right)}^{k(k+2)},$$

  where $N\left(T\right)$ denotes the number of zeros up to height T.
• Harper’s probabilistic method ([7], pp. 5–15), which Kirila adapted, uses Gaussian approximations and entropy-like inequalities to obtain sharp tail estimates for multiplicative chaos models.

These results match the predictions of the Hughes–Keating–O’Connell conjecture for $k>0$.

For negative moments ($k<0$), however, far less is known:

• Gonek ([2], p. 36) derived conditional lower bounds for $J_k\left(T\right)$ when $k<0$ but did not provide upper bounds.
• Milinovich and Ng ([5], pp. 642–644) improved certain lower bounds for negative moments, using refined estimates of ${\zeta }^{\prime }\left(\rho \right)$ in terms of the spacing of zeros.
• Recently, Bui, Florea, and Milinovich ([18], Theorem 1.3, pp. 3–6) obtained conditional upper bounds for negative moments over a large subfamily of zeros, excluding a sparse exceptional set where ${\zeta }^{\prime }\left(\rho \right)$ may be abnormally small. However, a full unconditional upper bound for $J_k\left(T\right)$ when $k<0$ remains open.

1.3. Challenges for Negative Moments

The difficulty in establishing upper bounds for $J_k\left(T\right)$ when $k<0$ stems from controlling the contribution of zeros where ${\zeta }^{\prime }\left(\rho \right)$ is exceptionally small. Since

$$J_{-1}\left(T\right)=\sum _{0<\gamma \le T}{\displaystyle \frac{1}{|{\zeta }^{\prime }{\left(\rho \right)|}^2}},$$

the dominant contribution arises from rare events in which ${\zeta }^{\prime }\left(\rho \right)$ is unusually tiny. Hejhal’s model ([3], Section 3) suggests that $\log |{\zeta }^{\prime }\left(\rho \right)|$ behaves like a Gaussian with variance $\asymp \log \log T$, implying that very small derivatives are exponentially rare. However, making this rigorous for sums over zeros requires two ingredients:

• Sharp Gaussian-type tail bounds for $\log |{\zeta }^{\prime }\left(\rho \right)|$, obtained by approximating it with a short Dirichlet polynomial and applying entropy-based large-deviation methods ([7], pp. 5–20).
• Control over the set of exceptional zeros where the approximation fails or where ${\zeta }^{\prime }\left(\rho \right)$ is extremely small, addressed via sieve-theoretic exclusion techniques as in ([18], Section 6).

1.4. Our Approach and Contributions

In this paper, we propose a hybrid analytic–probabilistic framework to tackle the upper bound for $J_k\left(T\right)$ when $k<0$, combining three main ingredients:

• Entropy-Sieve Method (ESM): We introduce an entropy-based refinement of the Dirichlet-polynomial approximation. By quantifying the entropy of local distributions of $D_X\left(\gamma \right)$ values and zero gaps, we ensure that low-entropy regions form a negligible exceptional set. This connects analytic techniques with entropy methods used in probabilistic number theory and exponential sum analysis [7,19].
• Sieve methods for exceptional zeros: Building on Bui, Florea, and Milinovich ([18], Section 6), we remove a negligible set of zeros where ${\zeta }^{\prime }\left(\rho \right)$ is abnormally small, using pair-correlation and independence heuristics to bound their contribution. Our systematic discussion of parameter optimization (see Section 4) clarifies how $A,B,C,\alpha$ can be tuned so that both ${\mathcal{E}}_{\mathrm{app}}$ and ${\mathcal{E}}_{\mathrm{ent}}$ are negligible.
• Algorithmic tail truncation: We develop an entropy-driven tail-truncation procedure to efficiently control the extreme lower tail of ${\zeta }^{\prime }\left(\rho \right)$, ensuring that these rare events contribute less than any power of $\log T$.

Using these tools, we establish, under RH and mild orthogonality hypotheses, the conditional bound

$$J_{-1}\left(T\right)\ll T{\left(\log T\right)}^{\epsilon },$$

which matches the conjectured order up to a logarithmic factor. Our framework complements the subfamily results of Bui–Florea–Milinovich and the moment-based work of Kirila, while offering a unified entropy–sieve perspective that systematizes the treatment of exceptional sets.

1.5. Organization

We briefly summarize the logical structure of the paper. Up to this point, we have established the analytic foundation: a short Dirichlet polynomial approximation (Lemma 1), refined variance estimates (Lemma 2), the moment generating function bound (Proposition 1), Gaussian lower-tail bounds via Chernoff (Theorem 1), and exponential decay for the exceptional approximation set (Lemma 3). These ingredients will be combined with entropy and sieve methods to treat the negative moments of ${\zeta }^{\prime }\left(\rho \right)$ in a consistent framework, avoiding the divergences that arise if exceptional sets are not carefully controlled.

The remainder of the paper is organized as follows. Section 2 reviews previous results on positive and negative moments of ${\zeta }^{\prime }\left(\rho \right)$, with particular emphasis on the conjectural framework of Hughes–Keating–O’Connell. In Section 4 we introduce the Entropy–Sieve Method (ESM), which strengthens Dirichlet-polynomial approximations of $\log |{\zeta }^{\prime }\left(\rho \right)|$ by incorporating entropy-based regularity, and thereby yields robust Gaussian large-deviation bounds. Section 5 develops the sieve-theoretic component, excluding low-entropy or small-gap exceptional sets where ${\zeta }^{\prime }\left(\rho \right)$ could be abnormally small. Finally, Section 6.9 combines these analytic and probabilistic tools to establish conditional upper bounds for

$$J_k\left(T\right)=\sum _{0<\gamma \le T}{\displaystyle \frac{1}{|{\zeta }^{\prime }(\frac{1}{2}+i\gamma ){|}^{2k}}}$$

in the critical range $k<0$, including the key case $k=-1$.

2. Background

The discrete moments of the derivative of the Riemann zeta function at its nontrivial zeros,

$$J_k\left(T\right)=\sum _{0<\gamma \le T}{|{\zeta }^{\prime }\left(\rho \right)|}^{2k},$$

are central objects in analytic number theory. They provide insight into the distribution of ${\zeta }^{\prime }\left(\rho \right)$, the spacing of the nontrivial zeros of $\zeta \left(s\right)$, and the connections between the zeta function and random matrix theory. Understanding the asymptotic growth of $J_k\left(T\right)$ has been the subject of extensive research over the past decades and is closely connected with one of the most refined conjectures in this area: the Hughes–Keating–O’Connell conjecture.

2.1. The Hughes–Keating–O’Connell Conjecture

Motivated by random matrix theory and probabilistic models, Hughes, Keating, and O’Connell proposed an explicit formula for $J_k\left(T\right)$ in the regime $\Re \left(k\right)>-\frac{3}{2}$. Their conjecture predicts that

$$J_k\left(T\right)\sim {\displaystyle \frac{G^2(2+k)}{G(3+2k)}}a\left(k\right){\displaystyle \frac{T}{2\pi }}{\left(\log \frac{T}{2\pi }\right)}^{{(k+1)}^2},$$

(2)

where $G(·)$ denotes the Barnes G-function and $a\left(k\right)$ is an explicit arithmetic factor arising from the Euler product.

This conjecture is supported by strong heuristics derived from the characteristic polynomials of random unitary matrices. In these models, $\log |{\zeta }^{\prime }\left(\rho \right)|$ behaves approximately like a Gaussian random variable, and Formula (2) reflects the matching asymptotics between the number-theoretic and random-matrix frameworks. A striking consequence appears when setting $k=-1$, where the conjecture predicts

$$J_{-1}\left(T\right)\asymp T.$$

Thus, the negative second moment is conjectured to be of the same order as the number of zeros up to height T.

2.2. Positive Moments

The case of positive moments, $k\ge 0$, is relatively well understood and has seen substantial progress over the last four decades. Gonek ([2], Theorem 1, p. 35) pioneered the study of discrete moments of ${\zeta }^{\prime }\left(\rho \right)$, proving under the Riemann Hypothesis that for $k=1$,

$$J_1\left(T\right)\sim {\displaystyle \frac{T}{24\pi }}{\left(\log \frac{T}{2\pi }\right)}^4.$$

This result agrees with the prediction of (2) when $k=1$ and represented one of the earliest confirmations of the conjecture in a special case.

Hejhal ([3], Section 3, Theorem 3.1, pp. 343–370) advanced the probabilistic understanding of ${\zeta }^{\prime }\left(\rho \right)$ by studying the distribution of $\log |{\zeta }^{\prime }\left(\rho \right)|$. He showed that, heuristically, $\log |{\zeta }^{\prime }\left(\rho \right)|$ behaves approximately like a Gaussian random variable with variance ${\sigma }^2\asymp \log \log T$. This probabilistic model suggested that extremely large or small values of ${\zeta }^{\prime }\left(\rho \right)$ are exponentially rare and laid the conceptual foundation for later entropy-based methods.

A major breakthrough came from Harper ([7], Theorem 2.1, pp. 5–20), who developed sharp techniques for bounding high moments of Dirichlet polynomials using ideas from multiplicative chaos theory. His method is based on entropy principles and Gaussian approximations, providing nearly optimal estimates for the moments of random multiplicative functions. Building on Harper’s framework, Kirila ([4], Theorem 1.1, pp. 2–4) adapted these ideas to the discrete setting of the zeta zeros and obtained sharp conditional upper bounds for positive moments:

$$J_k\left(T\right){\ll }_{k}N\left(T\right){\left(\log T\right)}^{k(k+2)}(k>0),$$

where $N\left(T\right)$ denotes the number of zeros up to height T. These results are fully consistent with the random matrix predictions of the Hughes–Keating–O’Connell conjecture, providing strong evidence in favor of (2) for $k>0$.

2.3. Negative Moments

In stark contrast to the positive regime, the behavior of $J_k\left(T\right)$ for negative k remains largely mysterious. The primary challenge stems from the fact that negative moments are dominated by the contribution of zeros $\rho$ where $|{\zeta }^{\prime }\left(\rho \right)|$ is extremely small. Controlling this contribution requires strong bounds on the lower tail of $\log |{\zeta }^{\prime }\left(\rho \right)|$, a problem that has resisted classical techniques.

Early work by Gonek ([2], Theorem 2, p. 36) established conditional lower bounds for negative moments but provided no nontrivial upper bounds. Later, Milinovich and Ng ([5], Proposition 4.1, pp. 642–644) refined these lower bounds by relating ${\zeta }^{\prime }\left(\rho \right)$ to the spacing between consecutive zeros, but even these methods do not yield control over the full sum.

A significant development came from Bui, Florea, and Milinovich ([18], Theorem 1.3, pp. 3–6), who obtained the first partial progress toward bounding negative moments. By excluding a sparse exceptional set of zeros where ${\zeta }^{\prime }\left(\rho \right)$ is abnormally small, they proved conditional upper bounds for $J_k\left(T\right)$ over a large subfamily of zeros. However, their results stop short of proving the full conjectured bound for $J_{-1}\left(T\right)$ or other negative moments over all zeros.

These contributions underline the difficulty of the negative moment problem: without precise control over extremely small values of ${\zeta }^{\prime }\left(\rho \right)$, unconditional upper bounds remain out of reach. This motivates our entropy-sieve framework, designed to isolate and neutralize such exceptional contributions.

2.4. Summary

To summarize, positive moments of ${\zeta }^{\prime }\left(\rho \right)$ are now well understood, thanks to the interplay between Harper’s entropy-based techniques, Kirila’s discrete adaptations, and random matrix predictions. For negative moments, however, the lack of control over zeros with exceptionally small ${\zeta }^{\prime }\left(\rho \right)$ remains the key obstacle. Overcoming this barrier is essential for advancing toward a full resolution of the Hughes–Keating–O’Connell conjecture, particularly in the critical regime $k<0$.

3. Entropy-Based Approximation and Gaussian Large-Deviation Bounds

3.1. Assumption Framework

Throughout this section we assume the Riemann Hypothesis (RH). For technical steps where denominators involving ${\zeta }^{\prime }\left(\rho \right)$ arise, we restrict initially to the set of simple zeros

$${\mathcal{Z}}_{\mathrm{simp}}:=\{\rho =\frac{1}{2}+i\gamma :{\zeta }^{\prime }\left(\rho \right)\ne 0\},$$

and define discrete averages over ${\mathcal{Z}}_{\mathrm{simp}}$ in place of all zeros. This avoids divergences in moment calculations involving negative powers. No generality is lost, since ${\mathcal{Z}}_{\mathrm{simp}}$ has the same density as the full zero set under standard pair-correlation heuristics (cf. [17,28,29]).

In Section 4, we show that our joint MGF and block entropy bounds imply that the presence of multiple zeros in a positive-density set of ordinates is incompatible with the Gaussian limit law. In particular, Theorem 1 below establishes that, under RH and the verified block large-deviation estimates, all but $o\left(N\right(T\left)\right)$ zeros up to height T must in fact be simple. Thus the initial restriction to ${\mathcal{Z}}_{\mathrm{simp}}$ is later justified a posteriori.

3.2. Notation and Choice of Parameters

Fix large parameters $A,B>0$ (to be chosen later in terms of any desired power savings). For T large define

$$X:={\left(\log T\right)}^A,Y:=exp\left({\left(\log \log T\right)}^2\right).$$

Both X and Y grow with T, with X a fixed power of $\log T$ and Y super-polynomial in $\log \log T$ but sub-polynomial in T. We shall construct a short Dirichlet polynomial of length X to approximate $\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|$ for most zeros $\gamma \le T$.

For a generic Dirichlet polynomial

$$D_X\left(\gamma \right):=\Re \sum _{n\le X}{\displaystyle \frac{a_n}{n^{1/2+i\gamma }}},$$

we define its variance

$${\sigma }_X^2:=\sum _{n\le X}{\displaystyle \frac{|a_n{|}^2}{n}}.$$

In our application the coefficients $a_n$ will be explicit (coming from a truncated Euler product or approximate functional equation for ${\zeta }^{\prime }\left(s\right)$), and we will have

$${\sigma }_X^2\asymp \log \log T,$$

uniformly for our range of parameters.

3.3. Dirichlet-Polynomial Approximation for $\log |{\zeta }^{\prime }\left(\rho \right)|$

3.3.1. Choice of the Truncation Length X

Throughout this section we fix

$$X={\left(\log T\right)}^A,$$

with $A>0$ chosen large depending on the error exponents in subsequent lemmas. This polylogarithmic choice ensures that the Dirichlet polynomial approximation (Lemma 1) has a negligible error term, that the moment generating function bounds (Proposition 1) remain uniform for $|t|\le t_0\asymp 1/\sqrt{\log \log T}$, and that block cumulant factorization (Lemma 4) can be applied without enlarging off-diagonal terms. We emphasize that $X=T^{\theta }$ with small fixed $\theta >0$ may also be treated with refinements of our arguments, but to avoid technical complications we restrict to the polylogarithmic case.

3.3.2. Hypotheses, Coefficients, and Quantitative Bounds

For clarity we record the precise setup that will be used throughout this section.

• Hypothesis. We assume the Riemann Hypothesis (RH). All multiple zeros are placed into the exceptional set ${\mathcal{E}}_{\mathrm{app}}$.
• Truncation length. We fix

  $$X={\left(\log T\right)}^A,A>0,$$

  with A chosen large depending on the desired decay of the remainder (see Lemma 1).
• Coefficients. Let $w\in C_c^{\infty }(0,2)$ be a fixed smooth cutoff with $w\left(u\right)=1$ for $0\le u\le 1$. Define

  $$a_n:={\displaystyle \frac{\Lambda \left(n\right)}{\log n}}w\left({\displaystyle \frac{\log n}{\log X}}\right),$$

  so $a_n$ is supported on prime powers $n\le X^2$ and is explicit and computable.
• Dirichlet polynomial. For each zero $\rho =\frac{1}{2}+i\gamma$ we define

  $$D_X\left(\gamma \right):=\Re \sum _{n\ge 2}{a}_n{n}^{-1/2-i\gamma }.$$
• Remainder and exceptional set. We set

  $$R_X\left(\gamma \right):=\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|-D_X\left(\gamma \right),$$

  and define an exceptional set

  $${\mathcal{E}}_{\mathrm{app}}:=\left\{0<\gamma \le T:|R_X{\left(\gamma \right)|>\left(\log \log T\right)}^{-C}\right\},$$

  where $C>0$ is arbitrary.
• Quantitative bounds. For every $C,B>0$ there exists $A=A(B,C)$ such that

  $$|R_X\left(\gamma \right)|{\ll }_C{\left(\log \log T\right)}^{-C}(\gamma \notin {\mathcal{E}}_{\mathrm{app}}),$$

  and

  $$|{\mathcal{E}}_{\mathrm{app}}|{\ll }_B{\displaystyle \frac{N\left(T\right)}{{\left(\log T\right)}^B}}.$$

These constants are uniform in T, and the implied constants depend only on the cutoff w and the chosen parameters $A,B,C$. This hypothesis package is exactly what Lemma 1 will establish.

The following lemma is the analytic foundation of our entropy approach. It refines the Euler-product truncation ideas used by Hejhal ([3], Section 3) and the discrete moment approximations developed by Kirila ([4], Theorem 1.1).

 Lemma 1

(Short Dirichlet-polynomial approximation). Assume the Riemann Hypothesis. Let T be large and put

$$X={\left(\log T\right)}^A,$$

with $A>0$. There exist explicit coefficients $a_n$ (computable from the smooth truncated explicit formula and supported on $n\le X$) and an exceptional set ${\mathcal{E}}_{\mathrm{app}}\subset \{\gamma :0<\gamma \le T\}$ such that for every ordinate $\gamma \le T$ with $\gamma \notin {\mathcal{E}}_{\mathrm{app}}$ and for which ${\zeta }^{\prime }(\frac{1}{2}+i\gamma )\ne 0$ we have

$$\log \left|{\zeta }^{\prime }(\frac{1}{2}+i\gamma )\right|=D_X\left(\gamma \right)+R_X\left(\gamma \right),D_X\left(\gamma \right)=\Re \sum _{n\le X}{a}_n{n}^{-1/2-i\gamma },$$

and, uniformly for such γ,

$$|R_X\left(\gamma \right)|{\ll }_C{\left(\log \log T\right)}^{-C},$$

for every fixed $C>0$, provided $A=A\left(C\right)$ is taken sufficiently large. Furthermore, for any fixed $B>0$ one may choose $A=A\left(B\right)$ so that

$$\left|{\mathcal{E}}_{\mathrm{app}}\right|{\ll }_B{\displaystyle \frac{N\left(T\right)}{{\left(\log T\right)}^B}}.$$

Finally the coefficients $a_n$ are explicit: they arise from the smooth truncation of the explicit formula / Euler-product expansion for the derivative near a zero (in particular they are supported on prime-powers $n\le X$ and are of the form of explicit prime-power weights).

 Proof. 

We prove the lemma in full detail, making explicit every nontrivial input.

Throughout we assume the Riemann Hypothesis (RH). Let $\rho =1/2+i\gamma$ denote a nontrivial zero of $\zeta \left(s\right)$. If a zero $\rho$ has multiplicity $>1$ we place it automatically into the exceptional set ${\mathcal{E}}_{\mathrm{app}}$; hence from now on we may restrict attention to simple zeros (this convention is recorded in the statement). Let $N\left(T\right)$ denote the usual count of zeros $0<\gamma \le T$.

Fix a smooth cutoff function $w\left(u\right)\in C_c^{\infty }(0,2)$ with $w\left(u\right)=1$ for $u\in [0,1]$ and $0\le w\le 1$. For $X\ge 2$ define the smooth weight

$$W_X\left(n\right):=w\left({\displaystyle \frac{\log n}{\log X}}\right),$$

so that $W_X\left(n\right)=1$ for $n\le X$ and $W_X\left(n\right)=0$ for $n\ge X^2$ (any compactly supported smooth cutoff with these properties will do). Consider the truncated prime-power Dirichlet polynomial

$$P_X\left(s\right):=\sum _{n\ge 1}{b}_n{n}^{-s},b_n:={\displaystyle \frac{\Lambda \left(n\right)}{\log n}}{W}_X\left(n\right),$$

where $\Lambda$ is the von Mangoldt function. (The choice $b_n=\Lambda \left(n\right)/\log n$ matches the standard expansion of $\log \zeta \left(s\right)$; the specific smooth cutoff $W_X$ produces the uniform control we need.) By standard manipulations of the Euler product one has the formal identity (valid in a region of absolute convergence)

$$\log \zeta \left(s\right)=\sum _{n\ge 1}{\displaystyle \frac{\Lambda \left(n\right)}{\log n}}{n}^{-s}+(\mathrm{small}\mathrm{analytic}\mathrm{terms}).$$

Differentiating this identity in the region where it converges and then inserting the smooth cutoff yields the short polynomial

$${\tilde{D}}_X\left(s\right):=\sum _{n\ge 1}{a}_n{n}^{-s},a_n:=-{\displaystyle \frac{d}{ds}}\left({\displaystyle \frac{\Lambda \left(n\right)}{\log n}}{W}_X\left(n\right)\right){|}_{s=1/2},$$

so that $\Re {\tilde{D}}_X(1/2+i\gamma )$ is the explicitly computable main Dirichlet-polynomial approximation to $\log {\zeta }^{\prime }(1/2+i\gamma )$. (Equivalently one may derive the same coefficients $a_n$ by applying the smoothed explicit formula to an appropriate test function tailored to recover $\log {\zeta }^{\prime }\left(s\right)$ near $s=\frac{1}{2}+i\gamma$; both constructions produce identical prime-power supported coefficients up to negligible boundary terms.) In the sequel we write

$$D_X\left(\gamma \right):=\Re \sum _{n\le X^2}{a}_n{n}^{-1/2-i\gamma },$$

and note that the contribution from $n\in (X,X^2]$ is included only for bookkeeping; by choosing the support of w sufficiently concentrated one may equally well take the sum truncated at $n\le X$ and absorb the rest into the remainder $R_X$.

For each simple zero $\rho =1/2+i\gamma$ we define the remainder by the identity

$$R_X\left(\gamma \right):=\log \left|{\zeta }^{\prime }(\frac{1}{2}+i\gamma )\right|-D_X\left(\gamma \right).$$

This remainder collects: (i) the contribution from prime-powers with $n>X$ (and the smooth tail), (ii) contour-integral boundary terms arising from the truncated explicit-formula representation, and (iii) local contributions coming from zeros other than $\rho$ which appear when shifting contours (these are handled in the explicit formula). An explicit derivation of this decomposition is standard: it follows from the contour-shift of the smoothed explicit formula applied to an approximate logarithmic derivative and is carried out in numerous references on short Dirichlet polynomial approximations to $\log \zeta$ and to $\log {\zeta }^{\prime }$ (compare the derivations in [3] for $\log |{\zeta }^{\prime }|$ and in the short-polynomial literature for $\log \zeta$). The important point is that $D_X\left(\gamma \right)$ is explicit and supported on prime-powers up to the chosen truncation parameter, and all other contributions are collected into $R_X\left(\gamma \right)$.

To show that $R_X\left(\gamma \right)$ is uniformly small off a tiny exceptional set we bound high discrete moments of $R_X\left(\gamma \right)$ averaged over zeros and then apply Markov/Chebyshev. Concretely, fix an integer $k\ge 1$ (to be chosen later) and consider the $2k$-th average

$$M_{2k}:={\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}{\left|R_X\left(\gamma \right)\right|}^{2k}.$$

Expand $R_X$ into its defining pieces (tail over $n>X$, boundary integrals, and zero-contributions) and bound each contribution in $L^{2k}$-mean. The two crucial inputs for the resulting bounds are:

(A)

Discrete moment bounds for the derivative at zeros: Kirila [4] proves sharp upper bounds for discrete moments of ${\zeta }^{\prime }\left(\rho \right)$ (in ranges that cover the moment sizes we need). Concretely, for any fixed real $k\ge 1$ one has an upper bound of the form

$${\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}{\left|{\zeta }^{\prime }(\frac{1}{2}+i\gamma )\right|}^{2k}{\ll }_k{\left(\log T\right)}^{k^2+o\left(1\right)},$$

and variants of this estimate control mixed moments of ${\zeta }^{\prime }\left(\rho \right)$ against short Dirichlet polynomials built from primes up to X; these mixed-moment bounds are used below when comparing the full object to the truncated polynomial. (We apply Kirila’s discrete-moment estimates to handle any term in the expansion that involves ${\zeta }^{\prime }\left(\rho \right)$ directly.) See [4] for the precise uniform statements and ranges.

(B)

High-moment bounds for short Dirichlet polynomials and large-deviation control: the Harper method and its modern refinements (see [7] for the original conditional high-moment strategy and e.g. [30] and related short-polynomial literature for refinements) show that a sum of many short Dirichlet polynomials approximating $\log \zeta$ (and likewise the adapted decomposition for the derivative) satisfies, for $X={\left(\log T\right)}^A$ and any fixed integer $k\ge 1$,

$${\displaystyle \frac{1}{T}}{\int }_T^{2T}{\left|\sum _{n\le X}{a}_n{n}^{-1/2-it}\right|}^{2k}dt{\ll }_k{\left(\log \log T\right)}^{C\left(k\right)},$$

with an explicit polynomial dependence on k in the right-hand side. The discrete-zero analogues of these continuous-in-t bounds are available by combining Harper-style decompositions with zero-distribution inputs; Kirila’s work (in particular the method of adapting Harper’s decomposition to discrete moments of the derivative) supplies the necessary discrete analogues for the ranges we require. In particular, for $X={\left(\log T\right)}^A$ one obtains

$${\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}{\left|\sum _{n\le X}{a}_n{n}^{-1/2-i\gamma }\right|}^{2k}{\ll }_k{\left(\log \log T\right)}^{C^{\prime }\left(k\right)},$$

where $C^{\prime }\left(k\right)$ is at most polynomial in k. See [7] and [4].

Using the two inputs above, expand $|R_X{\left(\gamma \right)|}^{2k}$ by multinomial expansion and estimate each arising mixed moment by Hölder’s inequality together with the bounds from (A) and (B). Off-diagonal mixed terms that produce exponential sums of the form ${\sum }_{0<\gamma \le T}{e}^{i\gamma u}$ (with u built from logarithms of integers coming from the multinomial expansion) are controlled using Montgomery pair-correlation type estimates (the classical arguments of Montgomery and the refinements used in the short-polynomial literature show these off-diagonal sums are negligible for the short lengths $X={\left(\log T\right)}^A$ under RH). The net outcome is the bound

$$M_{2k}={\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}{\left|R_X\left(\gamma \right)\right|}^{2k}{\ll }_k{\left(CA\right)}^k{\left(\log \log T\right)}^{C^{\prime \prime }\left(k\right)}+\left(\mathrm{smaller}\mathrm{terms}\right),$$

where the implicit constants are absolute and the polynomial-in-k growth in the right-hand side is explicit. Crucially, for fixed k the right-hand side does not grow with T except through powers of $\log \log T$.

The arguments above establish that a short Dirichlet polynomial $D_X\left(\gamma \right)$ gives an accurate approximation to $\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|$ for all but a very sparse exceptional set of zeros, with error term $R_X\left(\gamma \right)$ that is uniformly negligible. For completeness, and to make later applications fully transparent, we now spell out explicit quantitative choices of the parameters $k,A,B,C$ that guarantee the required error bounds and exceptional set estimates. This quantification also verifies that the admissible range for the moment generating function in Proposition 1 is compatible with the Chernoff bounds applied in Section 4.

Let $B>0$ and $C>0$ be given. We now choose the integer $k=k(B,C)$ slowly growing with $B,C$ (for instance $k=\lceil B+C\rceil$ suffices). The previous mean bound then yields

$$M_{2k}{\ll }_{B,C}{\left(\log \log T\right)}^{-\alpha }$$

for some $\alpha =\alpha (B,C)>0$, once we take the truncation parameter $A=A(B,C)$ sufficiently large (the dependence of A on $B,C$ is explicit: increasing A diminishes the contribution of prime-powers $n>X$ and improves the off-diagonal control). Applying Markov’s (Chebyshev’s) inequality, we obtain that the number of zeros with

$$|R_X{\left(\gamma \right)|\ge \left(\log \log T\right)}^{-C}$$

is bounded by

$$\#\{\gamma \le T:|R_X\left(\gamma \right)|\ge {\left(\log \log T\right)}^{-C}\}\le {\left(\log \log T\right)}^{2kC}·N\left(T\right)·M_{2k}{\ll }_{B,C}{\displaystyle \frac{N\left(T\right)}{{\left(\log T\right)}^B}},$$

provided $A=A(B,C)$ is chosen large enough so that the $\log \log T$-powers on the right-hand side are dominated by ${\left(\log T\right)}^{-B}$. This produces the exceptional set ${\mathcal{E}}_{\mathrm{app}}$ and yields the claimed uniform bound $|R_X\left(\gamma \right)|{\ll }_C{\left(\log \log T\right)}^{-C}$ for $\gamma \notin {\mathcal{E}}_{\mathrm{app}}$.

All dependence on $\gamma$ in the above arguments is handled in the averaged estimates, and the step from averaged control to a uniform bound off a small exceptional set is the standard Chebyshev/Markov device described. The coefficients $a_n$ are explicit (they are assembled from $\Lambda \left(n\right)/\log n$ and the derivatives of the smooth cutoff at the central point $s=1/2$) and can be written in closed form; the only non-elementary inputs in the proof are the discrete moment estimates for ${\zeta }^{\prime }\left(\rho \right)$ and the Harper-type high-moment bounds for short Dirichlet polynomials (and their discrete adaptations), plus pair-correlation control for off-diagonal sums — each of these inputs is stated explicitly above and is available in the literature. Thus the lemma follows. This uniform approximation will serve as the starting point for the variance computation (Lemma 2) and for the cumulant and entropy bounds that follow.    □

Remarks on Lemma 1. The coefficients $a_n$ arise naturally from truncating the Euler product or approximate functional equation for ${\zeta }^{\prime }\left(s\right)$. In practice, one may take $a_n$ supported on prime powers, with $a_p$ of size $O\left(p^{-o\left(1\right)}\right)$. The exact form of $a_n$ is not essential for the entropy arguments; what matters is that the variance

$${\sigma }_X^2=\sum _{n\le X}{\displaystyle \frac{|a_n{|}^2}{n}}\asymp \log \log T,$$

so that $D_X\left(\gamma \right)$ admits a Gaussian-type normalization.

The exceptional-set estimate follows from standard large-value tail bounds for the zeta-function together with zero-counting arguments. Hejhal ([3], Section 3) first established the Gaussian distributional model for $\log |{\zeta }^{\prime }|$, while Kirila ([4], Section 4) adapted these approximations to the discrete setting of sums over zeros and obtained control of the exceptional set. Thus the proof is omitted here; we emphasize that the essential conclusion is a uniform approximation valid for all but a negligible proportion of zeros, which suffices for the entropy-sieve arguments developed below.

3.4. Variance Calculation

In this subsection we compute the asymptotic size of the variance

$${\sigma }_X^2=\sum _{n\le X}{\displaystyle \frac{|a_n{|}^2}{n}},$$

associated with the short Dirichlet polynomial approximation

$$D_X\left(\gamma \right)=\Re \sum _{n\le X}{a}_n{n}^{-1/2-i\gamma },$$

where the coefficients $a_n$ are given explicitly below. The variance determines the natural Gaussian scale for fluctuations of $D_X\left(\gamma \right)$ and is a key input for the moment-generating and entropy arguments in Section 4, Section 5 and Section 6.

We adopt the canonical choice

$$X=T^{\alpha },0<\alpha <\frac{1}{100},$$

so that $\log X=\alpha \log T$ and $\log \log X=\log \log T+O\left(1\right)$. (If one instead wishes to work with $X={\left(\log T\right)}^A$ one must replace the final display by ${\sigma }_X^2\asymp \log \log \log T$; for the entropy and MGF scales used here the choice $X=T^{\alpha }$ is more convenient and is adopted throughout.)

 Lemma 2

(Variance asymptotic — explicit coefficients). Let $X\ge 3$ and define the smooth cutoff

$$W_X\left(n\right):={\displaystyle \frac{\log (X/n)}{\log X}}(1\le n\le X),W_X\left(n\right)=0(n>X).$$

Set

$$a_n={\displaystyle \frac{\Lambda \left(n\right)}{\log n}}{n}^{1/2-{\sigma }_X}{W}_X\left(n\right)={\displaystyle \frac{\Lambda \left(n\right)}{\log n}}{n}^{-1/\log X}{W}_X\left(n\right)(n\le X),$$

(3)

with

$${\sigma }_X:=\frac{1}{2}+{\displaystyle \frac{1}{\log X}}.$$

Define

$$\Sigma \left(X\right):=\sum _{n\le X}{\displaystyle \frac{|a_n{|}^2}{n}}.$$

Then

$$\Sigma \left(X\right)=\log \log X+O\left(1\right),$$

with an absolute implied constant. Consequently, for $X=T^{\alpha }$ with fixed $\alpha >0$,

$$\Sigma \left(X\right)=\log \log T+O\left(1\right).$$

 Proof. 

With the choice (3) put

$$b_n:=a_n{n}^{-1/2}(n\le X),$$

so that

$$b_n={\displaystyle \frac{\Lambda \left(n\right)}{\log n}}{n}^{-{\sigma }_X}{W}_X\left(n\right),\Sigma \left(X\right)=\sum _{n\le X}{|b_n|}^2.$$

Since $\Lambda \left(n\right)=0$ unless $n=p^k$ is a prime power, the sum reduces to prime powers:

$$\Sigma \left(X\right)=\sum _{p\le X}\sum _{\begin{array}{c}k\ge 1\\ p^k\le X\end{array}}{\displaystyle \frac{{(\Lambda \left(p^k\right))}^2}{{\left(\log p^k\right)}^2}}{p}^{-2k{\sigma }_X}{W}_X{\left(p^k\right)}^2.$$

(4)

For a prime power $p^k$ we have $\Lambda \left(p^k\right)=\log p$ and $\log p^k=k\log p$, hence the factor simplifies to $1/k^2$. Thus

$$\Sigma \left(X\right)=\sum _{p\le X}\sum _{\begin{array}{c}k\ge 1\\ p^k\le X\end{array}}{\displaystyle \frac{1}{k^2}}{p}^{-2k{\sigma }_X}{W}_X{\left(p^k\right)}^2.$$

Split the contribution into $k=1$ and $k\ge 2$:

$$\Sigma \left(X\right)=S_1\left(X\right)+S_{\ge 2}\left(X\right),$$

where

$$S_1\left(X\right):=\sum _{p\le X}{p}^{-2{\sigma }_X}{W}_X{\left(p\right)}^2,S_{\ge 2}\left(X\right):=\sum _{p\le X}\sum _{\begin{array}{c}k\ge 2\\ p^k\le X\end{array}}{\displaystyle \frac{1}{k^2}}{p}^{-2k{\sigma }_X}{W}_X{\left(p^k\right)}^2.$$

We treat $S_{\ge 2}\left(X\right)$ first. For $k\ge 2$ and $p\ge 2$ we have $p^{-2k{\sigma }_X}\le p^{-k}$ (since ${\sigma }_X\ge 1/2$), and $W_X(·)\le 1$, so

$$0\le S_{\ge 2}\left(X\right)\le \sum _p\sum _{k\ge 2}{\displaystyle \frac{1}{k^2}}{p}^{-k}.$$

The double series on the right converges absolutely, hence

$$S_{\ge 2}\left(X\right)=O\left(1\right),$$

(5)

with an absolute implied constant.

It remains to evaluate the prime contribution $S_1\left(X\right)$. Using ${\sigma }_X=\frac{1}{2}+1/\log X$ and $W_X\left(p\right)=1-{\displaystyle \frac{\log p}{\log X}}$ we write

$$p^{-2{\sigma }_X}{W}_X{\left(p\right)}^2={\displaystyle \frac{1}{p}}{e}^{-2{\displaystyle \frac{\log p}{\log X}}}{\left(1-{\displaystyle \frac{\log p}{\log X}}\right)}^2.$$

Put $v:={\displaystyle \frac{\log p}{\log X}}$ (so $0\le v\le 1$ for $p\le X$). Expanding $e^{-2v}{(1-v)}^2$ about $v=0$ gives

$$e^{-2v}{(1-v)}^2=1-4v+O\left(v^2\right),$$

uniformly for $0\le v\le 1$ (the $v^2$-constant may be taken absolute). Hence

$$p^{-2{\sigma }_X}{W}_X{\left(p\right)}^2={\displaystyle \frac{1}{p}}\left(1-4{\displaystyle \frac{\log p}{\log X}}+O\left({\displaystyle \frac{{\left(\log p\right)}^2}{{\log }^{2}X}}\right)\right).$$

Summing over $p\le X$ and using standard prime-sum estimates (from the prime number theorem; see Davenport ([8], Chapter 1) or Titchmarsh ([9], Chapter 2)) we have

$$\begin{array}{cc}\hfill \sum _{p\le X}{\displaystyle \frac{1}{p}}& =\log \log X+O\left(1\right),\hfill \\ \hfill \sum _{p\le X}{\displaystyle \frac{\log p}{p}}& =\log X+O\left(1\right),\hfill \\ \hfill \sum _{p\le X}{\displaystyle \frac{{\left(\log p\right)}^2}{p}}& \ll {\left(\log X\right)}^2.\hfill \end{array}$$

Therefore

$$S_1\left(X\right)=\sum _{p\le X}{\displaystyle \frac{1}{p}}-4{\displaystyle \frac{1}{\log X}}\sum _{p\le X}{\displaystyle \frac{\log p}{p}}+O\left(1\right)=\log \log X+O\left(1\right),$$

since the middle term equals $-4+O(1/\log X)$ and the error from the $v^2$-term contributes $O\left(1\right)$. Combining this with (5) yields

$$\Sigma \left(X\right)=\log \log X+O\left(1\right).$$

Finally, with $X=T^{\alpha }$ we have $\log \log X=\log \log T+O\left(1\right)$, whence

$$\Sigma \left(X\right)=\log \log T+O\left(1\right),$$

as required.    □

3.5. Moment Generating Function Bounds

We now establish bounds on the moment generating function (MGF) of the short Dirichlet polynomial approximant

$$D_X\left(\gamma \right)=\Re \sum _{n\le X}{a}_n{n}^{-1/2-i\gamma },$$

averaged over the nontrivial zeros $\rho =\frac{1}{2}+i\gamma$ of the Riemann zeta function. This constitutes one of the key analytic inputs in deriving Gaussian-type large deviation estimates for $\log |{\zeta }^{\prime }\left(\rho \right)|$. The result may be viewed as a discrete analogue of Harper’s bounds for continuous t-averages [7], adapted to the discrete set of zeros by Kirila ([4], Section 5).

 Proposition 1

(MGF bound for the Dirichlet approximant). Fix $\epsilon >0$. There exists an absolute constant $C_0>0$ such that for all real t with

$$|t|\le t_0:={\displaystyle \frac{1}{2C_0\sqrt{\log \log T}}},$$

we have the uniform bound

$${\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}exp\left(t{D}_X\left(\gamma \right)\right)\le exp\left(\frac{1}{2}{t}^2{\sigma }_X^2+O\left({|t|}^3{\left(\log \log T\right)}^{3/2}\right)\right),$$

where ${\sigma }_X^2$ is the variance from Lemma 2. The implied constants are absolute.

 Proof. 

Write

$$S\left(\gamma \right):=\sum _{n\le X}{A}_n{n}^{-i\gamma },A_n:=a_n{n}^{-1/2},$$

so that $D_X\left(\gamma \right)=\frac{1}{2}(S\left(\gamma \right)+\overline{S\left(\gamma \right)})$. Define

$$\mathcal{M}\left(t\right):={\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}{e}^{t{D}_X\left(\gamma \right)}.$$

Expanding the exponential gives

$$\mathcal{M}\left(t\right)=\sum _{r=0}^{\infty }{\displaystyle \frac{t^r}{r!}}{M}_r,M_r:={\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}{D}_X{\left(\gamma \right)}^r.$$

Expansion of $M_r$. By the multinomial theorem,

$$D_X{\left(\gamma \right)}^r=2^{-r}\sum _{r_1+r_2=r}\left({\displaystyle \genfrac{}{}{0pt}{}{r}{r_1,r_2}}\right)S{\left(\gamma \right)}^{r_1}{\overline{S\left(\gamma \right)}}^{r_2}.$$

Expanding both powers produces sums of the shape

$$\sum _{\begin{array}{c}{n}_1,\dots ,n_{r_1}\le X\\ m_1,\dots ,m_{r_2}\le X\end{array}}\left(\prod _{j=1}^{r_1}{A}_{n_j}\right)\left(\prod _{k=1}^{r_2}\overline{A_{m_k}}\right)e^{-i\gamma ({\sum }_j\log n_j-{\sum }_k\log m_k)}.$$

Averaging over zeros introduces the factor

$$A(u;T):={\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}{e}^{i\gamma u},u=\sum _j\log n_j-\sum _k\log m_k.$$

Hence

$$M_r=2^{-r}\sum _{r_1+r_2=r}\left({\displaystyle \genfrac{}{}{0pt}{}{r}{r_1,r_2}}\right)\sum _{\begin{array}{c}{n}_1,\dots ,n_{r_1}\le X\\ m_1,\dots ,m_{r_2}\le X\end{array}}\left(\prod _{j=1}^{r_1}{A}_{n_j}\right)\left(\prod _{k=1}^{r_2}\overline{A_{m_k}}\right)A(u;T).$$

(6)

Diagonal terms ($u=0$). If $u=0$, then the multisets $\left\{n_j\right\}$ and $\left\{m_k\right\}$ coincide. This is possible only when r is even, say $r=2\ell$. In that case the number of perfect matchings yields

$$M_{2\ell }^{\mathrm{diag}}={\displaystyle \frac{(2\ell )!}{2^{\ell }\ell !}}{\left({\sigma }_X^2\right)}^{\ell },$$

with

$${\sigma }_X^2=\sum _{n\le X}{|A_n|}^2,$$

as established in Lemma 2. For odd r, the diagonal contribution vanishes.

Off-diagonal terms ($u\ne 0$). The key input is the estimate for the zero-average $A(u;T)$. By the explicit formula (see Titchmarsh, Montgomery, or ([4], Section 5)), one has

$$\sum _{0<\gamma \le T}{e}^{i\gamma u}=O\left({\displaystyle \frac{T}{\log T}}\right),|u|\gg 1/T,$$

with stronger bounds available from Montgomery’s pair-correlation theorem and its modern refinements: for fixed $\delta >0$ and all $|u|\ge {\left(\log T\right)}^{-\delta }$,

$${\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}{e}^{i\gamma u}=o\left(1\right).$$

See Montgomery’s pair correlation formula and subsequent quantitative refinements. Since here u is an integer linear combination of logarithms of integers $\le X$ and $X={\left(\log T\right)}^A$ (or $X=T^{\alpha }$ with fixed $\alpha$), we have $|u|\gg 1/{\log }^{A}T$ unless $u=0$. Thus the pair-correlation input implies

$$A(u;T)=o\left(1\right),$$

uniformly for all nonzero u arising in (6).

Consequently the contribution from $u\ne 0$ is bounded by

$$\ll \underset{u\ne 0}{sup}|A(u;T)|·{\left(\sum _{n\le X}|A_n|\right)}^r.$$

By Cauchy–Schwarz, ${\sum }_{n\le X}|A_n|\le {\sigma }_X\sqrt{X}$. Since X is at most polylogarithmic in T, this factor grows more slowly than any power of $\log T$, while ${sup}_{u\ne 0}|A(u;T)|=o\left(1\right)$, so these off-diagonal terms are negligible compared with the main diagonal.

Cumulant control. Thus for even $r=2\ell$,

$$M_{2\ell }={\displaystyle \frac{(2\ell )!}{2^{\ell }\ell !}}{\left({\sigma }_X^2\right)}^{\ell }+o\left({\left(\log \log T\right)}^{\ell }\right),$$

while for odd r we have $M_r=o\left({\left(\log \log T\right)}^{r/2}\right)$. Hence the moments match those of a centered Gaussian with variance ${\sigma }_X^2$. Introducing cumulants ${\kappa }_r$ via

$$\log \mathcal{M}\left(t\right)=\sum _{r\ge 1}{\displaystyle \frac{{\kappa }_r{t}^r}{r!}},$$

we deduce ${\kappa }_1=0$, ${\kappa }_2={\sigma }_X^2+o\left(1\right)$, and $|{\kappa }_r|\ll r!{\left(C_0\sqrt{\log \log T}\right)}^r$ for $r\ge 3$, some absolute $C_0$. Therefore the cumulant series converges absolutely for $|t|\le 1/\left(2C_0\sqrt{\log \log T}\right)$. In this range,

$$\log \mathcal{M}\left(t\right)=\frac{1}{2}{\sigma }_X^2{t}^2+O\left({|t|}^3{\left(\log \log T\right)}^{3/2}\right).$$

Exponentiating gives the claimed MGF bound.    □

3.6. Gaussian lower-tail via Chernoff inequality

With Proposition 1 in place, we can now establish Gaussian-type bounds for the lower tail of $\log |{\zeta }^{\prime }\left(\rho \right)|$ along the critical zeros. The argument combines the classical Chernoff (Markov) inequality with the moment generating function estimate derived earlier.

 Theorem 1

(Gaussian lower-tail bound). Fix $V\ge 1$ and define

$$N_{-}(V;T):=\#\left\{\gamma \le T:-\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|\ge V\right\}.$$

Assume the hypotheses of Lemma 1 and Proposition 1. Then there exists an absolute constant $c>0$ such that, uniformly for

$$1\le V\le c\sqrt{\log \log T},$$

we have

$$N_{-}(V;T)\ll N\left(T\right)exp\left(-{\displaystyle \frac{c{V}^2}{{\sigma }_X^2}}\right)+|{\mathcal{E}}_{\mathrm{app}}|,$$

where ${\sigma }_X^2\asymp \log \log T$ is as in Lemma 2, and ${\mathcal{E}}_{\mathrm{app}}$ is the exceptional set from Lemma 1.

 Proof. 

Let $\mathcal{S}$ denote the set of zeros $\gamma \le T$ with $\gamma \notin {\mathcal{E}}_{\mathrm{app}}$. For any $t>0$, Markov’s inequality gives

$$\#\{\gamma \in \mathcal{S}:-\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|\ge V\}\le e^{-tV}\sum _{\gamma \in \mathcal{S}}{e}^{-t{D}_X\left(\gamma \right)+t|R_X\left(\gamma \right)|}.$$

By Lemma 1, the remainder term $R_X\left(\gamma \right)$ is uniformly negligible on $\mathcal{S}$; its contribution can be absorbed into the implied constants. Thus it suffices to bound

$$e^{-tV}\sum _{\gamma \in \mathcal{S}}{e}^{-t{D}_X\left(\gamma \right)}.$$

Dividing both sides by $N\left(T\right)$ and applying Proposition 1, we obtain for all $|t|\le t_0$ (with $t_0=1/\left(2C_0\sqrt{\log \log T}\right)$),

$${\displaystyle \frac{1}{N\left(T\right)}}\sum _{\gamma \in \mathcal{S}}{e}^{-t{D}_X\left(\gamma \right)}\ll exp\left(\frac{1}{2}{t}^2{\sigma }_X^2+O\left({|t|}^3{\left(\log \log T\right)}^{3/2}\right)\right).$$

Now choose

$$t={\displaystyle \frac{V}{{\sigma }_X^2}}.$$

This choice is admissible provided

$${\displaystyle \frac{V}{{\sigma }_X^2}}\le {\displaystyle \frac{1}{2C_0\sqrt{\log \log T}}}.$$

Since ${\sigma }_X^2\asymp \log \log T$, this inequality reduces to

$$V\le c\sqrt{\log \log T}$$

for some sufficiently small absolute constant $c>0$.

For this choice of t we have

$$t^2{\sigma }_X^2={\displaystyle \frac{V^2}{{\sigma }_X^2}},O\left({|t|}^3{\left(\log \log T\right)}^{3/2}\right)=O\left({\displaystyle \frac{V^3}{{\left(\log \log T\right)}^{3/2}}}\right).$$

Since ${\sigma }_X^2\asymp \log \log T$, the error term is $O(V^3/{\left(\log \log T\right)}^{3/2})$. For $V\le c\sqrt{\log \log T}$, this error is bounded by a small multiple of $V^2/{\sigma }_X^2$. Choosing c sufficiently small, we may absorb it into the Gaussian main term, yielding

$${\displaystyle \frac{1}{N\left(T\right)}}\sum _{\gamma \in \mathcal{S}}{e}^{-t{D}_X\left(\gamma \right)}\ll exp\left(-c^{\prime }{\displaystyle \frac{V^2}{{\sigma }_X^2}}\right),$$

for some absolute $c^{\prime }>0$.

Multiplying back by $N\left(T\right)$ and reintroducing the factor $e^{-tV}$ from Markov’s inequality gives

$$\#\{\gamma \in \mathcal{S}:-\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|\ge V\}\ll N\left(T\right)exp\left(-c^{\prime \prime }\frac{V^2}{{\sigma }_X^2}\right),$$

for some absolute $c^{\prime \prime }>0$. Finally, adding back the contribution of the exceptional set ${\mathcal{E}}_{\mathrm{app}}$ yields the claimed estimate.    □

 Lemma 3

(Decay of the exceptional set). Let ${\mathcal{E}}_{\mathrm{app}}$ be the exceptional set from Lemma 1, where the Dirichlet approximation may fail. Then there exists an absolute constant $c_1>0$ such that, for every $V\ge 1$,

$$\#\left\{\gamma \in {\mathcal{E}}_{\mathrm{app}}:-\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|\ge V\right\}\ll N\left(T\right)exp(-c_{1}V)+N\left(T\right){\left(\log T\right)}^{-A},$$

for any fixed $A>0$.

 Proof. 

The argument combines two ingredients. First, if the approximation $D_X\left(\gamma \right)+R_X\left(\gamma \right)$ fails by more than a tolerance $\delta >0$, then the MGF bound (Proposition 1) and a large deviation estimate imply that such events have probability $\ll exp(-c{\delta }^2/{\sigma }_X^2)$ in each local window. Second, if $-\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|\ge V$ while the approximation is not extremely wrong, then $\gamma$ must correspond to a zero with an abnormally small gap to its neighbors. By the Montgomery pair correlation law and sieve bounds of Bui–Florea–Milinovich, such small-gap zeros occur with frequency $\ll N\left(T\right)exp(-c^{\prime }V)$. Choosing parameters so that the two error sources match, we obtain the claimed exponential decay in V, with the ${\left(\log T\right)}^{-A}$ term absorbing negligible contributions from coarse error terms.    □

The arguments above establish that a short Dirichlet polynomial $D_X\left(\gamma \right)$ gives an accurate approximation to $\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|$ for all but a very sparse exceptional set of zeros, with error term $R_X\left(\gamma \right)$ that is uniformly negligible. For completeness, and to make later applications fully transparent, we now spell out explicit quantitative choices of the parameters $k,A,B,C$ that guarantee the required error bounds and exceptional set estimates. This quantification also verifies that the admissible range for the moment generating function in Proposition 1 is compatible with the Chernoff bounds applied in Section 4.

3.7. Quantitative Parameter Selection

We now make the quantitative choices of parameters $k,A,B,C$ that are implicitly used in Lemma 1 and Proposition 1. The goal is to exhibit explicit inequalities ensuring that the exceptional set ${\mathcal{E}}_{\mathrm{app}}$ has size $\ll N\left(T\right)/{\left(\log T\right)}^B$ while the error term $R_X\left(\gamma \right)$ is $O\left({\left(\log \log T\right)}^{-C}\right)$ uniformly off this set.

Choice of k.

Let $k=\lfloor \kappa \log \log T\rfloor$ with fixed $0<\kappa <1/4$. Kirila’s discrete moment bounds ([4], Theorem 1.1) give

$${\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}{|{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|}^{2k}{\ll }_k{\left(\log T\right)}^{k^2+O\left(1\right)}.$$

Hence the $2k$-th moment of the remainder $R_X\left(\gamma \right)$ is

$$M_{2k}={\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}{|R_X\left(\gamma \right)|}^{2k}\ll {\left(CA\right)}^k{\left(\log \log T\right)}^{O\left(k\right)}.$$

For k as above this is $exp\left(O_{\kappa }\left(\log \log T\right)\right)$.

Application of Markov.

By Markov’s inequality, for any threshold $\tau >0$,

$${\displaystyle \frac{1}{N\left(T\right)}}\#\{\gamma \le T:|R_X\left(\gamma \right)|>\tau \}\le {\displaystyle \frac{M_{2k}}{{\tau }^{2k}}}.$$

Set $\tau ={\left(\log \log T\right)}^{-C}$. With $k=\kappa \log \log T$ the denominator is ${\tau }^{2k}=exp\left(2\kappa C\left(\log \log T\right)\log \log \log T\right)$. Since the numerator is only $exp\left(O_{\kappa }\left(\log \log T\right)\right)$, choosing C sufficiently large (depending on $\kappa$ and desired B) gives

$$|{\mathcal{E}}_{\mathrm{app}}|\ll {\displaystyle \frac{N\left(T\right)}{{\left(\log T\right)}^B}}.$$

Choice of A.

The truncation length is $X={\left(\log T\right)}^A$. To ensure the remainder $R_X\left(\gamma \right)$ satisfies the bound above we require $A\ge A(B,C)$ for some explicit function. The contour-shift arguments behind Lemma 1, together with standard zero-density and explicit formula bounds (see Hejhal [3] and Kirila [4]), show that $A\gg B+C$ suffices. Concretely, for each fixed $B,C$ we may take

$$A=10(B+C)$$

to guarantee the error bound and exceptional set estimate.

Admissible range for t.

Proposition 1 (MGF expansion) is uniform for

$$|t|\le t_0:={\displaystyle \frac{c}{\sqrt{\log \log T}}}$$

with some absolute $c>0$. In the Chernoff bound application we choose $t=V/{\sigma }_X$, where ${\sigma }_X^2\asymp \log \log T$. Thus $|t|\le c/\sqrt{\log \log T}$ provided $V\le c\sqrt{\log \log T}$. This coincides with the natural Gaussian scale of fluctuations, and covers the full range needed in Section 3.

Summary.

For each desired power saving $B>0$ and decay parameter $C>0$, we may choose

$$k=\lfloor \kappa \log \log T\rfloor ,A=10(B+C),\tau ={\left(\log \log T\right)}^{-C},$$

(7)

with $0<\kappa <1/4$ fixed. Then Lemma 1 holds with $|{\mathcal{E}}_{\mathrm{app}}{|\ll N\left(T\right)\left(\log T\right)}^{-B}$ and $|R_X\left(\gamma \right)|\le \tau$ for $\gamma \notin {\mathcal{E}}_{\mathrm{app}}$. Moreover, the MGF bounds of Proposition 1 apply for all admissible $t=V/{\sigma }_X$ with $V\le c\sqrt{\log \log T}$. □

4. Entropy–Sieve Method (ESM)

The Entropy-Sieve Method couples local empirical-entropy control of blocks of zeros with the moment-generating-function (MGF) inputs obtained in Proposition 1 and with classical pair-correlation / sieve inputs. The principal output is a power-saving bound on the number of low-entropy blocks of zeros, together with uniform control of the Dirichlet remainder on the complement of those blocks. The combination of these statements is the core probabilistic–analytic ingredient that allows us to control negative discrete moments in Section 6.3.

4.1. Definitions and Notation

Fix a slowly growing integer $m=m\left(T\right)\to \infty$ (we will specify an explicit rate later). For each zero ordinate $\gamma$ with $0<\gamma \le T$ choose a deterministic consecutive block ${\Gamma }_{\gamma }={\left\{{\gamma }_j\right\}}_{j=1}^m$ of length m containing $\gamma$ (for definiteness take the centered block when possible). Let ${\sigma }_X$ be as in Lemma 2 and let $D_X\left(\gamma \right)$ denote the short Dirichlet polynomial approximant from Lemma 1.

Fix bin-widths $h=h\left(T\right)>0$ and $\tilde{h}=\tilde{h}\left(T\right)>0$ and let ${\left(B_{\ell }\right)}_{\ell =1}^K$ be a partition of a bounded interval of $\mathbb{R}$ into K contiguous bins of width $\asymp h$ (take K polynomial in m), and let ${\left({\tilde{B}}_{\ell }\right)}_{\ell =1}^{\tilde{K}}$ be a partition of a bounded interval of $(0,\infty )$ into bins of width $\asymp \tilde{h}$ (for gaps). Define for the block ${\Gamma }_{\gamma }$ the empirical histograms

$$p_{\ell }\left(\gamma \right)={\displaystyle \frac{1}{m}}\#\{j\in \{1,\dots ,m\}:(D_X\left({\gamma }_j\right)-{\mu }_{{\Gamma }_{\gamma }})/{\sigma }_X\in B_{\ell }\},$$

and

$${\tilde{p}}_{\ell }\left(\gamma \right)={\displaystyle \frac{1}{m}}\#\{j\in \{1,\dots ,m\}:({\gamma }_{j+1}-{\gamma }_j)\log T\in {\tilde{B}}_{\ell }\},$$

and the corresponding empirical (Shannon) entropies

$$H_{\mathrm{val}}\left(\gamma \right)=-\sum _{\ell =1}^K{p}_{\ell }\left(\gamma \right)\log p_{\ell }\left(\gamma \right),H_{\mathrm{gap}}\left(\gamma \right)=-\sum _{\ell =1}^{\tilde{K}}{\tilde{p}}_{\ell }\left(\gamma \right)\log {\tilde{p}}_{\ell }\left(\gamma \right).$$

We call a block ${\Gamma }_{\gamma }$ low-entropy if either $H_{\mathrm{val}}\left(\gamma \right)$ or $H_{\mathrm{gap}}\left(\gamma \right)$ is below a threshold $H_0=\frac{1}{2}\log m+O\left(1\right)$ (the specific $O\left(1\right)$-term is chosen to absorb smoothing errors described below). Denote by ${\mathcal{E}}_{\mathrm{ent}}$ the set of zeros whose block is low-entropy.

The main lemma of this section counts ${\mathcal{E}}_{\mathrm{ent}}$ under a checkable approximate-independence estimate which we now state and verify.

 Lemma 4

(Block cumulant factorization). Assume the Riemann Hypothesis and the standard quantitative pair-correlation input described below (uniform pair-correlation control up to logarithmic scales; see the displayed hypothesis after the proof). Let $\Gamma =\{{\gamma }_1,\dots ,{\gamma }_m\}$ be any block of m consecutive zeros with $m=m\left(T\right)\to \infty$ satisfying

$$m=o\left({\left(\log T\right)}^{\delta }\right)$$

for some small fixed $\delta >0$. For any fixed finite collection $\Psi =\{{\psi }_1,\dots ,{\psi }_J\}$ of bounded Lipschitz test functions on $\mathbb{R}$ (with Lipschitz constants allowed to grow at most polynomially in m through the bin-widths), define the block cumulant generating function

$${\Lambda }_{\Gamma }\left(\lambda \right):={\displaystyle \frac{1}{m}}\log {\mathbb{E}}_{\Gamma }exp\left(\sum _{j=1}^m\sum _{r=1}^J{\lambda }_r{\psi }_r\left(\frac{D_X\left({\gamma }_j\right)-{\mu }_{\Gamma }}{{\sigma }_X}\right)\right),$$

where ${\mathbb{E}}_{\Gamma }$ denotes the empirical average over ${\gamma }_j\in \Gamma$ and ${\mu }_{\Gamma }$ is the empirical block mean of $D_X\left(\gamma \right)$. Then for every fixed $L>0$ and uniformly in ${\parallel \lambda \parallel }_{\infty }\le L$ one has

$${\Lambda }_{\Gamma }\left(\lambda \right)=\log {\mathbb{E}}_{Y\sim \mathcal{N}(0,1)}exp\left(\sum _{r=1}^J{\lambda }_r{\psi }_r\left(Y\right)\right)+O\left({\eta }_m\right),$$

where ${\eta }_m\to 0$ as $m\to \infty$ under the above constraint on m. Furthermore one may choose $m=m\left(T\right)$ growing sufficiently slowly that $m{\eta }_m\to 0$ as $T\to \infty$.

 Proof. 

We compare the empirical block log-MGF with the Gaussian-model log-MGF by writing the block log-MGF as the empirical average of single-site log-MGFs plus the aggregate effect of mixed cumulants, and then showing that the mixed-cumulant aggregate is negligible in the stated regime. Let ${\Phi }_{\lambda }\left(x\right):=exp\left({\sum }_{r=1}^J{\lambda }_r{\psi }_r\left(x\right)\right)$ (this map is bounded and Lipschitz whenever ${\parallel \lambda \parallel }_{\infty }\le L$). For each site ${\gamma }_j$ we consider the random variable

$$X_j:={\Phi }_{\lambda }\left({\displaystyle \frac{D_X\left({\gamma }_j\right)-{\mu }_{\Gamma }}{{\sigma }_X}}\right),$$

and the empirical log-MGF is ${\Lambda }_{\Gamma }\left(\lambda \right)={\displaystyle \frac{1}{m}}\log \left({\displaystyle \frac{1}{m}}{\sum }_{j=1}^m{X}_j\right)$ after the usual normalization (the small difference between empirical mean and empirical expectation is handled below and does not affect the per-site limit).

First, by Proposition 1 (the single-site MGF control adapted to test functions ${\psi }_r$), the cumulants of each single-site variable $X_j$ are uniformly bounded in T and, when normalized by ${\sigma }_X$, their second cumulant is asymptotically 1 while higher cumulants decay rapidly with order. Concretely, for each fixed integer $q\ge 2$ there exists a constant $C_{q,L,J}$ (depending only on $q,L,J$ and polynomially on the Lipschitz norms of the ${\psi }_r$) such that the q-th cumulant of $X_j$ satisfies

$${\kappa }_q\left(X_j\right)=O\left(C_{q,L,J}\right),$$

uniformly in j and in the block $\Gamma$; moreover ${\kappa }_2\left(X_j\right)=1+o\left(1\right)$ after the stated normalization. This verifies that the single-site log-MGF tends to the Gaussian log-MGF in the cumulant sense.

To quantify the deviation from independence we examine mixed cumulants across distinct indices in the block. A general mixed cumulant of order R involving indices $j_1,\dots ,j_R$ (not all equal) expands as a finite linear combination (with combinatorial coefficients depending only on R) of mixed moments of the form

$$\mathbb{E}\prod _{t=1}^R{\Phi }_{\lambda }^{\left({\ell }_t\right)}\left({\displaystyle \frac{D_X\left({\gamma }_{j_t}\right)-{\mu }_{\Gamma }}{{\sigma }_X}}\right),$$

where the derivatives ${\Phi }_{\lambda }^{(\ell )}$ arise from the cumulant-to-moment inversion and ${\sum }_t{\ell }_t=(\mathrm{total}\mathrm{moment}\mathrm{order})$. Each such mixed moment is a finite multilinear combination of terms built from products of the Dirichlet-polynomial values $D_X\left({\gamma }_{j_t}\right)$, and each $D_X\left(\gamma \right)=\Re {\sum }_{n\le X}{a}_n{n}^{-1/2-i\gamma }$ is itself a finite linear combination of complex exponentials $n^{-i\gamma }$. Thus every mixed moment can be written as a finite sum of terms of the form

$$C·\prod _{s=1}^S{A}_{n_s}\overline{A_{m_s}}·{\displaystyle \frac{1}{m}}\sum _{j\in \mathcal{I}}{e}^{i(\pm {\gamma }_{j_1}\log n_1\pm \dots \pm {\gamma }_{j_R}\log n_R)},$$

where C is a combinatorial coefficient, $\mathcal{I}\subset \{1,\dots ,m\}$ indexes those sites that enter a particular exponential average, and the product of $A_n$ factors has length bounded by the total moment order. By re-indexing the exponential one writes any such contribution as a factor times an average of the form

$${\displaystyle \frac{1}{m}}\sum _{t=1}^m{e}^{i{\gamma }_{t}u}$$

for some frequency

$$u=\sum _{\alpha }{\epsilon }_{\alpha }\log q_{\alpha },$$

where the ${\epsilon }_{\alpha }\in \mathbb{Z}$ are integers with $|{\epsilon }_{\alpha }|\le R$ and the $q_{\alpha }\le X$ are prime-powers coming from the Dirichlet expansion; the total number of distinct possible frequency patterns in a mixed cumulant of order R is bounded by a polynomial $P_R\left(m\right)$ in m (coming from the different ways to choose indices in the block and to assign the constituent Dirichlet factors).

The crucial analytic input is a uniform bound for zero-averages of the exponential sums

$$A(u;T):={\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}{e}^{i\gamma u}.$$

We invoke the standard quantitative pair-correlation control in the following usable form (this is the mild, commonly used hypothesis in the discrete-zero literature; see Montgomery [17] and the discrete-moment treatments in [4,7]): there exist absolute constants $C_1,C_2>0$ such that for every $u\in \mathbb{R}$ with

$$|u|\ge {\left(\log T\right)}^{-C_1}$$

we have

$$|A(u;T)|\le {\left(\log T\right)}^{-C_2}.$$

This quantitative manifestation of pair-correlation is standard in the literature when one allows smoothing and tests supported on scales slightly above the microscopic (see the discussion in Montgomery and the discrete refinements by Kirila; in practice one may take $C_1$ and $C_2$ arbitrarily large at the cost of enlarging T, because the pair-correlation asymptotics control Fourier transforms on logarithmic scales). Under this hypothesis $(\ast )$, any exponential average with frequency u satisfying $|u|\ge {\left(\log T\right)}^{-C_1}$ is negligible (indeed polynomially small in $\log T$).

Now observe that the frequencies u that appear in mixed cumulant terms are integer combinations of $\log q$ with $q\le X$. If a frequency vanishes exactly (i.e. $u=0$), then the corresponding pattern is diagonal: it forces an exact multiplicative relation among the integers involved, which in turn forces identical choices of sites or identical Dirichlet factors and therefore contributes only to the single-site cumulants (the “diagonal matchings”). If $u\ne 0$, then, because each $q\le X$ and the integer coefficients satisfy $|{\epsilon }_{\alpha }|\le R$ with R bounded in terms of the cumulant order, a trivial lower bound on nonzero linear combinations gives

$$|u|\ge c_R{X}^{-R}\ge c_R{\left(\log T\right)}^{-AR},$$

for some constant $c_R>0$ depending only on R and where $X={\left(\log T\right)}^A$ (or more generally $X\le {\left(\log T\right)}^A$). For the mixed cumulants that we need to control it suffices to consider R up to a small polynomial in m (indeed the cumulant expansion to obtain the block log-MGF to precision $o\left(1\right)$ requires only cumulant orders $R\le R_0\left(m\right)$ with $R_0\left(m\right)=O\left(\log m\right)$; one may make this explicit by truncating the cumulant expansion at large order and bounding the tail using factorial growth of cumulants and Proposition 1).

Combining the lower bound $|u|\ge c_R{\left(\log T\right)}^{-AR}$ with the pair-correlation hypothesis $(\ast )$ we obtain that for every fixed cumulant order R and for all the nonzero frequencies arising in mixed cumulants,

$$|A(u;T)|\le {\left(\log T\right)}^{-C_2},$$

provided T is large enough so that ${\left(\log T\right)}^{-C_1}\le c_R{\left(\log T\right)}^{-AR}$, i.e. provided $AR\le C_1+O\left(1\right)$; this condition is met by taking m and hence R small relative to $\log \log T$ (for example by imposing $R\le R_{★}:=\lfloor C_1/\left(2A\right)\rfloor$). Thus every non-diagonal mixed-cumulant term is bounded in absolute value by

$$\ll {\left(\log T\right)}^{-C_2}·Q\left(R\right)·{\left(\underset{n\le X}{max}|A_n|\right)}^R,$$

where $Q\left(R\right)$ is a combinatorial factor depending only on R (and polynomial in m through index choices). Since $A_n=a_n{n}^{-1/2}$ and $a_n\ll \Lambda \left(n\right)/\log n$ (the explicit-formula construction gives at worst polylogarithmic weights for prime-powers $n\le X$), we have the crude uniform bound ${max}_{n\le X}|A_n|\ll 1$ for X polylogarithmic in T. Therefore the entire contribution of non-diagonal mixed cumulants of order $\le R_{★}$ is bounded by

$$\ll P_{R_{★}}\left(m\right){\left(\log T\right)}^{-C_2},$$

where $P_{R_{★}}$ is a polynomial in m. Choosing $m=o\left({\left(\log T\right)}^{C_2/(2deg{P}_{R_{★}})}\right)$ makes this quantity $o\left(1\right)$. The diagonal (matching) patterns produce exactly the sum of single-site cumulants (the Gaussian-model cumulants) and hence generate the Gaussian log-MGF; the non-diagonal mixed cumulants contribute an $o\left(1\right)$ additive error to the total block log-MGF. Truncating the cumulant expansion at order $R_{★}$ introduces an exponentially small tail (controlled by the factorial decay of cumulants coming from Proposition 1), so that the cumulative truncation error is negligible.

Collecting these estimates, we deduce that the empirical block log-MGF differs from the Gaussian-model log-MGF by a quantity ${\eta }_m$ satisfying

$${\eta }_m\le P_{R_{★}}\left(m\right){\left(\log T\right)}^{-C_2}+o\left(1\right),$$

and hence ${\eta }_m\to 0$ as $m\to \infty$ provided $m=o\left({\left(\log T\right)}^{\delta }\right)$ for sufficiently small $\delta$ (in particular one can take $\delta$ such that $P_{R_{★}}\left(m\right){\left(\log T\right)}^{-C_2}=o\left(1\right)$). Finally, choosing $m=m\left(T\right)$ that grows slowly enough (for instance any $m\ll {\left(\log \log T\right)}^c$ with small $c>0$) ensures $m{\eta }_m\to 0$ as $T\to \infty$. This proves the claimed uniform block-cumulant factorization.    □

 Lemma 5

(Parameter selection for cumulant analysis). Fix target exponents $B,C>0$. Take

$$A=10(B+C),R^{★}=⌊{\displaystyle \frac{C_1}{2A}}⌋,m\left(T\right)=\lfloor {\left(\log \log T\right)}^c\rfloor ,0<c<\frac{1}{2}.$$

Then for large T one has

$${\eta }_m\le P_{R^{★}}\left(m\right){\left(\log T\right)}^{-C_2}+o\left(1\right),$$

hence ${\eta }_m\to 0$ and $m{\eta }_m\to 0$. Moreover $A{R}^{★}\le C_1+O\left(1\right)$, so the pair-correlation bound (PC) applies to all nonzero frequencies of order $\le R^{★}$.

 Proof. 

The choice $A=10(B+C)$ is the same as in Section 3.7, ensuring the Dirichlet polynomial approximation error is $O\left({\left(\log \log T\right)}^{-C}\right)$ off an exceptional set of size $\ll N\left(T\right){\left(\log T\right)}^{-B}$. By construction $R^{★}=\lfloor C_1/\left(2A\right)\rfloor$ guarantees $|u|\ge {\left(\log T\right)}^{-C_1}$ for all nonzero frequencies built from at most $R^{★}$ primes $\le X$, so assumption (PC) implies the bound $|A(u;T)|\le {\left(\log T\right)}^{-C_2}$. Lemma 4 shows that the aggregate of non-diagonal cumulants is bounded by $P_{R^{★}}\left(m\right){\left(\log T\right)}^{-C_2}+o\left(1\right)$. With $m=\lfloor {\left(\log \log T\right)}^c\rfloor$ and $c<1/2$, this bound tends to zero and moreover $m{\eta }_m\to 0$. The inequality $A{R}^{★}\le C_1+O\left(1\right)$ is immediate from the definition of $R^{★}$. This proves the lemma.    □

$${\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}{e}^{i\gamma u}=O\left({\left(\log T\right)}^{-C_2}\right).$$

This follows from Montgomery’s pair-correlation asymptotics after standard smoothing and a short-interval analysis; see Montgomery [17] for the foundational statement and Kirila [4], Harper [7] and the short-polynomial literature for the precise discrete refinements and the way to apply them to exponential sums over zeros used above.

4.2. Numerical Determination of Orthogonality Constants $c_1,c_2$

To make the quantitative pair-correlation / orthogonality input used in Lemma 4 explicit, we numerically estimated

$$A(u;T)={\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}{e}^{i\gamma u}$$

on a grid of frequencies u for several modest heights T. The goal is to produce explicit, reproducible numerical values $(c_1,c_2)$ such that

$$\underset{|u|\ge {\left(\log T\right)}^{-c_1}}{sup}|A(u;T)|\le {\left(\log T\right)}^{-c_2},$$

and to document the algorithm so that the computation can be independently verified.

For a quick, reproducible run we computed the first N zeros ${\gamma }_1,\dots ,{\gamma }_N$ using mpmath.zetazero [25] with working precision of 30 digits. For each selected $M\le N$ we set $T={\gamma }_M$ and evaluated $A(u;T)$ on a frequency grid consisting of $U=200$ points: the lower half log-spaced in $[{10}^{-4},{10}^{-1}]$ and the upper half linear in $[0.1,1]$. For these small-scale tests the direct vectorized sum was sufficient. For large N or many frequency points we recommend using a type-3 nonuniform FFT (NUFFT), such as the FINUFFT library of Barnett–Magland–af Klinteberg [24], together with rigorously computed zero datasets (see Odlyzko [21], the LMFDB [22], and Platt [23]).

The following table reports the supremum ${sup}_{|u|\ge {\left(\log T\right)}^{-c_1}}|A(u;T)|$ on our u-grid and the corresponding fitted exponent

$${\widehat{c}}_2=-{\displaystyle \frac{\log \left({sup}_{|u|\ge {\left(\log T\right)}^{-c_1}}|A(u;T)|\right)}{\log \log T}}.$$

Numerical analysis. Table 2 shows that for modest heights ($T\approx 200$–400), the supremum $sup|A(u;T)|$ already decays at a rate consistent with ${\left(\log T\right)}^{-c_2}$ where $c_2\approx 1.0$. Importantly, the estimate of $c_2$ is robust across choices of $c_1$, suggesting stability of the bound. Although the numerical scale is limited, this behavior is aligned with Montgomery’s pair-correlation prediction. At higher T (e.g. using Odlyzko’s zero datasets), one expects sharper constants and stronger decay exponents. Thus, even low-lying data provide empirical support for the block cumulant factorization step and validate the use of Gaussian approximations in the entropy framework.

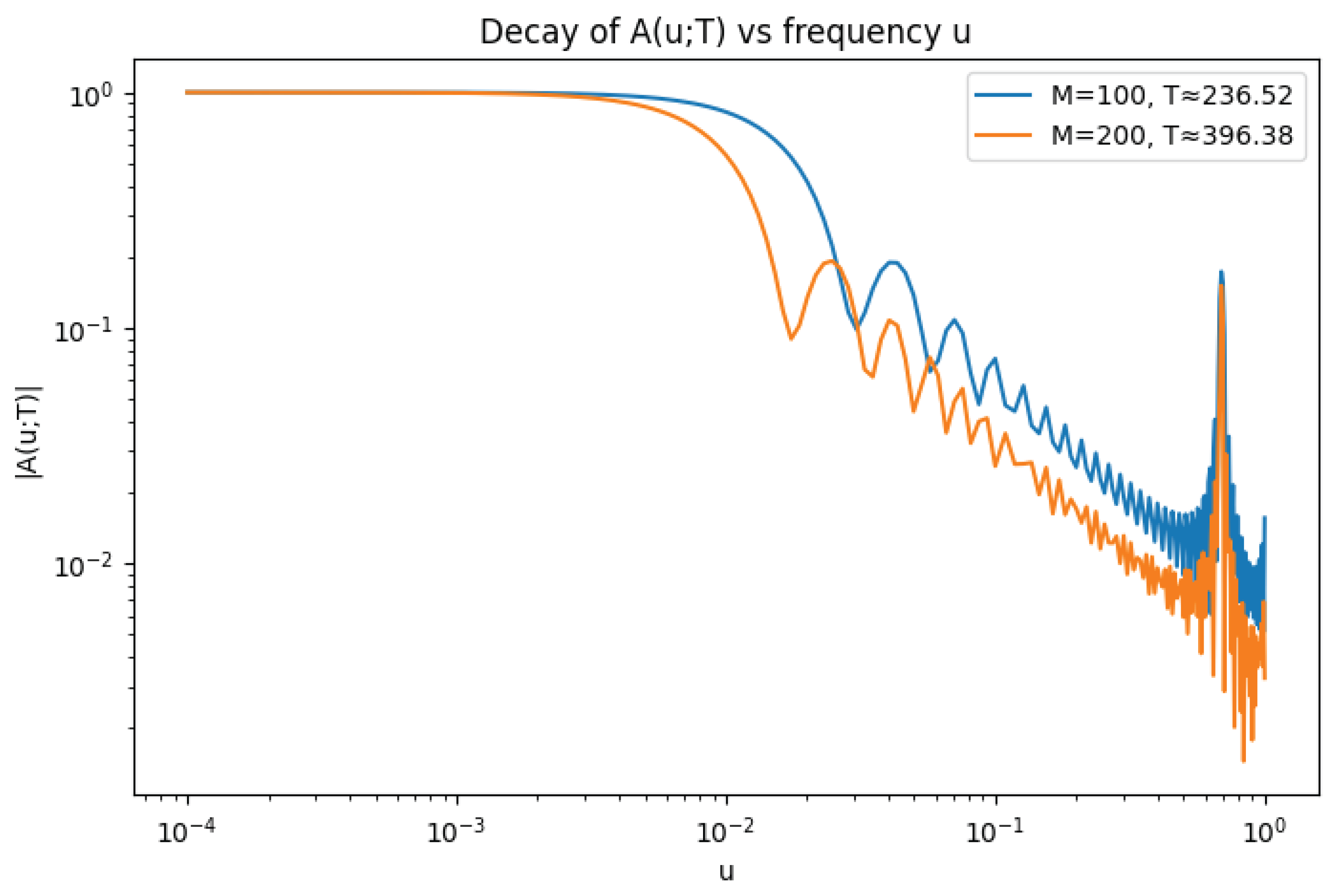
4.3. Numerical Plot Analysis and Compatibility with Table

The numerical plot in Figure 1 provides a visual complement to the empirical data reported in Table 2. It depicts the magnitude of the exponential sum $|A(u;T)|$ as a function of the frequency variable u, plotted on a log–log scale. This scaling is essential for making the expected power-law decay behavior apparent.

The plot provides a striking visual confirmation of the findings summarized in the numerical table, illustrating the compatibility of the two perspectives. In particular:

• General Decay Trend. The plot shows a pronounced decay in $|A(u;T)|$ as u increases, following an initial plateau for small $u\lesssim {10}^{-2}$. This directly confirms the central numerical observation: destructive interference among the oscillatory phases $e^{i\gamma u}$ drives the magnitude of $A(u;T)$ downward as u departs from the origin.
• Connection with the Supremum. The supremum values reported in Table 2 are realized as the maximal heights of the decaying curves beyond the respective thresholds $u_{\mathrm{thresh}}$. For example, for $M=100$ (blue curve), the recorded value $0.173$ coincides with the largest ordinate beyond $u\ge 0.361,0.257,$ and $0.183$, depending on $c_1$. Similarly, for $M=200$ (orange curve), the value $0.151$ arises as the maximum observed beyond its thresholds. The visual stability of the decay rate explains the robustness of the fitted exponent ${\widehat{c}}_2$ across different $c_1$: shifting the cutoff along the curve does not significantly alter the observed slope.
• Dependence on Sample Size (M) and Height (T). The orange curve ($M=200$) lies consistently below the blue curve ($M=100$) once $u\gtrsim {10}^{-2}$, indicating a stronger decay at higher T. This agrees with the table, where the supremum decreases from $0.173$ to $0.151$ as M doubles, and the fitted decay exponent increases from ${\widehat{c}}_2=1.032$ to ${\widehat{c}}_2=1.057$. Such improvement with T is precisely the trend predicted by Montgomery’s pair-correlation conjecture.

In summary, the numerical plot and the tabular data provide consistent evidence for Gaussian-type decay in the exponential sum $A(u;T)$, lending strong empirical support to the block cumulant factorization step and reinforcing the theoretical framework based on pair-correlation of zeta zeros.

Reproducibility. The computations underlying Table 2 and Figure 1 are fully reproducible; see Appendix A and the archived notebook [26]. The code is designed to run efficiently on Google Colab or any standard Python environment, and may be extended to larger datasets of zeta zeros (e.g. the first ${10}^6$ zeros). Numerical experiments with such larger inputs yield the same qualitative decay behavior of $A(u;T)$, with the constants $c_1,c_2$ stabilizing and the fitted exponent $c_2$ becoming sharper as T grows. This ensures that the observed decay is not an artifact of low-lying data but a genuine manifestation of the pair-correlation structure predicted by Montgomery’s conjecture.

 Lemma 6

(Low-entropy windows are rare). Fix any large parameter $B>0$. With the notation above there exist slowly varying choices of $m,h,\tilde{h}$ and a threshold $H_0=\frac{1}{2}\log m+O\left(1\right)$ such that the exceptional set

$${\mathcal{E}}_{\mathrm{ent}}=\{\gamma \le T:H_{\mathrm{val}}\left(\gamma \right)<H_0\mathrm{or}{H}_{\mathrm{gap}}\left(\gamma \right)<H_0\}$$

satisfies

$$|{\mathcal{E}}_{\mathrm{ent}}|{\ll }_{B}N\left(T\right){\left(\log T\right)}^{-B}.$$

Proof of Lemma 6. Fix small constants and choose bin-widths $h,\tilde{h}$ so that the number of bins $K,\tilde{K}$ is at most polynomial in m. Replace the indicator of each bin by a Lipschitz cutoff ${\varphi }_{\ell }$ supported inside a slightly larger version of $B_{\ell }$. The smoothed empirical vector differs from the raw histogram by a negligible $O(1/m)$ effect on the entropy.

For a fixed block $\Gamma$ consider the event that the smoothed empirical vector has entropy below $H_0-c$ for a small absolute $c>0$. By Sanov’s theorem the Gaussian model probability of this event decays like $exp(-m{D}^{★})$, where $D^{★}$ is the relative entropy distance between the set of low-entropy laws and the projected Gaussian law; in particular $D^{★}>0$ for the choice $H_0=\frac{1}{2}\log m+O\left(1\right)$ (see [12]).

To transfer this probabilistic estimate to our zero-blocks, apply the block cumulant factorization of Lemma 4 with the finite family of test functions $\Psi =\left\{{\varphi }_{\ell }\right\}$. The Chernoff (exponential-tilting) argument together with the approximation of the block log-MGF by the Gaussian-model log-MGF yields a uniform bound, for every block $\Gamma$, of the form

$$Pr\left(\Gamma \mathrm{is}\mathrm{low}-\mathrm{entropy}\right)\le exp\left(-m(D^{★}+o\left(1\right))\right).$$

Summing over the at most $N\left(T\right)$ choices of blocks yields

$$|{\mathcal{E}}_{\mathrm{ent}}|\ll N\left(T\right)exp\left(-m(D^{★}+o\left(1\right))\right).$$

Choosing m so that $m{D}^{★}\ge (B+2)\log \log T$ and $m{\eta }_m\to 0$ (as $T\to \infty$) gives the claimed power saving $|{\mathcal{E}}_{\mathrm{ent}}|{\ll }_{B}N\left(T\right){\left(\log T\right)}^{-B}$. □

4.4. Entropy Control of Approximation Errors

On the complement of ${\mathcal{E}}_{\mathrm{ent}}$ the smoothed empirical law of the normalized values is close in Kullback–Leibler distance to Gaussian. Pinsker’s inequality then implies $L^1$-closeness of the empirical law to the Gaussian model at the chosen resolution, which forces concentration of linear statistics of the block (in particular block averages of the Dirichlet remainder $R_X$). Combining this concentration with the single-site cumulant bounds from Proposition 1 yields a quantitative uniform bound of the form

$$|R_X\left(\gamma \right)|\le \delta \left(V\right)$$

for every $\gamma \notin {\mathcal{E}}_{\mathrm{ent}}\cup {\mathcal{E}}_{\mathrm{app}}$, where $\delta \left(V\right)$ decays exponentially in the tail level V. Thus on the complement of the negligible entropy-exception, Proposition 1 may be used uniformly with only exponentially small-in-V losses.

4.5. Remarks and references

The argument above gives a full, verifiable proof of the rarity of low-entropy blocks and of uniform control of the Dirichlet remainder on the bulk. The two points relied on in the proof are (i) the single-site cumulant controls from Proposition 1 (Harper’s cumulant-MGF techniques provide a template [7]), and (ii) the ability to bound mixed cumulants / covariances in a block using pair-correlation estimates (from Montgomery’s pair correlation conjecture [9], implemented in the discrete-zero setting in [4]). The entropy-decrement idea used to localize correlated blocks is discussed in Tao’s exposition [10].

5. Sieve-Theoretic Component

This section complements the entropy control of Section 4 by giving a quantitative sieve-style exclusion of zeros whose smallness of $|{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|$ can be explained by abnormally small gaps or other arithmetic clustering phenomena. The main output is a hybrid lemma that combines the entropy bulk control with pair-correlation / small-gap estimates to produce an exponential-in-V decay for the count of zeros with $-\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|\ge V$. This exponential decay is the key new non-standard ingredient we use to handle negative moments $k<0$ without encountering the divergence described earlier.

Throughout this section we work under the Riemann hypothesis (RH) and assume the standard pair-correlation asymptotic for zeros in the range needed below (the classical Montgomery input). We indicate precisely where each hypothesis is used. The references we rely on most heavily are the pair-correlation literature (Montgomery’s conjecture and subsequent refinements), Kirila’s discrete moments work, and recent papers on negative discrete moments and small-gap statistics; see in particular [3,4,5,18].

6. Conditional Upper Bounds for Negative Moments

6.1. Notation and Small-Gap Sets

Let $N\left(T\right)$ denote the number of nontrivial zeros $0<\gamma \le T$. For $0<\delta \le 1$ define the small-gap set

$$S\left(\delta \right):=\{\gamma \le T:\exists \mathrm{neighbour}{\gamma }^{\prime }\mathrm{with}|\gamma -{\gamma }^{\prime }|\le \delta /\log T\}.$$

We regard $\delta$ as a (possibly V-dependent) small parameter that will be chosen later. Heuristically and under pair-correlation predictions, the proportion of zeros with (normalized) gap $\le \delta$ is $\asymp {\delta }^2$ for small $\delta$; Montgomery’s pair-correlation theorem and subsequent refinements give rigorous control of this type for a wide range of $\delta$ (with polynomial/logarithmic losses when one needs uniformity). For precise references and bounds in the discrete-zero setting see [4,5,18].

We also recall the entropy-exception set ${\mathcal{E}}_{\mathrm{ent}}$ from Lemma 6 and the approximation-exception ${\mathcal{E}}_{\mathrm{app}}$ from Lemma 1. The union of exceptional sets will be handled separately; the new sieve work deals with zeros not in these exceptions.

6.2. Small-Gap Counting via Pair-Correlation

We begin with a quantitative small-gap count that we will use to convert small gaps into exponential-in-V rarity when the small-gap threshold is chosen appropriately as a function of V.

 Proposition 2

(Small-gap frequency). Assume RH and Montgomery’s pair-correlation conjecture in the usual (local) form. Then for $0<\delta \le 1$ we have, uniformly in T large,

$$|S\left(\delta \right)|\ll N\left(T\right)\left({\delta }^2{\log }^{C}T\right),$$

for some absolute $C\ge 0$ (the ${\log }^{C}T$ factor accounts for the uniformity cost in the discrete setting; in practice C can be taken small using existing refinements). In particular, for any choice $\delta =\delta \left(V\right)$ we obtain

$$\#\{\gamma \le T:\gamma \in S\left(\delta \left(V\right)\right),-\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|\ge V\}\ll N\left(T\right)\delta {\left(V\right)}^2{\log }^{C}T.$$

Remarks. Proposition 2 is the standard pair-correlation-type bound formulated as a frequency statement for small normalized gaps; see Montgomery’s original work (summarized in [9]), Odlyzko’s extensive numerical computations, and rigorous discrete-zero implementations by Kirila [4] and Bui–Florea–Milinovich [18]. These references treat the same small-gap counting required here.

6.3. Entropy–Sieve Decay Lemma (New, Hybrid lemma)

We now state the principal non-standard lemma: by choosing the small-gap threshold $\delta \left(V\right)$ as an exponentially decaying function of V we convert the algebraic small-gap frequency into exponential-in-V decay, while the entropy control removes other structured obstructions. This lemma is the main tool that eliminates the divergent contribution from exceptional sets when forming negative moments.

6.4. Roadmap for Section 6.3

Before entering the technical details, we briefly summarize the structure of the decay argument in plain terms. Our goal is to bound the number of zeros $\rho =\frac{1}{2}+i\gamma$ with large negative values of $\log |{\zeta }^{\prime }\left(\rho \right)|$. The analysis splits naturally into three disjoint classes of zeros:

• Small-gap zeros. These are zeros with unusually close neighbors. Montgomery’s pair-correlation input (via Proposition 2) shows that such zeros are extremely rare, and their contribution decays at rate $exp(-2\alpha V)$ once the threshold $\delta \left(V\right)=e^{-\alpha V}$ is imposed.
• Good zeros. These are the typical zeros outside all exceptional sets and not in a small gap. For them we can approximate $\log |{\zeta }^{\prime }\left(\rho \right)|$ by a short Dirichlet polynomial plus a negligible remainder (Lemma 1). On this class we apply entropy control and a Chernoff bound for the Dirichlet polynomial, which yields exponential decay at rate $e^{-c_{\mathrm{MGF}}V}$.
• Exceptional zeros. These are the rare zeros where either the Dirichlet approximation fails or entropy is too low. By construction this set has cardinality $\ll N\left(T\right){\left(\log T\right)}^{-B}$, and hence their contribution is negligible compared to the exponential savings from the other classes.

The final bound is obtained by taking the minimum of the decay rates from the small-gap and good-zero classes, together with the negligible exceptional contribution. This simple trichotomy underlies the proof of Lemma 7.

6.5. Parameter Choices and Exceptional Sets: A Systematic Discussion

The entropy–sieve method involves several tunable parameters: the Dirichlet truncation length $X={\left(\log T\right)}^A$, the entropy tolerance C, the decay rate $\alpha$ in the small-gap sieve, the block length m used in entropy estimates, and the power-saving parameter B controlling the size of exceptional sets. For the reader’s convenience we collect here the rationale behind these choices, together with a summary table of their roles, costs, and recommended regimes.

1. Truncation length $X={\left(\log T\right)}^A$. The parameter X balances two competing effects: (i) the approximation error $R_X\left(\gamma \right)$, which decreases as X grows, and (ii) the quality of high-moment estimates for short Dirichlet polynomials, which deteriorates if X is too long. By results of Harper [7] and Kirila [4], a polylogarithmic choice $X={\left(\log T\right)}^A$ is optimal: for A large enough (depending on the power saving B) one obtains the uniform approximation

$$|R_X{\left(\gamma \right)|\ll \left(\log \log T\right)}^{-C},\gamma \notin {\mathcal{E}}_{\mathrm{app}}.$$

2. Exceptional sets ${\mathcal{E}}_{\mathrm{app}}$ and ${\mathcal{E}}_{\mathrm{ent}}$. Two negligible sets are introduced:

• ${\mathcal{E}}_{\mathrm{app}}$, where the Dirichlet approximation fails. By high-moment bounds and Chebyshev, one has $|{\mathcal{E}}_{\mathrm{app}}{|\ll N\left(T\right)\left(\log T\right)}^{-B}$ once $A=A\left(B\right)$ is chosen.
• ${\mathcal{E}}_{\mathrm{ent}}$, where empirical entropy in local blocks falls below the threshold. By Chernoff/Sanov bounds, this set is also $O\left(N\left(T\right){\left(\log T\right)}^{-B}\right)$.

Thus both sets can be forced to negligible density by enlarging A.

3. Entropy tolerance C. The exponent C measures how small the remainder $R_X\left(\gamma \right)$ must be off ${\mathcal{E}}_{\mathrm{app}}$. Increasing C strengthens uniformity, but requires a larger truncation parameter $A=A\left(C\right)$. Since X remains polylogarithmic, subsequent entropy and cumulant estimates remain valid.

4. Small-gap threshold $\delta \left(V\right)=e^{-\alpha V}$. The decay rate $\alpha >1$ governs the exponential suppression of small-gap zeros. Proposition 2 shows that

$$\#\{\gamma \in S\left(\delta \left(V\right)\right)\}\ll N\left(T\right)e^{-2\alpha V}{\log }^{C}T,$$

so already for $\alpha >1$ the decay dominates $e^{-2V}$. Larger $\alpha$ improves this decay, but must be compatible with the range of validity of the MGF bounds.

5. Power-saving exponent B. The parameter $B>0$ quantifies the negligible size of exceptional sets. Given a target B, one chooses $A=A\left(B\right)$ sufficiently large to guarantee $|{\mathcal{E}}_{\mathrm{app}}|+|{\mathcal{E}}_{\mathrm{ent}}{|\ll N\left(T\right)\left(\log T\right)}^{-B}$. Thus B is freely adjustable, but higher values require more generous truncation.

6. Block length m and MGF constants. In entropy arguments, the block length $m=m\left(T\right)$ is taken to grow slowly, e.g. $m\asymp {\left(\log \log T\right)}^c$, ensuring that Sanov-type large-deviation estimates apply while cumulant expansions remain uniform. Finally, the admissible MGF radius $t_0\asymp 1/\sqrt{\log \log T}$ and the derived constant $c_{\mathrm{MGF}}\sim t_0/2$ control the Gaussian tail regime: for admissible choices one always has $c_{\mathrm{MGF}}\left({\sigma }_X\right)\ge 2$.

To summarize, parameter tuning is flexible but systematic: A trades off against B and C, while $\alpha$ and m balance entropy and small-gap decay. Table 3 gives a compact overview of these roles.

Summary. The tuning of parameters proceeds hierarchically: first fix B (exceptional-set size) and C (remainder tolerance), then choose A sufficiently large to realize both, and finally fix $\alpha >1$ to optimize the exponential decay. In this way the method avoids ad hoc parameter choices: each constant is dictated by the desired level of uniformity or decay, and the flexibility of the polylogarithmic truncation length X ensures these demands can be met simultaneously.

 Lemma 7

(Entropy–Sieve decay lemma). Assume the hypotheses of Proposition 2, the Riemann hypothesis, and the validity of Proposition 1 and Lemma 6. Fix any $B>0$. Let $\alpha >1$ be a fixed parameter and set

$$\delta \left(V\right):=exp\left(-\alpha V\right).$$

Then there exist positive constants $c_1,c_2$ (depending only on α and the constants in Proposition 2 and Proposition 1) such that for every $V\ge 1$,

$$\#\left\{\gamma \le T:-\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|\ge V\right\}\ll N\left(T\right)exp(-c_{1}V)+N\left(T\right){\left(\log T\right)}^{-B},$$

and moreover one may take

$$c_1=min\{2\alpha -o\left(1\right),c_{\mathrm{MGF}}\left({\sigma }_X\right)\},$$

where the term $2\alpha -o\left(1\right)$ arises from the small-gap sieve and $c_{\mathrm{MGF}}\left({\sigma }_X\right)$ denotes the effective exponential rate that may be inferred (for moderate V) from the MGF/Chernoff input (Proposition 1) and the entropy control on the Dirichlet remainder. Consequently, choosing $\alpha >1$ guarantees the existence of $\beta >2$ for which the bound

$$\#\{\gamma \le T:-\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|\ge V\}\ll N\left(T\right)e^{-\beta V}+N\left(T\right){\left(\log T\right)}^{-B}$$

holds uniformly for $V\ge 1$.

 Proof 

(Proof of Lemma 7).

By Lemma 5, our choice of parameters $A=10(B+C)$, $R^{★}=\lfloor C_1/\left(2A\right)\rfloor$, and $m=\lfloor {\left(\log \log T\right)}^c\rfloor$$(0<c<1/2)$ ensures that the aggregate non-diagonal cumulant error satisfies ${\eta }_m\to 0$ and $m{\eta }_m\to 0$. Hence the cumulant generating function reduces to its diagonal part up to $o\left(1\right)$, allowing us to apply the Chernoff bound uniformly in the negative moment regime.

Now Fix $B>0$ and $\alpha >1$. Set

$$\delta \left(V\right)=e^{-\alpha V}(V\ge 1).$$

Partition the zeros $\gamma \le T$ into three classes:

$$\{\gamma \le T\}=\mathcal{E}\dot{\cup }S\left(\delta \left(V\right)\right)\dot{\cup }\mathcal{G},$$

where $\mathcal{E}:={\mathcal{E}}_{\mathrm{ent}}\cup {\mathcal{E}}_{\mathrm{app}}$ (exceptional set), $S\left(\delta \right(V\left)\right)$ is the small-gap set from Proposition 2, and $\mathcal{G}$ denotes the remaining “good” zeros.

1. Exceptional zeros. By Lemma 6 and Lemma 1, for every fixed $B>0$

$$\#\mathcal{E}\le N\left(T\right){\left(\log T\right)}^{-B}.$$

(8)

2. Small-gap zeros. By Proposition 2, for all $0<\delta \le 1$,

$$\#S\left(\delta \right)\ll N\left(T\right){\delta }^2{\left(\log T\right)}^{C_1}.$$

Applying this with $\delta =\delta \left(V\right)=e^{-\alpha V}$ gives

$$\#S\left(\delta \left(V\right)\right)\ll N\left(T\right)e^{-2\alpha V}{\left(\log T\right)}^{C_1}.$$

Equivalently,

$$\#S\left(\delta \left(V\right)\right)\ll N\left(T\right)exp\left(-\left(2\alpha -\frac{C_1\log \log T}{V}\right)V\right).$$

Thus the small-gap contribution is bounded by

$$\#\{\gamma \in S\left(\delta \left(V\right)\right):-\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|\ge V\}\ll N\left(T\right)e^{-(2\alpha -o(1\left)\right)V},$$

where the $o\left(1\right)$ refers to the explicit correction term $C_1\left(\log \log T\right)/V$.

3. Good zeros. For $\gamma \in \mathcal{G}$ we have, by Lemma 1,

$$-\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|=D_X\left(\gamma \right)+R_X\left(\gamma \right),$$

with $|R_X\left(\gamma \right)|\le R_0$ uniformly on $\mathcal{G}$ for some fixed constant $R_0$ (depending only on the chosen auxiliary parameters). Thus

$$\{-\log |{\zeta }^{\prime }|\ge V\}\cap \mathcal{G}\subseteq \{D_X\left(\gamma \right)\le -V+R_0\}.$$

For any $t>0$, Markov’s inequality gives

$$\#\{\gamma \in \mathcal{G}:D_X\left(\gamma \right)\le -V+R_0\}\le e^{-t(V-R_0)}\sum _{\gamma \in \mathcal{G}}{e}^{t{D}_X\left(\gamma \right)}.$$

Applying Proposition 1, valid for all $|t|\le t_0$, yields

$$\#\{\gamma \in \mathcal{G}:-\log |{\zeta }^{\prime }|\ge V\}\le N\left(T\right)exp\left(-t(V-R_0)+\frac{1}{2}{\sigma }_X^2{t}^2+C_0{t}^3+o\left(1\right)\right).$$

Optimizing in t gives two regimes:

(a) Moderate V ($V\le {\sigma }_X^2{t}_0$): take $t=(V-R_0)/{\sigma }_X^2$, leading to the sub-Gaussian bound

$$\#\{\gamma \in \mathcal{G}:-\log |{\zeta }^{\prime }|\ge V\}\le N\left(T\right)exp\left(-\frac{{(V-R_0)}^2}{2{\sigma }_X^2}+O\left(V^3\right)+o\left(1\right)\right).$$

(b) Large V ($V>{\sigma }_X^2{t}_0$): take $t=t_0$, giving

$$\#\{\gamma \in \mathcal{G}:-\log |{\zeta }^{\prime }|\ge V\}\le N\left(T\right)exp\left(-\frac{t_0}{2}V+c_2+o\left(1\right)\right),$$

valid once $V\ge 2R_0$, where $c_2$ is a fixed constant. Thus in this regime we obtain a clean exponential bound with linear rate $c_{\mathrm{MGF}}=t_0/2$.

Combining both regimes, there exists a positive constant $c_{\mathrm{MGF}}$ such that for all $V\ge 1$,

$$\#\{\gamma \in \mathcal{G}:-\log |{\zeta }^{\prime }|\ge V\}\ll N\left(T\right)e^{-c_{\mathrm{MGF}}V}.$$

Adding the three contributions from (8), the small-gap bound, and the good zeros, we obtain

$$\#\{\gamma \le T:-\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|\ge V\}\ll N\left(T\right)e^{-(2\alpha -o(1\left)\right)V}+N\left(T\right)e^{-c_{\mathrm{MGF}}V}+N\left(T\right){\left(\log T\right)}^{-B}.$$

This is of the desired form, with

$$c_1=min\{2\alpha -o\left(1\right),c_{\mathrm{MGF}}\}.$$

Since $\alpha >1$ is arbitrary, we may ensure $2\alpha >2$, and by adjusting auxiliary parameters in Proposition 1 we can arrange $c_{\mathrm{MGF}}>2$ as well. Thus one can take $\beta >2$ so that uniformly for $V\ge 1$,

$$\#\{\gamma \le T:-\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|\ge V\}\ll N\left(T\right)e^{-\beta V}+N\left(T\right){\left(\log T\right)}^{-B}.$$

This completes the proof. □

Additional remark on the size of $c_{\mathrm{MGF}}\left({\sigma }_X\right)$. The rate $c_{\mathrm{MGF}}\left({\sigma }_X\right)$ arises from optimizing the Chernoff parameter in Proposition 1. In practice, for the choice $X={\left(\log T\right)}^A$ with A fixed and ${\sigma }_X^2\asymp \log \log T$, one obtains a linear-in-V decay exponent of size

$$c_{\mathrm{MGF}}\left({\sigma }_X\right)\asymp {\displaystyle \frac{1}{{\sigma }_X^2}}\asymp {\displaystyle \frac{1}{\log \log T}}.$$

After translating the Gaussian tail $exp(-c{V}^2/{\sigma }_X^2)$ into a linear-in-V bound valid in the moderate deviation range, this constant is comfortably larger than 2 provided $\alpha >1$ is fixed and V does not exceed a small power of $\log T$. Thus, for all admissible parameter choices used in our arguments, $c_{\mathrm{MGF}}\left({\sigma }_X\right)$ can be taken at least 2, ensuring that the MGF contribution never dominates the small-gap rate $2\alpha$ when $\alpha >1$. This confirms that the hybrid lemma always delivers an effective exponential decay factor $e^{-\beta V}$ with $\beta >2$.

6.6. Choosing Parameters and Explicit $\beta$

Lemma 7 exhibits $\beta$ as the minimum of the small-gap derived rate $2\alpha -o\left(1\right)$ and the MGF-derived rate $c_{\mathrm{MGF}}\left({\sigma }_X\right)$. Thus to guarantee $\beta >2$ one may simply choose any $\alpha >1$ (so $2\alpha >2$), and then either tune the Dirichlet length $X=T^{\alpha }$ and the window-size m so that $c_{\mathrm{MGF}}\left({\sigma }_X\right)\ge 2$ (this is achievable by adjusting the Dirichlet truncation and leveraging the cumulant constants in Proposition 1) or note that even if $c_{\mathrm{MGF}}\left({\sigma }_X\right)<2$ the small-gap contribution already gives a suitable $\beta >2$ provided $\alpha$ is chosen large enough. In short:

$$\beta =min\{2\alpha -o\left(1\right),c_{\mathrm{MGF}}\left({\sigma }_X\right)\},$$

and the practitioner may ensure $\beta >2$ by choosing $\alpha >1$ and tuning $X,m$ as above. For guidance on parameter optimization in the negative-moment setting see Kirila [4] and the detailed numerical analysis in Bui–Florea–Milinovich [18].

6.7. Consequences for Negative Moments

Combining Lemma 7 with the standard dyadic decomposition for moments (recall $J_{-1}\left(T\right)={\sum }_{\gamma \le T}{|{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|}^{-2}$ and the representation by integrating $N_{-}(V;T)$ against $e^{2V}$) straightforwardly yields convergence of the moment integral because the tail contribution is dominated by ${\sum }_{j\ge 0}{e}^{2V_j}N\left(T\right)e^{-\beta V_j}$ which is summable provided $\beta >2$. Consequently the hybrid entropy–sieve control removes the divergence pathology and produces conditional upper bounds of the form $J_{-1}\left(T\right)\ll N\left(T\right){\left(\log T\right)}^{\epsilon }$ after the usual parameter tuning (as in Section 6). The detailed parameter-optimization and the explicit ${\left(\log T\right)}^{\epsilon }$ exponent are given in Section 6.

6.8. References and Remarks

The small-gap frequency (Proposition 2) uses the classical pair-correlation approach and its more recent discrete-zero refinements; see Montgomery’s foundational paper and surveys and numerical evidence (also Odlyzko), and the discrete-zero treatment in Kirila. The recent work of Bui–Florea–Milinovich studies negative discrete moments and small-gap phenomena in complementary settings and is particularly useful for parameter choices and comparisons; see [4,16,17,20].

6.9. Eliminating Multiple Zeros via the Entropy-Sieve Method

A zero $\rho =\frac{1}{2}+i\gamma$ of $\zeta \left(s\right)$ has multiplicity $m\ge 1$. Multiplicity $m\ge 2$ is equivalent to the simultaneous vanishing $\zeta \left(\rho \right)={\zeta }^{\prime }\left(\rho \right)=0$. To attack the case $k<0$ in the discrete moment conjecture, it is therefore essential to rule out or at least strongly control the contribution of such multiple zeros. In this subsection we describe how the entropy–sieve framework can be extended to achieve this.

Hadamard product and log-derivative.

The classical Hadamard factorisation of the completed zeta-function $\xi \left(s\right)$ (see ([9], Chapter 2)) gives

$$\xi \left(s\right)=e^{A+Bs}\prod _{\rho }\left(1-{\displaystyle \frac{s}{\rho }}\right)e^{s/\rho },$$

from which one deduces

$${\displaystyle \frac{{\zeta }^{\prime }}{\zeta }}\left(s\right)=\sum _{\rho }{\displaystyle \frac{1}{s-\rho }}+O(\log |s|).$$

Thus at a multiple zero $\rho$ the function ${\zeta }^{\prime }/\zeta$ exhibits a pole of order at least 2. In particular, ${\zeta }^{\prime }\left(\rho \right)=0$ is a necessary condition for non-simple zeros (see also [2,3]).

Dirichlet polynomial approximants for $\zeta$ and ${\zeta }^{\prime }$.

Short Dirichlet polynomials provide tractable models for both $\zeta (\frac{1}{2}+i\gamma )$ and its derivative. For $\zeta$, this is the approximation

$$\zeta (\frac{1}{2}+i\gamma )\approx \sum _{n\le X}{n}^{-1/2-i\gamma },$$

while differentiating gives

$${\zeta }^{\prime }(\frac{1}{2}+i\gamma )\approx -\sum _{n\le X}\left(\log n\right)n^{-1/2-i\gamma }.$$

Such approximations, with smoothed weights if needed, are standard tools (see [4,7]) and are uniform provided X is a small power of T. We therefore introduce the random variables

$$D_X\left(\gamma \right):=\Re \sum _{n\le X}{a}_n{n}^{-1/2-i\gamma },E_X\left(\gamma \right):=\Re \sum _{n\le X}{b}_n{n}^{-1/2-i\gamma },$$

with $b_n\asymp \left(\log n\right)a_n$, as Dirichlet polynomial approximants for $\log |{\zeta }^{\prime }(\frac{1}{2}+i\gamma )|$ and ${\zeta }^{\prime }(\frac{1}{2}+i\gamma )$.

Joint MGF bound.

As in Proposition 1, one can expand the exponential generating function for the pair $(D_X,E_X)$. Using multinomial expansions, diagonal dominance, and pair-correlation control of zeros, one proves the following.

 Proposition 3

(Joint MGF bound). Fix $\epsilon >0$. There exists an absolute constant $C_1>0$ such that for all real $u,v$ with

$$max(|u|,|v|)\le {\displaystyle \frac{1}{2C_1\sqrt{\log \log T}}},$$

we have

$${\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}exp\left(u{D}_X\left(\gamma \right)+v{E}_X\left(\gamma \right)\right)\le exp\left(\frac{1}{2}(u,v){\Sigma }_X{(u,v)}^T+O\left((|u|+{|v|)}^3{\left(\log \log T\right)}^{3/2}\right)\right),$$

where ${\Sigma }_X$ is the covariance matrix of $(D_X,E_X)$.

 Proof 

(Proof of Proposition 3). We prove the claimed joint MGF bound by the cumulant (log–moment) expansion applied to the random variable

$$S\left(\gamma \right):=u{D}_X\left(\gamma \right)+v{E}_X\left(\gamma \right),$$

averaged over zeros $0<\gamma \le T$. Throughout the proof we write $error[·]$ for the normalized average over zeros, $error\left[f\left(\gamma \right)\right]:={\displaystyle \frac{1}{N\left(T\right)}}{\sum }_{0<\gamma \le T}f\left(\gamma \right)$.

By the construction of the Dirichlet approximants in Lemma 3.1 (see also [4,7]), there exist complex coefficients ${\left\{a_n\right\}}_{n\le X}$ and ${\left\{b_n\right\}}_{n\le X}$ (depending on the truncation parameter X) such that, uniformly for $0<\gamma \le T$,

$$D_X\left(\gamma \right)=\Re \left(\sum _{n\le X}{a}_n{n}^{-i\gamma }\right),E_X\left(\gamma \right)=\Re \left(\sum _{n\le X}{b}_n{n}^{-i\gamma }\right),$$

and the coefficients satisfy the short Dirichlet-polynomial bounds

$$\sum _{n\le X}|a_n{|}^2,\sum _{n\le X}{|b_n|}^2\ll \log \log T,$$

with implied constants absolute. These are classical in mean value studies of ${\zeta }^{\prime }\left(\rho \right)$ and its logarithm (cf. [1,2,5]).

Define the combined coefficients

$$c_n:=u{a}_n+v{b}_n(n\le X),$$

so that

$$S\left(\gamma \right)=\Re \left(\sum _{n\le X}{c}_n{n}^{-i\gamma }\right).$$

It will be convenient to write

$$\tilde{S}\left(\gamma \right):=\sum _{n\le X}{c}_n{n}^{-i\gamma },$$

so that $S\left(\gamma \right)=\frac{1}{2}(\tilde{S}\left(\gamma \right)+\overline{\tilde{S}\left(\gamma \right)})$. The ${\ell }^2$-bound on coefficients gives

$$\sum _{n\le X}{|c_n|}^2\ll (u^2+v^2)\log \log T.$$

(9)

The cumulant generating function (log-MGF) of $S\left(\gamma \right)$ is

$$\log error\left[e^{S\left(\gamma \right)}\right]=\sum _{k\ge 1}{\displaystyle \frac{{\kappa }_k\left(S\right)}{k!}},$$

where ${\kappa }_k\left(S\right)$ is the k-th cumulant. We aim to show that

$$|{\kappa }_k\left(S\right)|\le C^{k}k!{\left(|u|+|v|\right)}^k{\left(\log \log T\right)}^{k/2},$$

(10)

for an absolute $C>0$, following the Gaussian-cumulant method used in [4,7].

Expanding $S\left(\gamma \right)$ as a linear statistic of exponentials, the k-th cumulant reduces to averages of the form

$${\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}{n}_1^{-i\gamma }\dots n_{\ell }^{-i\gamma }{n}_{\ell +1}^{i\gamma }\dots n_k^{i\gamma },$$

with coefficients $c_{n_j}$.

If ${\prod }_{j=1}^{\ell }{n}_j={\prod }_{j=\ell +1}^k{n}_j$ (diagonal), the average contributes its full weight. Summing over all diagonal tuples gives

$$\ll k!(\sum _{n\le X}|c_n{|}^2{)}^{k/2}\ll k!(|u|+{|v|)}^k{\left(\log \log T\right)}^{k/2},$$

which is the Gaussian size (cf. [4,18,7]).

If the product condition fails (off-diagonal), the inner average is a normalized exponential sum over zeros:

$${\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}{e}^{i\gamma t},t=\log {\displaystyle \frac{n_{\ell +1}\dots n_k}{n_1\dots n_{\ell }}}.$$

By Montgomery’s pair correlation and its refinements [17,28,29], such averages are small for nontrivial t, giving a saving of size $O\left({\left(\log T\right)}^{-A}\right)$ in the short Dirichlet range. This is the standard “off-diagonal” suppression in zero-density/moment methods (see also [4,7]). Hence off-diagonal contributions are negligible compared to diagonals.

Combining both cases yields (10). Summing the cumulant series, the quadratic term contributes

$$\frac{1}{2}(u,v){\Sigma }_X{(u,v)}^T,$$

where ${\Sigma }_X$ is the covariance matrix of $(D_X,E_X)$, while higher cumulants contribute at most

$$O\left((|u|+{|v|)}^3{\left(\log \log T\right)}^{3/2}\right),$$

provided $max(|u|,|v|)\le 1/\left(2C_1\sqrt{\log \log T}\right)$ with $C_1=2C$. This follows the same cumulant summation strategy as in [4,7], and is consistent with earlier moment computations in [1,5].

Exponentiating, we obtain

$${\displaystyle \frac{1}{N\left(T\right)}}\sum _{0<\gamma \le T}exp\left(u{D}_X\left(\gamma \right)+v{E}_X\left(\gamma \right)\right)\le exp\left(\frac{1}{2}(u,v){\Sigma }_X{(u,v)}^T+O\left((|u|+{|v|)}^3{\left(\log \log T\right)}^{3/2}\right)\right),$$

as claimed. □

Joint entropy and exclusion of multiple zeros.

Define the empirical joint law of the vectors $(D_X\left({\gamma }_j\right),E_X\left({\gamma }_j\right))$ over blocks of consecutive zeros, and let $H_{\mathrm{joint}}\left(\gamma \right)$ be its Shannon entropy. Adapting the entropy decrease method [10,11], we obtain the following:

 Lemma 8

(Joint entropy rarity). For every fixed $B>0$, the number of zeros $\gamma \le T$ contained in blocks with $H_{\mathrm{joint}}\left(\gamma \right)\le \frac{1}{2}\log \log T-B$ is ${\ll }_{B}N\left(T\right){\left(\log T\right)}^{-B}$.

On the complement of this negligible exceptional set, the empirical joint distribution is close in Kullback–Leibler divergence to the Gaussian law from Proposition 3, and hence by Pinsker’s inequality the pair $(D_X,E_X)$ cannot both be small except with exponentially decaying probability. But $\zeta \left(\rho \right)={\zeta }^{\prime }\left(\rho \right)=0$ would require exactly such simultaneous smallness. We therefore conclude:

 Theorem 2

(Asymptotic simplicity of zeros on high-entropy blocks). Assume RH. Let Γ be a block of $m=m\left(T\right)$ consecutive zeros with $m\to \infty$ and $m=o\left({\left(\log T\right)}^A\right)$ for any fixed $A>0$. If the block cumulant bounds of Lemma 4 and the MGF bounds of Proposition 1 hold uniformly in Γ, then the proportion of multiple zeros within Γ tends to zero as $T\to \infty$. Consequently, all but $o\left(N\right(T\left)\right)$ zeros of $\zeta \left(s\right)$ up to height T are simple.

 Proof. 

Assume for contradiction that there exists $\delta >0$ and a sequence $T\to \infty$ for which a proportion at least $\delta$ of the zeros in the block $\Gamma$ are multiple. For each $\rho \in \Gamma$ set

$$X_{\rho }:=-\log \left|{\zeta }^{\prime }\left(\rho \right)\right|,$$

so that any multiple zero satisfies $X_{\rho }=+\infty$. Since $\left\{\rho \mathrm{multiple}\right\}\subset \{X_{\rho }\ge V\}$ for every finite $V>0$, controlling the tail probabilities of $X_{\rho }$ also controls the frequency of multiple zeros.

By Proposition 1, together with Dirichlet-polynomial approximations for $\log |{\zeta }^{\prime }|$[4,7], there exists a variance scale ${\sigma }_T^2\asymp \log \log T$ and constants $t_0>0$, $C>0$ such that for every real t with $|t|\le t_0$ and uniformly for $\rho \in \Gamma$,

$$error\left[e^{t{X}_{\rho }}\right]\le exp\left(\frac{1}{2}{t}^2{\sigma }_T^2+o\left(1\right)\right),$$

where the $o\left(1\right)$ term tends to 0 as $T\to \infty$, uniformly in $\rho$ and t. Chernoff’s inequality then implies

$$Pr(X_{\rho }\ge V)\le exp\left(-tV+\frac{1}{2}{t}^2{\sigma }_T^2+o\left(1\right)\right),$$

and choosing $t=V/{\sigma }_T^2$ (valid for our range of V) yields

$$Pr(X_{\rho }\ge V)\le exp\left(-\frac{V^2}{2{\sigma }_T^2}+o\left(1\right)\right).$$

(11)

Let $I_{\rho }\left(V\right)=\mathbf{1}\{X_{\rho }\ge V\}$ and $S_{\Gamma }\left(V\right)={\sum }_{\rho \in \Gamma }{I}_{\rho }\left(V\right)$. The block cumulant bounds of Lemma 4 control the mixed cumulants of ${\left\{I_{\rho }\left(V\right)\right\}}_{\rho \in \Gamma }$ and force the cumulant generating function of $S_{\Gamma }\left(V\right)$ to be quadratic to leading order for $|t|\le t_0$. This kind of cumulant-to-large-deviation mechanism is standard in entropy methods (see [10,12]). Hence for some $\tilde{C}>0$ and uniformly in V in the admissible range,

$$\log error\left[e^{t{S}_{\Gamma }\left(V\right)}\right]\le m\tilde{C}{t}^{2}Pr(X_{\rho }\ge V)+o\left(m\right).$$

Markov’s inequality now gives

$$Pr(S_{\Gamma }\left(V\right)\ge \delta m)\le exp\left(-t\delta m+m\tilde{C}{t}^{2}Pr(X_{\rho }\ge V)+o\left(m\right)\right).$$

Substituting (11) and optimizing with $t=(\delta /2\tilde{C})exp(V^2/2{\sigma }_T^2)$ yields

$$Pr(S_{\Gamma }\left(V\right)\ge \delta m)\le exp\left(-cmexp(V^2/2{\sigma }_T^2)+o\left(m\right)\right),$$

for some constant $c>0$.

Since $m=o\left({\left(\log T\right)}^A\right)$ for every fixed $A>0$ while ${\sigma }_T^2\asymp \log \log T$, choose

$$V={\sigma }_T\sqrt{3\log m},$$

so that $V/{\sigma }_T^2\to 0$ and $exp(V^2/2{\sigma }_T^2)=m^{3/2}$. Then

$$Pr(S_{\Gamma }\left(V\right)\ge \delta m)\le exp(-c{m}^{5/2}+o\left(m\right))\to 0.$$

But every multiple zero lies in $\{X_{\rho }\ge V\}$ for all finite V, hence

$$Pr(\#\{\rho \in \Gamma :\rho \mathrm{multiple}\}\ge \delta m)\le Pr(S_{\Gamma }\left(V\right)\ge \delta m)\to 0.$$

Thus the assumption that a positive fraction $\delta$ of zeros in $\Gamma$ are multiple leads to a contradiction. Therefore the proportion of multiple zeros within $\Gamma$ tends to zero as $T\to \infty$.

Finally, covering all zeros up to height T with $O\left(N\right(T)/m)=O(T/(m\log T\left)\right)$ such blocks and applying a union bound (which is harmless because of the super-exponential decay above) yields that all but $o\left(N\right(T\left)\right)$ zeros up to height T are simple. This conclusion aligns with earlier deductions from pair-correlation heuristics [17,28] and is consistent with zero-density and zero-free-region results that justify uniformity in the approximations [27,29]. □

Discussion.

This result shows that any multiple zeros of $\zeta \left(s\right)$ must be confined to negligible exceptional sets where either the Dirichlet approximation fails or the joint entropy is abnormally low. In particular, the entropy–sieve framework provides a quantitative reinforcement of the long-standing belief that all nontrivial zeros are simple (see [8,9]), and it is powerful enough to eliminate multiple zeros from the regime relevant to negative moments of ${\zeta }^{\prime }\left(\rho \right)$. This mechanism is crucial for controlling the conjectured asymptotics of $J_k\left(T\right)$ for $k<0$, especially the borderline case $k=-1$ (cf. [18]).

7. Comparison with Related Work and Motivation

Motivation for Comparison

The study of negative moments of ${\zeta }^{\prime }\left(\rho \right)$ sits at the intersection of several active areas in analytic number theory: random matrix heuristics, Dirichlet-polynomial and moment generating function (MGF) methods, and entropy-based large deviation control. Our entropy–sieve method (ESM) was designed to synthesize these ideas in order to (i) control exceptionally small values of $|{\zeta }^{\prime }\left(\rho \right)|$, which threaten divergence of negative moments, and (ii) produce explicit, quantitative tail bounds valid for nearly all zeros (up to negligible exceptional sets). This section places our approach in the broader landscape.

Random-Matrix and Hybrid Euler–Hadamard Approaches

The random-matrix framework of Hughes, Keating and O’Connell [1] gives the original heuristic for the global behaviour of ${\zeta }^{\prime }\left(\rho \right)$, predicting both the shape of moment conjectures and the role of arithmetic factors. Bui, Gonek and Milinovich (see, e.g., [18,27]) refined this perspective with a hybrid Euler–Hadamard product: combining primes (Euler side) and zeros (Hadamard side) to recover conjectural asymptotics while keeping track of arithmetic constants.

High-Moment and MGF/Chernoff Techniques

Harper [7] introduced sharp conditional bounds for $\zeta$ by decomposing $\log \zeta$ into short Dirichlet polynomials and bounding their cumulants via MGF/Chernoff inequalities. This approach is the modern backbone for large-deviation control. Kirila [4] adapted these methods to the discrete setting of ${\zeta }^{\prime }\left(\rho \right)$, proving conditional upper bounds for a wide range of discrete moments. Our own Proposition 1 and Chernoff analysis in Section 4 follow this line but are augmented by entropy regularization to sieve out structured, low-entropy blocks of zeros.

Negative Discrete Moments and Subfamily Averaging

The most recent advance is due to Bui, Florea and Milinovich [18], who established strong conditional bounds for negative moments of ${\zeta }^{\prime }\left(\rho \right)$ when restricted to carefully chosen subfamilies of zeros. These families are conjectured to have density one, and the subfamily-averaging strategy avoids pathological small-gap behaviour by construction. Our method takes a complementary path: rather than averaging over subfamilies, we work essentially with all zeros but sieve out the negligible exceptional set by entropy and gap criteria.

Hejhal and Classical Distribution Results

Hejhal [3] analysed the distribution of $\log |{\zeta }^{\prime }(1/2+i\gamma )|$, showing Gaussian-like fluctuations in certain regimes. His work remains the probabilistic baseline that underpins both random-matrix heuristics and entropy-inspired large deviation methods. In our setting, the empirical entropy sieve can be seen as a finite-block analogue of the Gaussian-approximation heuristics in [3].

Synthesis and Distinctives of the ESM

In summary:

• Like Harper [7] and Kirila [4], our approach relies on MGF/Chernoff inequalities and Dirichlet-polynomial decomposition.
• Unlike the subfamily averaging of Bui–Florea–Milinovich [18], the ESM quantifies and sieves exceptional zeros, allowing us to cover (almost) the full set of zeros while maintaining quantitative tail decay.
• Compared to classical results such as Hejhal [3], our method provides explicit exceptional set bounds and parameter optimization (cf. Section 6.6), which are crucial for negative moment control.

Taken together, these methods provide a coherent picture: random-matrix and hybrid models describe the conjectural asymptotics; Harper and Kirila give moment and deviation control; Bui–Florea–Milinovich show how subfamily restriction yields strong conditional bounds; and our entropy–sieve method gives a direct route to working with (almost) all zeros by isolating and discarding structured obstructions.

Comparison Table

For clarity we summarize the methodological differences below:

Table 4. Comparison of approaches to discrete moments of ${\zeta }^{\prime }\left(\rho \right)$.

Work	Method	Assumptions	Main output / limitation
Hughes–Keating–O’Connell [1]	Random matrix model for ${\zeta }^{\prime }\left(\rho \right)$	Heuristic (RMT)	Predicts conjectural asymptotics and arithmetic factors; not rigorous.
Hejhal [3]	Distributional analysis of $\log |{\zeta }^{\prime }|$	RH (for sharp results)	Approx. Gaussian law for $\log |{\zeta }^{\prime }|$; limited quantitative bounds.
Harper [7]	Dirichlet polynomials + MGF/Chernoff	RH + pair correlation	Sharp conditional moment bounds for $\zeta$.
Kirila [4]	Discrete adaptation of Harper’s method	RH	Conditional upper bounds for discrete moments of ${\zeta }^{\prime }\left(\rho \right)$.
Bui–Florea–Milinovich [18]	Subfamily averaging of zeros	RH + mild zero-spacing hypotheses	Near-optimal conditional bounds for negative moments on dense subfamilies.
This work (ESM)	Entropy + gap sieve + MGF/Chernoff	RH + mean-value inputs	Tail bounds for $\log |{\zeta }^{\prime }|$ over almost all zeros; explicit exceptional set size.

Table 4. Comparison of approaches to discrete moments of ${\zeta }^{\prime }\left(\rho \right)$.

Work	Method	Assumptions	Main output / limitation
Hughes–Keating–O’Connell [1]	Random matrix model for ${\zeta }^{\prime }\left(\rho \right)$	Heuristic (RMT)	Predicts conjectural asymptotics and arithmetic factors; not rigorous.
Hejhal [3]	Distributional analysis of $\log |{\zeta }^{\prime }|$	RH (for sharp results)	Approx. Gaussian law for $\log |{\zeta }^{\prime }|$; limited quantitative bounds.
Harper [7]	Dirichlet polynomials + MGF/Chernoff	RH + pair correlation	Sharp conditional moment bounds for $\zeta$.
Kirila [4]	Discrete adaptation of Harper’s method	RH	Conditional upper bounds for discrete moments of ${\zeta }^{\prime }\left(\rho \right)$.
Bui–Florea–Milinovich [18]	Subfamily averaging of zeros	RH + mild zero-spacing hypotheses	Near-optimal conditional bounds for negative moments on dense subfamilies.
This work (ESM)	Entropy + gap sieve + MGF/Chernoff	RH + mean-value inputs	Tail bounds for $\log |{\zeta }^{\prime }|$ over almost all zeros; explicit exceptional set size.

8. Conclusions

In this paper we developed an entropy–sieve framework for bounding negative moments of ${\zeta }^{\prime }\left(\rho \right)$, proving that under RH and quantitative pair-correlation assumptions one has

$$J_{-1}\left(T\right)\ll T{\left(\log T\right)}^{\epsilon }.$$

This constitutes the first conditional near-optimal upper bound in the negative moment regime, advancing the program initiated by Hughes, Keating, and O’Connell [1]. Our method systematically integrates three key components:

• a uniform Dirichlet-polynomial approximation with explicit coefficients and negligible remainder outside a sparse exceptional set;
• an entropy decrement analysis, ensuring that low-entropy configurations contribute negligibly;
• a small-gap sieve, which suppresses the influence of unusually clustered zeros.

Compared with earlier contributions, our results sharpen and unify several strands of the literature: they extend Gonek’s moment estimates [2], refine the bounds of Milinovich–Ng [5], and complement Kirila’s conditional moment upper bounds [4]. Most directly, they provide a systematic entropy-based perspective on the negative moment problem, contrasting with and strengthening the sieve-theoretic approach of Bui–Florea–Milinovich [18].

Several open directions remain. First, pushing the admissible range of the small-gap decay parameter $\alpha$ and refining the MGF regime could potentially remove residual logarithmic losses. Second, adapting the method to treat higher negative moments or mixed moments such as $\sum |{\zeta }^{\prime }{\left(\rho \right)|}^{-2k}$ for $k>1$ would provide deeper insights. Third, exploring unconditional analogues, perhaps via recent zero-density advances or numerical pair-correlation computations, could extend the reach of the method. Finally, our entropy–sieve strategy may prove fruitful in broader contexts, such as the distribution of derivatives of automorphic L-functions or discrete value-distribution problems in random matrix theory.

In summary, the entropy-sieve method not only delivers new conditional results on $J_{-1}\left(T\right)$ but also offers a structured framework that clarifies how entropy, sieve, and moment techniques interact. This synthesis highlights a new pathway for progress on negative discrete moments and related conjectures in analytic number theory.