Constructing 8×8 S-Boxes with Optimal Boolean Function Nonlinearity

1. Introduction

In modern block cipher algorithms, the substitution box (S-Box) is the fundamental nonlinear component that provides confusion and protects against classical cryptanalytic methods such as linear cryptanalysis and differential cryptanalysis. Formally, an S-Box can be represented as a vectorial Boolean function. The cryptographic strength of an S-Box is therefore determined by the properties of these functions. Nonlinearity (NL) is the most fundamental indicator, as it measures the distance from affine functions and directly reflects resistance to linear approximation attacks.

For 8-variable Boolean functions, corresponding to $8\times 8$ S-Boxes, the highest nonlinearity mathematically discovered so far for balanced functions is 116 [1,2,3]. However, constructing balanced S-Boxes that reach this bound has long been considered a major challenge in cryptography. Previous works based on algebraic transformations [4,5,6,7,8,9,10,11,12,13,14,15,16], chaotic systems [17,18,19,20,21,22,23,24,25,26,27], and hybrid approaches [28,29,30,31,32,33,34,35,36,37] have achieved significant progress, yet the highest reported nonlinearity has remainsed at $114.5$ [29], still below the theoretical maximum.

In addition to nonlinearity, other research directions have focused on optimizing different cryptographic aspects. Several studies aim to maximize the Strict Avalanche Criterion (SAC) [38,39,40], while others emphasize efficiency in hardware implementation [41,42,43,44,45,46,47]. Research on S-Boxes has also focused on optimizing parameters related to side-channel resistance [30,48,49], while other studies target optimization against advanced cryptanalytic techniques such as the Boomerang attack [50] or Differential and Linear Branch Numbers [51].

Although previous studies have made important progress in the design of S-Boxes, the fundamental challenge of attaining the maximum possible nonlinearity for balanced $8\times 8$ S-Boxes remains unresolved. In this paper, we focus on bridging these gaps by optimizing nonlinearity in conjunction with hardware efficiency. The main contributions of this work are summarized as follows:

• A novel construction method: We developed a systematic approach for building 8×8 S-Boxes from smaller $4\times 4$ component S-Boxes, which allows for a modular and efficient design.
• Optimal nonlinearity: The S-Boxes we constructed successfully achieve a nonlinearity of 116, reaching the theoretical maximum for 8-variable balanced Boolean functions.
• Comprehensive security analysis: Our analysis confirms that these new S-Boxes meet other critical security criteria, including the Strict Avalanche Criterion (SAC), Bit Independence Criterion (BIC), Differential Avalanche Probability (DAP), and Linear Avalanche Probability (LAP).
• Practical robustness: Side-channel attack experiments show that our S-Boxes offer resistance comparable to the Advanced Encryption Standard (AES) S-Box, proving their real-world applicability.
• Efficient hardware implementation: Our S-Boxes are designed for efficient hardware resource utilization, making them ideal for systems with limited resources.

The remainder of this paper is organized as follows. Section 2 reviews related work. Section 3 presents the theoretical background of Boolean functions and S-Box design criteria. Section 4 introduces the proposed construction method. Section 5 reports the cryptographic security analysis of the generated S-Boxes and presents experimental results of side-channel attack. Section 6 evaluates the hardware performance in terms of resource efficiency. Finally, Section 7 concludes the paper.

2. Related Works

A wide range of approaches have been proposed for the construction of S-Boxes, which can broadly be categorized into algebraic-based, chaotic-based, hybrid techniques, and composition methods using smaller substitution components. Below, we present some of the most recent studies in this field.

Several studies exploit algebraic structures and mathematical transformations for S-Box construction. In [8], Möbius transformation combined with permutations was applied to design S-Boxes that enhance IoT multimedia security. The study in [9] proposed constructing S-Boxes based on power associative loops, later applied to text encryption. The work in [20] employed Delannoy-derived sequences to generate a new chaotic S-Box. Dimitrov and Baicheva [52] analyzed the classification of 8-bit to 8-bit power mappings defined by pentanomials for S-Box generation. Waheed et al. [29] introduced S-Boxes constructed through a combination of linear fractional transformation and multilayer perceptrons, achieving the best reported nonlinearity of 114.5.

Chaotic dynamical systems have also been widely adopted for constructing S-Boxes. Boobalan et al. [18] proposed dynamic S-Boxes derived from Lorenz and Chua chaotic systems for efficient image encryption. A dynamic scheme based on Mordell elliptic curves over Galois fields was presented in [7]. Group-action-based S-Box generation was described in [6]. The approach in [32] combined chaotic maps with bit-level permutations to construct S-Boxes for medical data security. Furthermore, Zhang Lijun et al. [53] introduced S-Boxes generated via quantum random walks controlled by a hyper-chaotic map. These methods provide advantages in randomness and applicability to image encryption, but the achieved nonlinearity typically remains at medium–high levels, in most cases below 112, and still far from the theoretical optimum.

Other studies combine multiple methods or apply heuristic algorithms to strengthen S-Box properties. A cost-function-based approach for efficient S-Box construction was proposed in [5], while [31] employed a hybrid population-based hill climbing algorithm, where the nonlinearity stopped at 104. The work in [30] utilized rotation symmetry combined with heuristic search to generate S-Boxes. Malik et al. [33] constructed nonlinear components in the form of S-Boxes using hybrid pseudo-random binary sequences. In addition, Song and Zhao [17] focused on S-Box designs for secure image encryption, emphasizing a balance between robustness and efficiency.

Some works explored the construction of larger S-Boxes from smaller substitution components to achieve lightweight and efficient designs. The study in [45] introduced a Feistel-based composition method, while [47] extended the analysis to both Feistel and MISTY networks, highlighting their potential for systematic generation of lightweight substitution layers. High differential and linear branch numbers were targeted in [51] to improve diffusion, whereas [46] investigated hardware-oriented S-Box constructions combined with masking techniques to resist side-channel attacks. More recently, Yan et al. [48] developed substitution layers based on small S-Boxes that are resilient to differential power analysis, confirming the practicality of this direction. Collectively, these contributions underline that the primary motivation of composition-based methods lies in hardware efficiency and deployability rather than maximizing theoretical cryptographic metrics.

In summary, recent research has significantly expanded the design space of S-Boxes through diverse approaches. However, the gap between the best known result (114.5) and the theoretical maximum (116) persists, leaving an open challenge that the present study aims to address.

3. Background

3.1. Boolean Functions and Nonlinearity

Boolean functions [54] are at the heart of symmetric cryptography, where they provide the nonlinearity required to secure block ciphers against algebraic and statistical attacks. An n-variable Boolean function is formally defined as a mapping $f:{\mathbb{F}}_2^n\to {\mathbb{F}}_2$, where ${\mathbb{F}}_2$ denotes the binary field. For an input vector $x=(x_1,x_2,\dots ,x_n)\in {\mathbb{F}}_2^n$, the function outputs a single bit $f\left(x\right)\in \{0,1\}$. One of the most important cryptographic indicators of a Boolean function is its nonlinearity, which quantifies the minimum Hamming distance between f and the set of all affine functions. Formally, the nonlinearity of f is defined as Equation (1) [55].

$$NL\left(f\right)=\underset{g\in A_n}{min}{d}_H(f,g),$$

(1)

where $A_n$ is the set of affine functions in n variables and $d_H$ is the Hamming distance. High nonlinearity ensures that f cannot be closely approximated by linear or affine expressions, thereby strengthening resistance against linear cryptanalysis. The theoretical maximum nonlinearity of an n-variable Boolean function is given by Equation (2) [55].

$$NL\left(f\right)\le 2^{n-1}-2^{{\displaystyle \frac{n}{2}}-1}.$$

(2)

Bent functions represent Boolean functions that achieve the maximum possible distance from all affine functions, thereby providing the highest nonlinearity. However, a fundamental limitation is that bent functions are never balanced, which makes them unsuitable for S-Box design since balancedness is required to avoid biased outputs. Importantly, bent functions exist only when n is even. For instance, with $n=8$, the theoretical upper bound for unbalanced Boolean functions is 120, achieved by bent functions, whereas the best attainable value for balanced functions is strictly lower, at 116 [1,2,3]. This bound of 116 therefore constitutes the true optimal target for the coordinate functions of an $8\times 8$ S-Box.

The Walsh–Hadamard transform [56] is typically used to compute nonlinearity. For a Boolean function f, the Walsh spectrum is defined as Equation (3).

$$W_f\left(a\right)=\sum _{x\in {\mathbb{F}}_2^n}{(-1)}^{f\left(x\right)\oplus \langle a,x\rangle },$$

(3)

where $\langle a,x\rangle$ denotes the inner product of vectors a and x over ${\mathbb{F}}_2$. The nonlinearity can then be expressed equivalently as Equation (4).

$$NL\left(f\right)=2^{n-1}-{\displaystyle \frac{1}{2}}\underset{a\in {\mathbb{F}}_2^n}{max}\left|W_f\left(a\right)\right|.$$

(4)

From this perspective, minimizing the maximum Walsh coefficient directly maximizes the nonlinearity of f. This theoretical foundation highlights why constructing balanced 8-variable Boolean functions with nonlinearity 116 has been considered one of the most difficult open problems in symmetric cryptography.

3.2. Properties of Cryptographically Strong S-Boxes

Several well-established criteria are used to evaluate S-Box properties, including Nonlinearity (NL), Strict Avalanche Criterion (SAC), Bit Independence Criterion (BIC), Differential Approximation Probability (DAP), Linear Approximation Probability (LP) algebraic degree (AD), and some parameters related to side-channel attack, such as the Transparency Order (TO), Modified Transparency Order (MTO), Revised Transparency Order (RTO), Minimum Correlation Coefficient (MCC), Confusion Coefficient Variance (CCV), and Signal-to-Noise Ratio (SNR) [57,58,59,60,61,62,63]. The evaluation criteria for cryptographic S-Boxes have been presented in detail in many existing studies [21,64,65]. These metrics cover both classical cryptanalytic strength and resistance against side-channel attacks. For completeness, we provide in Table 1 a concise summary of the main properties and their desired values.

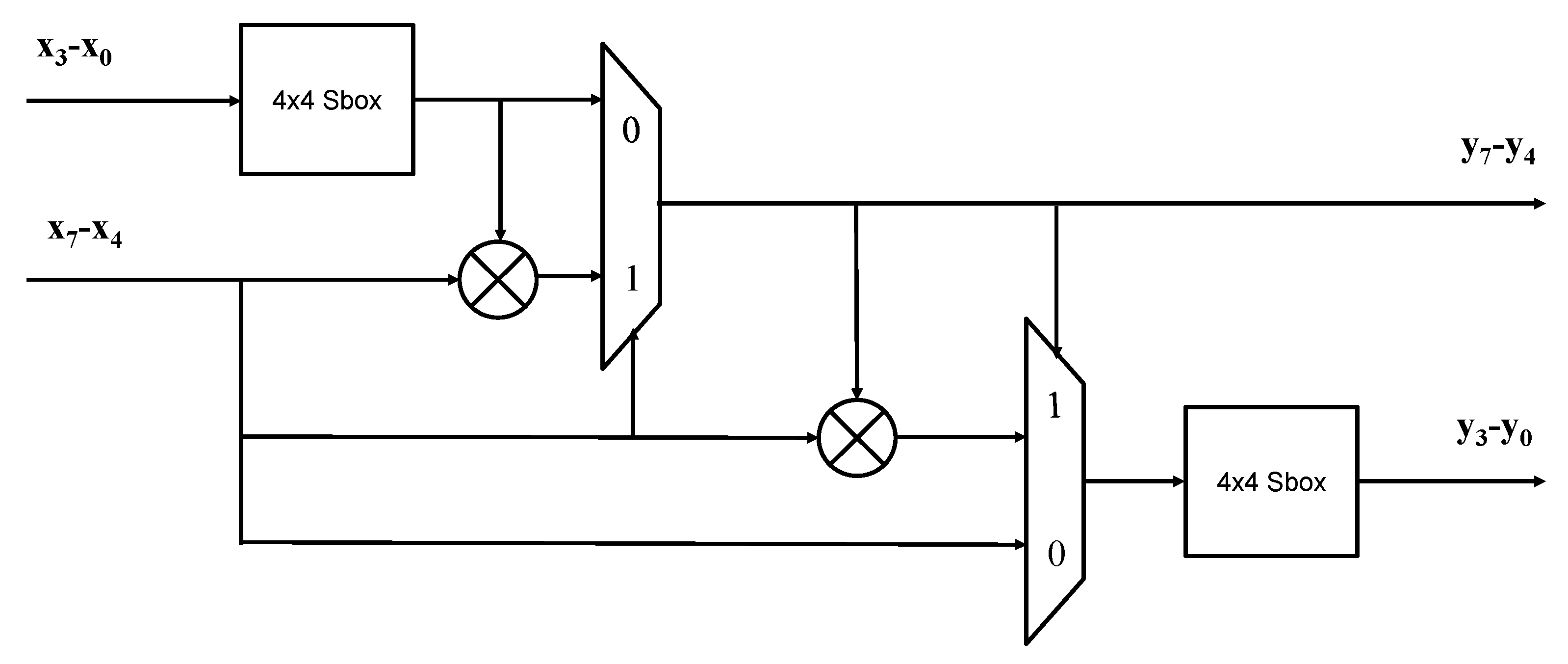
4. Proposed Method

4.1. Proposed Algorithm

In this study, we present a method to construct an 8×8 S-Box based on the combination of four $4\times 4$ S-Boxes and multiplication in the subfield $GF\left(2^4\right)$. The objective of the proposed method is to exploit both the strong nonlinearity of the $4\times 4$ lookup tables and the diffusion capability of finite field multiplication, thereby generating a mapping of sufficient complexity to resist modern cryptanalytic techniques. The algorithm takes as input an 8-bit word $x\in {\{0,1\}}^8$, and produces an 8-bit output $y\in {\{0,1\}}^8$. For computation, the input is divided into two halves: the upper nibble $x[7:4]$ and the lower nibble $x[3:0]$. Similarly, the output is represented by $y[7:4]$ and $y[3:0]$. Four independent $4\times 4$ S-Boxes, denoted $S_A,S_B,S_C,S_D$, are employed in the construction. These components provide nonlinearity in each transformation step, while multiplication in $GF\left(2^4\right)$, denoted by ⊗, ensures strong interdependence between the two halves of the data. The upper nibble of the output is computed as Equation (5).

$$y[7:4]=\left\{\begin{array}{cc}{S}_A\left(x[3:0]\right)\otimes x[7:4],\hfill & \mathrm{if}x[7:4]\ne 0,\hfill \\ S_B\left(x[3:0]\right),\hfill & \mathrm{if}x[7:4]=0,\hfill \end{array}\right.$$

(5)

that is, when the upper nibble of the input is nonzero, $S_A$ is applied to the lower nibble and the result is multiplied with the upper nibble; otherwise, $S_B$ is applied to the lower nibble. Next, the lower nibble of the output is computed as Equation (6).

$$y[3:0]=\left\{\begin{array}{cc}{S}_C(x[7:4]\otimes y[7:4]),\hfill & \mathrm{if}y[7:4]\ne 0,\hfill \\ S_D\left(x[7:4]\right),\hfill & \mathrm{if}y[7:4]=0.\hfill \end{array}\right.$$

(6)

Thus, the lower nibble depends on both halves of the input through the intermediate value $y[7:4]$, ensuring complete diffusion across the entire 8-bit word. Finally, the complete output is adjusted with a simple XOR by one ($y\leftarrow y\oplus 1$) to remove possible fixed points. This algorithm requires only two $4\times 4$ S-Box lookups, two multiplications in $GF\left(2^4\right)$, and one XOR operation. As a result, it achieves strong nonlinearity with low implementation complexity, which is advantageous for hardware-oriented designs under resource constraints. The combination of nonlinear substitution and finite field multiplication ensures that the high and low nibbles of the data remain strongly correlated, thereby strengthening resistance against differential and linear cryptanalysis.

4.2. Experimental

To specify multiplication ⊗ in $GF\left(2^4\right)$, three irreducible polynomials of degree four over $GF\left(2\right)$ are employed as Equation (7).

$$f_1\left(x\right)=x^4+x+1,f_2\left(x\right)=x^4+x^3+1,f_3\left(x\right)=x^4+x^3+x^2+x+1.$$

(7)

Each polynomial defines a distinct representation of the finite field, which leads to different multiplication tables and, consequently, different sets of $4\times 4$ S-Boxes.

The $4\times 4$ S-Boxes are generated from power mappings in the multiplicative group $GF{\left(2^4\right)}^{*}$ of order 15. A mapping $x\mapsto x^k$ is bijective if and only if $gcd(k,15)=1$. Therefore, the valid exponents are $k\in \{1,2,4,7,8,11,13,14\}$. Each exponent produces one distinct $4\times 4$ S-Box. Hence, for each irreducible polynomial $f_i$, eight S-Boxes are obtained, denoted as $S1$ through $S8$. Table 2 lists all resulting $4\times 4$ S-Boxes for the three polynomials.

During the experimentation, four S-Boxes were selected from each set of eight and assigned to $S_A,S_B,S_C,$ and $S_D$ in the proposed algorithm. For a single irreducible polynomial, this results in $8^4=4096$ possible configurations, and across the three considered polynomials the total number of generated S-Boxes reaches 12,288. The distribution of average Boolean function nonlinearities for these S-Boxes is summarized in Table 3. Among them, 2,304 S-Boxes achieve the optimal nonlinearity of 116 for all coordinate Boolean functions. This outcome highlights both the strength and flexibility of the proposed construction method, as it yields a large set of secure candidates from which practical designs can be selected. From this collection, we prioritize configurations with the lowest implementation cost, which corresponds to the case where all four component S-Boxes $S_A,S_B,S_C,$ and $S_D$ are identical. Using the irreducible polynomial $f_1\left(x\right)=x^4+x+1$, one representative configuration is obtained with four identical $4\times 4$ S-Boxes defined as [0, 1, 9, 14, 13, 11, 7, 6, 15, 2, 12, 5, 10, 4, 3, 8]. The detailed results for this representative S-Box are presented in Table 4.

5. Security Analysis

A variety of essential criteria for evaluating the cryptographic strength of S-Boxes have been discussed in [57,58,64,65]. Instead of restating the complete mathematical formulations for these metrics, we present only the corresponding analytical results, as the detailed definitions are readily available in existing S-Box literature. To support reproducibility, a dedicated program for computing all evaluation parameters of the S-Box has been developed and is publicly accessible at https://github.com/dpp291187/S-Box-Cryptanalysis.

5.1. Nonlinearity

By applying the standard formula for computing the nonlinearity of Boolean functions to each coordinate function of the S-Box, the results are obtained as shown in Table 5. Most existing constructions achieve average nonlinearity values in the range of 100–112, with the best reported results reaching about 114 on average. In contrast, the proposed S-Box achieves the maximum balanced nonlinearity of 116 uniformly across all eight Boolean functions, giving an average NL of 116.00. This uniform attainment of the theoretical optimum clearly surpasses all previously reported works and establishes a new benchmark for cryptographic S-Box design.

The constructed S-Box also achieves the maximum algebraic degree of 7. Although this value is commonly obtained in many strong S-Box designs, it remains a critical feature that prevents low-degree polynomial representations, thereby reinforcing robustness against algebraic cryptanalysis.

5.2. Strict Avalanche Criterion

One of the fundamental measures of diffusion in an S-Box is the Strict Avalanche Criterion (SAC), which evaluates whether flipping a single input bit produces random-like changes across the output bits with a probability close to 50%. When the SAC values approach 0.5, the S-Box is considered to exhibit strong randomness. Using the method described in [68], the SAC values for each coordinate function of the proposed S-Box were determined, and the outcomes are summarized in Table 6. The overall average value obtained is 0.5126, which is essentially optimal.

5.3. Bit Independence Criterion

The Bit Independence Criterion (BIC) serves as an important indicator of whether the output bits of an S-Box behave independently when a single input bit is modified. It is typically examined through two perspectives: the avalanche effect (BIC-SAC) and resistance to linear approximation (BIC-NL). The computed results, summarized in Table 7 and Table 8, show that the proposed S-Box attains an average BIC-NL of 111.64 and an average BIC-SAC of 0.5103. These values confirm that the design satisfies the independence requirement and exhibits strong cryptographic quality.

5.4. Differential Approximation Probability

An S-Box’s resistance to differential cryptanalysis is commonly evaluated through its differential uniformity, which reflects how evenly output differences are distributed when input differences are applied [58,64]. This behavior is summarized using the XOR distribution table as shown in Table 9, where each entry shows the frequency of specific input–output difference pairs.

Table 10 highlights the distribution of differences across the S-Box. The largest entry, denoted as the differential uniformity, shows the maximum probability of a specific difference pair occurring. Smaller values indicate stronger resistance against differential cryptanalysis. Based on the table, the maximum observed frequency leads to a differential uniformity of 6. Consequently, the DAP, obtained by normalizing this value over the full input space, equals $6/256=0.0234$.

5.5. Linear Approximation Probability

Another important property is the linear approximation probability, which evaluates the likelihood of linear relations existing between selected input and output bits of the S-Box [58,64]. This measure reflects vulnerability to linear cryptanalysis, where smaller values correspond to better resistance. The analysis shows that the S-Box under study achieves a maximum linear probability of 0.078, indicating that no strong linear correlations or structures are present. This outcome suggests that the transformation is resistant to linear approximations, thereby improving overall cryptographic strength.

The comparative results in Table 10 clearly demonstrate the superiority of the proposed S-Box over existing designs. In particular, our construction achieves the highest possible nonlinearity of 116, which significantly surpasses all previously reported works and reaches the theoretical optimum for balanced $8\times 8$ Boolean functions. Furthermore, the obtained BIC-NL of $111.64$ closely approaches the best results observed in strong S-Boxes such as [20], and AES S-Box [67], confirming its robustness against linear approximations of correlated outputs. With respect to the SAC and its BIC-SAC, the proposed design exhibits values close to the ideal $0.5$, indicating equivalent diffusion performance to state-of-the-art alternatives.

Although the DAP and LAP of our S-Box are slightly weaker compared to AES, they remain lower than or comparable to the majority of alternative S-Boxes surveyed, reflecting a favorable trade-off between resistance to differential and linear cryptanalysis. Another noteworthy strength of the proposed S-Box is the complete elimination of both fixed points and opposite fixed points. In this design, the number of fixed points is zero ($FP=0$), and likewise, the number of opposite fixed points is also zero ($OFP=0$). A fixed point corresponds to an input x such that $S\left(x\right)=x$, while an opposite fixed point arises when $S\left(x\right)=\overline{x}$, with $\overline{x}$ denoting the bitwise complement of x. The presence of such properties can weaken security by introducing predictable structures exploitable by adversaries. The absence of both FP and OFP in our construction ensures that no trivial input–output patterns exist, thereby enhancing unpredictability and reinforcing the overall cryptographic strength of the proposed S-Box.

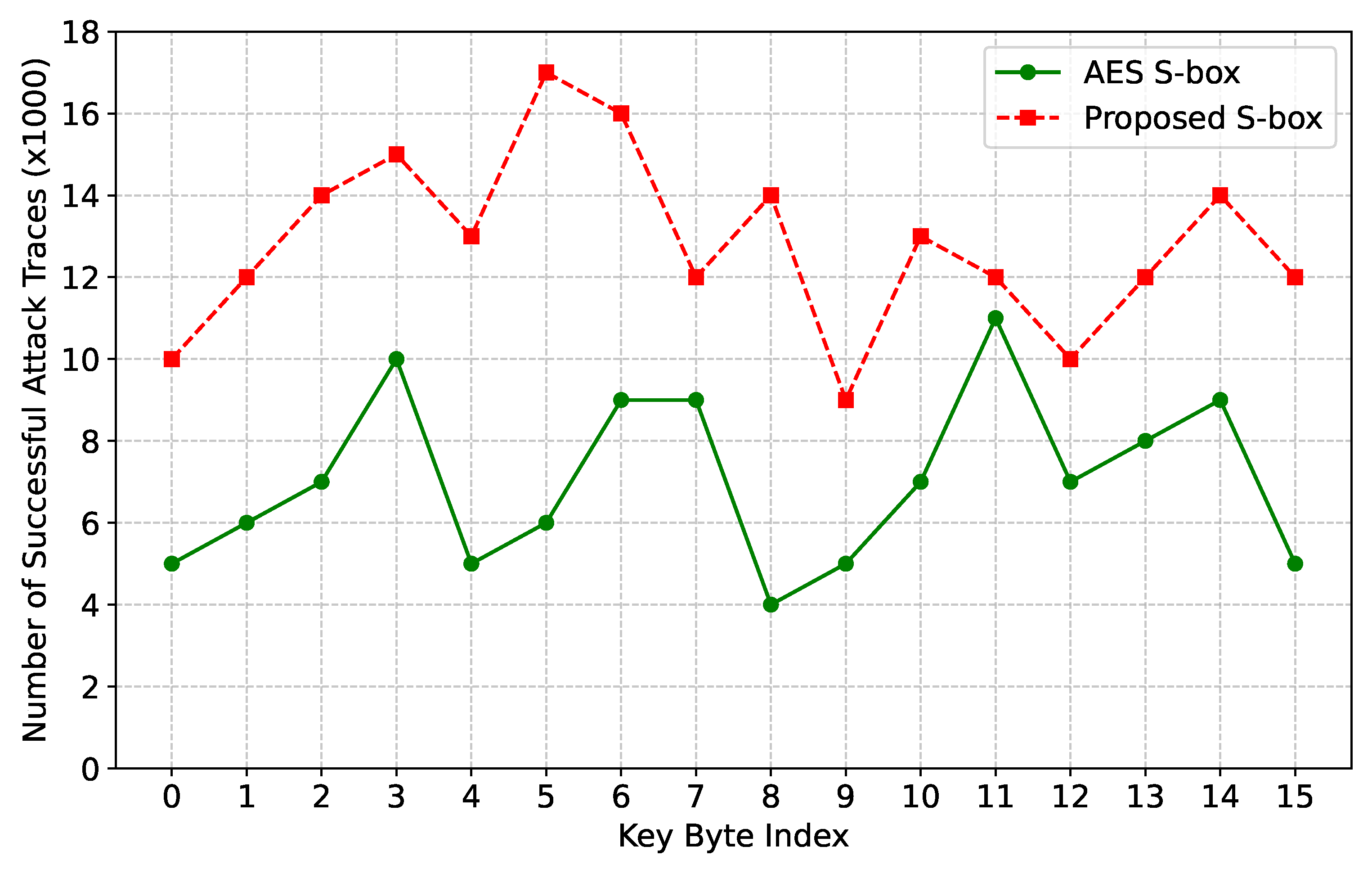
5.6. Side-Channel Attack Analysis

In addition to conventional cryptographic criteria, it is essential to assess the resistance of an S-Box against side-channel attacks. For this purpose, we computed several commonly used parameters, including TO. When making comparisons across different designs, however, the normalized forms $T{O}_0$, $MT{O}_0$, and $RT{O}_0$ are typically used, together with MCC, CCV, and SNR. These metrics provide a fair basis for evaluating how effectively an S-Box can mitigate leakage exploitable by power analysis or related techniques.

The results summarized in Table 11 show that the proposed design achieves parameter values closely aligned with those of AES and other recent strong constructions. The variations observed across different schemes are minimal, which indicates that at the theoretical level most modern S-Box designs, including the one proposed here, demonstrate a comparable degree of robustness against basic side-channel attacks. This also confirms that the cryptographic improvements obtained in the proposed S-Box do not compromise its side-channel security.

Since theoretical analysis alone cannot fully capture practical leakage behavior, the next section turns to hardware implementation and experimental attacks to provide a more reliable evaluation of the proposed S-Box in realistic scenarios.

To evaluate the resistance of the proposed S-Box against side-channel attacks, a trace acquisition scenario similar to [4] was conducted. AES-128 was implemented on the Sakura-X FPGA board with a single-cycle-per-round architecture. Random plaintexts were generated on a computer and encrypted using a fixed 128-bit key. During encryption, the oscilloscope recorded the power consumption of the FPGA, while the corresponding ciphertexts were synchronized and stored on the computer. In total, 30,000 power traces were collected for the analysis.

After trace acquisition, a Correlation Power Analysis (CPA) [69,70] targeting the last round of AES was performed. For each key byte, hypotheses were generated using the Hamming Distance power model, and the correlation coefficient between the hypothetical power values and the measured traces was computed. The correct key value was identified when its correlation clearly exceeded that of other hypotheses.

The evaluation considered two scenarios: AES with the standard Rijndael S-Box, and AES with the proposed S-Box.

• With the AES S-Box, approximately 9,000 traces were sufficient to recover 14 out of 16 key bytes, with the most difficult byte requiring about 11,000 traces.
• With the proposed S-Box, around 12,000 traces were necessary to recover 12 out of 16 key bytes, and the hardest byte required up to 17,000 traces.

As illustrated in Figure 1, the proposed S-Box requires more traces than the AES S-Box for successful key recovery. This suggests a marginal improvement in resistance to CPA; however, the difference remains insignificant in the unprotected evaluation setting. Overall, the results indicate that both S-Boxes exhibit comparable levels of side-channel resistance in practice.

6. Implementation

After selecting a representative configuration with four identical 4×4 S-Boxes that achieves both optimal nonlinearity and minimal implementation cost in the previous section, this section provides a detailed description of the hardware implementation in order to evaluate resource utilization. Since the 4×4 S-Box and the multiplication over $GF\left(2^4\right)$ are fundamental building blocks, the estimation of hardware cost is straightforward. According to Equations (5) and (6), the proposed architecture can be implemented with two 4×4 S-Box blocks, two multiplications in $GF\left(2^4\right)$, and two 2:1 multiplexers (each with 4-bit inputs). The overall hardware design is illustrated in Figure 2. In this figure, the two 4×4 S-Boxes are placed separately to compute output. However, to optimize resource usage, in practical implementation a single S-Box circuit can be reused sequentially for both computations through appropriate scheduling. In this way, the overall architecture not only reflects the algebraic definitions accurately but also achieves high efficiency in terms of hardware resource consumption.

Table 12 presents a benchmark of logic gate utilization for the proposed S-Box in comparison with several established designs. The proposed structure is composed of 43 XOR/XNOR gates, 39 AND gates, 6 OR gates, and 8 multiplexers ($2\times 4$ MUX21), while entirely avoiding NAND, NOR, and NOT gates. This configuration results in a compact circuit with moderate overall complexity.

Among these components, XOR gates are generally regarded as the most resource-demanding in terms of hardware cost. The proposed S-Box achieves a significant reduction in XOR usage compared to most prior works. For instance, Zhang [75] reports 154 XOR gates, Canright [71] 91 XOR gates, and Rashidi [74] 57 XOR gates, whereas our design employs only 43 XOR gates. This reduction is particularly important for hardware implementations, as it directly translates into lower area and power consumption.

The normalized hardware cost, expressed in Gate Equivalents (GE) based on STM 65nm technology parameters [73], further highlights the efficiency of the proposed design. The GE count of the proposed S-Box is calculated to be 159.75, which is smaller than most of the compared studies, including Canright (218.00 GE), Zhang (369.00 GE), and Kuznyechik (342.25 GE). Compared with the most efficient prior design by Maximov (168.00 GE), the proposed S-Box achieves a modest improvement, reducing the GE count by about 8.25. The results indicate that the proposed S-Box exhibits lower hardware resource consumption compared to most existing designs. While the main focus of this study lies in optimizing nonlinearity, the proposed S-Box simultaneously achieves improvements in hardware efficiency.

Overall, these results confirm that the proposed S-Box achieves an attractive balance between low gate complexity and strong cryptographic criteria. The significant reduction in XOR gates and the smallest GE count among all compared implementations highlight its suitability for resource-constrained environments such as embedded systems and lightweight cryptographic applications.

7. Conclusion

This paper presents a novel method for constructing 8×8 S-Boxes from smaller $4\times 4$ components, representing a significant advance in cryptographic design. Key findings and contributions are as follows:

• Optimal Nonlinearity: The S-Boxes developed using this new method achieve a nonlinearity of 116, which is the highest possible for balanced 8-variable Boolean functions. This breakthrough surpasses all previously reported results, setting a new benchmark in the field.
• Comprehensive Security: Beyond optimal nonlinearity, the S-Boxes also satisfy other key cryptographic criteria, including the Strict Avalanche Criterion (SAC), Bit Independence Criterion (BIC), Differential Avalanche Probability (DAP), and Linear Avalanche Probability (LAP), all at robust levels.
• Proven Robustness and Efficiency: Practical evaluations show that these S-Boxes are highly resilient. They offer side-channel attack resistance comparable to the AES S-Box and are designed for efficient hardware implementation, making them suitable for resource-constrained systems.

In summary, this research is a major step forward, providing a new S-Box construction method that is not only a theoretical breakthrough but also a practical, efficient, and highly secure solution for modern block ciphers and data protection systems.