Submitted:
28 August 2025
Posted:
01 September 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Material and Methods
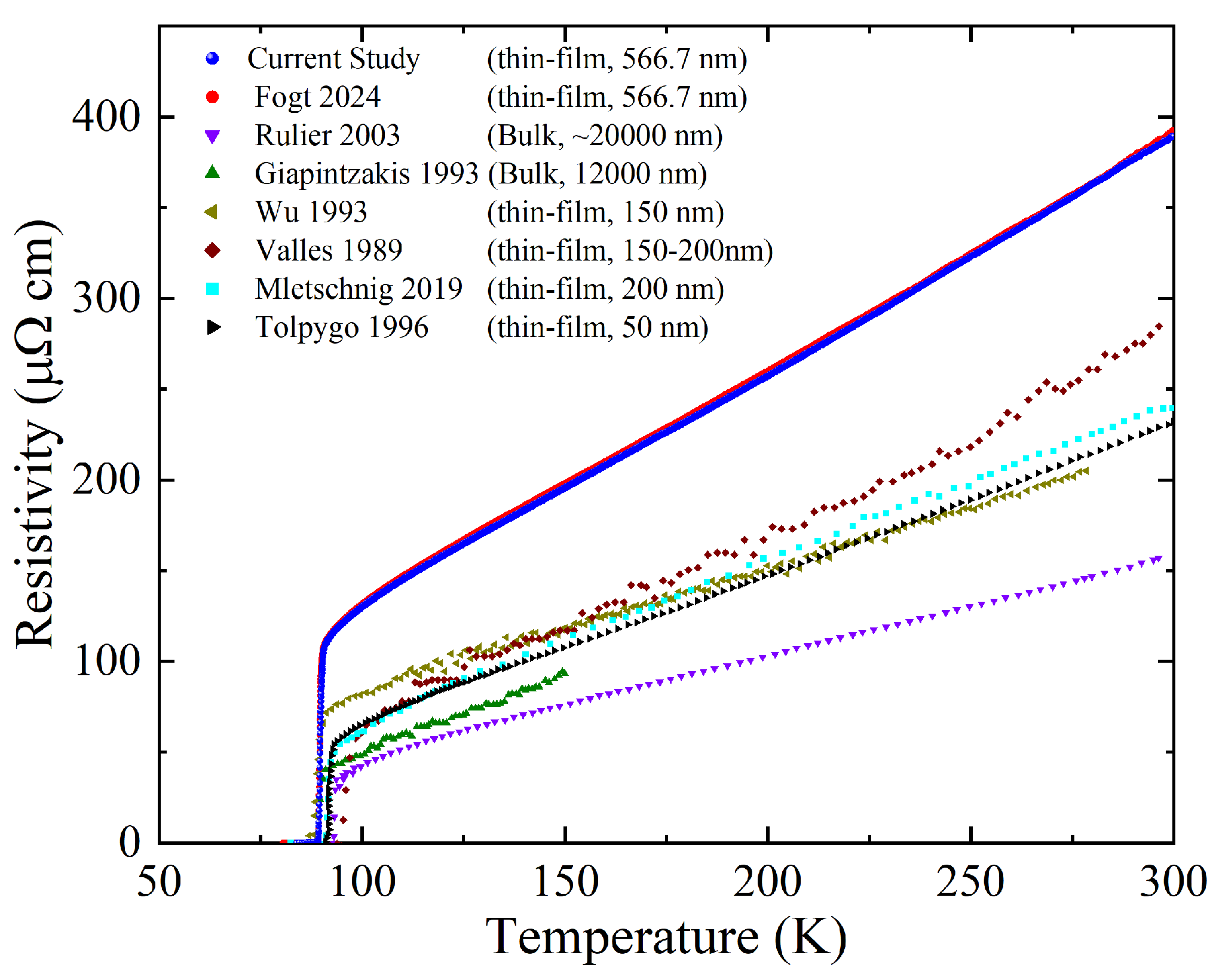
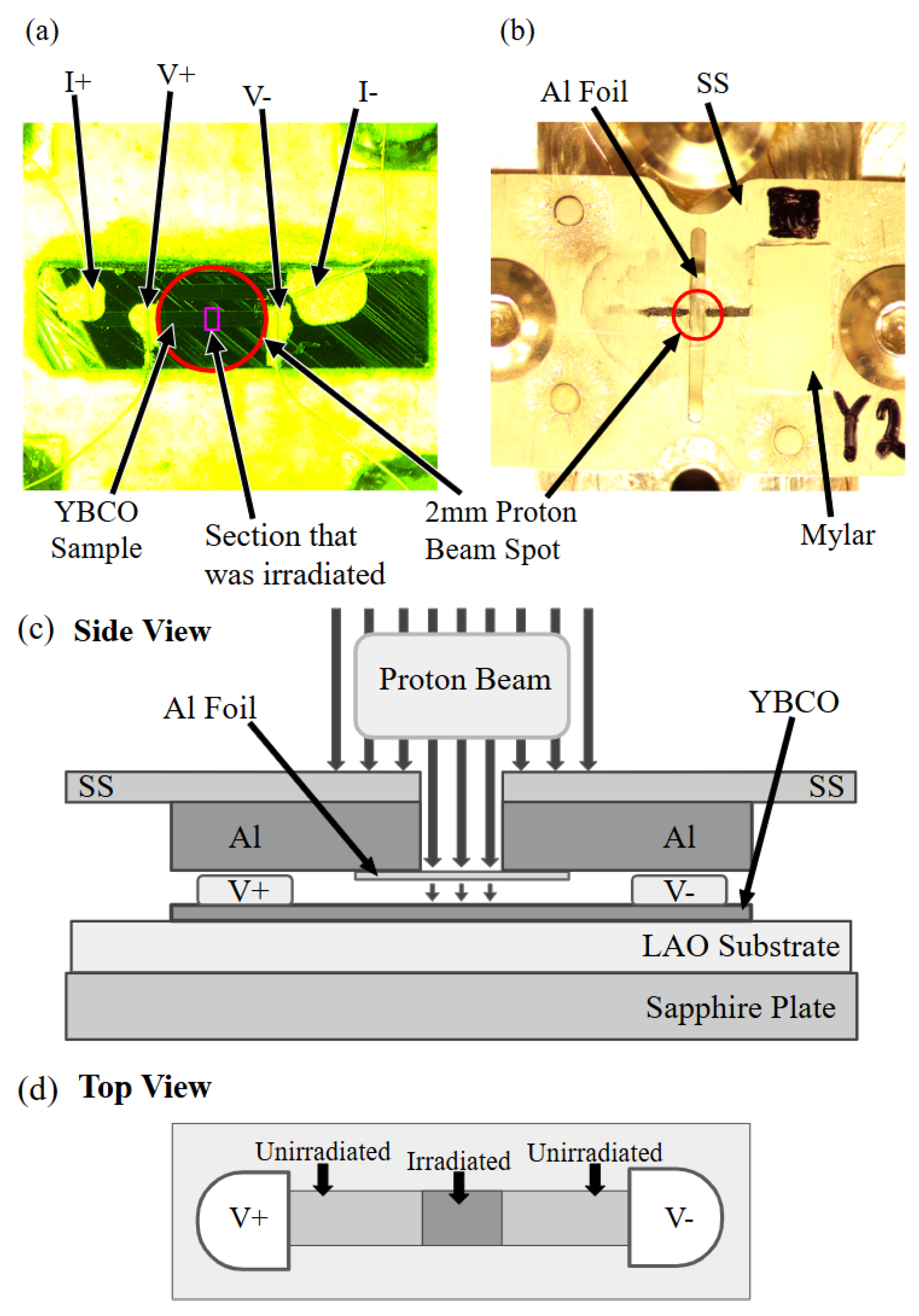
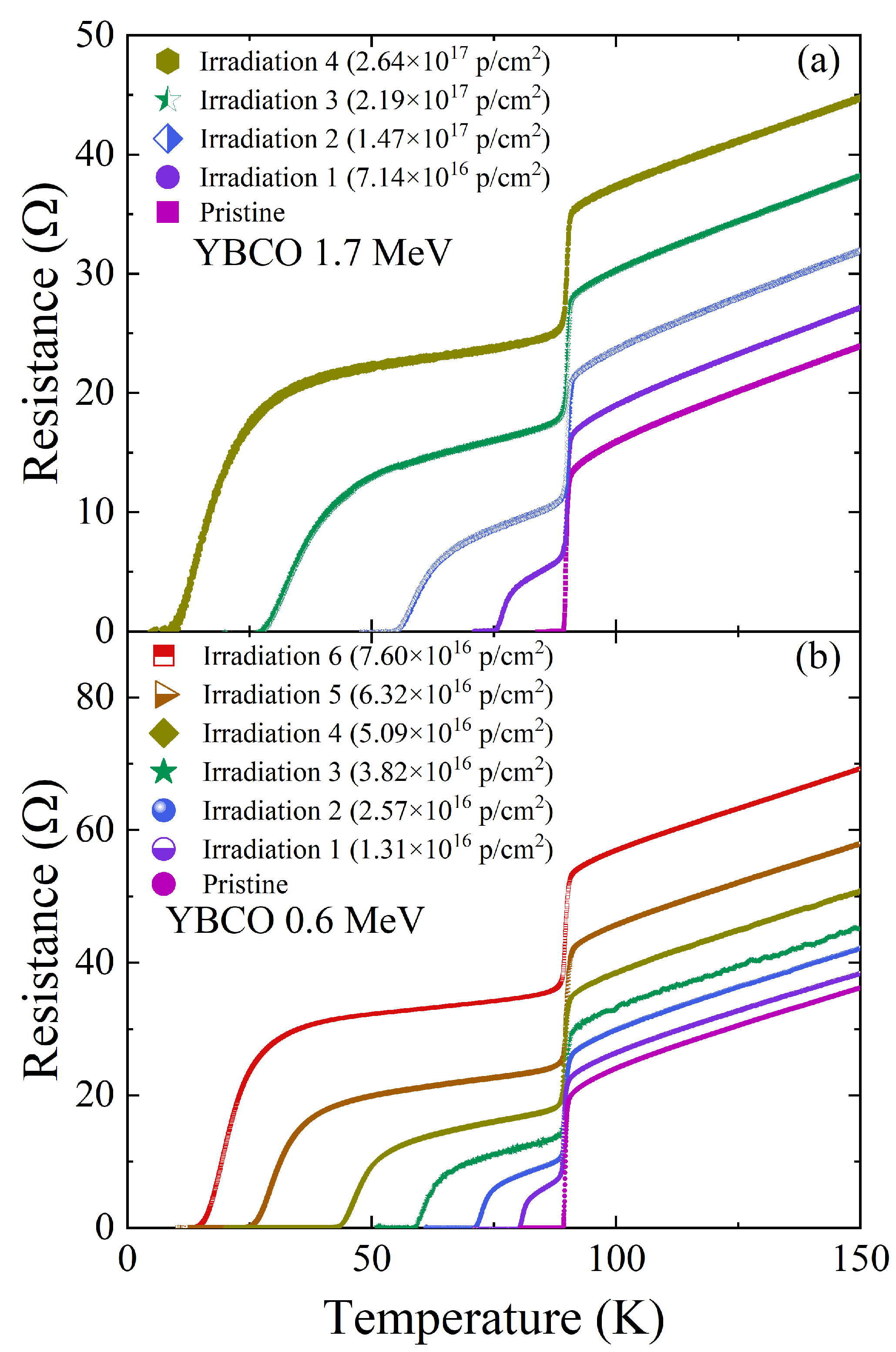
2.1. YBCO Thin-Film and Resistance Measurements
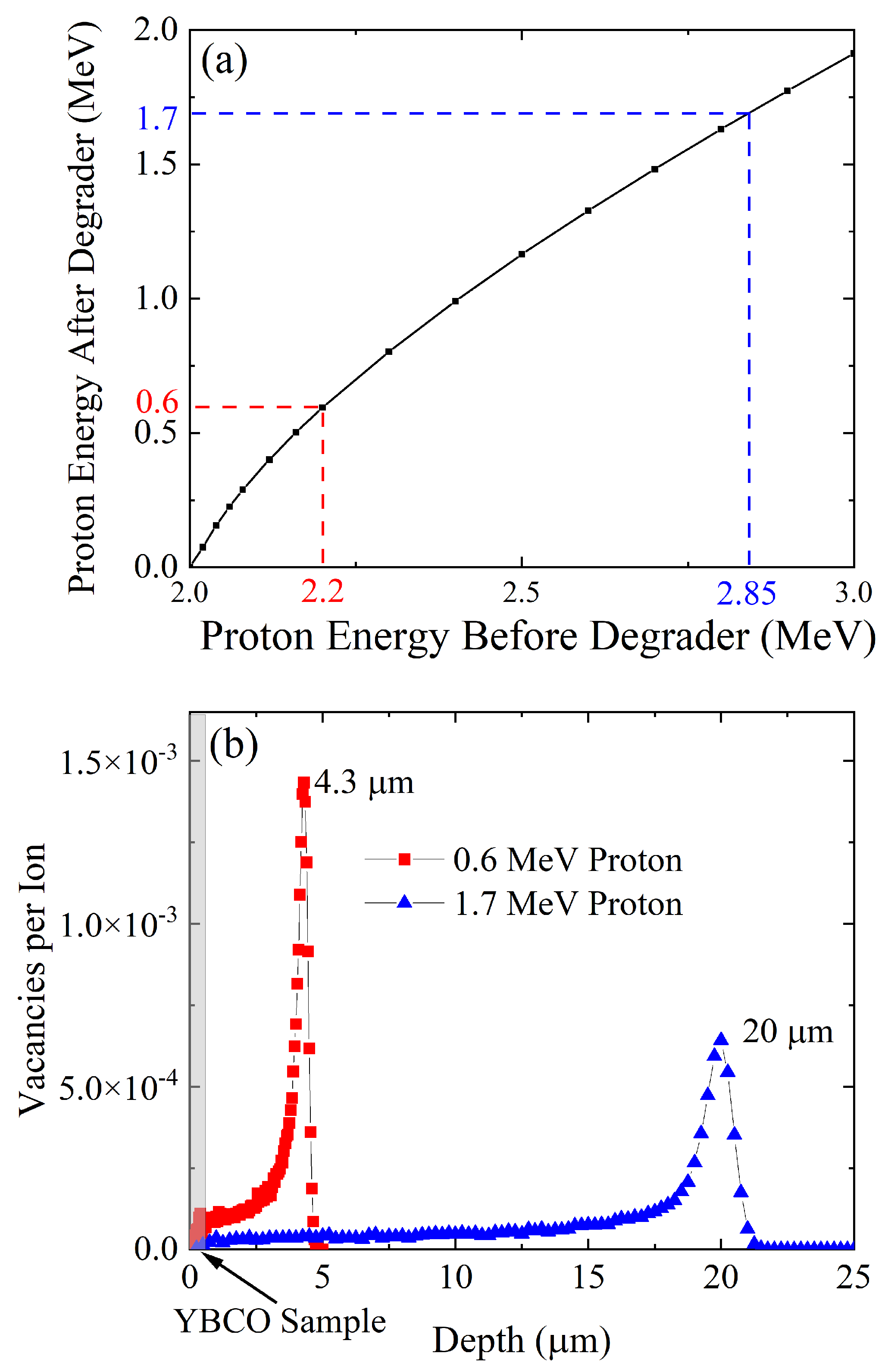
2.2. Energy Degrader and Homogeneous Proton Beam
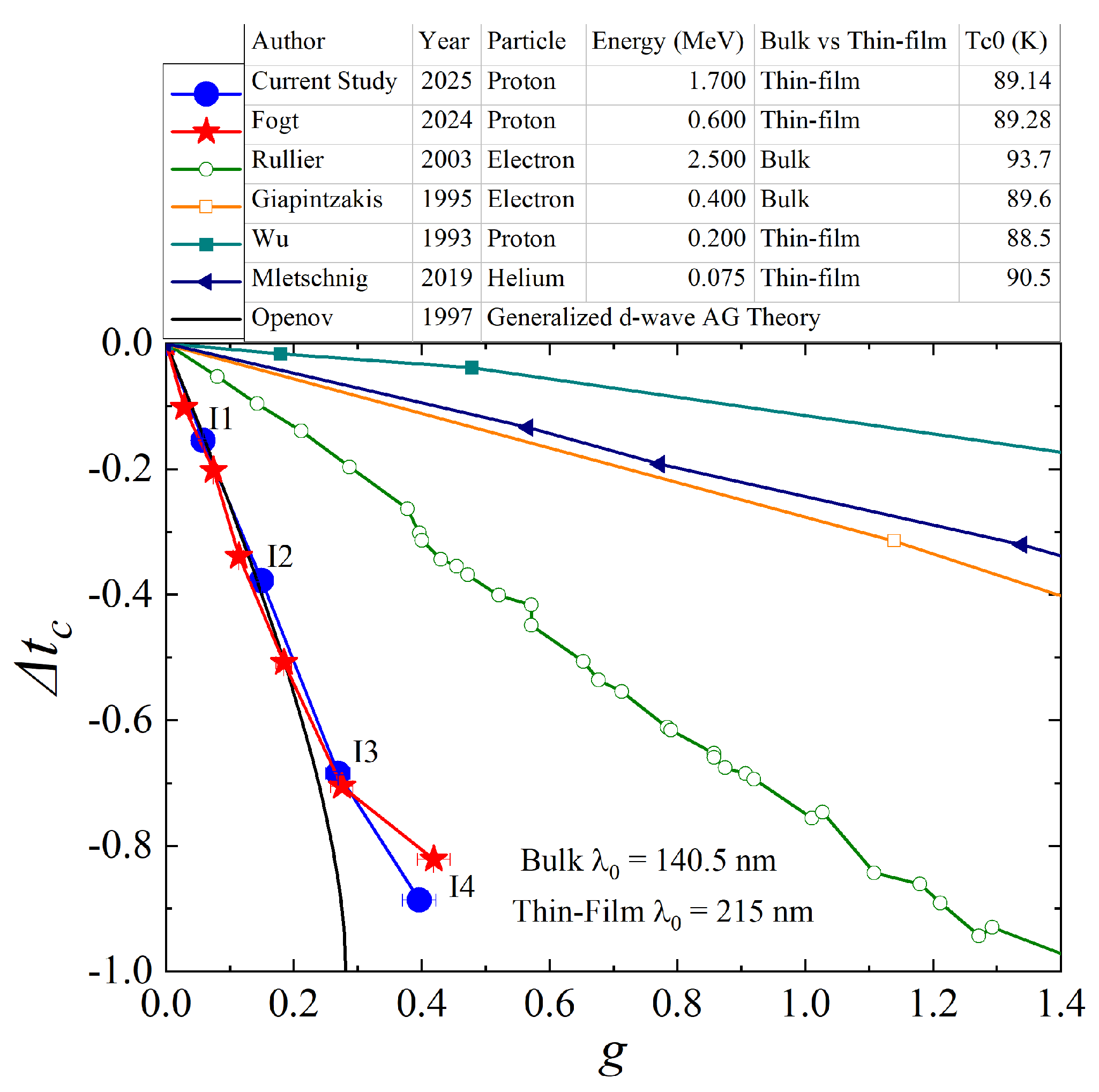
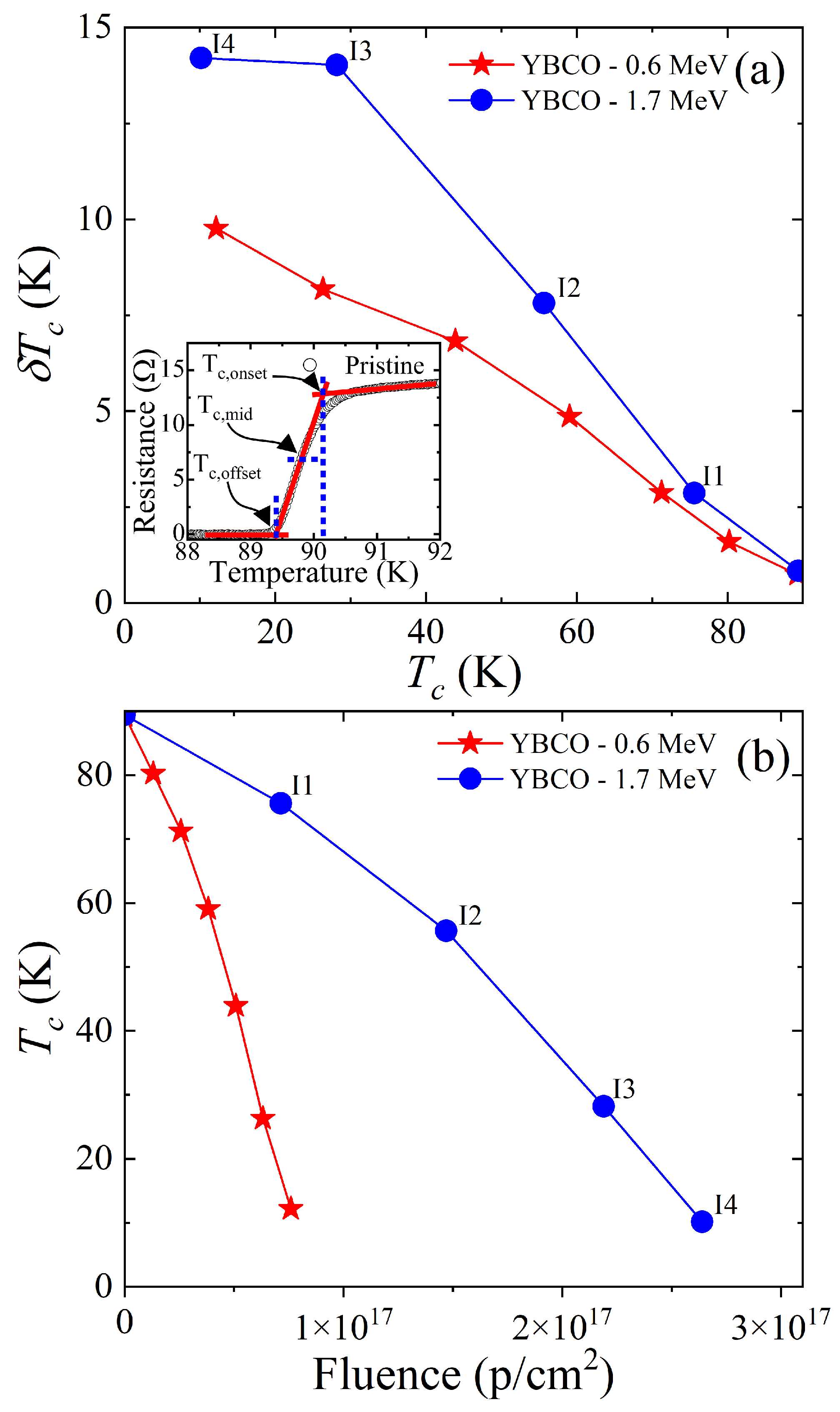
3. Results and Discussion
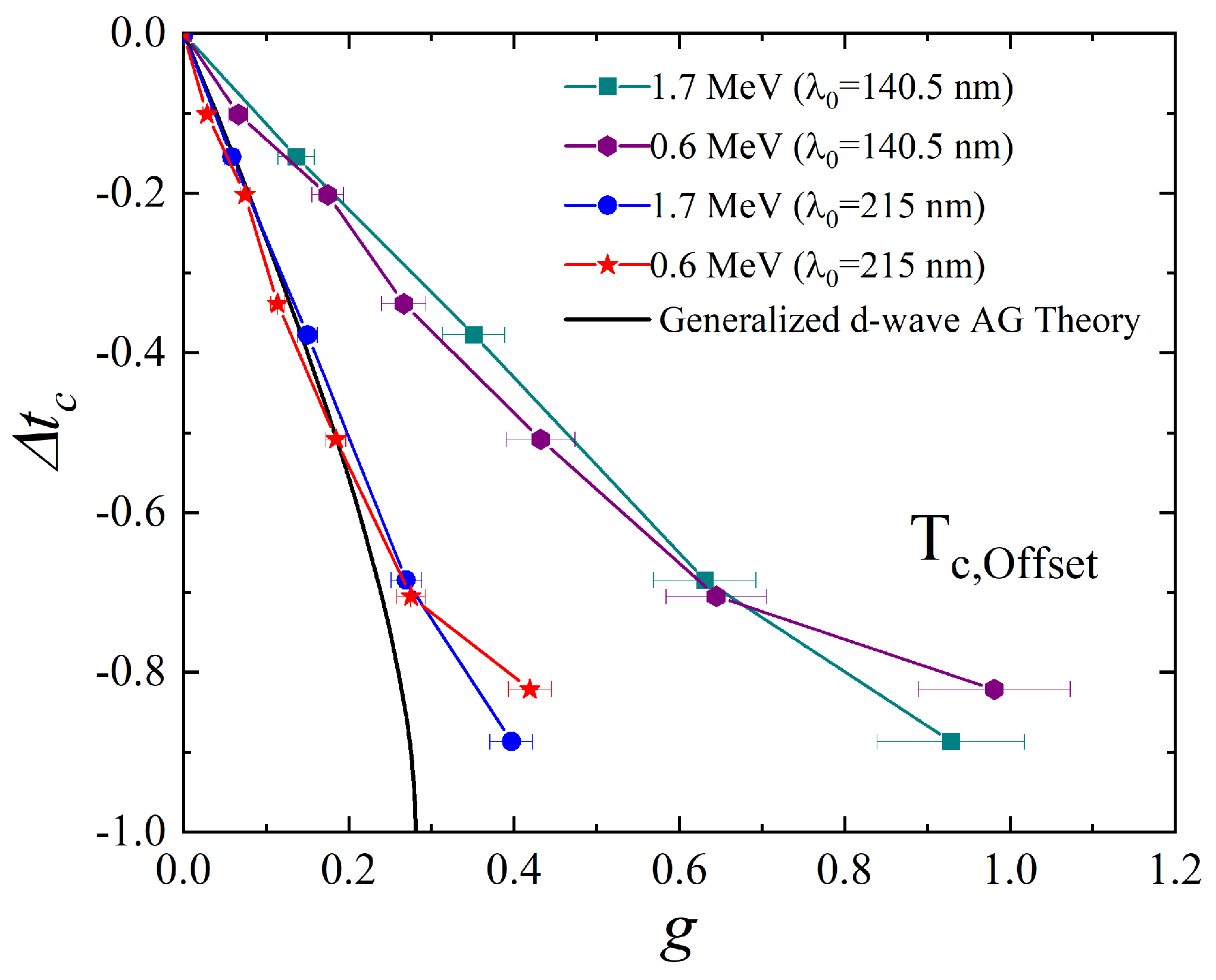
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bednorz, J.G.; Mueller, K.A. Possible high Tc superconductivity in the barium-lanthanum-copper-oxygen system. Z. Phys. B: Condens. Matter 1986, 64, 189–93. [Google Scholar] [CrossRef]
- Wu, M.K.; Ashburn, J.R.; Torng, C.J.; Hor, P.H.; Meng, R.L.; Gao, L.; Huang, Z.J.; Wang, Y.Q.; Chu, C.W. Superconductivity at 93 K in a new mixed-phase Y-Ba-Cu-O compound system at ambient pressure. Phys. Rev. Lett. 1987, 58, 908–910. [Google Scholar] [CrossRef] [PubMed]
- Hahn, S.; Kim, K.; Kim, K.; Hu, X.; Painter, T.; Dixon, I.; Kim, S.; Bhattarai, K.R.; Noguchi, S.; Jaroszynski, J.; et al. 45.5-tesla direct-current magnetic field generated with a high-temperature superconducting magnet. Nature 2019, 570, 496–499. [Google Scholar] [CrossRef] [PubMed]
- Molodyk, A.; Samoilenkov, S.; Markelov, A.; Degtyarenko, P.; Lee, S.; Petrykin, V.; Gaifullin, M.; Mankevich, A.; Vavilov, A.; Sorbom, B.; et al. Development and large volume production of extremely high current density YBa2Cu3O7 superconducting wires for fusion. Scientific Reports 2021, 11, 2084. [Google Scholar] [CrossRef]
- Tsuei, C.C.; Kirtley, J.R. Pairing symmetry in cuprate superconductors. Rev. Mod. Phys. 2000, 72, 969–1016. [Google Scholar] [CrossRef]
- Anderson, P.W. Theory of dirty superconductors. Journal of Physics and Chemistry of Solids 1959, 11, 26–30. [Google Scholar] [CrossRef]
- Abrikosov, A.A.; Gor’kov, L.P. Contribution to the theory of superconducting alloys with paramagnetic impurities. Zh. Eksp. Teor. Fiz. (Sov. Phys. JETP 12, 1243 (1961)) 1960, 39, 1781. [Google Scholar]
- Radtke, R.J.; Levin, K.; Schüttler, H.B.; Norman, M.R. Predictions for impurity-induced Tc suppression in the high-temperature superconductors. Phys. Rev. B 1993, 48, 653–656. [Google Scholar] [CrossRef]
- Openov, L.A. Combined effect of nonmagnetic and magnetic scatterers on the critical temperatures of superconductors with different anisotropies of the gap. Journal of Experimental and Theoretical Physics Letters 1997, 66, 661–667. [Google Scholar] [CrossRef]
- Mletschnig, K.; Lang, W. Nano-patterning of cuprate superconductors by masked He+ ion irradiation: 3-dimensional profiles of the local critical temperature. Microelectronic Engineering 2019, 215, 110982. [Google Scholar] [CrossRef]
- Rullier-Albenque, F.; Alloul, H.; Tourbot, R. Influence of Pair Breaking and Phase Fluctuations on Disordered High Tc Cuprate Superconductors. Phys. Rev. Lett. 2003, 91, 047001. [Google Scholar] [CrossRef] [PubMed]
- Giapintzakis, J.; Ginsberg, D.M.; Kirk, M.A. Determination of the symmetry of the superconducting pairing state and formation of a low-temperature normal metallic state in YBCO by electron irradiation. Technical Report 1995. [Google Scholar] [CrossRef]
- Cho, K.; Kończykowski, M.; Teknowijoyo, S.; Tanatar, M.A.; Liu, Y.; Lograsso, T.A.; Straszheim, W.E.; Mishra, V.; Maiti, S.; Hirschfeld, P.J.; et al. Energy gap evolution across the superconductivity dome in single crystals of Ba1-xKxFe2As2. Science Advances 2016, 2, e1600807. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Kończykowski, M.; Teknowijoyo, S.; Ghimire, S.; Tanatar, M.A.; Mishra, V.; Prozorov, R. Intermediate scattering potential strength in electron-irradiated YBa2Cu3O7-δ from London penetration depth measurements. Phys. Rev. B 2022, 105, 014514. [Google Scholar] [CrossRef]
- Wu, J.Z.; Yu, N.; Chu, W.K. Anisotropy of the ion-beam radiation effect in YBa2Cu3O7-δ (110) thin films. Phys. Rev. B 1993, 48, 9929–9931. [Google Scholar] [CrossRef]
- Torsello, D.; Fracasso, M.; Gerbaldo, R.; Ghigo, G.; Laviano, F.; Napolitano, A.; Iebole, M.; Cialone, M.; Manca, N.; Martinelli, A.; et al. Proton Irradiation Effects on the Superconducting Properties of Fe(Se,Te) Thin Films. IEEE Transactions on Applied Superconductivity 2022, 32, 1–5. [Google Scholar] [CrossRef]
- Konczykowski, M.; Rullier-Albenque, F.; Yacoby, E.R.; Shaulov, A.; Yeshurun, Y.; Lejay, P. Effect of 5.3-GeV Pb-ion irradiation on irreversible magnetization in Y-Ba-Cu-O crystals. Phys. Rev. B 1991, 44, 7167–7170. [Google Scholar] [CrossRef]
- Nakajima, Y.; Tsuchiya, Y.; Taen, T.; Tamegai, T.; Okayasu, S.; Sasase, M. Enhancement of critical current density in Co-doped BaFe2As2 with columnar defects introduced by heavy-ion irradiation. Phys. Rev. B 2009, 80, 012510. [Google Scholar] [CrossRef]
- Openov, L.A. Critical temperature of an anisotropic superconductor containing both nonmagnetic and magnetic impurities. Phys. Rev. B 1998, 58, 9468–9478. [Google Scholar] [CrossRef]
- Graser, S.; Hirschfeld, P.J.; Zhu, L.Y.; Dahm, T. Tc suppression and resistivity in cuprates with out of plane defects. Phys. Rev. B 2007, 76, 054516. [Google Scholar] [CrossRef]
- Garg, A.; Randeria, M.; Trivedi, N. Strong correlations make high-temperature superconductors robust against disorder. Nature Physics 2008, 4, 762–765. [Google Scholar] [CrossRef]
- Kemper, A.F.; Doluweera, D.G.S.P.; Maier, T.A.; Jarrell, M.; Hirschfeld, P.J.; Cheng, H.P. Insensitivity of d-wave pairing to disorder in the high-temperature cuprate superconductors. Phys. Rev. B 2009, 79, 104502. [Google Scholar] [CrossRef]
- Tang, S.; Dobrosavljević, V.; Miranda, E. Strong correlations generically protect d-wave superconductivity against disorder. Phys. Rev. B 2016, 93, 195109. [Google Scholar] [CrossRef]
- Fogt, J.; Weeda, H.; Harrison, T.; Miles, N.; Cho, K. Effect of Proton Irradiation on Thin-Film YBa2Cu3O7 Superconductor. Materials 2024, 17, 4601. [Google Scholar] [CrossRef] [PubMed]
- Remillard, S.K.; Kirkendall, D.; Ghigo, G.; Gerbaldo, R.; Gozzelino, L.; Laviano, F.; Yang, Z.; Mendelsohn, N.A.; Ghamsari, B.G.; Friedman, B.; et al. Microwave nonlinearity and photoresponse of superconducting resonators with columnar defect micro-channels. Superconductor Science and Technology 2014, 27, 095006. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Ziegler, M.; Biersack, J. SRIM– The stopping and range of ions in matter. Nuclear Instruments and Methods in Physics Research B 268, 1818–1823. [CrossRef]
- Miles, N.; Fogt, J.; Harrison, T.; Weeda, H.; Bunnell, A.; A. DeYoung, P.; Cho, K. Correcting Faraday Cup Measurements with Rutherford Backscattering Spectroscopy. Journal of Undergraduate Research in Physics and Astronomy 2025, xx, xxxxx. [Google Scholar]
- Prozorov, R.; Kończykowski, M.; Tanatar, M.A.; Thaler, A.; Bud’ko, S.L.; Canfield, P.C.; Mishra, V.; Hirschfeld, P.J. Effect of Electron Irradiation on Superconductivity in Single Crystals of Ba(Fe1-xRux)2As2 (x=0.24). Phys. Rev. X 2014, 4, 041032. [Google Scholar] [CrossRef]
- Cho, K.; Kończykowski, M.; Teknowijoyo, S.; Tanatar, M.A.; Prozorov, R. Using electron irradiation to probe iron-based superconductors. Superconductor Science and Technology 2018, 31, 064002. [Google Scholar] [CrossRef]
- Prozorov, R.; Giannetta, R.W.; Carrington, A.; Fournier, P.; Greene, R.L.; Guptasarma, P.; Hinks, D.G.; Banks, A.R. Measurements of the absolute value of the penetration depth in high-Tc superconductors using a low-Tc superconductive coating. Applied Physics Letters 2000, 77, 4202–4204. [Google Scholar] [CrossRef]
- Bernhard, C.; Niedermayer, C.; Binninger, U.; Hofer, A.; Wenger, C.; Tallon, J.L.; Williams, G.V.M.; Ansaldo, E.J.; Budnick, J.I.; Stronach, C.E.; et al. Magnetic penetration depth and condensate density of cuprate high-Tc superconductors determined by muon-spin-rotation experiments. Phys. Rev. B 1995, 52, 10488–10498. [Google Scholar] [CrossRef]
- Djordjevic, S.; de Vaulchier, L.A.; Bontemps, N.; Vieren, J.P.; Guldner, Y.; Moffat, S.; Preston, J.; Castel, X.; Guilloux-Viry, M.; Perrin, A. Low temperature penetration depth and the effect of quasi-particle scattering measured by millimeter wave transmission in YBa2Cu3O7-δ thin films. The European Physical Journal B - Condensed Matter and Complex Systems 1998, 5, 847–858. [Google Scholar] [CrossRef]
- Zaitsev, A.G.; Schneider, R.; Linker, G.; Ratzel, F.; Smithey, R.; Schweiss, P.; Geerk, J.; Schwab, R.; Heidinger, R. Microwave measurements of the absolute London penetration depth in double-sided YBa2Cu3O7—x thin films on sapphire. Review of Scientific Instruments 2002, 73, 335–344. [Google Scholar] [CrossRef]
- Bonn, D.A.; Liang, R.; Riseman, T.M.; Baar, D.J.; Morgan, D.C.; Zhang, K.; Dosanjh, P.; Duty, T.L.; MacFarlane, A.; Morris, G.D.; et al. Microwave determination of the quasiparticle scattering time in YBa2Cu3O6.95. Phys. Rev. B 1993, 47, 11314–11328. [Google Scholar] [CrossRef]
- Tinkham, M. Introduction to Superconductivity; McGraw Hill, 1996.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).