Maximizing Portfolio Diversification via Weighted Shannon Entropy: Application to the Cryptocurrency Market

1. Introduction

Portfolio optimization is a central problem in financial mathematics and investment science, concerned with determining the allocation of capital across multiple assets in order to balance expected return and risk exposure. The foundational contribution of Markowitz (1952) [1] introduced the mean–variance framework, which remains the cornerstone of modern portfolio theory. In this model, risk is quantified through the variance of returns, and efficient portfolios are constructed by either maximizing expected return for a given level of variance or minimizing variance for a targeted return. Despite its theoretical elegance, the model faces several limitations when applied in practice. It assumes normally distributed returns, requires precise estimates of variances and covariances, and often leads to unstable allocations in the presence of small sample sizes or heavy-tailed distributions.

To overcome these issues, alternative risk measures have been introduced. Konno and Yamazaki [2] proposed the mean–absolute deviation model, Speranza [3] developed semi-deviation formulations, while King [4] and Jensen [5] advanced semivariance approaches that focus more directly on downside risk. Other extensions have incorporated transaction costs, liquidity constraints, and nonlinear frictions [6,7,8]. Yet, empirical studies have often shown that even sophisticated models fail to consistently outperform naive diversification strategies such as the equally weighted portfolio [9]. This paradox highlights the need for frameworks that are more robust to model uncertainty and less reliant on restrictive distributional assumptions.

Within this broader context, entropy has emerged as a powerful tool for portfolio optimization. Originating from Shannon’s seminal work (1948) [10] in information theory, entropy provides a distribution-free and nonlinear measure of uncertainty, making it well-suited to complex and volatile financial markets. Philippatos and Wilson [11] were among the first to link entropy with financial risk, emphasizing its ability to capture diversification effects beyond variance. Subsequent studies extended this framework by considering generalized entropy measures such as Tsallis, Rényi, and Kaniadakis [12,13,14]. More recently, entropy has been applied in areas such as risk measurement, systemic analysis, and crypto-asset allocation, confirming its flexibility as a modeling tool under high uncertainty. These contributions highlight the potential of extending portfolio models beyond variance-based formulations, offering robust techniques that can be applied both in traditional finance and in emerging areas such as insurance and digital assets.

Despite these advances, relatively little attention has been devoted to the Weighted Shannon Entropy (WSE) formulation introduced by Guiasu [15], which incorporates asset-specific informational weights and thereby provides additional modeling flexibility. By adjusting the weights, investors can reflect asset-specific characteristics such as liquidity, reliability of information, or subjective confidence, while still preserving the mathematical tractability of the entropy framework. WSE thus extends the classical Shannon measure in a natural way, bridging the gap between theory and practice.

Further methodological contributions in the literature extend the application of entropy and risk measures in portfolio and financial modeling. Interval analysis has been widely employed for quantitative risk management in finance and insurance [16], while Value-at-Risk estimation has been analyzed through comparative approaches in optimization contexts [17]. Recent advances also highlight the role of fuzzy multi-objective programming in capturing Pareto optimality in uncertain environments [18]. In parallel, maximum entropy formulations have been proposed for large-scale portfolio optimization [19], and entropy has been directly integrated with mean–variance models in portfolio construction [20]. Additionally, stochastic modeling of cryptocurrency returns has further expanded the scope of risk and entropy-based analysis [21].

This paper contributes to the literature by formally developing and applying the WSE model for portfolio optimization in cryptocurrency markets. Cryptocurrencies are characterized by extreme volatility, structural instability, and non-normal return distributions, conditions under which entropy-based models are particularly advantageous. Using the principle of maximum entropy and the method of Lagrange multipliers, we derive analytical solutions in exponential form that inherently discourage concentration and promote diversification. The empirical validation is conducted on a portfolio composed of Bitcoin (BTC), Ethereum (ETH), Solana (SOL), and Binance Coin (BNB) with data from January–March 2025. The results confirm that entropy-based allocations provide robust and balanced portfolios compared to classical variance-based models, thereby reinforcing the role of entropy as both a theoretical and practical tool for portfolio diversification in complex financial environments.

The remainder of the paper is structured as follows. Section 2 presents the theoretical foundations of Weighted Shannon Entropy, its optimization framework and describes the empirical case study on a cryptocurrency portfolio. Section 3 discusses the results, highlighting the diversification and robustness benefits of entropy-based optimization. Finally, Section 4 concludes the paper by summarizing the contributions and outlining directions for future research

2. Materials and Methods

2.1. Weighted Shannon Entropy: Theoretical Background

Entropy, originally introduced by Shannon (1948) [10] in the context of information theory, quantifies the degree of uncertainty associated with a probability distribution. For a system of states $\mathit{X}=(\mathit{x}₁,\mathit{x}₂,...,{\mathit{x}}_{\mathit{N}})$ with the probability vector $(\mathit{p}₁,\mathit{p}₂,...,{\mathit{p}}_{\mathit{N}})$,$\sum _{\mathit{i}=1}^{\mathit{N}}{\mathit{p}}_{\mathit{i}}=1$. Shannon entropy is defined as

$$\mathbf{H}\left(\mathbf{X}\right)=-\sum _{\mathbf{i}=1}^{\mathbf{N}}{\mathbf{p}}_{\mathbf{i}}{(\mathbf{x}}_{\mathbf{i}})\mathbf{l}\mathbf{n}{{\mathbf{p}}_{\mathbf{i}}(\mathbf{x}}_{\mathbf{i}}).$$

To capture heterogeneity across assets, Guiasu [15] introduced the concept of

Weighted Shannon Entropy (WSE), which generalizes the classical definition by assigning strictly positive informational weights $\left\{{\mathit{u}}_{\mathit{i}}\right\},\mathit{i}=\overline{1,\mathit{n}}$.

$${\mathbf{H}}_{\mathbf{u}}\left(\mathbf{X}\right)=-\sum _{\mathbf{i}=1}^{\mathbf{N}}{\mathbf{u}}_{\mathbf{i}}{\mathbf{p}}_{\mathbf{i}}{(\mathbf{x}}_{\mathbf{i}})\mathbf{l}\mathbf{n}{{\mathbf{p}}_{\mathbf{i}}(\mathbf{x}}_{\mathbf{i}}),{\mathbf{u}}_{\mathbf{i}}>0$$

This weighted formulation allows entropy to reflect the relative importance of each asset, thus enhancing the flexibility of portfolio modeling. When all weights are set equal, the WSE reduces to the classical Shannon entropy. Beyond this equivalence, the introduction of weights provides a powerful mechanism for tailoring portfolio construction to heterogeneous financial contexts. For instance, higher informational weights may be assigned to assets with superior liquidity or more reliable historical data, while lower weights may be used for highly volatile or speculative assets. In this sense, WSE bridges the gap between purely statistical diversification and investor-specific preferences, making it particularly relevant in cryptocurrency markets where asset quality and stability vary substantially.

2.2. The Maximum Entropy Optimization Problem

The principle of maximum entropy, as formalized by Jaynes (1957) [22], asserts that among all feasible probability distributions satisfying given constraints, the one that maximizes entropy represents the most unbiased estimate consistent with the available information. This principle has broad applications in physics, statistics, and economics, and in the context of portfolio theory it translates into constructing allocations that maximize diversification while respecting investor-imposed return and risk constraints. Intuitively, such an allocation avoids overfitting to limited data or subjective assumptions, producing a distribution that is as non-committal as possible beyond what is dictated by the constraints. This makes entropy-based optimization particularly attractive in financial markets, where parameter uncertainty, heavy tails, and structural breaks often undermine variance-based approaches. Formally, the optimization problem can be expressed as maximizing Weighted Shannon Entropy subject to linear moment conditions on returns, variance, and informational weights, thereby ensuring that the resulting portfolio remains diversified, robust, and theoretically grounded.

max ${\mathit{H}}_{\mathit{u}}\left(\mathit{p}\right)=-\sum _{\mathit{i}=1}^{\mathit{N}}{\mathit{u}}_{\mathit{i}}{\mathit{p}}_{\mathit{i}}\mathit{l}\mathit{n}{\mathit{p}}_{\mathit{i}}$

$$\left\{\begin{array}{c}\sum _{\mathit{i}=1}^{\mathit{N}}{\mathit{p}}_{\mathit{i}}{\mathit{g}}_{\mathit{j}}{(\mathit{x}}_{\mathit{i}})=\mathbf{E}\left({\mathit{g}}_{\mathit{j}}\right),\mathbf{j}=1,2,\dots ,\mathbf{m}\\ \sum _{\mathit{i}=1}^{\mathit{N}}{\mathit{p}}_{\mathit{i}}=1,\end{array}\right.$$

where ${\mathit{g}}_{\mathit{j}}{(\mathit{x}}_{\mathit{i}})$ represent the constraints (e.g. expected return, variance, informational weights).

2.3. Solution via the Method of Lagrange Multipliers

To solve the problem, we introduce a set of Lagrange multipliers ${\mathit{\mu }}_{\mathit{i}}$, i = $\overline{0,\mathit{m}}$ corresponding to the constraints. The Lagrangian is defined as

L(p,$\mathit{\mu })$= - $\sum _{\mathit{i}=1}^{\mathit{N}}{\mathit{u}}_{\mathit{i}}{\mathit{p}}_{\mathit{i}}\mathit{l}\mathit{n}{\mathit{p}}_{\mathit{i}}$ + $({\mathit{\mu }}_0+1)\left(\sum _{\mathit{i}=1}^{\mathit{N}}{\mathit{p}}_{\mathit{i}}-1)+\sum _{\mathit{j}=1}^{\mathit{m}}{\mathit{\mu }}_{\mathit{j}}\right(\sum _{\mathit{i}=1}^{\mathit{N}}{\mathit{p}}_{\mathit{i}}{\mathit{g}}_{\mathit{j}}{(\mathit{x}}_{\mathit{i}})-\mathbf{E}\left({\mathit{g}}_{\mathit{j}}\right))$

The first-order optimality conditions yield exponential-form solutions:

${\mathit{p}}_{\mathit{i}}={\displaystyle \frac{\mathbf{e}\mathbf{x}\mathbf{p}(\sum _{\mathit{j}=1}^{\mathit{m}}{{\mathit{\mu }}_{\mathit{j}}\mathit{g}}_{\mathit{j}}{(\mathit{x}}_{\mathit{i}}\left)\right)}{{\sum }_{\mathit{k}=1}^{\mathit{N}}\mathbf{e}\mathbf{x}\mathbf{p}(\sum _{\mathit{j}=1}^{\mathit{m}}{{\mathit{\mu }}_{\mathit{j}}\mathit{g}}_{\mathit{j}}{(\mathit{x}}_{\mathit{k}}\left)\right)}}$, i=1,...,N.

Thus, the optimal portfolio weights adopt an exponential (softmax) form, where the multipliers ${\mathit{\mu }}_{\mathit{j}}$ are determined by the imposed constraints.

Substituting into the entropy functional, we obtain the dual problem:

max [$\mathbf{ln}\mathit{Z}-\sum _{\mathit{j}=1}^{\mathit{m}}{\mathit{\mu }}_{\mathit{j}}\mathbf{E}\left({\mathit{g}}_{\mathit{j}}\right)]$

This dual formulation is computationally advantageous, as it reduces the optimization problem to solving for the multipliers ${\mathit{\mu }}_{\mathit{j}}$

2.4. Portfolio Optimization Under Mean and Variance Constraints

In the context of portfolio selection, the constraints g_j(x_i) typically correspond to the mean and variance of returns. Let r_i denote the expected return of asset i, and σ² the variance of the portfolio. The optimization problem becomes:

max ${\mathit{H}}_{\mathit{u}}\left(\mathit{p}\right)=-\sum _{\mathit{i}=1}^{\mathit{N}}{\mathit{u}}_{\mathit{i}}{\mathit{p}}_{\mathit{i}}\mathit{l}\mathit{n}{\mathit{p}}_{\mathit{i}}$

$$\left\{\begin{array}{c}\sum _{\mathit{i}=1}^{\mathit{N}}\mathit{p}\mathrm{ᵢ}\overline{\mathit{r}}\mathrm{ᵢ}=\mathit{E}\\ \sum _{\mathit{i}=1}^{\mathit{N}}\sum _{\mathit{t}=1}^{\mathit{m}}{\mathit{p}}_{\mathit{i}}{({\mathit{r}}_{\mathit{i}\mathit{t}}-{\overline{\mathit{r}}}_{\mathit{i}})}^2={\mathit{\sigma }}_0^2,\\ \sum _{\mathit{i}=1}^{\mathit{N}}\mathit{p}\mathrm{ᵢ}=1\end{array}\right.$$

where $r_{it}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{s}\mathrm{s}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}t,t=\overline{1,m},$ ${\overline{r}}_i={\displaystyle \frac{1}{m}}\sum _{t=1}^m{r}_{it};E$ is the expected average return of the portfolio and the level ${\sigma }_0^2$ is assumed by the investor.

This system can be solved via numerical optimization methods (e.g., MATLAB, Python solvers), with the Lagrangian guaranteeing existence and uniqueness under convexity. The resulting allocations inherently discourage concentration in a single asset, promoting structural diversification.

2.5. Case Studies: Cryptocurrency Portfolio

To illustrate the applicability of the Weighted Shannon Entropy (WSE) model, we consider a portfolio consisting of four major cryptocurrencies: Bitcoin (BTC), Ethereum (ETH), Solana (SOL), and Binance Coin (BNB). These assets were selected based on their high liquidity, significant market capitalization, and consistent trading activity during the period January–March 2025. The cryptocurrency market is characterized by volatility, heavy tails, and nonlinear dependencies, conditions under which entropy-based approaches are particularly well-suited

2.5.1. Data and Model Setup

We computed monthly average returns for each cryptocurrency, along with variance–covariance estimates obtained from daily log-returns over the first quarter of 2025. The selected period, January to March 2025, captures a typical high-volatility environment for digital assets, characterized by both sharp price fluctuations and moderate cross-asset correlations. The mean returns were approximately 4.5% for BTC, 3.8% for ETH, 5.2% for SOL, and 4.1% for BNB, with moderate positive correlations across assets. These values are consistent with previous studies that documented elevated volatility clustering and interconnected dynamics in cryptocurrency markets.

The empirical setup follows the classical portfolio selection framework but replaces variance minimization with entropy maximization. Specifically, the optimization problem was formulated as the maximization of Weighted Shannon Entropy (WSE) under the constraints of full allocation, non-negativity, and target statistical moments of returns. Formally, the problem can be expressed as:

max ${\mathit{H}}_{\mathit{u}}\left(\mathit{p}\right)=-\sum _{\mathit{i}=1}^{\mathit{N}}{\mathit{u}}_{\mathit{i}}{\mathit{p}}_{\mathit{i}}\mathit{l}\mathit{n}{\mathit{p}}_{\mathit{i}}$

$$\left\{\begin{array}{c}\sum _{\mathit{i}=1}^{\mathit{N}}\mathit{p}\mathrm{ᵢ}\overline{\mathit{r}}\mathrm{ᵢ}=\mathit{E}\\ \sum _{\mathit{i}=1}^{\mathit{N}}\sum _{\mathit{t}=1}^{\mathit{m}}{\mathit{p}}_{\mathit{i}}{({\mathit{r}}_{\mathit{i}\mathit{t}}-{\overline{\mathit{r}}}_{\mathit{i}})}^2={\mathit{\sigma }}_0^2,\\ \sum _{\mathit{i}=1}^{\mathit{N}}\mathit{p}\mathrm{ᵢ}=1\end{array}\right.$$

where $r_{it}is\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{s}\mathrm{s}\mathrm{e}\mathrm{t}i\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}t,t=\overline{1,m},$ ${\overline{r}}_i={\displaystyle \frac{1}{m}}\sum _{t=1}^m{r}_{it};E$ is the expected average return of the portfolio and the level, ${\sigma }_0^2$ is assumed by the investor.

In practice, the specification of the target moments plays a decisive role in shaping the feasible solution space. The expected return constraint ensures that the optimized portfolio achieves a minimum performance level, while the variance constraint prevents the entropy maximization from producing allocations that are excessively exposed to risk. By embedding these statistical moments into the optimization framework, the WSE model can be tuned to reflect investor preferences and market conditions.

Moreover, the introduction of informational weights distinguishes WSE from purely return–risk formulations by allowing additional qualitative signals—such as liquidity, trading activity, or perceived reliability of each asset—to be incorporated. This layered structure provides a richer and more realistic representation of decision-making in cryptocurrency markets, where both quantitative volatility measures and qualitative assessments are essential for building robust portfolios.

2.5.2. Results

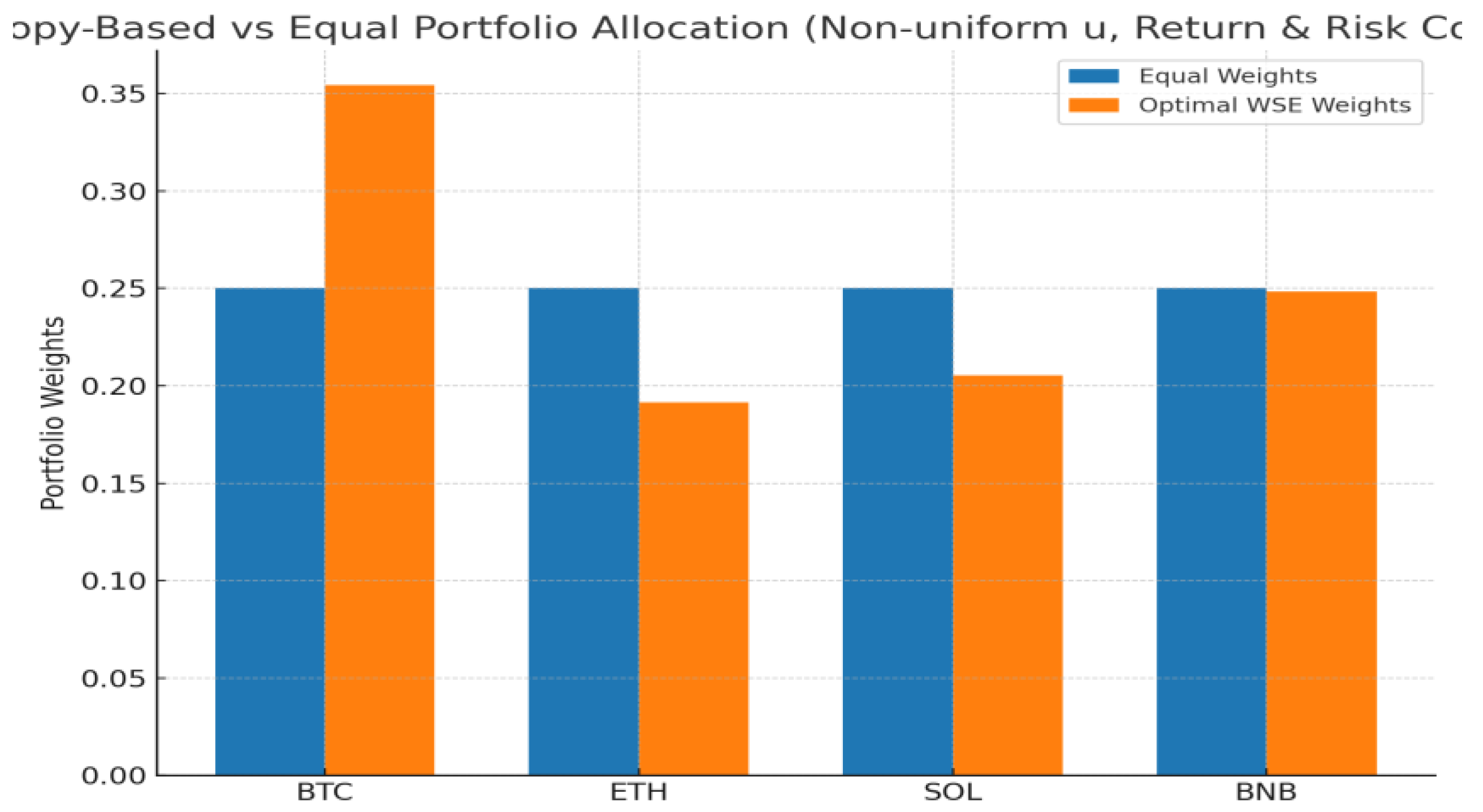
We first compared the entropy of the equally weighted portfolio (25% in each asset) with the entropy of the WSE-optimized portfolio obtained via numerical simulation. Table 1 reports the resulting allocations, while Figure 1 provides a visual comparison.

Informational weights u_i were set to the inverse of asset volatility (normalized). Targets: expected return ≥ 0.0446; variance ≤ 0.0356 (90% of equal-weight variance 0.0396). Entropy (WSE) equal-weights: 0.3466; optimized: 0.3398. Expected return equal-weights: 0.0440; optimized: 0.0441. Optimized variance: 0.0391.

How the Results Are Obtained

The results reported in Table 1 and illustrated in Figure 1 were obtained by solving the entropy-based optimization problem under realistic constraints. First, daily log-returns for Bitcoin, Ethereum, Solana, and Binance Coin were collected for the period January–March 2025. From these data, monthly average returns and the variance–covariance matrix were computed, providing the statistical foundation for the optimization.

Informational weights were defined as the inverse of asset volatility, u_i $\propto$1/σ_i, which assigns greater importance to assets with lower risk. To avoid trivial equal allocations, additional moment constraints were imposed: the expected portfolio return was required to exceed a robust target defined as the median return plus one-quarter of the interquartile range of individual asset returns, while the portfolio variance was restricted to be no greater than 90% of the equal-weight benchmark variance.

Formally, the optimization problem can be stated as:

max ${\mathit{H}}_{\mathit{u}}\left(\mathit{p}\right)=-\sum _{\mathit{i}=1}^{\mathit{N}}{\mathit{u}}_{\mathit{i}}{\mathit{p}}_{\mathit{i}}\mathit{l}\mathit{n}{\mathit{p}}_{\mathit{i}}$

$\left\{\begin{array}{c}\sum _{\mathit{i}=1}^{\mathit{N}}\mathit{p}\mathrm{ᵢ}\overline{\mathit{r}}\mathrm{ᵢ}\ge \mathit{E}\\ {\mathit{p}}^{\mathit{t}}\Omega p\le 0.9\\ \sum _{\mathit{i}=1}^{\mathit{N}}\mathit{p}\mathrm{ᵢ}=1\end{array}\right.{\mathit{V}}_{\mathit{e}\mathit{q}}$, where $\mathit{p}\mathrm{ᵢ}\ge 0$

Here, $\overline{\mathit{r}}\mathit{ᵢ}$ denotes the mean return of asset i, $\mathsf{\Omega }$ is the variance–covariance matrix, and ${\mathit{V}}_{\mathit{e}\mathit{q}}$ is the variance of the equally weighted portfolio. The optimization was solved numerically using Sequential Quadratic Programming (SLSQP), with initial allocations close to the equal-weight benchmark. This procedure generates the “Optimal WSE Weights” column in Table 1, which differs from the equal-weight allocation and illustrates the ability of Weighted Shannon Entropy to integrate informational weights and moment conditions. The resulting allocations demonstrate that entropy maximization, when combined with realistic constraints, produces diversified portfolios that remain robust while reflecting asset-specific characteristics.

As reported in Table 1 and illustrated in Figure 1, the entropy-based optimization with uniform weights reproduces the equally weighted portfolio, confirming that maximum entropy allocations coincide with balanced distributions under minimal information

2.5.3. Interpretation

The findings demonstrate the diversification power of entropy-based optimization. With uniform informational weights, the WSE framework naturally reproduces the equal-weighted allocation, which is theoretically justified as the entropy-maximizing distribution under minimal information. This provides a strong benchmark for portfolio construction, confirming that entropy discourages concentration in a single asset and promotes balance across available investments.

The advantage of WSE over classical Shannon entropy arises when non-uniform weights are introduced. By assigning higher informational weights to assets deemed more reliable or less risky, investors can tilt the allocation while still maintaining high entropy. This flexibility distinguishes WSE from unweighted formulations, allowing it to accommodate heterogeneous investor preferences or asset characteristics.

In cryptocurrency markets—where data quality, liquidity, and volatility vary significantly across tokens—the ability to incorporate informational weights provides a practical mechanism for tailoring portfolios to specific risk–return profiles. This not only strengthens the theoretical appeal of entropy-based methods but also enhances their operational relevance in environments where classical variance-based models tend to fail. In this sense, WSE can be viewed as a bridge between purely mathematical constructs of diversification and the practical needs of investors operating in turbulent and highly uncertain markets.

Another important implication of this interpretation is that WSE provides a unifying criterion capable of reconciling short-term market fluctuations with long-term portfolio stability. By embedding informational weights into the entropy framework, investors are not restricted to purely statistical considerations but can systematically integrate external signals such as market capitalization, trading volume, or regulatory confidence into the allocation process. This property is particularly relevant for digital assets, where the reliability of price dynamics varies sharply across tokens and where external shocks may rapidly alter the risk landscape. In this way, WSE offers not only a theoretical benchmark for diversification but also a flexible decision-making tool that adapts to evolving market conditions, thereby bridging the gap between static optimization models and dynamic investment realities. These insights provide the basis for the empirical evaluation are presented in Section 3.

3. Results and Discussions

The numerical results confirm the theoretical properties of the Weighted Shannon Entropy (WSE) framework. With uniform weights ui=1), the optimization process yields the equal-weighted portfolio, which is theoretically known to maximize entropy under minimal information. This outcome underscores the robustness of entropy as a diversification measure: portfolios with balanced allocations naturally achieve higher entropy values, reflecting greater uncertainty and reduced concentration risk.

From a comparative perspective, entropy-based optimization differs fundamentally from the mean–variance framework. In the classical Markowitz model, allocations often gravitate toward assets with higher expected returns, even if this leads to concentration in a few assets. While such portfolios may maximize return under variance constraints, they remain fragile to estimation errors, non-normal return distributions, and sudden market shocks. In contrast, entropy-based allocations inherently discourage over-concentration by penalizing distributions with excessive skewness toward individual assets. This property is particularly valuable in high-volatility markets, where robustness is essential.

The key advantage of WSE over classical Shannon entropy lies in its flexibility. By introducing asset-specific weights, the model allows investors to integrate qualitative or structural considerations—such as liquidity, reliability of data, or subjective confidence—into the optimization framework. For instance, assigning higher weights to assets with greater informational relevance can shift the portfolio toward those assets while maintaining a high level of diversification. Conversely, assigning lower weights to riskier or less liquid assets naturally reduces their impact on the overall allocation, without excluding them entirely. This adaptability allows entropy to move beyond a purely statistical measure and become an actionable tool for investor-specific strategies.

In the context of cryptocurrency markets, these properties are particularly valuable. Digital assets exhibit heavy-tailed return distributions, nonlinear correlations, and frequent structural breaks, which undermine the assumptions of variance-based models. Entropy’s distribution-free nature enables it to adapt to these conditions, offering resilience in environments where return distributions deviate significantly from normality. Moreover, entropy provides a unifying framework that integrates return, risk, and diversification into a single measure of portfolio quality, unlike variance-based models that often treat these dimensions separately.

The empirical results presented in this study highlight that entropy maximization leads to balanced allocations, avoiding the dominance of a single cryptocurrency. This aligns directly with the diversification principle, which is critical in markets where asset-specific risks are amplified by volatility and regulatory uncertainty. Importantly, the WSE framework introduces an additional degree of customization, enabling investors to model portfolios that reflect their unique preferences and informational priorities.

Beyond theoretical implications, these findings carry substantial practical relevance. Entropy-based portfolios can be employed in constructing cryptocurrency indices, stablecoin baskets, or digital asset funds, where robustness and diversification are essential. The analytical tractability of the entropy framework, supported by the method of Lagrange multipliers, further facilitates its integration into rule-based trading systems and algorithmic strategies. As such, WSE does not only contribute to the academic understanding of portfolio optimization but also provides an operational methodology suitable for implementation in real-world investment processes.

Overall, the discussion confirms that entropy is not merely a statistical measure of uncertainty but a structural force shaping portfolio construction. By reframing diversification as an entropy-maximization problem, investors gain access to allocations that are balanced, resilient to estimation risk, and robust under turbulent market conditions.

4. Conclusions

This paper has introduced the Weighted Shannon Entropy (WSE) framework as an alternative approach to portfolio optimization, extending the classical Shannon entropy by incorporating informational weights. Through analytical derivations based on the method of Lagrange multipliers, we demonstrated that the WSE model yields exponential-form solutions that inherently discourage concentration and promote diversification.

The empirical case study, conducted on a portfolio of four leading cryptocurrencies—Bitcoin, Ethereum, Solana, and Binance Coin—over the period January–March 2025, confirmed the theoretical insights. When uniform weights are applied, the WSE model reproduces the equally weighted allocation, which maximizes entropy under minimal information. This outcome highlights entropy’s role as a benchmark of structural diversification. More importantly, the weighted formulation offers investors an additional layer of flexibility by allowing the integration of qualitative and structural considerations, such as asset reliability, liquidity, or subjective confidence.

The results underscore the advantages of entropy-based optimization over variance-centered models, particularly in volatile and structurally unstable markets such as cryptocurrencies. While the mean–variance framework remains sensitive to estimation errors and normality assumptions, entropy-based approaches are distribution-free and inherently robust. By unifying return, risk, and diversification under a single criterion, WSE provides a comprehensive methodology for constructing resilient portfolios.

Moreover, the ability to incorporate informational weights grants investors an additional lever for tailoring portfolio construction to asset-specific characteristics, thereby bridging the gap between abstract theoretical models and practical decision-making in high-volatility environments.

Future research directions include extending the WSE framework to multi-period optimization, dynamic portfolio rebalancing, and integration with generalized entropy measures such as Tsallis and Kaniadakis entropy. Additional empirical testing across different asset classes and within institutional investment settings may further validate the operational value of WSE in modern financial environments. By building on both its mathematical foundation and empirical effectiveness, the WSE model represents a promising avenue for advancing portfolio theory in the age of digital finance.