Submitted:
30 August 2025
Posted:
02 September 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Background
1.2. Motivation
- Cost minimization, to stay within budget constraints.
1.3. Objective
1.4. Contributions
- Definition: We formally define ARCI′ as a cost-penalized connectivity index.
- Analysis: We investigate its mathematical behavior, including sensitivity to the penalty parameter.
- Simulation: We evaluate ARCI′ on synthetic network data and compare it with standard MST metrics.
- Application Potential: We discuss its relevance to rural road planning, sensor networks, and related infrastructure problems.
Section 2: Definition of ARCI′
2.1. Graph Model
2.2. ARCI′ Definition
2.3. Interpretation
- Higher population coverage → higher ARCI′.
- Higher cost → lower ARCI′ (penalized exponentially by α).
-
The parameter α determines the trade-off:
- ∘
- α≈1.0: low-cost penalty.
- ∘
- α>1.5: strong cost penalty.
2.4. Properties
- Positivity: ARCI′>0 for any connected graph.
- Monotonicity: ARCI′ decreases as α increases (for fixed cost and population).
- Scaling: If all edge costs are multiplied by k>0, then
Section 3: Experimental Results
3.1. Experimental Setup
- Number of nodes (villages): n=10
- Coordinates: Randomly sampled in a 100×100 plane.
- Population per node: Random integers between 100 and 1000.
- Edge cost: Euclidean distance multiplied by a terrain factor (random between 1.0 and 3.0).
- Population served per edge: Sum of the populations of its two endpoints.
3.2. ARCI′ Sensitivity to α
3.3. Visualization
3.4. Interpretation
- Trade-off Insight:
- 2.
- Parameter Tuning:
Section 4: Discussion
4.1. Key Findings
- For low values of α\alphaα (close to 1), ARCI′ values remain high. This indicates that the population component dominates, and the model favors networks that cover more people even if they are more expensive.
- As α\alphaα increases, ARCI′ decreases sharply. Cost minimization becomes the dominant factor, reducing ARCI′ to very small values for α>1.5.
4.2. Comparison with Traditional MST Metrics
- MST cost is constant for a given graph.
- ARCI′ reveals how that same MST performs when population is included as a priority.
4.3. Limitations
- Synthetic Data: The current experiments used artificial graphs, which may not reflect real-world complexity such as geographic obstacles, existing road layouts, or socio-political constraints.
- Single Objective Extension: While ARCI′ handles cost vs population, it does not yet include other factors such as reliability, redundancy, or maintenance cost.
- Parameter Selection: Choosing an appropriate α requires domain knowledge; the index alone does not prescribe the “best” value.
4.4. Future Work
- Real-World Case Studies: Apply ARCI′ to real African or Asian rural networks.
- Multi-Objective Optimization: Integrate ARCI′ into evolutionary algorithms to generate not just MST but Pareto-optimal networks.
- Theoretical Analysis: Prove formal properties (e.g., bounds, complexity, asymptotic behavior).
- Extension of Tareq Index (TI): Investigate how TI [17], originally for molecular graphs, can be generalized to networks like ARCI′, forming a family of indices for various domains.
Section 5: Conclusion
- ARCI′ decreases rapidly as α increases, reflecting the growing influence of cost penalties.
- Parameter values around α≈1.2–1.3 may achieve a practical balance for rural infrastructure contexts.
- ARCI′ can serve as an auxiliary evaluation tool for planners rather than a replacement for established algorithms like MST.
References
- Diestel, R. Graph Theory, 5th ed.; Springer: Berlin, 2017. [Google Scholar]
- Bondy, J. A.; Murty, U. S. R. Graph Theory with Applications; North-Holland: Amsterdam, 1976. [Google Scholar]
- Ahuja, R. K.; Magnanti, T. L.; Orlin, J. B. Network Flows: Theory, Algorithms, and Applications; Prentice Hall: New Jersey, 1993. [Google Scholar]
- Magnanti, T. L.; Wong, R. T. Network Design and Transportation Planning: Models and Algorithms. Transportation Science 1984, 18, 1–55. [Google Scholar] [CrossRef]
- Cormen, T. H.; Leiserson, C. E.; Rivest, R. L.; Stein, C. Introduction to Algorithms, 3rd ed.; MIT Press: Cambridge, 2009. [Google Scholar]
- Kruskal, J. B. On the Shortest Spanning Subtree of a Graph and the Traveling Salesman Problem. Proceedings of the American Mathematical Society 1956, 7, 48–50. [Google Scholar] [CrossRef]
- Prim, R. C. Shortest Connection Networks and Some Generalizations. Bell System Technical Journal 1957, 36, 1389–1401. [Google Scholar] [CrossRef]
- Magnanti, T. L.; Wong, R. T. Accelerating Benders Decomposition: Algorithmic Enhancement and Model Selection Criteria. Operations Research 1981, 29, 464–484. [Google Scholar] [CrossRef]
- Ghosh, D.; Das, S. Multi-objective Optimization for Rural Road Network Design. European Journal of Operational Research 2015, 243, 865–876. [Google Scholar]
- Gutjahr, W. J.; Dzubur, A. Bi-Objective Road Network Design with Minimal Cost and Maximal Connectivity. Annals of Operations Research 2013, 206, 63–90. [Google Scholar]
- Yeh, C.-H.; Chou, S.-Y. Multiobjective Optimization of Road Network Design Considering Traffic Safety and Cost. IEEE Transactions on Intelligent Transportation Systems 2011, 12, 1363–1371. [Google Scholar]
- Fan, Y.; Kalaba, R. Multiobjective Optimization for Transportation Networks. Applied Mathematics and Computation 2001, 117, 1–12. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; Wiley: Chichester, 2001. [Google Scholar]
- Chen, M.; Yang, H.; Lo, H. K. Capacity Reliability of a Road Network: An Assessment Methodology and Numerical Results. Transportation Research Part B: Methodological 2002, 36, 225–252. [Google Scholar] [CrossRef]
- Dijkstra, E. W. A Note on Two Problems in Connection with Graphs. Numerische Mathematik 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective Evolutionary Algorithms: A Comparative Case Study and the Strength Pareto Approach. IEEE Transactions on Evolutionary Computation 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Asaduzzaman, M. (2025). The Tareq Index (TI): A Novel Graph-Based Descriptor for Inorganic Acids. ChemRxiv. This content is a preprint and has not been peer-reviewed. [CrossRef]
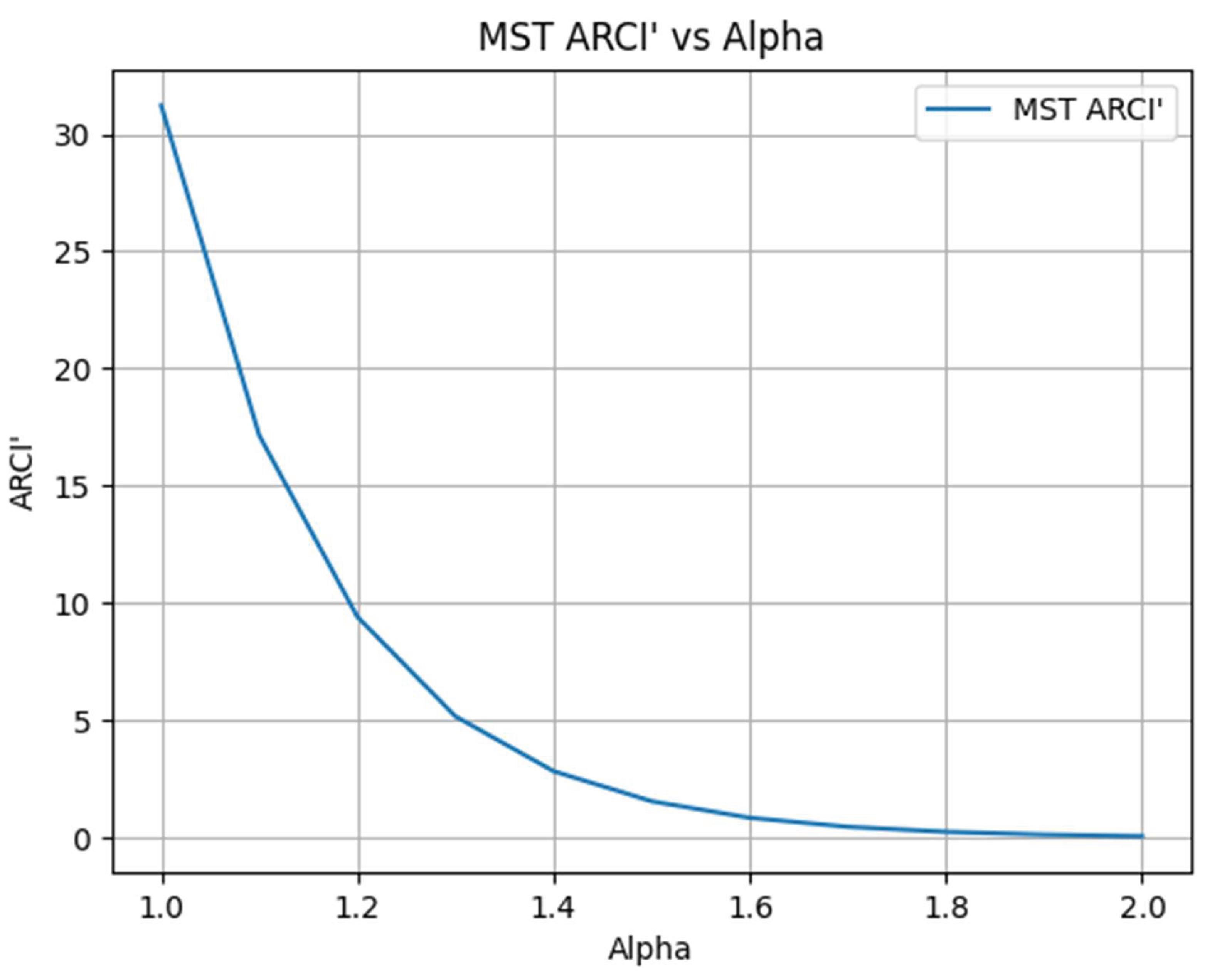
| α (alpha) | MST_ARCI′ |
| 1.0 | 31.218589 |
| 1.1 | 17.148364 |
| 1.2 | 9.419593 |
| 1.3 | 5.174180 |
| 1.4 | 2.842176 |
| 1.5 | 1.561207 |
| 1.6 | 0.857571 |
| 1.7 | 0.471063 |
| 1.8 | 0.258755 |
| 1.9 | 0.142134 |
| 2.0 | 0.078074 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





