Research on Hybrid Communication Strategy for Low-Power Battery-Free IoT Terminals

1. Introduction

With the continuous evolution of 5G communication technology, the era of 5G-Advanced has arrived. The number of intelligent IoT terminals is poised to cross the tens of billions threshold and will continue to exhibit exponential growth [1]. Against this backdrop, the energy resources and wireless spectrum underpinning IoT development face unprecedented strain. Concurrently, the burgeoning customized communication demands across vertical industries impose increasingly stringent challenges on IoT advancement at technological, cost, and security-related levels. Consequently, battery-free IoT technologies, exemplified by Energy Harvesting (EH) and Ambient Backscatter Communication (AmBC), offer promising solutions to overcome limitations inherent in conventional battery power. These technologies hold potential to alleviate pressure on energy and spectrum resources while delivering green, secure, low-energy communication solutions for diverse sectors.

In pursuit of sustainable alternatives to batteries that reduce maintenance costs and enable remote IoT deployment, various high-efficiency energy harvesting techniques have emerged as prominent research foci [2]. While there exist mature power generation technologies utilizing common ambient sources, such as solar, wind, vibrational, and thermal energy, their significant dependence on environmental factors like weather fluctuations results in insufficient stability for reliable IoT communication. Meanwhile, ambient Radio Frequency (RF) signals are becoming increasingly ubiquitous. The inherent portability, compact size, and low cost of RF energy harvesting systems align well with the requirements of IoT tags, positioning RF energy harvesting as a progressively viable power sourcing method. Furthermore, other harvesting approaches, including solar, can be integrated with RF energy harvesting to implement hybrid energy harvesting schemes leveraging diversified source availability.

In power-constrained wireless communication networks, AmBC has gained significant attention as a low-power communication solution synergistically paired with EH. This approach holds promise for addressing energy efficiency, spectral efficiency, and cost challenges inherent in massive machine-type communications (mMTC). Backscatter technology was first proposed by Stockman in 1948 [3] and rapidly emerged as a representative low-power communication technique, finding widespread application in consumer goods and sensor networks. Radio Frequency Identification (RFID) remains its most widely recognized implementation, relying on proximity excitation from a dedicated reader to backscatter information from tags [4]. However, conventional RFID systems exhibit notable limitations: short communication range, dependence on specialized readers, and significant self-interference caused by the integrated RF source/receiver design, which impairs communication performance. These drawbacks have constrained RFID’s applicability. The recent emergence of AmBC technology offers solutions to these limitations. AmBC leverages ambient RF signals (e.g., Wi-Fi, TV broadcasts, cellular signals) as both energy sources and carrier waves, which enables low-power communication by reflecting or modulating these existing signals. The authors designed a low-complexity tag utilizing digital TV signals for backscatter communication [5]. Theoretically, employing a passive coherent detection algorithm, the receiver achieved a 1 kbps data rate over a hundred-meter range. The passive tag presented in [6] backscatters Frequency Modulation (FM) broadcast signals. Its RF front-end, comprising the ultra-low-power microcontroller MSP430 and RF switch ADG902 [7,8], achieved ambient backscatter communication exceeding 5 meters at 2.5 kbps using On-Off Keying (OOK) modulation and a designed FM0 encoding scheme with the receiver. Reference [9] developed a low-power AmBC system utilizing ambient Wi-Fi signals as the RF source, achieving data rates of 5 kbps within 1 meter and 1 kbps within 5 meters. These studies collectively demonstrate that AmBC effectively extends the communication range compared to traditional RFID and exhibits greater development potential.

To further enhance the communication performance of AmBC devices, the authors introduced the concept of frequency-shifted backscatter [10]. This technique shifts ambient RF signals to adjacent frequency bands prior to backscatter communication, which eliminates self-interference at the receiver during data decoding from the reflected signal. It achieved a 50 kbps data rate with a bit error rate (BER) of 10-3 over 3.6 meters. The authors employed a multi-antenna interference cancellation design to increase the communication bit rate [11]. Concurrently, leveraging Code Division Multiple Access (CDMA), they developed an encoding scheme tailored for low-power devices to extend communication range, where longer spreading sequences effectively enhance signal-to-noise ratio (SNR). Addressing the challenge of weak backscatter signals in systems with multi-antenna tags and readers, the authors proposed utilizing orthogonal space-time block codes (OSTBC) [12]. They presented corresponding signal detection methods for scenarios with and without channel state information (CSI), alongside a multiple-input multiple-output (MIMO) channel model. The authors introduced an AmBC signal detector based on successive interference cancellation (SIC) for flat fading channels, deriving a closed-form expression for the BER [13]. Numerical results demonstrated that when the reflected signal shares the same periodicity as the RF source signal, the proposed SIC detector approaches the performance of the maximum likelihood detector in typical application scenarios. Furthermore, the authors proposed a blind signal detection method utilizing variational Bayesian inference and machine learning [14], addressing the difficulty of acquiring relevant CSI in AmBC systems. While this method outperforms traditional constellation learning approaches, the computational complexity of machine learning techniques warrants careful consideration regarding its impact on low-power tags. Collectively, these studies contribute diverse physical-layer modulation, coding, and interference cancellation schemes. They offer solutions, to a certain extent, to the limited coverage range of AmBC tags and the mutual interference between the RF source’s direct link and the backscatter link arising from spectrum sharing. These advancements hold significant importance for reducing BER in AmBC receivers and enhancing communication data rates.

Although significant progress has been made, existing research predominantly focuses on enhancing the communication performance of individual tags. Practical AmBC systems necessitate consideration of collaborative operation and access strategies among multiple tags. Reference [15] proposed a multi-tag transmission strategy based on tag selection. This approach divides each transmission slot into three sub-slots. In the first sub-slot, tags sequentially transmit signals to the reader using Time Division Multiplexing (TDM). In the second sub-slot, the reader performs tag selection based on received signal strength. In the third sub-slot, communication occurs between the reader and the selected tag(s) according to the selection outcome. Reference [16] investigated parameter design and device association schemes for scenarios involving multiple tags, multiple RF sources, and multiple readers from a networking perspective. Under CSI, they proposed an offline access strategy utilizing the convex-concave procedure (CCP) to transform the non-concave optimization problem into a concave one. For scenarios with unknown CSI, a combinatorial multi-armed bandit (MAB)-based controlled access strategy was introduced, effectively enhancing system throughput. Addressing coexistence within AmBC networks, Reference [17] adopted a cross-layer optimization approach. It studied networks where battery-free IoT devices coexist with devices employing Carrier Sense Multiple Access with Collision Notifications (CSMA/CNs). Through analysis of outage probability and carrier sensing metrics, the outage capacity of the coexisting CSMA/CNs and Backscatter Device (BD) system was derived. While the above strategies ensure signal transmission quality and system throughput, they overlook transmission fairness among tags. Recognizing the low throughput issue inherent in links with poor channel conditions, Reference [18] proposed an AmBC network resource allocation scheme based on maximizing the worst-link throughput. This scheme achieves improved throughput fairness while maintaining near-constant average throughput.

Leveraging advances in cognitive radio (CR) technology, researchers increasingly recognize the developmental potential of hybrid communication paradigms and actively explore AmBC network architectures incorporating spectrum sensing. Reference [19] addressed passive tag interference with the direct link’s primary user, categorizing tag operation modes into cooperative and coexistence scenarios based on interference levels. Employing the Lambert W function and BCD method, they derived the optimal time allocation scheme using Lagrangian duality theory. Reference [20] investigated a backscatter-assisted cognitive radio network with multiple devices in the primary communication link. Executing distinct decisions based on channel spectrum sensing outcomes, they formulated the sequential decision problem as a mixed observable Markov decision process (MOMDP), solved via the classic value iteration algorithm. This approach adapts flexibly to variations in energy availability and channel conditions. Reference [21] focused on a hybrid transmission mode combining passive backscatter communication with active wireless-powered communication. They formulated an optimization problem for transmitter operating mode selection and resource allocation, resolving this complex challenge via dynamic programming and a hierarchical optimization algorithm, validating the scheme’s superior throughput performance. Reference [22] proposed a novel dual-bargaining game model for time scheduling in AmBC-assisted CR networks, effectively sharing limited temporal resources while demonstrating responsive adaptability to current RF-CR system conditions. Collectively, AmBC networks under hybrid communication paradigms reveal expanded developmental possibilities for IoT. However, effectively resolving novel challenges arising from technology convergence to achieve synergistic gains (“1 + 1 > 2”) remains a significant challenge. To ensure access fairness for low-power terminals in passive hybrid communication systems, this study investigates terminal access strategies and system parameter optimization across communication modes based on the BCD algorithm. This approach aims to enhance system throughput while balancing throughput fairness among diverse links. The paper’s primary contributions are as following:

(1)

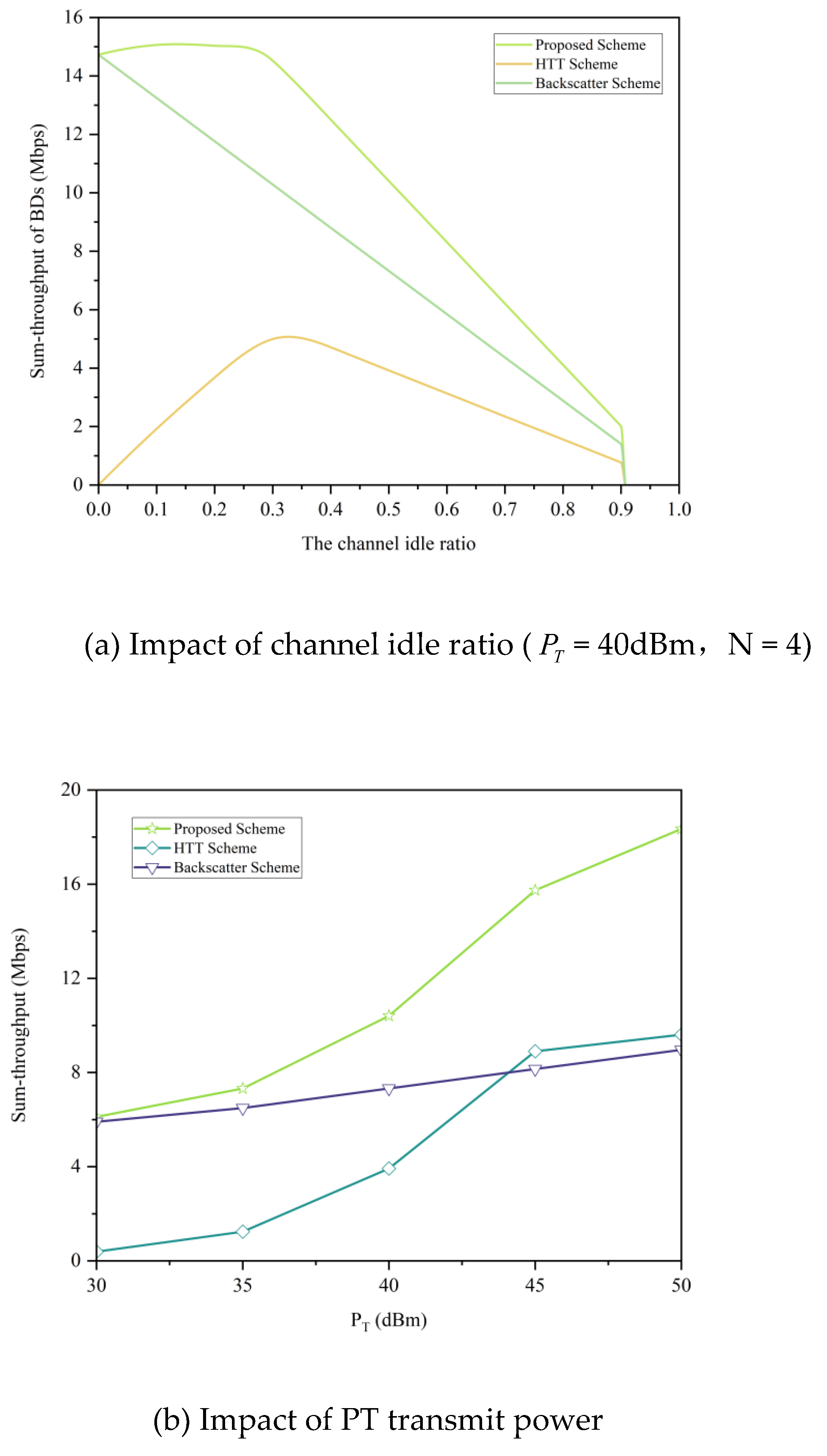
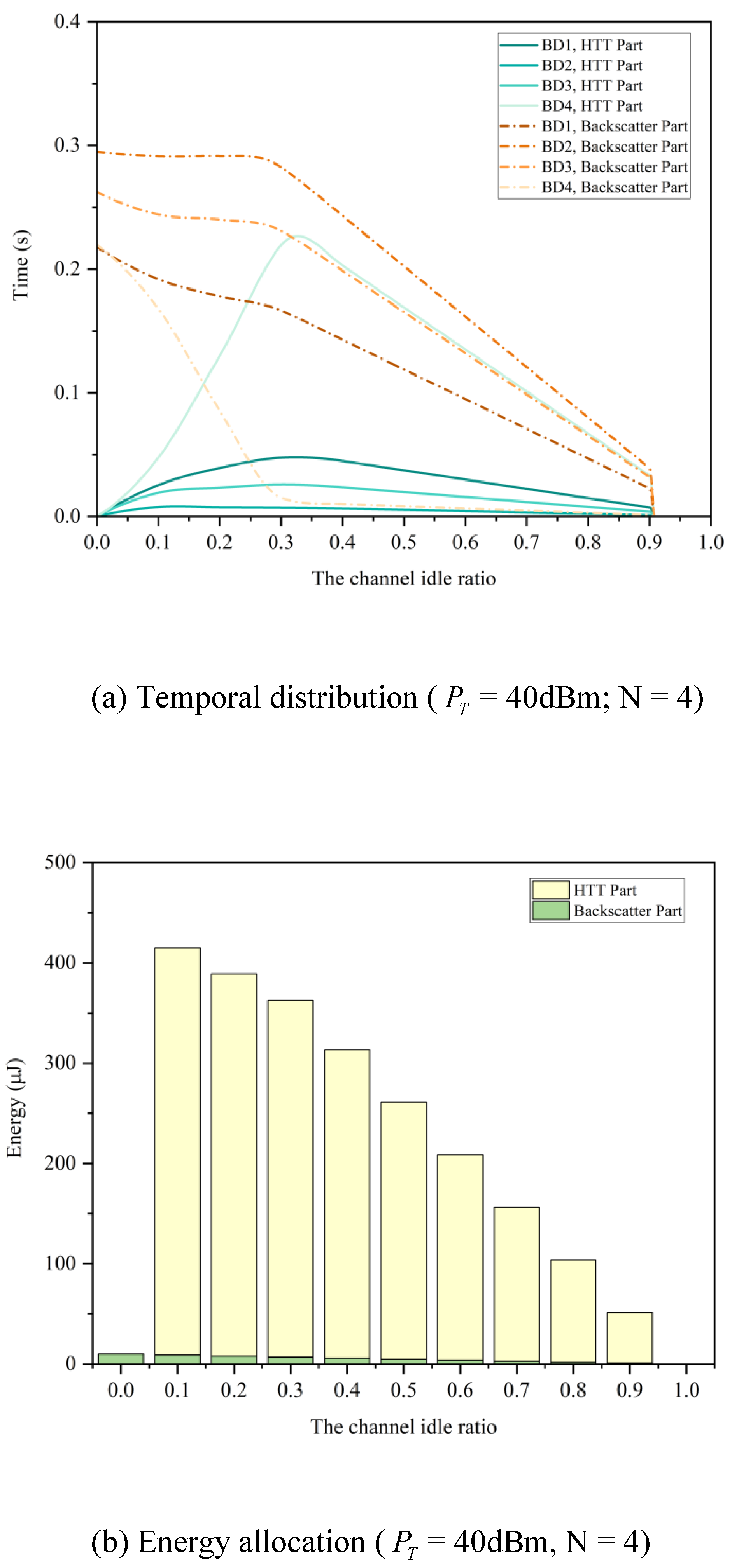
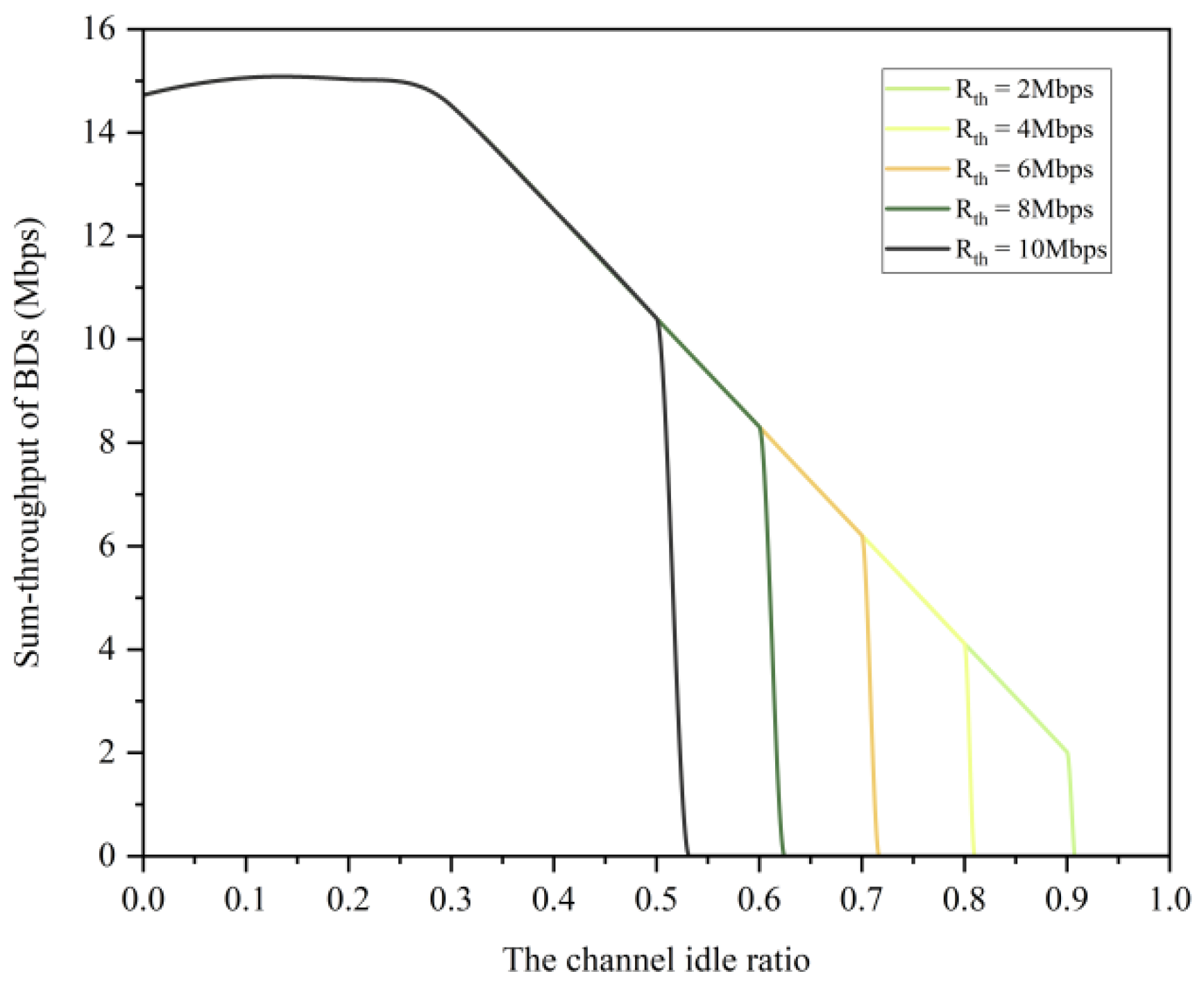
An innovative spectrum sensing-based low-power terminal access strategy is proposed. First, a communication frame structure for multi-AmBC transmitter scenarios is designed based on the underlay and interweave paradigms in cognitive radio. AmBC terminals perform spectrum sensing on licensed channel states: during busy channel conditions, they conduct RF energy harvesting from the primary link while engaging in ambient backscatter communication with the AmBC receiver to minimize interference to the primary link; during idle channel states, they activate active communication to enhance throughput on the backscatter link. Second, a mathematical model integrating energy harvesting, consumption, and hybrid communication is constructed under the QoS constraints of the primary link. Numerical simulations demonstrate the proposed hybrid access strategy significantly enhances system throughput compared to standalone AmBC or active communication modes.

(2)

Building upon this hybrid access strategy, the BCD-MLOP algorithm is designed to jointly optimize link fairness among AmBC terminals and overall system throughput across diverse channel conditions. The multi-objective optimization problem is decomposed into Max-min fairness and Max-throughput subproblems, with BCD methodology and auxiliary variables introduced to address non-convexity in individual subproblems. Each subproblem is alternately optimized using the CVX convex optimization toolkit to obtain the globally optimal solution. Numerical results validate the algorithm’s effectiveness and demonstrate the solution’s simultaneous excellence in link fairness and aggregate system throughput.

2. System Model

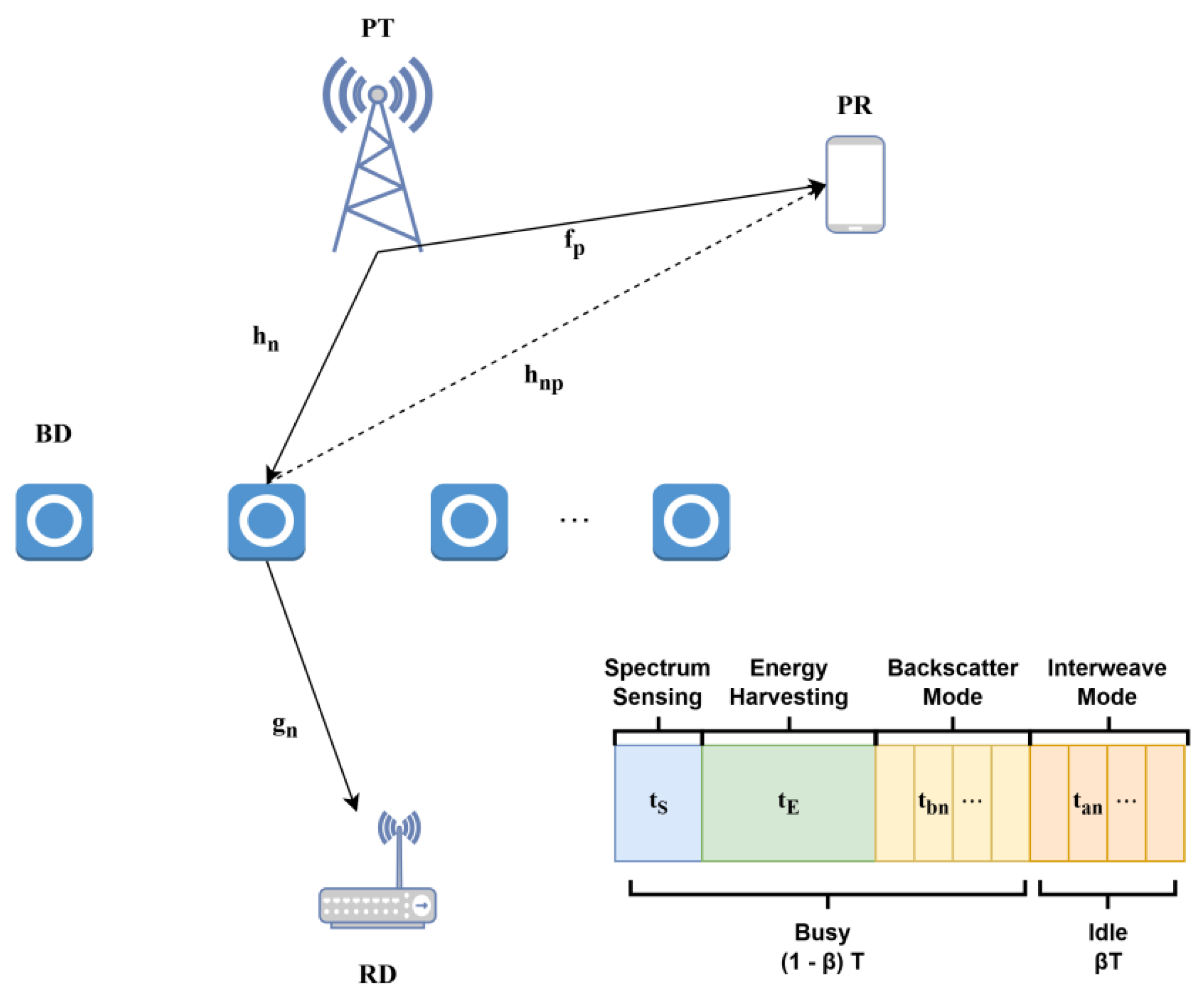
Consider a typical battery-free IoT communication scenario (e.g., logistics warehousing, smart home, or smart factory) where N unauthorized tags (Backscatter Devices, BDs) await access to a Reader (RD) for data upload. A Primary Transmitter (PT) (e.g., base station) is deployed near the N BDs to provide RF energy. Concurrently, the PT and a licensed Primary Receiver (PR) (e.g., mobile terminal) engage in data transmission using authorized spectrum resources, as illustrated in Figure 1.

The BDs form the set S = {n∈S | n=1, 2, …, N}. Assume all links experience independent block fading, with both RD and PR acquiring accurate channel state information via reliable channel estimation before each time block begins. Let$h_n$, $g_n$, $f_p$ and $h_{np}$denote the channel gains for the PT -, n-th BD, n-th BD-RD, PT-PR, and n-th BD-PR links, respectively, which can be given as following:

$$h_n={\displaystyle \frac{G_T{G}_B{\lambda }^2}{(4\pi {)}^2{L}_{TB}^{{\mathrm{v}}_1}}}$$

(1)

$${\mathrm{g}}_n={\displaystyle \frac{G_B{G}_R{\lambda }^2}{(4\pi {)}^2{L}_{BR}^{{\mathrm{v}}_2}}}$$

(2)

$$f_p={\displaystyle \frac{G_T{G}_U{\lambda }^2}{(4\pi {)}^2{L}_{TU}^{{\mathrm{v}}_3}}}$$

(3)

$$h_{np}={\displaystyle \frac{G_B{G}_U{\lambda }^2}{(4\pi {)}^2{L}_{BU}^{{\mathrm{v}}_4}}}$$

(4)

where $G_T$, $G_R$, $G_B$ and$G_U$ represent the antenna gains of PT, RD, BD, and PR, respectively; λ is the carrier wavelength; ν denotes the path-loss exponent; an L represents the communication distance for each link. As shown in Figure 1, the hybrid communication frame structure partitions the entire time block T into four sequential phases: $t_S$(spectrum sensing)，$t_E$(energy harvesting)，$t_{bS}$(backscatter communication) and $t_{aS}$(active communication). First, each BD consumes energy $E_S$for spectrum sensing during $t_S$. Based on the sensing outcome, it designates the primary link channel state as “busy” over duration $(1-\beta )T$ and “idle” during where $\beta (0\le \beta \le 1)$ represents the channel idle time ratio of the primary link. Simultaneously, during the spectrum sensing phase, the BD harvests a portion of RF energy $\eta P_T{h}_n{t}_E$, where $\eta (0<\eta <1)$ is the energy conversion efficiency, $P_T$ is the PT transmit power, and $\gamma (0<\gamma <1)$ is the energy harvesting duty cycle. Subsequently, during the primary link busy period $t_E$, the BD employs RF energy harvesting from the PT. Modeling energy harvesting as a linear process, the harvested RF energy is $\eta P_T{h}_n{t}_E$.

To enhance spectrum utilization efficiency in cognitive radio networks, unlicensed Secondary Users (SUs) can access the network through periodic spectrum sensing. SUs operate under either interweave mode or underlay mode^{Error! Reference source not found.}. In interweave mode, SUs access channels only during primary link idle periods, permitting higher transmit power for improved throughput. Conversely, in underlay mode, SUs access the primary channel with low transmit power even during primary user (PU) activity, provided interference to the Primary Receiver (PR) remains below acceptable thresholds. Extending the underlay paradigm, BDs employ AmBC to transmit low-rate data to the RD when spectrum is occupied, ensuring minimal interference to PR. Extending the underlay paradigm, BDs employ AmBC to transmit low-rate data to the RD when spectrum is occupied, ensuring minimal interference to PR. Let $c_n$ denote the information signal transmitted by the n-th BD to the RD, where $c_n\in \{0,1\}$. When $c_n$ = 1, the antenna matching state configures for backscatter communication mode, transmitting bit “1” to the RD. When $c_n$ = 0, the antenna matching state absorbs electromagnetic energy, yielding no backscattered information. BDs access the RD via Time Division Multiple Access (TDMA) for backscatter and active communication. Within a single time block, all BDs share licensed spectrum resources for AmBC or active transmission without mutual interference, conserving bandwidth. Thus, the received signal at the PR during the m-th time slot is:

$$y_U(m)=\sqrt{P_T}\left(\sqrt{f_p}+\sqrt{{\alpha }_n{h}_n{h}_{np}}{c}_n\right)x(m)+u_U(m)$$

(5)

where ${\alpha }_n(0\le {\alpha }_n\le 1)$denotes the backscattering coefficient of the n-th BD, $u_U(m)$represents additive white Gaussian noise (AWGN) at the PR receiver with$u_U(m)\sim CN(0,{\sigma }^2)$, and ${\sigma }^2$ is noise power. Here, $\sqrt{P_T{\alpha }_n{h}_n{h}_{np}}{c}_{n}x(m)$constitutes an interference signal at the PR. Assuming an authorized spectrum bandwidth W = 1MHz, the throughput of the PT-PR link is:

$$R_p={\displaystyle \sum _{n=1}^N{t}_{bn}}{\log }_2\left(1+{\displaystyle \frac{P_T{f}_p}{{\alpha }_n{P}_T{h}_n{h}_{np}+{\sigma }^2}}\right)$$

(6)

At the RD receiver, the received signal is expressed as:

$$y_R(m)=\sqrt{P_T{\alpha }_n{h}_n{g}_n}{c}_{n}x(m)+u_R(m)$$

(7)

The throughput for the n-th BD-RD link during the backscatter communication phase is:

$$R_{bn}=t_{bn}{\log }_2\left(1+{\displaystyle \frac{{\alpha }_n{P}_T{h}_n{g}_n}{{\sigma }^2}}\right)$$

(8)

Furthermore, during backscatter communication, the n-th BD may utilize a portion of harvested energy for self-powering. The harvested energy satisfies $\left(1-{\alpha }_n\right)\eta P_T{h}_n{t}_{bn}$. The energy consumed during antenna impedance switching for backscatter modulation is $P_{cb}{t}_{bn}$.

When licensed spectrum resources are released, during time segment $t_{aS}$, the n-th BD initiates active communication in interweave mode. Here, tags must generate carrier signals independently to enhance link throughput, consuming significantly more energy. The total energy expenditure per BD comprises transmit power and circuit consumption $\left(P_{an}+P_{ca}\right)t_{an}$. The received signal at the RD during active communication is:

$$y_R^{\text{'}}(m)=\sqrt{P_{an}{g}_n}{c}_{n}x(m)+u_R(m)$$

(9)

The resulting throughput for the n-th BD-RD link is:

$$R_{an}=t_{an}{\log }_2\left(1+{\displaystyle \frac{P_{an}{g}_n}{{\sigma }^2}}\right)$$

(10)

Additionally, accounting for BDs’ capability to harvest ambient non-RF energy (e.g., solar), the average harvested non-RF energy per BD per time block T is Eo.

3. Problem Formulation and Solution

Given heterogeneous channel conditions across links, throughput on severely degraded channels may become critically low. To ensure fairness among BDs while comprehensively addressing energy constraints, temporal resource limitations, and PT-PR link QoS requirements, we investigate rational resource allocation and system parameter design to maximize aggregate throughput under throughput fairness guarantees. This problem is formulated as an MLOP problem:

$$\mathrm{lex}\underset{t_{as},t_{bs},{\alpha }_s,P_{as}}{\max }\left(\underset{n\in S}{\min }{R}_n,{\displaystyle \sum _{n=1}^N{R}_n}\right)$$

(11)

$$\mathrm{s}.\mathrm{t}.{\displaystyle \sum _{n=1}^N{t}_{bn}}{\log }_2\left(1+{\displaystyle \frac{P_T{f}_p}{{\alpha }_n{P}_T{h}_n{h}_{np}+{\sigma }^2}}\right)⩾R_{th}$$

(12)

$$\begin{array}{c}\eta P_T{h}_n\left(t_E+{\displaystyle \sum _{i=1}^N{t}_{bi}}-t_{bn}+\gamma t_s\right)+\left(1-{\alpha }_n\right)\eta P_T{h}_n{t}_{bn}+E_0\\ ⩾\left(P_{an}+P_{ca}\right){\mathrm{t}}_{\mathrm{an}}+P_{cb}{t}_{bn}+E_s,\forall n\end{array}$$

(13)

$$t_E+{\mathrm{t}}_s+{\displaystyle \sum _{n=1}^N{t}_{\mathrm{bn}}}\le (1-\beta )T$$

(14)

$${\displaystyle \sum _{n=1}^N{t}_{\mathrm{an}}}\le \beta T$$

(15)

$$0\le {\alpha }_n\le 1,\forall n$$

(16)

$$P_{an},{\mathrm{t}}_{\mathrm{an}},t_{bn}\ge 0,\forall n,t_E,{\mathrm{t}}_s>0$$

(17)

From Eqs. (8) and (10), the throughput of the n-th BD is ${\mathrm{R}}_n={\mathrm{R}}_{bn}+{\mathrm{R}}_{an}=t_{bn}{\log }_2\left(1+{\alpha }_n{P}_T{h}_n{g}_n/{\sigma }^2\right)+t_{an}{\log }_2\left(1+P_{an}{g}_n/{\sigma }^2\right)$. Constraint (12) enforces the minimum tolerable QoS threshold${\mathrm{R}}_{th}$for the PT-PR link under BD-induced interference during AmBC. Constraint (13) ensures total harvested energy (RF + non-RF) covers transmission, circuit switching, and spectrum sensing expenditures. Temporal resource constraints during licensed spectrum occupancy and idleness are enforced via (14)-(15), while (16) bounds the backscattering coefficient design space. Non-negativity of transmit power and phase duration is mandated by (17).

Solving the MLOP in (11) presents two primary challenges. First, the near-far problem arising from varying BD-RD distances and disparate channel conditions necessitates rigorous throughput fairness provisioning. Achieving this requires judicious design of backscattering coefficients and active transmit powers, coupled with allocating extended backscatter communication and active communication durations to disadvantaged links for throughput enhancement. Second, the inherent coupling between ${\alpha }_n$ and $t_{bn}$ and that between $P_{an}$ and ${\mathrm{t}}_{\mathrm{an}}$, as shown in (12) and (13), renders (11) non-convex and generally intractable to global optimal. This challenge is addressed via the BCD algorithm, which alternately optimizes distinct variable blocks through iterative convexification. Following this rationale, the solution decomposes into two sequential phases: maximizing the BD throughput of the worst link and maximizing the total system throughput.

3.1. Max-Min Problem Solution

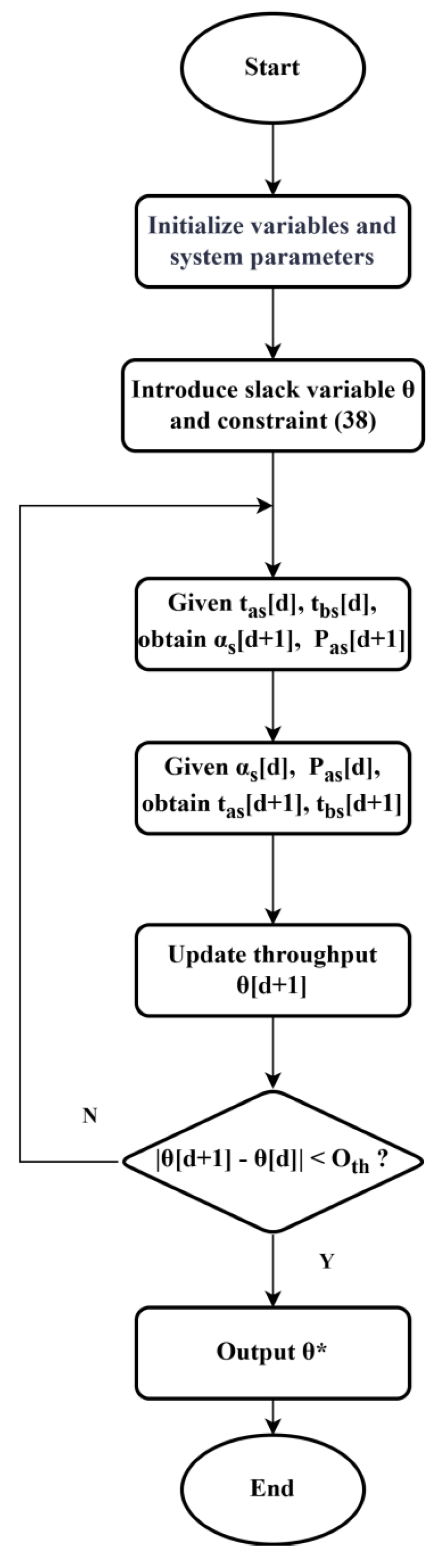
To solve the Max-min problem, we first introduce a slack variable $\theta =\underset{n\in S}{\min }{R}_n$ as the lower bound of the minimum throughput among BDs. This transforms the problem into an optimization with a linear objective, augmented by new constraints:

$$\underset{t_{aS},t_{bS},{\alpha }_S,P_{aS},\theta }{\max }\theta$$

(18)

$$\mathrm{s}.\mathrm{t}.{\displaystyle \sum _{n=1}^N{t}_{bn}}{\log }_2\left(1+{\displaystyle \frac{P_T{f}_p}{{\alpha }_n{P}_T{h}_n{h}_{np}+{\sigma }^2}}\right)⩾R_{th}$$

(19)

$$\begin{array}{c}\eta P_T{h}_n\left(t_E+{\displaystyle \sum _{i=1}^N{t}_{bi}}-t_{bn}+\gamma t_s\right)+\left(1-{\alpha }_n\right)\eta P_T{h}_n{t}_{bn}+E_0\\ ⩾\left(P_{an}+P_{ca}\right){\mathrm{t}}_{\mathrm{an}}+P_{cb}{t}_{bn}+E_s,\forall n\end{array}$$

(20)

$$t_E+{\mathrm{t}}_s+{\displaystyle \sum _{n=1}^N{t}_{\mathrm{bn}}}\le (1-\beta )T$$

(21)

$${\displaystyle \sum _{n=1}^N{t}_{\mathrm{an}}}\le \beta T$$

(22)

$$0\le {\alpha }_n\le 1,\forall n$$

(23)

$$P_{an},{\mathrm{t}}_{\mathrm{an}},t_{bn}\ge 0,\forall n,t_E,{\mathrm{t}}_s>0$$

(24)

$$R_n\ge \theta ,\forall n$$

(25)

Merging constraints (21) and (22), and noting that optimality requires equality in time allocation to ensure sufficient energy harvesting and communication for throughput enhancement, we obtain:

$$t_E+{\mathrm{t}}_s+{\displaystyle \sum _{n=1}^N{t}_{\mathrm{bn}}}+{\displaystyle \sum _{n=1}^N{t}_{\mathrm{an}}=T}$$

(26)

Substituting (26) into (20), for any given $t_{aS}[d]$ and $t_{bS}[d]$at the d (d≥1)-th iteration, the backscattering coefficients ${\alpha }_S$and active transmit powers ${\alpha }_S$are obtained by solving the following problem:

$$\underset{{\alpha }_s,P_{aS},\theta }{\max }\theta$$

(27)

$$\mathrm{s}.\mathrm{t}.{\displaystyle \sum _{n=1}^N{t}_{bn}}[d]{\log }_2\left(1+{\displaystyle \frac{P_T{f}_p}{{\alpha }_n{P}_T{h}_n{h}_{np}+{\sigma }^2}}\right)⩾R_{th}$$

(28)

$$\begin{array}{c}\eta P_T{h}_n\left(T-{\displaystyle \sum _{i=1}^N{t}_{ai}}+(\gamma -1)t_s\right)-\eta P_T{h}_n{\alpha }_n{t}_{bn}[d]+E_0\\ ⩾P_{an}{t}_{an}[d]+P_{ca}{\mathrm{t}}_{\mathrm{an}}[d]+P_{cb}{t}_{bn}[d]+E_s,\forall n\end{array}$$

(29)

$$0\le {\alpha }_n\le 1,\forall n$$

(30)

$$P_{an}\ge 0,\forall n,t_E,{\mathrm{t}}_s>0$$

(31)

$$R_n\ge \theta ,\forall n$$

(32)

Given $t_{aS}[d]$ and $t_{bS}[d]$, the left-hand side (LHS) of constraint (28) constitutes a monotonically decreasing convex function. Meanwhile, constraint (29) transforms into a linear constraint devoid of coupling variables, with remaining constraints also satisfying linearity conditions. Consequently, problem (27) reduces to a convex optimization problem solvable via the CVX convex optimization solverError! Reference source not found.. Similarly, during the d-th iteration with fixed ${\alpha }_S[d]$ and $P_{aS}[d]$, solve for backscattering coefficients $t_{aS}[d+1]$ and $t_{bS}[d+1]$:

$$\underset{t_{aS},t_{bS},\theta }{\max }\theta$$

(33)

$$\mathrm{s}.\mathrm{t}.{\displaystyle \sum _{n=1}^N{t}_{bn}}{\log }_2\left(1+{\displaystyle \frac{P_T{f}_p}{{\alpha }_n[d]P_T{h}_n{h}_{np}+{\sigma }^2}}\right)⩾R_{th}$$

(34)

$$\begin{array}{c}\eta P_T{h}_n\left(T-{\displaystyle \sum _{i=1}^N{t}_{ai}}+(\gamma -1)t_s\right)-\eta P_T{h}_n{\alpha }_n[d]t_{bn}+E_0\\ ⩾P_{an}[d]t_{an}+P_{ca}{\mathrm{t}}_{\mathrm{an}}+P_{cb}{t}_{bn}+E_s,\forall n\end{array}$$

(35)

$$0\le {\alpha }_n\le 1,\forall n$$

(36)

$${\mathrm{t}}_{\mathrm{an}},t_{bn}\ge 0,\forall n,t_E,{\mathrm{t}}_s>0$$

(37)

$$R_n\ge \theta ,\forall n$$

(38)

As this represents a canonical Linear Programming (LP) problem, it likewise admits solution via CVX. The iterative procedure is illustrated in Figure 2.

The iterative algorithm in Figure 2 decomposes the original non-convex problem into two blocks, namely (${\alpha }_n$, $t_{bn}$) and ($P_{an}$, ${\mathrm{t}}_{\mathrm{an}}$), via BCD. Each block is alternately optimized by solving the corresponding convex subproblem per iteration, with solutions propagated as inputs for subsequent iterations. Upon meeting termination criteria (i.e., throughput variation $\theta$ < $O_{th}$), the algorithm outputs the optimized solution vector ${\theta }^{*}$, which initializes the Max-throughput problem solution.

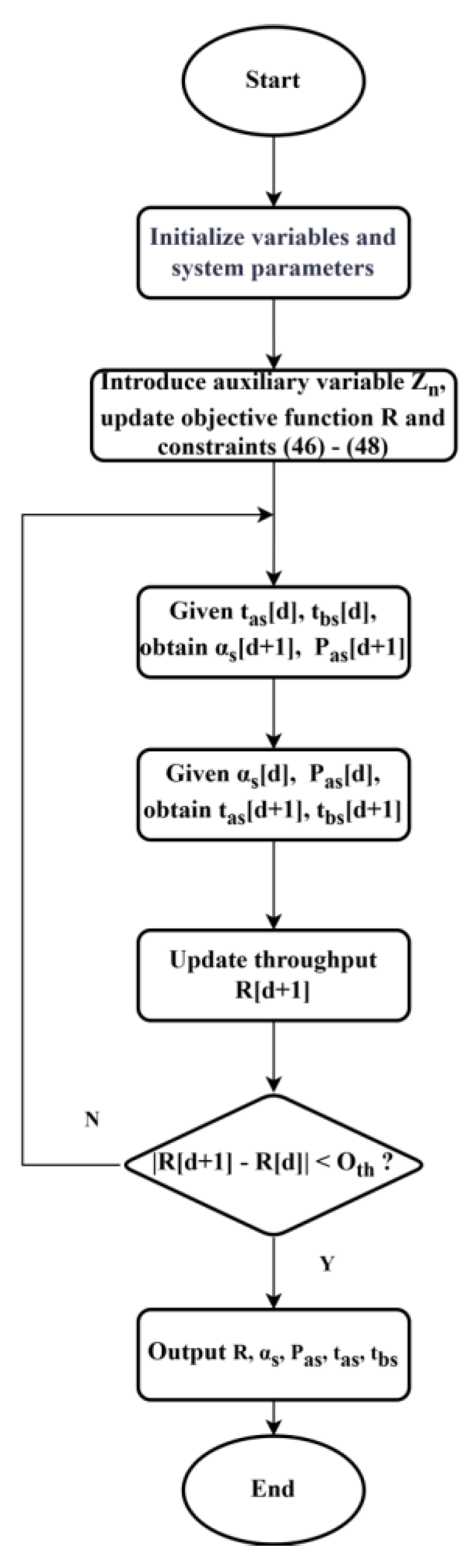
3.2. Max-throughput Problem Solution

Solving the max-throughout problem maximizes the aggregate throughput of all BDs while preserving fairness. Let $R={\displaystyle {\sum }_{n=1}^N{R}_n}$, input ${\theta }^{*}$ and revise constraint (25) to:

$$R_n\ge {\phi }_{n}R,\forall n$$

(39)

$${\phi }_{n}R\ge {\theta }^{*},\forall n$$

(40)

where ${\phi }_n$ denotes the throughput allocation coefficient for the n-th BD. The objective function is reformulated to maximize total system throughput ${\displaystyle {\sum }_{n=1}^N{\phi }_n=1;0\le {\phi }_n\le 1}$. By introducing auxiliary variable $Z_n={\phi }_n{\displaystyle {\sum }_{n=1}^N{R}_n}$, the single-objective optimization is solved as follows:

$$\underset{t_{aS},t_{bS},{\alpha }_S,P_{aS},Z_S,R}{\max }R$$

(41)

$$\mathrm{s}.\mathrm{t}.{\displaystyle \sum _{n=1}^N{t}_{bn}}{\log }_2\left(1+{\displaystyle \frac{P_T{f}_p}{{\alpha }_n{P}_T{h}_n{h}_{np}+{\sigma }^2}}\right)⩾R_{th}$$

(42)

$$\begin{array}{c}\eta P_T{h}_n\left(T-{\displaystyle \sum _{i=1}^N{t}_{ai}}+(\gamma -1)t_s\right)-\eta P_T{h}_n{\alpha }_n{t}_{bn}+E_0\\ ⩾P_{an}{t}_{an}+P_{ca}{\mathrm{t}}_{\mathrm{an}}+P_{cb}{t}_{bn}+E_s,\forall n\end{array}$$

(43)

$$0\le {\alpha }_n\le 1,\forall n$$

(44)

$$P_{an},{\mathrm{t}}_{\mathrm{an}},t_{bn}\ge 0,\forall n,t_E,{\mathrm{t}}_s>0$$

(45)

$$R_n\ge Z_n,\forall n$$

(46)

$${\theta }^{*}\le Z_n\le R,\forall n$$

(47)

$${\displaystyle \sum _{n=1}^N{Z}_n=R}$$

(48)

The presence of coupled variables in constraints (39) and (40) renders the optimization problem non-convex. To address this, auxiliary variables $Z_n$ are introduced. Constraints (46) and (47) ensure that the throughput of each link is greater than or equal to ${\theta }^{*}$and less than the total throughput. Here, the left-hand side of (46) constitutes a concave function, while (47) and (48) are affine, they all satisfy convexity requirements. The remaining non-convexity stems solely from variable coupling in (42) and (43). Mirroring the Max-min solution approach, we employ the BCD algorithm and CVX toolkit for alternating variable optimization. The algorithmic flow is detailed in Figure 3.

Finally, the proposed BCD-MLOP algorithm exhibits polynomial-time complexity. Each iteration in Phase 1 solves one LP and one convex optimization problem, while Phase 2 iterations solve two convex sub-problems, thus ensuring favorable convergence speed.

4. Simulation Results

4.1. Parameter Configuration

This study conducts numerical simulations to validate the proposed fair access strategy and system design methodology for spectrum sensing-based backscatter communication networks. To demonstrate the superiority of the hybrid communication scheme, two baseline schemes are evaluated across two dimensions: access fairness and aggregate system throughput. The first baseline (Hybrid-Throughput) employs hybrid communication while solely maximizing total system throughput. The second baseline (Single-Mode) operates exclusively in either pure backscatter communication or pure active communication with harvested energy. Parameter variations are implemented to comprehensively assess the performance of the proposed hybrid scheme.

Simulation parameters are configured as follows: The primary transmitter (PT) is deployed at (0, 0) m and primary receiver (PR) at (20, 0) m. Four (N=4) unlicensed BDs are randomly distributed within a 5m-radius circular area centered at the RD located at (-10, 0) m. System bandwidth is set to 1 MHz with time block duration T = 1s. Spectrum sensing time is fixed at Ts = 5ms, and channel idle ratio defaults to β = 0.5. Initial base station transmit power is 40 dBm with environmental noise power at -101 dBm. Circuit power consumption: 10 μW for backscatter communication and 1 mW for active communication. RF energy harvesting efficiency η = 0.8 and spectrum sensing energy conversion ratio γ = 0.5, both following a linear energy harvesting model. Mean energy consumption for spectrum sensing per time block is 1 mJ, while mean harvested non-RF energy is 1 mJ. Channel gains for backscatter and primary links are calculated using a path-loss model with uniform 1.5 dB antenna gains for PT, BD, PR, and RD. Path-loss exponent v is 3 for the primary link (PT-PR) and 2 for other links. The initial QoS threshold Rth for the primary link is 2 Mbps.

4.2. Simulation Results

Figure 4 compares the proposed fair access scheme against baseline schemes under varying channel gains, highlighting performance disparities between best- and worst-performing links. While baseline schemes achieve higher aggregate throughput, they exhibit >5 Mbps performance gaps across all channel conditions, a limitation effectively mitigated by our proposal while maintaining competitive system throughput. Critically, when channel gain divergence widens, baseline resource allocation disproportionately favors advantaged links, amplifying throughput disparity to 9.7 Mbps. Conversely, our scheme sustains robust throughput fairness even under significant channel gain discrepancies.

Figure 5(a) examines system throughput versus channel idle ratio (β) for hybrid, active-only, and backscatter-only schemes. Throughput in hybrid and active modes initially rises then declines as β increases. This trend arises because temporal resource allocation initially favors active communication, boosting throughput. However, extended active operation escalates power consumption while simultaneously compressing RF energy harvesting windows. Consequently, throughput degrades beyond critical β thresholds. The backscatter-only scheme demonstrates throughput reduction proportional to shortened communication time. Notably, all three schemes experience abrupt throughput collapse (reduction to 0) beyond β = 0.9, constrained by the primary link’s QoS threshold preventing indefinite backscatter time reduction. Crucially, the proposed hybrid communication consistently achieves superior throughput across all β regimes.

Figure 5(b) further examines system throughput under varying base station transmit power ($P_T$) for all three schemes. Elevated $P_T$ enhances tag energy availability for backscatter/active communication while simultaneously strengthening received signal power at the reader, progressively improving system throughput. The proposed hybrid scheme consistently demonstrates superior throughput performance across the entire transmit power range.

Figure 6 illustrates temporal and energy resource allocation dynamics versus increasing channel idle ratio β. Subfigure 6(a) reveals per-BD time resource variations: as β rises, backscatter communication duration decreases while active communication time exhibits initial expansion followed by contraction, constrained by harvested energy limitations. Critically, backscatter and active communication durations maintain an inversely proportional relationship across tags. Devices allocated extended backscatter time proportionally compensate by reducing active periods to preserve inter-link throughput fairness. Subfigure 6(b) details energy allocation per time block. Under persistent spectrum occupancy (β=0), minimal energy expenditure supports backscatter-only operation since carrier generation is unnecessary. Increasing β demands greater energy expenditure for active communication while simultaneously reducing RF harvesting opportunities from the primary link, progressively diminishing harvested energy. At full spectrum availability (β=1), BD operation ceases due to complete RF energy depletion.

Finally, the impact of varying QoS thresholds for the primary communication link on system throughput is analyzed. As shown in Figure 7, higher throughput demands in the primary link necessitate greater temporal allocation under fixed bandwidth and signal-to-noise ratio. Consequently, beyond critical channel idle ratios, the primary link fails to meet QoS requirements. To satisfy these constraints, tags must cease communications, indicating operational necessity to relax primary link QoS demands under high-idle-ratio regimes.

5. Conclusion

To address link fairness and communication rate enhancement in spectrum sensing-based backscatter systems, this study proposes a hybrid communication access strategy coupled with a BCD-enabled multi-objective optimization algorithm. Leveraging cognitive radio’s interweave and underlay paradigms, we design a time-block structure implementing RF energy harvesting, ambient backscatter communication, or active transmission according to primary link occupancy states. Energy consumption models and coexistence frameworks for primary and passive systems are analytically derived. The original non-convex optimization is transformed into tractable convex sub-problems via BCD methodology and variable substitution, obtaining optimal solutions for temporal partitioning and system parameters. Simulations demonstrate that the BCD-MLOP algorithm under hybrid communication outperforms conventional single-mode schemes and throughput-maximization approaches, delivering superior throughput while rigorously preserving fairness.