1. Introduction
The proposed paper continues a series of papers devoted to unsolved problems in the theory of stability and optimal control for stochastic systems (see [
1,
2,
3,
4,
5]). Here the problem of the controlled inverted pendulum is considered, which appears many years ago [
6] and has a long history (see [
7] and the references therein). The mathematical model of the controlled inverted pendulum has the form of nonlinear differential equation of the second order
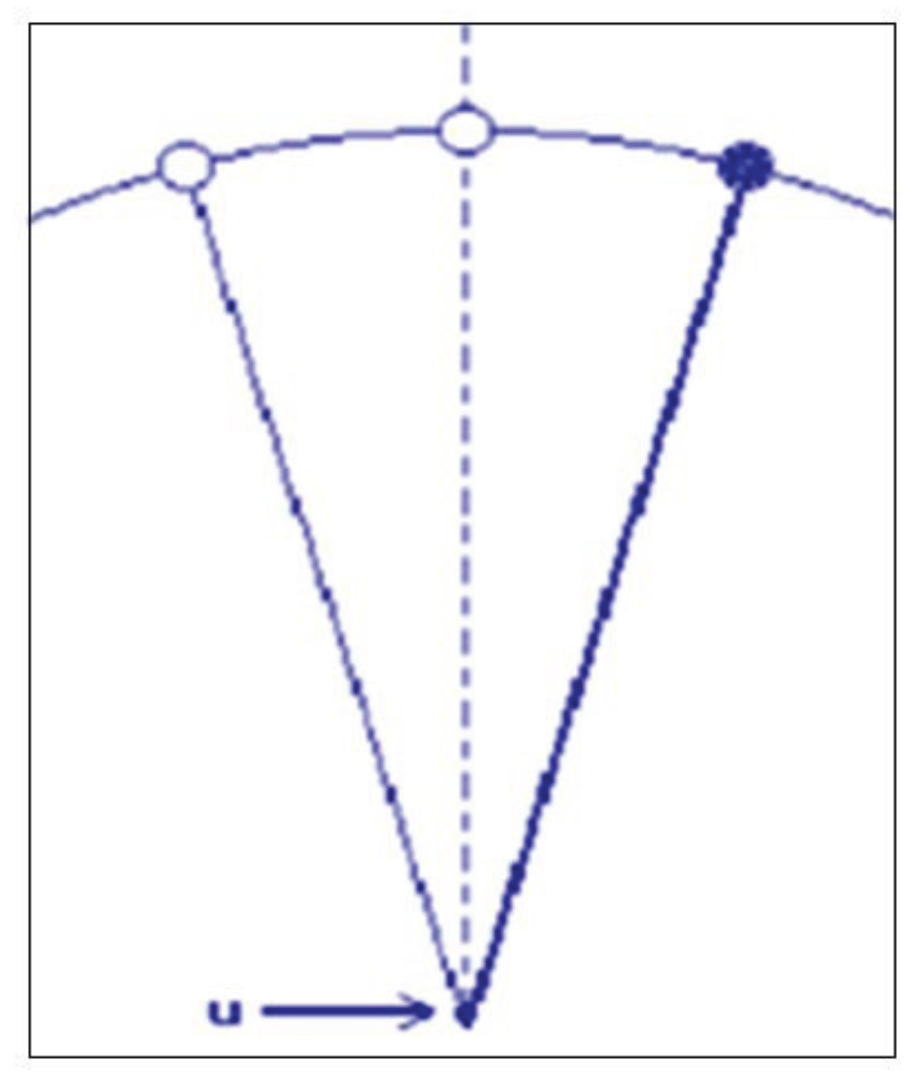
where
measures the angle between the rod and the upward vertical (
Figure 1).
The classical way of stabilization for the equation (
1) uses [
6] the control
, which is a linear combination of the state and velocity of the pendulum, i.e.,
But this type of control, which represents instantaneous feedback, is quite difficult to realize because usually it is necessary to have some finite time to make measurements of the coordinates and velocities, to treat the results of the measurements and to implement them in the control action.
Unlike of the classical way of stabilization another way of stabilization is considered in [
8]. It is supposed that only the trajectory of the pendulum is observed and the control
does not depend on the velocity, but depends on the all previous values of the trajectory
,
, and is given in the form
where the kernel
is a continuous from the right function of bounded variation on
and the integral is understood in the Stieltjes sense. It means, in particular, that both distributed and discrete delays can be used depending on the concrete choice of the kernel
.
2. Zero and Nonzero Equilibria
It is clear that (
1), (
2) define the delay differential equation
which has the zero solution. However, this equation has not the zero solution only. Put
and note that the nonzero equilibrium
of the equation (
3) is a root of the equation
or
, where
Remark 1.
As it is noted in [7] for all
where . Therefore, if
or
then there exists at least one nonzero root of the equation (5).
3. Two Types of Stochastic Perturbations
In addition, it is supposed that the pendulum is under influence of stochastic perturbations, so, the considered stabilization problem is a problem of the theory of stochastic functional differential equations [
8,
9,
10].
Let
be a complete probability space,
be a nondecreasing family of sub-
-algebras of
, i.e.,
for
,
be the mathematical expectation with respect to the probability
. Let
and
be respectively
-measurable the Wiener and the Poisson processes,
,
,
[
9,
10],
Supposing for the beginning that the parameter
a in (
1) is influenced by additive stochastic perturbations, i.e.,
, where
is defined in (
6), and using the control (
2), rewrite the equation (
1) as
or, using
,
and (
6), in the form of the system of stochastic differential equations [
9,
10] with the zero solution
From the other hand let us suppose that the equation (
3) is influenced by additive stochastic perturbations of the form
, where
is a nonzero root of the equation (
5) and
is defined in (
6). Then similarly to (
8) we obtain the system of stochastic differential equations with the solution
,
:
Using the general method of Lyapunov functionals construction [
8], in [
7] the following two theorems about stability in probability (see definition in [
7,
8]) have been proven
Theorem 1.
Let be
where , , are defined in (4). Then the zero solution of the equation (7) (or the system (8)) is stable in probability.
Theorem 2.
Let be
where , , are defined in (4). Then the nonzero equilibrium of the system (9) is stable in probability.
4. Unsolved Problems
Let us consider the mathematical model of two coupled controlled inverted pendulums in the form of the system of two nonlinear differential equations of the second order:
It is assumed that only the trajectories of both pendulums are observed, the controls
and
do not depend on the velocity, but depend respectively on all previous values of the trajectories
and
,
, and are given in the form
Similarly to (
2) here it is supposed that
and
are continuous from the right functions of bounded variation on
and the integrals are understood in the Stieltjes sense.
If
then the system (
12), (
13) splits into two independent equations, for each from which the statements of both Theorems 1 and 2 can be formulated.
Putting
we obtain the following two problems.
4.1. The Problem 1
Supposing that the parameters
,
, in (
12) are influenced by stochastic perturbations
where
,
and
are mutually independent the Wiener and the Poisson processes, we obtain
or
Problem 1: Formulate and prove for the system (14) an analogue of the Theorem 1. 4.2. The Problem 2
The nonzero equilibrium
of the system (
12), (
13) is a solution of the system of algebraic equations
where
,
, and is also the equilibrium of the system
Problem 2: Formulate and prove for the system (16) an analogue of the Theorem 2. 5. Conclusions
The list of the author’s unsolved problems continues to increase. But the author continues to hope that his unsolved problems will be solved someday, and invites interested readers to help him with this.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- L. Shaikhet, Two unsolved problems in the stability theory of stochastic differential equations with delay. Appl. Math. Lett. 25, 2012, 636-637, doi:10.1016/j.aml.2011.10.002.
- L. Shaikhet, Some unsolved problems in stability and optimal control theory of stochastic systems. Special Issue “Models of Delay Differential Equations–II”, MDPI Mathematics, 10(3), 2022, 474, p.1-10, Pub.online: 01 Feb 2022, . [CrossRef]
- L. Shaikhet, About an unsolved problem of stabilization by noise for difference equations. MDPI, Mathematics, 12(1), 2024, 110, 11p., https://www.mdpi.com/2227-7390/12/1/110.
- L. Shaikhet, Unsolved problem about stability of stochastic difference equations with continuous time and distributed delay. Modern Stochastics: Theory and Applications, 11(4), 2024, 395-402, . [CrossRef]
- L. Shaikhet, About some unsolved problems in the stability theory of stochastic differential and difference equations. MDPI, Axioms, 14(6), 2025, 452, 10p, . [CrossRef]
- P.L. Kapitza, Dynamical stability of a pendulum when its point of suspension vibrates, and pendulum with a vibrating suspension. In: ter Haar D (ed) Collected papers of P.L. Kapitza. Pergamon Press, London, 2, 1965, 714-737.
- L. Shaikhet, About Stabilization of the Controlled Inverted Pendulum under Stochastic Perturbations of the Type of Poisson’s Jumps. MDPI, Axioms, Special Issue: “Advances in Mathematical Optimal Control and Applications”, 14(1), 2025, 29, 14p., . [CrossRef]
- L. Shaikhet, Lyapunov Functionals and Stability of Stochastic Functional Differential Equations, Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013, https://link.springer.com/book/10.1007/978-3-319-00101-2.
- I.I. Gikhman, A.V. Skorokhod, Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 1972.
- I.I. Gikhman, A.V. Skorokhod, The theory of stochastic processes, v.III, Berlin: Springer-Verlag; 1979.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).