About Some Unsolved Problems in the Stability Theory of Stochastic Differential and Difference Equations

1. Introduction

The unsolved problems proposed here continue a series of unsolved problems in stability and optimal control theory for stochastic differential and stochastic difference equations, that have been presented during the recent years at some international conferences and papers (see [1,2,3,4,5,6,7,8,9,10]). All these problems still need to be solved.

Let $\{\mathrm{\Omega },\mathfrak{F},\mathbf{P}\}$ be a complete probability space, ${\left\{{\mathfrak{F}}_t\right\}}_{t\ge 0}$ be a nondecreasing family of sub-$\sigma$-algebras of $\mathfrak{F}$, i.e., ${\mathfrak{F}}_s\subset {\mathfrak{F}}_t$ for $s<t$, $\mathbf{E}$ be the expectation with respect to the measure $\mathbf{P}$, $H_2$ be the space of ${\mathfrak{F}}_0$-adapted stochastic processes $\phi \left(s\right)$, $s\le 0$, ${\parallel \phi \parallel }^2=\underset{s\le 0}{sup}\mathbf{E}{\left|\phi \left(s\right)\right|}^2$.

Following Gikhman and Skorokhod [11,12], let us consider the stochastic delay differential equation

$$\begin{array}{c}dx\left(t\right)=\left(Ax\left(t\right)+{\displaystyle \sum _{i=1}^k}{B}_{i}x(t-h_i)\right)dt+{\displaystyle \sum _{i=1}^m}{C}_i\left(t\right)x\left(t\right)d{w}_i\left(t\right)\\ +\int G(t,u)x\left(t\right)\tilde{\nu }(dt,du),t\ge 0,\\ x\left(s\right)=\varphi \left(s\right)\in H_2,s\in [-h,0],h=\underset{i=1,\dots ,k}{max}{h}_i,\end{array}$$

(1)

where $x\left(t\right)\in {\mathbf{R}}^n$, $A,B_i,C_i\left(t\right),G(t,u)$ are $n\times n$-matrices, $h_i>0$, $w_1\left(t\right),...,w_m\left(t\right)$ are mutually independent standard Wiener processes, which are also independent of the Poisson measure $\nu (t,A)$,

$$\mathbf{E}\nu (t,A)=t\mathrm{\Pi }\left(A\right),\tilde{\nu }(t,A)=\nu (t,A)-t\mathrm{\Pi }\left(A\right).$$

1.1. Auxiliary Definitions and Statements

Let $x\left(t\right)$ be a solution of the Equation (1) in the time moment t, $x_t=x(t+s)$, $s<0$, be a trajectory of the Equation (1) solution until the time moment t. Consider a functional $V(t,\phi ):[0,\infty )\times H_2\to {\mathbf{R}}_{+}$ that can be presented in the form $V(t,\phi )=V(t,\phi (0),\phi (s\left)\right)$, $s<0$, and for $\phi =x_t$ put

$$\begin{array}{c}{V}_{\phi }(t,x)=V(t,\phi )=V(t,x_t)=V(t,x,x(t+s)),\\ x=\phi \left(0\right)=x\left(t\right),s<0.\end{array}$$

(2)

Let D be a set of functionals $V(t,\phi )$, for which the function $V_{\phi }(t,x)$ defined in (2) has a continuous derivative with respect to t and two continuous derivatives with respect to x. Let ′ be the sign of transpose, $\nabla V_{\phi }(t,x)$ and ${\nabla }^2{V}_{\phi }(t,x)$ be respectively the first and the second derivatives of the function $V_{\phi }(t,x)$ with respect to x. For the functionals from D the generator L of the Equation (1) has the form [11,12,13]

$$\begin{array}{cc}LV(t,x_t)=\hfill & {\displaystyle \frac{\partial }{\partial t}}{V}_{\phi }(t,x\left(t\right))+\nabla V_{\phi }^{\prime }(t,x\left(t\right))\left(Ax\left(t\right)+{\displaystyle \sum _{i=1}^k}{B}_{i}x(t-h_i)\right)\\ \hfill & +{\displaystyle \frac{1}{2}}{\displaystyle \sum _{i=1}^m}{x}^{\prime }\left(t\right)C_i^{\prime }\left(t\right){\nabla }^2{V}_{\phi }(t,x\left(t\right))C_i\left(t\right)x\left(t\right)\\ \hfill & +\int [V_{\phi }(t,x\left(t\right)+G(t,u)x\left(t\right))-V_{\phi }(t,x\left(t\right))\\ & -\nabla V_{\phi }^{\prime }(t,x\left(t\right))G(t,u)x\left(t\right)]\mathrm{\Pi }\left(du\right).\end{array}$$

(3)

Definition 1.

[13] The zero solution of the Equation (1) is called:

- 

mean square stable if for each $\epsilon >0$ there exists a $\delta >0$ such that ${\mathbf{E}\left|x\left(t\right)\right|}^2<\epsilon$, $t\ge 0$, provided that ${\parallel \varphi \parallel }^2<\delta$;

- 

asymptotically mean square stable if it is mean square stable and for each initial function $\varphi \left(s\right)$ the solution $x\left(t\right)$ of the Equation (1) satisfies the condition $\underset{t\to \infty }{lim}\mathbf{E}{\left|x\left(t\right)\right|}^2=0$.

Theorem 1.

[13] Let there exist a functional $V(t,\phi )\in D$, positive constants $c_1$, $c_2$, $c_3$, such that the following conditions hold:

$$\begin{array}{c}\mathbf{E}V(t,x_t)\ge c_1\mathbf{E}|x\left(t\right){|}^2,\mathbf{E}V(0,\varphi )\le c_2{\parallel \varphi \parallel }^2,\\ \mathbf{E}LV(t,x_t)\le -c_3\mathbf{E}{\left|x\left(t\right)\right|}^2.\end{array}$$

Then the zero solution of the Equation (1) is asymptotically mean square stable.

Some particular cases of the Equation (1) are considered in [14,15], where it is proven that if the stochastic perturbations fade on the infinity quickly enough then the asymptotically stable zero solution of the corresponding deterministic system remains asymptotically mean square stable regardless of the level of these stochastic perturbations.

In particular, in [15] the asymptotic mean square stability of the zero solution of the Equation (1) with $k=m=1$ is proven by virtue of the general method of Lyapunov functionals construction [13,16] and the method of Linear Matrix Inequalities (LMIs) [17,18,19]. By that it is supposed that for some positive definite matrix P the following conditions hold

$$C^{\prime }\left(t\right)PC\left(t\right)\le {\sigma }^2\left(t\right)P,G^{\prime }(t,u)PG(t,u)\le {\gamma }^2(t,u)P,$$

$$\rho \left(t\right)={\sigma }^2\left(t\right)+\int {\gamma }^2(t,u)\mathrm{\Pi }\left(du\right),{\int }_0^{\infty }\rho \left(t\right)dt<\infty ,$$

(4)

and the Lyapunov functional $V(t,x_t)$ is constructed in the form $V(t,x_t)=V_1(t,x\left(t\right))+V_2(t,x_t)$, where

$$\begin{array}{c}{V}_1(t,x\left(t\right))=e^{-{\int }_0^t\rho \left(s\right)ds}{x}^{\prime }\left(t\right)Px\left(t\right),P>0,\\ V_2(t,x_t)={\int }_{t-h}^t{e}^{-{\int }_0^{s+h}\rho \left(\tau \right)d\tau }{x}^{\prime }\left(s\right)Rx\left(s\right)ds,R>0.\end{array}$$

(5)

Remark 1.

Note that in order for the constructed Lyapunov functional $V(t,x_t)$ (5) to satisfy the conditions of Theorem 1 the integrability condition (4) of the function $\rho \left(t\right)$ must be satisfied. This condition means that stochastic perturbations fade on the infinity quickly enough. Below another situation is studied. It is supposed that stochastic perturbations can fade on the infinity either slowly or not fade at all. By that some unsolved problem is also proposed.

2. About One Problem of Stability

2.1. Equation Without Delays

Consider at first the Equation (1) without delays, i.e., by the condition

$$B_i=0,i=1,...,k.$$

(6)

Let L be the generator of the Equation (1), (6). Then via (3) for the function $V\left(x\left(t\right)\right)={\left|x\left(t\right)\right|}^2$ we have

$$\begin{array}{c}LV\left(x\left(t\right)\right)=2x^{\prime }\left(t\right)Ax\left(t\right)+{\displaystyle \sum _{i=1}^m}{x}^{\prime }\left(t\right)C_i^{\prime }\left(t\right)C_i\left(t\right)x\left(t\right)\\ +\int x^{\prime }\left(t\right)G^{\prime }(t,u)G(t,u)x\left(t\right)\mathrm{\Pi }\left(du\right)\\ =x^{\prime }\left(t\right)[A+A^{\prime }+Q\left(t\right)]x\left(t\right),\end{array}$$

(7)

where

$$Q\left(t\right)=\sum _{i=1}^m{C}_i^{\prime }\left(t\right)C_i\left(t\right)+\int G^{\prime }(t,u)G(t,u)\mathrm{\Pi }\left(du\right).$$

Let $\rho \left(t\right)=\parallel Q\left(t\right)\parallel$ be the norm of the matrix $Q\left(t\right)$, i.e.,

$$x^{\prime }Q\left(t\right)x\le \rho \left(t\right){\left|x\right|}^2.$$

(8)

Assume that the symmetric matrix $A+A^{\prime }$ is a negative definite matrix, i.e.,

$$x^{\prime }(A+A^{\prime })x\le -\alpha {\left|x\right|}^2,\alpha >0,$$

(9)

and, besides, suppose that

$$\underset{t\ge 0}{sup}\rho \left(t\right)<\alpha \mathrm{or}{\int }_0^{\infty }\rho \left(t\right)dt<\infty .$$

(10)

Put also

$$\mu \left(t\right)={\displaystyle \frac{1}{t}}{\int }_0^t\rho \left(s\right)ds,\mu =\underset{t\to \infty }{lim\; sup}\mu \left(t\right).$$

(11)

Remark 2.

Note that if the first or the second condition (10) holds then respectively $\mu <\alpha$ or $\mu =0<\alpha$. But the condition $\mu <\alpha$ can be hold even by the condition

$${\int }_0^{\infty }\rho \left(t\right)dt=\infty .$$

(12)

For example, for the function $\rho \left(t\right)={\displaystyle \frac{2\alpha }{t+1}}$ none of the conditions (10) are satisfied, but the both conditions $\mu =0<\alpha$ and (12) are obviously satisfied.

Theorem 2.

Let α and μ, defined in (9) and (11), satisfy the condition $\mu <\alpha$. Then the zero solution of the Equation (1), (6) is asymptotically mean square stable.

Proof. 

Using the generator (7) and the definitions (8), (9) for $\rho \left(t\right)$ and $\alpha$, we have

$$LV\left(x\left(t\right)\right)\le {(-\alpha +\rho \left(t\right))\left|x\left(t\right)\right|}^2.$$

From this and Dynkin’s formula [11]

$$\mathbf{E}V\left(x\left(t\right)\right)=\mathbf{E}V\left(x\left(0\right)\right)+{\int }_0^t\mathbf{E}LV\left(x\left(s\right)\right)ds$$

for the function $V\left(x\left(t\right)\right)={\left|x\left(t\right)\right|}^2$ it follows that

$${\displaystyle \frac{d}{dt}}{\mathbf{E}\left|x\left(t\right)\right|}^2=\mathbf{E}LV\left(x\left(t\right)\right)\le (-\alpha +\rho \left(t\right))\mathbf{E}{\left|x\left(t\right)\right|}^2$$

or

$${\displaystyle \frac{{d\mathbf{E}\left|x\left(t\right)\right|}^2}{{\mathbf{E}\left|x\left(t\right)\right|}^2}}\le (-\alpha +\rho \left(t\right))dt.$$

Integrating this inequality and using (11), we obtain

$$\begin{array}{c}{\mathbf{E}\left|x\left(t\right)\right|}^2\le {\mathbf{E}\left|x\left(0\right)\right|}^{2}exp\left\{-\alpha t+{\int }_0^t\rho \left(s\right)ds\right\}\\ =\mathbf{E}{\left|x\left(0\right)\right|}^{2}exp\left\{(-\alpha +\mu \left(t\right))t\right\}.\end{array}$$

From this and $\mu <\alpha$ it follows that ${\mathbf{E}\left|x\left(t\right)\right|}^2\le \mathbf{E}{\left|x\left(0\right)\right|}^2$ and $\underset{t\to \infty }{lim}\mathbf{E}{\left|x\left(t\right)\right|}^2=0$, i.e., the zero solution of the Equation (1), (6) is asymptotically mean square stable. The proof is completed. □

Remark 3.

Note that the condition (4) of integrability of the function $\rho \left(t\right)$ is not a necessary condition for asymptotic mean square stability of the zero solution of the stochastic differential Equation (1). For instance, for a simple scalar equation of the type of (1) with constant coefficients

$$dx\left(t\right)=-ax\left(t\right)dt+\sigma x\left(t\right)dw\left(t\right)+\int \gamma \left(u\right)x\left(t\right)\tilde{\nu }(dt,du),$$

(13)

where $a>0$ and $\rho \left(t\right)$ is the constant, i.e.,

$$\rho ={\sigma }^2+\int {\gamma }^2\left(u\right)\mathrm{\Pi }\left(du\right),$$

the condition (12) holds, but the zero solution of the Equation (13) is asymptotically mean square stable if $\rho <2a$.

Unsolved problem. The proof of asymptotic mean square stability of the zero solution of the stochastic delay differential Equation (1) under the condition (12) is currently an unsolved problem, which is offered to the attention of potential readers.

3. About the Problem of Stabilization by Noise

Note that the problem of stabilization has a long history, in particular, very popular problem of stabilization of the inverted pendulum is considered in a lot of works: for example, the well known work of Kapitsa [20] and many others [21,22,23,24,25,26,27,28,29,30,31,32]. Below the problem of stabilization by noise is discussed.

Consider the scalar linear Ito’s stochastic differential equation [11]

$$\begin{array}{c}dx\left(t\right)=\left(ax\right(t)+bx(t-h\left)\right)dt+\sigma x\left(t\right)dw\left(t\right),\\ x\left(s\right)=\varphi \left(s\right),s\in [-h,0],\end{array}$$

(14)

where a, b and $\sigma$ are constants and $w\left(t\right)$ is the standard Wiener process.

Definition 2.

[13,33] The zero solution of the Equation (14) is called stable in probability if for any ${\epsilon }_1>0$

and ${\epsilon }_2>0$ there exists $\delta >0$ such that the solution $x(t,\varphi )$ of the Equation (14) satisfies the condition

$\mathbf{P}\left\{{sup}_{t\ge 0}\left|x(t,\varphi )\right|>{\epsilon }_1\right\}<{\epsilon }_2$ for any initial function $\varphi \left(s\right)$, such that $\mathbf{P}\left\{{sup}_{s\in [-h,0]}\left|\varphi \left(s\right)\right|<\delta \right\}=1$.

3.1. Equation Without Delay

Consider now the Equation (14) by the condition $b=0$, i.e., without delay:

$$\begin{array}{c}dx\left(t\right)=ax\left(t\right)dt+\sigma x\left(t\right)dw\left(t\right),\\ x\left(s\right)=\varphi \left(s\right),s\in [-h,0].\end{array}$$

(15)

Khasminskii shows [33] that unstable by the conditions $a>0$ and $\sigma =0$ the zero solution of the Equation (15) becomes stable by the presence of a big enough level of noise. More exactly, by the condition

$$0<2a<{\sigma }^2$$

(16)

so-called "stabilization by noise" occurs and the zero solution of the Equation (15) becomes stable in probability.

Really, let L be the generator [11,12,13,33] of the Equation (15). Then for the Lyapunov function

$$v\left(x\right)={\left|x\right|}^{\nu },\nu =1-{\displaystyle \frac{2a}{{\sigma }^2}}\in (0,1),$$

we have

$$\begin{array}{cc}Lv\left(x\right)& ={\displaystyle \frac{dv\left(x\right)}{dx}}ax+{\displaystyle \frac{1}{2}}{\displaystyle \frac{d^{2}v\left(x\right)}{d{x}^2}}{\sigma }^2{x}^2\hfill \\ & ={\nu \left|x\right|}^{\nu -1}ax+{\displaystyle \frac{1}{2}}{\nu (\nu -1)\left|x\right|}^{\nu -2}{\sigma }^2{x}^2\hfill \\ & \le a\nu {\left|x\right|}^{\nu }\left(1-(1-\nu ){\displaystyle \frac{{\sigma }^2}{2a}}\right)=0.\hfill \end{array}$$

It is known [13,33] that if there exist a Lyapunov function $v\left(x\right)$ with the condition $Lv\left(x\right)\le 0$ then the zero solution of the Equation (15) is stable in probability.

3.2. Purely Stochastic Equation

From the condition (16) it follows, in particular, that the zero solution of the "purely stochastic" differential equation

$$dx\left(t\right)=\sigma x\left(t\right)dw\left(t\right)$$

(17)

is stable in probability for arbitrary $\sigma$. Moreover, the larger $\left|\sigma \right|$, the faster the trajectories of the solution of the Equation (17) converge to zero.

Note that the solution of the Equation (17) has the form [11]

$$x\left(t\right)=x\left(0\right)exp\left\{-{\displaystyle \frac{1}{2}}{\sigma }^{2}t+\sigma w\left(t\right)\right\}.$$

(18)

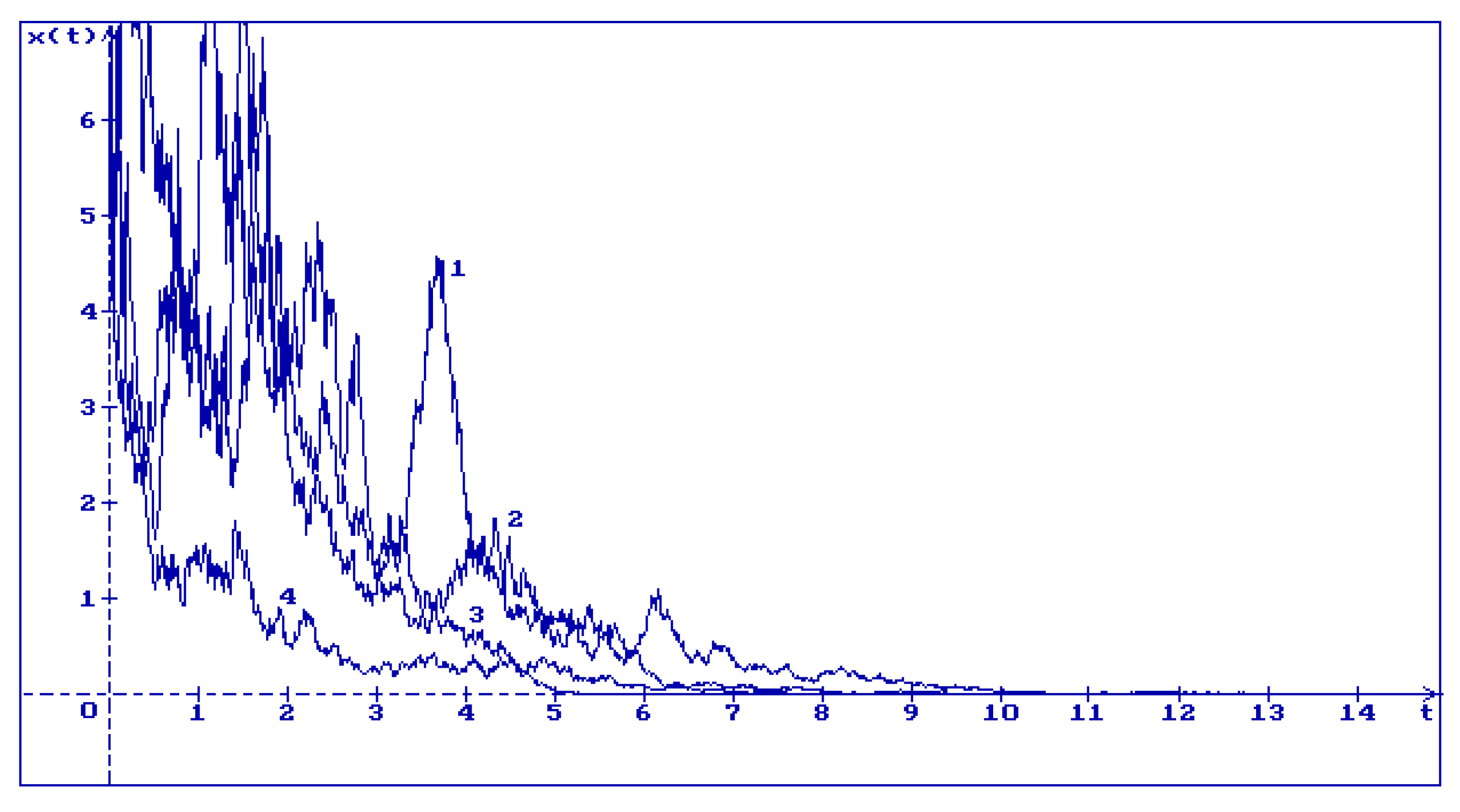
In Figure 1 one can see 4 trajectories of the solution (18) of the Equation (17) for $x\left(0\right)=6$ and different values of $\sigma$:

$$1)\sigma =0.8,2)\sigma =0.9,3)\sigma =1.0,4)\sigma =1.1,$$

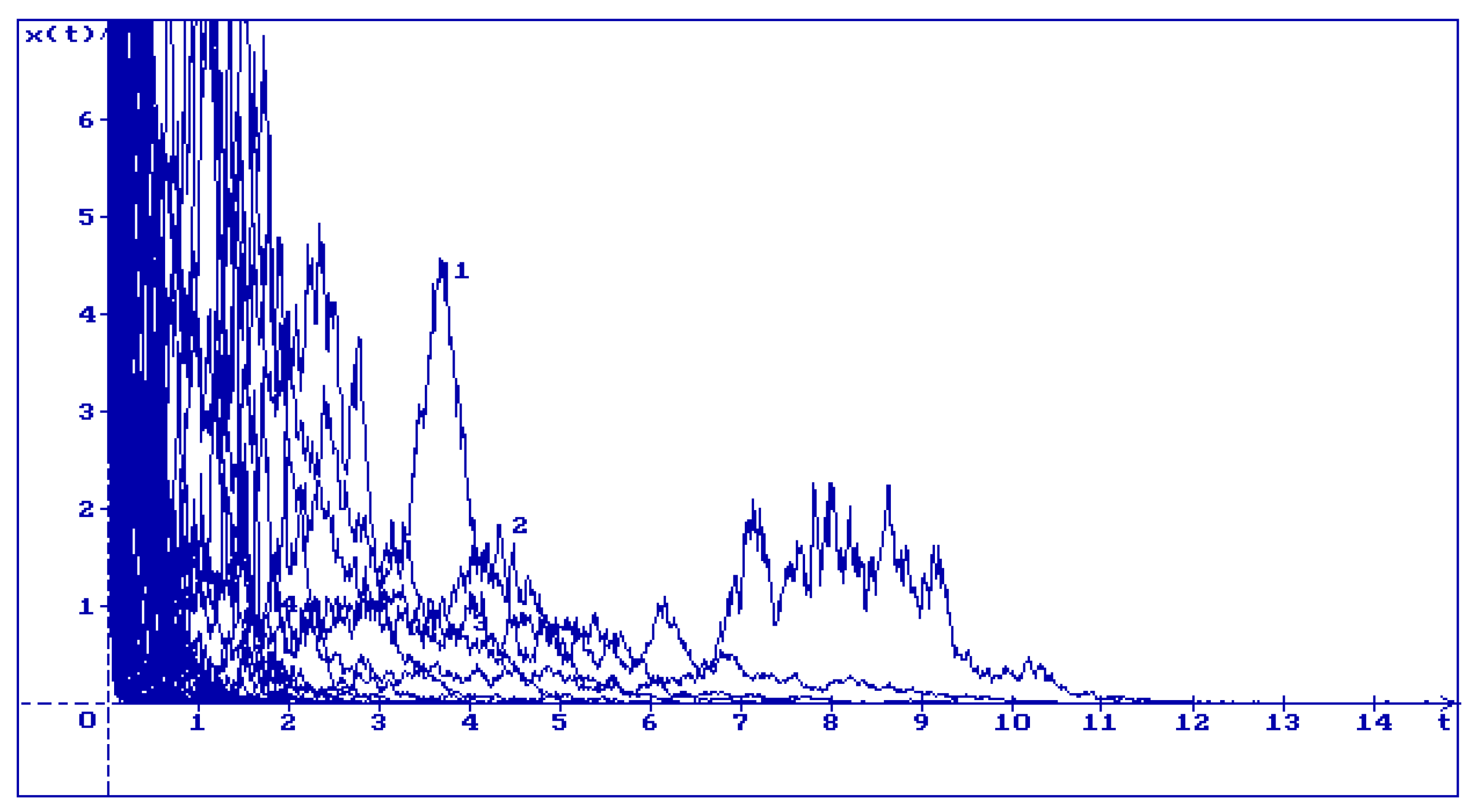
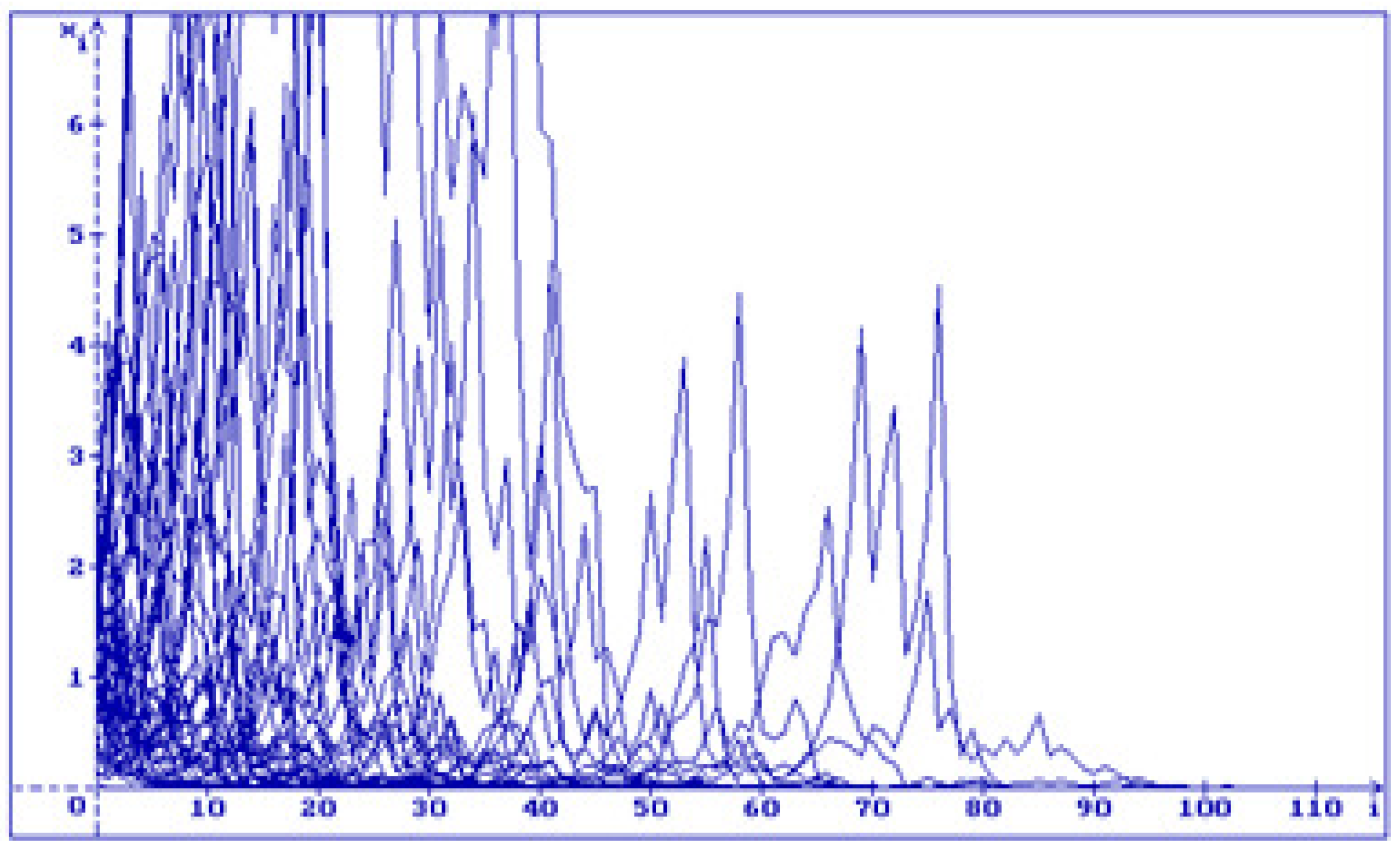
In Figure 2 one can see 50 trajectories of the solution (18) of the Equation (17) for $x\left(0\right)=6$ and different values of $\sigma$:

$$1)\sigma =0.8,2)\sigma =0.9,...,49)\sigma =5.6,50)\sigma =5.7.$$

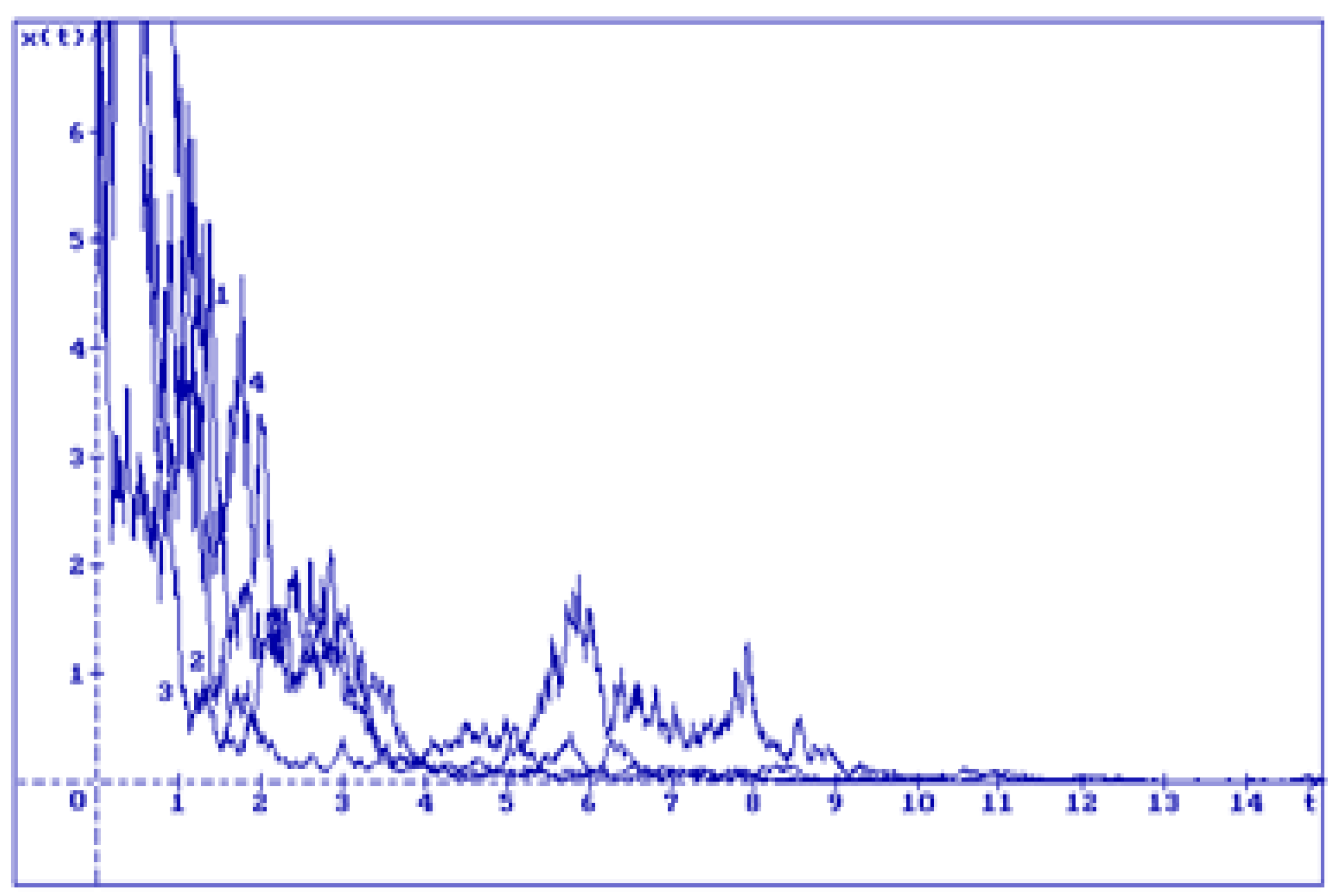
A similar situation is demonstrated by 50 trajectories with negative $\sigma$: in Figure 3 for

$$1)\sigma =-1.2,2)\sigma =-1.3,3)\sigma =-1.4,4)\sigma =-1.5,$$

and in Figure 4 for

$$5)\sigma =-1.6,6)\sigma =-1.7,...,49)\sigma =-6.0,50)\sigma =-6.1.$$

Remark 4.

From Figs.1-4 one can see that if $\left|\sigma \right|$ increases then the trajectories of the solution (18) converge to the zero faster.

Remark 5.

Note that by numerical simulation of the solution (18) for simulation of trajectories of the Wiener process $w\left(t\right)$ the special algorithm was used described in [13].

Unsolved problem. A generalization of Khasminskii’s statement (16) about stabilization by noise for the delay differential Equation (14) is currently the unsolved problem.

3.3. Stochastic Difference Equation

Consider now the scalar linear stochastic difference equation

$$x_{i+1}=a_1{x}_i+{\sigma }_1{x}_i{\xi }_{i+1},i=0,1,...,$$

(19)

where $a_1$ and ${\sigma }_1$ are constants and ${\xi }_i$, $i=1,2,...$, is a sequence of mutually independent random values with the conditions

$$\mathbf{E}{\xi }_i=0,\mathbf{E}{\xi }_i^2=1.$$

(20)

It is known that by the condition

$$a_1^2+{\sigma }_1^2<1$$

(21)

the zero solution of the Equation (19) is asymptotic mean square stable [16].

Let us consider an analogue of the condition (16) for the linear stochastic difference Equation (19) by the condition $a_1>1$. For this aim let us represent the difference analogue of the Equation (15) in the form (19).

Put $t_i=i\Delta$, $i=0,1,...$, $\Delta >0$, $x_i=x\left(t_i\right)$, $w_i=w\left(t_i\right)$. Then the difference analogue of the Equation (15) takes the form

$$x_{i+1}-x_i=a{x}_i\Delta +\sigma x_i(w_{i+1}-w_i).$$

(22)

Note that

$${\xi }_{i+1}={\displaystyle \frac{1}{\sqrt{\Delta }}}(w_{i+1}-w_i)$$

(23)

satisfies the conditions (20). Using (23) rewrite the Equation (22) as follows:

$$x_{i+1}=(1+a\Delta )x_i+\sigma \sqrt{\Delta }{x}_i{\xi }_{i+1},$$

i.e., in the form (19) with the coefficients

$$a_1=1+a\Delta ,{\sigma }_1=\sigma \sqrt{\Delta }.$$

(24)

From (24) we have

$$a={\displaystyle \frac{a_1-1}{\Delta }},\sigma ={\displaystyle \frac{{\sigma }_1}{\sqrt{\Delta }}},$$

and via (16) we obtain

$$0<2{\displaystyle \frac{a_1-1}{\Delta }}<{\displaystyle \frac{{\sigma }_1^2}{\Delta }},$$

i.e., the condition

$$0<2(a_1-1)<{\sigma }_1^2.$$

(25)

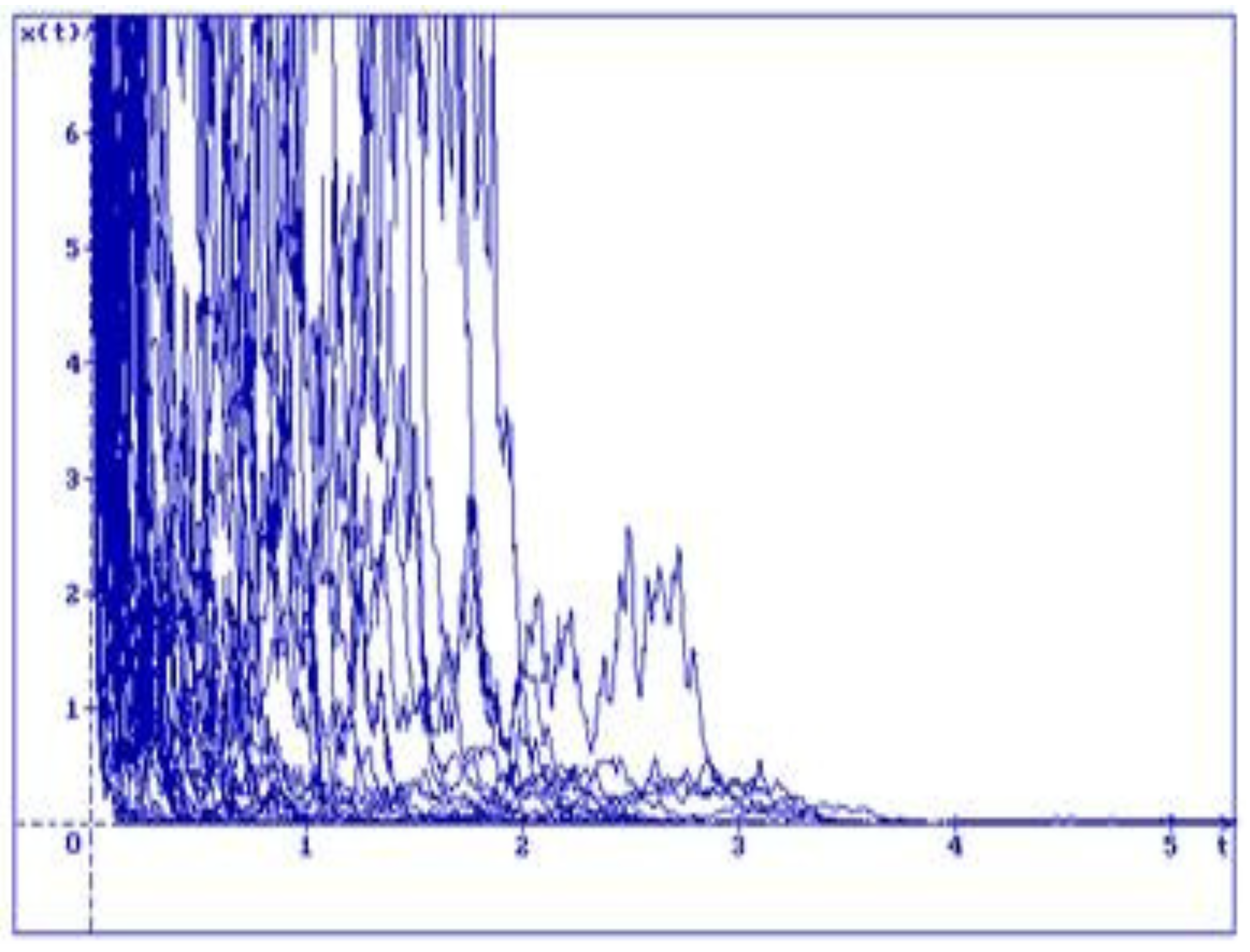
In Figure 5 50 trajectories of the Equation (19) are shown for $a_1=1.05$, ${\sigma }_1=0.5$ and different initial conditions:

$$1)x_0=0.05,2)x_0=0.10,...,49)x_0=2.45,50)x_0=2.50.$$

By that the condition (25) holds, all trajectories converge to the zero.

So, we obtain the following

Hypothesis 1.

If the condition (25) holds then the zero solution of the Equation (19) is stable in probability.

Unsolved problem. Can the above reasoning be considered as a proof of the Hypothesis 1 or not? And why?

4. Conclusions

Some unsolved problems in the field of stability of differential and difference equations under stochastic perturbations are proposed to attention of potential readers. There is a hope that the solution of these problems will contribute to the emergence of new ideas and the further development and improvement of the theory of stability of stochastic systems.