About Stability of One System of Stochastic Difference Equations with Exponential Nonlinearity

1. Introduction

Systems of both difference and differential equations with different forms of exponential nonlinearities are very popular in research and various applications (see, for instance, [1,2,3,4,5,6,7,8,9,10,11,12] and references therein), in particular, the model of Nicholson’s blowflies [1] or Mosquito population equation [8].

Here, similarly to [10], the stability of the positive equilibrium of a system with exponential nonlinearity is investigated under stochastic perturbations via the general method of Lyapunov functionals construction [11,13,14,15] and the method of linear matrix inequalities (LMIs) [16,17,18,19,20,21,22,23,24]. However, unlike, for instance, [3,10], where the exponential nonlinearity in each equation depends on only one variable, here each equation exponentially depends on all variables of the system under consideration. The obtained results are illustrated via examples and figures with the equilibrium and numerical simulation of the solution of the considered system of difference equations. Numerical analysis of the considered LMIs is carried out using MATLAB.

Consider the system of two nonlinear difference equations

$$\begin{gathered} x_1(n+1)=a_1+b_1{x}_1(n-1)+c_1{x}_1(n-1)e^{-p_1{x}_1\left(n\right)-q_1{x}_2\left(n\right)}, \\ {x}_2(n+1)=a_2+b_2{x}_2(n-1)+c_2{x}_2(n-1)e^{-p_2{x}_1\left(n\right)-q_2{x}_2\left(n\right)}, \\ n\in N=\{0,1,...\}, \end{gathered}$$

(1)

with positive parameters, $b_i<1$, and positive initial conditions $x_i\left(j\right)={\varphi }_i\left(j\right)$, $i=1,2$, $j\in N_0=\{-1,0\}$.

1.1. Equilibrium

It is clear that the equilibrium $(x_1,x_2)$ of the system (1) is defined by the system of two algebraic equations

$$\begin{gathered} x_1=a_1+b_1{x}_1+c_1{x}_1{e}^{-p_1{x}_1-q_1{x}_2}, \\ {x}_2=a_2+b_2{x}_2+c_2{x}_2{e}^{-p_2{x}_1-q_2{x}_2}. \end{gathered}$$

(2)

Presenting the first equation (2) in the form

$$e^{q_1{x}_2}\left(1-b_1-{\displaystyle \frac{a_1}{x_1}}\right)=c_1{e}^{-p_1{x}_1}$$

(3)

and calculating the logarithm, we get

$$x_2=f_1\left(x_1\right):={\displaystyle \frac{1}{q_1}}\left(ln{c}_1-p_1{x}_1-ln\left(1-b_1-{\displaystyle \frac{a_1}{x_1}}\right)\right),x_1>{\displaystyle \frac{a_1}{1-b_1}}.$$

(4)

Similarly, from the second equation (2) we have

$$e^{p_2{x}_1}\left(1-b_2-{\displaystyle \frac{a_2}{x_2}}\right)=c_2{e}^{-q_2{x}_2}$$

(5)

and

$$x_1={\displaystyle \frac{1}{p_2}}\left(ln{c}_2-q_2{x}_2-ln\left(1-b_2-{\displaystyle \frac{a_2}{x_2}}\right)\right),x_2>{\displaystyle \frac{a_2}{1-b_2}}.$$

(6)

It is clear that the function $x_2=f_1\left(x_1\right)$ given by (4) is defined and positive if $x_1\in (x_{1min},x_{1max})$, where $x_{1min}={\displaystyle \frac{a_1}{1-b_1}}$ and $x_{1max}$ is a unique root of the equation

$$1-b_1-{\displaystyle \frac{a_1}{x_1}}=c_1{e}^{-p_1{x}_1},$$

(7)

which follows from (3) by $x_2=0$.

Calculating the derivative in (4)

$$x_2^{\prime }={\displaystyle \frac{1}{q_1}}\left(-p_1-{\displaystyle \frac{a_1}{((1-b_1)x_1-a_1)x_1}}\right)<0,$$

it is easy to see that $x_2=f_1\left(x_1\right)$ is strictly decreasing function. Moreover, $\underset{x_1\to x_{1min}}{lim}{f}_1\left(x_1\right)=+\infty$ and $f_1\left(x_{1max}\right)=0$.

Calculating the derivative of the function $x_2=f_2\left(x_1\right)$, defined implicitly by (6), we have

$$p_2=-\left(q_2+{\displaystyle \frac{a_2}{((1-b_2)x_2-a_2)x_2}}\right)x_2^{\prime }>0,$$

i.e., $x_2^{\prime }<0$. It means that $x_2=f_2\left(x_1\right)$ is strictly decreasing function for $x_1\ge 0$. Moreover, $\underset{x_1\to \infty }{lim}{f}_2\left(x_1\right)={\displaystyle \frac{a_2}{1-b_2}}$ and $x_2=f_2\left(0\right)$ is a unique root of the equation

$$1-b_2-{\displaystyle \frac{a_2}{x_2}}=c_2{e}^{-q_2{x}_2},$$

(8)

which follows from (5) by $x_1=0$. It is easy to see that the root $x_2$ of this equation satisfies the condition $x_2>{\displaystyle \frac{a_2}{1-b_2}}$.

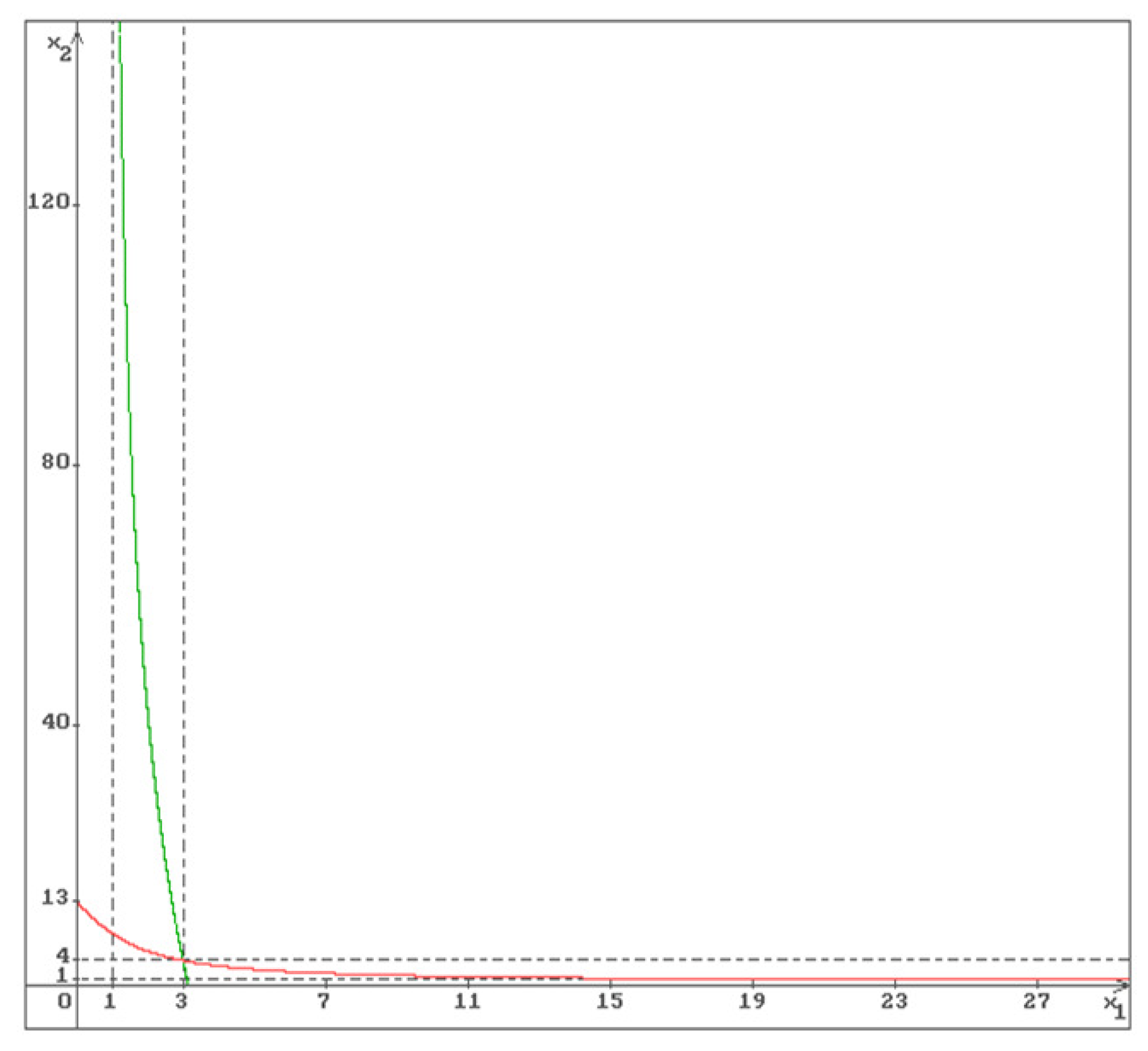
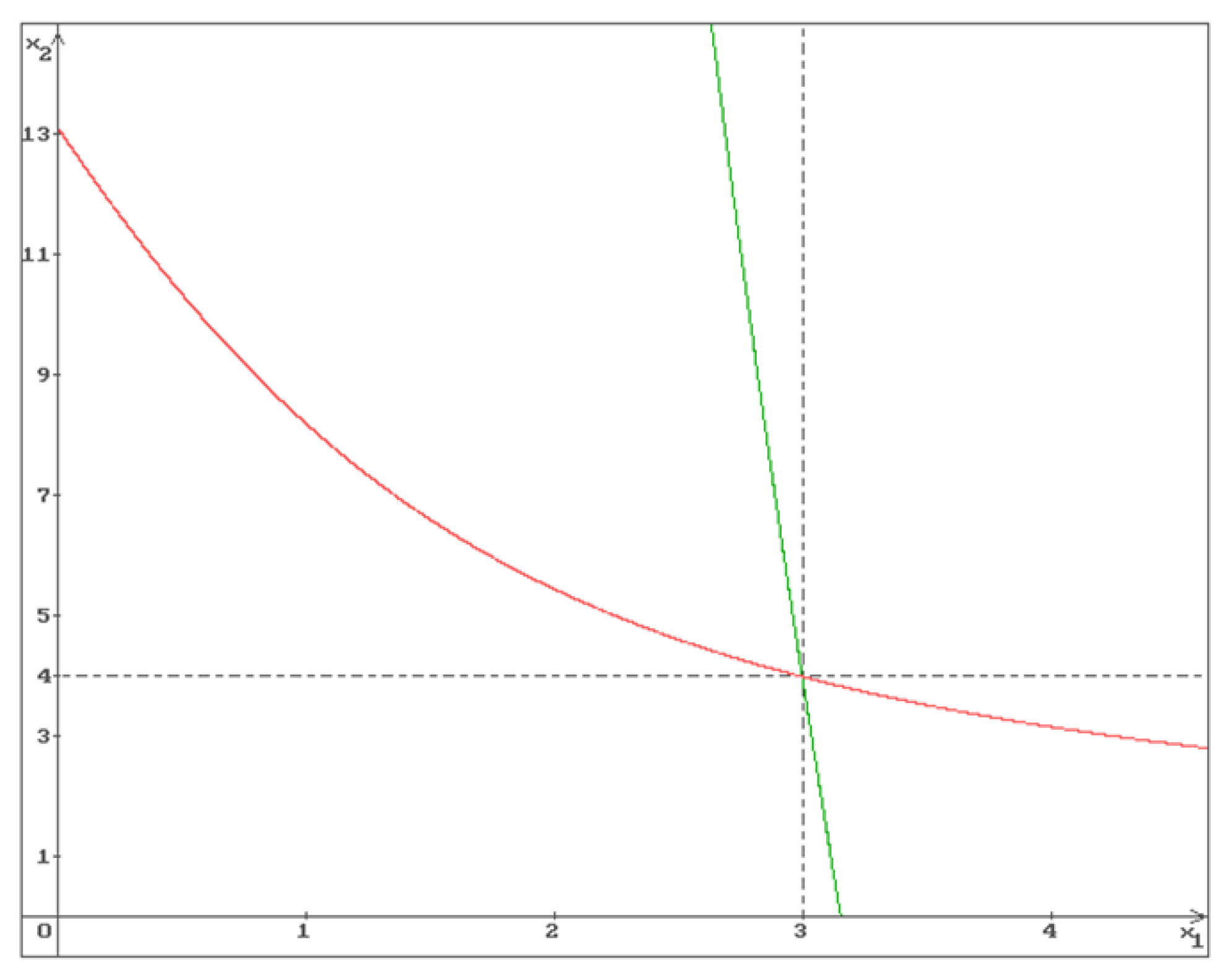
It is clear that two strictly decreasing functions $x_2=f_1\left(x_1\right)$ and $x_2=f_2\left(x_1\right)$ have (see Figure 1 and Figure 2) one common point, which is a solution of the system (2) and is the unique equilibrium $(x_1^{*},x_2^{*})$ of the system (1).

Remark 1. 

The equilibrium $(x_1^{*},x_2^{*})$ of the system (1) satisfies the conditions

$$x_1^{*}\in \left({\displaystyle \frac{a_1}{1-b_1}},x_{1max}\right),x_2^{*}\in \left({\displaystyle \frac{a_2}{1-b_2}},x_{2max}\right),$$

(9)

where $x_{1max}$ and $x_{2max}$ are roots of the equations (7) and (8) respectively.

Example 1. 

Consider the system (1) with

$$a_1=0.3,a_2=0.4,b_1=0.7,b_2=0.6,c_1=0.2810,c_2=0.4215,p_1=p_2=0.1,q_1=q_2=0.01.$$

Then the solution of the system (2) is $(x_1^{*},x_2^{*})=(3,4)$, from (9) and (7), (8) it follows that $x_{1min}=1$, $x_{2min}=1$, $x_{1max}=3.156$, $x_{2max}=13.147$. In Figure 1 and Figure 2 the graphs of the functions $x_2=f_1\left(x_1\right)$ (green), $x_2=f_2\left(x_1\right)$ (red) and the equilibrium $(x_1^{*},x_2^{*})$ are shown.

In Figure 1 also the asymptotes $x_1={\displaystyle \frac{a_1}{1-b_1}}=1$ and $x_2={\displaystyle \frac{a_2}{1-b_2}}=1$ of the functions $f_1\left(x_1\right)$ and $f_2\left(x_1\right)$ respectively are shown.

2. Stochastic Perturbations and the System Transformation

Let $\{\Omega ,\mathfrak{F},\mathbf{P}\}$ be a basic probability space, ${\mathfrak{F}}_n\in \mathfrak{F}$, $n\in N$, be a nondecreasing family of sub-$\sigma$-algebras of $\mathfrak{F}$, i.e., ${\mathfrak{F}}_{n_1}\subset {\mathfrak{F}}_{n_2}$ for $n_1<n_2$, $\mathbf{E}$ be the mathematical expectation with respect to the measure $\mathbf{P}$, ${\xi }_1\left(n\right)$ and ${\xi }_2\left(n\right)$, $n\in N$, be two mutually independent sequences with ${\mathfrak{F}}_n$-adapted mutually independent random values such that [11]

$$\mathbf{E}{\xi }_i\left(n\right)=0,\mathbf{E}{\xi }_i^2\left(n\right)=1,\mathbf{E}{\xi }_i\left(n\right){\xi }_j\left(m\right)=0\mathrm{if}i\ne j\mathrm{or}n\ne m,i,j=1,2.$$

(10)

Let us assume that the system (1) is exposed to stochastic perturbations that are directly proportional to the deviation of the system state $(x_1\left(n\right),x_2\left(n\right))$ from the equilibrium $(x_1^{*},x_2^{*})$. Then the system (1) takes the form

$$\begin{gathered} x_1(n+1)=a_1+b_1{x}_1(n-1)+c_1{x}_1(n-1)e^{-p_1{x}_1\left(n\right)-q_1{x}_2\left(n\right)}+{\sigma }_1(x_1\left(n\right)-x_1^{*}){\xi }_1(n+1), \\ {x}_2(n+1)=a_2+b_2{x}_2(n-1)+c_2{x}_2(n-1)e^{-p_2{x}_1\left(n\right)-q_2{x}_2\left(n\right)}+{\sigma }_2(x_2\left(n\right)-x_2^{*}){\xi }_2(n+1). \end{gathered}$$

(11)

Remark 2. 

Note that the such type of stochastic perturbations was firstly proposed in [25] for a system of Ito’s stochastic delay differential equations and was later used in many other works for both differential and difference equations (see, for instance, [11,15] and references therein). With this type of stochastic perturbations, the equilibrium of the original deterministic system remains also a solution of the stochastically perturbed system.

Presenting the solution of the system (11) in the form $(x_1\left(n\right),x_2\left(n\right))=(y_1\left(n\right)+x_1^{*},y_2\left(n\right)+x_2^{*})$, we get

$$\begin{array}{lll}{y}_1(n+1)+x_1^{*}& =& a_1+b_1(y_1(n-1)+x_1^{*})\\ & +& c_1(y_1(n-1)+x_1^{*})e^{-p_1{y}_1\left(n\right)-q_1{y}_2\left(n\right)}{e}^{-p_1{x}_1^{*}-q_1{x}_2^{*}}+{\sigma }_1{y}_1\left(n\right){\xi }_1(n+1),\\ y_2(n+1)+x_2^{*}& =& a_2+b_2(y_2(n-1)+x_2^{*})\\ & +& c_2(y_2(n-1)+x_2^{*})e^{-p_2{y}_1\left(n\right)-q_2{y}_2\left(n\right)}{e}^{-p_2{x}_1^{*}-q_2{x}_2^{*}}+{\sigma }_2{y}_2\left(n\right){\xi }_2(n+1).\end{array}$$

(12)

Using (2) with $(x_1,x_2)=(x_1^{*},x_2^{*})$, from the first equation (12) we have

$$\begin{array}{lll}{y}_1(n+1)& =& a_1+b_1{x}_1^{*}-x_1^{*}+b_1{y}_1(n-1)\\ & & +c_1(y_1(n-1)+x_1^{*})e^{-p_1{y}_1\left(n\right)-q_1{y}_2\left(n\right)}{e}^{-p_1{x}_1^{*}-q_1{x}_2^{*}}+{\sigma }_1{y}_1\left(n\right){\xi }_1(n+1)\\ & =& b_1{y}_1(n-1)-c_1{x}_1^{*}{e}^{-p_1{x}_1^{*}-q_1{x}_2^{*}}\\ & & +c_1(y_1(n-1)+x_1^{*})e^{-p_1{y}_1\left(n\right)-q_1{y}_2\left(n\right)}{e}^{-p_1{x}_1^{*}-q_1{x}_2^{*}}+{\sigma }_1{y}_1\left(n\right){\xi }_1(n+1)\\ & =& \left(b_1+c_1{e}^{-p_1{x}_1^{*}-q_1{x}_2^{*}}{e}^{-p_1{y}_1\left(n\right)-q_1{y}_2\left(n\right)}\right)y_1(n-1)\\ & & -c_1{x}_1^{*}{e}^{-p_1{x}_1^{*}-q_1{x}_2^{*}}\left(1-e^{-p_1{y}_1\left(n\right)-q_1{y}_2\left(n\right)}\right)+{\sigma }_1{y}_1\left(n\right){\xi }_1(n+1).\end{array}$$

Similarly, for the second equation (12) we get

$$\begin{array}{lll}{y}_2(n+1)& =& a_2+b_2{x}_2^{*}-x_2^{*}+b_2{y}_2(n-1)\\ & & +c_2(y_2(n-1)+x_2^{*})e^{-p_2{y}_1\left(n\right)-q_2{y}_2\left(n\right)}{e}^{-p_2{x}_1^{*}-q_2{x}_2^{*}}+{\sigma }_2{y}_2\left(n\right){\xi }_2(n+1)\\ & =& b_2{y}_2(n-1)-c_2{y}^{*}{e}^{-p_2{x}_1^{*}-q_2{x}_2^{*}}\\ & & +c_2(y_2(n-1)+x_2^{*})e^{-p_2{y}_1\left(n\right)-q_2{y}_2\left(n\right)}{e}^{-p_2{x}_1^{*}-q_2{x}_2^{*}}+{\sigma }_2{y}_2\left(n\right){\xi }_2(n+1)\\ & =& \left(b_2+c_2{e}^{-p_2{x}_1^{*}-q_2{x}_2^{*}}{e}^{-p_2{y}_1\left(n\right)-q_2{y}_2\left(n\right)}\right)y_2(n-1)\\ & & -c_2{x}_2^{*}{e}^{-p_2{x}_1^{*}-q_2{x}_2^{*}}\left(1-e^{-p_2{y}_1\left(n\right)-q_2{y}_2\left(n\right)}\right)+{\sigma }_2{y}_2\left(n\right){\xi }_2(n+1).\end{array}$$

As a result we obtain the nonlinear system with the zero solution:

$$\begin{array}{lll}{y}_1(n+1)& =& \left(b_1+c_1{e}^{-p_1{x}_1^{*}-q_1{x}_2^{*}}{e}^{-p_1{y}_1\left(n\right)-q_1{y}_2\left(n\right)}\right)y_1(n-1)\\ & & -c_1{x}_1^{*}{e}^{-p_1{x}_1^{*}-q_1{x}_2^{*}}\left(1-e^{-p_1{y}_1\left(n\right)-q_1{y}_2\left(n\right)}\right)+{\sigma }_1{y}_1\left(n\right){\xi }_1(n+1),\\ y_2(n+1)& =& \left(b_2+c_2{e}^{-p_2{x}_1^{*}-q_2{x}_2^{*}}{e}^{-p_2{y}_1\left(n\right)-q_2{y}_2\left(n\right)}\right)y_2(n-1)\\ & & -c_2{x}_2^{*}{e}^{-p_2{x}_1^{*}-q_2{x}_2^{*}}\left(1-e^{-p_2{y}_1\left(n\right)-q_2{y}_2\left(n\right)}\right)+{\sigma }_2{y}_2\left(n\right){\xi }_2(n+1),\end{array}$$

(13)

Remark 3. 

Note that stability of the zero solution of the system (13) is equivalent to stability of the equilibrium $(x_1^{*},x_2^{*})$ of the system (11).

Using (2) and the linear approximation $e^{-x}=1-x+o\left(x\right)$, where $\underset{x\to 0}{lim}{\displaystyle \frac{o\left(x\right)}{x}}=0$, we obtain the linear part of the system (13)

$$\begin{gathered} z_1(n+1)=\left(1-{\displaystyle \frac{a_1}{x_1^{*}}}\right)z_1(n-1)-((1-b_1)x_1^{*}-a_1)(p_1{z}_1\left(n\right)+q_1{z}_2\left(n\right))+{\sigma }_1{z}_1\left(n\right){\xi }_1(n+1), \\ {z}_2(n+1)=\left(1-{\displaystyle \frac{a_2}{x_2^{*}}}\right)z_2(n-1)-((1-b_2)x_2^{*}-a_2)(p_2{z}_1\left(n\right)+q_2{z}_2\left(n\right))+{\sigma }_2{z}_2\left(n\right){\xi }_2(n+1). \end{gathered}$$

(14)

Representing the linear system (14) in the matrix form, we get

$$z(n+1)=-Az\left(n\right)+Bz(n-1)+\sum _{i=1}^2{C}_{i}z\left(n\right){\xi }_i(n+1),$$

(15)

where

$$\begin{gathered} z\left(n\right)=\left[\begin{array}{c}{z}_1\left(n\right)\\ z_2\left(n\right)\end{array}\right],A=\left[\begin{array}{cc}{\alpha }_1{p}_1& {\alpha }_1{q}_1\\ {\alpha }_2{p}_2& {\alpha }_2{q}_2\end{array}\right],B=\left[\begin{array}{cc}{\beta }_1& 0\\ 0& {\beta }_2\end{array}\right],C_1=\left[\begin{array}{cc}{\sigma }_1& 0\\ 0& 0\end{array}\right],C_2=\left[\begin{array}{cc}0& 0\\ 0& {\sigma }_2\end{array}\right],{\alpha }_i=(1-b_i)x_i^{*}-a_i, \\ {\beta }_i=1-{\displaystyle \frac{a_i}{x_i^{*}}},i-1,2. \end{gathered}$$

(16)

3. Stability

3.1. Some Necessary Definitions and Statements

Let ′ be the transposition sign. Put now

$$y\left(n\right)={(y_1\left(n\right),y_2\left(n\right))}^{\prime },z\left(n\right)={(z_1\left(n\right),z_2\left(n\right))}^{\prime },n\in N,\varphi \left(j\right)={({\varphi }_1\left(j\right),{\varphi }_2\left(j\right))}^{\prime },j\in N_0.$$

Definition 1.([11]). The zero solution of the system (13) is called stable in probability if for any $\epsilon >0$ and ${\epsilon }_1\in (0,1)$ there exists a $\delta >0$ such that the solution $y\left(n\right)=y(n,\varphi )$ of the system (13) satisfies the inequality $\mathbf{P}\{\underset{n\in N}{sup}\left|y\left(n\right)\right|>\epsilon \}<{\epsilon }_1$ for any initial function $\varphi \left(j\right)$ such that $\mathbf{P}\{\parallel \varphi {\parallel }_0<\delta \}=1$, where ${\parallel \varphi \parallel }_0=\underset{j\in N_0}{max}\left|\varphi \left(j\right)\right|$.

Definition 2.([11]). The zero solution of the system (14) is called mean square stable if for each $\epsilon >0$ there exists a $\delta >0$ such that ${\mathbf{E}\left|z\left(n\right)\right|}^2<\epsilon$, $n\in N$, for any initial function $\varphi \left(j\right)$ such that ${\parallel \varphi \parallel }^2=\underset{j\in N_0}{max}\mathbf{E}{\left|\varphi \left(j\right)\right|}^2<\delta$; asymptotically mean square stable if it is mean square stable and for each initial function $\varphi \left(j\right)$ such that ${\parallel \varphi \parallel }^2<\infty$ the solution $z\left(n\right)$ of the system (14) satisfies the condition $\underset{n\to \infty }{lim}\mathbf{E}{\left|z\left(n\right)\right|}^2=0$.

Let ${\mathbf{E}}_n=\mathbf{E}\{./{\mathfrak{F}}_n\}$ be the conditional expectation with respect to the $\sigma$-algebra ${\mathfrak{F}}_n$, $U_{\epsilon }=\{y:|y|\le \epsilon \}$, $\epsilon >0$, and $\Delta V\left(n\right)=V(n+1)-V\left(n\right)$.

Theorem 1.([11]). Let for the system (13) there exists a functional $V\left(n\right)=V(n,y(-1),...,y(n\left)\right)$ satisfying the conditions

$$\begin{array}{l}V(n,y(-1),...,y\left(n\right))\ge c_0{\left|y\left(n\right)\right|}^2,\\ V(0,\phi (-1),\phi \left(0\right))\le c_1{\parallel \phi \parallel }_0^2,\\ {\mathbf{E}}_n\Delta V(n,y(-1),...,y\left(n\right))\le 0,y\left(j\right)\in U_{\epsilon },-1\le j\le n,n\in N,\end{array}$$

(17)

where $\epsilon >0$, $c_0>0$, $c_1>0$. Then the zero solution of the system (13) is stable in probability.

Theorem 2.([11]). Let for the system (14) there exists a nonnegative functional $V\left(n\right)=V(n,z(-1),...,z(n\left)\right)$ satisfying the conditions

$$\begin{array}{l}\mathbf{E}V(0,\varphi (-1),\varphi \left(0\right))\le c_1{\parallel \varphi \parallel }^2,\\ \mathbf{E}\Delta V\left(n\right)\le -c_2\mathbf{E}{\left|z\left(n\right)\right|}^2,n\in N,\end{array}$$

(18)

where $c_1>0$, $c_2>0$. Then the zero solution of the system (14) is asymptotically mean square stable.

Remark 4. 

Note that the system (13) has an order of nonlinearity higher than one. It is known [11] that in this case sufficient conditions for asymptotic mean square stability of the zero solution of the linear system (14) are also sufficient conditions for stability in probability of the zero solution of the nonlinear system (13).

3.2. Stability conditions

Theorem 3. 

Let there exist positive definite $2\times 2$-matrices P and R such that the following linear matrix inequality (LMI)

$$\left[\begin{array}{cc}{A}^{\prime }PA+S_0+R-P& A^{\prime }PB\\ B^{\prime }PA& B^{\prime }PB-R\end{array}\right]<0$$

(19)

holds, where

$$S_0=\sum _{i=1}^2{C}_i^{\prime }P{C}_i=\left[\begin{array}{cc}{\sigma }_1^2{p}_{11}& 0\\ 0& {\sigma }_2^2{p}_{22}\end{array}\right],$$

(20)

the matrices $C_1$, $C_2$ are defined in (16) and $p_{11},p_{22}$ are diagonal elements of the matrix P. Then the equilibrium $(x_1^{*},x_2^{*})$ of the system (11) is stable in probability.

Proof. 

Following the general method of Lyapunov functionals construction [11,13,14,15], consider the functional $V\left(n\right)$ in the form $V\left(n\right)=V_1\left(n\right)+V_2\left(n\right)$, where $V_1\left(n\right)=z^{\prime }\left(n\right)Pz\left(n\right)$, $P>0$, $z\left(n\right)$ is defined in (16) and the additional functional $V_2\left(n\right)$ will be chosen below. For the functional $V_1\left(n\right)$ via (15) we have

$$\begin{array}{ll}\mathbf{E}\Delta V_1\left(n\right)& =\mathbf{E}[V_1(n+1)-V_1\left(n\right)]\\ & =\mathbf{E}[z^{\prime }(n+1)Pz(n+1)-z^{\prime }\left(n\right)Pz\left(n\right)]\\ & =\mathbf{E}[\left(-z^{\prime }\left(n\right)A^{\prime }+z^{\prime }(n-1)B^{\prime }+\sum _{i=1}^2{z}^{\prime }\left(n\right)C_i^{\prime }{\xi }_i(n+1)\right)\\ & *P\left(-Az\left(n\right)+Bz(n-1)+\sum _{i=1}^2{C}_{i}z\left(n\right){\xi }_i(n+1)\right)-z^{\prime }\left(n\right)Pz\left(n\right)].\end{array}$$

From here via (10) and (20) it follows that

$$\begin{array}{ll}\mathbf{E}\Delta V_1\left(n\right)& =\mathbf{E}[z^{\prime }\left(n\right)(A^{\prime }PA+S_0-P)z\left(n\right)+z^{\prime }\left(n\right)A^{\prime }PBz(n-1)\\ & +z^{\prime }(n-1)B^{\prime }PAz\left(n\right)+z^{\prime }(n-1)B^{\prime }PBz(n-1)]\end{array}$$

or in the matrix form

$$\mathbf{E}\Delta V_1\left(n\right)=\mathbf{E}{\left[\begin{array}{c}z\left(n\right)\\ z(n-1)\end{array}\right]}^{\prime }\left[\begin{array}{cc}{A}^{\prime }PA+S_0-P& A^{\prime }PB\\ B^{\prime }PA& B^{\prime }PB\end{array}\right]\left[\begin{array}{c}z\left(n\right)\\ z(n-1)\end{array}\right].$$

(21)

Using the additional functional $V_2\left(n\right)=z^{\prime }(n-1)Rz(n-1)$, $R>0$, with $\Delta V_2\left(n\right)=z^{\prime }\left(n\right)Rz\left(n\right)-z^{\prime }(n-1)Rz(n-1)$, for the functional $V\left(n\right)=V_1\left(n\right)+V_2\left(n\right)$ from (21) we obtain

$$\mathbf{E}\Delta V\left(n\right)=\mathbf{E}{\left[\begin{array}{c}z\left(n\right)\\ z(n-1)\end{array}\right]}^{\prime }\left[\begin{array}{cc}{A}^{\prime }PA+S_0+R-P& A^{\prime }PB\\ B^{\prime }PA& B^{\prime }PB-R\end{array}\right]\left[\begin{array}{c}z\left(n\right)\\ z(n-1)\end{array}\right].$$

(22)

From (22) and the LMI (19) for some $c>0$ we have $\mathbf{E}\Delta V\left(n\right)\le -{c\mathbf{E}\left|z\left(n\right)\right|}^2$, i.e., the constructed functional $V\left(n\right)$ satisfies the conditions of Theorem 2. Therefore, the zero solution of the linear equation (15) is asymptotically mean square stable. Via Remarks 4 and 3 it means that the equilibrium $(x_1^{*},x_2^{*})$ of the system (11) is stable in probability. The proof is completed. □

Remark 5. 

Note that instead of the LMI (19) for definition of stability some other LMIs also can be used. Using, for instance, the additional functional $V_2\left(n\right)$ in the form $V_2\left(n\right)=z^{\prime }(n-1)(R+B^{\prime }PB)z(n-1)$ instead of the LMI (19) we obtain the LMI

$$\left[\begin{array}{cc}{A}^{\prime }PA+B^{\prime }PB+S_0+R-P& A^{\prime }PB\\ B^{\prime }PA& -R\end{array}\right]<0.$$

(23)

If at least one from the LMIs (19) and (23) holds then the equilibrium $(x_1^{*},x_2^{*})$ of the system (11) is stable in probability. Other ways to get appropriate LMIs are shown also in [10].

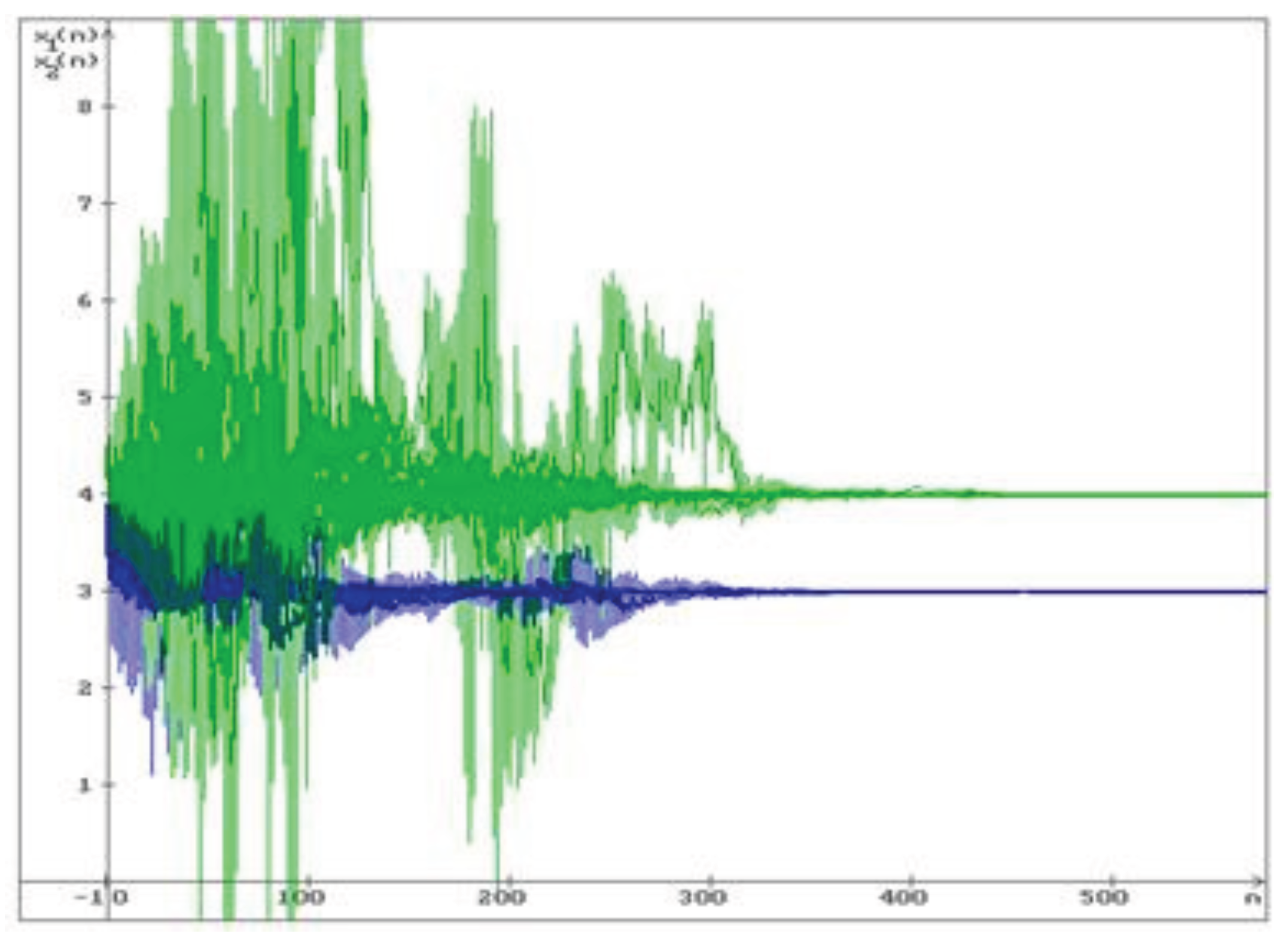
Example 2. 

Consider the system (11) with the values of the parameters given in Example 1. Via MATLAB the maximal values of ${\sigma }_1=0.232$ and ${\sigma }_2=0.384$ were obtained, by which the LMIs (19) and (23) hold respectively for the positive definite matrices

$$P=\left[\begin{array}{cc}10240.838& 914.037\\ 914.037& 545.487\end{array}\right],R=\left[\begin{array}{cc}8820.374& 827.335\\ 827.335& 456.341\end{array}\right],$$

and

$$P=\left[\begin{array}{cc}7031.372& 627.491\\ 627.491& 374.625\end{array}\right],R=\left[\begin{array}{cc}361.556& 59.703\\ 59.703& 9.976\end{array}\right].$$

In Figure 3 50 trajectories of the solution of the system (11) are shown. All trajectories converge to the stable equilibrium $(x_1^{*},x_2^{*})=(3,4)$.

4. Conclusions

Stability of a system of nonlinear difference equations under stochastic perturbations is investigated. The nonli-nearity of exponential form in each equation depends on all variables of the system under consideration. The conditions of stability in probability for positive equilibrium of the considered system, obtained via the general method of Lyapunov functionals construction, are formulated in terms of linear matrix inequalities (LMIs) and are illustrated by numerical examples and figures. The method of stability investigation, used in the paper, can be applied to many other types of systems with high-order nonlinearity, for both difference and differential equations in various applications.