About Asymptotic Properties of Bilinear Difference Equations Under Stochastic Perturbations

1. Introduction

During the last two decades, rational difference equations, in particular, rational bilinear difference equations have become very popular in research (see, for instance, [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] and references therein). Various interesting results related to the solvability and stability of equations of this type are obtained. In particular, stability of the bilinear difference equation

$$\begin{gathered} x_{n+1}=a{x}_n+{\displaystyle \frac{b{x}_n{x}_{n-1}}{c{x}_n+d{x}_{n-1}}},n=0,1,..., \\ {x}_n={\varphi }_n,n=-1,0, \end{gathered}$$

with positive parameters $a,b,c,d$ and initial values ${\varphi }_{-1}$, ${\varphi }_0$ is studied in [7].

It is clear that, without loss of generality, one of the parameters $b,c,d$ in this equation can be equated to 1. Let $d=1$. So, we will consider the bilinear difference equation

$$\begin{gathered} x_{n+1}=a{x}_n+{\displaystyle \frac{b{x}_n{x}_{n-1}}{c{x}_n+x_{n-1}}},n=0,1,..., \\ {x}_n={\varphi }_n,n=-1,0, \end{gathered}$$

(1)

with positive $a,b,c$ and ${\varphi }_{-1}$, ${\varphi }_0$.

The following two statements, obtained in [7], for the Equation (1) take the form:

Statement 1 If $(1-a)(c+1)\ne b$ then the unique equilibrium of the Equation (1) is $x^{*}=0$.

Statement 2 If $(1-a)(c+1)>b$ then the zero solution of the Equation (1) is locally asymptotically stable.

Below, the bilinear difference Equation (1) is studied under stochastic perturbations that are directly proportional to the deviation of the current value of the solution of the stochastic bilinear difference equation under consideration from the zero or nonzero equilibrium of the Equation (1). To the best of author’ knowledge stochastic bilinear difference equations have not yet been considered.

Based on the obtained results, a hypothesis is proposed and discussed about the possibility of "stabilization by noise" for stochastic difference equations. The well-known effect of "stabilization by noise" for stochastic differential equations still has no analogue for stochastic difference equations. Here, this hypothesis is tested by numerical simulation and confirmed, but the formal proof of this hypothesis is still an unsolved problem.

1.1. Equilibria of the Equation (1)

Putting $x_n=x^{*}$ for $n\ge -1$, we obtain that the equilibrium $x^{*}$ of the Equation (1) is defined by the equation

$$x^{*}\left(1-a-{\displaystyle \frac{b}{c+1}}\right)=0.$$

(2)

It is clear that if

$$a+{\displaystyle \frac{b}{c+1}}\ne 1$$

(3)

then $x^{*}=0$ only can be the equilibrium of the Equation (1) (that coincides with Statement 1).

From the other hand, by the assumption

$$a+{\displaystyle \frac{b}{c+1}}=1$$

(4)

each $x^{*}\in \mathbf{R}$ is a solution of the Equation (2) and $x_n=x^{*}$, $n\ge -1$, is a solution of the Equation (1).

Remark 1. 

Note that by the condition (4) from the equality $x_m=x_{m-1}=x^{*}$ for some $m\ge 0$ from (1) it follows that $x_n=x^{*}$ also for all $n>m$.

Below stability of the zero and nonzero equilibria of the Equation (1) is investigated under stochastic perturbations.

2. Some Transformations of the Initial Equation

Let $n\in Z\bigcup Z_0$ be a discrete time, $Z=\{0,1,...\}$, $Z_0=\{-1,0\}$. Let $\{\mathrm{\Omega },\mathfrak{F},\mathbf{P}\}$ be a basic probability space, ${\mathfrak{F}}_n\in \mathfrak{F}$, $n\in Z$, be a nondecreasing family of $\sigma$-algebras, $\mathbf{E}$ be the expectation, ${\left({\xi }_n\right)}_{n\in Z}$ be a sequence of ${\mathfrak{F}}_n$-adapted mutually independent identically distributed random variables such that $\mathbf{E}{\xi }_n=0$, $\mathbf{E}{\xi }_n^2=1$, $n\in Z$ [18].

Note that via Remark 1 by the condition (4) and $x_0=x_{-1}$ the Equation (1) has the equilibrium $x^{*}=x_0$. Let us assume that the Equation (1) is exposed to stochastic perturbations that are directly proportional to the deviation of the solution $x_n$ from the equilibrium $x^{*}$, i.e., the Equation (1) takes the form of the stochastic difference equation [18]

$$x_{n+1}=a{x}_n+{\displaystyle \frac{b{x}_n{x}_{n-1}}{c{x}_n+x_{n-1}}}+\sigma (x_n-x^{*}){\xi }_{n+1},n=0,1,...,$$

(5)

where $\sigma$ is a constant. By that the solution $x_n=x^{*}$ of the Equation (1) is also the solution of the Equation (5).

Remark 2. 

Note that stochastic perturbations of the type (5) were first used for a system of stochastic delay differential equations in [19] and later in many other different research both for differential and for difference equations (see, for instance, [18,20] and references therein).

Putting in (5) $x_n=y_n+x^{*}$, we obtain

$$y_{n+1}=a(y_n+x^{*})-x^{*}+{\displaystyle \frac{b(y_n+x^{*})(y_{n-1}+x^{*})}{c(y_n+x^{*})+y_{n-1}+x^{*}}}+\sigma y_n{\xi }_{n+1}$$

or

$$y_{n+1}=a{y}_n+(a-1)x^{*}+{\displaystyle \frac{b[{\left(x^{*}\right)}^2+(y_n+y_{n-1})x^{*}+y_n{y}_{n-1}]}{(c+1)x^{*}+c{y}_n+y_{n-1}}}+\sigma y_n{\xi }_{n+1}.$$

(6)

Lemma 1. 

Let the condition (4) holds and $x^{*}\ne 0$. Then the linear part of the Equation (6) has the form

$$z_{n+1}=A{z}_n+B{z}_{n-1}+\sigma z_n{\xi }_{n+1},n=0,1,...,z_n={\varphi }_n,n=-1,0,$$

(7)

where

$$A=a+{\displaystyle \frac{b}{{(c+1)}^2}},B={\displaystyle \frac{bc}{{(c+1)}^2}},A+B=1.$$

(8)

Proof. 

Using the equality

$${\displaystyle \frac{1}{p+y}}={\displaystyle \frac{1}{p}}-{\displaystyle \frac{y}{p^2}}+o\left(y\right),\mathrm{where}p\ne 0\mathrm{and}\underset{y\to 0}{lim}{\displaystyle \frac{o\left(y\right)}{y}}=0,$$

we have

$$\begin{gathered} {\displaystyle \frac{b[{\left(x^{*}\right)}^2+(y_n+y_{n-1})x^{*}+y_n{y}_{n-1}]}{(c+1)x^{*}+c{y}_n+y_{n-1}}} \\ =b[{\left(x^{*}\right)}^2+(y_n+y_{n-1})x^{*}+y_n{y}_{n-1}]\left({\displaystyle \frac{1}{(c+1)x^{*}}}-{\displaystyle \frac{c{y}_n+y_{n-1}}{{(c+1)}^2{\left(x^{*}\right)}^2}}+o\left(y\right)\right) \\ ={\displaystyle \frac{b{x}^{*}}{c+1}}-{\displaystyle \frac{b}{{(c+1)}^2}}(c{y}_n+y_{n-1})+{\displaystyle \frac{b}{c+1}}(y_n+y_{n-1})+o\left(y\right). \end{gathered}$$

(9)

Substituting (9) into (6), neglecting the nonlinear terms and using (2), we obtain

$$\begin{gathered} z_{n+1}=a{z}_n+(a-1)x^{*}+{\displaystyle \frac{b{x}^{*}}{c+1}}-{\displaystyle \frac{b}{{(c+1)}^2}}(c{z}_n+z_{n-1})+{\displaystyle \frac{b}{c+1}}(z_n+z_{n-1})+\sigma z_n{\xi }_{n+1} \\ =\left(a-1+{\displaystyle \frac{b}{c+1}}\right)x^{*}+\left(a+{\displaystyle \frac{b}{c+1}}-{\displaystyle \frac{bc}{{(c+1)}^2}}\right)z_n+\left({\displaystyle \frac{b}{c+1}}-{\displaystyle \frac{b}{{(c+1)}^2}}\right)z_{n-1}+\sigma z_n{\xi }_{n+1} \\ =\left(a+{\displaystyle \frac{b}{{(c+1)}^2}}\right)z_n+{\displaystyle \frac{bc}{{(c+1)}^2}}{z}_{n-1}+\sigma z_n{\xi }_{n+1}, \end{gathered}$$

that via (8) gives (7). The proof is completed. □

3. Stability

Consider the scalar stochastic difference equation [18]

$$\begin{array}{cc}{x}_{n+1}\hfill & =a{x}_n+b{x}_{n-1}+\sigma x_n{\xi }_{n+1},i\in Z,\\ x_n\hfill & ={\varphi }_n,n\in Z_0,\end{array}$$

(10)

where a, b, $\sigma$ are constants and ${\xi }_{n+1}$ is described above.

Definition 1. 

The zero solution of the Equation (10) is called stable in probability if for any $\epsilon >0$ and ${\epsilon }_1\in (0,1)$ there exists a $\delta >0$ such that the solution $x_n$ of the Equation (10) satisfies the inequality $\mathbf{P}\{\underset{n\in Z}{sup}|x_n|>\epsilon /{\mathfrak{F}}_0\}<{\epsilon }_1$ for any initial function ϕ such that $\mathbf{P}\left\{\underset{n\in Z_0}{max}\right|x_n|<\delta \}=1$.

Definition 2. 

The zero solution of the Equation (10) is called:

- mean square stable if for each $\epsilon >0$ there exists a $\delta >0$ such that $\mathbf{E}{x}_n^2<\epsilon$, $n\in Z$, for any initial function $\varphi \left(n\right)$ such that ${\parallel \varphi \parallel }^2=\underset{n\in Z_0}{max}\mathbf{E}{\left|\varphi \left(n\right)\right|}^2<\delta$;

- asymptotically mean square stable if it is mean square stable and for each initial function $\varphi \left(n\right)$ such that ${\parallel \varphi \parallel }^2<\infty$ the solution $x_n$ of the Equation (10) satisfies the condition $\underset{n\to \infty }{lim}\mathbf{E}{x}_n^2=0$.

Remark 3. 

It is clear that stability of the equilibrium $x^{*}$ of the Equation (5) is equivalent to stability of the zero solution of the Equation (6). It is known [18] that the investigation of stability in probability of the zero solution of a nonlinear stochastic difference equation with an order of nonlinearity higher than one can be reduced to the investigation of asymptotic mean square stability of the zero solution of the linear part of this equation. So, to get conditions for stability in probability of the equilibrium $x^{*}$ of the nonlinear stochastic difference Equation (5) it is enough to get conditions for asymptotic mean square stability of the zero solution of the linear stochastic difference Equation (7) that is the linear part of the nonlinear difference Equation (6).

Remark 4. 

Note that the method of studying the stability in probability of nonlinear stochastic difference equations, presented in Remark 3, is also applicable to stochastic nonlinear differential equations with the order of nonlinearity higher than one (see [20,21,22,23]).

Lemma 2. 

If

$$\left|a\right|+\left|b\right|<\sqrt{1-{\sigma }^2}$$

(11)

then the zero solution of the Equation (10) is asymptotically mean square stable.

Lemma 3. 

The inequalities

$$\left|b\right|<1,\left|a\right|<1-b,{\sigma }^2<{\displaystyle \frac{1+b}{1-b}}\left[{(1-b)}^2-a^2\right],$$

(12)

are the necessary and sufficient conditions for asymptotic mean square stability of the zero solution of the Equation (10).

Remark 5. 

Note that the stability conditions (11) and (12) are obtained via the general method of Lyapunov functionals construction [18].

Theorem 1. 

If

$$a+{\displaystyle \frac{b}{c+1}}<\sqrt{1-{\sigma }^2}$$

(13)

then the equilibrium $x^{*}=0$ of the Equation (5) is stable in probability.

Proof. 

From the condition (3) it follows that by the condition (13) the Equation (5) has the equilibrium $x^{*}=0$ only. Note also that

$$a+{\displaystyle \frac{b}{{(c+1)}^2}}+{\displaystyle \frac{bc}{{(c+1)}^2}}=a+{\displaystyle \frac{b}{c+1}}.$$

So, for the Equation (7) the condition (11) takes the form (13). Via Lemma 2 it means that by the condition (13) the equilibrium $x^{*}=0$ of the Equation (7) is asymptotically mean square stable and via Remark 3, the equilibrium $x^{*}=0$ of the Equation (5) is stable in probability. The proof is completed. □

Remark 6. 

Note that the conditions (12) for the Equation (7) take the form

$$a+{\displaystyle \frac{b}{c+1}}<1,{\sigma }^2<{\displaystyle \frac{{(c+1)}^2+bc}{{(c+1)}^2-bc}}\left[{\left(1-{\displaystyle \frac{bc}{{(c+1)}^2}}\right)}^2-{\left(a+{\displaystyle \frac{b}{{(c+1)}^2}}\right)}^2\right].$$

(14)

Thus, the inequalities (14) are necessary and sufficient conditions for asymptotic mean square stability of the zero solution of the Equation (7) and, therefore, via Remark 3, sufficient conditions for stability in probability of the solution $x^{*}$ of the Equation (5).

Remark 7. 

Note that by $\sigma =0$ each from the conditions (13) and (14) coincides with the inequality inStatement 2 .

Remark 8. 

Note that in all examples below for numerical simulation of solutions of the Equation (5) the random value ${\xi }_{n+1}$ is used in the form ${\xi }_{n+1}=\sqrt{12}(\eta -0.5)$, where η is a random value uniformly distributed on the interval $\left[0.1\right]$ with $\mathbf{E}\eta =0.5$ and $\mathbf{D}\eta =1/12$. So, $\mathbf{E}{\xi }_{n+1}=0$, $\mathbf{D}{\xi }_{n+1}=\mathbf{E}{\xi }_{n+1}^2=1$.

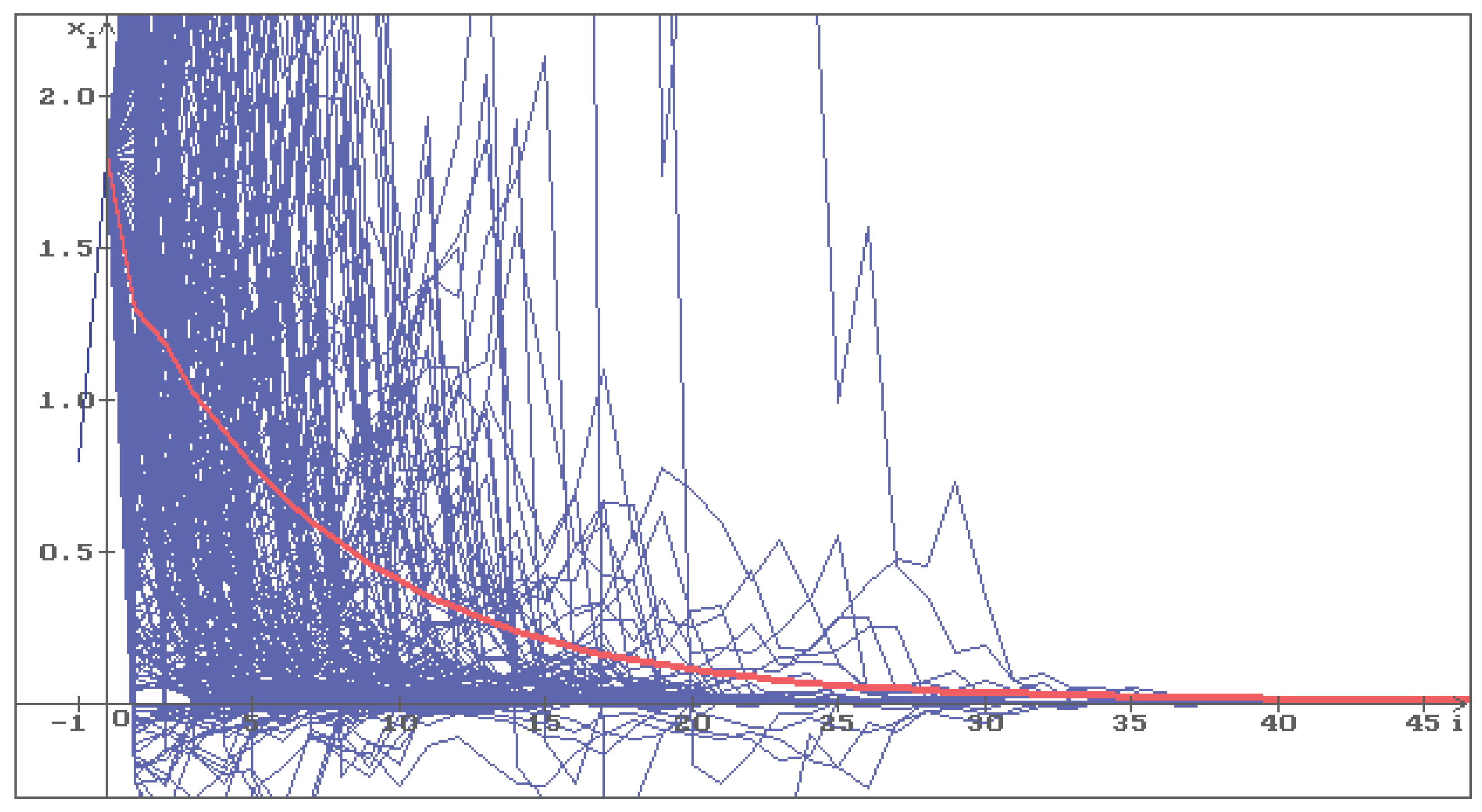
Example 1. 

Put $a=0.5$, $b=0.7$, $c=1$, $\sigma =0.5$. The condition (13) holds: $a+{\displaystyle \frac{b}{c+1}}=0.85<\sqrt{1-{\sigma }^2}=0.866$. Besides, the conditions (13) and (14) give respectively ${\sigma }^2<0.28$ and ${\sigma }^2<0.32$. Via Theorem 1 the zero solution of the Equation (5) with $x^{*}=0$ is stable in probability. In Figure 1 500 trajectories (blue) of the solution of the Equation (5) are shown with the initial conditions $x_{-1}=0.8$, $x_0=1.8$, all trajectories converge to zero. The red line corresponds to the deterministic case, i.e., $\sigma =0$.

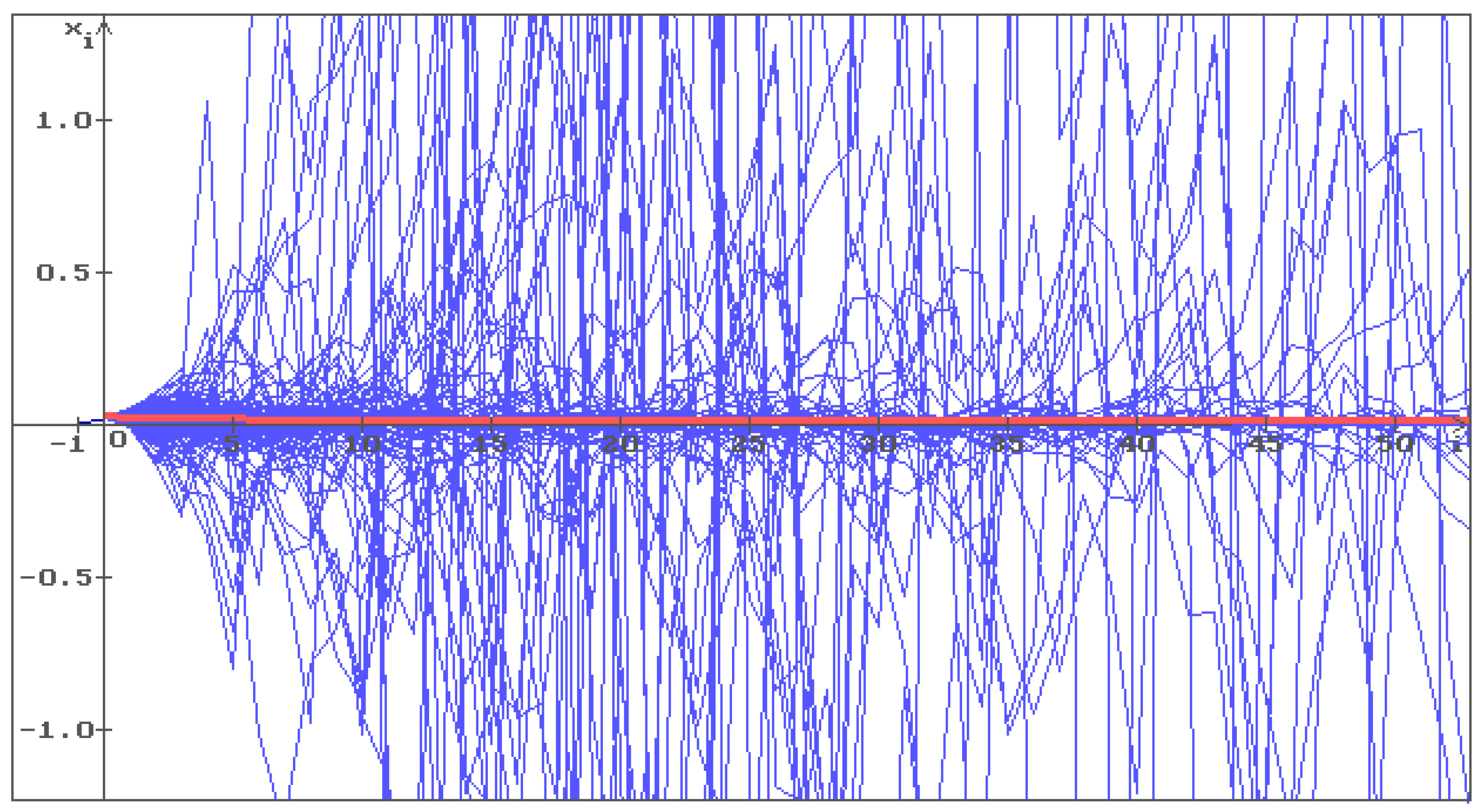
Example 2. 

Put now $\sigma =0.95$ with the same values of all other parameters as in Example 1. The conditions (13) and (14) do not hold. In Figure 2 500 trajectories (blue) of the solution of the Equation (5) with $x^{*}=0$ are shown with the initial conditions $x_{-1}=0.01$, $x_0=0.02$. The zero solution is unstable and the trajectories fill the whole space. The red line corresponds to the deterministic case, i.e., $\sigma =0$.

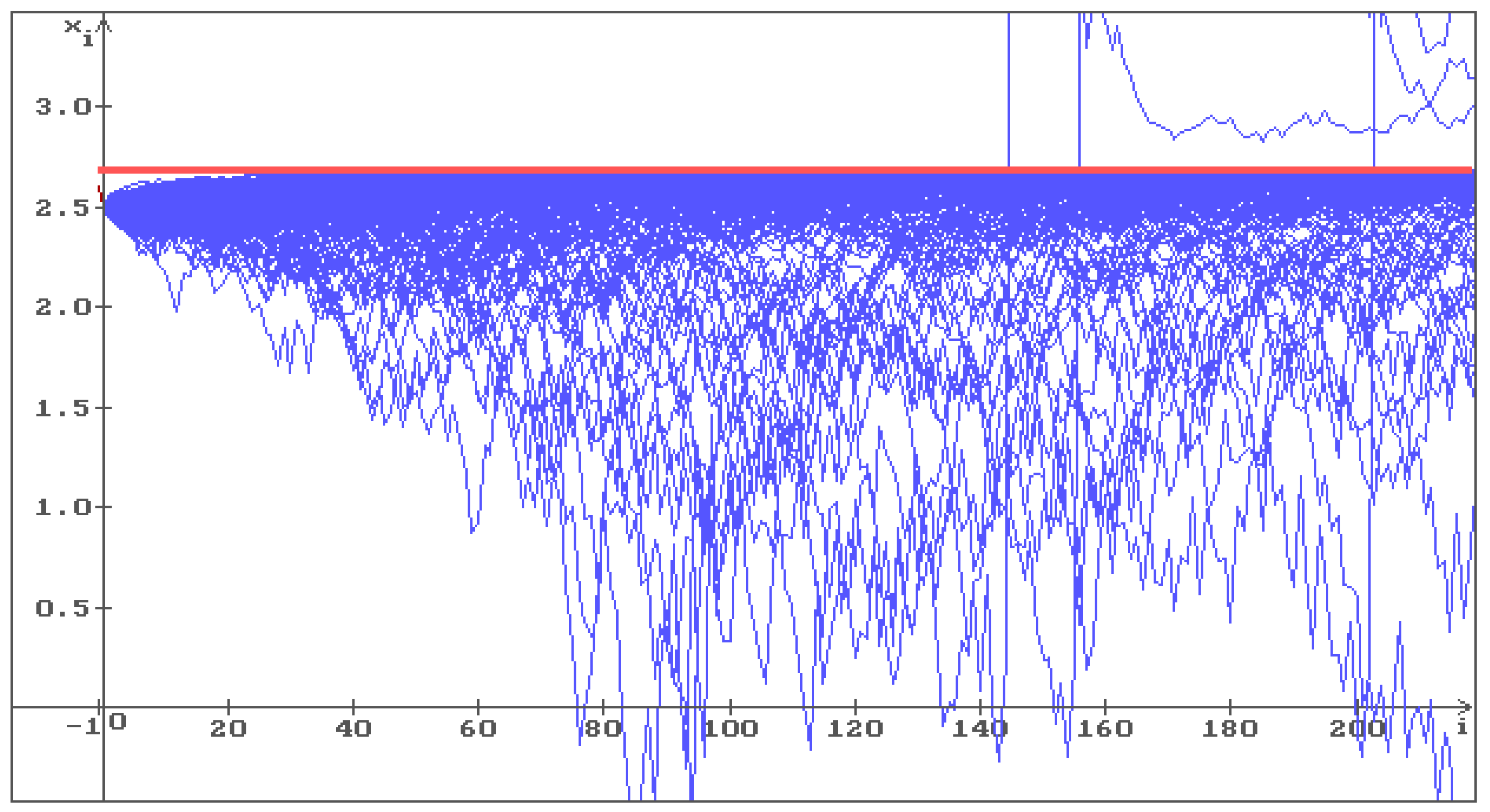
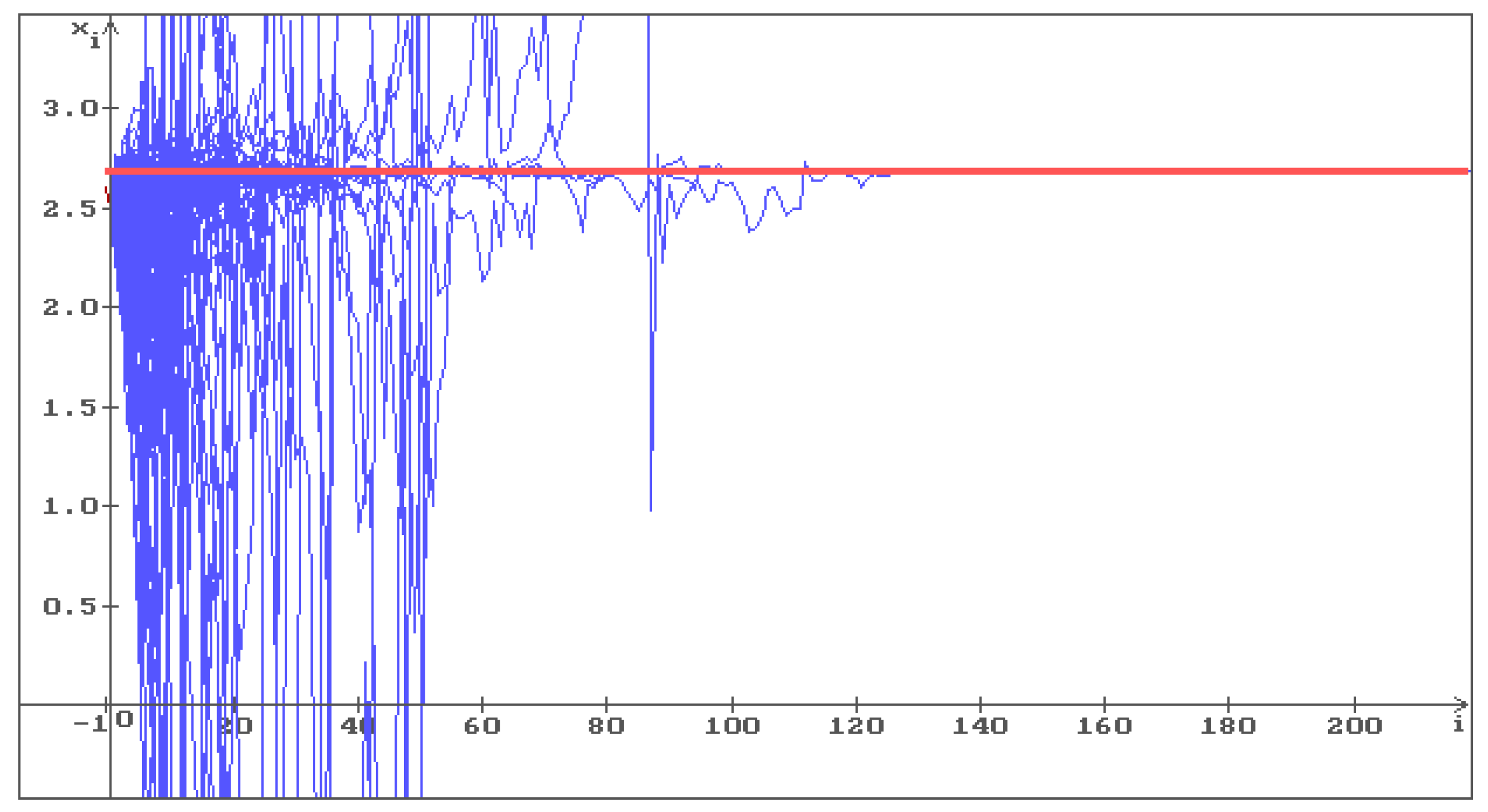
Example 3. 

Put $a=0.65$, $b=0.7$, $c=1$, $\sigma =0.15$, $x^{*}=2.7$. Wherein $a+{\displaystyle \frac{b}{c+1}}=1$, therefore, the condition (4) holds, the conditions (13) and (14) do not hold. In Figure 3 the red straight corresponds to the constant solution $x_n=x^{*}$, $n\ge -1$, 500 trajectories (blue) of the solution of the Equation (5) are shown with the initial conditions $x_{-1}=x^{*}-0.1=2.6$, $x_0=x^{*}-0.2=2.5$. The solution $x_n=x^{*}$ is unstable, so, the trajectories fill the whole space.

4. About One Unsolved Problem of Stabilization by Noise

More than 50 years ago Khasminskii shows [24] that unstable by the conditions $a>0$ and $\sigma =0$ the zero solution of the differential equation

$$dx\left(t\right)=ax\left(t\right)dt+\sigma x\left(t\right)dw\left(t\right)$$

(15)

becomes stable by the presence of a big enough level of noise. More exactly, by the condition

$$0<2a<{\sigma }^2$$

(16)

so-called "stabilization by noise" occurs and the zero solution of the Equation (15) becomes stable in probability.

Really, let L be the generator [20,24,25] of the stochastic differential Equation (15). For the Lyapunov function $v\left(x\right)$ it has the form

$$Lv\left(x\right)=v^{\prime }\left(x\right)ax+{\displaystyle \frac{1}{2}}{v}^{\prime \prime }\left(x\right){\sigma }^2{x}^2.$$

So, via (16) for the Lyapunov function

$$v\left(x\right)={\left|x\right|}^{\nu },\nu =1-{\displaystyle \frac{2a}{{\sigma }^2}}\in (0,1),$$

we have

$$\begin{gathered} Lv\left(x\right)={\nu \left|x\right|}^{\nu -1}ax+{\displaystyle \frac{1}{2}}{\nu (\nu -1)\left|x\right|}^{\nu -2}{\sigma }^2{x}^2 \\ \le a\nu {\left|x\right|}^{\nu }\left(1+(\nu -1){\displaystyle \frac{{\sigma }^2}{2a}}\right)=0. \end{gathered}$$

From the obtained condition $Lv\left(x\right)\le 0$ it follows that the zero solution of the Equation (15) is stable in probability [20,24].

As it is noted in [26] any similar result for the stochastic difference Equation (10) is absent until now even in the case $b=0$. But the following example shows that the effect of stabilization by noise can take a place for difference equations too.

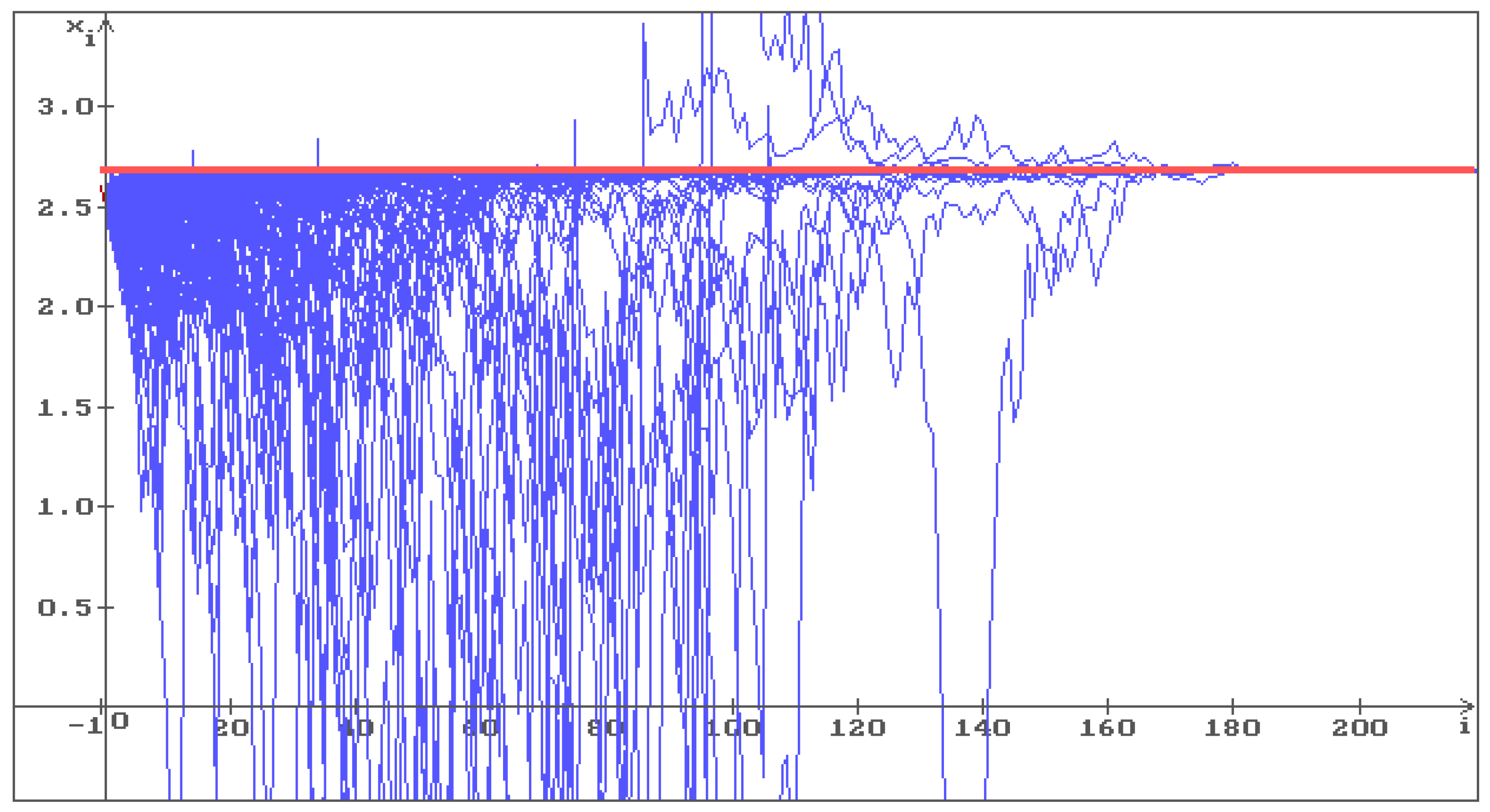
Example 4. 

Consider Example 3 again with $\sigma =0.45$ and the same values of all other parameters. In Figure 4 one can see that all 500 trajectories converge to the solution $x_n=x^{*}=2.7$ of the Equation (5). Putting $\sigma =0.75$, i.e., increasing once more the level of noise, we obtain (see Figure 5) that all 500 trajectories converge to the solution $x_n=x^{*}=2.7$ of the Equation (5) faster than in Figure 4. So, the solution $x_n=x^{*}=2.7$ of the Equation (5), that is unstable by the small level of noise (Figure 3, $\sigma =0.15$), becomes stable by increasing the level of noise.

Thus, the Hypothesis about stabilization by noise for stochastic difference equations may well take a place. However, the proof of this Hypothesis is currently an unsolved problem.

5. Conclusions

In conclusion, one would like to note that the study of the asymptotic properties of a bilinear difference equation under stochastic perturbations is carried out here for the first time, and that the research method used here can be extended to the following natural directions of research development:

1) Bilinear difference equations of other forms, for instance, obtained from this one

$$\begin{gathered} x_{n+1}=a{x}_n\pm {\displaystyle \frac{b{x}_n{x}_{n-1}}{c{x}_n\pm d{x}_{n-1}}},n=0,1,..., \\ {x}_n={\varphi }_n,n=-1,0, \end{gathered}$$

using different combinations of plus and minus. In each case, one can expect the appearance of new features of the solution behavior.

2) Different mathematical models in various applications, described by nonlinear stochastic difference equations of a more complex form.

3) Formulate and prove for difference equations a statement similar to Khasminsky’s statement about "stabilization by noise", which has been well known in the theory of stochastic differential equations for more than 50 years, but still has no analogue for stochastic difference equations.