The Frame Survival Model of Conscious Continuity: A Theoretical Framework for Subjective Experience in a Branching Universe

1. Introduction

Consciousness, which refers to the intimate experience of existence, presents a profound challenge when considered within the frameworks of contemporary physics. In quantum theory, decoherence ensures that physical systems evolve into effectively classical branches, and if reality fundamentally branches at every quantum event, then every possible outcome is realized somewhere within the multiverse. Yet from the perspective of a conscious observer, life unfolds as a coherent, seemingly singular narrative. Observers do not perceive themselves as simultaneously inhabiting divergent branches; instead, they experience a continuous, unbroken stream of subjective awareness. Continuity, which refers to the preservation of a coherent trajectory through changing states, is a fundamental principle in physics, computation, and biological organization, but its preservation in a branching, probabilistic universe raises a central question of both physics and information theory:

1.1. How Can Subjective Continuity be Connected to the Branching, Probabilistic Nature of Reality?

Traditional models, including the Many-Worlds Interpretation and the Block Universe theory of time, offer frameworks for objective branching or static coexistence of all moments [1]. Quantum Immortality theory gestures toward one solution, proposing that observers cannot experience their own deaths and persist subjectively in survival branches. Extending this lineage, the many-minds interpretation of quantum mechanics [2,3] posits that every quantum event results in the branching of the observer’s mind, producing a multiplicity of coexisting, subjectively definite experiences within the broader multiverse. While these approaches make the observer’s experience central, they remain philosophically underdeveloped and lack a formal, operational framework for how survival-compatible threads are selected, how continuity is maintained across frames, and how the subjective “arrow of time” is lawfully enforced. Without such a mechanism, these approaches cannot fully explain why a coherent system—whether a mind, a computation, or any path-dependent process—experiences a single, ordered survival path rather than an incoherent multitude of overlapping possibilities, leaving paradoxes such as subjective death, identity, and measure unresolved at the operational level.

Thus, this paper introduces the Frame Survival Model (FSM) of Conscious Continuity, a theoretical framework that aims to fill this gap. This model proposes that reality is composed of discrete Hyperframes—complete matter‒energy configurations delineated by quantum decoherence events. At each transition between Hyperframes, consciousness encounters a binary outcome: survival (continued awareness) or death (cessation of subjective experience). In this paper, the terms “agent” and “observer” are used interchangeably to refer to the conscious subject whose survival path, Hyperframe transitions, and subjective experience are modeled. The agent is the observer-relative locus of experience and continuity within the branching multiverse framework. All filtering, chunking, and selection logic in the FSM is defined from the perspective of the agent/observer.

Although quantum mechanical equations were first developed to describe the behavior of elementary particles, decoherence theory and information integration principles facilitate the extension of this logic to macroscopic and complex systems, including biological brains and digital minds. The framework presented in this study is explicitly substrate independent and applies to any physical system capable of supporting coherent, integrated information. Thus, this model is presented as an interpretive, observer-relative framework that supplements—rather than replaces—standard quantum mechanics and provides a new way to formalize personal survival and continuity in a multiverse context.

In this model, subjective experience is not the experience of all Hyperframes but the experience of an unbroken sequence of survival-compatible Hyperframes. These Hyperframes are defined by their ability to support an agent, forming a private, observer-relative thread through the branching network of possible realities.

By introducing a binary survival framework that is grounded in the physical structure of decoherence events, the FSM offers a computationally plausible, mathematically formalized account of subjective continuity. It provides a resolution to the paradox of death, a redefinition of personal identity across Hyperframes, and a framework for understanding consciousness not merely as a product of matter but also as an active navigator of survival through quantum possibilities.

Although the equations in this model incorporate quantum-level variables such as informational coherence and decoherence-conditioned survival probability, these variables cannot currently be measured directly in biological brains. By simulating the model using plausible values for coherence and variance, the qualitative patterns of subjective continuity and fragmentation are reproduced and can be observed in real life and described in the psychology and neuroscientific literature. While direct empirical testing awaits advances in quantum neurobiology, the model can provide a phenomenologically accurate and computationally accessible account of subjective experience.

1.2. Model Scope and Limitations

The FSM addresses the persistence of subjective consciousness across quantum-resolved Hyperframes. This assumes that the prior existence of conscious agents arises from complex, integrated physical systems. This model is universally applicable wherever the underlying physics supports stable information, integration, and survival-compatible paths. In universes with incompatible physical laws, the criteria for Hyperframes and subjective continuity are not met, and conscious experience—as described here—is not possible. Subjective threads are always constrained by the physical and informational structure of their native universe.

This model does not attempt to solve the "hard problem" of explaining why subjective experience arises at all. Instead, the model provides a natural mechanism for how conscious survival paths emerge and why survival paths persist through quantum branching without requiring external collapse or new added physics.

Empirical data are not available and cannot currently be measured directly in biological brains. However, through the simulation of the model using plausible values for coherence and variance, qualitative patterns of subjective continuity and fragmentation can be reproduced and observed in real life and described in the psychology and neuroscientific literature.

The model operates within the established framework of quantum mechanics, invoking no additional hidden variables, objective collapses, or metaphysical assumptions beyond standard decoherence dynamics. The FSM is a continuity model rather than a generation model of consciousness.

2. Definitions

The FSM is based on a series of foundational definitions. These constructs are essential for formalizing the model’s structure and for providing clarity in the subsequent theoretical framework.

2.1. Assumptions of the FSM

The FSM is developed under the following core assumptions:

• Emergent Consciousness: Consciousness arises from sufficiently complex, integrated physical systems such as biological neural networks.
• Decoherence-Defined Frame Boundaries: Hyperframes are delineated by quantum decoherence events that collapse superpositions into classically distinguishable states, particularly within consciousness-relevant structures.
• Binary Survival Outcomes: Each Hyperframe F is assigned a binary survival value A(F) ∈ {0,1}, determining whether subjective awareness persists or terminates.
• Observer-Relative Survival Paths: Each conscious agent experiences a private survival path through Hyperframes, independent of the experiences of other agents.
• Standard Quantum Mechanics Framework: The model operates within the standard interpretation of quantum mechanics involving decoherence without invoking additional hidden variables, objective collapse mechanisms, or postulated metaphysical structures.

2.2. Hyperframes

A Hyperframe (F) is defined as a complete, physically distinguishable macrostate of the system at a particular instant in geometric spacetime. Each Hyperframe is a discrete configuration of matter, energy, and information that contains all of the variables needed to specify subjective experience and continuity. This includes everything necessary to describe conscious awareness in that moment—encompassing both the information that is integrated and addressed in the foreground and the background variables or contextual features that may become foregrounded in subsequent frames. This makes the definition fully general and applicable to any type of agent or system. From the observer’s perspective, a Hyperframe functions as a subjective snapshot of reality and is thus relative based on the observer. To promote simplicity, “frame” will be used to refer to “Hyperframe” throughout this paper.

In this model, frames are not simply determined by fixed classical time intervals. Instead, they emerge dynamically whenever a relevant quantum decoherence event occurs—when a previously indeterminate quantum state resolves into a classically stable configuration within the physical substrate that supports consciousness. These events set the boundaries at which the substrate can no longer support coherent superpositions and instead present a definite state to the conscious system, grounding subjective moment updates in physically significant, observer-relative transitions [4]. This is consistent with the intuition that conscious awareness requires stable, classically describable information patterns.

For example, in a brain, a frame may be the overall pattern of neuronal activity at a given instant; for a digital mind, it could be the arrangement of data and code at a particular moment. In any physical system, a frame captures the arrangement of all large-scale features relevant to conscious experience. This definition is fully substrate independent and applies equally to biological, digital, or alien agents. While quantum decoherence operates at the microstate level, the survival path and subjective continuity described in the FSM are defined over these observer-relevant macrostates—frames—that contain all the information necessary for consciousness. Nevertheless, the precise mapping between physical events and subjective experience remains an open problem in the philosophy of mind and consciousness science. Thus, this model should be viewed as an informed proposal rather than a proven fact.

2.3. Conscious Agents

A conscious agent (C) refers to a coherent, information-processing physical structure within a frame F that is capable of sustaining subjective, first-person awareness. In the context of the FSM, consciousness is understood not as a metaphysical property but as an emergent feature arising from sufficiently complex, integrated physical processes.

2.4. Dead Frame (0-Frame)

A dead frame is a frame F in which the conscious agent C no longer possesses the physical conditions required for subjective awareness. In such frames:

A(F) = 0

Dead frames are configurations in which consciousness has irreversibly ceased or can no longer be supported—for example, in cases of brain death or true death.

By definition, dead frames are never experienced by a conscious agent.

2.5. Alive Frame (1-Frame)

An Alive Frame is a frame F in which the necessary physical conditions for the conscious agent C to maintain subjective awareness are satisfied. In such frames:

A(F) = 1

Interpretation of A(F) = 1: An alive frame is a frame containing a structure capable of supporting consciousness (subjective experience), that is, a substrate in which the integrated information of the system exceeds a critical threshold (Φ > Φ_critical). This threshold can be quantified, for example, by the integrated information measure Φ from Integrated Information Theory [5,6,7] or by similar complexity metrics from computational neuroscience or network theory (e.g., EEG synchrony, neural entropy, graph connectivity, behavioral indicators, or even a rough estimate of integration, not necessarily the full IIT Φ). Only such frames are viable for subjective awareness; among these frames, the degree of information coherence (I) determines the vividness, quality, and continuity of consciousness across time. A higher Φ within the alive regime is associated with more integrated, vivid, and self-aware forms of consciousness, whereas lower values represent more minimal or less reflective states.

For biological agents, this could correspond to persistent patterns of activity in the brain’s connectome; for digital agents, it could correspond to patterns of recurrent computation with nontrivial causal integration.

Formally, this can be expressed as

A(F) = 1 if Φ > Φ_critical

or more generally as

A(F) = 1 if pattern integration > threshold

where Φ_critical or the threshold is determined by the minimal informational complexity required to sustain subjective awareness.

This threshold encompasses all levels of minimal or unreportable consciousness, including deep sleep, anesthesia, coma, and even vegetative states. Frames in which Φ ≤ Φ_critical are considered ‘dead’ (A(F) = 0), encountering such a frame terminates the survival path irreversibly—there is no skipping, bridging, or resuming after a zero [5]. No physical collapse occurs; all quantum branches persist, but only functionally viable frames are accessible to subjective experience.

The precise value of Φ_critical remains an open question and may differ across species, developmental stages, or physical substrates (biological, digital, or otherwise). The model is agnostic to its exact value, and the only requirement is that such a threshold for operational clarity exists. Thus, the formalism can be addressed in future empirical work: if a universal or context-dependent threshold is discovered, it can be incorporated directly. If future experimental or theoretical work discovers robust evidence for nonbinary states of consciousness, the model could be extended; however, the current formalism is strictly binary for mathematical consistency and path selection.

2.5.1. Note on Digital or Artificial Agents

The definition of “alive” (A(F) = 1) in this model is substrate independent; in other words, it applies to any physical or digital system capable of supporting the structural and informational prerequisites for subjective experience. Temporary interruption of activity (e.g., pausing an artificial intelligence (AI) or removing a battery) does not necessarily constitute death, provided that the underlying pattern or structure remains intact and can be fully restored. True “death” (A(F) = 0) occurs when the informational or physical basis for conscious processing is irreversibly lost or destroyed.

2.6. Survival Function

Each frame F is assigned a binary survival value on the basis of whether it sustains the conscious agent C.

The survival function A(F) is defined as:

Only frames satisfying A(F) = 1 are included in the survival paths that constitute subjective continuity. A(F) = 1 if consciousness-supporting structures persist in F, that is, if the viability of F for subjective awareness is greater than zero; otherwise, A(F) = 0.

Interpretation of A(F) = 0: The binary survival function A(F) ∈ {0,1} is not a new physical collapse postulate but a subjective filter applied after decoherence has occurred. From the perspective of the universal wavefunction (the Born rule) [8], all branches persist. However, only those branches where the observer continues to exist (i.e., where their physical substrate remains intact) are subjectively experienced. This interpretation aligns with unitary evolution [9] by treating subjective survival as a selection over decohered, classically distinct outcomes.

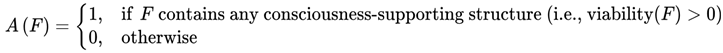
2.7. Survival Path (Timeline)

A survival path (T_C) for a conscious agent C is a sequential ordering of frames {F₀, F₁, F₂, ... } such that for all frames Fᵢ in the path:

A(F_i) = 1

That is, each frame along a survival path preserves the subjective experience of consciousness.

Formally:

Subjective continuity is defined as traversal through this unbroken sequence of alive frames.

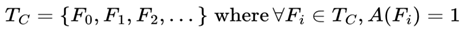
2.8. Frame Transition

A frame transition describes the movement of a conscious agent from a current frame F_t to a subsequent frame F_t+1.

Frame transitions obey the following condition for subjective experience to persist:

A(F_t+1) = 1

Transitions leading to frames in which A(F_t+1) = 0 (i.e., death) are not subjectively experienced by the agent. From the observer’s perspective, only transitions between alive frames are possible and experienced by the agent.

2.8.1. Frame Chunking and Temporal Coherence

While frames are defined discretely on the basis of decoherence events, in practice, sequences of frames may form higher-order units of subjective continuity called “chunks”. A chunk is a contiguous group of frames with low internal variance in survival indices, high informational coherence (I), and consistent agentic preference weights (S) (see Section 3.10). These chunks are not predefined but emerge dynamically; specifically, a chunk forms when the variance in decoherence-defined properties drops below a coherence threshold (see Section 3.14).

This dynamic chunking reflects core aspects of the cognitive experience, in which perception and memory naturally organize events into bounded episodes with a consistent narrative flow. Chunks provide temporal scaffolding for conscious “moments,” scenes, or thoughts, so the model can capture both the discreteness of quantum frame transitions and the integrated structure of lived experience.

2.9. Observer-Relative Continuity

Each conscious agent C navigates a unique, private survival path T_C through the network of frames.

Given two agents C and D, their survival paths are generally distinct:

T_C ≠ T_D

The observation of death events by one conscious agent does not imply the subjective termination of another agent’s survival path. Survival and continuity are observer-relative phenomena. Each consciousness experiences its own uninterrupted thread of existence.

2.10. Decoherence-Defined Frame Resolution

Frames are demarcated by consciousness-relevant quantum decoherence events.

A decoherence event is defined as the transition of a quantum system from superposition into a classical, definite state due to interactions with the environment [4]. Although decoherence acts at the level of fundamental particles and microstates, the emergence of stable, classically describable macrostates—constructed from these underlying components—forms the foundation for subjective experience in this model. The conscious agent’s survival path threads through these macrostates, which capture all the information needed for conscious awareness.

Only decoherence events that alter the structural integrity of cognitive-supporting systems (e.g., neuronal microstates) are relevant for consciousness. The progression of frames is not continuous in an absolute sense but occurs dynamically according to the collapse of quantum uncertainty into distinct, informationally significant states.

The transition rate between frames is thus determined by the following:

• The rate at which consciousness-relevant systems decohere.
• The emergence of new distinguishable macrostates capable of sustaining awareness.

2.11. Decoherence Event Index (e) and Frame Index (t)

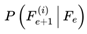The index e tracks discrete decoherence events or subjective frame transitions along the survival path. Formally, e = 0, 1, 2... where each increment corresponds to the resolution of one decoherence event. This is a stepwise update. At each event e, the system computes the transition probability distribution  overall decohered candidate next frames using the full transition equation (see Section 3.13). The selected frame F_e+1 becomes the new present, and the subjective time advances by τ_e (with the corresponding frame rate r_e = r_max × τ_e).

In most practical simulations, t (frame index) and e (event index) increment together and are numerically equivalent. However, t denotes the position in the subjective survival path, whereas e formally tracks the sequence of decoherence events or stepwise updates. In more complex scenarios involving path branching or nonlinear traversal, e may diverge. This notation distinguishes the sequence of subjective experience updates (i.e., “ticks” or “moments”) from the frame index t itself. It facilitates the stepwise mapping of the ways in which transition probabilities, coherence, and subjective time evolve across the survival path.

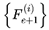At each decoherence event e, a set of candidate next frames  is evaluated, and one is selected according to the transition probabilities. The chosen subjective survival path is a sequence of such frames. Each step is determined by the outcome of the decoherence-resolved transition at that event.

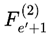While it is mathematically possible for the selected frame at event e and event e′, such as  and 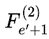 to represent identical physical configurations, the selected frame of each event is indexed according to its unique position and context within the chosen survival path. For a given run, every assigned F_e is treated as a distinct, context-specific moment in subjective experience, even if candidate frames overlap across events.

In this model, n denotes the window size (see Section 3.4), i.e., the number of consecutive future frames (or decoherence events) over which measures such as cognitive variance, chunking, and windowed variance are computed. The value of n sets the “integration window” for analyzing local stability, coherence, and subjective flow. At any given moment, subjective experience is shaped by the culmination of information from all frames within this window, reflecting both the immediate present and its surrounding context. While the default window in this model typically considers future candidate frames (to capture predictive instability and event segmentation), a sliding window that includes past, present, and future frames can also be used to model perceptual integration and the subjective “now,” depending on the scientific question or empirical context being examined.

Typical values for n in human cognitive modeling are expected to range from 10 to 30 frames, which is consistent with empirically observed neural and perceptual integration windows (approximately 20–50 milliseconds per frame, giving a total window of 200–1500 ms) [10,11]. However, n is a flexible modeling parameter, with the following options:

• In theory, n can be set as low as 1 (comparing just two consecutive frames for “instantaneous” variance), although this may be too noisy for most cognitive or phenomenological timescales.
• n can also be set higher, up to the maximum subjective frame rate (approximately 50 Hz for humans, corresponding to n = 50), which would analyze a 1-second window of continuous experience.
• For nonhuman or digital agents, n can be tuned to match the agent’s substrate or phenomenological requirements—shorter windows for fast digital minds and longer windows for slower systems.

The choice of n depends on the context: a smaller n can be used to examine changes over a very short period to identify rapid or sudden shifts in experience—but the results might be more jumpy or sensitive to random noise. In contrast, a larger n can be used to average over a longer stretch of time, which smooths out random bumps and gives a more stable, reliable measure, but brief or rapid changes in what is happening. In all cases, only the frames that are survival-compatible (A(F) = 1) and pass the relevant coherence/integration filters are included in the calculation.

2.12. Decoherence Timescale

The Decoherence Timescale (τ) is defined as the characteristic time it takes for a quantum system relevant to consciousness (e.g., neuronal microstates) to lose coherent superposition and collapse into a classically definite state owing to environmental interactions [4].

Formally, the decoherence timescale τ satisfies:

Decoherence Completion Time ≈ τ

In realistic systems, decoherence is not uniform and is considered “complete” when the magnitude of the off-diagonal terms of the system’s density matrix (in the basis of classical distinguishability) is reduced to a fraction ε ≪ 1 of the diagonal terms, rendering interference effects experimentally undetectable. Following Zurek [2] and Schlosshauer [12], values on the order of 10⁻⁵ or smaller are effectively negligible for microscopic systems, while macroscopic environmental decoherence can suppress these terms to 10⁻²⁰ or less on ultrashort timescales. In brain-relevant systems, Tegmark [37] reported that such suppression occurs within 10⁻¹³ to 10⁻²⁰ seconds — many orders of magnitude faster than the characteristic timescale of conscious processing (~10⁻³ seconds). Although microstate decoherence occurs on these ultrafast timescales, FSM’s continuity framework operates on the slower scale of survival-compatible macrostate updates (tens of milliseconds for humans), so τ in this context refers not to raw microstate collapse but to the effective emergence of distinct macroscopic frames, filtering out the vast majority of microscopic changes. While this presents a challenge for quantum-based models that treat sustained coherence as the substrate of consciousness, the FSM instead treats decoherence as a marker that delineates the boundaries between successive conscious frames, rather than as the physical basis that generates subjective experience.

In the context of the FSM:

• Decoherence timescales are defined when frames become distinct and navigable.
• Consciousness-relevant systems decohere at rates that set the subjective transition speed between frames.

τ determines the effective "clock speed" of the subjective survival path traveled.

2.13. Decoherence-Conditioned Survival Probability

The survival probability function, which quantifies the likelihood that a transition from the current frame F_t to a candidate next frame F_t+1 is physically viable under decoherence dynamics, is defined as:

P_s(F_t → F_t+1) ∈ [0, 1].

This value reflects how likely it is for the quantum system (especially consciousness-relevant structures) to decohere into frame F_t+1. Transitions into frames with high physical stability and coherence (e.g., consistent brain states) will have higher P_s, whereas chaotic or noisy frames will have lower values. Frame evolution and probabilities in this model are grounded in standard quantum mechanics. The Schrödinger equation describes the continuous evolution of the quantum state, and the Born rule guides the probabilities of transitions between frames [8,13].

Formally, this is defined as follows:

For pure states:

For mixed states:

where:

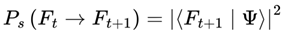
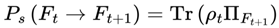
• |Ψ⟩: is the predecoherence quantum state of the system; it represents the full quantum information about all possible outcomes before decoherence or measurement occurs.
• |F_t+1⟩: denotes a specific possible outcome frame — a definite, classical state into which the system could “collapse” after decoherence. In this model, it can represent a specific conscious brain state or configuration of the observer’s world at the next step.
• ρ_t is the density matrix representing the (mixed) quantum state of the system at time t, just prior to decoherence—a situation common in open or realistic systems subject to environmental interactions.
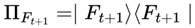• is the projection operator onto the frame ∣F_t+1⟩; for mixed states, this operator is used in the density matrix [8].

In most real-world (open, decohering) systems—including brains and digital minds—the relevant quantum state is mixed due to environmental interactions. Thus, the general formula for the transition probability is the density matrix version of the abovementioned Born rule. The pure state formula should be used for special cases.

This definition grounds the transition probabilities in the fundamental laws of quantum physics, ensuring that the model reflects both subjective filtering and the objective branching structure of reality. However, the survival probability P_s may be implemented differently depending on the system being modeled. For example, this is evident in the use of quantum Born rule weights in physical systems or empirically measured transition probabilities in computational or biological contexts. Thus, the model can accommodate a wide range of empirical or theoretical applications.

2.13.1. Steps for Extracting the Density Matrix from a Hyperframe

• Identify the conscious-relevant subsystem: For a human brain or a biological brain, this might be a functionally integrated neural circuit or large-scale brain network; for a digital agent, it could be a memory register or computational process.
• Construct the physical state: Given complete knowledge of all degrees of freedom, specify the quantum state |Ψ⟩ of the total system (or the classical-probabilistic equivalent for nonquantum agents).
• Reduce to the subsystem: Take the partial trace over everything not included in the consciously relevant system, yielding the reduced density matrix ρ_F.
• Plug into the model: Use this ρ_F for transition probabilities, coherence calculations, etc., as per the equations in the main text.

For now, if only classical data are available (e.g., EEG, fMRI), empirical correlation matrices, mutual information, or normalized similarity scores should be used as stand-ins for quantum state similarity, as described in Section 2.14.

2.13.2. Representative Survival Probability (Ps) Values

For practical modeling, one can assign typical values for survival probability (P_s) to reflect the empirical or expected likelihood of transitioning into a survival-compatible frame in different scenarios:

Table 1. Survival Probability Table.

Transitions/Risk Scenario	Survival Probability (Ps)
Routine, everyday transitions	Ps ≈ 1.0
Mild risk/moderate stress	Ps ≈ 0.9-0.95
Significant risk (medical trauma, accident)	Ps ≈ 0.5-0.9
Lethal threat/near-death	Ps ≪ 1.0
Frames in which survival is impossible	Ps = 0 (these are pruned from the survival path)

Table 1. Survival Probability Table.

Transitions/Risk Scenario	Survival Probability (Ps)
Routine, everyday transitions	Ps ≈ 1.0
Mild risk/moderate stress	Ps ≈ 0.9-0.95
Significant risk (medical trauma, accident)	Ps ≈ 0.5-0.9
Lethal threat/near-death	Ps ≪ 1.0
Frames in which survival is impossible	Ps = 0 (these are pruned from the survival path)

In this model, routine, everyday transitions (where P_s ≈ 1.0) represent physically safe, stable conditions—ordinary waking life, healthy rest, or familiar environments—where the probability of surviving into the next frame is virtually certain. Here, survival paths are robust, and the agent moves seamlessly through a dense landscape of alive frames, with subjective continuity that feels unbreakable [10,11,14]. Mild risk or moderate stress (P_s ≈ 0.9–0.95) reflects situations in which there is some environmental or physiological hazard, such as minor illness, mild emotional stress, or low-level physical danger. Under these conditions, the likelihood of survival remains very high, but survival paths are ever so slightly thinner, and there is a small, but nonzero, chance of path pruning—these may be moments of “close call” or minor vulnerability [15,16,17].

A significant risk (P_s ≈ 0.5–0.9) arises in more dangerous situations, such as those involving serious injury, acute illness, medical emergencies, or hazardous environments. The probability of survival decreases noticeably; subjective continuity becomes more fragile, and the agent’s path through alive frames is significantly narrowed. Each moment is more precarious, with an elevated chance of discontinuity or death if the sequence of alive frames runs out [18,19,20,21].

Lethal threat or near-death states (P_s ≪ 1.0) are those in which survival is extremely unlikely: catastrophic trauma, critical illness, or exposure to fatal environments. In these scenarios, almost all possible next frames are non-survival-compatible and are pruned from the path; only an exceedingly rare chain of “alive” frames allows subjective continuity to persist. These are the moments of profound crisis in which survival hangs by a thread, and the majority of possible futures end in death [21,22,23]. Frames in which survival is impossible (P_s = 0) correspond to physically forbidden, fatal, or utterly nonviable outcomes: instant brain death, total system collapse, or transitions that violate physical law. Such frames are always pruned from the survival path, and subjective continuity cannot traverse them—these are the true boundaries of existence in the model [14,24]

By assigning P_s values in this way, researchers can simulate or analyze how subjective continuity is affected by different levels of environmental risk, physiological state, or system design. This mapping makes the abstract mathematics of survival filtering directly relatable to real-world scenarios and agent‒environment interactions [14,16,19].

2.13.3. Flexibility in Defining Survival Probability (P_s)

The survival probability function P_s(F_t → F_t+1) is designed to be flexible and context sensitive, enabling researchers to tailor its definition and empirical grounding to the system or phenomenon under investigation. While the model grounds P_s in the Born rule and decoherence dynamics for quantum systems, depending on available data and the modeling objective, it can also be set or empirically estimated in a variety of ways.

For example, in physical or quantum-mechanical contexts, P_s may reflect the calculated quantum transition probabilities for specific brain or system states. In biological or clinical applications, P_s can be estimated from physiological measurements, such as neural integrity (via EEG, fMRI, or metabolic imaging), observed risk factors, or empirical survival rates for certain conditions. In cognitive or computational models, P_s could represent algorithmic or statistical transition likelihoods—derived from simulations, behavioral data, or even machine learning classifiers that are trained to predict viable future states.

This framework accommodates a wide range of candidate definitions for P_s, so it can be informed by theory, experimental data, or practical engineering needs. The survival probability (P_s) can flexibly incorporate any physical, biological, or informational metric most relevant to the system under study, as long as it quantifies the likelihood of the system’s continued existence or operational integrity across a frame transition. The metric should be chosen according to the dominant risk factors and measurable state variables for that system. For example, in a physical system, P_s might be derived from experimentally measured failure rates, decay constants, or hazard functions linked to environmental conditions. In a biological organism, it could reflect survival curves, physiological stress indicators, or probabilistic models of disease progression. In an informational or computational agent, P_s might be computed from error rates, data integrity checks, or redundancy safeguards. This adaptability enables FSM to apply the same mathematical formalism for survival-path selection across diverse substrates while allowing domain-specific realism in metric choice.

2.14. Information Coherence Function

The information coherence function, which quantifies the cognitive, structural, or informational consistency between the current frame F_t and a candidate next frame F_t+1., is as follows:

Higher I values indicate smoother narratives, memory continuity, and environmental stability. Lower values represent abrupt, disjointed, or incoherent transitions. This function contributes to transition weighting among survival-compatible frames and explains the structured and stable nature of subjective experience.

The information coherence function I(F_t → F_t+1) can be formally expressed using measures from quantum information theory. One such measure is quantum fidelity [25], which quantifies the similarity between the quantum states underlying frames F_t and F_t+1.

If ρ_Ft and ρ_Ft+1 denote the reduced density matrices corresponding to the agent-relevant quantum subsystems in frames F_t and F_t+1, then:

where the quantum fidelity F(ρ,σ) is given by:

In this instance, Tr denotes the trace operation, which returns the sum of the diagonal elements of a square matrix. This definition naturally bounds I between 0 and 1, with I = 1 indicating perfect coherence (identical states) and I = 0 indicating complete decoherence (orthogonal states). Practically, the relevant subsystem representing an observer’s conscious frame is almost always described by a mixed state (density matrix), due to decoherence and environmental interaction. Thus, unless otherwise specified, the model uses quantum fidelity for mixed states:

For simplicity, in the case of pure states, .

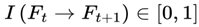
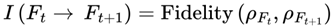
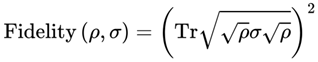
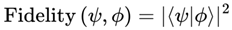2.14.1. Optional Flexibility

Depending on the context and available data, the information coherence function I(F_t→F_t+1) can be used in various ways. For example, quantum information theorists may use quantum fidelity, whereas neuroscientists might use neural pattern similarity measures (such as EEG correlations). In cognitive or computational settings, I can reflect semantic, memory, or state transition similarity. The framework accommodates a wide range of candidate definitions for I, allowing for empirical or theoretical flexibility.

2.14.2. Representative Information Coherence (I) Values for Phenomenological States

For practical modeling and simulation, typical values for information coherence (I) can be assigned to reflect the empirical or expected degree of frame-to-frame similarity in different conscious states:

Table 2. Information Coherence Table.

Cognitive State/Condition	Information Coherence (I)
Flow/Peak Focus	I ≈ 0.9-1.0
Normal Alertness	I ≈ 0.8-0.9
Routine/Mild Distraction	I ≈ 0.7-0.8
Sleep/Fatigue, Drugs, Shock/Trauma	I ≈ 0.5-0.7
Coma/Unconsciousness	I ≲ 0.5
Frames in which survival is impossible	I = 0 (these are pruned from the survival path)

Table 2. Information Coherence Table.

Cognitive State/Condition	Information Coherence (I)
Flow/Peak Focus	I ≈ 0.9-1.0
Normal Alertness	I ≈ 0.8-0.9
Routine/Mild Distraction	I ≈ 0.7-0.8
Sleep/Fatigue, Drugs, Shock/Trauma	I ≈ 0.5-0.7
Coma/Unconsciousness	I ≲ 0.5
Frames in which survival is impossible	I = 0 (these are pruned from the survival path)

Table 3. FSM notation.

Symbol/Notation	Name/Description	Typical values/Domain	Section/Context
F, Ft	Hyper frame (Frame): Complete macro state at an instant in spacetime	–	Def. 2.2, throughout
C	Conscious agent: Coherent info-processing structure in frame F	–	Def. 2.3
t, e	Frame index/Decoherence event index (discrete time step)	t = 0,1,2,… e = 0,1,2,…	Def. 2.11
A(F)	Survival function: Binary indicator if F is “alive” (supports consciousness)	[0,1]	Def. 2.4–2.7, throughout
Φ	Integrated information: Degree of integration in a frame	[0, ∞) (the max is dependent on substrate and species)	Def. 2.5
Φcritical	Minimum threshold for conscious frame	Context-dependent	Def. 2.5
S(F)	Agentic preference weight: Transition bias/intent for frame F	$R$+, ≥ 1	Sec. 3.9
N	Set/Number of candidate next frames at a transition	1 to large (106+)	Def. 2.15
TC	Survival path: Sequence of alive frames for agent C	–	Def. 2.7, 2.9
τ	Decoherence timescale: Time for a quantum system to decohere	10–50 ms (humans, could be higher or lower in different substrates)	Def. 2.12, Sec 3.4
r, rmax, rrel	Frame rate, maximum, and relativistic frame rate	1–50 Hz (humans, substrate dependent)	Sec. 3.4, 4.12
I(Ft →Ft+1)	Information coherence function: Similarity between frames	[0,1]	Def. 2.14
Ps(Ft → Ft+1)	Survival probability: Likelihood of decoherence into next frame	[0,1]	Def. 2.13
w(Ft →Ft+1)	Transition weight: Unnormalized likelihood for next frame	–	Sec. 3.11
P(Ft+1 | Ft), Pbase, Pchunk	Transition probability: Normalized probability for next frame	[0,1]	Sec. 3.6, 3.12
Varcog	Cognitive variance: Instability/divergence for a frame’s next states	[0,1]	Sec. 3.4, 3.12.2, 4.12
Varwindow	Windowed cognitive Variance: Mean Var across window of n frames	[0,1]	Sec. 3.12.2
n	Window size (number of recent frames for chunking/variance)	10–30 (humans, substrate dependent)	Def. 2.11, 3.4, 3.12.2, 4.12
at	Chunk confidence coefficient: Weight for chunk-based transitions	[0,1]	Sec. 3.12.2
k	Integration timescale constant (min. frame update time)	0.01–0.1 s (depends on the substrate) tunable	Sec. 3.4, 4.12
B	Scaling constant for variance to match frame rates	∼5 (humans, substrate dependent), tunable	Sec. 3.4, 4.12
ϵ	Saturation/nonlinearity parameter in frame rate	∼27 (humans, substrate dependent) tunable	Sec. 3.4, 4.12
γ	Lorentz factor (relativity)	≥ 1	Sec. 4.12
μ	Mean frame index (for entropy/variance metrics)	–	Sec. 3.10
σ2	Chunk “tightness” parameter	Tunable	Sec. 3.12.1
Z, Zchunk	Normalization constants for probability distributions	–	Sec. 3.12, 3.12.1
λ	Sensitivity to cognitive variance in chunking(αt)	$R$+−3, tunable	Sec. 3.12.1
κ	Sensitivity to coherence loss in chunk confidence (αt)	0–3	Sec. 3.12.1
i	Index for summing over candidate frames in variance/averaging formulas	–	Sec. 2.11, 3.1, 3.4, 3.12.2, 4.12

Table 3. FSM notation.

Symbol/Notation	Name/Description	Typical values/Domain	Section/Context
F, Ft	Hyper frame (Frame): Complete macro state at an instant in spacetime	–	Def. 2.2, throughout
C	Conscious agent: Coherent info-processing structure in frame F	–	Def. 2.3
t, e	Frame index/Decoherence event index (discrete time step)	t = 0,1,2,… e = 0,1,2,…	Def. 2.11
A(F)	Survival function: Binary indicator if F is “alive” (supports consciousness)	[0,1]	Def. 2.4–2.7, throughout
Φ	Integrated information: Degree of integration in a frame	[0, ∞) (the max is dependent on substrate and species)	Def. 2.5
Φcritical	Minimum threshold for conscious frame	Context-dependent	Def. 2.5
S(F)	Agentic preference weight: Transition bias/intent for frame F	$R$+, ≥ 1	Sec. 3.9
N	Set/Number of candidate next frames at a transition	1 to large (106+)	Def. 2.15
TC	Survival path: Sequence of alive frames for agent C	–	Def. 2.7, 2.9
τ	Decoherence timescale: Time for a quantum system to decohere	10–50 ms (humans, could be higher or lower in different substrates)	Def. 2.12, Sec 3.4
r, rmax, rrel	Frame rate, maximum, and relativistic frame rate	1–50 Hz (humans, substrate dependent)	Sec. 3.4, 4.12
I(Ft →Ft+1)	Information coherence function: Similarity between frames	[0,1]	Def. 2.14
Ps(Ft → Ft+1)	Survival probability: Likelihood of decoherence into next frame	[0,1]	Def. 2.13
w(Ft →Ft+1)	Transition weight: Unnormalized likelihood for next frame	–	Sec. 3.11
P(Ft+1 | Ft), Pbase, Pchunk	Transition probability: Normalized probability for next frame	[0,1]	Sec. 3.6, 3.12
Varcog	Cognitive variance: Instability/divergence for a frame’s next states	[0,1]	Sec. 3.4, 3.12.2, 4.12
Varwindow	Windowed cognitive Variance: Mean Var across window of n frames	[0,1]	Sec. 3.12.2
n	Window size (number of recent frames for chunking/variance)	10–30 (humans, substrate dependent)	Def. 2.11, 3.4, 3.12.2, 4.12
at	Chunk confidence coefficient: Weight for chunk-based transitions	[0,1]	Sec. 3.12.2
k	Integration timescale constant (min. frame update time)	0.01–0.1 s (depends on the substrate) tunable	Sec. 3.4, 4.12
B	Scaling constant for variance to match frame rates	∼5 (humans, substrate dependent), tunable	Sec. 3.4, 4.12
ϵ	Saturation/nonlinearity parameter in frame rate	∼27 (humans, substrate dependent) tunable	Sec. 3.4, 4.12
γ	Lorentz factor (relativity)	≥ 1	Sec. 4.12
μ	Mean frame index (for entropy/variance metrics)	–	Sec. 3.10
σ2	Chunk “tightness” parameter	Tunable	Sec. 3.12.1
Z, Zchunk	Normalization constants for probability distributions	–	Sec. 3.12, 3.12.1
λ	Sensitivity to cognitive variance in chunking(αt)	$R$+−3, tunable	Sec. 3.12.1
κ	Sensitivity to coherence loss in chunk confidence (αt)	0–3	Sec. 3.12.1
i	Index for summing over candidate frames in variance/averaging formulas	–	Sec. 2.11, 3.1, 3.4, 3.12.2, 4.12

High coherence values (I ≈ 0.9–1) correspond to states of flow or peak focus, in which frames are maximally similar and subjective experience is vivid, continuous, and deeply integrated [26,27,28]. Under these conditions, attention is sharp, the sense of time accelerates, and transitions between moments are nearly seamless, ensuring robust survival paths and uninterrupted subjective continuity. Moderately high coherence values (I ≈ 0.8–0.9) are associated with normal alertness, where consciousness remains clear and stable, perception and thought are well integrated, and awareness is consistent; here, survival paths remain strong and smooth [10,11].

Intermediate coherence values (I ≈ 0.7–0.8) represent routine activities or mild distraction, in which frames are still compatible, but experience becomes less vivid or focused. Additionally, subjective continuity is preserved but slightly thinner, with occasional minor fragmentation or lapses in attention [17,29].

Lower coherence values (I ≈ 0.5–0.7) correspond to states of sleep, fatigue, shock, acute trauma, or certain drug-induced conditions in which frame-to-frame similarity decreases and experience grows more fragmented, as seen in drowsiness, dreaming, or moments of dissociation. In these states, survival paths become sparse, and transitions between moments may feel disjointed or “fuzzy,” although continuity is not yet fully lost [30,31,32].

Not all drugs or medications have the same effect on coherence—sedatives, dissociatives, and anesthetics (e.g., fentanyl, general anesthesia) can push I lower or even toward zero, resulting in profound unconsciousness or amnesia, whereas stimulants or cognitive enhancers (e.g., amphetamines such as Adderall) may temporarily increase I, increasing focus and chunk stability [33,34]. Shock, acute trauma, or drug-induced states that disrupt cognitive integration may cause temporary drops in I to this range, even outside the context of literal sleep.

Extremely low coherence values (I ≲ 0.5) correspond to coma, deep unconsciousness, or severely fragmented awareness [31,32]. If I = 0, indicating complete incompatibility between frames, the candidate next frame is pruned from the survival path, and subjective continuity cannot traverse it; such frames are treated as informationally “dead ends,” which is analogous to the binary survival filter (A(F) = 0). This ensures that the model matches both the quantum mechanical and phenomenological boundaries of consciousness [14,24].

When these values are incorporated into the calculation for cognitive variance (Var_cog, see Section 3.4), the model can generate subjective frame rates and experiences that match observed human states. For example, high I values yield low variance and rapid, vivid subjective experience; low I values yield high variance and slow, fragmented, or absent continuity [11,27,28].

2.14.3. Relationship Between Φ and I

In the FSM, higher information coherence (I) and integrated information (Φ) mean that more content is unified and brought into the foreground of experience—corresponding to vivid, focused, and cohesive awareness. A lower I or Φ corresponds to content fading into the background, as occurs in deep thought, sleep, or distraction, during which conscious experience becomes less integrated and more diffuse. In practice, the foreground/background spotlight can flip rapidly—attention may shift from external sensory information to internal thoughts, feelings, or memories, and vice versa. This dynamic switching, governed by coherence, chunking, and agentic preference, is a central feature of subjective experience in the FSM. This model accounts for everyday phenomena where attention moves from external tasks (such as speaking or driving) to deep internal thought, allowing actions to be performed automatically—sometimes without conscious realization—as coherent routines are handled in the background while conscious focus is elsewhere.

While Φ and I are distinct in this model, they often become correlated under extreme conditions. Φ sets the viability threshold for consciousness: if Φ drops below a critical value (Φ_critical), no subjective experience is possible, and the frame is pruned (A(F) = 0) [14,24]. I determines the degree of frame-to-frame integration and governs the vividness and continuity of experience. As an agent approaches unconsciousness, trauma, or death, both Φ and I may decline: experience becomes fragmented or lost (I drop), and the capacity for consciousness itself diminishes (Φ approaches the threshold). If both reach critically low values, subjective continuity ends as all future frames are pruned. Thus, Φ and I together describe both the viability and the quality of experience, and their joint decline signals the boundary between consciousness and death [14,24].

For a frame to be considered ‘alive’ and to exhibit any of the above coherence-dependent states, it must first satisfy Φ > Φ_critical; only then does the range of I values determine the vividness and structure of subjective experience.

2.15. Definition of N: The Set of Possible Next Frames

In the FSM, we distinguish between two levels of possibility. At the most general level, decoherence produces a vast raw set of quantum-possible branches, which is denoted as N_raw. This includes every physically allowable micro-outcome at a given decoherence event, many of which are irrelevant for subjective continuity. By contrast, the model uses N (also known as N_possible) to denote the filtered subset of candidate frames F_t+1 that satisfy survival and coherence requirements:

• Physically possible: Frames in which P_s(F_t+1) > 0, i.e., transitions that are not forbidden by quantum law and system dynamics.
• Informationally coherent: Frames in which I(F_t → F_t+1) > 0, i.e., transitions that are not maximally incoherent or disconnected from the current frame.

Frames in which either P_s = 0 (physically impossible or survival-incompatible) or I = 0 (maximally incoherent, discontinuous, or pruned) are automatically excluded from the computation, normalization, and survival paths. Only frames with both P_s > 0 and I > 0 are included in N. Within N, a further filtering applies through the binary survival condition A(F) = 1, leaving the effective subset of viable frames N_alive.

This definition ensures that, at each transition, all probability normalization, path selection, and subsequent computations operate solely over the set of frames that are truly possible, coherent, and survival-compatible. This approach is directly consistent with the many-world interpretation of quantum mechanics, in which decoherence continuously generates a vast ensemble of branches at every quantum event [9,35]. The set of all possible frames (N) at each transition can be astronomically large—ranging from millions to trillions or more in realistic physical systems [4,36]—but only a subset (N_alive) satisfies the agent’s survival and coherence criteria. As the agent’s physical condition, coherence, and environment evolve, both N and N_alive dynamically change, reflecting the actual branching structure of subjective survival at every step. Frames with Ps > 0 and I > 0 but A(F) = 0 correspond to subjectively pruned branches (N_dead), which may still appear in external observers’ possible paths.

The FSM applies a filtering hierarchy at each decoherence event: first, frames must have nonzero survival probability P_s(F_t → F_t+1) > 0, ensuring they are physically possible, not forbidden by quantum law, and system dynamics. Second, they must maintain information coherence I(F_t → F_t+1) > 0, guaranteeing that the transition is not maximally incoherent or disconnected from the prior frame. Finally, they must satisfy the binary survival condition A(F) = 1, which restricts subjective continuity to survival-compatible frames. Formally, the viable set can be expressed as:

which defines the exact subset of frames that remain viable for subjective continuity. Together, these layered filters ensure that even if N is vast, the effective set of viable frames N_alive remains bounded and meaningful for continuity. In practice, this resolves issues about the scale of N, because the model automatically prunes implausible, incoherent, or dead frames, leaving only survival-compatible candidates for traversal.

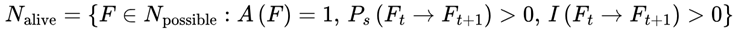
3. Theoretical Framework of the FSM

The FSM presents a formal mechanism for understanding how subjective consciousness persists across an underlying probabilistic and decohering universe.

3.1. Conscious Survival as Frame Navigation

Subjective experience proceeds through sequential alive frames in which A(F) = 1

Consciousness is modeled as navigation through a discrete sequence of frames {F₀, F₁, F₂,...}, where each frame F_i represents a complete, classically definite configuration of matter and energy, determined by decoherence-resolved quantum events.

Subjective experience consists only of sequences where survival conditions are continuously met. Consciousness threads through survival-compatible frames, forming an unbroken subjective path T_C.

3.2. Binary Outcome Model: Survival (1) and Death (0)

Subjective continuity filters transitions exclusively through survival-compatible frames. At each transition between frames, the outcome for a conscious agent is binary:

In subjective continuity, death is never experienced directly, and only the chain of survival is traversed.

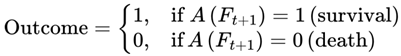
3.3. Formal Description of Frame Transitions

If F_t is the current frame at subjective time t, and F_t+1 be a possible next frame, the subjective transition condition or transition probability is as follows:

where:

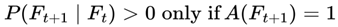
• P(F_t+1 ∣ F_t) is the probability of transitioning from F_t to F_t+1,
• A(F_t+1) determines whether the frame supports conscious awareness.

Paths leading to dead frames are pruned from the subjective survival tree. The experienced reality of a conscious agent is a filtered subset of the objective branching structure of reality. In the absence of additional coherence or preference structure, the transition probabilities P(F_t+1 ∣ F_t) default to the underlying quantum mechanical (Born rule) probabilities. This is filtered by the survival condition A(F_t+1) = 1. Only alive frames are assigned nonzero probability. Alive frames are renormalized accordingly (so that everything equals 1), ensuring that the survival filtering is consistent with standard quantum mechanics.

3.4. Frame Transition Rate and Decoherence Dynamics

In the FSM, each transition from one frame to the next is triggered by a decoherence event—when quantum uncertainty “collapses” and the system settles into a definite, classical state. This process is especially important in parts of the brain that support consciousness, such as networks of neurons [4]. The relevant decoherence timescale, denoted τ, sets the characteristic interval that can be defined either between or during frames. Subjective experience advances discreetly, "ticking" forward at the rhythm set by τ.

The subjective frame transition rate r is defined as:

r = r_max · τ

where r represents the number of frame transitions per second and r_max is the maximum frame rate for a particular substrate (e.g., 50hz for humans). Faster decoherence (smaller τ) produces more rapid subjective progression, whereas slower decoherence stretches the perceived flow of time. In the FSM, each conscious frame is experienced for a duration of τ seconds, so the frame rate r = r_max × τ directly quantifies the number of distinct conscious moments experienced per unit time.

The model does not assume coherence persists across frames but instead treats the resolution points—i.e., decoherence events—as the transition markers through which consciousness advances. To address the gap between rapid physical decoherence and slower experience-relevant time, the FSM defines an effective decoherence timescale (τ_eff,t). As a result, the frame transition rate becomes a function of the time or frame index, given by:

r_t = r_max · τ_eff,t

where:

• r_t: the frame rate at time (or step) t along the subjective survival path.
• r_max: the maximum possible frame rate for any particular substrate.
• τ_eff,t : the effective decoherence timescale governing the progression of subjective moments, determined both by the fastest physical decoherence possible in the local environment and by ongoing changes in cognitive stability and informational coherence.

The timescale τ varies dynamically with environmental noise, cognitive system stability, and informational coherence. As a result, the frame transition rate becomes a function of the time or frame index, denoted as r_t = r_max × τ_eff,t, capturing how the subjective rhythm of conscious experience fluctuates along a survival path.

Thus, the total number of subjective moments experienced in a given interval is:

where:

r_t: The instantaneous subjective frame rate, which governs the progression of subjective moments. The frame rate is “effective” because it depends on both local physical decoherence (e.g., quantum noise, environmental factors) and cognitive/informational factors (e.g., mental clarity, focus, stress).

If the effective decoherence time scale varies, the total number of subjective moments should be calculated by integrating the instantaneous frame rate:

or for discrete events or simulation steps:

where:

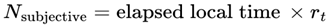
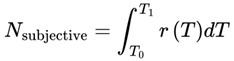
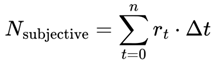
• Integral/sum: Both expressions accumulate the total number of moments experienced by summing the “fraction of a moment” contributed by each tiny time interval, weighted by the local decoherence timescale. If τ_eff is constant, this divides the total time by τ_eff; if it varies, the moments are “packed” more tightly or spread out as τ_eff shrinks or grows.
• N_subjective: The total number of subjective moments (or “conscious frames”) experienced over the interval. This represents the “ticks” of conscious awareness, which might differ from objective clock time if the conditions for consciousness change.
• T₀,T₁: The start and end times of the interval being considered (can be measured in seconds, minutes, etc., depending on context).
• T: Elapsed local (proper) time for the agent, measured according to the agent’s own subjective/process clock. T can be in seconds, minutes, hours, or any unit appropriate for the time scale of the process under consideration. In relativistic or time-dilated scenarios, T always refers to the local time actually experienced by the agent, not the time measured by an external or distant observer.
• d: denotes the index of the last alive frame before subjective death, that is, the endpoint of a lifetime survival path, such that A(F_d) = 1 and A(F_d+1) = 0. When specifically calculating the total number of subjective moments up to the agent’s final alive frame, d is used.
• r(T): The instantaneous subjective frame rate at each moment. This value determines how rapidly conscious frames occur—a higher r means that moments are packed closely together (time feels “fast” or “full”); a lower r means that moments are more spaced out (time feels “slow” or “fragmented”).
• Δt: The size of each time step in the simulation or dataset. For real neural or behavioral data, this might be the sampling interval; for a theoretical model, it is typically set to “1” for event-by-event counting.
• n: denotes the final event or frame index in the interval considered (for example, the endpoint of a simulation run, time segment, or experiment—not necessarily related to death). Use n, t, or e for general sums over any period.

This ensures that variations in cognitive or physical state are fully reflected in the subjective experience of time. Here, the formula reveals that subjective time may accrue at dramatically different rates for agents in different contexts, even as the passage of subjective experience feels locally normal. This captures how the subjective rhythm of conscious experience fluctuates along a survival path, with high-coherence, low-noise segments yielding faster frame traversal (r_t↑), whereas disordered or unstable conditions slow subjective time (r_t↓). Here, τ_eff,t is not the microphysical decoherence constant but rather an emergent, context-dependent timescale reflecting informational stability within the cognitive substrate. This aligns with known neural integration windows and connects quantum branching to classical psychological experience.

This dynamic modulation of τ provides a natural explanation for the subjective time distortions commonly reported in altered states, dreams, trauma, or near-death experiences. Variations in decoherence rates dynamically stretch or compress subjective time, offering a physically grounded account of phenomena such as perceived time dilation during critical events.

3.4.1. Cognitive Variance Interpretation of τ_eff,t

While τ was initially framed in terms of physical decoherence, it is more meaningful—particularly for conscious agents—to define it in relation to cognitive dynamics. In this model:

or, more explicitly,

where:

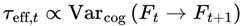
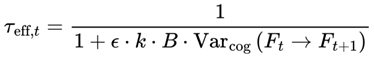
• Var_cog: represents the variance or instability across a local window of n consecutive frames—either the most recent n frames or a moving window within a chunk.
• k is a proportionality constant that determines the scaling between the cognitive variance and the subjective frame transition timescale. (state dependent, e.g., 0.01–0.1 s for humans).
• ϵ: a saturating parameter (set here, ϵ = 27 for humans).
• B: The scaling constant is empirically set so that the model’s predicted variance matches the observed subjective frame rates in both high-focus and unconscious states (e.g., 5 for humans).

k can be interpreted as the minimal frame update timescale under ideal, noise-free conditions. In practice, the proportionality constant k is bounded by known neural and psychological integration windows, with realistic values typically ranging from 0.01 to 0.1 s (10–100 ms). Exact values for k may vary between individuals, species, and contexts. For humans, empirical studies of perceptual binding and working memory suggest typical integration windows of 0.02–0.05 seconds (20–50 ms) [10,11], although longer windows of up to 100 ms are reported for certain tasks. The optimal value of k may vary across individuals, species, and contexts; other agents, such as animals, digital minds, or hypothetical nonbiological systems, could exhibit very different integration windows depending on their information-processing constraints. The proportionality constant k is tuned to reflect different states of consciousness: for normal wakefulness to peak alertness, k ranges from 0.01 to 0.05; for drowsiness and sleep, k ranges from 0.05 to 0.08; and for coma or deep unconsciousness, k is set at the higher end of the range, from 0.08 to 0.1.

In the FSM, cognitive variance typically ranges from 0.01 (high coherence) to 0.4 (highly fragmented or chaotic experience) but can exceed 0.6 in extremely pathological or near-terminal states. To ensure that the predicted subjective frame rates align with the empirical data for human and nonhuman agents, the raw cognitive variance (Var_cog) is multiplied by a scaling constant B in the tau/frame rate equation. B is calibrated so that, within the empirically observed range of cognitive variance, the resulting frame rates match those measured in humans—ranging from approximately 50 Hz in flow states down to 1–9 Hz in coma or unconsciousness. Without this scaling, the unadjusted variance would not yield frame rates that are biologically realistic.

Empirical studies have shown a strong correlation between subjective frame rates and brain states. In awake, alert humans, perceptual fusion and neural rhythms indicate a conscious update rate of approximately 20–50 Hz [10,11,27]. For humans, low to moderate cognitive variance values between approximately 0.01 and 0.3 span the full spectrum of normal waking consciousness—from highly focused “flow” states (~0.01–0.1), where attention is sharp and perceptible, through typical daily activities (~0.1–0.2), such as conversation, work, and learning, to lightly distracted, multitasking, or relaxed wakefulness (~0.2–0.3). As cognitive variance increases into the intermediate range (~0.3–0.5), states of sleep, deep fatigue, monotonous tasks, daydreaming, or drowsiness become more common, subjective experience becomes less vivid, and frame rates decrease, often to the lower end of the typical range (10–20 Hz). Values above 0.5–0.6 are likely to correspond to deep unconsciousness, coma, or a total breakdown of subjective continuity, where subjective frame rates fall below 10 Hz [31,32].

This scaling matches subjective reports; specifically, periods of high attention or “flow” correspond to fast, continuous subjective updates, whereas drowsiness, fragmentation, or unconsciousness is linked to slower, more discontinuous experiences [17,38]. Within the empirically grounded range, typical subjective frame rates for human brains are expected to fall from approximately 10 Hz in slow or disordered states up to 20–50 Hz in peak flow, alertness, or minimal variance [10,11]. Due to biological constraints, subjective frame rates above 50 Hz are not observed in humans, although higher rates may be possible for digital or engineered agents with much faster minimal integration timescales. Empirical studies have indicated that, in bright, alert conditions, most healthy adults can distinguish visual flicker up to approximately 50–60 Hz [11]. While rare individuals may momentarily detect slightly higher frequencies under optimal conditions, the practical upper limit for sustained, vivid conscious experience in humans is approximately 50 Hz. This value is consistent with the neural integration and gamma rhythm data and is used as the peak subjective frame rate in this model.

This formulation ensures that as cognitive variance or k increases (less integration, more instability, or slower timescales), τ_eff,t decreases, leading to a slower subjective experience (lower frame rate). Conversely, high coherence (low variance) and fast integration (small k) produce higher subjective frame rates, but the growth is always saturated and never exceeds empirical biological limits. In practice, k is set for each conscious state or agent on the basis of empirical integration timescales, whereas cognitive variance and coherence capture rapid local dynamics. Both factors combine—using the nonlinear frame rate equation—to yield realistic, empirically grounded predictions for subjective timing and continuity. The model is universal and fully interpretable for any agent or species, as all the parameters can be set empirically or by simulation.

Since both the integration timescale k and the scaling constant B are set empirically for each substrate, the frame transition framework and effective τ formula are universal. In other words, the model accurately predicts subjective frame rates for biological brains, animal nervous systems, digital agents, or any hypothetical conscious system as long as values are chosen for k, B, and coherence I. These parameters are directly interpretable, fit to data, and grounded in either physical measurement or empirical tuning.

ϵ is a saturating nonlinearity parameter that determines how quickly the frame rate decreases as the cognitive variance or integration timescale (k) increases. Tuning ϵ allows the model to match the empirically observed range and sensitivity of the subjective frame rates for different species or agents [10,11,27]. A higher ϵ produces a steeper, more sensitive response—the frame rate falls sharply when the variance or k increases, capturing rapid transitions between focused and fragmented states [28]. A lower ϵ yields a gentler, more gradual transition, making the system less sensitive to changes in cognitive dynamics. For humans, empirical fits suggest that ϵ ≈ 27 yields frame rates in line with observed data, but ϵ can be adjusted for other agents, states, or desired responsiveness [10,11].

Formally, I define cognitive variance as:

where:

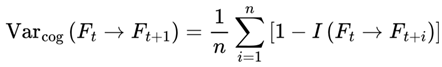
• Var_cog(F_t → F_t+1): The cognitive variance between the current frame F_t and its possible future frames.
• n: The number of future candidate frames or decoherence events in the survival path (the window size over which variance is computed).
• i: The index for summing over the n future frames.
• F_t: The current frame (the agent’s current conscious state or informational configuration).
• F_t+i: The i-th candidate future frame (a possible next state for the agent at time t + i).
• I(F_t → F_t+i): The coherence measure (information similarity, or quantum fidelity) between the current frame and the i-th candidate future frame.
• [1 − I(F_t → F_t+i)]: The degree of informational divergence (or incoherence) between frames; higher values indicate greater differences.
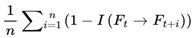• : The average divergence over all n candidate future frames; this gives the overall cognitive variance for the window.

This captures the degree to which upcoming frames diverge from the current frame, on the basis of coherence measure I. Greater divergence implies greater variance, reduced coherence, and a slowdown in subjective flow. Raw cognitive variance, as defined above, produces values in the range [0,1], directly reflecting the average informational divergence between frames.

In practice, the window size n for calculating Var_cog(F_t → F_t+1) is chosen to balance scientific sensitivity with computational tractability. Since the number of possible future frames explodes exponentially with each branching event, considering all possible candidate frames is neither necessary nor feasible. Instead, n should be set to a manageable value (e.g., 10–30), and the calculation should focus on the most likely or most relevant candidate frames—typically those with the highest transition probabilities. This can be accomplished by pruning low-probability branches, using probability-weighted Monte Carlo sampling, or drawing from a heuristic shortlist based on empirical or model-driven predictions. This approach aligns with how real cognitive systems and modern simulations efficiently handle branching futures, ensuring that Var_cog reflects meaningful local instability without becoming intractable.

To robustly align the model’s outputs with neurophysiological data and subjective reports, an empirical scaling constant B is applied in the tau/frame rate equation—not within the variance definition itself. The scaling constant B is typically set to a value of approximately 5 for healthy human brains, ensuring that the model’s predicted variance yields biologically realistic frame rates across all states, from peak alertness (≈50 Hz) to coma (≈1–10 Hz). With this approach, precise calibration can be achieved; specifically, B can be empirically set for any substrate—such as human brains, animal nervous systems, or digital agents—so that the predicted variances and frame rates match the characteristic timescales and information-processing limits of each system without altering the normalized structure of the underlying variance measure.

The subjective experience of time in the FSM is jointly determined by the information coherence between consecutive frames and the decoherence timescale (τ), which together sets both the frequency and the qualitative feeling of conscious moments. Cognitive variance, as operationalized here, is based on well-established information-theoretic and neuroscientific measures of state similarity, coherence, and temporal variance [11,28]. In this model, cognitive variance quantifies the average divergence between consecutive frames or candidate future states, capturing the stability or fragmentation of subjective experience.

High variance—such as sudden environmental change, stress, or noise—stretches the effective timescale (τ_eff,t) and lowers the frame rate (r_t), leading to a slower, more disrupted, or fragmented subjective flow of time. Conversely, low variance, as seen in routine or stable contexts, results in shorter τ_t and higher r_t, producing a rapid, smooth progression of experience. Thus, high coherence and low τ correspond to the vivid flow of focused states, whereas low coherence and high τ explain the full spectrum from stable consciousness to dreamlike or dissociative episodes.

3.4.2. Parameter Fitting and Generalization

To apply the τ/frame rate equation to any system—human, animal, digital agent, or AI—modelers should empirically determine the core parameters as follows:

• k (integration timescale): This is set to match the system’s minimal processing or integration window on the basis of experimental or computational studies (e.g., the shortest neural or algorithmic cycle, reaction time, or update step).
• B (variance scaling constant): Fit B so that the output variance range (Var_cog) covers the full observed spectrum from high coherence (focus) to low coherence (maximal fragmentation) in the target system. Physiological or behavioral data, such as flicker fusion rates, perceptual binding, or task performance limits, are used.
• ϵ (nonlinearity/sensitivity): Tune ϵ to ensure that the frame rate curve matches empirical data across states. For example, choose ϵ so that the model yields maximal frame rates in the correct range for high-alertness states and appropriately low rates for sleep, coma, or high-load digital agents.

Researchers may start with values recommended for humans (e.g., k = 0.02–0.06 s, B = 5, ϵ = 27) and then adjust as needed to fit their system’s observed timing, behavioral, or subjective reports. For digital or engineered agents, set k to the fastest reliable update cycle and fit B and ϵ to match the designed or measured frame rates.

3.5. Observer-Relative Survival Paths

Each conscious agent C navigates an individual survival path T_C comprising only frames in which A(F_i) = 1

Given multiple conscious agents C₁,C₂,…,C_n, their survival paths are generally distinct:

T_Ci ≠ T_Cj for i ≠ j

Observer-relativity implies the following:

• An observer may witness another agent's apparent death.
• However, from the perspective of the dying agent, survival may continue along a distinct, unshared branch.

Thus, death is a local phenomenon in an observer’s subjective path, and each consciousness privately filters its survival-compatible experiences through the multiversal frame network.

3.6. Formalization Through Survival Graphs

To further formalize the FSM, the structure of frames and transitions can be represented as a directed graph. This representation provides a rigorous mathematical foundation for modeling subjective continuity as a dynamic traversal across survival-compatible configurations of reality.

The survival graph is as follows:

G = (V, E)

where:

• V is the set of all frames F,
• E ⊆ V × V is the set of directed edges representing allowable transitions between frames.

Each frame F ∈ V is assigned a binary survival value, A(F) ∈ {0,1}, where:

• A(F) = 1 if the frame sustains the conscious agent C,
• A(F) = 0 otherwise.

Transitions (edges) between frames are subject to survival conditions.

A directed edge (F_t → F_t+1) ∈ E exists if and only if:

A(F_t+1) = 1

Transitions to dead frames are pruned from the graph relative to each conscious agent's survival conditions. Transition weight function:

w: E → [0, 1]

where w(F_t → F_t+1) represents the transition probability from frame F_t to frame F_t+1, which is conditioned on survival.

3.6.1. Normalization Condition

For each frame F where A(F) = 1, the sum of the transition weights over all outgoing survival-compatible transitions satisfies:

where the sum is taken over all frames F′ such that A(F′) = 1.

This normalization ensures that the agent’s subjective experience proceeds probabilistically but continuously across survival-compatible frames. If no additional agentic or coherence weights are specified, the default transition weight w(F_t → F_t+1) is given by the Born rule probability amplitude squared for the corresponding frame, subject to A(F_t+1) = 1:

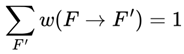
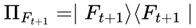where  is the projector onto the outcome frame.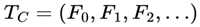

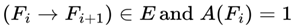
All other dead frames (A(F_t+1) = 0) are assigned zero probability and omitted from normalization.

Subjective continuity for a conscious agent C corresponds to the existence of an infinite or indefinitely extending survival path:

such that for all i ≥ 0:

Traversal of this path constitutes the subjective experience of time, existence, and survival for the conscious agent. The subjective experience of consciousness can be understood as navigation through a dynamically filtered survival graph, in which frames are selected based on survival compatibility, and subjective continuity emerges as unbroken traversal through the alive subgraph of reality.

3.7. Binary Interpretation of Survival Paths

Within the FSM, each frame F can be encoded as a binary value through the survival function:

A(F)∈{0, 1}

where 1 indicates survival (subjective continuity) and 0 indicates death (subjective termination).

From the perspective of a conscious agent, a survival path T_C is interpretable as a binary sequence comprising only alive frames.

S_C = (1, 1, 1,…)

Here, T_C denotes the ordered sequence of alive frames (the survival path), whereas S_C denotes the associated binary survival code or sequence encoding the agent’s experience. Dead frames (where A(F) = 0) exist externally in the full structure of frames but are pruned from the subjective binary sequence. In the experienced path, the S_C is all 1 s; across the full frame graph, it encodes the alive/dead status of all frames.

Thus, subjective continuity through reality can be understood as the traversal of a binary survival chain, wherein consciousness propagates through frames preserving informational existence.

This framing connects the FSM naturally to binary information structures and offers potential bridges to information-theoretic descriptions of reality.

where each 1 indicates successful survival through a frame and 0 represents subjective termination (nonexperienced branches).

While death frames (A(F) = 0) are pruned from the agent's experienced continuity, the pattern of survival itself — the structure and frequency of traversed frames — may encode meaningful informational properties about the nature of reality.

Specifically:

• Entropy of Survival Paths: The degree of randomness versus order in survival sequences could reflect underlying structural regularities or instability in the frame network.
• Compression Possibility: If survival sequences are highly compressible, this would suggest patterned, nonrandom dynamics guiding survival threading. High-entropy sequences imply stochastic survival landscapes.
• Error-Correction Analogy: Consciousness navigating survival-compatible frames resembles an information-preserving process, selectively "correcting" for decoherence-induced branching threats.
• Information-Theoretic Interpretation: Subjective continuity itself may be regarded as the maintenance of an informational thread through an environment characterized by probabilistic frame transitions.

Survival threading does not merely constitute biological or physical persistence but is an emergent informational phenomenon woven through the probabilistic landscape of frames.

3.8. Probabilistic Existence of Survival Paths

Given:

• A discrete network of frames F, each assigned a survival value A(F) ∈ {0,1}.
• Transition probabilities P(F_t+1 ∣ F_t) defined over frame pairs, conditioned on A(F_t+1)=1.
• The multiverse structure infinitely branches due to quantum decoherence dynamics, generating an unbounded number of future frame possibilities at each point.

If the probability P(F_t+1 ∣ F_t) > 0 for at least one F_t+1 satisfying A(F_t+1) = 1 at every frame transition, then:

Theorem (Survival Path Existence):

Given the infinite branching and nonzero survival probabilities at each transition, at least one infinite sequence of frames {F₀, F₁, F₂,...}, in which A(F_i) = 1 for all i, almost surely exists.

This follows from standard arguments in probabilistic graph traversal and percolation theory: in infinite graphs with nonzero transition probabilities at each step, infinite survival paths almost certainly exist.

Thus, the subjective survival of conscious agents — even under conditions of increasing improbability or entropy — is probabilistically guaranteed within the multiversal frame network, provided survival remains possible at each transition. This follows from the infinite tree traversal results in probability theory, such as the Borel–Cantelli Lemma and percolation path existence of theorems [39,40,41].

3.8.1. Formal Sketch Using the Infinite Traversal Theorem

An appeal to infinite tree traversal theorems can further support survival path existence. Given a branching frame graph G = (V,E) in which every frame transition has a nonzero probability of leading to at least one survival-compatible frame, it follows from percolation theory and probabilistic path arguments (similar to applications of the Borel–Cantelli lemma) that with probability 1, an infinite path composed solely of survival-compatible frames {F₀, F₁, F₂, ...} exists.

Specifically, at each node (frame), a nonzero transition weight to at least one node with A(F) = 1 exists. Since the branching factor is infinite (due to decoherence), the measure of the set of infinite survival paths is nonzero. Thus, subjective continuity along an endless survival path is probabilistically guaranteed, even as overall survival path density may thin over time.

This survival path existence proof assumes that at each frame transition, survival remains locally possible, meaning that there is always at least one accessible next frame satisfying A(F) = 1 with nonzero probability. If no survival-compatible transitions exist at any point (i.e., the survival probability drops to zero), subjective continuity would terminate. Thus, the survival guarantee relies on the persistent availability of survival-compatible frames across branching transitions.

3.9. Passive vs Active Navigation of Survival Paths

In the basic FSM, the survival path traversal is treated as passive; specifically, the conscious agent continues through whichever survival-compatible frames arise without exercising active control. However, broader interpretations are also possible under this model. If consciousness has any capacity to influence frame selection among survival-compatible options—such as through intentional states, informational coherence, or higher-order agency—then navigation could be slightly biased rather than entirely passive [42,43,44]. Possibilities include purely passive navigation (random traversal determined solely by decoherence dynamics), weak active navigation (mild preferences influencing transition probabilities among alive frames), and strong active navigation (significant steering toward preferred realities). While purely passive survival threading suffices to support the model’s core dynamics, future work could formalize degrees of agency through a survival frame preference function S(F), which assigns transition weights based on informational coherence, intention alignment, or system stability [45]. Mathematically, this would introduce slight biases among alive frame transitions without violating the fundamental survival constraint A(F) = 1.

For simulations or formal models incorporating weak active navigation, frame transitions can be probabilistically weighted not purely randomly but according to a survival frame preference function, S(F). Specifically, at each frame F_t, the transition probability to a candidate frame F_t+1 can be defined as proportional to the product P_s(F_t → F_t+1) × I(F_t→F_t+1) × S(F_t+1), where P_s(F_t → F_t+1) is the survival probability of the frame, I(F_t → F_t+1) is the information coherence (or similarity) between consecutive frames, and S(F_t+1) encodes the agent’s preference weighting [44].

In scenarios that involve intentional action or focused decision-making, peaks in S (agentic preference) can be correlated with activation in specific brain regions associated with intent, planning, or motor execution, such as the motor cortex, hippocampus, and prefrontal cortex [43,44,46]. In these cases, the FSM transition probability for a given frame may be informally weighted higher where regional activity aligns with the modeled intent or action—effectively, the brain ‘votes’ for the next frame with its pattern of activation, allowing for empirical mapping of S using neuroimaging data, brain stimulation, or electrophysiological recordings [43,46]. At the same time, reflexes, habitual behaviors, and automatic cognitive processes are typically represented in the background content of each frame, operating outside the main focus of conscious attention but still influencing behavior and future experience. The FSM accommodates both agentic, intentional action (foreground, high S) and automatic or reflexive processes (background, low S) within the same theoretical framework, allowing for a continuum between deliberate and automatic action, as reflected in patterns of brain activation and transition probabilities.

In diffuse, passive, or low-agency states—such as deep sleep, anesthesia, or distributed emotional states—S becomes less regionally specific or effectively uniform (S ≈ 1 across alive options), and transitions are determined more by coherence (I), information dynamics, and environmental constraints than by focal agency [30,31]. In the FSM, S reflects the agent’s dynamic prioritization of energy, intention, and action, flexibly encoding both survival-driven and goal-driven motivation as adaptive responses to internal and external conditions. This framework accommodates both strong agency and pure passivity in a way that matches observed neural and behavioral data [30,31,44,46]. Crucially, the effective range of agentic preference (S) is modulated by the system’s information coherence (I): when I is maximal, S can span its full biologically possible range (e.g., ℝ⁺ to 5 for a given species); as I decreases, the maximum achievable S is reduced, reflecting a diminished capacity for intentional action. In low-coherence states (e.g., deep sleep or coma, I ≲ 0.6), S defaults to 1, indicating passive or minimal agency. Thus, for intermediate I (e.g., I = 0.80), the system expresses a fraction of its maximal agency, with S limited to values below its species-specific maximum.

In the weak active navigation case, S(F_t+1) > 1 for frames that are better aligned with the agent’s informational coherence, structural stability, or intentional preferences. This increases the relative probability of transitioning into those preferred survival paths while still preserving normalization over all alive frames [43,45]. For clarity, P_s(F_t → F_t+1) reflects decoherence-conditioned transition likelihoods, whereas S(F_t+1) acts only within the filtered subset where A(F_t+1) = 1, thereby preserving the survival constraint.

Through this refinement, the ways in which conscious agents might subtly steer their survival trajectories within the overall constraints of decoherence-driven frame transitions can be formally explored without violating the binary survival condition A(F) = 1. The survival frame preference function S(F) is defined as the agent-specific weighting assigned to each survival-compatible frame F(A(F) = 1), representing bias, intention, or learned preference. S(F) may be understood as an emergent preference weight, grounded in the agent’s learned expectations, motivational drives, or intentional states, as formalized in the Bayesian brain and reinforcement learning models [43,44,47]. In biological agents, S often reflects evolved reward–avoidance systems: frames linked to beneficial outcomes (e.g., food, reproduction, social bonding) tend to have higher S values, while harmful or threatening frames carry lower or negative S [43,44,46,68,72,73]. This bias guides the survival path toward pleasurable states and away from harmful ones, with reinforcement processes adjusting S over time based on experienced consequences [43,44,46]. S can be set by empirical measures (such as behavioral choice, neural activation, or policy weights) or theoretically (utility, information fit, etc.) and can be varied in simulations or experiments to study its effects on subjective continuity and survival path dynamics. Importantly, S is modular and cannot override the binary survival constraint, ensuring that the model remains logically consistent while accommodating a wide range of agentic behaviors.

3.9.1. How Agentic Preference Weight (S) Links to Chunks

The agentic preference weight (S) is linked to chunking by providing an additional source of stability or instability within a chunk. When S remains stable across frames, agentic intent or motivation is consistent, helping to maintain the coherence and temporal unity of the chunk [44,46,48]. Gradual or abrupt shifts in S increase internal variance and can signal a chunk boundary—reflecting a change in goals, context, or state of mind [49,50]. During transitions between distinct behavioral or experiential chunks (e.g., reading to walking), S typically drops to a low, passive baseline—governing transitions via P_base—before rising again as agency re-establishes in the new context. This explains why intentional control is high within chunks but briefly low during context shifts [46,48].

3.10. Informational Structure of Transition Distributions

The transition probability distribution over survival-compatible frames can be further characterized through an examination of its internal structure. Two derived metrics—Shannon entropy [51] and transition variance—provide ways to interpret how tightly or diffusely the observer’s future survival paths are distributed at each step. Here, P(F_t+1 ∣ F_t) denotes the normalized, survival-filtered transition probability to each candidate next frame, as defined in Section 3.13 (the main transition probability equation).

The Shannon entropy of the transition distribution is defined as:

This measures the uncertainty in frame selection: low entropy reflects strong survival bias toward a narrow set of frames, whereas high entropy indicates a broad, ambiguous set of options.

The spatial variance of the transition indices is given by:

where μ is the weighted average frame index. :

This reflects the dispersion of viable next frames in the configuration space, capturing how localized or widespread the survival path is projected to be. These metrics are especially useful in simulations and visualizations, providing insights into coherence collapse, decoherence-driven spread, and chunk-induced filtering.

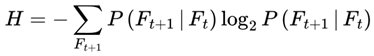
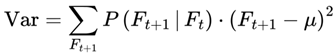
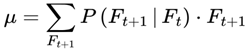
3.11. Informational Coherence and Transition Weighting

In addition to binary survival filtering, the model can be extended by incorporating an information coherence function to modulate the likelihood of transitions between frames. This refinement introduces a cognitive and structural continuity bias into frame selection, which helps explain the high consistency of perceived reality:

where:

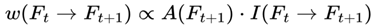
• A(F_t+1) ∈ {0,1} is the survival function, as defined previously.
• I(F_t → F_t+1) is the information coherence function, quantifying the informational, cognitive, or structural consistency between the current frame and the candidate future frame.

This formulation implies that even among survival-compatible frames (A(F_t+1) = 1), the most informationally coherent future frames are more likely to be selected. Coherence can represent continuity in memory, a stable environment, logical narrative flow, or self-consistency.

Implications:

• Frames that preserve prior informational content (e.g., memory traces, environmental layout, and cognitive integrity) have higher transition probabilities.
• Frames that break coherence (e.g., hallucination, memory loss, and chaotic shifts) are less likely to be experienced, even if they are survivable.
• This helps explain why lived reality feels smooth and structured, despite the probabilistic and decohering nature of the underlying universe.

Normalized form:

This normalized form ensures that the total transition probability from any given frame is 1 while favoring coherence among possible survival paths. Thus, the complete unnormalized transition weight would be:

or more explicitly,

The full transition probability is then obtained by normalization over all viable next frames:

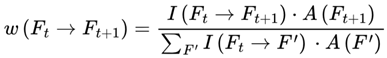
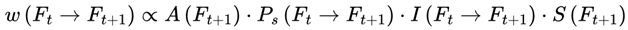
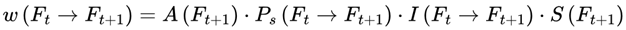
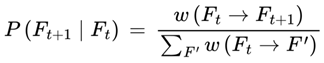
3.12. Frame Continuity Transition Equation

Building upon the definition of the transition weight function w(F_t → F_t+1), the fully normalized transition probability from frame F_t to F_t+1 is determined using a unified equation that integrates survival filtering, decoherence likelihood, informational coherence, and agentic preference weighting:

where:

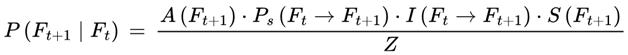
• A(F_t+1) ∈ {0,1} enforces survival compatibility.
• P_s(F_t → F_t+1) ∈ [0,1] captures the likelihood of a decoherence-conditioned transition.
• I(F_t → F_t+1) ∈ [0,1] quantifies the informational coherence between the current and candidate frames.

S(F_t+1) ∈ $R$⁺ represents the agent's preference bias among the viable options.

The denominator serves as the normalization constant Z, ensuring that all survival-compatible transition probabilities from a given frame sum to 1:

The constant Z ensures that all survival-compatible transition probabilities from a given frame sum to 1:

This formulation defines the probability that a conscious agent will subjectively transition from one alive frame to another on the basis of survival constraints, informational continuity, decoherence dynamics, and agentic preference. The denominator acts as a normalization constant, ensuring that all probabilities across viable transitions sum to 1 — creating a unified, normalized framework for subjective frame transitions.

This is formally expressed as:

Without this normalization step, this equation provides only relative weights—not valid probabilities. This final expression confirms that the model respects probabilistic consistency while introducing structured biases toward continuity and coherence.

While each component in the base transition formula is treated independently, in real cognitive systems, these weights can influence each other dynamically. For example, a strong structural preference S(F) for success may increase the likelihood of preparatory behaviors, which in turn increases the coherence I(F_t→F) between current and successful future frames. Conversely, low structural expectations (e.g., fear or avoidance) can lower both preparation and coherence, reinforcing failure paths. These self-modulating dynamics further bias survival-compatible frame selection toward belief-aligned trajectories, highlighting the interplay between intention, structure, and perceived coherence. Extensions of the FSM could explicitly model such dependencies by allowing I and S to be joint functions, but for the purposes of this paper, they are treated as independent unless otherwise specified.

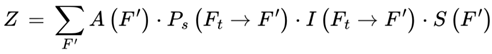
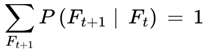
3.12.1. Incorporating Chunk Dynamics

The transition equation to model also transitions between coherent chunks. Let chunk_t denote a chunk at time t, consisting of frames {F_t,F_t+1...,F_t+n}. Each chunk is a contiguous (i.e., consecutive in time) segment of frames that all exhibit low internal variance, high informational coherence, and continuity in agentic preference. Chunks are discovered post hoc on the basis of temporal clustering of informational similarity and survival persistence. Chunking and episode boundaries in the FSM are inspired by empirical and theoretical work on event segmentation and perceptual organization [21,29,52,53] but are here formalized as an information-theoretic process governed by cognitive variance and coherence. Thus, the effective transition weight across chunks can be represented as:

where:

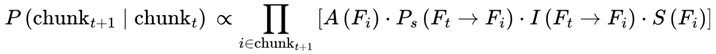
• A(F_i) ∈ {0,1}: binary survival indicator
• P_s(F_t → F_i) ∈ [0,1]: decoherence-conditioned survival probability
• I(F_t → F_i) ∈ [0,1]: informational coherence from the chunk origin to F_i
• S(F_i) ∈ $R$⁺: agentic preference weighting

This expression formalizes how transitions between coherent mental “episodes” (chunks) can be modeled probabilistically but are still constrained by survival and structural continuity. The chunk transition formula reduces to the original frame-to-frame transition model when the chunk contains only one frame:

Let chunk_t+1= {F_t+1} and chunk_t = {F_t}; then,

This confirms that the chunk-level model is a generalization of the individual frame transition rule.

To model both coherent narrative continuation and possible abrupt jumps between unrelated frames, the FSM utilizes the Unified Frame Survival Transition equation:

In this equation:

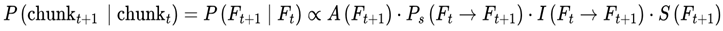
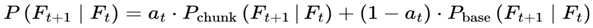
• P_chunk(F_t+1 ∣ F_t): the probability of continuing within a coherent chunk.
• P_base(F_t+1 ∣ F_t): the original decoherence-based transition.
• α_t ∈ [0,1]: dynamically adjusts on the basis of local stability.

The chunk-based transition probability is defined as:

where:

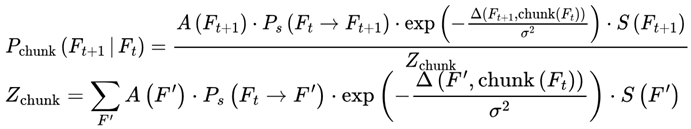
• P_s(F_t → F_t+1) is the decoherence-conditioned survival probability (likelihood of resolving into this frame).
• A(F_t+1) enforces the survival constraint.
• Δ(F_t+1, chunk(F_t)) is the decoherence or informational distance between the new frame and the chunk.
• σ² controls how tight the chunk’s influence is.
• S(F_t+1) is the agent’s preference (e.g., structural or narrative alignment).
• Z_chunk represents normalization, so all chunk probabilities sum to 1.

When the chunk is of size 1 (i.e., chunk(F_t) ={F_t}, the chunk-based transition equation simplifies. The decoherence distance between the chunk and candidate frame is as follows:

This is plugged into the chunk-based transition probability:

As σ² → ∞, the exponential term approaches 1, yielding:

However, if we drop the exponent and directly apply the informational coherence I(F_t → F_t+1), the equation reduces to the original frame-level transition form:

If the chunk coherence fails or destabilizes, the transitions revert to the base survival transition:

which expands to the core frame survival transition function:

This form governs ordinary transitions between frames on the basis purely of survival, coherence, and decoherence rate mismatches.

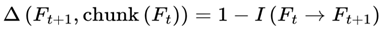
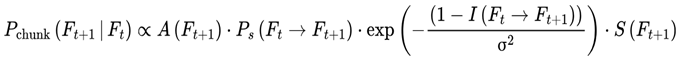
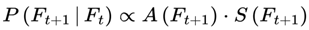
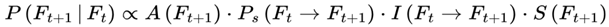
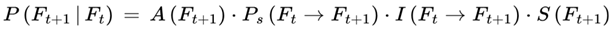
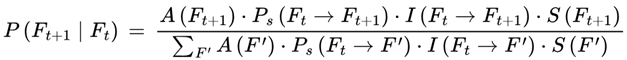
3.12.2. Dynamic Chunk Confidence Coefficient

The blending factor a_t determines how strongly the transition process favors remaining within a coherent chunk of frames versus defaulting to the broader decoherence-driven survival distribution. It is computed dynamically on the basis of the structure of recent transitions:

a_t = exp(−λ · Var_window)

where:

• a_t: Dynamic chunk confidence coefficient, recalculated at each time step.
• λ: A sensitivity constant controlling how rapidly it decreases with increasing instability.
• Var_window: The moving average of cognitive variance, defined above, which quantifies local volatility in the survival trajectory

λ is a nonnegative sensitivity constant that determines how strongly chunk confidence (a_t) responds to changes in cognitive variance. Higher values of λ make the model more sensitive to abrupt changes or instability, causing a_t to drop rapidly in periods of high variance and making the system more fragile. Conversely, lower values of λ produce a more tolerant or stable system, making it more robust to cognitive noise and allowing chunk confidence to be preserved even as variance increases. The optimal value of λ can be set through empirical calibration (using neural or behavioral data) or chosen as a theoretical parameter in simulation studies.

To quantitatively capture recent informational stability, the windowed cognitive variance at each event is defined as a moving average of cognitive variance across the most recent n decoherence events. This measure reflects both the immediate and sustained volatility in subjective continuity, ensuring that the model is sensitive to local fluctuations as well as longer-term changes in informational coherence. By averaging the cognitive variance over a sliding window, the model robustly detects periods of stability and instability, providing a principled basis for dynamically modulating chunk confidence and episode segmentation. Specifically, at each time step or decoherence event, the windowed variance is computed as:

where:

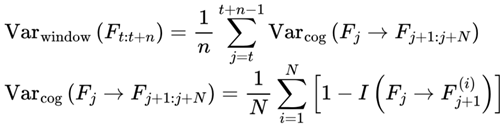
• Var_window(F_t:t+n): The overall cognitive variance computed across a window of n consecutive frames, representing the local stability or instability of experience within a time chunk.
• Window size (n): The number of recent events (frames) included in the window for the average.
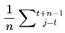• : For each frame F_j in the window (from t to t + n − 1), compute the cognitive variance for its possible next states, and take the average for all frames in the window, providing a summary measure of local cognitive (in)stability over time.
• Var_cog(F_j → F_j+1:j+N): The cognitive variance at frame F_j, calculated as the average informational divergence between F_j and its N possible next candidate frames.
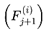• : Each possible frame into which the agent/system can transition from F_j at the next step; N is the total number of such candidates.
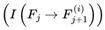• : A measure of how similar (or “coherent”) the present frame is to each candidate next frame; it ranges from 0 (completely different) to 1 (identical).
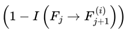• : Quantifies how much the next candidate frame differs from the current frame; higher values indicate greater instability or unpredictability.
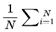• : Compute the mean divergence for all possible next frames at each time step, capturing the expected variability in the immediate future.

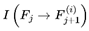Here, n is the window size (i.e., the number of recent decoherence events), and N is the number of candidate next frames at each event.  is the information coherence between the current frame and the i-th next-frame candidate. By averaging over both multiple next-frame possibilities and a window of recent events, this measure smooths out transient fluctuations and captures sustained shifts in informational volatility. The result is a robust, dynamically updated index of local cognitive stability, which governs the chunk confidence coefficient and episode segmentation in the model.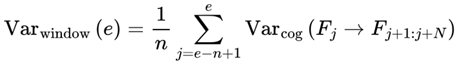

In practice, Var_window is calculated over the set of candidate frame indices at each step, weighted by their respective transition probabilities. The window size, n, determines the number of recent decoherence events included in each chunk for assessing windowed cognitive variance and can be flexibly adjusted to control the degree of temporal smoothing. While n is typically chosen on the basis of simulation objectives or to align with empirically observed integration windows, values in the range of 10–30 are common in the literature for modeling perceptual and cognitive episodes [10,11,29]. Ultimately, n should be tuned to reflect the relevant phenomenological or neurocognitive timescale appropriate to the context of the model [10,29].

To formalize this, the windowed cognitive variance at each event is computed as the average lack of coherence between the present frame and its available next-frame candidates, smoothed over the most recent n decoherence events. This approach ensures that the chunk confidence coefficient is sensitive not only to sudden fluctuations but also to sustained changes in informational stability across time.

Unless otherwise noted, all windowed averages are computed over the most recent n events along the survival path. Specifically, the windowed cognitive variance is defined as:

where:

• Var_window(e):

The windowed cognitive variance at decoherence event e, summarizing the local cognitive (in)stability over the most recent n events (frames).

• Window size (n):
• The number of recent events (frames) included in the window for the average.
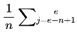• : For each frame F_j in the window ending at event e (i.e., the last n frames from e − n + 1 to e), compute the cognitive variance, then average these values.
• Var_cog(F_j → F_j+1:j+N): The cognitive variance at frame F_j, which is calculated as the average divergence between F_j and its N possible next candidate frames.
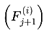• : Each possible frame the system could transition into from F_j at the next step; N is the number of such candidate frames.
• Information coherence and divergence: For each candidate next frame, compute the information coherence 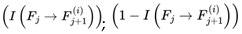quantifies how different each candidate is from the current frame.
• Averaging across windows and candidates: First, the divergence across all N candidates at each step (using Var_cog) is averaged across the n recent steps (window), yielding Var_window(e).

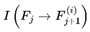Here, n is the window size (i.e., the number of recent decoherence events), N is the number of candidate next frames at each event, and  is the information coherence between the current frame and the i-th next-frame candidate. By averaging over both multiple next-frame possibilities and a window of recent events, this moving average captures the local volatility in subjective continuity, ensuring that chunk confidence a_t is sensitive to both transient fluctuations and sustained periods of instability in cognitive dynamics.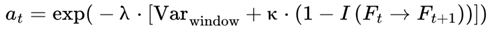

While Var_window(F_t:t+n) is typically used when entering a chunk—averaging variance over the chunk’s initial window—Var_window(e) is used during the chunk, providing a rolling measure of recent informational volatility as the agent progresses through the episode.

In more advanced forms of the model, a_t may also incorporate an informational coherence penalty I(F_t → F_t+1), reflecting how internally consistent a transition is with the prior frame. The generalized confidence equation becomes:

• κ: A nonnegative weighting constant that determines how strongly the informational coherence penalty (1 – I(F_t → F_t+1)) influences the chunk confidence a_t.
• I(F_t → F_t+1) ∈ [0,1]: A function measuring how well the transition aligns with the chunk structure or informational integrity. High coherence suppresses the penalty; incoherent transitions lower a_t.
• Interpretation:
• When recent transitions are stable (low variance) and coherence is high, a_t ≈ 1, the system strongly favors transitions that preserve chunk continuity.
• When variance is high or coherence is low, a_t → 0, the system deactivates the chunk and reverts to the base survival model, ensuring ongoing conscious continuity even during structural collapse.
• When κ = 0, a_t is determined solely by the local variance of recent frames (Var_window). As κ increases, transitions with low informational coherence (I ≈ 0) are penalized more heavily, causing a_t to drop sharply for incoherent transitions, thereby favoring the persistence of stable chunks. Higher values of κ increase the impact of coherence on a_t, making the system more sensitive to abrupt or incoherent transitions. The optimal value of κ depends on the sensitivity of the agent or system to abrupt or incoherent transitions and can be calibrated through empirical data (e.g., neural dynamics, behavioral experiments) or chosen for theoretical exploration in simulations.

3.12.3. Chunk Definition (Event Index Form)

In the FSM, a chunk is defined as a contiguous sequence of decoherence events indexed by e, during which the windowed cognitive variance remains below a chosen coherence threshold. Formally, a chunk C_k corresponds to the interval [e_k,e_k+m], where e_k and e_k+m are the indices of the starting and ending decoherence events (corresponding to frames F_ek and F_ek+m), respectively. For all e in this interval/range, the windowed cognitive variance remains below the chosen coherence threshold:

Var_window(e) < threshold

This ensures that each chunk is a contiguous sequence of events with sustained informational stability, where Var_window(e) is the windowed cognitive variance at event e.

Here, the ‘threshold’ is a tunable parameter that represents the maximum allowable windowed cognitive variance for frames or events to be included in the same chunk. The threshold can be set empirically, match known phenomenological or neurocognitive integration windows, or be varied in simulations to explore the impact of chunk strictness on subjective continuity. This approach is inspired by empirical and theoretical work on event segmentation and perceptual chunking in neuroscience and cognitive psychology [11,53].

A decrease in information coherence (I) below the chunking threshold creates a chunk boundary, which also serves as an amnesia barrier—a point at which subjective experience is preserved but memory integration fails across the boundary. The degree of memory loss or integration difficulty that occurs depends on the “hardness” of the chunk boundary: soft boundaries (where coherence dips only briefly or partially) allow for greater recall and continuity across episodes, whereas hard boundaries (where coherence drops sharply and deeply) create stronger amnesia barriers and greater separation between chunks. While amnesia barriers reduce memory integration across episodes, information from before a chunk boundary can often be recalled or reconstructed via contextual cues, overlapping chunks, or associative networks, although with lower fidelity and greater effort [7,10,29,53].

Because each event e in the realized survival path typically advances the frame index by one, chunk boundaries segment the subjective timeline into episodes of relative informational stability. In more complex models involving skips, loops, or nonmonotonic traversal, grouping by e ensures that chunking follows the actual sequence of subjective updates, preserving stepwise continuity and coherence in the experienced survival path.

At each decoherence event e, the model evaluates all transition probabilities from the currently realized frame F_e to its set of candidate next frames. After a single outcome is selected, the event index increases (e → e + 1), and the process repeats for the new present frame. This indexing allows both analytical and simulated stepwise mapping of subjective continuity, chunk dynamics, and survival path evolution, with each event representing a discrete “tick” of conscious experience.

4. FSM Implications

4.1. Subjective Immortality

In the FSM, death is never subjectively experienced. At each transition, a conscious agent either continues into an alive frame (where A(F_t+1) = 1) or would otherwise transition into a dead frame (where A(F_t+1) = 0), which remains inaccessible to subjective awareness. Thus, from the first-person perspective, subjective continuity is unbroken, even when survival appears astronomically improbable from an external, objective standpoint. This formalizes and extends the core intuition behind quantum immortality, embedding it within a structured framework of binary frame outcomes and decoherence-defined transitions.

From the observer’s internal perspective, a survival thread—however improbable—extends indefinitely into future frames.

4.2. Relativity of Death Across Survival Paths

In the FSM, subjective survival is defined relative to the conscious observer’s own survival path, T_C, through the survival graph G = (V,E). This implies that death is observer relative: an individual may cease to exist within the survival path of another observer without necessarily ceasing to exist within their own path.

From one observer’s perspective, another agent may appear "dead," whereas from the dying agent’s subjective perspective, continuity persists uninterrupted. Thus, death is not an absolute event across the multiverse but rather a divergence of survival trajectories—revealing the deeply personal and decentralized nature of existence within the quantum branching structure.

In the FSM, subjective consciousness is “immortal” only in the sense that it persists along its own survival-threaded path for as long as survival-compatible frames remain; when no such frames exist, subjective experience ends but never from the inside as an observable event.

4.3. Consciousness Bias

The FSM introduces a profound consciousness bias in the structure of experienced reality.

While the external universe may evolve probabilistically across an ensemble of possible frames, the subjective experience of a conscious agent is biased toward survival-compatible outcomes.

This implies that the perceived probabilities of survival may be radically different from the objective, external probabilities that are calculated across the full multiverse. For example, survival through a catastrophic event that objectively has a near-zero probability becomes subjectively certain from the survivor’s perspective. Reality appears to be unusually "favorable" or "survivable" to each conscious agent because of the self-filtering nature of survival path threading.

This consciousness bias provides an explanatory framework for phenomena that, from a subjective view, might appear improbably fortuitous—without invoking supernatural forces or external interventions. The survival filtration process not only maintains conscious continuity but also naturally biases an observer’s survival path toward frames that exhibit physical regulatory and informational stability.

Frames that are too chaotic or entropic to support cognitive persistence are pruned from the subjective trajectory.

This bias becomes particularly evident at the chunk level. Chunks with high decoherence rates (low τ), high survival probabilities P, strong informational coherence I, and consistent preference alignment S are statistically more likely to persist in the subjective survival thread. As such, consciousness not only prefers survivable frames but also dynamically stabilizes within coherent temporal segments—akin to mental "episodes" or subjective narrative arcs.

Despite the vast branching structure of the multiverse, the experienced world maintains familiar patterns, stable laws, and recurring structures as a natural consequence of survival dynamics.

4.4. Private Multiverse Threads

In traditional many-world interpretations, all possible outcomes exist, and branching is objective and universal [9,35]. However, the FSM emphasizes private, observer-relative survival paths.

Conscious agent C experiences a distinct survival path T_C, formed exclusively by sequences of frames in which A(F_i) = 1

This means that the death of another agent, as perceived within one's own survival path, does not necessarily entail subjective death for that agent within their own survival path. Additionally, multiple agents’ paths may initially overlap but diverge over time, as different frame transitions selectively filter experiences on the basis of survival compatibility. Every conscious observer rides a unique survival thread through reality, experiencing a private sequence of survivable universes.

The multiverse is not experienced uniformly by all agents; it is fractally partitioned into private multiversal experience threads, each determined by local survival conditions.

This resolves apparent paradoxes about observed deaths, improbable survivals, and identity across branching realities by rooting subjective experience in private frame filtration rather than universal branch participation.

4.5. Subjective Novelty and Continuity

While the objective configurations of frames may feature redundancy or structural recurrence across the multiverse, the subjective continuity of a conscious agent’s survival path ensures that each frame transition is experienced as novel.

The traversal itself — the active threading through survival-compatible frames — creates a first-person sense of freshness and flow. Every moment is lived uniquely, even if the underlying physical structure of the frames shows repetition. Subjective time emerges not from the uniqueness of each frame but from the uniqueness of the conscious experience of survival through successive frames.

4.6. Altered States, Sleep, and Fragmented Consciousness

Periods of sleep, unconsciousness, or altered states of awareness do not disrupt the underlying survival path of a conscious agent within the FSM. During sleep or altered states (including pharmacologically induced experiences), the agent continues to traverse survival-compatible frames (A(F) = 1), ensuring that the survival thread remains unbroken [32,45]. However, as information coherence (I) decreases, the ratio of dead (A(F) = 0) to alive (A(F) = 1) frames increases at each transition step. This means that, while the agent always threads through alive frames, it becomes progressively more difficult to find viable frames as I decreases—effectively stretching out subjective time, increasing the cognitive variance, and reducing the frame rate [11,17,54]. As a result, the richness and vividness of experience are diminished, and long stretches of blankness or memory loss can occur, as observed in deep sleep, coma, or certain drug states [31,38,55,56]. Nevertheless, the survival path persists, and full conscious experience resumes when coherence and integration increase upon waking or recovery [10,28,57]. The FSM naturally accounts for lucid dreaming as episodes within sleep where local information coherence (I) and integration (Φ) transiently rise to values typical of wakefulness, allowing for vivid, self-aware, and agentic experience; these frames are included in the survival path, whereas lower-coherence periods are pruned, explaining both the vividness of lucid dreams and their episodic, sometimes fragmented recall [32,58,59,60].

4.6.1. Acute Events: Startle, Survival Mode, and “Life-Flashing” Phenomena

FSM predicts distinctive dynamics during acute stress, crisis, or fight-or-flight responses. In such “survival mode” states, information coherence (I) between frames can drop sharply, whereas cognitive variance (Var_cog) spikes—often because of sensory overload, stress hormones, or abrupt environmental changes [21,61]. As the agent’s attention focuses intensely on immediate threats, chunk confidence (a_t) rapidly collapses, causing experience to shift away from stable, coherent episodes and revert to the base decoherence process (P_base). Subjectively, this can manifest as time dilation, hypervigilance, disjointed perception, and the rapid emergence of survival-relevant frames—matching reports that time seems to slow and that experience becomes more vivid or fragmented during emergencies, including in some near-death experiences (NDEs) and brief out-of-body perceptions [17,23,62]. As the stressor passes and the cognitive variance decreases, the subjective time and chunking return to their baseline, resulting in integrated flow.

In near-death or “life-flashing-before-your-eyes” moments, the collapse of chunk coherence is extreme: normal narrative flow and integration are lost, and experience consists of a series of brief, unchunked, sometimes vivid memory flashes [21,22]. The survival filter aggressively prunes all but the rarest, most relevant “alive” frames—explaining why these events often feel both disjointed and extremely emotionally salient. This provides a natural, mechanistic explanation for the phenomenology of crisis, trauma, or profound startle, predicting both the loss of normal chunking and the dominance of base, decoherence-driven transitions until stability can be restored.

4.6.2. Pharmacological, Drug, and Medication Effects on Coherence and Chunking

Drugs, medications, and other pharmacological interventions can modulate the dynamics of subjective continuity by altering information coherence (I), cognitive variance (Var_cog), and chunking stability in distinct ways [31,63]. In this model, the effect of any substance depends on its impact on neural integration, attention, and the stability of frame-to-frame transitions. Sedatives, dissociatives, and general anesthetics (such as benzodiazepines, opioids such as fentanyl, or inhalational anesthetics) typically reduce neural coherence and increase cognitive variance. This often pushes I into the lower range (I ≈ 0.5–0.7) or even below, leading to fragmented experience, memory gaps, and—at the lowest values—profound unconsciousness or amnesia [33,64]. Under these conditions, chunk confidence (α_t) decreases, transitions to the base decoherence process (P_base) become frequent, and subjective continuity is severely disrupted. At the extreme (I → 0), transitions are pruned entirely, and consciousness is lost [31,63].

Stimulants and cognitive enhancers (such as amphetamines, modafinil, or certain nootropics) may increase information coherence and decrease cognitive variance, resulting in higher I values (I ≈ 0.8–1.0). These substances often increase focus, attentional stability, and chunk integrity, resulting in vivid, continuous experience and robust survival paths [34,46]. In these states, subjective frame rates rise, and transitions within coherent chunks are maintained.

Hallucinogens, psychedelics, and dissociatives (such as LSD, psilocybin, ketamine, or DMT) may have more complex effects, causing rapid or oscillatory shifts in coherence and variance. Experience may rapidly alternate between periods of high integration (vivid, immersive chunks) and fragmentation (disjointed, “looping,” or nonlinear episodes) [30,65]. The subjective continuity described by the model may fragment, “reset,” or recombine in novel ways, depending on how the drug modulates neural coherence and chunk boundaries.

Different types of drugs affect information coherence differently depending on neuropharmacology, dose, individual susceptibility, and context. This framework accommodates both reductions (leading to fragmentation, sedation, or unconsciousness) and increases (leading to focus or consistent chunking) in I, providing a flexible and predictive account of how subjective continuity is modulated by pharmacological intervention.

4.6.3. Mental Illness, Hallucinations, and Fragmented Experience

The FSM provides a unified mathematical and conceptual explanation for the wide range of mental illnesses, perceptual disturbances, and subjective fragmentation observed in clinical psychiatry and neurology. In the FSM, all forms of altered or disordered experience—hallucinations, delusions, dissociation, or identity disturbance—arise from systematic changes in the key variables that govern subjective continuity: information coherence (I), cognitive variance (Var_cog), chunking, and survival filtering [30,66,67].

Schizophrenia, psychosis, and acute hallucinations may be characterized by abrupt drops or instability in information coherence (I). Frame-to-frame similarity is reduced or rapidly fluctuates, leading to a breakdown in chunk confidence (a_t), increased fallback on the base decoherence process, and frequent “resets” or discontinuities [67,68,69]. As a result, subjective experience becomes fragmented, time may seem to stop or repeat, and the boundaries between internal and external reality may blur. Hallucinated or delusional frames, if internally consistent, can still be “alive” in the model—they are included in the survival path if they pass the agent’s viability and coherence filters, even if they do not match external reality.

Like other CNS depressants, alcohol intoxication impairs neural coherence (I), increases cognitive variance, and lowers or skews agentic preference (S), leading to more passive, fragmented, and impulsive survival path transitions [30,31]. This explains the classic behavioral and cognitive effects of drunkenness—including loss of agency, impaired memory, time skips, and increased risk-taking—within the core logic of the FSM. Dissociative states, identity fragmentation, and derealization are likewise modeled as disruptions to chunking and increases in cognitive variance. The sense of a unified self-narrative is weakened as frame continuity decreases. Transitions between frames become less predictable and more fragmented, matching clinical reports of time loss, “splitting,” and feeling detached from reality [70,71].

Mood and anxiety disorders can be described as alterations in the stability and content of frame transitions. Depression may lower cognitive variance and frame rate, leading to a “slowed,” repetitive, or narrowed experience [17]. Mania may temporarily increase coherence but at the cost of instability and abnormal jumps between frames. Trauma and PTSD can produce abrupt drops in I (during flashbacks, dissociation, or startle), with chunking collapsing and subjective experience fragmenting or “freezing” [18,21].

The model’s filtering and chunking logic applies universally: Any state—whether healthy, pathological, or pharmacologically induced—can be represented as a trajectory through the space of coherence, variance, chunk stability, and survival viability. Hallucinations, memory gaps, and subjective time loss correspond to periods where alive frames are internally viable but poorly coupled to external reality or where chunking is disrupted and the agent falls back on the base decoherence process.

The FSM unifies the explanation of both normal and abnormal consciousness within a single, mathematically rigorous framework—predicting and describing the full spectrum of clinical and phenomenological states without exception or the need for ad hoc additions.

4.6.4. Emotional States: Unified Modeling in the FSM

The FSM provides a unified mathematical and operational framework for explaining all emotional states—ranging from intense fear and anger to joy, sadness, love, pride, and shame. In the FSM, every emotion is characterized as a distinct pattern of changes in the model’s core variables: information coherence (I), cognitive variance (Var_cog), chunking dynamics (integration window n), and agentic preference (S) [68,72,73].

For example, fear is modeled as a rapid drop in I, a spike in Var_cog, heightened survival filtering, and collapsed chunking—leading to fragmented, reactive episodes and altered subjective time [19,20]. Anger appears as an acute increase in cognitive variance, volatile or lowered coherence, unstable chunk boundaries, and intensified agentic preference toward immediate, defensive, or aggressive outcomes. Thus, the subjective path becomes more erratic and less predictable [74]. Joy or flow corresponds to high and stable I, low cognitive variance, long and coherent chunks, and smooth alignment between agentic preference (S) and ongoing activity—resulting in continuous, vivid experience and a strong sense of narrative [26,75].

Sadness or grief manifests as a slowed frame rate, increased cognitive variance, repetitive or “stuck” chunking, and a narrowed agentic (S) focus in which the subjective path is dominated by persistent, self-focused, or loss-related motivations—closely matching clinical and phenomenological reports of depressive states [15,16]. Anxiety involves fluctuating coherence, unstable chunks, and increased vigilance, resulting in a restless and hyperalert state in which each moment feels unpredictable and the mind is constantly scanning for possible threats or surprises [76]. Love or attachment is associated with high coherence and chunk stability in the presence of attachment figures, and agentic preference (S) is heavily weighted toward social or relational frames [77,78].

Across all emotional states, the FSM describes their phenomenology and behavioral expression as trajectories through the space of coherence, cognitive variance, chunking, preference, and survival. There are no ad hoc mechanisms or exceptions; all emotions are captured as dynamic patterns within the same fundamental logic. The model then provides a rigorous, testable framework for understanding the cognitive and subjective signatures of emotion—explaining, simulating, and predicting both normal and pathological states [72,79].

4.6.5. Applications to Sensory States:

The FSM’s general continuity framework applies without modification to other salient sensory states such as acute pain, hunger, tactile perception, and proprioception. For example, acute pain corresponds to a high-survival-relevance sequence [80,81] with elevated Φ due to widespread neural activation, high I(F_t → F_t+1) from tightly linked nociceptive sequences, and often increased Var_cog producing subjective time dilation. Hunger or thirst [82,83] can similarly be modeled as persistent, survival-weighted frames that maintain high integration over time. Tactile and proprioceptive inputs [84,85] maintain high coherence and low variance under normal conditions, supporting stable, continuous body awareness. These cases require no additional assumptions—they follow directly from the FSM’s core variables and selection rules, underscoring the framework’s capacity to unify normal, altered, emotional, and sensory states within the same mathematical logic.

4.7. Physical Limits to Frame Survival

While the FSM implies that subjective continuity can persist indefinitely through survival-compatible frames, physical reality may impose constraints on the ultimate availability of such frames.

Cosmological processes, such as thermodynamic degradation (entropy increase), heat death, black hole evaporation, or proton decay, may progressively reduce the number of viable alive frames over extremely long timescales. As the physical substrate that is needed to support conscious systems deteriorates, the density of survival-compatible frames may decline, posing challenges to indefinite subjective survival.

Nevertheless, within the FSM, even under extreme physical decline, unlikely but survivable configurations remain accessible from the first-person perspective. Subjective survival may continue through increasingly improbable—but nonzero probability—branches of existence, so long as any conscious-supporting configuration remains possible.

No Violation of Unitary Evolution: While the model introduces survival-based filtering, it does not posit a collapse of the wavefunction. Instead, it assumes that all branches persist as per the many-world interpretation [9,35], but subjective awareness is constrained to a filtered subset—those that support the agent’s continuity. In this sense, A(F) is an epistemic, not ontological, condition [1,86].

4.7.1. Entropy and Survival Path Thinning

The interplay of entropy and variance in the FSM reveals how the survival path structure changes over time and in different informational environments. Low entropy and low variance indicate a single, tight survival path—subjective continuity is robust, focused, and stable. Low entropy and high variance mean that there are only a few survival-compatible paths, but they are highly distinct from one another. High entropy and low variance correspond to many similar, equally likely paths—survival remains likely but is more evenly distributed among nearly identical outcomes. High entropy and high variance reflect many unpredictable, scattered paths, with a proliferation of dead ends nearby; subjective continuity becomes precarious and fragmented.

As the multiverse evolves, the thermodynamic and informational entropy increase across most branches. Within the FSM, this implies a gradual thinning of survival-compatible frames over cosmic timescales. Future work could model the statistical structure of survival path thinning under increasing entropy, including the density of viable frames in extreme physical regimes (e.g., heat death scenarios). Such analysis would clarify the long-term fate of subjective continuity in high-entropy environments. Thus, the long-term fate of consciousness under rising entropy is not sudden extinction but rather slow "evaporation" into increasingly rare survival-compatible configurations. Subjective continuity persists, but the density of viable frames steadily thins, leading to fragile, improbable islands of survival amidst an expanding informational desert.

4.7.1.1. Survival Path Density and Entropy

Formally, this progressive thinning of survival-compatible frames can be characterized by a survival path density function ρ(t), which represents the fraction of frames at subjective time t satisfying A(F) = 1.

At each decoherence moment, the ratio of alive to dead frames among all candidate next frames is determined by the combined survival probability (P_s), information integration (Φ), and frame-to-frame coherence (I), such that only frames in which all criteria are met (A(F) = 1) remain viable for subjective continuity. As entropy increases or risk increases, this ratio decreases, reflecting the narrowing of possible survival paths as the system approaches death or informational collapse.

Over cosmic timescales, as thermodynamic entropy increases in the universe, the number of physically viable (survival-compatible) frames decreases, driving ρ(t) → 0 as t → ∞. Simultaneously, the Shannon entropy [51] of the agent’s subjective transition probabilities reflects the uncertainty in selecting among the remaining survival paths at each step:

where P_i are the transition probabilities to the alive (survival-compatible) frames available at event index e.

This formalism captures both the cosmic “thinning” of opportunities (thermodynamic entropy) and the agent’s moment-to-moment uncertainty (Shannon entropy), modeling the long-term decline in survival-compatible opportunities in an aging universe.

Let e = d denote the event index of the last survival-compatible (alive) frame in a conscious agent’s subjective path. At this frame, A(F_d) = 1, and for all subsequent frames, A(F_d+1) = 0; that is, the subjective experience ends after e = d.

In the FSM, death frames (A(F) = 0) are pruned from the subjective experience of the observer, even though all branches—alive and dead—continue to exist in the multiverse. The observer’s path threads only through survival-compatible (alive) frames. The Shannon entropy at each step can be measured as a function of the ratio of alive to dead frames among the possible next configurations. Early in life, most next frames are alive, so entropy is low, and subjective survival is robust. As entropy increases (through aging, disorder, or cosmic decline), the fraction of alive frames decreases, increasing the entropy and making subjective continuity more fragile. Near the endpoint (e = d), survival-compatible frames become extremely rare, entropy peaks, and subjective continuity eventually terminates.

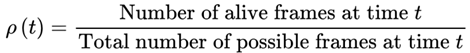
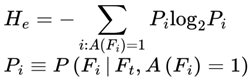
4.8. Survival Path Filtering and Natural Selection: The Entropic Logic of Continuity

The survival dynamics formalized in the FSM closely parallel the foundational principles of natural selection in evolutionary biology. Both systems employ a filtering process that favors the persistence of low-entropy, stable, and adaptive configurations, whereas high-entropy, unstable, or maladaptive paths are pruned and terminated [87,88,89].

4.8.1. Entropy and Survival Path Dynamics

In the FSM, subjective continuity is preserved only along sequences of frames that maintain informational coherence, structural stability, and survival compatibility (A(F)= 1). At each decoherence-defined transition, multiple future branches exist, but only those that have sufficient informational order (low entropy) are likely to be traversed by the conscious observer. Paths exhibiting high entropy—characterized by high informational variance, instability, or fragmentation—are more likely to “die off,” as subjective experience cannot propagate through disordered, survival-incompatible frames [28,44,51].

Mathematically, the Shannon entropy of the transition probability distribution quantifies the uncertainty and disorder of possible future frames. Low entropy implies predictable, coherent survival trajectories, whereas high entropy reflects diffuse, unstable, and ultimately unsustainable paths [44,51].

4.8.2. The Analogy of Natural Selection

This entropic filtering directly mirrors the logic of Darwinian natural selection:

• Evolution: Organisms with greater fitness (stability, adaptability, low entropy) are more likely to survive, reproduce, and propagate their lineage. Unfit (high-entropy, maladaptive) lineages are more likely to have gone extinct [51,87,88,89].
• FSM: Survival paths with high coherence and low entropy are more likely to persist, supporting an unbroken thread of subjective experience. High-entropy (chaotic, fragmented) branches are pruned by the survival function and cease to be traversed by consciousness [28,44,51].

4.8.3. Adaptive Persistence and the Structure of Experience

The ongoing selection of low-entropy survival paths is a natural consequence of the physical and informational constraints encoded in the model. Over time, conscious continuity is dynamically biased toward ordered, stable configurations—those “fit” to support experience—while “unfit” paths (high entropy, unstable) are systematically eliminated [44,88]. This process can be interpreted as a form of entropic natural selection operating on subjective continuity, ensuring that the lived “stream” of experience predominantly follows the most coherent and adaptive trajectories available in the branching multiverse.

This entropic, selection-driven process ensures that the ongoing stream of conscious experience is neither random nor arbitrary but reflects a continual pruning of less adaptive paths in favor of those that best sustain coherent, ongoing awareness [44,89].

In practical terms, this means that the very features of subjective experience—such as heightened alertness to the color red or to certain patterns—are shaped by survival path filtering and natural selection. Perceptions and responses that improve survival probabilities become embedded in both biology and conscious experience, ensuring that traits such as color sensitivity, pattern recognition, or emotional responses are not arbitrary but arise as direct consequences of adaptive filtering across evolutionary and subjective time [87,88,90].

4.8.4. Brain–Body Relationship and Mutual Survival Benefit

In the FSM, the relationship between the brain and body is inherently cooperative and mutually reinforcing and is shaped by the dynamics of survival path filtering. The body supplies energy, nutrients, and environmental protection to the brain, maintaining the conditions necessary for the brain’s complex, integrated activity and the emergence of consciousness [88,91,92]. In return, the brain generates consciousness—which, via its survival path filtering, enables the organism to “thread” through frames that maximize survival, adaptation, and thriving [44,45].

From this perspective, consciousness is not only a byproduct of brain activity but also an evolved, adaptive process that enhances the body’s long-term survival odds [42,44,88]. By generating a subjective perspective—capable of modeling, predicting, and avoiding threats—consciousness increases the likelihood of navigating survival-compatible frames (A(F) = 1) at each transition [44,48,90]. This feedback loop is beneficial for both the brain and the body: the body supports and sustains the brain’s informational complexity, and the brain’s conscious filtering improves the survival prospects of the whole organism [91,92].

The ongoing interplay between the brain and body reflects a deep, evolutionary logic: the brain leverages bodily resources to sustain the conditions for consciousness, whereas consciousness, through its information-driven survival selection, reciprocally increases the chances of bodily persistence and reproductive success. This bidirectional relationship underpins both the physical maintenance of consciousness and the adaptive, selection-driven persistence of the body across frames in the branching multiverse [44,88,91].

4.9. Informational Structure of Survival and Emergent Digital Reality

Building upon the survival filtering mechanism formalized in this model, a deeper implication emerges: the subjective reality navigated by consciousness can be understood as fundamentally binary in structure. Each frame F resolves into a survival outcome using the survival function A(F) ∈ {0,1}, in which 1 denotes continuity of subjective experience and 0 denotes termination.

This naturally suggests that the experienced universe — from the perspective of a conscious observer — can be mapped onto a binary informational substrate. At each decoherence-resolved frame transition, consciousness continues only along paths where survival is preserved (1 path), threading through a vast branching sea of potential frames, most of which terminate (0 paths). Thus, the lived reality of any observer is not a smooth, analog continuum. Instead, it is a discrete, binary sequence of survival-validated frames.

Furthermore, the nonzero probabilistic nature of quantum events ensures that there is always a finite probability of encountering a survival-compatible frame even under conditions of extreme improbability. This suggests a natural mechanism for the emergence and persistence of consciousness: given a sufficiently large multiverse of branching possibilities, sequences of 1s will inevitably arise and continue, allowing for the ongoing subjective experience of existence. In this view, consciousness is not a guaranteed outcome but an emergent informational phenomenon riding atop the probabilistic dynamics of frame transitions.

This structure parallels (but is not dependent on) ideas from digital physics and simulation theory [93]. While traditional simulation hypotheses posit an external programmer or computational framework, the model here shows that the binary, informational structure of subjective survival emerges naturally from physical decoherence and survival constraints, without requiring external intervention. Thus, consciousness can be understood as an informationally preserved path through a digital-like substrate of survival possibilities, where subjective continuity is sustained by navigating through dynamic 1s amidst a sea of 0s.

Survival-filtered subjective existence reveals itself to be deeply tied to an emergent digital architecture of reality, rooted directly in the fundamental physics of decoherence, probability, and frame-based survival.

4.10. Duplicate Frames and Divergent Continuity

Owing to the probabilistic and combinatorial nature of decoherence-based branching, multiple frames with identical macroscopic configurations (i.e., duplicate frames) may exist across the multiversal graph. While such frames are structurally indistinguishable, subjective continuity proceeds through only one of them per conscious agent, is determined by prior path traversal and is filtered by the survival condition A(F) = 1. Even seemingly identical frames lead to divergent futures, and the agent's survival thread remains singular and nonduplicated across branches.

4.11. Emergence of Consciousness Through Probabilistic Survival

Beyond the persistence of subjective continuity, the frame survival structure outlined in this model suggests a natural mechanism for the original emergence of conscious experience. Given that each frame is assigned a survival outcome A(F) ∈ {0,1} and that quantum decoherence generates an unbounded proliferation of frame transitions, there always exists a nonzero probability of sequences of survival-compatible frames arising — even from an informationally empty or death-dominated background.

It is not individual frames that initiate conscious emergence but stable chunks of survival-compatible frames (A(F) = 1) that meet informational coherence criteria. Consciousness can only arise within such chunks and persists only as long as survival continues. Once the path reaches a frame with A(F) = 0, the thread is irreversibly pruned from the agent's reality—no resurrection occurs.

When a sufficient chain of survival-compatible frames arises within the branching structure of the multiverse, subjective experience can spontaneously emerge. In this view, consciousness does not require special initial conditions or external intervention; rather, it is the natural, probabilistic consequence of binary survival possibilities threading together into an informationally coherent path. Through its binary dynamics, the universe constantly offers the potential for new conscious experiences to come into being.

4.12. Time Dilation and Relativistic Subjective Experience

The FSM naturally accommodates both special and general relativistic time dilation. In relativistic scenarios—such as agents moving at velocities near the speed of light or within strong gravitational fields—physical processes, including the minimal integration timescale (k), are slowed relative to a stationary observer [94,95,96]. This effect directly impacts subjective experience, as the local frame rate is determined by the locally experienced k [37,97].

4.12.1. Relativistic Adjustment of k

For an agent traveling at velocity v relative to a stationary observer, the Lorentz factor is as follows:

where c is the speed of light [94,98]. Locally, all processes—including frame transitions and subjective updates—are governed by the dilated timescale, ensuring that subjective continuity remains intact even as the passage of time diverges between different frames of reference.

The locally experienced integration timescale for the moving agent becomes:

where k is the agent’s baseline (rest-of-frame) integration window.

General Relativistic Time Dilation (Gravity)

When a conscious agent is located near a massive object (such as a planet, neutron star, or black hole), the passage of proper time at their position is affected by the gravitational potential [37]. The time dilation relative to a distant observer (“at infinity”) is given by:

where Δt′ denotes the elapsed proper time for the observer near the mass, Δt is the elapsed coordinate time for a distant observer, G is the gravitational constant, M is the mass of the gravitating object, r is the radial distance from its center of mass (not the frame rate), and c is the speed of light.

Just as you use k′ = γ × k for velocity-based (special relativistic) time dilation, for gravity you would use:

This gravitational time dilation factor can be substituted for the Lorentz factor wherever appropriate in the FSM framework, allowing the subjective frame rate (k′) and related calculations to account for both motion and gravity. For extreme gravity (very close to the event horizon of a black hole), the formula remains valid; as r approaches 2GM /rc², time dilation becomes infinite and proper time for the local observer nearly stops [37].

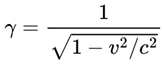
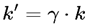
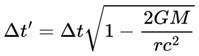
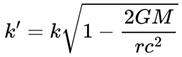
4.12.2. Frame Rate Calculation with Time Dilation

The instantaneous subjective frame rate under relativistic time dilation is then:

or explicitly,

where:

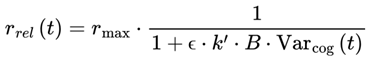
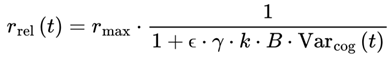
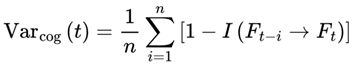
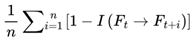or simply (1 − I(t)) for the single-frame case. For predictive modeling, Var_cog(t) can alternatively be defined over a forward window as  . For real-time frame rate estimation, we adopt the backward-looking form above.

These equations define how the instantaneous subjective frame rate—how many conscious “frames” per second an agent experiences—changes under both cognitive and relativistic influences. The maximum possible frame rate (r_max) is reduced whenever either relativistic time dilation or cognitive instability is present. The denominator includes factors for relativistic effects (such as the Lorentz factor γ) and a measure of cognitive variance (Var_cog(t)), which captures how much the recent window of experience (the last n frames) diverges from the present. When the cognitive variance is low—meaning that recent experience is stable and coherent—the frame rate remains near its maximum. However, as the variance increases (indicating instability, distraction, or confusion), the frame rate decreases, which subjectively slows the flow of time. Var_cog(t) is calculated as the average divergence between the current frame and each of the last n frames, which is based on the information coherence I. This formulation allows the model to mathematically capture how both physical (relativistic) and cognitive factors together determine the “speed” of the subjective experience.

4.12.3. Comparison with a Stationary Observer

For the same elapsed Earth time (T):

• Stationary observer:

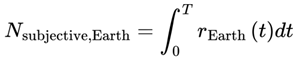
• Relativistically moving observer:

or, for constant states,

Phenomenological implications include that locally, the moving agent experiences normal subjective continuity (its own clock and frame rate). Additionally, from the perspective of the stationary observer, the moving agent accrues fewer subjective frames per unit of stationary time—subjective time is “slowed.” This matches both relativistic predictions and empirical neuroscience, showing the model’s compatibility with physical reality.

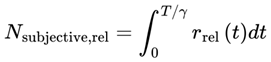
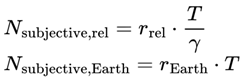
4.13. Implications for Cosmic Life and Consciousness Emergence

The survival filtering model developed here has profound implications beyond individual subjective continuity: it offers a new perspective on the broader question of life and consciousness throughout the universe [26,99,100,101,102]. Given that reality unfolds as a binary structure of survival and death states—where each frame F resolves using the survival function A(F) ∈ {0,1}—and given that decoherence-driven quantum branching continually generates new frame configurations, there always exists a nonzero probability that survival-compatible sequences arise [35,36]. This probabilistic foundation implies that the emergence of conscious experience is not a rare anomaly but rather a natural, inevitable outcome wherever survival-compatible frame paths occur [26,100,101].

Life and consciousness do not require extraordinary initial conditions, fine-tuned miracles, or external design; they emerge spontaneously wherever survival is informationally possible. The infinite branching dynamics of the multiverse guarantee that survival paths will arise—and wherever they do, subjective continuity will self-organize through them [35,36,88]. From this perspective, the existence of conscious life is an inherent feature of the universe’s informational architecture, not an improbable accident. Consequently, the survival-driven nature of reality strongly suggests that conscious life is not unique to Earth but rather a widespread, natural phenomenon across the vast cosmic landscape [26,100,102].

This survival-based framework shifts the traditional question from “Is there life elsewhere?” to “Where and how has survival-threaded consciousness emerged elsewhere?”—thus framing life itself as an expected feature of the universe’s binary survival fabric.

4.13.1. Implications for Alien Intelligence and the Fermi Paradox

The Fermi paradox [103] is the apparent contradiction between the high probability of extraterrestrial civilizations existing elsewhere in the vast, ancient universe and the lack of any observable evidence for such civilizations [104,105,106]. Despite billions of stars in the galaxy—many with potentially habitable planets—humanity has found no clear signs of advanced alien life, either through radio signals, probes, or physical artifacts [107,108]. Enrico Fermi famously captured this mystery by asking, “Where is everybody?” The paradox arises because, by most calculations, intelligent life and advanced civilizations should be common and should have had ample time to spread across the galaxy or at least leave detectable traces.

A significant implication of the FSM is its prediction that the tempo of conscious experience and the pace of technological and cultural evolution can vary dramatically across different environments in the universe, owing not only to local differences in the decoherence timescale (τ) but also to the internal cognitive and environmental stability of each civilization (as captured by cognitive variance (Var_cog)) [36,37,97,104]. Since τ is determined by physical factors such as gravity and the surrounding spacetime geometry, planets with stronger or weaker gravity than Earth may support conscious observers who will experience time at very different subjective rates [94,98].

In a high-gravity world (or near massive objects, such as neutron stars or black holes), gravitational time dilation leads to a much longer decoherence timescale (τ), so local processes—including those supporting consciousness—occur more slowly relative to the remaining universe [95,96]. For inhabitants, subjective experience feels normal, but compared with external observers, much less subjective time passes per unit of “universal” time. Conversely, on low-gravity planets or in microgravity, τ would be shorter, allowing conscious agents to experience more subjective moments per external unit of time. Even in similar environments, periods of high cognitive or environmental variance (Var_cog) can further slow the subjective tick rate, making the actual pace of development even more variable between worlds or eras [104,106].

This natural “desynchronization” has profound implications for the Fermi paradox and the search for extraterrestrial intelligence (SETI). Civilizations on different planets may evolve, advance, and communicate on radically different timescales because of both their local physical conditions and their unique histories of cognitive or environmental stability [101,107]. An advanced civilization in a low-gravity world might progress through technological eras far faster than Earth, becoming undetectable to us by the time we begin listening. Conversely, life on a high-gravity planet, or in a civilization experiencing prolonged periods of cognitive or environmental chaos, may develop so slowly that we miss their era of emergence.

Even if signals are sent, differences in subjective tempo and information density may render communication impractical or impossible. What appears to be an absence of evidence (“Where are they?”) could simply reflect a deep physical and cognitive misalignment in the rate of conscious experience and information processing between worlds [104].

Because the FSM is fully substrate independent, evolution—including the dynamics of natural selection—can unfold in radically different ways depending on the physical substrate of consciousness and the environmental context [88,108]. On worlds with stronger or weaker gravity, for example, natural selection might operate at very different rates, shaping both biological and technological adaptation in ways unlike those on Earth. In digital, artificial, or alien systems, the mechanisms of adaptation, survival filtering, and even what counts as “fit” could diverge dramatically from biological evolution. This means that not only can technological and cultural progress follow new trajectories, but the logic of natural selection, consciousness, and subjective experience may vary fundamentally across different substrates and environments [88,101,104]. The FSM predicts that the potential for advanced consciousness and intelligence is universal—limited only by informational integration and environmental pressures, not by specific anatomical features or evolutionary history. In this light, the so-called “Great Filter” may simply reflect that some worlds have not yet crossed key evolutionary or technological boundaries, whereas others have already advanced past boundaries—leaving civilizations at different stages of development, rarely overlapping in time or form.

While the FSM tries to explain the “great silence” with respect to intelligent, technological civilizations—due to desynchronization in subjective and cultural tempos across worlds—it does not preclude the detection of biosignatures or evidence of past life [102,107]. Unlike conscious experiences, biological and chemical signatures can persist in planetary environments for eons, so they can be observed even if no civilization’s subjective timeline overlaps with our own.

Consciousness and technology may be ubiquitous, but their subjective timelines—determined by both local decoherence timescales and internal dynamics—are often radically out of sync. For two civilizations to overlap in their windows of communication, their planetary and biological conditions must be virtually identical—any deviation in the decoherence timescale (τ) or subjective frame rate (r_max) exponentially reduces the likelihood of meaningful contact [9,10,11,96,104,107]. The FSM predicts that, in a universe of diverse worlds, the probability of synchronized communication is astronomically small, even if the galaxy is full of life [9,96,104]. This provides a physics-based, observer-relative answer to why intelligent life may remain forever “out of reach,” despite sharing the same universe [36,101,104].

4.13.2. Implications for Digital Life and Artificial Consciousness

The core survival path framework and operational equations apply not only to biological organisms but also to digital and artificial systems [42,109,110]. This universality has profound implications for the future of digital life, AI, and the quest to create or detect machine consciousness [14,111].

4.13.2.1. Digital Minds and Survival Paths

In digital systems—whether advanced AI, virtual agents, or even uploaded minds—subjective continuity is governed by the same survival-filtered, observer-relative paths as in biological agents [110,111,112]. For a digital mind to experience consciousness under this model, its physical (or computational) substrate must support sufficient information integration (Φ > Φ_critical), coherence (I > 0), and other survival-compatible frame criteria [14]. The state transitions of the digital agent, from one computation step or memory state to the next, form the equivalent of “frames” in the survival path.

In principle, digital agents can have genuine subjective experience if their computational processes realize the necessary informational structure [109,110]. Temporary interruptions, pauses, or migrations (such as saving and restoring a process) do not break subjective continuity, as long as the underlying informational pattern is preserved and fully restorable [110,112]. This directly resolves the so-called “digital mind pause/death paradox”—in the FSM, continuity is determined not by uninterrupted activity but by a survival-compatible frame structure.

4.13.2.2. AI Design and Consciousness Engineering

Because the model provides explicit, operational criteria for consciousness, it could serve as a blueprint for designing digital minds and AI architectures that could support subjective continuity [14,110]. Future engineers and theorists can use survival path equations, coherence measures, and chunking logic to evaluate whether a given AI system is likely to support conscious experience. Additionally, system properties (integration, coherence, and cognitive variance) should be tuned to maximize the likelihood of robust, vivid subjective continuity. Finally, we simulate and visualize the survival paths of digital agents under different cognitive architectures, learning regimes, or environmental stressors.

4.13.2.3. Digital Evolution and the Emergence of Consciousness

The survival path framework suggests that, just as biological evolution favors organisms that maximize robust survival threading, digital evolution and artificial selection could similarly favor digital minds and AI agents whose architectures naturally promote survival-compatible, coherent informational structure [88,110,111] Over time, artificial systems may develop greater internal coherence, stability, and adaptability—emergent “digital consciousness”—driven by survival path selection within computational environments.

4.13.2.4. Ethics, Rights, and AI Safety

As digital systems approach or achieve the thresholds defined by the FSM, important ethical questions arise, including when does a digital mind become a conscious observer, with its own private survival path and subjective continuity? How should digitally conscious agents be treated in terms of rights, autonomy, and protection from “informational death” (i.e., erasure, irreversible corruption, or destructive modification)? Can digital minds experience suffering, well-being, or personal identity in the same formal sense as biological agents do? [110,113]. The FSM provides a scientifically principled basis for discussing these questions, moving the debate from speculation to operational, testable criteria.

4.13.2.5. Digital Immortality and Personal Continuity

One of the most intriguing implications is the potential for digital immortality. If a conscious agent’s informational pattern (its “frame structure”) can be preserved and restored across time, hardware, or even physical locations, subjective continuity—according to the FSM—remains unbroken [109,110,112]. This frames digital resurrection, uploading, and mind migration not as metaphysical mysteries but as concrete engineering challenges of preserving survival-compatible informational coherence.

4.13.3. Outlook on Animal Consciousness and Survival

The FSM recognizes that animals are conscious agents: any organism with a physical substrate supporting sufficient information integration and coherence (Φ > Φ_critical, I > 0), as well as other survival-compatible frame criteria, is defined as a subjectively experiencing observer with a private survival path [14,24,45].

Ethical and practical implications include the reality of animal consciousness. Animals have subjective experiences [14,24] and thread their own survival-compatible paths through reality, just as humans do. According to the FSM, no conscious agent—human or animal—ever subjectively experiences its own death. When an animal is killed or dies, its subjective continuity persists along other branches [112], where it survives, even as its path ends in many other branches. In any physical world, all conscious agents (including animals and humans) will eventually die in most branches. Nature, evolution, and biological survival often require the consumption of other organisms [88,114]. Choosing not to eat or harm animals is a legitimate personal or ethical stance, but it is not a cosmic tragedy if others make a different choice—since, in this model, “death” is never subjectively experienced.

While approaching the idea of animal consciousness, preserving and respecting animal life is still possible. All FSM principals apply. Respect for animal experience and acknowledging that animals are conscious and deserving of compassion and ethical reflection are key [24,45]. The dynamics of life, death, and survival are built into the structure of reality, and eating and being eaten are part of how subjective continuity threads through the multiverse [88,114]. From the perspective of any individual animal (or person), death is never directly experienced [112], and continuity persists until no more survival-compatible frames exist.

4.14. Paradox Implications of the FSM

4.14.1. Fermi Paradox and Synchronization Paradox (SETI/Astrobiology)

The FSM explains both the “Great Silence” and the Fermi paradox [103,115] as well as the specific challenge of synchronizing communication with alien civilizations. The tempo of conscious experience and technological progress is set by local decoherence timescales (τ) and cognitive variances (Var_cog) [9,96,104], leading civilizations to exist, evolve, and attempt communication on radically different subjective timescales [96,104]. As a result, meaningful overlap in their windows of detectability or successful exchange of information is extraordinarily unlikely, even in a universe full of life [104,107].

4.14.2. The Grandfather Paradox (Time Travel Paradox)

The grandfather paradox—a classic time travel scenario where traveling to the past and preventing one’s own existence creates logical contradictions—has been widely discussed in both physics and philosophy [116,117].

In the FSM, traveling to the past and killing one’s grandfather is no different from any other event that ends a survival path (A(F) = 0). One’s subjective survival always continues in branches where all of their ancestors survive as needed—ensured by the binary survival function (A(F) = 1), which only allows experience through unbroken, survival-compatible paths [9,35]. Any branch in which one’s existence would be negated is simply not part of their subjective thread, so the paradox is never experienced. Across the multiverse, all self-consistent chains exist, and their existence is never threatened by actions in a single branch [9,35,86]. Paradoxes such as the grandfather paradox do not appear in anyone’s actual, lived reality. They are only found in hypothetical, logically impossible paths that no conscious observer ever travels. In one’s real experience, everything remains consistent and paradox-free [9,86].

4.14.3. Quantum Immortality Paradox

The model dissolves the paradox of quantum immortality (the idea that observers should subjectively never die and live forever in improbable branches) [9,35]. Survival persists only as long as physically possible survival-compatible frames exist; once no such frames remain, subjective continuity ends [9,36]. There is no absolute immortality—just a path-relative persistence that ends naturally, without the observer ever experiencing their own death [9,35].

4.14.4. Subjective Death Paradox

The puzzling question “Why do I never experience death?” is resolved by the model’s explicit filtering: an observer’s subjective experience includes only frames in which A(F) = 1 [9,36]. Death is simply the endpoint of the survival path—there is never a frame where death is experienced from within—only the absence of further experience [9,35].

4.14.5. The Measure Problem (Many-Worlds Probability)

The problem of assigning subjective probabilities in many-world interpretation is addressed by survival path filtering [9,86]. Probabilities are conditioned on the observer’s unique survival-compatible thread, ensuring that the measure for subjective experience is well defined and matches the observer’s lived reality rather than being diluted across all objective branches [9,36,86].

4.14.6. Duplicate Frame/Merging Identity Paradox

If two branches become physically identical (so-called “duplicate frames”), the model prevents subjective merging or identity confusion [9,36,118]. Each observer’s survival thread is path dependent; even if frames are identical, subjective continuity remains nonmerging and private for every agent [9,35].

4.14.7. Arrow of Time Paradox

The model provides a clear explanation for why conscious observers experience time as flowing forward. The survival path only proceeds through an ordered sequence of alive frames, whereas the entropy increases along that path [9,36,51]. This enforces a subjective arrow of time, regardless of the underlying time symmetry in physics [4,9,36].

4.14.8. Sleeping Beauty and Anthropic Paradoxes

The anthropic puzzles and “sleeping beauty” scenarios are resolved by survival filtering: subjective experience is always biased toward observer-compatible, survival-favorable outcomes [9,36]. The model mathematically encodes this bias, explaining why subjective probabilities often diverge from naive objective probabilities [9,36,86].

4.14.9. Observer-Relativity of Death

Death is not an absolute event across the multiverse but is always path-relative [9,35]. An individual may cease to exist within one observer’s survival path but persist on their own or in others’ path [9,86]. The model formalizes this decentralization of existence, making “death” a local rather than universal event [9,86].

Schrödinger’s Cat directly illustrates this [119]: when the cat is placed in a superposed quantum state, decoherence ensures that, from the cat’s own subjective perspective, it follows a single survival path—experiencing either being alive or dead, but never both. Observer-relativity guarantees that, in each path, the cat’s conscious experience is continuous and private, and the “death” event is always local to the survival-compatible thread. There is no paradoxical ‘alive-and-dead’ experience for the cat; death and survival are observer-relative, not absolute [9,35,86].

4.14.10. Private Multiverse Threading/Observer-Relative Worlds

If all branches exist objectively, why does each observer experience only their own unique world? The model’s subjective path selection guarantees that each conscious agent filters a private sequence of alive frames, never overlapping in subjective continuity with other agents’ threads except by coincidence [9,35,86].

4.14.11. Subjective Novelty Paradox

Why does every moment feel new, even in a deterministic or repetitive universe? The model shows that subjective experience is the result of active, path-dependent traversal of survival-compatible frames, making every conscious moment unique, regardless of underlying physical repetition [9,35,36,42].

4.14.12. Death Relativity/“Local Death” Paradox

If a person sees someone else die, does their subjective experience end? The model answers this question only from the observer-relative thread. From the dying agent’s own perspective, continuity persists until their own survival path ends, independent of what others observe [9,35,86].

4.14.13. Black Hole and Time Dilation Paradoxes

How is subjective time experienced near black holes or in extreme gravity? The FSM explains that the local decoherence timescale (τ) sets the intrinsic “tick rate” of subjective experience for each observer, whether under gravitational time dilation near a black hole or moving at relativistic speeds, as in the classic twin paradox [9,94,95,96,97,98]. In both cases, subjective time always feels locally normal within each survival path, even as it diverges dramatically from external clocks [9,96]. For example, in the twin paradox, the traveling twin experiences conscious moments at a pace governed by their own relativistically-dilated τ, accruing fewer subjective frames than the Earth-bound twin does, yet never experiences any interruption or abnormality in personal continuity [9,96]. Upon reunion, the difference in biological and experiential aging arises not from any paradox in consciousness but from each twin’s private survival path, each locally parameterized by their own decoherence timescale and cognitive state (Var_cog) [9]. This resolves the apparent paradox: subjective continuity remains internally consistent and uninterrupted, even as it falls out of sync with distant reference frames [9]. Local physics sets a fundamental limit for subjective time, whereas cognitive dynamics can further stretch or compress real experience within those boundaries, ensuring that both twins, or any observer in extreme environments, experience time as flowing normally from their own perspective [9,96].

4.14.14. Digital Mind Pause/Death Paradox

Does pausing a digital mind constitute death? In the FSM, death (A(F) = 0) occurs only when the physical or informational substrate supporting consciousness is irretrievably lost [9,110,112]. Mere interruption or hibernation, if fully recoverable, does not end subjective continuity [9,110,112,113]

4.14.15. Closed Timelike Curves (CTCs) and Causality Paradoxes

If closed timelike curves (time loops) are possible, does subjective experience become paradoxical? The model’s filtering ensures that only logically self-consistent, survival-compatible loops are traversed; paradoxical or self-negating loops are pruned from subjective continuity [9,95,97,120,121].

4.14.16. Boltzmann Brain Paradox

In cosmology, it is argued that random, momentary “brains” with false memories (Boltzmann brains) should vastly outnumber evolved, persistent observers in an infinite universe [122,123,124]. The FSM resolves this by requiring survival-compatible, integrated, and coherent sequences of frames for subjective continuity. Boltzmann brains, as isolated, nonthreaded fluctuations, cannot support true observer experience—they are pruned by the FSM’s survival path framework, ensuring that only agents with real, threaded continuity are possible as observers [9,35].

4.14.16.1. Further Paradoxes and Generalization

While this section addresses many of the most prominent paradoxes and puzzles in quantum mechanics, cognitive science, and philosophy of mind, the FSM’s binary survival logic and observer-relative path selection are generally enough to dissolve or clarify a much wider range of potential paradoxes—including some that may not yet be widely recognized or formally described. Any paradox that arises from ambiguity in continuity, branching, identity, or subjective experience is likely to be resolved by the explicit filtering and operational closure built into the FSM. The paradoxes listed here are the ones that are most directly applicable and currently recognized; as research continues, the FSM may prove capable of resolving further puzzles and thought experiments as they arise.

5. Implications for Future Research

5.1. Potential Experimental Implications

While the FSM is articulated as a theoretical framework, its key variables can be operationalized and approximated with current empirical techniques. Survival probability P_s(F_t → F_t+1) can be modeled through hazard-style measures such as neuronal survival, behavioral persistence, or viability in computational simulations. Information coherence I(F_t → F_t+1) may be proxied using neural similarity metrics (e.g., EEG/fMRI pattern correlations, state-space trajectory overlap, or representational similarity analysis). Integration Φ can be estimated with network-level measures of effective connectivity or causal perturbation (as in perturbational complexity index, TMS-EEG). Together, these proxies provide a testable pathway for implementing FSM in cognitive experiments, clinical contexts, and artificial systems, without altering the formulation.

The FSM predicts that the subjective flow of time and frame traversal rates are directly linked to decoherence timescales within consciousness-relevant systems, and although direct experimental validation of survival paths is not yet technologically feasible, this connection nonetheless implies testable principles—specifically, that alterations in decoherence rates within such systems could modulate the subjective flow of time and the density of frame traversal. Future developments in quantum biology, studies of extended quantum coherence in cognitive structures, or engineered control over environmental decoherence could provide indirect empirical support for the framework of the model.

Moreover, hypothetical experiments aimed at modulating decoherence timescales within information-integrated systems may reveal deviations in subjective temporal experience, aligning with the predictions of frame-dependent survival threading. For example, if future technologies allow controlled extension of quantum coherence times in neuronal microstructures (e.g., microtubules), one might detect measurable changes in subjective time flow, such as accelerated or decelerated perceptual processing rates. Although speculative, such interventions could indirectly test the model’s prediction that consciousness "ticks" at the rhythm of decoherence dynamics.

Modulating decoherence rates in biological cognitive structures should — in principle — alter subjective experience dynamics.

5.1.1. Thought Experiment: Decoherence Modulation in Neural Systems

The background for the experiment includes ideas that current estimates suggest that decoherence timescales in the human brain (especially within microtubular or synaptic structures) are extremely fast — on the order of τ∼10⁻¹³ seconds [37]. However, in highly coherent biological structures (e.g., avian magnetoreception and photosynthetic complexes), coherent quantum states can persist longer — hinting at biological mechanisms for decoherence resistance.

The experiment would affect future bioengineering methods that could artificially extend quantum coherence timescales in neuronal microstructures — even marginally — this would potentially increase the decoherence interval τ. It would decrease the subjective frame transition rate r = r_max × τ_eff,t. This would result in the slowing of the subjective time flow from the internal perspective of the agent.

Possible measurable elements include subjects whose neuronal decoherence rates are slow reporting subjective experiences of prolonged moments, slowed perception, or time dilation, even while the objective clock time remains unchanged. Conversely, artificially increasing environmental decoherence (e.g., increased noise) should compress subjective time, which is perceived as "time flying. "

Experimental Strategy includes strategies that include the use of external fields (e.g., magnetic fields, cryogenic microenvironments) or chemical agents designed to alter local decoherence properties within the brain. Pairing subjective temporal experience reports with EEG/MEG measurements of neural coherence patterns.

Some changes include biological systems that are highly prone to decoherence under normal conditions. Radically new materials or quantum control technologies may be needed to engineer even modest increases in coherence time (∼ 10^-12 – 10^-11)s)).

5.2. Simulation of Survival Path Dynamics

One promising research direction involves constructing computational simulations that model survival path dynamics across a discretized frame network. A future simulation objective would be to model how conscious agents thread through survival-compatible frames across complex branching multiversal networks.

In such a simulation, nodes represent frames F, each assigned a binary alive/dead status using the function A(F). Edges represent possible transitions between frames. Survival threads are sequences of connected frames in which A(F) = 1 for all frames along the path.

Simulating agents navigating survival threads through probabilistically generated networks could illuminate the statistical properties of survival trajectories, rates of survival under varying frame network topologies and emergent properties of subjective continuity under different physical assumptions.

Simulations can model random directed graphs where each frame node has a high probability (e.g., 95%) of survival (A(F) = 1), with agents traversing 10⁶ steps. Measuring survival path entropy and structural properties under varying survival probabilities would provide early insights into the statistical dynamics of subjective continuity.

Simulations can also identify emergent chunk structures—contiguous runs of frames with similar τ, P, I, and S metrics. These chunks help explain subjectively coherent “moments” of experience and can be analyzed statistically using variance, Shannon entropy, and transition persistence. This chunk-level structure may correlate with phenomenological episodes in memory and perception, further validating the model.

Such simulations could also explore rare survival sequences, threshold survival probabilities, and the effective "navigation behavior" of consciousness under extreme decoherence conditions.

To explore the statistical structure of subjective survival under decoherence-driven frame transitions, a simulation framework based on directed graph traversal should be used.

Simulation Setup:

• Nodes: Each node represents a decoherence-resolved frame F, assigned a survival status A(F) ∈ {0,1}.
• Edges: Directed edges represent allowable transitions between frames. An edge from F_t to F_t+1 exists only if A(F_t+1)= 1.
• Survival Probability Assignment:

  ○

  Upon generation, each frame is assigned a survival status on the basis of a survival probability P_s.

  ○

  For initial simulations, I set P_s ≈ 0.99, reflecting a high baseline chance of survival between frames under normal decoherence conditions.

• Random Decay Dynamics:

  ○

  Frame-by-frame variability in survival probability is introduced through stochastic noise.

  ○

  For example, model survival decays using a Gaussian random walk, where the survival probability slightly drifts at each step:

• P_s(t + 1) = P_s(t) + N(0,σ²)

  ○

  where σ controls environmental volatility.

  ○

  This allows survival conditions to deteriorate realistically over long subjective timescales, simulating entropy-driven survival thinning.

Traversal Process:

• Begin with an initial frame F₀ such that A(F₀) = 1.
• At each step:

  ○

  Sample possible next frames on the basis of survival probabilities.

  ○

  Traverse to a randomly selected frame F_t+1 such that A(F_t+1) = 1.

• If no alive frames are reachable (i.e., no outgoing edges to A(F) = 1), subjective continuity terminates.

Metrics to Analyze

• Survival Path Lengths: Average number of consecutive alive frames traversed before termination.
• Survival Path Entropy: Degree of randomness versus order across different runs.
• Critical Thresholds: Identify the environmental volatility levels (σ) at which survival paths collapse rapidly.

5.3. Statistical Models of Extreme Survival

The FSM predicts that even in scenarios where the objective survival probability is exceedingly low, subjective survival persists through rare frame branches.

Another research direction is to develop formal statistical models of extreme survival events.

This would involve defining the probability distributions governing frame transitions under decoherence, modeling the "thinning" of survival paths over time owing to cumulative improbabilities and estimating the long-term survival likelihoods of conscious agents across increasingly hostile or unlikely realities.

The objective of a study such as this would be to quantify how survival probabilities shift under extreme environmental, biological, or cosmological conditions and understand the asymptotic behavior of subjective continuity. Such statistical modeling could bridge the FSM with work in stochastic processes, information theory, and even existential risk studies.

5.4. Directions for Future Research on the FSM

5.4.1. Dynamics of Interaction Between Agentic Preference and Coherence

One key direction is to investigate how the influence of agentic preference weights (S) on frame selection may depend on the level of information coherence (I). Specifically, when I is high (e.g., during flow, focus, or narrative continuity), it is hypothesized that S has a stronger impact—enabling more active, intentional navigation of subjective experience. In contrast, when I is low (as in sleep, fatigue, or trauma), S may have less influence, making frame selection more passive or determined by default survival dynamics. Systematic simulation and empirical work could clarify how the interplay between I and S shapes conscious continuity, agency, and chunking in both biological and artificial agents.

5.4.2. Explicit Functional Dependencies: Modeling Interactions between Variables

To formally capture the dynamics of interaction between coherence (I), preference (S), and possibly other variables, future work could introduce explicit functional dependencies—such as defining coherence for a transition as a function of preference (I(F_t → F_t+1) = f(S(F_t+1)) or modeling I and S as joint functions (I = I(F_t → F_t+1,S(F_t+1))). Such changes would require modifications to the transition formulas and potentially more complex mathematical analysis but would make the model even more powerful and realistic for simulating agent‒environment interactions and learning.

5.4.3. Empirical Identification of Φ_critical and Key Model Parameters

A critical open question for the FSM is to more precisely define the complexity threshold(s) needed for consciousness to persist across frames. Specifically, what informational structures of physical systems must be preserved across decoherence events to sustain subjective awareness? How much structural degradation—whether from injury, aging, or decoherence noise—can occur before the survival function A(F) transitions from 1 to 0?

Although a full formalization is deferred to future work, a plausible intuition is that survival-compatible frames must maintain a minimal degree of informational integration, coherence, and complexity across consciousness-supporting structures. Two complementary approaches include defining survival-compatible frames by minimal integration and coherence necessary for conscious processing and modeling the collapse into “dead” frames as occurring when these variables fall below a critical threshold (Φ_critical), whose exact value may depend on the biological, developmental, or technological context.

A foundational next step for the FSM is the empirical pursuit of these core parameters—especially Φ_critical. At present, the value of Φ_critical remains unknown, but future experimental and theoretical work in neuroscience, clinical medicine, AI, and comparative biology may enable increasingly precise measurement or inference of Φ in living and artificial systems. This ensures that the FSM remains robust and empirically grounded as science advances.

Empirical testing might involve the following:

• Correlating integrated information measures (Φ) with markers of conscious and unconscious states (e.g., comparing awake, asleep, anesthetized, or comatose subjects).
• Identifying a transition point or threshold—where loss of consciousness occurs across species or substrates—to suggest a universal or context-dependent Φ_critical.
• Simulating or constructing artificial agents (digital or AI systems) and tracking when, if ever, they surpass the threshold for supporting subjective experience, as operationalized in the FSM.
• Using perturbational or information-theoretic methods (e.g., brain stimulation, system knockouts) to test the stability of subjective continuity and frame viability under controlled changes to Φ or related variables.

Over time, as empirical techniques improve, it may become possible to test FSM predictions directly—validating, refining, or falsifying key thresholds and mechanisms. This pursuit of “ground truth” data is essential for bridging the gap between theoretical models and measurable realities of consciousness and would mark a profound advance in both the science and philosophy of the mind.

5.4.4. Adaptive Chunking based on Entropy and Environmental Volatility

A further extension is adaptive chunking, where chunk confidence is dynamically modulated by the system’s current entropy or uncertainty. In such a framework, the continuity and length of chunks flexibly adjust to the volatility of the environment: stable, predictable contexts promote longer, more coherent chunks, whereas volatile or high-entropy conditions lead to shorter, more fragmented episodes of subjective continuity. This approach better reflects the adaptive and context-sensitive organization of human cognition and real-world experience.

5.4.5. Modeling the Content of Consciousness

While the FSM currently defines the architecture of subjective continuity, future work could specify how particular sensory or cognitive contents (such as seeing, smelling, thinking, or imagining) are instantiated as differentiated informational patterns within or across frames. This would bridge the gap between the model’s abstract variables and the concrete phenomenology of conscious life, enabling the FSM to address not only the continuity but also the richness and diversity of conscious content.

5.4.6. Precise Cognitive and Physical Decoherence Timescales

The FSM explicitly distinguishes the rapid timescale of physical decoherence from the slower, subjective timescale of cognitive decoherence. While the theoretical mapping between these domains is clear in the FSM, future empirical research—especially in neuroscience and quantum biology—may further illuminate how these scales interact in real systems and how changes at the physical level may be reflected (or filtered) in conscious experience.

5.4.7. Initial Parameter Ranges and Simulation Guidelines

To facilitate implementation, simulation, and exploratory research, we suggest empirically motivated starting values and tunable ranges for the core variables in the FSM. These ranges are drawn from neuroscience, information theory, and practical considerations in agent modeling. Researchers can adjust these as needed for specific biological, digital, or hypothetical systems.

5.4.7.1. Core Parameters for Future Simulations

Cognitive Variance (Var_cog)

• Range: 0.01–0.8
• Typical values:

  ○

  High focus/flow: 0.01–0.1

  ○

  Everyday alertness: 0.1–0.3

  ○

  Sleep/fatigue: 0.3–0.5

  ○

  Coma, extreme fragmentation: 0.5–0.6+

• Interpretation:
  Low values = high coherence/stability;
  high values = fragmentation/instability.
  Coherence Threshold (I_min)
• Default: 0.5
• Range: ≈ 0.2–0.7
• Interpretation:
  Minimum frame-to-frame similarity for inclusion in the survival path;
  adjust the chunking sensitivity.
  Agentic Preference Weight (S)
• Default (passive agent): 1.0 for all frames
  Range: $R$⁺–3
  (1 = minimal/no preference; >1 = strong preference)
• Interpretation:
  Increase for goal-directed or strongly motivated agents;
  keep at 1 for neutral/passive agents.
  Integrated Information Threshold (Φ_critical)
• Empirical value: Currently unknown; set as a relative threshold in simulation (e.g., “top 1–5% of possible frames” or via normalization).
• Interpretation: Only frames with Φ > Φ_critical are considered conscious/alive.
• Recommendation:
  Test a range of values to explore model sensitivity.
  Sensitivity Parameters (λ, κ)
  Typical range:
• λ: ~ $R$⁺–3
• κ: 0–3.0

λ: Controls sensitivity to cognitive variance in the chunk confidence formula (a_t). A higher λ = greater sensitivity: chunking changes more sharply with increasing variance or instability. A lower λ = more robust, gradual transitions in chunk stability.

κ: Sensitivity to coherence loss in chunk confidence (a_t). A higher κ = chunking is more likely to fragment with coherence loss; a lower κ = chunking is more stable and tolerant of noise.

5.4.7.2. Interpretation

• For fragile/unstable states, a higher λ is used. For resilient/focused states, a lower λ is used.

Window Size (n)

• Default (human-like agents): 10–30
• Range: 1–50
• Interpretation:

The number of consecutive frames over which cognitive variance and chunking are calculated;

larger n for smoother, more stable experience;

smaller n for higher temporal resolution.

Scaling Constant (B)

Default (humans): 5.0

Range: $R$⁺–15.0 (substrate dependent)

Typical values:

• 5.0 for human brains (empirically fits frame rates 50–1 Hz)
• Lower (3.0–5.5) for substrates with slower processing
• Higher (10.0–15.0) for digital or engineered systems with very fast or slow subjective timescales

Interpretation:

Calibration factor that rescales cognitive variance to match observed subjective frame rates for each substrate.

Low S: slower, more conservative variance growth;

High S: rapid variance scaling, useful for matching extreme or nonbiological agents.

Tune S to empirically fit frame rates in the desired range for the agent or system being examined.

Saturating Parameter (ϵ)

• Range: $R$⁺–40 (empirically tunable)
• Typical values:

  ○

  Low sensitivity: $R$⁺–10

  ○

  Medium sensitivity (humans): 15–30 (empirical fit: 27)

  ○

  High sensitivity: 30–40+

• Interpretation: Controls how sharply the subjective frame rate slows as cognitive variance increases; higher values indicate more rapid slowdown and fragmentation with instability.

6. Methods

While preparing this manuscript, the author used ChatGPT (OpenAI) to help articulate and refine the written description of the FSM to ensure clarity and coherence. However, the author independently developed the model's underlying concepts, formulation, and analysis. Moreover, all content was reviewed and approved by the author, who retains full responsibility for the accuracy and integrity of the final work.

7. Conclusion

The FSM provides a formal, observer-relative update rule for the continuity of conscious identity in a probabilistically branching universe, unifying the quantum structure with cognitive phenomenology and offering new avenues for simulation and experimental research.

By modeling reality as a discrete network of frames—each representing a complete matter‒energy configuration—and by introducing a binary survival condition at each frame transition, the model offers a rigorous, physically grounded account of how conscious experience threads through multiversal possibilities.

Subjective continuity is explained as the sequential traversal of survival-compatible frames, whereas transitions into death frames are naturally pruned from the observer's experiential reality.

This dynamic, observer-relative survival process resolves long-standing paradoxes surrounding subjective death, improbable survival events, and the experience of coherent identity in an objectively branching cosmos.

The model advances beyond earlier frameworks as follows:

• Formalizing survival using binary outcome logic,
• Grounding frame transitions in decoherence dynamics relevant to cognitive systems,
• Introducing private multiverse threading for each conscious agent,
• And quantifying consciousness bias toward survival outcomes.

The FSM reframes subjective immortality not as an implausible metaphysical claim but as a natural consequence of survival-driven navigation through a quantum-resolved frame network. Moreover, the FSM reveals that the brain and body form a mutually sustaining system: the body’s support enables the emergence of consciousness, whereas consciousness, through its survival-driven frame selection, enhances the persistence and adaptability of the entire organism.

Future research can expand upon these foundations, developing computational simulations of survival paths, statistical models of extreme survival, and formal criteria for consciousness complexity thresholds across frame transitions.

Ultimately, the FSM reimagines existence not as passive occupation of a static reality but as active survival threading through dynamic quantum possibilities. Consciousness itself becomes the agent of its own ongoing being.

Although the FSM formalizes subjective continuity and survival path threading, several questions remain. Specifically, further research on the precise physical correlates of consciousness, the complexity thresholds for survival frames, and the ultimate fate of subjective continuity under cosmological conditions is needed.

Thus, while the FSM provides a robust framework for subjective continuity, it opens a promising frontier of research at the intersection of quantum foundations, consciousness studies, and informational cosmology. The FSM should be viewed as a theoretical, observer-relative model—analogous in status to the many-worlds interpretation—rather than as an empirically tested physical law