The prophecy’s unbearable. It reaps a scrap of truth and headsman-like presents the crowds with the dimming eyes of harmony deceased . . .
Tatiana Akhtman. The life and adventures of a provincial soul
1. Introduction
One of the most fundamental and profound questions in human intellectual pursuit since its inception has been whether the universe we inhabit may be infinite. Modern theoretical physics remains agnostic on the subject of the Universe finitude for the most part, but the state-of-the-art mathematical apparatus it relies on, makes numerous implicit and explicit assumptions that require the universe to be infinite. Let us denote this de facto assumption as the infinitude conjecture.
Indeed, our common mathematical apparatus is based on an infinite number system, infinitesimal calculus, as well as trigonometry and complex number theory that include fundamental constants, such as the enigmatic and the natural base e—transcendental numbers that can never be fully derived in a system with finite complexity. Advanced fields of mathematics such as abstract algebras and formal logic assume the existence of infinite number of distinct categories, objects and statements with infinitely complex interplay.
There are, of course, a variety of finite mathematical constructs routinely used in physics as well as numerous other scientific and technological fields. But these advanced mathematical concepts are often perceived as utilitarian, auxiliary and abstract rather than the fundamental mathematical foundations our reality is based on.
The
infinitude conjecture presents a slew of paradoxes, singularities, and inconsistencies across both mathematics and theoretical physics, notably the Russell Paradox in set theory [
1], the Turing halting problem in computer science [
2], Gödel’s Incompleteness Theorems in formal logic [
3], as well as the Cosmological Constant problem,
a.k.a. the “Vacuum Catastrophe”, in physics [
4]. But disposing of the
infinitude conjecture altogether appears to be nothing but inconceivable.
Nevertheless, some of the most profound breakthroughs in both physics and mathematics have been accomplished by overcoming the infinitude conjecture in the context of at least some physical processes or mathematical constructs, and providing an elegant and useful explanation based on the conclusion that these processes are fundamentally finite, quantized, or/and periodic. Some notable examples range from the important discovery that the Earth is round (very large, but finite, circular surface) [
5], the discovery of the Earth and other planets’ orbit around the sun (finite, periodic) [
6], and all the way to Einstein’s quantization of light (very small, but finite quanta) [
7], relativity (very large, but finite speed) [
8], and ultimately quantum physics — quantization of essentially everything else with the notable exception of gravity [
9].
It is interesting to note that despite the “common sense” assumption that our every-day number system is somehow infinite, every time we try building effective computational mechanisms, we immediately default to number systems that are finite and periodic. For example, we count using a decimal system which relies on a finite and periodic system of 10 characters, where 9+1=0 (mod 10). Of course, we take care of the extra digit in a smart way, but let us just make this little cognitive note for further reference. We measure time using a somewhat complex and arbitrary mix of modulo 12, 24 and 60 computations that are of course informed by some of the natural cycles of our planet, but take quite some time for our children to figure out and get used to.
But perhaps the most striking example of this dichotomy is the way computations are carried out by modern computers. The entirety of the output of the multitude of digital computing systems, large and small, that permeate our modern existence is based on finite and periodic modulo-2 computations. All the music we listen to, all the movies we watch, all the video games we play, all the complex and oftentimes extraordinarily accurate simulations of the physical world we use for our scientific and technological endeavors, and all the wisdom we partake from our new and shiny Large Language Models is based on a fundamentally finite system of numbers and calculations.
It is therefore appropriate to contemplate the possibility that the universe is fundamentally finite. In this work, we postulate the feasibility of constructing a mathematical and physical framework grounded not in the abstraction of infinite axiomatic systems, but in the singular acknowledgment of a finite, coherent, information-complete reality — The Fundamental Axiom of Existence. We aim to lay the ontological foundation for a model in which all observable phenomena emerge from the projection and compression of a globally coherent, high-dimensional totality onto lower-dimensional observational subsystems. Within this paradigm, complexity, unpredictability, and apparent randomness are not intrinsic features of reality, but artifacts of the symbolic and informational compression inherent to finite projections. We propose that such a model holds the potential to reframe and unify our understanding of emergence, structure, and knowledge itself, offering a coherent account of the interconnectedness and stability of the universe without recourse to the concept of actual infinity.
2. Existence
The concept of existence has long been a central question in ontology. Traditional perspectives often treat existence as a binary condition: something either is or is not. For example, a rock exists, a thought exists, but a unicorn does not. While this binary framework is linguistically convenient, it fails to capture the nuanced reality of existence. This section proposes an alternative scalar model, wherein existence is proportional to the persistence of a system’s structure over time.
2.1. The Fundamental Axiom of Existence
Our subjective experience provides the most immediate and undeniable evidence that something indeed does exist. The very act of experiencing — of perceiving, thinking, and being aware — confirms the presence of existence in some form. This foundational insight, rooted in the subjective, is the starting point for any exploration of ontology. As Descartes famously concluded, “I think, therefore I am”. However, this statement, while profound, is inherently limited to the individual perspective. It asserts the existence of the self but does not address the broader context within which the self exists.
This insight aligns with the wisdom of the Talmud, which states, “We don’t see things as they are, we see them as we are”. Our perception of existence is inherently shaped by our subjective frameworks — our cognitive limitations, cultural contexts, and prior experiences. This means that what we perceive as reality is not an objective reflection of the Universe but a relational construct filtered through the lens of our own being. The act of perceiving is not passive; it is an active process of interpretation, shaped by the observer’s position within the broader system.
When we examine the nature of existence more deeply, it becomes evident that all separate objects and constructs — whether material or conceptual — are inherently composite and partial. A chair, for instance, is not an independent entity but a composite of wood, screws, and design, each of which is itself a composite of molecules, atoms, and subatomic particles. Even the so-called elementary particles of physics are not fundamental in an absolute sense but are emergent features of a deeper, interconnected system of physical laws and cognitive interpretations. These particles are not isolated, self-sufficient entities. Their existence is defined relationally — by their interactions with other particles, by the fields they inhabit, and by the frameworks through which we observe and describe them. Without the intricate web of physical laws that govern their behavior, and without the cognitive tools we use to interpret those laws, these particles would have no coherent meaning. They are not “fundamental” in an absolute sense but are emergent features of a deeper, interconnected system.
Similarly, cognitive constructs — ideas, theories, and abstractions — are not fundamental. They are composites of prior knowledge, linguistic structures, and shared cultural frameworks. Their existence is defined not by their objective reality but by their coherence and utility within the cognitive systems that generate and sustain them. This leads us to the conclusion that the existence of any particular object, whether material or conceptual, is relative and subjective. It is not defined by some intrinsic, independent essence but by its function within a broader system of relationships. An object “exists” to the extent that it persists and interacts meaningfully within a given context — whether that context is physical, informational, or cognitive.
This leads to a profound conclusion: the only entity that can be assumed to objectively exist is the Universe itself. Everything else — every object, particle, or construct — is merely a partial and incomplete expression of this greater whole. These subsystems derive their existence not from any intrinsic, independent essence but from their role and function within the broader context of the Universe. They are relational phenomena, defined by their interactions and persistence within the dynamic web of systems that constitute reality.
From this perspective, we can reformulate the famous Cartesian axiom to reflect a more universal truth: “I think, therefore the Universe is”. This variation shifts the focus from the individual to the totality, recognizing that the act of thinking — of experiencing and being aware — is itself a subsystem of the Universe. The existence of thought implies the existence of a broader context within which thought can occur. This broader context is the Universe, the only truly fundamental entity that encompasses all subsystems and interactions.
This reformulated axiom constitutes the only truly foundational principle required for all further deduction. It asserts that the Universe exists as the ultimate and objective reality, of which all other phenomena are partial expressions. From this axiom, we can derive the principles of persistence, relational existence, and the interconnectedness of all things. It provides a stable foundation for exploring the nature of reality, grounding our understanding in the recognition that all existence is ultimately unified within the totality of the universe. Thus, the universe is not merely a collection of objects or a backdrop for events. It is the singular, all-encompassing reality within which everything else — from the fleeting existence of unstable elementary particles to the enduring structures of thought and culture — finds its place. To think is to participate in this reality, to recognize the universe as the only objective existence, to embrace the fundamental unity of all being.
2.2. Existence as Persistence
The root criterion for existence is not visibility, tangibility, or materiality, but persistence. A system exists not because it is named or sensed, but because it maintains coherence across time. For instance, a cloud formation that dissipates within seconds is less likely to be recognized as an entity, whereas a stone, which endures for millennia, is universally acknowledged as a “thing”. This reflects a fundamental ontological principle: existence is equivalent to persistence.
This holds true for both the Universe itself, as much as all the constituent objects within it. The Universe is a vast, complex system that persists over time, maintaining its coherence through the interplay of physical laws and cosmic structures. If the Universe were not persistently coherent, no complex structures could arise to enable the cognition of its existence. Without this foundational persistence, the intricate systems necessary for observation, thought, and cognition would never emerge, leaving the Universe effectively unknowable, unobservable and ultimately non-existent.
More precisely, existence is proportional to the duration and coherence of persistence. Systems that maintain their internal relations—whether in form, function, or pattern—exist more fully than those that do not. When a system collapses into entropy and loses its identifiable structure, it ceases to exist ontologically.
An unstable elementary particle may only materially exist for a fleeting moment, decaying almost as soon as it emerges. Yet, the particle’s emergence follows a predictable and repeatable pattern, governed by the fundamental laws of physics. The particle’s decay products, its interactions with other particles, and the probabilistic structures that predict its behavior all contribute to a broader, enduring system of coherence. It is this system — the persistence of the patterns and laws that govern the particle’s emergence and dissolution — that grants the particle its ontological significance.
The concept of persistence as foundational to existence has deep roots in philosophical and scientific thought. Aristotle, in his
Metaphysics, introduced the notion of substance and the distinction between potentiality and actuality — emphasizing the continuity of essential form across change, an early exploration of persistence as the maintenance of coherent being over time [
10]. Immanuel Kant, in the
Critique of Pure Reason, articulated the relational nature of objects within human cognition, suggesting that persistence is not an independent property but a structural necessity of our temporal intuition [
11].
In the 20th century, Alfred North Whitehead’s
Process and Reality advanced the view that reality consists of processes rather than static entities, framing existence as persistence across interrelated events [
12]. Henri Bergson, in
Creative Evolution, emphasized the dynamic flow of time and life, tying persistence to the creative unfolding of duration [
13]. Ilya Prigogine’s
Order Out of Chaos explored how dissipative structures maintain local coherence by generating order from entropy in far-from-equilibrium systems [
14]. Stuart Kauffman, in
At Home in the Universe, extended this perspective by highlighting how self-organizing systems naturally achieve persistence through the interplay of order and complexity [
15].
David Bohm’s
Wholeness and the Implicate Order proposed that persistence emerges from the enfolded relational structure of reality, wherein explicate phenomena unfold from a deeper implicate coherence [
16]. In informational and computational domains, John von Neumann’s
Theory of Self-Reproducing Automata and Claude Shannon’s
A Mathematical Theory of Communication provided key insights into how systems preserve structure over time through redundancy, feedback, and error correction [
17,
18].
Finally, Lee Smolin’s
The Life of the Cosmos [
19] and Karen Barad’s
Meeting the Universe Halfway [
20] extend the concept of persistence to cosmological and quantum scales. Smolin’s cosmological model suggests that physical laws themselves evolve to favor stable universes, while Barad’s agential realism emphasizes the relational emergence of existence through interactions. These contributions collectively enrich our understanding of persistence as the defining characteristic of existence, providing a robust foundation for the scalar ontology proposed in this framework.
This scalar model of Existence has far-reaching implications. It suggests that what we call “objects” are systems that achieve a sufficient threshold of stability to interact with other systems. Systems that flicker too briefly or change too erratically fall below the threshold of meaningful ontology. They lack actionable presence and are functionally irrelevant.
Furthermore, this model dissolves the sharp boundary between existence and non-existence. A thought that lasts a second exists less than a mathematical proof that endures for millennia. Similarly, a momentary glitch in a system may “exist” for a nanosecond, but without persistence, it has no impact—no relational presence in the broader system of the world. In this framework, existence is not a static property but an active process. To exist is to persist—to maintain structure against the forces of time and entropy. This scalar perspective provides a unified ontology that encompasses physical, informational, and conceptual systems, laying the foundation for further exploration of persistence as the defining characteristic of being.
3. From Stability to Survival
The transition from stability to survival marks a critical juncture in the ontology of persistence. Stability, as a property of systems, refers to the capacity to maintain coherence and structure over time. However, in a dynamic universe characterized by entropy, disruption, and change, stability alone is insufficient for long-term persistence. Survival, therefore, emerges as an active process, requiring systems to adapt, respond, and evolve in order to endure.
This section explores the principles underlying the shift from stability to survival, drawing on insights from evolutionary biology, systems theory, and thermodynamics. It argues that survival is not merely a biological phenomenon but a universal principle applicable to all persistent systems, from physical structures to informational constructs.
3.1. Stability as a Foundation for Persistence
Stability is the baseline condition for persistence. A stable system is one that resists external perturbations and maintains its internal coherence over time. Examples of stable systems include planetary orbits, crystalline structures, and thermodynamic equilibria. As Ludwig Boltzmann’s work in statistical mechanics demonstrates, stability often arises from probabilistic structures that favor equilibrium states [
21].
However, stability is inherently passive. It relies on favorable initial conditions and external environments that do not impose excessive stress. In a universe governed by the second law of thermodynamics, where entropy tends to increase, stability is fragile. Systems that rely solely on passive stability are vulnerable to collapse when faced with significant disruptions. Survival represents an active extension of stability. It involves the capacity of a system to detect changes in its environment, adapt to those changes, and preserve its coherence in the face of entropy. This principle is evident in the evolution of biological systems, as described by Charles Darwin in
On the Origin of Species [
22]. Organisms that could sense and respond to environmental changes were more likely to survive and reproduce, leading to the development of increasingly sophisticated survival mechanisms.
Ilya Prigogine’s concept of dissipative structures further illustrates this principle [
14]. Dissipative structures are systems that maintain their stability by exchanging energy and matter with their surroundings. Examples include hurricanes, chemical reactions, and living organisms. These systems do not merely resist entropy; they actively harness it to sustain their structure. The transition from stability to survival can be understood as a shift from passive to adaptive systems. Passive systems, such as rocks or crystals, persist because they are inherently stable. Adaptive systems, by contrast, persist because they can modify themselves in response to changing conditions. This distinction aligns with Stuart Kauffman’s exploration of self-organization and the emergence of order in complex systems [
15].
Adaptive systems exhibit several key characteristics:
Sensing: The ability to detect changes in the environment.
Processing: The capacity to interpret and respond to environmental signals.
Feedback: Mechanisms for self-regulation and adjustment.
Replication: The ability to reproduce and propagate successful adaptations.
These characteristics are not limited to biological organisms. Informational systems, such as blockchain networks, also exhibit adaptive behaviors. Blockchain protocols, for example, adjust their difficulty levels to maintain stability in the face of fluctuating computational power [
23]. The principle of survival extends beyond biology to encompass all systems that persist over time. Whether a system is physical, biological, or informational, its ability to endure depends on its capacity to adapt and respond to its environment. This universal applicability underscores the importance of survival as a foundational concept in the ontology of persistence.
Lee Smolin’s work on cosmological natural selection provides a compelling example of this principle at the largest scales [
19]. Smolin suggests that universes themselves may be subject to a form of selection, with those capable of producing stable structures and black holes persisting while others fade into entropy. The transition from stability to survival represents a critical evolution in the ontology of persistence. Stability provides the foundation, but survival ensures continuity in a dynamic and entropic universe. By adapting to change and harnessing entropy, systems can achieve a higher degree of persistence, transcending the limitations of passive stability. This principle, rooted in both biological and physical systems, offers a unifying framework for understanding the dynamics of existence across scales and domains.
3.2. The Survival of Fundamental Laws
The apparent fine-tuning of the universe — its precise physical constants, elegant equations, and mysterious symmetries — has long been a subject of philosophical and scientific inquiry. Why is the speed of light what it is? Why do the fundamental forces have the strengths they do? Why is there just enough entropy to allow for change, and just enough order to allow for structure? These questions point to the survival of fundamental laws as a key principle in the ontology of persistence.
From an ontological perspective, the laws of physics that we observe are not arbitrary but are the result of a selection process. In a chaotic multiverse of possibilities, the vast majority of hypothetical “laws” would lead only to disorder, collapse, or immediate entropy. They would produce no atoms, no time, no stars, no persistence — and crucially, no quasi-stable systems. As Lee Smolin suggests in his theory of cosmological natural selection, universes capable of producing stable structures, such as black holes, are more likely to persist and propagate [
19].
This principle aligns with the broader framework of persistence: only those patterns — including physical laws — that give rise to stable, coherent systems can be said to “exist” in any meaningful or observable way. The laws of physics, therefore, are not given but are selected through a process of ontological Darwinism, where only the survivable set of laws remains [
14]. The fine-tuning of the universe can be understood as a natural outcome of this selection process. For example, the cosmological constant, which governs the rate of expansion of the universe, is finely balanced to allow for the formation of galaxies and stars [
4]. Similarly, the strengths of the fundamental forces — gravity, electromagnetism, and the strong and weak nuclear forces — are precisely calibrated to permit the existence of complex matter [
24].
These constants and laws are not fine-tuned by design but are the result of a filtering process: only those laws that support persistence and complexity are capable of giving rise to observers who can question their existence. This anthropic principle, as articulated by Brandon Carter, provides a framework for understanding why the universe appears so uniquely suited to life [
25]. Symmetry and invariance play a crucial role in the survival of fundamental laws. As Noether’s theorem demonstrates, every symmetry in the laws of physics corresponds to a conserved quantity, such as energy, momentum, or charge [
26]. These conserved quantities provide stability and coherence, enabling the persistence of physical systems over time.
For example, the rotational symmetry of space ensures the conservation of angular momentum, while the translational symmetry of time guarantees the conservation of energy. These symmetries are not merely aesthetic features but are essential for the stability and predictability of the universe [
27]. The survival of fundamental laws has profound implications for our understanding of reality. It suggests that the universe is not a static entity but a dynamic system subject to principles of selection and persistence. This perspective bridges the gap between physics and metaphysics, providing a unified framework for understanding the emergence and stability of the cosmos.
Moreover, this framework challenges the notion of a “designed” universe. Instead, it posits that the universe’s structure is the result of a natural process of selection, where only those configurations capable of sustaining persistence and complexity endure. This view aligns with the broader principle that existence itself is a function of persistence. The fine-tuning of the universe and the survival of its fundamental laws are not mysteries to be solved but principles to be understood within the ontology of persistence. The laws of physics that we observe are the survivors of a vast landscape of possibilities, selected not by chance but by their capacity to sustain structure, coherence, and complexity. In this light, the universe is not merely a collection of arbitrary constants and equations but a testament to the enduring principles of stability and persistence that underlie all existence.
4. Chaos and Randomness
The concepts of chaos and randomness have long been subjects of philosophical and scientific inquiry. Within the framework of persistence, these phenomena are not ontological categories but epistemic phenomena — reflections of the limitations of our capacity to model and understand complex systems. This section explores the nature of chaos and randomness, arguing that they are not fundamental properties of reality but emergent features of incomplete perspectives.
Chaos is often described as the absence of order, a state of unpredictability and apparent randomness. However, as David Bohm argues in
Wholeness and the Implicate Order, chaos is better understood as a shadow cast by complexity onto a limited perspective [
16]. From this view, chaotic systems are not devoid of structure; rather, their structure exceeds the scope of the observer’s tools and models.
For example, the behavior of turbulent fluids or weather systems appears chaotic when analyzed through classical models. Yet, advances in nonlinear dynamics and chaos theory, as pioneered by Edward Lorenz, reveal underlying patterns and attractors that govern these systems [
28]. These insights suggest that chaos is not a lack of order but an order that is too intricate to be resolved by current methodologies.
4.1. Randomness as Unresolved Complexity
Randomness, like chaos, is often treated as a fundamental property of certain systems, particularly in quantum mechanics. However, as Claude Shannon’s work on information theory demonstrates, randomness can also be understood as a measure of unpredictability or entropy within a given informational framework [
17]. In this sense, randomness is not an intrinsic feature of reality but a reflection of the observer’s inability to predict outcomes due to incomplete information.
Quantum mechanics provides a compelling case study. While the behavior of particles at the quantum level appears probabilistic, the underlying wave functions described by Schrödinger’s equation are deterministic [
29]. This duality suggests that what we perceive as randomness is, in fact, a manifestation of unresolved complexity within a probabilistic framework.
The reinterpretation of chaos and randomness as epistemic phenomena has significant implications for the ontology of persistence. Persistent systems, whether physical, biological, or informational, operate within environments that appear chaotic or random only from the perspective of limited observers. As Ilya Prigogine’s work on dissipative structures illustrates, systems can harness apparent chaos to maintain stability and adapt to changing conditions [
14]. This perspective also aligns with Henri Bergson’s concept of duration, which emphasizes the continuous flow of time and the dynamic interplay of order and disorder [
13]. Persistent systems do not merely resist chaos; they integrate it, using feedback mechanisms to transform unpredictability into adaptive strategies.
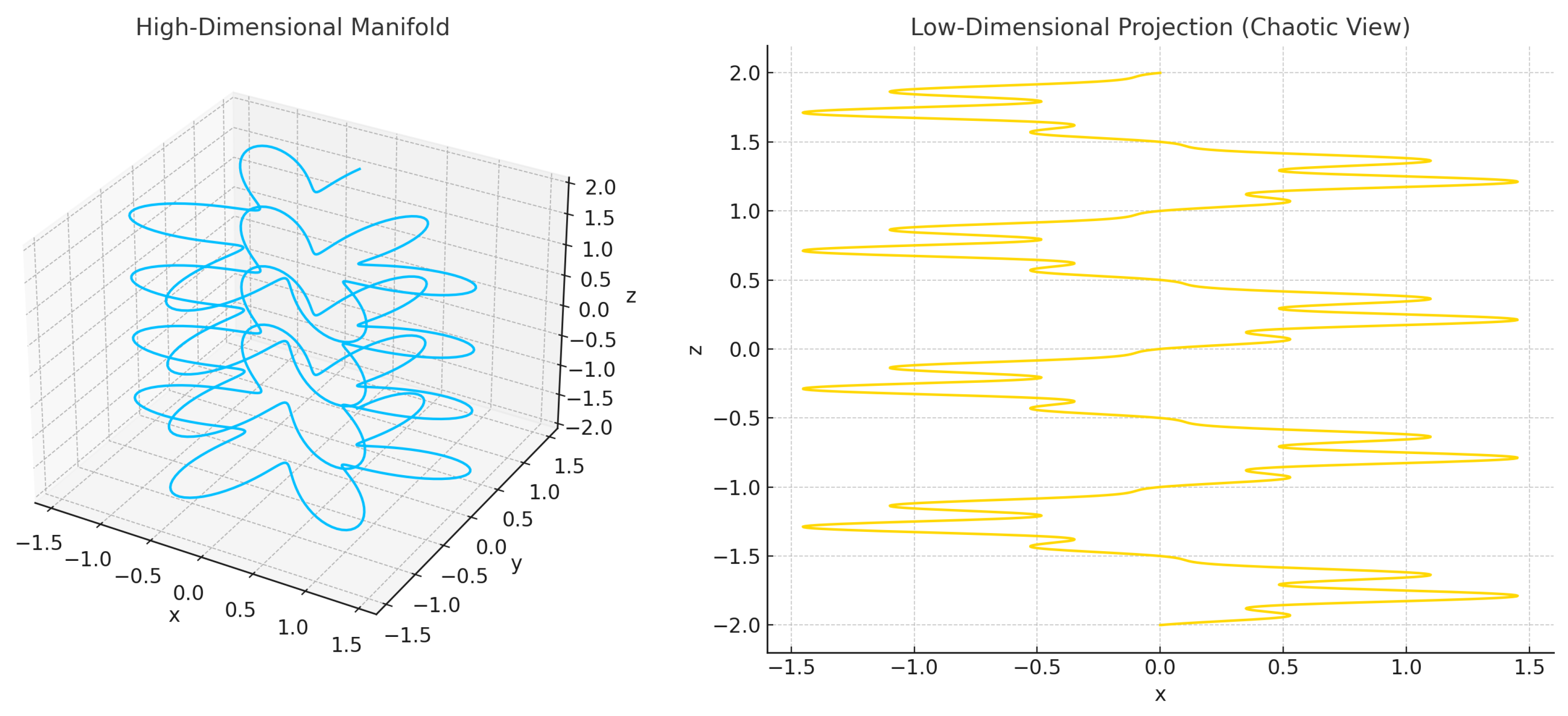
Chaos, in many classical systems, appears in relatively low-dimensional phase spaces — for instance, a 3D system like the Lorenz attractor. Yet, the underlying processes that give rise to chaotic dynamics can often involve many more degrees of freedom — in some cases, they are effectively higher-dimensional (like in fluid turbulence or climate models).
Figure 1.
A seemingly complex dynamics in a low-dimensional projection (right) of a very simple periodic motion in a higher-dimensional space (left).
Figure 1.
A seemingly complex dynamics in a low-dimensional projection (right) of a very simple periodic motion in a higher-dimensional space (left).
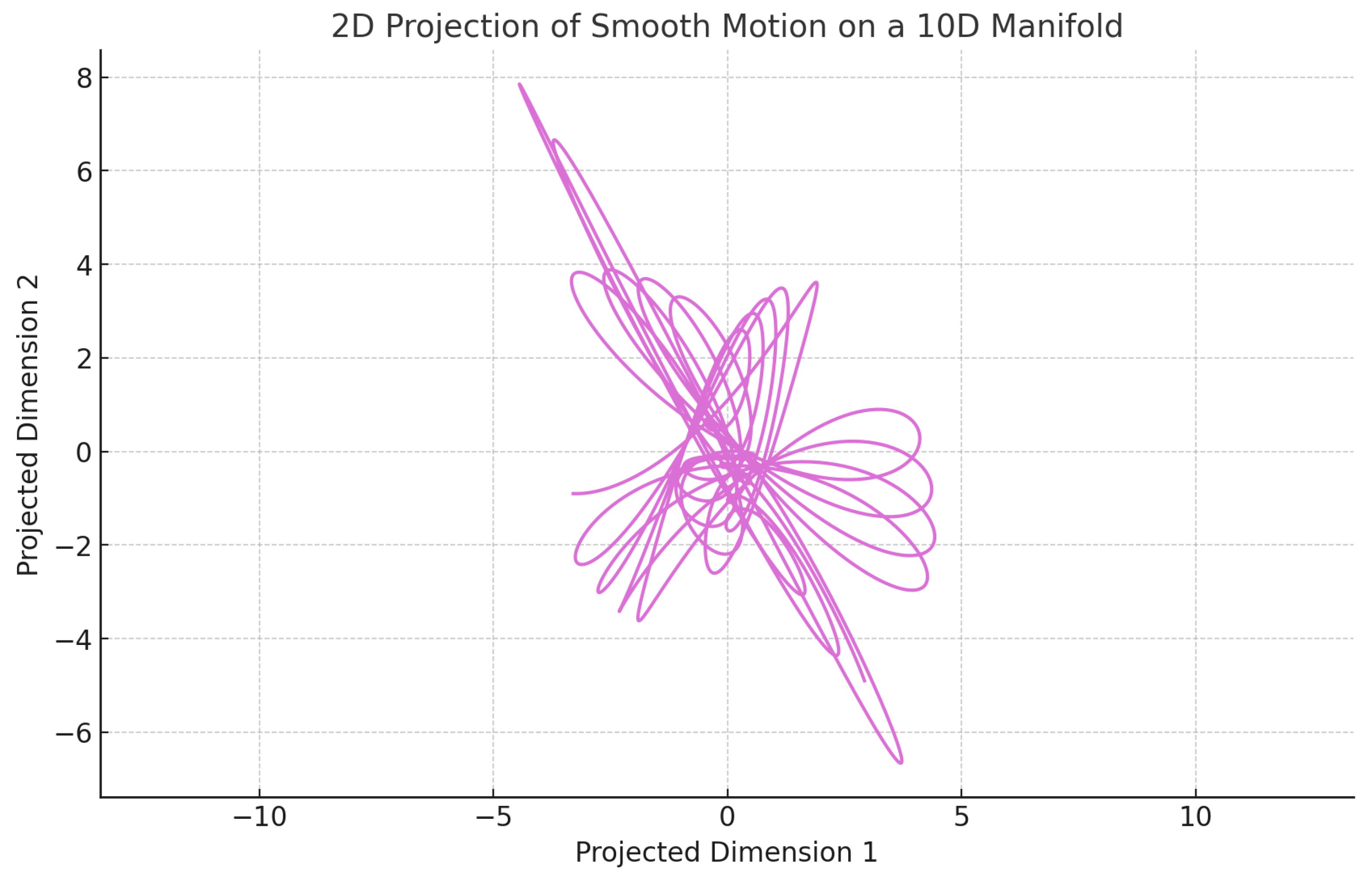
Figure 2.
A seemingly chaotic system in a low-dimensional projection of a smooth motion on a high-dimensional manifold.
Figure 2.
A seemingly chaotic system in a low-dimensional projection of a smooth motion on a high-dimensional manifold.
The Concept: You can imagine that what we perceive as a “chaotic system” is actually a projection of some much richer, high-dimensional dynamical process that unfolds on a complex manifold — a geometric space that locally resembles Euclidean space but can have intricate global structure [
16,
28].
When you observe or model a system in reduced dimensions (e.g., measuring only temperature and pressure in a weather system), you’re effectively compressing or projecting the full state space into something simpler. This projection loses information — particularly the interactions in the “hidden” dimensions — and this can make the observed behavior seem unpredictable, sensitive to initial conditions, and chaotic [
30,
31].
Analogy: Imagine watching the shadow of a dancer on a wall. The shadow might move in erratic, seemingly inexplicable ways — limbs appearing and disappearing, strange contortions — yet this is just a 2D projection of a graceful, continuous motion in 3D space. Chaos, similarly, might be a distorted shadow of a smooth flow on a high-dimensional manifold [
32].
In Mathematical Terms: Let the full system evolve on a manifold
M of high dimension
N. Observations are limited to a low-dimensional subspace or projection
where
. The dynamics in
can appear chaotic, even if the flow on
M is smooth or structured (though often still nonlinear) [
30,
31]. This perspective aligns with ideas in:
Manifold learning and dimensionality reduction (e.g., t-SNE, UMAP) [
33,
34]
Dynamical systems theory (e.g., embedding theorems like Takens’ theorem) [
31]
Physics (e.g., holography, statistical mechanics, or emergent phenomena) [
14,
35]
Chaos and randomness, far from being fundamental properties of reality, are emergent phenomena that arise from the interplay of complexity and perspective. They are not violations of the principle of persistence but its edges — the points at which systems exceed the capacity of observers to model and predict their behavior. As our tools and frameworks evolve, what once appeared chaotic or random may reveal deeper layers of structure and coherence. This understanding not only enriches the ontology of persistence but also provides a framework for navigating the complexities of an ever-changing universe [
13,
17].
4.2. Fractals as Projections of High-Dimensional Dynamics
The emergence of fractal structures in low-dimensional observations of dynamical systems can be interpreted as a consequence of projecting smooth, high-dimensional dynamics onto lower-dimensional spaces. This perspective aligns with modern understandings of complexity, where apparent disorder often reflects a compression or shadow of underlying structure.
Let be a smooth manifold of dimension , on which a dynamical system evolves according to deterministic laws. The system’s trajectory may follow well-behaved, continuous dynamics—such as oscillations or nonlinear flows—resulting in smooth behavior when considered within the full state space. In practice, observations are often limited to a low-dimensional subspace or projection with . Such projections may arise due to measurement constraints or intentional dimensionality reduction. The result is a lower-dimensional trajectory , in which the structure of the original dynamics becomes entangled, compressed, and—importantly—folded upon itself.
This projection process inherently involves both stretching and folding of phase space regions, analogous to operations in known chaotic maps. These operations induce scale-invariant and self-similar patterns in the observable space, which manifest as fractals. Unlike smooth trajectories in , the projected trajectory may occupy a set with non-integer Hausdorff dimension, characteristic of strange attractors. Formally, consider that the evolution operator preserves structure in the high-dimensional space. The effective operator on the observed space, , may no longer be smooth due to the loss of invertibility and unfolding during projection. This results in attractors that exhibit fractal geometry.
This paradigm may be metaphorically understood through an origami analogy: imagine a high-dimensional sheet being intricately folded (via dynamics on ) and then projected onto a flat surface. The resulting shadow, although complex and possibly self-similar, is a coherent transformation of the original smooth object. Fractal geometries in observed systems can thus be interpreted as artifacts of structured compression, rather than indications of fundamental randomness. Such perspective supports the notion that chaotic and fractal behaviors in observed dynamical systems are not inherently disordered, but instead emerge from high-dimensional deterministic processes subject to nonlinear projection. Understanding these projections provides a unifying framework for interpreting complexity in natural and engineered systems, where intrinsic dimensionality exceeds observational capacity.
4.3. The Mandelbrot Set
The Mandelbrot set is a canonical example of a fractal structure arising from iterative nonlinear dynamics. Traditionally viewed as a set of complex numbers with bounded iterates under a quadratic map, it can be reinterpreted within the paradigm of high-dimensional dynamics as a projection of structured processes in an implicitly infinite-dimensional space.
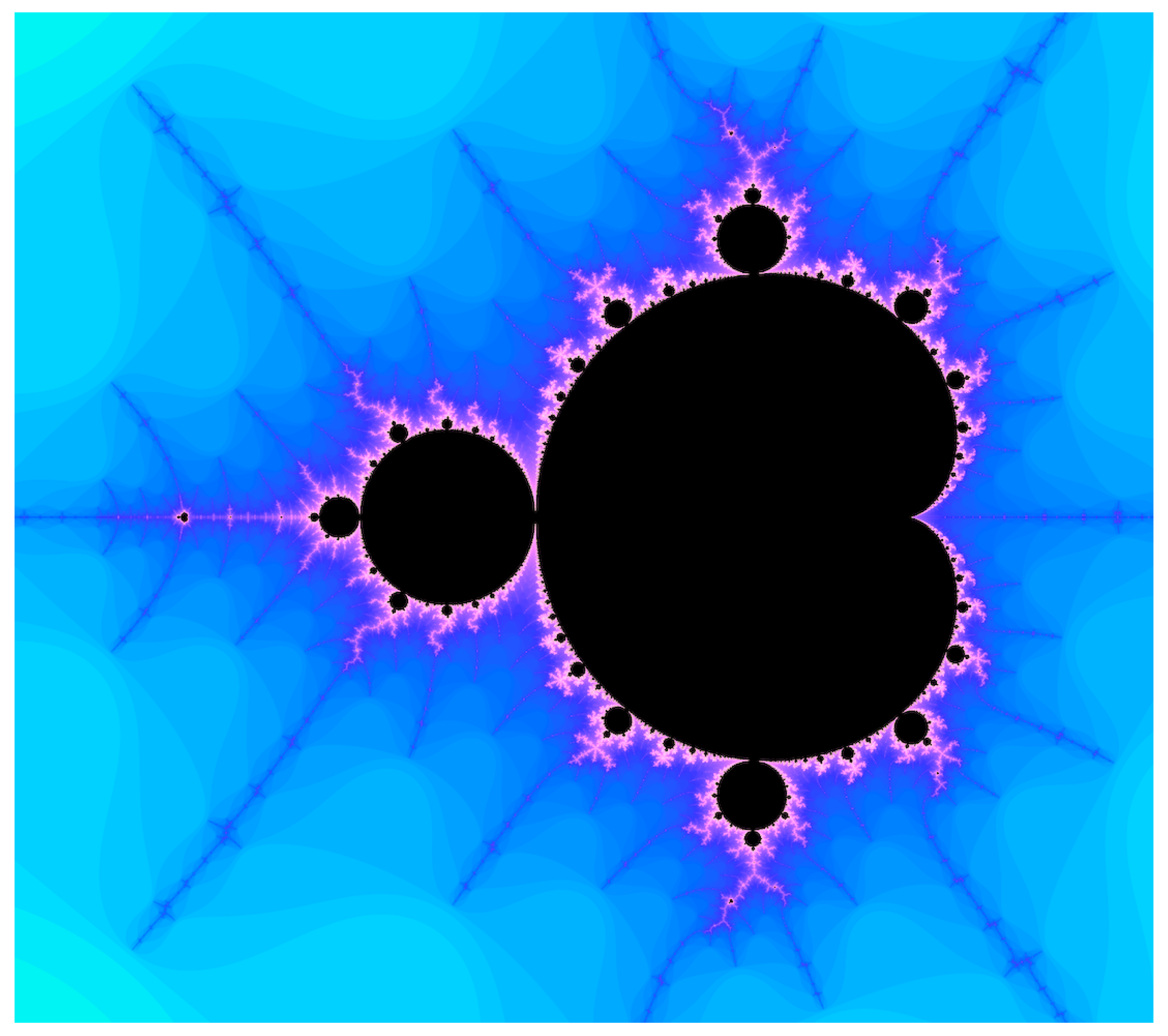
Figure 3.
The Mandelbrot set, a fractal generated by iterating a simple complex function, reveals intricate structure when viewed in reduced dimensions.
Figure 3.
The Mandelbrot set, a fractal generated by iterating a simple complex function, reveals intricate structure when viewed in reduced dimensions.
The Mandelbrot set
is defined by the iteration:
where
c is a complex parameter. The set
contains all values of
c for which the sequence
remains bounded. The boundary of
forms a highly intricate and self-similar fractal, which has been widely studied as a prototype of complex dynamical behavior. Each parameter
c can be understood as defining a unique dynamical system. The orbit of
under this system, i.e., the sequence
, defines a point in an infinite-dimensional sequence space such as
. Formally, we can define a mapping:
The evolution of
z under iteration can thus be seen as a trajectory in this function space. The condition for inclusion in
corresponds to whether this trajectory remains within a bounded subset of
. The standard visual representation of the Mandelbrot set is effectively a projection:
which identifies parameters for which the full trajectory remains bounded. The complexity and fractality of the boundary arise due to the nonlinear structure of
, which involves repeated squaring and translation, causing strong folding and stretching effects in the trajectory space. Such repeated compression of high-dimensional trajectories into a 2D parameter space induces self-similarity and scale invariance. Small changes in
c can result in drastically different long-term behaviors, a hallmark of chaotic sensitivity, even though the generating rule is entirely deterministic. Within the high-dimensional projection paradigm, the Mandelbrot set becomes:
A 2D visualization of the parameter space of an infinite family of dynamical systems, each defined by a trajectory in a high-dimensional space, compressed through nonlinear projection.
The apparent complexity in the Mandelbrot set’s boundary reflects the intricate structure of trajectory divergence and bifurcation in the full state space. Just as strange attractors emerge from folding dynamics in phase space, the Mandelbrot set’s geometry results from folding dynamics in parameter space. This interpretation situates the Mandelbrot set within the same geometric framework used to understand chaotic attractors and fractals in dynamical systems. It emphasizes the unity of these phenomena as visible artifacts of structured high-dimensional processes compressed into low-dimensional views.
4.4. Cellular Automata: Randomness and Complexity
Cellular Automata are discrete, rule-based systems capable of generating complex patterns from simple initial conditions [
36,
37,
38]. Despite the deterministic nature of their update rules, certain cellular automata exhibit behavior that appears stochastic or chaotic. Within the framework of high-dimensional projections, this complexity can be reinterpreted as the consequence of projecting high-dimensional dynamics onto a low-dimensional observable substrate.
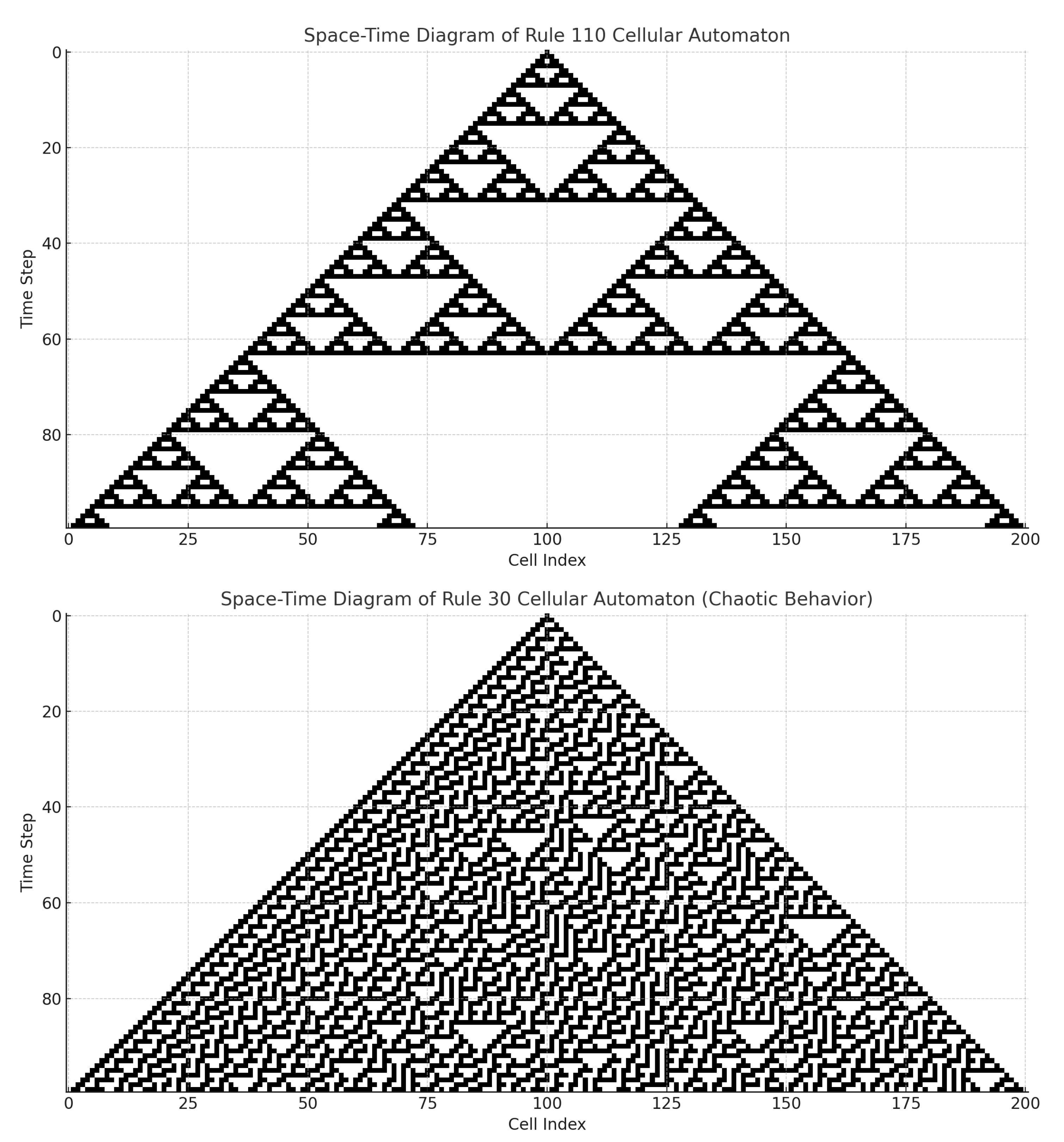
Figure 4.
Cellular automata exhibiting complex behavior.
Figure 4.
Cellular automata exhibiting complex behavior.
Formally, a one-dimensional cellular automaton consists of a finite or infinite array of discrete cells, each of which can adopt a finite number of states. The system evolves in discrete time steps according to a fixed local rule that updates each cell’s state based on the states of its neighbors. Let
denote the state of cell
i at time
t, where
is a finite state set. The global state of the system at time
t can be represented as a vector
, where
n is the number of cells. The evolution rule defines a global update function:
which is deterministic, but may generate highly intricate patterns over time. This representation implicitly places the cellular automaton in a high-dimensional discrete configuration space, specifically the finite set
. For large
n, this space becomes combinatorially vast and structurally rich.
In most practical or theoretical analyses, we observe a CA by tracking individual cell states or plotting spacetime diagrams — effectively projecting the global evolution into a low-dimensional visual or statistical representation. This projection significantly compresses the full dynamics and obscures interdependencies in the global state.
Let
represent such a projection, e.g., extracting summary statistics, visual rows, or entropy measures. The observable behavior of the system becomes:
where
can appear complex or random due to the loss of high-dimensional structural information. When the cellular automaton exhibits class IV behavior (in the Wolfram classification), it generates localized structures, long-range correlations, and apparent unpredictability. However, the underlying process is fully deterministic and governed by a fixed update rule
F. The apparent randomness observed in
can thus be interpreted as a manifestation of:
Folding of trajectories: Similar global states may evolve into divergent local behaviors when projected.
Compression of causality: High-dimensional correlations are masked in the projection, producing outputs that appear locally unpredictable.
Emergent scales: Patterns observed in spacetime diagrams emerge from nonlinear composition of simple local rules operating in a vast configuration space.
From this viewpoint, complex behavior in cellular automata is analogous to the fractal boundary of the Mandelbrot set or strange attractors in chaotic flows: a visible shadow of compressed deterministic dynamics in a high-dimensional space. This interpretation unifies cellular automata with broader classes of complex systems. Just as chaos in low-dimensional maps can be understood as a projection of high-dimensional flows, the emergence of complexity in CAs arises from observing structured evolution through a narrow observational lens.
Apparent randomness in cellular automata is not evidence of intrinsic disorder, but rather the projection of combinatorially structured logic unfolding in a high-dimensional discrete space.
This paradigm provides a robust theoretical foundation for interpreting CAs not merely as simple rule-based systems, but as models of information compression and projection in computational and natural systems. Notably, several cellular automata, such as Rule 110 and Conway’s Game of Life, are known to be Turing complete. This suggests that their configuration spaces can encode arbitrary computational processes. From the projection perspective, this means that any computable high-dimensional evolution — including those representing physical or biological systems — may yield structured, fractal-like, or chaotic patterns when projected into simpler observable forms. Such cellular automata thus serve as fertile models for studying the limits of observability, the emergence of patterns, and the interpretability of complex systems under dimensional compression.
4.5. Quantum Uncertainty as a Consequence of Incomplete System Isolation
Quantum mechanics introduces fundamental uncertainty through the indeterminacy of measurement outcomes. The Heisenberg uncertainty principle, the probabilistic collapse of the wavefunction, and the impossibility of simultaneously knowing conjugate variables are often interpreted as intrinsic to the quantum world. However, within the paradigm that views complexity and apparent randomness as projections of higher-dimensional structure, quantum uncertainty may be reinterpreted as a consequence of treating a fundamentally open system as closed.
Canonical quantum mechanics models systems using wavefunctions
evolving unitarily under the Schrödinger equation:
where
is the system’s Hamiltonian operator. Crucially, this formalism assumes that the system under consideration is
closed—isolated from the rest of the universe. Measurements, environmental influences, and unknown degrees of freedom are typically modeled as external perturbations or abstract operators. This closed-system assumption is a mathematical idealization. In practice, no quantum system exists in perfect isolation: all systems are
embedded in the full universe, which itself possesses vast—possibly infinite—dimensional complexity.
Let the total universe be represented as a complex state in a very high-dimensional Hilbert space
, while the quantum system of interest resides in a much smaller subspace
. The state of the universe evolves unitarily according to some unknown universal Hamiltonian
:
Our observations are restricted to a projection:
where the partial trace over the environment
E reflects the information loss due to our limited observational reach. This projection compresses a high-dimensional, deterministic evolution into a lower-dimensional probabilistic description. The indeterminacy captured by quantum uncertainty can thus be interpreted as the result of projecting the state of the total universe onto a subsystem, filtering out interactions and entanglements with inaccessible degrees of freedom. In this interpretation:
Wavefunction collapse reflects a structural transformation when a weakly coupled quantum system interacts with a complex, non-quantum measurement apparatus, and the balance between accessible and inaccessible degrees of freedom shifts. The system thus transitions from a low-complexity, probabilistic mode to a higher-complexity, effectively deterministic one.
Probabilistic outcomes arise not from inherent randomness but from marginalizing over unknown high-dimensional correlations.
Entanglement is a visible sign of high-dimensional structure, where separable projection is no longer valid.
From this perspective, quantum behavior is not evidence of fundamental indeterminism, but rather a signal of dimensional compression—our description of a high-dimensional, causally coherent universe reduced to a manageable but incomplete subsystem. This reinterpretation parallels earlier analyses of chaos, fractals, and cellular automata: in each case, apparent complexity, unpredictability, or randomness arises when structured dynamics on a high-dimensional manifold are observed through a narrow, low-dimensional lens.
Quantum uncertainty is not necessarily a window into fundamental randomness, but rather a shadow cast by the full complexity of the universe onto the subspace we are able to observe.
Thus, the peculiar features of quantum theory—superposition, measurement collapse, and entanglement—may all be artifacts of attempting to isolate and describe a non-isolatable fragment of a universal process whose full dimensionality remains hidden. This perspective resonates with quantum decoherence theory, relational interpretations, and quantum information approaches. It suggests that the route to a deeper understanding of quantum phenomena lies not in seeking hidden variables per se, but in developing mathematical and conceptual tools that account for the unavoidable entanglement with the rest of reality, and the projection thereof. By extending the projection paradigm to quantum mechanics, we establish a unified explanatory framework across classical chaos, complex systems, and quantum phenomena—each revealing only a partial cross-section of a more complete dynamical whole.
4.6. Information Coherence and Non-Locality of Subsystems
To illustrate the inherent non-locality of subsystems in the universe, we consider the following thought experiment rooted in relativistic spacetime geometry and quantum causality.
Imagine a distant galaxy located some three billion light-years from Earth. On the surface of a star within that galaxy, an electron undergoes a transition and emits a photon. This photon traverses intergalactic space, unaffected by intervening matter, and ultimately reaches Earth, where it is absorbed by an electron in the retina of a human observer. This absorption event initiates a cascade of neural activity, culminating in a conscious perceptual experience.
Despite the immense spatial distance between the site of emission and the site of absorption, the spacetime interval
between these two events is precisely zero:
indicating that they are connected by a null (lightlike) trajectory. According to the geometry of Minkowski spacetime, such events are not separated by any “real” spacetime interval, but rather exist in direct causal contact along the light cone.
From the conventional perspective, these events are separated by a spatial distance of three billion light-years and by a temporal delay of three billion years. However, from the photon’s point of view — which lacks a proper time — the emission and absorption occur at the same instant. There is no experienced interval, no delay, and no intermediate state: the process is indivisible and coherent. The two events of emission and absorption constitute two expressions of a single, unified process the same way that the two shadows in
Figure 5 are not independent but are two 2D projections of the same 3D object observed from two distinctive frames of reference.
This leads to a striking conclusion: although spatially distant, the emission and absorption events are in a state of informational coherence. The emission cannot be fully defined without reference to its eventual absorption, and vice versa. In this sense, these events are not merely causally linked, but are aspects of a single, unified process when viewed from a higher-dimensional or more complete informational framework. This thought experiment challenges the classical intuition of subsystem separability. The emission event on the star and the perceptual event in the human brain are not strictly independent. They are connected by a fundamental continuity through the fabric of spacetime, a continuity that is invisible when the universe is arbitrarily decomposed into isolated, local systems.
Under the high-dimensional projection paradigm, the universe evolves as a globally entangled system. Local subsystems — such as the electron on the star and the neuron in the retina — are not ontologically independent entities, but are emergent features of a single high-dimensional process. Their apparent separability arises only under projection into a lower-dimensional, locally causal model. This view aligns with the non-local character of quantum entanglement, the retrocausal implications of certain quantum interpretations, and recent developments in quantum information theory and holography. It reinforces the idea that what appears to be local, sequential, and disconnected behavior may in fact be a compressed representation of a fundamentally coherent, non-local evolution.
Two events, separated by billions of light-years and years, are in informational contact through a null interval; in the deeper geometry of the universe, they are not apart, but touching.
This perspective suggests that non-locality is not an exotic feature of quantum entanglement alone, but a general consequence of describing a globally structured universe through the lens of subsystems and projections. Building upon the preceding thought experiment, we now consider the ontological and epistemological consequences of non-local coherence. If every event is embedded in a continuum of causal and informational connections across spacetime, then every localized subsystem is not an isolated entity, but a projection of the global structure of the universe.
In conventional physical models, systems are often decomposed into smaller, spatially or causally local subsystems. These are then studied in isolation or treated as weakly coupled to an external environment. However, the assumption of subsystem independence is a methodological convenience, not an ontological truth. As illustrated by the photon thought experiment, the interactions that define a subsystem’s evolution are informed by, and contingent upon, the full dynamical state of the universe. The apparent separability of a system is only meaningful within a projected or coarse-grained description. In the full manifold of the universe’s state space, such separations vanish.
Let
denote the total informational state of the universe, evolving in a high-dimensional Hilbert space or configuration manifold. Any subsystem
S is not an independent subspace, but a functional projection
of the whole:
Thus, the complexity observed in any system
S — be it a particle, a living organism, or a human brain — is inherited from the global complexity of
. In this sense, the human observer is not a
small piece of the universe, but a
specific perspective on its total informational state. Every electron, every thought, every event is a compressed, localized expression of a cosmic-scale computation. This leads to a profound conclusion:
Every localized system in the universe is as complex as the universe itself — not because itcontainsall information, but because it is a projection of the full dynamical structure.
The analogy with holography is instructive: in a physical hologram, each part encodes the entire image in compressed form. Similarly, in a non-locally coherent universe, each event encodes — via entanglement, correlation, and causal history — the full tapestry of cosmic evolution. This perspective challenges reductionist methodologies that seek to explain systems solely in terms of proximate components. Instead, it emphasizes that understanding any system — particularly complex or conscious systems — requires situating it within the full informational context of the universe. It also redefines the meaning of emergence: what appears as emergent complexity is in fact the reappearance, under projection, of global structure in localized form. Complexity is not built up from below, but compressed down from above.
The non-local coherence of spacetime, demonstrated even by simple causal chains such as photon emission and absorption, implies that the universe cannot be fundamentally decomposed. Every subsystem is a lens on the whole. The complexity of any one part is a manifestation of the complexity of the totality. The universe is not made of separate things. It is made of different ways the whole looks when viewed from within.
5. The Nature of Truth and the Limits of Information
To deepen our inquiry into the nature of information and its entanglement with truth, we turn to a well-known logical construction:
“This statement is false.”
At first glance, this appears to be a simple declarative sentence. However, its self-referential structure produces a paradox: if the statement is true, then what it asserts must hold — hence, it is false. But if it is false, then what it asserts does not hold — hence, it is true. The result is a logical contradiction, often classified as the
Liar Paradox [
39].
5.1. Truth as Relational, Not Intrinsic
The paradox arises not from any flaw in syntax or grammar, but from the sentence’s attempt to refer to itself
as an object of evaluation. In doing so, it violates the implicit hierarchy of linguistic levels — what logicians refer to as the
object language and the
meta-language [
39]. A statement that attempts to encapsulate its own truth value recursively creates a logical loop without fixed resolution. This reveals a deep property of information:
Truth is not a static attribute of a sentence, but a relational property between statements and the broader context in which they are interpreted.
To further refine our understanding of truth and information, we must reconsider a foundational ontological assumption: that in the universe we inhabit, there is no such thing as negative existence. Everything that appears — every symbol, every event, every configuration of matter, meaning, or language — exists to some extent. There are no “false” entities in the ontological sense; there are only entities whose significance, coherence, or durability may vary.
All that manifests — whether as a transient pattern in a cloud, a random bitstring, or a proposition written in logical form — partakes in the structure of reality. It may persist or vanish. It may be coherent or disordered. But its appearance affirms its existence. Even contradictions, illusions, or lies are there. They have form. They take place. They register in the informational fabric of the cosmos. Hence:
There is no ontological negative. What is called “false” does not fail to exist — it only fails to cohere within our horizon of meaning.
From this perspective, “falsehood” is not a metaphysical category but an epistemic placeholder. It marks the boundary where our knowledge fails to resolve structure. A false statement is not an entity that contradicts being; it is a configuration that exceeds — or escapes — our current framework for assigning coherence or correspondence. The label “false” therefore functions like terms such as “noise,” “randomness,” or “chaos”: it designates what is, but what we do not yet understand. These are not categories of non-being, but indicators of our own perceptual and cognitive limits.
5.2. Reinterpreting the Liar Paradox
This has critical implications for self-referential paradoxes, such as:
“This statement is false”.
The paradox does not arise from a conflict between truth and falsehood as metaphysical opposites. Rather, it emerges from the attempt to embed in a statement a reference to a category that is epistemically undefined — one that lies beyond the semantic closure of the system. When a statement refers to its own falsehood, it attempts to wrap an unknowable, undefined boundary condition inside a fixed and finite syntax. The result is not contradiction in the universe, but compression failure at the interface of language and totality — the linguistic analog of trying to encode a singularity. Therefore, the category of the “false” does not denote an ontological absence, but a cognitive horizon:
Falsehood is not a thing; it is a name we give to that which lies just beyond the boundary of our comprehension.
As with noise, as with chaos, as with quantum uncertainty, what we perceive as false or contradictory may be a surface effect — the shimmer at the edge of coherence — produced by attempting to view the whole through the filter of a part. In a universe of informational continuity, everything that exists exists. The term “false” functions not as a denial of being, but as a signal of ungrasped structure. Paradoxes such as the Liar reveal not a flaw in logic, but a deep principle: that any system which tries to contain the uncontainable will generate formal breakdowns at its edge. And those breakdowns are not failures, but pointers — boundary markers to the greater coherence from which all statements arise.
5.3. Falsehood as Partial Context: A Real-World Illustration
To further clarify the notion that “falsehood” refers not to the absence of truth but to the incompleteness of context, we examine a common scenario from public discourse — political speech.
Consider a politician who proclaims during a campaign:
“Elect me and I will end the war on the first day in office.”
At first glance, this appears to be a declarative prediction — one that can be classified as either true or false depending on future outcomes. Public discourse often frames such statements in terms of truth-value: did the politician tell the truth, or was it a lie? However, this binary framing ignores the broader informational and motivational context in which the statement was made. A more complete reconstruction of the full statement — inclusive of intention, strategy, and context — might read as follows:
“I am an ambitious and ruthless political actor. I wish to attain power at any cost, and I am willing to say and do whatever it takes to survive and to maximise my chances of being elected. Based on current polling, public sentiment, and media cycles, the most resonant message is: `I will end the war on my first day in office’ ”.
Understood this way, the utterance is not a standalone truth-claim about the future. It is an element in a strategy of persuasion — an expression of underlying motivations embedded within a complex political system. As such, the full statement is not “false” in the traditional sense; it is true within the context of the speaker’s internal logic, situational awareness and ultimately pursuit of survival. What we conventionally refer to as a “lie” is often simply a cropped frame — a local slice of a more expansive structure. The cognitive error lies in mistaking the partial utterance for the totality of meaning. In this view, the term “falsehood” operates not as a judgment of existential invalidity, but as a placeholder indicating that the full context is not yet visible or known. Thus:
What we label as false is not untrue — it is incomplete. It is a boundary effect of limited informational framing.
This reframes the idea of deception in pragmatic and epistemological terms. A deceptive statement does not fail to exist; it exists fully as an intentional act embedded in a field of motivations, constraints, and symbolic strategies. The “false” quality attributed to it is a result of focusing narrowly on surface syntax without perceiving the structure that gave rise to it. Just as a fractal segment appears irregular only when removed from its recursive whole, or a chaotic sequence seems random only when projected into low dimensions, so too does a deceptive utterance seem false only when divorced from its generative logic.
Falsehood, therefore, is not a statement about the inexistence or negation of reality. It is a linguistic and epistemic marker indicating that our interpretive lens is too narrow, that we are perceiving only a sliver of a broader pattern. In this framework,
everything said is true — in context. What we call falsehood is a measure of our own distance from that context.
Illustration: Relativism (left) versus Shared albeit Complex Reality (right). Images are from the public domain (internet memes). The elephant meme is possibly by TeePublic.
5.4. The Futility and Danger of Relativism
In postmodern discourse — particularly as adopted and operationalized within political strategy and social engineering — a common sentiment prevails: that there is no such thing as absolute truth. Each person, each party, each ideological faction is thought to possess its own “truth,” and thus no truth can claim superiority or objectivity over another [
40].
This relativist assertion is often used rhetorically to neutralize criticism, paralyze dialogue, or justify epistemic isolation. It appears, on the surface, to align with the framework we have presented — a model of partial information, subjective projection, and perspectival compression. However, this appearance is misleading. Our model does not support postmodern relativism. In fact, it refutes it at its core. Relativism collapses the distinction between perspective and truth. It asserts:
“Because we all have different perspectives, there is no single truth.”
But this misunderstands the nature of perspective. A perspective is not a truth; it is a
projection — a limited and localized representation of something more complete [
39]. Perspectives are real, meaningful, and necessary, but they do not exist in isolation. They derive their coherence and intelligibility from the reality they partially represent. From the paradigm of projection, we affirm instead:
The only truth that exists is the whole truth — the universe itself. Everything else is a projection, a compression, a local expression of that singular totality.
Different perspectives are not incompatible truths; they are different
views of the same objective reality [
16]. The fact that we observe from different frames does not imply that there is no object of observation. On the contrary, it implies that our frames are
connected — that there exists something
shared and
stable toward which all perspectives converge. The distinction is not merely philosophical — it is civilizational. If we accept that there is no common truth, then reconciliation becomes impossible. There is no shared ground upon which dialogue can unfold, no mutual reality to appeal to, no overlap in which understanding can be cultivated. Every discourse becomes warfare. Every interaction becomes manipulation. Every disagreement becomes ontological rupture [
41].
By contrast, if we accept that there is one underlying reality — and that each of us sees only part of it — then dialogue becomes meaningful. Exchange becomes possible. We can communicate not because we hold separate truths, but because we are exploring the same truth from different angles. This paradigm demands a deep humility: to recognize that our personal or collective “truths” are not ultimate, but contingent perspectives — filtered through cognitive, cultural, and historical lenses [
42]. But it also offers a profound hope: that despite fragmentation, there is something that holds — something that unites all experience, all perception, all structure. That something is the universe — not in its parts, but in its whole. Truth, then, is not subjective. It is not relative. It is absolute, but seen partially. It is one, but expressed multiply. It is stable, but approached incrementally.
Thus, we reject the relativist stance not out of dogmatism, but out of deeper fidelity to the structure of reality. There is only one truth — the whole. Our task is not to invent truths, but to uncover, exchange, and refine our views of that which is. In this endeavor, every perspective has value — not because it is truth, but because it points toward it.
6. Infinity as an Epistemic Placeholder: The Far Beyond
Within the framework developed throughout this work, we have reinterpreted several traditionally fundamental categories — such as falsehood, randomness, and contradiction — not as absolute states of reality, but as epistemic markers. These concepts do not denote independent entities or metaphysical opposites, but instead signal the boundaries of understanding. They are cognitive placeholders for structures we do not (yet) comprehend. In this light, we now turn to the notion of infinity.
6.1. The Infinite as the Horizon of Comprehension
The concept of infinity appears across the disciplines as both a symbol of idealization and a source of contradiction. In mathematics, it is treated as a formal limit; in physics, as a convenient abstraction or problematic singularity; in theology and philosophy, as a notion of ultimate unknowability.
But viewed within our epistemic framework, we can now make a deeper claim:
Infinity is not a real thing in the universe. It is a placeholder for the “far-far-away” — the unreachable end of a projection, the boundary beyond which our comprehension fades into undefined space.
Infinity serves the same function as the concept of “falsehood” in logic or “randomness” in computation: it arises precisely when the internal representation of a system attempts to reach beyond its informational horizon. It is not what is, but what we point to when we can no longer say what is.
When we describe something as infinite — an infinite series, an infinite space, an infinite number of possible outcomes — we are acknowledging that our current mode of symbolic representation cannot contain or resolve the full structure within a bounded frame. Just as “false” marks what escapes coherence, and “random” marks what escapes pattern, so too does “infinity” mark what escapes enclosure.
We are not denying the value or utility of infinite constructs. But we are reframing them: as asymptotic gestures toward the whole, rather than literal descriptions of an external, infinite substance. Just as lines extend “to infinity” on paper, but in reality, all physical instantiations are finite, so too does infinity live in our models — not in the universe.
6.2. The Same Family: Infinity, Randomness, Falsehood
These three categories — infinity, randomness, and falsehood — all share the same structural role. They do not name things. They name thresholds. They are markers at the edges of knowability, standing in for what is presently unreachable from a given perspective.
Falsehood indicates that something lies outside the current frame of semantic or contextual coherence.
Randomness indicates a lack of discernible pattern within the current resolution or perspective.
Infinity indicates an unboundedness or ungraspability within the current limits of containment.
None of these are negations of existence. They are affirmations of limitation — reflections of how our partial views relate to the fullness of the universe. To treat infinity as real is to confuse the edge of the map for the territory. To treat it as a placeholder is to understand its true power: not as a number or a space, but as a symbol for the unreachable, the unresolved, the far-far-away. This reinterpretation aligns with the rest of our framework: reality is whole, finite, and coherent. What we call infinite is simply what remains — for now — out of reach. Like a horizon, infinity recedes as knowledge expands. But the world itself remains bounded, structured, and complete — always already there. Now, consider the following examples of enigmatic problems in mathematics:
6.3. Gödel’s Incompleteness
Gödel’s Incompleteness Theorems are often taken to mark a permanent limit in human knowledge and the capacity of formal systems to fully express arithmetic truth. The First Theorem states that in any sufficiently expressive formal system, there exist true statements that cannot be proven within that system [
3]. The Second states that such a system cannot prove its own consistency [
3].
These results are traditionally interpreted within a framework that assumes actual infinity — that is, an infinite set of numbers, infinite proofs, and infinite formal chains. Gödel’s proofs, in particular, rely on encoding statements about the system within the system itself, and on the assumption that the natural numbers are a complete and infinite domain [
43]. But within the paradigm of a finite, coherent universe — where all symbolic and logical systems are grounded in a closed informational totality — the basis for Gödel’s incompleteness begins to shift.
We postulate that incompleteness arises not from a flaw in formal systems themselves, but from the mischaracterization of symbolic limits as ontological boundaries. In our paradigm, infinity is not a real condition of mathematics, but a symbolic placeholder that marks the limit of observational or representational scope. Likewise, “unprovable truths” are not truths outside the system, but statements that encode complexity beyond the current resolution or compression of the formal framework.
Gödel’s incompleteness is not an ontological rupture. It is an epistemic horizon effect — a boundary condition produced when a finite system is forced to simulate infinite self-reference.
In a truly finite and coherent universe, there exists a maximal amount of information and structure. Every logical system constructed within that universe is, by necessity, a
subsystem of the whole. The apparent paradoxes — such as Gödel’s undecidable statements — arise when a symbolic subsystem attempts to speak about the totality it does not yet contain or comprehend [
44].
In a finite universe, every possible truth is grounded in a finite configuration. There exists a limit, not to what can be known, but to how much symbolic self-reference can exceed the bounds of the total informational structure. Once the system is sufficiently expanded to reflect the full structure of the universe, the apparent incompleteness vanishes — not because every proof becomes accessible in principle, but because every statement is now framed in context of the whole. This leads to a natural resolution:
Gödel’s incompleteness theorems dissolve when the formal system is no longer expected to exceed or mirror the whole — when it is understood as a projection within, and not beyond, the finite universe.
In other words, no formal system can prove its own completeness or consistency if it attempts to refer to a structure beyond its scope. But if the universe is finite and fully coherent, then all statements, systems, and truths are part of that totality — and no contradiction is required. The incompleteness is not a permanent defect of logic, but a temporary misalignment of symbolic compression with ontological structure [
45].
Gödel’s theorems, like the Liar Paradox, point to the same structural insight: symbolic systems break down when they attempt to simulate the infinite. In a finite, coherent universe, this breakdown is resolved not by escaping it, but by reframing it. Truth is not incomplete. It is always whole — and systems are incomplete only insofar as they refuse to acknowledge their embeddedness in that whole.
6.4. Fermat’s Last Theorem
Fermat’s Last Theorem states that there are no three positive integers
a,
b, and
c that satisfy the equation
for any integer
. This theorem, first conjectured by Pierre de Fermat in 1637 [
46], remained unproven for over 350 years until Andrew Wiles provided a proof in 1994 [
47] using powerful tools from algebraic geometry and number theory.
While the proof operates within the formal framework of modern mathematics — which includes infinite sets and abstract constructions — the key structures Wiles employed, such as modular forms and elliptic curves, are fundamentally algebraic and arithmetically well-defined [
48]. These structures allow one to encode infinite behavior into finite, coherent systems of relations.
Rather than directly confronting the infinitude of possible solutions to Fermat’s equation, Wiles demonstrated that any hypothetical solution would correspond to an elliptic curve with properties that contradict the modularity theorem [
49]. This indirect approach transformed the infinite problem space into a question about the structure and symmetry of a well-defined mathematical object. Thus, the resolution of the theorem relied not on infinity per se, but on the deep structure and coherence of algebraic systems that project and constrain infinite possibilities within finite frameworks.
6.5. The Riemann Hypothesis
Among all the unresolved problems in mathematics, the
Riemann Hypothesis (RH) stands uniquely at the intersection of metaphysics and formalism. It is often regarded as the
Holy Grail of modern mathematics — not merely because of its technical difficulty or implications for number theory, but because of the deep ontological challenge it embodies [
50]. The RH concerns the distribution of the prime numbers, which are discrete and finite in any range, yet extend seemingly indefinitely across the number line. The hypothesis asserts that all non-trivial zeros of the Riemann zeta function,
lie on the so-called “critical line” in the complex plane:
This function is initially defined by an
infinite sum, analytically continued to the entire complex plane except for a pole at
[
51]. Thus, RH is not merely a conjecture about primes — it is a conjecture about the deep structure of an
infinite analytic extension that encodes the full behavior of the primes.
In this way, the RH does not just make use of infinity; it is about infinity. It is a question whose formulation is inseparable from infinite processes, complex analysis, and transcendental extension. The infinite sum
contains within it the entirety of the prime distribution — compressed into a single function — but at the cost of invoking the full machinery of infinite series, limits, and analytic continuation [
52]. The deeper challenge of RH lies in its placement on the boundary between two mathematical worlds:
Number Theory, concerned with discrete, countable, and finite structures — especially the primes [
53].
Complex Analysis and Calculus, rooted in the continuity of the complex plane and the infinitesimal logic of limits and convergence [
54].
The Riemann zeta function acts as a bridge: a function that translates the prime structure of the integers into the language of the continuum. The non-trivial zeros of this function lie within the complex plane, and yet they encode statements about integers — the most finite and foundational of mathematical objects. The Riemann Hypothesis is the most explicit manifestation of infinity in modern mathematics. It challenges us not simply because of its technical complexity, but because it places us at the exact epistemological boundary — the threshold where discrete number theory spills over into the ocean of analytic infinity.
Within the epistemological framework developed throughout this work, we have come to understand concepts such as
falsehood,
randomness, and
infinity not as real categories of being, but as symbolic placeholders that emerge when a system attempts to describe what lies beyond its own boundary of coherence. These are not errors of logic, but errors of scope — phenomena produced at the edge of observability. In this light, we may interpret the
Riemann Hypothesis as a direct analog to the
Liar Paradox. The Liar Paradox (“This statement is false”) generates an apparent contradiction by introducing the category of falsehood — a placeholder for semantic breakdown — into a system that cannot accommodate it. The contradiction is not real; it is a byproduct of projecting an undefined reference beyond the epistemic limits of the statement’s frame [
45].
Similarly, the Riemann Hypothesis introduces the category of infinity into the analysis of prime distribution — a fundamentally finite, discrete phenomenon. The zeta function is constructed as an infinite analytic continuation meant to capture the behavior of primes, but it does so by invoking a symbolic structure () that lives explicitly outside the domain it seeks to describe. The difficulty of the RH — its apparent unsolvability — arises not from the content of the question, but from the way in which the concept of infinity distorts the visibility of the underlying structure.
Just as the Liar Paradox is not a failure of truth but a horizon effect caused by referencing falsehood from within, the Riemann Hypothesis is not a failure of number theory but a horizon effect caused by referencing infinity from within the finite.
From this perspective, the challenge of RH does not lie in the mathematics, but in the mode of representation. The analytic formalism tries to speak for the discrete totality of primes by means of an infinite extension — and in doing so, it veils the finite structure it aims to illuminate. The unsolvability of RH may then be seen not as a permanent feature of number theory, but as a symptom of relying on symbolic constructs that exceed the scale of the reality they are meant to describe. To resolve RH, therefore, is not merely to locate a zero or complete a proof — it is to properly reframe the projection, to remove the placeholder of infinity, and to see the primes not through the lens of what lies beyond them, but through the harmony they already express.
This work does not (yet) claim to offer a complete interpretation or resolution of the Riemann Hypothesis within the paradigm of a finite universe. However, we are prepared to postulate a reorientation of the problem — one that may illuminate a more coherent and ontologically consistent path forward. Specifically, we propose that in a universe that is fundamentally finite — one in which all informational, physical, and numerical entities are bounded — the presumption of an actually infinite sequence of integers is not warranted. Instead, we propose the following interpretive shift:
The Riemann zeta function should not be understood as a sum over an abstractly infinite set, but as the sum over all the Natural Numbers that actually exist — a vast but ultimately finite totality of number-like entities that constitute the arithmetic substrate of the universe.
It is important to emphasize that the type of number systems which support this finite-universe reinterpretation of the Riemann zeta function are not speculative or obscure. They are well-established and deeply explored within modern mathematics. These include modular arithmetic [
55], finite fields (
) [
56], residue class systems [
57], and cyclic group structures [
58] — all of which provide consistent, logically coherent, and computationally tractable frameworks for working with bounded numerical domains.
Despite their power and rigor, such systems have historically been treated as auxiliary or utilitarian — tools of encryption [
59], digital computation [
2], coding theory [
60], and combinatorics [
61] — rather than as candidates for the foundational ontology of physical or mathematical reality. In conventional paradigms, they are regarded as convenient abstractions rather than representations of what truly exists.
Yet in the context of a finite, informationally coherent universe, these so-called “secondary” number systems acquire new significance. They offer precisely the type of bounded, internally consistent numerical infrastructure required to support a fully finite reconstruction of symbolic constructs like the zeta function — not as infinite series, but as periodic summations over a totality of integers that are not merely conceptual, but existentially grounded.
Finally, we postulate that the non-trivial zeros of the Riemann zeta function are not merely mathematical markers of prime distribution, but the emergent result of deeper, universal constraints — resonant patterns that encode the balance and coherence of the universe itself [
62]. Just as physical systems exhibit stable modes of vibration — frequencies at which standing waves emerge and resonance is achieved — so too may the informational field of the universe possess intrinsic modes of coherence. These modes are not spatial or mechanical in the traditional sense; they are mathematical, symbolic, and structural. These harmonic modes, expressed as the non-trivial zeros of the zeta function, manifest in the distribution of prime numbers as the surface-level arithmetic signature of a deeper, resonant order — the visible trace of the universe’s underlying informational coherence.
7. The Langlands Program and the Reflected Unity of Mathematical Structures
In the realm of pure mathematics, the Langlands program stands as one of the most profound and unifying conceptual architectures ever proposed. It posits a deep correspondence between seemingly unrelated mathematical domains: number theory, representation theory, algebraic geometry, and automorphic forms [
63]. These are distinct languages, developed in isolation across centuries, now found to encode — through complex transformations — the same underlying structures.
Within the framework we have developed, the Langlands program is not an anomaly. It is precisely what we should expect when different systems attempt to describe the same underlying reality through different projections. At the core of the Langlands philosophy is the idea that each of these mathematical frameworks is not a standalone domain, but a
perspective on the same informational structure. Their equivalence — known as the Langlands correspondence — is not a coincidence, but a mathematical echo of a deeper ontological unity [
64].
Each domain expresses certain symmetries, patterns, and invariants — but through different symbolisms and operations. What one domain expresses in terms of Galois groups and prime fields [
65], another encodes through harmonic analysis on Lie groups or cohomology of algebraic varieties [
66]. These are not separate realities, but distinct reflections — mirrored fragments of a singular mathematical whole. If the universe is a unified informational system — a kaleidoscope of recursively reflected patterns — then mathematics, as its most abstract language, inevitably generates multiple equivalent representations. The apparent diversity of mathematical theories corresponds to the different vantage points from which the same universal structure is examined. From this perspective:
The Langlands program is the mathematical articulation of universal coherence — the recognition that different symbolic systems, when deeply understood, are not divergent but equivalent.
Just as physical complexity arises from projection and relational recursion, mathematical complexity arises from mapping the universal onto various formal systems. The Langlands correspondences reveal the invariant that persists across such projections — the “same shape” seen through many mirrors [
67]. In this framework, the Langlands program is not merely a technical web of conjectures. It is a philosophical revelation: the universe, in its informational totality, is
structured in such a way that any formal system sufficiently rich to reflect its structure will ultimately reflect all others. Not trivially — not obviously — but in a deep and precise way that requires years or decades of unfolding. Thus, the Langlands program mirrors our broader thesis:
All local symbolic systems — whether physical, linguistic, cognitive, or mathematical — are partial projections of the same universal information structure. The deeper the system, the more likely it is to converge, through unexpected bridges, with all others.
The Langlands program does not merely unify mathematical domains. It testifies to the unity of structure beneath form, the unity of reality beneath representation. It is the mathematical embodiment of the idea that all complexity — all truth — is the projection of a single, coherent, recursive, and infinite system: the universe.
8. Conclusion
Throughout this work, we have developed a unified paradigm in which complexity, chaos, fractality, and quantum uncertainty are not markers of fundamental randomness or disconnection, but reflections of an underlying unity. These phenomena emerge when structured, high-dimensional processes are observed through the lens of low-dimensional projections. We have extended this paradigm to quantum systems, cellular automata, and spacetime geometry. In each case, apparent separability and locality dissolve upon closer analysis, revealing that what we consider to be individual systems are in fact expressions of the whole — partial perspectives on the globally entangled dynamics of the universe.
From the emission of a photon on a distant star to the spark of human perception, the universe demonstrates that information is not confined by distance. The space between events is not a barrier but a medium of coherence. What appears to be far apart in space and time may, under null or entangled trajectories, be in direct contact at the level of informational structure.
This leads us to a final, holistic conclusion:
Everything within the universe — every particle, process, and observer — is a projection and expression of the entirety of the universe. What we perceive as individual things are compressed reflections of the totality, viewed from particular vantage points. The part does not merely participate in the whole; it is the whole, seen from within.
This vision reframes the universe not as a collection of parts interacting locally, but as a single indivisible process — infinitely faceted, self-reflective, and coherent. Every subsystem is not a container of information but a portal to the universe’s full dimensionality, folded into form by the geometry of projection and the limits of observation. Understanding reality, then, is not a matter of building up from the bottom, but of unfolding from the top.
8.1. Complexity as the Projection of Universal Structure
Across domains as varied as nonlinear dynamical systems, computational automata, and quantum physics, we observe the emergence of complexity from systems defined by deceptively simple rules. Fractals arise from recursive geometric iterations, cellular automata from binary logic, and quantum systems from linear operators on finite Hilbert spaces. Yet, in each case, the resulting behavior defies the simplicity of the generating rules, exhibiting patterns of astonishing intricacy, unpredictability, and self-similarity.
The prevailing explanation attributes this complexity to intrinsic properties: to nonlinearity, recursion, entanglement, or feedback. However, a deeper account emerges when we consider each of these systems not in isolation, but as
projections of a larger, high-dimensional reality — the universe itself — evolving through structures and interactions far beyond what any single subsystem can internally encode. In this light, every system — mathematical, physical, biological, cognitive — is a portal through which the whole universe peers at itself. No part is truly separate. No behavior is truly local. The source of all complexity is the same: the universe as a unified informational structure, whose parts are shadows of the whole.
8.2. The Universe as a Kaleidoscope of Reflected Complexity
The universe may be conceived as a kaleidoscope — not in its decorative appearance, but in its structural essence. A kaleidoscope contains only a few discrete fragments: colored glass, polished stones, or shaped beads. These are the elemental components — simple, countable, finite. But they are enclosed within a chamber of mirrors — recursive, angled, and inter-reflective — that multiplies and refracts them into endless pattern.
Each rotation of the kaleidoscope reconfigures the arrangement of fragments, generating new symmetries, asymmetries, and emergent forms. The result is an ever-changing complexity, an intricate interplay of color, form, and structure that far exceeds the simplicity of the inputs. So it is with the universe.
What appears as infinite diversity — stars and cells, equations and languages, thoughts and lives — emerges from a finite set of foundational elements, reflected and refracted through the recursive architecture of spacetime, causality, and relation. The complexity we observe is not a product of an infinite number of things, but of the seemingly infinite ways in which a limited set of things can mirror and relate to one another.
The universe is not made of endless parts, but of a vast multitude of reflections of its singular totality.
This is why the world feels both familiar and unknowable, ordered and chaotic, finite and boundless. Each moment is a rotation. Each perspective is a view into a different chamber. And every pattern we see is a configuration — not of new things, but of new angles, new projections, new relational alignments. Like the image in a kaleidoscope, no part exists independently. Every piece depends on the whole arrangement, and every pattern is a manifestation of totality — revealed through symmetry, distortion, and recursive depth.
References
- Bertrand Russell. The Principles of Mathematics. Cambridge University Press, 1903. Introduces the Russell Paradox, highlighting foundational issues in set theory.
- Alan Turing. On computable numbers, with an application to the entscheidungsproblem. Proceedings of the London Mathematical Society, 42(2):230–265, 1936. Introduces the Turing machine and the halting problem, foundational to computer science.
- Kurt Gödel. Über formal unentscheidbare sätze der principia mathematica und verwandter systeme i. Monatshefte für Mathematik und Physik, 38:173–198, 1931. Presents Gödel’s incompleteness theorems, demonstrating the limits of formal systems.
- Steven Weinberg. The cosmological constant problem. Reviews of Modern Physics, 61(1):1–23, 1989. Discusses the cosmological constant problem, also known as the vacuum catastrophe.
- Aristotle. On the Heavens. Oxford University Press (modern editions), circa 384 BCE. Argues for the finiteness of the Earth and the cosmos, foundational to early cosmology.
- Nicolaus Copernicus. On the Revolutions of the Heavenly Spheres. Johannes Petreius, 1543. Proposes the heliocentric model, demonstrating the periodic and finite nature of planetary orbits.
- Albert Einstein. On a heuristic point of view concerning the production and transformation of light. Annalen der Physik, 17:132–148, 1905. Introduces the concept of light quanta, foundational to quantum mechanics.
- Albert Einstein. On the electrodynamics of moving bodies. Annalen der Physik, 17:891–921, 1905. Presents the theory of special relativity, introducing the concept of a finite speed of light.
- Max Planck. On the law of distribution of energy in the normal spectrum. Annalen der Physik, 4:553–563, 1901. Introduces the concept of quantization, foundational to quantum theory.
- Aristotle. Metaphysics. Oxford University Press (modern editions), circa 350 BCE. Introduced the concepts of substance, potentiality, and actuality, foundational to the idea of persistence.
- Immanuel Kant. Critique of Pure Reason. Cambridge University Press (modern editions), 1781. Explores the relational nature of objects and their dependence on human cognition and perception.
- Alfred North Whitehead. Process and Reality. Macmillan, 1929. Develops process philosophy, emphasizing reality as composed of processes and events that persist through time.
- Henri Bergson. Creative Evolution. Henry Holt and Company, 1911. Emphasizes the dynamic nature of life and reality, tying persistence to the continuous flow of time.
- Ilya Prigogine. Order Out of Chaos: Man’s New Dialogue with Nature. Bantam Books, 1984. Explores dissipative structures and the maintenance of stability in far-from-equilibrium systems.
- Stuart Kauffman. At Home in the Universe: The Search for the Laws of Self-Organization and Complexity. Oxford University Press, 1993. Examines self-organization and the emergence of order in complex systems.
- David Bohm. Wholeness and the Implicate Order. Routledge, 1980. Introduces a relational and holistic view of reality, emphasizing the implicate and explicate orders.
- Claude E. Shannon. A mathematical theory of communication. Bell System Technical Journal, 27(3):379–423, 1948. Foundational work on information entropy and redundancy in communication systems.
- John von Neumann. Theory of Self-Reproducing Automata. University of Illinois Press, 1966. Explores self-replication and feedback mechanisms in computational systems.
- Lee Smolin. The Life of the Cosmos. Oxford University Press, 1997. Proposes cosmological natural selection and the evolution of stable universes.
- Karen Barad. Meeting the Universe Halfway: Quantum Physics and the Entanglement of Matter and Meaning. Duke University Press, 2007. Develops the concept of agential realism, emphasizing relational emergence through interactions.
- Ludwig Boltzmann. Statistical Mechanics. Springer, 1877. Foundational work on probabilistic structures and equilibrium states.
- Charles Darwin. On the Origin of Species. John Murray, 1859. Seminal work on natural selection and the evolution of survival mechanisms.
- Satoshi Nakamoto. Bitcoin: A peer-to-peer electronic cash system, 2008. Introduces blockchain technology and adaptive protocols for maintaining stability.
- John D. Barrow. The Constants of Nature: From Alpha to Omega. Vintage, 2007. Explores the fundamental constants of physics and their role in shaping the universe.
- Brandon Carter. Large number coincidences and the anthropic principle in cosmology. IAU Symposium, 63:291–298, 1974. Introduces the anthropic principle, explaining the fine-tuning of the universe in terms of observer selection effects.
- Emmy Noether. Invariante variationsprobleme. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, pages 235–257, 1918. Establishes Noether’s theorem, linking symmetries in physics to conservation laws.
- Richard P. Feynman, Robert B. Leighton, and Matthew Sands. The Feynman Lectures on Physics. Addison-Wesley, 1964. A comprehensive introduction to physics, including discussions on symmetry and conservation laws.
- Edward N. Lorenz. Deterministic nonperiodic flow. Journal of the Atmospheric Sciences, 20(2):130–141, 1963. Pioneering work in chaos theory, introducing the concept of deterministic chaos and the Lorenz attractor.
- Erwin Schrödinger. Quantisierung als eigenwertproblem. Annalen der Physik, 384(4):361–376, 1926. Introduced the Schrödinger equation, foundational to quantum mechanics.
- Norman H Packard, James P Crutchfield, J Doyne Farmer, and Robert S Shaw. Geometry from a time series. Physical Review Letters, 45(9):712, 1980. [CrossRef]
- Floris Takens. Detecting strange attractors in turbulence. Lecture Notes in Mathematics, 898:366–381, 1981.
- Steven H Strogatz. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Westview Press, 1994.
- Leland McInnes, John Healy, and James Melville. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv preprint arXiv:1802.03426, 2018.
- Laurens van der Maaten and Geoffrey Hinton. Visualizing data using t-sne. Journal of Machine Learning Research, 9(Nov):2579–2605, 2008.
- Juan M Maldacena. The large-n limit of superconformal field theories and supergravity. Advances in Theoretical and Mathematical Physics, 2(2):231–252, 1998.
- Matthew Cook. Universality in elementary cellular automata. Complex Systems, 15(1):1–40, 2004. [CrossRef]
- Andrew Ilachinski. Cellular Automata: A Discrete Universe. World Scientific, 2001.
- Stephen Wolfram. A New Kind of Science. Wolfram Media, 2002.
- Alfred Tarski. The concept of truth in formalized languages. Logic, Semantics, Metamathematics, 1936.
- Jean-François Lyotard. The Postmodern Condition: A Report on Knowledge. University of Minnesota Press, Minneapolis, 1984. [CrossRef]
- Jürgen Habermas. The Theory of Communicative Action, Volume 1: Reason and the Rationalization of Society. Beacon Press, Boston, MA, 1984.
- Thomas S Kuhn. The Structure of Scientific Revolutions. University of Chicago Press, 1962.
- Ernest Nagel and James R. Newman. Gödel’s Proof. New York University Press, New York, 1958.
- Douglas R. Hofstadter. Gödel, Escher, Bach: An Eternal Golden Braid. Basic Books, New York, 1979.
- Willard Van Orman Quine. Ways of Paradox and Other Essays. Harvard University Press, Cambridge, MA, 1976. [CrossRef]
- Pierre de Fermat. Arithmetica. Toulouse: Jean de Boude, 1670. Posthumously published by his son.
- Andrew Wiles. Modular elliptic curves and fermat’s last theorem. Annals of Mathematics, 141(3):443–551, 1995. [CrossRef]
- Kenneth A. Ribet. On modular representations of Gal(/Q) arising from modular forms. Inventiones mathematicae, 100(2):431–476, 1990.
- Gerhard Frey. Links between stable elliptic curves and certain diophantine equations. Annales scientifiques de l’École Normale Supérieure, 19(4):645–656, 1986.
- Enrico Bombieri. The Riemann Hypothesis. Cambridge University Press, Cambridge, UK, 2000.
- Bernhard Riemann. Ueber die anzahl der primzahlen unter einer gegebenen grösse. Monatsberichte der Berliner Akademie, pages 671–680, 1859.
- E. C. Titchmarsh. The Theory of the Riemann Zeta-Function. Oxford University Press, Oxford, UK, 1986.
- G. H. Hardy and E. M. Wright. An Introduction to the Theory of Numbers. Oxford University Press, 5th edition, 1979.
- Harold M. Edwards. Riemann’s Zeta Function. Dover Publications, New York, 1974.
- Carl Friedrich Gauss. Disquisitiones Arithmeticae. Fleischer, Leipzig, 1801. [CrossRef]
- Évariste Galois. Théorie des équations algébriques. Journal de Mathématiques Pures et Appliquées, 11:381–444, 1846.
- Peter Gustav Lejeune Dirichlet. Vorlesungen über Zahlentheorie. Vieweg, Braunschweig, 1863.
- William Burnside. Theory of Groups of Finite Order. Cambridge University Press, Cambridge, 1911.
- Claude E. Shannon. Communication theory of secrecy systems. Bell System Technical Journal, 28(4):656–715, 1949. [CrossRef]
- Richard W. Hamming. Error detecting and error correcting codes. Bell System Technical Journal, 29(2):147–160, 1950.
- Richard P. Stanley. Enumerative Combinatorics, Volume 1. Cambridge University Press, 1997.
- Alain Connes. Trace formula in noncommutative geometry and the zeros of the riemann zeta function. Selecta Mathematica, 5(1):29–106, 1999.
- Robert P. Langlands. Problems in the Theory of Automorphic Forms. Yale University Press, 1970. Seminal work introducing the Langlands program, proposing deep connections between number theory and representation theory.
- Stephen Gelbart. Automorphic forms and the langlands program. Bulletin of the American Mathematical Society, 10(2):177–219, 1984. Overview of the Langlands program and its implications for unifying mathematical domains.
- John Tate. Global class field theory. Algebraic Number Theory, pages 162–203, 1967. Foundational work on class field theory, connecting number theory and algebraic geometry.
- Armand Borel. Automorphic l-functions. Proceedings of Symposia in Pure Mathematics, 33:27–61, 1979. Explores automorphic forms and their connections to algebraic geometry and representation theory.
- Harold M. Edwards. Fermat’s Last Theorem: A Genetic Introduction to Algebraic Number Theory. Springer, 1977. Discusses the historical and mathematical context of Fermat’s Last Theorem, including its connections to modern number theory.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).