Submitted:
18 August 2025
Posted:
19 August 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Analytical Approach
3. The Equations of Motion
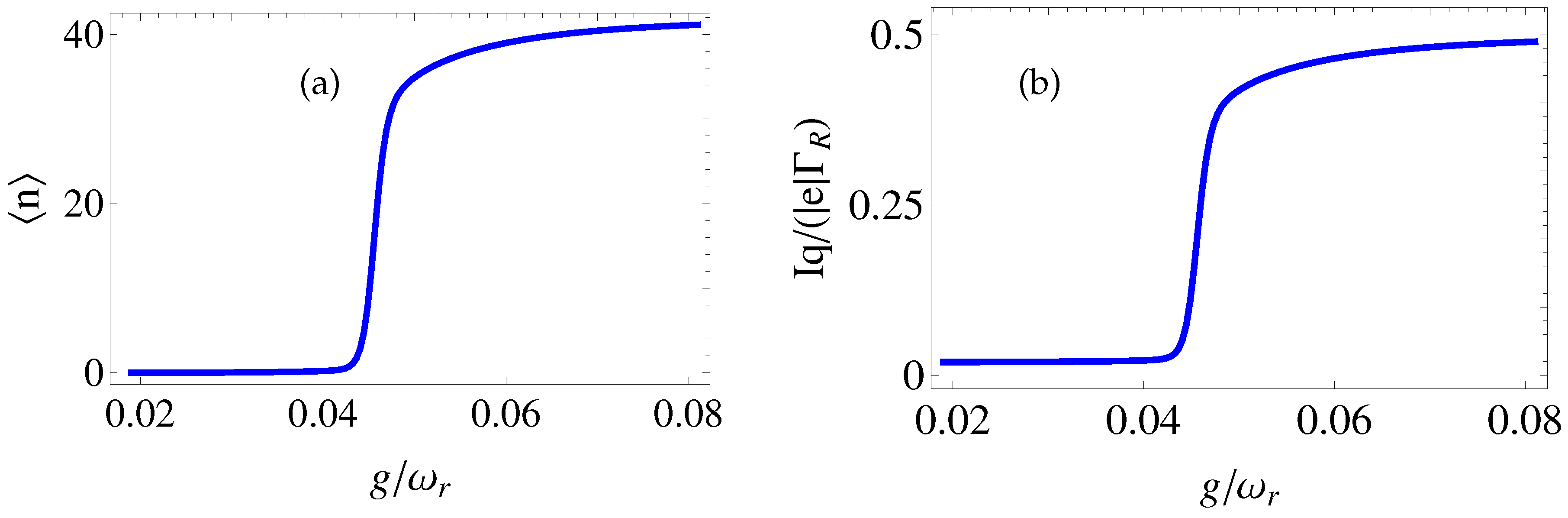
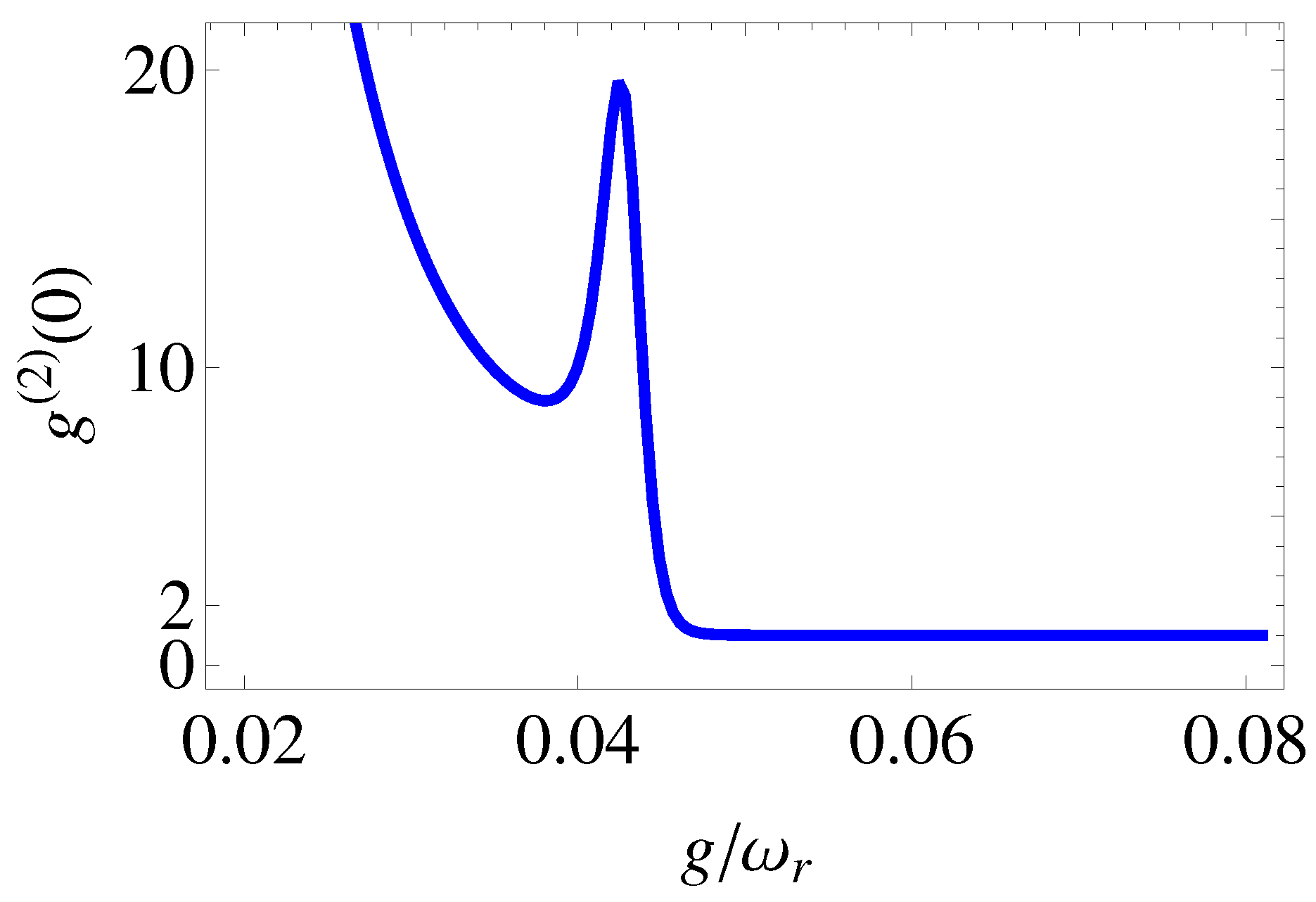
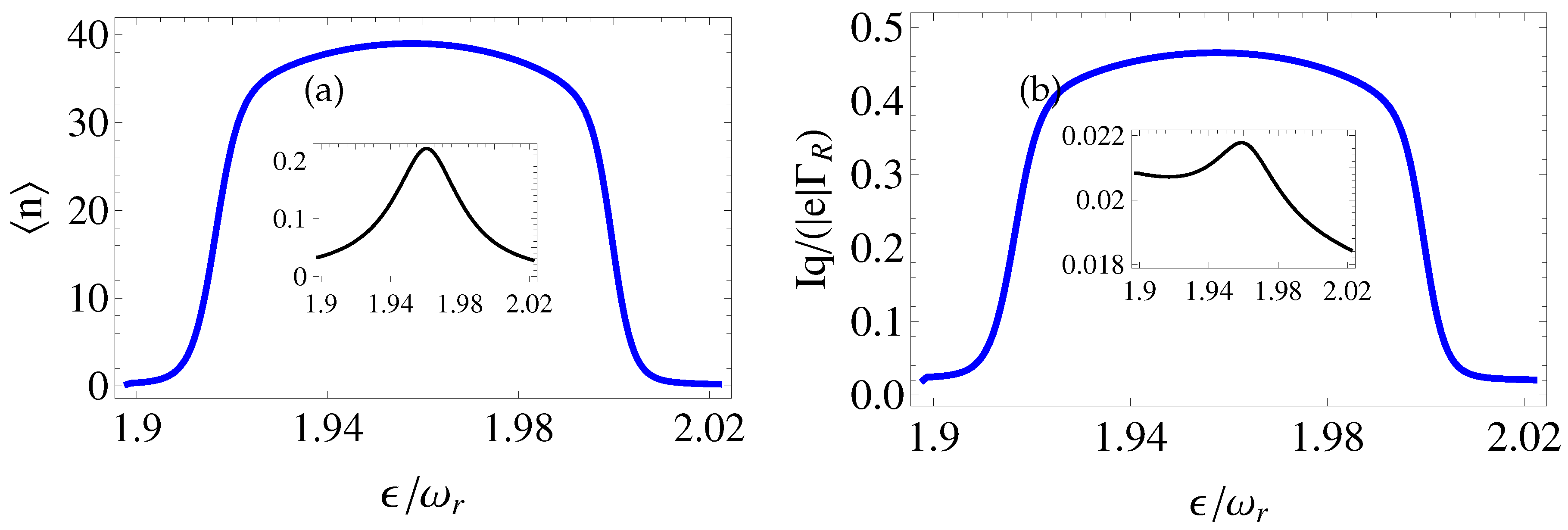
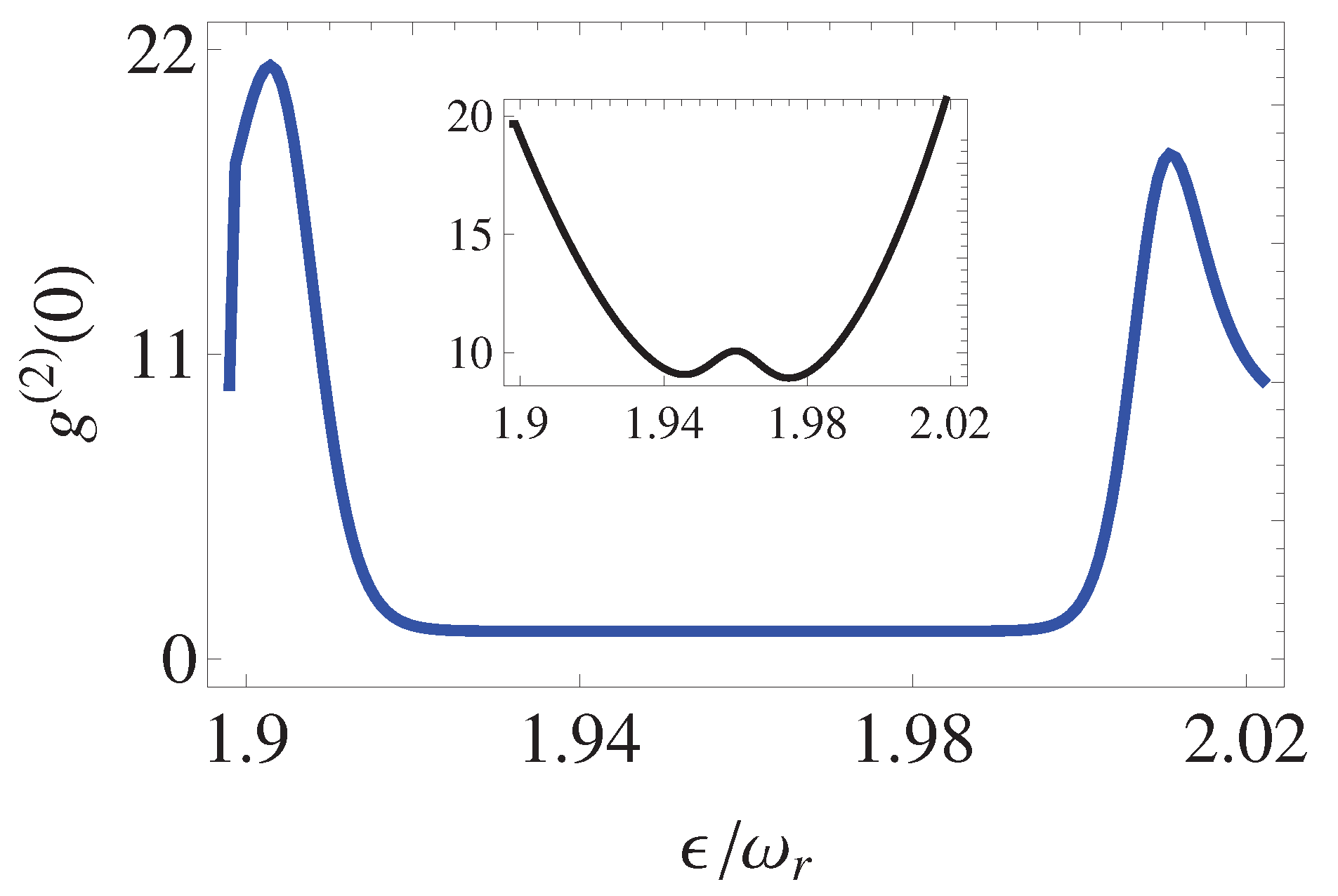
4. Results and Discussion
5. Summary
Acknowledgments
References
- Bruhat, L. E.; Cubaynes, T.; Viennot, J. J.; Dartiailh, M. C.; Desjardins, M. M.; Cottet, A.; Kontos, T. Circuit QED with a quantum-dot charge qubit dressed by Cooper pairs. Phys. Rev. B 2018, 98, 155313. [Google Scholar] [CrossRef]
- Burkard, G.; Gullans, M. J.; Mi, X.; Petta, J. R. Superconductor-semiconductor hybrid-circuit quantum electrodynamics. Nat. Rev. Phys. 2020, 2, 129–140. [Google Scholar] [CrossRef]
- Haldar, S.; Barker, D.; Havir, H.; Ranni, A.; Lehmann, S.; Dick, K. A.; Maisi, V. F. Continuous Microwave Photon Counting by Semiconductor-Superconductor Hybrids. Phys. Rev. Lett. 2024, 133, 217001. [Google Scholar] [CrossRef] [PubMed]
- Stanisavljević, O.; . Philippe, J.-C.; Gabelli, J.; Aprili, M.; Estéve, J.; Basset, J. Efficient Microwave Photon-to-Electron Conversion in a High-Impedance Quantum Circuit. Phys. Rev. Lett. 2024, 133, 076302. [Google Scholar] [CrossRef] [PubMed]
- de Sá Neto, O.P.; de Oliveira, M.C. Signal, detection and estimation using a hybrid quantum circuit. Sci. Rep. 2024, 14, 15225. [Google Scholar] [CrossRef]
- Brandes, T. Coherent and collective quantum optical effects in mesoscopic systems. Phys. Rep. 2005, 408, 315. [Google Scholar] [CrossRef]
- Kulkarni, M.; Cotlet, O.; Türeci, H. E. Cavity-coupled double-quantum dot at finite bias: analogy with lasers and beyond. Phys. Rev. B 2014, 90, 125402. [Google Scholar] [CrossRef]
- Liu, Y.-Y.; Stehlik, J.; Eichler, C.; Mi, X.; Hartke, T. R.; Gullans, M. J.; Taylor, J. M.; Petta, J. R. Threshold Dynamics of a Semiconductor Single Atom Maser. Phys. Rev. Lett. 2017, 119, 097702. [Google Scholar] [CrossRef]
- Tabatabaei, S. M.; Neda, J. Lasing in a coupled hybrid double quantum dot-resonator system. Phys. Rev. B 2020, 101, 115135. [Google Scholar] [CrossRef]
- Gu, X.; Kockum, A.F.; Miranowicz, A.; Liu, Y.X.; Nori, F. Microwave photonics with superconducting quantum circuits. Phys. Rep. 2017, 1, 718–719. [Google Scholar] [CrossRef]
- Scarlino, P.; van Woerkom, D. J.; Stockklauser, A.; Koski, J. V.; Collodo, M. C.; Gasparinetti, S.; Reichl, C.; Wegscheider, W.; Ihn, T.; Ensslin, K.; Wallraff, A. All-Microwave Control and Dispersive Readout of Gate-Defined Quantum Dot Qubits in Circuit Quantum Electrodynamics. Phys. Rev. Lett. 2019, 122, 206802. [Google Scholar] [CrossRef] [PubMed]
- Khan, W.; Potts, P. P.; Lehmann, S.; Thelander, C.; Dick, K. A.; Samuelsson, P.; Maisi, V. F. Efficient and continuous microwave photoconversion in hybrid cavity-semiconductor nanowire double quantum dot diodes. Nat. Commun. 2021, 12, 5130. [Google Scholar] [CrossRef] [PubMed]
- Havir, H.; Haldar, S.; Khan, W.; Lehmann, S.; Dick, K. A.; Thelander, C.; Samuelsson, P.; Maisi, V. F. Quantum dot source-drain transport response at microwave frequencies. Phys. Rev. B 2023, 108, 205417. [Google Scholar] [CrossRef]
- Nian, L.-L.; Hu, S.; Xiong, L.; Lü, J.-T.; Zheng, B. Photon-assisted electron transport across a quantum phase transition. Phys. Rev. B 2023, 108, 085430. [Google Scholar] [CrossRef]
- Wallraff, A.; Schuster, D. I.; Blais, A.; Frunzio, L.; Huang, R.- S.; Majer, J.; Kumar, S.; Girvin, S. M.; Schoelkopf, R. J. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 2004, 431, 162. [Google Scholar] [CrossRef]
- Stockklauser, A.; Scarlino, P.; Koski, J. V.; Gasparinetti, S.; Andersen, C. K.; Reichl, C.; Wegscheider, W.; Ihn, T.; Ensslin, K.; Wallraff, A. Strong Coupling Cavity QED with Gate-Defined Double Quantum Dots Enabled by a High Impedance Resonator. Phys. Rev. X 2017, 7, 011030. [Google Scholar] [CrossRef]
- Gu, S.-S.; Kohler, S.; Xu, Y.-Q.; Wu, R.; Jiang, Sh.-L.; Ye, Sh.-K.; Lin, T.; Wang, B.-Ch.; Li, H.-O. Probing Two Driven Double Quantum Dots Strongly Coupled to a Cavity. Phys. Rev. Lett. 2023, 130, 233602. [Google Scholar] [CrossRef]
- Ungerer, J. H.; Pally, A.; Kononov, A.; Lehmann, S.; Ridderbos, J.; Potts, P. P.; Thelander, C.; Dick, K. A.; Maisi, V. F.; Scarlino, P.; Baumgartner, A.; Schönenberger, C. Strong coupling between a microwave photon and a singlet-triplet qubit. Nat. Commun. 2024, 15, 1068. [Google Scholar] [CrossRef]
- Wong, C. H.; Vavilov, M. G. Quantum efficiency of a single microwave photon detector based on a semiconductor double quantum dot. Phys. Rev. A 2017, 95, 012325. [Google Scholar] [CrossRef]
- Ghirri, A.; Cornia, S.; Affronte, M. Microwave photon detectors based on semiconducting double quantum dots. Sensors 2020, 20, 4010. [Google Scholar] [CrossRef]
- Nian, L.-L.; Zheng, B.; Lü, J.-T. Electrically driven photon statistics engineering in quantum-dot circuit quantum electrodynamics. Phys. Rev. B 2023, 107, L241405. [Google Scholar] [CrossRef]
- Brandes, T. Coherent and collective quantum optical effects in mesoscopic systems. Phys. Rep. 2005, 408, 315. [Google Scholar] [CrossRef]
- Sánchez, R.; Platero, G.; Brandes, T. Resonance Fluorescence in Transport through Quantum Dots: Noise Properties. Phys. Rev. Lett. 2007, 98, 146805. [Google Scholar] [CrossRef]
- Xu, C.; Vavilov, M. G. Full counting statistics of photons emitted by a double quantum dot. Phys. Rev. B 2013, 88, 195307. [Google Scholar] [CrossRef]
- Agarwalla, B. K.; Kulkarni, M.; Mukamel, S.; Segal, D. Tunable photonic cavity coupled to a voltage-biased double quantum dot system: Diagrammatic nonequilibrium Green’s function approach. Phys. Rev. B 2016, 94, 035434. [Google Scholar] [CrossRef]
- Chen, C.-C.; Stace, T. M.; Goan, H.-S. Full-polaron master equation approach to dynamical steady states of a driven two-level system beyond the weak system-environment coupling. Phys. Rev. B 2020, 102, 035306. [Google Scholar] [CrossRef]
- Hazra, S. K.; Addepalli, L.; Pathak, P. K.; Dey, T. N. Nondegenerate two-photon lasing in a single quantum dot. Phys. Rev. B 2024, 109, 155428. [Google Scholar] [CrossRef]
- Jin, J.; Marthaler, M.; Jin, P.-Q.; Golubev, D.; Schön, G. Noise spectrum of a quantum dot-resonator lasing circuit. New J. Phys. 2013, 15, 025044. [Google Scholar] [CrossRef]
- Lambert, N.; Flindt, C.; Nori, F. Photon-mediated electron transport in hybrid circuit-QED. EPL 2013, 103, 17005. [Google Scholar] [CrossRef]
- Shi, P.; Hu, M.; Ying, Y.; Jin, J. Noise spectrum of quantum transport through double quantum dots: Renormalization and non-Markovian effects. AIP Adv. 2016, 6, 095002. [Google Scholar] [CrossRef]
- Karlewski, C.; Heimes, A.; Schön, G. Lasing and transport in a multilevel double quantum dot system coupled to a microwave oscillator. Phys. Rev. B 2016, 93, 045314. [Google Scholar] [CrossRef]
- Jin, J. Nonequilibirum noise spectrum and Coulomb blockade assisted Rabi interference in a double-dot Aharonov-Bohm interferometer. Phys. Rev. B 2020, 101, 235144. [Google Scholar] [CrossRef]
- Drummond P., D.; Walls, D. F. Quantum theory of optical bistability. I. Nonlinear polarisability model. J. Phys. A 1980, 13, 725. [Google Scholar] [CrossRef]
- Macovei, M. A. Measuring photon-photon interactions via photon detection. Phys. Rev. A 2010, 82, 063815. [Google Scholar] [CrossRef]
- Zenelaj, D.; Potts, P. P.; Samuelsson, P. Full counting statistics of the photocurrent through a double quantum dot embedded in a driven microwave resonator. Phys. Rev. B 2022, 106, 205135. [Google Scholar] [CrossRef]
- Zenelaj, D.; Samuelsson, P.; Potts, P. P. Wigner-function formalism for the detection of single microwave pulses in a resonator-coupled double quantum dot. Phys. Rev. Research 2025, 7, 013305. [Google Scholar] [CrossRef]
- Jin, P.-Q.; Marthaler, M.; Cole, J. H.; Shnirman, A.; Schön, G. Lasing and transport in a quantum-dot resonator circuit. Phys. Rev. B 2011, 84, 035322. [Google Scholar] [CrossRef]
- Rastelli, G.; Governale, M. Single atom laser in normal-superconductor quantum dots. Phys. Rev. B 2019, 100, 085435. [Google Scholar] [CrossRef]
- Mantovani, M.; Armour, A. D.; Belzig, W.; Rastelli, G. Dynamical multistability in a quantum-dot laser. Phys. Rev. B 2019, 99, 045442. [Google Scholar] [CrossRef]
- Agarwalla, B. K.; Kulkarni, M.; Segal, D. Photon statistics of a double quantum dot micromaser: Quantum treatment. Phys. Rev. B 2019, 100, 035412. [Google Scholar] [CrossRef]
- Tabatabaei, S. M.; Jahangiri, N. Lasing in a coupled hybrid double quantum dot-resonator system. Phys. Rev. B 2020, 101, 115135. [Google Scholar] [CrossRef]
- Stace, T. M.; Doherty, A. C.; Barrett, S. D. Population Inversion of a Driven Two-Level System in a Structureless Bath. Phys. Rev. Lett. 2005, 95, 106801. [Google Scholar] [CrossRef] [PubMed]
- Müller, C.; Stace, Th. M. Deriving Lindblad master equations with Keldysh diagrams: Correlated gain and loss in higher order perturbation theory. Phys. Rev. A 2017, 95, 013847. [Google Scholar] [CrossRef]
- Mihaescu, T.; Isar, A.; Macovei, M. A. Two-quanta processes in coupled double-quantum-dot cavity systems. arXiv 2025, arXiv:2501.05967v1. [Google Scholar]
- Nian, L.-L.; Wang, Y.-Ch.; Wang, J.-Y.; Xiong, L.; Zheng, B.; Lü, J.-T. Dissipative quantum phase transitions in electrically driven lasers. arXiv 2025, arXiv:2501.10997v2. [Google Scholar]
- Agarwal, G. S. Quantum Statistical Theories of Spontaneous Emission and their Relation to Other Approaches; Springer: Berlin, 1974. [Google Scholar]
- Kiffner, M.; Macovei, M.; Evers, J.; Keitel, C. H. Vacuum induced processes in multilevel atoms. Prog. Opt. 2010, 55, 85. [Google Scholar]
- James, D. F. V. Quantum Computation with Hot and Cold Ions: An Assessment of Proposed Schemes. Fort. Phys. 2000, 48, 823. [Google Scholar] [CrossRef]
- Tan, R.; Li, G.-X.; Ficek, Z. Squeezed single-atom laser in a photonic crystal. Phys. Rev. A 2008, 78, 023833. [Google Scholar] [CrossRef]
- Quang, T.; Freedhoff, H. Atomic population inversion and enhancement of resonance fluorescence in a cavity. Phys. Rev. A 1993, 47, 2285. [Google Scholar] [CrossRef]
- Mihaescu, T.; Cecoi, E.; Macovei, M. A.; Isar, A. Geometric discord for a driven two-qubit system. Rom. Rep. Phys. 2021, 73, 101. [Google Scholar]
- Glauber, R. J. The Quantum Theory of Optical Coherence. Phys. Rev. 1963, 130, 2529. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




