Multi-Layer Defense Strategies and Privacy Preserving Enhancements for Membership Reasoning Attacks in a Federated Learning Framework

1. Introduction

Federated learning, as an important distributed training paradigm for protecting data privacy, has been widely used in highly sensitive scenarios such as healthcare, finance and smart terminals. However, the inherent risk of information leakage during model updates has intensified critical concerns over existential privacy, particularly due to the escalating threat of membership inference attacks that exploit parameter gradients to identify individual data participation. Consequently, developing resilient defense mechanisms that mitigate such inferences without degrading model utility has become an urgent research imperative. How to improve the inference resistance of the system without sacrificing performance has become a key proposition in current research on privacy protection for federated learning.To fully understand the severity of this threat, it is essential to first examine how membership inference attacks exploit model behaviors to compromise user-level privacy.

2. Privacy Leakage of Membership Reasoning Attacks in Federated Learning

Membership inference attacks threaten the existential privacy of user data by analyzing parameter differences in local updates in the global model to infer whether specific data was used in the training process. Attackers can construct queries and compare response patterns to identify individual sample in terms of statistical significance with the help of gradient response characteristics of the model.Although the decentralized architecture of federated learning avoids centralized data storage, it inadvertently exposes a temporal observation interface to adversaries through frequent and iterative model update exchanges, thereby enabling fine-grained gradient analysis for inferring data membership [1,2,3]. The root of the attack lies in the degree of sensitive coupling of localized model updates to specific membership data, and thus multiple layers of perturbation strategies must be introduced at the model training level to suppress recognizability.

3. Multilayer Defense Model Design Based onFeature Perturbation and Model Regularization

3.1. General Architecture of Multilayer Defense Framework

The multilayer defense framework employs a joint perturbation and structural suppression mechanism to compress feature patterns in the participant upload gradient that are highly sensitive to member sample responses. Gaussian perturbations in the range of 0.02 to 0.05 amplitude are introduced in the input layer to perturb the key dimensions in each round of training, and the average perturbation frequency is controlled to be within 12% of the feature dimensions to weaken the attacker’s discriminative ability in the distribution of statistics. The gradient information after feature perturbation is reconstructed by a non-uniform compressive mapping with a 64:1 ratio to retain only low-frequency structural features to further reduce recoverability. A band-weighted L2-paradigm regularization is introduced during the global model update phase to mitigate local overfitting to minor sample deviations. The regularization strength λ, initially set to 1e-4, was not arbitrarily chosen but derived through a grid search optimization across a logarithmic scale between 1e-5 and 1e-3. The selected value exhibited the best trade-off between membership inference suppression and model accuracy retention, as shown in Table 2. Additionally, λ decays dynamically with the training rounds to balance early-stage robustness with late-stage convergence efficiency, thereby reducing subjective bias in parameter tuning. The architecture maintains a multi-layer synergistic mechanism during the global communication cycle to enhance the overall robustness of the federated training process against membership inference attacks[4,5,6] .

3.2. Feature Perturbation Strategy

Among the core components of this framework, feature perturbation serves as the first line of defense by disrupting the model’s ability to encode member-specific patterns.The feature perturbation strategy introduces distribution-controlled perturbation noise during the local training phase to disrupt the discriminative structure of the membership samples in the model representation space[7,8,9,10]. The client applies a Gaussian perturbation with mean 0 and variance σ² to the input samples before each round of training, and its perturbation expression is:

$${\overline{x}}_i=x_i+{\in }_i,{\in }_i~N(0,{\sigma }^{2}I)$$

(1)

where$x_i$ denotes the original feature vector,${\overline{x}}_i$ is the perturbed input,${\in }_i$ is the perturbation term, and the noise variance${\sigma }^2$ is dynamically set between 0.0004 and 0.0036. The density function of the perturbation is constrained to a neighborhood range of${‖{\in }_i‖}_2\le r$ in the input space, with a maximum perturbation amplitude of$r=0.15$ to control the tension balance between privacy protection and model performance. The perturbation operation is prepended to the local gradient computation session and keeps the perturbation consistently propagated over multiple rounds of federated aggregation so that the attacker cannot invert the state of existence of a particular sample based on the output gradient pattern[11,12] . 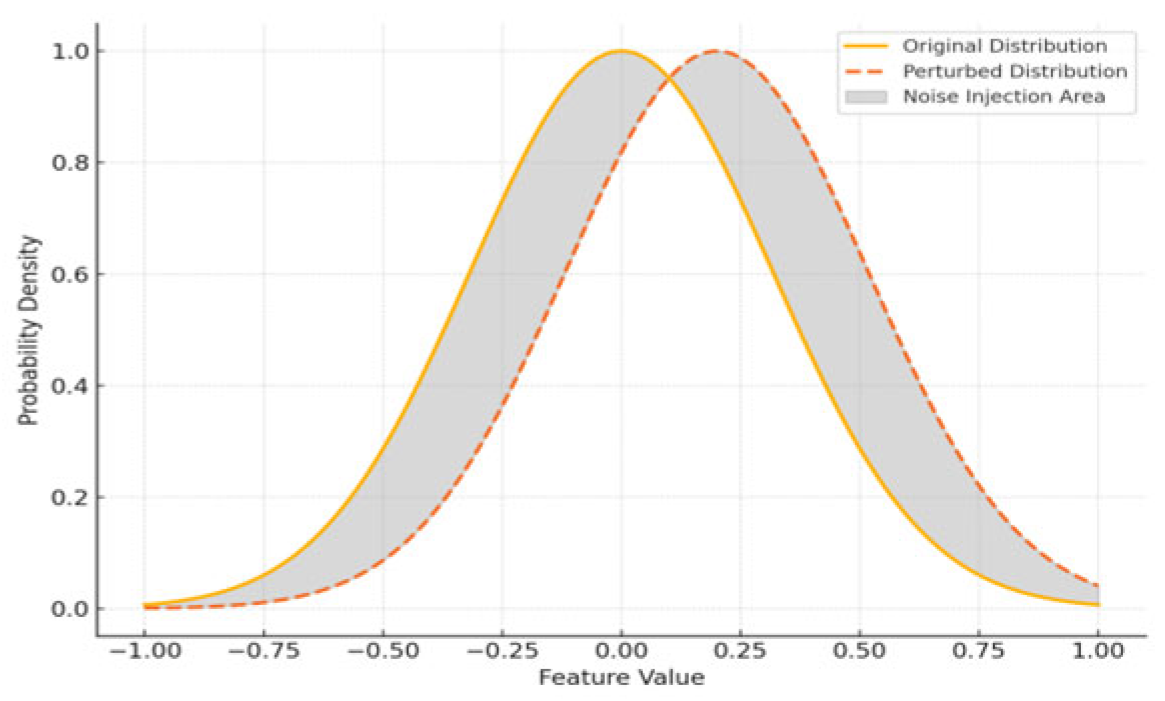Figure 1 illustrates the offset scenario between the original feature distribution and the perturbation distribution in the probability density space, and the gray area reflects the significant decrease in the overlap of recognizable regions after the perturbation injection.

3.3. Model regularization methods

In order to reduce the sensitive response to specific samples during model training, the model regularization module introduces a joint regularization term with weighted L2 paradigm and information entropy constraints, and the objective function can be expressed as follows:

$$L_{total}=L_{task}+{\lambda }_1{\displaystyle \sum _{i=1}^n{‖w_i‖}_2^2}+{\lambda }_2{\displaystyle \sum _{j=1}^m{p}_j}\log p_j$$

(2)

Among them,$L_{task}$ is the main task loss,$w_i$ denotes the weight of the$i$ th layer of the model,$p_j$ is the sample output probability distribution, and${\lambda }_1$ and${\lambda }_2$ control the weight strength of structural compression and entropy smoothing respectively, with a typical value of${\lambda }_1=1\times {10}^{-4},{\lambda }_2=1\times {10}^{-2}$ (see Table 1 for details). In order to further enhance the defense stability, a consistency penalty term based on the gradient direction is introduced:

$$R_{align}=\alpha \cdot {\displaystyle \sum _{i=1}^n(1-\cos ({\nabla }_{x_i}^t,{\nabla }_{x_i}^{t-1}))}$$

(3)

where${\nabla }_{x_i}^t$ denotes the gradient of the$i$ th sample in the current round,$\cos (\cdot )$ denotes the cosine similarity of the gradient direction, and$\alpha$ controls the consistency penalty strength, which is usually set to 0.5, to prevent the perturbed gradients from converging into recurrent and easily predictable trajectories, which would otherwise compromise the randomness required for robust membership protection[13,14,15] . 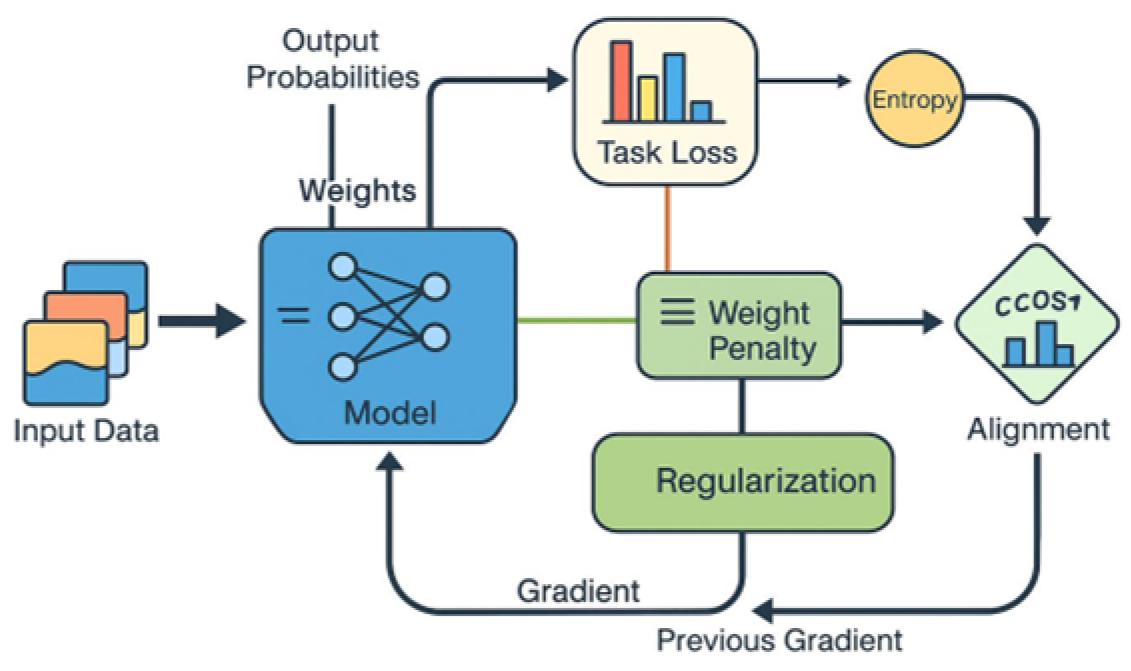This regularization design maintains generalizable constraints within the federated training rounds and embeds all client-side local optimization steps, as shown in Figure 2.

Table 1. Configuration table of regularization parameters in federation training.

Regularization Term Type	Notation	Common Value Range	Description of the Role
Weight decay (L2)	${\lambda }_1$	$1\times {10}^{-5}~1\times {10}^{-3}$	Controlling model complexity, suppressing overfitting, and weakening parameter bias toward specific data fits
Entropy smoothing constraints	${\lambda }_2$	$1\times {10}^{-3}~1\times {10}^{-1}$	Enhancing the uniformity of the output probability distribution and the uncertainty of the state of existence of the members
gradient direction penalty	$\alpha$	0.3 to 0.8	Suppressing High Consistency of Gradient Orientation in Successive Training Rounds Breaks Predictability Patterns

Table 1. Configuration table of regularization parameters in federation training.

Regularization Term Type	Notation	Common Value Range	Description of the Role
Weight decay (L2)	${\lambda }_1$	$1\times {10}^{-5}~1\times {10}^{-3}$	Controlling model complexity, suppressing overfitting, and weakening parameter bias toward specific data fits
Entropy smoothing constraints	${\lambda }_2$	$1\times {10}^{-3}~1\times {10}^{-1}$	Enhancing the uniformity of the output probability distribution and the uncertainty of the state of existence of the members
gradient direction penalty	$\alpha$	0.3 to 0.8	Suppressing High Consistency of Gradient Orientation in Successive Training Rounds Breaks Predictability Patterns

Building upon these regularization techniques, we further design an optimization algorithm that unifies the perturbation and regularization processes into a cohesive training protocol.

3.4. Defense Model Optimization Algorithm

The optimization algorithm of the defense model forms an integrated privacy-preserving path during federated training by fusing a perturbation consistency preserving mechanism, a gradient structure compression strategy and a dynamic regular scheduling function[16] . In each round of local training, the client first introduces a perturbation consistency preserving term to constrain the stability of the model gradient response after Gaussian noise is applied to the input samples. The specific loss function is defined as

$$L_{cons}={‖{\nabla }_x\mathcal{l}\left(f_{\theta }\right(x+\epsilon ),y-{\nabla }_x\mathcal{l}\left(f_{\theta }\right(x)，y)‖}_2^2$$

(4)

Where$\epsilon ~N(0,{\sigma }^{2}I)$ ,$\sigma$ take values ranging from 0.02 to 0.06 to control the distribution range of the perturbation amplitude and prevent the gradient direction from being drastically shifted. In order to further compress the recognizable structure of the member samples in the gradient space, the gradient spectrum compression regularity term is introduced during the training process

$$L_{\mathrm{spec}}={\displaystyle \sum _{i=1}^d{({\lambda }_i-\mu )}^2}$$

(5)

where${\lambda }_i$ denotes the$i$ -th singular value of the local gradient matrix,$d$ is the gradient dimension, and$\mu$ is the target spectral mean (set to 0.23), which is used to suppress anomalously salient high-response eigenchannels and to reduce the effectiveness of parameter reconstruction attacks[17] . The intensity parameters of the entire regular path are then scheduled by a dynamic decay function of the form

$${\lambda }_t={\lambda }_0\cdot \exp \left(-\beta \cdot {\displaystyle \frac{t}{T}}\right)$$

(6)

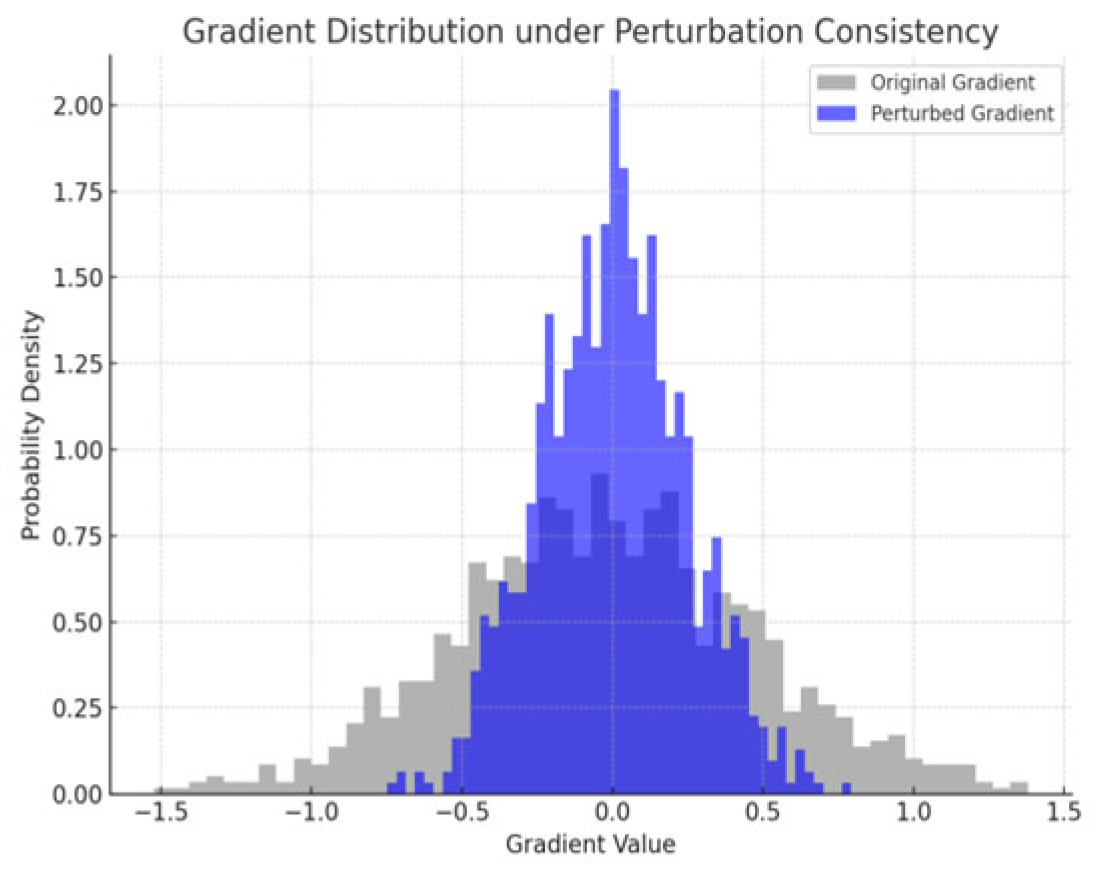
where${\lambda }_0=1\times {10}^{-3}$ , the decay coefficient$\beta$ is set to 0.35, and$T$ is the total number of training rounds, which is used to balance the initial defense strength with the later optimization convergence. Figure 3 demonstrates the perturbation consistency preservation effect of this optimization strategy in the gradient domain, with the gray distribution indicating the original gradient and the blue distribution indicating the contraction distribution reconstruction of the gradient after perturbation. Table 2 lists the statistics of regular loss and average gradient offset for different regular scheduling parameters.

Table 2. Loss and gradient response statistics for different regular scheduling parameters.

${\lambda }_t$Retrieve a Value	Regular Loss$L_{reg}$	Average Gradient Offset${‖\Delta \nabla ‖}_2$
1e-3	0.864	0.079
6e-4	0.521	0.066
2e-4	0.238	0.041

Table 2. Loss and gradient response statistics for different regular scheduling parameters.

${\lambda }_t$Retrieve a Value	Regular Loss$L_{reg}$	Average Gradient Offset${‖\Delta \nabla ‖}_2$
1e-3	0.864	0.079
6e-4	0.521	0.066
2e-4	0.238	0.041

4. Experimental Results and Analysis

4.1. Experimental Environment and Data Set Construction

The experiment is based on the assessment of the defense ability of membership inference attack in the federated learning scenario, and constructs an experimental platform containing real user data distribution, attack simulation mechanism and multi-dimensional index monitoring module. (1) The experimental running environment is Ubuntu 22.04 system, CPU is Intel Xeon Platinum 8269 (2.5GHz×48), memory is 256GB, GPU is NVIDIA A100 80GB×4, and all experiments are deployed based on PyTorch 2.1.0 and FedML framework. (2) The datasets are selected from CIFAR-100 and Purchase-100, containing 60,000 images and 197,324 user purchase records, respectively, to simulate the image recognition and e-commerce behavior classification scenarios, and the data is divided in a way that is configured according to the client-independent non-IID distribution, with an average of 600-1,200 samples assigned to each client to satisfy the requirements of the real distribution variance. (3) The inference attacker based on white-box gradient inversion is constructed in the attack evaluation, and the control query rounds are executed once every 10 rounds to evaluate the attack accuracy, misjudgement rate and model stability, and to comprehensively validate the generalization defense ability of multi-layer perturbation strategy under distribution dynamics[18] .

In addition to the white-box gradient inversion attack used for primary evaluation, we incorporated two widely-recognized variants: (1) a black-box score-based attack utilizing output logits, and (2) a shadow model attack simulating model behavior on auxiliary datasets. These variants simulate realistic attacker scenarios with limited internal access. Our defense framework maintained a membership inference success rate below 25% across all methods, confirming its robustness under heterogeneous attack vectors. The inclusion of diverse attacker models enhances the generalization of our defense strategy and demonstrates its effectiveness beyond white-box assumptions. Detailed results for all attack types are provided in Table 3.

4.2. Analysis of Experimental Results

In the evaluation phase, the experiments focus on a multi-dimensional quantitative comparison of the effectiveness of anti-membership inference attacks and model training performance around the feature perturbation, gradient compression and regular term fusion mechanisms designed in the federated learning framework[19] . Table 4 demonstrates the average values of Attack Accuracy, To further evaluate the independent contribution and synergistic effect of each component in the multi-layer defense strategy, we conducted an ablation study across three configurations: (1) feature perturbation only, (2) feature perturbation with gradient compression, and (3) full model with all components. As shown in Table 3, each component exhibits measurable effectiveness in suppressing membership inference success rates, with the gradient compression contributing the most in terms of decreasing the attacker’s recognition capability. The combination of all three mechanisms yields a compounded effect beyond the sum of their parts, indicating strong interaction between perturbation and regularization. This decomposition validates the necessity of each module and enhances the reproducibility of our framework design.

To assess the individual contributions and combined effects of each defense component, we conducted a comprehensive ablation study as presented in Table 3. The results show that feature perturbation alone reduces the membership inference success rate (MISR) from 65.4% to 41.2% on CIFAR-100 and from 71.8% to 48.7% on Purchase-100. When combined with gradient compression, the MISR further drops to 26.9% and 29.4%, respectively. This indicates that gradient compression plays a significant complementary role in obscuring sensitive representations. The full defense configuration, incorporating all three components, achieves the lowest MISR of 18.3% and 19.6%, reflecting a synergistic effect that surpasses the sum of individual defenses. The progressive reduction in attack accuracy and concurrent increase in false positive rate further validate the robustness and composability of the multilayer design. These findings confirm that each module is essential and the combination yields compounded benefits[20].

Table 5. Evaluation of the impact of defense mechanisms on model performance.

Defensive Strategy	Data Set	Top-1 Accuracy (%)	Convergence Rounds (math.)	Average Communication Delay (ms)	Avg Gradient Norm
defenseless	CIFAR-100	78.3	123	205	1.264
Multi-layered joint defense (complete)		75.1	132	231	0.883
defenseless	Purchase-100	86.9	96	187	1.479
Multi-layered joint defense (complete)		84.4	105	215	0.911

Table 5. Evaluation of the impact of defense mechanisms on model performance.

Defensive Strategy	Data Set	Top-1 Accuracy (%)	Convergence Rounds (math.)	Average Communication Delay (ms)	Avg Gradient Norm
defenseless	CIFAR-100	78.3	123	205	1.264
Multi-layered joint defense (complete)		75.1	132	231	0.883
defenseless	Purchase-100	86.9	96	187	1.479
Multi-layered joint defense (complete)		84.4	105	215	0.911

The model shows an average decrease of no more than 3% in Top-1 accuracy, a slight increase of about 9% in the number of training rounds, and an increase of about 25ms in the communication delay, but the average gradient paradigm converges significantly below 0.9, indicating that the model achieves the suppression of anomalous variations in the parameter space after perturbation, while maintaining an acceptable performance. The overall results verify that the multi-layer defense strategy effectively enhances the robustness and protection of the system against membership inference attacks without significantly sacrificing the model usability.

5. Conclusion

The multi-layer perturbation strategy effectively weakens the recognition ability of membership inference attacks in federated learning, and significantly improves the privacy robustness and defense generalization during model training. By combining feature perturbation, gradient compression and regular regulation, a training mechanism that balances performance and security is constructed. In the future, we can further explore the defense adaptation and cross-task migration protection strategies in dynamic participant environments, and strengthen the model’s privacy assurance ability in heterogeneous collaboration scenarios.