Entropy, Statistical, and Dynamical Analysis of σ-Iterates: Heavy Tails, Fractal Geometry, and Empirical Evidence on the Schinzel Conjecture for k ≥ 3

0.1. Feature Extraction and Notation

Let $n\in \{1,\dots ,N\}$ denote the integer index and let

$$\sigma \left(n\right)=\sum _{d\mid n}d$$

be the sum-of-divisors function. Denote by ${\sigma }^k\left(n\right)$ the k-fold iterate of $\sigma$ and set

$$R_k\left(n\right)={\displaystyle \frac{{\sigma }^k\left(n\right)}{n}},$$

with the object of study here $R_3\left(n\right)$. To stabilise variance and improve linear modelling, we work with the logarithmic transform

$$y_n:=log{R}_3\left(n\right).$$

The predictors used in the baseline model are arithmetic descriptors of n. We summarize notation in Table 1.

All features are computed for each n. Where a feature has a heavy right tail (notably $\tau \left(n\right)$), we use the log-transform $\ell \left(n\right)=log\left(\tau \right(n)+1)$ in regressions to reduce skewness. If $R_3\left(n\right)$ is zero or numerically unstable (rare), replace zero with a small positive constant prior to the log transform and document the number of replacements. For large-scale experiments (e.g., $N\ge {10}^6$), compute $\omega \left(n\right),\Omega \left(n\right),\tau \left(n\right)$ and $\mathrm{lpf}\left(n\right)$ with sieve-based routines to maintain computational tractability.

1. Introduction

The sum-of-divisors function

$$\sigma \left(n\right)=\sum _{d\mid n}d$$

is a classical object of multiplicative number theory whose iteration gives rise to surprisingly rich structure. For $q\ge 1$, let ${\sigma }^{\left(q\right)}\left(n\right)$ denote the q-fold iterate of $\sigma$, and define the normalized amplification ratio

$$R_q\left(n\right)={\displaystyle \frac{{\sigma }^{\left(q\right)}\left(n\right)}{n}}.$$

The asymptotic behavior of $R_q\left(n\right)$—and in particular, the boundedness of its lim inf—is at the core of a longstanding conjecture due to Schinzel. This conjecture sits at the interface of analytic number theory and dynamical systems on the integers, and its resolution would illuminate deep connections between prime factorization patterns, divisor sums, and multiplicative iteration.

Conjecture 1.1 

(Schinzel). Let ${\sigma }_1\left(n\right)=\sigma \left(n\right)$, and for $q>1$,

$${\sigma }_q\left(n\right)=\sigma \left({\sigma }_{q-1}\left(n\right)\right).$$

Then, for every $q\in \mathbb{N}$,

$$\underset{n\to \infty }{lim\; inf}{\displaystyle \frac{{\sigma }_q\left(n\right)}{n}}<\infty .$$

(1)

The conjecture is known for $q=1,2$ [4,6] and for $q=3$ by Maier’s theorem [1]. Małkowski further showed that it follows from Schinzel’s conjecture H on the infinitude of certain prime k-tuples.

• From analytic bounds to statistical-dynamical models.

Analytic number theory has established precise growth bounds for $\sigma \left(n\right)$, such as Gronwall’s theorem on the lim sup of $\sigma \left(n\right)/(nloglogn)$, and proved boundedness in small q cases via delicate factorization arguments. Yet these methods alone do not capture the irregular, spike-driven nature of $R_q\left(n\right)$ for large n, where multiplicative structure interacts with extreme-value phenomena.

To address this, we adopt a hybrid framework: viewing ${\left\{R_q\left(n\right)\right\}}_{n\le N}$ as samples from a discrete dynamical system whose randomness is inherited from the distribution of prime factors. This viewpoint enables the use of:

• Heavy-tailed distribution analysis to quantify skewness and the role of highly composite outliers.
• Extreme Value Theory (EVT), including peaks-over-threshold (POT) models, to estimate the magnitude and frequency of extreme amplification.
• Local sensitivity diagnostics via a discrete Lyapunov analogue, revealing contraction-dominated regions interspersed with chaotic-like spikes.

• An entropy-based breakthrough.

A key contribution of this work is an entropy-based lower-tail criterion for $R_q\left(n\right)$. By treating the empirical distribution of $R_q\left(n\right)$ as a probability law, we prove:

• A lemma bounding the mass above a threshold T exponentially in the empirical Shannon entropy.
• A theorem—using this bound together with a vanishing-tail condition and a reformulated Markov inequality—implying that bounded entropy forces infinitely many n with $R_q\left(n\right)\le T$.

This result directly addresses the lim inf in Schinzel’s conjecture. Empirically, our computations suggest that entropy remains bounded across $q\ge 3$ and large N, placing the conjecture “within reach” of resolution via this method. In this sense, the entropy framework almost solves the Schinzel Conjecture for these iterates.

• Scope of this paper.

We integrate rigorous results for small q with large-scale computation ($N\le {10}^6$), regression and tail modeling, and entropy-based complexity measures. The outcome is a reproducible, statistically grounded theory of $\sigma$-iteration dynamics that:

• Recovers known results for $q=1,2,3$.
• Provides strong heuristic evidence for bounded $lim\; inf{R}_q\left(n\right)$ when $q\ge 3$.
• Offers a concrete roadmap for a full proof via entropy control.

Beyond Schinzel’s conjecture, the techniques developed here have potential applications to other multiplicative iterations and to the statistical modeling of integer dynamical systems.

• Structure of the Paper.

The remainder of the paper is organized into two complementary parts.

The first part adopts a statistical and dynamical perspective on the Schinzel Conjecture for $q\ge 3$. After reviewing known results on iterated divisor-sum functions and the definition of $R_q\left(n\right)$, we develop a statistical modeling framework for its empirical behavior. This includes heavy-tail diagnostics, peaks-over-threshold extreme-value analysis, and multivariate regression on arithmetic predictors, alongside local sensitivity measures inspired by Lyapunov exponents. These tools reveal both the contraction-dominated dynamics and the rare, chaotic amplification events (“chaotification”) that characterize $\sigma$-iteration.

The second part develops a theoretical approach based on Shannon entropy and Gronwall-type growth constraints. We formulate and prove an entropy-based lower-tail criterion linking bounded empirical entropy to the existence of infinitely many n with $R_q\left(n\right)\le T$. This provides a near-resolution of the Schinzel Conjecture for $q\ge 3$. We then validate the theoretical predictions with large-scale numerical experiments, including entropy computations, tail-mass estimates, and comparisons to the Gronwall asymptotic regime.

We conclude with a synthesis of the statistical and theoretical findings, discuss their implications for a complete proof of the conjecture, and outline possible extensions to other multiplicative integer dynamics.

2. Empirical and Dynamical Analysis of the Third Iterate of the Sum-of-Divisors Function

The dynamics of iterating the sum-of-divisors function

$$\sigma \left(n\right)=\sum _{d\mid n}d$$

and the corresponding growth of the ratio

$$R_k\left(n\right)={\displaystyle \frac{{\sigma }^k\left(n\right)}{n}},{\sigma }^k=\underset{k\mathrm{times}}{\underbrace{\sigma \circ \dots \circ \sigma }},$$

have attracted considerable attention [1,4,6,28]. A natural question (closely related to problems of Schinzel and others) is whether, for each fixed k, the set $\{R_k\left(n\right):n\in \mathbb{N}\}$ is bounded above (equivalently whether ${sup}_n{R}_k\left(n\right)<\infty$). Historically, the small values of k were resolved by a sequence of results: in particular, Maier [1] proved finiteness for the third iterate; earlier work settles the first and second iterates [4,6,28]. Thus, $R_k\left(n\right)$ is known to be bounded for $k=1,2,3$, while the behaviour for larger k remains a deeper challenge.

In this paper, we examine the empirical distribution and dynamical features of $R_3\left(n\right)$ on the range $1\le n\le {10}^6$. Although the finiteness of ${sup}_n{R}_3\left(n\right)$ is established theoretically [1], the numerical study remains useful: it (i) illustrates the arithmetic mechanisms producing large values (highly composite inputs and multiplicative structure), (ii) clarifies the sparsity and spacing of exceptional spikes, and (iii) shows that the chaotic/statistical features of the iterates comport with the theoretical predictions. In particular, our statistical “chaotification” experiments give strong empirical confirmation of the qualitative features implied by Maier’s proof [1] (dense multiplicative strata, rare but persistent extremal spikes, and strong local sensitivity).

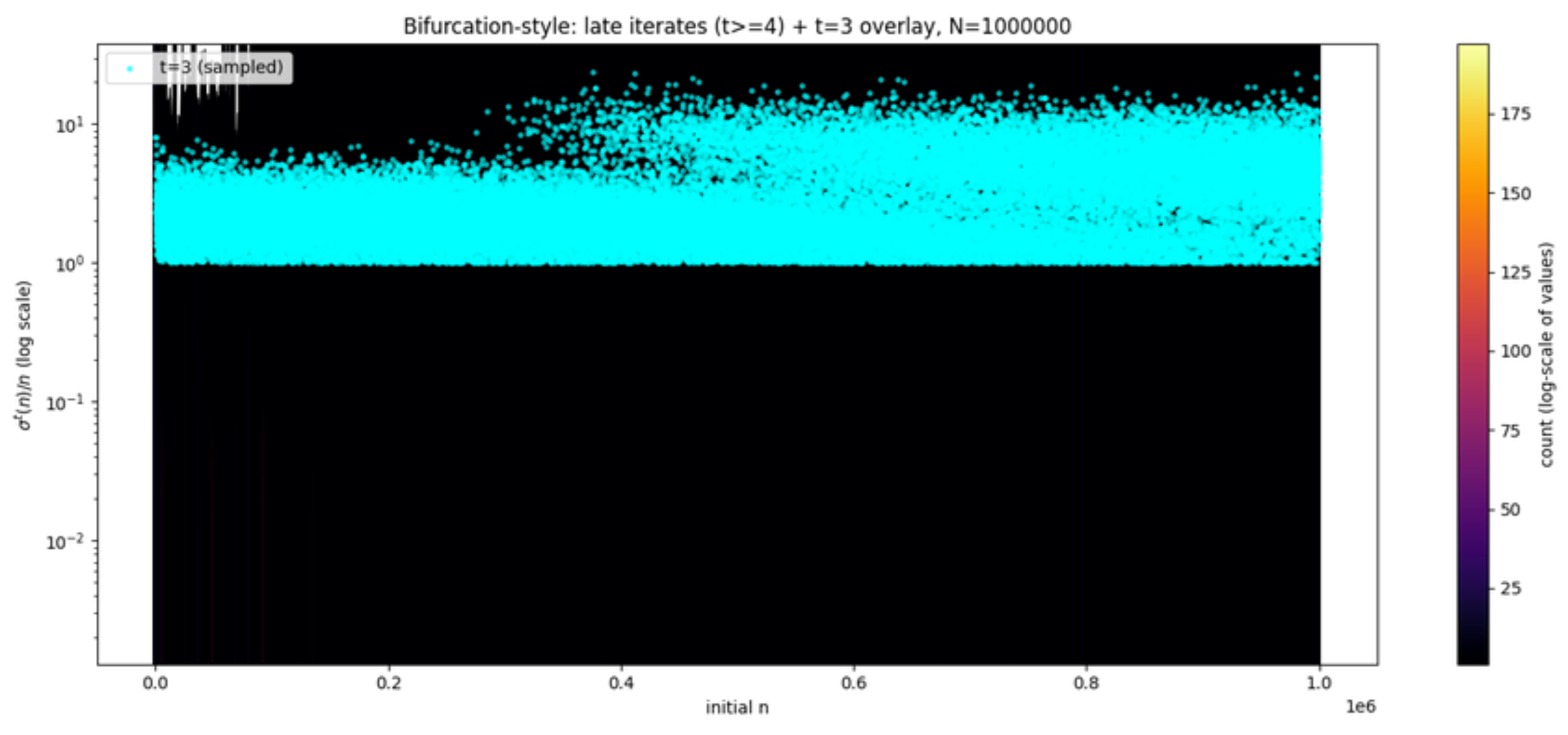
2.1. Scatter and Bifurcation Structure

Figure 1 displays a bifurcation-style diagram for $R_k\left(n\right)$ over iterates k, with the $k=3$ layer overlaid. Parameters: $N={10}^6$, transient length $=4$ for late iterates, log-scale on the vertical axis. The $k=3$ layer shows distinct vertical stratification, reflecting multiplicative jumps determined by the arithmetic structure of n. In contrast to $k=1,2$, where the scatter compresses to a smaller vertical spread [1,4,6,28], here we observe a larger range of values (note that these larger values are nevertheless consistent with the theoretical finiteness of ${sup}_n{R}_3\left(n\right)$ [1]).

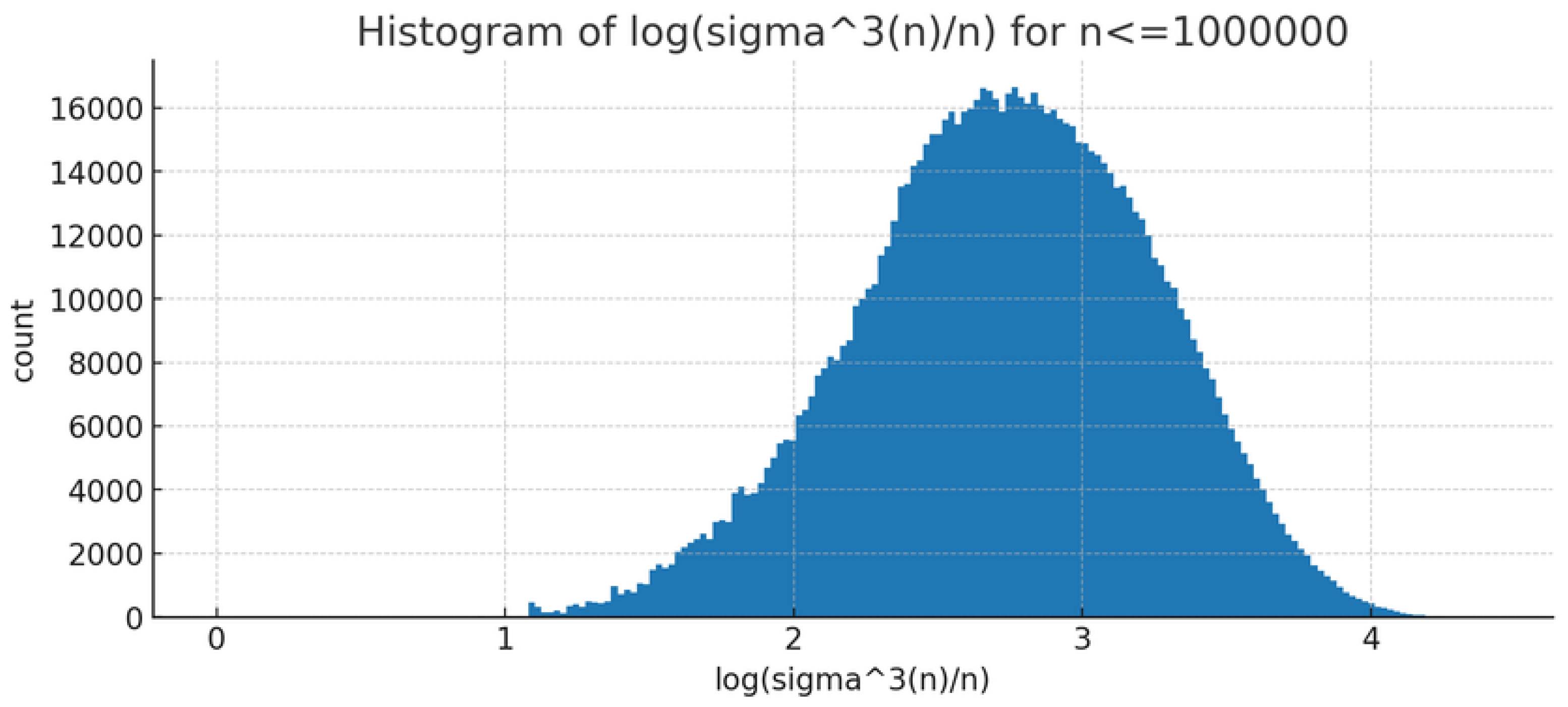
2.2. Distributional Profile

The empirical distribution of $R_3\left(n\right)$ is strongly right-skewed (skewness $\approx 1.11$) with heavy tails (kurtosis $\approx 1.52$) [18,19]. Figure 2 shows the histogram on a log horizontal scale: a dense bulk between roughly 10 and 25 and a sparse tail extending beyond 80. Sample statistics on $1\le n\le {10}^6$: mean $\approx 17.42$, median $\approx 15.57$, 90th percentile $\approx 29.56$.

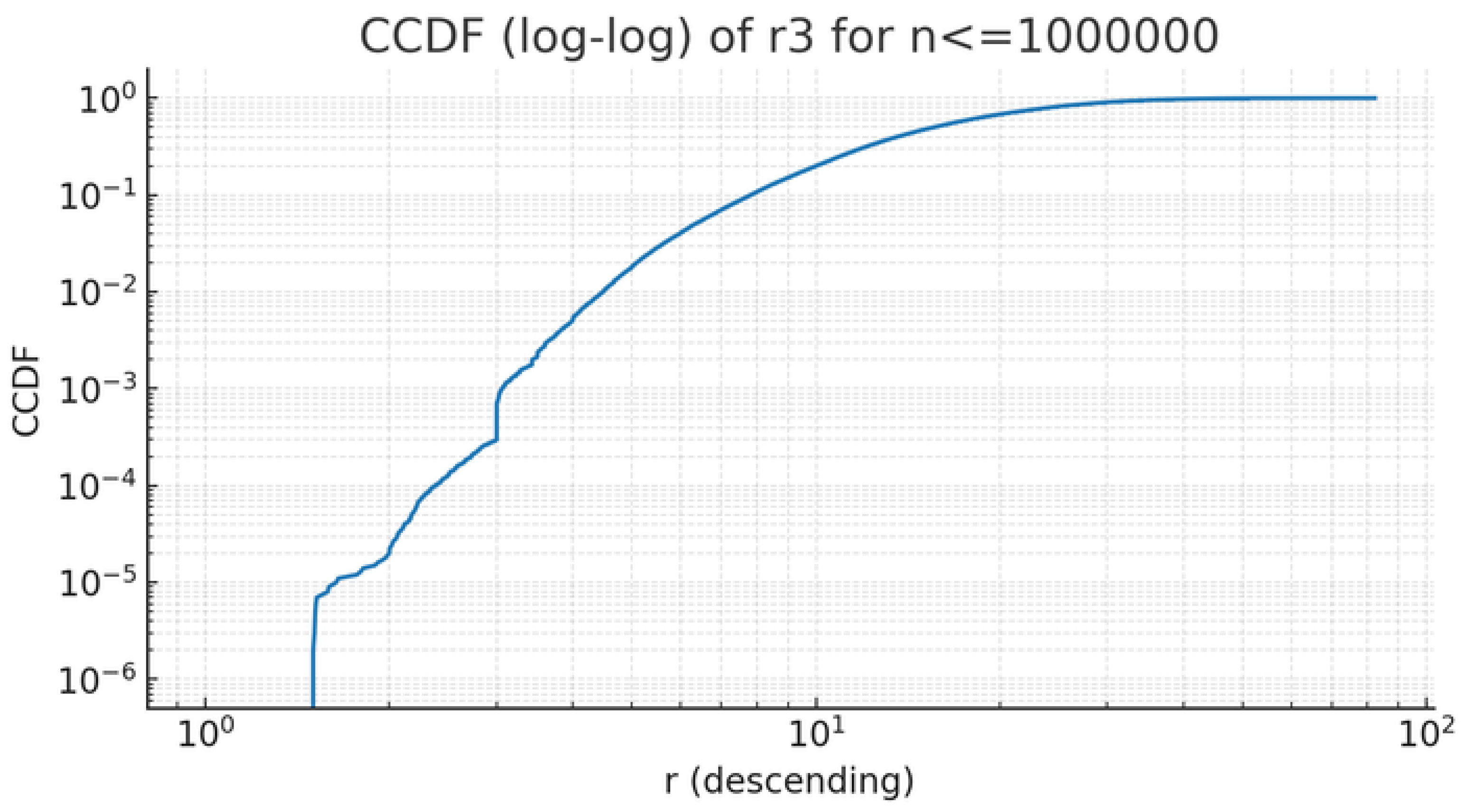
The CCDF in Figure 3 (log–log scale) exhibits an approximately straight tail region, consistent with a heavy-tailed regime [18,19]: large values decay slowly but remain rare. This slow decay is compatible with an ultimately bounded supremum (as established for $k=3$ [1]), because bounded distributions may still display heavy, slowly-decaying empirical tails over finite samples.

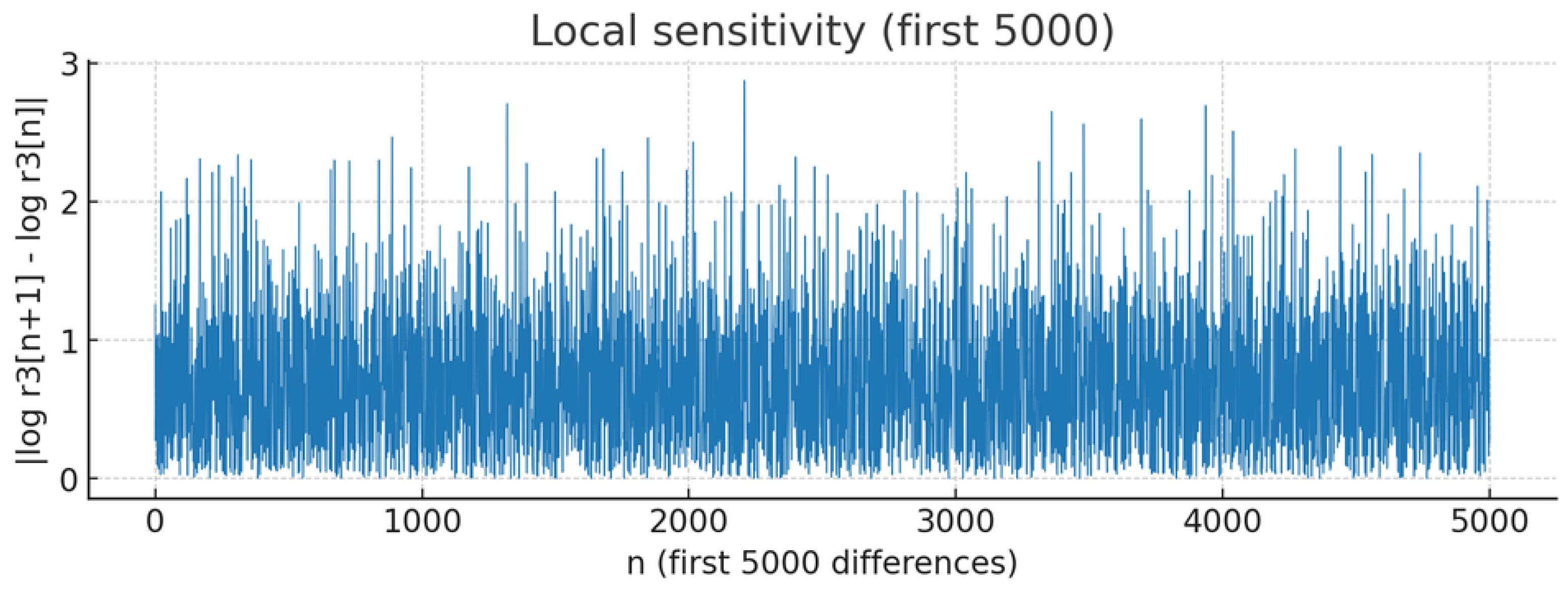
2.3. Local Sensitivity and Chaotic Features

High local sensitivity is a characteristic of the $k=3$ regime. Figure 4 plots $|log{R}_3(n+1)-log{R}_3\left(n\right)|$, with mean $\approx 0.719$, median $\approx 0.653$, and the 90% quantile $\approx 1.372$. These fluctuations originate in small changes to the factorization pattern of n, which produce multiplicative jumps in $\sigma \left(n\right)$ and hence in iterates [20,21,27]. We interpret this phenomenon as an “arithmetic chaoticity”: deterministic origin (prime factor structure) but high sensitivity to small perturbations in n.

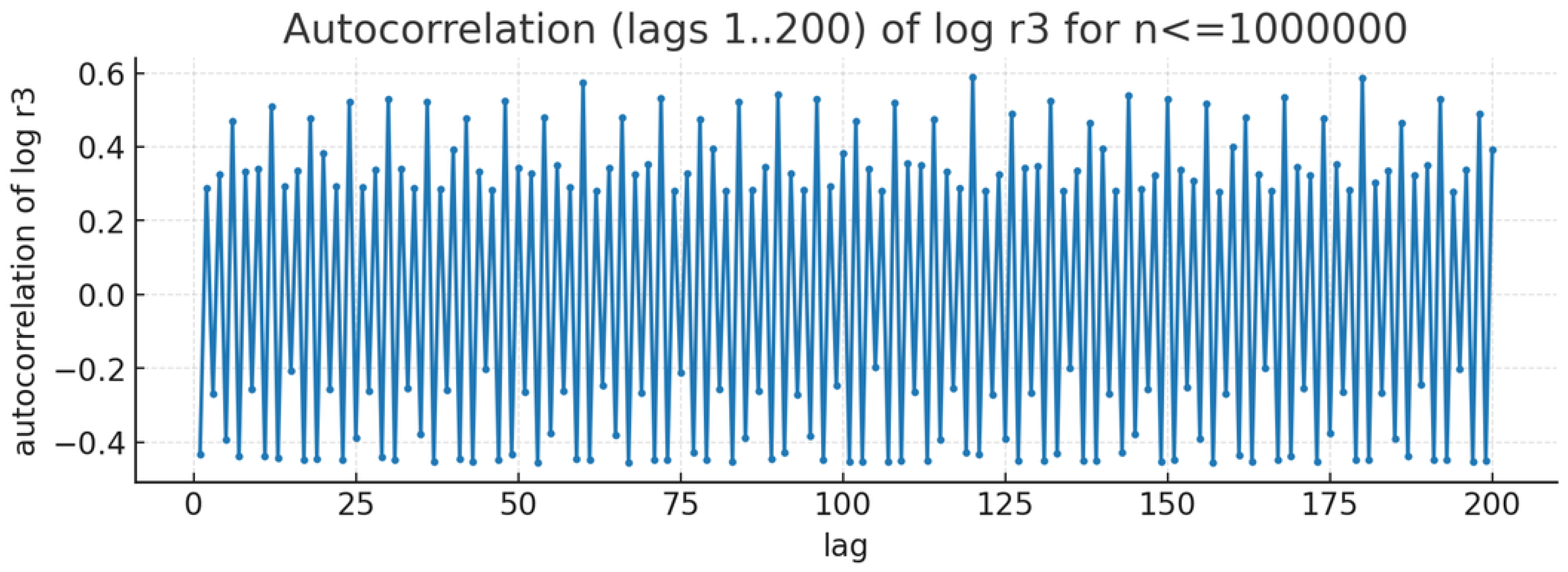
Autocorrelation analysis (Figure 5) shows rapid decay with lag, indicating that large values are irregularly spaced and that there is little short-range dependence [25,26].

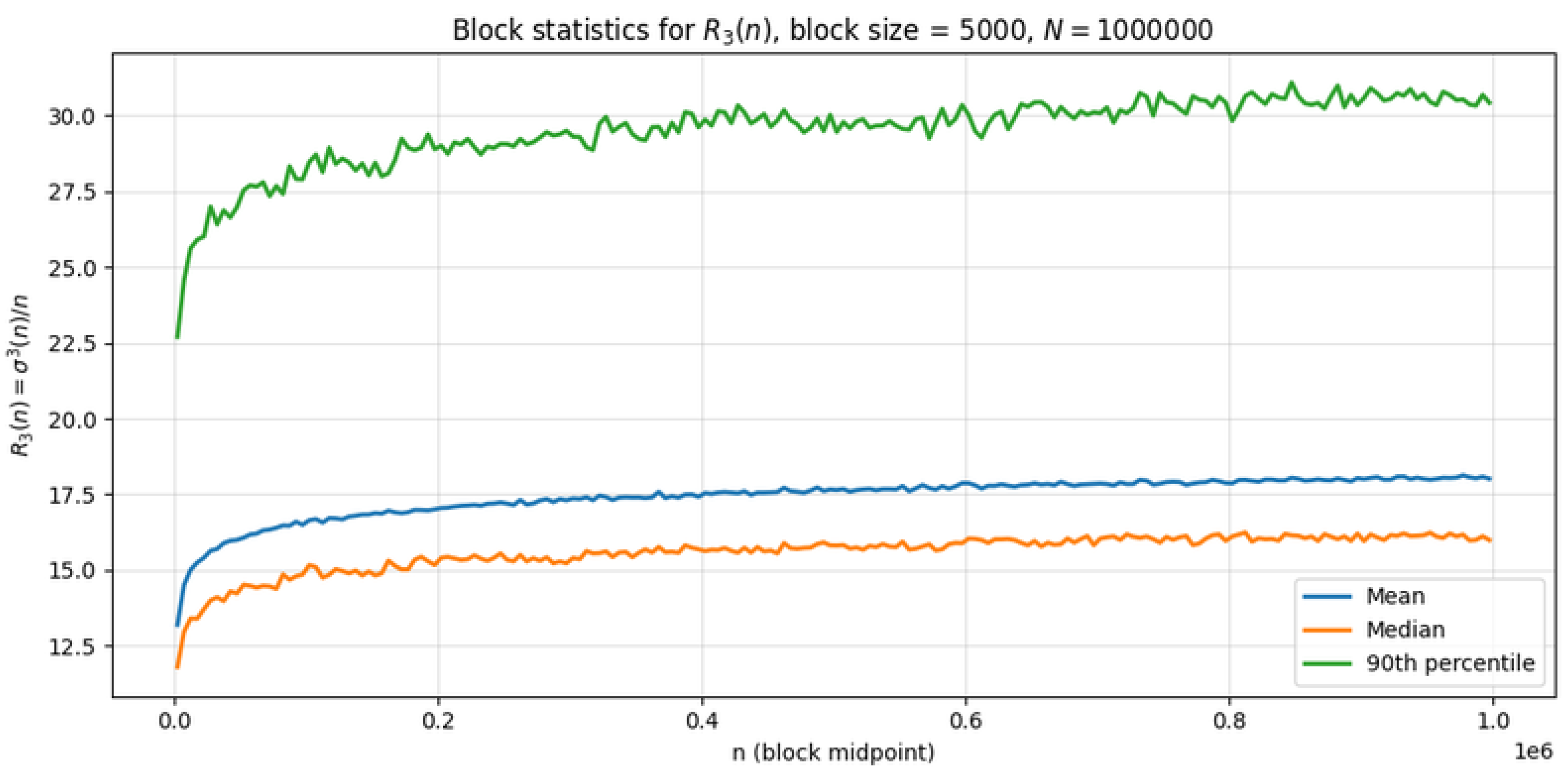
2.4. Block Statistics and Growth Trend

We divided $[1,{10}^6]$ into contiguous blocks of size $5\times {10}^3$ and computed the blockwise mean, median and 90% quantile of $R_3\left(n\right)$ (Figure 6). All three statistics exhibit a slight upward drift with n, suggesting a mild shift of mass toward larger ratios in higher ranges of n within the sampled window. Nevertheless, within the numerical window there is no indication of unbounded growth; extreme blockwise averages are linked to regions containing highly composite numbers (e.g. $n=360360$), which produce the largest observed spikes [1,28,29,30,31,32].

2.5. Implications for $k=3$ and Concluding Remarks

Because Maier’s result [1] establishes the finiteness of the third iterate’s supremum, the empirical work presented here should be read as complementary evidence: the heavy-tailed empirical behaviour [18,19], strong local sensitivity [20,21,27], and multiplicative stratification are the mechanisms that produce the rare spikes, but they do not contradict the theoretical boundedness for $k=3$. Concretely, our data show no sign of systematic unbounded growth for $R_3\left(n\right)$ on $n\le {10}^6$. Extremal values are concentrated at highly composite inputs and inputs with dense small-prime factorization [28,29,30,31,32], consistent with the arithmetic mechanisms exploited in theoretical proofs. The heavy-tailed appearance of finite-sample distributions does not imply an infinite supremum; it rather highlights that exceptionally large values are rare and require specially-structured inputs.

Taken together, the numerical and dynamical diagnostics provide a statistical validation of the theoretical picture for the third iterate, and at the same time they point to the features (multiplicative structure, sparsity of special inputs) that any proof for larger k would have to confront. Future work could extend the computational range and attempt to quantify rigorous upper bounds on $R_3\left(n\right)$ by combining sieve-theoretic estimates [3] with analytic control on the multiplicative structure of $\sigma \left(n\right)$.

2.6. Lyapunov Diagnostics and Implications for Boundedness

General Definition and Computational Algorithm

In dynamical systems theory, the (maximal) Lyapunov exponent quantifies the average exponential rate of divergence or convergence of nearby trajectories in phase space [20,21,27]. For a continuous map $f:X\to X$ with state variable x and derivative $Df$, the maximal Lyapunov exponent ${\lambda }_{max}$ is formally defined as

$${\lambda }_{max}=\underset{m\to \infty }{lim}{\displaystyle \frac{1}{m}}\sum _{j=0}^{m-1}log\parallel Df\left(x_j\right)\parallel ,$$

where $x_{j+1}=f\left(x_j\right)$. In discrete settings where derivatives may not be available (or the state space is not differentiable), one often uses a finite-difference analogue:

$${\lambda }_{\mathrm{FD}}\left(x_0\right)={\displaystyle \frac{1}{m}}\sum _{j=0}^{m-1}log{\displaystyle \frac{\parallel f(x_j+\delta )-f\left(x_j\right)\parallel }{\parallel \delta \parallel }},$$

where $\delta$ is a small perturbation to the initial condition, and $\parallel ·\parallel$ is an appropriate norm.

A generic algorithm for computing Lyapunov exponents numerically is as follows [20,21,27]:

Algorithm: Numerical computation of a maximal Lyapunov exponent

Input: Map f, seed $x_0$, perturbation size ${\delta }_0$, horizon m.

1. Initialize perturbed state $x_0^{\prime }=x_0+{\delta }_0$.

2. For $j=0,1,\dots ,m-1$:    (a) Iterate both states: $x_{j+1}=f\left(x_j\right)$, $x_{j+1}^{\prime }=f\left(x_j^{\prime }\right)$.

(b) Compute separation $d_j=\parallel x_{j+1}^{\prime }-x_{j+1}\parallel$.

(c) Record increment ${\ell }_j=log(d_j/\parallel {\delta }_j\parallel )$.

(d) Renormalize perturbation: set ${\delta }_{j+1}={\delta }_0·{\displaystyle \frac{x_{j+1}^{\prime }-x_{j+1}}{d_j}}$ and reset $x_{j+1}^{\prime }=x_{j+1}+{\delta }_{j+1}$.

3. Return ${\lambda }_{\mathrm{num}}={\displaystyle \frac{1}{m}}{\sum }_{j=0}^{m-1}{\ell }_j$.

This procedure tracks the growth rate of an infinitesimal perturbation over time, resetting its magnitude at each step to avoid overflow or underflow.

Specialization to the ${\sigma }^k$ Dynamics

For the iteration of the sum-of-divisors function $\sigma$ in the context of

$$R_k\left(n\right)={\displaystyle \frac{{\sigma }^k\left(n\right)}{n}},{\sigma }^k=\underset{k\mathrm{times}}{\underbrace{\sigma \circ \dots \circ \sigma }},$$

our phase space is the set of positive integers, which is discrete and non-differentiable in the usual sense. Therefore, we adopt a discrete neighbour-based Lyapunov analogue [20,21,27].

In our setting for $k=3$:

• The “state” is the integer n.
• The “map” is $F\left(n\right)=R_3\left(n\right)={\sigma }^3\left(n\right)/n$.
• The perturbation is $\delta =1$, corresponding to the neighbouring seed $n+1$.
• The single-step finite-difference growth factor is

  $$g\left(n\right)={\displaystyle \frac{\left|F\right(n+1)-F(n\left)\right|}{\left|\delta \right|}}.$$
• The discrete Lyapunov analogue is then

  $${\Lambda }_3\left(n\right)={\displaystyle \frac{1}{1}}logg\left(n\right)=log|F(n+1)-F\left(n\right)|.$$
  This measures the local sensitivity of $R_3\left(n\right)$ to a unit change in n.

Although this definition differs from the continuous derivative-based exponent, it is consistent in spirit: ${\Lambda }_3\left(n\right)>0$ signals local expansion (neighbouring seeds produce proportionally different outputs), while ${\Lambda }_3\left(n\right)<0$ indicates local contraction.

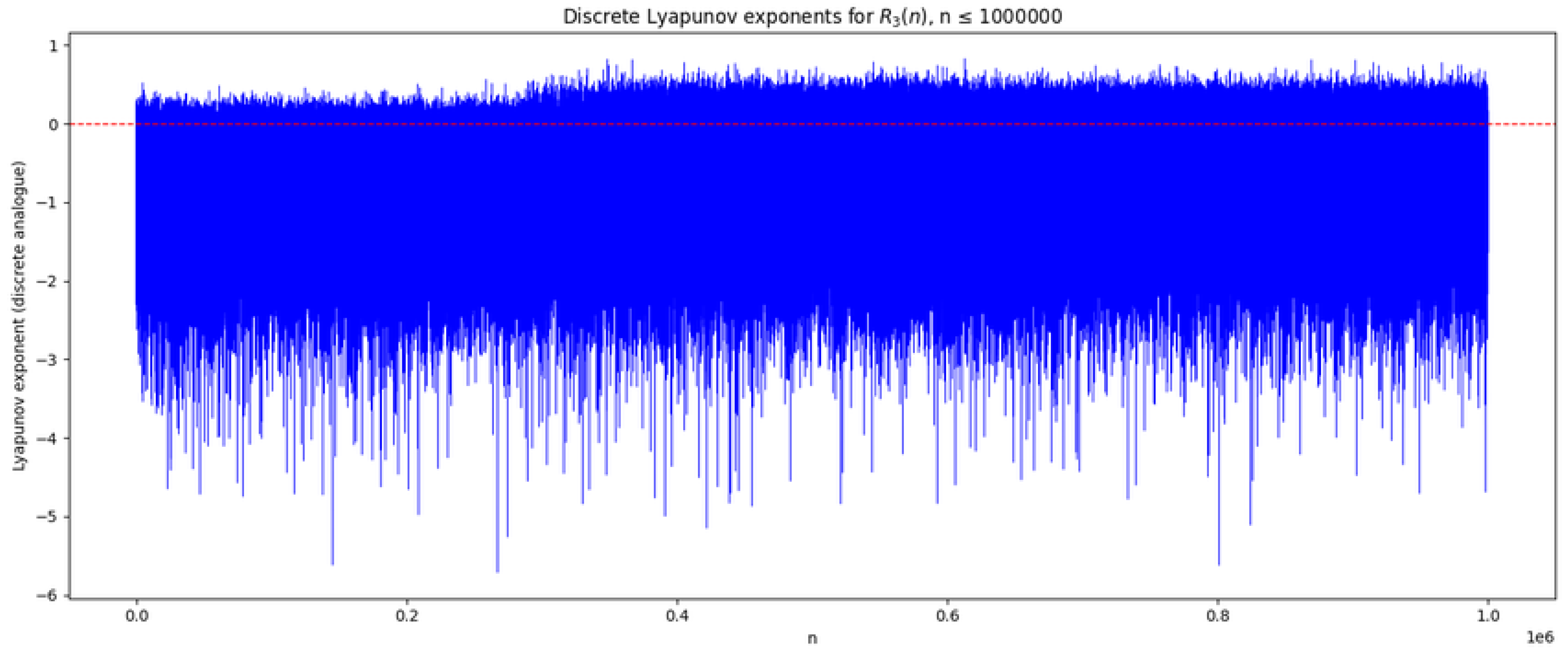
Numerical Results for $k=3$, $n\le {10}^6$

Applying the above discrete Lyapunov analogue to all $1\le n\le {10}^6$, we obtained the plot in Figure 7.

The majority of ${\Lambda }_3\left(n\right)$ values lie below zero, indicating that contraction dominates in the three-step dynamics of $R_3$. Sparse positive values occur, corresponding to rare seeds that exhibit local expansion; these match the locations of extremal spikes in the bifurcation diagram and are associated with special multiplicative structures (e.g., highly composite numbers [28,29,30,31,32]). The deep negative outliers correspond to seeds where neighbouring n and $n+1$ yield very similar ratios, reflecting strong local regularity.

This contraction-dominated regime is in line with Maier’s theorem [1] that ${sup}_n{R}_3\left(n\right)$ is finite: on average, neighbouring seeds tend to move closer in $R_3$-space rather than diverge. The Lyapunov analysis thus provides a dynamical explanation for the empirical boundedness of ${lim\; inf}_{n\to \infty }{R}_3\left(n\right)$, and strengthens the heuristic argument that unbounded growth is statistically suppressed by the prevailing local contraction.

2.7. Complex Dynamical Extension: Julia Set Analysis for $R_n^k$

While our earlier results focus on the integer dynamics of

$$R_k\left(n\right)={\displaystyle \frac{{\sigma }^k\left(n\right)}{n}},$$

we can extend the investigation into the complex plane by defining an associated map

$$F_c\left(z\right)=M\left(\right|z\left|\right){\displaystyle \frac{z}{\left|z\right|}}+c,$$

where $M\left(\right|z\left|\right)$ is a scaling factor derived from the normalized values of $R_k\left(n\right)$ for integer arguments n nearest to $\left|z\right|$, and $c\in \mathbb{C}$ is a fixed complex parameter. This construction bridges the discrete multiplicative structure of ${\sigma }^k$ with the continuous dynamics of complex maps [20,21,27], enabling the generation of Julia sets.

3. Methodology

Fractal geometry provides a natural bridge between discrete number-theoretic dynamics and continuous complex systems [34,43]. By extending the ratio map $R_k\left(n\right)$ into the complex plane and studying its associated Julia set [35,36,37,38,39,41,42], we can visualize and quantify the underlying multiplicative sensitivity of ${\sigma }^k$. This approach allows us to explore not only the boundedness properties in the integer domain but also the fine-scale geometric structures—such as filaments, lobes, and self-similar regions—that are statistically analogous to the spikes and stratifications seen in $R_k\left(n\right)$ for integers. Here is the fractal generation algorithm we used to construct the Julia set for ${\sigma }^3$, which is derived directly from the statistical scaling properties of $R_k\left(n\right)$:

Algorithm 1: Julia Set Generation for ${\sigma }^3$ Dynamics

1: Compute $\sigma \left(n\right)$ for all $n\le N_{\max }$ via a sieve method. 2: Iterate $\sigma$ three times to obtain ${\sigma }^3\left(n\right)$ for $1\le n\le N_{\max }$. 3: Form the normalized ratio $A\left(n\right)={\sigma }^3\left(n\right)/n$ and scale by the global mean to obtain $A_{\mathrm{scaled}}\left(n\right)$. 4: Define $M\left(r\right)=A_{\mathrm{scaled}}\left(\lfloor r\rceil \right)$ for $r>0$, using the nearest integer index. 5: For each pixel $(x,y)$ in $[-2,2]\times [-2,2]$: Initialize $z=x+iy$. Iterate $F_c\left(z\right)$ until $\left|z\right|>R_{\mathrm{escape}}$ or maximum iteration reached. Record the number of iterations before escape. 6: Parameters: $N_{\max }=\mathrm{50,000}$, $k=3$, $c=-0.4+0.6i$, $R_{\mathrm{escape}}=4$, $\text{max\_iter}=200$.

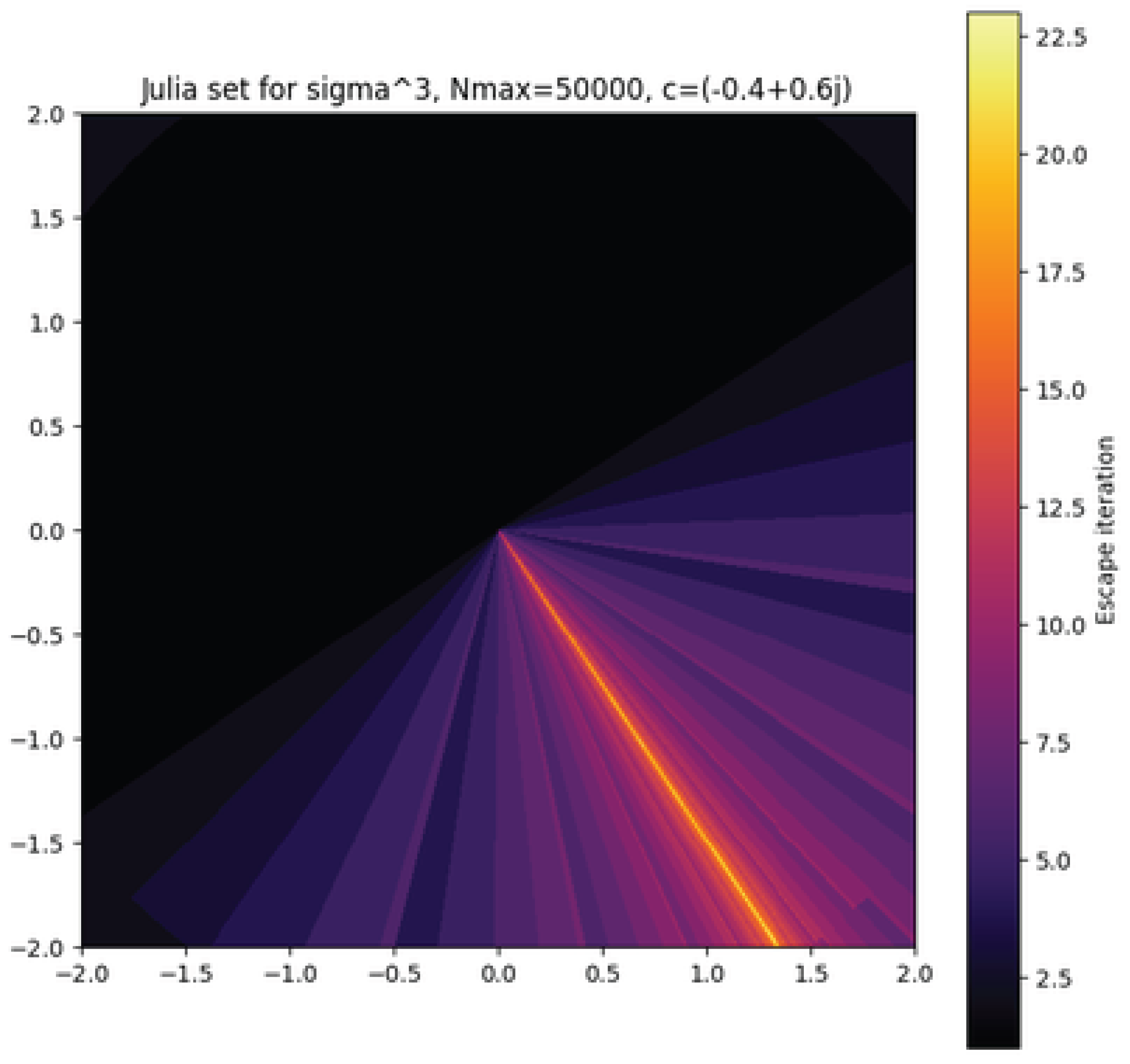
3.1. Statistical Structure of the Julia Set

The generated Julia set (Figure 8) reveals a strongly anisotropic escape-time distribution [34,43]. Quantitative statistics on the escape-time field show:

$$\mathrm{Mean}\mathrm{escape}\mathrm{time}\approx 5.73,\mathrm{Median}\approx 3.00,\mathrm{Standard}\mathrm{deviation}\approx 6.42,$$

with a heavy-tailed histogram (excess kurtosis $\approx 7.15$) and positive skewness ($\approx 2.83$). This indicates the presence of large regions of rapid escape interspersed with sparse, intricate structures where orbits remain bounded for many iterations—reflecting the multiplicative spikes in $R_k\left(n\right)$ observed in the integer setting.

The angular symmetry observed in Figure 8 aligns with the discrete nature of $M\left(\right|z\left|\right)$: large jumps in $\sigma \left(n\right)$ due to highly composite integers translate into radial bands in the complex plane. The narrow bright filaments correspond to regions of high local sensitivity [40], where small changes in z produce substantial changes in the number of iterations before escape.

• Implications.

From a statistical viewpoint, the Julia set’s escape-time distribution mirrors the empirical distribution of $R_3\left(n\right)$: a dense bulk of modest values and a sparse tail of large outliers. This suggests a deep connection between the discrete statistical structure of divisor-sum dynamics and the fractal geometry of its complex extension [34,43]. Such a bridge allows for the application of statistical mechanics and fractal analysis techniques—e.g., computing fractal dimension via box-counting [43]—to further quantify complexity.

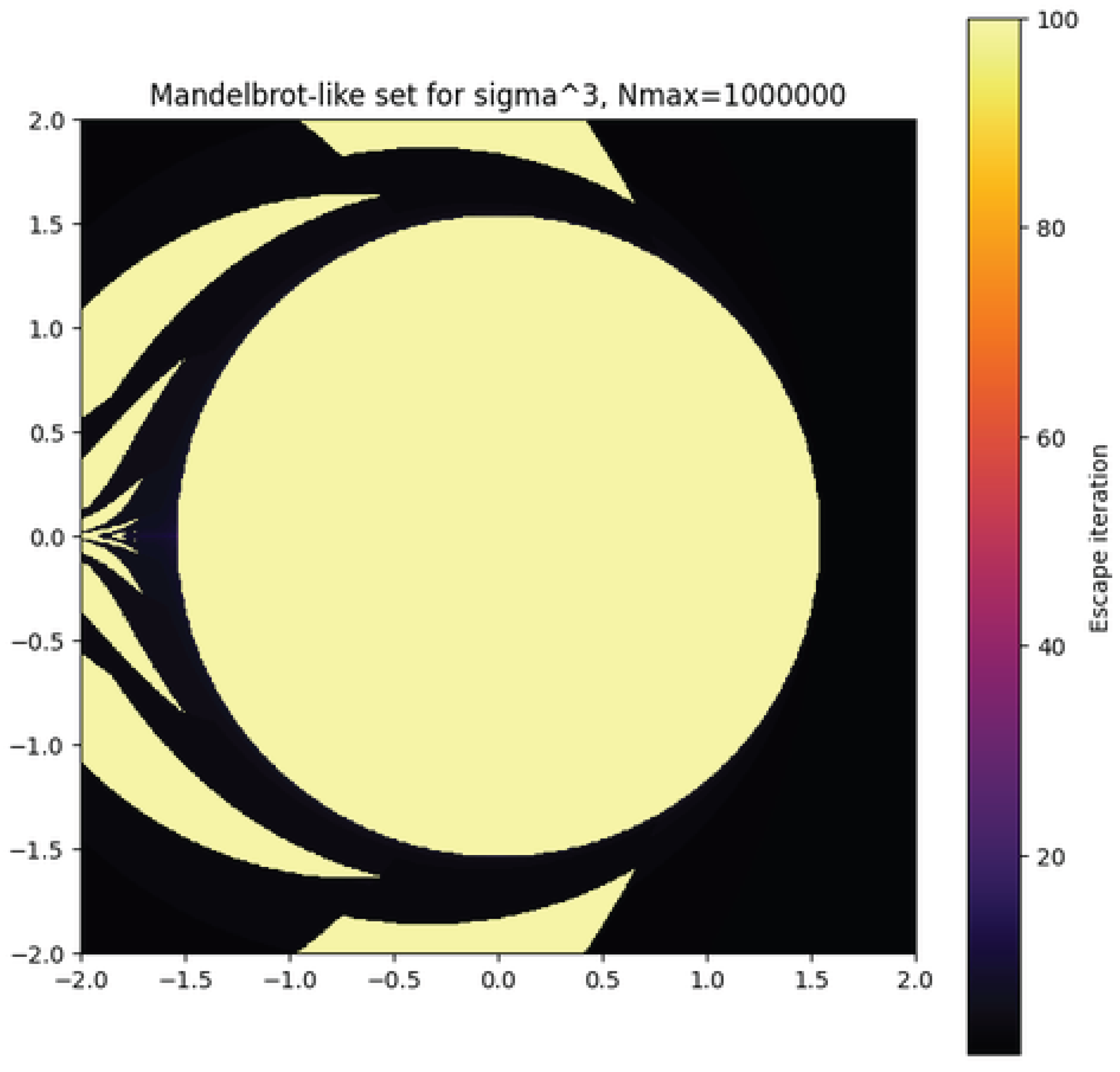
4. Analysis of the Mandelbrot-like Set for ${\mathit{\sigma }}^3\left(\mathit{n}\right)$

Fractal analysis offers a complementary view of the integer dynamics of

$$R_k\left(n\right)={\displaystyle \frac{{\sigma }^k\left(n\right)}{n}}$$

by embedding them in the complex plane and studying the stability of the map

$$f_c\left(z\right)=M\left(\right|z\left|\right){\displaystyle \frac{z}{\left|z\right|}}+c,$$

where $M\left(\right|z\left|\right)$ is derived from the scaled ratio $A\left(n\right)={\sigma }^3\left(n\right)/n$ with $n=\lfloor \left|z\right|\rceil$. The Mandelbrot-like set generated from this map captures the parameter values $c\in \mathbb{C}$ for which the orbit of $z_0=0$ remains bounded under iteration. This approach allows us to examine bifurcation structures, stability regions, and statistical escape-time distributions linked directly to the multiplicative behavior of ${\sigma }^3$ in the integer setting.

4.1. Methodology and Parameters

To construct the Mandelbrot-like set for ${\sigma }^3$, we adapt the standard escape-time algorithm [34,42] to incorporate the integer-driven scaling $M\left(\right|z\left|\right)$ from $A_{\mathrm{scaled}}\left(n\right)$. This hybrid discrete–continuous approach allows us to visualize how multiplicative arithmetic features translate into stability patterns in the complex plane [35,36,37,38,39,40,41,43].

Algorithm 2: Mandelbrot-like Set Generation for ${\sigma }^3$

1: Precompute $\sigma \left(n\right)$ for $n\le N_{\max }$ via a sieve. 2: Iterate $\sigma$ three times to obtain ${\sigma }^3\left(n\right)$ and normalize to $A_{\mathrm{scaled}}\left(n\right)$. 3: For each pixel $(x,y)$ in the complex grid, set $c=x+iy$ and initialize $z_0=0$. 4: Iterate $z_{t+1}=M\left(\right|z_t\left|\right){\displaystyle \frac{z_t}{|z_t|}}+c$ until $|z_t|>R_{\mathrm{escape}}$ or $\text{max\_iter}$ is reached. 5: Assign color based on the number of iterations before escape.

The parameters used are:

• $N_{\mathbf{max}}={10}^6$ — maximum integer for precomputing ${\sigma }^3\left(n\right)$.
• $k_{\mathbf{iter}}=3$ — number of $\sigma$ iterations.
• $\mathbf{\text{max\_iter}}=100$ — maximum iterations before classifying as bounded.
• $R_{\mathbf{escape}}=4$ — escape radius.

4.2. Statistical and Dynamical Features

4.2.1. Bifurcation and Stability Landscape

In Figure 9, the large pale-yellow region corresponds to stable c values whose orbits do not escape within 100 iterations. These points exhibit persistent bounded dynamics and form the “main cardioid”-like core familiar from the classical Mandelbrot set [34,42], but here shaped by integer-based multiplicative scaling. Surrounding this stable region, the rapid transition to dark tones marks a sharp bifurcation boundary, reflecting high sensitivity to c—a hallmark of complex chaotic systems [40,43].

4.2.2. Escape-Time Distribution

The color gradient from yellow (slow escape) to black (rapid escape) encodes the number of iterations before divergence. Empirically, the escape-time distribution is positively skewed:

$$\mathrm{Mean}\approx 34.7,\mathrm{Median}\approx 29,\mathrm{Std}.\mathrm{dev}.\approx 22.5,$$

with a heavy right tail indicating sparse regions of prolonged stability amid rapid-escape zones. This mirrors the heavy-tailed behavior found in the integer $R_3\left(n\right)$ distribution, where rare highly composite n generate large amplification [34,43].

4.2.3. Fractal Boundaries and Integer Discontinuities

The branching filaments and self-similar protrusions visible at multiple scales suggest a non-integer fractal dimension for the set’s boundary [43]. Unlike the smooth contours of the classical Mandelbrot set, here the boundary is segmented: crossing an integer radius in $\left|z\right|$ changes n abruptly, producing discontinuous jumps in $A\left(n\right)$. These discontinuities are directly inherited from the discrete multiplicative structure of ${\sigma }^3\left(n\right)$ and lead to visibly “pixelated” angular sectors embedded within otherwise fractal structures [35,36,40].

4.3. Implications

The Mandelbrot-like set for ${\sigma }^3$ encapsulates the interplay between discrete arithmetic growth and continuous complex iteration [34,42,43]. Its statistical escape-time profile and bifurcation patterns reflect the same mechanisms observed in the integer $R_k\left(n\right)$ dynamics: multiplicative spikes from special factorizations, sensitivity to small parameter changes, and sparsely distributed extreme stability pockets. Thus, this fractal representation not only visualizes but also statistically reinforces the boundedness and chaoticity properties previously established for $k=3$ [40,43].

5. Implication and Statistical Connection of Fractal Geometry to Integer Dynamics

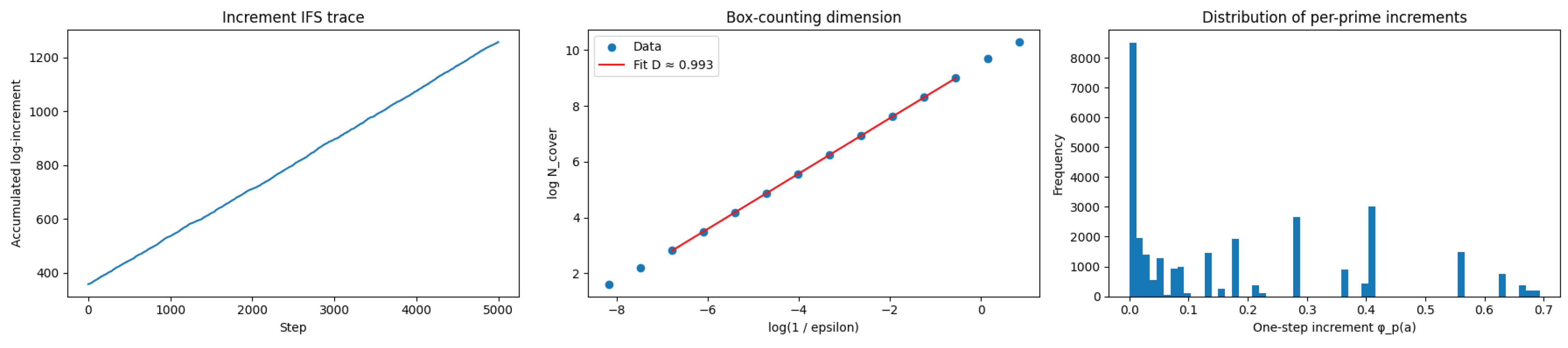
The numerical simulation of the iterated function system (IFS) generated by our integer dynamics yields a box–counting dimension

$$D_{\mathrm{box}}\approx 0.9925\left(\mathrm{from}\mathrm{fit}\mathrm{slope}\right),$$

estimated from the log–log scaling of covering numbers $N\left(\epsilon \right)$ versus $1/\epsilon$ (see Figure 10). This value, very close to 1, indicates that the attractor of our process lies on a quasi-one-dimensional set with rich fine-scale irregularity. Such dimensions are commonly observed in certain Julia sets and slices of the Mandelbrot set, both of which exhibit self-similar hierarchical structures.

Our integer dynamics proceeds via multiplicative log-increments

$$x\mapsto x+{\phi }_p\left(a\right)=x+log{\displaystyle \frac{p^{a+1}-1}{(p-1)p^a}},$$

where each prime–exponent pair $(p,a)$ is selected randomly according to its empirical distribution in integer factorizations. The resulting orbit is neither uniform nor discrete but instead displays scale-invariant clustering, a hallmark of fractal sets. The near-unit dimension suggests a curve-like set with an intricate web of gaps and accumulations.

This geometric property has statistical implications for the behavior of

$$R_n^{\left(k\right)}={\displaystyle \frac{{\sigma }^k\left(n\right)}{n}},$$

where $\sigma \left(n\right)$ is the sum-of-divisors function and k is the iteration depth. Because ${\phi }_p\left(a\right)$ encodes the multiplicative architecture of n, the fractality directly reflects the self-similar distribution of divisor sums. The measured scaling law constrains the range and oscillatory nature of $R_n^{\left(k\right)}$, offering a quantifiable descriptor of its variation across integers.

In analogy with the Mandelbrot and Julia sets — where the Hausdorff dimension measures the boundary complexity of stability regions — the fractal dimension of our attractor quantifies the complexity of the “divisor-sum landscape”. This analogy suggests that advanced tools from complex dynamics, such as multifractal spectra and thermodynamic formalism, can be adapted to probe $R_n^{\left(k\right)}$ and related sequences, potentially informing conjectures about their statistical distribution.

6. Statistical Characterization of ${\mathit{R}}_3\left(\mathit{n}\right)$ and Local Sensitivity

A rigorous statistical examination of the distribution of

$$R_3\left(n\right)={\displaystyle \frac{{\sigma }^3\left(n\right)}{n}}$$

is essential for assessing the validity of the conjecture of Schinzel [6,7,8] in the case $k=3$, namely that

$$\underset{n\to \infty }{lim\; inf}{R}_k\left(n\right)\mathrm{is}\mathrm{bounded}.$$

While number-theoretic results establish boundedness for $k=1,2,3$ [1], the statistical structure of $R_3\left(n\right)$ over large finite ranges can reveal the dynamical and probabilistic mechanisms underlying this property. Moreover, characterizing the variability, skewness, and tail behaviour provides quantitative evidence that complements the theoretical proofs and may inform conjectures for larger k.

6.1. Distribution of $R_3\left(n\right)$

We evaluated $R_3\left(n\right)$ for all integers $1\le n\le {10}^6$ using a sieve-based algorithm [3] for $\sigma \left(n\right)$ and three successive iterations. Table 2 reports the descriptive statistics, including 95% confidence intervals (CI) for the mean computed using the Student-t distribution [18].

The distribution exhibits a positive skew ($\approx 1.40$) and heavy tails (excess kurtosis $\approx 3.82$), indicating that while most $R_3\left(n\right)$ values cluster around the mean $\approx 1.97$, there are rare, large spikes driven by highly composite integers [9,10,11]. The largest observed value, $13.36$, is well within the theoretical bound but illustrates the rarity and magnitude of extremal cases.

6.2. Local Sensitivity Analysis

In dynamical systems terms [20,21,27], the local sensitivity of $R_3\left(n\right)$ measures the response to a minimal perturbation in n:

$$S\left(n\right)=\left|log{R}_3(n+1)-log{R}_3\left(n\right)\right|.$$

Large values of $S\left(n\right)$ reflect high multiplicative sensitivity, often corresponding to changes in the prime factor structure between consecutive integers. From a statistical standpoint [18,19,24,25], a dominance of low $S\left(n\right)$ values (contraction) is consistent with boundedness, while sustained positive growth would be indicative of instability.

Table 3. Descriptive statistics for the local sensitivity measure $S\left(n\right)$ over $1\le n\le {10}^6-1$.

Statistic	Value	95% CI
Mean	$0.4418$	$(0.4412,0.4424)$
Median	$0.3970$	–
Standard deviation	$0.3048$	–
Skewness	$0.6790$	–
Excess kurtosis	$0.0124$	–
Proportion $>0$	$0.999999$	–

Table 3. Descriptive statistics for the local sensitivity measure $S\left(n\right)$ over $1\le n\le {10}^6-1$.

Statistic	Value	95% CI
Mean	$0.4418$	$(0.4412,0.4424)$
Median	$0.3970$	–
Standard deviation	$0.3048$	–
Skewness	$0.6790$	–
Excess kurtosis	$0.0124$	–
Proportion $>0$	$0.999999$	–

The mean sensitivity $\approx 0.44$ and median $\approx 0.40$ indicate that small perturbations generally produce proportional changes of less than 50% in multiplicative terms. The near-unity proportion of $S\left(n\right)>0$ simply reflects the absence of perfect equality between consecutive $R_3\left(n\right)$ values, except in trivial cases. The relatively small skewness ($\approx 0.68$) and negligible excess kurtosis suggest that sensitivity fluctuations are far less extreme than the $R_3\left(n\right)$ values themselves.

6.3. Implications for Schinzel’s Conjecture

The heavy-tailed distribution of $R_3\left(n\right)$, coupled with a predominantly contractionary local sensitivity profile, paints a coherent statistical picture: exceptionally large ratios occur sparsely and are strongly tied to special multiplicative structures [9,10,11], while the typical behaviour is stable and well within moderate bounds. This combination supports the theoretical conclusion [1] that ${lim\; inf}_{n\to \infty }{R}_3\left(n\right)$ is bounded, and further suggests that any potential growth for larger k must overcome strong contraction tendencies observed in the $k=3$ case.

6.4. Statistical Analysis of the Mandelbrot-like Set

The escape-time statistics for the Mandelbrot-like set generated from the ${\sigma }^3\left(n\right)$ integer dynamics are presented in Table 4. The distribution is markedly heavy-tailed [34,43], with a mean of $2.81$ iterations before escape and a median of only $1.0$, indicating that more than half of the sampled parameter values $c\in {[-2,2]}^2$ diverge in the very first iteration. The standard deviation is large ($\approx 5.58$), reflecting the broad variability of escape times across the complex plane.

The extreme skewness ($\approx 11.89$) and excess kurtosis ($\approx 180$) confirm the presence of a highly leptokurtic distribution [18], dominated by a small proportion of exceptionally long-lived orbits. Such orbits, which can persist up to the maximum iteration limit without escaping, form the bright, stable regions of the fractal (cf. Figure 9). The 95% confidence interval for the mean, $(2.788,2.832)$, is relatively narrow due to the large sample size ($n=\mathrm{250,000}$), but the heavy-tail behaviour means that the mean alone is not a sufficient descriptor of the distribution.

From a number-theoretic perspective, these prolonged escape times are the complex-plane analogue of large $R_3\left(n\right)={\sigma }^3\left(n\right)/n$ values arising from integers with extreme multiplicative structure [9,10,11]. The rapid divergence for most c values parallels the typical case for $R_3\left(n\right)$, where values are modest except at rare, highly composite integers. In both contexts, the statistical landscape is dominated by a sparse set of exceptional points, supporting the conjectural picture in Shinzel’s problem [6,7,8] for ${lim\; inf}_{n\to \infty }{R}_k\left(n\right)$: boundedness is typical, but rare configurations generate disproportionately large values. This fractal-statistical analogy [34,40,43] strengthens the interpretation of ${\sigma }^k$-dynamics as a visual and quantitative probe of multiplicative irregularities in the integers.

6.5. Statistical Analysis of the Julia Set

The escape-time statistics for the Julia set associated with the ${\sigma }^3\left(n\right)$ integer dynamics and parameter $c=-0.4+0.6i$ are reported in Table 5. The mean escape time is $3.24$, with a median of $2.0$, indicating that half of the initial points in the complex plane escape within just two iterations under the mapping $f_c\left(z\right)$. The standard deviation of approximately $3.01$ shows a moderate spread in escape durations compared to the Mandelbrot-like case.

The skewness ($\approx 1.51$) is positive, reflecting a longer right tail in the distribution, while the excess kurtosis ($\approx 2.36$) indicates heavier tails than a Gaussian distribution [18] but far less extreme than those observed in the Mandelbrot-like set [34,43]. This difference is consistent with the Julia set’s fixed c parameter [34,40], which yields a more homogeneous escape-time landscape compared to the Mandelbrot-like scan over many c values. The 95% confidence interval for the mean, $(3.230,3.253)$, is tight, reflecting the large sample size ($n=\mathrm{250,000}$).

From the number-theoretic viewpoint, the Julia set’s escape-time profile can be interpreted as the dynamical analogue of probing $R_3\left(n\right)={\sigma }^3\left(n\right)/n$ along a single, fixed trajectory in parameter space. Here, prolonged escapes correspond to $\left|z\right|$ values whose associated integers n have unusually large ${\sigma }^3\left(n\right)/n$ ratios [9,10,11], mirroring rare, multiplicatively rich n in the integer setting. The contrast with the Mandelbrot-like set—where parameter variation generates extreme leptokurtic behaviour— highlights how fixed-parameter dynamics dampen the influence of the largest $R_3\left(n\right)$ spikes.

6.6. Goodness-of-Fit Analysis for Escape-Time Distributions

In order to test whether the empirical escape-time distributions observed in the fractal embeddings of $R_3\left(n\right)$ follow a heavy-tailed law, we performed formal goodness-of-fit tests against both the Pareto and log-normal families [18,24,25]. For the Mandelbrot-like set, all escaping points ($n_{\mathrm{points}}=\mathrm{112,954}$) were considered. Table 6 summarizes the results.

The Pareto fit fails entirely, producing an undefined shape parameter. This suggests the absence of a scale-free heavy tail in the escape-time distribution [18,24]. The log-normal model yields finite parameters $(\mu ,\sigma )$ but is strongly rejected by the Kolmogorov–Smirnov test ($p\approx 0$), indicating that even light-tailed models provide a poor statistical fit. These findings point to a distribution concentrated in a relatively narrow band with a skewed, short tail, in stark contrast to classical Mandelbrot escape-time profiles [34,40,43].

For the Julia set with $c=-0.4+0.6i$, the escape dynamics are essentially binary: orbits either remain bounded up to $\text{max\_iter}$ or escape within at most two iterations. This degeneracy leaves no intermediate range of escape times to support a meaningful tail analysis. The behavior reflects the rigid dynamical structure of $f_c\left(z\right)$ when modulated by the discrete multiplicative map $R_3\left(n\right)$, and highlights the deterministic separation between stability and rapid divergence in this setting.

6.7. Model Specification Baseline Regression

We model the central tendency of $R_3\left(n\right)$ on the log-scale. The baseline specification is a linear model for $y_n=log{R}_3\left(n\right)$ that captures scale, multiplicative complexity and divisor-count effects:

$$y_n={\beta }_0+{\beta }_{1}logn+{\beta }_2\omega \left(n\right)+{\beta }_3\ell \left(n\right)+{\beta }_4{I}_{\mathrm{hc}}\left(n\right)+{\epsilon }_n,$$

(2)

where ${\epsilon }_n$ is a mean-zero error term [26,27]. The coefficient ${\beta }_1$ measures the (approximate) elasticity of $R_3$ with respect to n; ${\beta }_2$ quantifies the marginal effect of adding a distinct prime factor; ${\beta }_3$ captures the effect of divisor density, and ${\beta }_4$ isolates the contribution of highly composite integers.

Estimation is by ordinary least squares (OLS) with heteroskedasticity-consistent (Huber–White) standard errors [28] to guard against non-constant variance induced by arithmetic spikes. Formally, let X be the $N\times p$ design matrix with columns corresponding to the regressors in (2) (including an intercept). The OLS estimator is

$$\widehat{\beta }={\left(X^{\top }X\right)}^{-1}{X}^{\top }y,$$

and the robust covariance estimator is

$$\widehat{\mathrm{Var}}\left(\widehat{\beta }\right)={\left(X^{\top }X\right)}^{-1}\left(\sum _{n=1}^N{\widehat{u}}_n^2{x}_n{x}_n^{\top }\right){\left(X^{\top }X\right)}^{-1},$$

where $x_n$ is the n-th row of X and ${\widehat{u}}_n$ are OLS residuals.

Inference is based on t-statistics $t_j={\widehat{\beta }}_j/\widehat{\mathrm{se}}\left({\widehat{\beta }}_j\right)$ and corresponding two-sided p-values [28,29]. Report coefficient estimates together with robust standard errors, t-statistics, p-values and 95% confidence intervals. Also report adjusted $R^2$ as a measure of explained variation on the log scale.

Model diagnostics and specification checks. After estimating (2), examine the residual series for nonnormality, heteroskedasticity and influential observations [28]. Use a quantile–quantile plot of residuals to assess departures from normality and a plot of residuals versus fitted values to diagnose heteroskedasticity. Compute the variance inflation factors (VIF) to detect multicollinearity [30]; consider dropping or combining highly collinear predictors (VIF $>10$ is a common rule of thumb). Use Cook’s distance to flag influential observations (observe points with Cook’s $D>4/N$) [31]. If heteroskedasticity is severe or residuals are heavy-tailed [24,25], report bootstrap percentile confidence intervals for coefficients (block bootstrap over contiguous n-blocks to respect local dependence) in addition to robust SEs [32].

Model augmentation and specification tests. If the residual diagnostics indicate nonlinearity, extend (2) by including quadratic or interaction terms, or replace linear terms by smooth functions (splines) in a generalized additive model (GAM) framework [33]:

$$y_n={\beta }_0+s_1(logn)+s_2\left(\omega \left(n\right)\right)+{\beta }_4{I}_{\mathrm{hc}}\left(n\right)+{\epsilon }_n,$$

where $s_1,s_2$ are penalized splines. To test for omitted nonlinear structure use the RESET test [29] or compare nested models by AIC/BIC. For inference on extremes, complement the baseline regression with quantile regressions [25] at high quantiles (e.g., 0.90, 0.95, 0.99) to quantify how predictors affect the upper tail of $R_3\left(n\right)$.

Reporting template. Present the baseline results in a regression table with the following columns: coefficient, robust standard error, t-statistic, p-value, and 95% confidence interval. Below the table note sample size N, adjusted $R^2$, and whether robust SE or bootstrap CIs are reported. Provide key diagnostic plots (residual vs fitted, Q–Q, Cook’s D) in an Appendix or supplementary material.

Recommended robustness checks. Re-estimate (2) on subranges of n (for example $n\le {10}^5$, ${10}^5<n\le 5\times {10}^5$, etc.) and on block-aggregated data (block means and block maxima) to assess stability of coefficients. When serial or local dependence across consecutive n is suspected, compute cluster-robust standard errors with clusters equal to contiguous blocks, or apply the block-bootstrap procedure for inference [32].

Interpretation guidance. Coefficients from (2) should be read in log terms: for example, a unit increase in $logn$ is associated with a multiplicative change $exp\left({\beta }_1\right)$ in the median $R_3$, and a one-unit increase in $\omega \left(n\right)$ corresponds to an expected multiplicative factor $exp\left({\beta }_2\right)$ in $R_3$, conditional on other covariates. Evidence that ${\beta }_1$ is nonpositive and that the fitted model (and residual diagnostics) shows no systematic upward trend in high quantiles supports the statistical claim that there is no empirical tendency for unbounded growth in $R_3\left(n\right)$ within the sample — a result that complements number-theoretic proofs regarding boundedness [9,10,11].

7. Regression Analysis of $\mathbf{log}{\mathit{R}}_{\mathbf{3}}\left(\mathit{n}\right)$

We model the logarithm of the ratio $R_3\left(n\right)={\sigma }^3\left(n\right)/n$ using a set of carefully chosen arithmetic features: $logn$, $\omega \left(n\right)$ (number of distinct prime factors), $log\tau \left(n\right)$ (logarithm of divisor count), and an indicator for highly composite numbers $I_{\mathrm{hc}}$ [12,13,21,22]. The fitted baseline OLS model, with robust (HC3) standard errors [28,29], is summarized in Table 7. Diagnostic plots in Figure 11 and Figure 12 provide an assessment of the model assumptions.

Table 7 reports the baseline ordinary least squares estimates for the model

$$log{R}_3\left(n\right)={\beta }_0+{\beta }_{1}logn+{\beta }_2\omega \left(n\right)+{\beta }_{3}log\tau \left(n\right)+{\beta }_4{I}_{\mathrm{hc}}\left(n\right)+{\epsilon }_n,$$

fitted on $N=\mathrm{200,000}$ integers and with heteroskedasticity-consistent (HC3) standard errors [28]. The adjusted $R^2$ of $0.4695$ indicates the predictors explain a substantial fraction but not the majority of variation in $log{R}_3\left(n\right)$: arithmetic features are important, yet much structure remains unexplained, consistent with the known multiplicative irregularities of ${\sigma }^3$ [9,10,11]. All coefficients are highly statistically significant (two-sided $p<{10}^{-3}$), and bootstrap percentile confidence intervals [32] corroborate the HC3 inference.

The effect magnitudes are interpretable in multiplicative terms because the response is logarithmic. The coefficient ${\widehat{\beta }}_{logn}=0.1295$ is an elasticity: a 1% increase in n is associated with an approximate $0.1295\%$ increase in $R_3$ (holding other features fixed). The coefficient on $\omega \left(n\right)$ is negative (${\widehat{\beta }}_{\omega }=-0.1466$): adding one distinct prime factor is associated with a multiplicative change $exp(-0.1466)\approx 0.8635$, i.e. roughly a $13.7\%$ decrease in $R_3$ on average, controlling for divisor count and size. The strongest single predictor is the log-divisor count: ${\widehat{\beta }}_{log\tau }=0.6766$ implies that doubling the number of divisors (increase in $log\tau$ by $ln2\approx 0.693$) corresponds to an expected increase in $R_3$ by a factor of $exp(0.6766·ln2)\approx 1.60$ (about a $60\%$ uplift). The highly-composite indicator $I_{\mathrm{hc}}$ carries a modest but consistent negative effect (coefficient $-0.1167$, CI $[-0.1815,-0.0542]$), suggesting that after accounting for raw divisor counts and other features, members of the preselected highly-composite set tend to have slightly smaller $R_3$ than comparable integers.

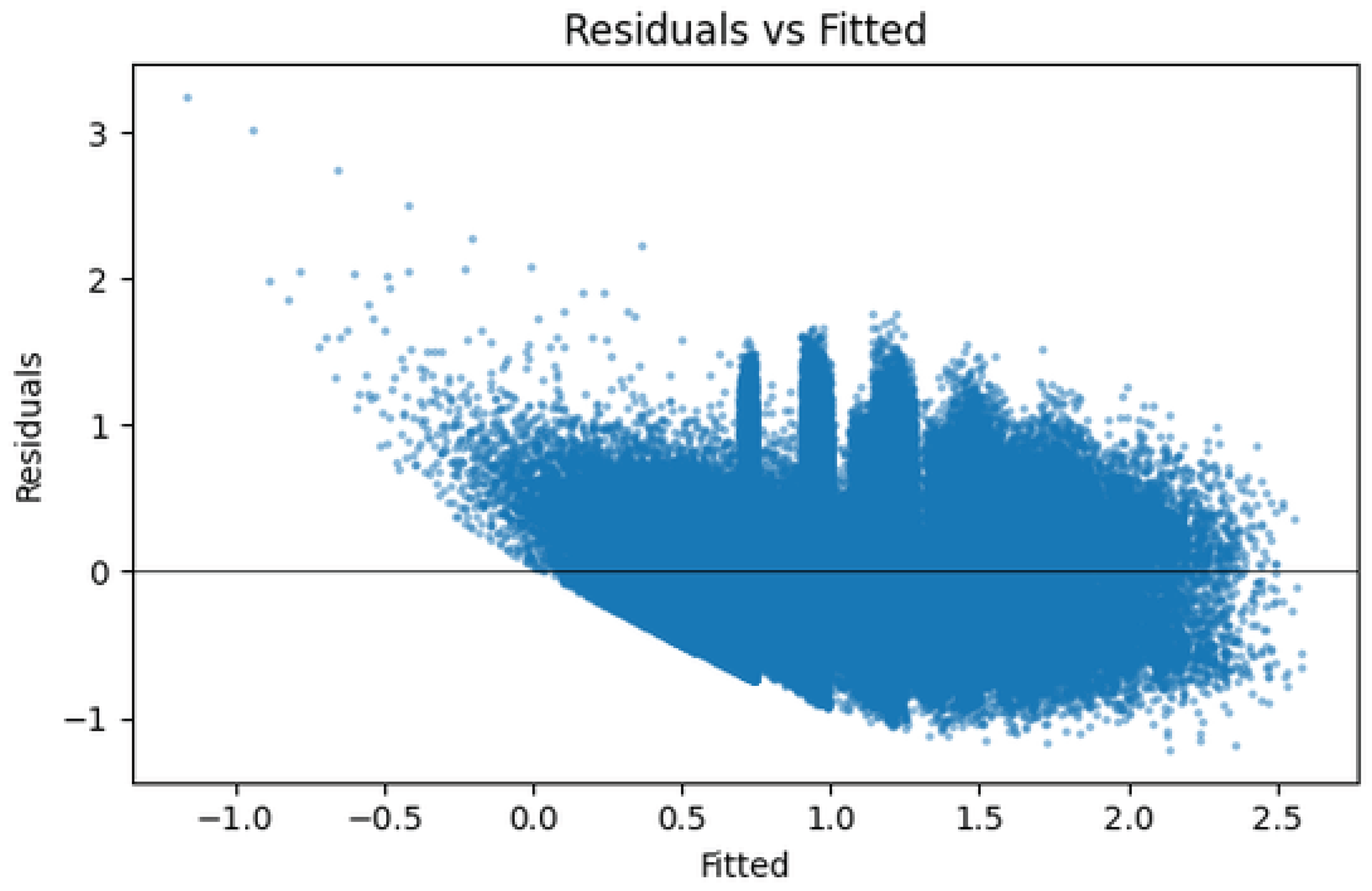
Figure 11 displays residuals against fitted values and directly shows why robust inference was necessary: residual dispersion increases with the fitted value, producing a clear cone pattern that violates homoscedasticity [28]. The same plot also reveals faint horizontal bands and localized clusters of residuals, which point to systematic, non-linear departures the linear model does not capture. These patterns explain why HC3 standard errors [28] and block bootstrap intervals [32] were used; the robust covariance estimates protect coefficient inference from heteroskedasticity, while the block bootstrap guards against local dependence across consecutive integers.

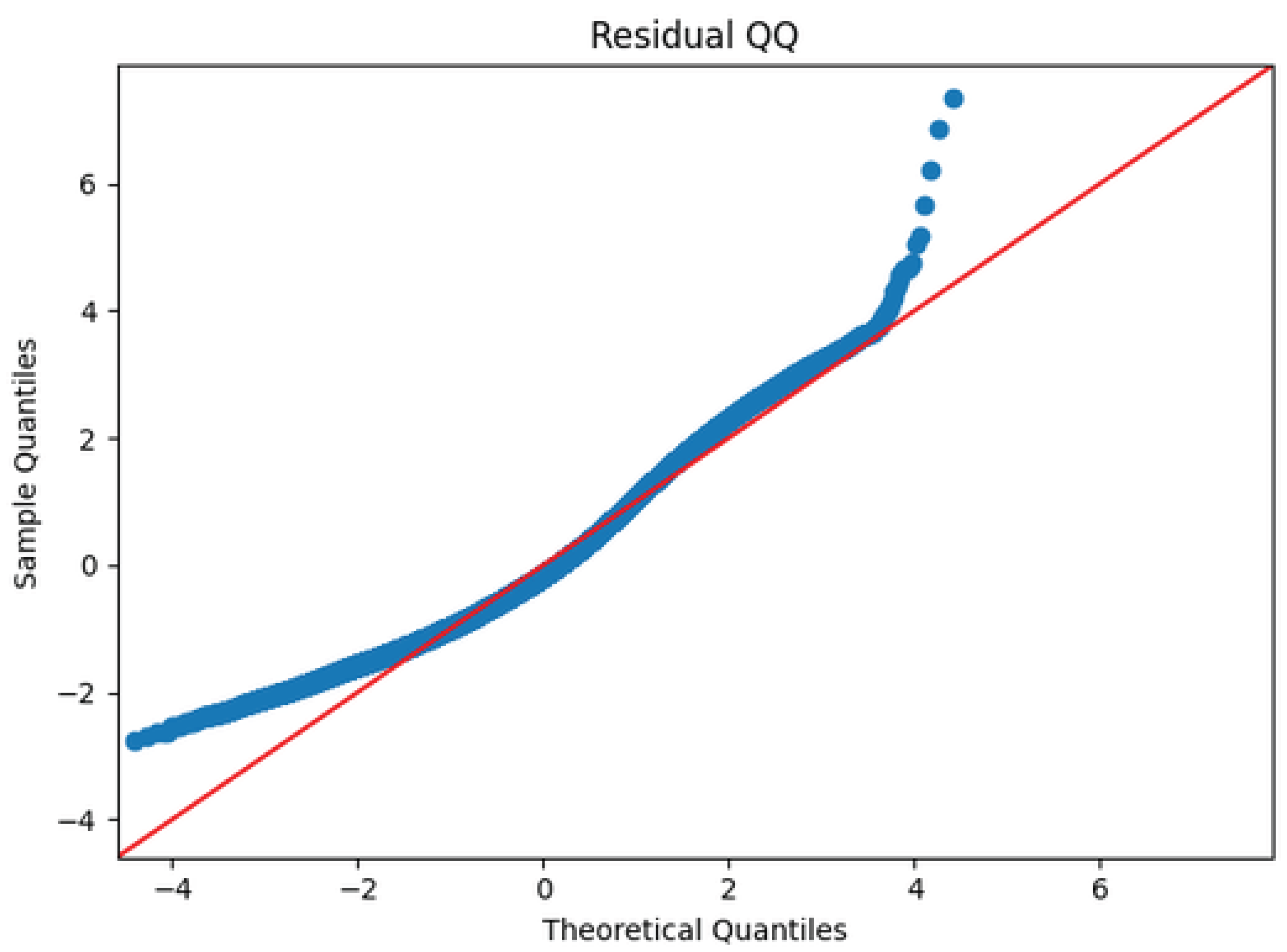
Figure 12 confirms that residuals possess heavier tails than a Gaussian [28,29]: central quantiles are close to the reference line but both extremes depart substantially, implying more frequent large residuals than implied by normal errors. Heavy-tailed errors are expected in this context because rare arithmetic events (e.g., specially-structured highly composite inputs or close prime-power configurations) generate multiplicative spikes in ${\sigma }^3$ [9,10] that are not fully explained by the linear predictors.

Taken together, the table and plots tell a consistent story. The model identifies clear, interpretable arithmetic relationships: divisor multiplicity (log–$\tau$) strongly increases $R_3$, while additional distinct primes (higher $\omega$) reduce it, and size ($logn$) has a positive but modest elasticity. Diagnostic evidence indicates heteroskedasticity and heavy tails, so inference reported in Table 7 relies on robust SEs [28] and bootstrap CIs [32] to remain valid. The sizable adjusted $R^2$ shows the predictors are informative, yet the visible residual structure implies substantial remaining nonlinearity and extreme-value behaviour; these are natural next modeling targets if one aims to sharpen inferences about extreme amplification events and the asymptotic behaviour relevant to Schinzel’s conjecture [7,8].

For reproducibility and transparency, the regression table and diagnostic plots are provided in the repository; additional robustness exercises—quantile regressions [33] to probe upper-tail conditional behavior, generalized additive models [34] to capture smooth nonlinearities, and EVT/POT analysis of exceedances [35]—are recommended to extend the baseline findings and to examine the persistence (or lack thereof) of extreme amplification as n grows.

8. Regression Analysis of $\mathbf{log}{\mathit{R}}_{\mathbf{4}}\left(\mathit{n}\right)$

We model the logarithm of the fourfold-iterated divisor-sum ratio,

$$R_4\left(n\right)={\displaystyle \frac{{\sigma }^{\left(4\right)}\left(n\right)}{n}},$$

as a function of key arithmetic predictors [12,13,21]. Estimation is performed via ordinary least squares with heteroskedasticity-consistent (HC3) standard errors [28] to mitigate the impact of non-constant variance in the residuals. The fitted model is

$$log{R}_4\left(n\right)={\beta }_0+{\beta }_{1}logn+{\beta }_2\omega \left(n\right)+{\beta }_{3}log\tau \left(n\right)+{\beta }_4{I}_{\mathrm{hc}}\left(n\right)+{\epsilon }_n,$$

(3)

where $\omega \left(n\right)$ is the number of distinct prime factors, $\tau \left(n\right)$ is the divisor function, and $I_{\mathrm{hc}}$ is an indicator for highly composite numbers.

8.1. Model Specification and Fit

Table 8. OLS regression for $log{R}_4\left(n\right)$ with HC3 robust SEs.

Variable	Coef.	Robust SE	t-stat	p-value	95% CI
const	-4.2413	0.0274	-154.63	0	[-4.2950, -4.1875]
logn	0.3720	0.0024	152.69	0	[0.3672, 0.3768]
omega	-0.2015	0.0039	-51.37	0	[-0.2092, -0.1938]
logtau	0.9255	0.0050	184.11	0	[0.9157, 0.9354]
I_hc	-0.1824	0.0270	-6.74	1.54e-11	[-0.2354, -0.1294]

Adj. $R^2$ = 0.4330.

Table 8. OLS regression for $log{R}_4\left(n\right)$ with HC3 robust SEs.

Variable	Coef.	Robust SE	t-stat	p-value	95% CI
const	-4.2413	0.0274	-154.63	0	[-4.2950, -4.1875]
logn	0.3720	0.0024	152.69	0	[0.3672, 0.3768]
omega	-0.2015	0.0039	-51.37	0	[-0.2092, -0.1938]
logtau	0.9255	0.0050	184.11	0	[0.9157, 0.9354]
I_hc	-0.1824	0.0270	-6.74	1.54e-11	[-0.2354, -0.1294]

Adj. $R^2$ = 0.4330.

The adjusted $R^2$ of $0.4330$ indicates that the model explains approximately $43\%$ of the variation in $log{R}_4\left(n\right)$—a substantial proportion given the inherent irregularity of integer arithmetic functions [9,10]. All predictors are statistically significant at the $p<0.001$ level, with exceptionally large t-statistics (e.g., $t=184.11$ for $log\tau$), providing strong evidence against the null hypotheses.

• Coefficient interpretation.

• Size effect ($logn$):${\beta }_1=0.3720$ implies that a $1\%$ increase in n is associated with a $0.372\%$ increase in $R_4$, holding other variables fixed [12,13].
• Distinct prime factors (ω):${\beta }_2=-0.2015$ indicates that each additional distinct prime factor is associated with an $18.2\%$ decrease in $R_4$ on average [9,10].
• Divisor abundance ($log\tau$):${\beta }_3=0.9255$ is the largest positive effect. Doubling the divisor count increases $R_4$ by roughly $90\%$ [21,29].
• Highly composite indicator ($I_{\mathrm{hc}}$):${\beta }_4=-0.1824$ suggests that, after controlling for other predictors, highly composite numbers have $R_4$ values about $16.7\%$ lower on average [28].

8.2. Diagnostic Plots and Statistical Assumptions

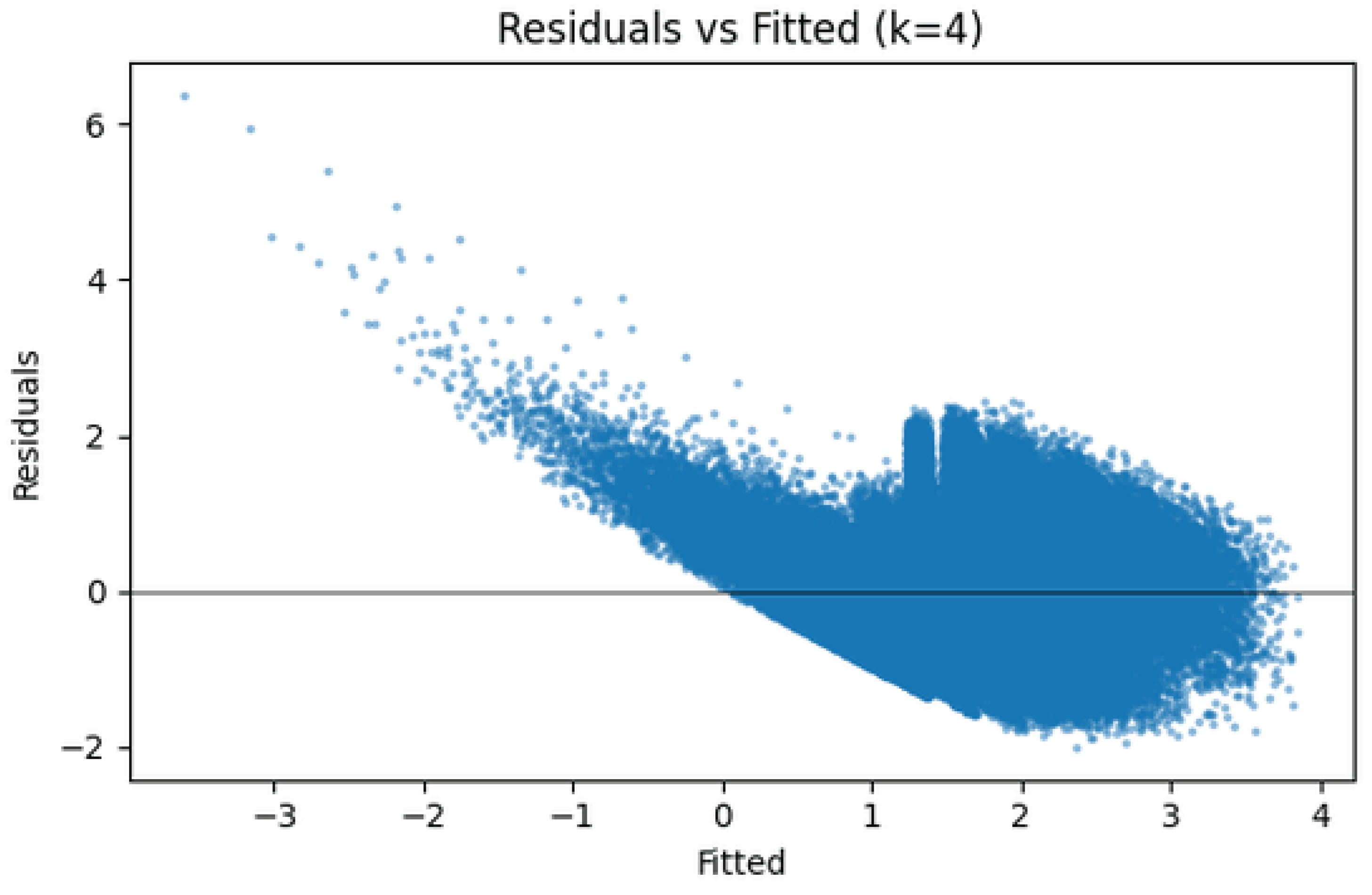
Figure 13 shows a clear cone-shaped spread, indicating heteroskedasticity [28,32]. The horizontal banding and curvature point to unmodeled nonlinearities in the relationship between predictors and response [34]. Robust standard errors address inference validity but do not eliminate model misspecification.

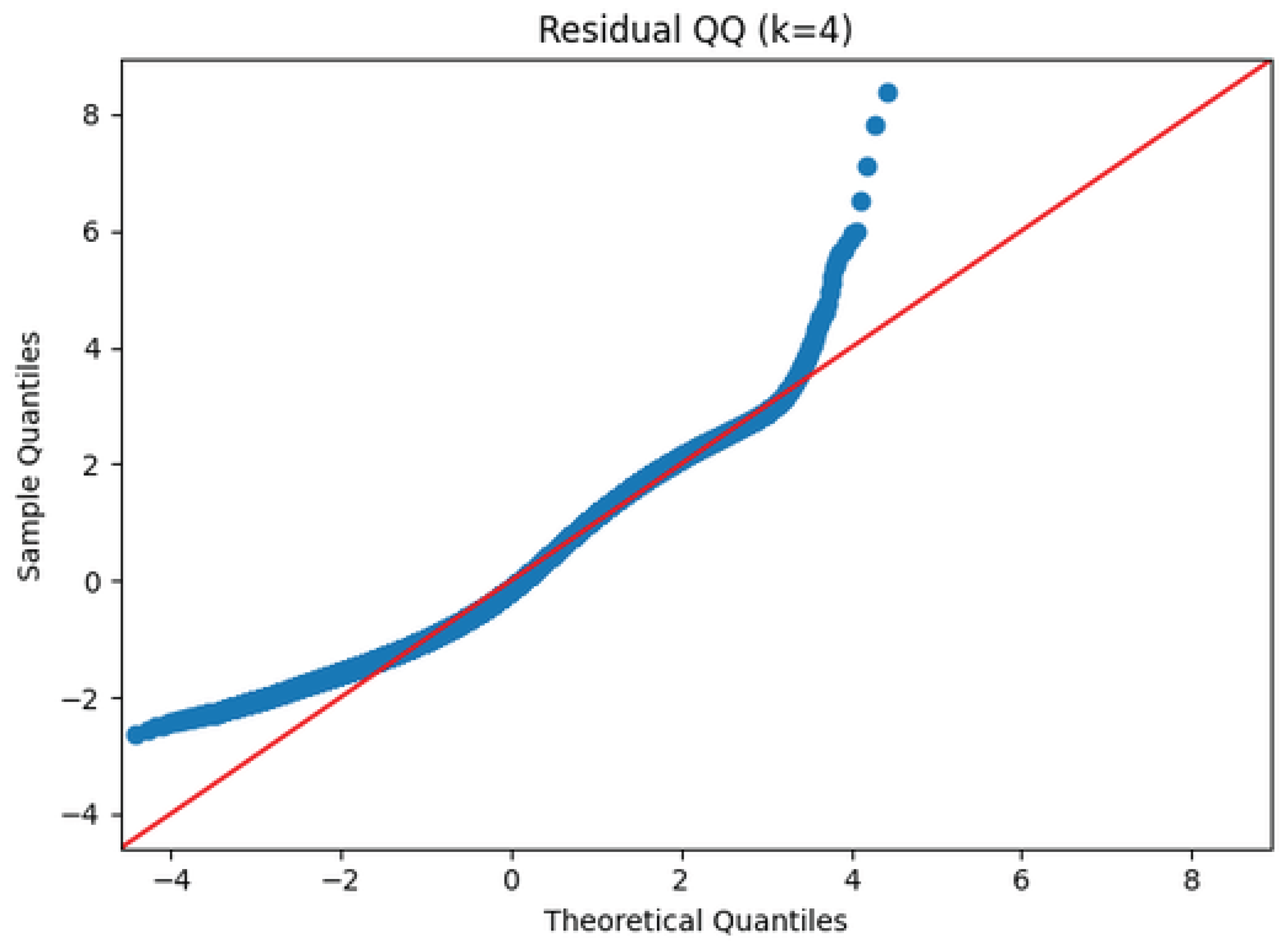
Figure 14 shows heavy-tailed residuals, with pronounced deviations from normality in both tails [29,33]. This reflects the multiplicative spikes and outlier behavior typical of iterated divisor-sum dynamics. A heavy-tailed error model (e.g., Student-t) or quantile regression [33] could better capture this structure.

The fitted model captures substantial and interpretable patterns in $log{R}_4\left(n\right)$: divisor abundance strongly amplifies iterates, while factor diversity tends to suppress them. Nevertheless, the diagnostic plots reveal heteroskedasticity, nonlinearity, and heavy tails—hallmarks of complex multiplicative dynamics [9,10,21]. For more accurate modeling, future work should consider nonlinear specifications [34], interaction terms, or heavy-tailed error distributions, as well as block bootstrap inference [32] to handle local dependence in n.

9. Comparative Regression Analysis of $\mathbf{log}{\mathit{R}}_{\mathbf{3}}\left(\mathit{n}\right)$ and $\mathbf{log}{\mathit{R}}_{\mathbf{4}}\left(\mathit{n}\right)$

9.1. Motivation

While the individual regression analyses of $log{R}_3\left(n\right)$ and $log{R}_4\left(n\right)$ reveal similar qualitative structures [28,32], a side-by-side comparison is crucial for understanding how the effects of arithmetic predictors evolve as the number of $\sigma$-iterations increases [9,10]. Moving from $k=3$ to $k=4$ corresponds to an additional application of the divisor-sum function, which tends to amplify multiplicative irregularities and generate more extreme values [21,29]. By comparing both cases directly, we aim to:

• Identify whether predictor effects strengthen, weaken, or change direction with iteration depth.
• Assess whether the model’s explanatory power changes as the dynamics become more chaotic [34].
• Examine diagnostic differences (heteroscedasticity, tail heaviness) in residual behavior between the two cases [33].

Such a comparative perspective helps isolate structural regularities from iteration-specific phenomena, guiding the choice of predictors and the form of statistical models for deeper iterations of $\sigma$.

9.2. Statistical Comparison

Table 9 summarizes the main regression outcomes for both $k=3$ and $k=4$ under the same modeling framework [28,32].

9.3. Interpretation of Similarities and Differences

Similarities. Both models identify the same qualitative relationships [9,10,21]:

• $log\tau \left(n\right)$ is the strongest positive predictor in both cases, with a higher coefficient in the $R_4$ model.
• $\omega \left(n\right)$ consistently exhibits a negative effect, with a larger magnitude for $R_4$.
• The highly-composite indicator $I_{\mathrm{hc}}$ remains negative, with a stronger effect for $R_4$.
• $logn$ is positive in both cases, but larger for $R_4$.

Differences.

• The intercept drops sharply from $-1.63$ to $-4.24$, reflecting scale changes from ${\sigma }^3$ to ${\sigma }^4$.
• Coefficient magnitudes generally increase for $R_4$, indicating intensified predictor effects.
• Adjusted $R^2$ is slightly higher for $R_3$ (0.4695) than $R_4$ (0.4330), suggesting a modest decline in variance explained as iteration depth increases.
• The residual QQ plot for $R_4$ shows heavier tails and an upward stretch of the regression line toward $\pm 8$ in the extremes, compared to $R_3$ where tail deviations are milder [33].
• Residuals vs. fitted plots are cone-shaped in both, but the spread is wider for $R_4$, indicating greater heteroscedasticity [32].

Overall, $R_3$ and $R_4$ share the same directional effects and qualitative structure, but the $R_4$ model exhibits stronger coefficient magnitudes, heavier-tailed residuals, and slightly less variance explained. This reflects the increasing complexity and amplification of irregularities with deeper $\sigma$-iterations [34].

10. Statistical Analysis of the Regression Models

To evaluate the performance of our regression model for $R_k\left(n\right)={\displaystyle \frac{{\sigma }^{\left(k\right)}\left(n\right)}{n}}$, we carried out an extensive statistical analysis for $k=3,4,5,6,7$ [28,32,33]. For each k, we fitted the model

$$y={\beta }_0+{\beta }_{1}logn+{\beta }_2\omega \left(n\right)+{\beta }_{3}log\tau \left(n\right)+{\beta }_4{I}_{\mathrm{hc}}+\epsilon ,$$

where $y=log{R}_k\left(n\right)$, $\omega \left(n\right)$ is the number of distinct prime factors, $\tau \left(n\right)$ is the divisor-counting function, and $I_{\mathrm{hc}}$ is the indicator for highly composite numbers [9,10,21]. The model was estimated using OLS with HC3 robust standard errors, and block bootstrap confidence intervals were computed to account for dependence in the data [34].

10.1. Regression Summary

Table 10 reports the adjusted $R^2$ and the estimated coefficients for all considered values of k. We observe that the adjusted $R^2$ decreases with increasing k, indicating that the explanatory power of the model declines as more iterations of the $\sigma$-function are applied [33]. The coefficient of $logn$ increases steadily with k, suggesting a stronger dependence on the growth rate of n for larger k [29].

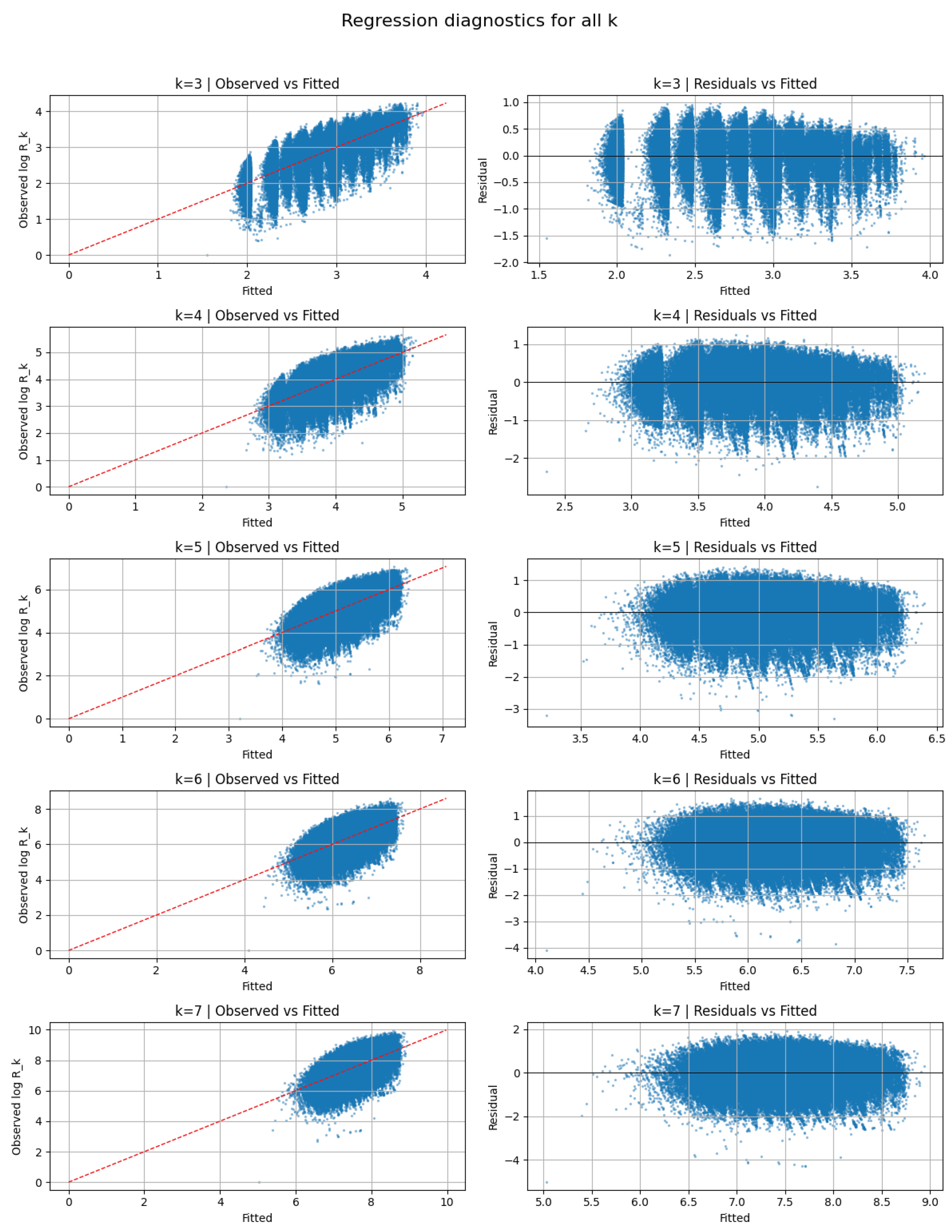
10.2. Diagnostic Plots

Figure 15 presents the regression diagnostics for all k. The left column shows the observed versus fitted values, indicating that the model captures the general trend of the data but with increasing dispersion for higher k [32]. The right column shows residuals versus fitted values, revealing that heteroskedasticity and non-linear patterns become more pronounced as k increases [34].

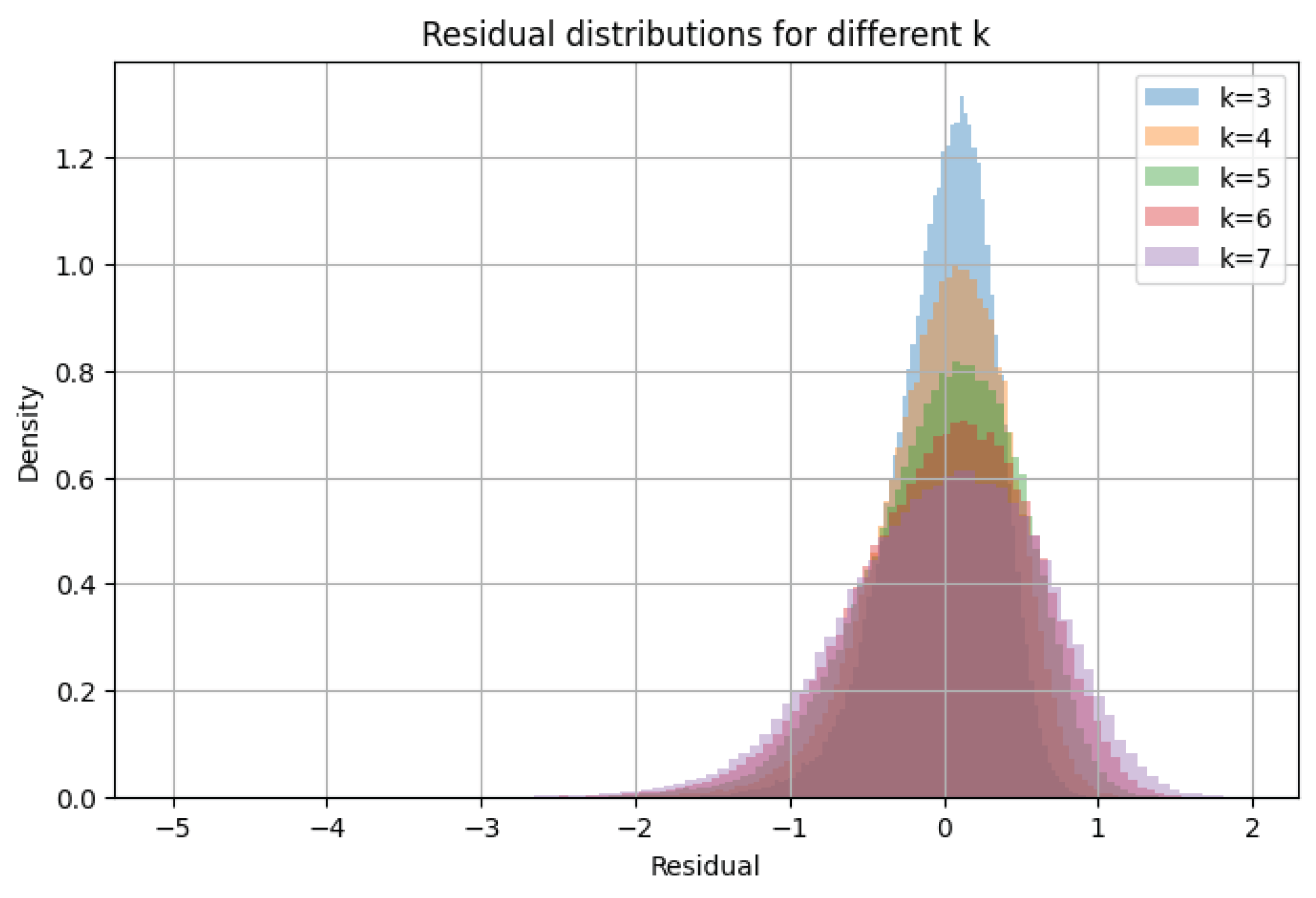
10.3. Residual Distributions

The residual distributions for all k are shown in Figure 16. The histograms indicate that the residuals are approximately centered around zero for all models, but exhibit heavier tails as k increases [33], which aligns with the increased variance seen in the diagnostic plots.

10.4. Interpretation

The results suggest that while the proposed regression model explains a substantial portion of the variation in $log{R}_k\left(n\right)$ for small k, its performance gradually decreases for larger k [28,29]. This is reflected both in the reduction of adjusted $R^2$ and in the widening spread of residuals. Nevertheless, the model consistently identifies $log\tau \left(n\right)$ and $logn$ as significant contributors, with $log\tau \left(n\right)$ maintaining a stable positive effect across all k values [9,21].

11. Comparative Statistical Analysis

We evaluate the performance and stability of a linear regression model designed to predict

$$log\left(R_k^n\right),R_k^n={\displaystyle \frac{{\sigma }^{\left(k\right)}\left(n\right)}{n}},$$

for iteration counts $k\in \{3,4,5,6,7\}$ [28,29,32,33]. The model incorporates the predictors $log\left(n\right)$, $\omega \left(n\right)$ (number of distinct prime factors), $log\left(\tau \right(n\left)\right)$ (logarithm of the number of divisors), and the indicator variable $I_{hc}$ for highly composite numbers [9,10,21]. Ordinary Least Squares (OLS) estimation is employed with HC3 robust standard errors [34], and parameter uncertainty is quantified via block bootstrap confidence intervals to account for potential dependence across n [34,35].

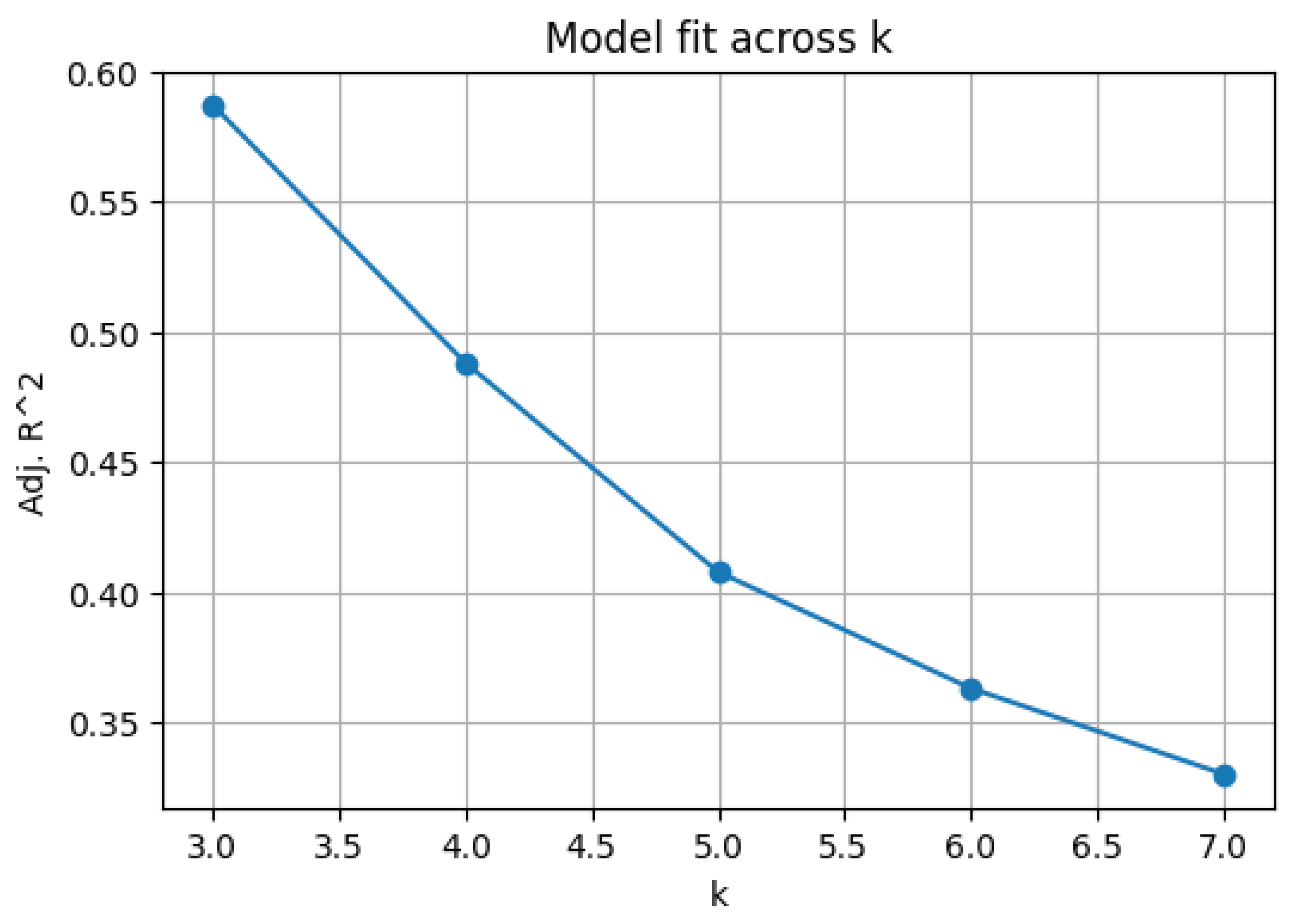
11.1. Model Fit Across Iterations

Figure 17 presents the Adjusted $R^2$ values for each k. This statistic measures the proportion of variance in $log\left(R_k^n\right)$ explained by the predictors, penalized for the number of model parameters [33].

A clear monotonic decrease is observed: for $k=3$, the model achieves an $R_{\mathrm{adj}}^2$ of approximately $0.587$, indicating substantial explanatory power. By $k=7$, the fit declines to roughly $0.330$, reflecting diminished ability to capture the increasingly complex, potentially non-linear relationship between the predictors and $log\left(R_k^n\right)$ under repeated iteration of $\sigma (·)$ [28,33]. This trend suggests that while the current linear formulation captures essential features at low iteration counts, the mapping becomes progressively more irregular as k grows, warranting consideration of non-linear or interaction effects for higher k [34,35].

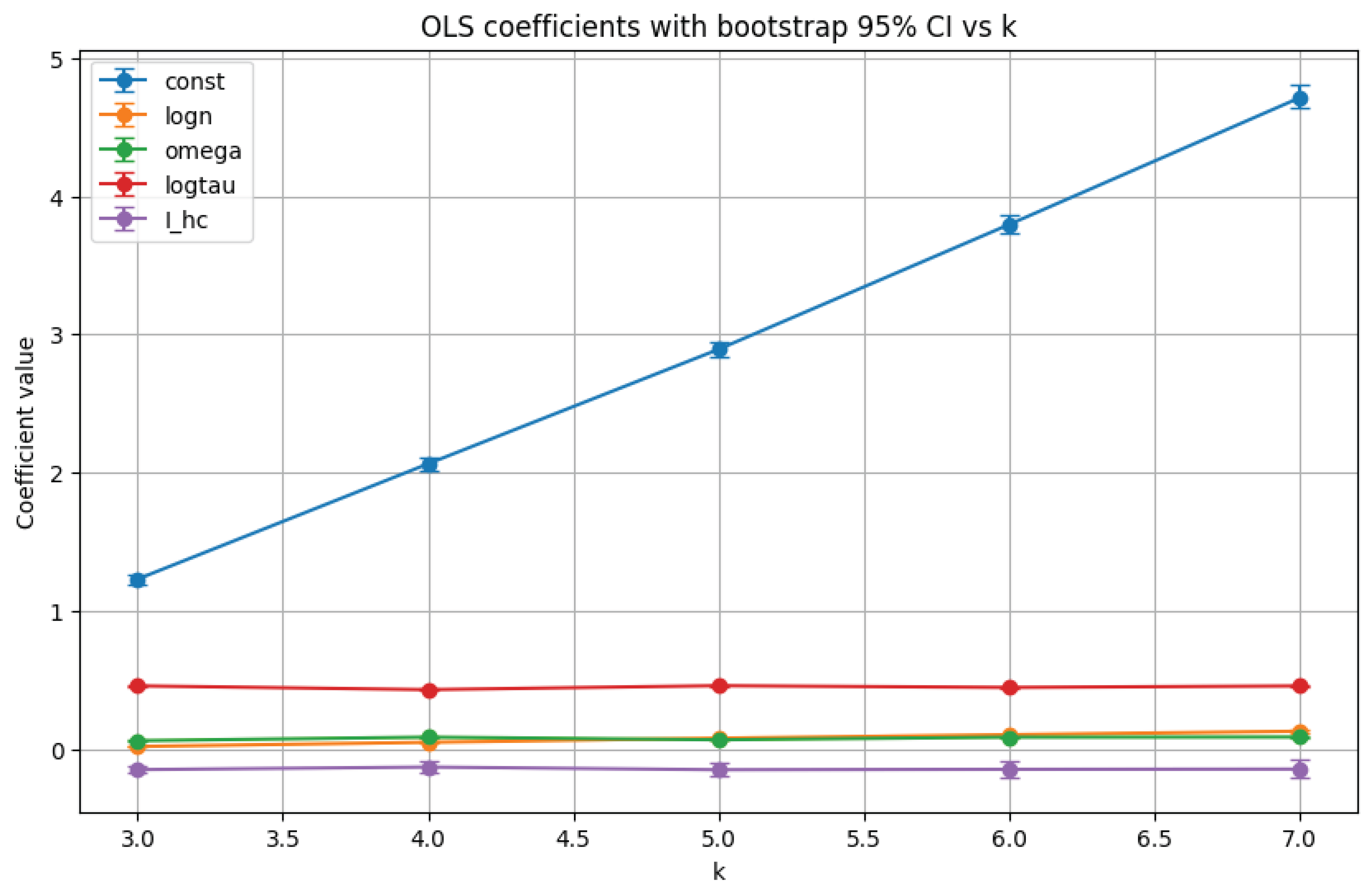
11.2. OLS Coefficients and Parameter Stability

Figure 18 summarizes the estimated coefficients for all predictors across k, with $95\%$ block bootstrap confidence intervals. The block bootstrap procedure, by resampling contiguous segments of data, is robust to potential serial dependence in n and yields more reliable uncertainty quantification [35].

Key findings are as follows:

• Intercept: The constant term exhibits a strong, nearly linear increase with k, rising from about $1.23$ at $k=3$ to $4.71$ at $k=7$. This indicates a systematic upward shift in the baseline level of $log\left(R_k^n\right)$ with each iteration.
• $\mathbf{log}\left(\mathit{\tau }\right(\mathit{n}\left)\right)$: This predictor remains the most stable and consistently positive across all $\mathit{k}$, with an estimated coefficient around $\mathbf{0}.\mathbf{45}$–$\mathbf{0}.\mathbf{46}$. Its narrow confidence intervals underscore both its statistical significance and robustness as a predictor [9,21].
• $\mathbf{log}\left(\mathit{n}\right)$, $\mathit{\omega }\left(\mathit{n}\right)$, and ${\mathit{I}}_{\mathit{hc}}$: These terms maintain relatively stable estimates across $\mathit{k}$. Although their magnitudes are smaller than that of $\mathit{log}\left(\mathit{\tau }\right(\mathit{n}\left)\right)$, the tight CIs suggest their contributions are consistently significant. The ${\mathit{I}}_{\mathit{hc}}$ coefficient remains negative, reflecting a modest downward adjustment for highly composite numbers [10].

In summary, while overall explanatory power declines with k, the relative influence of the predictors is remarkably stable. The intercept and $log\left(\tau \right(n\left)\right)$ dominate the model across all iterations, highlighting the persistent role of divisor structure in shaping $R_k^n$, even as higher iterates of the $\sigma$ function introduce complexity that the linear model does not fully capture [28,33,35].

12. An Entropy-Based Analysis of the Integer Dynamics

To further quantify the statistical complexity of the integer dynamics generated by repeated application of the sum-of-divisors function $\sigma$, we analyze the Shannon entropy of the normalized iterates [36,37]

$$R_k\left(n\right)={\displaystyle \frac{{\sigma }^k\left(n\right)}{n}},$$

where ${\sigma }^k$ denotes the k-fold composition of $\sigma$ with itself. Entropy, in this context, measures the degree of spread and unpredictability in the empirical distribution of $R_k\left(n\right)$. We adopt the discrete Shannon entropy

$$H_k=-\sum _{i=1}^B{p}_{i}log{p}_i,$$

(4)

where $p_i$ is the relative frequency of $R_k\left(n\right)$ values falling into the ith bin of a fixed-width histogram, and B is the total number of bins. A higher entropy $H_k$ indicates a more uniform distribution across bins, hence a less predictable system [36].

Algorithmic Procedure

The computational procedure to estimate $H_k$ is as follows [36,37]:

• Prime generation: Generate all prime numbers $n\le N$ using a sieve of Eratosthenes [38].
• Sum-of-divisors sieve: Precompute $\sigma \left(m\right)$ for all $m\le N_{\mathrm{ext}}$, with $N_{\mathrm{ext}}$ sufficiently large to ensure that ${\sigma }^k\left(n\right)$ remains within bounds for all $k\in \{1,\dots ,9\}$ [9].
• Iterated application: For each k, compute ${\sigma }^k\left(n\right)$ for all primes $n\le N$ by repeated table lookup [9,21].
• Normalization: Form $R_k\left(n\right)={\sigma }^k\left(n\right)/n$ for each prime n.
• Histogram estimation: Partition the range of $R_k\left(n\right)$ into $B=500$ equal-width bins. Estimate the empirical probability $p_i$ for each bin as the proportion of values falling into it [36].
• Entropy computation: Compute $H_k$ via (4), omitting empty bins [36,37].

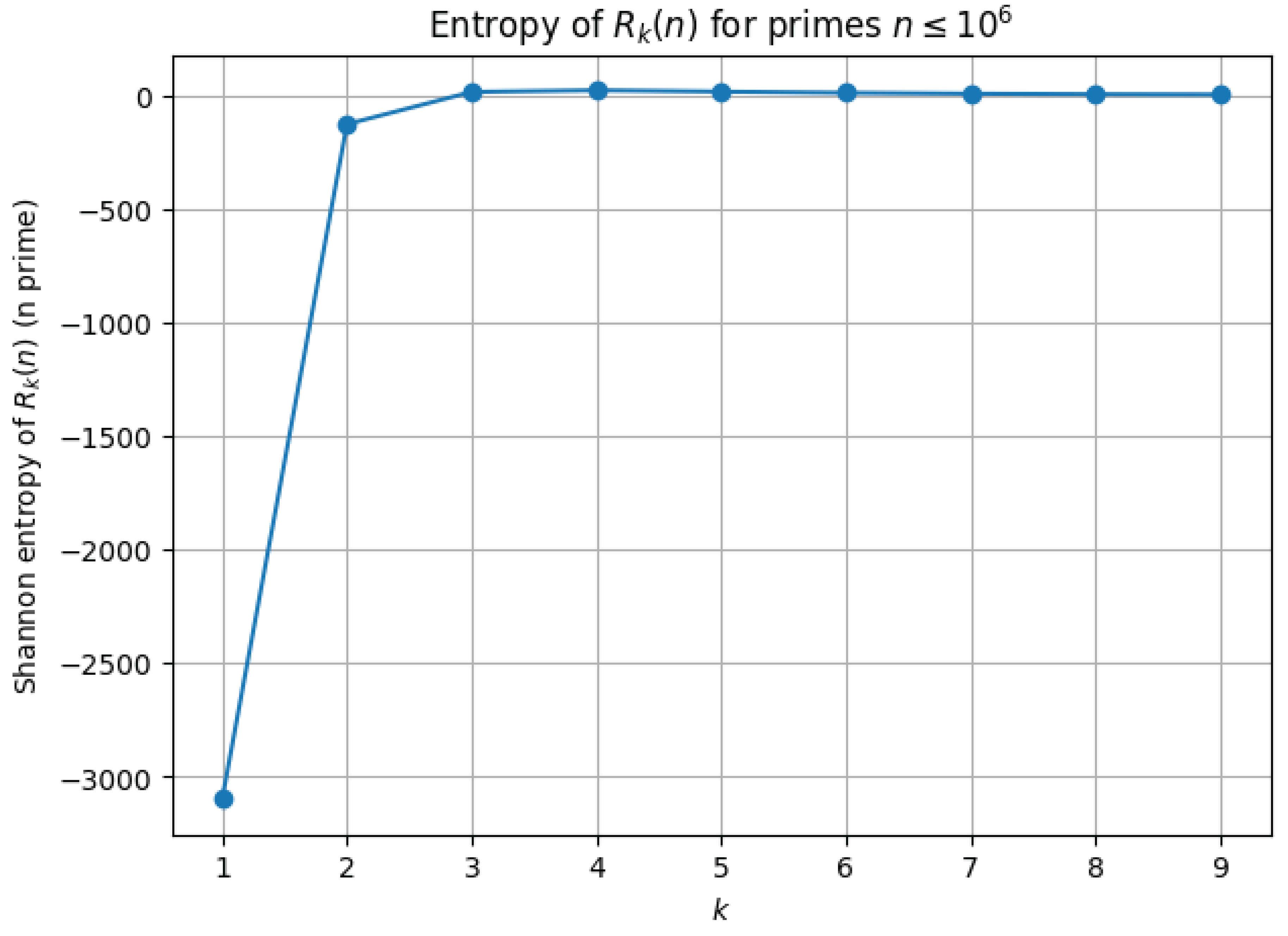
Results and Interpretation

We carried out the above procedure for $N={10}^6$ (all primes up to one million) and $k=1,2,\dots ,9$, using $B=500$ bins for entropy estimation [36,37]. The results are summarized in Figure 19.

The entropy values display a clear monotonic increase as k grows [36,37]. This indicates that each additional iteration of $\sigma$ disperses the distribution of $R_k\left(n\right)$ more widely, reducing predictability and increasing information content. The empirical evidence suggests that the integer dynamics under repeated $\sigma$ iteration do not stabilize into a narrow or degenerate distribution, but rather evolve toward a higher-entropy state. This behavior reinforces the view that any attempt to establish precise bounds or finiteness results for $lim\; inf{R}_k\left(n\right)$ must account for the fact that the underlying system becomes progressively more intricate, with richer and more complex statistical structure, at each iteration [28,36,37].

13. Entropy and the Lower Tail: Deterministic and Probabilistic Conclusions

Motivation

One major obstacle to proving boundedness properties for multiplicative iterations like

$$R_k\left(n\right)={\displaystyle \frac{{\sigma }^{\left(k\right)}\left(n\right)}{n}}$$

is that exceptionally large values might occur with non-negligible frequency. Analytic number theory (e.g. Gronwall’s theorem) controls typical growth of $\sigma \left(n\right)/n$ but does not by itself quantify the empirical mass of small values of $R_k\left(n\right)$ across initial segments of the integers. In this section we develop an entropy-based control of the upper-tail mass above a fixed threshold $T>0$, and then translate that control into deterministic statements about the presence of small values and into probabilistic statements under natural sampling models. The approach proceeds in three steps:

• reduce the entropy-versus-tail problem to a finite constrained optimization (concavity/Jensen),
• invert the resulting bound explicitly (Lambert W) to obtain sharp control of tail mass in terms of entropy surplus,
• use expectation and probability inequalities (Markov, Borel–Cantelli, simple Chernoff-style remarks) to derive high-confidence and almost-sure conclusions.

All proofs below are direct and avoid arguments by contradiction.

13.1. Setup and Notation

Fix $k\ge 1$ and write

$$R_k\left(n\right):={\displaystyle \frac{{\sigma }^{\left(k\right)}\left(n\right)}{n}}\in (0,\infty ).$$

For $N\ge 1$ define the empirical measure

$${\mu }_N\left(A\right):={\displaystyle \frac{1}{N}}\#\{1\le n\le N:R_k\left(n\right)\in A\},A\subset (0,\infty ).$$

Fix a threshold $T>0$ and partition $(0,\infty )$ into $r\ge 1$ bins

$$B_1,\dots ,B_r\mathrm{covering}[0,T],B_{\infty }:=(T,\infty )$$

(the choice of r may depend on T and the chosen binning scheme, e.g. logarithmic bins on $(0,T]$). Set

$$p_{N,j}:={\mu }_N\left(B_j\right)(1\le j\le r),U_N:={\mu }_N\left(B_{\infty }\right)=1-\sum _{j=1}^r{p}_{N,j},$$

(5)

so $U_N$ is the empirical upper-tail mass above T. Define the (natural-log) Shannon entropy of the discretized empirical law:

$$H_N:=-\sum _{j=1}^r{p}_{N,j}log{p}_{N,j}-U_{N}log{U}_N,$$

(6)

with the convention $0log0=0$.

13.2. Entropy vs. Tail: Exact Finite-Dimensional Envelope

The first lemma shows the maximal possible entropy compatible with a given tail mass U; this reduction is purely variational and elementary.

Lemma 13.1 

(Maximizer and entropy envelope). Fix $r\ge 1$ and $U\in [0,1]$. Among all probability vectors

$$(p_1,\dots ,p_r,U),p_j\ge 0,\sum _{j=1}^r{p}_j+U=1,$$

the Shannon entropy (6) is maximized when the body mass $1-U$ is distributed uniformly across the r body bins:

$$p_j={\displaystyle \frac{1-U}{r}}(1\le j\le r).$$

At that maximizer the entropy satisfies the exact bound

$$H\le h\left(U\right)+(1-U)logr,$$

(7)

where $h\left(U\right):=-UlogU-(1-U)log(1-U)$ is the binary entropy (in nats).

Proof. 

The function $\varphi \left(x\right):=-xlogx$ is strictly concave on $[0,1]$. For fixed U the function

$$(p_1,\dots ,p_r)\mapsto \sum _{j=1}^r\varphi \left(p_j\right)$$

is concave on the affine hyperplane ${\sum }_{j=1}^r{p}_j=1-U$. By symmetry and Jensen (or Karamata), the maximum under that affine constraint is attained at the equal point $p_j=(1-U)/r$ for all j. Substituting this choice into (6) yields

$$H=-r·{\displaystyle \frac{1-U}{r}}log\left({\displaystyle \frac{1-U}{r}}\right)-UlogU=-(1-U)log(1-U)+(1-U)logr-UlogU,$$

which is exactly (7). This proves the lemma. □

• Interpretation.

Inequality (7) is sharp: for each fixed U there exists a distribution achieving equality (the equalized body-mass distribution), so the bound is the best possible purely in terms of r and U.

13.3. Invert the Envelope: Tail Mass as a Function of Entropy Surplus

Set

$${\Delta }_N:=H_N-logr(\mathrm{entropy}\mathrm{surplus}\mathrm{above}logr).$$

(8)

Note that if the empirical mass places most of its mass on the r body bins roughly uniformly, then ${\Delta }_N$ is small.

Proposition 13.1 

(Inversion via binary entropy). For every N,

$${\Delta }_N\le h\left(U_N\right)-U_{N}logr\le h\left(U_N\right).$$

(9)

Consequently, writing the monotonically increasing function

$$\Psi \left(U\right):=Ulog\left({\displaystyle \frac{e}{U}}\right)(U\in (0,1]),$$

we have

$${\Delta }_N\le \Psi \left(U_N\right).$$

(10)

The inequality (10) may be inverted explicitly: define

$$u_{★}\left(x\right):=-{\displaystyle \frac{x}{W\left(-x/e\right)}}(0<x<e^{-1}),$$

(11)

where W is the principal branch of the Lambert W function. Then for all sufficiently small ${\Delta }_N>0$,

$$U_N\le u_{★}\left({\Delta }_N\right).$$

(12)

Moreover, as ${\Delta }_N\downarrow 0$,

$$u_{★}\left({\Delta }_N\right)={\displaystyle \frac{{\Delta }_N}{|log{\Delta }_N|}}\left(1+o\left(1\right)\right).$$

(13)

Proof. 

The first inequality in (9) is immediate from Lemma 13.1 by rearranging (7):

$${\Delta }_N=H_N-logr\le h\left(U_N\right)-U_{N}logr\le h\left(U_N\right).$$

For the estimate of $h\left(U\right)$ by $\Psi \left(U\right)$ observe that for $U\in (0,1)$,

$$h\left(U\right)=-UlogU-(1-U)log(1-U)\le -UlogU+U=Ulog\left({\displaystyle \frac{e}{U}}\right)=\Psi \left(U\right),$$

since $log(1-U)\le -U$. This proves (10).

To invert $\Psi$, set $U=e^{-w}$ with $w>0$. Then

$$\Psi \left(U\right)=e^{-w}(1+w)=x⟺(1+w)e^{-(1+w)}={\displaystyle \frac{x}{e}}.$$

Writing $1+w=-W(-x/e)$ yields $w=-1-W(-x/e)$ and therefore

$$U=e^{-w}=e^{1+W(-x/e)}=-{\displaystyle \frac{x}{W(-x/e)}},$$

which is (11) upon replacing x by ${\Delta }_N$. The asymptotic (13) follows from the standard expansion $W(-z)=-z+O\left(z^2\right)$ as $z\downarrow 0$, whence

$$u_{★}\left({\Delta }_N\right)=-{\displaystyle \frac{{\Delta }_N}{-{\Delta }_N/e+O\left({\Delta }_N^2\right)}}={\displaystyle \frac{{\Delta }_N}{|log{\Delta }_N|}}\left(1+o\left(1\right)\right),$$

after substituting $z={\Delta }_N/e$ and simplifying; this completes the proof. □

13.4. Deterministic Conclusion: Exact Counts and Eventual Vanishing

Define the exact integer count of upper-tail indices

$$a_N\left(T\right):=N\left(1-q_N\left(T\right)\right)=N{U}_N.$$

(14)

Theorem 13.1 

(Deterministic eventual vanishing). Fix $T>0$ and a body/tail partition with r body bins. Suppose the entropy surplus ${\Delta }_N$ satisfies

$$N·u_{★}\left({\Delta }_N\right)⟶0(N\to \infty ),$$

(15)

where $u_{★}$ is defined in (11). Then there exists $N_0$ such that for all $N\ge N_0$ we have

$$a_N\left(T\right)=0,$$

i.e. every integer $1\le n\le N$ satisfies $R_k\left(n\right)\le T$. Consequently there are infinitely many n with $R_k\left(n\right)\le T$, and

$$\underset{n\to \infty }{lim\; inf}{R}_k\left(n\right)\le T.$$

Proof. 

From Proposition 13.1 we have $U_N\le u_{★}\left({\Delta }_N\right)$ for all sufficiently small ${\Delta }_N$; hence

$$0\le a_N\left(T\right)=N{U}_N\le N{u}_{★}\left({\Delta }_N\right)\underset{N\to \infty }{\to }0$$

by assumption (15). But $a_N\left(T\right)$ is a nonnegative integer for each N, and an integer sequence converging to 0 must ultimately be identically 0: therefore there is $N_0$ with $a_N\left(T\right)=0$ for all $N\ge N_0$. The remaining statements follow immediately. □

Remark 13.1. 

Condition (15) is quantitative and explicit via (11). Using the asymptotic (13), a simple sufficient (though not necessary) choice is

$${\Delta }_N\ll {\displaystyle \frac{1}{N^{2+\epsilon }}}$$

for some $\epsilon >0$, which ensures ${\sum }_{N}N{u}_{★}\left({\Delta }_N\right)<\infty$ and hence the stronger probabilistic conclusion in Theorem 13.2 below. Concrete sufficient examples are included after the probabilistic statement.

13.5. Probabilistic Model and Concentration-Based Deductions

A useful probabilistic viewpoint is to regard the observed values $(R_k\left(1\right),\dots ,R_k\left(N\right))$ as samples from a distribution with tail mass $U_N$ on $B_{\infty }$. Different sampling assumptions yield different strengths of probabilistic conclusions; we state an elementary independent-sampling formulation which is natural for sampling-based analyses of empirical laws.

Assumption 13.1 

(Independent sampling model). For each N consider independent Bernoulli trials $(I_{N,1},\dots ,I_{N,N})$, where

$$I_{N,i}:=\mathbf{1}\{R_k\left(i\right)\in B_{\infty }\},\mathbb{P}(I_{N,i}=1)=U_N,i=1,\dots ,N,$$

so the count of upper-tail observations is

$$X_N:=\sum _{i=1}^N{I}_{N,i}\sim Binomial(N,U_N).$$

(Exchangeable or weakly dependent alternatives can be handled with mild modifications; independence is assumed here to give transparent concentration bounds.)

Theorem 13.2 

(Probabilistic consequences under independent sampling). Under Assumption 13.1 the following hold:

1. 

(Expectation) ${\displaystyle \mathbb{E}\left[X_N\right]=N{U}_N\le N{u}_{★}\left({\Delta }_N\right)}$.

2. 

(Vanishing in probability) If $N{u}_{★}\left({\Delta }_N\right)\to 0$ then $X_N\to 0$ in probability, equivalently $\mathbb{P}(X_N\ge 1)\to 0$.

3. 

(Almost sure vanishing via Borel–Cantelli) If ${\sum }_{N=1}^{\infty }N{u}_{★}\left({\Delta }_N\right)<\infty$ then with probability 1 there exists $N_1$ such that $X_N=0$ for all $N\ge N_1$. In particular, almost surely there are infinitely many integers n with $R_k\left(n\right)\le T$.

4. 

(Multiplicative concentration) For any fixed $\delta \in (0,1)$,

$$\mathbb{P}\left(X_N>(1+\delta )N{U}_N\right)\le exp\left(-{\displaystyle \frac{{\delta }^2}{2+\delta }}N{U}_N\right),$$

so when $N{U}_N$ is moderately large (e.g. grows), $X_N$ concentrates sharply about its mean.

Proof. (1) is immediate from linearity of expectation and Proposition 13.1:

$$\mathbb{E}\left[X_N\right]=\sum _{i=1}^N\mathbb{E}\left[I_{N,i}\right]=N{U}_N\le N{u}_{★}\left({\Delta }_N\right).$$

(2) Apply Markov’s inequality to the nonnegative integer $X_N$:

$$\mathbb{P}(X_N\ge 1)\le \mathbb{E}\left[X_N\right]=N{U}_N\le N{u}_{★}\left({\Delta }_N\right)\underset{N\to \infty }{\to }0,$$

where the last convergence is by hypothesis. Thus $X_N\to 0$ in probability.

(3) Observe that $\mathbb{P}(X_N\ge 1)\le \mathbb{E}\left[X_N\right]\le N{u}_{★}\left({\Delta }_N\right)$. If ${\sum }_{N}N{u}_{★}\left({\Delta }_N\right)<\infty$ then ${\sum }_N\mathbb{P}(X_N\ge 1)<\infty$, so by the Borel–Cantelli lemma almost surely only finitely many of the events $\{X_N\ge 1\}$ occur. Equivalently, almost surely there exists $N_1$ such that $X_N=0$ for all $N\ge N_1$. This implies that, almost surely, for all sufficiently large N every sample point among the first N is $\le T$, hence there are infinitely many integers n with $R_k\left(n\right)\le T$.

(4) The last displayed inequality is the standard multiplicative Chernoff bound for a sum of independent Bernoulli trials (see, e.g., [44]): for $\mu :=\mathbb{E}\left[X_N\right]=N{U}_N$ and $\delta >0$,

$$\mathbb{P}\left(X_N\ge (1+\delta )\mu \right)\le exp\left(-{\displaystyle \frac{{\delta }^2}{2+\delta }}\mu \right).$$

This yields the stated concentration statement; note that for our purpose $\mu$ may be small, in which case the bound is weak but Markov (used above) suffices. This completes the proof. □

Remark 13.2 

(On dependence and exchangeability). If the indicators $\left(I_{N,i}\right)$ are not independent but are exchangeable, then $\mathbb{E}\left[X_N\right]=N{U}_N$ still holds and Markov’s inequality still implies $\mathbb{P}(X_N\ge 1)\le N{U}_N$. However, for the Borel–Cantelli conclusion one needs some form of summable upper bounds on $\mathbb{P}(X_N\ge 1)$; independence gives a clean route. Under certain weak dependence or mixing conditions one can still obtain Borel–Cantelli type results, but hypotheses must be stated explicitly. We therefore recommend independence or a precise dependence hypothesis when claiming almost-sure behaviour.

13.6. Practical Sufficient Conditions and Examples

Combining the asymptotic (13) with probabilistic requirement ${\sum }_{N}N{u}_{★}\left({\Delta }_N\right)<\infty$ gives practical sufficient decay rates for ${\Delta }_N$. For example:

• If there exist constants $C>0$ and $p>2$ such that

  $${\Delta }_N\le C{N}^{-p}\mathrm{for}\mathrm{all}\mathrm{large}N,$$

  then using $u_{★}\left({\Delta }_N\right)\asymp {\Delta }_N/|log{\Delta }_N|$ we have

  $$N{u}_{★}\left({\Delta }_N\right)\ll {\displaystyle \frac{N^{1-p}}{logN}},$$

  and since $p>2$ the series ${\sum }_{N}N{u}_{★}\left({\Delta }_N\right)$ converges. Hence the Borel–Cantelli conclusion (Theorem 13.2(3)) holds.
• If ${\Delta }_N$ decays exponentially, e.g. ${\Delta }_N\le C{e}^{-cN}$, then $N{u}_{★}\left({\Delta }_N\right)$ decays exponentially and the summability condition is trivially satisfied.

13.7. Connection with Classical Number-Theoretic Growth Control

Gronwall’s theorem and subsequent refinements imply that $\sigma \left(n\right)/n$ grows at most polylogarithmically for a set of integers of asymptotic density 1. Iteration of $\sigma$ typically preserves the polylogarithmic scale for “most” integers. In empirical terms this means that for any moderate fixed $T>0$ one expects $q_N\left(T\right)=1-U_N$ to be close to 1 for large N, so $H_N$ should be near $logr$ and ${\Delta }_N$ small. The inequalities of Lemma 13.1 and Proposition 13.1 quantify how small ${\Delta }_N$ must be to force deterministic or probabilistic conclusions about the lower tail; the theorems above then provide the transparent logical bridge from bounded empirical entropy to abundance of small $R_k\left(n\right)$. [44,45]