Application of Machine Learning Algorithm to Assess and Minimize Credit Risks

1. Introduction

Historically, a proper credit risk management plays a key role in the normal functioning of the economy and in the prevention of financial crises. Thus, for example, the global financial crisis of 2008 indicated how important it is to precisely manage the credit risk (Siddique et al., 2022). The Basel Committee on Banking Supervision also emphasizes the active and coordinated management of such type of risk, which contributes to the stability of the banking system (Curcio & Hasan, 2015).

At the time of lending credit organizations often apply various developed models in order to assess the credit risk of an individual, for example, FICO Scoring model (Addo et al., 2018). FICO credit scoring solutions provide a better understanding of credit risk in lending to consumers and businesses. The introduction of broad-based credit scores by FICO more than 30 years ago has transformed economic growth in the US and globally - making access to credit more efficient and objective while protecting the financial stability of lenders by enabling decisions that limit risk (Klein & Thompson, 2021).

This model and its analogues are “black box” and credit organizations often can not clearly understand the reason for the formation of this or that score point, as well as those models are often built based on data of borrowers from only few countries and in essence do not describe the social-economic situation of the operation region of a credit organization. For the same reasons for the accurate evaluation and credit risk management credit organizations often collect the information on their borrowers and the quality of provided loans themselves and based on all that data they build models (Addo et al., 2018). Historically, logistic regression model is used often in order to solve such problems. Though, recently it is noticed that modern ML models are also often used in order to solve this problem, for example, XGBoost, LightGBM, Neural Network etc. (Zhang et al., 2020).

The aim of this research work is to investigate the behavoiur of borrowers based on real data, applying the ideas of known ML models to develop new algorithms for solving binary classification problems. The aim is also to develop local score system of the given bank based on the data of the borrowers available to us by using new algorithms.

The results of achieving the goal of this research can be used by credit organizations, which will contribute to the optimal credit risk management and to the cost reduction in the given organizations.

2. Literature Review

Within the framework of this research many scientific works of others have been studied. We shall consider some of them.

In the article named “Advancing credit risk modelling with Machine Learning: A comprehensive review of the state-of-the-art” the authors studied the granting of the loans as the most important part of the banking activity and credit risk originating from it. In this research work the literature, which refers to modeling of consumer credit risk by means of ML, has been studied. The authors analyzed strengths and weaknesses of the ML, the pre-processing of the data, the choice of the variables and optimization and other important phases of the modeling. The results of the research work show, that the implementation of ML in the field of management of the financial risk is increasing. However, standardized modeling procedures are necessary before difficult ML classifiers can be deployed commercially (Montevechi, et al., 2024).

In the article named “Machine Learning for Credit Risk Prediction: A Systematic Literature Review” the authors raise the question of necessity of use of Artificial intelligence (AI) and ML by financial institutions in order to evaluate credit risk by analyzing large amounts of information. Analyzing popular databases the researchers have discovered 52 researches, which are related to the microfinance lending sector. Research has shown that boosted models are the most researched among ML models, and most often, in order to evaluate the quality of models, such metrics as Area Under Curve (AUC), Accuracy (ACC), Recall, precision measure F1 (F1) and Precision (Niu & Zheng, 2020) are used.

In the article named “Credit Risk Prediction Using Machine Learning and Deep Learning: A Study on Credit Card Customers” the researchers studied approaches predicting default of the credit card customers using various models of ML including neural networks, logistic regression, AdaBoost, XGBoost and LightGBM. The results of the research work show, that XGBoost outperforms other models reaching 99,4% accuracy. The study has shown that application of algorithms of ML and deep learning (DL) significantly improved accuracy of forecasts in the field of customer default (Chang, et al., 2024).

In the article named “Machine learning-driven credit risk: a systemic review” the researchers studied a number of major research works over the last eight years (76 articles), where in order to solve credit risk problems statistical, ML and DL methods were used. Using available datasets a new classification methodology of ML-based credit risk algorithms and their efficiency ranking was proposed. The research has shown, that deep learning models for the credit risk assessment are more accurate than statistical algorithms of ML. Authors also mention that ensemble methods provide higher accuracy than separate models (Shi, et al., 2022).

In the article named “Financial Inclusion in Emerging Economies: The Application of Machine Learning and Artificial Intelligence in Credit Risk Assessment” as a result of the conducted research, it was revealed, that ML and artificial intelligence (AI) have a significant impact on the credit risk assessment, during which various available data is also used. All this allows lenders to conduct in-depth research of the behavior of the borrowers. The authors advise financial organizations to invest in AI and ML fields (Mhlanga, 2021).

In the article named “Machine Learning for an Enhanced Credit Risk Analysis: A Comparative Study of Loan Approval Prediction Models Integrating Mental Health Data” the researchers studied two subsets: the data about the mental health of people and choice about the loan approval. The data was generated in terms of 1991 people. This study work shows how chosen ML algorithms can distinguish risky and non-risky customers (Alagic, et al., 2024).

In the article named “Responsible Credit Risk Assessment with Machine Learning and Knowledge Acquisition” the authors mention, that human experience can be used for correction of an inaccurate data. In the research ML algorithms were used on a small amount of data, then errors in the data were corrected through human experience using Ripple-Down rules. As a result, it was revealed, that combined model, which learned from small amount of data works in the same way as the model, which learned from big amount of data. The presented approach is universal and can be applied to improve the validity of decisions on lending (Guan, et al., 2023).

In the article named “Machine Learning for Enhanced Credit Risk Assessment: An Empirical Approach” ten ML models are evaluated using more than 2,5 million observations. The results of the research show, that ensemble models, especially, XGBoost model qualitatively is better than traditional algorithms such as logistic regression (Suhadolnik, Ueyama, & Da Silva, 2023).

In the article named “Comparison of the impact of dimensionality reduction and data splitting on classification performance in credit risk assessment” it has been studied how changes in data dimension affect the efficiency of classification algorithms. In the research work data dimension was carried out using PCA method, and in order to solve the classification problem Random Forest, Logistic Regression, Decision Tree and Naive Bayes algorithms were used. The research showed, that the models, that were built based on that dataset, which consists of a total of 20 features, which are expressed with 13 PC, show same or better results, than the models, that are have been developed using the original database (Bulut & Arslan, 2024).

In the article named “A study on credit scoring modeling with different feature selection and machine learning approaches” it was demonstrated, that when building a credit score it is possible to improve the forecast results by choosing the right combination of different variable selection methods and ML algorithms. In this research work available credit data from Germany was used. In this study work an analysis was carried out, as a result of which the best combination between ML models and variable selection methods was revealed: random forest and Chi-Square (Trivedi, 2020).

Summarizing the reviewed researches we can mention, that in the scientific world various literature is often studied and in practical model building known models of ML are used. For that reason, within the framework of this research work the results of the conducted research are even more up-to-date.

3. Research Methodology

Within the framework of this research various data processing methods were used. In order to identify patterns in the data the correlation analysis method was used.

Correlation is a bivariate analysis that measures the strength of association between two variables and the direction of the relationship (Smith & Brown, 2020): This coefficient shows a linear relationship between variables.

Taking into account that the dataset contains categorical variables, that data was processed using One Hot Encoding method.

One Hot Encoding is a method for converting categorical variables into a binary format. It creates new binary columns (0s and 1s) for each category in the original variable. Each category in the original column is represented as a separate column, where a value of 1 indicates the presence of that category, and 0 indicates its absence (Smith & Brown, 2020).

Taking into account that the dataset contains numeric variables, the data was processed using StandardScaler method.

StandardScaler is a versatile and widely used preprocessing technique that contributes to the robustness, interpretability, and performance of machine learning models trained on diverse datasets.

StandardScaler operates on the principle of normalization, where it transforms the distribution of each feature to have a mean of zero and a standard deviation of one. This process ensures that all features are on the same scale, preventing any single feature from dominating the learning process due to its larger magnitude (Zhang & Wang, 2020).

In order to solve the classification problem within the framework of this research a new binary classification algorithm has been developed, which consists of the following steps mentioned below:

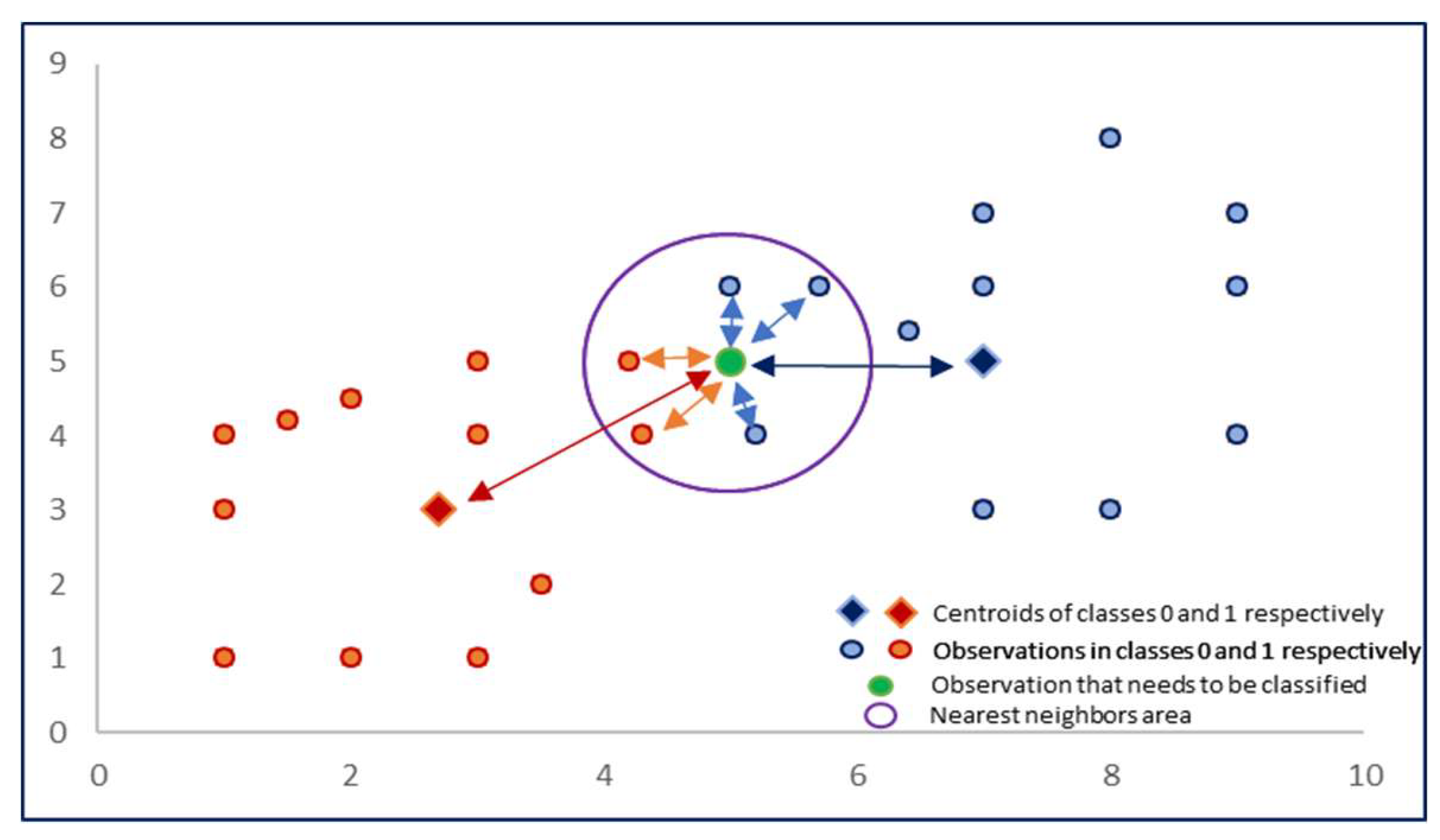
• Depending on the depent variable (y) it is necessary to divide the existing dataset (S) into two subsets. First subsets will consist of (S0) those observations, for which y takes the value of 0, and second (S1)՝ y takes the value of 1. It is appropriate

  $$S_0=\left\{x_i\in S\right|y_i=0\},S_1=\left\{x_i\in S\right|y_i=1\},$$

  where ${\mathrm{x}}_{\mathrm{i}}$: i is the vector of the observation variable, S is the initial dataset.

  $$S=\begin{array}{ccc}{x}_{11}& x_{12}& \begin{array}{ccc}\dots & x_{1j}& y_1\end{array}\\ x_{21}& x_{22}& \begin{array}{ccc}\dots & x_{2j}& y_2\end{array}\\ \begin{array}{c}⋮\\ x_{31}\end{array}& \begin{array}{c}⋮\\ x_{32}\end{array}& \begin{array}{ccc}\begin{array}{c}\ddots \\ \dots \end{array}& \begin{array}{c}⋮\\ x_{ij}\end{array}& \begin{array}{c}⋮\\ y_i\end{array}\end{array}\end{array}y\in \left(\mathrm{0,1}\right),$$

  $$S_0=\begin{array}{ccc}{x}_{11}& x_{12}& \begin{array}{cc}...& x_{1j}\end{array}\\ x_{21}& x_{22}& \begin{array}{cc}...& x_{2j}\end{array}\\ \begin{array}{c}⋮\\ x_{31}\end{array}& \begin{array}{c}⋮\\ x_{32}\end{array}& \begin{array}{c}\begin{array}{cc}\ddots & ⋮\end{array}\\ \begin{array}{cc}...& x_{ij}\end{array}\end{array}\end{array}y=0,$$

  $$S_1=\begin{array}{ccc}{x}_{11}& x_{12}& \begin{array}{cc}\dots & x_{1j}\end{array}\\ x_{21}& x_{22}& \begin{array}{cc}\dots & x_{2j}\end{array}\\ \begin{array}{c}⋮\\ x_{31}\end{array}& \begin{array}{c}⋮\\ x_{32}\end{array}& \begin{array}{c}\begin{array}{cc}\ddots & ⋮\end{array}\\ \begin{array}{cc}\dots & x_{ij}\end{array}\end{array}\end{array}y=1$$
• For each subset obtained in point 1 we find the centroid of the given group according to the formulas given below:

  $$C_0=\left({\displaystyle \frac{1}{s_0}}\sum _{i=1}^n{x}_{i1},{\displaystyle \frac{1}{s_0}}\sum _{i=1}^n{x}_{i2},\dots ,{\displaystyle \frac{1}{s_0}}\sum _{i=1}^n{x}_{ij}\right),$$

  $$C_1=\left({\displaystyle \frac{1}{s_1}}\sum _{i=1}^n{x}_{i1},{\displaystyle \frac{1}{s_1}}\sum _{i=1}^n{x}_{i2},\dots ,{\displaystyle \frac{1}{s_1}}\sum _{i=1}^n{x}_{ij}\right),$$

  where $C_0$ and $C_1$ are the centroids of the choices, and $s_0$ and $s_1$ is the amount of the relevant subsets.
• We calculate the distances from the point subject to classification to the centroid of each group and between given selected point and N neighbors. The distance can be measured using various methods. Within the framework of this study Euclidean distance was applied according to the formula given below (Gallet & Gowanlock, 2022):

  $$\begin{gathered} p=\left(p_1,p_2,\dots ,p_n\right)q=(q_1,q_2,\dots ,q_n) \\ d\left(p,q\right)=\sqrt{{\left(p_1-q_1\right)}^2+{\left(p_2-q_2\right)}^2+\dots +{\left(p_n-q_n\right)}^2}=\sqrt{\sum _{k=1}^n{\left(p_k-q_k\right)}^2}, \end{gathered}$$

  where p and q are two points in n-dimensional space.
• Applying the distances obtained in point 3 we calculate the influence of each centroid and each nearest neighbor according to the formula mentioned below:

  $$Impact={\displaystyle \frac{1}{{d(p,q)}^k+e}},$$

  where d(p,q) is the distance between p and q points, and k is the impact factor, e is a the rational number.
• The probability of belonging to the class 0 and 1 of the point subject to classification are calculated according to the formulas given below:

  $$Impact\left(0\right)=Impact\left(C_0\right)+\sum _{i=1}^{N0}Impact\left({d0}_i\right),N0\in N$$

  $$Impact\left(1\right)=Impact\left(C_1\right)+\sum _{i=1}^{N1}Impact\left({d1}_i\right),N1\in N$$

  $$Probability\left(0\right)={\displaystyle \frac{Impact\left(0\right)}{Impact\left(0\right)+Impact\left(1\right)}},$$

  $$Probability\left(1\right)={\displaystyle \frac{Impact\left(1\right)}{Impact\left(0\right)+Impact\left(1\right)}},$$

  where $Impact\left(C_0\right)$ and $Impact\left(C_1\right)$ are the influence of class centroids 0 and 1, $Impact\left({d0}_i\right)$ and $Impact\left({d1}_i\right)$ are the influences from a given point to the N nearest neighbors (0 and 1 class neighbors), Probability(0) and Probability(1)՝ the probabilities of belonging to groups 0 and 1 of the point subject to classification.

Figure 1. Classification algorithm diagram.

Figure 1. Classification algorithm diagram.

4. Analysis

The research is based on real credit information by example of “Unibank” OJSC. In this dataset there are 13 variables:

• Marital Status․ In the original data, this variable had the values M1, M2, M3, and M4. Each value has been changed to “Married”, “Widow”, “Divorced”, and “Single”, respectively;
• Education․ In the original data, this variable had the values E1, E2, E3, and E4. Each value has been changed to “Academic degree”, “Higher education”, “Medium professional”, and “High school”, respectively;
• Availability of property․ In the original data, this variable had the values P1, P2, P3, and P4. Each value has been changed to “Availability of real estate”, “Availability of movable property”, “Availability of real estate and movable property”, and “Absence”, respectively;
• Sex․ In the original data, this variable had the values S1 and S2. Each value has been changed to “Female”, and “Male”, respectively;
• Borrower’s Age․ The variable is numeric and contains values from 20 to 65;
• Number of days past due in the last 12 months. The variable is numeric and contains values from 0 to 1600;
• Number of delays. The variable is numeric and contains values from 1 to 67. This variable contains missing data. Based on the information received from the bank, it became clear that these clients do not have overdue debts. Based on this, the missing values were changed to 0;
• Number of changes in risk classes. The variable is numeric and contains values from 0 to 28;
• Credit load. The variable is numeric and contains values from 0 to 2,984,303. Data are presented in AMD;
• Credit history length. The variable is numeric and contains values from 0 to 488. Data is presented in days;
• Maximum repaid loans. The variable is numeric and contains values from 0 to 25,131,048. Data are presented in AMD;
• Contract sum. The variable is numeric and contains values from 30,000 to 2,300,000. Data are presented in AMD. There are some outliers in the data. These are the clients to whom the bank has issued a loan in the amount of more than AMD 1,000,000. There are 7 such observations in the sample. It was calculated that the removal of observational data does not significantly affect the quality of the models. Therefore, when creating models, these observations were not removed from the dataset;
• Default. Binary data is presented. 1 - default, 0 - no default. Based on the information received from the bank, a default is considered the presence of overdue obligations for 90 days or more at least once in the last year.

In the Dataset there are 4603 observations. For modeling purposes Default variable was chosen as the dependent variable.

Both the analysis and the model building were carried out with the help of the Excel program, Python programming language and its appropriate libraries, which are Pandas, Matplotlib, Seaborn, Scikit-learn libraries.

In the Table 1 a descriptive statistics of numerical variables is presented. It can be seen that there are no omissions in the data, because in all variables the quantity is mentioned to be 4603. The statistical average for all the variables is represented in the table, minimum and maximum values, as well as 25%, 50% և 75% percentiles (Thompson & Lee, 2022).

A correlation matrix was constructed for the numerical variables (Table 2), which shows that there is a moderate connection between “Number of changes in risk classes” and “Number of delays”, “Credit history length” and “Credit load” variables.

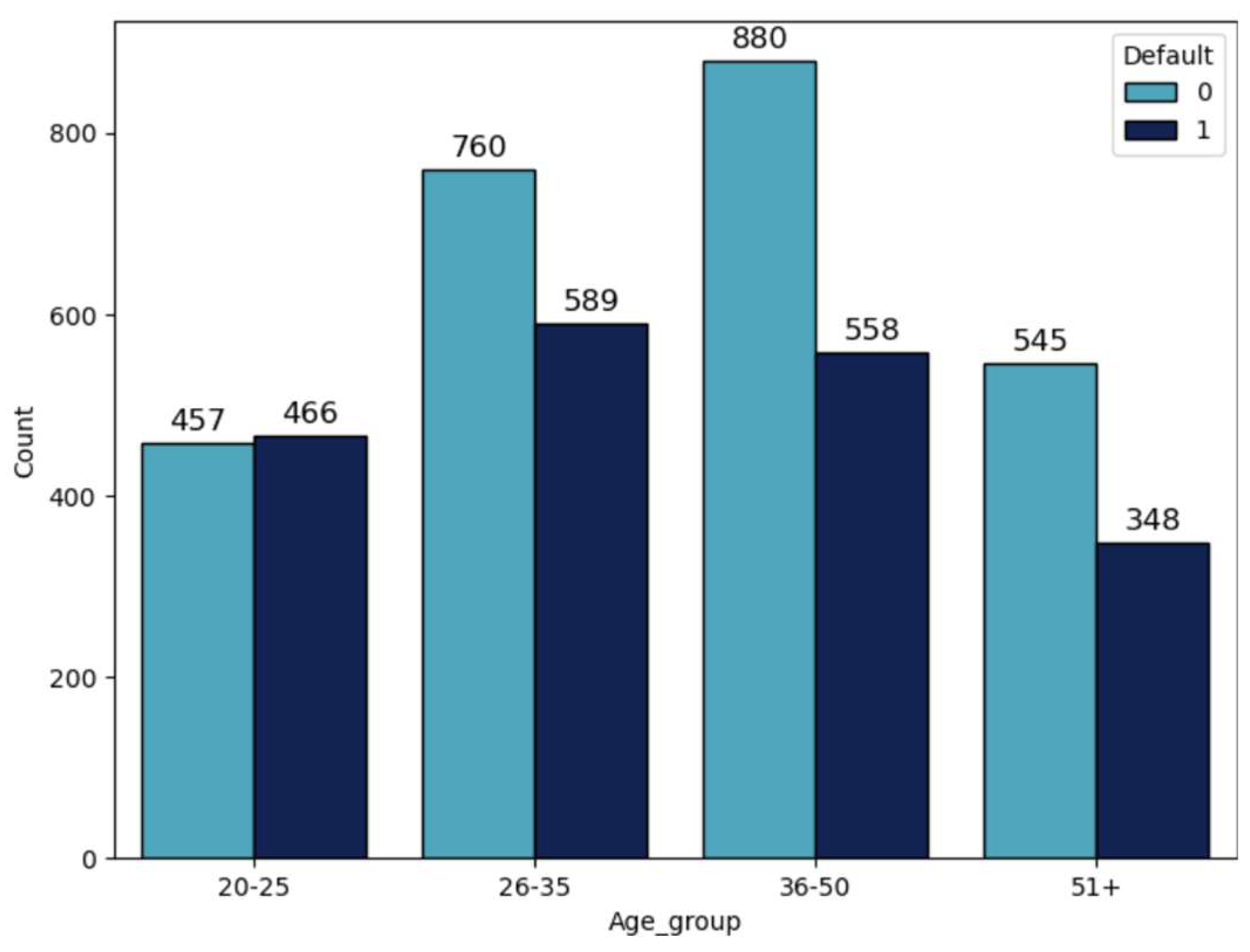
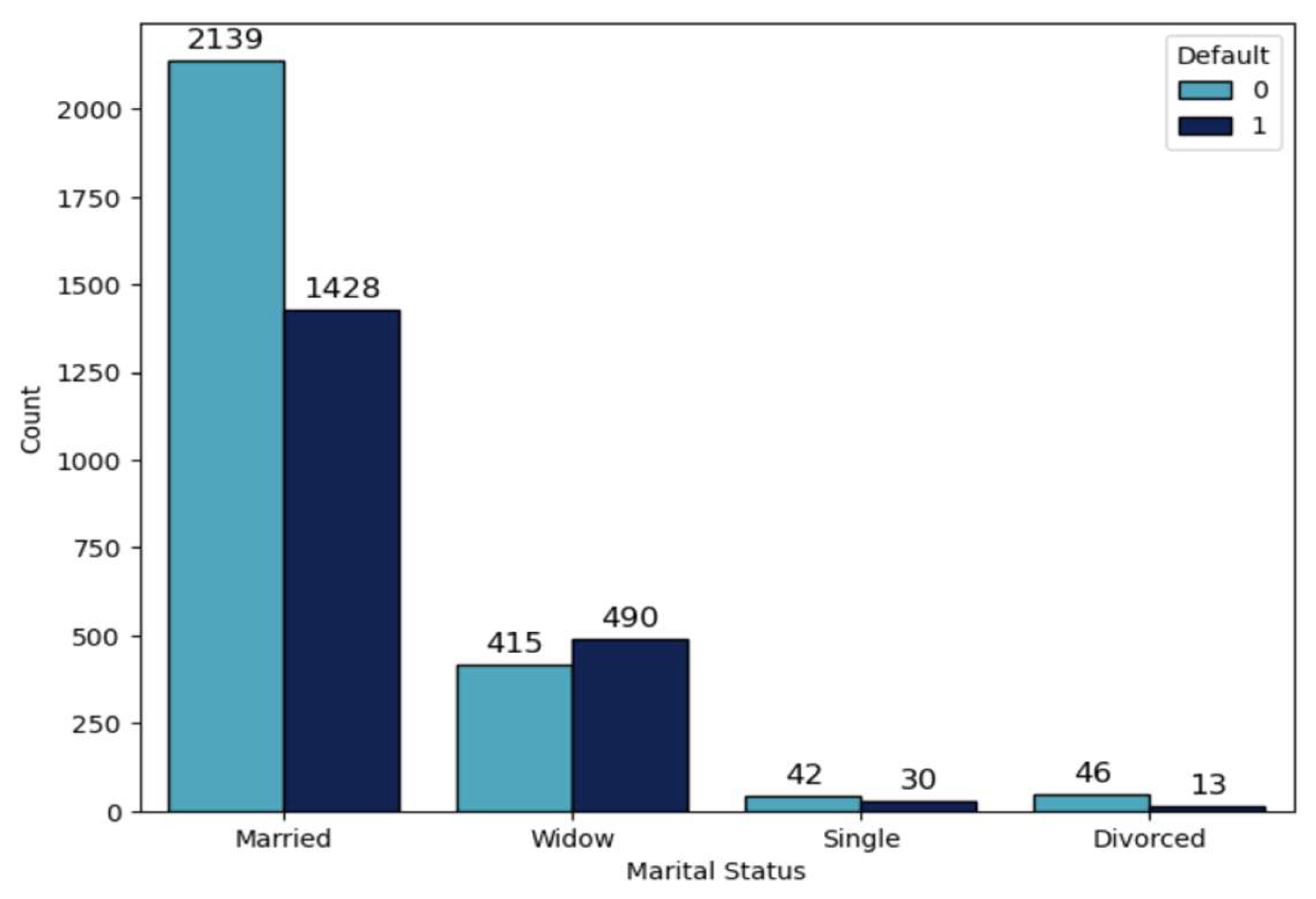
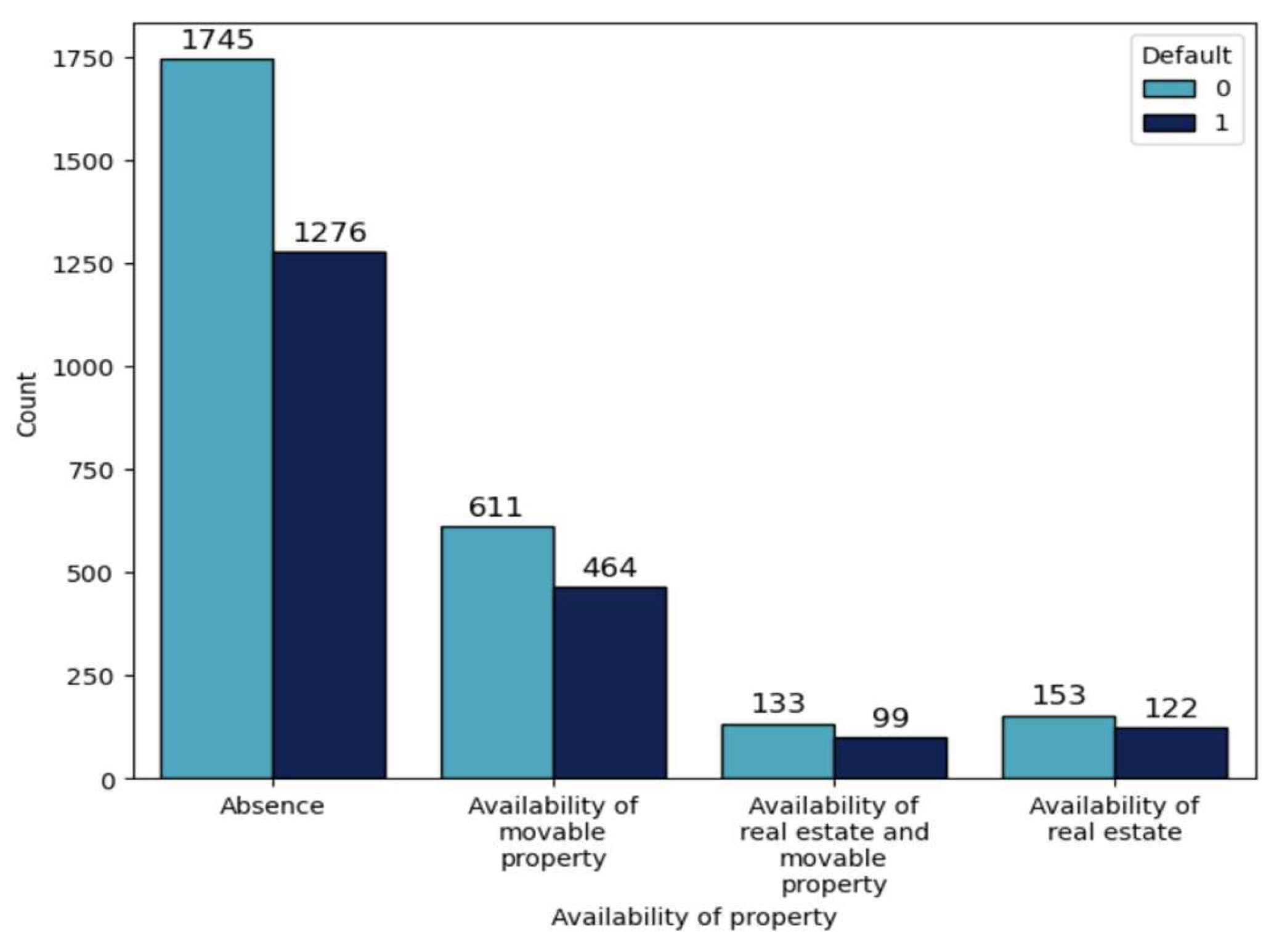
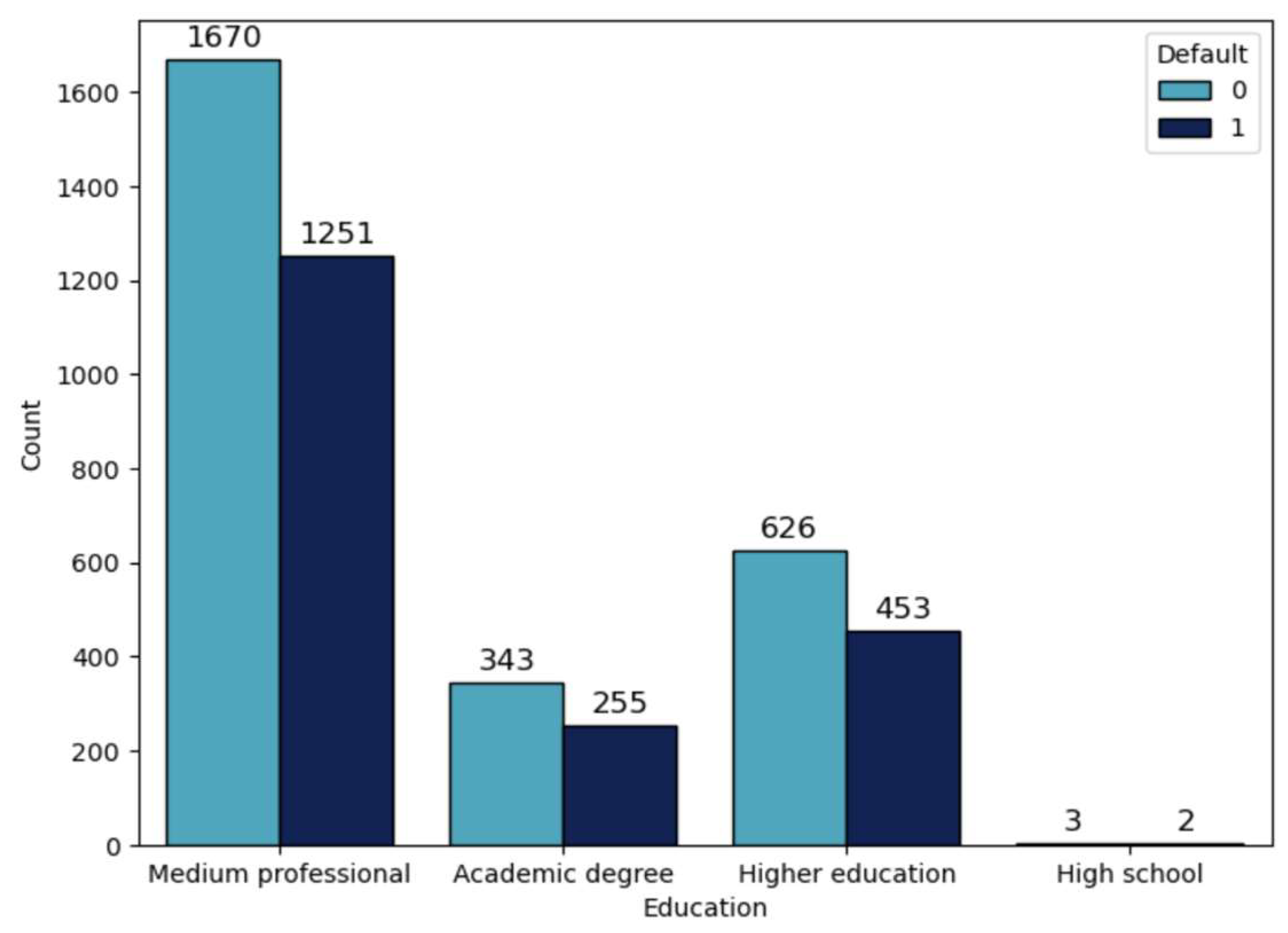
Within the framework of this research work various variables were analyzed, which shows that default is accumulated in in the age group of 20-25 (50,49%, Table 3, Figure 2), in the “widow” group of customers (54,14%, Table 4, Figure 3), as well as in the group of customers that have real estate (44,36%, Table 5, Figure 4) and in the group of customers that have medium professional education level (42,83%, Table 6, Figure 5).

After completing the analysis it is necessary to develop a classification model according to the methodology mentioned in this research, to evaluate the qualitative indicators of that model and to modify the obtained probabilities into 300-850 score points.

For the modeling purposes certain modifications have been made to the existing data, in accordance with the points mentioned below:

• The entire dataset was divided into training (80%) and testing (20%) subsets;
• For each subset obtained in the point 1 - “Contract sum”, “Age”, “Credit load”, “Credit history length”, “Number of days past due in the last 12 months”, “Number of delays” and “Maximum repaid loans” variables were standardized, using StandardScaler instrument of Sklearn library of Python programming language (Pedregosa et al., 2011).
• For all categorical variables dummy variables were created, using get_dummies instrument of Pandas library of Python programming language (Pandas Development Team, 2023).

In the Research methodology section of this research the proposed methodology was implemented using Python programming language. The amount of N neighbors was chosen from the range of 2 - 15, and k coefficient from the range of 0.0001 - 0.2001. N was chosen to be 12, and k to be 0.0001, because that combination provided the best result for the model.

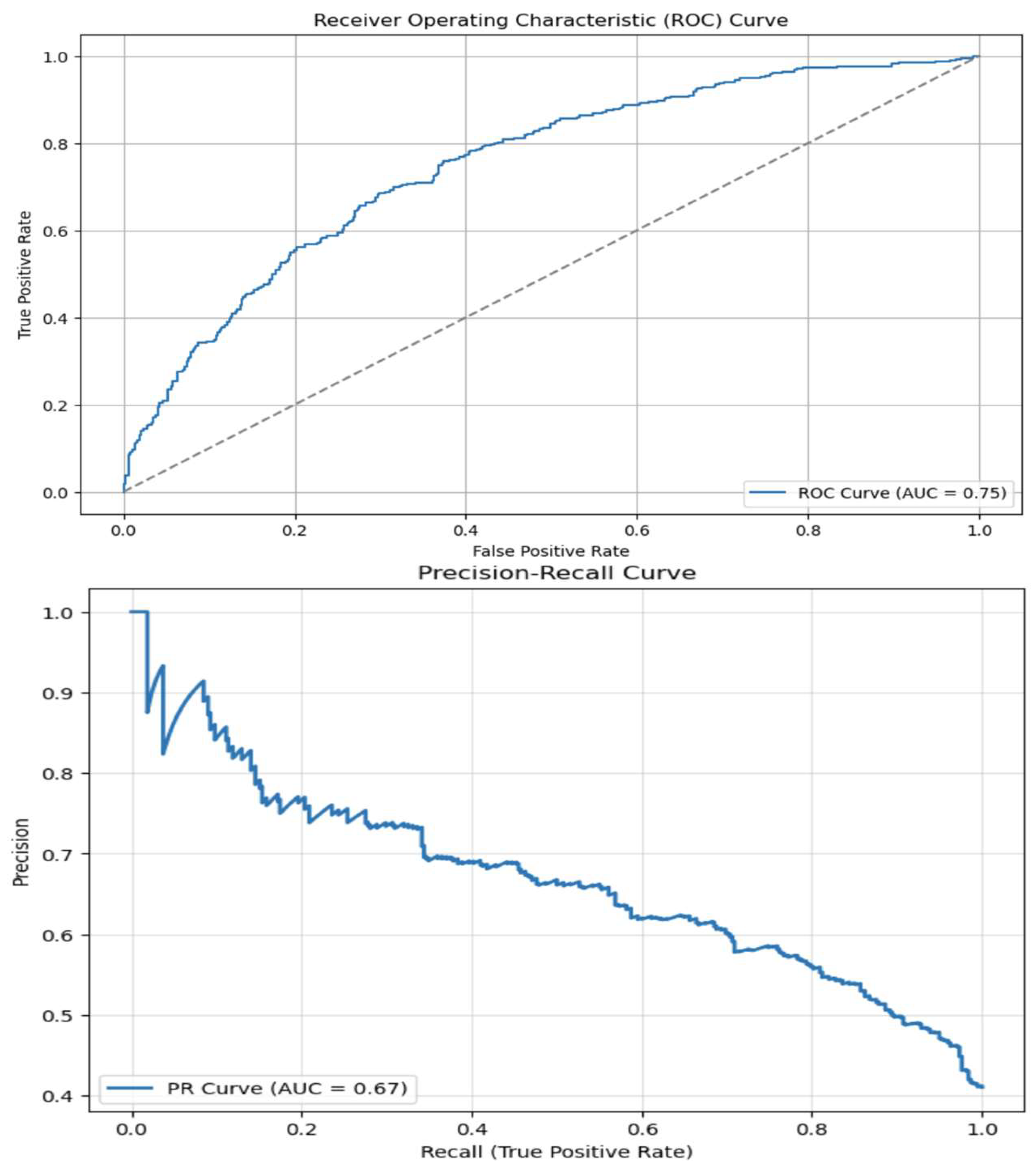
In the figure 6 ROC and PR curves and appropriate AUC coefficients are presented (Bradley, 1997).

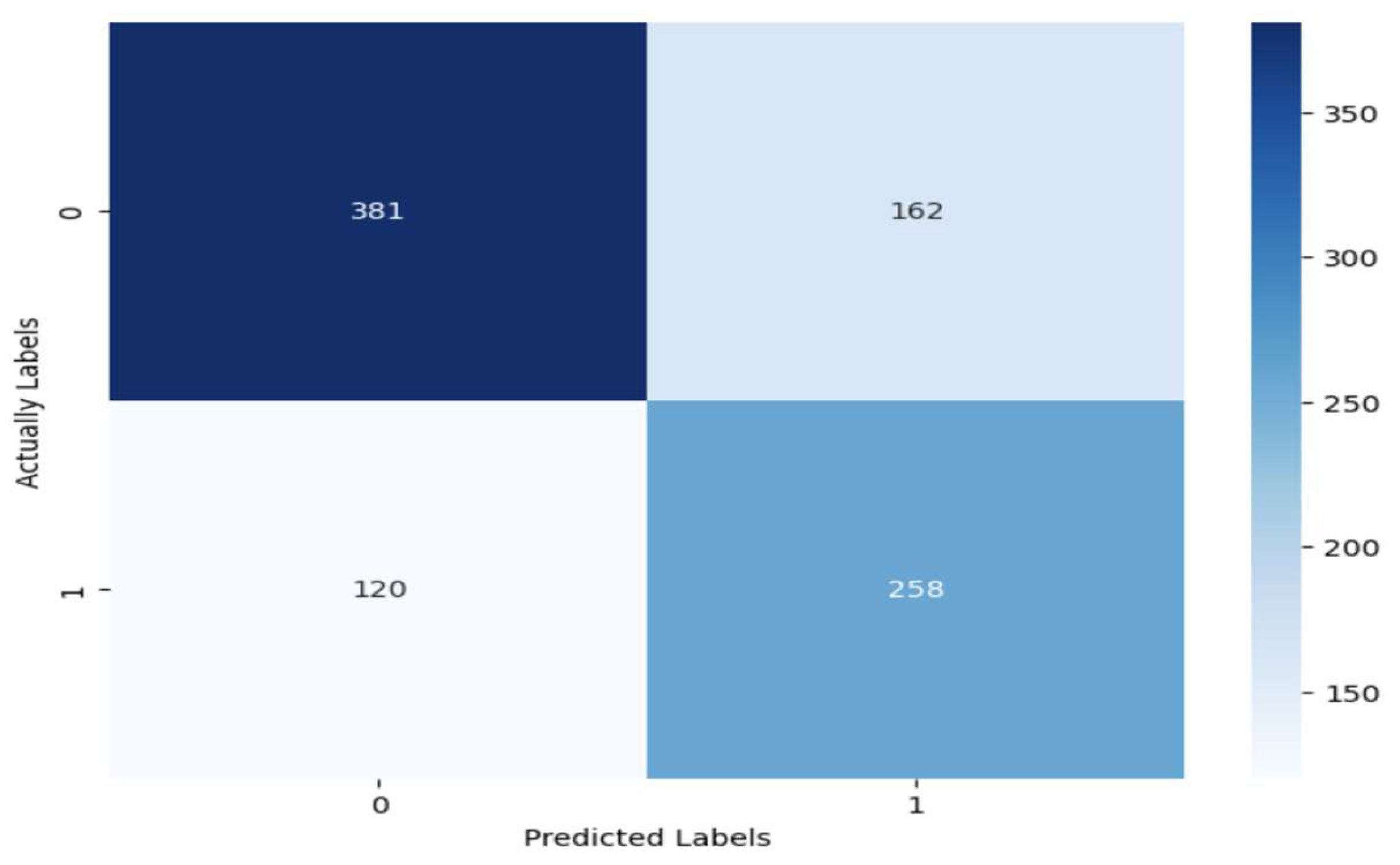
As the best threshold of the model the threshold of 0.4286 was chosen, in which case the accuracy is equal to 0.6938, Precision is equal to 0.7005, Recall is equal to 0.6938, and F1 Score is equal to 0.6957: In the figure 7 the Confusion matrix of the built model is presented, from which it is evident that the model revealed around 68% of defaults (258/378), but at the same time it refuses 162 good customers, which makes around 30% (162/543) of the good customers in the test subset (Dyrland et al., 2023).

After the above as a result of the prediction of the test subset the probability of obtained 0 class was modified into score points, which can be in the range of 300 – 850. The modification is carried out according to the following formula:

$$\begin{gathered} Score=\left(\ln \left({\displaystyle \frac{P\left(y=0\right)}{1-P\left(y=0\right)}}\right)\mathrm{*}{\displaystyle \frac{850-300}{\left|{Percentile}_1\right|+\left|{Percentile}_{99}\right|}}\right) \\ +\left(850-{\displaystyle \frac{850-300}{\left|{Percentile}_1\right|+\left|{Percentile}_{99}\right|}}\mathrm{*}{Percentile}_1\right), \end{gathered}$$

where Score is a score point, $P\left(y=0\right)$ is the probability of class 0, ${Percentile}_1$ and ${Percentile}_{99}$ are the 1st and 99th percentiles of the logarithmic row.

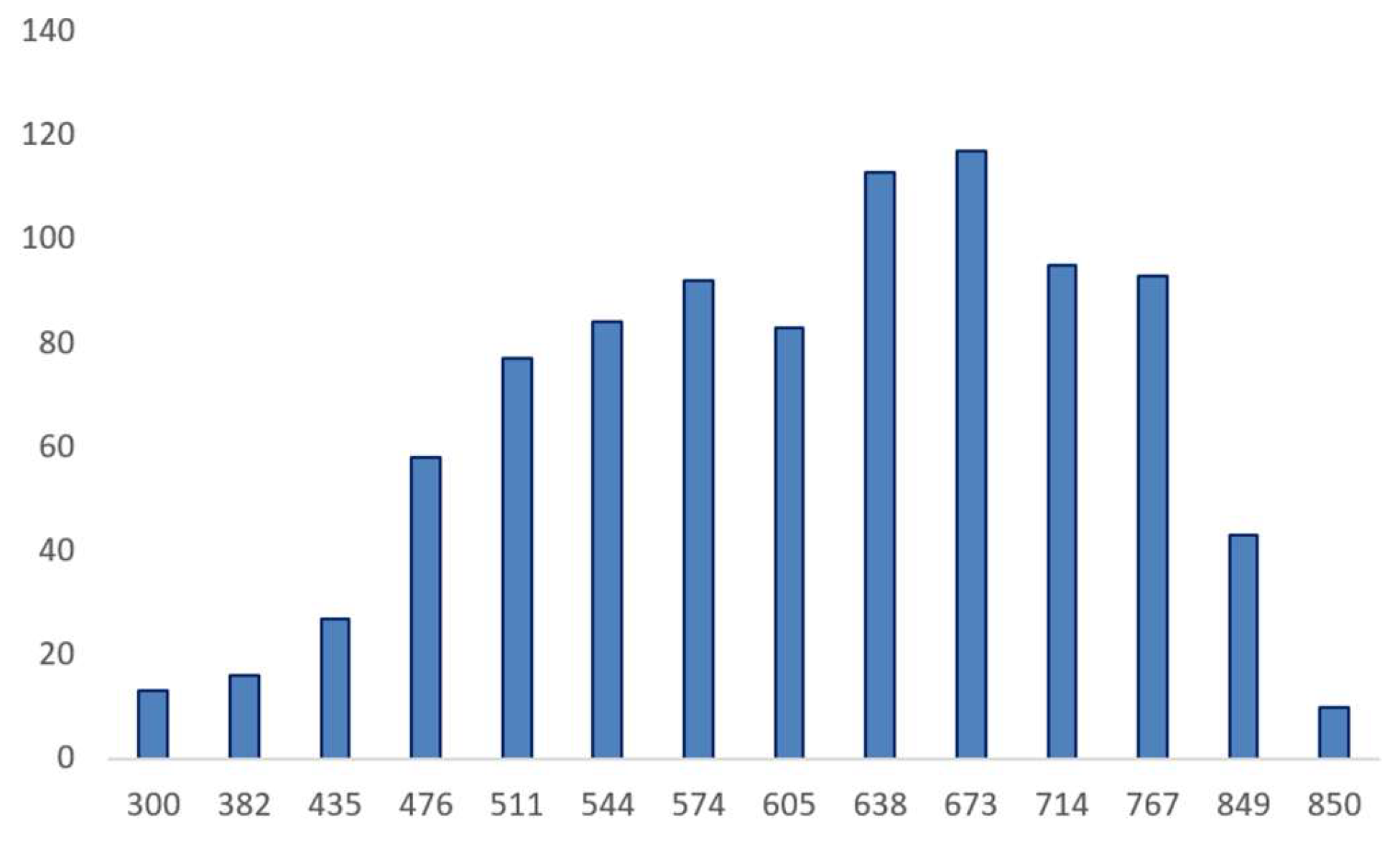
In the Figure 8 the distribution of the resulting score groups is presented.

Figure 6. Curves ROC and PR.

Figure 6. Curves ROC and PR.

Figure 7. Confusion matrix.

Figure 7. Confusion matrix.

Figure 8. Distribution of scores.

Figure 8. Distribution of scores.

5. Conclusions

It is important for every credit organization to identify and manage credit risks. In order to mitigate that risk, it is important to implement a reasonable decision-making system. The aim of this research was to develop a new machine learning model for binary classification. The results of this research work show, that as a result of a combination of ideas leaning in the foundation of the well-known classic models it is possible to get a new algorithm, which will show quite a big result. Within the framework of this topic the use of new algorithms of this type can mitigate credit risk encountered by the credit organizations and the losses resulting from it.