Electromagnetically Induced Transparency in a GaAs Coupled Quantum Dot-Ring

1. Introduction

Quantum nanostructures such as quantum dots [1,2,3], lens-shaped structures [4,5,6], and tetrapods [7] exhibit unique electronic and optoelectronic properties, which make them suitable for applications in multiple fields, from bioimaging [8] to photovoltaics [9]. Among these, quantum rings (QR) [10,11,12] have attracted particular interest due to their unique electronic and optical characteristics, including Aharonov-Bohm oscillations and quantum interference effects [13,14], which open possibilities for their integration into optoelectronic devices and quantum information technologies [15,16,17].

During the characterization and fabrication process of such structures, it has been possible to experiment with various geometries [18,19,20,21], many of which are based on coupling structures. In recent years, coupled quantum dot-ring (CQDR) systems [22,23,24,25] have attracted significant attention due to their highly tunable electronic states, which can be modified by external factors such as electric and magnetic fields, hydrostatic pressure, and structural parameters [26]. This tunability makes CQDRs promising candidates for applications in optoelectronic devices, optical modulators [27], and quantum communication technologies [28]. These structures, formed by a QR coupled to a concentric quantum dot (QD), offer a versatile way to explore quantum interference phenomena and electromagnetically induced transparency (EIT).

CQDRs have also gained relevance due to their ability to host localized electronic states with versatile optical properties [24,26,29,30]. External perturbations on the structure, such as electric and magnetic fields, can substantially modify the electronic structure of these systems [31,32,33,34]. For example, the application of an electric field along the growth direction introduces Stark shifts and dipole moment variations [35,36,37]. This motivates continued studies that include these external perturbations.

Recent studies on the interaction between donors and structures have yielded interesting conclusions. Some have concluded that the interaction between the confined electron and the neutral donor center results in position-dependent modifications to transition energies and absorption properties[32,38,39]. Shallow donors add a layer of complexity to CQDRs due to their position within the structure [40,41], which plays a critical role in shaping electronic states and optical absorption spectra. Furthermore, recent studies on doubly ionized donors confined in CQDRs have provided information on the role of donor states and their interaction with external probes, such as hydrostatic pressure, electric fields, and temperature variations [26]. The present study explores the interaction between a shallow donor and a CQDR.

Such facts motivate the present study of the energy levels of a ${\mathrm{GaAs/Al}}_{0.3}{\mathrm{Ga}}_{0.7}$As CQDR, along with a detailed analysis of the consequences of external factors, such as magnetic and electric fields, while identifying the optoelectronic properties of the heterostructure. Furthermore, the study examines the phenomenon of EIT, in which quantum interference suppresses absorption while maintaining significant nonlinear optical properties [42,43].

This paper is organized as follows: in Section 2, we describe the theoretical model, outlining the fundamental principles that govern the electronic and optical properties of CQDRs, along with a description of the basic theory. Section 3 presents and discusses our numerical results, highlighting the impact of external perturbations and structural parameters on the electronic states and optical responses. Finally, our main conclusions are provided in Section 4.

2. Theoretical Framework

In this work, we analyze the energy states and their associated wavefunctions in a CQDR structure under the influence of external electric and/or magnetic fields applied in the z-direction. To complete our study, we investigate optoelectronic properties via EIT in a ladder or cascade configuration and linear optical absorption.

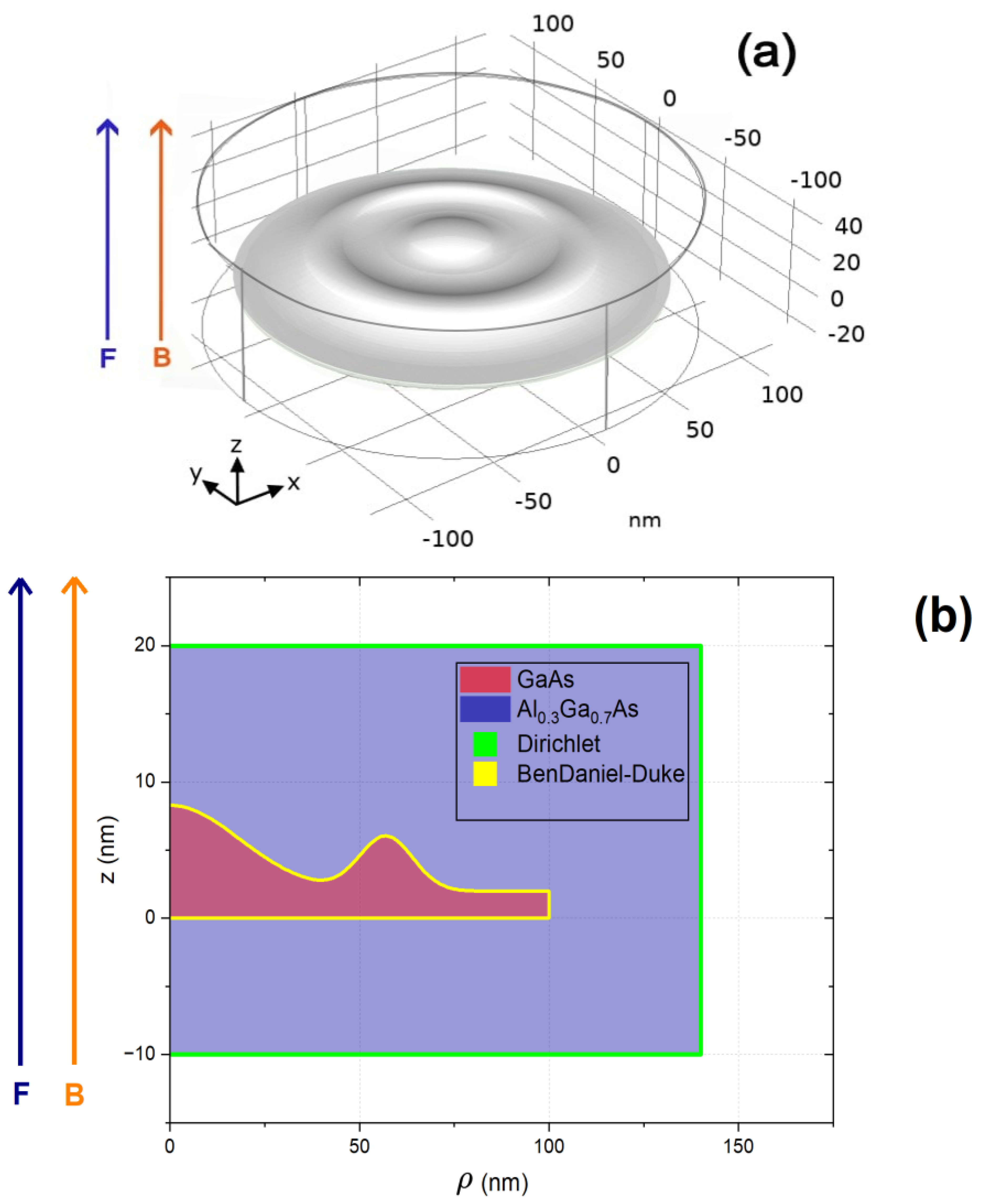
Figure 1 presents a schematic view of the CQDR under study, together with the main dimensions of the heterostructure. A 3D view of the nanostructure is shown in panel (a), obtained by revolution around the z-axis of Figure 1(b). A cross-section of the structure (the $\varphi =0$ plane) is shown in panel (b), where the two composing materials are easily identified, i.e., the GaAs and the ${\mathrm{Al}}_x{\mathrm{Ga}}_{1-x}$As. The latter displays a barrier-like behavior, while the former presents a well-like behavior. This configuration is suitable for building a 2D-axisymmetric model where azimuthal symmetry reduces the computational cost of numerically solving the three-dimensional Schrödinger equation. The geometry of the nanostructure is a variation of a theoretical function [32] that accurately reproduces an experimental profile of a GaAs CQDR, as obtained via the AFM technique by Somaschini [24]. To enhance the visibility of the ring’s influence, the height of the central region (dot) has been deliberately reduced by 65% compared to the original geometry. For the sake of clarity, the reference system and the directions of the external fields are also depicted. The CQDR is made of GaAs, whereas the cylindrical host matrix in which it is embedded is made of ${\mathrm{Al}}_x{\mathrm{Ga}}_{1-x}$As with $x=0.3$.

The mathematical function describing the height, $h\left(\rho \right)$, as depicted in Figure 1 (a), is formally expressed as[26]:

$$h\left(\rho \right)=h_{d}exp\left[-{\left({\displaystyle \frac{\rho }{w_d}}\right)}^2\right]+h_{r}exp\left[-{\left({\displaystyle \frac{\rho -d_r}{w_r}}\right)}^2\right]+w_l.$$

(1)

In this equation, $h_d$ represents the height of the central dot, $w_d$ denotes its characteristic width, $h_r$ signifies the height of the ring, $d_r$ corresponds to the radius of the ring, $w_r$ indicates the width of the ring and $w_l$ establishes the baseline height. For the specific nanostructure under investigation, the precise values assigned to these parameters are as follows: $h_d=6.3\mathrm{nm}$, $w_d=26\mathrm{nm}$, $h_r=4\mathrm{nm}$, $d_r=57\mathrm{nm}$, $w_r=10\mathrm{nm}$, and $w_l=2\mathrm{nm}$.

Using the effective mass approximation and taking the assumption of parabolic conduction bands, the Schrödinger equation of an electron interacting with external electric and magnetic fields is written in cylindrical coordinates as follows:

$$\left\{{\displaystyle \frac{1}{2}}\left[\left(-i\hslash \overrightarrow{\nabla }+e\overrightarrow{A}\right){\displaystyle \frac{1}{m_j^{*}\left(\overrightarrow{r}\right)}}\left(-i\hslash \overrightarrow{\nabla }+e\overrightarrow{A}\right)\right]+e\overrightarrow{F}·\overrightarrow{r}+V(\rho ,z)\right\}{\mathsf{\Psi }}_i\left(\overrightarrow{r}\right)=E_i{\mathsf{\Psi }}_i\left(\overrightarrow{r}\right),$$

(2)

where i designates each of the quantized states, i.e., the value $i=1$ represents the ground state and $i\ge 2$ corresponds to the excited states. The j-index identifies each one of the two materials that make up the CQDR, and e is the absolute value of the electron charge. The values of the effective mass and $V(\rho ,z)$ depend on the region where the Schrödinger equation is solved, as shown in Figure 1 (a). The effective mass is considered to be position-independent within each material. The effective mass and the confining potential are taken for the calculations in the following way:

$$V(\rho ,z)=\left\{\begin{array}{cc}0,\hfill & (\rho ,z)\in \mathrm{CQDR},\hfill \\ V_0,\hfill & (\rho ,z)\in \mathrm{cylindrical}\mathrm{matrix},\hfill \\ \infty ,\hfill & elsewhere,\hfill \end{array}\right.$$

(3)

and

$$m_j^{*}\left(\overrightarrow{r}\right)=\left\{\begin{array}{cc}{m}_{GaAs}^{*},\hfill & j=1,\hfill \\ m_{A{l}_{x}G{a}_{1-x}As}^{*},\hfill & j=2.\hfill \end{array}\right.$$

(4)

In this work, both electric and magnetic fields are applied along the z-direction, i.e., $\overrightarrow{F}=(F_{\rho },F_{\phi },F_z)=(0,0,F_z)$ and $\overrightarrow{B}=(B_{\rho },B_{\phi },B_z)=(0,0,B)$.

The gauge chosen for the description of the magnetic field effect entails the following conditions for the magnetic vector potential, $\overrightarrow{A}$: (i)$\overrightarrow{\mathbf{\nabla }}·\overrightarrow{A}=0$ and (ii)$\overrightarrow{A}=-{\displaystyle \frac{1}{2}}\overrightarrow{r}\times \overrightarrow{B}$. Under these two conditions, the Hamiltonian in Eq. 2 takes the form:

$$\left[-{\displaystyle \frac{{\hslash }^2}{2m_j^{*}}}\left({\displaystyle \frac{{\partial }^2}{\partial {\rho }^2}}+{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial }{\partial \rho }}+{\displaystyle \frac{1}{{\rho }^2}}{\displaystyle \frac{{\partial }^2}{\partial {\phi }^2}}\right)-{\displaystyle \frac{ei\hslash B}{2m_j^{*}}}{\displaystyle \frac{\partial }{\partial \phi }}+{\displaystyle \frac{e^2{B}^2{\rho }^2}{8m_j^{*}}}+e{F}_{z}z+V(\rho ,z)\right]{\mathsf{\Psi }}_i\left(\overrightarrow{r}\right)=E_i{\mathsf{\Psi }}_i\left(\overrightarrow{r}\right).$$

(5)

This Hamiltonian is separable, $H(\rho ,\phi ,z)=H_{\phi }\left(\phi \right)+H_{\rho ,z}(\rho ,z)$, which allows to replace ${\mathsf{\Psi }}_i\left(\overrightarrow{r}\right)=R_i(\rho ,z)e^{il\phi }$ in Eq. 5 (here $l=0,\pm 1,\pm 2,...$). Taking the derivatives with respect to $\phi$, the Schrödinger equation for the radial function $R_i(\rho ,z)$ can be written as:

$$\left[-{\displaystyle \frac{{\hslash }^2}{2m_j^{*}}}\left({\displaystyle \frac{{\partial }^2}{\partial {\rho }^2}}+{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial }{\partial \rho }}-{\displaystyle \frac{l^2}{{\rho }^2}}\right)+{\displaystyle \frac{e\hslash Bl}{2m_j^{*}}}+{\displaystyle \frac{e^2{B}^2{\rho }^2}{8m_j^{*}}}+e{F}_{z}z+V(\rho ,z)\right]R_i(\rho ,z)=E_i^{\prime }{R}_i(\rho ,z),$$

(6)

where $E_i^{\prime }$ are the eigenvalues associated with the 2D-wavefunctions $R_i$. The solution of Eq. 6 was investigated using the finite element method (FEM) as implemented in the COMSOL-Multiphysics software [44]. The boundary conditions were imposed in the following way: (i) BenDaniel-Duke boundary condition for wave function continuity on the core-shell interface, $R_{GaAs}=R_{A{l}_{x}G{a}_{1-x}As}$, (ii) BenDaniel-Duke boundary condition for the wave function first derivative continuity: ${\displaystyle \frac{1}{m_{GaAs}^{*}}}{\displaystyle \frac{\partial R_{GaAs}}{\partial X}}={\displaystyle \frac{1}{m_{A{l}_{x}G{a}_{1-x}As}^{*}}}{\displaystyle \frac{\partial R_{A{l}_{x}G{a}_{1-x}As}}{\partial X}}$ with $X=\rho ,z$ and (iii) Dirichlet boundary conditions on the outer surface of the embedding ${\mathrm{Al}}_x{\mathrm{Ga}}_{1-x}$As matrix: $R(\rho ,z)=0$.

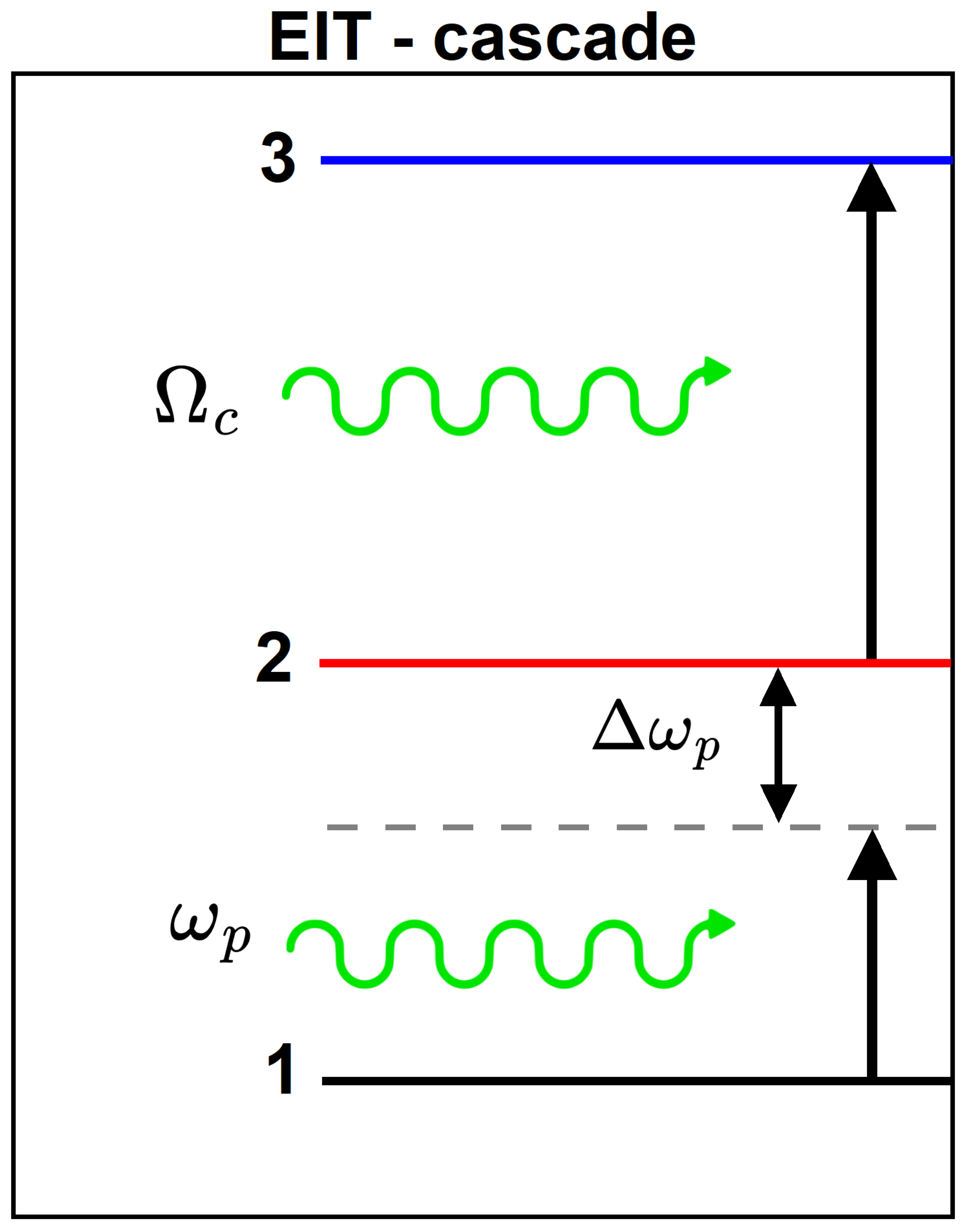
The cascade configuration chosen for the EIT analysis comprises the first three $l=0$ energy levels and is modeled in Figure 2.

Within the density matrix approach, an expression for the imaginary part of the linear susceptibility can be derived in terms of the probe field and Rabi frequencies as follows [31]:

$${\chi }^{\prime \prime }\left({\omega }_p\right)={\displaystyle \frac{{\left|{\tilde{M}}_{21}\right|}^2{\sigma }_{12}}{\hslash {\epsilon }_0{\epsilon }_r}}\times {\displaystyle \frac{{\mathsf{\Gamma }}_{13}\left({\mathsf{\Gamma }}_{12}{\mathsf{\Gamma }}_{13}-{\Delta }_p^2+{\mathsf{\Omega }}_c^2/4\right)+{\Delta }_p^2\left({\mathsf{\Gamma }}_{12}+{\mathsf{\Gamma }}_{13}\right)}{{\left({\mathsf{\Gamma }}_{12}{\mathsf{\Gamma }}_{13}-{\Delta }_p^2+{\mathsf{\Omega }}_c^2/4\right)}^2+{\Delta }_p^2{\left({\mathsf{\Gamma }}_{12}+{\mathsf{\Gamma }}_{13}\right)}^2}},$$

(7)

where ${\Delta }_p=\left({\omega }_2-{\omega }_1\right)-{\omega }_p$ is the detuning between the probe field frequency ${\omega }_p$ and that of the $|1\rangle \to |2\rangle$ transition,

${\tilde{M}}_{ij}=e\langle {\mathsf{\Psi }}_i|\overrightarrow{r}·{\widehat{u}}_p|{\mathsf{\Psi }}_j\rangle$ is the electric dipole matrix element for a transition between states $|i\rangle$ and $|j\rangle$ induced by a light field with polarization vector ${\widehat{u}}_p$. While the general notation uses indices $i,j$, the specific transition from the ground state to the first excited state ($|1\rangle \to |2\rangle$) is represented by the element ${\tilde{M}}_{21}$, as shown in the formula, ${\mathsf{\Omega }}_c$ is the Rabi frequency associated with the aforementioned $|1\rangle \to |2\rangle$ transition, ${\sigma }_{12}$ stands for the population difference between the two involved levels, and ${\mathsf{\Gamma }}_{ij}$ are the decay rates for the $|i\rangle \to |j\rangle$ transition. The Rabi frequency is taken to be fixed for the material throughout this study. The imaginary part of the linear susceptibility is related to the linear optical absorption, allowing for the EIT calculation as in [31]:

$${\alpha }_{EIT}\left({\omega }_p\right)={\displaystyle \frac{{\omega }_p}{c_m}}{\chi }^{\prime \prime }\left({\omega }_p\right),$$

(8)

where $c_m$ is the speed of light in the medium, $c_m=c_{vacuum}/\sqrt{{\mu }_r{\epsilon }_r}$. Finally, the linear optical absorption coefficient (LOAC) for the transition $|1\rangle \to |2\rangle$ can be deduced from Eq. 8, subtracting all contributions coming from the third level, i. e., ${\mathsf{\Omega }}_c$, ${\mathsf{\Gamma }}_{13}\to 0$.

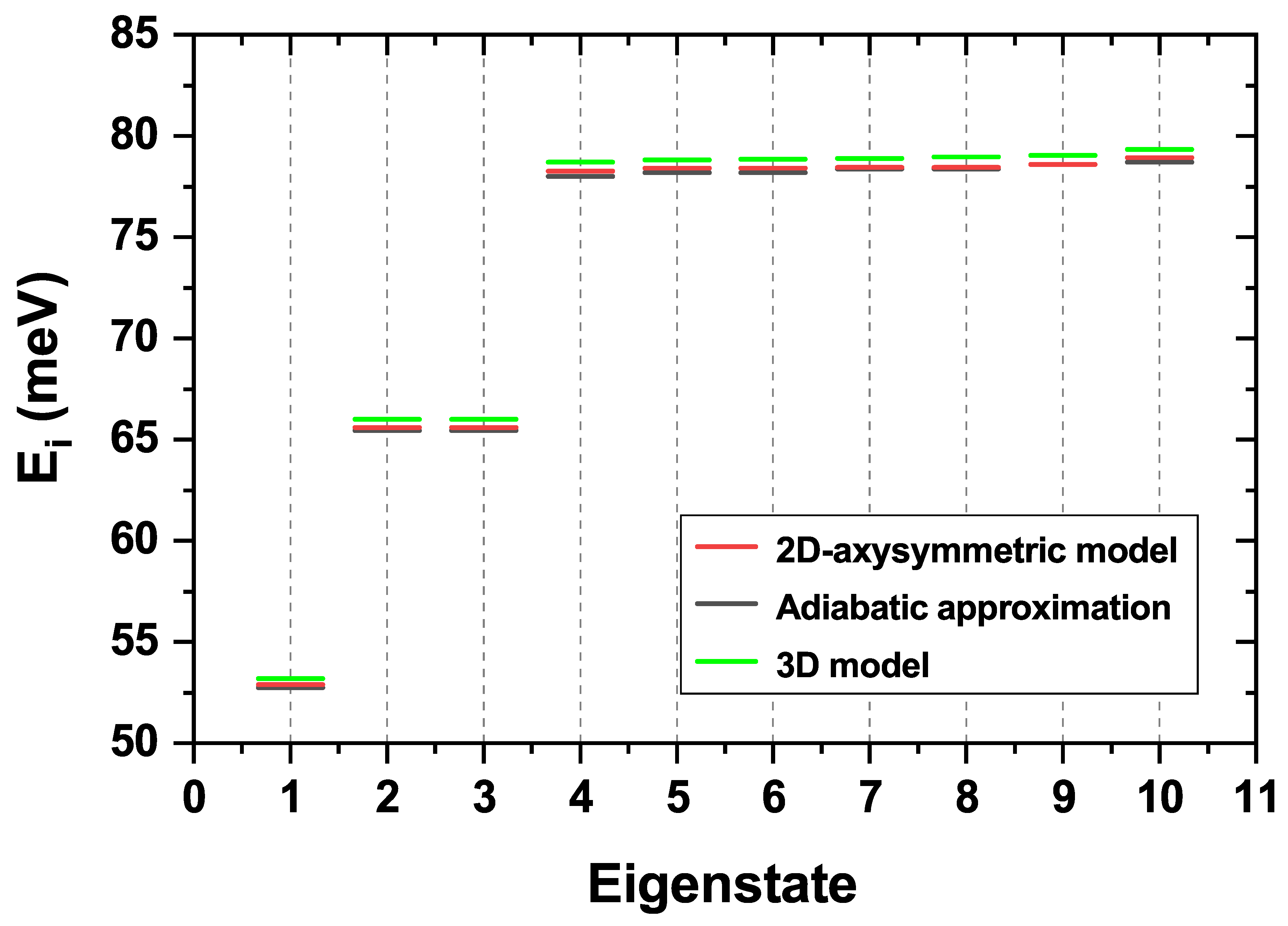
To close this section, we provide in Figure 3 the comparison of the first ten electron eigenenergies obtained by solving the three-dimensional Schrödinger equation, by implementing the adiabatic approximation, and through the 2D-axisymmetric model described along this section. The use of the adiabatic approximation is justified by the system’s morphological features, where confined carriers experience significantly greater quantum confinement in the z-direction than in the $z=0$ plane [32]. This geometric asymmetry supports the decoupling of the electron’s motion into two separate kinetic contributions (z-axis and $xy$-plane). The procedure begins by "freezing" the $xy$-plane motion to solve a one-dimensional Schrödinger equation for the z-axis. The resulting eigenvalues are then introduced into the $xy$-plane Schrödinger equation, reducing the original three-dimensional Hamiltonian to a simplified and numerically solvable two-dimensional problem.

As Figure 3 shows, the results from all three methods are in very good agreement, the 3D model being the most precise. Therefore, we can confidently conclude that the implementation of the simpler axisymmetric model is justified for our analysis. At this point, it is worth mentioning that the fact of having seven eigenstates with similar energies does not mean a seven-fold degeneracy, given that the eigenenergies associated with the dot are mixed with those associated with the ring. The latter will be thoroughly discussed later on.

3. Results and discussion

The Schrödinger equation, given in Eq. 6, was solved using the FEM via the COMSOL-Multiphysics software [44] within the effective mass approximation. We computed the lowest confined electron energy states in a GaAs CQDR embedded in an ${\mathrm{Al}}_x{\mathrm{Ga}}_{1-x}$As cylindrical matrix with $x=0.3$ applying external electric and/or magnetic fields perpendicular to the structure. We calculated the EIT and the LOAC in the presence and absence of the fields mentioned above. The parameters for electrons adopted in the numerical calculations are $m_{\mathrm{GaAs}}^{*}=0.067m_0$, $m_{{\mathrm{Al}}_{0.3}{\mathrm{Ga}}_{0.7}\mathrm{As}}^{*}=0.092m_0$ (here, $m_0$ is the free electron mass) [45] and the barrier height of $V_0=262$ meV [46]. Calculations were performed for negative and positive values of the electric field F. The CQDR profile under study is an adaptation of AFM measurements [24]. In the first stage, the study will focus on analyzing the effects of electric and/or magnetic fields on electron energy levels when the fields are applied perpendicular to the structure.

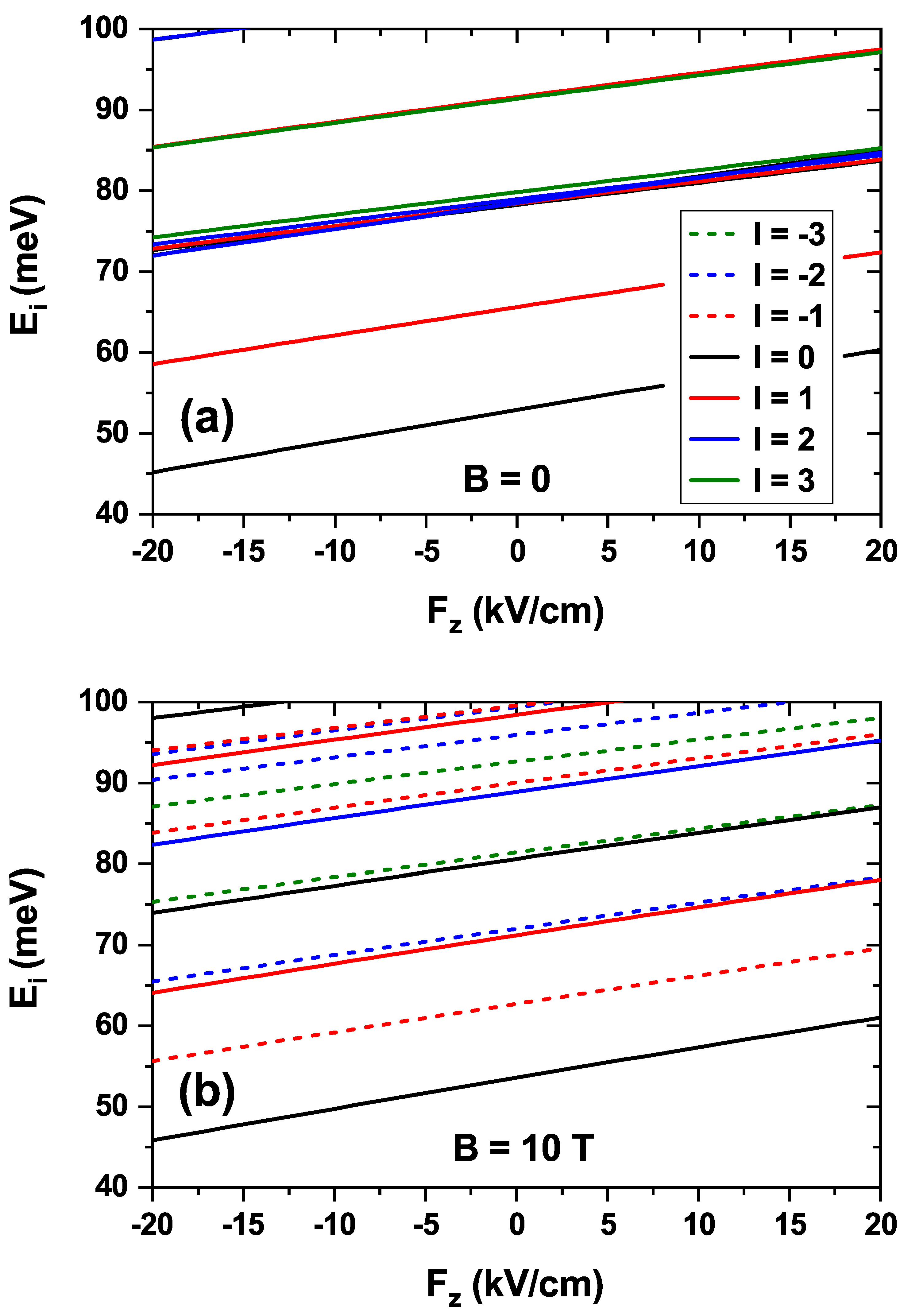
Figure 4 shows the variation in the electron energies of the first states obtained by applying an electric field directed along the z-axis. Negative field values indicate that the field points in the negative z-direction. The implementation of a 2D-axisymmetric model allows the distinction of states according to the quantum number l. In this work, the first states with $\left|l\right|=0,1,2,3$ are analyzed. Panel (a) of Figure 4 is devoted to the case in which no magnetic field is applied, and, therefore, the states with positive (solid lines) and negative (dashed lines) l are superimposed, as is straightforward from Eq. 6. The energy of the states increases as the electric field shifts from negative to positive values, given that the electron wave function is pushed towards the lower region of the CQDR, becoming more confined as the field intensity increases. The following states, after the first $l=0$ and $\left|l\right|=1$ states, which correspond to the dot, are concentrated in less than 5 meV. Here, the ring states appear and are intermixed with the dot states. To complete this analysis, panel (b) shows the energy variation with the electric field in the presence of a magnetic field, also applied along the z-direction. This magnetic field is responsible for the degeneracy breaking of the energies associated with $l=+1$ and $l=-1$. Comparing panels (a) and (b) of Figure 4, states with $l\ge 0$ ($l<0$) are found to display higher (lower) energies than in the absence of the magnetic field. At the same time, all of them show increasing energies as the electric field intensity ranges from more negative to more positive values. In both the absence and the presence of an external magnetic field, a linear increasing trend in the energy levels is observed as the electric field ranges from $-20$ to $+20$kV/cm, such that the levels are practically parallel. A linear fit of these allows the calculation of an average slope, which, in the case of a zero magnetic field, is $\approx 0.2977$meV cm/kV, while in the case of a $10$T magnetic field it is of $\approx 0.2988$meV cm/kV. The relative standard deviation in the first case is $11.9\%$ and in the second case is $10.7\%$. The value of this slope can be related to the Stark shift [47,48].

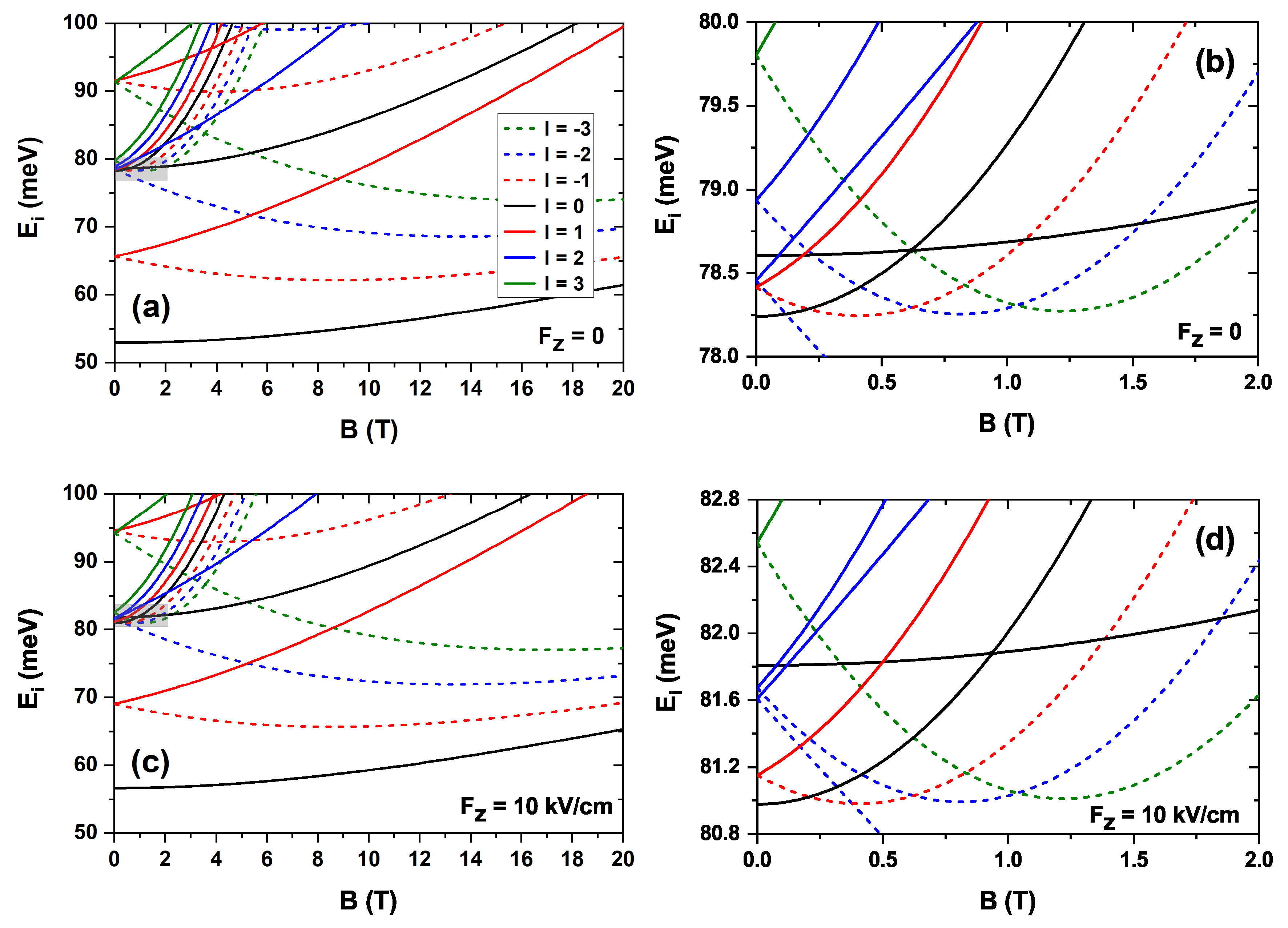
For the sake of completeness, the variation in electron energy is now analyzed in the presence of an externally applied magnetic field, both in the absence and in the presence of an electric field, with both fields parallel to the z-axis. The results are shown in Figure 5, which distinguishes the states based on the quantum number l, as previously discussed. Both levels whose energy decreases with the magnetic field (typically of QDs) and levels whose energy increases (typically of QRs) are observed. Panels (a) and (c) show the first electron energies as a function of the magnetic field without an electric field and with an electric field of $F_z=10$ kV/cm applied to the nanostructure, respectively. From the comparison between them, it is concluded that the electric field does not alter the main features of the electronic structure, but increases the energies associated with all states. As discussed in Figure 4, the accumulation of states observed corresponds to the emergence of the ring states. Panels (b) and (d) correspond to a zoom of the shadow region in panels (a) and (c), respectively. The Aharanov-Bohm oscillations, typical of this kind of structure [49], are observed.

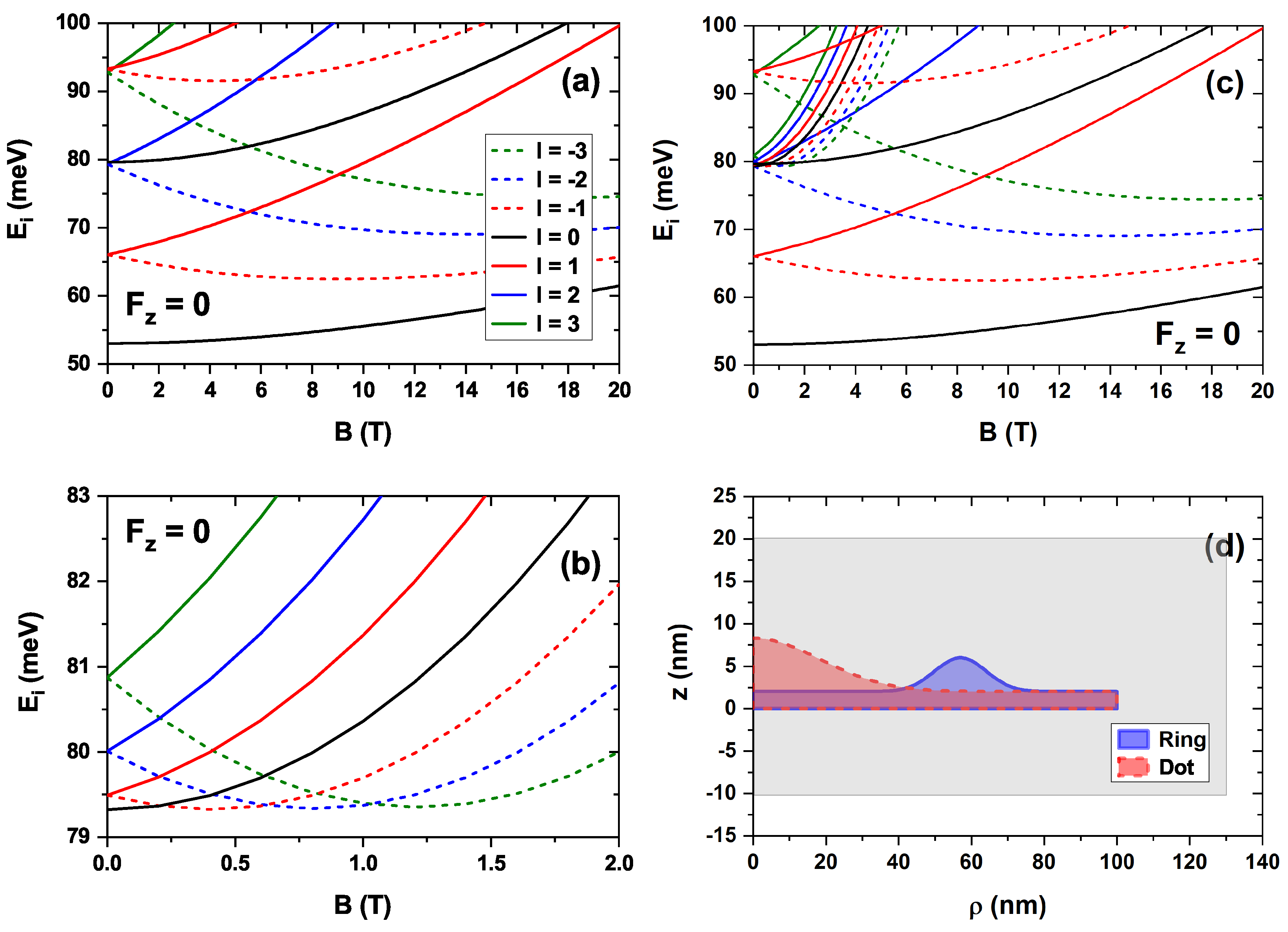
The energy spectrum observed in Figure 5 can be better understood by decomposing the CDQR into a colloidal quantum dot (CQD) and a colloidal quantum ring (CQR) with the same wetting layer and dimensions as those shown in Figure 1. The results of this decomposition are shown in Figure 6, where panel (a) corresponds to the CQD and panel (b) corresponds to the CQR. The magnetic field sweep is selected according to panels (a) and (c) of Figure 5. For simplicity, only the case with no external electric field applied to the nanostructure is analyzed. The superposition of panels (a) and (b) of Figure 6 is shown in panel (c), from which it is clear that the results obtained for the CQDR in Figure 5 (a) and (c) are consistent with the aforementioned decomposition of the nanostructure, where the coupling between its components causes them to interact and exhibit slight differences.

The second part of this work is devoted to calculating the EIT in the ladder configuration and LOAC for various values of the electric and magnetic fields.

To begin with, Figure 7 illustrates the EIT calculation as a function of the probe field energy, $E_p$, and the LOAC as a function of the incident photon energy, $E_{ph}$, for three different values of the electric field with and without a magnetic field applied to the nanostructure. Looking at panel (a) of Figure 7, it is straightforward that the two peaks associated with the EIT present a slightly appreciable blueshift as the absolute value of the electric field increases. Additionally, it is worth noting that the magnitude of the peaks also increases with the absolute value of the electric field. Finally, a particularity arises for the positive value of the electric field, where no EIT is observed. The latter is due to the term of the electric dipole moment matrix corresponding to the transitions involved in the ladder configuration, i.e., between the ground and the first two excited states. This kind of EIT requires an allowed $|1\rangle \to |2\rangle$ transition and a nearly suppressed $|1\rangle \to |3\rangle$ transition. The panel (a) of Figure 6 illustrates how these matrix terms change their behavior at approximately $F=-7.5$ kV/cm, making zero the EIT for positive F-values. The blueshift is justified by the energy levels features shown in Figure 4 (a). When a magnetic field $B=10$ T is applied together with the electric field, the EIT in the ladder configuration is observed for positive and negative values of the electric field. This is illustrated on panel (b) of Figure 7 and is justified by the dipole moment matrix terms displayed in Figure 8(b). A slight blueshift occurs as the electric field ranges from positive to negative values. On the other hand, shadowed regions on panels (a) and (b) of Figure 7 show the LOAC as a function of the incident photon energy, which is centered at the minimum located between the two EIT peaks. Again, the term of the zero electric dipole matrix for the transition $|1\rangle \to |2\rangle$ at positive electric field values is responsible for the zero LOAC in (a).

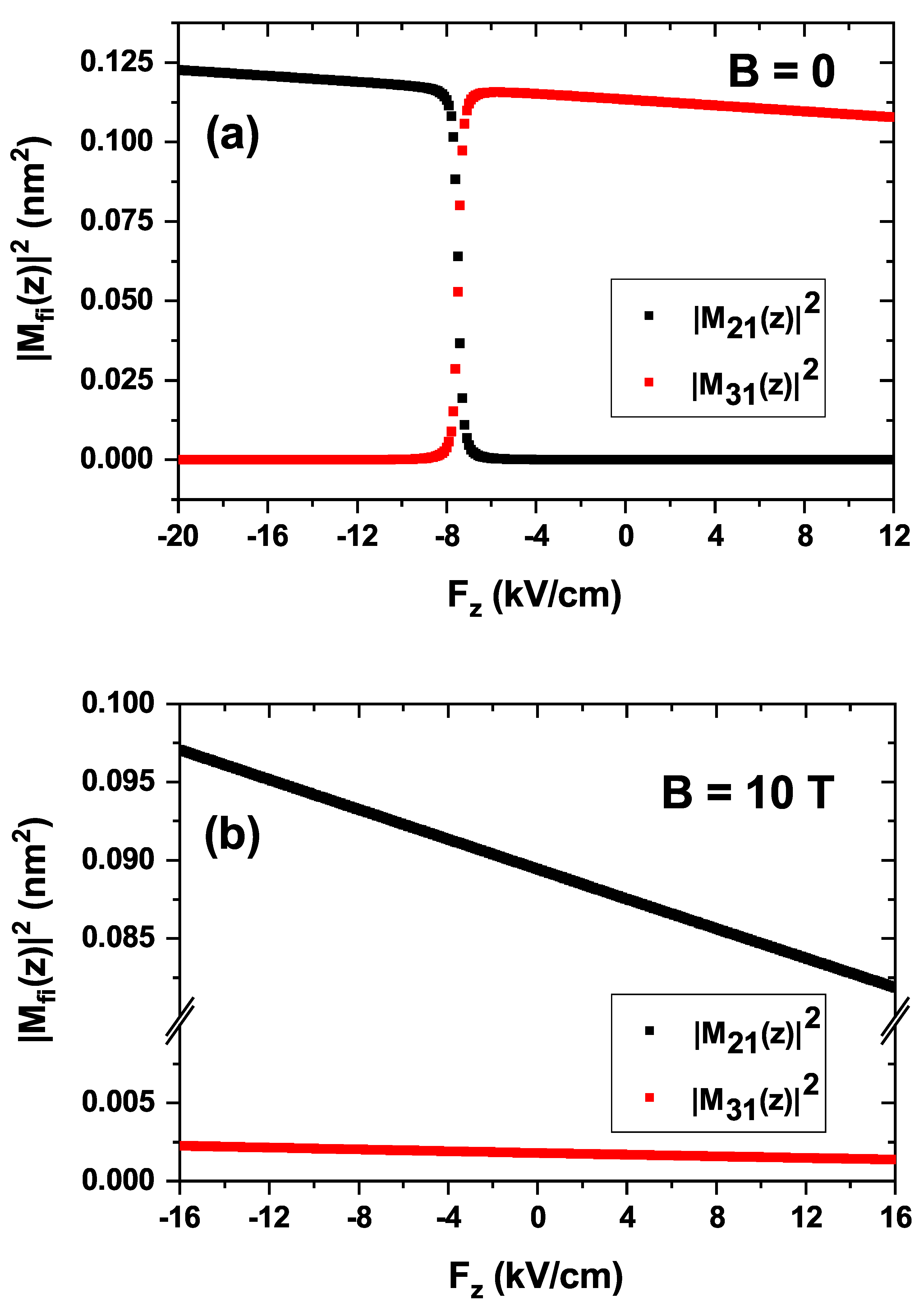
The behavior of the dipole matrix terms shown in Figure 8, which directly impacts the EIT spectra in Figure 7, is governed by the energy shifts of the electronic states under external fields. To illustrate this dependence, Figure 9 plots the energies of the first three states with angular momentum $l=0$, denoted as $E_{i,l}$ (where $i=1,2,3$ is the principal quantum number and $l=0$), as a function of the applied electric field. Panel (a) shows the case without a magnetic field (B = 0 T), while panel (b) corresponds to a magnetic field (B = 10 T). The gray shaded areas indicate the specific electric field values used for the calculations in Figure 7.

To better visualize the non-linear component of the Stark effect, which is crucial for determining the dipole moments, a dominant linear trend has been subtracted from the energy values. This data processing step allows the quadratic shifts and level anti-crossings which are otherwise obscured to be clearly observed, providing a direct insight into the physics governing the dipole matrix elements.

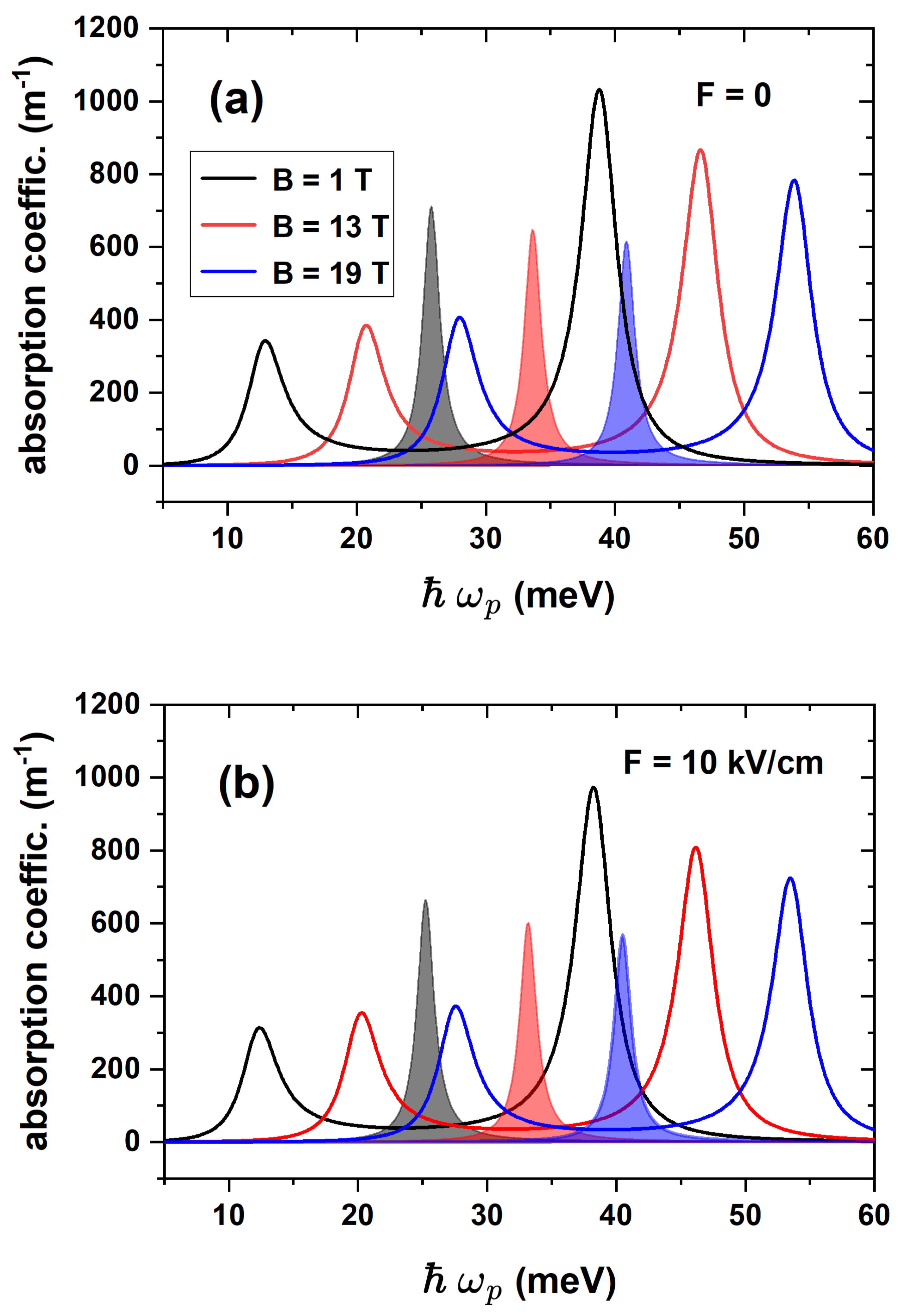
Figure 10 illustrates the dependence of the EIT and LOAC on the magnetic field, both in the absence and presence of an external electric field. Panel (a) shows the results for a zero electric field, it is clear that the EIT peaks shift toward higher energies as the magnetic field strength increases and that the LOAC peaks undergo the same energy shift. Panel (b) is homologous to (a), but subjecting the system to an external electric field of $F=10$ kV/cm. Comparing the EIT and LOAC peaks in both panels, it is straightforward that the effect of the electric field is practically negligible compared to the magnetic field, with only a slight variation in the magnitude and position of the peaks being observed. The magnitude of the EIT peaks decreases slightly between (a) and (b), and the shift of the peaks to lower energies in the presence of the electric field is practically imperceptible. The electric field causes once more the emergence of the LOAC peaks at lower energies and their magnitude to be slightly lower compared to the case without the electric field. All this is justified by the electronic structure shown in Figure 5.

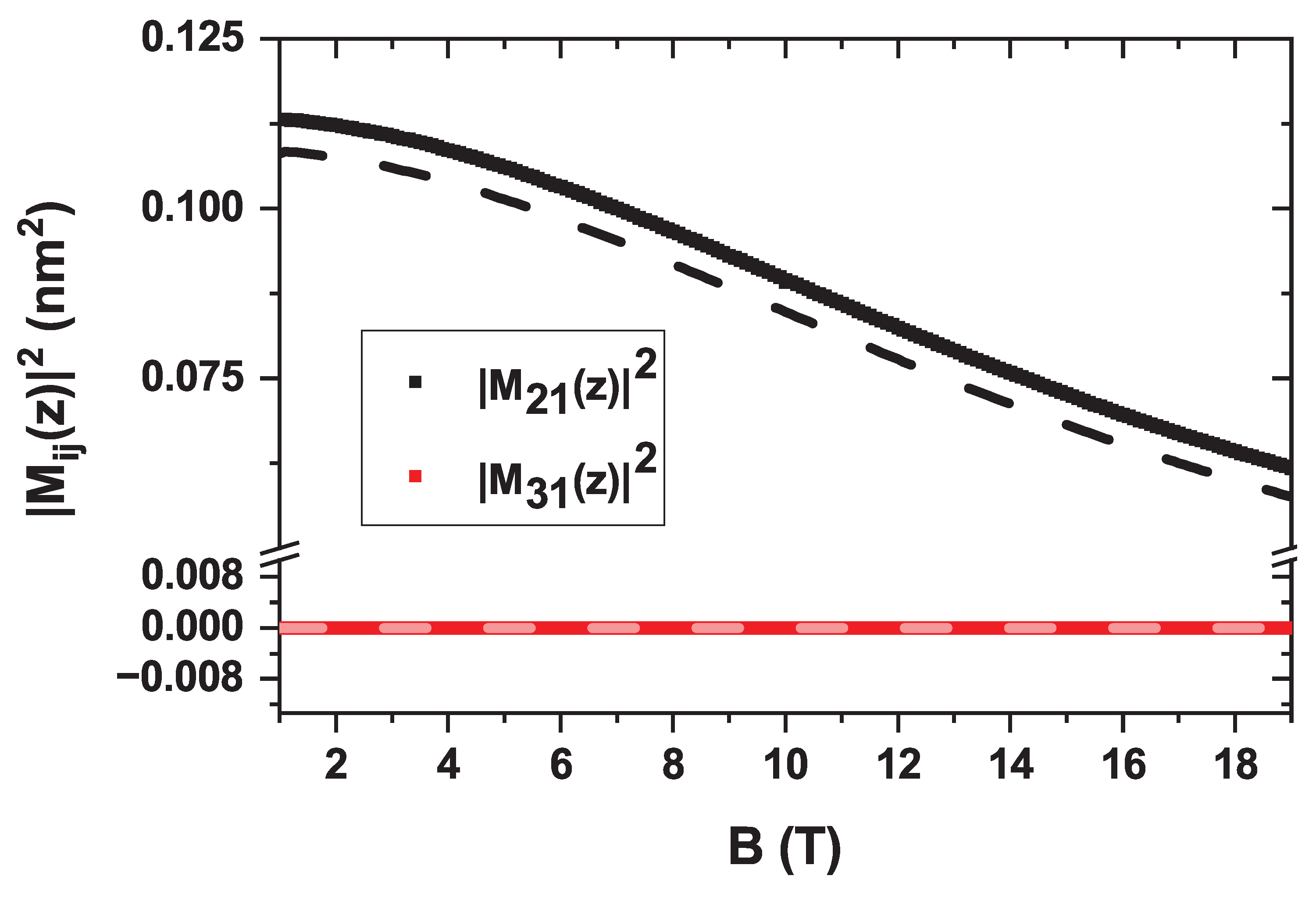
In contrast to Figure 7, the non-zero EIT shown in Figure 10 is explained by the behavior of the electric dipole matrix elements, which are depicted in Figure 11. This figure displays the squared dipole moments for the $|1\rangle \to |2\rangle$ transition (${\tilde{M}}_{21}$) and the $|1\rangle \to |3\rangle$ transition (${\tilde{M}}_{31}$) as a function of the magnetic field. The results are shown for both a zero electric field (solid lines) and an external electric field of $F=10$ kV/cm (dashed lines).

A direct comparison between the solid and dashed curves reveals that the influence of the electric field on the dipole moments is minimal, confirming that the system’s optical response is predominantly governed by the magnetic field. The most significant trend observed is the systematic decrease of the primary dipole matrix element, ${\tilde{M}}_{21}$, as the magnetic field strength increases. This behavior is a direct consequence of magnetic confinement. The applied Lorentz force radially compresses the electron wavefunctions, leading to a reduced spatial overlap for the dipole transition. Consequently, the magnitude of ${\tilde{M}}_{21}$ is diminished, which directly suppresses the transition probability and, therefore, the overall absorption intensity [50]. It is also noteworthy that the ${\tilde{M}}_{31}$ element is nearly zero across the entire range, indicating that the $|1\rangle \to |3\rangle$ transition is dipole-forbidden for this light polarization, consistent with the selection rules.

4. Conclusions

In this study, we have analyzed the electronic structure and optical properties of a ${\mathrm{GaAs/Al}}_{0.3}{\mathrm{Ga}}_{0.7}$As CQDR system under the influence of external electric and magnetic fields. Using a finite element method within the effective mass approximation, we have demonstrated that both fields significantly influence the confined electron energy levels, with the magnetic field producing notable Aharonov-Bohm oscillations and a more substantial impact on the energy spectrum than the electric field. These external fields not only shift the electronic states but also modulate the LOAC and EIT behavior, thereby providing mechanisms for dynamic control of the nanostructure’s optoelectronic response.

The EIT phenomenon in a ladder configuration was thoroughly investigated, revealing that its occurrence and intensity are highly sensitive to the direction and magnitude of the applied electric field. In particular, a suppression of EIT was observed for positive electric field values in the absence of a magnetic field, an effect traced to vanishing dipole transition matrix elements. Conversely, applying a magnetic field restored the EIT for all electric field values, leading to an overall enhancement in the tunability of optical transparency and absorption. These findings highlight the superior role of magnetic fields in precisely modulating light-matter interactions in CQDRs.

Overall, our results demonstrate that CQDR systems are promising platforms for developing tunable optoelectronic devices, with magnetic fields offering a more robust control parameter than electric fields for manipulating EIT and LOAC. These findings contribute to the understanding of quantum interference effects in complex nanostructures, opening pathways for their application in photonic devices and quantum information processing technologies.