A Short Computer Program That Computes in the Limit a Non-Computable Function from N to N

1. A program that computes in the limit a function $f:\mathbb{N}\to \mathbb{N}$ which eventually dominates every computable function $g:\mathbb{N}\to \mathbb{N}$

Theorem 1. 

([5, p. 118]). There exists a limit-computable function $f:\mathbb{N}\to \mathbb{N}$ which eventually dominates every computable function $g:\mathbb{N}\to \mathbb{N}$.

We present an alternative proof of Theorem 1. For $n\in \mathbb{N}$, $f\left(n\right)$ denotes the smallest $b\in \mathbb{N}$ such that if a system of equations $\mathcal{S}\subseteq E_n$ has a solution in ${\mathbb{N}}^{n+1}$, then $\mathcal{S}$ has a solution in ${\{0,\dots ,b\}}^{n+1}$. The function $f:\mathbb{N}\to \mathbb{N}$ is computable in the limit and eventually dominates every computable function $g:\mathbb{N}\to \mathbb{N}$, see [7]. 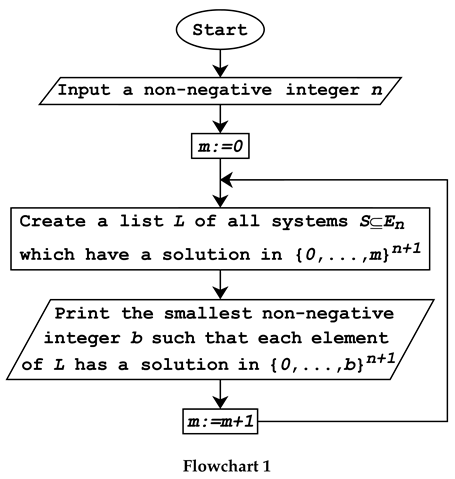The term "dominated" in the title of [7] means "eventually dominated". Flowchart 1 shows a semi-algorithm which computes $f\left(n\right)$ in the limit, see [7].

A semi-algorithm which computes $f\left(n\right)$ in the limit

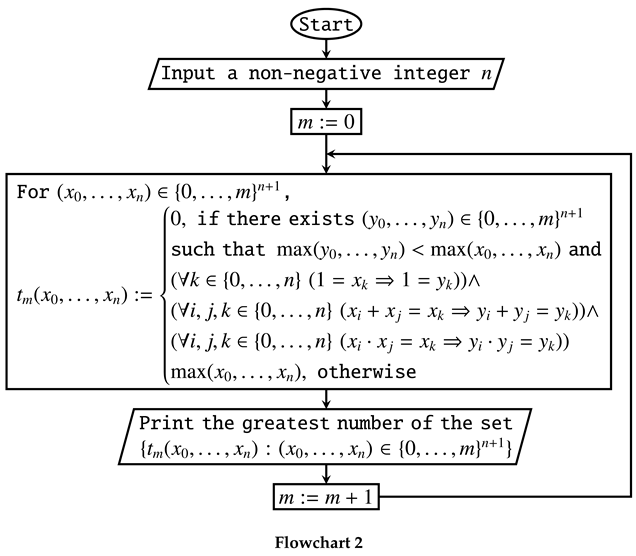
Flowchart 2 shows a simpler semi-algorithm which computes $f\left(n\right)$ in the limit.

A simpler semi-algorithm which computes $f\left(n\right)$ in the limit

Lemma 1. 

For every $n,m\in \mathbb{N}$, the number printed by Flowchart 2 does not exceed the number printed by Flowchart 1.

Proof. 

For every $(a_0,\dots ,a_n)\in {\{0,\dots ,m\}}^{n+1}$,

$$E_n\supseteq \{1=x_k:(k\in \{0,\dots ,n\})\wedge (1=a_k)\}\cup$$

$$\{x_i+x_j=x_k:(i,j,k\in \{0,\dots ,n\})\wedge (a_i+a_j=a_k)\}\cup$$

$$\{x_i·x_j=x_k:(i,j,k\in \{0,\dots ,n\})\wedge (a_i·a_j=a_k)\}$$

   □

Lemma 2. 

For every $n,m\in \mathbb{N}$, the number printed by Flowchart 1 does not exceed the number printed by Flowchart 2.

Proof. 

Let $n,m\in \mathbb{N}$. For every system of equations $\mathcal{S}\subseteq E_n$, if $(a_0,\dots ,a_n)\in {\{0,\dots ,m\}}^{n+1}$ and $(a_0,\dots ,a_n)$ solves $\mathcal{S}$, then $(a_0,\dots ,a_n)$ solves the system of equations

$$\tilde{\mathcal{S}}:=\{1=x_k:(k\in \{0,\dots ,n\})\wedge (1=a_k)\}\cup$$

$$\{x_i+x_j=x_k:(i,j,k\in \{0,\dots ,n\})\wedge (a_i+a_j=a_k)\}\cup$$

$$\{x_i·x_j=x_k:(i,j,k\in \{0,\dots ,n\})\wedge (a_i·a_j=a_k)\}$$

   □

Theorem 2. 

For every $n,m\in \mathbb{N}$, Flowcharts 1 and 2 print the same number.

Proof. 

It follows from Lemmas 1 and 2.    □

MuPAD is a part of the Symbolic Math Toolbox in MATLAB R2019b. The following program in MuPAD implements the semi-algorithm shown in Flowchart 2.

input("Input a non-negative integer n",n):

m:=0:

while TRUE do

X:=combinat::cartesianProduct([s $s=0..m] $t=0..n):

Y:=[max(op(X[u])) $u=1..(m+1)^(n+1)]:

for p from 1 to (m+1)^(n+1) do

for q from 1 to (m+1)^(n+1) do

v:=1:

for k from 1 to n+1 do

if 1=X[p][k] and 1<>X[q][k] then v:=0 end_if:

for i from 1 to n+1 do

for j from i to n+1 do

if X[p][i]+X[p][j]=X[p][k] and X[q][i]+X[q][j]<>X[q][k] then v:=0 end_if:

if X[p][i]*X[p][j]=X[p][k] and X[q][i]*X[q][j]<>X[q][k] then v:=0 end_if:

end_for:

end_for:

end_for:

if max(op(X[q]))<max(op(X[p])) and v=1 then Y[p]:=0 end_if:

end_for:

end_for:

print(max(op(Y))):

m:=m+1:

end_while:

The author is not aware about computer programs by other authors which compute in the limit non-computable functions from $\mathbb{N}$ to $\mathbb{N}$.

For $n\in \mathbb{N}$, $h\left(n\right)$ denotes the smallest $b\in \mathbb{N}$ such that if a system of equations $\mathcal{S}\subseteq \{x_i+1=x_k,x_i·x_j=x_k:i,j,k\in \{0,\dots ,n\}\}$ has a solution in ${\mathbb{N}}^{n+1}$, then $\mathcal{S}$ has a solution in ${\{0,\dots ,b\}}^{n+1}$. From [7] and Lemma 3 in [6], it follows that the function $h:\mathbb{N}\to \mathbb{N}$ is computable in the limit and eventually dominates every computable function $g:\mathbb{N}\to \mathbb{N}$. A bit shorter program in MuPAD computes h in the limit.

2. A program that computes in the limit a function $\beta :\mathbb{N}\to \mathbb{N}$ of unknown computability which eventually dominates every function $\delta :\mathbb{N}\to \mathbb{N}$ with a single-fold Diophantine representation

    The Davis-Putnam-Robinson-Matiyasevich theorem states that every listable set $\mathcal{M}\subseteq {\mathbb{N}}^n$$(n\in \mathbb{N}\setminus \{0\left\}\right)$ has a Diophantine representation, that is

$$(a_1,\dots ,a_n)\in \mathcal{M}⟺\exists x_1,\dots ,x_m\in \mathbb{N}W(a_1,\dots ,a_n,x_1,\dots ,x_m)=0\left(\mathtt{R}\right)$$

(1)

for some polynomial W with integer coefficients, see [2]. The representation (R) is said to be single-fold, if for any $a_1,\dots ,a_n\in \mathbb{N}$ the equation $W(a_1,\dots ,a_n,x_1,\dots ,x_m)=0$ has at most one solution $(x_1,\dots ,x_m)\in {\mathbb{N}}^m$.

Hypothesis 1. 

([1, pp. 341–342], [3, p. 42], [4, p. 745]). Every listable set $\mathcal{X}\subseteq {\mathbb{N}}^k$$(k\in \mathbb{N}\setminus \{0\left\}\right)$ has a single-fold Diophantine representation.

For $n\in \mathbb{N}$, $\beta \left(n\right)$ denotes the smallest $b\in \mathbb{N}$ such that if a system of equations $\mathcal{S}\subseteq E_n$ has a unique solution in ${\mathbb{N}}^{n+1}$, then this solution belongs to ${\{0,\dots ,b\}}^{n+1}$. The computability of $\beta$ is unknown.

Theorem 3. 

The function $\beta :\mathbb{N}\to \mathbb{N}$ is computable in the limit and eventually dominates every function $\delta :\mathbb{N}\to \mathbb{N}$ with a single-fold Diophantine representation.

Proof. 

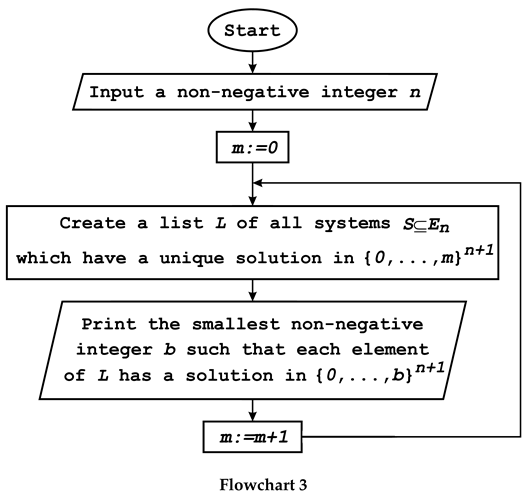
This is proved in [7]. Flowchart 3 shows a semi-algorithm which computes $\beta \left(n\right)$ in the limit, see [7].

A semi-algorithm which computes $\beta \left(n\right)$ in the limit    □

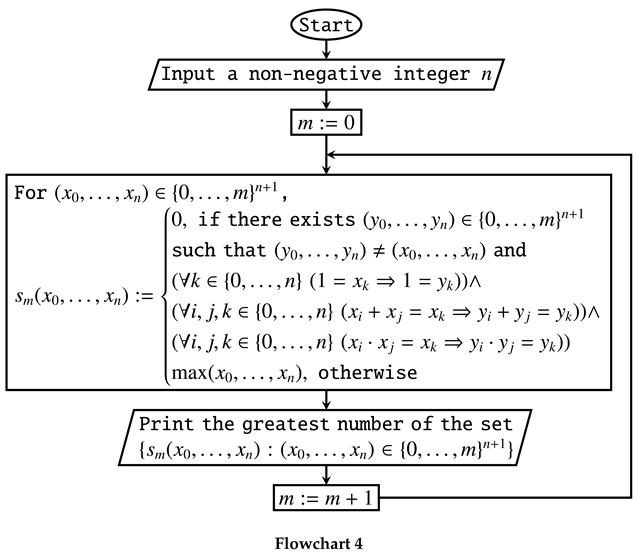
Flowchart 4 shows a simpler semi-algorithm which computes $\beta \left(n\right)$ in the limit.

A simpler semi-algorithm which computes $\beta \left(n\right)$ in the limit

Lemma 3. 

For every $n,m\in \mathbb{N}$, the number printed by Flowchart 4 does not exceed the number printed by Flowchart 3.

Proof. 

For every $(a_0,\dots ,a_n)\in {\{0,\dots ,m\}}^{n+1}$,

$$E_n\supseteq \{1=x_k:(k\in \{0,\dots ,n\})\wedge (1=a_k)\}\cup$$

$$\{x_i+x_j=x_k:(i,j,k\in \{0,\dots ,n\})\wedge (a_i+a_j=a_k)\}\cup$$

$$\{x_i·x_j=x_k:(i,j,k\in \{0,\dots ,n\})\wedge (a_i·a_j=a_k)\}$$

   □

Lemma 4. 

For every $n,m\in \mathbb{N}$, the number printed by Flowchart 3 does not exceed the number printed by Flowchart 4.

Proof. 

Let $n,m\in \mathbb{N}$. For every system of equations $\mathcal{S}\subseteq E_n$, if $(a_0,\dots ,a_n)\in {\{0,\dots ,m\}}^{n+1}$ is a unique solution of $\mathcal{S}$ in ${\{0,\dots ,m\}}^{n+1}$, then $(a_0,\dots ,a_n)$ solves the system of equations

$$\widehat{\mathcal{S}}:=\{1=x_k:(k\in \{0,\dots ,n\})\wedge (1=a_k)\}\cup$$

$$\{x_i+x_j=x_k:(i,j,k\in \{0,\dots ,n\})\wedge (a_i+a_j=a_k)\}\cup$$

$$\{x_i·x_j=x_k:(i,j,k\in \{0,\dots ,n\})\wedge (a_i·a_j=a_k)\}$$

By this and the inclusion $\widehat{\mathcal{S}}\supseteq \mathcal{S}$, $\widehat{\mathcal{S}}$ has exactly one solution in ${\{0,\dots ,m\}}^{n+1}$, namely $(a_0,\dots ,a_n)$.    □

Theorem 4. 

For every $n,m\in \mathbb{N}$, Flowcharts 3 and 4 print the same number.

Proof. 

It follows from Lemmas 3 and 4.    □

The following program in MuPAD implements the semi-algorithm shown in Flowchart 4.

input("Input a non-negative integer n",n):

m:=0:

while TRUE do

X:=combinat::cartesianProduct([s $s=0..m] $t=0..n):

Y:=[max(op(X[u])) $u=1..(m+1)^(n+1)]:

for p from 1 to (m+1)^(n+1) do

for q from 1 to (m+1)^(n+1) do

v:=1:

for k from 1 to n+1 do

if 1=X[p][k] and 1<>X[q][k] then v:=0 end_if:

for i from 1 to n+1 do

for j from i to n+1 do

if X[p][i]+X[p][j]=X[p][k] and X[q][i]+X[q][j]<>X[q][k] then v:=0 end_if:

if X[p][i]*X[p][j]=X[p][k] and X[q][i]*X[q][j]<>X[q][k] then v:=0 end_if:

end_for:

end_for:

end_for:

if q<>p and v=1 then Y[p]:=0 end_if:

end_for:

end_for:

print(max(op(Y))):

m:=m+1:

end_while: