Submitted:
17 May 2023
Posted:
18 May 2023
You are already at the latest version
Abstract
Keywords:
MSC: 11D61; 11D85
1. Epistemic Notions Increase the Scope of Mathematics
2. Composite Numbers of the Form
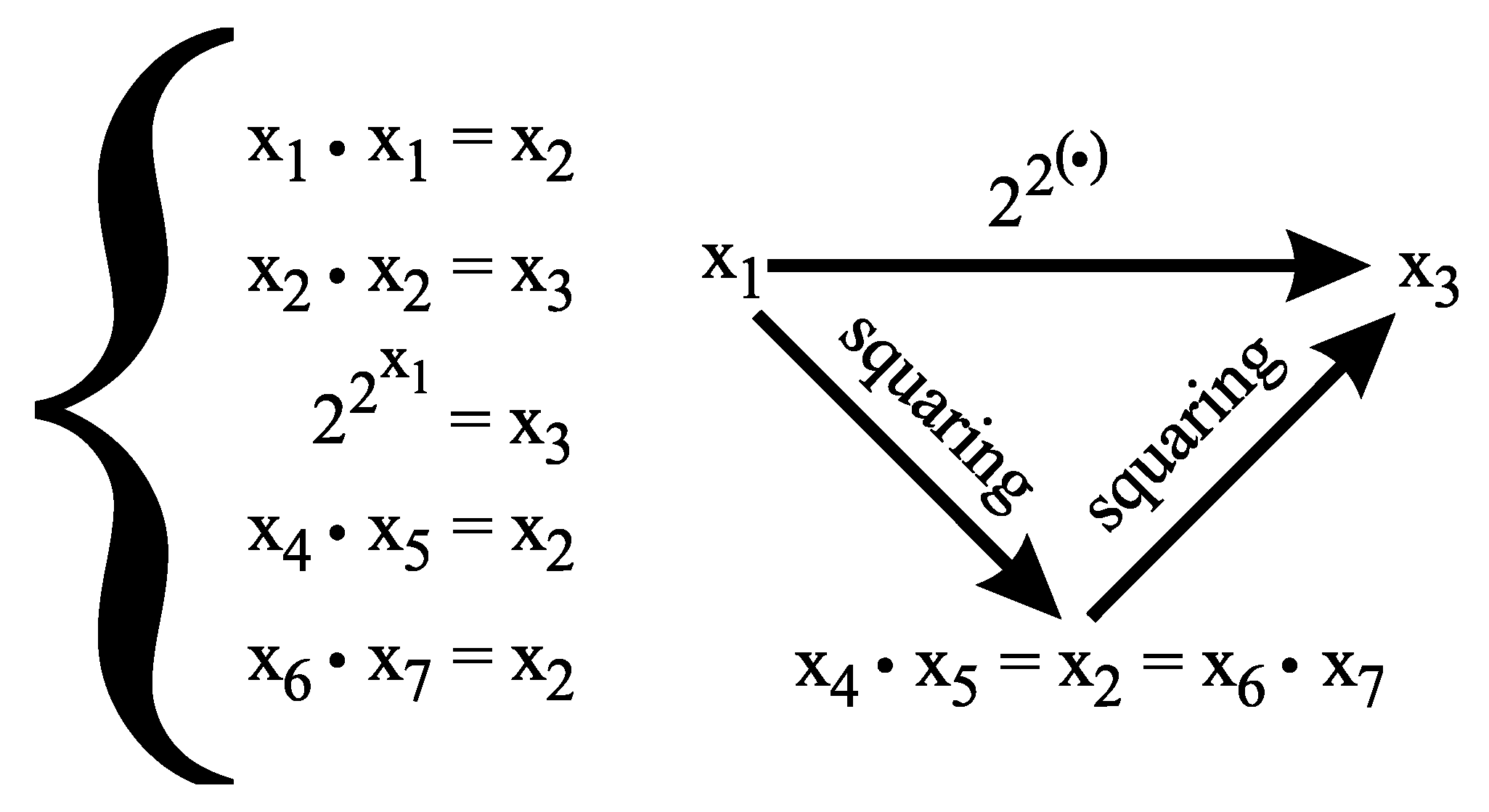
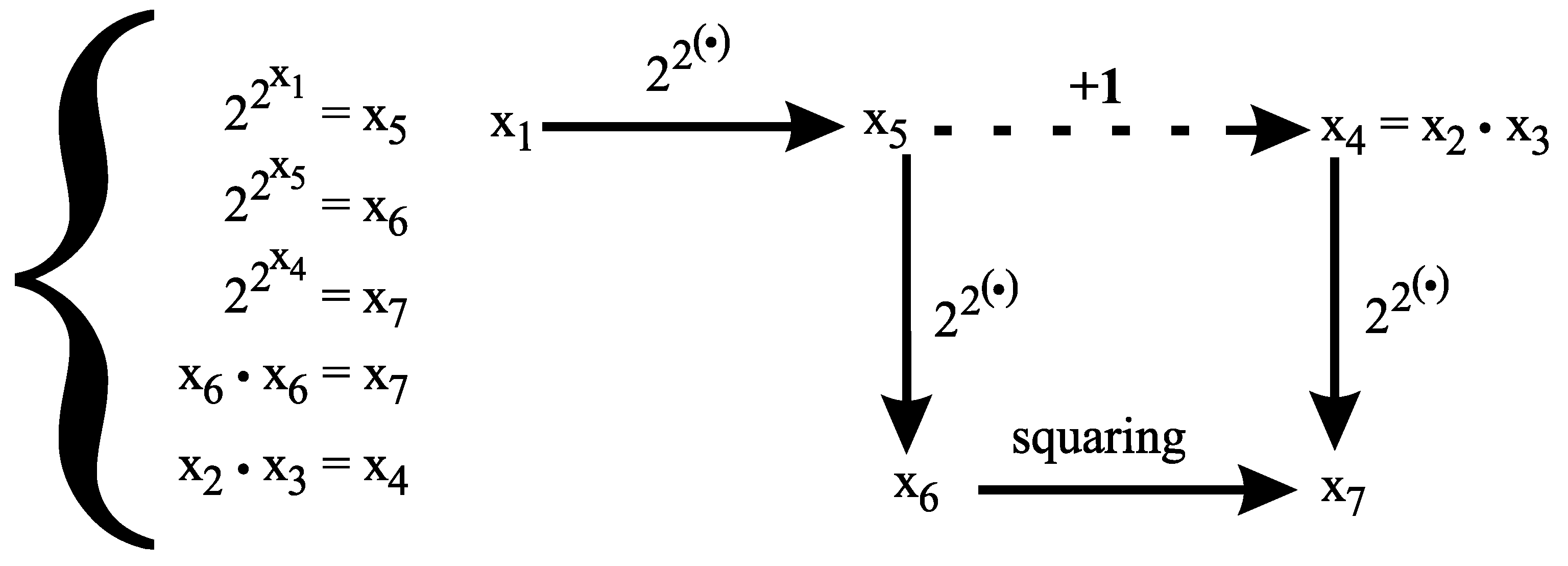
3. The Brocard-Ramanujan equation
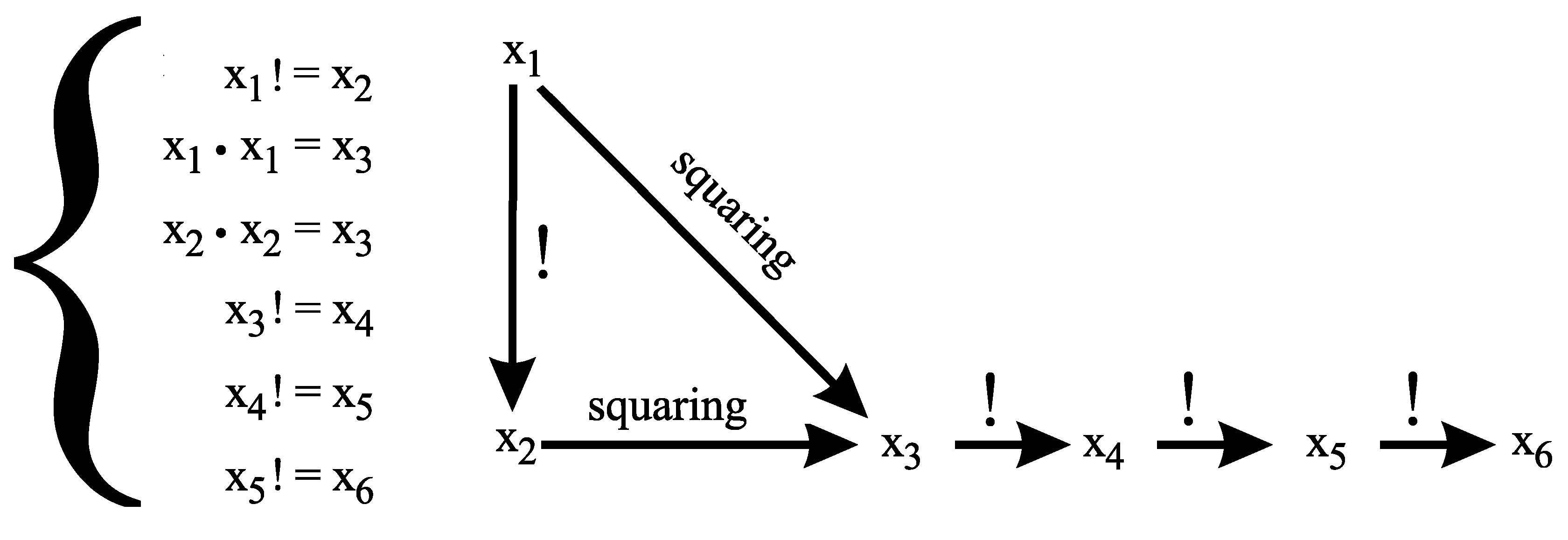
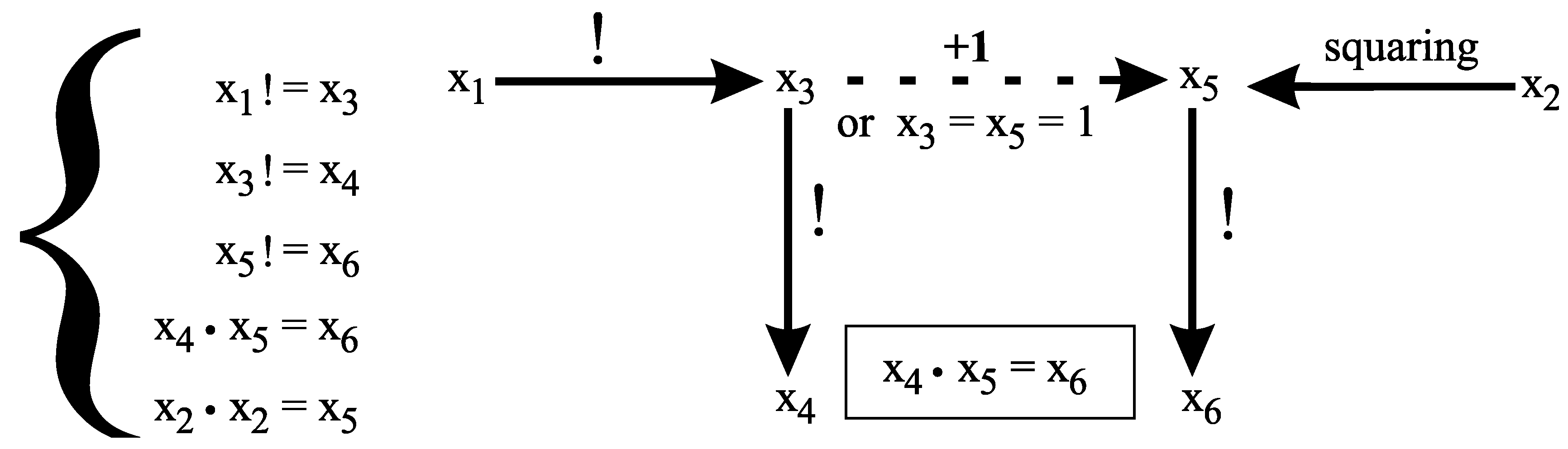
4. Erdös’ Equation
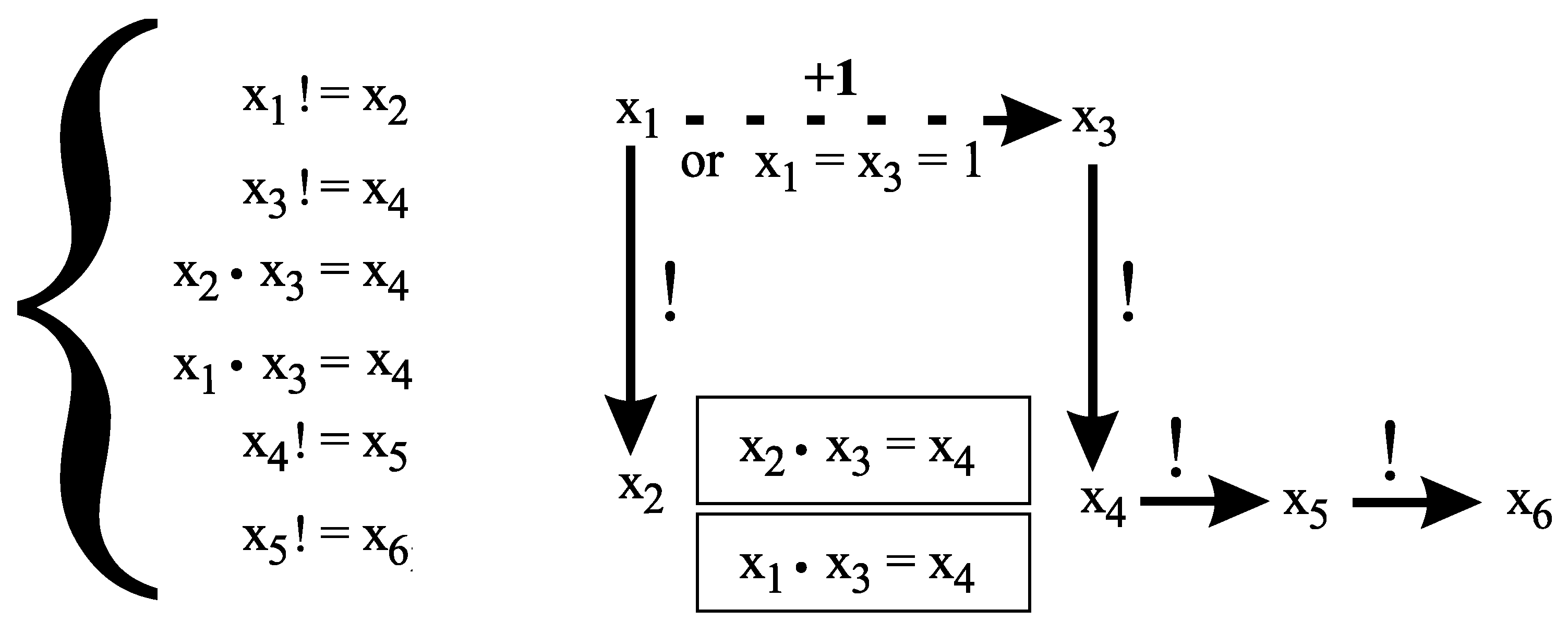
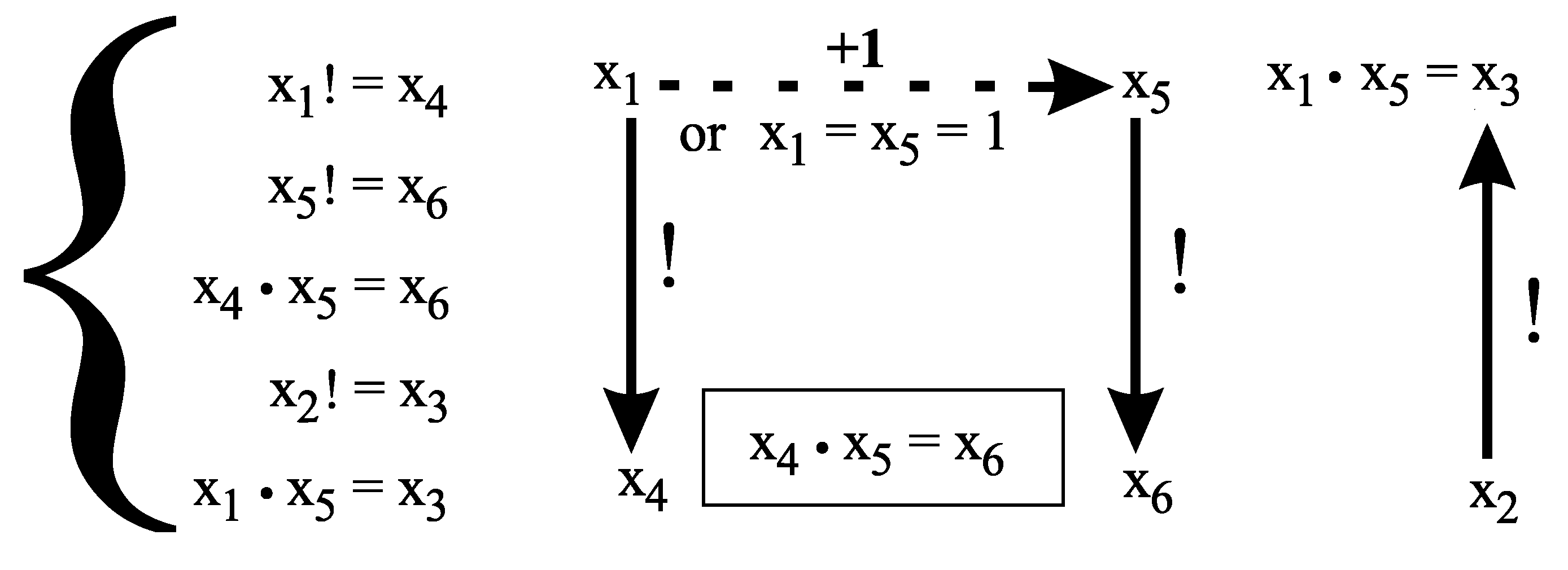
5. Conjectures 3 and 5 Cannot Be Generalized to An Arbitrary Number of Variables
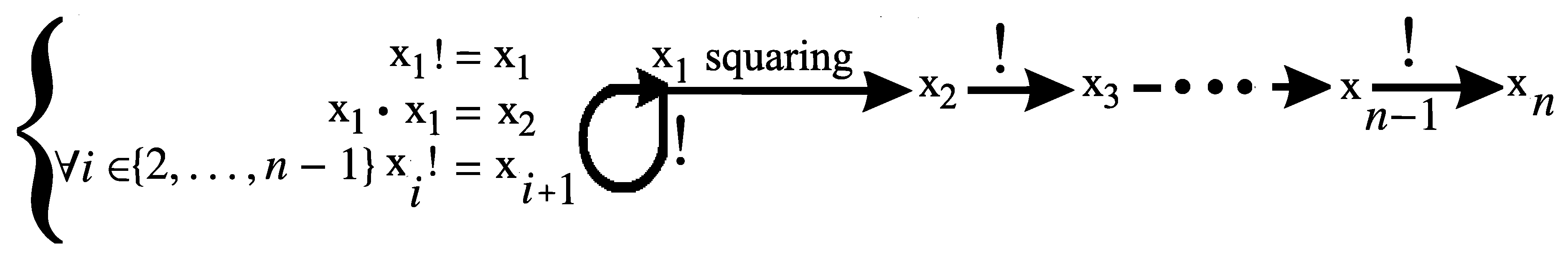
6. Equivalent Forms of Conjectures 1–5
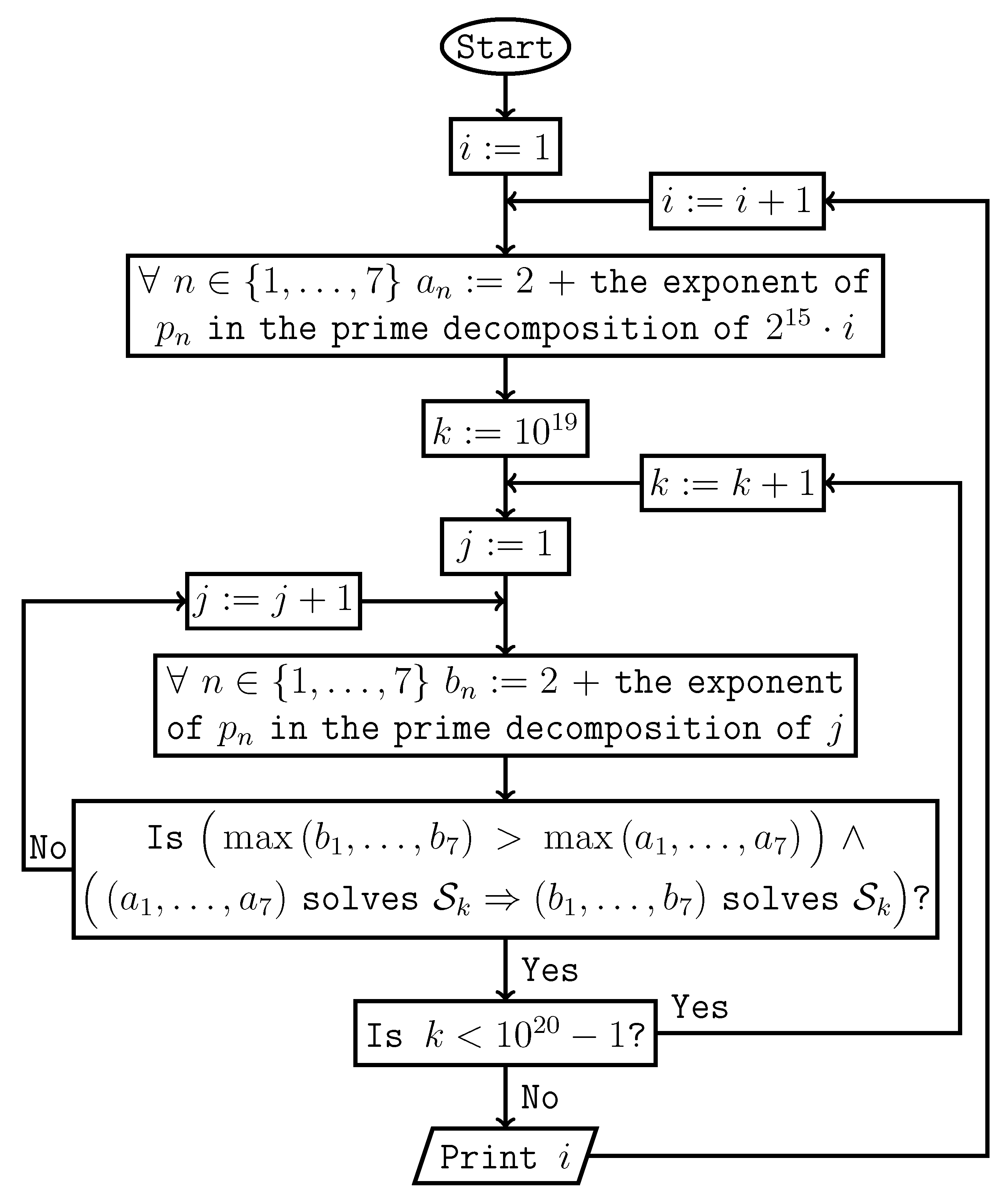
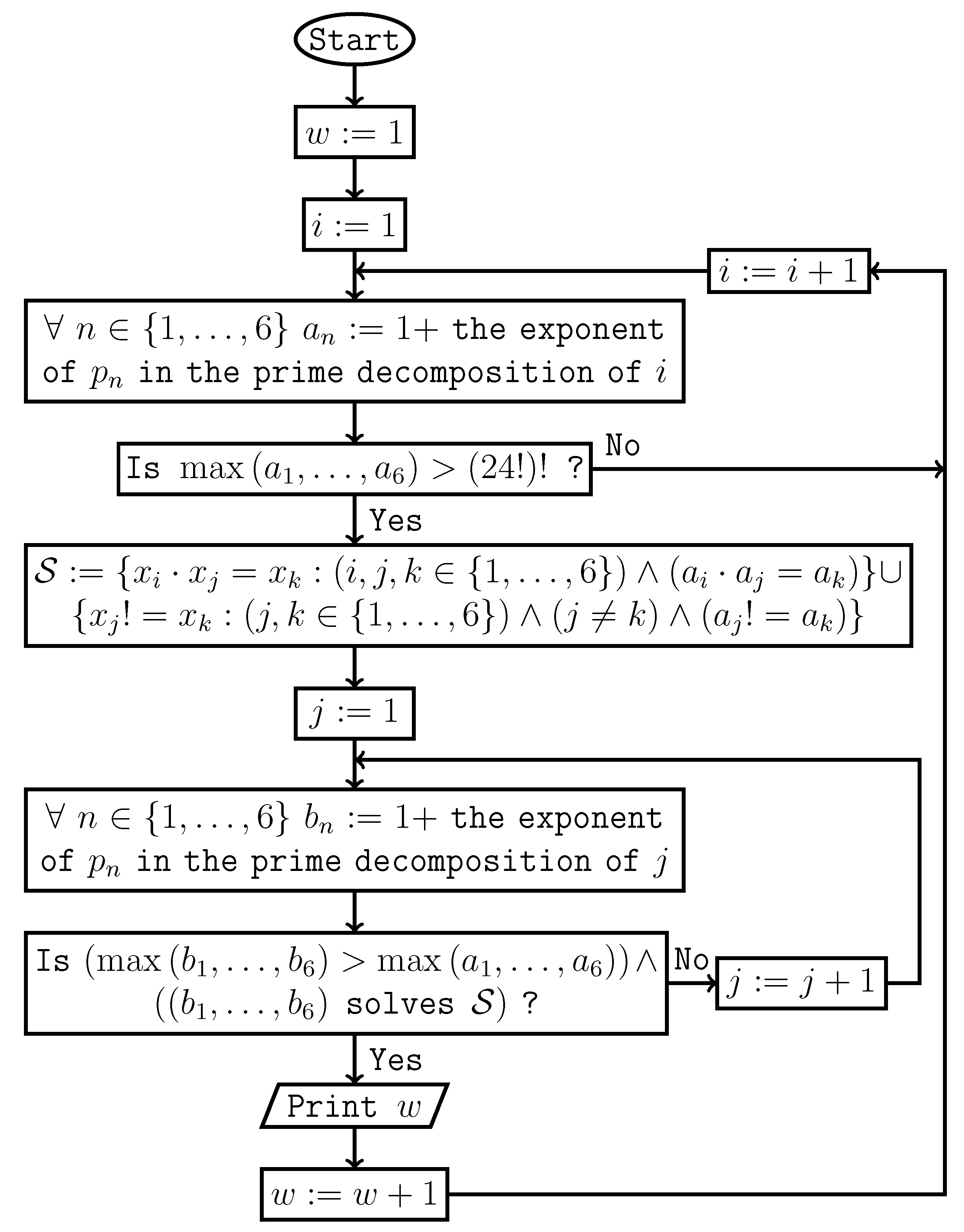
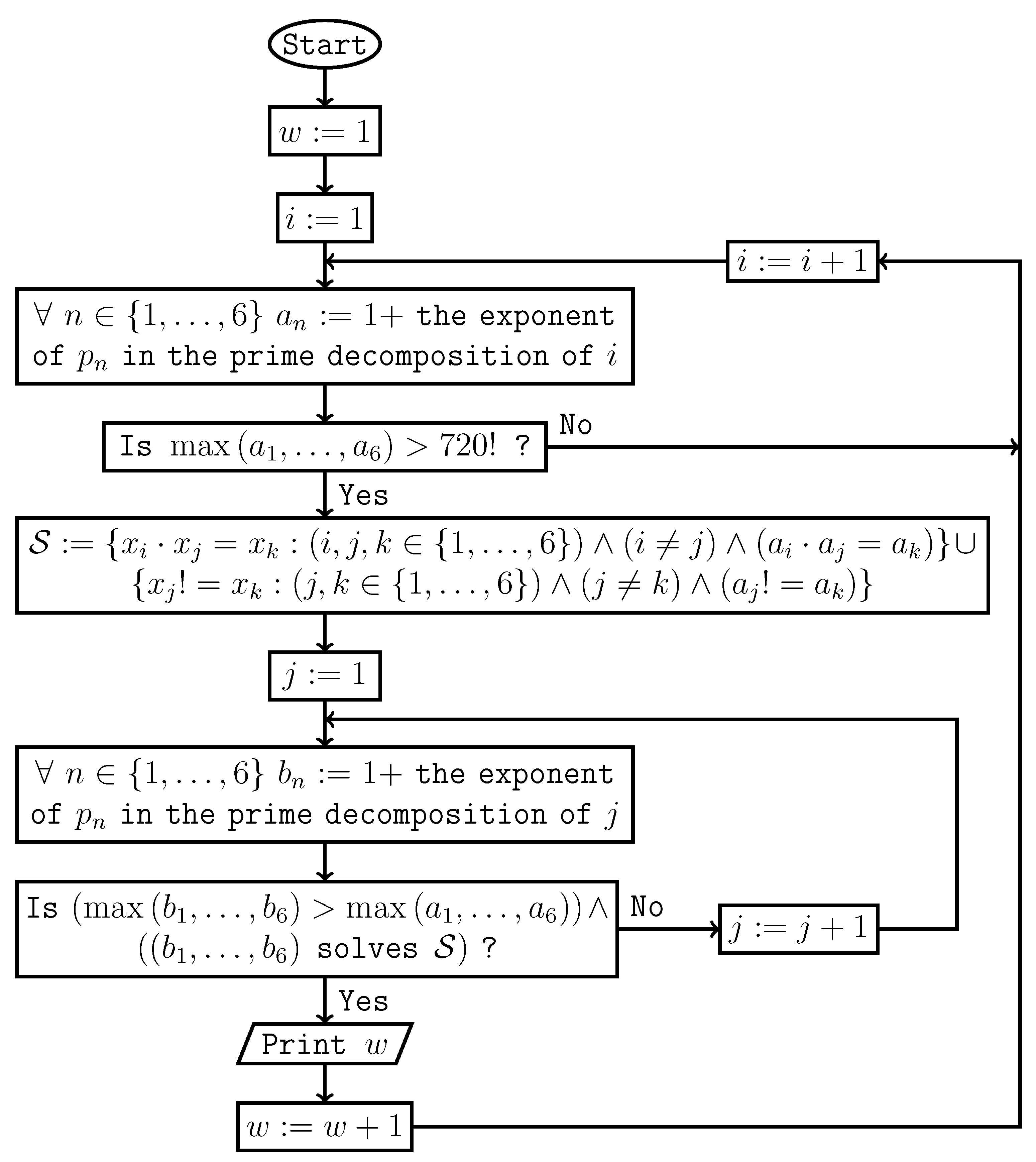
References
- N. D. Goodman, The Knowing Mathematician. Synthese 1984, 60, 21–38, Available online: http://link.springer.com/article/10.1007/BF00485616 Reprinted in: H. Leblanc, E. Mendelson, A. Orenstein, Foundations: Logic, Language, and Mathematics, Springer, 1984; pp. 21–38, Available online: http://link.springer.com/book/10.1007/978-94-017-1592-8.
- A. Tyszka, A hypothetical upper bound on the heights of the solutions of a Diophantine equation with a finite number of solutions. Open Comput. Sci. 2018,8, 109–114. [CrossRef]
- J.-M. De Koninck and F. Luca. Analytic Number Theory: Exploring the Anatomy of Integers; American Mathematical Society: Providence, RI, 2012.
- M. Křížek, F. Luca, L. Somer, 17 Lectures on Fermat Numbers: From Number Theory to Geometry, Springer: New York, 2001.
- D. Berend and J. E. Harmse, On polynomial-factorial Diophantine equations, Trans. Amer. Math. Soc.2006, 358, 1741–1779.
- F. Luca, The Diophantine equation P(x) = n! and a result of M. Overholt, Glas. Mat. Ser. III 2002, 37, 269–273.
- Yu. Matiyasevich, Existence of noneffectivizable estimates in the theory of exponential Diophantine equations, J. Sov. Math. 1977, 8, 299–311. [CrossRef]
- E. W. Weisstein. CRC Concise Encyclopedia of Mathematics, 2nd ed., Chapman & Hall/CRC: Boca Raton, FL, 2002.
- M. Overholt, The Diophantine equation n! + 1 = m2, Bull. London Math. Soc.1993, 25, 104.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




