1. Introduction
Space robotics has been a very active research area in the past decade due to its potential and important applications in on-orbit servicing (OOS) whose term implies maintenance of space systems in orbit [
1,
2]. OOS operations include assembly, refueling, repair and upgrading of spacecraft after being deployed. However, the US National Aeronautics and Space Administration (NASA) already recognized the importance of robotics for space operations as early as the 1980s [
3,
4] and considered using robot manipulators and astronauts to construct the International Space Station (ISS) as the first step to establish permanent human presence in space [
5]. In light of the potential danger astronauts could encounter while constructing the ISS in space, NASA’s intention to build the ISS sparked an intensive and controversial debate in the space community about whether or not the ISS construction should be carried out fully robotically or by an optimal balance of astronauts and autonomous robots. In the end, the ISS was built through a collaboration between astronauts and robot manipulators such as the Canadarm, well-known as the Shuttle Remote Manipulator System (SRMS) and the Canadarm2, well-known as the Space Station Remote Manipulator system (SSRMS) [
6]. The SRMS and the SSRMS were used to deploy, retrieve, and maneuver large modules and other heavy pieces of equipment in the Shuttle’s cargo bay or from the ISS for installation onto a location of the ISS. They were also employed to carry and position astronauts during spacewalks and to provide them with a stable platform to work from. On the other hand, astronauts, after being placed at a desired location by the above manipulators, carried out tasks including joining modules, installing equipment, and making crucial connections for power, data, and fluid lines, sometimes manually or with robotic assistance. In addition, astronauts inside the Space Shuttle or the ISS teleoperated the above manipulators to maneuver modules, deploy elements, and berth visiting spacecraft. NASA’s initial vision of using fully autonomous robots to construct the ISS was not realized due to the lack of advanced technology in the 1990’s for the development of sophisticated robots to perform complicated tasks required for the construction.
During the last decade, advancements in AI and related areas including smart sensors, smart materials, soft actuators, machine learning and intelligent control have substantially motivated researchers to develop robot manipulators capable of autonomously performing complicated tasks for space operations without human intervention [
2]. In order to be autonomous and effective, manipulators should be equipped with position and vision sensors to be aware of their locations and force sensors to effectively interact with their working environment. In addition, robotic controllers should be developed to take sensor information and work in a closed-loop mode to automatically control the position and force of the manipulator to achieve the task objective.
Traditional robot manipulators whose joints and links are actuated in series are classified as serial robot manipulators (SRM) [
7]. SRMs generally have long reach, large workspace and are capable of entering small spaces because of their compactness. However, their cantilever-like structure causes them to have low stiffness and consequently undesirable dynamic characteristics, especially at high speed and large payload. In addition, they have low strength-to-weight ratios due to the fact that the payload is not uniformly distributed to the actuators. Finally, the fact that relatively large position error occurs at the last link because the joint errors are accumulated throughout manipulator structure suggests that SRMs are not suitable for high precision tasks such as part assembly. On the other hand, robot manipulators whose actuators are arranged in parallel are classified as parallel robot manipulators (PRM) and generally have relatively small workspace and low maneuverability. In return to these disadvantages, they possess high positioning capability produced by their high structural rigidity and noncumulative actuator errors. PRMs also have higher strength-to-weight ratios as compared to SRMs because the payload is proportionally distributed to the links. Finally, the inverse kinematics of PRMs has simple closed-form solutions.
Implementation of the parallel structure concept first appeared in the Stewart Platform [
8] which was originally designed as an aircraft simulator. A typical Stewart Platform consists of two platforms driven by a number of parallel actuators. The invention of the Stewart platform has attracted tremendous robot designer’s attention, and its mechanism was used in many robotic applications [
9,
24]. Dieudonne [
10] and his coworkers de-rived an actuator extension transformation and presented experimental results of a Stew-art Platform-based simulator built at NASA Langley Research Center to train aircraft operators. A finite element program was used by Hoffman and McKinnon [
11] to simulate the motion of the Stewart Platform whose mechanism was later applied by McCallion and Truong [
12] to design an automatic assembly table. Hunt [
13] conducted a systematic study of in-parallel-actuated robot arms and presented the structural kinematic problem of this type of manipulators. Sugimoto and Duffy [
14] developed a general technique to describe the instantaneous link motion of a single closed-loop mechanism by employing linear algebra elements to screw systems. Kinematic problems and practical construction of the Stewart Platform were later considered by Fichter [
17]. Sugimoto [
18] studied kinematics and dynamics of parallel manipulators and Lee [
19] derived dynamical equations for a 3 degree-of-freedom (DOF) CKC manipulator. Nguyen and Pooran [
20] developed a learning control scheme for a 2 DOF CKC manipulator performing repetitive tasks.
An autonomous wrist for space assembly (AWSA) was developed and built as a prototype to investigate the feasibility of robotic assembly in space, which required the wrist to have the ability to autonomously perform fine and precise compliant motion [
21]. Parallel structure instead of serial structure was selected for the design of the AWSA due to its accurate positioning capability despite its small workspace and low maneuverability, which does not pose an issue for part assembly. The AWSA with its six linear actuators driven by dc motors and ball screw drives enables an end-effector attached to it to carry out the delicate motions required for assembly tasks.
The paper is organized as follows.
Section 2 gives an overview of robotic construction of the international space station (ISS) and
Section 3 describes the main components of the AWSA and their functions. The design and component selection of the linear dc actuator for the AWSA will be presented and discussed in
Section 4.
Section 5 provides a brief analysis of the AWSA inverse and forward kinematics and
Section 6 discusses three control schemes proposed for motion control of the AWSA. Concluding the paper,
Section 7 provides a summary of the paper’s contents and offers future research directions.
2. Robotic Construction of the International Space Station
In 1984, President Ronald Reagan approved the construction of the International Space Station (ISS) with international partners including Canada, Japan and Russia and many nations of the European Space Agency [
6]. The design of the ISS took place between 1984 and 1993, and its components were built all over the US, Canada, Japan, and Europe starting in the late 1980s. The ISS, a large spacecraft orbiting the Earth at an altitude of about 248 miles with a speed of about 17,500 mph, was originally planned to be a laboratory and observatory and to serve as a low orbit staging base for future missions to the Moon and Mars. NASA planned to use the SRMS of the Space Shuttle to perform the construction of the ISS in space. Brushless dc servomotors were used to drive the six joints and the end effector of the 50 ft long SRMS to provide both teleoperation and automatic control of the arm movements. While the SRMS, a serial robot manipulator, was developed to assist astronauts to deploy, retrieve, and handle big payloads in free space, (
Figure 1), it was not suitable for carrying out motions needed in typical tasks of the ISS construction where the manipulator would be constantly in contact with the environment. Thus, there was a need to develop a mechanism to be mounted between the end of the SRMS and an end-effector to enable it to perform fine and precise motions while complying with the contact force generated by the environment it was in contact with. This type of compliant motion is often required in an assembly task of the construction of the ISS. Such an above idea was thought for the old Canadarm (SRMS), now retired, but now can be applied to Canadarm2 (SSRMS) which is a larger, more advanced robotic arm developed for the ISS. As a matter of fact, the above type of mechanism was already incorporated into the special-purpose robot Dextre that was integrated into the SSRMS to carry out specific tasks required for the ISS assembly and maintenance (
Figure 2).
3. The Autonomous Wrist for Space Assembly (AWSA)
Based on the discussion in
Section 2 about the need for the development of a robot manipulator system to perform tasks required for the construction, maintenance and repair of the ISS,
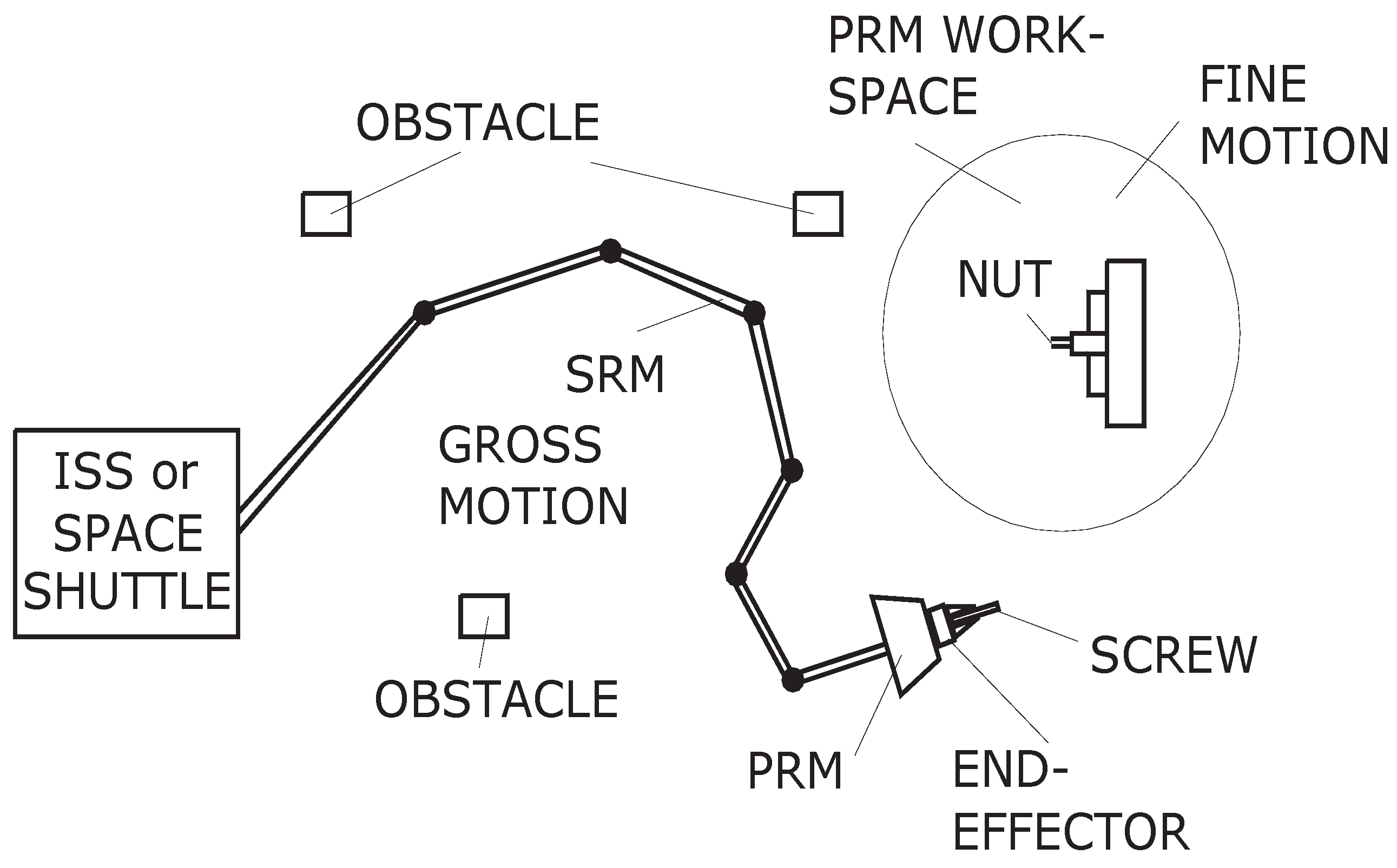
Figure 3 illustrates a proposed a hybrid concept of combining a SRM with a PRM to accomplish the above tasks. One end of the SRM is connected to either a space shuttle or a location of the ISS and its other end is connected to the PRM. An end-effector (tool) is mounted to the PRM to carry out robotic tasks. With a serial structure where the manipulator links are coupled serially, the SRM has long reach and large workspace, but also suffers from severe actuator backlash making the manipulator incapable of carrying out precise motions. On the other hand, despite its small workspace, the PRM in a parallel arrangement of its actuators is capable of performing precise motions due to its low backlash and non-accumulating link errors. The proposed concept illustrated in
Figure 3 considers strengths and weaknesses of the SRM and the PRM and assigns them to perform the type of motions that they are most suitable for.
There are two types of motions a robot manipulator performs, namely, the gross motion and the fine motion [
24]. While gross motion refers to the overall movements a robot manipulator makes to bring itself or an object to within its workspace, fine motion deals with precise and controlled movements required for tasks like part assembly where accuracy of position and force is essential. To carry out a particular task such as assembly of a part on the ISS, it is envisioned that the SRM performs the gross motion autonomously or by teleoperation to move the end-effector into the workspace of the PRM. During the gross motion phase, collision avoidance strategies may be employed to avoid colliding with other structures or spacecrafts around the workspace. After the SRM finishes its gross motion, it renders motion control to the PRM that then carries out the fine motion to complete the assembly task. Since the end-effector will be constantly in contact with the structure of the ISS, compliant motion control may be employed to avoid damage to the end-effector and the ISS structure by excessive contact forces and torques.
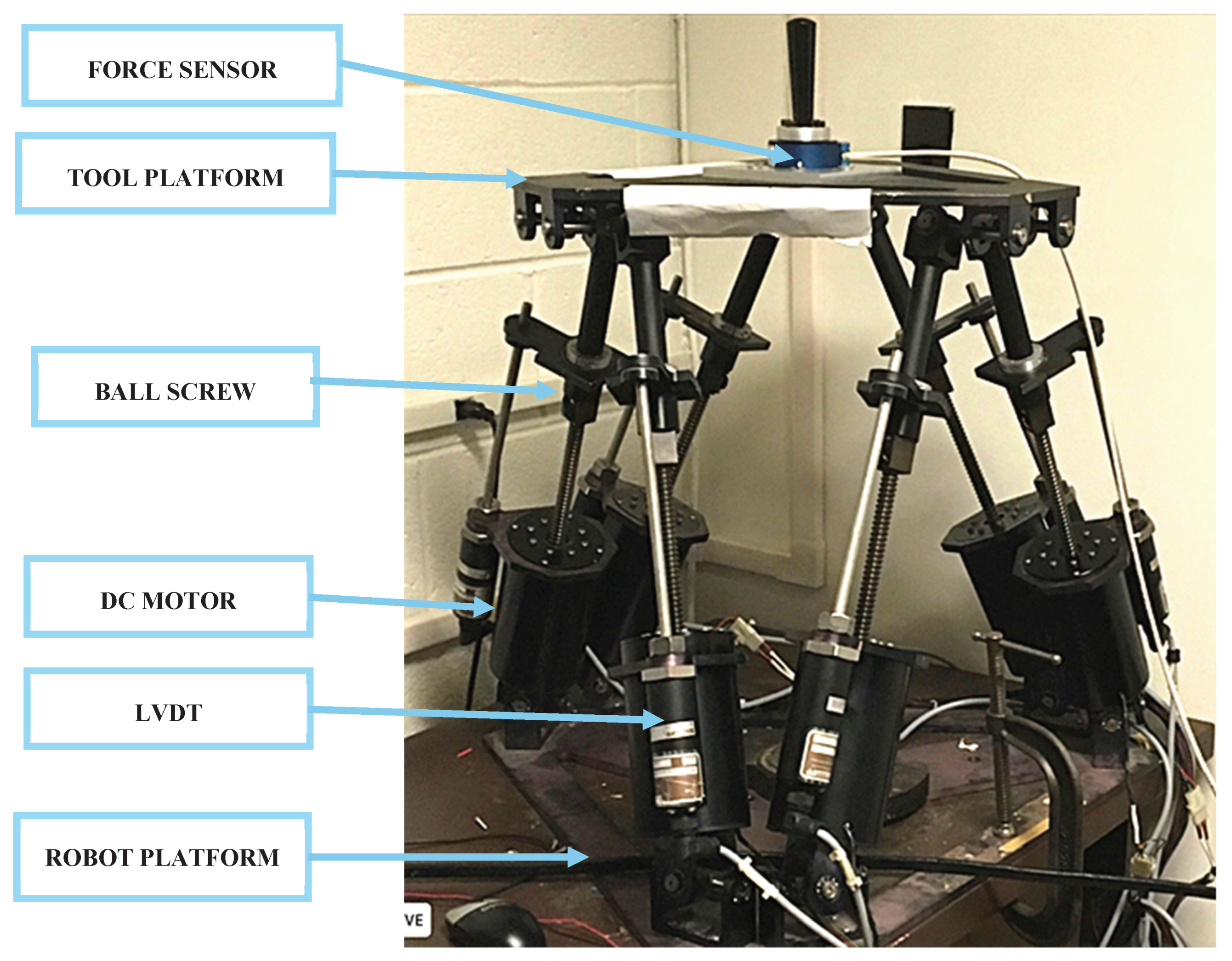
Figure 4 shows a prototype of the PRM, named Autonomous Wrist for Space Assembly (AWSA) that was designed and built to study the feasibility of using parallel robot manipulators for in-space robotic operations including maintaining and repairing NASA spacecrafts including the ISS or satellites [
21]. The wrist is composed of two platforms, the Tool Platform (TP) and the Robot Platform (RP). Referring to
Figure 3, an end-effector is connected to the TP of the AWSA via a force sensor and one end of the SRM is connected to the RP of the AWSA. As shown in
Figure 4, the TP is coupled to the RP through six links. Each link constitutes a linear actuator comprising a DC motor and a linear ball screw drive. The ends of the links are connected to the TP and RP through ball joints. The AWSA possesses six degrees of freedom because it has six linear actuators coupled together in a parallel structure through the TP and RP. The linear actuators are equipped with linear voltage differential transducers (LVDT) that measure the actuator lengths and provide them for joint position feedback control.
4. The Linear DC Motor Actuator
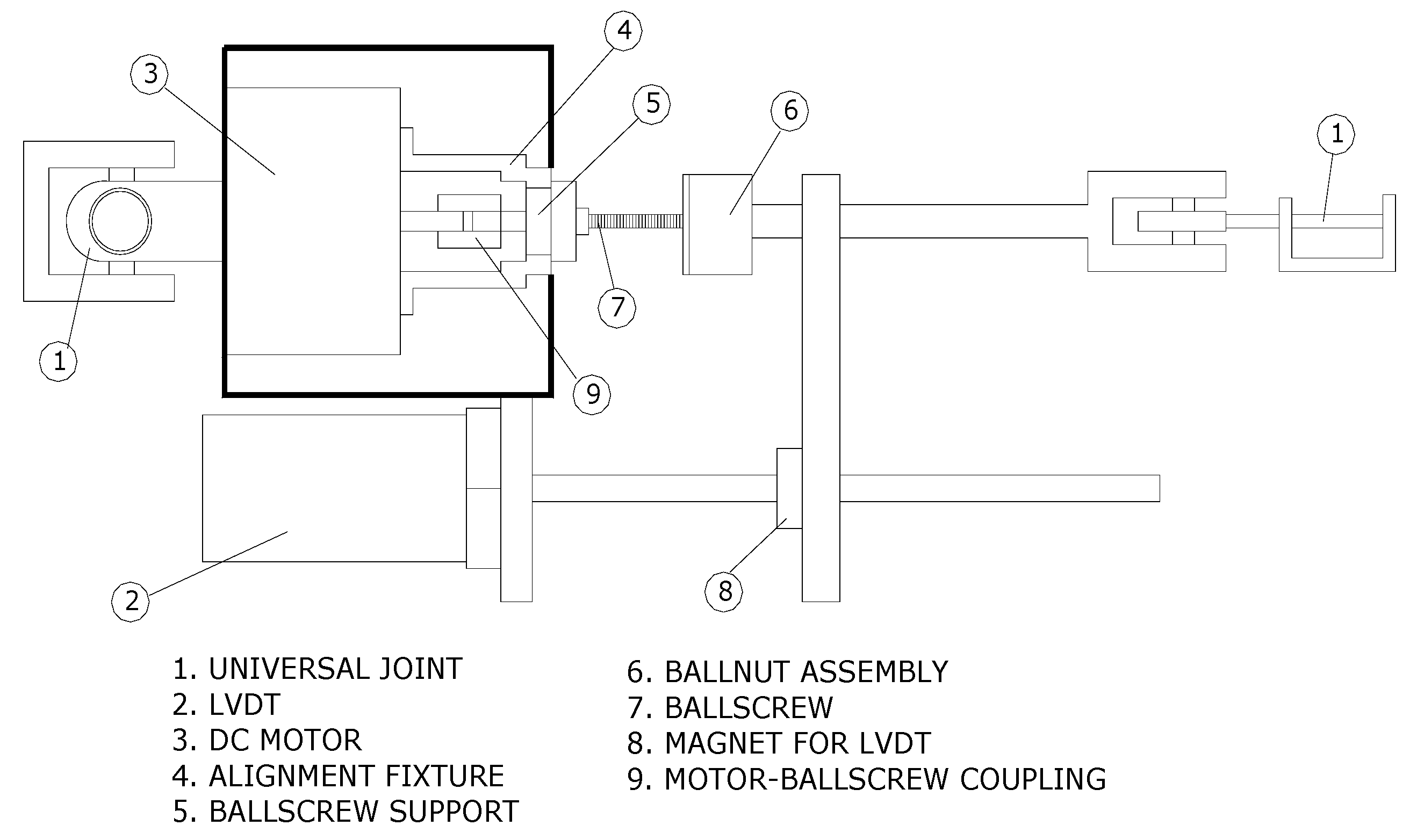
Figure 5 shows the details of the linear actuator of the AWSA, which is mainly composed of a dc motor and a ball joint drive comprising a ball screw and a ball nut. An LVDT is mounted along the length of the actuator to acquire its length for feedback control.
We now discuss the design and selection of the linear actuator components that are divided into two categories, the structural components, and the dynamic components. The structural components are the main load bearing components responsible for holding the actuator together. The dynamic components are those providing the actuator with movement capability and thus comprise the dc motor, the ball joint drive and the LVDT. In order to minimize costs and system downtime, parts of the above components are selected to be off-the-shelf items. The ball screw is selected by considering its maximum lead,
that is calculated by [
22]
where
and
are the desired actuator resolution and maximum resolution of the motor, respectively. The minimum lead
can be calculated by
where
and
are the desired maximum linear velocity and the assumed maximum rotational velocity of the selected motor, respectively. It is important to select a ball screw whose lead lies within the range of lead specified by
and
. The maximum allowable rotational velocity
of the ball screw must be calculated to assure that its resonant frequency is greater than the operating frequency, namely
where
f is the coefficient specified by the ball screw mounting method,
d is the inside diameter of the screw and
L is the length of the screw. We also are aware that the above range satisfies only the motion requirements of the ball screw but does not dictate the behavior of the ball screw as a load bearing element. The maximum axial load
for the selected ball screw can be determined by
Where m is a coefficient determined by the way the ball screw is supported. Now based on Equations (1)-(4), a suitable ball screw can be properly selected. If a motor is not available for the selected ball screw, the above process of ball screw selection must be repeated with some different ball screw parameters until a ball screw can be selected for an existing motor.
The motor selection is performed with a compromise between size, weight, torque and speed. The selected motor should have a maximum operating rotational velocity
to allow the actuator to travel at the desired linear velocity by the selected ball screw. However, the selected motor should have a resolution
to achieve the desired actuator resolution
. The lifting capacity of the selected motor is determined by its average operating torque,
that is given by
where
= the maximum reaction load of the AWSA
L = the lead of the selected ball screw
k = the product of the unit conversion factor and the efficiency factor of the ball screw (=5.654)
Although a motor may be capable of supplying ample torque to sustain a load, it may not be able to supply the torque at the desired speed. Therefore, the Torque-Speed curve of the selected motor must be analyzed to determine if the selected motor can provide the required torque. However, if the Torque-Speed curve is not available, the delivered torque
at a specific rotational velocity
can be computed by
where
= the motor’s torque constant
= the motor’s terminal voltage
= the motor’s back EMF
= the motor’s viscous damping constant
= the motor’s terminal resistance
= the average frictional torque of the motor
Using Equation (6), the deliverable torque at a given rotational velocity for a specific motor can be calculated. However, to determine if a motor has the minimum power
to sustain
at a given velocity, we use
Based on specifications expressed by Equations (1)-(7), the PMI motor, model SM6HI and NSK Ball Screw with a 2.5mm lead and 10mm diameter were selected. The motor was hard coupled to the ball screw to reduce vibration.
The LVDT size should be selected to minimize the chance of colliding with the linear actuator or the TP and the RP during the movement of the AWSA. The selected LVDT should have a resolution which is equal or smaller than that of the linear actuator. Furthermore, the LVDT traverse velocity, defined as the maximum allowable speed of retraction or extension of LVDT should be equal or greater than the actuator’s maximum velocity. Finally, the LVDT should be insensitive to mechanical vibrations and electromagnetic interferences due to its planned mounting on the motor housing. Based on the above specifications, the BALLUFF LDT, Series BTL with a resolution of 0.003 inches, a maximum traverse velocity of 13 inches/sec and output voltage range of 0-10 volts, was selected.
5. Kinematic Analysis of the AWSA
This section gives an overview of the solutions for the forward kinematics and inverse kinematics of the AWSA. Readers interested in detailed derivations of the kinematic solutions should consider Reference [
21].
5.1. The AWSA Inverse Kinematics
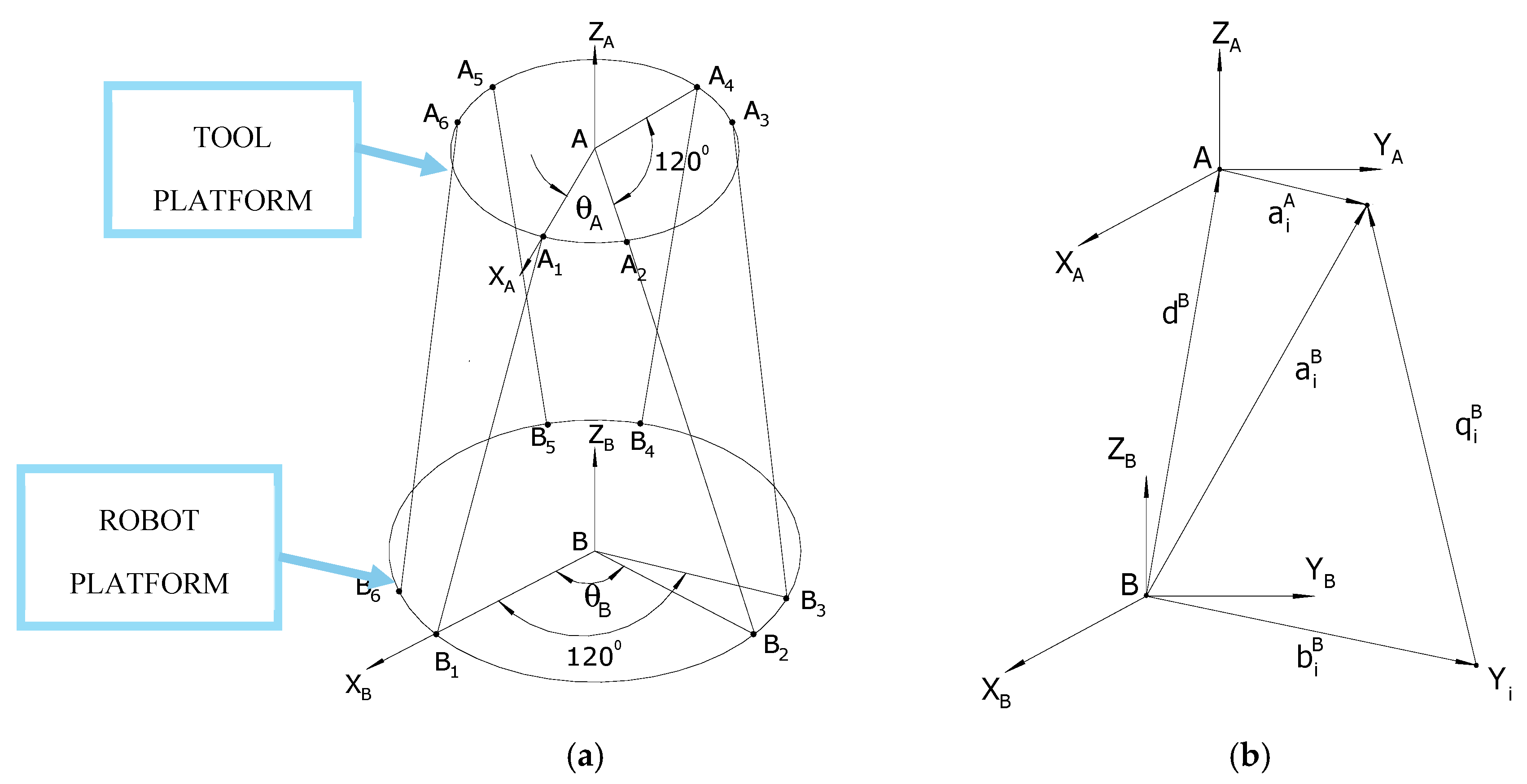
Figure 6 shows the frame assignment and vector diagram of the AWSA. To represent the configuration (position and orientation) of the TP with respect to the RP, Frame {B} whose origin is at the centroid of the RP and Frame {A} whose origin is at the centroid of the TP are assigned as seen in
Figure 6a. The assignment of the above frames follows right-hand rule. Points A
i and points B
i are the attachment points of actuator
i to the TP and RP, respectively. In addition, each pair of ball joints on the platforms is distributed symmetrically with a separation angle of 120 degrees.
Referring to
Figure 6b, the fixed position vectors
,
describe the position of the ball joints at
,
with reference to Frame {A} and Frame {B}, respectively. The radii of the TP and RP are denoted by
and
, respectively. In
Figure 6a let
represent the angle between ball joints
and
, which is the same between
and
, and
and
. Furthermore, if the angle between
and
-axis is denoted by
then the fixed position vector
can be determined with
and
being functions of
and
. Similarly, if the angle between
and
-axis is denoted by
, then the fixed position vector
can be calculated with
and
being functions of
and
. In
Figure 6b, Vector
expressing the position of point A with respect to frame {B} is given by
It is noted that the Cartesian variables
x, y and
z also represent the position of the TP with respect to the RP. Furthermore, if the orientation of Frame {A} of the TP with respect to Frame {B} of the RP is specified by the orientation matrix
as
then from [ ] there is a closed-form solution for the inverse kinematics of the AWSA, given by
where
is the length of Actuator
i. In other words, if a set of actuator lengths
,
,
,
, and
must be determined to yield a desired configuration of the TP with respect to the RP, expressed by the desired position in Equation (8) in terms of Cartesian variables x, y and z and by the desired orientation in Equation (9) in terms of the element of the orientation matrix
, then Equation (10) can be employed to accomplish this objective.
5.2. The AWSA Forward Kinematics
The forward kinematics of the above AWSA deals with the determination of the Cartesian configuration of the TP with respect to the RP, specified by
x,
y,
z, and
for
i =1,2,…6 in Equation (9) based on the actuator lengths,
for
i = 1, 2…6. Unfortunately, Equation (10) provides six nonlinear simultaneous equations with six unknowns that lead to no closed-form solutions for the forward kinematic problem. As a result, this problem is extremely difficult and needs to be solved by using iterative numerical methods such as the Newton Raphson’s Method [
10].
6. Motion Control of the AWSA
This section proposes some control schemes for the motion control of the AWSA. In robot kinematics, we deal with two types of variables, the Cartesian variables, and the joint variables. Cartesian variables include positional variables x, y and z expressing the position of the end-effector with respect to a reference frame and three orientational variables such that Euler Angles expressing the orientation of the end-effector with respect to the same reference frame. In serial robot manipulators, joint variables are the angles of revolute joints or distances of prismatic joints. For parallel manipulators, joint variables are typically the lengths of the actuators. Thus, for the AWSA, the joint variables are the lengths of the six actuators, , , , , , and . In the following, we will discuss three control schemes, namely, a Cartesian space control scheme, a joint-space control scheme and a model reference adaptive control scheme, which are proposed to control the motion of the AWSA.
6.1. The Cartesian Space Control Scheme
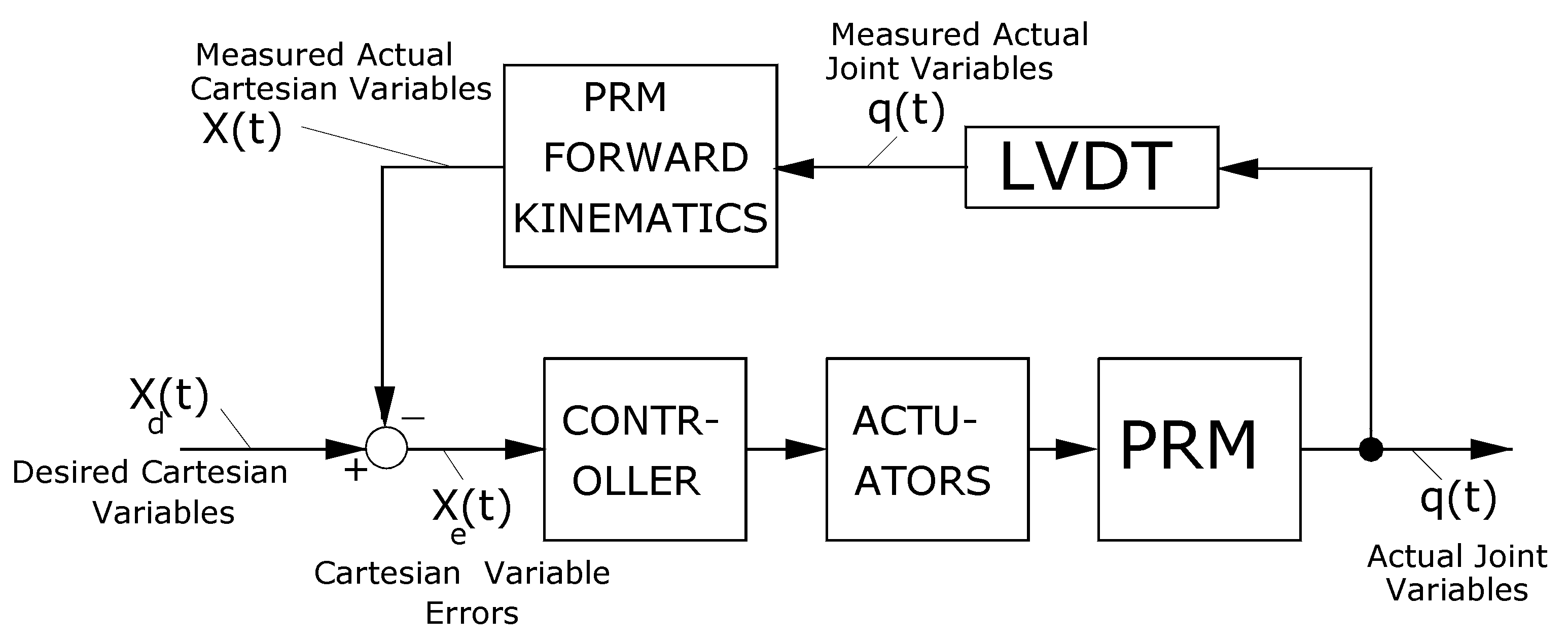
Figure 7 presents the structure of a Cartesian Space Control Scheme (CSCS) employed to control the Cartesian variables of the AWSA. As shown in the figure, the LVDTs measure the actual joint variables contained in Vector
q(t) and provide the measured actual joint variables to the Forward Kinematics block. Using an iterative numerical method, the Forward Kinematics block computes the measured actual Cartesian variables from the measured actual joint variables, that are then subtracted from desired Cartesian variables contained in Vector
to produce the Cartesian variables errors
. The Cartesian variables errors are then fed to a controller which could be a Proportional (P) controller, or a Proportional-Derivative (PD) controller or a Proportional-Derivative-Integral (PID) controller. A particular type of the above controllers is selected to satisfy the control requirements. In general, P-controller is suitable for point to point control while D-controller and P-controller are employed to controlling the transient behavior and the steady-state errror of the system output, respectively. The gains of the above controller could be set at certain values to stabilize and optimize the closed-loop feedback control system using standard control techniques including linearization and pole placement, etc. The outputs of the controller then drive the actuators so that the Cartesian variable errors are minimized and eventually settle to zero. We observe that this Cartesian space control scheme as its name implies controls the Cartesian variables directly. The only disadvantage of this control scheme is that it does not have a closed-form solution of the AWSA Forward Kinematics and must evaluate the Forward Kinematics numerically, which could cause its implementation to be computationally intensive. As a result, the CSCS may not be suitable for real time applications.
6.2. The Joint-Space Control Scheme
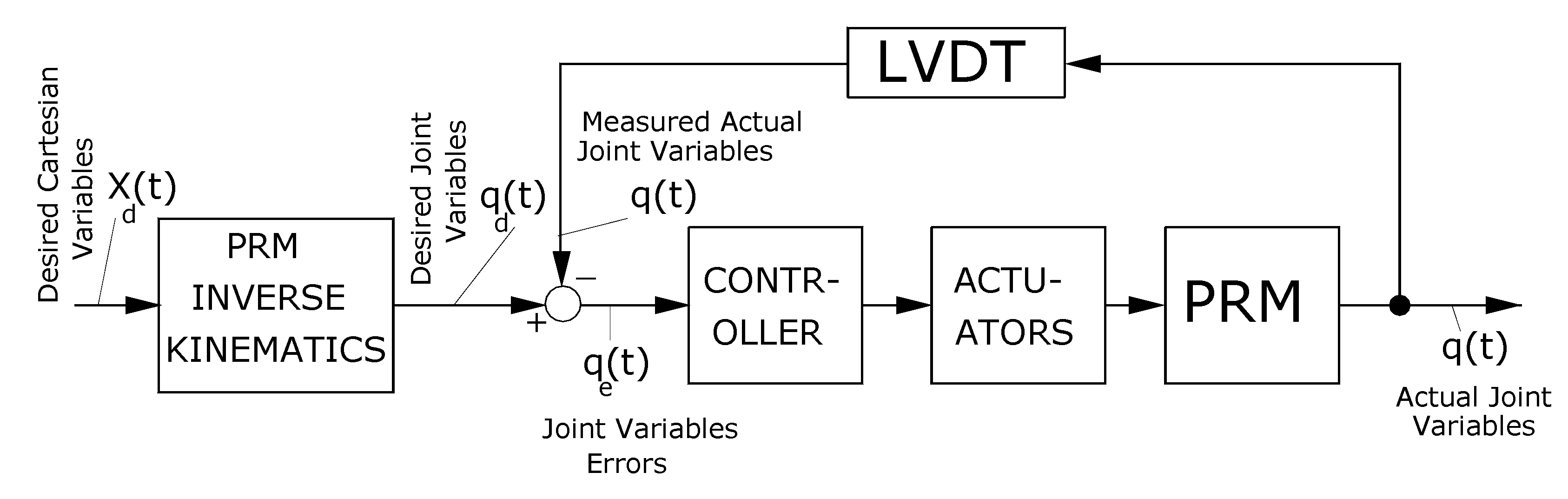
A joint-space control scheme (JSCS) illustrated in
Figure 8 can be applied to control the joint variables (actuator lengths) of the AWSA. As shown in the figure, the JSCS takes advantage of the existence of a closed-form solution for the AWSA inverse kinematics and uses its to convert the desired Cartesian variables expressed in Vector
to the desired joint variables contained in Vector
. The actual joint variables expressed by Vector
q(t) are measured by the LVDTs and then the measured actual joint variables are subtracted from the desired joint variables contained in Vector
to produce the joint variables errors expressed by Vector
. The joint variables errors are then sent to a controller which could be a Proportional (P) controller, or a Proportional-Derivative (PD) controller or a Proportional-Derivative-Integral (PID) controller. Similar to the above CSCS, the controller gains in this case could be set at certain fixed values using standard control techniques including linearization and pole placement to stabilize the closed-loop control system. The actuators are then driven by the controller outputs so that the joint variable errors are minimized and utimately converge to zero. We observe that the JSCS controls the joint variables directly as its name implies. Since it has a closed-form solution for the inverse kinematics, the implemenation of its control law is less computationally intensive than that of the CSCS and consequently, it is more suitable for real time applications than the CSCS.
6.3. Adaptive Control Scheme
As discussed in
Section 6.1 and
Section 6.2, the gains of the CSCS and the JSCS are fixed and set by using standard control techniques. Since the AWSA dynamics and its working environment are not constant but fluctuate due to temperature, humidity, actuator backlash, and sudden change in payload, controllers with constant gains do not perform well under the above conditions. To handle this problem, we consider model reference adaptive control (MRAC) [
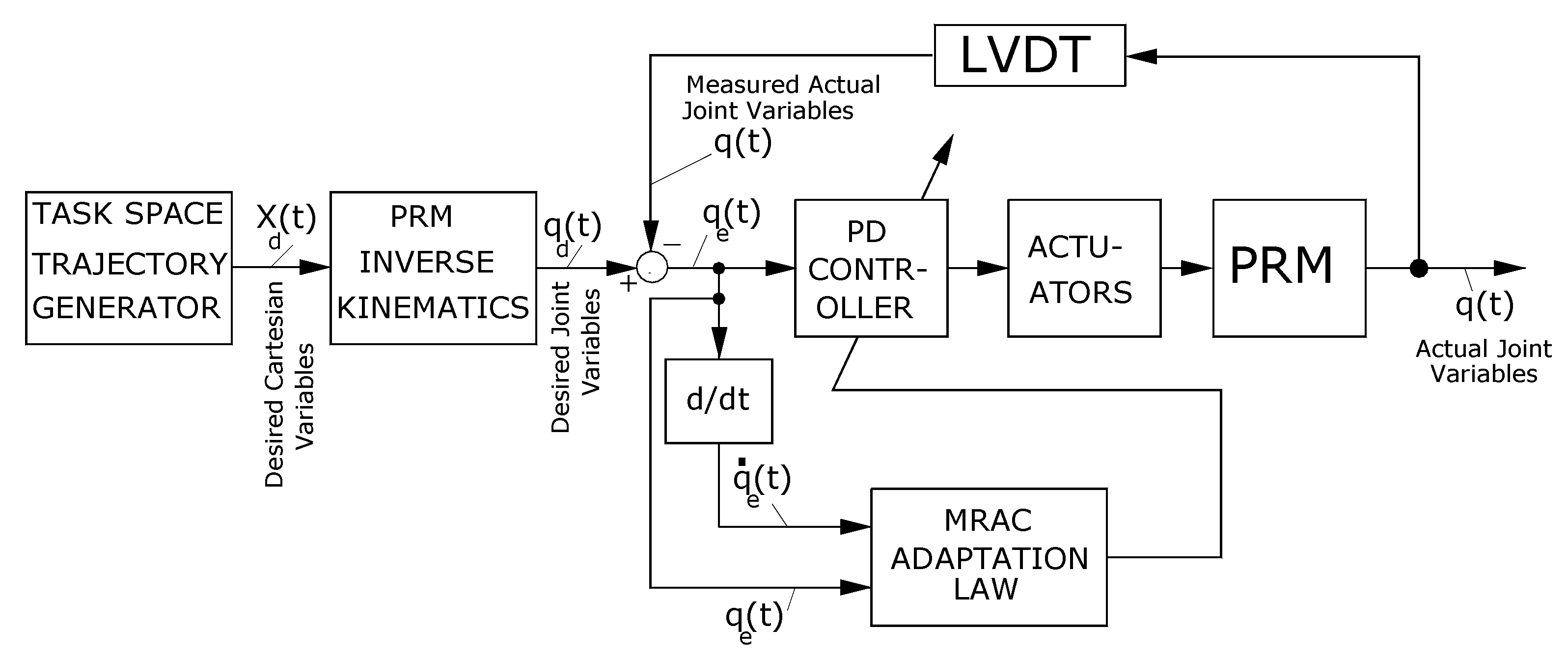
29] which is a control technique that could make the closed-loop feedback control system of the AWSA behave like a desired reference model even though the system dynamics and the working environment change over time. An MRAC system achieves the above objective by continuously adjusting the gains of the PID controllers based on the error between the reference model output and the system output. A PD-MRAC scheme is given in
Figure 9.
As shown in
Figure 9, similar to the CSCS and JSCS, the measured actual joint variables
q(t) are obtained from the LVDTs and subtracted from the desired joint variables
to generate the joint variable errors
. On the input side, a task space trajectory generator produces the desired Cartesian variables
according to the task to be completed. Then the closed-form AWSA Inverse Kinematics converts the desired Cartesian variables
to the desired joint variables
. The MRAC adaptation law block takes the joint variable errors
and its derivative
and generates gain adjusting actions based on the adaptation law and constantly adjusts the gains P and D of the PD controller in real time accordingly. The adaptation law of the MRAC scheme is derived based on a specified reference model that is designed to satisfy the control requirements of the system. We see an obvious advantage of this adaptive control scheme is that it has the ability to monitor the change in manipulator dynamics and working environment through the joint variable errors and its derivatives and to constantly adjust the gains of the PD controller so that the closed-loop system follows the specified reference model very closely. In addition, the real time implementation of the MRAC adaptation law does not require the dynamics of the AWSA and its working environment and as a result it is very computationally efficient making it very suitable for real time applications.
7. Conclusions
This paper considered the design, analysis and control of a robotic wrist, named AWSA that was designed and built to study the feasibility of using autonomous robot manipulators to perform precise motion required by assembly tasks in space. Parallel structure was selected in the development of AWSA because this structure had better positioning capability than its counterpart, the serial structure. AWSA comprised six linear actuators each of which consisted of a dc motor and a ball screw drive. The paper presented the mechanical design of various components of the wrist and explained their selections. In addition, it derived a closed-form solution for the inverse kinematics of the AWSA and suggested a numerical iterative method for the solution of its forward kinematics. It also introduced a hybrid concept for robotic space operations combining a SRM performing gross motion and a PRM like AWSA performing fine and precise motion required by space operation tasks. Several control schemes including Cartesian and joint space control schemes and MRAC scheme were presented and proposed for motion control of AWSA.
Future work on AWSA is recommended as follows.
Computer simulation and experiments should be conducted to obtain the reachable and dexterous workspaces of AWSA to assess the type of assembly it is suitable for.
Advanced control schemes such as intelligent control schemes in [
26,
27,
28] should be studied for potential application in motion and force control of AWSA.
AWSA should be considered for other industrial and medical applications such as force-reflecting hand controller for space teleoperation, patient training device for medical physical therapy and microgravity hand trainer for astronauts.
Author Contributions
Conceptualization, C.C.N.; methodology, C.C.N., H.T.T.N. and T.T.C.D; software, H.T.T.N., T.T.C.D. and A.N.; validation, C.C.N., H.T.T.N., T.T.C.D. and A.N.; formal analysis, C.C.N., H.T.T.N., T.T.C.D.; investigation, C.C.N., H.T.T.N., T.T.C.D.; resources, C.C.N.; data curation, C.C.N., H.T.T.N., T.T.C.D. and A.N.; writing—original draft preparation, C.C.N.; writing—review and editing, C.C.N., H.T.T.N. and T.T.C.D.; visualization, H.T.T.N., T.T.C.D. and A.N.; supervision, C.C.N.; project administration, C.C.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
All authors announce that they have no conflicts of interest in relation to the publication of this article.
Abbreviations
The following abbreviations are used in this manuscript:
| ISS |
International Space Station |
| AWSA |
Autonomous Wrist for Space Assembly |
| SRM |
Serial Robot Manipulator |
| PRM |
Parallel Robot Manipulator |
| CSCS |
Cartesian Space Control System |
| JSCS |
Joint Space Control System |
| MRAC |
Model Reference Adaptive Control |
| SRMS |
Shuttle Remote Manipulator System |
| SSRMS |
Space Station Remote Manipulation System |
References
- Flores-Abad, A.; Ma, O.; Pham, K.; Ulrich, S. A review of space robotics technologies for on-orbit servicing. Progress in Aerospace Sciences, 2014, 68, 1–26. [Google Scholar] [CrossRef]
- Fallahiarezoodar, N.; Zhu, Z.H. Review of autonomous space robotic manipulators for on-orbit servicing and active debris removal. Space: Science & Technology, 2025, 5, Article ID: 0291. [Google Scholar] [CrossRef]
- Miller, R.; Minsky, M.; Smith, D. Space applications of automation, robotics and machine intelligence systems (ARAMIS). NASA Technical Report. 1982, NASA-CR162079. [Google Scholar]
- Dubowsky, S. Advanced methods for the dynamic control of high performance robotic devices and manipulators with potential for applications in space. NASA Technical Report. 1987, NASA-CR-181061.
- Hinkal, S.W.; Andary, J.F.; Watzin, J.G.; Provost, D.E. The flight telerobotic servicer (FTS): A focus for automation and robotics on the space station. Acta Astronautica, 1988, 17, 759–786. [Google Scholar] [CrossRef]
- Delucas, L.J. International space station. Acta Astronautica, 1996, 38, 613–619. [Google Scholar] [CrossRef]
- Merlet, J.P. Parallel Robots; Springer Science & Business Media: Berlin, Germany, 2006; Volume 128. [Google Scholar]
- Stewart, D. A Platform with Six Degrees of Freedom Proc. Inst. Mech. Eng. 1965, 180, 371–386. [Google Scholar] [CrossRef]
- Dasgupta, B.; Mruthyunjaya, T.S. The Stewart platform manipulator: A review. Mech. Mach. Theory 2000, 35, 15–40. [Google Scholar] [CrossRef]
- Dieudonne, J.E. An actuator extension transformation for a motion simulator and an inverse transformation applying Newton-Raphson’s method. NASA Technical Report, 1972, NASA-D-7067.
- Hoffman, R.; McKinnon, M.C. Vibration modes of an aircraft simulator motion system. In Proceedings of The Fifth World Congress for the Theory of Machines and Mechanisms, USA; 1979. [Google Scholar]
- McCallion, H.; Truong, P.D. The analysis of a six-segree-of-freedom work station for mechanised sssembly. Proceedings of The Fifth World Congress for the Theory of Machines and Mechanisms, USA; 1979. [Google Scholar]
- Hunt, K. H. Kinematic Geometry of Mechanisms, Oxford University: London, 1978.
- Sugimoto, K.; Duffy, J. Application of linear algebra to screw systems. Mech.Mach. Theory, 1982, 17, 73–83. [CrossRef]
- Hunt, K. H. Structural kinematics of in-parallel-actuated robot arms. Trans. ASME, J. Mech., Transmis., Automa. in Des., 1983, 105, 705–712.
- Nguyen, C.C. Pooran, F.J.; Premack, T. Control of robot manipulatorcompliance. In Recent Trends in Robotics: Modeling, Control and Education, 1st ed.; Jamshidi, M., Luh, J.Y.S., Shahipoor, M., Eds.; North Holland: New York, USA, 1986; Volume 1, pp. 237–242. [Google Scholar]
- Fichter, E.F. Fichter, E.F. A Stewart platform-based manipulator: general theory and practical construction. Int. Journal of Robotics Research, 1986, 5, 157–182. [CrossRef]
- Sugimoto, K. Kinematic and dynamic analysis of parallel manipulators by means of motor algebra. ASME Journal of Mechanisms, Transmissions, and Automation in Design. 1986, 109, pp. 1–5. [CrossRef]
- Lee, K. M.; Chao, A.; Shah, D. K. A three degrees of freedom in-parallel actuated manipulator. Proceedings of IASTED Int. Conf., 1986., 10 December.
- Nguyen, C.C.; Pooran, F.J. Learning-based control of a closed-kinematic chain robot end-effector performing repetitive tasks. International Journal of Microcomputer Applications, 1990, 9, 9–15. [Google Scholar]
- Nguyen, T.T. Intelligent Control of Closed-Kinematic Chain Robot Manipulators. Ph.D. Dissertation, The Catholic University of America, Washington, DC, USA, 2020. [Google Scholar]
- Smith, W.F.; Nguyen, C.C. On the mechanical design of a Stewart platform-based robotic end-effector. In IEEE Proceedings of the SOUTHEASTCON ‘91, Williamsburg, VA, USA, 7 April, 1991.
- Nguyen, C.C. Pooran, F.J., “Adaptive Force/Position Control of Robot Manipulators with Closed-Kinematic Chain Mechanism. In Recent Trends in Robotics: Modeling, Control and Education, 1st ed.; Jamshidi, M., Ed.; ASME Press: New York, USA, 1988; Volume 1, pp. 177–186, Behi, F. Kinematic analysis for a six-degree-of-freedom 3-PRPS parallel mechanism. IEEE Journal of Robotics and Automation, 1988, 5, 561–565. [Google Scholar]
- Fu, K.S.; Gonzalez, R.C.; Lee, C.S.G. Robotics: Control, Sensing, Vision, and Intelligence, 1st Ed. McGraw-Hill: New York, USA, 1987.
- Nguyen, C.C; Zhou, Z.; Antrazi, S.S.; Campbell, C.E. Efficient computation of forward kinematics and Jacobian matrix of a Stewart platform-based manipulator. In Proceedings of the IEEE Proc. SOUTHEASTCON ‘91, USA; 1991. [Google Scholar]
- Nguyen, T. T.; Nguyen, C. C.; Nguyen, M. T; Duong, T. C. T.; Ngo, T. T. H.; Lu, S. ; Decentralized adaptive control of closed-kinematic chain mechanism manipulator. Machines 2025, 13, 331. [Google Scholar] [CrossRef]
- Duong, T.T.C.; Nguyen, C.C.; Tran, T.D. Synchronization Sliding Mode Control of Closed-Kinematic Chain Robot Manipulators with Time-Delay Estimation. Appl. Sci. 2022, 12, 5527. [Google Scholar] [CrossRef]
- Nguyen, C.C.; Nguyen, T. T.; Duong, T. C.; Nguyen, M. T; Ngo, T. T. H.; Lu, S. Real-time experiments for decentralized adaptive synchronized motion control of a closed-kinematic chain mechanism robot manipulator. Machines 2025, 13, 652. [Google Scholar] [CrossRef]
- Seraji, H. Decentralized adaptive control of manipulators: Theory, simulation, and experimentation. IEEE Trans. Robot. Autom. 1989, 5, 183–201. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).