Performance Evaluation of a Salinity Gradient Solar Pond with Different Geometric Designs: A Numerical Study

1. Introduction

A salinity gradient solar pond (SGSP) is a large pool wherein the solar energy is collected and stored as thermal energy for a long period (months, seasons, years). It is filled with a mixture of water and salt and constituted by three different zones from the top to the bottom. The top zone is named an upper convective zone (UCZ) and exposed to the atmosphere. The middle zone represents the non–convective zone (NCZ) and plays the role of a thermal insulator. The lower zone, named a heat storage zone (HSZ), is saturated in salt water. The HSZ is a convective zone in where solar radiations are collected and stored as thermal energy. Because of the heat storage capacity, SGSPs are used in different processes of seawater desalination, and various industrial applications (e.g., heating of buildings, thermal power industrial, refrigeration, electric power generation, agricultural processes, etc.), and recognized more attention from various research laboratories everywhere and every research work tried to ameliorate the heat storage performance of SGSPs by using different techniques. Among these techniques, the geometric design is considered to be an important parameter in improving the heat storage capacity of SGSPs. In this context, Assari et al. [1] experimentally studied the thermal performance of rectangular and circular SGSPs with the same areas and volumes. The authors concluded that the temperature of the rectangular SGSP is higher than that of the circular one. Besides, Hongsheng et al. [2] studied experimentally and numerically the thermal performance of rectangular and trapezoidal SGSPs. The researchers showed that the temperature of trapezoidal pond is higher as compared to the rectangular one. More recently, square and circular SGSPs have been studied experimentally by Dehghan et al. [3]. The authors showed that the circular pond gives the maximum temperature of heat storage as compared to the square one. Similarly, Khalilian [4] studied the thermal efficiency of circular, square, and rectangular solar ponds both experimentally and numerically by using one-dimensional model. Their results showed that circular pool provides the highest heat storage temperature when compared to the square one. They also demonstrated that geographical directions have a significant influence on the thermal efficiency of square and rectangular solar ponds. The square solar pond gives the greatest heat storage temperature if it is directed in the North-South, and the rectangular solar pond attains a maximum heat storage temperature if its width is directed in the North-South. In another research, Jubran et al. [5] numerically studied the influence of the sloped wall on the generation of convective cells in the solar pond by using PHOENICS program. They concluded that the size of convective cells increases with decreasing in the angle of the sloped wall which is heated by a constant heat flux. For the similar goal but by utilizing phase change materials (PCMs), Sayer et al. [6] confirmed by an experimental study that using a thin layer of liquid paraffin in the top of the SGSP can suppress evaporative heat losses and, therefore, enhances the pond’s heat storage performance. Besides, Ines et al. [7] demonstrated experimentally that the use of salt hydrates as PCMs increases the heat storage performance of a SGSP. In addition, Beik et al. [8] studied numerically the thermal behavior of a SGSP by developing a 1D–model of transient heat transfer process in the presence of PCM (Paraffin Wax). The authors concluded that the use of PCM in the SGSP produces a constant temperature during the extraction of the stored thermal energy. More recently, other researchers suggested using nanoparticles and PCMs in order to boost the heat storage performance of SGSPs such as nanofluid [9], a mixture of encapsulated PCM and nanoparticles [10], Paraffin Wax [11], a mixture of coated magnesium powder and Paraffin Wax [12], silica microparticles added to paraffin wax [13], a mixture of CuO as nanoparticles and Paraffin [14], and a mixture of AgTiO₂ as nanoparticles and Paraffin Wax as PCM [15]. Besides, Choubani et al. [16] experimentally studied the heat and mass transfers performance of a SGSP by using Paraffin Wax as PCM. The researchers concluded that the SGSP in the presence of PCM provides the highest temperature and concentration as compared to the pond without PCM. Moreover, Wang et al. [17] proposed to add Steel-Wires and Paraffin Wax as mixed PCMs for boosting the heat storage performance of a SGSP. The authors concluded that the use of these PCMs enhances the heat storage temperature in a SGSP. In another research, the effect of external magnetic field on the heat storage capacity of a SGSP has been numerically studied by Tian et al. [18]. The researchers showed that the magnetic field increases the heat storage performance of a SGSP.

In the present paper, three geometric designs of SGSP having the same area of upper free–surface and depth, namely, Rectangular Salinity Gradient Solar Pond (RSGSP), Salinity Gradient Solar Pond with One Inclined Wall (SGSP-OIW), and Salinity Gradient Solar Pond with Two Inclined Walls (SGSP-TIWs) are studied and compared numerically to evaluate the impact of geometric design’s SGSP on its heat storage performance. While the shading area influences the SGSP’s heat storage efficiency, the shading area of each zone is assessed and compared between the three proposed designs. As shown from the above literature and to the greatest of our understanding, transient hydrodynamic behavior, heat transfer and mass transfer processes in a SGSP with different designs has not been examined yet. Therefore, the novelty of the present numerical study is to evaluate how different designs of SGSP influence the heat storage performance. Based on numerical data, the heat storage performance (velocities, temperature and salt concentration distribution, average temperature and concentration, and thermal energy stored in the HSZ) of the three proposed designs has been analyzed, which will offer real aides to store solar energy as thermal energy in the SGSP for several thermal engineering applications.

2. Problem Statement and Mathematical Formulation

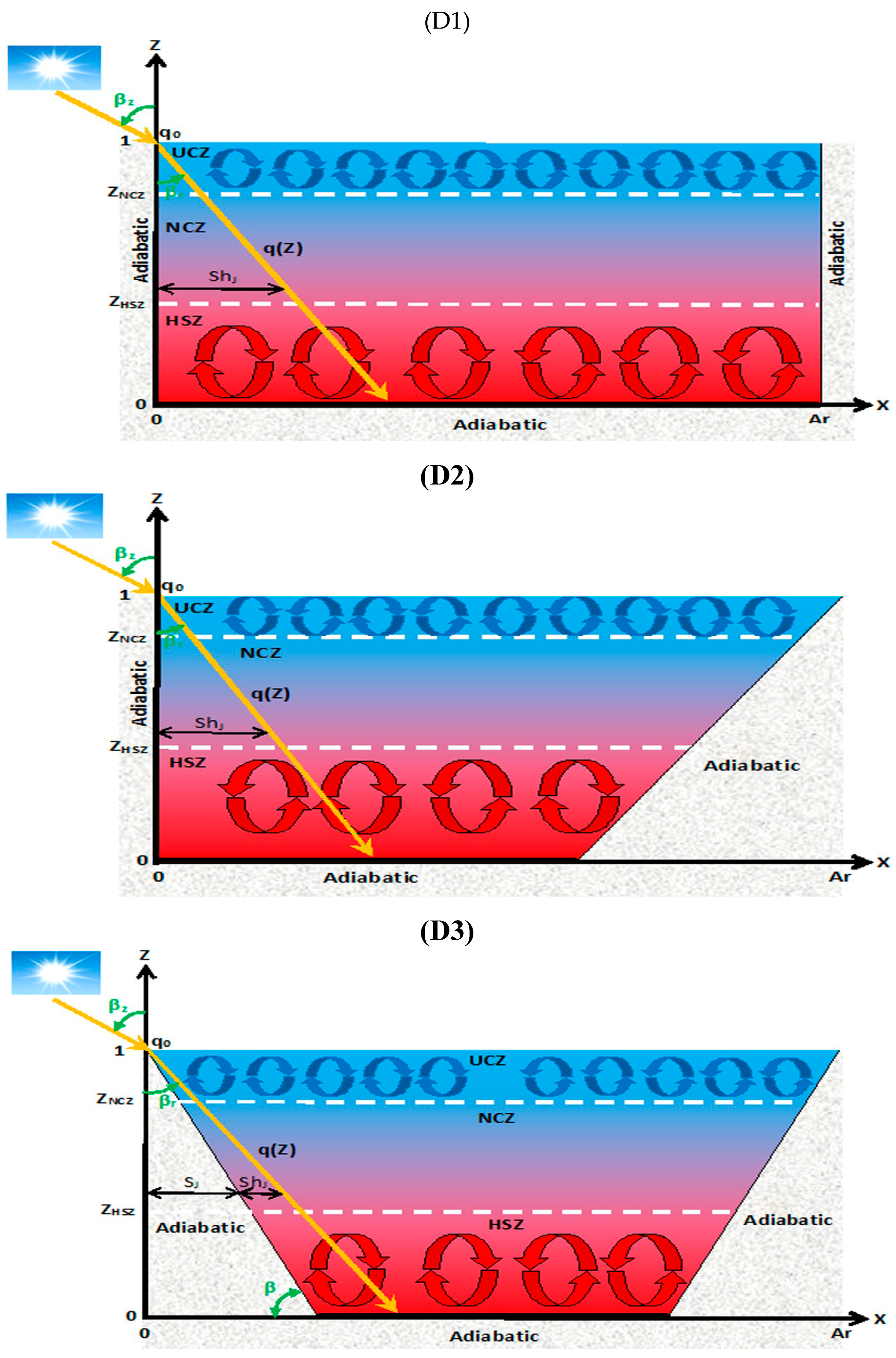
2.1. Schematic Representation

The present numerical study aims to ameliorate the heat storage performance of a SGSP. To attain this objective, three SGSPs having the same area of upper free–surface and depth are designed, namely, Rectangular Salinity Gradient Solar Pond (RSGSP), Salinity Gradient Solar Pond with One Inclined Wall (SGSP–OIW), and Salinity Gradient Solar Pond with Two Inclined Walls (SGSP–TIWs) as shown in Figure 1(a)–(c), respectively. In the present paper, the shading area of each zone is considered into account for the three proposed designs. Each design of SGSP is divided into three zones with different salt concentrations. The aspect ratio "Ar" is defined as the length "L" divided by the height "H" of the SGSP.

2.2. Simplifying Assumptions

A SGSP is a device where the simulation of unsteady thermosolutal natural convection is very complicated. Due to this complication, the process of thermosolutal natural convection is handled as bi-dimensional model in unsteady regime. Besides, the vertical and inclined sidewalls, and the bottom of the three designs of SGSP are adiabatic and impermeable. Also, at the upper free–surface of each design, convective, evaporative and radiative heat losses have been considered. In addition, we suppose that the intensity of solar radiation penetrating the upper free–surface of each design is constant during heat storage process.

At the matte black background of each design, the quantity of solar radiation intensity is wholly absorbed by the salt water. This latter is Newtonian and incompressible. Moreover, the thermophysical properties of salt water are constant, while the density is varied as function of both the temperature and the concentration. According to Boussinesq approximation, this density is expressed as follows:

$$\mathsf{\rho }(\mathrm{T},\mathrm{C})={\mathsf{\rho }}_{\mathrm{r}}\left[1-{\mathsf{\beta }}_{\mathrm{T}}\left(\mathrm{T}-{\mathrm{T}}_{\mathrm{a}}\right)+{\mathsf{\beta }}_{\mathrm{C}}\left(\mathrm{C}-{\mathrm{C}}_{\mathrm{l}}\right)\right]$$

(1)

2.3. Governing Equations

By using the above illustrated assumptions, the process of thermosolutal natural convection inside the SGSP with different designs is governed by the following dimensional equations:

Continuity equation:

$$\mathrm{d}\mathrm{i}\mathrm{v}\overrightarrow{\mathrm{v}}=0$$

(2)

Momentum equation in dimensional horizontal axis:

$${\displaystyle \frac{\partial \mathrm{u}}{\partial \mathrm{t}}}+\mathrm{d}\mathrm{i}\mathrm{v}\left(\mathrm{u}\overrightarrow{\mathrm{v}}-\mathsf{\nu } \overrightarrow{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}} \mathrm{u}\right)=-{\displaystyle \frac{1}{{\mathsf{\rho }}_{\mathrm{r}}}} {\displaystyle \frac{\partial \mathrm{p}}{\partial \mathrm{x}}}$$

(3)

Momentum equation in dimensional vertical axis:

$${\displaystyle \frac{\partial \mathrm{w}}{\partial \mathrm{t}}}+\mathrm{d}\mathrm{i}\mathrm{v}\left(\mathrm{w} \overrightarrow{\mathrm{v}}-\mathsf{\nu } \overrightarrow{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}} \mathrm{w}\right)=-{\displaystyle \frac{1}{{\mathsf{\rho }}_{\mathrm{r}}}} {\displaystyle \frac{\partial \mathrm{p}}{\partial \mathrm{z}}}+\left[{\mathsf{\beta }}_{\mathrm{T}}\left(\mathrm{T}-{\mathrm{T}}_{\mathrm{a}}\right)-{\mathsf{\beta }}_{\mathrm{C}}\left(\mathrm{C}-{\mathrm{C}}_{\mathrm{l}}\right)\right] \mathrm{g}$$

(4)

Heat transfer equation with thermal energy source term:

$${\displaystyle \frac{\partial \mathrm{T}}{\partial \mathrm{t}}} + \mathrm{d}\mathrm{i}\mathrm{v}\left(\mathrm{T} \overrightarrow{\mathrm{v}} - \mathsf{\alpha } \overrightarrow{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}} \mathrm{T}\right)={\displaystyle \frac{\dot{\mathrm{q}}}{{\mathsf{\rho }}_{\mathrm{r}}{\mathrm{C}}_{\mathrm{p}}}}$$

(5)

Mass transfer equation:

$${\displaystyle \frac{\partial \mathrm{C}}{\partial \mathrm{t}}}+\mathrm{d}\mathrm{i}\mathrm{v}\left(\mathrm{C} \overrightarrow{\mathrm{v}}-\mathrm{D} \overrightarrow{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}} \mathrm{C}\right)=0$$

(6)

The term $\dot{\mathrm{q}}$ in Eq. (5) denotes the proportion of thermal energy generation per unit volume in a salt water layer located between z and (z + dz), causing from the absorbed solar radiation intensity. In this present numerical work, the mitigation of intensity of solar radiation attaining a depth z in the SGSP with different designs is delivered by Sodha et al. [19] to provide more precision. This quantity of intensity of solar radiation can be expressed as follows:

$$\mathrm{q}(\mathrm{z}) ={\mathrm{q}}_0{\displaystyle \sum _{\mathrm{i}=1}^5{\mathsf{\psi }}_{\mathrm{i}}}\exp \left[-{\mathsf{\mu }}_{\mathrm{i}} \left(\mathrm{H}-\mathrm{z}\right)\right] = {\mathrm{q}}_0 {\displaystyle \sum _{\mathrm{i}=1}^5{\mathsf{\psi }}_{\mathrm{i}} \exp \left[- {\mathsf{\Phi }}_{\mathrm{i}} \left(1 - \frac{\mathrm{z}}{\mathrm{H}}\right)\right]}$$

(7)

Therefore, the term $\dot{\mathrm{q}}$ can be written as follows:

$$\dot{\mathrm{q}} = {\displaystyle \frac{\partial \mathrm{q}(\mathrm{z})}{\partial \mathrm{z}}}={\mathrm{q}}_0 {\displaystyle \sum _{\mathrm{i}=1}^5{\mathsf{\psi }}_{\mathrm{i}}{\mathsf{\mu }}_{\mathrm{i}} \exp \left[- {\mathsf{\Phi }}_{\mathrm{i}} \left(1 - \mathrm{Z}\right)\right]}$$

(8)

The quantity of thermal energy stored in the HSZ can be expressed in dimensional form as follows:

$${\mathrm{E}}_{\mathrm{t}\mathrm{h}}={\displaystyle \iint {\mathsf{\rho }}_{\mathrm{r}}{\mathrm{C}}_{\mathrm{p}}\left(\mathrm{T}-{\mathrm{T}}_{\mathrm{a}}\right)\mathrm{d}\mathrm{x}\mathrm{d}\mathrm{z}}$$

(9)

By introducing the following dimensionless variables:

X= x/H, Z=z/H, U=u/(α/H), W=w/(α/H), τ = t/(H²/α), P = p/(ρ₀α²/H²), θ=(T–T_a)/ΔT,

φ=(C–C_l)/ΔC, Ra_IE=Ra_I/Ra_E, Br=β_CΔC/(β_TΔT), Pr=ν/α, Le=α/D

(10)

the following dimensionless governing equations of continuity, momentum, heat transfer with thermal energy source term, and mass transfer are obtained and solved numerically to produce the time–wise distribution of velocity, temperature and concentration fields inside the SGSP with different designs.

$$\mathrm{d}\mathrm{i}\mathrm{v} \overrightarrow{\mathrm{V}}=0$$

(11)

$${\displaystyle \frac{\partial \mathrm{U}}{\partial \mathsf{\tau }}} +\mathrm{d}\mathrm{i}\mathrm{v}({\overrightarrow{\mathrm{J}}}_{\mathrm{U}}) = {\mathrm{S}}_{\mathrm{U}}$$

(12)

With: ${\overrightarrow{\mathrm{J}}}_{\mathrm{U}} = \mathrm{U} \overrightarrow{\mathrm{V}} - \mathrm{Pr} \overrightarrow{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}} \mathrm{U}$ and ${\mathrm{S}}_{\mathrm{U}} = - {\displaystyle \frac{\partial \mathrm{P}}{\partial \mathrm{X}}}$

$${\displaystyle \frac{\partial \mathrm{W}}{\partial \mathsf{\tau }}} + \mathrm{d}\mathrm{i}\mathrm{v}({\overrightarrow{\mathrm{J}}}_{\mathrm{W}}) = {\mathrm{S}}_{\mathrm{W}}$$

(13)

With: ${\overrightarrow{\mathrm{J}}}_{\mathrm{W}} = \mathrm{W} \overrightarrow{\mathrm{V}} - \mathrm{Pr} \overrightarrow{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}} \mathrm{W}$ and ${\mathrm{S}}_{\mathrm{W}} = - {\displaystyle \frac{\partial \mathrm{P}}{\partial \mathrm{Z}}} + \mathrm{Pr} \mathrm{R}{\mathrm{a}}_{\mathrm{E}} \left(\mathsf{\theta } - \mathrm{B}\mathrm{r} \phi \right)$

$${\displaystyle \frac{\partial \mathsf{\theta }}{\partial \mathsf{\tau }}} + \mathrm{d}\mathrm{i}\mathrm{v}({\overrightarrow{\mathrm{J}}}_{\mathsf{\theta }}) = {\mathrm{S}}_{\mathsf{\theta }}$$

(14)

With: ${\overrightarrow{\mathrm{J}}}_{\mathsf{\theta }} = \mathsf{\theta } \overrightarrow{\mathrm{V}} - \overrightarrow{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}} \mathsf{\theta }$

$${\displaystyle \frac{\partial \phi }{\partial \mathsf{\tau }}} + \mathrm{d}\mathrm{i}\mathrm{v}({\overrightarrow{\mathrm{J}}}_{\phi }) = {\mathrm{S}}_{\phi }$$

(15)

With: ${\overrightarrow{\mathrm{J}}}_{\phi } = \phi \overrightarrow{\mathrm{V}} - {\displaystyle \frac{1}{\mathrm{L}\mathrm{e}}} \overrightarrow{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}} \phi$ and ${\mathrm{S}}_{\phi } = 0$In Eqs. (12)-(15), ${\overrightarrow{\mathrm{J}}}_{\mathrm{U}}$, ${\overrightarrow{\mathrm{J}}}_{\mathrm{W}}$, ${\overrightarrow{\mathrm{J}}}_{\mathsf{\theta }}$ and ${\overrightarrow{\mathrm{J}}}_{\phi }$ represent the dimensionless flux vector of U, W, θ and φ, respectively. Also, S_U, S_W, S_θ and S_φ represent the source term of U, W, θ and φ, respectively. The heat source term S_θ in Eq. (14) is expressed in dimensionless form as follows:

$${\mathrm{S}}_{\mathsf{\theta }} =\mathrm{R}{\mathrm{a}}_{\mathrm{I}\mathrm{E}}{\displaystyle \sum _{\mathrm{i}=1}^5{\mathsf{\Psi }}_{\mathrm{i}}{\mathsf{\Phi }}_{\mathrm{i}}}\exp \left[-{\mathsf{\Phi }}_{\mathrm{i}} \left(1-\mathrm{Z}\right)\right]$$

(16)

where Ψ_i and Φ_i are the portion of intensity of solar radiation and dimensionless coefficient of solar radiation absorption, respectively. These values are mentionned in Table 1.

Moreover, the dimensionless average temperature of the HSZ and the UCZ inside the SGSP with different designs is evaluated, respectively, by Eq. (17) and Eq. (18) at each dimensionless time "τ".

$${\overline{\mathsf{\theta }}}_{\mathrm{H}\mathrm{S}\mathrm{Z}} = {\displaystyle \frac{{\displaystyle {\int }_0^{{\mathrm{Z}}_{\mathrm{H}\mathrm{S}\mathrm{Z}}}{\displaystyle {\int }_0^{\mathrm{A}\mathrm{r}}\mathsf{\theta }(\mathsf{\tau },\mathrm{X},\mathrm{Z})\mathrm{d}\mathrm{X}\mathrm{d}\mathrm{Z}}}}{{\displaystyle {\int }_0^{{\mathrm{Z}}_{\mathrm{H}\mathrm{S}\mathrm{Z}}}{\displaystyle {\int }_0^{\mathrm{A}\mathrm{r}}\mathrm{d}\mathrm{X}\mathrm{d}\mathrm{Z}}}}}$$

(17)

$${\overline{\mathsf{\theta }}}_{\mathrm{U}\mathrm{C}\mathrm{Z}} = {\displaystyle \frac{{\displaystyle {\int }_{{\mathrm{Z}}_{\mathrm{N}\mathrm{C}\mathrm{Z}}}^1{\displaystyle {\int }_0^{\mathrm{A}\mathrm{r}}\mathsf{\theta }(\mathsf{\tau },\mathrm{X},\mathrm{Z})\mathrm{d}\mathrm{X}\mathrm{d}\mathrm{Z}}}}{{\displaystyle {\int }_{{\mathrm{Z}}_{\mathrm{N}\mathrm{C}\mathrm{Z}}}^1{\displaystyle {\int }_0^{\mathrm{A}\mathrm{r}}\mathrm{d}\mathrm{X}\mathrm{d}\mathrm{Z}}}}}$$

(18)

The thermal energy stored in the HSZ can be written in dimensionless form as follows:

$${\mathrm{E}}_{\mathrm{t}\mathrm{h},\mathrm{H}\mathrm{S}\mathrm{Z}}^{*} = {\displaystyle \iint \mathsf{\theta }(\mathsf{\tau },\mathrm{X},\mathrm{Z})\mathrm{d}\mathrm{X}\mathrm{d}\mathrm{Z}}$$

(19)

2.4. Initial and Boundary Conditions

As initial conditions, at τ = 0, the salt water is motionless. Hence, the initial dimensionless values of velocities components (U, W) are equal to zero. Also, the initial temperature of salt water is equal to ambient temperature. So, the initial dimensionless value of temperature (θ) is equal to zero. Besides, the initial dimensionless value of pressure is equal to zero. The initial dimensionless salt concentration is expressed as follows:

φ = 1 for 0 ≤ Z ≤ Z_HSZ

(20a)

$$\phi = {\displaystyle \frac{\mathrm{Z}}{\left({\mathrm{Z}}_{\mathrm{H}\mathrm{S}\mathrm{Z}} - {\mathrm{Z}}_{\mathrm{N}\mathrm{C}\mathrm{Z}}\right)}} - {\displaystyle \frac{{\mathrm{Z}}_{\mathrm{N}\mathrm{C}\mathrm{Z}}}{\left({\mathrm{Z}}_{\mathrm{H}\mathrm{S}\mathrm{Z}} - {\mathrm{Z}}_{\mathrm{N}\mathrm{C}\mathrm{Z}}\right)}}\mathrm{for}{\mathrm{Z}}_{\mathrm{HSZ}}\le \mathrm{Z}\le {\mathrm{Z}}_{\mathrm{NCZ}}$$

(20b)

φ = 0 for Z_NCZ ≤ Z ≤ 1

(20c)

Considering the region {0 ≤ X ≤ Ar; 0 ≤ Z ≤ 1}, the boundary conditions are detailed as follows:

The velocities components (U, W) are equal to zero on the vertical and sloped walls, and the bottom of the pond, but on the top surface of each design of the SGSP the following boundary conditions are applied.

$${\displaystyle \frac{\partial \mathrm{U}}{\partial \mathrm{Z}}} = 0\mathrm{and}\mathrm{W}=0\mathrm{for}\mathrm{Z}=1$$

(21)

Besides, the vertical and sloped walls of each SGSP’s design are adiabatic and impermeable.

For the RSGSP and SGSP–TIWs, we consider only the half of the pond and the following boundary conditions along the symmetrical vertical plane are applied.

$$\mathrm{U} = 0, {\displaystyle \frac{\partial \mathrm{W}}{\partial \mathrm{X}}} = 0, {\displaystyle \frac{\partial \mathsf{\theta }}{\partial \mathrm{X}}} = 0, {\displaystyle \frac{\partial \phi }{\partial \mathrm{X}}} = 0\hspace{1em}\mathrm{for}\mathrm{X}=\mathrm{Ar}/2$$

(22)

Also, the bottom and the top surface of each design of the SGSP are impermeable. In addition, the following boundary condition of heat transfer is applied through the bottom of each design of the SGSP.

$$-{\displaystyle \frac{\partial \mathsf{\theta }}{\partial \mathrm{Z}}} =\mathrm{R}{\mathrm{a}}_{\mathrm{I}\mathrm{E}}{\displaystyle \sum _{\mathrm{i}=1}^5{\mathsf{\Psi }}_{\mathrm{i}}}\exp \left[-{\mathsf{\Phi }}_{\mathrm{i}} \right]\hspace{1em}\mathrm{for}\mathrm{Z}=0$$

(23)

Finally, the boundary condition of thermal transfer through the top surface (Z = 1) of each design of the SGSP is mentionned in Appendix A.

2.5. Dimensionless Numbers

In Eq. (12)-(15), one can observe the presence of five dimensionless numbers:

external Rayleigh number which designates thermal Rayleigh number

$$\mathrm{R}{\mathrm{a}}_{\mathrm{E}} = {\displaystyle \frac{\mathrm{g}{\mathsf{\beta }}_{\mathrm{T}}\left({\mathrm{T}}_{\mathrm{h}}-{\mathrm{T}}_{\mathrm{l}}\right){\mathrm{H}}^3}{\mathsf{\alpha }\mathsf{\nu }}}$$

(24)

internal to external Rayleigh number

$$\mathrm{R}{\mathrm{a}}_{\mathrm{I}\mathrm{E}} = {\displaystyle \frac{\mathrm{R}{\mathrm{a}}_{\mathrm{I}}}{\mathrm{R}{\mathrm{a}}_{\mathrm{E}}}}$$

(25)

where Ra_I is the internal Rayleigh number, which characterizes the internal heating of salty water as a result of the absorption of sunrays by salty water layers. This number is expressed as follows:

$$\mathrm{R}{\mathrm{a}}_{\mathrm{I}} = {\displaystyle \frac{\mathrm{g}{\mathsf{\beta }}_{\mathrm{T}}{\mathrm{q}}_0{\mathrm{H}}^4}{\mathsf{\alpha }\mathsf{\nu }{\mathsf{\lambda }}_{\mathrm{W}}}}$$

(26)

Prandtl number

$$\mathrm{Pr} = {\displaystyle \frac{\mathsf{\nu }}{\mathsf{\alpha }}}$$

(27)

Lewis number

$$\mathrm{Pr} = {\displaystyle \frac{\mathsf{\alpha }}{\mathrm{D}}}$$

(28)

Buoyancy ratio

$$\mathrm{B}\mathrm{r} = {\displaystyle \frac{{\mathsf{\beta }}_{\mathrm{C}}\left({\mathrm{C}}_{\mathrm{h}}-{\mathrm{C}}_{\mathrm{l}}\right)}{{\mathsf{\beta }}_{\mathrm{T}}\left({\mathrm{T}}_{\mathrm{h}}-{\mathrm{T}}_{\mathrm{l}}\right)}}$$

(29)

Each of these dimensionless numbers influences the transient evolution of fluid flow, heat and mass transfer inside the SGSP.

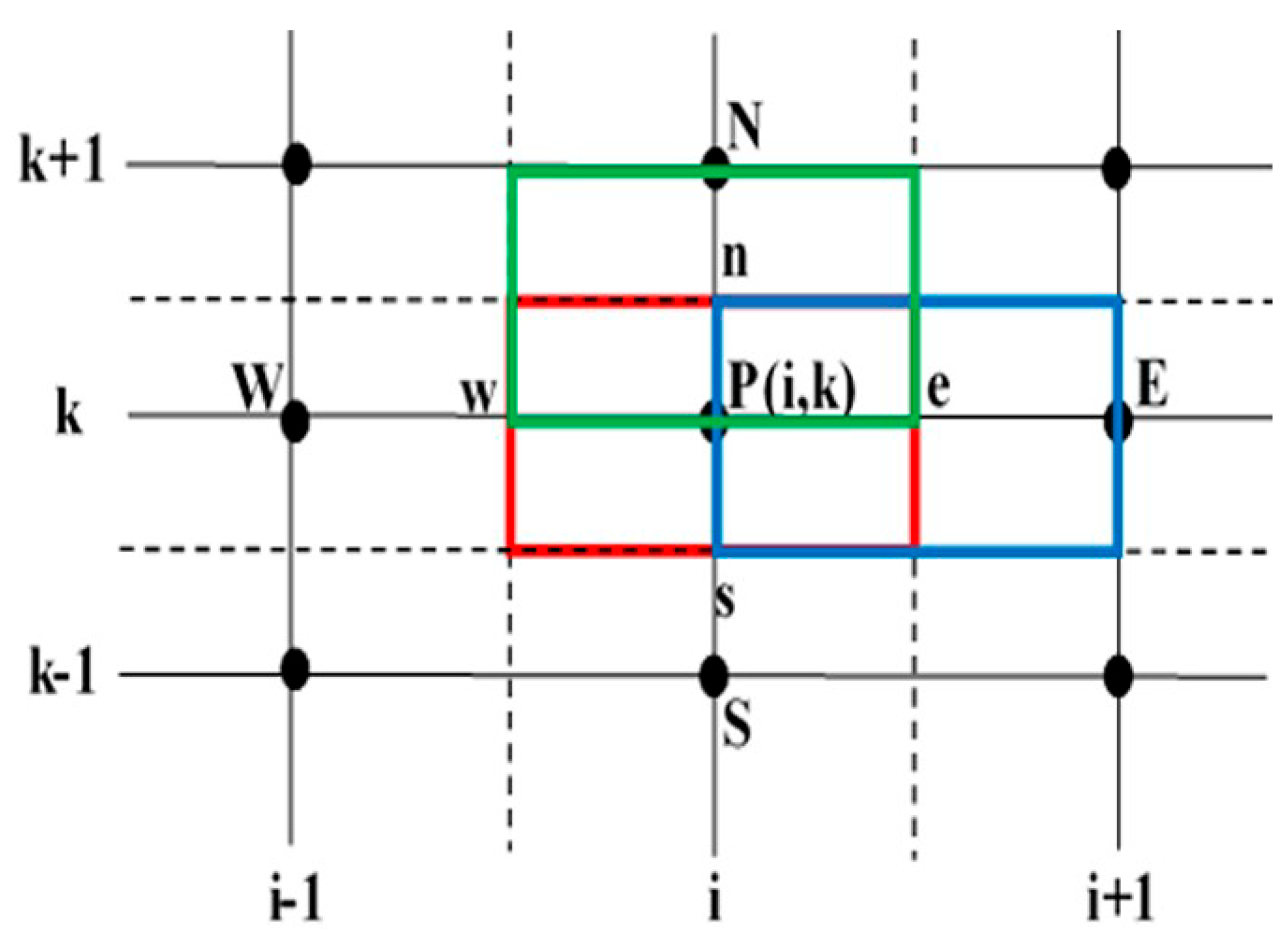
3. Numerical Procedure

The dimensionless governing equations (11)-(15) connected to the initial and boundary conditions have been numerically solved via the employ of a computer code developed in Fortran specifically for the present work and founded on the finite–volume method described in [20]. These equations can be written in general conservation form as follows:

$${\displaystyle \frac{\partial \mathrm{F}}{\partial \mathsf{\tau }}} + \mathrm{d}\mathrm{i}\mathrm{v}({\overrightarrow{\mathrm{J}}}_{\mathrm{F}}) = {\mathrm{S}}_{\mathrm{F}}$$

(30)

With: ${\overrightarrow{\mathrm{J}}}_{\mathrm{F}} = \mathrm{F} \overrightarrow{\mathrm{V}} - {\mathsf{\Gamma }}_{\mathrm{F}} \overrightarrow{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}} \mathrm{F}$

In Eq. (30), ${\overrightarrow{\mathrm{J}}}_{\mathrm{F}}$, ${\mathsf{\Gamma }}_{\mathrm{F}}$ and S_F represent the flux vector, conductance coefficient and source term of dimensionless transported variable F, respectively. They are offered in Table 2.

The studied domain is subdivided in a two–dimensional elementary control volumes Ω_F surrounding each node of the mech. Figure 2 showed three different control volumes for a given node, such as P(i,k). The first control volume for the horizontal velocity component (traced in blue), the second control volume for the vertical velocity component (traced in green), and the third control volume for the scalar variables (traced in red), thus being a staggered mesh. In this numerical study, the mesh tightening, in horizontal or vertical direction, is managed by a node distribution function which is written in the following form:

$$\mathrm{f}(\mathrm{q}) = {\displaystyle \frac{1-{\mathrm{q}}^{\left(\mathrm{n}-{\mathrm{n}}_{\mathrm{b}}\right)}}{1-{\mathrm{q}}^{\left({\mathrm{n}}_{\mathrm{e}}-{\mathrm{n}}_{\mathrm{b}}\right)}}}$$

(31)

The function “f” represents either X or Z. Parameters n, n_b and n_e designate the index I (or k), the index at the beginning of the domain and the index at the end of the same domain, respectively. The indexes I and k varies from 1 to NX and from 1 to NZ, respectively. The parameters NX and NZ represent, respectively, the number of nodes in dimensionless horizontal and in dimensionless vertical directions. The variable “q” is the tightening key of mesh. In the present paper, this variable is equal to one In order to obtain”a un’form mesh spacing In dimensionless horizontal and in dimensionless vertical directions.

Figure 2. Three different two–dimensional control volumes.

Figure 2. Three different two–dimensional control volumes.

Then, Eq. (31) is integrated over its proper control volume as follows:

$${\displaystyle {\iiint }_{{\mathsf{\Omega }}_{\mathrm{F}}}\frac{\partial \mathrm{F}}{\partial \mathsf{\tau }} \mathrm{d}\mathsf{\upsilon } = }- {\displaystyle {\iiint }_{{\mathsf{\Omega }}_{\mathrm{F}}}\mathrm{d}\mathrm{i}\mathrm{v}{\overrightarrow{\mathrm{J}}}_{\mathrm{F}} \mathrm{d}\mathsf{\upsilon }} + {\displaystyle {\iiint }_{{\mathsf{\Omega }}_{\mathrm{F}}}{\mathrm{S}}_{\mathrm{F}} \mathrm{d}\mathsf{\upsilon }}$$

(32)

By introducing the Gauss–Ostrogradsky transformation, the equation (32) can be written as follows:

$${\displaystyle {\iiint }_{{\mathsf{\Omega }}_{\mathrm{F}}}\frac{\partial \mathrm{F}}{\partial \mathsf{\tau }}\mathrm{d}\mathsf{\upsilon }}= -{\displaystyle {\iint }_{\sum }{\overrightarrow{\mathrm{J}}}_{\mathrm{F}}\overrightarrow{\mathrm{n}} \mathrm{d}\mathrm{S}}+{\displaystyle {\iiint }_{{\mathsf{\Omega }}_{\mathrm{F}}}{\mathrm{S}}_{\mathrm{F}}\mathrm{d}\mathsf{\upsilon }}$$

(33)

$\overrightarrow{\mathrm{n}}$ is the normal to the surface Σ delimiting the control volume Ω_F.

The equation (33) is spatially discretized for each dimensionless transported variable "F" by using the hybrid scheme.

Concerning temporal discretization, the Alternating Direction Implicit (ADI) technique has been used to resolve the time–wise transported variable in Eq. (32).

The pressure–velocity correction was solved by the SIMPLER algorithm detailed in [20].

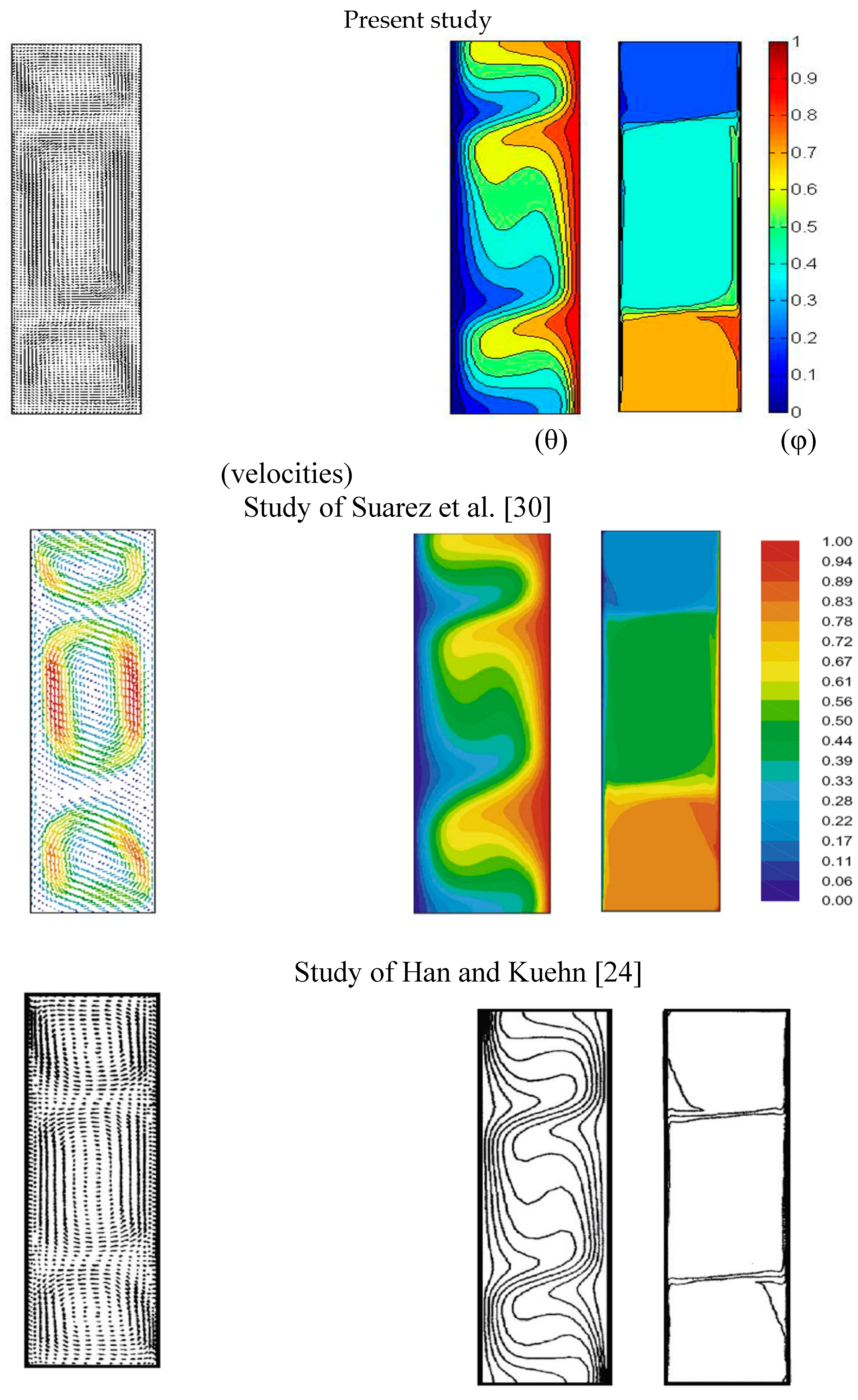
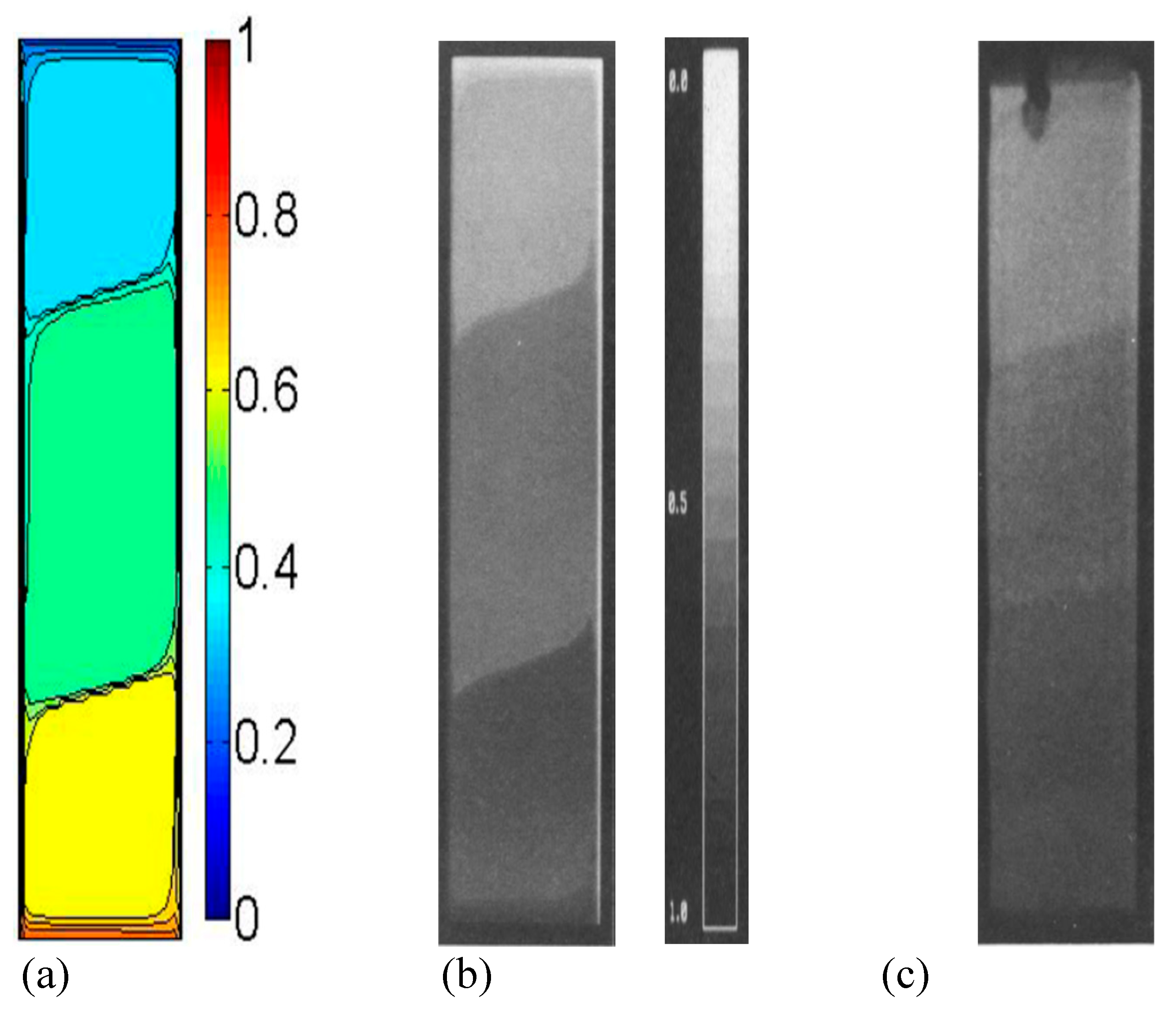
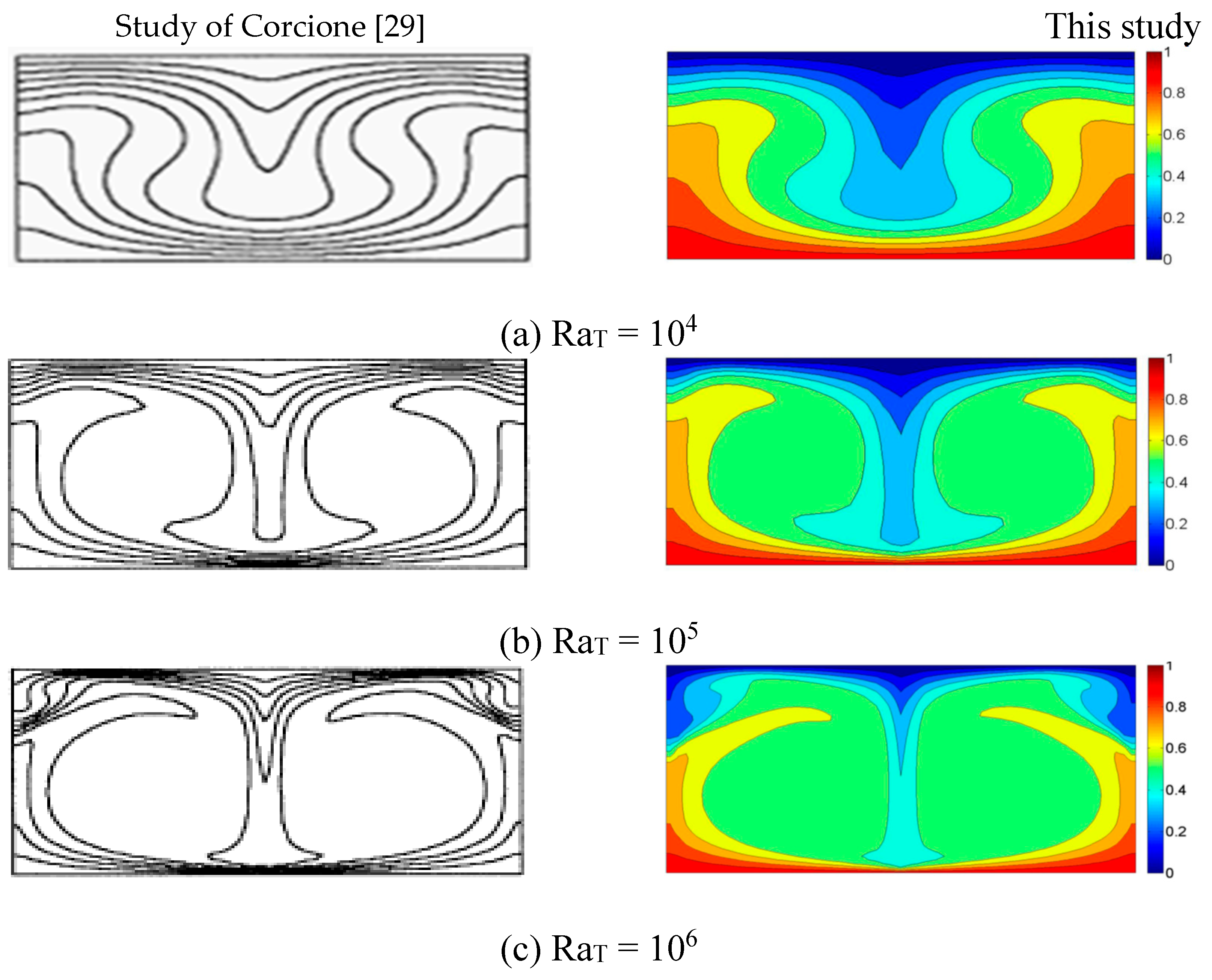
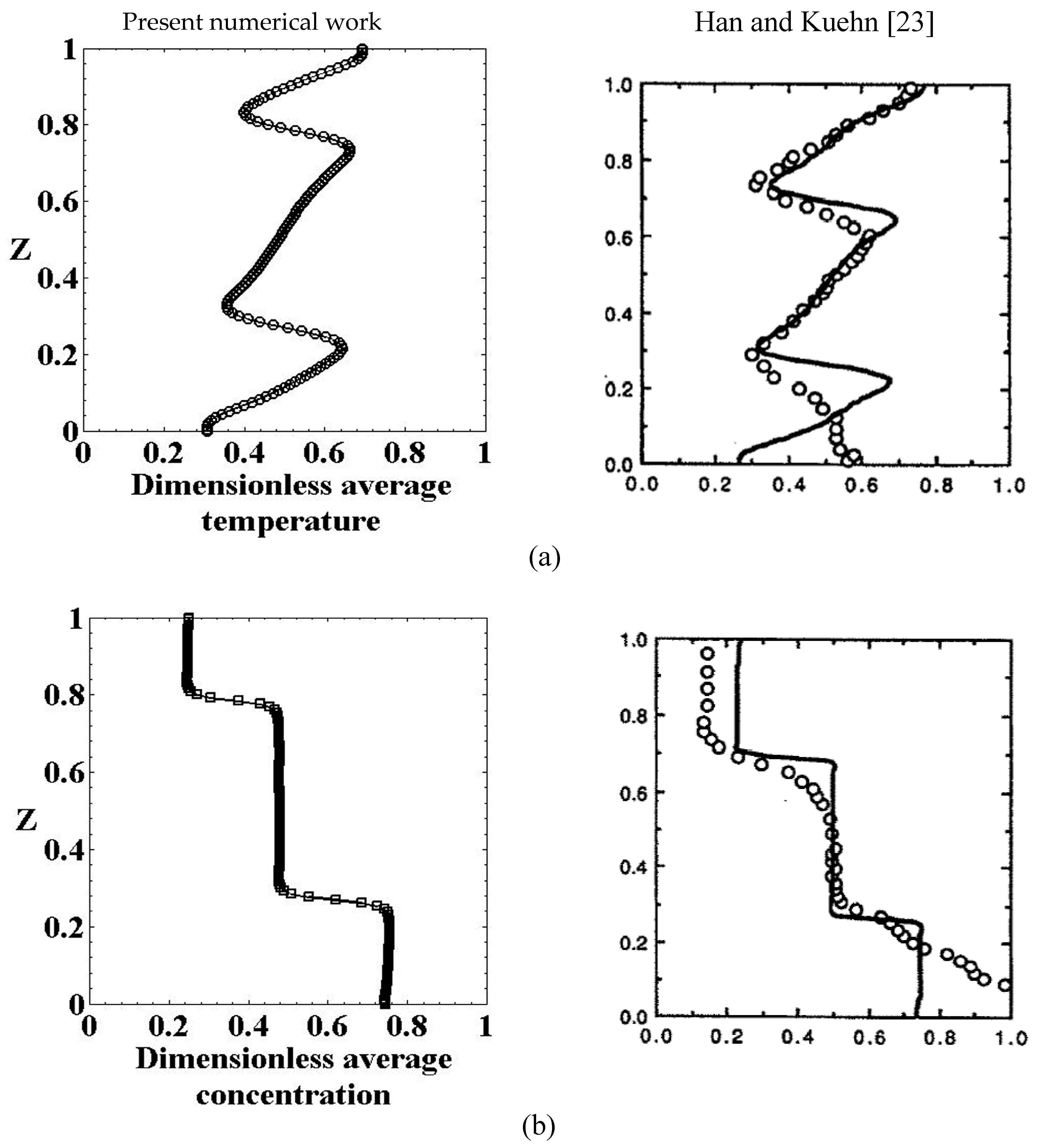
4. Verification of Grid Independent and Validation of Computer Program

To warrant the correctness of the numerical results produced by the constructed computer program, numerous uniform grids have been tested in our previous work [21]. The obtained numerical results demonstrated that the 100×100 uniform grid nodes seem to be greatly satisfactory for producing correctness numerical results with a dimensionless time step equal to 10^-8.

Because the results of experimental studies on the complicated process of thermosolutal natural convection inside the SGSP are not available in literature, the computer program developed in Fortran specially for this research was validated in four manners.

In the first manner, the current numerical results of a steady state simulation were compared with numerical results presented by Han and Kuehn [23], and Suarez et al. [30] which refer to a vertical rectangular enclosure in absence of internal warming of fluid. This comparison is illustrated in Figure 3.

As a second manner of verification, the computer program is validated with Han and Kuehn [23,28] which studied experimentally and numerically the distribution of concentration in a vertical rectangular enclosure in absence of internal warming of fluid in a steady state. This comparison is displayed in Figure 4.

Besides, as a third manner of verification, the computer program is validated with Corcione [29] for natural convection in a rectangular enclosure in a steady state. This comparison is displayed in Figure 5.

As another manner of verification, the computer program is validated with Han and Kuehn [23] which presented an experimental and numerical profiles of dimensionless average temperature and salt concentration inside a rectangular enclosure in absence of internal warming of fluid. The comparison is presented in Figure 6. It can be noted that the numerical results produced in this research show good agreement with those from the previous studies. Hence, these numerical results supply trust to the rationality and accuracy of the present computer program.

5. Evaluation of Dimensionless Shadow Area for Different Designs of SGSP

The shadow area is an important parameter which affects the heat storage performance of a SGSP. In order to investigate the effect of shadow area on different SGSP’s designs, various solar radiation angles are required as shown in Figure 1. The first important angle is the solar zenith angle "β_z", which can be written in degree as [31]:

cosβ_z = cosχcosβ_d[tgχtgβ_d + cosω]

(34)

where χ, β_d and ω are the latitude of SGSP, the declination angle and the hour angle, respectively. The angle β_d is expressed in degree by [31]:

$${\mathsf{\beta }}_{\mathrm{d}} = 23.45\sin \left[2\mathsf{\pi }\left({\displaystyle \frac{284+\mathrm{n}}{365}}\right)\right]$$

(35)

where n represents the number of day in year.

The angle ω is expressed in degree as follows:

$$\mathsf{\omega } = 2\mathsf{\pi }\left({\displaystyle \frac{\mathrm{t}-12}{24}}\right)$$

(36)

where t represents the local time.

Also, the rays of sunlight reaching the free–surface of SGSP are refracted with the angle β_z and, then, penetrating into salt water layers with an angle of refraction "β_r", which is expressed in degree by [31]:

$$\sin {\mathsf{\beta }}_{\mathrm{r}} = {\mathrm{k}}_{\mathrm{r}}^{-1}\sin {\mathsf{\beta }}_{\mathrm{z}}$$

(37)

where k_r is a coefficient of refraction. For water, k_r = 1.33 [32].

To evaluate the expression of dimensionless shading area of UCZ, NCZ and HSZ inside each design of SGSP, the dimensionless height of the SGSP is divided into 30 layers with a dimensionless thickness of 0.033 for each layer. These layers are numbered from the water free–surface to the bottom of each design. Therefore, the UCZ, NCZ and HSZ are constituted by 6 layers, 12 layers and 12 layers, respectively.

The dimensionless shading area of UCZ in the RSGSP and SGSP–OIW is expressed as follows:

$${\mathrm{A}}_{\mathrm{s}\mathrm{h},\mathrm{U}\mathrm{C}\mathrm{Z}}^{\mathrm{R}\mathrm{S}\mathrm{G}\mathrm{S}\mathrm{P}} = {\mathrm{A}}_{\mathrm{s}\mathrm{h},\mathrm{U}\mathrm{C}\mathrm{Z}}^{\mathrm{S}\mathrm{G}\mathrm{S}\mathrm{P}-\mathrm{O}\mathrm{I}\mathrm{W}} = \left({\mathrm{J}}_{\mathrm{U}\mathrm{C}\mathrm{Z}}-1\right)\mathsf{\Delta }\mathrm{Z}\tan {\mathsf{\beta }}_{\mathrm{r}}$$

(38)

The dimensionless shading area of NCZ in the RSGSP and SGSP–OIW is expressed as follows:

$${\mathrm{A}}_{\mathrm{s}\mathrm{h},\mathrm{N}\mathrm{C}\mathrm{Z}}^{\mathrm{R}\mathrm{S}\mathrm{G}\mathrm{S}\mathrm{P}} = {\mathrm{A}}_{\mathrm{s}\mathrm{h},\mathrm{N}\mathrm{C}\mathrm{Z}}^{\mathrm{S}\mathrm{G}\mathrm{S}\mathrm{P}-\mathrm{O}\mathrm{I}\mathrm{W}} = \left(\left(1-{\mathrm{Z}}_{\mathrm{N}\mathrm{C}\mathrm{Z}}\right)+\left({\mathrm{J}}_{\mathrm{N}\mathrm{C}\mathrm{Z}}-1\right)\mathsf{\Delta }\mathrm{Z}\right)\tan {\mathsf{\beta }}_{\mathrm{r}}$$

(39)

The dimensionless shading area of HSZ in the RSGSP and SGSP–OIW is expressed as follows:

$${\mathrm{A}}_{\mathrm{s}\mathrm{h},\mathrm{H}\mathrm{S}\mathrm{Z}}^{\mathrm{R}\mathrm{S}\mathrm{G}\mathrm{S}\mathrm{P}} = {\mathrm{A}}_{\mathrm{s}\mathrm{h},\mathrm{H}\mathrm{S}\mathrm{Z}}^{\mathrm{S}\mathrm{G}\mathrm{S}\mathrm{P}-\mathrm{O}\mathrm{I}\mathrm{W}} = \left(\left(1-{\mathrm{Z}}_{\mathrm{H}\mathrm{S}\mathrm{Z}}\right)+\left({\mathrm{J}}_{\mathrm{H}\mathrm{S}\mathrm{Z}}-1\right)\mathsf{\Delta }\mathrm{Z}\right)\tan {\mathsf{\beta }}_{\mathrm{r}}$$

(40)

where J_UCZ, J_NCZ and J_HSZ are the numbers of layers constituting the UCZ, NCZ and HSZ, respectively. The parameter ΔZ is the dimensionless thickness of a layer.

The dimensionless shading area of UCZ in the SGSP–TIWs is expressed as follows:

$${\mathrm{A}}_{\mathrm{s}\mathrm{h},\mathrm{U}\mathrm{C}\mathrm{Z}}^{\mathrm{S}\mathrm{G}\mathrm{S}\mathrm{P}-\mathrm{T}\mathrm{I}\mathrm{W}\mathrm{s}} = \left({\mathrm{J}}_{\mathrm{U}\mathrm{C}\mathrm{Z}}-1\right)\mathsf{\Delta }\mathrm{Z}\tan {\mathsf{\beta }}_{\mathrm{r}}-{\mathrm{S}}_{\mathrm{j}} = \left({\mathrm{J}}_{\mathrm{U}\mathrm{C}\mathrm{Z}}-1\right)\mathsf{\Delta }\mathrm{Z}\left(\tan {\mathsf{\beta }}_{\mathrm{r}}-\tan \mathsf{\beta }\right)$$

(41)

where S_j is the dimensionless horizontal space between the dimensionless vertical direction and the inclined wall of SGSP at the J^th layer.

The dimensionless shading area of NCZ in the SGSP–TIWs is expressed as follows:

$${\mathrm{A}}_{\mathrm{s}\mathrm{h},\mathrm{N}\mathrm{C}\mathrm{Z}}^{\mathrm{S}\mathrm{G}\mathrm{S}\mathrm{P}-\mathrm{T}\mathrm{I}\mathrm{W}\mathrm{s}} = \left(\left(1-{\mathrm{Z}}_{\mathrm{N}\mathrm{C}\mathrm{Z}}\right)+\left({\mathrm{J}}_{\mathrm{N}\mathrm{C}\mathrm{Z}}-1\right)\mathsf{\Delta }\mathrm{Z}\right)\left(\tan {\mathsf{\beta }}_{\mathrm{r}}-\tan \mathsf{\beta }\right)$$

(42)

The dimensionless shading area of HSZ in the SGSP–TIWs is expressed as follows:

$${\mathrm{A}}_{\mathrm{s}\mathrm{h},\mathrm{H}\mathrm{S}\mathrm{Z}}^{\mathrm{S}\mathrm{G}\mathrm{S}\mathrm{P}-\mathrm{T}\mathrm{I}\mathrm{W}\mathrm{s}} = \left(\left(1-{\mathrm{Z}}_{\mathrm{H}\mathrm{S}\mathrm{Z}}\right)+\left({\mathrm{J}}_{\mathrm{H}\mathrm{S}\mathrm{Z}}-1\right)\mathsf{\Delta }\mathrm{Z}\right)\left(\tan {\mathsf{\beta }}_{\mathrm{r}}-\tan \mathsf{\beta }\right)$$

(43)

where β is the angle of the sloped wall of SGSP with the dimensionless horizontal direction. In the present paper, this angle is fixed at 45°.

The values of dimensionless shadow area of the three zones for different designs of SGSP are displayed in Table 3.

As shown in Table 3, the SGSP–TIWs decreases the dimensionless shading area of UCZ, NCZ and HSZ by 88.7%, 88.45% and 88.54%, respectively, as compared to the SGSP–OIW and RSGSP.

6. Numerical Results and Discussion

A numerical investigation has been executed on the effect of geometric design on the hydrodynamic, heat and mass transfer behaviors in a SGSP during the storage of solar energy as thermal energy. To evaluate the heat storage performance of the three considered SGSPs, the results are established in the form of time–wise evolutions of temperature, salt concentration and velocities fields, and average temperature and salt concentration profiles for Pr = 6 and Sc = 1000 which represents the diffusion of salt into water, see [21,22] and also [24]. These numerical results are produced under the same dimensionless parameters which are presented in Table 4.

With the aim of clearly showing the field, the scale of the three different designs of SGSP is not indicated in the present numerical results.

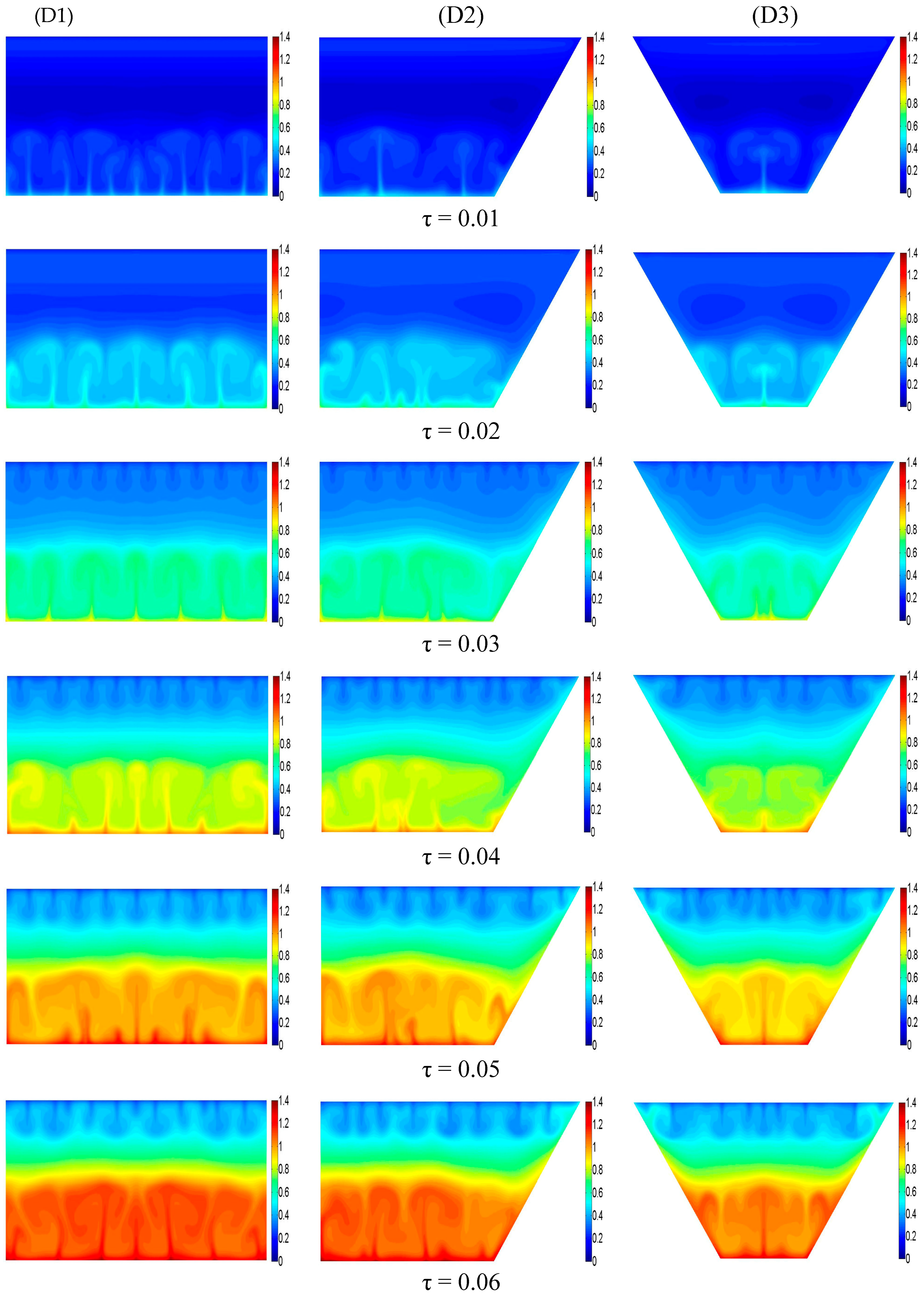
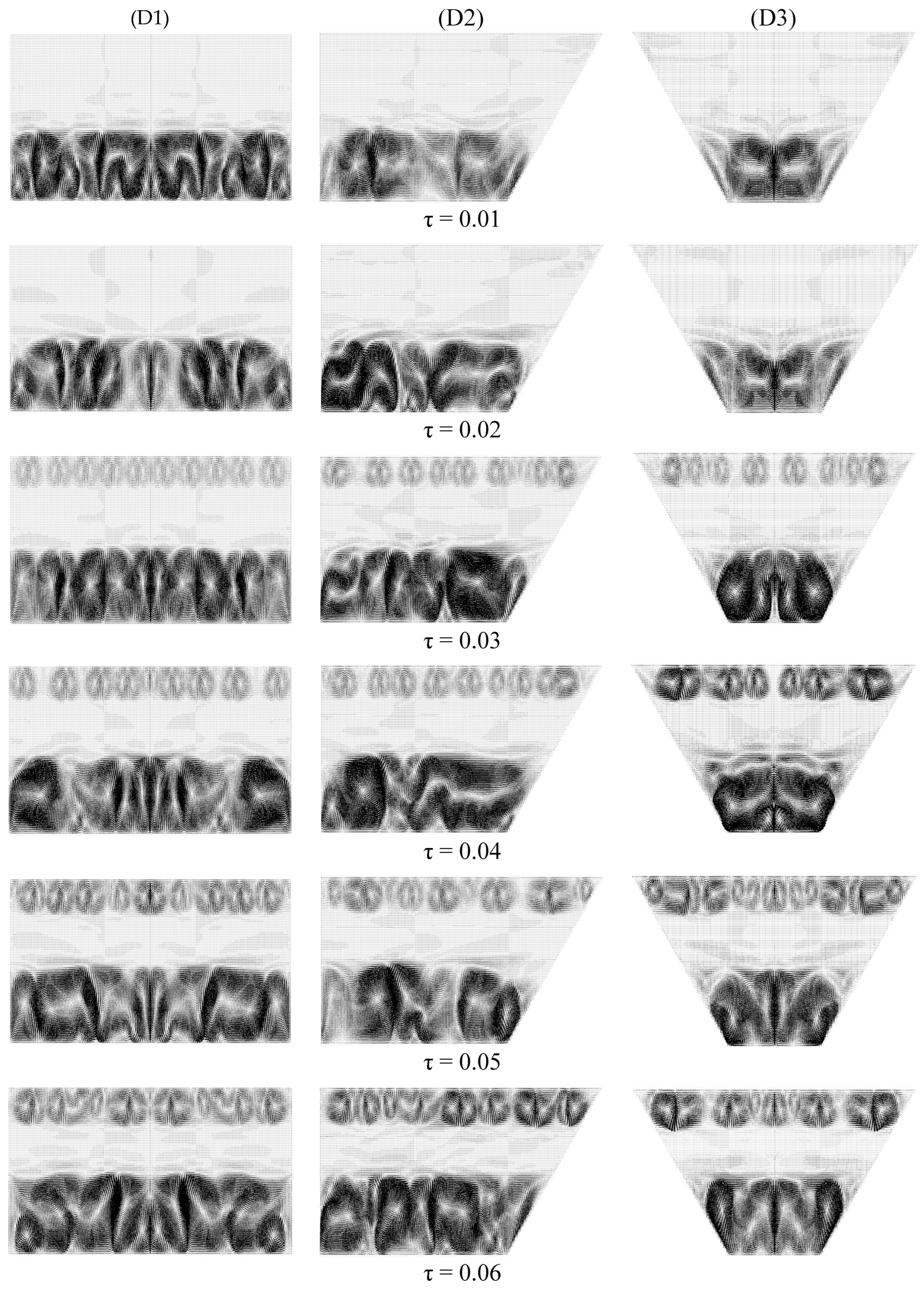
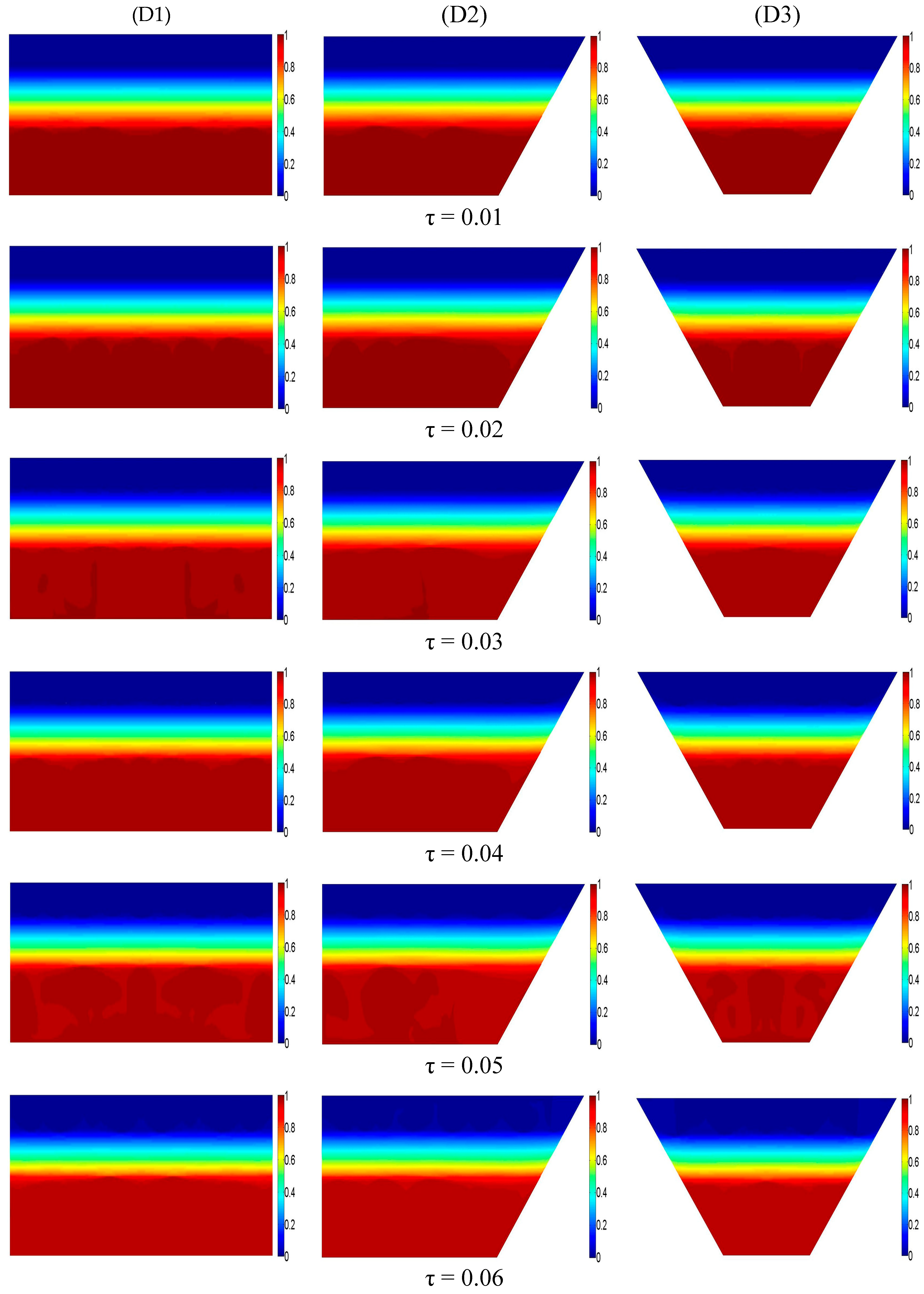
6.1. Time–Wise Evolutions of Temperature, Velocity and Concentration Fields in the SGSP

Figure 7 shows the time–wise evolution of temperature field in the RSGSP, SGSP–OIW and SGSP–TIWs for Ra_IE = 14, Pr = 6, Sc = 1000, Ar = 3, and Br = 10.

As shown in Figure 7, the temperature of water in the UCZ is similar for the three designs of SGSP at τ = 0.01 and 0.02, and after that the temperature of SGSP–TIWs becomes greater than that of the SGSP–OIW and RSGSP in the same zone until τ = 0.06. Looking at the HSZ, the SGSP–TIWs provides a higher temperature when compared to the SGSP–OIW and RSGSP for each solar heating time. This confirms that the two inclined walls are useful to rise the temperature of salt water in the HSZ. This numerical result is due to the smaller volume of salt water inside the SGSP–TIWs compared to the SGSP–OIW and RSGSP, and the two inclined sidewalls effectively decrease the impact of shadows on the intensity of solar radiation transmitted into the bottom, which leads to an augmentation in the temperature of salt water in the HSZ.

So as to get a profounder comprehension into the hydrodynamic behaviour for the three considered SGSPs, the time–wise evolution of velocities field is displayed in Figure 8 for the following parameters: Ra_IE = 14, Pr = 6, Sc = 1000, Br = 10, and Ar = 3. It is observed an immobile water in the top zone of RSGSP, SGSP–OIW and SGSP–TIWs at τ = 0.01 and 0.02, and after that a series of small convective swirls are mentionned in the same zone. It is also observed that from τ = 0.04 to τ = 0.06, the size of these swirls produced in the UCZ of the SGSP–TIWs becomes grander when compared to the RSGSP and SGSP–OIW. On the other hand, it can be seen that the number of big convective swirls produced in the HSZ of the SGSP–TIWs is lesser than that of the RSGSP and SGSP–OIW. This because of the small area of HSZ in the SGSP–TIWs as compared to the RSGSP and SGSP–OIW.

With regard to the Figure 9 which represents the time–wise evolution of salt concentration field in the three designs of SGSP for Ra_IE = 14, Pr = 6, Sc = 1000, Br = 10, and Ar = 3, it can be seen that the salt concentration in the UCZ rests practically the same for the RSGSP, SGSP–OIW and SGSP–TIWs during solar heating operation. In the HSZ, for a higher solar heating time, we can indicate an increasing of salt concentration in the SGSP–TIWs as compared to the SGSP–OIW and RSGSP. This because the volume of salt water is lesser in the HSZ of the SGSP–TIWs compared to the SGSP–OIW and RSGSP.

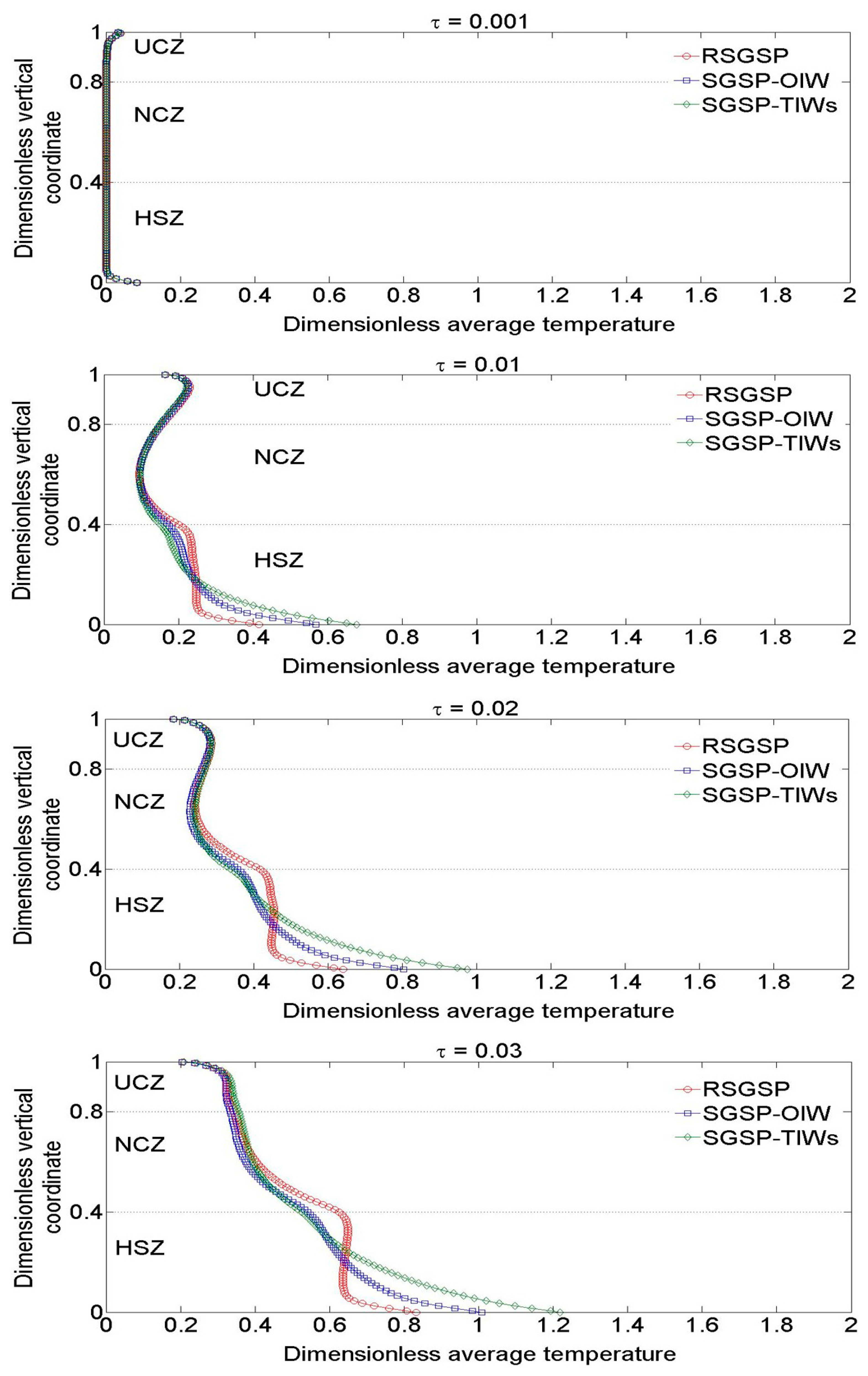
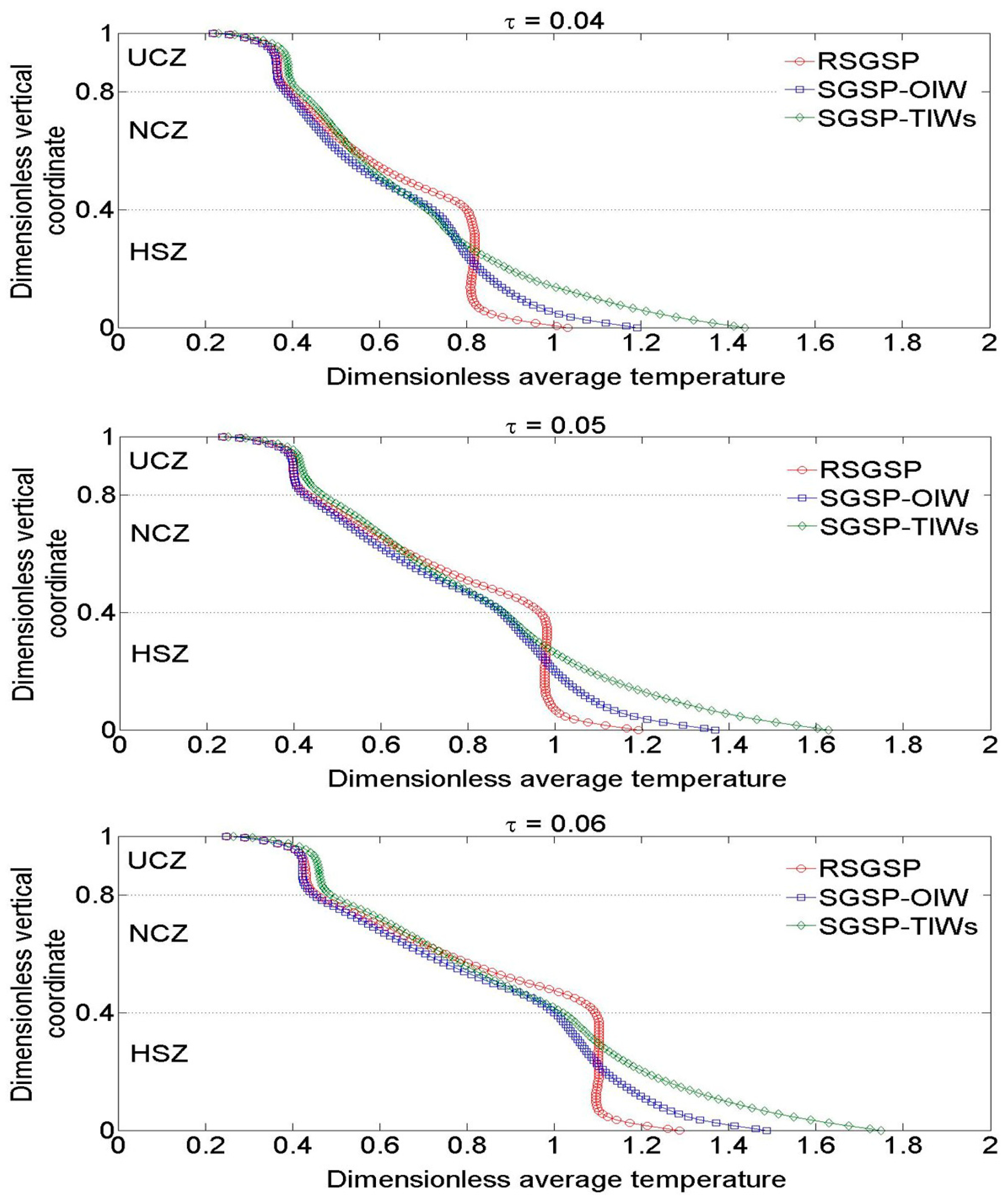
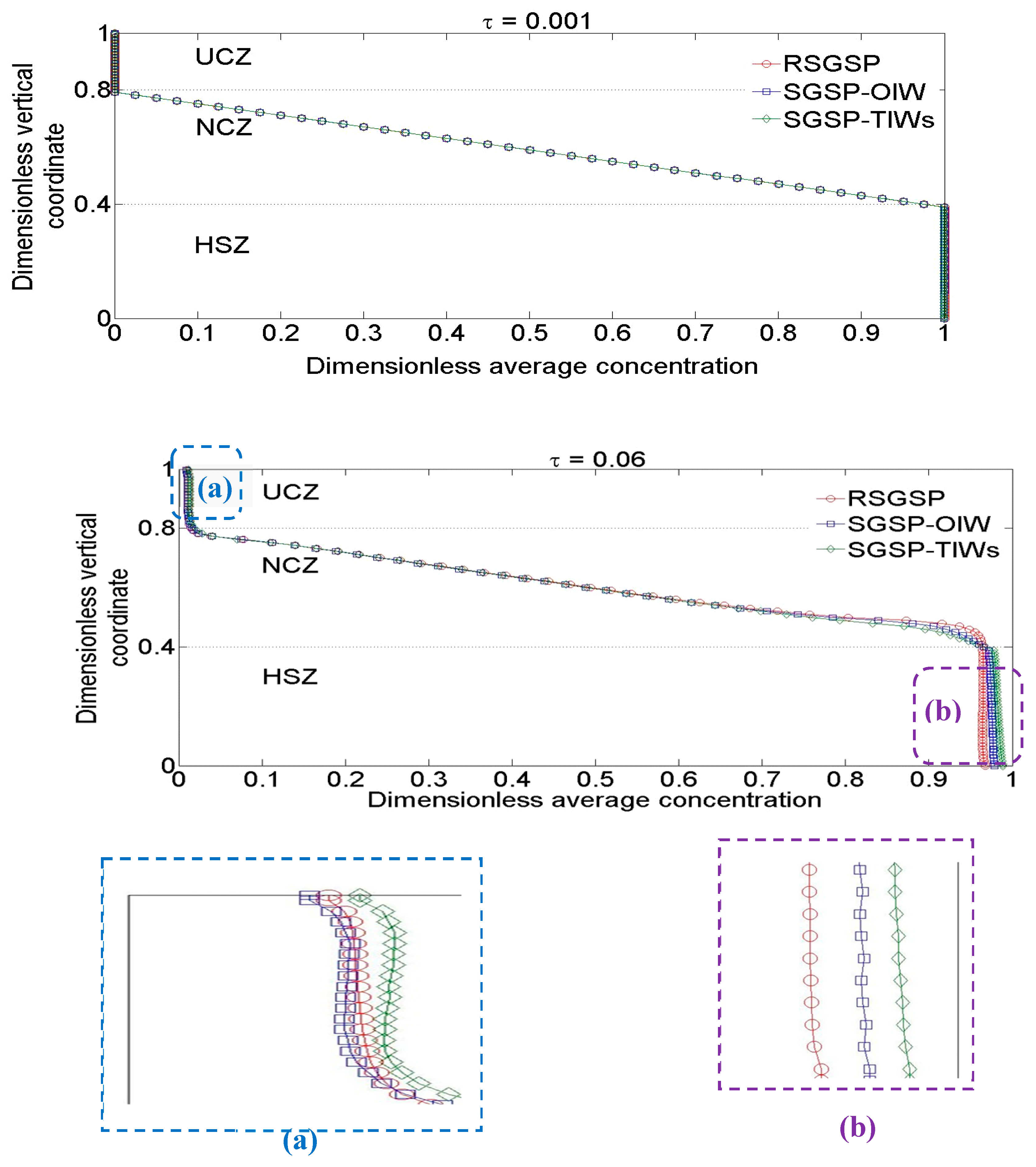
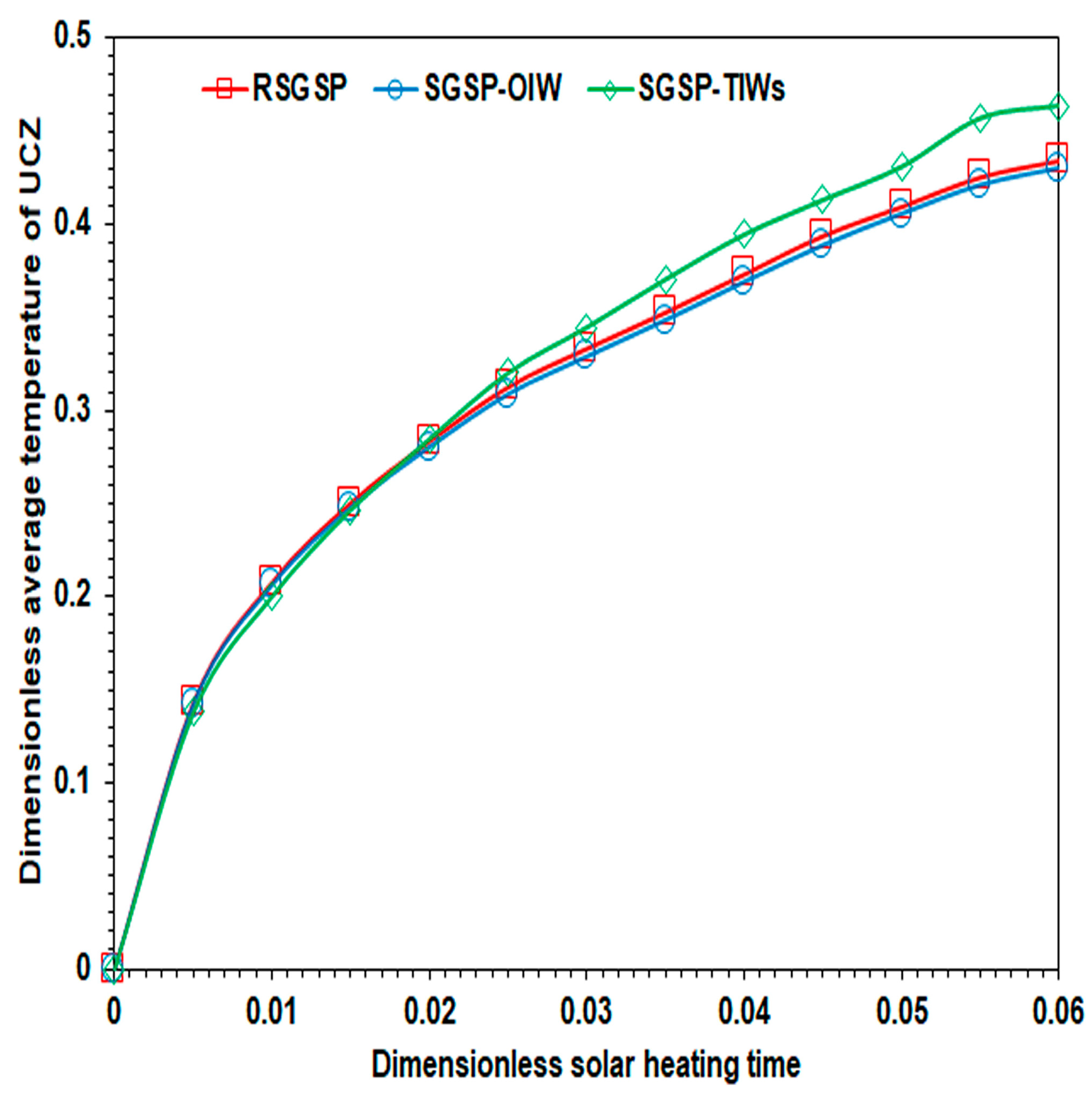
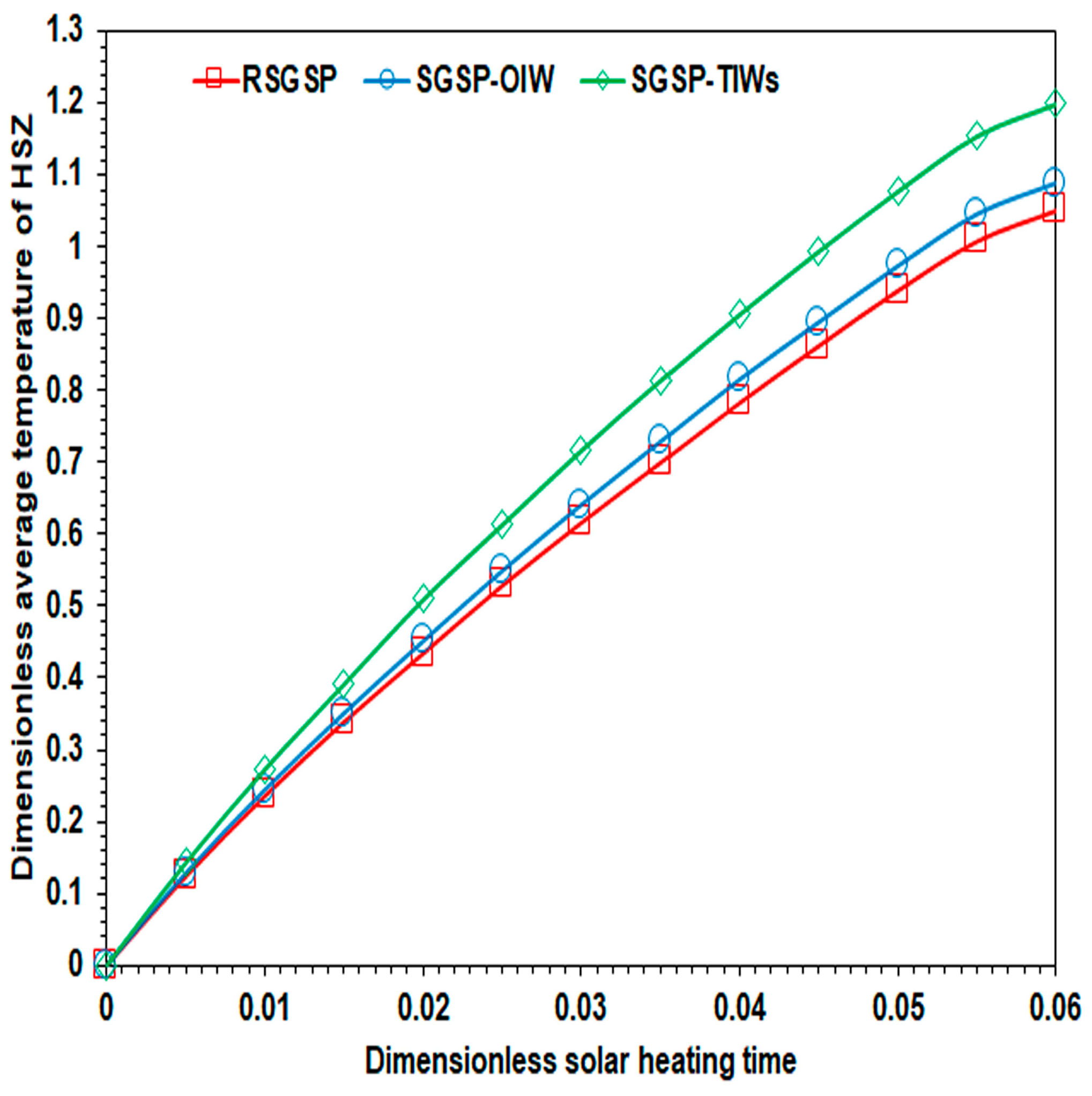
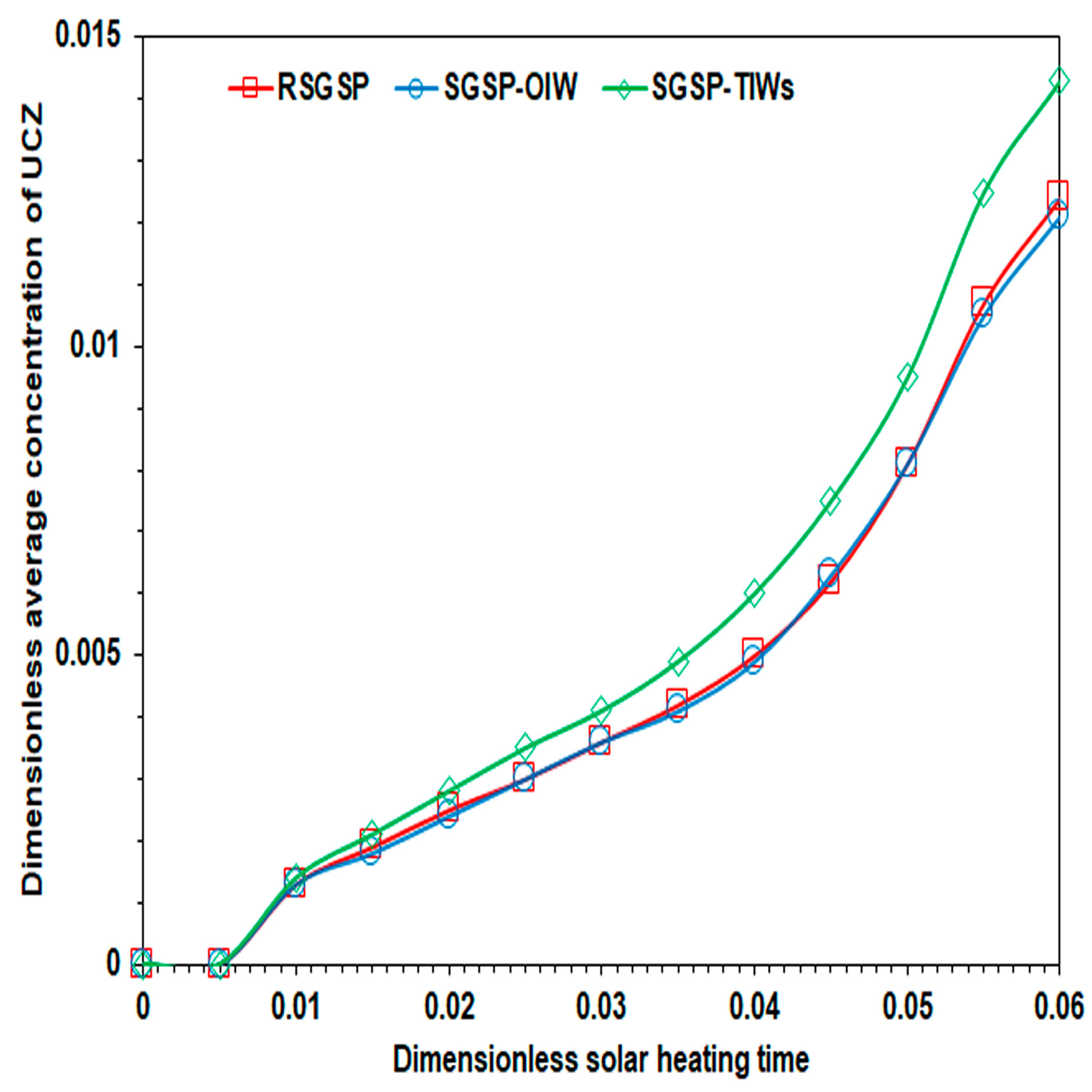
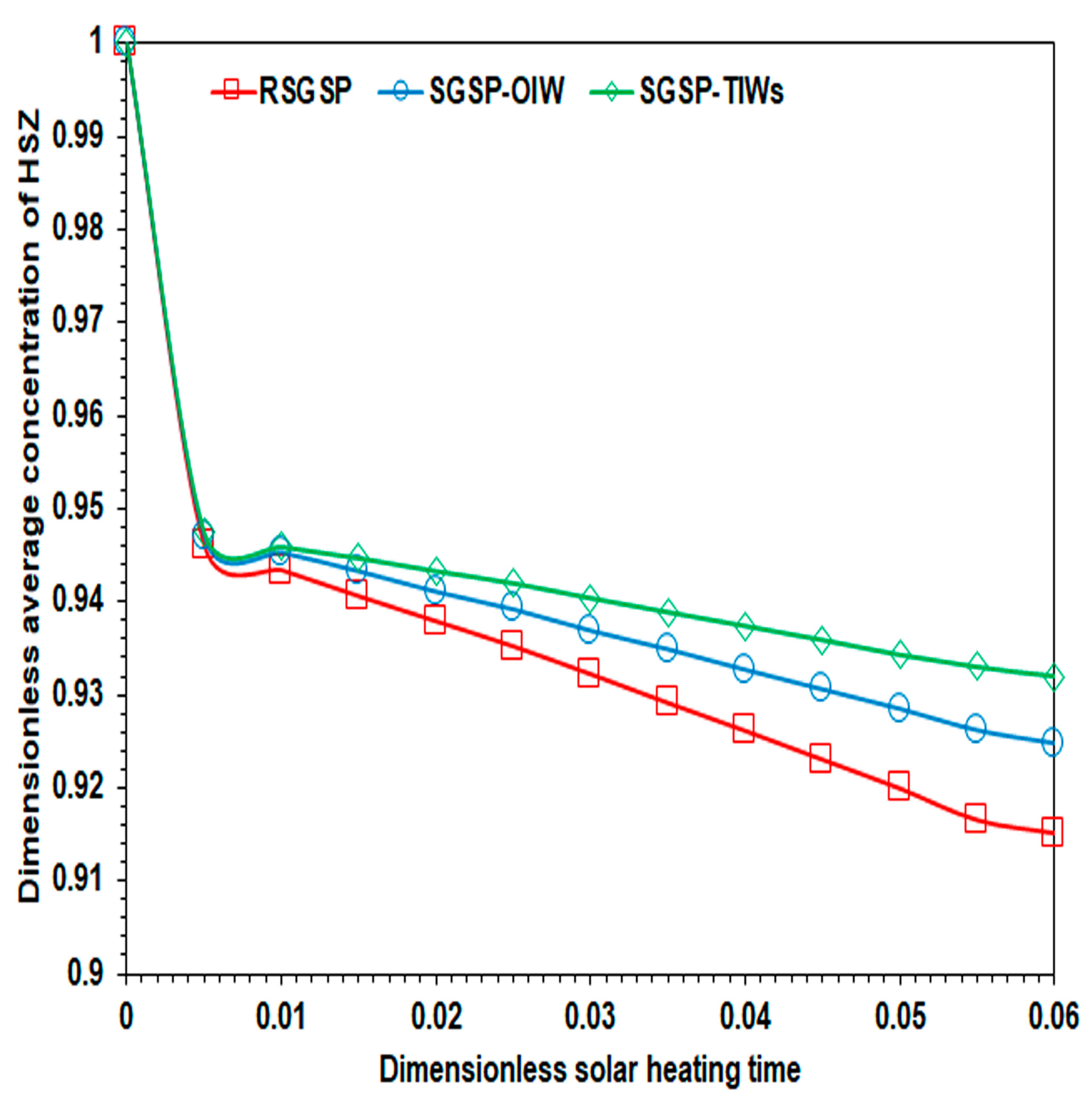
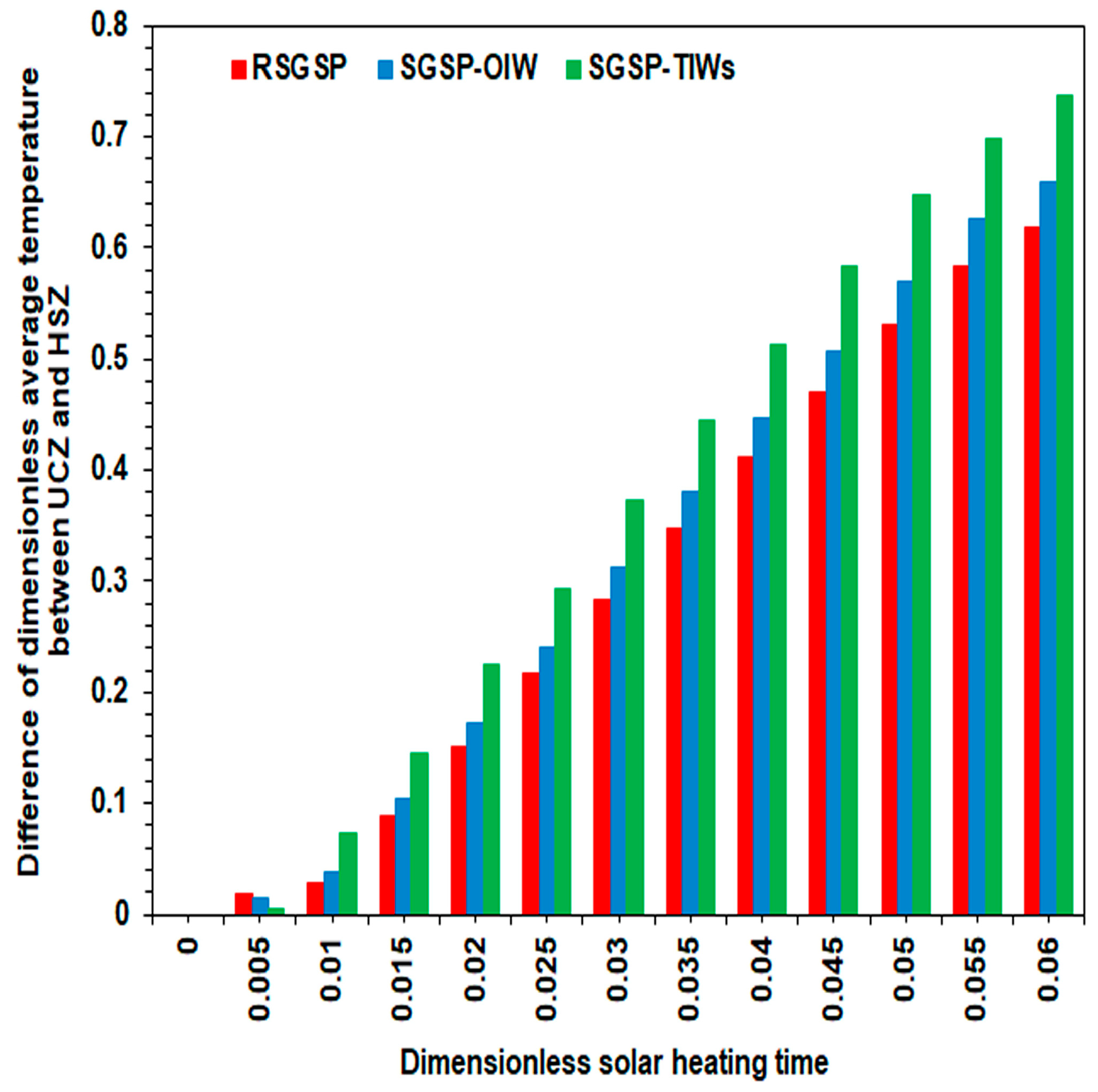
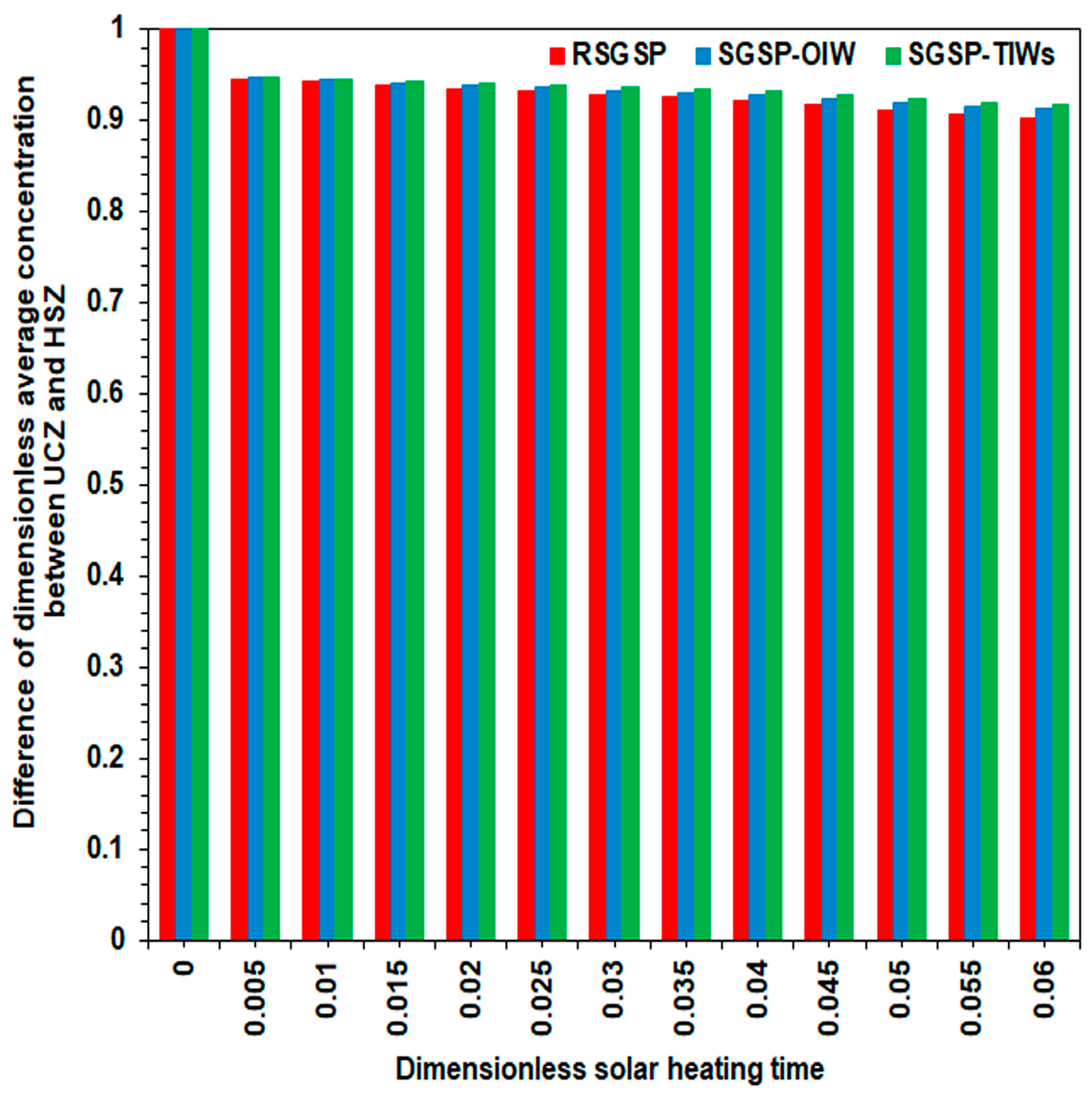
6.2. Time–Wise Evolution of the Dimensionless Average Temperature and Concentration

In order to clearly examine the heat and mass transfer behaviours inside the RSGSP, SGSP–OIW and SGSP–TIWs during the heat storage operation, we demonstrated in Figure 10 and Figure 11, respectively, the time–wise development of the dimensionless average temperature and salt concentration profiles for Ra_IE = 14, Pr = 6, Sc = 1000, Br = 10, and Ar = 3. According to Figure 10, the profile of dimensionless average temperature of the three designs of SGSP is identical at τ = 0.001. At τ = 0.01 and 0.02, the profile of average temperature of both SGSPs in the UCZ is confused and after that the important increase in this profile occurred for the SGSP–TIWs in the same zone. From τ = 0.01 to τ = 0.06, the maximum profile of dimensionless average temperature of SGSP–TIWs in the HSZ is greater than that of the SGSP–OIW and RSGSP. This is because the area of shadow created in the SGSP–TIWs is smaller than that in the SGSP–OIW and RSGSP.

With regard to the Figure 11, the initial profile of dimensionless average salt concentration is confused for the RSGSP, SGSP–OIW and SGSP–TIWs at τ = 0.001. However, at τ = 0.06, the slight increase in the profile of dimensionless average salt concentration indicated by the SGSP–TIWs in the UCZ and HSZ as compared to the other two designs of SGSP.

To better understanding the impact of SGSP’s geometric shape on the heat and mass transfer, the time–wise variation of dimensionless average temperature and salt concentration of UCZ and HSZ in both SGSPs is established in Figs. 12-15 for Ra_IE = 14, Pr = 6, Sc = 1000, Br = 10 and Ar = 3. As it is indicated in Figure 12, it is evident that increasing the solar heating time leads to rise in the dimensionless average temperature of UCZ for the three considered SGSPs. From τ = 0 to τ = 0.02, the dimensionless average temperature of UCZ has the same value for the three SGSPs and after that the dimensionless average temperature of UCZ in the SGSP–TIWs becomes slightly larger than that of the other two SGSPs. As seen in Figure 13, the dimensionless average temperature of HSZ in the SGSP–TIWs is greater when compared to the RSGSP and SGSP–OIW. In fact, at τ = 0.06, the dimensionless average temperature of HSZ in the RSGSP reaches a value of 1.05. With the SGSP–OIW, the dimensionless average temperature of HSZ reaches 1.1 for the same τ. Because of the inclination of single wall of the conventional SGSP, the dimensionless average temperature of HSZ rises by 0.05 and this represents 4.762% greater than the RSGSP.

When using the SGSP–TIWs, the dimensionless average temperature of HSZ reaches 1.2 for the same τ. Because of the inclination of two walls of the conventional SGSP, the dimensionless average temperature of HSZ rises by 0.15 and this represents 14.3% greater than the RSGSP.

The time–wise variation of dimensionless average temperature of HSZ for the three different designs of SGSP is numerically correlated by Eqs. (44)-(46).

- For the RSGSP, the numerical correlation equation is written as follows:

$${\overline{\mathsf{\theta }}}_{\mathrm{H}\mathrm{S}\mathrm{Z}} = - 102.45 {\mathsf{\tau }}^2 + 23.814 \mathsf{\tau }$$

(44)

where ${\overline{\mathsf{\theta }}}_{\mathrm{H}\mathrm{S}\mathrm{Z}}$ is the dimensionless average temperature of HSZ and τ is the dimensionless solar heating time. R² = 0.9997 is the value of R-squared of the obtained numerical correlation.

- For the SGSP–OIW, the numerical correlation equation is written as follows:

$${\overline{\mathsf{\theta }}}_{\mathrm{H}\mathrm{S}\mathrm{Z}} = - 108.26 {\mathsf{\tau }}^2 + 24.796 \mathsf{\tau }$$

(45)

with R² = 0.9997 is the value of R-squared of the obtained numerical correlation.

- For the SGSP–TIWs, the numerical correlation equation is written as follows:

$${\overline{\mathsf{\theta }}}_{\mathrm{H}\mathrm{S}\mathrm{Z}} = - 130.12 {\mathsf{\tau }}^2 + 27.976 \mathsf{\tau }$$

(46)

with R² = 0.9998 is the value of R-squared of the obtained numerical correlation.

Eqs. (44)-(46) are obtained for the following parameters: Ra_IE = 14, Pr = 6, Sc = 1000, Br = 10 and Ar = 3.

As can be observed in Figure 14, it is evident that the dimensionless average salt concentration of UCZ increases with the increase of dimensionless solar heating time for the three SGSPs. On the other hand, the dimensionless average salt concentration of UCZ in the RSGSP and SGSP–OIW has practically the same values during solar heating operation. Whereas, the values of dimensionless average salt concentration of UCZ in the SGSP–TIWs are slightly upper than the RSGSP and SGSP–OIW from τ = 0.01 to τ = 0.06.

As appreciated in Figure 15, with the increase of dimensionless solar heating time, the dimensionless average salt concentration of HSZ in the three SGSPs diminishes. This because of the upward salt diffusion in both SGSPs. It is also observed that the dimensionless average salt concentration of HSZ in the SGSP–TIWs is slightly grander as compared to the RSGSP and SGSP–OIW. At τ = 0.06, the dimensionless average salt concentration of HSZ in the RSGSP attains a value of 0.91. However, the dimensionless average salt concentration of HSZ in the SGSP–OIW attains 0.92 for the same τ. Due to the inclination of single wall of the conventional SGSP, the dimensionless average salt concentration of HSZ enhances by 0.01 and this represents 1.1% higher than the RSGSP. With the use of the SGSP–TIWs, the dimensionless average salt concentration of HSZ attains a value of 0.93 for the same τ. Because of the inclination of two walls of the conventional SGSP, the dimensionless average salt concentration of HSZ rises by 0.02 and this represents 2.2% higher than the.

The time–wise variation of dimensionless average temperature and concentration difference between UCZ and HSZ in the three considered SGSPs has been demonstrated in Figure 16 and Figure 17. As observed in these figures, at τ = 0.06, the difference of dimensionless average temperature between UCZ and HSZ in the RSGSP, SGSP–OIW and SGSP–TIWs is 0.62, 0.66 and 0.74, respectively. Also, the difference of dimensionless average salt concentration between UCZ and HSZ in the RSGSP, SGSP–OIW and SGSP–TIWs is 0.9, 0.913 and 0.92, respectively.

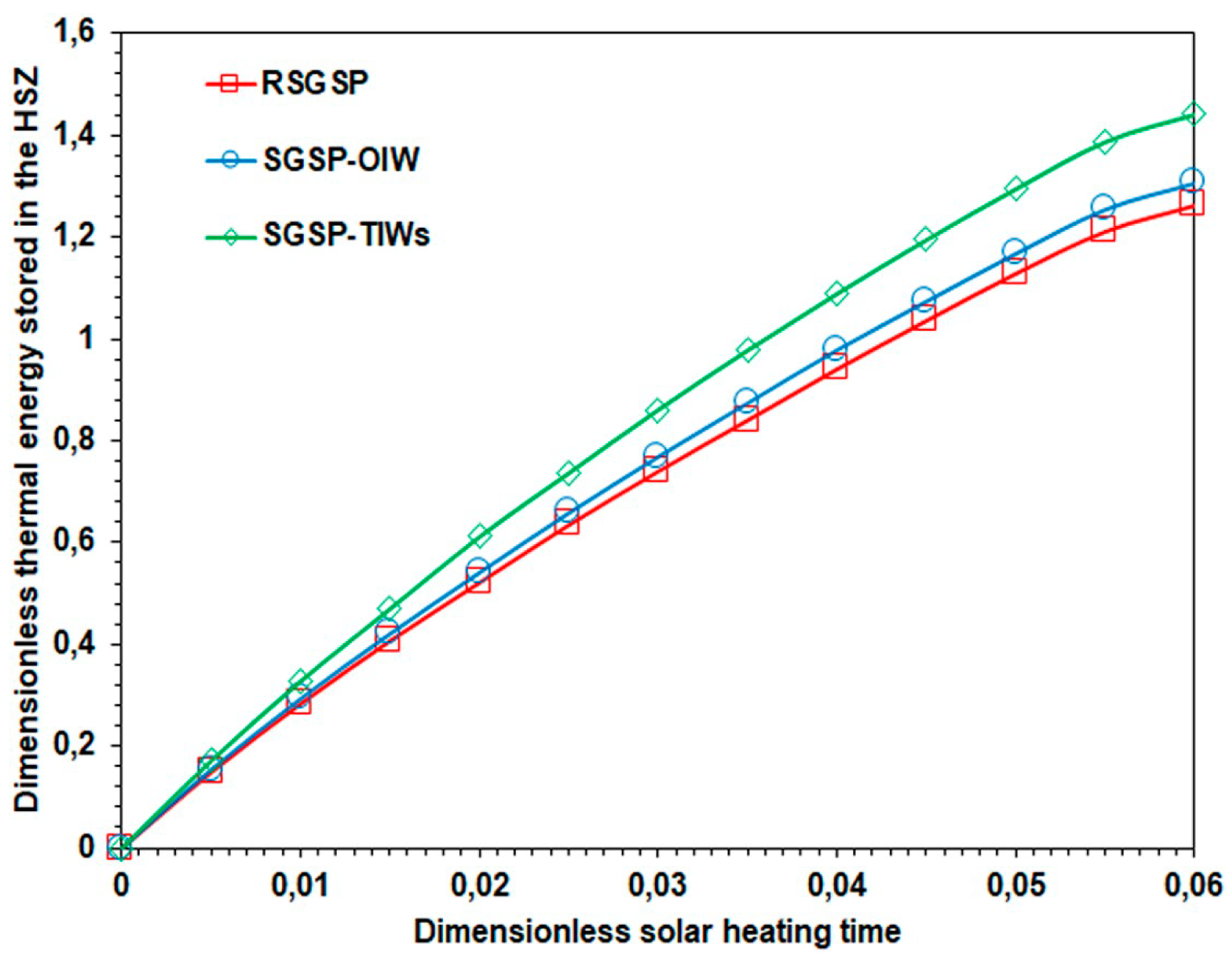
6.3. Time–Wise Evolution of the Dimensionless Thermal Energy Stored in the HSZ

Figure 18 shows the temporal evolution of dimensionless thermal energy stored in the HSZ of the three considered SGSPs for Ra_IE = 14, Pr = 6, Sc = 1000, Br = 10 and Ar = 3. As shown in Figure 18, these curves have the identical style as the dimensionless average temperature of HSZ. This is because the dimensionless thermal energy stored in the HSZ is strictly connected to the dimensionless temperature in the same zone through Eq. 19. Besides, the dimensionless thermal energy stored in the HSZ inside the three proposed geometry designs of SGSP rises successively until the dimensionless solar heating time of 0.06 to attain 1.25, 1.3 and 1.44 for the RSGSP, SGSP–OIW and SGSP–TIWs, respectively. The use of one inclined wall boosts the dimensionless stored thermal energy by 4 % compared to the RSGSP. Whereas the use of two inclined walls boosts the dimensionless stored thermal energy by 15.2% compared to RSGSP. Furthermore, the use of two inclined walls boosts the dimensionless stored thermal energy by 10.8% as compared to SGSP–OIW. This is due to the highest dimensionless average temperature of HSZ in the SGSP–TIWs as compared to the SGSP–OIW and RSGSP.

7. Conclusions

The numerical investigation on the effect of geometric design on the heat storage performance of salinity gradient solar pond revealed that the use of two inclined walls in SGSPs decreases the impact of shadow on the intensity of solar radiation transmitted into the bottom of the pond. Also, the volume of salt water inside the SGSP–TIWs is lesser than the SGSP–OIW and RSGSP, and from which the SGSP–TIWs has the greatest dimensionless average temperature of HSZ. The maximum dimensionless average temperature of RSGSP and SGSP–OIW in the HSZ is 1.05 and 1.1, respectively. Due to the use of one inclined wall, the SGSP–OIW enhanced the dimensionless average temperature of HSZ by 4.762% more than that of the RSGSP. Besides, the maximum dimensionless average temperature of RSGSP and SGSP–TIWs in the HSZ is 1.05 and 1.2, respectively. Due to the use of two inclined walls, the SGSP–TIWs boosted the dimensionless average temperature of HSZ by 14.286% more than that of the RSGSP. The dimensionless average temperature of HSZ as a function of dimensionless solar heating time can be provided by the following numerical correlations:

For the RSGSP: ${\overline{\mathsf{\theta }}}_{\mathrm{H}\mathrm{S}\mathrm{Z}} = - 102.45 {\mathsf{\tau }}^2 + 23.814 \mathsf{\tau }$

For the SGSP–OIW: ${\overline{\mathsf{\theta }}}_{\mathrm{H}\mathrm{S}\mathrm{Z}} = - 108.26 {\mathsf{\tau }}^2 + 24.796 \mathsf{\tau }$

For the SGSP–TIWs: ${\overline{\mathsf{\theta }}}_{\mathrm{H}\mathrm{S}\mathrm{Z}} = - 130.12 {\mathsf{\tau }}^2 + 27.976 \mathsf{\tau }$The dimensionless value of thermal energy stored in the HSZ for the RSGSP is 1.25. But, this becomes equal to 1.3 for the SGSP–OIW. While, the dimensionless value of thermal energy stored in the HSZ for the SGSP–TIWs is 1.44. The SGSP–TIWs boosts the storage quantity of thermal energy in the HSZ by 10.8% and 15.2% as compared to the SGSP–OIW and RSGSP, respectively. On the whole, the use of two inclined walls in SGSPs supplied better heat storage performance than the one inclined wall and vertical walls.

The obtained dimensionless numerical results can be used to determine appropriate operation and geometric parameters of the solar pool design.