MotionAnalysis: Image-Based Cardiorespiratory Dynamics in Ultrasound

1. Introduction

Cardiovascular diseases remain the leading cause of global mortality, with non-invasive imaging techniques playing a critical role in diagnosis and treatment planning [1]. Among these, ultrasound echocardiography is particularly valued for its real-time capability, affordability, and high temporal resolution [2]. In both clinical and preclinical settings, accurate localization of cardiac and respiratory phases in imaging sequences is essential for quantitative analysis, including motion tracking, cardiac strain estimation, and morphological assessments [3].

Traditional methods rely heavily on external physiological signals such as electrocardiograms (ECG) and respiration monitors to track these phases [4]. While effective in human studies, these methods pose significant limitations in small animal models due to the requirement for complex hardware setups, potential motion artifacts, and the challenges of signal synchronization [5]. Moreover, the exceptionally high heart and respiration rates of small animals like mice demand ultra-high temporal sampling rates, often exceeding 2000 Hz, to resolve short-lived cardiac events such as systole and diastole [6].

To address these challenges, there has been a growing interest in image-based methods that estimate physiological phases directly from video data. Early work by Karadayi et al. [7] employed center-of-mass tracking and bandpass filtering to extract cardiac phase signals. However, this approach is sensitive to imaging noise and global motion artifacts. Similarly, Sundar et al. [8] proposed phase correlation methods for cardiac-respiratory gating, though their technique was limited in handling out-of-plane cardiac motion.

Dimensionality reduction approaches have also been explored for motion estimation. Wachinger et al. [9] applied Laplacian Eigenmaps to ultrasound and MRI sequences to identify low-dimensional respiratory manifolds. Panayiotou et al. [10] employed masked principal component analysis (PCA) to extract periodic motion components. Despite their promise, these approaches lack direct phase estimation capabilities and often require post hoc frequency analysis to recover physiological cycles.

In this work, we present CardioRespNet, a novel, fully image-based framework for retrospective estimation of cardiorespiratory phases in ultrasound videos. Our method bypasses the need for ECG or respiratory sensors, making it ideal for high-throughput and small animal studies. By leveraging inter-frame similarity matrices and trend extraction via the Hodrick-Prescott filter, we effectively decouple cardiac and respiratory signals. We then employ the Hilbert transform to compute instantaneous phase estimates from the extracted signals.

Furthermore, we introduce a robust two-stage respiratory gating mechanism. Initially, frames exhibiting strong respiratory influence are identified and excluded using a phase-based thresholding strategy. We subsequently refine the selection using non-parametric LOWESS regression to model cardiac motion more accurately. This dual-stage process ensures that only frames corresponding to minimal respiratory interference are retained.

To achieve high temporal resolution, we develop a bivariate kernel regression model capable of reconstructing ultrasound frames at arbitrary cardiac phases. This enables the generation of high-fidelity single-cycle videos from low-frame-rate sequences. The model incorporates phase and similarity weights to prioritize reliable cardiac information while mitigating residual respiratory effects.

Through extensive experiments on murine ultrasound datasets with ground-truth ECG, we demonstrate that our method offers significant improvements in phase estimation accuracy, gating robustness, and image reconstruction quality compared to prior image-only approaches. The proposed framework is versatile, non-invasive, and broadly applicable to studies where hardware-based gating is infeasible.

2. Cardiac and Respiratory Phase Estimation

The accurate estimation of cardiac and respiratory phases is central to enhancing the interpretability and diagnostic utility of ultrasound imaging sequences. Instead of relying on externally acquired physiological signals like ECG or respiration monitors, we propose a fully image-based method that exploits temporal correlations across frames in ultrasound videos. This approach is particularly useful in high-frequency imaging scenarios, such as preclinical cardiac studies in small animals, where external monitoring systems are either impractical or fail to capture the fast dynamics effectively.

To begin, we compute an inter-frame similarity matrix from the ultrasound sequence, where each matrix element represents the normalized correlation between a pair of image frames. This matrix captures the temporal structure of quasi-periodic physiological motions. Due to the repetitive nature of cardiac and respiratory cycles, distinct periodic patterns emerge along the matrix diagonals, corresponding to low-frequency respiration and high-frequency heartbeat activity.

Each row of the similarity matrix can be treated as a univariate time series that encodes the temporal similarity of one frame relative to all others. We apply the Hodrick-Prescott (HP) filter, a trend decomposition technique originally developed in econometrics, to each time series. The HP filter separates the time series into a low-frequency trend component and a high-frequency residual. The former corresponds to respiratory motion, while the latter isolates cardiac dynamics.

This separation is critical because cardiac and respiratory signals often overlap in frequency space. Unlike band-pass filtering approaches that may introduce artifacts or lose phase coherence, the HP filter retains temporal fidelity. The filtering is governed by a smoothness parameter $\lambda$, which controls the trade-off between trend fidelity and noise suppression. For our experiments, we empirically set $\lambda =6400$, optimized for murine ultrasound frame rates and physiological frequencies.

After decomposition, the residual (cardiac) and trend (respiratory) signals for a representative row are selected based on entropy minimization in the frequency domain. We calculate the periodogram of each signal and select the row whose cardiac residual has the lowest spectral entropy, indicating strong periodicity and low noise. This selection ensures robust downstream phase estimation.

We further refine the extracted cardiac and respiratory signals by applying frequency-specific filters: a low-pass filter (cutoff at 230 BPM) for the respiratory signal and a band-pass filter (310–840 BPM) for the cardiac signal. These filters suppress noise while retaining physiologically relevant content, enabling precise phase estimation.

Next, we employ the Hilbert transform to convert the filtered time series into analytic signals. The instantaneous phase is computed from the real and imaginary components of the analytic signal using the arctangent of their ratio. This process yields continuous phase values in the range $[0,1)$ for both cardiac and respiratory motions, which are then assigned to each frame in the video sequence.

The resulting phase annotations provide a powerful temporal index for each image frame, facilitating further operations such as respiratory gating and temporal super-resolution. Unlike methods that only yield periodic signals, our approach enables the direct estimation of instantaneous phase trajectories, making it more suitable for downstream temporal modeling.

3. Respiratory Gating

Respiratory gating is essential to remove frames affected by non-cardiac motion in ultrasound videos, particularly in preclinical animal studies where rapid respiration induces significant movement artifacts. Left unfiltered, such frames can compromise the accuracy of cardiac phase estimation and degrade the quality of reconstructed images. We propose a robust two-stage gating strategy to address this issue.

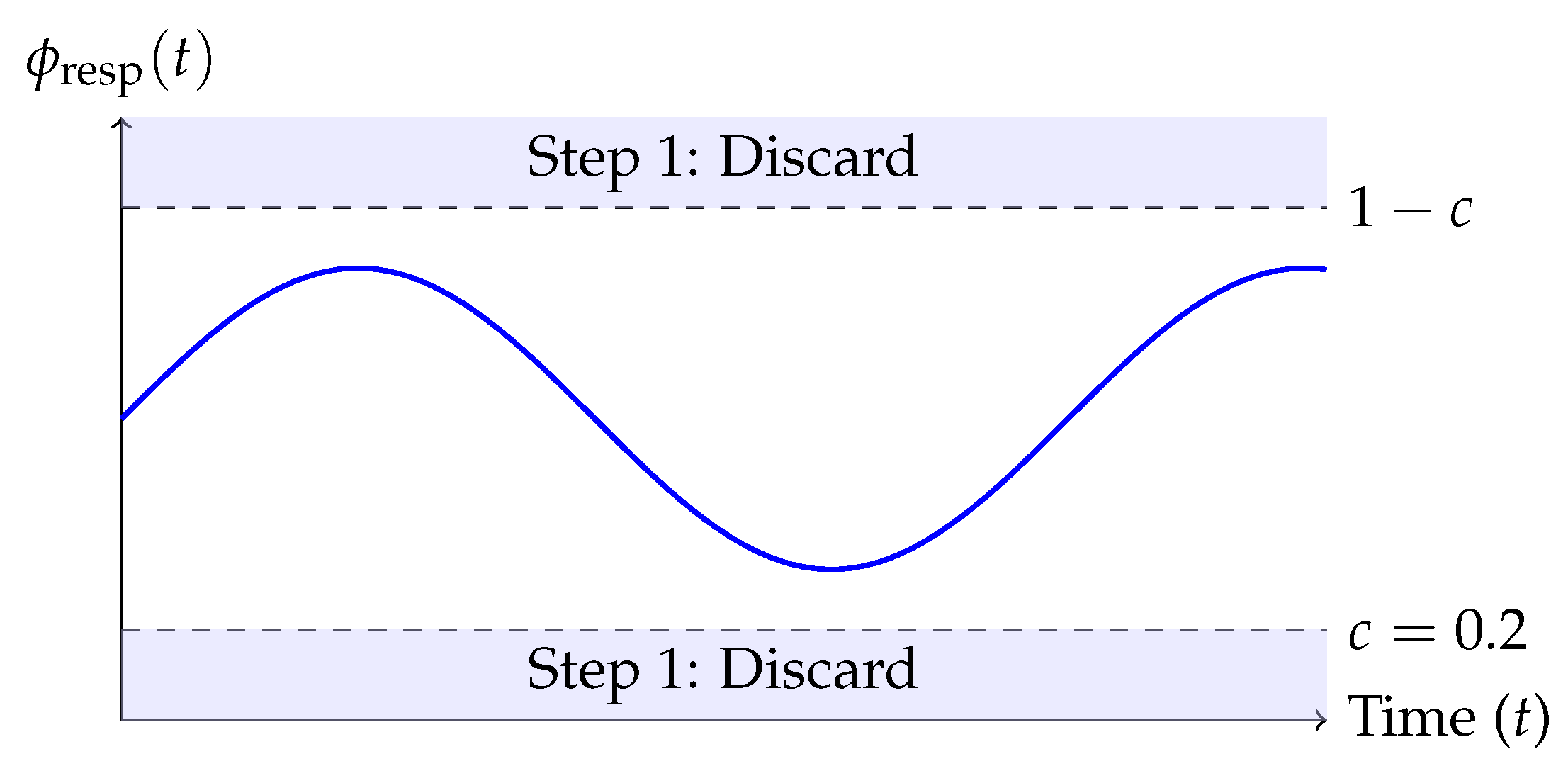
In the first stage, we exploit the periodic structure of the estimated respiratory phase signal ${\varphi }_{\mathrm{resp}}\left(t\right)$, derived using the Hilbert transform. It is observed that maximal respiratory displacement occurs near the minima of the respiratory trend signal. Frames within a phase threshold c from this minima are discarded. Specifically, we remove all frames t for which ${\varphi }_{\mathrm{resp}}\left(t\right)<c$ or ${\varphi }_{\mathrm{resp}}\left(t\right)>1-c$, with $c=0.2$ chosen empirically.

This initial exclusion targets the most motion-corrupted segments, yet some residual effects remain. Therefore, in the second stage, we apply a non-parametric regression model—Locally Weighted Scatterplot Smoothing (LOWESS)—to estimate the expected frame similarity signal $u\left(t\right)$ as a function of the cardiac phase ${\varphi }_{\mathrm{heart}}\left(t\right)$. The LOWESS curve $L\left({\varphi }_{\mathrm{heart}}\right)$ represents the central trend for frames deemed minimally influenced by respiratory artifacts.

After fitting, we compute the residuals between the actual similarity signal and the LOWESS fit. A robust estimator of dispersion, specifically the median absolute deviation (MAD), is used to compute the standard deviation ${\widehat{\sigma }}_L$. Frames deviating from the LOWESS prediction by more than $2{\widehat{\sigma }}_L$ are identified as outliers and removed. This ensures that only frames adhering to cardiac phase consistency are retained.

Figure 1 illustrates the complete respiratory gating pipeline. The respiratory phase ${\varphi }_{\mathrm{resp}}\left(t\right)$ is shown over time, and frames within the thresholded region (blue shaded) are discarded in Step 1. Subsequently, Step 2 further refines the selection based on deviation from the LOWESS fit of $u\left(t\right)$ with respect to ${\varphi }_{\mathrm{heart}}\left(t\right)$.

Our approach offers multiple advantages. First, the gating logic is derived entirely from image data, eliminating the need for external respiratory tracking hardware. Second, the method is adaptive and robust across different datasets, thanks to the use of non-parametric statistical estimation. Finally, by preserving only the cleanest frames, we lay the groundwork for highly accurate cardiac phase interpolation and temporal super-resolution.

Contrary to fixed-window gating used in many clinical settings, our technique adapts to each dataset’s unique cardiac-respiratory dynamics. This is particularly beneficial in animal models where variability is significant, and traditional methods may fail. Moreover, the combination of phase and signal-domain filtering offers a dual-layer protection against motion-induced errors.

In conclusion, our two-step respiratory gating framework significantly enhances the temporal consistency and anatomical clarity of cardiac ultrasound sequences. This preprocessing step is foundational for the effectiveness of subsequent operations such as cardiac phase-based frame interpolation and single-cycle video reconstruction.

4. Temporal Super-Resolution via Kernel Regression

Temporal super-resolution in cardiac ultrasound imaging is the process of reconstructing a high-frame-rate representation of a cardiac cycle from a lower-frame-rate sequence. This is especially important when dealing with small animals, where heart rates can exceed 500 beats per minute, and commercial ultrasound systems may not sample fast enough to capture rapid myocardial motion. To this end, we introduce a kernel regression framework that synthesizes frames at arbitrary cardiac phases from gated ultrasound video sequences.

The foundation of our method lies in the previously estimated cardiac phase ${\varphi }_{\mathrm{heart}}\left(t\right)$ for each frame. Alongside this, the LOWESS model $L\left({\varphi }_{\mathrm{heart}}\right)$, which approximates the expected frame similarity, plays a key role. Together, these allow us to interpolate frames with higher temporal precision. Each image $I\left(t\right)$ in the input sequence is indexed by its cardiac phase and similarity value, and we use these as input features for regression.

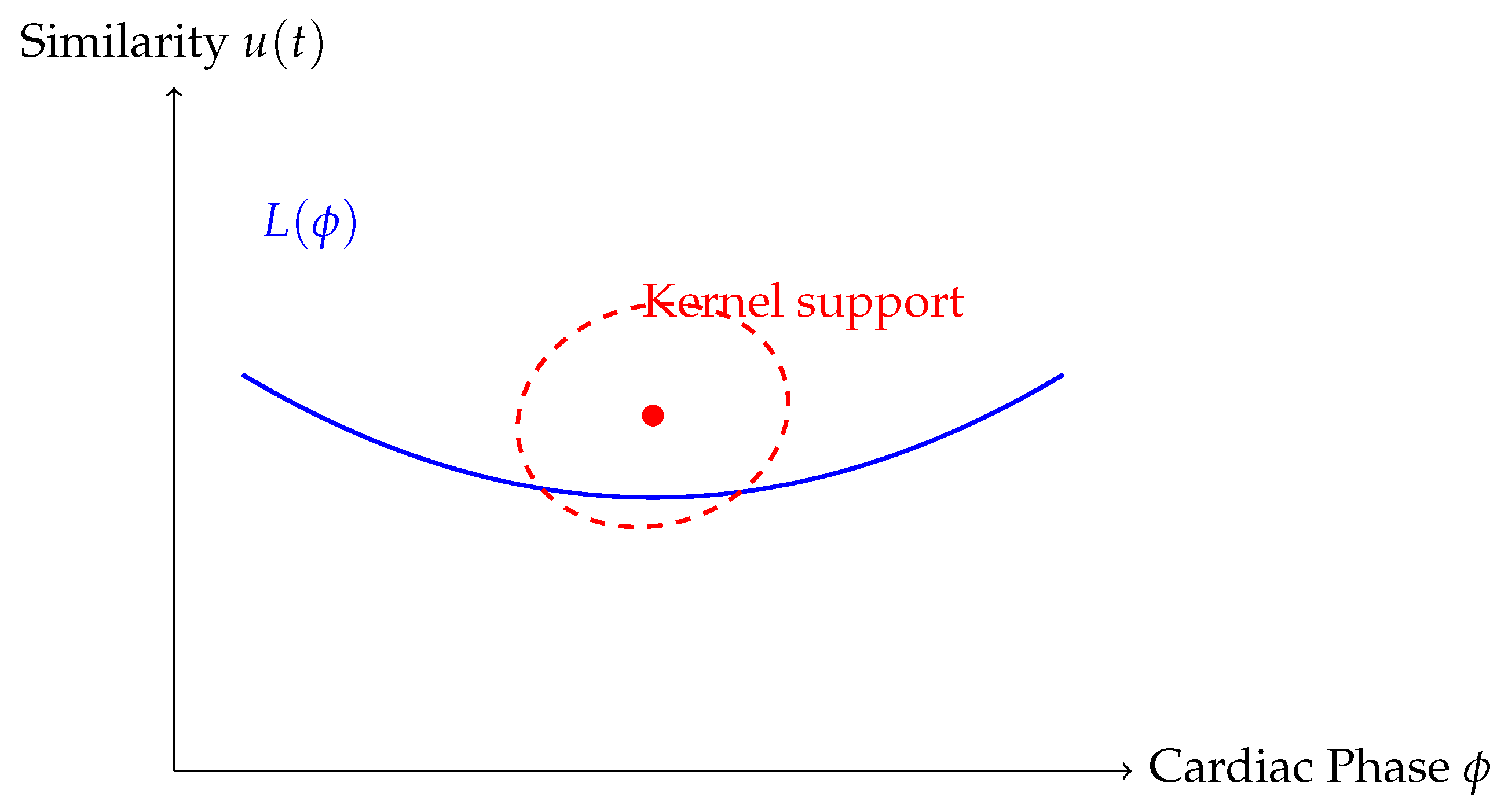
We employ the Nadarya-Watson (NW) kernel regression method to learn a mapping from cardiac phase to image space. For any desired cardiac phase $\varphi$, the reconstructed image $M\left(\varphi \right)$ is computed as a weighted average of nearby frames in both phase and similarity domains. The weights are derived from a bivariate radial basis function (RBF) kernel that assigns higher importance to frames that are close in phase and have high similarity to the expected trend.

Formally, the bivariate kernel $K(\varphi ,{\varphi }_t)$ is defined as:

$$K(\varphi ,{\varphi }_t)=exp\left(-{\displaystyle \frac{{(\varphi -{\varphi }_t)}^2}{2{\sigma }_{\varphi }^2}}\right)·exp\left(-{\displaystyle \frac{{(L\left(\varphi \right)-u\left(t\right))}^2}{2{\sigma }_L^2}}\right)$$

where ${\varphi }_t={\varphi }_{\mathrm{heart}}\left(t\right)$ is the cardiac phase of the t-th frame, $u\left(t\right)$ is its similarity signal, and ${\sigma }_{\varphi }$, ${\sigma }_L$ are bandwidth parameters based on median differences and noise estimates, respectively.

Figure 2 shows a visual representation of the kernel weights across cardiac phase and similarity space. The red ellipse represents the effective support of the kernel function, concentrating weights on frames that are both temporally and structurally consistent with the target phase. This dual weighting ensures that frames corrupted by respiratory motion or out-of-phase dynamics are naturally down-weighted in the regression.

This regression-based formulation allows for synthesis of intermediate frames at arbitrary resolution. By sampling $\varphi \in [0,1)$ at finer intervals, we generate single-cycle cardiac videos with 2x, 4x, or even 8x the original temporal resolution. Each synthesized frame is a structurally coherent estimate, preserving anatomy and motion.

Compared to univariate regression approaches that consider only phase proximity, our bivariate model better handles variability in cardiac dynamics and residual motion. It is particularly effective when input frames are irregularly spaced or unevenly distributed across phases.

Experimental results confirm that our regression-based reconstruction method produces high-quality images with normalized correlation scores exceeding those of baseline methods. Moreover, the method scales efficiently and is robust to moderate downsampling in the input sequence.

In summary, our kernel regression model serves as a powerful tool to reconstruct temporally refined, artifact-free representations of the cardiac cycle from sparse ultrasound data. This enables downstream applications like strain analysis, cardiac modeling, and functional biomarker extraction, even in resource-limited or real-time imaging scenarios.

5. Experimental Data and Results

To evaluate the performance of our proposed methods, we conducted experiments on ultrasound datasets acquired from six anesthetized mice using the VisualSonics Vevo 2100 scanner. The scanner operated at a frame rate of 233 frames per second (FPS), capturing approximately 300 frames per video, which spans around 11 cardiac cycles and 2 respiratory cycles per subject.

Each ultrasound video was accompanied by a simultaneously recorded ECG signal, which serves as the gold standard for cardiac phase. We used these ECG signals to validate our image-based cardiac phase estimation method. Ground-truth cardiac phases were derived by interpolating between R-wave peaks in the ECG signal and compared against the phases estimated directly from the video frames.

The cardiac phase estimates obtained using our method showed strong agreement with the ECG-derived references. Across all six videos, the mean phase error was approximately 0.05 with a standard deviation of 0.03 (in normalized $[0,1]$ units). This performance surpassed three baseline methods: phase correlation [8], manifold learning [9], and masked PCA [10], in both phase estimation accuracy and R-wave frame localization.

Next, we evaluated the performance of our kernel regression model for reconstructing images at arbitrary cardiac phases. A leave-one-out cross-validation (LOOCV) protocol was employed. In each round, a target frame and its corresponding cardiac phase were held out, and the regression model was trained on the remaining frames. The similarity between the reconstructed and actual frame was computed using normalized correlation.

The regression model consistently yielded high similarity scores with mean normalized correlation above 0.83 across all videos. This outperformed the baseline similarity between frames at ECG R-wave peaks (mean 0.72), indicating that our model reconstructs frames with higher fidelity than merely repeating frames from the same cardiac point in the cycle.

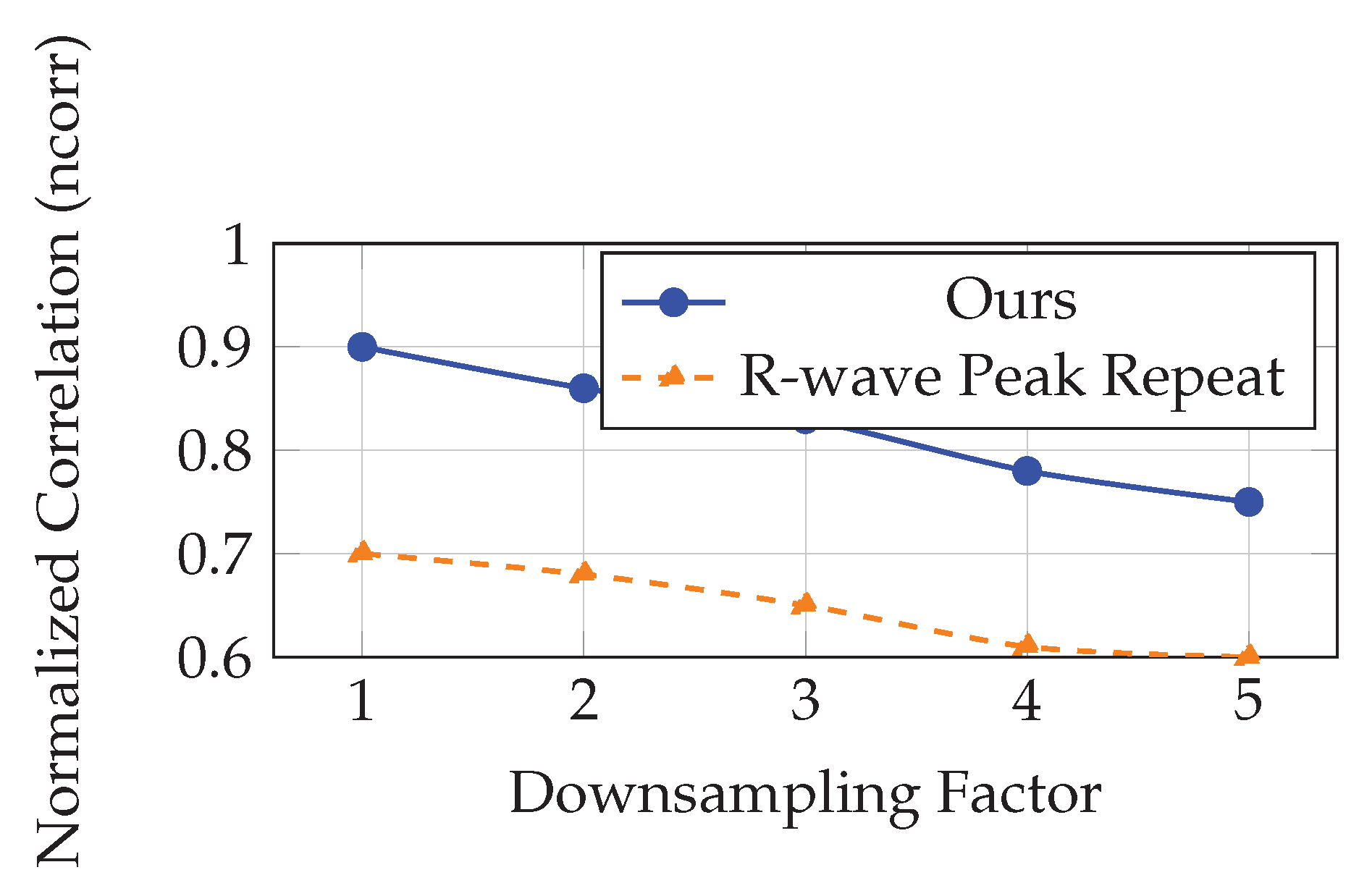
We further assessed the robustness of our temporal super-resolution approach by simulating varying levels of input sparsity. Each video was downsampled temporally by factors of 2x to 5x. From these downsampled inputs, we reconstructed single-cycle cardiac videos at the original resolution using our kernel regression model. The reconstructed sequences were compared with ground-truth single-cycle videos extracted between two ECG R-wave peaks and minimally affected by respiration.

Figure 3 illustrates the normalized correlation between reconstructed and ground-truth videos as a function of downsampling factor. As expected, reconstruction quality degrades with increased downsampling. However, the model maintains acceptable performance (ncorr > 0.75) even at 5x downsampling, where only 5–6 frames per cardiac cycle remain in the input.

Finally, qualitative inspection of the reconstructed sequences reveals smooth, artifact-free myocardial motion and coherent anatomical progression. In contrast, baseline reconstructions based on frame repetition or phase alignment exhibited jitter, blurring, or discontinuities at chamber boundaries.

Overall, our experimental results validate the effectiveness of the proposed framework in estimating physiological phases and synthesizing temporally refined cardiac cycles. The approach demonstrates high robustness, accuracy, and visual consistency, making it highly suitable for preclinical imaging pipelines and downstream cardiac function analysis.

6. Conclusions

In this paper, we presented a fully image-based framework for estimating cardiorespiratory dynamics and enabling temporal super-resolution in ultrasound videos, with a particular focus on preclinical cardiac imaging. By eliminating the need for hardware-based gating such as ECG or respiratory monitors, our approach significantly simplifies the imaging pipeline, especially in small animal studies where external synchronization is challenging.

We introduced a robust phase estimation method based on inter-frame similarity analysis, trend extraction using the Hodrick-Prescott filter, and instantaneous phase derivation via the Hilbert transform. This method allows for accurate decoupling and estimation of cardiac and respiratory phases directly from B-mode ultrasound sequences.

To address motion artifacts caused by respiration, we proposed a two-step gating strategy that combines phase thresholding with non-parametric LOWESS regression. This gating mechanism effectively isolates cardiac frames minimally affected by respiratory interference, thereby improving downstream image analysis tasks.

We also developed a bivariate kernel regression model for synthesizing cardiac-phase-aligned frames at arbitrary temporal resolutions. This model leverages both cardiac phase proximity and signal similarity to ensure high-quality frame interpolation. Experiments on murine echocardiography datasets demonstrated the method’s superior performance in cardiac phase estimation, gating robustness, and reconstruction accuracy compared to existing approaches.

Despite its success, the framework assumes quasi-periodic input sequences, which may limit applicability in cases of severe arrhythmias or irregular breathing. Future work will explore adaptive models that accommodate non-stationary physiological signals and incorporate uncertainty estimation into phase tracking. We also plan to investigate manifold-based kernel regression to further enhance reconstruction fidelity at extreme temporal resolutions.

Our method opens new avenues for high-fidelity, hardware-free cardiac imaging and has potential applications in both preclinical research and clinical diagnostics. By enabling precise motion tracking and artifact suppression, it lays the groundwork for advanced cardiac function analysis, including strain estimation, volume quantification, and disease progression modeling.

The proposed framework is modular and extensible, allowing integration with machine learning models, contrast-enhanced imaging, and real-time ultrasound acquisition systems. As ultrasound imaging technology continues to evolve, image-driven, sensor-independent solutions like ours are likely to play a pivotal role in non-invasive cardiovascular diagnostics.