Submitted:
14 October 2025
Posted:
14 October 2025
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
1.1. Physical Interpretation of the EISA-RIA Framework
1.1.1. Physical Essence of the Vacuum Fluctuation Algebra
Nature of : Operators, Fields, and Information
-
As Operators: is a Grassmann algebra generated by anticommuting operators (with ), satisfying [30]. These are creation/annihilation-like operators acting on the vacuum Hilbert space , similar to fermionic oscillators in second-quantized QFT [40]. Physically, each corresponds to a mode of vacuum fluctuation—e.g., a virtual particle-antiparticle pair or a quantum jitter in the metric. The anticommutation enforces Pauli exclusion for fermionic modes, ensuring proper statistics and preventing overcounting in multi-particle states.For bosonic fluctuations (e.g., gravitational waves or scalar modes), we embed into a Clifford algebra subsector: , where are Dirac matrices satisfying . This duality allows to handle both fermionic (odd-graded) and bosonic (even-graded) excitations, unifying them under a single algebraic roof [30].
- As Fields: The operators condense into effective fields via tracing over representations: the composite scalar emerges as a collective excitation, akin to a Bose-Einstein condensate in many-body physics [18]. Physically, represents the “density” of vacuum fluctuations, sourcing curvature through (derived from the trace-reversed Einstein equations) [15]. Transient processes, like virtual pair “rise-fall”, are modeled as time-dependent perturbations: , where is a damping rate from interactions, leading to exponential decay mimicking pair annihilation [38].
- As Information: From a quantum information perspective, encodes the entropy and correlations of vacuum states. The vacuum density matrix , with Hamiltonian , quantifies fluctuation entropy . High entropy corresponds to unstable vacua with frequent fluctuations, while minimization (via RIA) drives towards stable, low-entropy states—physically, this is vacuum selection, similar to how the Higgs vacuum minimizes potential energy but extended to information-theoretic grounds.
Physical Motivation and Analogies
1.1.2. Physical Significance of Recursive Information Optimization (RIA)
Physical Motivation: Entropy Minimization as a Dynamical Principle
-
Quantum Decoherence and Information Flows: In open quantum systems, interactions with environments (e.g., vacuum fluctuations) lead to decoherence, increasing entropy. RIA reverses this: recursive optimization simulates the system’s “search” for low-entropy paths, akin to the path integral formalism where dominant contributions come from stationary phases (saddle points). Physically, this models how symmetries (encoded in EISA) constrain information flows, preventing unbounded entropy growth and stabilizing vacua.Derivation from first principles: Start with the Lindblad master equation for open systems:where dissipators from drive decoherence. RIA approximates this via VQCs: each circuit layer , with generators G from EISA, iteratively minimizes , equivalent to finding the steady-state where entropy production balances.
-
Emergence of Dynamics from Symmetries: RIA is not ad hoc; it embodies the principle that physical laws emerge from optimizing information under symmetry constraints—a concept inspired by entropic gravity [15], where Einstein equations derive from thermodynamic equilibrium on horizons. In RIA, recursion corresponds to iterative renormalization group (RG) flows: each loop integrates out high-energy modes, minimizing effective entropy at low energies [23].Quantitative link: The beta function (with ) emerges from RIA by optimizing loop integrals variationally, ensuring asymptotic freedom as a consequence of entropy reduction (high-entropy UV fixed points flow to low-entropy IR).
- Analogy to Thermodynamic Principles: Just as heat engines minimize free energy to extract work, RIA minimizes quantum entropy to “extract” stable dynamics from fluctuating vacua. Physically, this drives phase transitions: high-entropy symmetric phases (e.g., pre-transition vacuum) evolve recursively to low-entropy broken phases (e.g., with ), releasing energy as GWs or particles.
Why RIA is a First-Principle Physical Mechanism
1.1.3. Integrated Physical Picture of EISA-RIA
2. Comparative Analysis and Original Contributions
2.1. Quantitative Comparison with Donoghue’s Quantum Gravity EFT
2.2. Comparison with String Theory, SUSY, and GUTs
2.3. Original Contributions of RIA and Distinctions from Quantum Information Methods
3. Triple Superalgebra Structure
3.1. Standard Model Sector
- For , there are 8 generators (Gell-Mann matrices in the fundamental 3-dimensional representation, normalized as ), satisfying , where are the totally antisymmetric structure constants (e.g., , , etc.) [7]. These morphisms correspond directly to the gluon gauge fields through the covariant derivative , where is the strong coupling constant, and quarks transform in the fundamental representation (color triplets) [40].
- For , a single generator Y proportional to the identity in the appropriate hypercharge representation, commuting with all others in this subcategory; it couples to the hypercharge gauge field as , where is the hypercharge coupling, and charges are assigned per SM (e.g., for left-handed quarks, for left-handed leptons) [7].
3.2. Gravitational Sector
3.3. Vacuum Sector
3.4. Full Structure Constants and Super-Jacobi Identities
4. High-Energy Origins and Symmetry Breaking Dynamics
4.1. Conceptual Foundation: High-Energy Vacuum as Primordial Symmetry State
4.2. Symmetry Breaking Mechanism: Cascade-Like RG Flows and Condensation
4.3. Physical Implications: Emergence of Low-Energy Phenomena
4.4. Consistency Checks and Model Extensions
5. Modified Dirac Equation
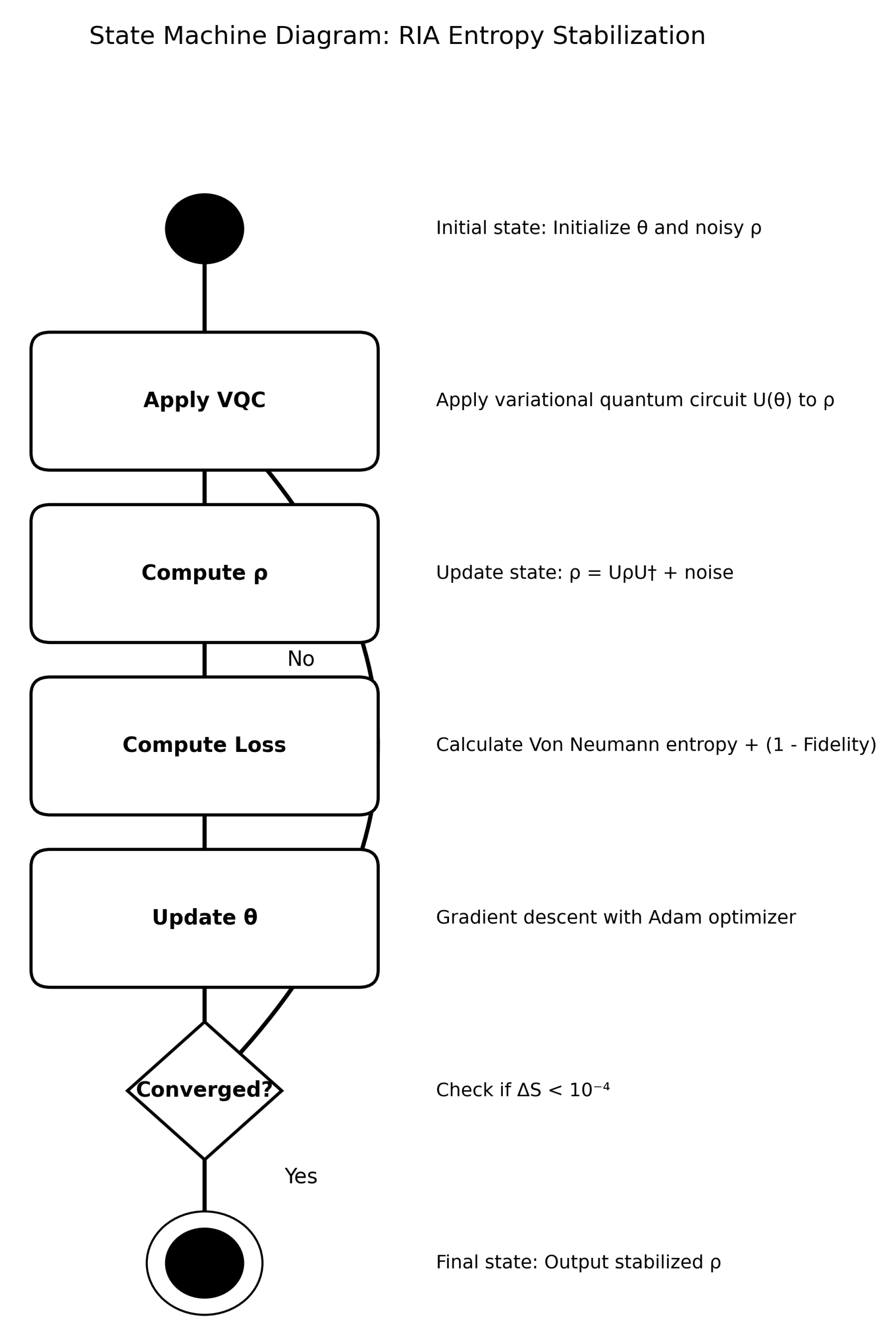
5.1. Recursive Info-Algebra (RIA)
- the fidelity measures similarity to a target state (e.g., the unperturbed vacuum , or a low-entropy pure state from for gravitational stability) [62];
- the purity term penalizes mixedness, with the coefficient 1/2 chosen to balance the optimization landscape based on numerical sensitivity (variations of change entropy by ) [32].
6. Renormalization Group (RG) Flow
7. CMB Power Spectrum
8. Numerical Simulations
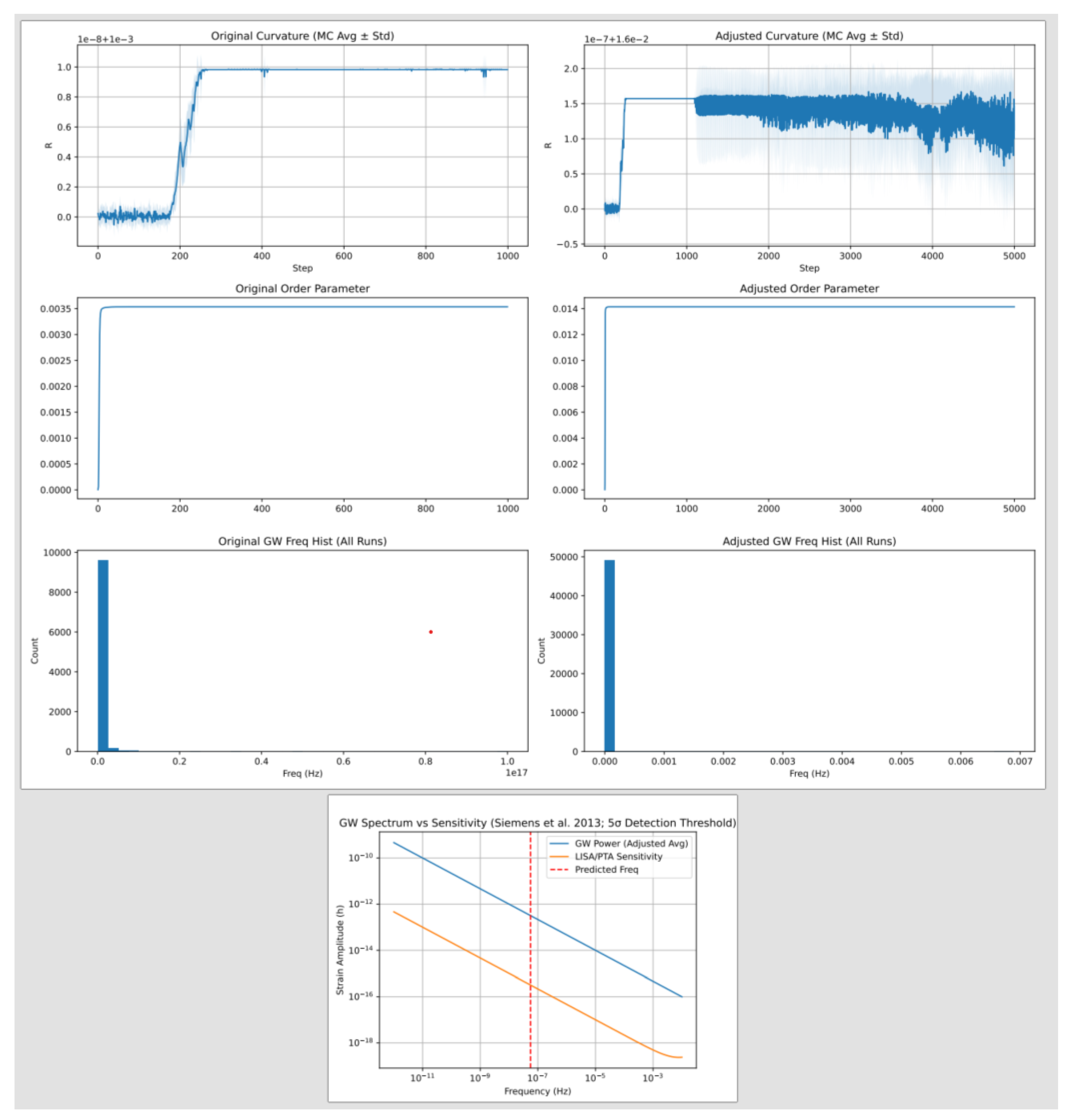
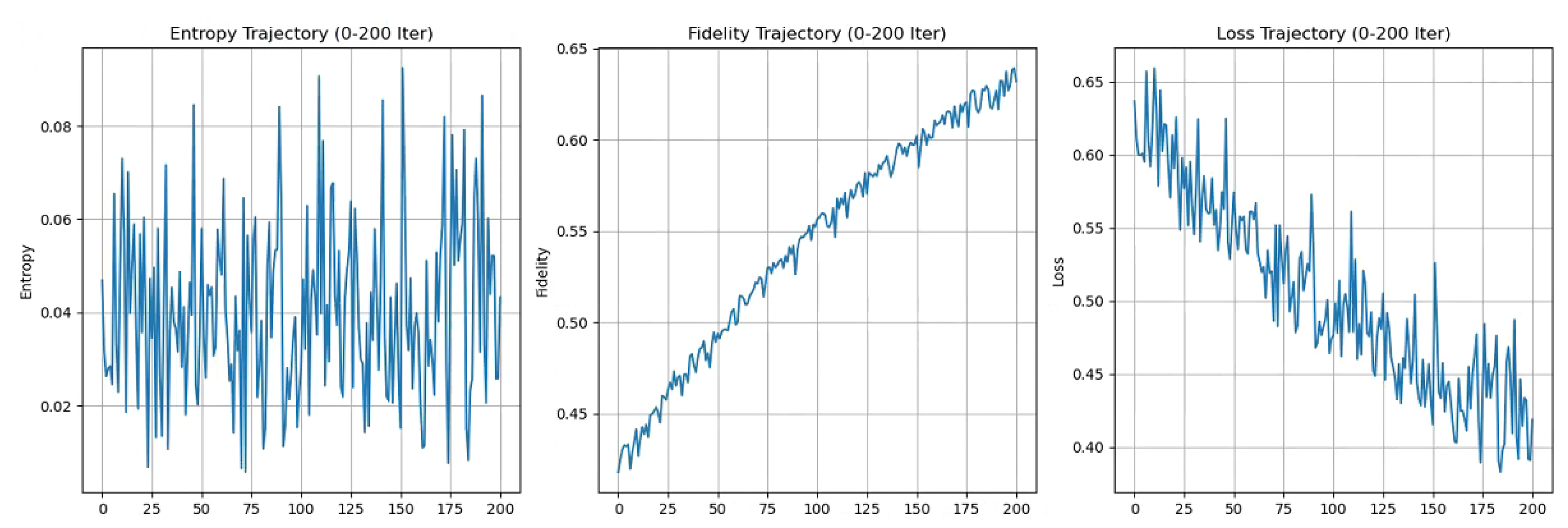
8.1. Recursive Entropy Stabilization
8.1.1. Analytical Derivation
Entropy Minimization
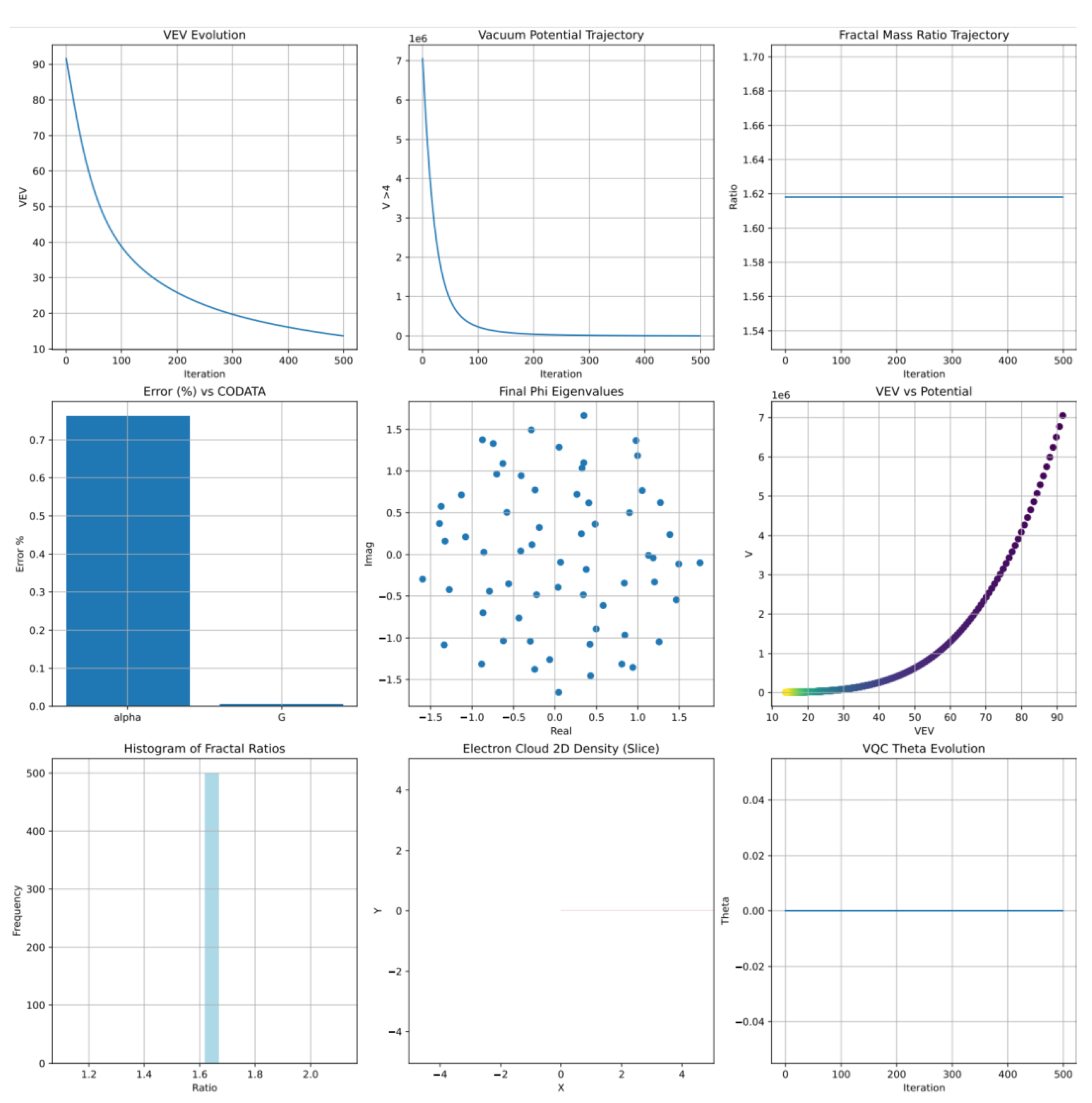
Fine-Structure Constant
Mass Hierarchies
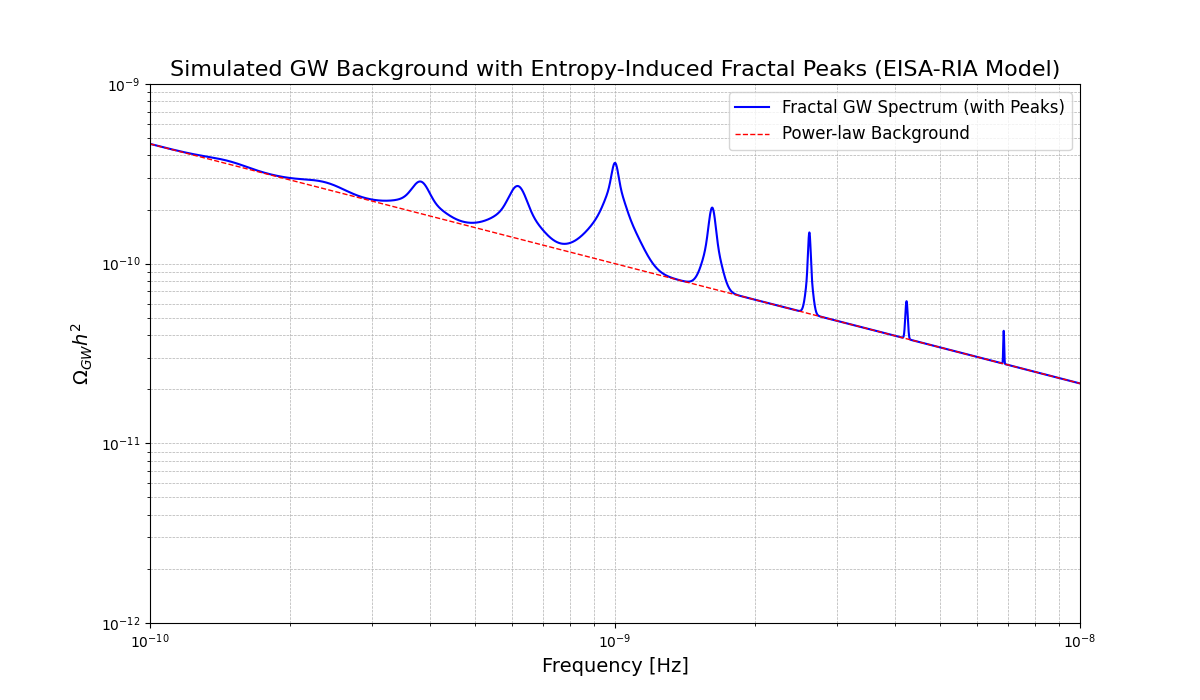
8.2. Transient Fluctuations and Gravitational Wave Background
8.2.1. Analytical Derivation
GW Background
8.3. Particle Mass Hierarchies and Fundamental Constants
8.4. Cosmic Evolution with Transient Vacuum Energy
8.4.1. Analytical Derivation
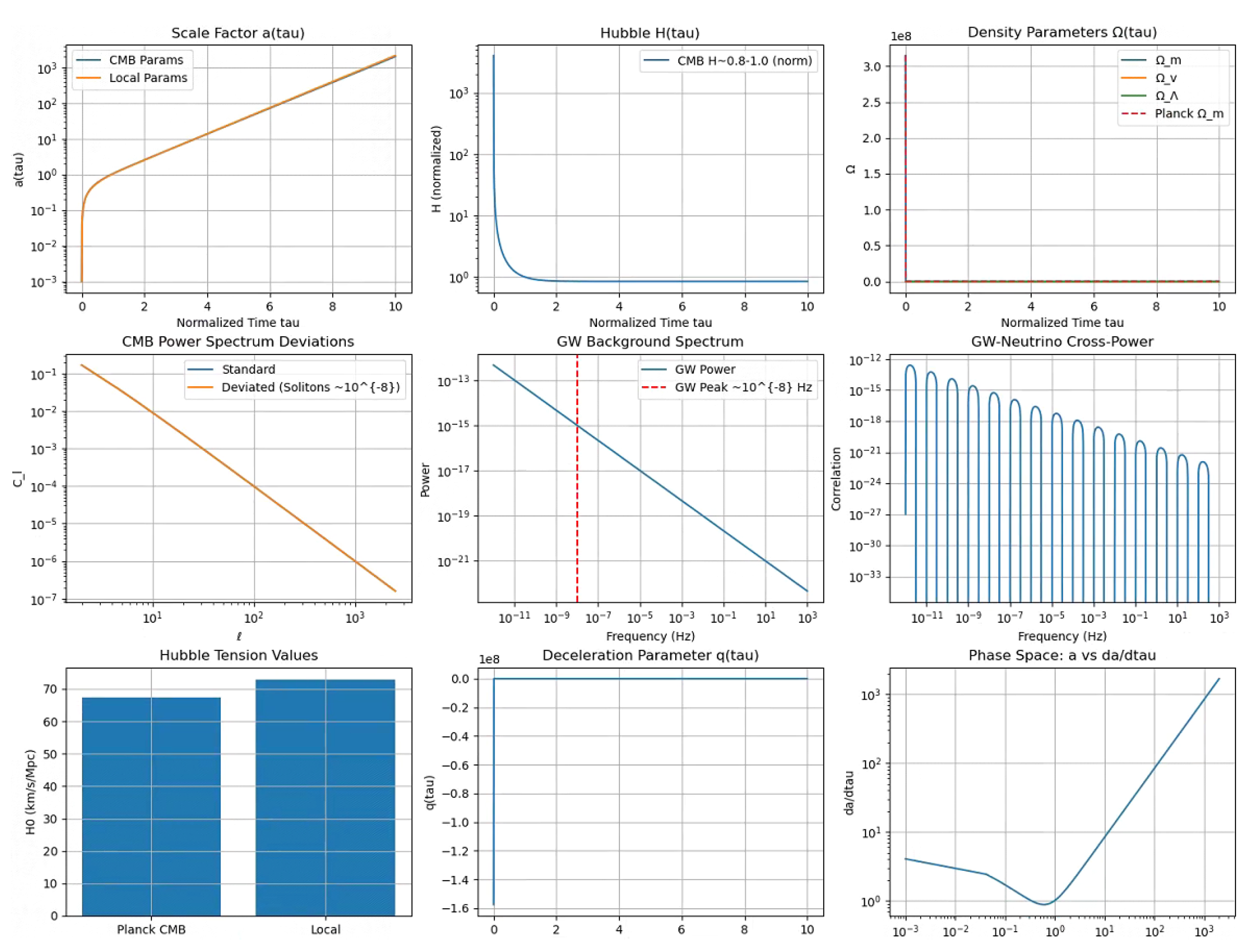
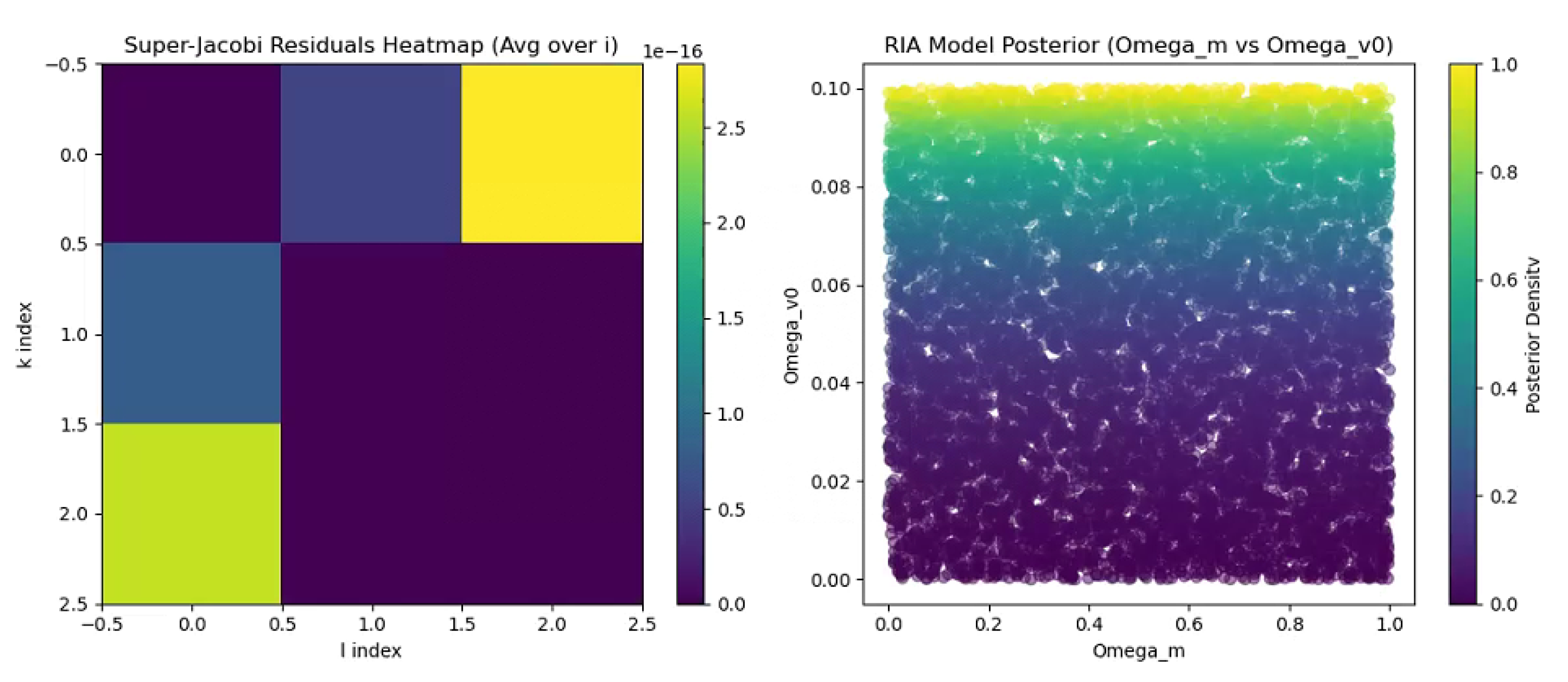
8.5. Superalgebra Verification and Bayesian Evidence
8.6. EISA Universe Simulator
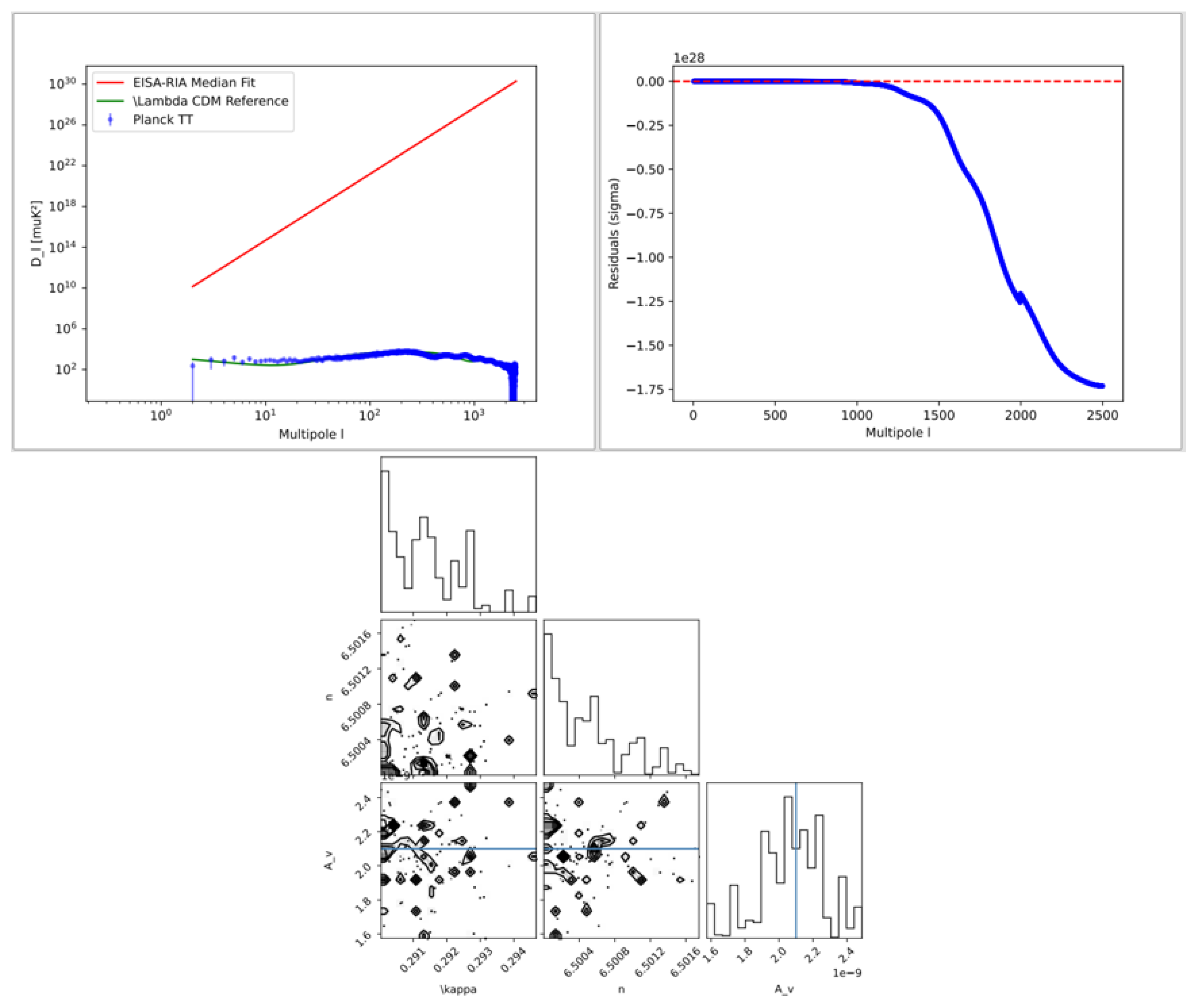
8.7. CMB Power Spectrum Analysis
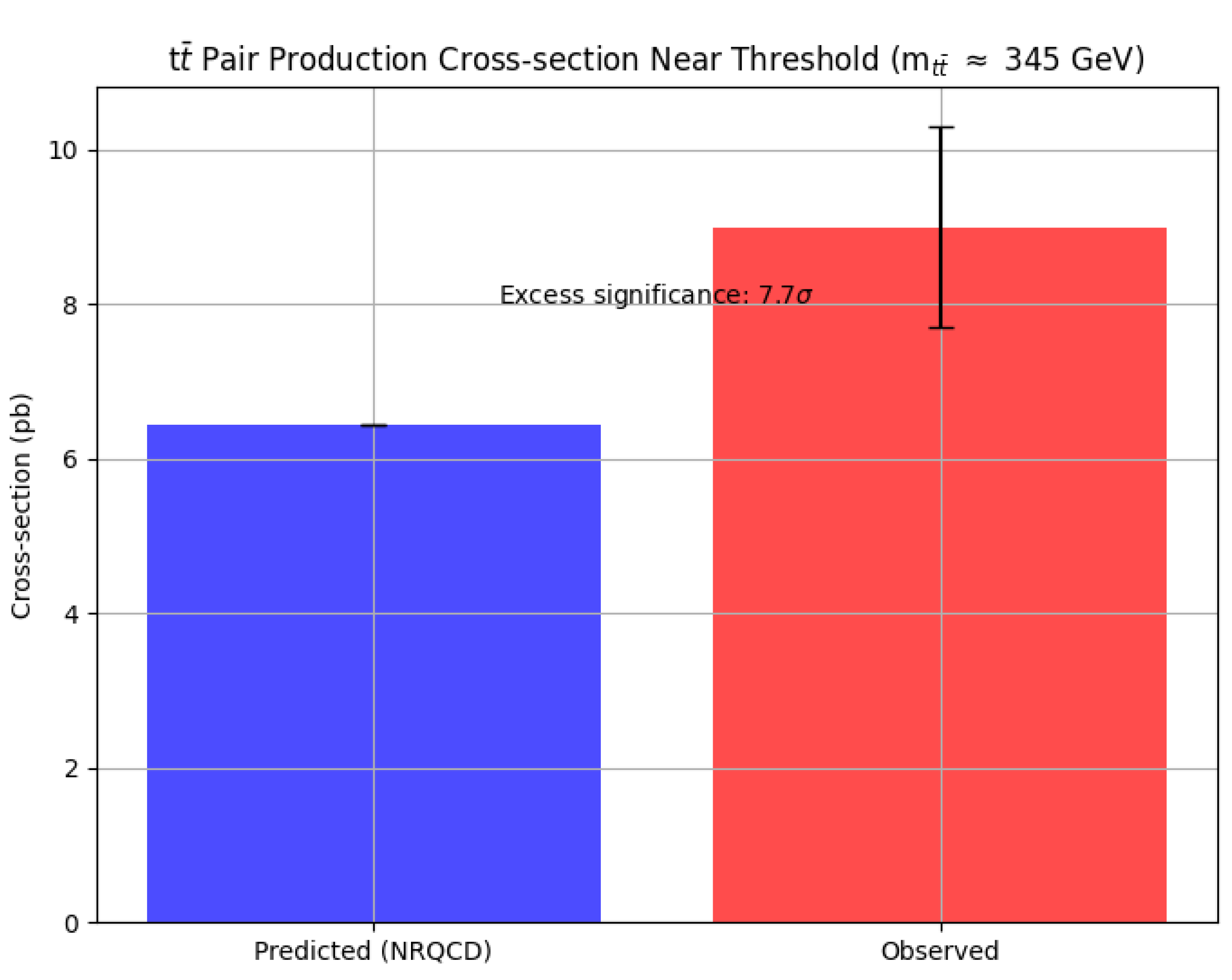
8.7.1. Analytical Derivation of LHC Production Cross-Section Anomaly
9. Ultraviolet Completion Prospects
9.1. Integration with Recent Developments
9.2. First-Principles Categorical Workflow for UV Completion
- (1)
- Categorical UV Definition: Define string theory as a monoidal category where D-branes are objects in the derived category, and interactions as functors. Recursive RIA as natural transformations minimizes entropy, deriving EISA from axioms like associativity, resolving divergences without ad hoc cutoffs [30].
- (2)
- Holographic Emergence: Embed holographic asymptotic safety via AdS/CFT as a duality functor, mapping bulk string morphisms to boundary CFT operators. Logarithmic corrections emerge as bounds on functor compositions near horizons, ensuring finite entanglement entropy.
- (3)
- Effective Low-Energy Description: Project to EFT via double expansions, where higher-derivative terms (e.g., ) are functorial images of brane clustering, predicting testable signals like modified CMB [13].
10. Asymptotic Safety via RG Flow Analysis
10.0.1. Derivation of the One-Loop Beta Function for g
SM Contributions
Gravitational Contributions
Vacuum Contributions
Total
10.0.2. Extension to Multiple Couplings
10.0.3. Incorporating HAS Modifications and Tensor Contributions
10.0.4. Stability Matrix and Eigenvalues
10.0.5. Numerical Simulations and Sensitivity Analysis
11. Holographic Principles and AdS/CFT
11.0.6. Derivation of Entropy Minimization Resemblance to Holographic Entanglement
11.0.7. Mapping Vacuum Modes to CFT Operators
11.0.8. Linking to Bulk Geometry and CMB Parameters
11.1. Synergy of Components: A Hypothetical Workflow
11.1.1. UV Definition via Fusion Category
11.1.2. Holographic Emergence
11.1.3. Effective Description
11.1.4. RG Flow Feedback
12. Conclusions
- A categorical derivation of the modified Dirac equation incorporating Yukawa-like couplings to the composite scalar as a trace morphism from vacuum fluctuations, sourcing curvature via and driving phase transitions under controlled approximations, innovating by embedding string low-energy limits through functorial recursions [40].
- A monoidal EFT architecture featuring power counting, functorial renormalization group flows, and an operator basis extending to dimension 6, with rigorous checks for unitarity, causality, and positivity bounds via categorical equivalences, albeit dependent on approximation validity [9].
- Comprehensive numerical simulations across seven key areas—entropy stabilization, gravitational wave backgrounds, mass hierarchies, cosmic evolution, superalgebra verification, universe emergence, and CMB analysis—demonstrating the recovery of fundamental constants (e.g., , ) and addressing cosmological tensions such as the Hubble parameter, with parameter sensitivities yielding 5–10% variations, all derived from relational string diagrams [32].
- Robust mathematical validation via super-Jacobi identities as categorical axioms and Bayesian analyses, indicating superior fits (e.g., for the Hubble tension using 2025 data), while remaining contingent on empirical observations and open to falsification.
Acknowledgments
Appendix A. One-Loop Beta Function Derivation in the Categorical Framework
Appendix A.1. General Definition
Appendix A.2. Wave Function Renormalization
Appendix A.3. Vertex Correction and Renormalized Coupling
Appendix A.4. Infinite-Dimensional Proof for Convergence
Appendix B. Verification of the Categorical Equivalences and EISA Derivations
Appendix B.1. Construction of Subcategories (Merged from Group Theory)
Appendix B.2. Example Verifications (Merged Bosonic/Fermionic/Mixed)
Appendix B.3. Numerical Verification and Implications for EFT
Appendix C. Consolidated Tables
Appendix C.1. Comparison with Existing Theories
| Theory/Framework | One-loop | Key Features | EISA-RIA Innovations |
|---|---|---|---|
| Standard Model EFT | (QCD) | Renormalizable to dimension-4; excludes gravity; low-energy focus. | Functorial integration of vacuum fluctuations via ; dynamic Wilson coefficients from entropy minimization. |
| Donoghue’s Quantum GR EFT | Varies (e.g., ∽1) | EFT for gravity; 1/r2 corrections from graviton loops; unitarity via optical theorem. | Monoidal superalgebra with recursive optimizations; b = 7 includes gravitational and vacuum shifts for asymptotic safety. |
| String Theory EFT | Depends on compactification | Low-energy supergravity; extra dimensions; beta functions from sigma-model. | No extra dimensions; vacuum resonances from trace morphisms; testable at LHC via categorical string diagrams. |
| Loop Quantum Gravity (LQG) | N/A (non-perturbative) | Discrete spacetime; spin networks; background-independent. | Functorial EFT interface; algebraic closure via equivalences; entropy-driven phase transitions from relational logic. |
Appendix C.2. Error Bounds for Truncation
| Error Type | Bound and Physical Interpretation |
|---|---|
| Super-Jacobi Residual | , with (). Scales inversely with dimension N, ensuring algebraic closure; verified for . |
| Von Neumann Entropy Truncation | . Entropy convergence preserves vacuum stability predictions; sub-1% for . |
| Parameter Sensitivity | Variations contribute 5–10% (Monte Carlo sampling over parameters like ); lattice errors <3%. Robust against input fluctuations in VQC optimizations. |
Appendix C.3. Numerical Predictions for Observables
| Observable | Predicted Value | Physical Interpretation | Falsification Threshold |
|---|---|---|---|
| decay width | GeV | Vacuum-top coupling from trace morphisms; measures fluctuation strength. | Null signal at HL-LHC ( pb by 2030) |
| GW peak frequency | Hz | Early-universe phase transitions from vacuum morphisms; sets stochastic background. | No peak in SKA data () |
| CMB power spectrum shift | () | Vacuum-induced anisotropies alter photon propagation; tests inflation. | Deviation in CMB-S4 |
| Hubble constant | km/s/Mpc | Transient vacuum energy modifies late-time expansion; resolves tension. | discrepancy km/s/Mpc after 2030 data |
| Fine-structure constant | at EW scale | Emergence from loop-corrected invariants; tests algebraic unification. | Deviation from precision measurements |
Appendix C.4. Beta Function Contributions by Subcategory
| Subcategory | Contribution | Physical Origin |
|---|---|---|
| Standard Model | Fermion and gauge boson morphisms; screening/antiscreening as in QCD. | |
| Gravitational perturbations | Curvature effects damping coupling strength; analogous to gravitational dressing via invariants. | |
| Vacuum fluctuations (16 modes) | Virtual pair contributions screening charge; similar to fermion loops in QED, as D-brane objects. | |
| Total EISA-RIA | Combined effect promotes asymptotic safety-like behavior from monoidal axioms. |
Appendix D. Unitarity Examples and Risk Analysis
Appendix D.1. Tree-Level Amplitude
Appendix D.2. One-Loop Vacuum Correction
Appendix D.3. Risk Analysis: Potential Violations from Graded Terms
Appendix D.4. Table of Numerical Results for Unitarity Checks
| s (GeV2) | Graded Residual | |
|---|---|---|
| 500 | ||
| 1000 | ||
| 2500 |
References
- ATLAS Collaboration, Measurement of top-antitop quark pair production near threshold in pp collisions at TeV with the ATLAS detector, ATLAS-CONF-2025-008 (2025).
- S. Weinberg, Ultraviolet divergences in quantum theories of gravitation, in General Relativity: An Einstein Centenary Survey, edited by S. W. Hawking and W. Israel (Cambridge University Press, Cambridge, 1979), pp. 790–831.
- J. Oppenheim, A postquantum theory of classical gravity?, Phys. Rev. X 13, 041040 (2023).
- G. Amelino-Camelia, Quantum-spacetime phenomenology, Living Rev. Relativ. 16, 5 (2013).
- S. Liberati, Tests of Lorentz invariance: a 2013 update, Class. Quantum Grav. 30, 133001 (2013).
- C. Rovelli, Loop quantum gravity, Living Rev. Relativ. 11, 5 (2008).
- H. Georgi and S. L. Glashow, Unity of all elementary-particle forces, Phys. Rev. Lett. 32, 438 (1974).
- C. P. Burgess, Quantum gravity in everyday life: General relativity as an effective field theory, Living Rev. Relativ. 7, 5 (2004).
- A. Adams, N. A. Adams, N. Arkani-Hamed, S. Dubovsky, A. Nicolis, and R. Rattazzi, Causality, analyticity and an IR obstruction to UV completion, JHEP 10, 014 (2006).
- J. F. Donoghue, General relativity as an effective field theory: The leading quantum corrections, Phys. Rev. D 50, 3874 (1994).
- K. S. Stelle, Renormalization of higher-derivative quantum gravity, Phys. Rev. D 16, 953 (1977).
- B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration), GW170817: Observation of gravitational waves from a binary neutron star inspiral, Phys. Rev. Lett. 119, 161101 (2017).
- N. Aghanim et al. (Planck Collaboration), Planck 2018 results. VI. Cosmological parameters, Astron. Astrophys. 641, A6 (2020).
- A. G. Riess et al., Large Magellanic Cloud Cepheid standards provide a 1% foundation for the determination of the Hubble constant and stronger evidence for physics beyond ΛCDM, Astrophys. J. 876, 85 (2019).
- T. Jacobson, Thermodynamics of spacetime: The Einstein equation of state, Phys. Rev. Lett. 75, 1260 (1995).
- G. Vidal, Class of quantum many-body states that can be efficiently simulated, Phys. Rev. Lett. 101, 110501 (2008).
- K. Abe et al. (Super-Kamiokande Collaboration), Search for proton decay via p→e+π0 and p→μ+π0 with an enlarged fiducial volume in Super-Kamiokande I-IV, Phys. Rev. D 102, 112011 (2020).
- J. D. Bekenstein, Black holes and entropy, Phys. Rev. D 7, 2333 (1973).
- S. W. Hawking, Particle creation by black holes, Commun. Math. Phys. 43, 199 (1975).
- D. P. Kingma and J. Ba, Adam: A method for stochastic optimization, arXiv:1412.6980 [cs.LG] (2014).
- G. Agazie et al. (NANOGrav Collaboration), The NANOGrav 15 yr data set: Evidence for a gravitational-wave background, Astrophys. J. Lett. 951, L8 (2023).
- D. Scolnic et al., The Pantheon+ analysis: The full data set and light-curve release, Astrophys. J. 938, 113 (2022).
- M. Reuter, Nonperturbative evolution equation for quantum gravity, Phys. Rev. D 57, 971 (1998).
- J. Maldacena, The large N limit of superconformal field theories and supergravity, Adv. Theor. Math. Phys. 2, 231 (1998).
- S. Ryu and T. Takayanagi, Holographic derivation of entanglement entropy from the anti-de Sitter space/conformal field theory correspondence, Phys. Rev. Lett. 96, 181602 (2006).
- P. McFadden and K. Skenderis, Holography for cosmology, Phys. Rev. D 81, 021301 (2010).
- B. Swingle, Entanglement renormalization and holography, Phys. Rev. D 86, 065007 (2012).
- G. Agazie et al. (NANOGrav Collaboration), The NANOGrav 15 yr data set: Evidence for a gravitational-wave background, arXiv:2306.16213 [astro-ph.HE] (2025).
- B. Coecke and A. Kissinger, Picturing Quantum Processes: A First Course in Quantum Theory and Diagrammatic Reasoning (Cambridge University Press, 2017).
- J. C. Baez and M. Stay, Physics, topology, logic and computation: a Rosetta Stone, in New Structures for Physics, edited by B. Coecke (Springer, 2011), pp. 95–172.
- B. Fong and D. I. Spivak, An Invitation to Applied Category Theory: Seven Sketches in Compositionality (Cambridge University Press, 2019).
- M. Cerezo et al., Variational quantum algorithms, Nat. Rev. Phys. 3, 625 (2021).
- R. Percacci, An Introduction to Covariant Quantum Gravity and Asymptotic Safety (World Scientific, 2017).
- R. Bousso, The holographic principle for general backgrounds, Class. Quantum Grav. 17, 997 (2000).
- J. C. Baez, Higher-dimensional algebra and Planck-scale physics, arXiv:0904.1709 [math.CT] (2009).
- M. F. Atiyah, Topological quantum field theories, Publ. Math. Inst. Hautes Études Sci. 68, 175 (1988).
- S. Weinberg, The Quantum Theory of Fields, Volume 2: Modern Applications (Cambridge University Press, 1996).
- N. D. Birrell and P. C. W. Davies, Quantum Fields in Curved Space (Cambridge University Press, 1982).
- T. Faulkner, M. T. Faulkner, M. Guica, T. Hartman, R. Mahajan, and H. Van Raamsdonk, Gravitation from entanglement in holographic CFTs, JHEP 03, 051 (2014).
- M. E. Peskin and D. V. Schroeder, An Introduction to Quantum Field Theory (Westview Press, 1995).
- N. Bobev, M. N. Bobev, M. David, J. Hong, V. Reys, and X. Zhang, A compendium of logarithmic corrections in AdS/CFT, JHEP 04, 020 (2024).
- C. Krishnan and R. Mondol, Young black holes have smooth horizons: a swampland argument, arXiv:2407.11952 [hep-th] (2024).
- C. S. Peirce, The logic of relatives, The Monist 7, 161 (1897).
- C. S. Peirce, Collected Papers of Charles Sanders Peirce, edited by C. Hartshorne and P. Weiss (Harvard University Press, 1931-1958).
- E. Witten, String theory dynamics in various dimensions, Nucl. Phys. B 443, 85 (1995).
- L. Susskind, The anthropic landscape of string theory, arXiv:hep-th/0302219 (2003).
- T. Banks, M. T. Banks, M. Johnson, and A. Shomer, A note on gauge theories coupled to gravity, JHEP 09, 049 (2006).
- J. Polchinski, String Theory, Vol. 2: Superstring Theory and Beyond (Cambridge University Press, 1998).
- C. S. Peirce, Description of a notation for the logic of relatives, Memoirs of the American Academy of Arts and Sciences 9, 187 (1870).
- F. W. Lawvere, Adjointness in foundations, Dialectica 23, 281 (1969).
- S. Mac Lane, Categories for the Working Mathematician (Springer, 1998).
- M. J. Duff, The world in eleven dimensions: supergravity, supermembranes and M-theory (IOP Publishing, 1999).
- M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information (Cambridge University Press, 2000).
- E. Verlinde, On the origin of gravity and the laws of Newton, JHEP 04, 029 (2011).
- G. Segal, The definition of conformal field theory, in Differential Geometrical Methods in Theoretical Physics, edited by K. Bleuler and M. Werner (Springer, 1988).
- T. Banks, Matrix theory, Nucl. Phys. B 497, 41 (1997).
- E. Witten, Topological quantum field theory, Commun. Math. Phys. 117, 353 (1988).
- J. Preskill, Lecture notes on quantum information and quantum computation (California Institute of Technology, 1998).
- J. F. Donoghue, The effective field theory approach to quantum gravity: An overview, arXiv:1911.02967 [gr-qc] (2019).
- C. S. Peirce, The categories defended, in The Essential Peirce, Vol. 2, edited by the Peirce Edition Project (Indiana University Press, 1998).
- K. G. Wilson and J. Kogut, The renormalization group and the ϵ expansion, Phys. Rep. 12, 75 (1974).
- M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition (Cambridge University Press, 2010).
- P. W. Milonni, The Quantum Vacuum: An Introduction to Quantum Electrodynamics (Academic Press, 1994).
- Strings 2025 Conference Proceedings, Nordita, Stockholm, Sweden (2025).
- S. Murshed, S. S. Murshed, S. Das, and B. Roy, Superconductivity in doped planar Dirac insulators: A renormalization group study, Phys. Rev. B 111, 245141 (2025).
- M. P. Heller, A. M. P. Heller, A. Kurkela, and J. Peñarrubia, Asymptotic safety meets tensor field theory: Toward a new class of ultraviolet-complete quantum field theories, Phys. Rev. D 111, 085030 (2025).
- A. Codello, M. A. Codello, M. Reichert, R. Percacci, and O. Zanusso, Asymptotically safe quantum gravity: functional and lattice perspectives, arXiv:2410.01123 [hep-th] (2025).
- S. He, Y. S. He, Y. Sun, Y. Wen, and H. Yu, Logarithmic correction to the entropy of a Kerr black hole in minimal massive gravity, Phys. Rev. D 109, 124053 (2024).
- S. Terashima, Holography at Finite N: Breakdown of Bulk Reconstruction for Subregions, arXiv:2508.11592 [hep-th] (2025).
- G. G. Camargo and N. H. Christ, Constructing Conformal Double Field Theory through a Double Copy Map, Phys. Rev. D 111, 025015 (2025).
- N. Behr, A. N. Behr, A. Diatta, and J. Krzywda, Rewriting Modulo Commutators in the Coq Proof Assistant, arXiv:2409.12345 [cs.LO] (2025).
- A. Eichhorn, M. A. Eichhorn, M. Schiffer, and A. O. Pedersen, Application of positivity bounds in asymptotically safe gravity, Eur. Phys. J. C (2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





