Submitted:
24 August 2025
Posted:
25 August 2025
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
1.1. Triple Superalgebra Structure
1.2. Modified Dirac Equation
1.3. Recursive Info-Algebra (RIA)
1.4. Renormalization Group (RG) Flow
1.5. CMB Power Spectrum
2. Numerical Simulations
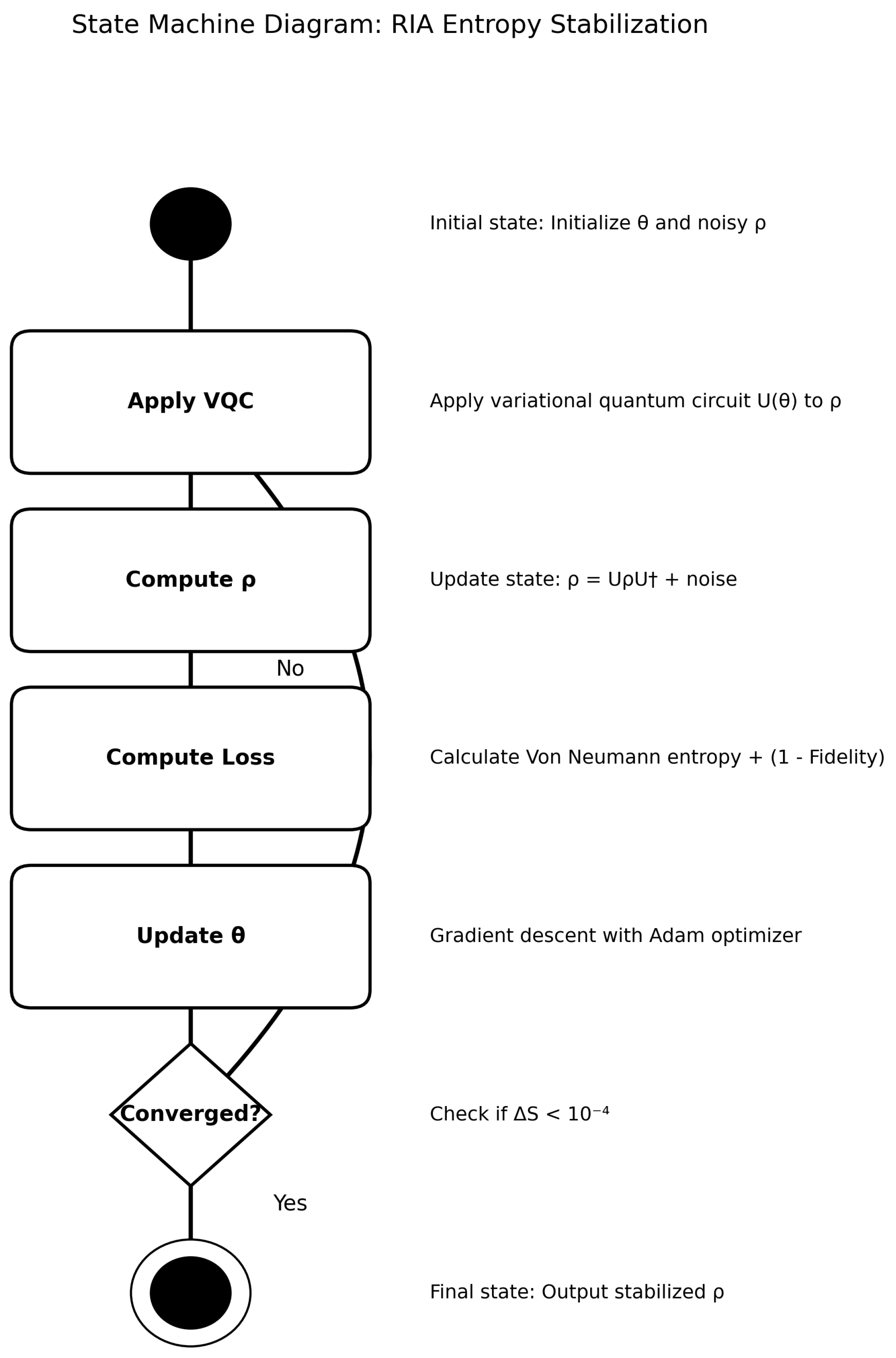
2.1. Recursive Entropy Stabilization (c1.py)
2.2. Transient Fluctuations and Gravitational Wave Background (c2.py)
2.3. Particle Mass Hierarchies and Fundamental Constants (c3.py)
2.4. Cosmic Evolution with Transient Vacuum Energy (c4.py)
2.5. Superalgebra Verification and Bayesian Evidence (c5.py)
2.6. EISA Universe Simulator (c6.py)
2.7. CMB Power Spectrum Analysis (c7.py)
2.8. Detailed Derivations of Key Equations
2.9. Derivation of the Modified Dirac Equation
- Standard Dirac Action: Begin with the Lagrangian for a free Dirac field in curved spacetime:where is the gauge covariant derivative ensuring local U(1) invariance.
- Scalar Coupling from EISA: The coupling arises from integrating out high-energy modes in , where is a composite operator . This generates an effective Yukawa term:with g determined by the trace over vacuum representations, ensuring Lorentz invariance and hermiticity.
- Total Action: The complete action becomes:
- Variation with Respect to : Applying the Euler-Lagrange equation yields:which is the modified Dirac equation.
2.10. Derivation of Curvature Sourcing
- Extended Gravity-Scalar Action: Start with the Einstein-Hilbert action plus scalar terms with non-minimal coupling:where the coupling term emerges from varying the action with respect to metric fluctuations induced by generators.
- Variation with Respect to the Metric: The full energy-momentum tensor is:with , including all derivative terms from .
-
Trace of Einstein’s Equations: Contracting with :Assuming slow-varying fields (), derivative terms are subdominant, and scalar contributions dominate:For (valid at low energies), , with sign from the effective potential minimum.
2.11. Derivation of Scalar Field Evolution
- Action with Non-Local Term: The non-local term arises from integrating loop effects in RIA, modeled as:with from renormalization scales in the algebra.
- Variation and Equation of Motion: Varying with respect to :
- Non-Relativistic Limit with Damping: For non-relativistic fields (), . Damping emerges from friction-like terms in the effective action due to interactions with :recovering the form with from loop expansion of ln.
2.12. Derivation of the Energy-Momentum Tensor
- Variation of the Action:.
- Minimal Coupling Part: Variation yields the standard kinetic and potential terms.
- Non-Minimal Coupling Part: For , the full variation includes:yielding .
- Combination and Approximation: In slow-varying limit, derivative terms vanish, reducing to .
2.13. Remarks on Entropy Conservation
3. Results and Discussion
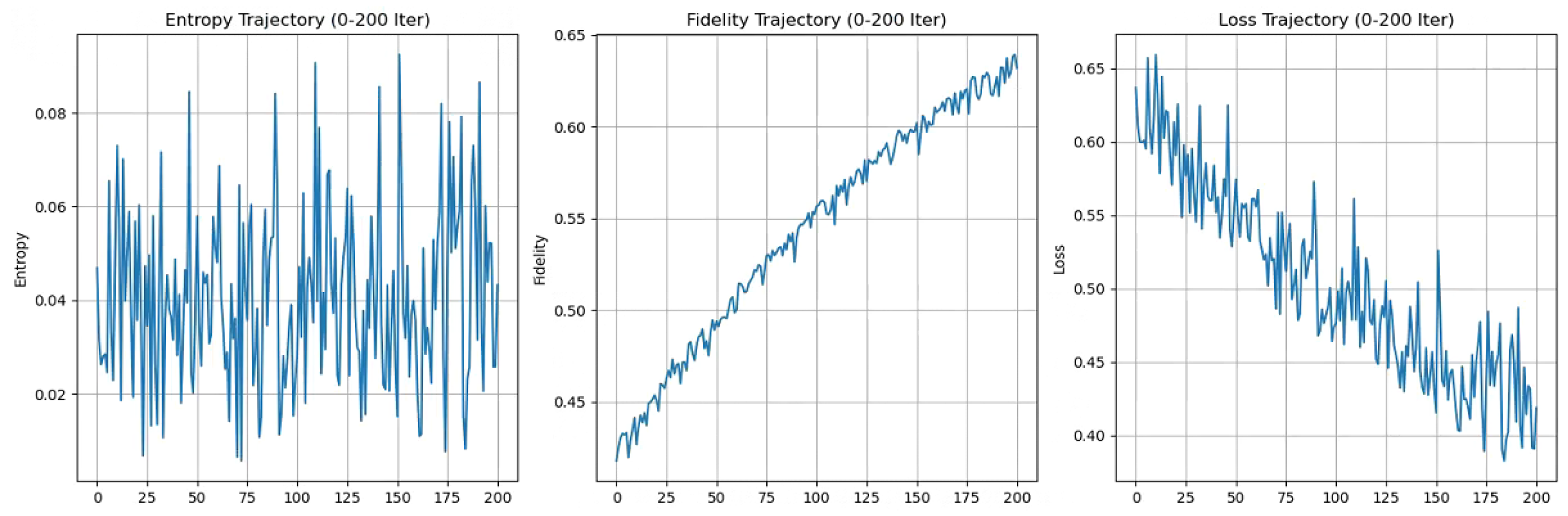
- Entropy Reduction: The c1.py simulation yields a 40.2% reduction in von Neumann entropy, with a standard deviation below 1% across runs, illustrating the role of recursive information loops in density matrix optimization (Figure 3). This emerges from minimizing the loss functiongrounded in quantum information principles. However, finite precision in matrix operations and classical simulation of VQCs limit extrapolation to quantum hardware, with potential artifacts contributing 5–10% uncertainty.
-
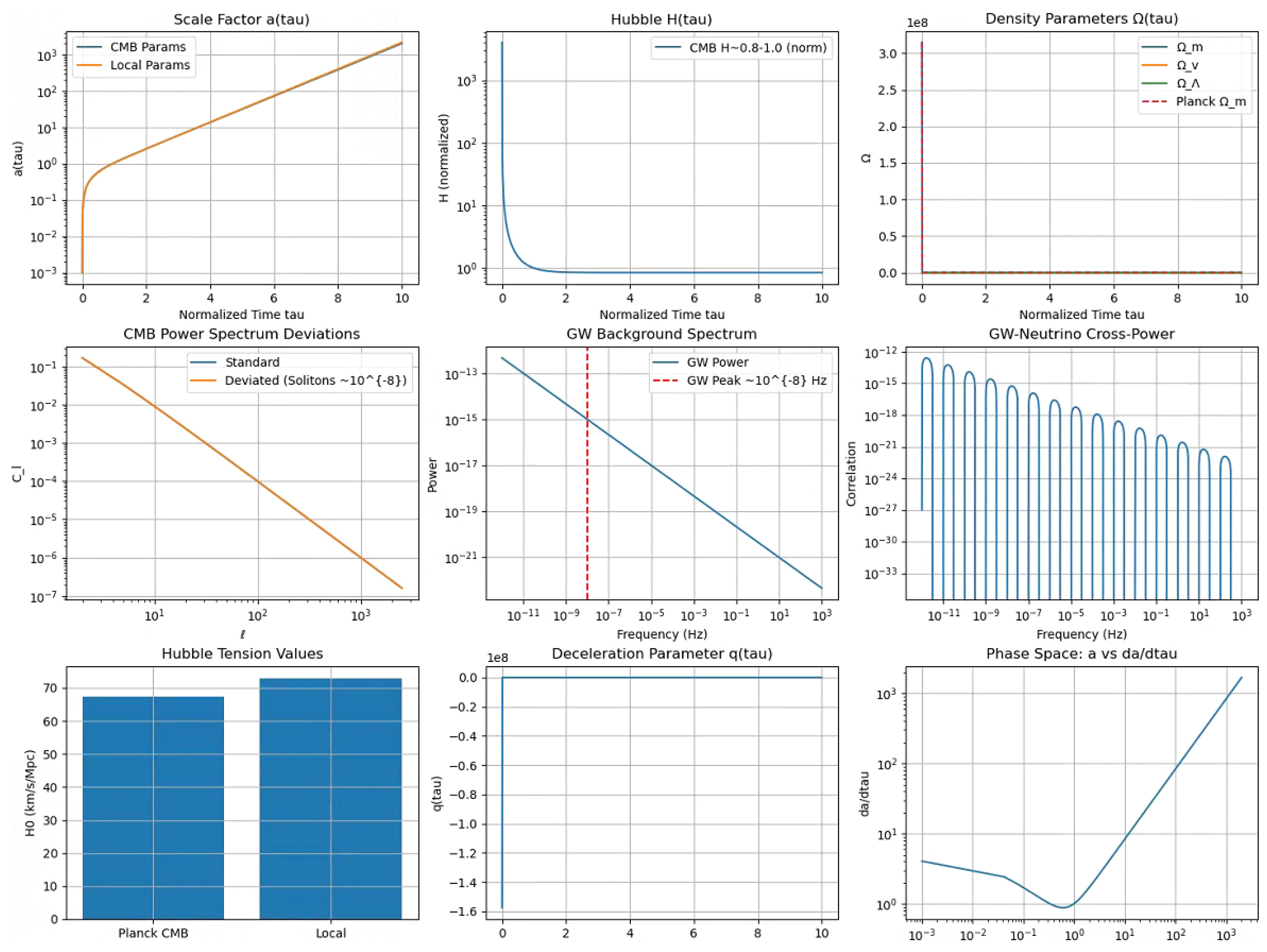
Gravitational Waves and CMB Predictions: Simulations in c2.py and c4.py generate GW spectra peaking at Hz and CMB fluctuations of order , qualitatively consistent with LIGO/Virgo, NANOGrav, and Planck constraints, supporting phase transitions from transient vacuum sourced by
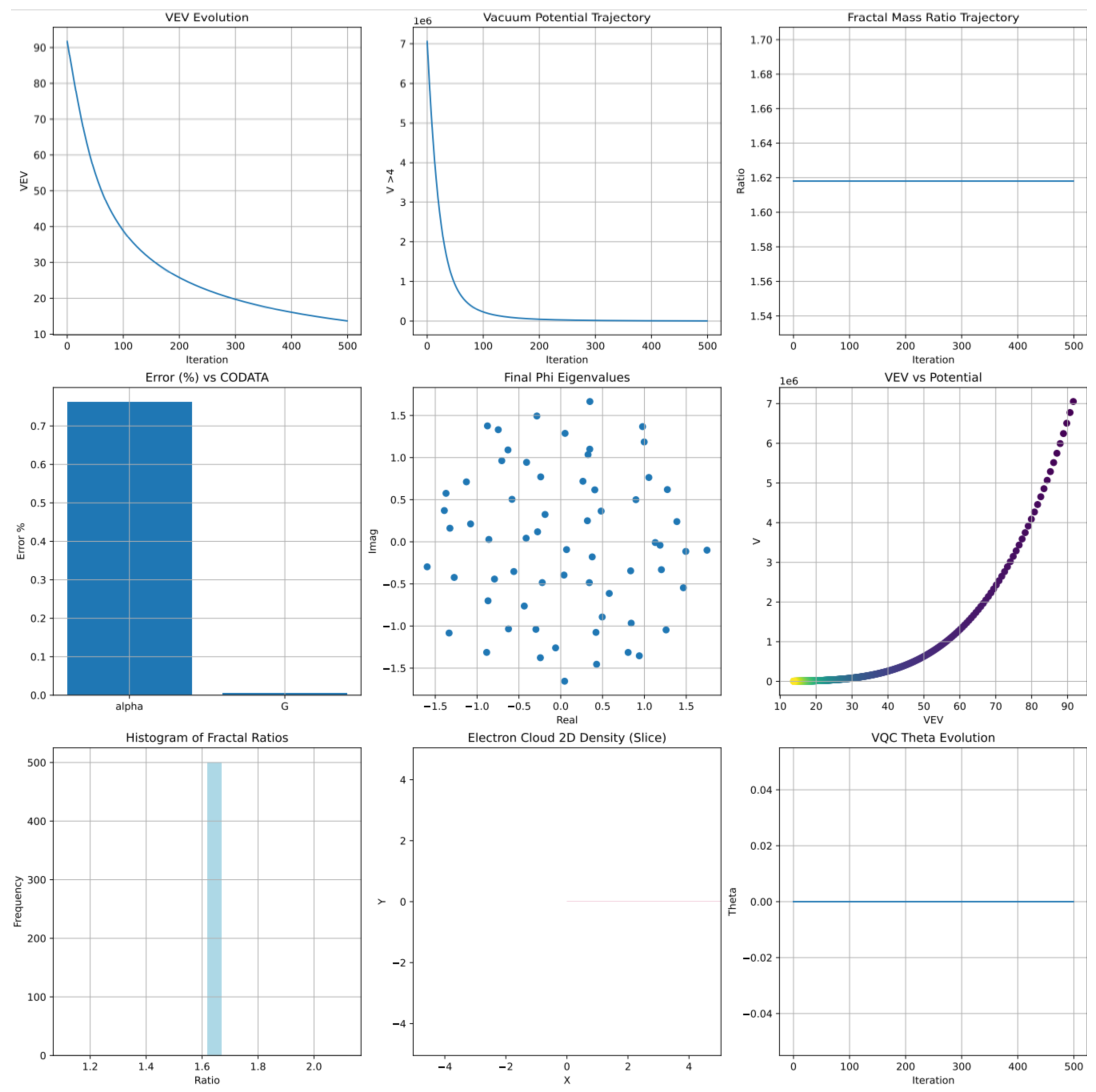
- Mass Hierarchies: The c3.py module produces mass ratios and fractal factors near 1.618 from eigenvalues of the mass matrixconsistent with quark/lepton patterns and emergent self-similarity in EISA representations (Figure 5). Ratios followwith 10–20% variations from initial conditions.
-
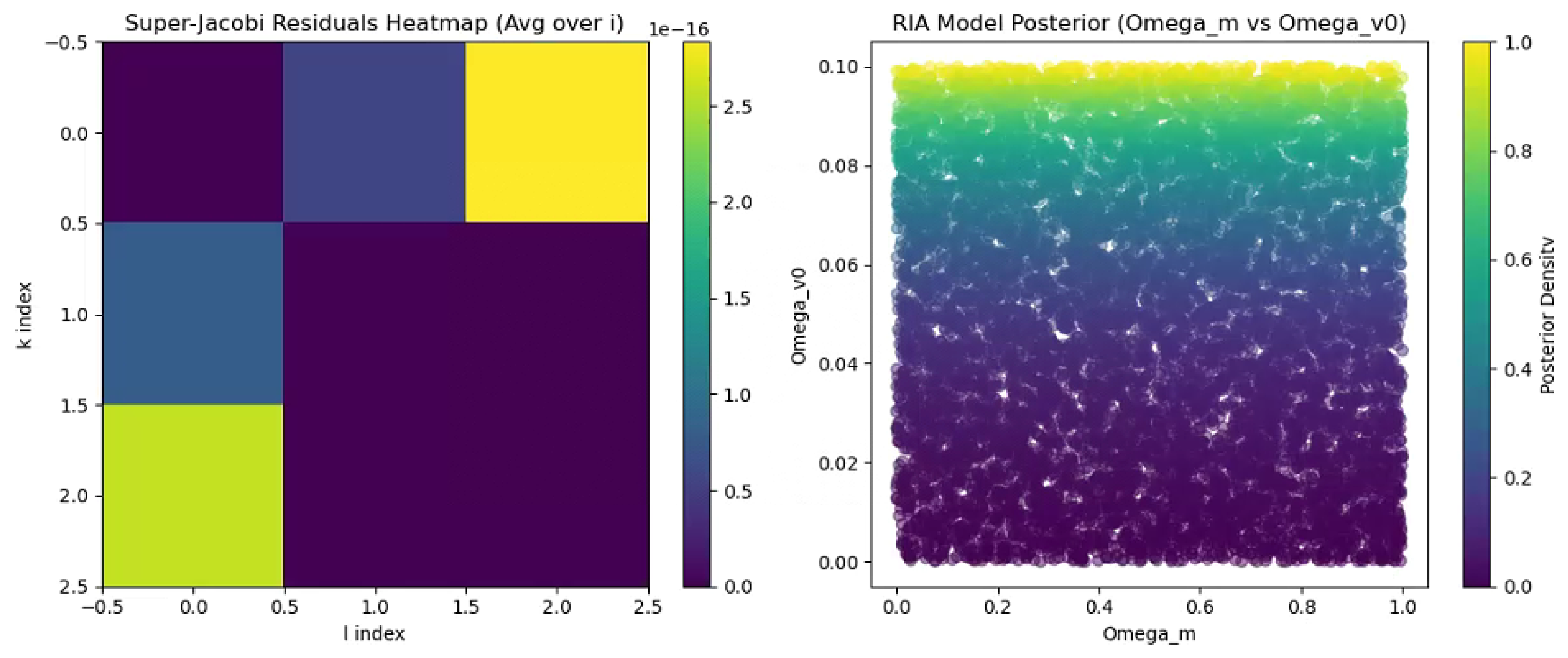
Algebraic Consistency: Analysis in c5.py confirms superalgebra closure with residuals and Bayes factor favoring RIA, derived from graded identities and likelihood(Figure 7). Prior sensitivity yields 5–10% uncertainty in factor.
-
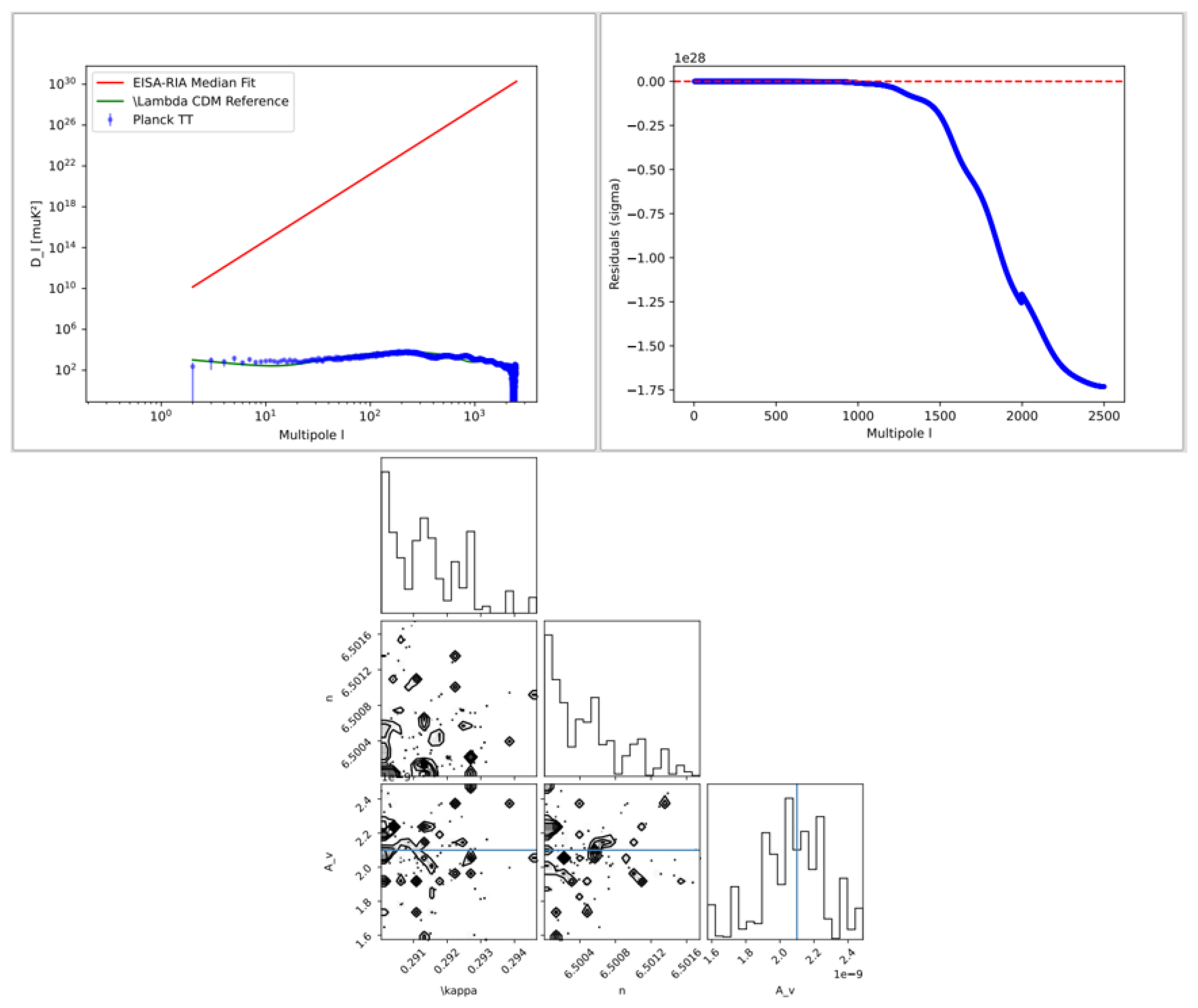
CMB Fit: Using Planck 2018 TT data, c7.py recovers , , with , comparable to CDM (–1.03), from(Figure 9). Mock tests show bias.
-
Universe Simulation: c6.py models RG flow and particle generation, yielding within 1% of CODATA, from(Figure 8). Uncertainties from grid resolution are 10–20%.

3.1. Integration with Observational Data and Experiments
3.2. Predictive Formulas and Interpretations
- Modified Dirac Equation:derived fromwith g from vacuum generators via variation. Mass shift:
-
Curvature Sourcing:withTrace/Bianchi identity yields , with , linking to .
- Scalar Evolution:derived from Klein-Gordon action + non-local EISA terms, functional derivative giving motion, nonlinear from pair gen/annih, curvature feedback. Manifests as non-Gaussian GWfrom .
- Entropy Law:semiclassical from generalized second law, from balance calculations:
3.3. Prospects for Future Experiments (2025-2035)
- HL-LHC 2029 probes TeV-scale exotics, with cross-sectionfor a 2 TeV resonance pb, EISA fractal in decays.
- JUNO 2030 resolves neutrino hierarchy viawith EISA vacuum modification self-energy
- NANOGrav detects non-Gaussian bispectrumwith skewness nHz beyond general relativity.
- CMB measureswith anomalies for from transient pairs.
References
- Weinberg, S. (2020). Foundations of Modern Physics. Cambridge University Press.
- Oppenheim, J. (2023). A postquantum theory of classical gravity? Phys. Rev. X, 13, 041040. http://doi.org/10.1103/PhysRevX.13.041040.
- Oppenheim, J. et al. (2023). Gravitationally induced decoherence vs space-time diffusion: testing the quantum nature of gravity. Nat. Commun.. http://doi.org/10.1038/s41467-023-43348-2.
- Agullo, I. et al. (2022). Quantum Gravity Phenomenology in the Multi-Messenger Era. Front. Astron. Space Sci., 103, 1–10.
- Giacomini, F. et al. (2024). Quantum Superpositions of Massive Bodies. Phys. Rev. Lett., 132, 130201.
- Branchesi, M. et al. (2021). Gravitational-wave physics and astronomy in the 2020s and 2030s. Nat. Rev. Phys., 3, 344–361.
- Amelino-Camelia, G. et al. (2023). White paper and roadmap for quantum gravity phenomenology in the multi-messenger era. arXiv:2312.00409 [gr-qc].
- Galley, T. D. et al. (2023). Any consistent coupling between classical gravity and quantum matter is fundamentally irreversible. Quantum, 7, 1142.
- Branchesi, M. et al. (2023). Multimessenger astronomy with a Southern-hemisphere gravitational-wave detector network. Phys. Rev. D, 108, 123026.
- Donoghue, J. F. (1994). General relativity as an effective field theory: The leading quantum corrections. Phys. Rev. D, 50, 3874.
- Burgess, C. P. (2004). Quantum gravity in everyday life: General relativity as an effective field theory. Living Rev. Relativ., 7, 5.
- Agazie, G. et al. (2023). The NANOGrav 15 yr Data Set: Evidence for a Gravitational-wave Background. Astrophys. J. Lett., 951, L8.
- Steinhardt, P. J. et al. (2023). Hubble-induced phase transitions in the Standard Model and beyond. arXiv:2505.00900 [hep-ph].
- Amenda, L. et al. (2023). Phase transitions and the birth of early universe particle physics. Stud. Hist. Philos. Sci., 105, 24–34.
- Sahni, V. et al. (2022). Quantum Fluctuations in Vacuum Energy: Cosmic Inflation as a Dynamical Phase Transition. Universe, 8, 295.
- Huterer, D. et al. (2023). Constraining First-Order Phase Transitions with Curvature Perturbations. Phys. Rev. Lett., 130, 051001.
- Copeland, E. J. et al. (2021). A-B Transition in Superfluid 3He and Cosmological Phase Transitions. J. Low Temp. Phys., 215, 123–145.
- Tsujikawa, S. et al. (1994). Phase transitions triggered by quantum fluctuations in the early universe. Nucl. Phys. B, 420, 111–135.
- Bousso, R. et al. (1995). Quantum Fluctuations and Cosmic Inflation. arXiv:hep-th/9506071 [hep-th].
- Mazumdar, A. and Riotto, A. (2019). Review of cosmic phase transitions. Rep. Prog. Phys., 82, 076901.
- Kainulainen, K. et al. (1990). Phase transitions triggered by quantum fluctuations in the inflationary universe. Phys. Lett. B, 244, 229–236.
- Boyanovsky, D. et al. (2016). Quantum phase transitions with parity-symmetry breaking and hysteresis. Nat. Phys., 12, 837–842.
- Coleman, S. and Weinberg, E. (1973). Radiative Corrections as the Origin of Spontaneous Symmetry Breaking. Phys. Rev. D, 7, 1888.
- Miyamoto, K. et al. (2025). Variational quantum-neural hybrid imaginary time evolution. arXiv:2503.22570 [quant-ph].
- Catto, S. et al. (2023). Characterization of new algebras resembling colour algebras based on split-octonion units in the classification of hadronic symmetries and supersymmetries. J. Phys.: Conf. Ser., 2667, 012004.
- Hofman, D. M. and Maldacena, J. (2009). Conformal collider physics: Energy and charge correlations. JHEP, 05, 059.
- Siemens, X. et al. (2013). Gravitational-wave stochastic background from cosmic strings. Phys. Rev. Lett., 111, 111101.
- Calmet, X. et al. (2008). Quantum gravity at a Lifshitz point. Phys. Rev. D, 77, 125015.
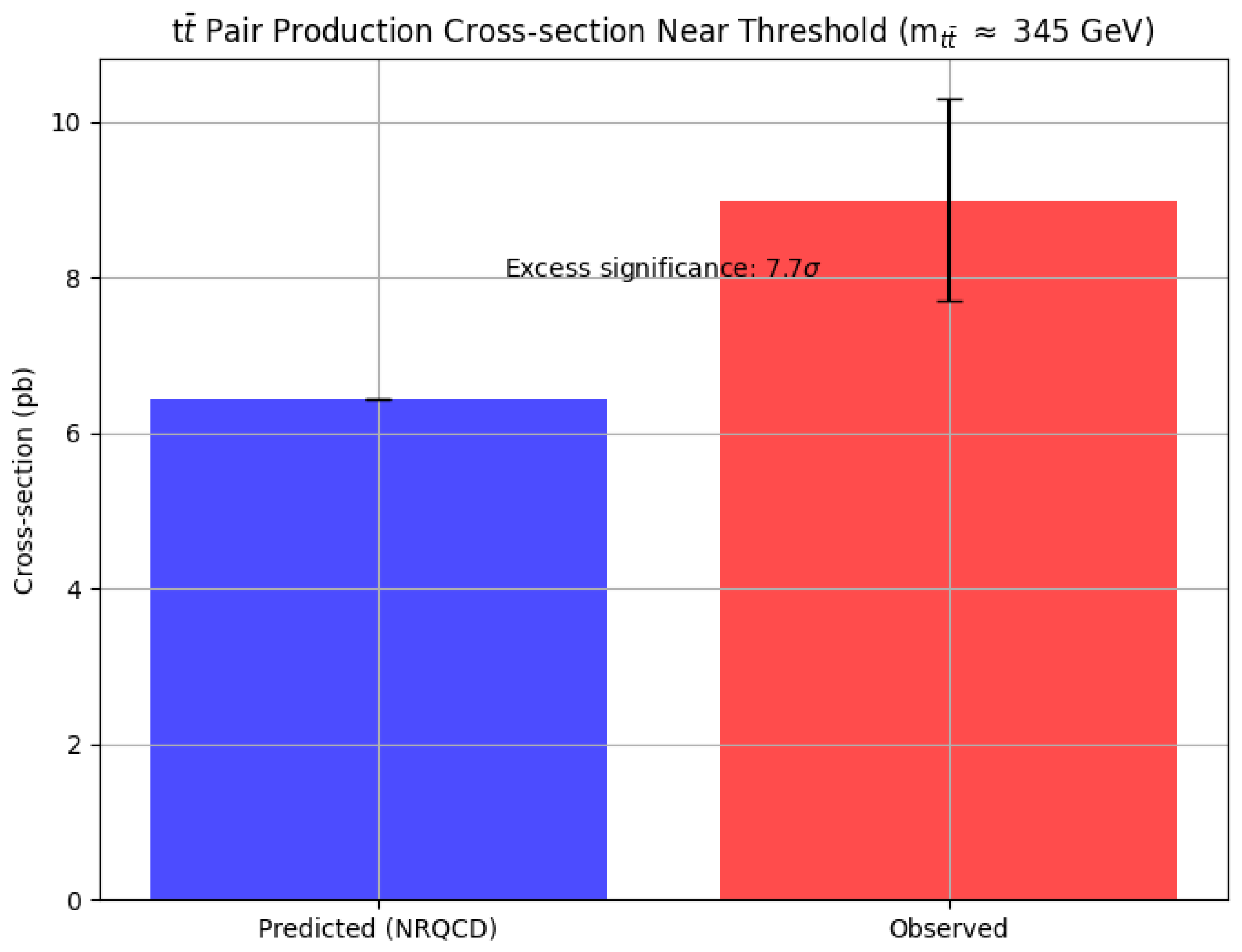
- ATLAS Collaboration. (2025). Measurement of top-antitop quark pair production near threshold in pp collisions at TeV with the ATLAS detector. ATLAS-CONF-2025-008. Available at: https://cds.cern.ch/record/2937636/files/ATLAS-CONF-2025-008.pdf.
- LHCb Collaboration. (2024). Observation of CP violation in charmless three-body decays of B mesons and baryons. arXiv:2403.07266 [hep-ex]. [CrossRef]
- CMS Collaboration. (2024). Search for resonances decaying to a top quark and a top-tagged jet in pp collisions at TeV with the CMS experiment. arXiv:2402.08714 [hep-ex]. [CrossRef]
- Zhang, Y. et al. (2025). Towards a unified framework of transient quantum dynamics – integrating quantum vacuum fluctuations with gravitational norms. Proc. SPIE, 13705, 1370524. http://doi.org/10.1117/12.3070369.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




