Formulation of the Transfer Matrix of the Invers Electrophysiology of the Heart Activation Inside Homogeneous and Inhomogeneous Volume Conductor

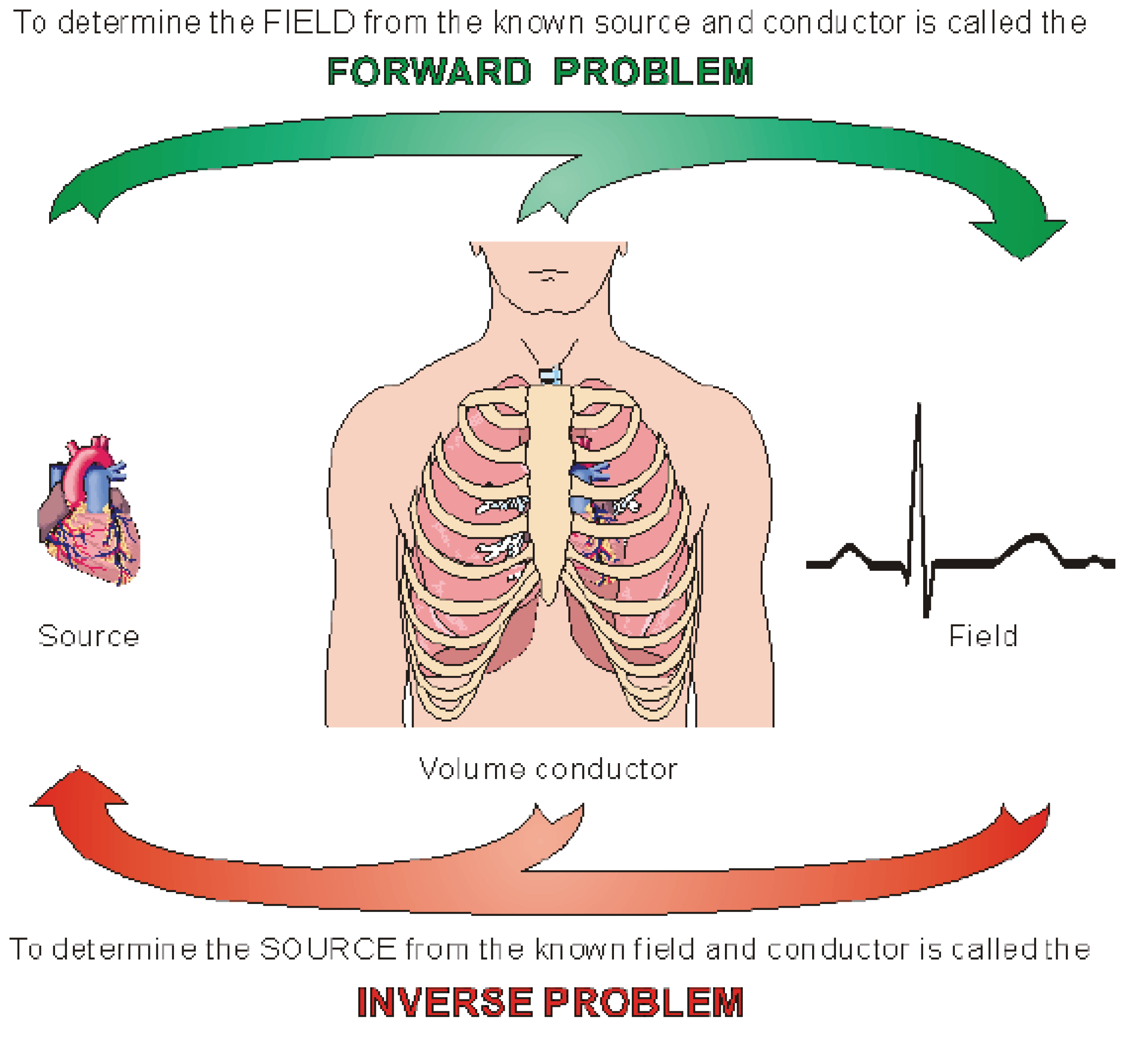
1. Introduction

There are two problems in modeling the electrophysiology of the heart: the Forward Problem and the Inverse Problem [1]. The heart Forward Problem involves designing a model that is capable of determining the field on the surface of known body (conductor) that is generated by electrical-sources inside the heart. Solving the Forward Problem requires the development of electrical models which are capable of describing the bioelectrical criteria of the heart and the body (Figure 1).

Formulating the Inverse Problem requires identifying the configuration of the volume source. The heart can be considered as one dipole source that generate the field as introduced in [2,3,4], where in Cartesian coordinates, six parameters are required to identify that source; three for location and three for direction. One of the most used source models is the potential distribution on the Epicardium surface from the body surface reading as described in [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. This will provide an indication about the source distribution inside the heart. Finally, the most recent models use the multiple pole source distribution, where it is required to identify the distribution of electrical sources in the heart volume directly [20,21,22,23,24,25,26,27]. Instead of formulating the Inverse Problem in terms of current densities distributions as demonstrated in other research, the formulation of the problem in this research will be in terms of transmembrance potentials.

Formulating the problem in terms of TMP reduces the solution domain size to the 1/3 of the current density solutions, as each location inside the heart will be represented as one variable instead of the three variables for each component of the current density vector. Some operations (matrix multiplication and matrix inversion) of the Inverse Problem solutions are of cubic complexity, O(N³), and so reducing the solution domain size will decrease the computation cost.

Moreover, reducing the solution domain size will reduce the ‘underdeterminity’ of the system since providing fewer unknowns (independent variables) to the regularization process with the same number of results (dependent variables) will lead to a better solution.

The stages of the Inverse Problem solution are performed as shown in Figure 2, where the heart model [28,29,30,31,32,33,34] and the body model [35] are used to build the lead field transfer matrix and the BSPM (the output of the Forward Model solution) [36] is used as the dependent variables vector.

The main objective here is to build a transfer matrix A that maps the transmembrance potentials x to the body surface potential b such that

$$b=Ax$$

(1)

where A is MxN transfer matrix, b is Mx1 body surface reading vector, and x is Nx1 TMP vector.

Formulation of the Inverse Problem is introduced for both homogeneous and inhomogeneous volume conductor and the volume source conductivity-tensor can be either isotropic or anisotropic, leading to different lead field transfer matrices. Three settings are introduced in this research, isotropic volume source in infinite homogeneous volume conductor, anisotropic volume source in infinite homogeneous volume conductor and anisotropic volume source in inhomogeneous volume conductor. The first is the simplest setting which requires the least information about the volume source and the volume conductor, but it is also the most inaccurate model among the three models.

2. Transfer Matrix of Isotropic Volume Source in Infinite Homogeneous Volume Conductor

Consider the equation of calculating the potential in an infinite homogenous volume conductor:

$${\varphi }_0={\displaystyle \frac{-1}{4\pi {\sigma }_0}}{\displaystyle \underset{v}{\int }\begin{array}{cc}\frac{{\sigma }_i\nabla V_m\cdot r}{|r{|}^3}& dv\end{array}}$$

(2)

where σ₀ is the homogeneous volume conductor conductivity, σ_i is the volume source conductivity tensor, V_m is the transmembrance potential, and r is the observation point to source point vector.

By assuming isotropic conductivity-tensor of the source and equal to the conductivity of the volume source medium then equation (2) can be written as

$${\varphi }_0={\displaystyle \frac{-1}{4\pi }}{\displaystyle \underset{v}{\int }\begin{array}{cc}\frac{\nabla V_m\cdot r}{|r{|}^3}& dv\end{array}}$$

(3)

and then

$${\varphi }_0={\displaystyle \frac{-{\delta }_v}{4\pi }}{\displaystyle \sum _{i=1}^N\frac{\nabla V_{m_i}\cdot r_i}{|r_i{|}^3}}$$

(4)

where N is the number of sources and δ_v is a unit volume. The gradient of transmembrance potential and the vector r can be written in Cartesian coordinates as

$$\nabla V_m={\displaystyle \frac{\partial V_m}{\partial x}}\overline{X}+{\displaystyle \frac{\partial V_m}{\partial y}}\overline{Y}+{\displaystyle \frac{\partial V_m}{\partial z}}\overline{Z}$$

(5)

$$r=r_x\overline{X}+r_y\overline{Y}+r_z\overline{Z}$$

(6)

then

$${\displaystyle \frac{\nabla V_m\cdot r}{|r{|}^3}}={\displaystyle \frac{\partial V_m}{\partial x}}{\displaystyle \frac{r_x}{|r{|}^3}}+{\displaystyle \frac{\partial V_m}{\partial y}}{\displaystyle \frac{r_y}{|r{|}^3}}+{\displaystyle \frac{\partial V_m}{\partial z}}{\displaystyle \frac{r_z}{|r{|}^3}}$$

(7)

using Taylor’s theorem

$${\displaystyle \frac{\partial V_m}{\partial x}}{\displaystyle \frac{r_x}{|r{|}^3}}={\displaystyle \frac{V_{m(x+1,y,z)}-V_{m(x-1,y,z)}}{2h_x}}{\displaystyle \frac{r_x}{|r{|}^3}}$$

(8)

Then in the X direction, the current element will contribute by ${\displaystyle \frac{-{\delta }_v}{4\pi }}\left[{\displaystyle \frac{r_x}{2h_x|r{|}^3}}\right]$ to the next element and by ${\displaystyle \frac{-{\delta }_v}{4\pi }}\left[{\displaystyle \frac{-r_x}{2h_x|r{|}^3}}\right]$to the previous element, and so on for Y and Z directions.

Finally, each element in the transfer matrix A can be built as

$$A_{(i,j)}={\displaystyle \frac{-{\delta }_v}{4\pi }}\left[\begin{array}{l}{\displaystyle \frac{r_{x1}}{2h_x|r_1{|}^3}}-{\displaystyle \frac{r_{x2}}{2h_x|r_2{|}^3}}+{\displaystyle \frac{r_{y3}}{2h_y|r_3{|}^3}}-{\displaystyle \frac{r_{y4}}{2h_y|r_4{|}^3}}\\ \begin{array}{cccc}& & & \end{array}+{\displaystyle \frac{r_{z5}}{2h_z|r_5{|}^3}}-{\displaystyle \frac{r_{z6}}{2h_z|r_6{|}^3}}\end{array}\right]$$

(9)

where these elements represents the six orthogonal neighbors of the current node with respect to an observation point in the Cartesian coordinate system. Then, for M body-surface locations, the forward solution of the infinite homogeneous volume conductor can be written as

$$b_0=A_{0}x$$

(10)

where b₀ is the vector of the dependent variables, x is the vector of the independent variables, and A₀ is the lead field transfer matrix.

3. Transfer Matrix of Anisotropic Volume Source in Infinite Homogeneous Volume Conductor

The approach is taken as the previous section, but the conductivity tensor of the source is considered here to be anisotropic. Due to orthogonality of the conductivity tensor, the calculations can be in terms of the principal direction (first eigenvector) of the tensor. Equation (11) shows the equation in terms of principal direction e as

$${\varphi }_0={\displaystyle \frac{-{\sigma }_t}{4\pi {\sigma }_0}}{\displaystyle \underset{v}{\int }\begin{array}{cc}\frac{\nabla V_m\cdot r}{|r{|}^3}& dv\end{array}}+{\displaystyle \frac{-({\sigma }_l-{\sigma }_t)}{4\pi {\sigma }_0}}{\displaystyle \underset{v}{\int }\begin{array}{cc}\frac{e{e}^T\nabla V_m\cdot r}{|r{|}^3}& dv\end{array}}$$

(11)

where e is the tensor’s principal direction vector, e^T is the transpose of this vector, and σ_l and σ_t is the longitudinal and traverse conductivities, respectively. The term ${\displaystyle \frac{e{e}^T\nabla V_m\cdot r}{|r{|}^3}}$ can be written in the X coordinate as

$${\displaystyle \frac{\partial V_m}{\partial x}}\left[e_x{e}_x+e_x{e}_y+e_x{e}_z\right]{\displaystyle \frac{r_x}{|r{|}^3}}={\displaystyle \frac{V_{m(x+1,y,z)}-V_{m(x-1,y,z)}}{2h_x}}\left[e_x{e}_x+e_x{e}_y+e_x{e}_z\right]{\displaystyle \frac{r_x}{|r{|}^3}}$$

(12)

Finally, each element in the transfer matrix A_(i,j) can be built as

$$A_{(i,j)}={\displaystyle \frac{-{\delta }_v}{4\pi {\sigma }_0}}\left\{\begin{array}{l}\left[{\displaystyle \frac{r_{x1}}{2h_x|r_1{|}^3}}-{\displaystyle \frac{r_{x2}}{2h_x|r_2{|}^3}}\right]\cdot \left[{\sigma }_t+({\sigma }_l-{\sigma }_t)(e_x{e}_x+e_x{e}_y+e_x{e}_z)\right]+\\ \left[{\displaystyle \frac{r_{x1}}{2h_x|r_1{|}^3}}-{\displaystyle \frac{r_{x2}}{2h_x|r_2{|}^3}}\right]\cdot \left[{\sigma }_t+({\sigma }_l-{\sigma }_t)(e_x{e}_y+e_y{e}_y+e_y{e}_z)\right]+\\ \left[{\displaystyle \frac{r_{x1}}{2h_x|r_1{|}^3}}-{\displaystyle \frac{r_{x2}}{2h_x|r_2{|}^3}}\right]\cdot \left[{\sigma }_t+({\sigma }_l-{\sigma }_t)(e_x{e}_z+e_y{e}_z+e_z{e}_z)\right]\end{array}\right\}$$

(13)

and the forward solution will be the same as equation (10)

4. Transfer Matrix of a Volume Source in Inhomogeneous Volume Conductor

The equation that calculates the potential field at any point inside an inhomogeneous volume conductor is defined as [Ref_102]:

$$\varphi ={\varphi }_{\infty }+{\displaystyle \frac{1}{4\pi {\sigma }_0}}\left[{\displaystyle \sum _{k=1}^L{\displaystyle \underset{S_k}{\int }\left(\frac{({\sigma }_k^{"}-{\sigma }_k^{\text{'}})\varphi (r_k)r_k^{\text{'}}\cdot \overrightarrow{n_k}}{|r_k^{\text{'}}{|}^3}\right)}d{S}_k}\right]$$

(14)

where ${\varphi }_{\infty }$is the potential of the infinite homogeneous volume conductor (eq. 2), k is the organ’s number, L is the number of organs, S_k is the surface of the organ, ${\sigma }_k^{\text{'}\text{'}}$ and ${\sigma }_k^{\text{'}}$ are the conductivities just inside and just outside the organ’s boundary, $\varphi (r_k)$is the equation (2), $r_k$is the displacement vector from primary source to a point on the organ boundary, $r_k^{\text{'}}$ is the displacement vector from boundary surface (secondary source) to body surface and $\overrightarrow{n_k}$is the normal vector on the organ’s boundary surface and it points to the outside of the organ. Then, for an observation point W, ${\varphi }_{\infty }$and $\varphi (r_k)$can be written as in equation (10) as the following

$$\begin{array}{l}{\varphi }_{\infty }=A_{0W}x\\ \varphi (r_1)=A_{1W}x\\ \varphi (r_2)=A_{2W}x\\ .\\ .\\ \varphi (r_L)=A_{LW}x\end{array}$$

(15)

such that A_kT represents the row of elements (a vector transpose) belonging to the observation point W in the matrix A of the organ k. For any point W on the body surface, equation (14) can be written as

$$\begin{array}{l}\varphi =A_{0}x+{\displaystyle \frac{1}{4\pi {\sigma }_0}}\left[{\displaystyle \sum _{k=1}^L({\sigma }_k^{"}-{\sigma }_k^{\text{'}}){\displaystyle \underset{S_k}{\int }\left(\frac{(A_{kW}x)r_{kW}^{\text{'}}\cdot \overrightarrow{n_k}}{|r_{kW}^{\text{'}}{|}^3}\right)}d{S}_k}\right]\\ =A_{0}x+{\displaystyle \frac{1}{4\pi {\sigma }_0}}\left[{\displaystyle \sum _{k=1}^L({\sigma }_k^{"}-{\sigma }_k^{\text{'}}){\displaystyle \sum _{j=1}^{P_k}\left(\frac{{\delta }_{Skj}(A_{kW}x)r_{kWj}^{\text{'}}\cdot \overrightarrow{n_{kj}}}{|r_{kWj}^{\text{'}}{|}^3}\right)}}\right]\\ =\left\{A_0+{\displaystyle \frac{1}{4\pi {\sigma }_0}}\left[{\displaystyle \sum _{k=1}^L({\sigma }_k^{"}-{\sigma }_k^{\text{'}}){\displaystyle \sum _{j=1}^{P_k}\left(\frac{{\delta }_{Skj}{A}_{kW}{r}_{kWj}^{\text{'}}\cdot \overrightarrow{n_{kj}}}{|r_{kWj}^{\text{'}}{|}^3}\right)}}\right]\right\}x\end{array}$$

(16)

where P_k denotes the number of surfaces in the organ k, δ_S is a surface element area, r is the vector from an observation point W to a point on the surface of an organ k, and n is the normal vector at this point. Then for each organ, the partial transfer matrix will be

$$\overline{A_W}={\displaystyle \frac{({\sigma }^{"}-{\sigma }^{\text{'}})}{4\pi {\sigma }_0}}{\displaystyle \sum _{j=1}^P\left(\frac{{\delta }_{Sj}{A}_W{r}_{Wj}^{\text{'}}\cdot \overrightarrow{n_j}}{|r_{Wj}^{\text{'}}{|}^3}\right)}={\displaystyle \sum _{j=1}^P\left(A_W\frac{{\delta }_{Sj}({\sigma }^{"}-{\sigma }^{\text{'}})}{4\pi {\sigma }_0}\frac{r_{Wj}^{\text{'}}\cdot \overrightarrow{n_j}}{|r_{Wj}^{\text{'}}{|}^3}\right)}$$

(17)

Building the partial transfer matrix using equation (17) can be performed as follows

1-

Compute the transfer matrix A of the organ or the body torso to all sources inside the heart using Equation 13. (Equation 9 can be used also in case of no information about fibers directions).

2-

Tessellate the organ’s surface into triangular elements and calculate the normal vectors on each surface element done by cross product of any two edges of the triangle in anti-clock-wise direction and calculate the area of the triangle element can be derived from the dot product of two these edges.

$$Normal=\overrightarrow{n}=AB\times AC={[\begin{array}{ccc}{n}_x& n_y& n_z\end{array}]}^T$$

$$Area={\delta }_s={\displaystyle \frac{1}{2}}\sqrt{\left|AB{|}^2\right|AC{|}^2-{(AB\cdot AC)}^2}$$

3-

From each point on the body surface, compute the vector r to a point on an organ surface element.

$$r={[\begin{array}{ccc}rx& ry& rz\end{array}]}^T$$

4-

Compute the scalar

$$U={\displaystyle \frac{{\delta }_s({\sigma }_k^{"}-{\sigma }_k^{\text{'}})}{4\pi {\sigma }_0}}{\displaystyle \frac{[n_x{r}_x+n_y{r}_y+n_z{r}_z]}{|r{|}^3}}$$

5-

Multiply the last scalar by the corresponding row (the row of the current observation point) in the corresponding A matrix, and add this row in a new matrix $\overline{A}$.

When applying these steps to all organs, Equation 16 becomes

$$\varphi =[A_0+\overline{A_1}+\mathrm{....}+\overline{A_k}]x$$

(18)

which can be written as

$$\varphi =Ax$$

(19)

or in the form of equation (1)

$$b=Ax$$

(20)

Then this proves a linear relation between the body surface potential readings and the transmembrance potential which is the necessary condition for using any linear regularization methods such as MN, WMN [37,38,39] and LORETA [40].

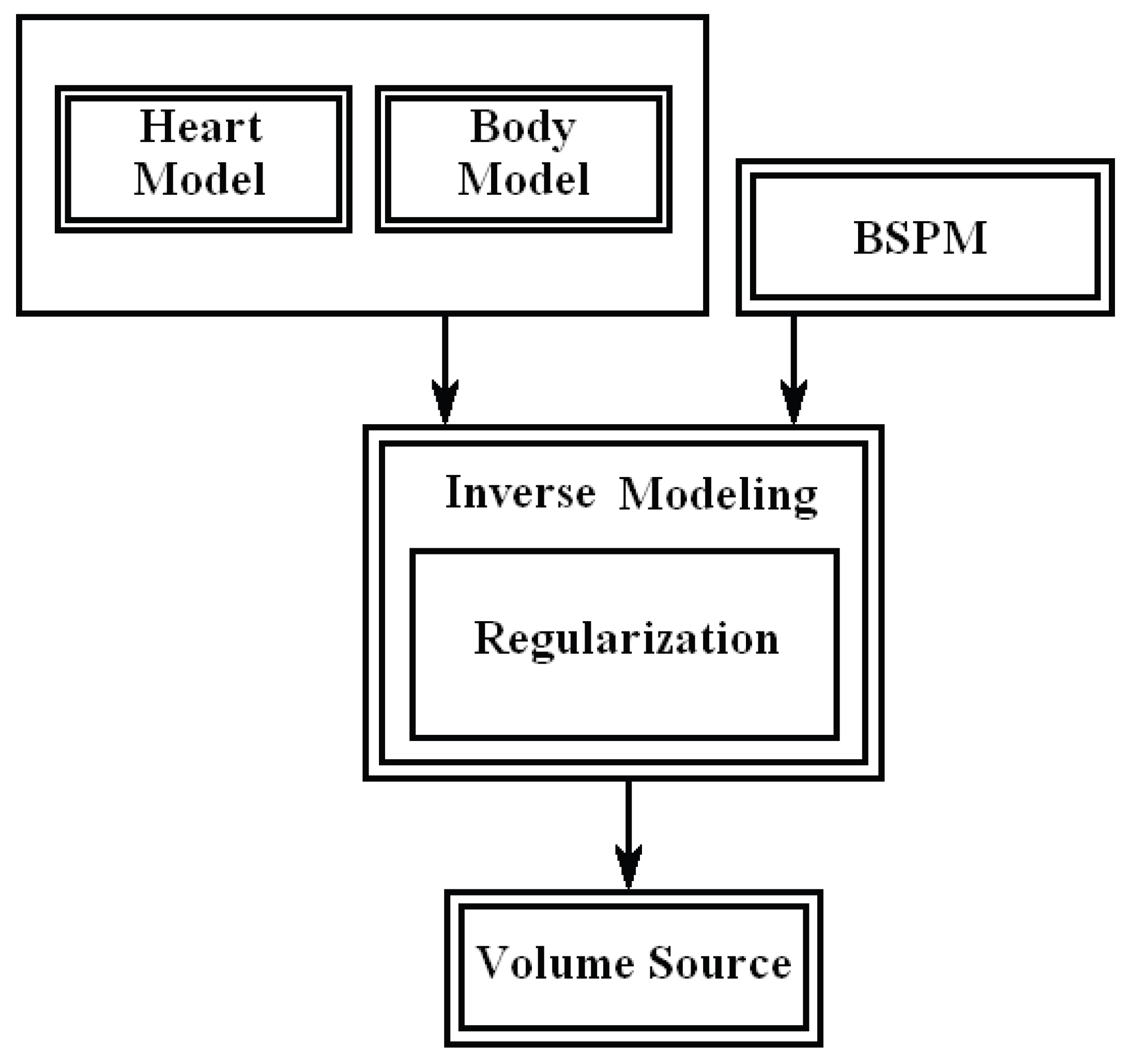
5. Conclusions

This research develops a comprehensive framework for modeling and solving the cardiac Inverse Problem using transmembrance potentials. By reformulating the problem in terms of TMPs instead of current densities, the solution space is reduced by two-thirds, resulting in significant computational efficiency and improved system conditioning. The study derives and constructs lead field transfer matrices under three increasingly complex biophysical conditions: isotropic-homogeneous, anisotropic-homogeneous, and anisotropic-inhomogeneous conductors. The final formulation maintains linearity, ensuring compatibility with established linear regularization techniques such as MN, WMN, and LORETA. This approach provides a robust foundation for accurate non-invasive cardiac source imaging, potentially enhancing clinical diagnosis and treatment planning in electrophysiology.