I. Introduction
Modern physics faces deep conceptual and mathematical challenges, especially in reconciling quantum field theory (QFT) [
1,
2] with general relativity. The standard model of particle physics, built upon a smooth continuum spacetime, gives rise to a series of unresolved problems: infinite vacuum energy densities, ultraviolet (UV) divergences in self-energy calculations, and singularities in gravitational collapse [
3]. These pathologies are not merely technical nuisances—they reveal deep inconsistencies in our foundational understanding of spacetime and field interactions.
One of the most glaring examples is the so-called vacuum catastrophe [
4], where theoretical predictions of the vacuum energy density exceed observed cosmological values by up to 120 orders of magnitude [
5]. This discrepancy—often cited as the worst theoretical prediction in physics—arises from summing zero-point energies [
6] of quantum fields over all modes in a continuum background. Yet despite the widespread assumption of vacuum energy, no direct experimental measurement confirms its absolute existence [
7].
The traditional cure for these divergences is renormalization [
8,
9], a mathematically successful but conceptually unsatisfying procedure that subtracts infinities by hand. Meanwhile, gravitational singularities, such as those predicted at the center of black holes and at the Big Bang, signal the breakdown of general relativity at small scales [
10]. These singularities indicate the need for a theory that modifies or replaces the continuum assumption at Planck-scale distances.
We show that the lattice spacetime structure reproduces the uncertainty principle [
9] as a geometric constraint without invoking canonical operator postulates. Furthermore, the lattice breaks both global and local U(1) symmetries [
10], providing a natural explanation for mass generation without the Higgs mechanism [
11]. It eliminates zero-point energy, resolves singularity divergences [
12], and avoids the need for renormalization altogether.
As a concrete test, we reinterpret the Casimir effect [
13,
14]—not as a manifestation of vacuum fluctuations, but as a radiation pressure imbalance that depends on ambient thermal conditions. This leads to distinct experimental predictions, enabling falsifiability of the lattice spacetime interpretation [
15].
By grounding quantum theory in a finite, causal, and physically meaningful geometry, our framework offers a new path forward. It removes the conceptual inconsistencies of the continuum model, avoids singularities, and offers a unified basis for field dynamics, cosmology, and quantum phenomena without speculative constructs or fine-tuning.
II. Causal Quantized Spacetime as Origin for Uncertainty Principle
In this section, we shall show that the commutation relations, derived from lattice operators, geometrically enforce non-commutativity and thereby reproduce uncertainty relations without invoking quantum postulates.
2.1. Position and Lattice Shift Operators
In a discretized spacetime lattice, coordinates are represented by the integer multiples of the lattice constant. We first consider a 2D lattice spacetime, and we define two conjugate pairs of coordinate operators , and a displacement operator along the spatial and temporal axes as
(1A)
where L and T are the fundamental length and time units of the lattice spacetime, one obtais and Thus, one obtains the following commutation relation . Likewise, one obtains the following commutation relation for time as . The unit length and time are related by the speed of light, i.e., L = cT. In 4D spacetime, one obtains the following commutation relations
(2)
or, in normalized operator form, concerning the unit lattice constant. The above commutation relation is related to Heisenberg’s uncertainty principle [
19] in continuum spacetime by relating the momentum operator
to the spatial displacement operator
. Because
and
are non-commutative, they cannot be scalars and can be represented by a matrix. Consequently, the function
It cannot be a scalar function. To the lowest order of representation, one can use a 2 by 2 matrix for these operators and
as a 2 by 1 vector function, which is isomorphic to a complex-valued function. Thus, spacetime quantization automatically leads to the necessity of a complex wave function, and equivalently, the natural emergence of wave-particle duality without ad hoc proposition by de Broglie’s matter-wave hypothesis as the foundation of Schrodinger wave mechanics or Heisenberg’s matrix mechanics.
2.2. Lattice Shift Operator as a Unitary Transformation
We define the displacement operator as a unitary operator generating finite spatial translations D = exp(i LP /ħ) and P = (ħ/iL)ln(D), using the Baker–Campbell–Hausdorff (BCH) identity. this gives D X D⁻¹ = X + L
D⁻¹ X D = X – L . (3)
This mirrors the canonical momentum relation [P, X] = -iħ, but implemented via finite translations on the lattice.
2.3. Uncertainty Relation
Define dimensionless position X̂ = X / L. Now, using the conjugation relation:
D⁻¹ X̂ D = X̂ - 1. (4)
We define the dimensionless momentum operator as the antisymmetric generator of lattice translations:
P̂ = (i / 2) [D⁻¹ X̂ D - D X̂ D⁻¹] . (5)
This leads to canonical commutation relations:
[X̂, P̂] = i. (6)
2.4. Absence of Zero-Point Vacuum Energy and Vacuum Catastrophe
We now define the annihilation and creation operators analogous to standard QFT based on dimensionless position and momentum operators as
a = (1/√2)(X̂ + i P̂), a† = (1/√2)(X̂ - i P̂) (7)
These satisfy the canonical algebra [a, a†] = 1. By defining H = ħω N, with the number operator N = a† a and N|n⟩ = n |n⟩, one obtains
N|0⟩ = a† a |0⟩= 0, (8)
because a|0⟩ = 0.
In the lattice spacetime formulation, the field Hamiltonian does not rely on the concept of a harmonic oscillator. In contrast, in standard QFT, the field Hamiltonian is based on the harmonic oscillator formalism to describe field amplitude oscillations, which includes the zero-point term intrinsic to the harmonic oscillator model. One has
H = (1/2)(P² + ω²X²) = ħω(a†a + 1/2). (9)
The +1/2 term arises from the symmetric ordering of X and P and assumes an underlying harmonic oscillator structure.
However, in our lattice spacetime framework, H = a†a. This Hamiltonian is purely a counting operator. Since there is no vacuum fluctuation and no oscillator-based dynamics, the ground state energy is strictly zero H|0⟩ = 0. This eliminates the concept of zero-point energy and avoids ultraviolet divergences and the vacuum catastrophe.
In standard QFT, zero-point energy arises because the Hamiltonian is quantized from classical harmonic oscillators and involves symmetric ordering of non-commuting operators. In the lattice model, no such oscillator structure exists. Therefore, there is no need for symmetric ordering, and the Hamiltonian H = ħωN leads naturally to a zero vacuum energy state. The position and momentum-like operators emerge from discrete symmetries, and the zero-point energy is naturally excluded, providing a divergence-free and geometrically grounded foundation for quantum theory.
In this framework, we propose that the discreteness of spacetime—manifested through a causal lattice with finite length and time intervals—is not merely a mathematical artifact or regularization scheme, but the true physical origin of all quantum behavior.
This interpretation offers a natural explanation for the rrise of Planck’s quantized energy: Instead of being imposed by harmonic oscillator eigenmodes or boundary conditions, energy quantization arises directly from discrete time evolution.
That is, the quantified frequency condition E = ħω emerges because T = 2π/ω is itself discretized.
Now, we discuss the role in Heisenberg’s uncertainty principle [
19]: Arising from the non-commutativity of discrete operators, such as [X, D] = L·D, it implies ΔX · ΔP ≥ ħ/2 without the need for operator postulates or canonical quantization. In this view, Planck’s constant ħ is not a mysterious universal constant but a direct reflection of the underlying geometric structure of quantized spacetime itself.
In analogy to the conventional quantum theory in continuum spacetime, we can define the creation, annihilation, and occupation number operators a = (1/√2)(X̂ + i P̂), a† = (1/√2)(X̂ - i P̂), one obtains Since for the vacuum state , and, where . To generalize this result by including y and z-directions.
One concludes the vacuum state has no zero-point energy, i.e., This result, based on the lattice spacetime, is drastically different from the standard continuum model with where the creation and annihilation operators are defined as the position and annihilation operators of a harmonic oscillator. The absence of zero-point vacuum energy has a very important implication that leads to no vacuum catastrophe, no ultraviolet divergence and no singularities. All differential equations and integral equations must be replaced by difference and summation equations at very small time and space scales.
2.5. Displacement Operators and Global Causality in Lattice Spacetime
In conventional quantum theory, the position and momentum operators can be represented by two non-commutative infinite-dimensional matrices in the Hilbert space. In addition, momentum operators along different spatial axes are commutative. However, such a representation is inconsistent with causality due to the finite light’s speed. In this work, we focus on the global causal structure of the discretized lattice spacetime. In conventional special relativity, the invariant interval is given by x² + y² + z² - c² t² = constant, which ensures Lorentz invariance and global causality. We shall show that the Lorentz invariance as a causality constraint leads to a non-commutative quaternionic representation for the momentum operators.
To mirror this structure in our lattice model, we associate the spatial displacement operators with quaternionic basis elements Dx ∼ e₁, Dy ∼ e₂, Dz ∼ e₃, where e₁, e₂, and e₃ are the standard imaginary units of the quaternion algebra, satisfying eᵢ eⱼ = -δᵢⱼ + εᵢⱼₖ eₖ.The temporal displacement is assigned the imaginary scalar: Dt = i c, where i is the complex unit and c is the speed of light. This assignment ensures the Euclidean form of the invariant becomes x² + y² + z² + (i c t)² = constant.
This formalism captures the geometric essence of global causality without invoking the full operator structure needed to encode micro-causal dynamics. The quaternionic assignment for space offers a clean and compact representation of 3D spatial structure, while the imaginary scalar time direction preserves commutativity and allows the use of Euclidean invariants.We emphasize that this formulation deliberately avoids the more involved algebra of non-commuting operators and time-as-generator structures (e.g., γ⁰ or e₄). Those aspects, including their implications for micro-causality, mass generation, and symmetry breaking, will be treated in a separate report.
Here, our main focus is to show that even at the global level, discretized lattice spacetime naturally supports a quaternionic interpretation of spatial displacement and accommodates the causal structure of special relativity through an imaginary time axis. This sets the foundation for the deeper algebraic structures that emerge when local interactions and internal symmetries are included.
2.6. Violation of the Massless Klein-Gordon Equation and U(1) Symmetry on the Lattice
In the continuum, the massless Klein–Gordon (KL) equation [
16,
17] for a scalar field, or Higgs field [
18], is given by
□φ = (∂²/∂t² - ∇²) φ = 0, which leads to the dispersion relation E² = p₁² + p₂² + p₃². On a discrete lattice, we replace derivatives with second-order finite difference operators:
δₜ² φ(n₀) = [φ(n₀+1) + φ(n₀−1) − 2φ(n₀)] / T²,
δᵢ² φ(nᵢ) = [φ(nᵢ+1) + φ(nᵢ−1) − 2φ(nᵢ)] / L². (4A)
Assuming a discrete plane-wave solution, φ(n) = exp[i(p · n − E·n₀)], the modified dispersion relation becomes
(4/T²) sin²(ET/2) = ∑₁³ (4/L²) sin²(pᵢL/2). (4B)
This differs fundamentally from the continuum relation. The equality E² = p² no longer holds unless ET → 0 and pL → 0. For finite lattice units T and L, and energy-momentum values as multiples of the inverse lattice spacing, we generically find E² − p² ≠ 0. Thus, in lattice spacetime, the massless KL equation in continuum spacetime becomes a KL equation for a massive scalar boson, i.e., the massless boson acquires a mass, not through the Higgs mechanism [
18] but due to U(1)-symmetry breaking due to the lattice structure of the spacetime.
Simply put, the Klein–Gordon equation is violated at the fundamental level in causal lattice spacetime. As a result, one concludes:
The global U(1) symmetry for massless scalar fields is broken.
The local U(1) symmetry associated with electromagnetic and fermion fields is also broken, leading to natural mass generation without requiring a scalar Higgs field or spontaneous symmetry breaking.
These conclusions underscore how spacetime discretization alone suffices to explain particle masses and symmetry breaking — a major departure from the conventional Higgs paradigm. In short, based on the causal lattice spacetime framework, we show that the Klein-Gordon equation for a scalar Higgs field is violated at the fundamental level in lattice spacetime. In addition to the global U(1)-symmetry breaking, one can also prove a breaking of the local U(1)-symmetry for Maxwell’s electromagnetic field and a Dirac fermion field, which leads naturally to mass acquisition without the Higgs mechanism. Details will be presented elsewhere.
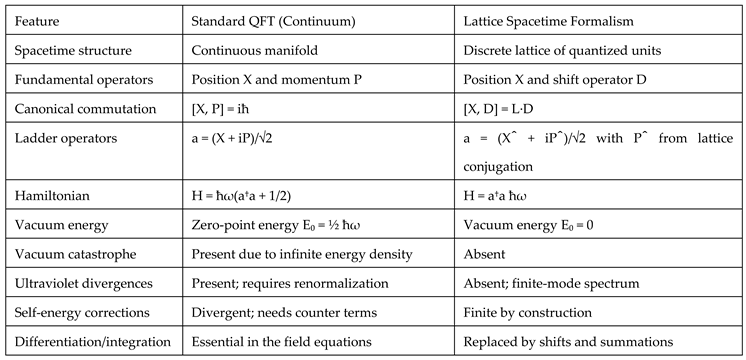
2.7. Comparison between Continuous and Lattice Spacetime
The following table compares key aspects of the standard quantum harmonic oscillator formalism in continuum quantum field theory (QFT) with the proposed lattice spacetime framework. This highlights how our model resolves foundational issues through a finite, discrete, and causal structure.
Table 1.
Comparison of quantum field theories based on continuous vs. lattice spacetime.
Table 1.
Comparison of quantum field theories based on continuous vs. lattice spacetime.
IV. Experimental Proposal to test the Radiation-Based Casimir Effect in Lattice Spacetime QFT
This approach echoes Einstein’s principle that physical theories must be grounded in observable effects, not mathematical artifacts. In the standard quantum field theory (QFT), the Casimir effect is attributed to vacuum fluctuations and the associated zero-point energy. In contrast, the lattice spacetime quantum field theory posits that vacuum energy is strictly zero, and the Casimir force instead arises from the imbalance in ambient radiation pressure between the inside and outside of two conducting plates.
In a vacuum chamber, the Casimir force should depend on the thermal radiation present in the environment. By controlling the temperature of surrounding walls and apparatus, one should observe a corresponding change in the measured Casimir force—something not predicted by standard QFT. We propose an experiment that provides a clear and controlled method to test the physical origin of the Casimir effect. If the force varies with ambient temperature, it will support the view that it is a result of real thermal and blackbody radiation pressure, not abstract zero-point energy. This would validate lattice spacetime interpretation and resolve long-standing conceptual paradoxes such as the vacuum catastrophe and infinite self-energy.
By experimentally verifying the temperature dependence of the Casimir effect, we can determine whether zero-point energy is a physically necessary concept. The results could reshape our understanding of vacuum, radiation, and field quantization.
V. Discussion and Implications
The lattice spacetime model offers a profound departure from conventional quantum field theory (QFT). While standard QFT is built on a smooth spacetime manifold allowing infinite field modes and divergences, the lattice framework imposes a discrete, finite geometry that transforms both interpretation and computation.
In standard QFT, vacuum energy arises from summing zero-point fluctuations, leading to divergences and cosmological contradictions. The lattice model rejects vacuum energy as physically meaningful, removing the need for renormalization and avoiding the vacuum catastrophe.
In lattice quantum chromodynamics (QCD) [
20], the lattice is a numerical scaffolding for solving field theories on a computer, not physically fundamental. In contrast, in this model, the lattice is the physical and causal backbone of reality, fundamentally altering the origin of quantum rules, eliminating zero-point energy, and replacing divergent infinities with finite, bounded structures.
The uncertainty principle, introduced axiomatically in standard theory, arises here from finite signal propagation and discrete geometry, offering a causal, deterministic interpretation. Likewise, the Casimir effect—traditionally linked to vacuum fluctuations—is attributed instead to thermal radiation pressure differentials, offering an experimentally testable distinction between the models.
Singularities, such as those in black holes or the Big Bang, are unavoidable in continuous models due to infinite curvature. In lattice geometry, maximal compression replaces singularities, allowing cyclic cosmology without infinite densities. The field spectrum becomes finite, and the vacuum is reconceptualized not as an energetic state but as the absence of excitation within a discrete structure. This reframing simplifies physical law and avoids longstanding paradoxes.
VI. Conclusions and Outlook
We have presented a lattice spacetime framework that resolves core problems in quantum field theory by replacing the continuum with a finite, discrete structure. This model naturally enforces uncertainty through geometric constraints, eliminates vacuum zero-point energy, avoids divergences, and removes singularities.
Reinterpreting the Casimir effect as a thermal radiation phenomenon opens a path to experimental tests that distinguish between this model and standard QFT. Temperature-dependent Casimir force measurements could empirically challenge the zero-point energy hypothesis and support the lattice view.
The model also supports a cyclic cosmological picture, avoiding singularities and aligning with bounded geometric evolution. It provides a physically coherent and mathematically consistent pathway for integrating quantum field theory and gravity without invoking speculative constructs or fine-tuning.
Future work includes extending the lattice framework to incorporate gauge fields, fermions, and black hole thermodynamics. This approach may provide a physically grounded, unified foundation for fundamental physics beyond current paradigms.
VII. Summary
Here, we use the following list to summarize the key results of this work:
Classical continuum spacetime is replaced by an intrinsic discrete lattice structure with minimum length and time scales.
Planck’s quantized energy arises naturally due to spacetime quantization.
• Heisenberg’s uncertainty principle emerges naturally from geometric micro-causality rather than operator axioms.
• Vacuum zero-point energy is eliminated, resolving the vacuum catastrophe.
• The Casimir effect is explained as thermal radiation pressure, enabling experimental validation.
• No ultraviolet divergences or singularities arise; renormalization is unnecessary.
• The model recovers quantum dynamics, gauge symmetries algebraically through hypercomplex operators, naturally leading to mass acquisition via symmetry-breaking without the ad hoc Higgs mechanism.
• SU(3) color symmetry and octonionic spinors emerge naturally.
• This framework unifies particle physics and quantum spacetime geometry under one causal lattice-spacetime QFT framework.
We are presently expanding this framework to analyze the leptons and quarks, to resolve unsolved puzzles in the Standard Model, such as their mass hierarchy, electric and color charges, the mechanism behind neutrino oscillations, the origin of three generations, quantization of gravity, and grand unification. These results will be published elsewhere.
Author Contributions
J. Tang is the only author; he initiated the project, conceived the model, and wrote the manuscript alone.
Funding
The author is a retired professor with no funding agency to be acknowledged.
Data Availability Statement
There are only analytical equation derivations, but no computer numerical simulations. All reasonable questions about the data or derivations can be requested by contacting the corresponding author.
References
- Weinberg, S. The Quantum Theory of Fields, Vol. 1. Cambridge Univ. Press ( 1995.
- Peskin, M. E. & Schroeder, D. V. An Introduction to Quantum Field Theory. Westview Press ( 1995.
- Carroll, S. M. The cosmological constant. Living Rev. Relativ. 4, 1 (2001).
- Padmanabhan, T. Cosmological constant—the weight of the vacuum. Phys. Rep. 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Burgess, C. P. The cosmological constant problem: why it’s hard to get dark energy from micro-physics. Princeton Univ. Lect. Notes ( 2007.
- Narodny, L.; Feynman, R. QED: The Strange Theory of Light and Matter. Leonardo 1991, 24, 493. [Google Scholar] [CrossRef]
- Peebles, P. J. E. & Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 75, 559–606 (2003).
- Hooft, G. '.; Veltman, M. Regularization and renormalization of gauge fields. Nucl. Phys. B 1972, 44, 189–213. [Google Scholar] [CrossRef]
- Heisenberg, W. The Physical Principles of the Quantum Theory. Univ. of Chicago Press ( 1930.
- Hawking, S.W.; Ellis, G.F.R.; Sachs, R.K. The Large Scale Structure of Space-Time
. Phys. Today 1974, 27, 91–93. [Google Scholar] [CrossRef]
- Englert, F.; Brout, R. Broken Symmetry and the Mass of Gauge Vector Mesons. Phys. Rev. Lett. 1964, 13, 321–323. [Google Scholar] [CrossRef]
- Penrose, R. & Hawking, S. W. The singularities of gravitational collapse. Proc. R. Soc. Lond. A 314, 529–548 (1970).
- Casimir, H. B. G. On the attraction between two perfectly conducting plates. Proc. K. Ned. Akad. Wet. 51, 793 (1948).
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press (OUP):Oxford,UK, 2009.
- Lamoreaux, S. K. Demonstration of the Casimir force in the 0.6 to 6 µm range. Phys. Rev. Lett. 78, 5–8 (1997).
- Klein, O. & Gordon, W. Quantum theory and five-dimensional relativity. Z. Phys. 12, 307–326 (1926).
- Bjorken, J. D. & Drell, S. D. Relativistic Quantum Fields. McGraw-Hill (1965).
- Wilson, K. G. Confinement of quarks. Phys. Rev. D 10, 2445–2459 (1974).
- Cohen-Tannoudji, C. , Diu, B. & Laloë, F. Quantum Mechanics. Wiley-VCH (1977).
- Weinberg, S. A model of leptons. Phys. Rev. Lett. 19, 1264–1266 (1967).
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).