Multiscale Modeling of Tumor Angiogenesis and Resistance Evolution: A Hybrid PDE–ABM Framework for Cancer Prediction and Therapy Planning

1. Introduction

Understanding how spatially variable drug penetration and hypoxia shape tumor evolution is essential to improve cancer therapy and motivates the development of multiscale mathematical models. Chemotherapy and targeted therapy are the main cancer treatments, especially in patients ineligible for curative surgery or those requiring perioperative intervention [1,2,3,4,5,6,7]. Nevertheless, their efficacy is often impaired by drug resistance [8]. This process is complex and is caused by intrinsic processes, i.e., preexisting genetic alterations, or by acquired modifications, e.g., therapy-generated mutations, epigenetic reprogramming, or microenvironmental selection [8,9,10,11,12]. As the disease advances and treatments continue, most of the tumors exhibit ongoing evolutionary dynamics in reaction to therapy. This gives rise to multiple drug-resistant subclones and treatment failure [13,14]. Additionally, heterogeneity of the tumor microenvironment (TME), e.g., hypoxic regions and heterogeneous drug delivery, significantly affects drug distribution and uptake. These heterogeneities promote resistant clones’ survival and dominance [15,16,17]. Modeling cell type competition, drug stress survival patterns, and tumor growth in a temporally and spatially heterogeneous microenvironment is thus most crucial for the prediction of therapy response as well as the design of personalized, effective treatment plans.

To address these challenges, researchers increasingly use mathematical modeling to study resistance mechanisms and predict treatment outcomes quantitatively [18,19]. Mathematical approaches encompass genetic, epigenetic, and microenvironmental drivers of resistance [20]. They also include evolutionary dynamics [21] and use multi-omics data with machine learning [22]. Spatial differences and environmental interactions, such as low oxygen levels, are key resistance factors [23,24,25]. Low oxygen occurs when blood flow does not meet the metabolism of rapidly growing tumors. This activates survival pathways driven by hypoxia-inducible factor-$1\alpha$ (HIF-$1\alpha$) and encourages blood vessel growth through vascular endothelial growth factor (VEGF) [26,27,28]. Pathological neovascularization partially alleviates oxygen deficits but creates heterogeneous drug distribution landscapes that select resistant phenotypes.

This interplay between vascular dynamics and therapy resistance motivates mathematical work on angiogenesis and resistance evolution [29,30,31,32,33]. Early models employed reaction-diffusion systems to describe tumor-induced vessel formation and validated traveling wave solutions for vessel tips [34,35]. The Keller-Segel model describes biased movement of cells (e.g., endothelial cells) in response to chemical gradients such as tumor angiogenic factor (TAF). The original equations are [36]:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\partial }_{t}n=D_n\Delta n-\chi ·\nabla (n\nabla c),\hfill \\ {\partial }_{t}c=D_c\nabla c-g(c,n).\hfill \end{array}\right.\end{array}$$

(1.1)

Here, n denotes cell density, c chemoattractant concentration, $D_n$ and $D_c$ diffusion coefficients and $g(c,n)$ chemical kinetics. Subsequent angiogenesis models introduced thermodynamically consistent continuum descriptions of interfacial growth. A key contribution [37] couples endothelial proliferation and VEGF diffusion:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\partial }_t{c}^{+}=\Delta c^{+}-c^{+},\hfill & \mathrm{in}{V}^{+}\left(t\right),\hfill \\ {\partial }_t{c}^{-}=\Delta c^{-}-c^{-},\hfill & \mathrm{in}{V}^{-}\left(t\right),\hfill \end{array}\right.\end{array}$$

(1.2)

where $V^{+}\left(t\right)$ and $V^{-}\left(t\right)$ denote time-dependent extracellular and capillary lumen volumes, $c^{+}$ and $c^{-}$ corresponding VEGF concentrations, with appropriate boundary conditions at $\Sigma \left(t\right)$ (endothelial layer interface) and $\partial V_t\left(t\right)$ (tumor surface).

Agent-based models (ABMs) are based on these studies. They simulate how individual cells act within heterogeneous microenvironments. ABMs can show processes at various levels, ranging from molecular signaling to tissue characteristics. This ability helps us examine cancer progression, immune interactions, and responses to therapy [38,39,40]. ABMs show how microenvironmental niches affect drug resistance [24], how spatial limits influence residual disease [41], and how both internal and external factors impact drug resistance [42]. Despite these developments, few models can combine dynamic changes in blood vessel adaptation with growing tumor resistance during treatment. This gap makes it hard to understand how angiogenesis influences selective pressures.

Continuum models, for example, reaction-diffusion systems, can capture overall tumor dynamics but cannot capture single-cell stochasticity. Agent-based approaches address heterogeneity but lack rigorous coupling to continuum-scale physics. To bridge this gap, we propose a hybrid discrete-continuous (HDC) framework coupling agent-based tumor/endothelial cell dynamics with reaction-diffusion-chemotaxis equations for oxygen, drug, and TAF:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\partial }_{t}n=D_n\Delta n-\nabla ·(\chi \left(c\right)n\nabla c),\hfill \\ {\partial }_{t}u=D_u\Delta u+f_{u,\mathrm{source}}-f_{u,\mathrm{sink}}.\hfill \end{array}\right.\end{array}$$

(1.3)

Here n denotes endothelial cell density, $u\in \{c,d,o\}$ represents TAF (c), drug (d), and oxygen (o) fields, $\chi \left(c\right)$ the chemotactic function, and $f_{u,\mathrm{source}}$, $f_{u,\mathrm{sink}}$ source/sink terms. Tumor cell agents have state variables:

$$\begin{array}{c}\hfill a=\left\{{\mathrm{id}}_a,a^{(X,Y)}\left(t\right),a^o\left(t\right),a^d\left(t\right),a^{dam}\left(t\right),a^{death}\left(t\right),a^{age}\left(t\right),a^{mat}\right\},\end{array}$$

with random motility via Wiener processes:

$$\begin{array}{c}\hfill d{a}^{\left(X,Y\right)}=\epsilon d{W}_t^a.\end{array}$$

Vessel agents follow:

$$\begin{array}{c}\hfill b=\{{\mathrm{id}}_b,b^{(X,Y)}\left(t\right),b^{age}\left(t\right)\}.\end{array}$$

The discrete component simulates tumor cells (proliferation, apoptosis, mutation, motility) and endothelial cells (chemotaxis, branching, anastomosis). The continuous component models diffusion, decay, production, and uptake of biochemical fields, incorporating chemotaxis and cellular consumption/production. This integration analyzes how vascular remodeling influences drug penetration, hypoxia-driven adaptation, and clonal competition, elucidating feedback loops between angiogenesis and resistance. We discretize the endothelial chemotaxis equation using probabilistic finite differences and solve reaction-diffusion equations via semi-implicit alternating direction implicit (ADI) methods. Simulations reproduce hypoxia-induced angiogenesis and investigate preexisting versus spontaneous mutations in resistance evolution.

The remainder of the paper is organized as follows. Section 2 presents modeling and computational techniques; namely, Section 2.1 advances the partial differential equation (PDE) formulation, Section 2.2 the agent-based approach to tumor and vessel cells, and Section 2.3 the numerical discretization of the model. Section 3 presents simulations of the impact of angiogenesis on resistance evolution and optimal drug delivery strategies. Section 4 discusses biological implications, e.g., reconciliation of mutually contradictory experimental results, and posits possible model extensions. Section 5 closes the research.

2. Materials & Methods

2.1. PDE Model for Continuous Fields

We model tumor progression and angiogenesis using spatially resolved reaction-diffusion equations for endothelial cells n, TAF c, drug d, and oxygen o, where each field couples to discrete tumor cells ($a\in {\Lambda }_t$) and vessel sites ($v\in V_t$). We denote the collection of tumor cells and vessel agents at time t by ${\Lambda }_t$ and $V_t$, respectively. Tumor cells partition into normoxic ($a\in {\Lambda }_t^n$) and hypoxic ($a^{\prime }\in {\Lambda }_t^h$) subpopulations, with local environments mediating angiogenic signaling and drug resistance.

Endothelial cells undergo diffusive and chemotactic migration:

$$\begin{array}{c}\hfill {\partial }_{t}n=D_n\Delta n-\nabla ·\left(\chi \left(c\right)n\nabla c\right),\chi \left(c\right)={\displaystyle \frac{{\chi }_0{k}_1}{k_1+c}},\end{array}$$

(2.1)

where $D_n$ denotes the diffusion coefficient and $\chi \left(c\right)$ is the chemotactic sensitivity function. This $\chi \left(c\right)$ adheres to receptor-kinetics law [43,44,45,46,47], where ${\chi }_0$ is the maximal chemotactic coefficient and $k_1>0$ modulates TAF sensitivity.

TAF dynamics combine diffusion, decay, hypoxic cell secretion, and vessel uptake:

$$\begin{array}{c}\hfill {\partial }_{t}c=D_c\Delta c-{\xi }_{c}c+\eta \sum _{a\in {\Lambda }_t^h}{\chi }_a-\lambda c\sum _{v\in V_t}{\chi }_v,\end{array}$$

(2.2)

The indicator functions ${\chi }_a$ and ${\chi }_v$ are 1 within radius $R_c$ of tumor cell a or vessel agent v, and 0 otherwise:

$$\begin{array}{c}\hfill {\chi }_a(x,t)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}∥x-a^{\left(X,Y\right)}\left(t\right)∥\le R_c,\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\mathrm{and}{\chi }_v(x,t)=\left\{\begin{array}{cc}1\hfill & if∥x-v^{\left(X,Y\right)}\left(t\right)∥\le R_c,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

The positions $a^{(X,Y)}\left(t\right)$ and $v^{(X,Y)}\left(t\right)$ denote the centers of hypoxic tumor cell $a\in {\Lambda }_t^h$ and vessel site $v\in V_t$ at time t. Parameter $D_c$ represents the TAF diffusion rate, ${\xi }_c$ the natural decay rate, $\eta$ the production rate per hypoxic tumor cell, and $\lambda$ the endothelial uptake rate.

Drug dynamics include diffusion, degradation, uptake by tumor cells, and delivery by vessels:

$$\begin{array}{c}\hfill {\partial }_{t}d=D_d\Delta d-{\xi }_{d}d-{\rho }_{d}d\sum _{a\in {\Lambda }_t}{\chi }_a+S_d\left(t\right)\sum _{v\in V_t}{\chi }_v.\end{array}$$

(2.3)

Here, $D_d$ is the diffusion rate, ${\xi }_d$ the decay rate, ${\rho }_d$ the tumor cell uptake rate, and $S_d$ the time-dependent vessel supply rate.

Oxygen follows analogous dynamics, but with feedback-limited vessel supply:

$$\begin{array}{c}\hfill {\partial }_{t}o=D_o\Delta o-{\xi }_{o}o-{\rho }_o\sum _{a\in {\Lambda }_t}{\chi }_a+S_o(o_{max}-o)\sum _{v\in V_t}{\chi }_v,\end{array}$$

(2.4)

where $D_o$ is the diffusion rate, ${\xi }_o$ the decay rate, ${\rho }_o$ the tumor and endothelial cell uptake rate, $S_o$ the vessel supply rate, and $o_{max}$ the saturation concentration. This feedback mechanism suppresses oxygen release at high concentrations.

Homogeneous Neumann boundary conditions ensure mass conservation in the isolated tissue domain:

$$\begin{array}{c}\hfill \overrightarrow{n}·\nabla \varphi {|}_{\partial U}=0,\varphi \in \{n,c,d,o\},\end{array}$$

where $\overrightarrow{n}$ is the unit outward normal vector on the boundary $\partial U$. The chemotaxis equation (2.1) is discretized using the forward Euler method, while the remaining reaction-diffusion equations are solved via an alternating direction implicit (ADI) scheme. The governing processes incorporated in each PDE are summarized in Table 1.

We non-dimensionalize the system using characteristic scales for length L, diffusion time $\tau =L^2/D$, and field concentrations ($n_0,c_0,d_0,o_{max}$). These are summarized in Table 2. Here, D denotes a representative diffusion coefficient, chosen such that $\tau =L^2/D=5.76\times {10}^4$ s for a spatial scale $L=5\times {10}^{-3}$ m.

With

$$\begin{array}{cc}\hfill & {\tilde{D}}_n={\displaystyle \frac{D_n}{D}},{\tilde{\chi }}_0={\displaystyle \frac{{\chi }_0{c}_0}{D}},\alpha ={\displaystyle \frac{c_0}{k_1}},{\tilde{D}}_c={\displaystyle \frac{D_c}{D}},\hfill \\ \hfill & \tilde{\eta }={\displaystyle \frac{\eta \tau n_0}{c_0}},\tilde{\lambda }=\lambda \tau n_0,{\tilde{\xi }}_c=\tau {\xi }_c,\hfill \\ \hfill & {\tilde{D}}_d={\displaystyle \frac{D_d}{D}},{\tilde{\xi }}_d=\tau {\xi }_d,{\tilde{\rho }}_d={\rho }_d\tau n_0,{\tilde{S}}_d={\displaystyle \frac{S_d\tau n_0}{d_0}},\hfill \\ \hfill & {\tilde{D}}_o={\displaystyle \frac{D_o}{D}},{\tilde{\xi }}_o=\tau {\xi }_o,{\tilde{\rho }}_o={\displaystyle \frac{{\rho }_o\tau n_0}{o_{max}}},{\tilde{S}}_o=S_o\tau n_0,\hfill \end{array}$$

we obtain the non-dimensionalized systems by dropping the tildes:

$$\begin{array}{cc}\hfill {\partial }_{t}n& =D_n\Delta n-\nabla ·\left({\displaystyle \frac{{\chi }_0}{1+\alpha c}}n\nabla c\right),\hfill \end{array}$$

(2.5)

$$\begin{array}{cc}\hfill {\partial }_{t}c& =D_c\Delta c-{\xi }_{c}c+\eta \sum _{a\in {\Lambda }_t^h}{\chi }_a-\lambda c\sum _{v\in V_t}{\chi }_v,\hfill \end{array}$$

(2.6)

$$\begin{array}{cc}\hfill {\partial }_{t}d& =D_d\Delta d-{\xi }_{d}d-{\rho }_{d}d\sum _{a\in {\Lambda }_t}{\chi }_a+S_d\sum _{v\in V_t}{\chi }_v,\hfill \end{array}$$

(2.7)

$$\begin{array}{cc}\hfill {\partial }_{t}o& =D_o\Delta o-{\xi }_{o}o-{\rho }_o\sum _{a\in {\Lambda }_t}{\chi }_a+S_o(1-o)\sum _{v\in V_t}{\chi }_v,\hfill \end{array}$$

(2.8)

All fields $\varphi \in \{n,c,d,o\}$ satisfy homogeneous Neumann (no-flux) boundary conditions in dimensionless form:

$$\begin{array}{c}\hfill \overrightarrow{n}·\nabla \varphi {|}_{\partial U}=0.\end{array}$$

Table 3 gives an overview of all model parameters used in the study, both for the PDE system, the ABM, and non-dimensionalization. Each parameter is listed with a brief description of how it enters the modeling framework.

We list all assumptions in our work:

(i)

Tumor cells consume oxygen and TAF at fixed rates.

(ii)

Drug diffusion and decay are assumed isotropic and linear.

(iii)

Angiogenic tip cells follow TAF gradients via chemotaxis.

(iv)

Mutation is modeled as a neutral stochastic process.

(v)

DNA repair is included but lacks mechanistic biochemical modeling.

Quantitative estimation of critical parameters predicts whether reaction or diffusion dominates. Key biological implications arise: high decay (${\xi }_i$) or uptake (${\rho }_i$) rates induce spatial heterogeneity, forming hypoxic cores and hypoxia-driven resistance when diffusion is low ($D_o\ll 1$). Pathologic vasculature generates low $S_o$ and $S_d$; upon normalization, this predicts poor tumor response to hypoxia-targeted and vascular normalization therapies. Optimal dosing regimens are defined by drug properties: low diffusivity ($D_d$) prevents penetration, so local delivery or carriers are necessary; rapid decay (${\xi }_d$) necessitates high infusion rates due to short half-life; and high uptake (${\rho }_d$) leads to saturation, best with chronic low-dose over pulsed high-dose schedules.

This PDE model gives a rigorous mathematical framework for tumor growth and resistance to therapy, grounded in biological mechanisms. Reaction-diffusion equations model heterogeneity in the microenvironment by diffusion, decay, and local production/consumption, accounting for effects like hypoxic cores where blood vessels poorly supply certain regions, limited penetration of drugs, and TAF-induced chemotactic angiogenesis. The bidirectional PDE-ABM coupling enables multiscale modeling of cellular heterogeneity: cells respond to local signaling fields while dynamically altering them via production and consumption. This computationally efficient multiscale framework readily extends to incorporate advanced cellular behaviors and microenvironment interactions.

2.2. Agent-Based Model

2.2.1. Tumor Dynamics

Tumor cells are modeled as discrete agents on a 2D lattice that interact with continuum microenvironmental fields governed by PDEs (Section 2.1). Each cell follows a set of biologically motivated and mathematically explicit rules for proliferation, apoptosis, mutation, and motility. Spatial interactions among agents and their motility are constrained by the lattice neighborhood structure. Figure 1 compares two such structures: the Von Neumann neighborhood, comprising the four adjacent lattice sites (left, right, down, up), and the Moore neighborhood, consisting of all eight surrounding sites, including diagonals.

We characterize each tumor cell $a\in {\Lambda }_t$ by:

$$\begin{array}{c}\hfill a=\left\{{\mathrm{id}}_a,a^{(X,Y)}\left(t\right),a^o\left(t\right),a^d\left(t\right),a^{dam}\left(t\right),a^{death}\left(t\right),a^{age}\left(t\right),a^{mat}\left(t\right)\right\},\end{array}$$

where $a^{(X,Y)}\left(t\right)$ is the center position of the cell, $a^o\left(t\right)$ the oxygen concentration, $a^d\left(t\right)$ the accumulated drug level, $a^{dam}\left(t\right)$ the drug-induced DNA damage, $a^{death}\left(t\right)$ the death threshold, $a^{age}\left(t\right)$ the time elapsed since thelast division, and $a^{mat}$ the maturation time to achieve proliferation competence.

We assign each cell $a\in {\Lambda }_t$ a unique lineage identifier ${\mathrm{id}}_a=(k,i_1,\dots ,i_n)$, where:

(i)

$k\in \{1,\dots ,N_0\}$ is the index of the ancestor cell,

(ii)

$i_j\in \{1,2\}$ records the branching decision at the j-th division,

(iii)

$n\in \mathbb{N}$ counts mitotic generations since initiation.

The initial population ($n=0$) has identifiers ${\mathrm{id}}_a=\left(k\right)$. For any n-generation cell with ${\mathrm{id}}_a=(k,i_1,\dots ,i_n)$, mitosis produces two $(n+1)$-generation daughter cells with:

$$\begin{array}{c}\hfill {\mathrm{id}}_{a^{\prime }}=(k,i_1,\dots ,i_n,i_{n+1}),i_{n+1}=1,2.\end{array}$$

Tumor cells move passively through Brownian dynamics:

$$\begin{array}{c}\hfill d{a}^{(X,Y)}=\epsilon d{W}_t^a,{\left\{W_t^a\right\}}_{a\in {\Lambda }_t}\mathrm{i}.\mathrm{i}.\mathrm{d}.\mathrm{Brownian}\mathrm{motions},\end{array}$$

where $\epsilon =0.01$ (dimensionless) regulates noise strength. Positions update via Euler-Maruyama:

$$\begin{array}{c}\hfill a^{(X,Y)}(t+\Delta t)=a^{(X,Y)}\left(t\right)+\epsilon \sqrt{\Delta t}{Z}_t^a,Z_t^a\sim \mathcal{N}(0,1)\mathrm{i}.\mathrm{i}.\mathrm{d}.\end{array}$$

This random movement, together with division-induced daughter cell displacement, is the only migration mechanism.

At each time step, tumor cells sense local chemical fields:

$$\begin{array}{c}\hfill a^o(t+\Delta t)=o(a^{(X,Y)}\left(t\right),t),a^d(t+\Delta t)=a^d\left(t\right)+d(a^{(X,Y)}\left(t\right),t)\Delta t.\end{array}$$

DNA damage evolves through:

$$\begin{array}{c}\hfill a^{dam}(t+\Delta t)=a^{dam}\left(t\right)+\left[d\left(a^{(X,Y)}\left(t\right),t\right)-p_r{a}^{dam}\left(t\right)\right]\Delta t,\end{array}$$

where $p_r$ is the DNA repair rate. Cell death occurs when $a^{dam}\left(t\right)>a^{death}\left(t\right)$. The death threshold follows:

$$\begin{array}{c}\hfill a_R^{death}=\theta a_S^{death},\theta \ge 1,\end{array}$$

where $\theta$ is the resistance factor ($\theta =T{h}_{multi}$ fixed for preexisting resistance, mutation-dependent otherwise).

Cells are classified according to oxygen level $a^o\left(t\right)$:

(i)

Normoxic ($a\in {\Lambda }_t^n$) if $a^o\left(t\right)>o_{hyp}$,

(ii)

Hypoxic ($a\in {\Lambda }_t^h$) if $o_{apop}<a^o\left(t\right)\le o_{hyp}$,

(iii)

Apoptotic (removed immediately from ${\Lambda }_t$) if $a^o\left(t\right)\le o_{apop}$, where $o_{apop}<o_{hyp}$ are critical thresholds.

Cells age only when normoxic:

$$\begin{array}{c}\hfill a^{age}(t+\Delta t)=\left\{\begin{array}{cc}{a}^{age}\left(t\right)+\Delta t\hfill & \mathrm{if}{a}^o\left(t\right)>o_{hyp},\hfill \\ a^{age}\left(t\right)\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

Normoxic cells divide when $a^{age}\left(t\right)\ge a^{mat}\left(t\right)$, where maturation time depends on division rate ${\alpha }_n$:

$$\begin{array}{c}\hfill a^{mat}\left(t\right)={\displaystyle \frac{log\left(2\right)}{{\alpha }_n}}.\end{array}$$

We express the local cell density, $F(x,t)$, in terms of the indicator function ${\chi }_{B_{R_c}}\left(x\right)$, which merely checks whether a point x lies within a circular region (a ball) of radius $R_c$, centered at the origin:

$$\begin{array}{c}\hfill F(x,t)=\sum _{\tilde{a}\in {\Lambda }_t}{\chi }_{B_{R_c}}\left(x-{\tilde{a}}^{(X,Y)}\left(t\right)\right).\end{array}$$

This measurement of density at the cell’s position, $F(a^{(X,Y)}\left(t\right),t)$, plays a crucial part in determining whether a cell can divide or not. If the density at the cell’s position is greater than some threshold $F_{max}$, then the cell will not divide at this time step. It keeps the same age it has now and must wait until the next time step before trying again. In 2D, when cells are disks that interact with one another through forces like those of the Lennard-Jones potential, they spontaneously organize into close-packed hexagonal patterns [25]. In the ideal close-packed arrangement, this pattern restricts each cell to roughly six immediate neighbors, so one would naively choose $F_{max}=6$ to allow for close-packing. Tumor cells are more densely packed than this. To allow for denser packing arrangements without permitting cells to overlap too much, we choose the cutoff $F_{max}=10$.

When the density is within acceptable levels, for example, if $F(a^{(X,Y)}\left(t\right),t)\le F_{max}$, the cell continues to divide. It divides into two daughter cells, which are denoted $a_1$ and $a_2$, and they each inherit new spatial coordinates according to the division process:

$$\begin{array}{cc}\hfill a_1^{(X,Y)}\left(t\right)& =a^{(X,Y)}\left(t\right),\hfill \end{array}$$

(Daughter 1)

$$\begin{array}{cc}\hfill a_2^{(X,Y)}\left(t\right)& =a^{(X,Y)}\left(t\right)+0.1(cos\left(2\pi \theta \right)\Delta x,sin\left(2\pi \theta \right)\Delta y),\hfill \end{array}$$

(Daughter 2)

where $\theta \sim \mathrm{Uniform}[0,1]$ and $\Delta x,\Delta y$ are spatial discretizations. If $a_2^{(X,Y)}\left(t\right)$ overlaps with existing cell center positions ${\tilde{a}}^{(X,Y)}\left(t\right)$, $\theta$ is resampled until a valid non-overlapping position is found. We propose an alternative daughter placement rule: one daughter inherits the mother’s position, while the other occupies a random vacant site in the Moore neighborhood. Division is blocked if no space is available, retaining the mother in the proliferative phase.

Upon division, daughter cells $a_1$ and $a_2$ inherit half of the mother cell a’s damage and drug load:

$$\begin{array}{c}\hfill a_i^{dam}\left(t\right)={\displaystyle \frac{1}{2}}{a}^{dam}\left(t\right),a_j^d\left(t\right)={\displaystyle \frac{1}{2}}{a}^d\left(t\right),i,j\in \{1,2\},\end{array}$$

and reset their age to 0. The oxygen levels in daughter cells depend on local oxygen concentrations. Daughter cells retain their mother’s death threshold, proliferation rate, and oxygen consumption rate.

We initialize the zeroth-generation cells with the state vector:

$$\begin{array}{c}\hfill a=\left\{\left(k\right),a^{(X,Y)}\left(t\right),o\left(a^{(X,Y)}\left(t\right),t\right),0,0,T_k,N_k,M_k\right\},\end{array}$$

with $M_k\sim \mathrm{Uniform}[7.776\times {10}^4,9.504\times {10}^4]\mathrm{s}$ days, $N_k\sim \mathrm{Uniform}[0,M_k]$, and $T_k=0.5$ for all $k\in \{1,\dots ,N_0\}$ in preexisting resistance scenario. For spontaneous mutation, we set $a_R^{death}=3a_S^{death}=1.5$.

Existing mutation models include:

(i)

Random mutation, where one of $N>1$ predefined phenotypes is selected with equal probability $p={\displaystyle \frac{1}{N}}$ during mutation [54];

(ii)

Linear mutation, where phenotypes evolve deterministically along a predefined trajectory of increasing resistance and aggressiveness. Although linear mutation avoids abrupt phenotypic jumps, it enforces a deterministic progression toward aggressive phenotypes, disregarding microenvironmental selection pressures.

To address these limitations, we introduce a neutral, non-directional mutation algorithm that prevents abrupt trait shifts and enables unbiased phenotypic evolution. Mutations follow a Poisson process with intensity $\mu >0$ per cell per time step:

$$\begin{array}{c}\hfill \mathbb{P}\left(\mathrm{mutation}\mathrm{in}[t,t+\Delta t]\right)=1-e^{-\mu \Delta t}\approx \mu \Delta t\end{array}$$

Every cell attribute $x_i$ changes with some random multiplier:

$$\begin{array}{c}\hfill x_{i,\mathrm{new}}=r_i\times x_{i,\mathrm{current}},r_i\sim \mathrm{Uniform}[0.7,1.7],\end{array}$$

with bounds ensuring biologically plausibility:

$$\begin{array}{c}\hfill 0.5x_{i,\mathrm{baseline}}\le x_{i,\mathrm{new}}\le 4x_{i,\mathrm{baseline}}.\end{array}$$

Note that mutations are not directly coupled with cell proliferation. Instead, they are the result of internal cell mechanisms and environmental stresses [62]. We simulate this using a Poisson process, modeling the memoryless property of mutation events. This serves to decouple mutation timing consistently, both analytically tractable and reproducible, regardless of a cell’s division history.

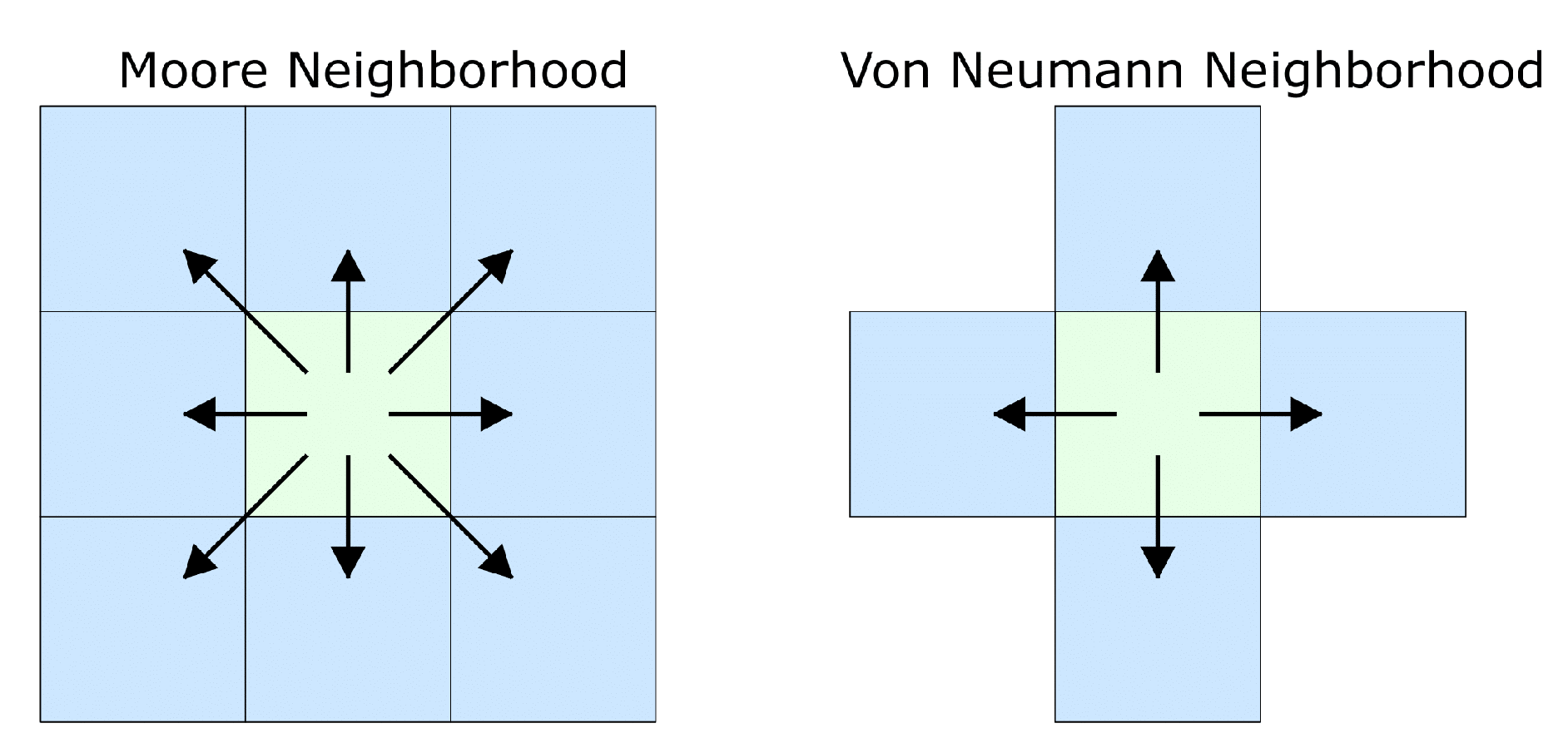
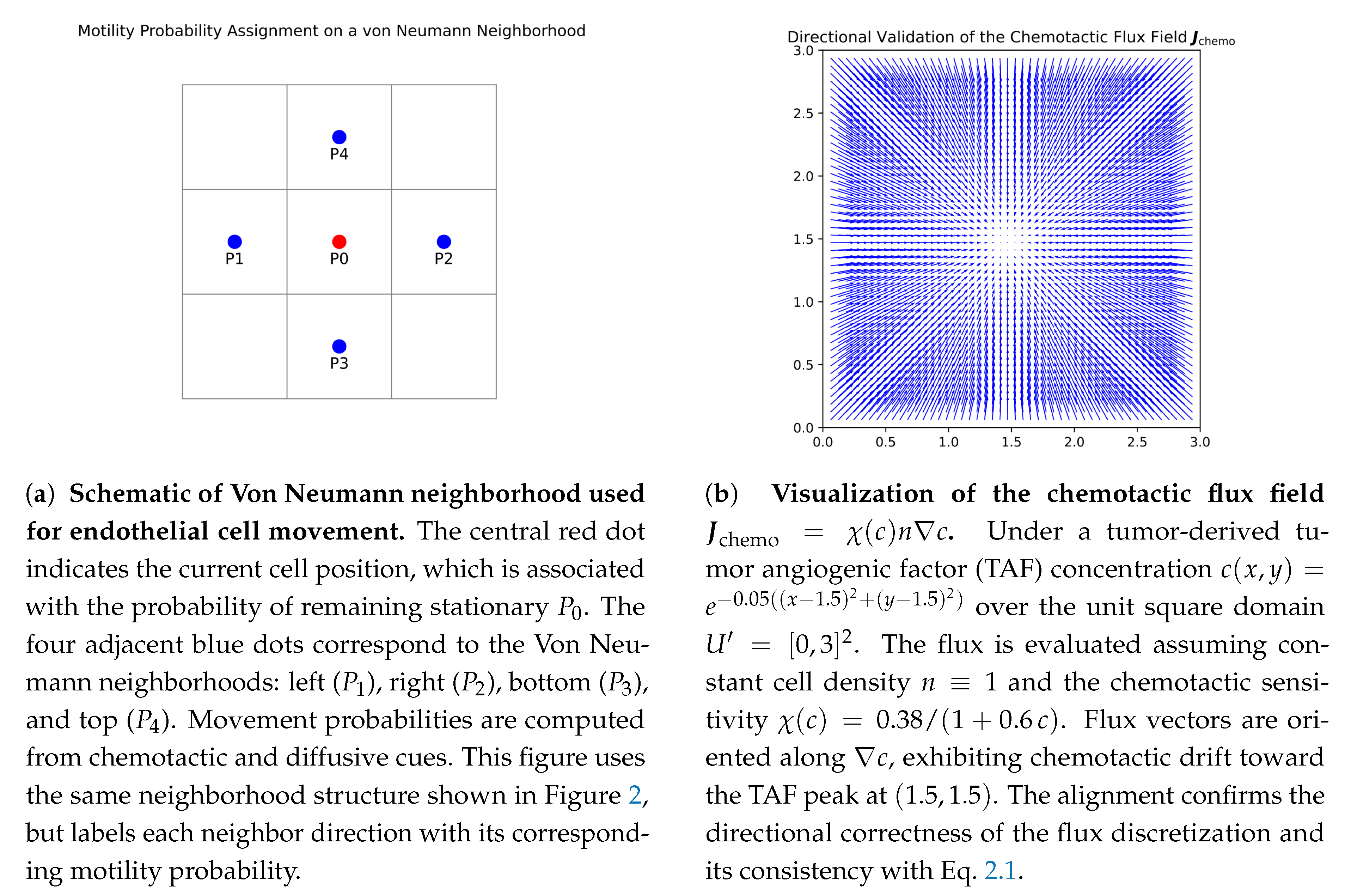
2.2.2. Angiogenesis Dynamics

Endothelial tip cells and vessel cells are modeled as discrete agents $b\in T_t$ and $v\in V_t$, respectively, where angiogenesis is driven by chemotaxis, branching, and anastomosis. The set $T_t$ denotes all tip cells at time t. Each tip cell b is characterized by:

$$\begin{array}{c}\hfill b=\{{\mathrm{id}}_b,b^{(X,Y)}\left(t\right),b^{age}\left(t\right)\},\end{array}$$

where $b^{(X,Y)}\left(t\right)$ denotes spatial coordinates and $b^{age}$ tracks time since last branching. The unique identifier ${\mathrm{id}}_b$ records lineage from branching events. The tip cell age evolves as:

$$\begin{array}{c}\hfill b^{age}(t+\Delta t)=b^{age}\left(t\right)+\Delta t.\end{array}$$

Tip cells migrate on a lattice via chemotaxis-diffusion dynamics, with movement probabilities $P_0$ (stationary), $P_1$ (left), $P_2$ (right), $P_3$ (down), and $P_4$ (up) derived from the TAF gradient (see Section 2.3):

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_0=\begin{array}{ccc}\hfill & 1-4{\displaystyle \frac{D_n\Delta t}{\Delta x^2}}\hfill & \hfill -{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i+1,j}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i+1,j}-c_{i,j})\\ \hfill & \hfill & \hfill +{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i-1,j}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i,j}-c_{i-1,j})\\ \hfill & \hfill & \hfill -{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i,j+1}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i,j+1}-c_{i,j})\\ \hfill & \hfill & \hfill +{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i,j-1}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i,j}-c_{i,j-1})\end{array}\hfill \\ P_1=\begin{array}{ccc}\hfill & {\displaystyle \frac{D_n\Delta t}{\Delta x^2}}\hfill & \hfill -{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i+1,j}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i+1,j}-c_{i,j})\end{array}\hfill \\ P_2=\begin{array}{ccc}\hfill & {\displaystyle \frac{D_n\Delta t}{\Delta x^2}}\hfill & \hfill +{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i-1,j}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i,j}-c_{i-1,j})\end{array}\hfill \\ P_3=\begin{array}{ccc}\hfill & {\displaystyle \frac{D_n\Delta t}{\Delta x^2}}\hfill & \hfill -{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i,j+1}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i,j+1}-c_{i,j})\end{array}\hfill \\ P_4=\begin{array}{ccc}\hfill & {\displaystyle \frac{D_n\Delta t}{\Delta x^2}}\hfill & \hfill +{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i,j-1}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i,j}-c_{i,j-1})\end{array}\hfill \end{array}\right.\end{array}$$

(2.9)

These probabilities govern directional movement on a discrete grid with Von Neumann neighborhoods, coupling discrete agents to continuum PDE dynamics.

We model tip branching as a Poisson process with intensity dependent on TAF concentration:

$$\begin{array}{c}\hfill {\lambda }_{br}(b,t)=c_{br}{\displaystyle \frac{c(b^{(X,Y)}\left(t\right),t)}{{\parallel c(·,t)\parallel }_{\infty }}}H(b^{age}\left(t\right)-\psi ),\end{array}$$

where $c_{br}=1$ denotes the baseline branching rate, ${\parallel c(·,t)\parallel }_{\infty }$ represents the maximum TAF concentration, and H is the Heaviside function ensuring branching occurs only after maturity time $\psi =0.5$ days. A branching event occurs if $b^{age}>\psi$, at least one Moore neighbor is vacant, and

$$\begin{array}{c}\hfill \mathrm{Uniform}[0,1]<1-e^{-{\lambda }_{br}(b,t)\Delta t}\approx {\lambda }_{br}(b,t)\Delta t.\end{array}$$

Upon branching, one daughter cell remains at the original location, while the other occupies a randomly selected vacant Moore neighbor, with both resetting their age to 0.

Anastomosis occurs when a migrating tip enters a site occupied by another tip or vessel agent. The invading tip ceases migration and branching, converting into a vessel segment and contributing to a closed-loop vascular network. This mechanism yields a dynamically evolving vascular network with loops and branches, consistent with physiological neovascularization.

Endothelial tip cell proliferation follows a fixed doubling time $\tau =18$ hours, with each division event elongating the vascular sprout by one cell length. The model tracks tip cell proliferation explicitly, disregarding non-tip endothelial cell proliferation since their contribution to sprout elongation is identical.

The motion of an individual endothelial cell at the capillary sprout tip governs the entire sprout’s movement because the remaining endothelial cells lining the sprout wall are contiguous [52]. Thus, the cumulative paths of tip cells define the angiogenic network:

$$\begin{array}{c}\hfill A_t=\bigcup _{b\in T_t}\left\{b^{(X,Y)}\left(s\right):0\le s\le t\right\}.\end{array}$$

Each lattice site intersecting $A_t$ becomes a vessel agent $v=\left\{v^{(X,Y)}\left(t\right)\right\}\in V_t$, modeled as a circle of radius $R_c$ inscribed in that site. These vessel agents act as sources of oxygen and drug delivery in the PDEs, coupling the PDE model and ABM. The current formulation, however, excludes explicit mechanical interactions (e.g., Lennard-Jones potentials) between endothelial and tumor cells. This simplification isolates chemotactic and proliferative angiogenic dynamics from mechanical effects. Although these interactions could be incorporated via established force models, their exclusion here facilitates a focused study of tumor evolution under microenvironmental regulations.

For clarity and reproducibility, we summarize the angiogenesis module per time step: each tip cell moves probabilistically via $P_i$ (derived from diffusion-chemotaxis dynamics), and anastomosis occurs if the destination site is occupied. Branching follows a Poisson process with probability ${\lambda }_{br}(b,t)\Delta t$. Newly migrated, fused, and branched cells are converted to vessel segments, and the tip cell list and vessel agent collection are updated accordingly.

2.2.3. Biological and Modeling Implications

Hybrid models that integrate agent-based dynamics with continuum reaction–diffusion processes are critical for studying tumor proliferation, angiogenesis, and response to treatment in dynamic TME. We list the biological significance:

(i)

Multiscale Coupling Validity: The result ensures that stochastic cell-scale events (division, migration, vessel remodeling) can be consistently embedded into tissue-scale PDE frameworks.

(ii)

Predictive Stability: The simulation results on hypoxic zones, nutrient distribution, and vascular remodeling demonstrate mathematical robustness rather than being numerical artifacts.

(iii)

Groundwork for Control and Optimization: Well-formulated mathematical model creates possibilities to study therapeutic methods such as chemotherapy scheduling and anti-angiogenic therapy through a rigorous mathematical oncology framework.

The mathematical basis ensures that the simulation results accurately represent stable model behaviors. This result confirms that hybrid PDE–ABM systems are mathematically sound and biologically credible for modeling complex tumor–vasculature interactions.

2.3. Discretization Framework

Building upon the mathematical framework established in Section 2.1 and Section 2.2, we now detail the computational methodology. This section rigorously analyzes discretization schemes, stability properties, and conservation laws essential for simulating coupled tumor-vascular dynamics.

To simulate the coupled tumor-vascular dynamics governed by (2.2)-(2.4), we implement a hybrid numerical strategy. Specifically, we solve the reaction-diffusion equations that govern the drug, oxygen, and TAF fields (Eqs. 2.2-2.4) using an ADI method, which offers unconditional stability and allows for longer time steps than explicit methods. The endothelial cell equation (Eq. 2.1) includes a nonlinear chemotactic flux, and we employ a forward Euler method with a CFL-constrained time step. This scheme reflects the model’s multiscale nature, enabling robust simulation of emergent vascular structures.

A regular Cartesian grid containing $(N_x+1)\times (N_y+1)=100\times 100$ nodes spans the $2.5\times {10}^{-5}{\mathrm{m}}^2$ tissue region with equal spacing $\Delta x=\Delta y=5.0\times {10}^{-5}$ m. The PDE solver operates with a fixed time step of $\Delta t=0.005$ (corresponding to $\Delta t=2.88\times {10}^2$ s). The ABM runs with a coarser time step $\Delta t^{\prime }=0.1$ ($\Delta t^{\prime }=5.76\times {10}^3$s), and is synchronized with the PDE solver at each $\Delta t^{\prime }$ interval. This time-step difference follows multiscale modeling principles to ensure accurate interaction between continuous fields and discrete agents.

We discretize the endothelial cell equation.

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial n}{\partial t}}=D_n\Delta n-\nabla ·\left(\chi \left(c\right)n\nabla c\right),\end{array}$$

using central differences:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial n}{\partial t}}& \approx {\displaystyle \frac{n_{i,j}^{k+1}-n_{i,j}^k}{\Delta t}},\hfill \\ \hfill D_n\Delta n& \approx D_n{\displaystyle \frac{n_{i-1,j}^k+n_{i+1,j}^k+n_{i,j-1}^k+n_{i,j+1}^k-4n_{i,j}^k}{\Delta x^2}}.\hfill \end{array}$$

The nonlinear chemotaxis term $-\nabla ·\left(\chi \right(c)n\nabla c)$ is discretized using a probabilistic finite difference method inspired by the HDC framework [52,63,64]. This method encodes the directional bias of cell movement as a movement probability within a Von Neumann neighborhood, which is consistent with biological chemotaxis behavior.

The chemotactic term is discretized as follows:

$$\begin{array}{cc}\hfill \nabla ·(\chi n\nabla c)& \approx {\displaystyle \frac{F_{i+\frac{1}{2},j}-F_{i-\frac{1}{2},j}}{\Delta x}}+{\displaystyle \frac{G_{i,j+\frac{1}{2}}-G_{i,j-\frac{1}{2}}}{\Delta x}},\hfill \end{array}$$

where the chemotactic fluxes are defined by

$$\begin{array}{cc}\hfill F_{i+{\displaystyle \frac{1}{2}},j}& \chi (c_{i+{\displaystyle \frac{1}{2}},j})n_{i+{\displaystyle \frac{1}{2}},j}{\displaystyle \frac{c_{i+1,j}-c_{i,j}}{\Delta x}}\hfill \\ \hfill F_{i-{\displaystyle \frac{1}{2}},j}& \chi (c_{i-{\displaystyle \frac{1}{2}},j})n_{i-{\displaystyle \frac{1}{2}},j}{\displaystyle \frac{c_{i,j}-c_{i-1,j}}{\Delta x}}\hfill \\ \hfill G_{i,j+{\displaystyle \frac{1}{2}}}& \chi (c_{i,j+{\displaystyle \frac{1}{2}}})n_{i,j+{\displaystyle \frac{1}{2}}}{\displaystyle \frac{c_{i,j+1}-c_{i,j}}{\Delta x}}\hfill \\ \hfill G_{i,j-{\displaystyle \frac{1}{2}}}& \chi (c_{i,j-{\displaystyle \frac{1}{2}}})n_{i,j-{\displaystyle \frac{1}{2}}}{\displaystyle \frac{c_{i,j}-c_{i,j-1}}{\Delta x}}\hfill \end{array}$$

with half-index values approximated by linear interpolation, for example:

$$\begin{array}{c}\hfill \chi (c_{i+{\displaystyle \frac{1}{2}},j})={\displaystyle \frac{\chi (c_{i+1,j})+\chi (c_{i,j})}{2}},n_{i+{\displaystyle \frac{1}{2}},j}={\displaystyle \frac{n_{i+1,j}+n_{i,j}}{2}}.\end{array}$$

The same approach applies to calculating the values of $\chi (c_{i-{\displaystyle \frac{1}{2}},j}),\chi (c_{i,j+{\displaystyle \frac{1}{2}}}),\chi (c_{i,j-{\displaystyle \frac{1}{2}}})$ and $n_{i-{\displaystyle \frac{1}{2}},j},n_{i,j+{\displaystyle \frac{1}{2}}},n_{i,j-{\displaystyle \frac{1}{2}}}$ in the remaining directions. Substituting these expressions, we get the following discrete scheme:

$$\begin{array}{c}\hfill n_{i,j}^{k+1}=n_{i,j}^k+\Delta t\left({\displaystyle \frac{D_n}{\Delta x^2}}{\delta }^2{n}_{i,j}^k-{\displaystyle \frac{1}{\Delta x}}(\delta F_{i,j}+\delta G_{i,j})\right)\end{array}$$

(2.10)

To interpret this update probabilistically, we recast the scheme as a weighted sum of contributions from local Von Neumann neighborhoods:

$$\begin{array}{c}\hfill n_{i,j}^{k+1}=n_{i,j}^k{P}_0+n_{i+1,j}^k{P}_1+n_{i-1,j}^k{P}_2+n_{i,j+1}^k{P}_3+n_{i,j-1}^k{P}_4,\end{array}$$

(2.11)

where $P_0$ is proportional to the probability of remaining stationary, and $P_1$ through $P_4$ correspond to movement into the four Von Neumann neighboring grid points.

The movement probabilities are derived as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_0=\begin{array}{ccc}\hfill & 1-4{\displaystyle \frac{D_n\Delta t}{\Delta x^2}}\hfill & \hfill -{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i+1,j}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i+1,j}-c_{i,j})\\ \hfill & \hfill & \hfill +{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i-1,j}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i,j}-c_{i-1,j})\\ \hfill & \hfill & \hfill -{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i,j+1}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i,j+1}-c_{i,j})\\ \hfill & \hfill & \hfill +{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i,j-1}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i,j}-c_{i,j-1})\end{array}\hfill \\ P_1=\begin{array}{ccc}\hfill & {\displaystyle \frac{D_n\Delta t}{\Delta x^2}}\hfill & \hfill -{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i+1,j}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i+1,j}-c_{i,j})\end{array}\hfill \\ P_2=\begin{array}{ccc}\hfill & {\displaystyle \frac{D_n\Delta t}{\Delta x^2}}\hfill & \hfill +{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i-1,j}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i,j}-c_{i-1,j})\end{array}\hfill \\ P_3=\begin{array}{ccc}\hfill & {\displaystyle \frac{D_n\Delta t}{\Delta x^2}}\hfill & \hfill -{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i,j+1}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i,j+1}-c_{i,j})\end{array}\hfill \\ P_4=\begin{array}{ccc}\hfill & {\displaystyle \frac{D_n\Delta t}{\Delta x^2}}\hfill & \hfill +{\displaystyle \frac{\Delta t{\chi }_0}{4\Delta x^2}}\left({\displaystyle \frac{1}{1+\alpha c_{i,j-1}}}+{\displaystyle \frac{1}{1+\alpha c_{i,j}}}\right)(c_{i,j}-c_{i,j-1})\end{array}\hfill \end{array}\right.\end{array}$$

(2.12)

Here, the chemotactic sensitivity is modeled as $\chi \left(c\right)={\displaystyle \frac{{\chi }_0}{1+\alpha c}}$. These probabilistic coefficients $P_i$ account for both diffusion (symmetric contributions) and chemotaxis (biased contributions via centered differences), driving net movement toward higher TAF concentrations.

To implement movement based on these coefficients, we interpret them as discrete probabilities. These coefficients define the likelihood of each possible movement direction, enabling a stochastic update of cell positions at each time step based on local chemotactic cues and diffusion. Specifically, we compute five movement probabilities: $P_0$ for remaining stationary and $P_1$–– $P_4$ for movement to the Von Neumann neighbors (left, right, down, up, respectively; see Figure 2a). Non-negative values for probabilities are achieved by setting negative values to zero before normalizing all values so that ${\sum }_{i=0}^4{P}_i=1$. The uniform distribution $\mathrm{Uniform}[0,1]$ provides random numbers which determine movement direction through comparison with the cumulative distribution of $P_i$. Specifically, the cell moves in the direction corresponding to the interval $R_j$ containing the sampled value:[52,63,64]

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill R_0& =[0,P_0],\hfill \\ \hfill R_j& =\left(\sum _{i=0}^{j-1}{P}_i,\sum _{i=0}^j{P}_i\right]\mathrm{for}j=1,\dots ,4.\hfill \end{array}\end{array}$$

(2.13)

This representation ensures the partitioning of the unit interval by cumulative probabilities.

To validate the directional behavior of the chemotactic flux field ${\mathbf{J}}_{\mathrm{chemo}}=\chi \left(c\right)n\nabla c$ in Eq. 2.1, we visualize the flux field under a representative tumor-derived TAF distribution $c(x,y)=e^{-0.05({(x-1.5)}^2+{(y-1.5)}^2)}$. As illustrated in Figure 2b, the flux vectors align with the gradient of the TAF concentration field $c(x,y)$, consistently pointing toward the chemotactic source. This spatial alignment confirms the correct implementation of the discretized flux term and demonstrates directional consistency under the assumed tumor-induced configuration of the TAF field.

To efficiently solve the diffusion-dominated PDEs that govern other quantities (e.g., Equations (2.2)–(2.4)), we employ the ADI method [65]. It is unconditionally stable for linear diffusion and computationally efficient on large spatial grids.

At each time step, we solve two sequential tridiagonal systems: first implicit in the x-direction and explicit in y, then swapped. We handle reaction terms explicitly. To remain consistent with the chemotaxis update in Equation (2.1), we adopt a uniform time step of $\Delta t=0.01$; however, larger time steps such as $\Delta t=0.1$ can also be used for efficient long-term simulations without stability constraints from diffusion terms.

Assume a reaction-diffusion equation of the form

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial u}{\partial t}}=D\Delta u+f(u,x,y,t),\end{array}$$

Then the ADI method is implemented as follows:

$$\begin{array}{cc}\hfill \left(1-{\displaystyle \frac{D\Delta t}{2\Delta x^2}}{\delta }_x^2\right)U^{k+1/2}& =\left(1+{\displaystyle \frac{D\Delta t}{2\Delta y^2}}{\delta }_y^2\right)U^k+{\displaystyle \frac{\Delta t}{2}}f\left(U^k\right),\hfill \\ \hfill \left(1-{\displaystyle \frac{D\Delta t}{2\Delta y^2}}{\delta }_y^2\right)U^{k+1}& =\left(1+{\displaystyle \frac{D\Delta t}{2\Delta x^2}}{\delta }_x^2\right)U^{k+1/2}+{\displaystyle \frac{\Delta t}{2}}f\left(U^k\right),\hfill \end{array}$$

where $U^{k+1/2}\approx u((k+1/2)\Delta t)$ is the intermediate solution at time $(k+1/2)\Delta t$. ${\delta }_x^2$ and ${\delta }_y^2$ are the second-order central difference operators in the x and y directions, respectively. This hybrid explicit-implicit approach strikes a balance between stability and computational efficiency for complex reaction-diffusion dynamics.

3. Results

3.1. Parameterization and Non-dimensionalization

To establish biologically relevant scales while ensuring numerical stability, we non-dimensionalize the model using characteristic length $L=5\times {10}^{-3}$ m, time $\tau =L^2/D=5.76\times {10}^4$ s with a representative diffusion rate D, cell density $n_0=6.4\times {10}^{13}\mathrm{cells}/{\mathrm{m}}^3$[54], and concentration $c_0=1.0\times {10}^{-7}\mathrm{mol}/{\mathrm{m}}^3$ [52]:

$$\begin{array}{c}\hfill \tilde{n}={\displaystyle \frac{n}{n_0}},\tilde{c}={\displaystyle \frac{c}{c_0}},\tilde{t}={\displaystyle \frac{t}{\tau }}.\end{array}$$

The non-dimensionalization framework facilitates direct comparison of scaled dynamics across systems and yields the dimensionless parameters summarized in Table 4. These parameters integrate experimental measurements, established literature values, and calibrated constants tailored for tumor-vascular modeling. The numerical stability of the model required key parameter calibrations such as TAF production rate ($\eta$) and oxygen uptake rate (${\rho }_o$). The model uses a dimensionless time unit of $t=0.5$ to represent $2.88\times {10}^4$ s to match biological observations [56,57,58,59,60,61]. Furthermore, we calibrated the oxygen supply ($S_o$) to model the saturation of growth under hypoxic conditions, which acts as the primary control factor for angiogenesis and tumor growth behavior.

3.2. Agent-based Simulation Design

We implement an agent-based simulation framework that couples PDEs for oxygen, TAF, and drug diffusion with agent-based rules for tumor and vessel dynamics. This hybrid approach links spatial concentration fields to stochastic cellular behaviors. Endothelial motility responds to TAF gradients via probabilistic direction sampling. Tumor and vessel cells evolve through mutation, branching, anastomosis, and apoptosis. Although simplified to 2D for computational tractability, the design preserves spatially heterogeneous behaviors characteristic of 3D systems [54], enabling vascular network emergence.

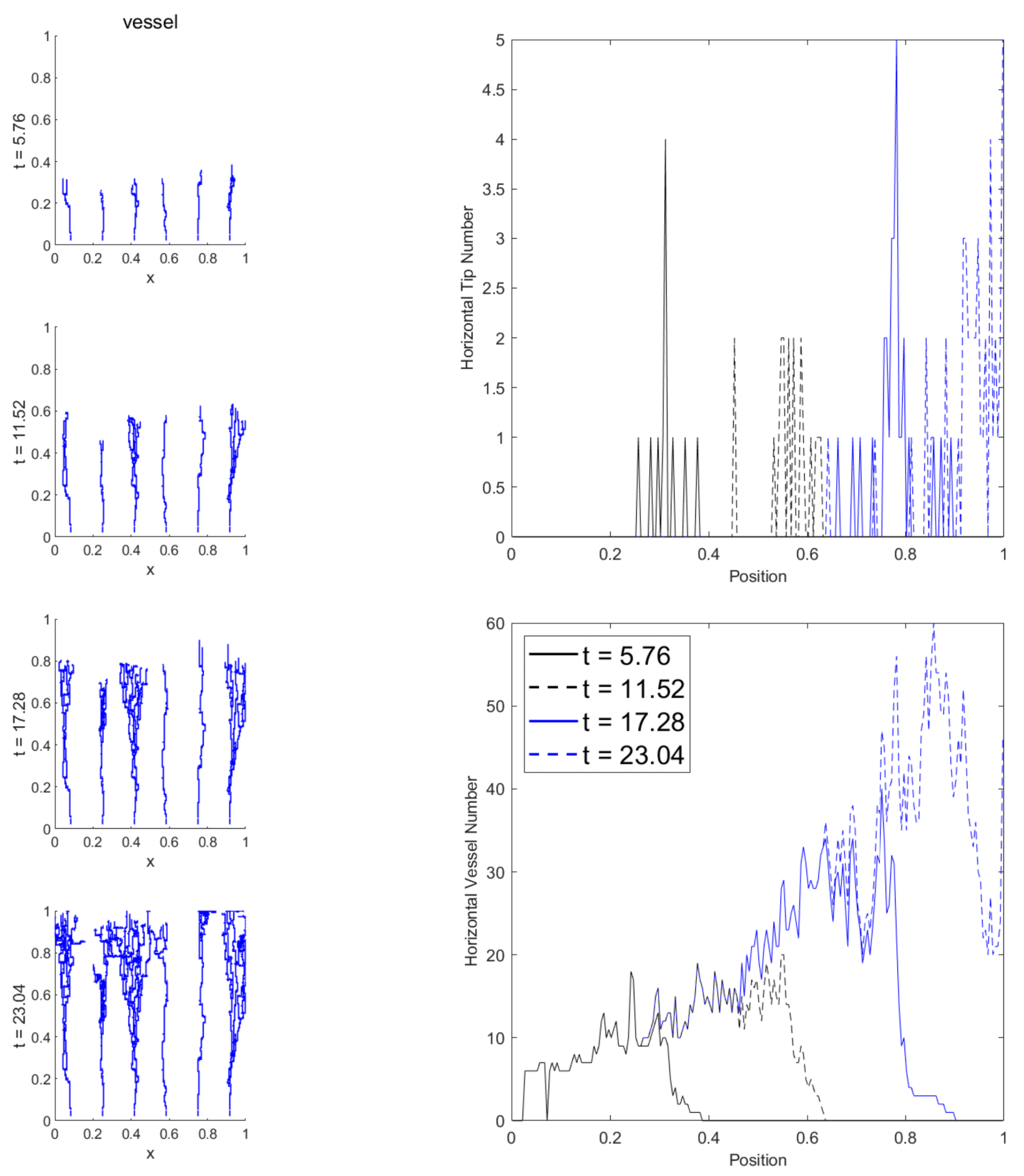
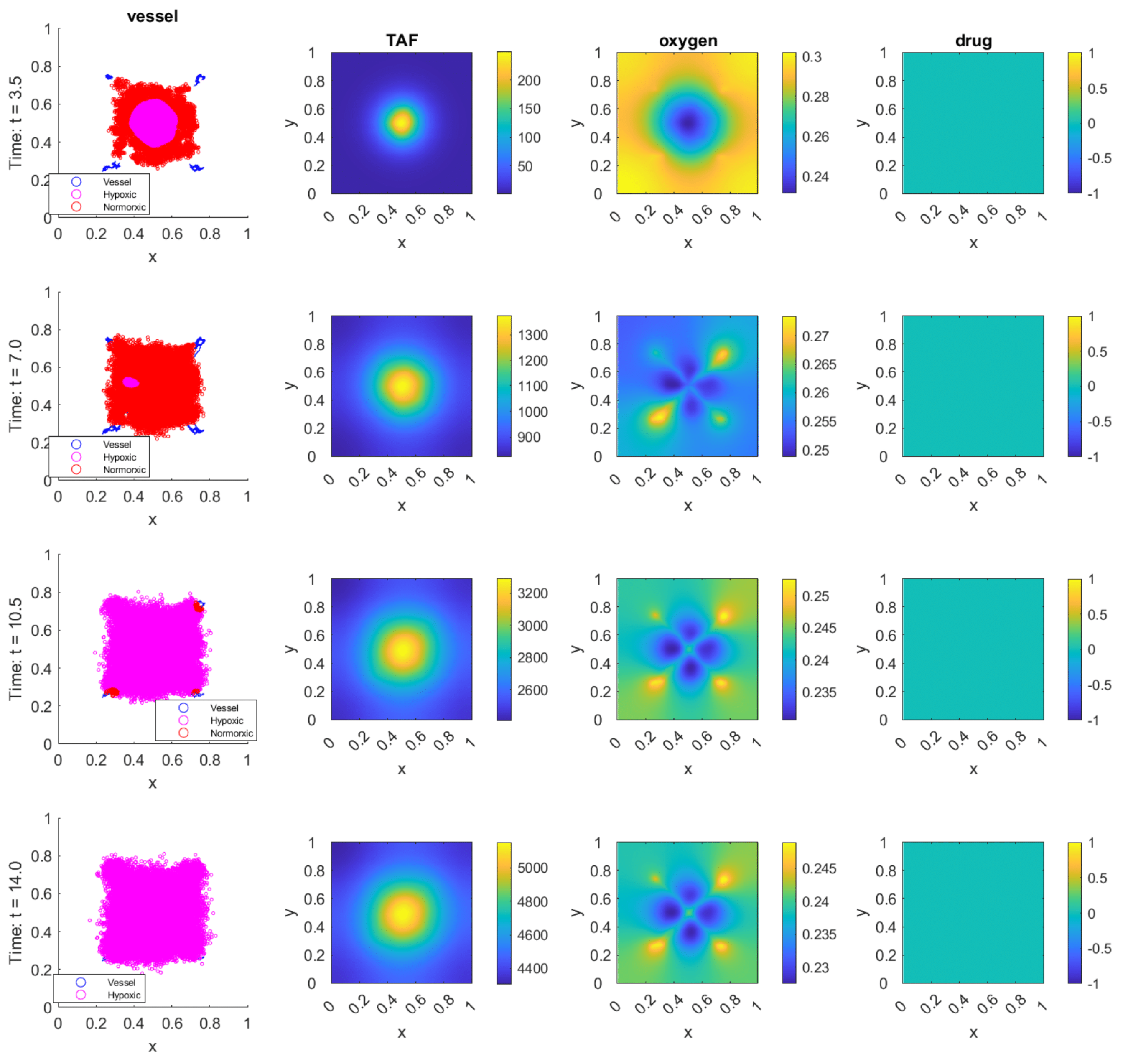
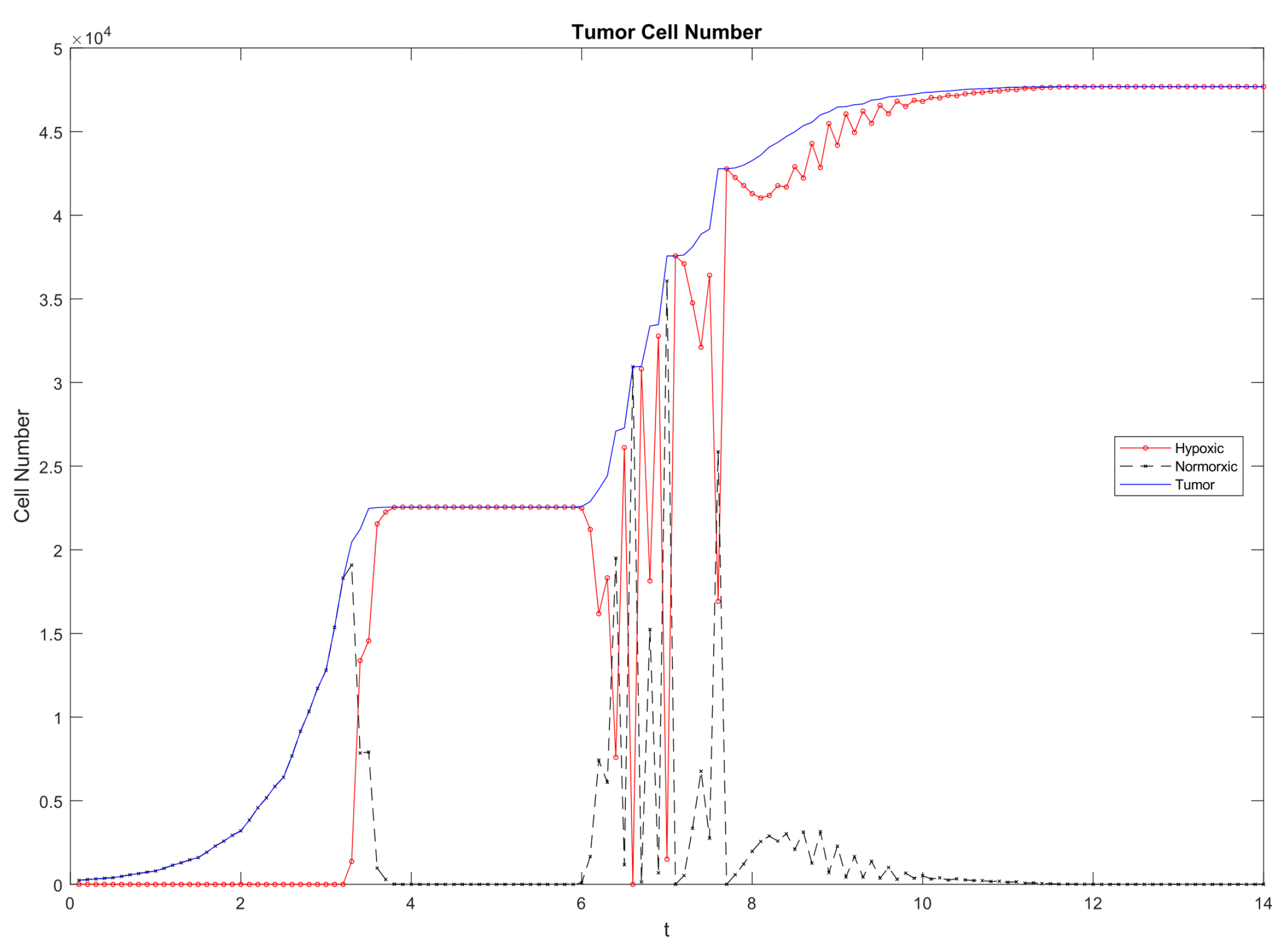
3.3. Emergent Vascularization and Tumor Growth

We simulate emergent vascularization and tumor-independent angiogenesis by prescribing a linear TAF field $c(x,y,0)=5y$, consistent with previous models [66]. This initialization induces vessel formation on a time scale of approximately $1.22\times {10}^6$ s, in agreement with experimental data [34]. Simulations reveal non-perfusing and nonfunctional self-loops ($>95\%$ of anastomosis events) [67] and traveling wave propagation of vessel fronts (Figure 3), matching theoretical predictions [34,35,66]. The brush border pattern forms near the tumor source at $y=1$, where the intensification of branching occurs along with increased tip density [52]. The oxygen supply rate $S_o$ controls the long-term growth behavior because low supply levels ($S_o=3$) stop growth, yet high levels ($S_o=5$) lead to unlimited growth; while a moderate level ($S_o=3.5$) maintains a stable, hypoxia-dominated equilibrium state. This oxygen-limited steady state limits future tumor growth and influences drug response and resistance trajectories.

Figure 4 and Figure 5 show the tumor-vascular feedback loop: exponential expansion induces core hypoxia (Figure 4), hypoxia-driven TAF secretion triggers angiogenesis, and oxygen consumption fluctuations continue until supply and demand are balanced. This vascular template lays the foundation for therapeutic research.

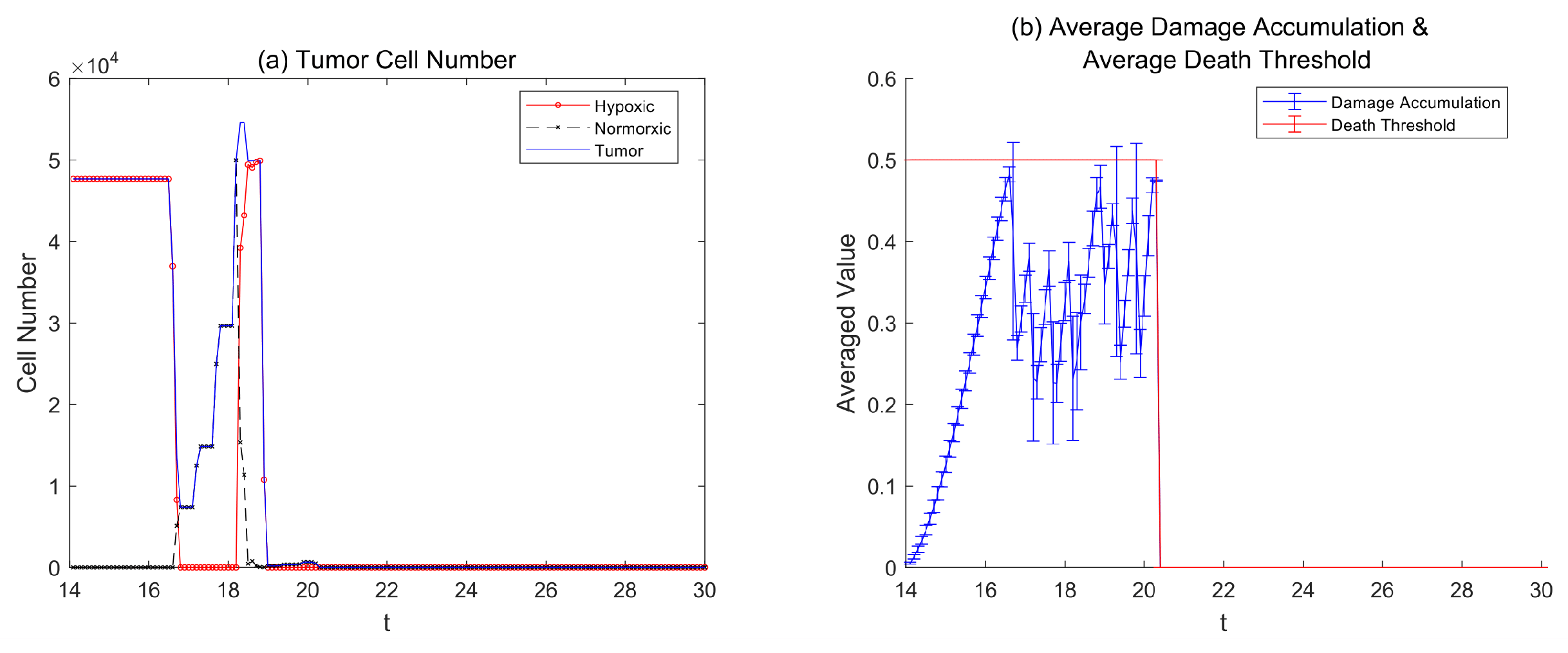
3.4. Therapy Without Resistance

We simulate treatment in the absence of resistance to establish a baseline therapeutic response. Under continuous drug infusion ($S_d=0.05$), tumors are fully eradicated (Figure 6). Apoptosis transiently releases space, restoring normoxia and enabling regrowth. As cell divisions resume, damage is diluted via symmetric partitioning between daughter cells, reducing intracellular drug burden by half. This interplay between damage accumulation, cell death, and proliferative dilution gives rise to oscillatory dynamics in average damage levels. These cycles reflect a balance between drug-induced cytotoxicity and damage dilution through synchronized mitosis.

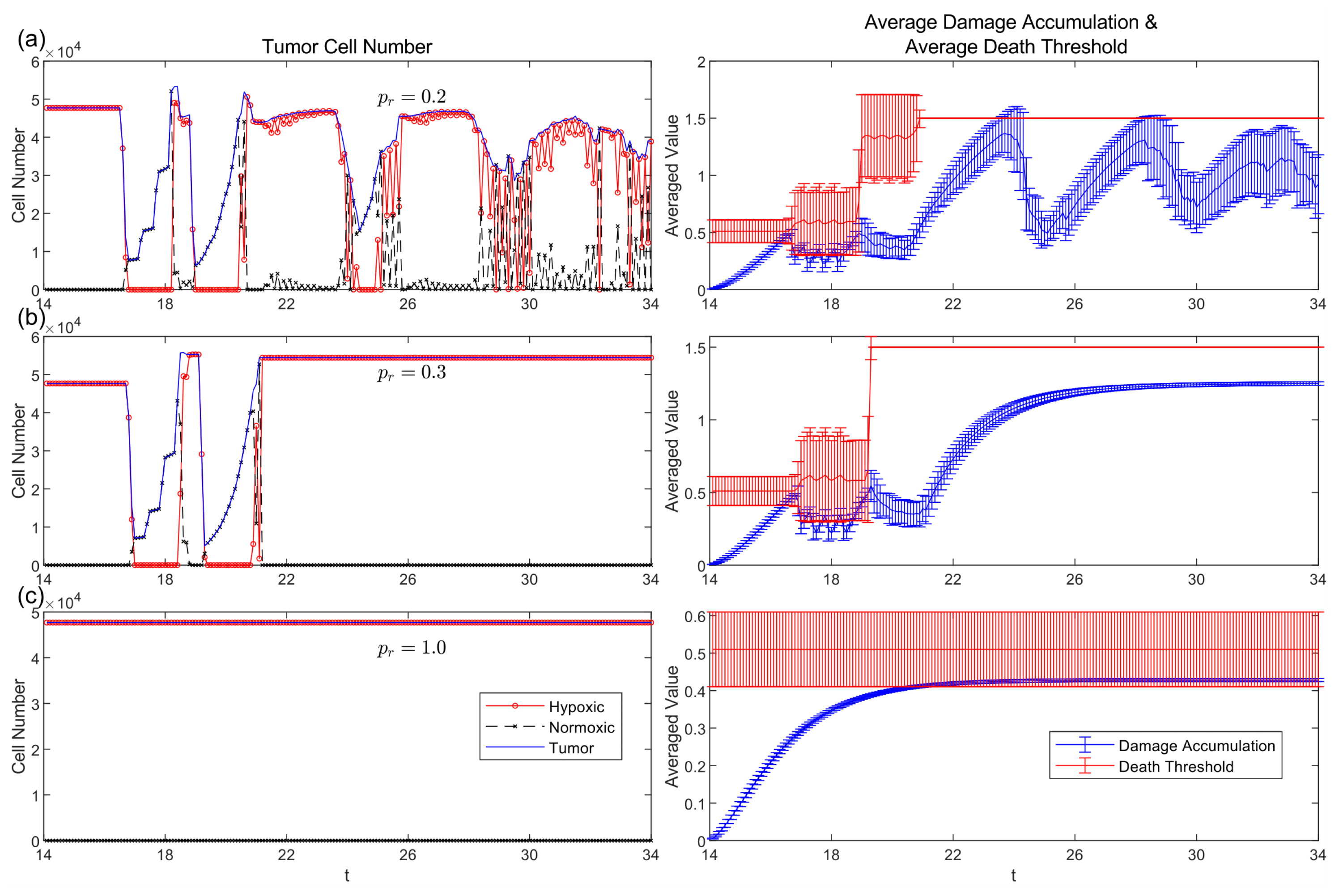
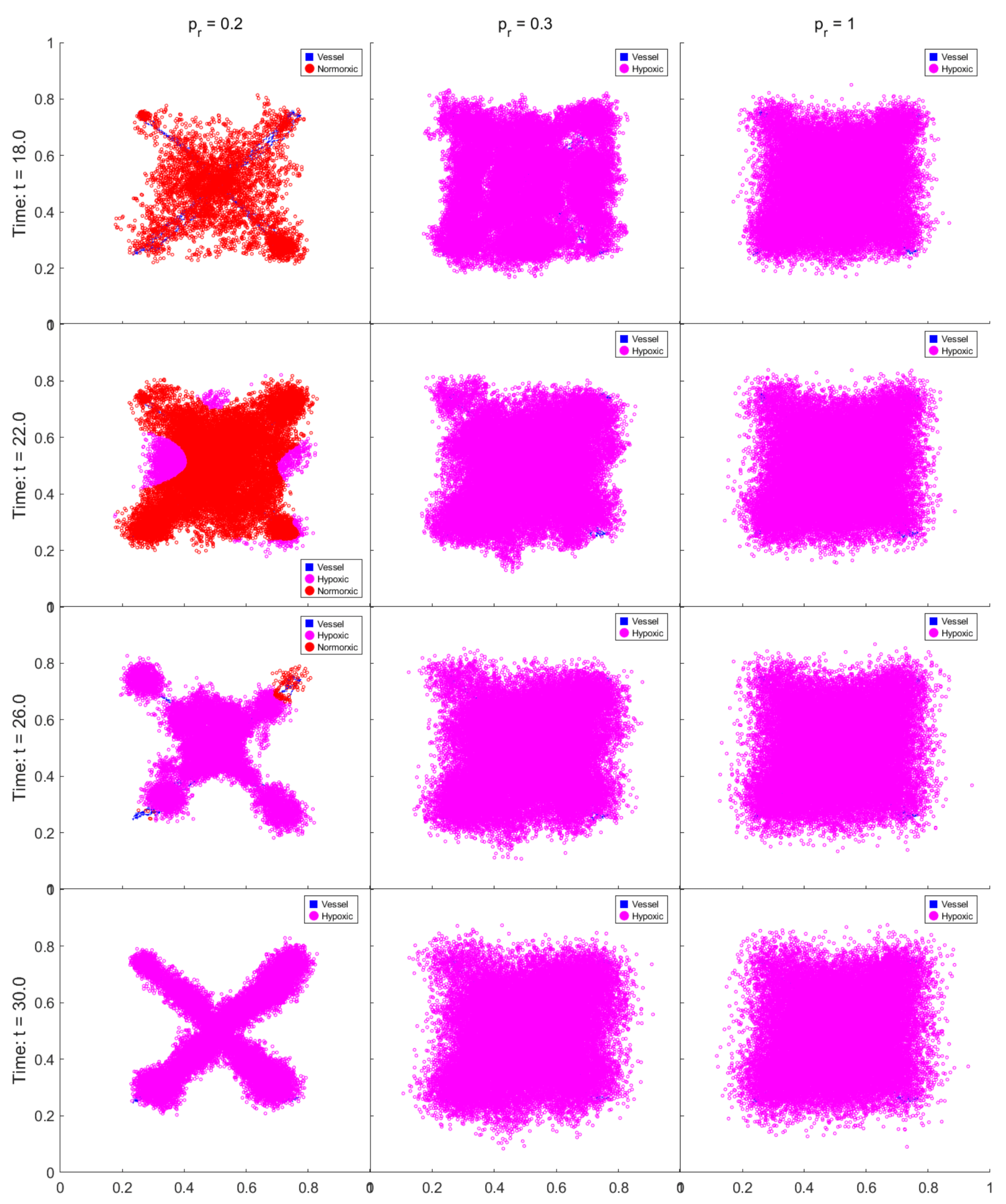
3.5. Passive and Active Resistance Mechanisms

Introducing $1\%$ preexisting resistance fundamentally alters treatment outcomes. As shown in Figure 7, resistant clones—defined by elevated death thresholds—eventually dominate under lower clearance conditions ($p_r=0.2,0.3$). At low clearance rates ($p_r=0.2$), sensitive cells are eliminated, while resistant cells persist through oscillatory apoptosis-division dynamics driven by damage accumulation and proliferative dilution. Intermediate clearance ($p_r=0.3$) accelerates resistance without oscillation. At maximal clearance ($p_r=1$), damage is fully repaired at each time step, rendering therapy ineffective and preserving both sensitive and resistant populations.

Spatially (Figure 8), resistant cells preferentially localize near vasculature under low clearance ($p_r=0.2$), exploiting oxygen-rich sanctuaries where proliferation-enabled dilution offsets linear drug damage accumulation. As clearance increases, spatial bias diminishes and tumor distributions become more homogeneous, consistent with reduced therapy efficacy.

Spontaneous mutations complement preexisting resistance by enabling adaptive evolution and conferring active resistance during treatment. Empirical studies estimate stem cell mutation rates per division to lie between ${10}^{-6}$–${10}^{-2}$[68,69]. We model mutation events as a Poisson process with intensities $\mu ={10}^{-1},{10}^{-2},{10}^{-3},{10}^{-4}$ per time step $\Delta t^{\prime }=0.1$, assuming all mutation initiate at therapy onset. Tumor dynamics exhibit strong sensitivity to the mutation rate $\mu$. For $\mu \ge {10}^{-3}$, resistance emerges progressively, sustaining tumor burden via cycles of apoptosis and regrowth (Figure 9). In contrast, $\mu ={10}^{-4}$ results in eventual eradication.

Temporal profiles of oxygen uptake and proliferation (Figure 10) reveal a self-reinforcing feedback loop: rapidly proliferating cells generate more mutations, while highly resistant mutants preferentially survive. This bidirectional coupling accelerates the dominance of fast-cycling, drug-resistant phenotypes. The resulting co-selection produces coupled evolutionary trajectories, as evidenced by the spatial co-localization of high proliferation and resistance traits in Figure 11 and Figure 12. Notably, oxygen consumption undergoes neutral drift under weak selection, in contrast to proliferation and resistance, which are strongly co-selected.

3.6. Comparative Strategy Evolution

We assess the clinical implications of our mechanistic model through the evaluation of seven iso-dosed regimens, including both pulsed and continuous protocols with different resistance scenarios. Table 5 presents a summary of treatment plans and their results at various combinations of resistance mechanism and mutation rate. The continuous administration of high-dose therapy ($S_d=10$) achieves universal success, while pulsed and low-dose regimens do not work even when mutation rates are moderate ($\mu \ge 0.001$). Three fundamental factors combine to determine treatment success: resistance level, mutation rate, and dosing protocol. The success of intermediate dose regimens depends on low mutation rates and the absence of preexisting resistance, which highlights the need for treatment approaches based on evolutionary dynamics.

4. Biological Implications and Future Directions

Our model conceptualizes tumor resistance as an emergent phenotype driven by mutation, drug exposure, and microenvironmental heterogeneity. This framework matches clinically observed dynamics that occur in non-small cell lung cancer (NSCLC) with epidermal growth factor receptor (EGFR)–mutant. The T790M mutation, when co-occurring with activating mutations L858R or exon 19 deletions, confers both therapeutic resistance and enhanced oncogenicity [70,71]. Paradoxically, experimental studies demonstrate that T790M creates a growth disadvantage [55], implying synergistic tumor-promoting activities arise from non-T790M genetic alterations that enable aggressive phenotypic shifts. Our simulations successful demonstrate this contradiction through two mechanisms: (i) higher mutation rates confer survival advantages, which reducs treatment efficacy (Figure 9), and (ii) proliferation and resistance traits become mutually reinforced leading to simultaneous emergence and the spatial co-localization of highly proliferative, resistant cells (Figure 10, Figure 11 and Figure 12).

Although molecular mechanisms remain abstracted, these emergent dynamics directly inform clinical translation strategies. We treat T790M not as a discrete genetic driver, but as a survival-enhanced phenotype with therapy-altered dynamics. This abstraction captures divergent outcomes (regression or progression) without detailed EGFR pharmacodynamics, supporting the hypothesis that tumor fate depends equally on spatial ecology and genetics.

To transform this phenotypic abstraction into precision oncology tools, we propose coupling intracellular signaling models with our hybrid PDE–ABM framework. The simulation of resistance mutations, including EGFR T790M in NSCLC, phosphoinositide 3-kinase (PI3K)/protein kinase B (AKT) in breast cancer, and mitogen-activated protein kinase (MAPK) in melanoma, can be performed through modular ordinary differential equations (ODEs) or logic-based networks that control cellular decisions. The modular system governs cellular decisions about division, apoptosis, and repair based on extracellular oxygen levels and drug concentrations, which connect genotypic information to phenotypic characteristics within our spatial ecology framework.

Operationalizing this integration requires scalable computational methods. Tools like MaBoSS, BioNetGen, or PySB could embed molecular systems biology within agent-based platforms, simulating mutation-specific dynamics (e.g., constitutively active EGFR or phosphatase and tensin homolog (PTEN) loss) alongside spatially varying therapy. This would enable predictions of resistance, synergy, and adaptive responses.

Collectively, these extensions would advance multiscale simulations of combined therapies and resistance evolution, providing mechanistic insights into combination strategies, evolutionary steering, and sequential regimens tailored to pathway-specific vulnerabilities. Key extensions include: (i) in silico validation of anti-angiogenic/cytotoxic combinations supporting [72,73]; (ii) vascular intravasation/extravasation models capturing dissemination [74,75]; (iii) incorporation of metabolic reprogramming [76,77], TME remodeling [78,79], and stemness enhancement [80,81] to model collaborative resistance; and (iv) vascular permeability modulation via $S_d\left(t\right)\to P_v{S}_d\left(t\right)$ addressing current extravasation assumptions and reflecting clinical variability in vascular permeability [82,83,84,85,86,87,88,89]. While these extensions enhance predictive capacity, our current framework already delivers critical insights into resistance evolution, as consolidated below.

5. Discussion and Conclusions

The core understanding from these findings reveals that the HDC model proves that hypoxia-vascularization-drug gradient interactions control resistant subclone development as well as their spatial patterns throughout chemotherapy. Hypoxia-driven angiogenesis restores oxygen levels while simultaneously producing uneven drug distribution patterns that establish evolutionary "safe zones" where resistant phenotypes thrive and expand to become dominant. Therapeutic resistance emerges through dynamic connections between vascular plasticity and microenvironmental selection mechanisms.

These mechanistic understanding extends prior spatial cancer evolution models [24,41,52,90], yet advance the field by explicitly coupling angiogenic remodeling with resistance evolution within a unified framework. Unlike compartmental or continuum models that neglect stochastic cellular events or handle static vasculature, our model reproduces tip cell sprouting, anastomosis, and hypoxic cores, validating biological relevance.

Basic models fail to properly describe the intricate relationship between vascularization and resistance. The positive relationship between vessel density and drug penetration exists, although densely packed tissue with high interstitial pressure reduces perfusion according to Jain et al. [91]. Resistance still emerges in well-perfused tumor regions through random mutations, yet the slower emergence rate makes DNA repair kinetics and mutation rates essential for in vivo calibration.

The study demonstrates both nuanced findings along recognized limitations about tumor analysis and modeling. 2D domain analysis and simulation oversimplify 3D tumor complexity, even though it retains computational tractability, yet the angiogenesis module abstracts key molecular pathways like VEGF signaling and endothelial-pericyte interactions. The model improves its prediction power through additional biochemical details, but this advancement requires more parameters, together with increased computational resources. Additionally, single-drug assumptions with uniform pharmacodynamics contrast with clinical combination therapies.

The model delivers usable principles that extend across different scientific fields despite its operational constraints. Mathematical biologists receive a flexible and rigorous framework that connects stochastic and deterministic processes. Cancer researchers obtain a mechanistic understanding of why anti-angiogenic treatments may fail to achieve long-term resistance prevention while showing initial drug delivery enhancements. Medical practitioners, along with pharmaceutical developers, must develop time-based drug protocols that focus on particular microenvironmental areas to achieve enduring therapeutic success. Public discussion gains value through this model because it disproves basic misconceptions that link more blood vessels to improved outcomes.

By unifying previously isolated modeling approaches (e.g., discrete evolutionary modeling, dynamic vascular remodeling), we reveal emergent behaviors like angiogenesis’s paradoxical dual role in both therapeutic success and failure. This foundational framework prioritizes mechanistic plausibility over data-fitting, with credibility established through validation against: (i) tumor progression from avascular to vascular stages (Figure 4 and Figure 5), (ii) TAF-driven angiogenesis wave propagation (see Figure 3 and [34,35,66]), and (iii) established principles of drug heterogeneity in pharmacokinetics and pharmacodynamics [92,93,94].

Advancing this framework into patient-specific predictive tools requires: (i) genomics-informed calibration of mutation rates ($\mu$) based on EGFR-mutant NSCLC sequencing data [95], (ii) validation of vascular architectures using dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) [96,97,98], and (iii) integration of pharmacokinetic heterogeneity via $P_v{S}_d$ modeling [82,83,84,85,86,87,88,89].

Ultimately, this work establishes a biologically grounded mathematical framework that interconnects angiogenesis, hypoxia, drug distribution, and resistance evolution. By elucidating how vascular adaptation may inadvertently foster treatment failure, we emphasize the critical need for spatially informed therapies—repositioning hybrid modeling from mechanistic explanatory tools to predictive engines guiding cancer discoveries and precision oncology envisioned in this Special Issue.