1. Introduction
Natural stones are used in jewellery, as souvenirs, for decoration and are thought to have metaphysical and healing properties. They are favourite items of collectors and have high market values. Also natural stones with larger dimensions are used as kitchen countertops (e.g. granite, marble, quartzite, soapstone, slate, and limestone) and their density is an important parameter in determining their durability, mechanical properties and therefore market price.[
1,
2,
3] Most natural stones are not single crystals but rather an aggregate of smaller crystal particles (i.e. grains) and are therefore polycrystalline.[
4] Some natural stones are mixtures of grains of different crystalline materials (e.g. granite composed of feldspar, quartz, mica, and amphiboles).[
5,
6] Also some natural stones are not even crystalline but rather amorphous (e.g. obsidian, opal, and moldavite) so lack a regular arrangement of atoms in a lattice.[
7,
8,
9] For this reason their structural determination by means of crystallography (i.e. X-ray, neutron diffraction) is sometimes challenging which is the typical method used in mineralogy to determine the density of single crystals.[
10,
11,
12,
13] It is therefore useful to report the densities and morphology of some common natural stones found in museums and souvenir shops as a means of their identification for collectors and merchants of these stones. Furthermore, it is useful to explore the various methods and techniques to measure the density of natural stones to quantify which method has the highest accuracy-to-cost ratio.
The concept of density of a material is of high importance in many fields and is therefore thought early on in education. However, to quantify the density of materials is taught at university level courses in chemistry, physics, engineering, materials science and many other disciplines. Also, the density of materials is assessed in many commercial settings to access the quality of a material. For example, denser materials have a larger degree of chemical bonding between the atoms of the material an therefore are expected to have enhanced mechanical properties. It also indicates that there is smaller number of defects in the structure which can considerably affect chemical and mechanical properties of the material. Lastly, for allotropes it is a measure of the void space in a material which is an important parameter in materials design.
The density of material is defined by the mass of the material divided by the volume of the material. The mass is easier to measure using a scale, however, there has been considerable efforts to obtain an accurate measurement of the volume of an object. The volume of a stone can be accurately measured if the stone has a geometric shape (e.g. sphere, cube) but in the case of stones with an arbitrary shape, the volume has to be measured either by submerging the stone into a liquid and measuring the volume of the displaced liquid or by measuring pressure changes in a gas (e.g. Helium), when a known volume of it is introduced inside a closed chamber that contains the stone, with the use of Boyle’s law (i.e. P1V1 = P2V2). In this study we use water as the fluid to measure the volume 27 natural stones. Water is non-toxic compared to other liquids such as mercury, which has also been used for volume measurements of solids via the displacement method.
There are also digital/optical methods of calculating the volume of a 3D object such as 3D photogrammetry, 3D laser scanning and micro-CT. 3D photogrammetry uses photographs of the object at various angles to reconstruct the shape of the object. [
14] This technique has a higher cost (~
$3000) and it has limitations on the size of the object that can be scanned and its transparency. It uses software such as Meshlab (which calculates the volume of the object by summing triangular pyramids that are fitted within the volume of the object). This technique has accuracies of estimating the volume of about 95%.
A more recent technique, 3D laser scanning is generally more accurate than 3D photogrammetry because it uses a laser beam to calculate the distance between a laser beam source and the surface of the object. [
15] These distance measurements generate a point cloud that then is used to calculate the volume, which can be as accurate as 98%. The instruments for this technique can cost (
$500-
$3000).
The best and most expensive technique to scan the volume of stones is micro-CT which uses X-ray images (radiographs) and rotates the object through 360 degrees and then uses the 2D images to digitally reconstruct a 3D volume. This technique has the advantage of being able to reveal the internal and external structure of an object so it will take in account if there is porosity within the micrometre range within the stone [
16] and has accuracy of the volume to about 99%. This technique is rather expensive with some instruments sold in the range of
$200,000 to over
$1,000,000 and is therefore only used in specialised labs.
In this paper we evaluate various inexpensive yet accurate empirical methods to evaluate the density of natural stones. This is particularly important for educators that would like to assess this physical parameter using inexpensive equipment in activities that enhance the experiential learning. Also, collector can use our method to measure the density of various natural stones in combination with their morphological examination. In addition, we show how to calibrate scales, and how to calculate the accuracy and precision of these techniques. Finally, we propose a design of a new chemistry glassware that can determine the density of natural stones in a non-destructive way using the displacement of fluids in a thin, transparent tube with well-defined geometric parameters.
2. Materials and Methods
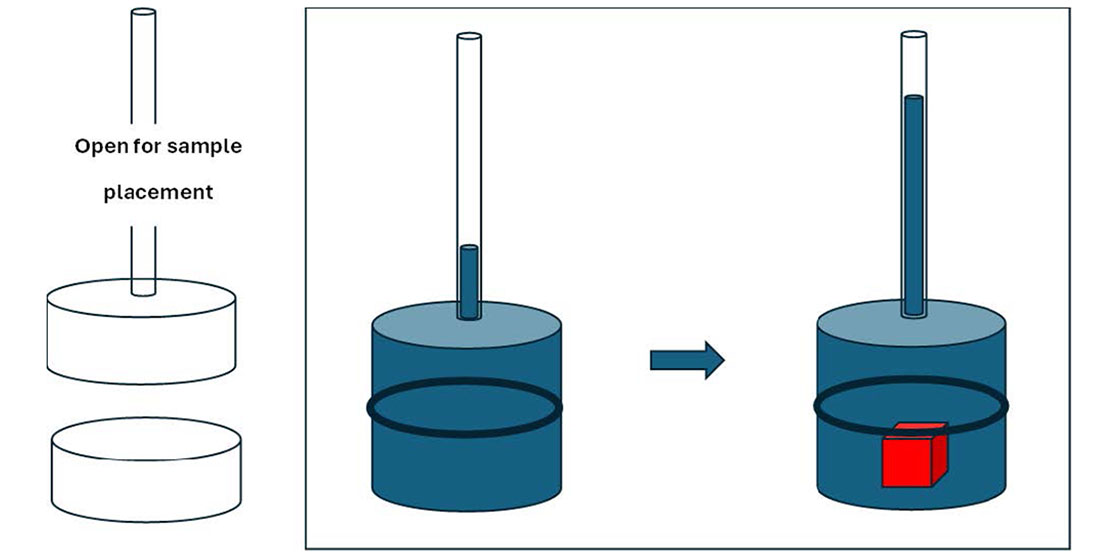
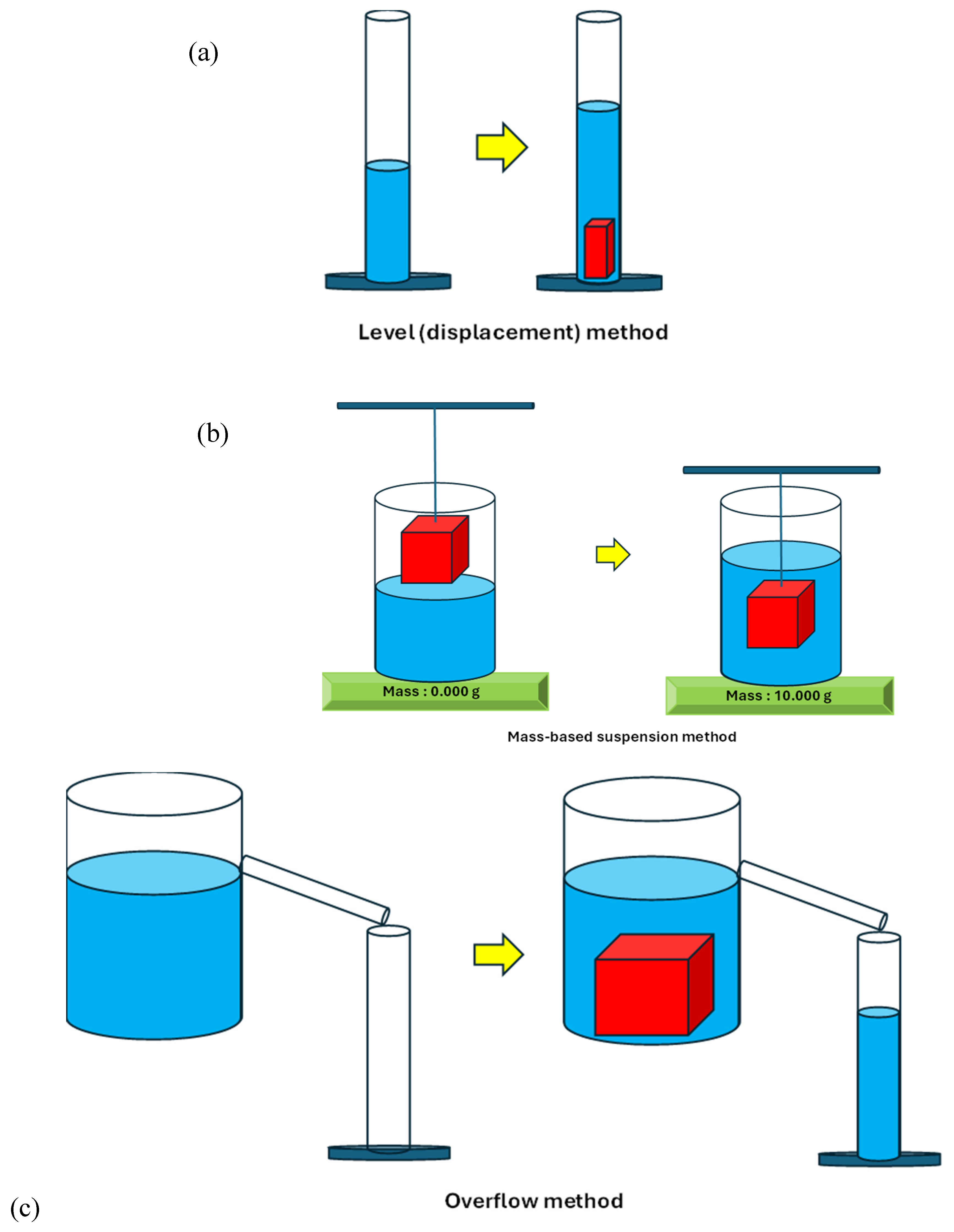
Typically, there are three methods that the density of a material can be measured in the chemistry, physics, engineering and materials science classroom. The first method is the level method (i.e. displacement) method. The second method is the overflow method, and the third method is the mass-based suspension method that employs Archimedes’ principle to measure the volume of a stone. These three methods are depicted in the following simplified schematic.
Archimedes’ principle states that the buoyant force of a partially or fully submerged object in a fluid is given by
Where
is the buoyant force,
is the density of the liquid,
is the acceleration due to gravity and
is the volume of the submerged object or the volume of the displaced fluid. This force is exerted onto the scale due to Newton’s third law (action-reaction law) when the stone is submerged into water (see
Scheme 1(c) ).
Scheme 1.
Simplified schematic of the (a) level (displacement) method, (b) overflow method and (c) mass-based suspension method used to determine the density of natural stones used in this study.
Scheme 1.
Simplified schematic of the (a) level (displacement) method, (b) overflow method and (c) mass-based suspension method used to determine the density of natural stones used in this study.
So the mass measured on the scale is
Combination of equations 1 and 2 yields that the mass measured on the scale is
And since the fluid we used was water at 20 °C which has a density of 0.9982 g cm-
3 the volume of the stone is given by,
Lastly the density of the stone is calculated by measuring the mass of the stone (
) on the scale and dividing by the volume of the stone (
) calculated using Archimedes principle, given by
For these methods we have used an inexpensive jewellery scale (~
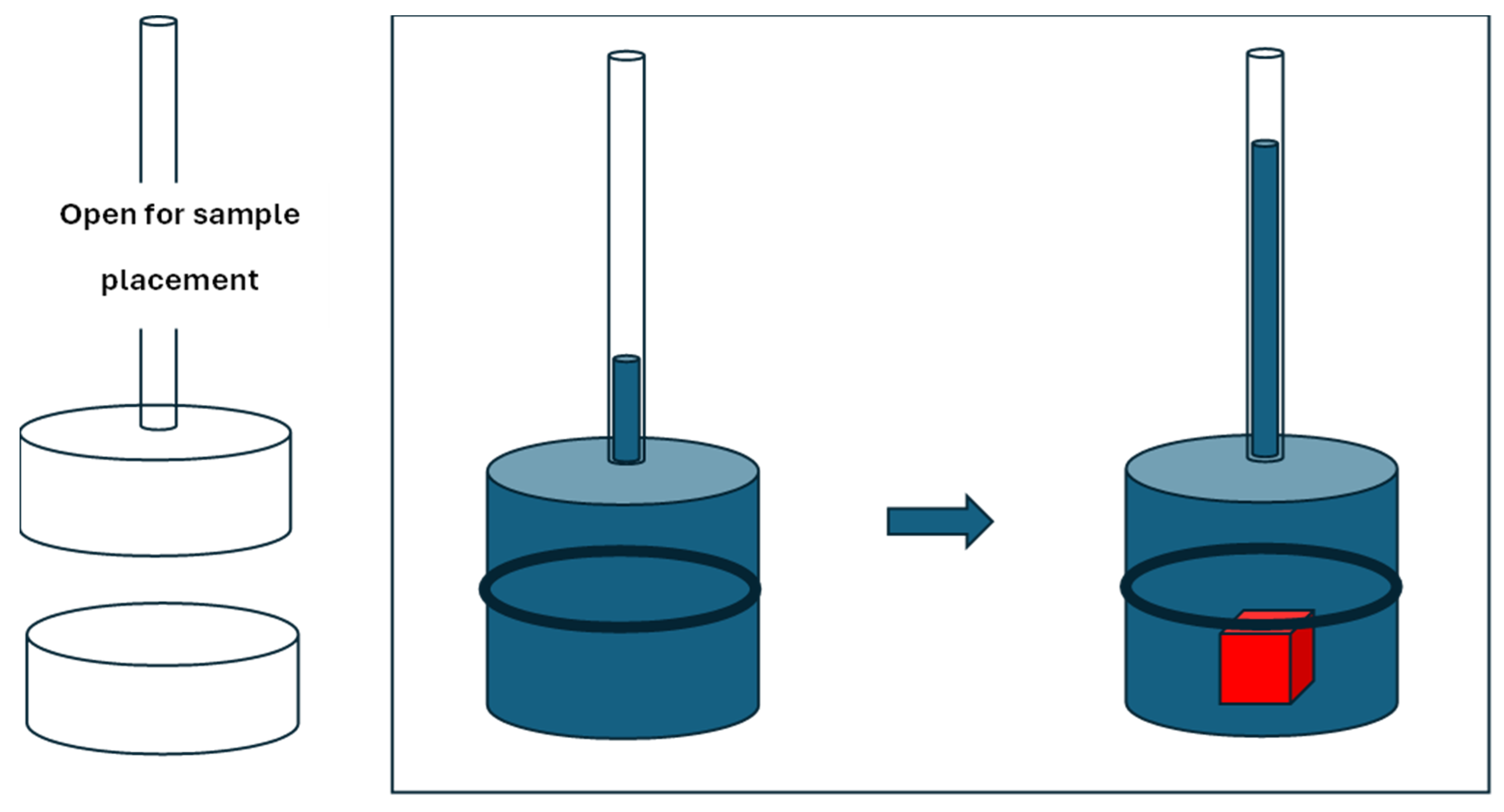
$15-20) which measures a maximum mass of 50.000g with a precision of 0.001g (see
Figure 1) according to the manufacturer. The accuracy of the scale was assessed with a calibration set chrome plating scale weights set that included the following weights: 1g, 2g, 5g, 10g, 20g and 50g, shown in
Figure 1(a). The experimental setup for the mass-based suspension method using the jewellery scale is shown in
Figure 1(b). In this, the natural stone is suspended from a horizontal beam using a 0.20 mm in diameter metal wire, measured with a digital metal calliper with an accuracy of 0.01 mm. The length of the wire that is submerged in the liquid is about 5 cm, which results in an error of the volume of the submerged stone of 1.57×10
-3 cm
3. This corresponds to an error in the determination of the volume of the natural stone using Archimedes' principle that is of the order of the accuracy (1×10
-3 g) of the jewellery scale. Using this method, the natural stone is preserved as there is no requirement to drill a hole to suspend the stone by other means. This method can also be used to support stones of any shape and a large range of masses, depending on the range of the scale making the method very versatile. During the measurement, the natural stone is fully submerged in deionised water, without touching the bottom or the side walls of a 120 ml capacity polypropylene (PP) sample vial, without a lid. The use of a plastic rather than a glass beaker is to reduce the mass exerted on the jewellery scale, which has a measuring range of 1-50 g, which enhances the mass range of natural stone specimens that can be measured. Also, the size of the sample vial is such that it fits exactly on to the measuring platform of the jewellery scale. With this experimental setup we were able to measure the density of natural stones that had volumes smaller than 10 cm
3, which is the typical size of natural stones commercially available.
In order to check the accuracy of the mass-based suspension method using a 3 d.p. jewellery scale we have also measured the densities with 4 d.p. accuracy using a closed system and an analytical balance by Fisher (analytical series FAS224/E). For these measurements we have used deionised water 18.2 MΩ·cm (Elga – Pure lab chorus). The pressure inside the lab was about 759 Torr, measured with an analogue barometer. The pH of deionised water was roughly 7 within the time of the experiment (10-15 sec) and the temperature of water, once equilibrated with the lab temperature, was 21.9 °C. The rate of evaporation of water inside the lab was slightly higher than under ambient conditions was of the order of 0.0005 g⋅min-1 and the measured mass using the suspension method was determined within 10-15 sec as the use of the metal wire made the adjustment of height and lateral position of the stone very fast minimising therefore the loss of water mass due to evaporation. Additionally, we used a closed system to minimise the effect of water evaporation. The measurements of densities using a 4 d.p. analytical balance within a lab environment were only slightly affected by the negative pressure (-0.1 Torr). The agreement between the method developed in this manuscript using the jewellery scale and the more accurate analytical balance measurements were found to be in good agreement for the 27 natural stones, with an average percent error of 0.3% error, between the two methods. Also, the uncertainty of the density measurement with the mass-based suspension method due to the error in the determination of the volume with a jewellery balance is of the order of 0.1% error, which was assessed with a copper density reference cube (d = 2.54 cm and 99.95% purity).
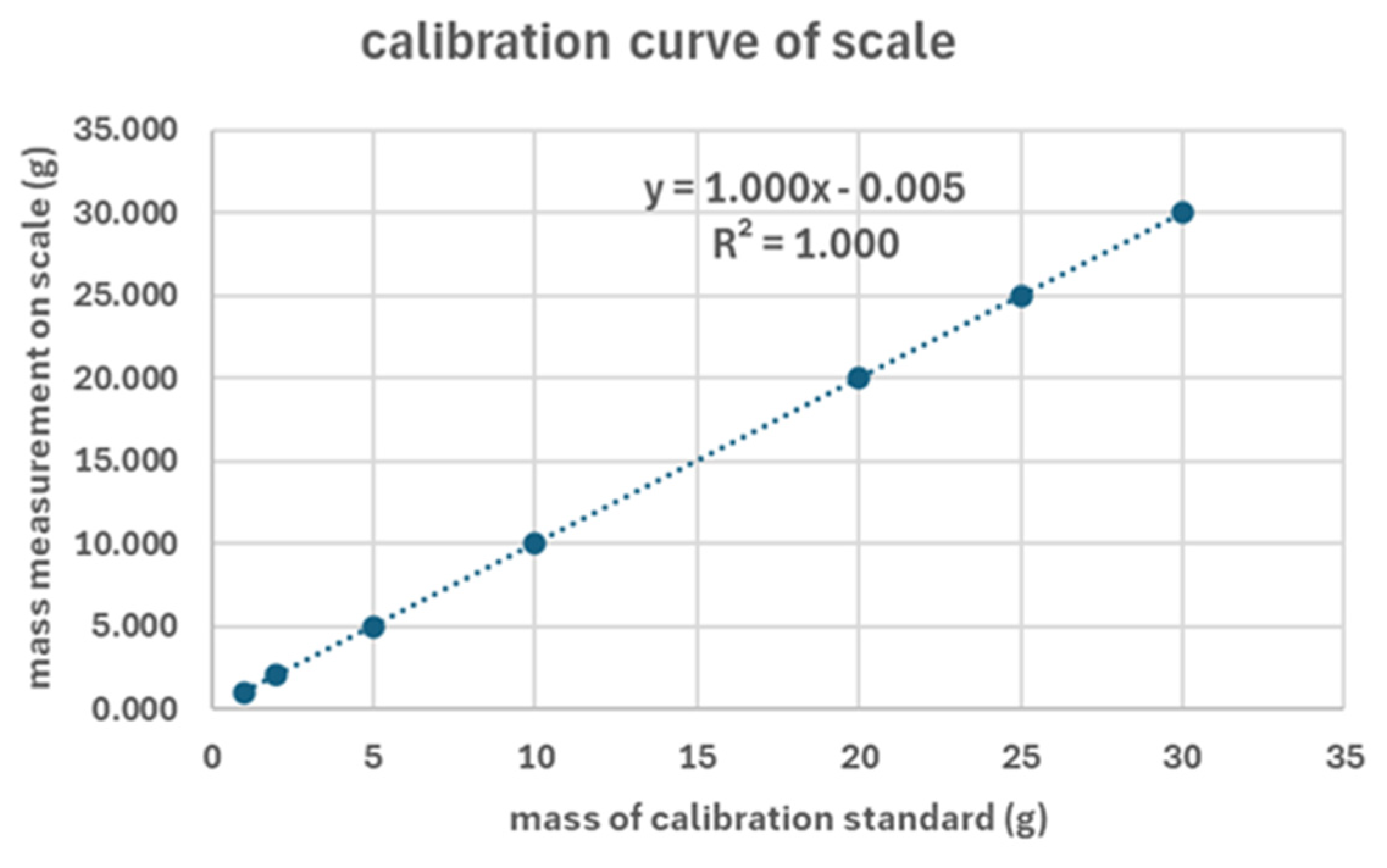
The systematic error of the jewellery balance was corrected with the use of a linear calibration curve using standard weights within the measured range (0-30g) of the balance (Axel Taube, Dr. Ellen Hage, Dr. Julian Haller, Niclas Ludolph, White paper: Use of laboratory balances in the pharmaceutical industry, October 2021). The calibration curve of the jewellery scale (see
Figure 2) showed that the correlation between chrome-platted standard masses and the measured mass on the scale is perfectly linear (R
2 = 1.000) within the range of 1 – 30 g. Also, the equation of the trendline from linear regression suggests that this correlation between theoretical and empirical mass is linear with a small correction factor of 0.005g which must be added to the measured masses on the jewellery scale to take into account the systematic error of the jewellery balance. Additionally, the maximum standard deviation observed in the mass measurements is 0.002 g with an average value of the standard deviation of all measurements of 0.0004 g. This suggests that this scale is accurate to 0.001 g ± 0.0004 g once the correction factor of 0.005 g has been added to every individual mass measurement. On this scale the calibration of the mass was initially done at 20 g and 40 g using the standard weights that were supplied with the scale. However, to test the accuracy of this calibration method we have used chrome plating scale weights from a different supplier to obtain the calibration curve data which are presented in
Table 1.
The dimensions of these natural stones were such that the overflow method was not found to be an accurate method for the determination of densities of natural stones with volumes less than 10 cm
3. We find that the accuracy of the overflow method can be improved by measurement of the mass of the overflown water on the jewellery scale rather than the volume of the overflown water in a graduated cylinder as shown in
Scheme 1(b). The overflow method was tested with two commercially available overflow vessels shown in
Figure 3. One was a 500 ml capacity borosilicate displacement vessel and the second a 500 ml tin displacement vessel, and the volume of the stone was measured by measuring the mass of the displaced water collected in a beaker placed on the jewellery scale. One advantage of using the overflow vessel was that we could measure the volume of larger natural stones, whereas with the graduated cylinder only small in dimensions specimens could be measured. In general, the use of the displacement vessel gave more accurate readings for the volume, especially when the mass of the displaced water was measured. One drawback of the borosilicate displacement vessel was that the side tube inner diameter was 4.8 mm and therefore some displaced water would remain in the glass tube. We have therefore used the tin displacement vessel with a side tube inner diameter of 11.5 mm to report volume of stones when the stones had volumes that exceeded 10 cm
3. However, these results are not reported due to errors introduced using the overflow method due to the small volume ( < 10 cm
-3) of the natural stone specimens examined in this study.
The third method we used to measure the density of these natural stones was the level (i.e. displacement) method (
Scheme 1(a)). In this method the density is determined by changes in the height of the water level inside a graduated cylinder made from borosilicate glass. In this cylinder water forms a meniscus at the surface, but we have also examined the use of graduated cylinders by Clementoni which are made from a plastic in which water has a flat surface due to the absence of strong adhesive forces of water with the cylinder walls. This makes the measurement of the height of water more accurate and precise as there is an absence of a meniscus, the height of which may be difficult to observe. For consistency among the measured volumes in the level method the volume of most natural stones was measured using a 100 ± 1 ml graduated cylinder (here we are able to measure volumes to within 0.5 ml by observation of the meniscus that is in between two lines) in which deionised water was poured and the bottom of the meniscus of water was observed. We have also used a 250 ± 2 ml graduated cylinder for the volume measurement of one stone with larger dimensions. However, this method was not found very accurate in the determination of the volume of natural stones, as there was a great uncertainty in the measurement of the water level in the graduated cylinder. So this method was only used for one natural stone that had larger dimensions and therefore could not be measured with the jewellery scale.
The natural stones for which we determined the density is given in
Table 2 along with their common name, their dominant chemical formula and the correct mineral name.
3. Results and Discussion
In general, the measurement of mass is more accurate than the measurement of volume. Almost every lab nowadays has 4 decimal place (d.p.) analytical balance with can measure masses to within ±0.0001 g. There are also some labs that use ±0.000001 g microbalance which achieve even higher accuracy. This is the reason that for example pipettors used in chemistry, biology and biomedical labs are calibrated using a mass-based method, where the mass of water is measured rather than the volume and then using the equation V = m / ρ (where V is the volume , ρ the density of water and m the mass of water) the accuracy of the pipettor can be estimated and also calibrated in some pipettors.[
14]
The measurement of volume by displacement of a fluid in graduated cylinder is less accurate as a 100 ml graduated cylinder (i.e. volumetric cylinder) has an accuracy of 1 ml. This means that a rock of a typical natural stone which has a volume of 5 - 10 cm
3 there will be a 10 - 20% error in the volume determination by use of the water displacement method. It has therefore been suggested that a mass-based method where the mass of the displaced water is measured using an overflow vessel is more accurate and precise (see
Figure 3). [
32]
Another educational study has compared the level (i.e. displacement method) to the overflow and suspension method based on Archimedes’ principle and found that the latter is the most accurate among the three methods in determining the volume of an object for density determination.[
33] The % errors reported in this study for volume determination where 1.7 ± 8.5 % for the level (i.e. displacement) method, 0.09 ± 3.0 % for the overflow method and 0.04 ± 0.43 % for the suspension method.[
33]
Natural stone densities vary between 1.05 g/cm
3 for Amber to 19.32 g/cm
3 for gold. This suggests that their density in combination with morphological characterisation (colour, patterns and shape of natural stones) maybe useful for collectors and educators that seek a quick method to determine the kind of natural stone and as an activity in the chemistry/physics/materials science lab. We therefore determine accurate densities and provide high-clarity pictures of the morphological characteristics of a collection of natural stones shown in
Figure 4.
3.1. Densities of Natural Stones
We find that the water overflow method using a 500 ml borosilicate or tin overflow vessel gives inconsistent results for the amount of displaced water. These results are not reported because for some smaller volume stones (e, g, n, I, j, k, l, m, n, p, r, s, t, v, w) this method did not result in any overflow. Currently, the availability of 100 ml overflow vessels, which would have been more appropriate for the volume of the natural stones measured here, is not commercially available. The only natural stone that gave reliable results with the overflow method was specimen w which had a volume of 16.1 cm3. Also, some natural stones seemed to just change the surface tension of water (or even the density) and the additional volume of the natural stone had no effect on the height of the water meniscus, resulting in a lack of overflow when the natural stone was added to the liquid.
The level method (i.e. water displacement method) gave relatively accurate results for the small stones with an average percent error given by the following equation,
where n is the number of measurements, the density of the natural stone measured with the less accurate method and the density measured with the more accurate method.
The percent error of the mass-based suspension method using the 3 d.p. jewellery scale was calculated using the following equation,
where is the density measured with the mass-based suspension method and the density of 99.95 % Cu reference cube at 300K and 1 bar pressure.
Using equation 1 we can assess by what degree density measurements of the level method differ from the mass-based suspension method. This average % error was found to be 9.3% for natural stones in the range of 2 - 50 g. It also requires a volumetric cylinder in addition to the jewellery scale whereas the mass-based suspension method requires only a plastic beaker, the jewellery scale and a small diameter wire. We therefore are in agreement with the earlier study by W. H. Stephen [
33] that the mass-based suspension method is the most accurate among the three methods in determining the density of objects with irregular shape and this is due to the higher accuracy of mass measurement compared to volume measurement by the instruments used in this study.
As the measurements of the volume of the Cu (1 inch) reference cube revealed that the suspension method had an inherent error of the order of 0.1% which is mainly due to the inaccuracies in the measurement of the volume of the object. So for a natural stone with 5 cm3 volume the error in the volume measurement would be 0.005 cm3. This suggest that densities with this method with the jewellery scale should be reported up to 2 d.p.. Densities using the level method were reported to 2. d.p. as we could read volumes that have a precision of 0.5 ml on the 100 ml graduated cylinder. To confirm the validity of our density measurements, we have also measured the densities of the various natural stones using a 4 d.p. analytical balance in a closed system, and we report these densities as reference values of the natural stones examined
In
Table 3 we tabulate the measured densities for the level method, the mass-based suspension method using the a 3 d.p. jewellery scale and the mass-based suspension method using the 4 d.p. analytical scale. The agreement of the two later methods is 0.3% (average % error) based on the average percent error which indicates that the density measurement protocol developed is accurate.
Polycrystallinity is expected to reduce the density of natural stones compared to the density of single crystals. For most specimens, the main crystal structure was amorphous silicon dioxide, which is known to have a lower density than quartz; however, depending on the second phase in the solid, some stones that were primarily silica (SiO2) had higher densities compared to α-quartz. It would be interesting to explore this aspect in a subsequent study more detailed study in which also temperature effects could be addressed.
The volume in the density determination was either from the level method or from the changes in mass of the suspension method due to Archimedes principle. The densities determined by the later method show higher precision and accuracy which is reflected in the significant figures reported for these measurements.
If we compare the accuracies of the densities determined by the simple and inexpensive suspension method, we reach the conclusion that this technique is accurate and cost-effective. We therefore recommend that educators, collectors and merchants of natural stones use this technique as a way to identify natural stones in combination with morphological characterisation. By using a more accurate digital balance of 4 d.p., we find that the average percent error (% err.) between the suspension method using the 3 d.p. jewellery balance and the more accurate 4 d.p. balance by Fisher analytical series FAS224/E is only 0.3%. However, the average percent error of the level method and the suspension method using the jewellery balance was 9.2%. This suggests that the methodology developed with the suspension method and the jewellery balance is accurate to the 2 d.p. with an average percent error of 0.3 %.
The uncertainty of the measurement of the density using the 3 d.p. jewellery balance was assessed using a copper density reference cube ( d = 1 inch = 2.54 cm) mainly to validate the accuracy of the volume measurement of the stone. To increase the accuracy of the volume determination of this geometric cube, we have used a digital calliper with 0.001 cm accuracy. This resulted in a volume of the reference cube of 16.406 cm-3. This was very close to the volume of the metal cube measured from the mass-based suspension method on a 3 d.p. digital jewellery balance, which was found to be 16.421 cm-3. So the differences in volume between the exact geometric shape of the reference cube and the volume calculated from the mass-based suspension method are of the order of 0.01 cm-3. From this one measurement of the copper density reference cube we find that the uncertainty of the technique with the 3 d.p. jewellery scale is of the order of 0.02%. This suggests that the densities with the 3 d.p. jewellery scale can be reported with accuracy up to 3 d.p..
3.2. Gas Pycnometry – Non-Destructive Density of Solids via Boyle’s Law
Gas pycnometers calculate the actual volume of a solid by measuring pressure changes (ΔP) that happen when helium with a known mass expands from a reference chamber into a sample chamber of unknown volume. The sample volume and density can be obtained from the ΔP reading with the ideal gas law (P·V = constant at constant T) without immersing the sample in liquid or making a powder from it. Helium is preferred for this application because its tiny kinetic diameter of 0.26 nm enables it to access most open porosity spaces while remaining unable to pass through crystalline lattice structures. The commercial tools automate the expansion process by utilising highly accurate pressure transducers (±0.0001 psi) and chambers with precise temperature control (±0.01 K).
Table 4 summarises current models and costs.
3.3. Precision-to-Cost Comparison
We have performed a brief market search on instruments that can measure the density of stones in a non-destructive way to make a comparison with the mass-based suspension method suggested in this work. We calculate the ratio between precision of the instrument per the cost of the instrumental setup and find the following results.
A higher precision-per-cost ratio makes an instrument considerably more accessible and practical for educators and collectors who need an affordable method to measure stone densities. While gas pycnometers provide tenfold greater absolute precision, the suspension technique using a jewellery scale achieves approximately 9000 times better for each dollar invested, demonstrating its value for classroom demonstrations and routine gem identification.
3.4. Future Directions in Improving the Measurement of Densities of Natural Stones
Based on our study, we estimate that an overflow vessel with a square cross-section tube emerging from the main vessel would dispense water more accurately, as the water meniscus perimeter would be co-linear with the opening of the square tube. Currently the small circular diameter tube used in commercially available borosilicate overflow vessels of 500 ml capacity retains some of the overflown water inside the tube due to the formation of a double meniscus at the tip of the overflow tube (see
Figure 5) due to adhesive forces of water with the walls of the class tube (e.g. capillary effect).
This capillary effect would be limited by the use of a 1 x 1 cm square overflow tube that would be large enough to eliminate the formation of the double meniscus at the overflow tube. Also, the availability of inexpensive jewellery scales with a higher measuring range would significantly improve versatility of the mass-based suspension method.
In the chemistry laboratory the density of liquids and solid powders is usually measured using a liquid pycnometer which was an invention of Dmitri Ivanovich Mendeleev and the German glassworker, Heinrich Geissler in 1959. A method to measure the density of metals and gemstones was first described in the book of the Iranian polymath scholar al-Beruni (Abu al-Rayan Muhammad ibn Ahmad al-Biruni, 973 - after 1050 A.D.) with the title ‘The book most comprehensive in knowledge of precious stones’ (Translation by Hakim Mohammad Said, No. 66, ISBN 969-8016-28-7, Pakistan Hijra Council). In this book he used the hydrostatic method of finding the specific gravity and density of metals and gemstones with precision with a conical instrument in which he placed a certain mass of a solid (100 Mithqāl = 425 g) and measured the mass of overflown water through a semi-circular tube that was pierced to reduce the water capillary effect which was called the ‘Conical instrument of Abū al-Rayān’.
In this glassware the weight of the liquid displaced by the solid is determined by subtracting the weight of the pycnometer and liquid from the weight of the pycnometer, solid, and liquid. This weight difference is the liquid that was displaced from the closed pycnometer and using the density of water one can calculate the volume of the solid inside the pycnometer. This technique although works very well for liquids and powdered solids it has the limitation that it a destructive method for natural stones as they would have to be powdered to fit in the liquid pycnometer.
We suggest that the level method could be improved using a sealed compartment that would fit the natural stone in a non-destructive way and then this compartment with a small diameter graduated cylinder at the top would increase the accuracy of the volume measurement. A simplified device is shown in
Figure 6 which shows the liquid pycnometer in an open and closed position. It also shows the level of the displaced liquid inside the capillary tube at the top of the pycnometer.
The volume of the water inside the top graduated cylinder could be measured by a geometric equation at correlates the inner diameter of the tube to the change of height of water inside the tube using the geometry equation of a cylinder,
The inner diameter of the glass tube could be measured very accurately with a calliper that has a typical precision of ±0.02 mm which would result in a precision of the volume of the order of 10-8 cm-3 calculated using equation . Also, thin glass tubes can be made to have accurate diameters of ±0.005 mm error in the diameter value. This would be an improved design of the liquid pycnometer which is currently destructive and needs the solid sample to be made in a powder first to measure its volume.
Such a glassware would also make possible to study the expansion of liquids as a function of temperature or due to changes of solute concentration so it could be used in research activities.
Author Contributions
Conceptualization, C.D.Z.; methodology, C.D.Z.; validation, C.D.Z., D.D. and E.L.; formal analysis, C.D.Z., D.D. and E.L.; investigation, C.D.Z., D.D. and E.L.; resources, C.D.Z; data curation, C.D.Z, D.D. and E.L..; writing-original draft preparation, C.D.Z. and E.L.; writing—review and editing, C.D.Z., E.L. and D.D.; project administration, C.D.Z; funding acquisition, C.D.Z. Authors have read and agreed to the published version of the manuscript.
Figure 1.
(a) Jewellery scale with 3 d.p. accuracy and a set of chrome plating scale weights used for calibration of the scale. (b) Experimental setup for the suspension method determination of density.
Figure 1.
(a) Jewellery scale with 3 d.p. accuracy and a set of chrome plating scale weights used for calibration of the scale. (b) Experimental setup for the suspension method determination of density.
Figure 2.
Calibration curve of jewellery scale with chrome scaling weights.
Figure 2.
Calibration curve of jewellery scale with chrome scaling weights.
Figure 3.
Picture of commercially available (a) borosilicate overflow vessel (500 ml) and (b) tin overflow vessel (500 ml) that can measure the volume of an object with irregular shape by water overflow and collection of the water in a graduated cylinder or in a beaker that is on a scale.
Figure 3.
Picture of commercially available (a) borosilicate overflow vessel (500 ml) and (b) tin overflow vessel (500 ml) that can measure the volume of an object with irregular shape by water overflow and collection of the water in a graduated cylinder or in a beaker that is on a scale.
Figure 4.
Various natural stones for which the densities were determined in this study. (a) Carnelian, (b) Clear quartz, (c) Blue banded agate, (d) Nummite, (e) Snowflake obsidian, (f) Malachite, (g) Rose quartz, (h) Nephrite jade, (i) Petrified wood, (j) Brecciated jasper, (k) Dalmatian jasper, (l) Turritela agate, (m) Aquamarine, (n) Green aventurite fluorite, (o) Pink agate, (p) Brecciated jasper, (q) Opalite, (r) Yellow ocean jasper cabochon, (s) Fuchsite, (t) Orange moonstone, (u) Shiva lingam, (v) Amber, (w) White quartz, (x) Yellow fluorite, (y) Green fluorite, (z) Blue fluorite, (aa) Red jasper.
Figure 4.
Various natural stones for which the densities were determined in this study. (a) Carnelian, (b) Clear quartz, (c) Blue banded agate, (d) Nummite, (e) Snowflake obsidian, (f) Malachite, (g) Rose quartz, (h) Nephrite jade, (i) Petrified wood, (j) Brecciated jasper, (k) Dalmatian jasper, (l) Turritela agate, (m) Aquamarine, (n) Green aventurite fluorite, (o) Pink agate, (p) Brecciated jasper, (q) Opalite, (r) Yellow ocean jasper cabochon, (s) Fuchsite, (t) Orange moonstone, (u) Shiva lingam, (v) Amber, (w) White quartz, (x) Yellow fluorite, (y) Green fluorite, (z) Blue fluorite, (aa) Red jasper.
Figure 5.
Double meniscus formed by water adhesion to glass tube walls.
Figure 5.
Double meniscus formed by water adhesion to glass tube walls.
Figure 6.
Simplified schematic of a proposed inexpensive pycnometer for natural stones to which a known mass of water is added first without the stone using an accurate syringe or pipettor (e.g. 1ml) and then the same amount of water is added with the stone inside the pycnometer.
Figure 6.
Simplified schematic of a proposed inexpensive pycnometer for natural stones to which a known mass of water is added first without the stone using an accurate syringe or pipettor (e.g. 1ml) and then the same amount of water is added with the stone inside the pycnometer.
Table 1.
Calibration curve data for the measurement of mass between 0-30 g on a jewellery scale along with mean value of the mass and standard deviation reported for each measurement.
Table 1.
Calibration curve data for the measurement of mass between 0-30 g on a jewellery scale along with mean value of the mass and standard deviation reported for each measurement.
| mass of calib. stand. |
Mass measurement on scale |
|
|
| |
measur. 1 |
measur. 2 |
measur. 3 |
Mean Value |
Stand. Dev. |
| (g) |
(g) |
(g) |
(g) |
(g) |
(g) |
| 1 |
0.996 |
0.995 |
0.996 |
0.996 |
0.001 |
| 2 |
1.996 |
1.995 |
1.993 |
1.995 |
0.002 |
| 5 |
5.000 |
5.000 |
5.000 |
5.000 |
0.000 |
| 10 |
9.995 |
9.994 |
9.993 |
9.994 |
0.001 |
| 20 |
20.000 |
20.000 |
20.000 |
20.000 |
0.000 |
| 25 |
25.006 |
25.006 |
25.006 |
25.006 |
0.000 |
| 30 |
30.000 |
30.000 |
30.000 |
30.000 |
0.000 |
| * the mass of 25g was 20g standard plus 5g standard and the mass of 30g was the 20g standard plus the 10g standard |
Table 2.
List of label, chemical formula and name of natural stones investigated for their density.
Table 2.
List of label, chemical formula and name of natural stones investigated for their density.
| Label |
Name (common) |
Correct mineral name |
Dominant formula |
Key citation |
| a |
Carnelian |
Chalcedony (var. of Quartz) |
SiO₂ (with Fe³⁺ inclusions) |
USGS Quartz entry [17] |
| b |
Clear quartz |
α-Quartz |
SiO₂ |
[17] |
| c |
Blue banded agate |
Blue lace agate (Chalcedony) |
SiO₂ + Al-Fe-Mn oxides |
[18] |
| d |
Nummite |
Amphibole mix (Anthophyllite-Gedrite) |
(Mg,Fe)₇Si₈O₂₂(OH)₂ |
[19] |
| e |
Snowflake obsidian |
Volcanic glass with cristobalite spherulites |
Amorphous SiO₂ + Al₂O₃ + FeO |
[20] |
| f |
Malachite |
Malachite |
Cu₂CO₃(OH)₂ |
USGS Malachite [21] |
| g |
Rose quartz |
Rose Quartz |
SiO₂ (Ti-Fe-Mn impurities) |
[17] |
| h |
Nephrite jade |
Actinolite-Tremolite solid solution |
Ca₂(Mg,Fe)₅Si₈O₂₂(OH)₂ |
[22] |
| i |
Petrified wood |
Silicified wood (Quartz + minor calcite) |
SiO₂ ± CaCO₃ |
[7] |
| j |
Brecciated jasper |
Jasper (opaque Quartz) |
SiO₂ with Fe-oxide cement |
[18] |
| k |
Dalmatian jasper |
Igneous rhyolite (spotty quartz-feldspar) |
(Na,K)AlSi₃O₈ + SiO₂ |
[23] |
| l |
Turritella agate |
Fossiliferous Chalcedony |
SiO₂ + CaCO₃ shells |
[24] |
| m |
Aquamarine |
Beryl |
Be₃Al₂Si₆O₁₈ |
USGS Beryl
[25] |
| n |
Green aventurine |
Quartz with fuchsite mica |
SiO₂ + K(Al,Cr)₂(Si₃AlO₁₀)(OH)₂ |
[26] |
| o |
Pink agate |
Dyed Chalcedony |
SiO₂ |
[18] |
| p |
Brecciated jasper |
seej |
SiO₂ |
[18] |
| q |
Opalite (man-made) |
Opalite glass |
SiO₂·nH₂O (amorphous) |
[27] |
| r |
Yellow ocean jasper |
Orbicular Chalcedony |
SiO₂ + Fe-oxides |
[18] |
| s |
Fuchsite |
Fuchsite |
K(Al,Cr)₂(Si₃AlO₁₀)(OH)₂ |
[26] |
| t |
Orange moonstone |
Orthoclase feldspar |
(Na,K)AlSi₃O₈ |
[28] |
| u |
Shiva lingam |
Crypto-crystalline Quartz/Hematite |
SiO₂ + Fe₂O₃ |
[29] |
| v |
Amber |
Fossilised tree resin |
(C₁₀H₁₆O)ₙ |
[30] |
| w |
White quartz |
α-Quartz |
SiO₂ |
[17] |
| x |
Yellow fluorite |
Fluorite |
CaF₂ |
USGS Fluorite [31] |
| y |
Green fluorite |
Fluorite |
CaF₂ |
[31] |
| z |
Blue fluorite |
Fluorite |
CaF₂ |
[31] |
| aa |
Red jasper |
Hematitic Jasper |
SiO₂ + Fe₂O₃ |
[18] |
Table 3.
Label, measured mass, average measured mass (av. m), standard deviation (σ) of measured mass and calculated density of the various natural stone specimen listed in
Table 2 using the level method (
ρ1) and the mass-based suspension method using the jewellery scale (
ρ2) and the mass-based suspension method using the analytical 4 d.p. balance (
ρ3). Values are also compared to literature values for the density (
ρlit).
Table 3.
Label, measured mass, average measured mass (av. m), standard deviation (σ) of measured mass and calculated density of the various natural stone specimen listed in
Table 2 using the level method (
ρ1) and the mass-based suspension method using the jewellery scale (
ρ2) and the mass-based suspension method using the analytical 4 d.p. balance (
ρ3). Values are also compared to literature values for the density (
ρlit).
| Label |
m1
|
m2
|
m3
|
av. m |
σ |
Vstone
|
mstone
|
ρ1
|
ρ2
|
ρ3
|
% err. |
ρlit
|
| (g) |
(g) |
(g) |
(g) |
(g) |
(cm3)4
|
(g) |
(g/cm3)1
|
(g/cm3)2
|
(g/cm3)5
|
|
(g/cm3) |
| a |
5.227 |
5.225 |
5.224 |
5.220 |
0.002 |
5.230 |
13.684 |
2.27 |
2.61 |
2.6123 |
0.0 |
2.64 [17] |
| b |
7.033 |
7.036 |
7.032 |
7.029 |
0.002 |
7.041 |
15.519 |
2.38 |
2.20 |
2.1952 |
0.3 |
2.648 [17] |
| c |
5.619 |
5.618 |
5.620 |
5.614 |
0.001 |
5.624 |
14.603 |
2.42 |
2.59 |
2.5889 |
0.1 |
2.60 [18] |
| d |
5.793 |
5.794 |
5.795 |
5.789 |
0.001 |
5.799 |
13.768 |
2.75 |
2.37 |
2.3658 |
0.2 |
3.01(anthophyllite) [19] |
| e |
2.820 |
2.821 |
2.821 |
2.816 |
0.001 |
2.821 |
6.617 |
2.20 |
2.34 |
2.3384 |
0.0 |
2.38 ± 0.05 (obsidian) [7] |
| f |
7.894 |
7.895 |
7.893 |
7.889 |
0.001 |
7.903 |
30.618 |
3.82 |
3.87 |
3.8641 |
0.1 |
4.03 [21] |
| g |
2.486 |
2.484 |
2.485 |
2.480 |
0.001 |
2.484 |
6.591 |
2.63 |
2.64 |
2.6411 |
0.0 |
2.65 [17] |
| h |
2.645 |
2.643 |
2.644 |
2.639 |
0.001 |
2.644 |
7.062 |
2.82 |
2.66 |
2.6554 |
0.2 |
2.95 ± 0.05 [22] |
| i |
2.462 |
2.463 |
2.462 |
2.457 |
0.001 |
2.462 |
6.557 |
2.62 |
2.65 |
2.6469 |
0.2 |
2.60 [34] |
| j |
3.504 |
3.505 |
3.507 |
3.500 |
0.002 |
3.507 |
10.175 |
2.54 |
2.89 |
2.8874 |
0.2 |
2.60 [18] |
| k |
3.880 |
3.879 |
3.878 |
3.874 |
0.001 |
3.881 |
10.13 |
2.53 |
2.60 |
2.6043 |
0.0 |
2.58 [23] |
| l |
3.537 |
3.536 |
3.535 |
3.531 |
0.001 |
3.537 |
9.206 |
3.06 |
2.60 |
2.5883 |
0.3 |
2.60 [24] |
| m |
3.295 |
3.299 |
3.297 |
3.292 |
0.002 |
3.298 |
8.237 |
2.35 |
2.49 |
2.4857 |
0.2 |
2.641 [25] |
| n |
4.000 |
4.000 |
4.000 |
3.995 |
0.000 |
4.002 |
12.718 |
3.17 |
3.17 |
3.1667 |
0.1 |
2.65 [26] |
| o |
9.076 |
9.075 |
9.074 |
9.070 |
0.001 |
9.086 |
23.537 |
2.93 |
2.59 |
2.5838 |
0.1 |
2.60 [18] |
| p |
2.569 |
2.565 |
2.567 |
2.562 |
0.002 |
2.567 |
8.217 |
3.28 |
3.19 |
3.1923 |
0.1 |
2.60 [18] |
| q |
4.000 |
3.995 |
3.996 |
3.992 |
0.003 |
3.999 |
9.632 |
2.40 |
2.40 |
2.4006 |
0.1 |
2.20 (glass) [27] |
| r |
3.340 |
3.342 |
3.340 |
3.336 |
0.001 |
3.342 |
8.858 |
2.52 |
2.64 |
2.6372 |
0.2 |
2.60 [18] |
| s |
4.633 |
4.632 |
4.631 |
4.627 |
0.001 |
4.635 |
12.551 |
2.66 |
2.70 |
2.6962 |
0.2 |
2.88 [26] |
| t |
2.208 |
2.207 |
2.208 |
2.203 |
0.001 |
2.207 |
10.483 |
2.75 |
4.73 |
2.6543 |
0.0 |
2.56 [35] |
| u |
2.387 |
2.386 |
2.386 |
2.381 |
0.001 |
2.386 |
8.028 |
2.67 |
3.35 |
2.7891 |
0.2 |
2.70 [29] |
| v |
1.658 |
1.657 |
1.656 |
1.652 |
0.001 |
1.655 |
1.784 |
0.67 |
1.07 |
1.0799 |
0.8 |
1.05 [30] |
| w3 |
- |
- |
- |
- |
- |
16.1 |
49.406 |
2.90 |
3.07 |
2.6279 |
4.4 |
2.648 [17] |
| x |
9.250 |
9.252 |
9.249 |
9.245 |
0.002 |
9.262 |
25.231 |
3.14 |
2.72 |
2.7204 |
0.0 |
3.18 [31] |
| y |
8.009 |
8.008 |
8.005 |
8.002 |
0.002 |
8.017 |
21.819 |
2.72 |
2.72 |
2.7142 |
0.2 |
3.18 [31] |
| z |
9.743 |
9.741 |
9.740 |
9.736 |
0.002 |
9.754 |
26.413 |
2.63 |
2.71 |
2.7041 |
0.0 |
3.18 [31] |
| aa |
1.888 |
1.889 |
1.888 |
1.883 |
0.001 |
1.887 |
5.225 |
2.61 |
2.76 |
2.7625 |
0.3 |
2.60 [18] |
| Cu ref. |
16.370 |
16.363 |
16.361 |
16.370 |
0.005 |
16.426 |
146.67 |
|
|
|
0.17
|
8.929 |
| d6 (cm) |
2.542 |
2.540 |
2.541 |
|
0.001 |
16.406 |
|
|
|
|
|
8.940 |
| |
1 Displacement of water was used to measure the volume of the natural stone using eqn.4. |
|
|
| |
2 Mass-based suspension method employing Archimedes principle. |
|
|
| |
3 This natural stone specimen mass exceeded the measuring range of the jewellery scale so the level method was used instead
4 density of water used to calculate Vstone 0.9982 g⋅cm-3 at 20 °C (UKAS ISO/IEC17025 and ISO Guide 34 certified).
5 density of water at 21.9 °C was 0.9977956 g⋅cm-3 (CRC handbook of physics and chemistry) 18.2 MΩ·cm deionised water by ELGA (Pure lab chorus).
6 the dimensions of the copper reference cube were measured with a 3 d.p. digital caliper (Draper Expert) and the density of deionised water was taken as 0.99656 g cm-3 (300K, 1 bar). The density of 99.95% w/w copper at 300K is 8.930 g cm-3 (https://www.engineeringtoolbox.com/copper-density-specific-heat-thermal-conductivity-vs-temperature-d_2223.html) The mass of the Cu ref. cube was measured with a 2 d.p. accuracy professional digital scale (146.67 g) and was taken as the average of three measurements (146.66 g, 146.68 g and 146.67 g).
7 Percent error of the mass-based suspension method with a 3 d.p. jewellery scale calculated from Eqn 7 |
|
|
Table 4.
Gas Pycnometer Models: Sample Capacity, Accuracy and Market Price.
Table 4.
Gas Pycnometer Models: Sample Capacity, Accuracy and Market Price.
| Model |
Sample volume range |
Stated precision (g cm⁻³) |
Typical price (USD)* |
| Micromeritics AccuPyc II 1340 |
0.1–135 cm³ |
±0.0001 |
5 k (refurbished)–18 k (new) [36] |
| Anton Paar Ultrapyc 5000 |
0.5–100 cm³ |
±0.0002 |
18–25 k [37] |
| OEM bench-top units (China) |
1–50 cm³ |
±0.001–0.002 |
1–3 k [38] |