Submitted:
23 July 2025
Posted:
24 July 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Methodology
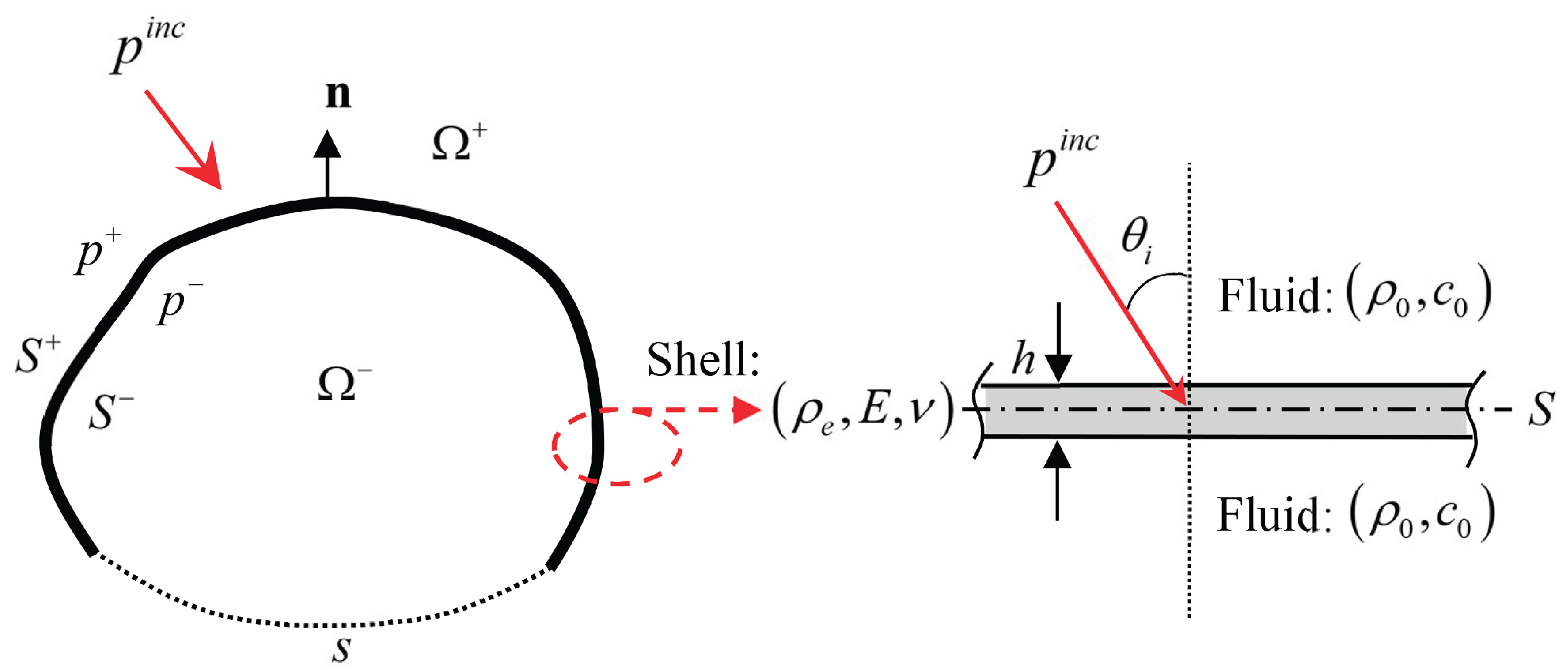
2.1. Thin-shell integral formulation
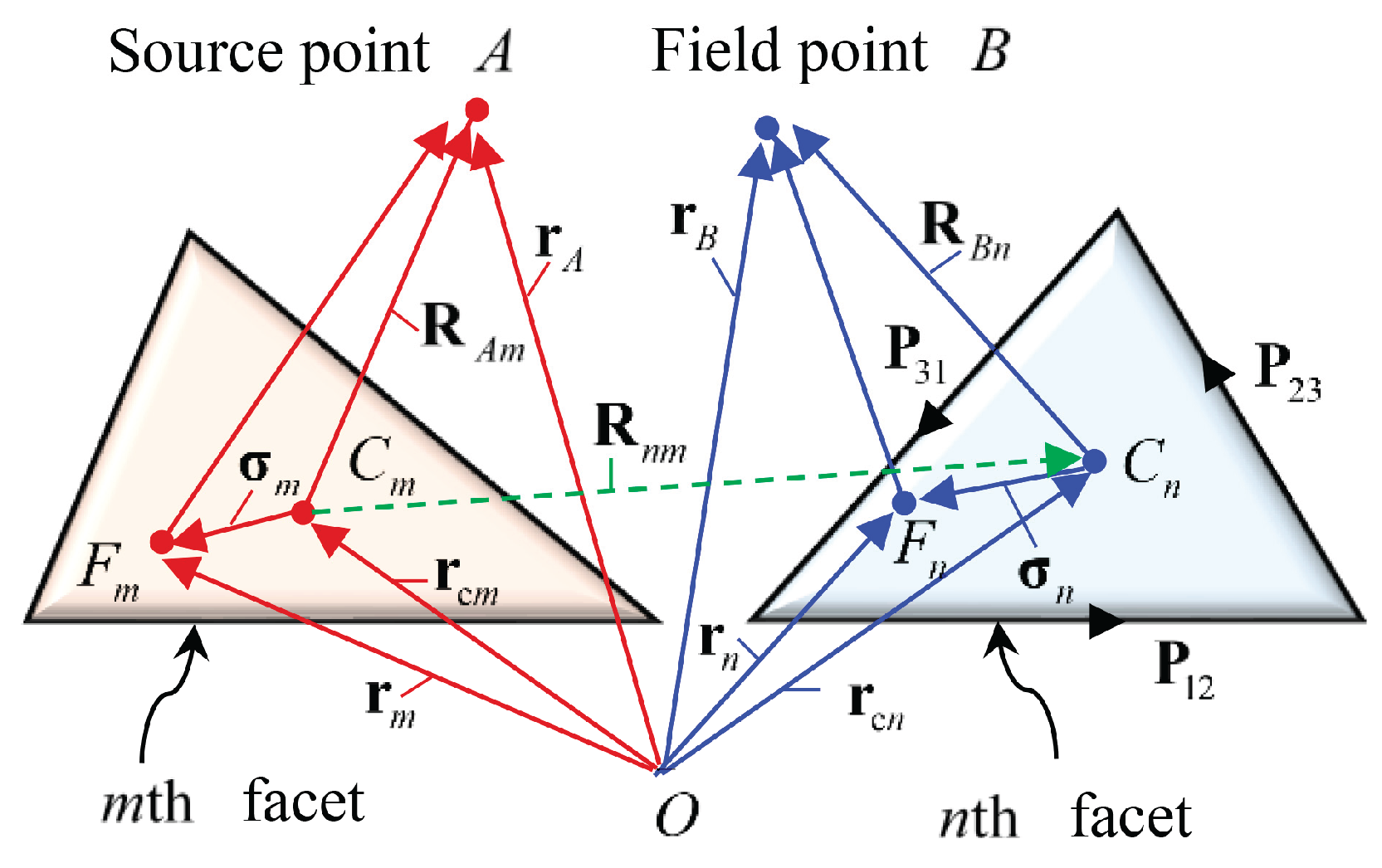
2.2. Discretization and numerical implementation
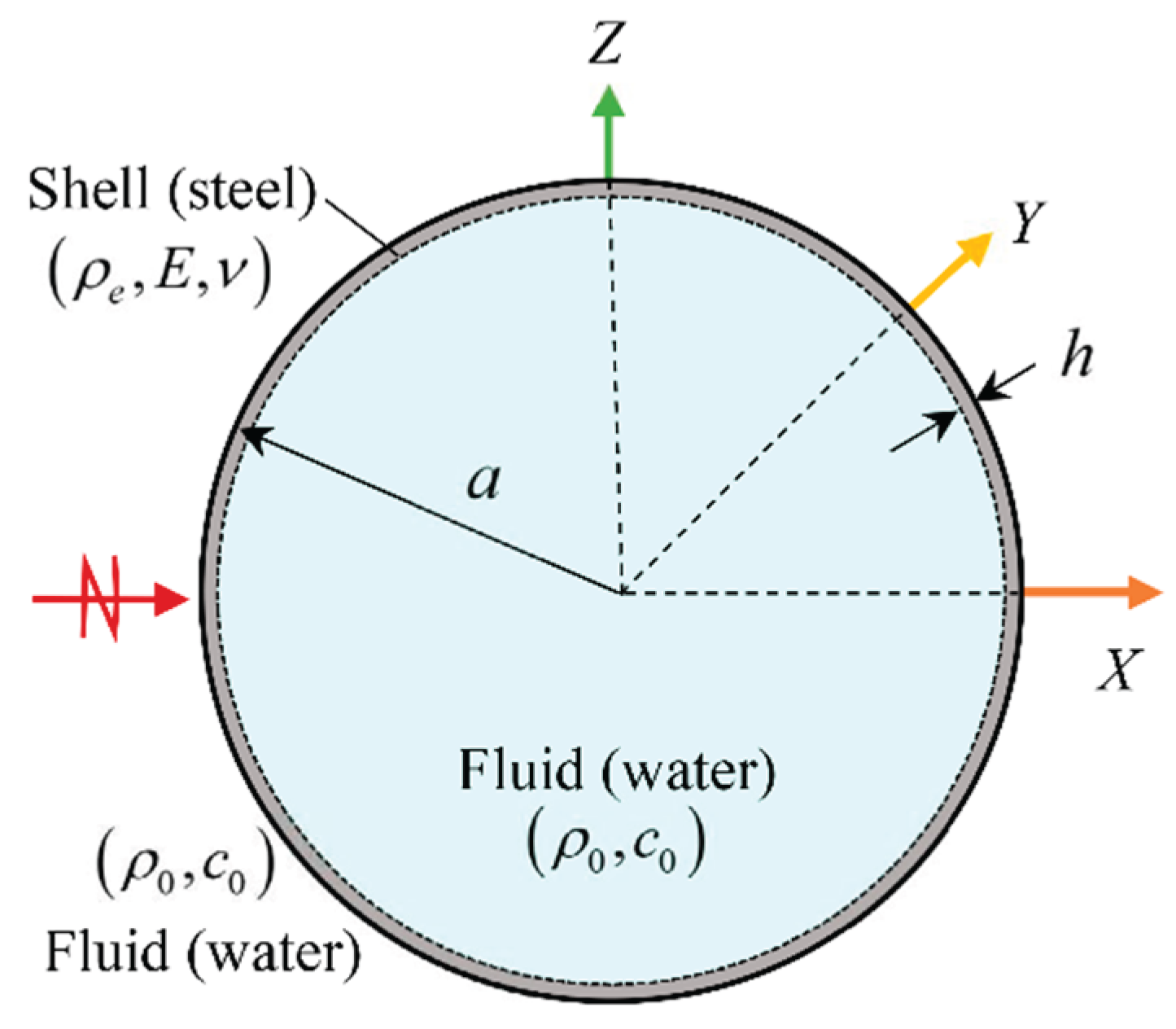
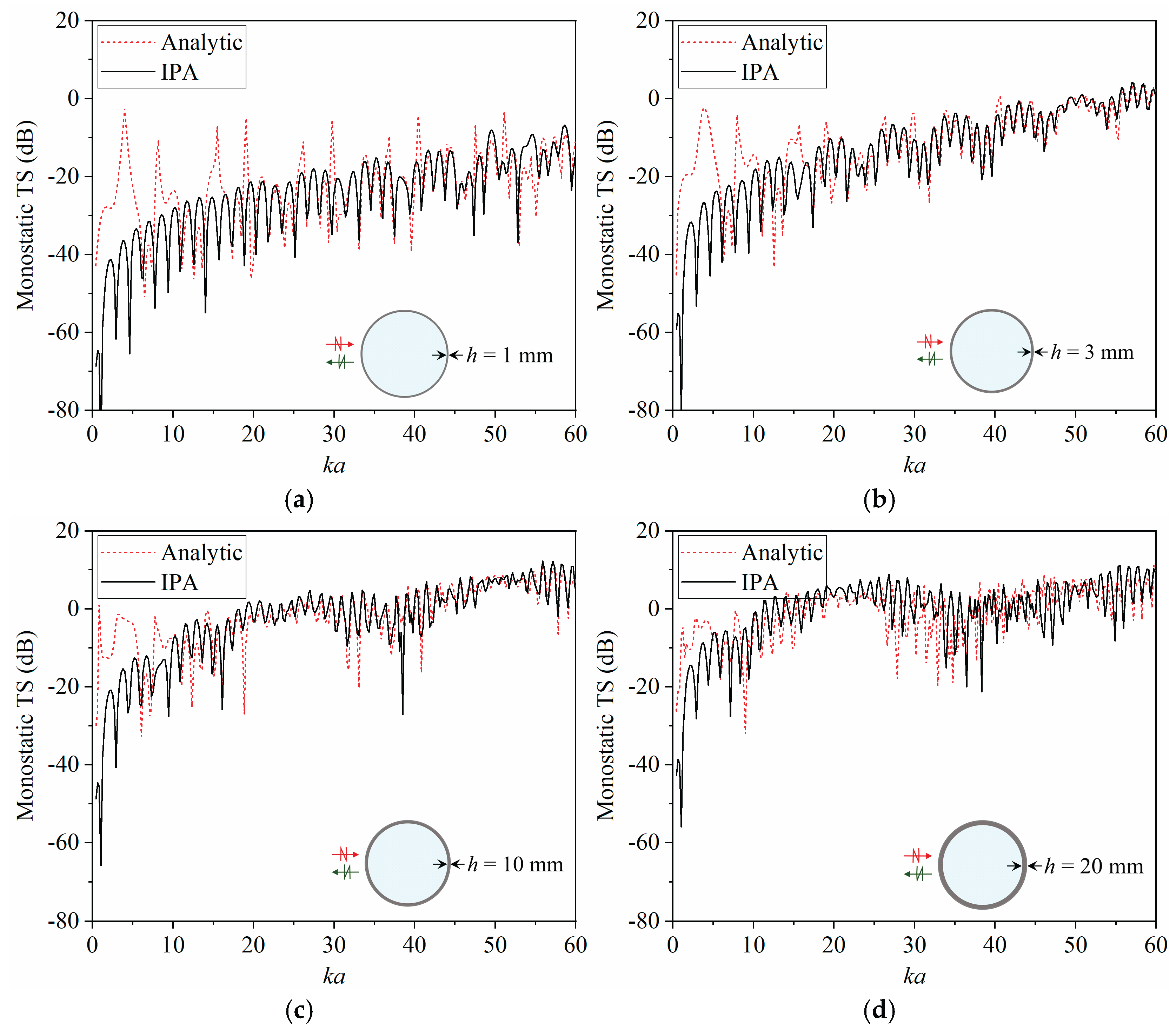
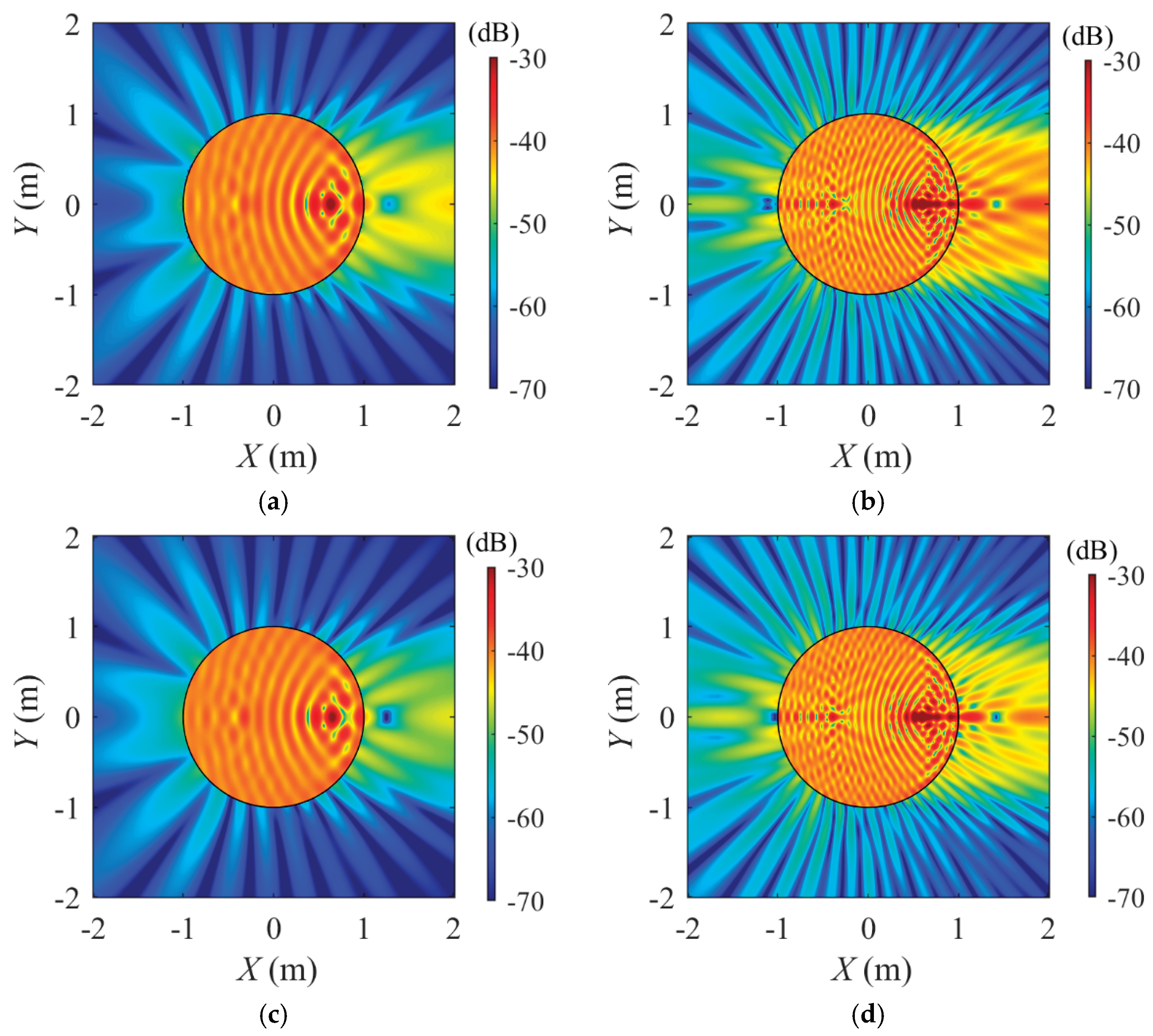
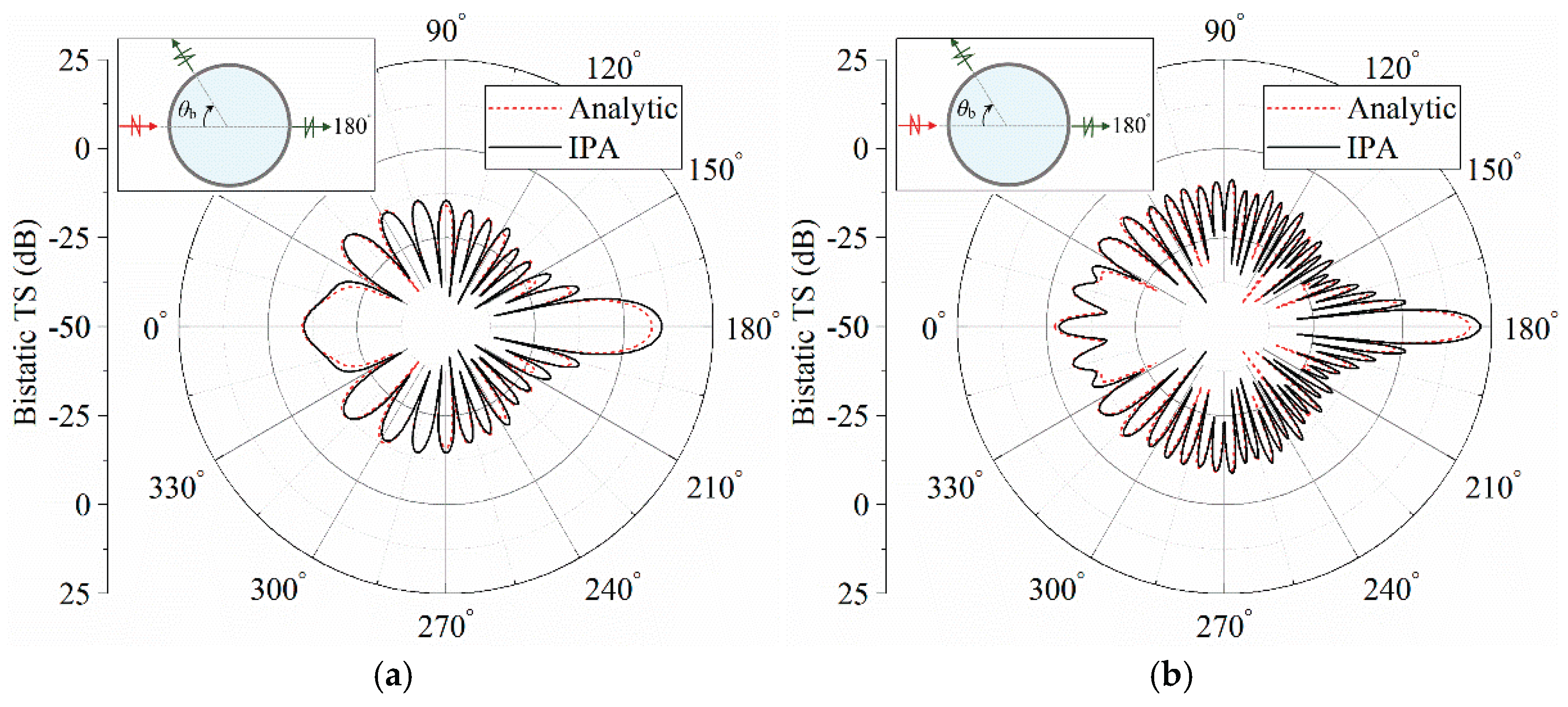
2.3. Numerical validation
3. Sail scattering modeling and experimental validation
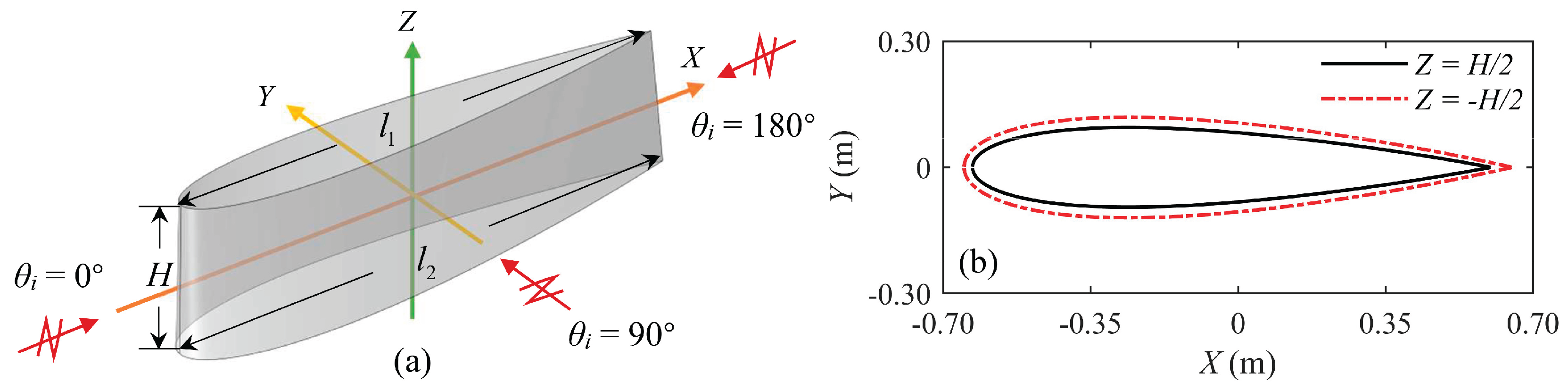
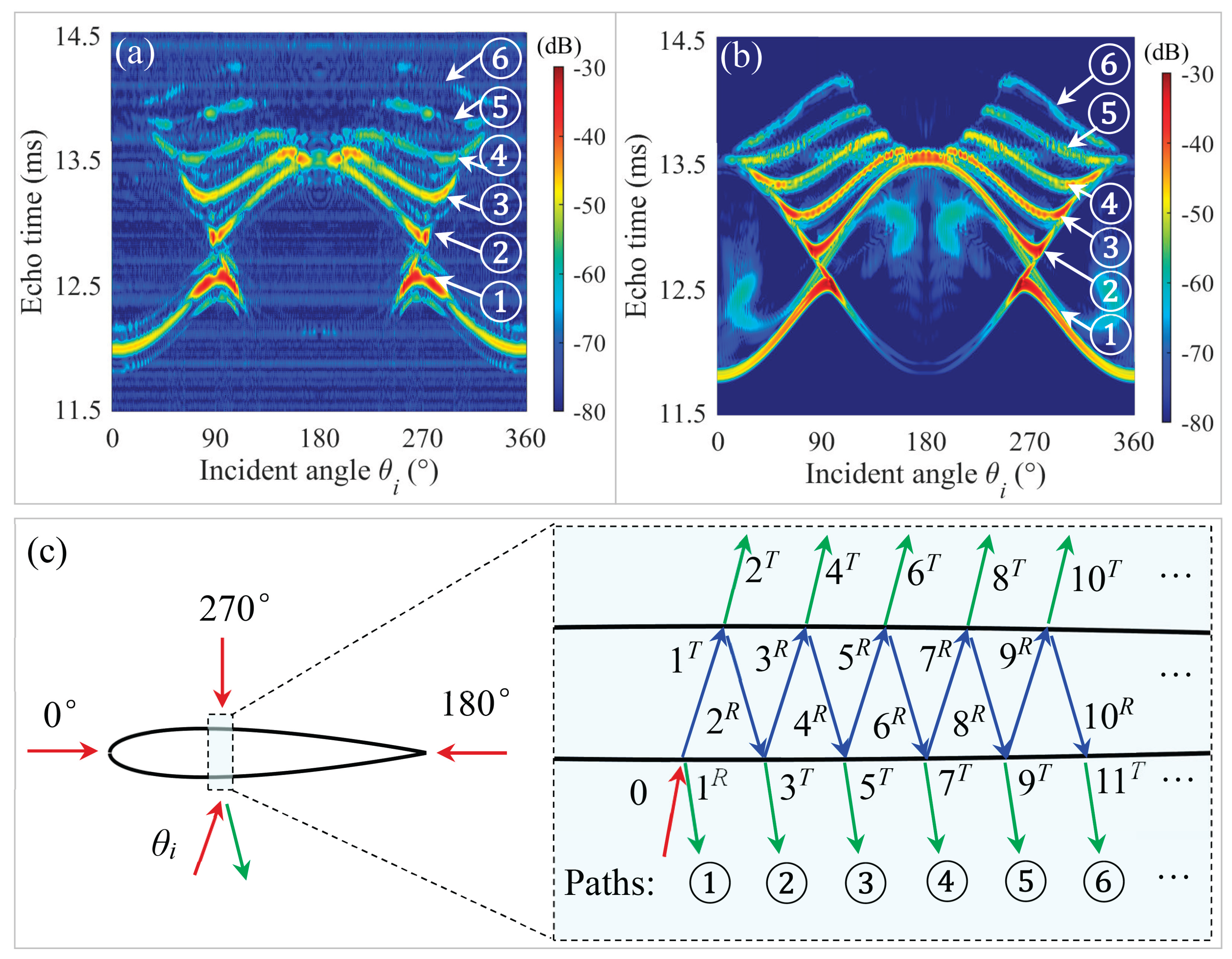
3.1. IPA-based sail scattering modeling
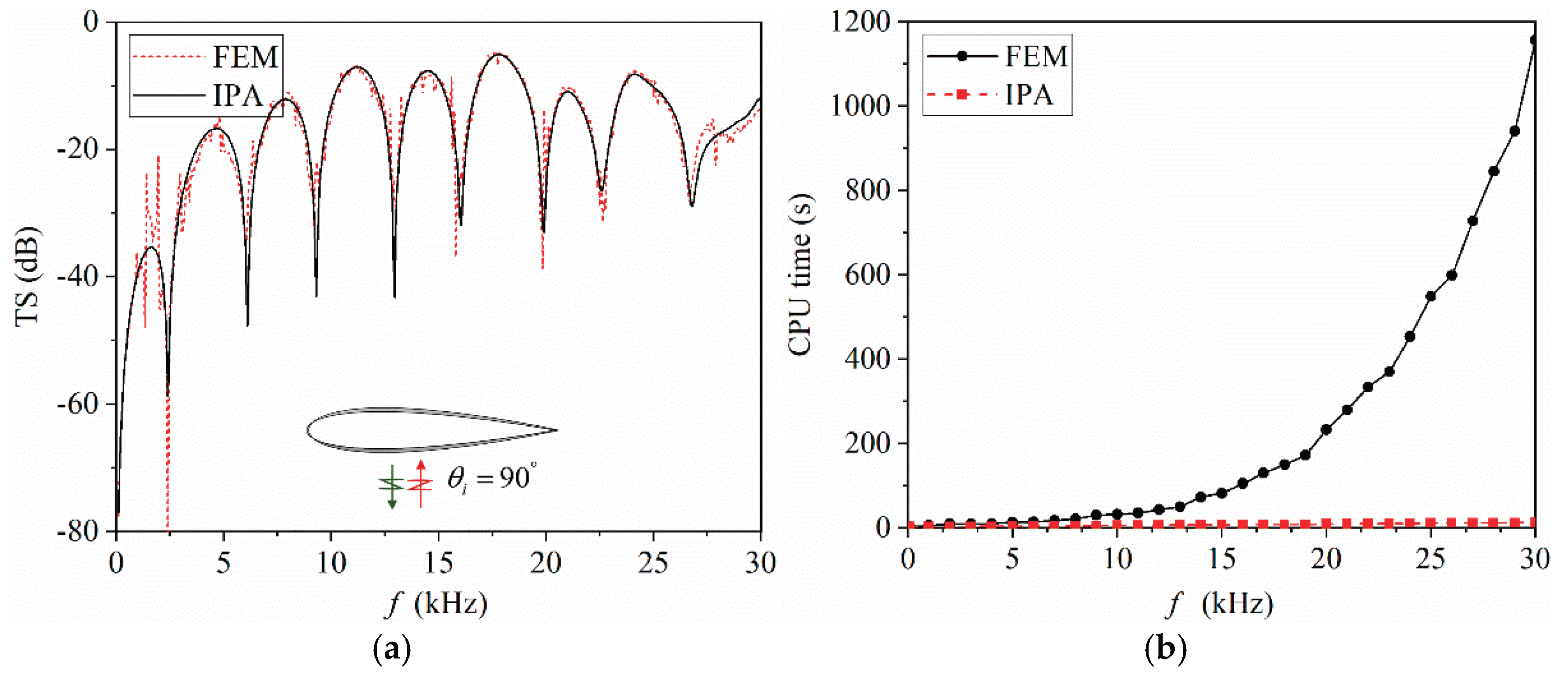
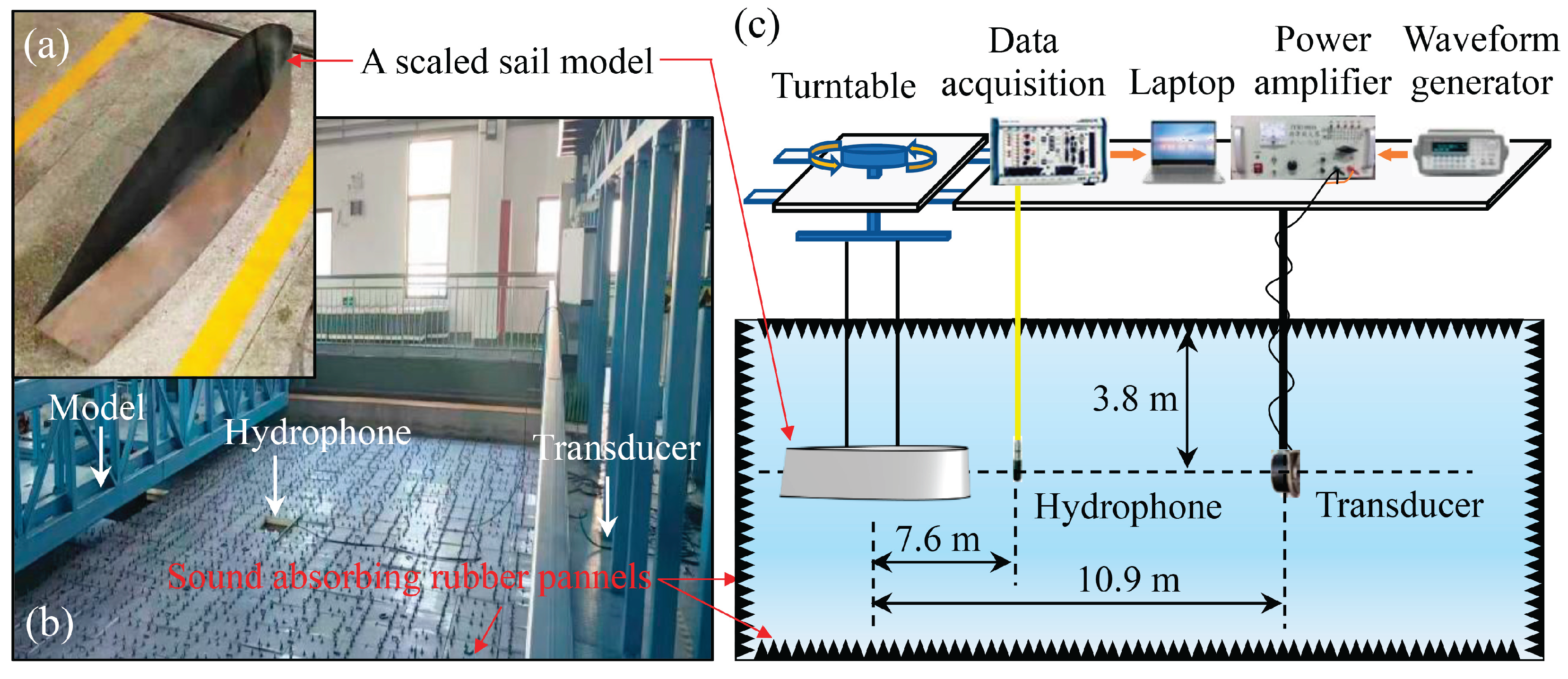
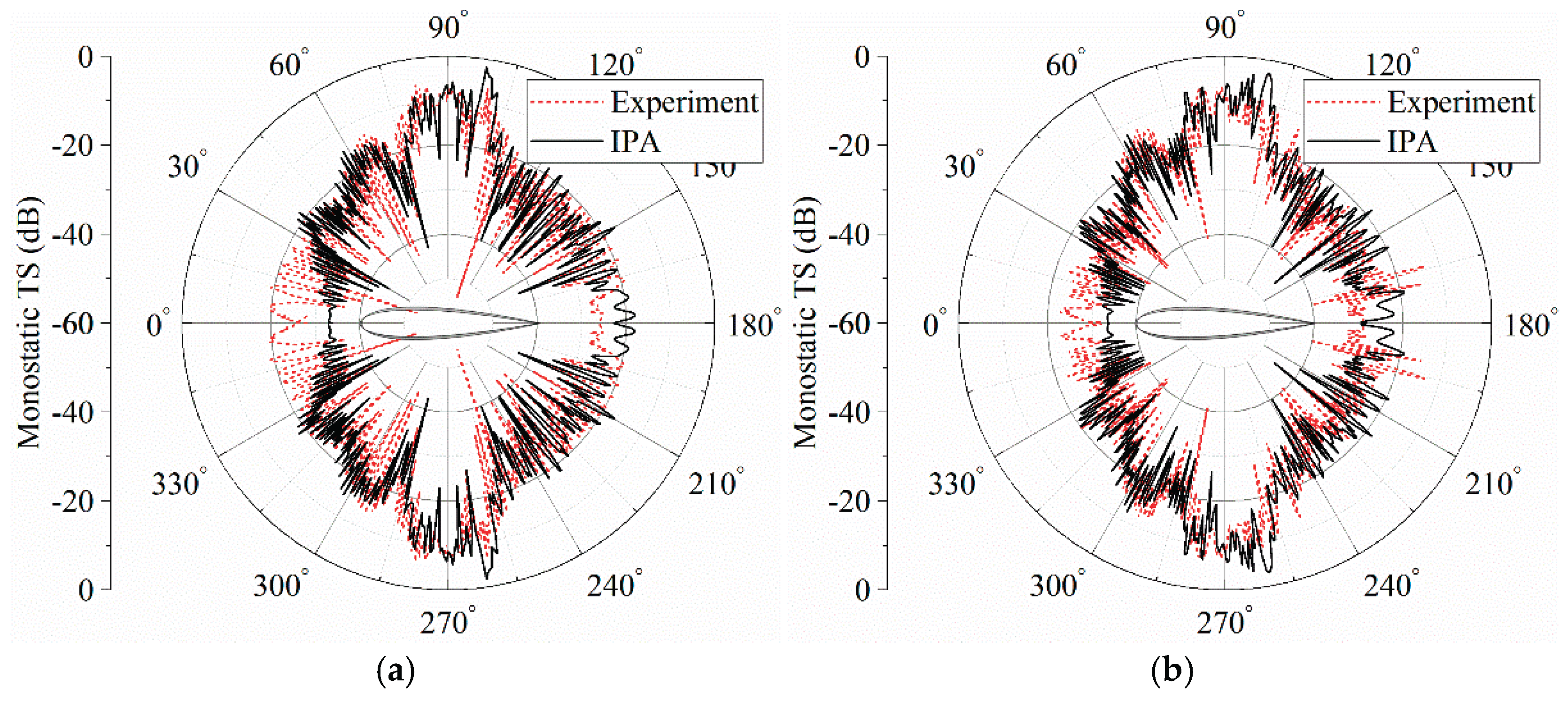
3.2. Sail scattering experiment and validation
4. Conclusions
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aslam, M.A.; Zhang, L.; Liu, X.; Irfan, M.; Xu, Y.; Li, N.; Zhang, P.; Jiangbin, Z.; Yaan, L. Underwater sound classification using learning based methods: A review. Expert Systems with Applications 2024, 255, 124498. [Google Scholar] [CrossRef]
- Urick, R.J. Principles of underwater sound, second ed.; McGraw-Hill: New York, 1975. [Google Scholar]
- Werby, M.F.; Überall, H. A systematic study of water-filled submerged elastic spherical shells and the resolution of elastic- and water-included resonances. The Journal of the Acoustical Society of America 2002, 112, 896–905. [Google Scholar] [CrossRef] [PubMed]
- España, A.L.; Williams, K.L.; Plotnick, D.S.; Marston, P.L. Acoustic scattering from a water-filled cylindrical shell: Measurements, modeling, and interpretation. The Journal of the Acoustical Society of America 2014, 136, 109–121. [Google Scholar] [CrossRef] [PubMed]
- Gaunaurd, G.C.; Werby, M.F. Lamb and creeping waves around submerged spherical shells resonantly excited by sound scattering. The Journal of the Acoustical Society of America 1987, 82, 2021–2033. [Google Scholar] [CrossRef]
- Gaunaurd, G.C.; Werby, M.F. Sound scattering by resonantly excited, fluid-loaded, elastic spherical shells. The Journal of the Acoustical Society of America 1991, 90, 2536–2550. [Google Scholar] [CrossRef]
- Brill, D.; Gaunaurd, G.C. Acoustic resonance scattering by a penetrable cylinder. The Journal of the Acoustical Society of America 1983, 73, 1448–1455. [Google Scholar] [CrossRef]
- Everstine, G.C. Finite element formulatons of structural acoustics problems. Computers & Structures 1997, 65, 307–321. [Google Scholar] [CrossRef]
- Kirkup, S. The Boundary Element Method in Acoustics: A Survey. Applied Sciences 2019, 9, 1642. [Google Scholar] [CrossRef]
- Everstine, G.C.; Henderson, F.M. Coupled finite element/boundary element approach for fluid–structure interaction. The Journal of the Acoustical Society of America 1990, 87, 1938–1947. [Google Scholar] [CrossRef]
- Wu, H.; Yu, L.; Jiang, W. A coupling FEM/BEM method with linear continuous elements for acoustic-structural interaction problems. Applied Acoustics 2019, 150, 44–54. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Woinowsky-Krieger, S. Theory of plates and shells; McGraw-Hill Companies: New York, 1959. [Google Scholar]
- Burgschweiger, R.; Ochmann, M.; Schäfer, I. Implementation and results of a mass inertia coupling as an extension of the BEM for thin shells. In Proceedings of the 22nd International Congress on Sound and Vibration (ICSV), Florence, ITALY, Jul 12-16, 2015. [Google Scholar]
- Chernokozhin, E.; Tsinovoy, A.; Boag, A. Scattering by thin shells in fluids: Fast solver and experimental validation. JASA Express Letters 2021, 1, 016002. [Google Scholar] [CrossRef]
- Chernokozhin., E.; Boag., A. Numerical Modeling of Acoustic Scattering by Thin Elastic Shells Immersed in Fluids. TechRxiv 2024.
- Williams, K.L.; Marston, P.L. Backscattering from an elastic sphere: Sommerfeld–Watson transformation and experimental confirmation. The Journal of the Acoustical Society of America 1985, 78, 1093–1102. [Google Scholar] [CrossRef]
- Yang, Y.; Norris, A.N.; Couchman, L.S. Ray tracing over smooth elastic shells of arbitrary shape. The Journal of the Acoustical Society of America 1996, 99, 55–64. [Google Scholar] [CrossRef]
- Fawcett, J.A. Computing the Scattering From Slightly Deformed Spherical Shells—A Ray-Based Approach. IEEE Journal of Oceanic Engineering 2018, 43, 1161–1170. [Google Scholar] [CrossRef]
- Jun Fan, T.L., Weilin Tang. The structure of highlight echoes due to specular reflection from shells of immerged target. Technical Acoustics 2002, 153-157+170.
- Liszka, E.G.; McCoy, J.J. Scattering at a rough boundary—Extensions of the Kirchhoff approximation. The Journal of the Acoustical Society of America 1982, 71, 1093–1100. [Google Scholar] [CrossRef]
- McCammon, D.F.; McDaniel, S.T. Surface velocity, shadowing, multiple scattering, and curvature on a sinusoid. The Journal of the Acoustical Society of America 1986, 79, 1778–1785. [Google Scholar] [CrossRef]
- Dacol, D.K. The Kirchhoff approximation for acoustic scattering from a rough fluid–elastic solid interface. The Journal of the Acoustical Society of America 1990, 88, 978–983. [Google Scholar] [CrossRef]
- Lieuwen, T. Explicit results for wave scattering and transmission through a rough fluid–fluid interface. Applied Acoustics 2002, 63, 1031–1050. [Google Scholar] [CrossRef]
- Ganesh, M.; Hawkins, S.C. A fast algorithm for the two-dimensional Helmholtz transmission problem with large multiple scattering configurationsa). The Journal of the Acoustical Society of America 2024, 156, 752–762. [Google Scholar] [CrossRef]
- Yitong Tang, B.W. , Jun Fan. Study on target strength prediction method of water-filled acoustic transparent structure. Technical Acoustics 2021, 40, 316–323. [Google Scholar] [CrossRef]
- Junger, M.C.; Feit, D.; Greenspon, J.E. Sound, structures, and their Interaction; MIT Press: Cambridge, 1972. [Google Scholar]
- Wang, W.; Wang, B.; Fan, J. Time-domain Kirchhoff approximation extensions modeling of acoustic camera imagery with multiple scattering. Applied Acoustics 2023, 211, 109465. [Google Scholar] [CrossRef]
- Wang, W.; Wang, B.; Fan, J.; Zhou, F.; Zhao, K.; Jiang, Z. A simulation method on target strength and circular SAS imaging of X-rudder UUV including multiple acoustic scattering. Defence Technology 2023, 23, 214–228. [Google Scholar] [CrossRef]
- Pierce, A.D.; Beyer, R.T. Acoustics: an introduction to its physical principles and applications; Acoustical Society of America: New York, 1991. [Google Scholar]
- Wang, B.; Wang, W.-h.; Fan, J.; Zhao, K.-q.; Zhou, F.-l.; Tan, L.-w. Modeling of bistatic scattering from an underwater non-penetrable target using a Kirchhoff approximation method. Defence Technology 2022, 18, 1097–1106. [Google Scholar] [CrossRef]
- Marten Nijhof, L.F., Layton Gilroy, Jan Ehrlich, Ingo Schäfer. BeTSSi IIb: Submarine target strength modeling workshop. In Proceedings of the UACE2017 - 4th Underwater Acoustics Conference and Exhibition, 2017; pp. 377–384.
- Wu, T.W.; Wan, G.C. Numerical modeling of acoustic radiation and scattering from thin bodies using a Cauchy principal integral equation. The Journal of the Acoustical Society of America 1992, 92, 2900–2906. [Google Scholar] [CrossRef]
- Lee, K.; Seong, W. Time-domain Kirchhoff model for acoustic scattering from an impedance polygon facet. The Journal of the Acoustical Society of America 2009, 126, EL14–EL21. [Google Scholar] [CrossRef]
- Gordon, W. Far-field approximations to the Kirchoff-Helmholtz representations of scattered fields. IEEE Transactions on Antennas and Propagation 1975, 23, 590–592. [Google Scholar] [CrossRef]
- Multiphysics, C. Available online: http://cn.comsol.com.
- Frisk, G.V.; Dickey, J.W.; Überall, H. Surface wave modes on elastic cylinders. The Journal of the Acoustical Society of America 1975, 58, 996–1008. [Google Scholar] [CrossRef]
- Ufimtsev; Yakovlevich, P. Fundamentals of the physical theory of diffraction; Wiley: New York, 2007. [Google Scholar]
| Parameter name | Symbol | Value | Unit |
|---|---|---|---|
| Density of water | 1000 | ||
| Longitudinal velocity of water | 1500 | ||
| Density of shell | 7800 | ||
| Young's modulus of shell | 200 | GPa | |
| Poisson's ratio of shell | 0.30 | / | |
| Outer radius | 1 | m | |
| Thickness of shell | 3 | mm |
| Parameter name | Symbol | Value | Unit |
|---|---|---|---|
| Length of upper surface | 1.23 | m | |
| Length of lower surface | 1.30 | m | |
| Height | 0.35 | m | |
| Shell thickness | 1.50 | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





