Introduction
By analyzing Gurzadyan and Penrose’s anisotropic distribution of concentric low-variance circles (LVCs) [
1,
2,
3] with the Planck Collaboration’s large-scale temperature extrema [
4,
5] in the CMB, we propose a mechanism initiating the Big Bang: the Universe would emerge from the collapse of the densest object in a previous-aeon black hole [
6]. Where the collapse occurred, or the Center of this Universe, would currently be about 30 billion light years away from us and around Galactic coordinates
. If we look from where we are, i.e. the Local Supercluster (LS), to the Center, the Universe would spin clockwise.
In this report, we provide the Friedmann equation for the spinning Universe, and then use it to study the Hubble tension, and to calculate the angle that the Universe has spun since photon decoupling.
Theory
Newtonian mechanics has proven to be valid for the study of most of the aspects of the Friedmann Equation [
7]. Suppose a homogeneous sphere of matter that is rotating about its center and is expanding with time, for a test mass
m at the surface of the equator of the sphere, a centrifugal force will be experienced:
Therefore, the total force will be:
By writing the radius in the form:
, we have
Assuming that the angular momentum is conserved (after photon decoupling, the Universe was large enough, and hence would not be significantly affected by its surroundings):
Multiply by
and integrate:
For a perfectly flat Universe, the integration constant
[
7]. As the sphere is homogeneous:
, we have:
Thus we have a modified Friedmann equation for a flat Universe with spin in the mass-dominated era:
where
is the Hubble parameter for a spinning Universe. If
, then the Friedmann equation for a non-spinning Universe is:
Therefore, for the spinning Universe, we have:
The Universe at present is large enough that
; hence the Hubble parameter that we measure locally can be regarded as the non-spinning Hubble parameter. Traditionally, we report it as the Hubble constant:
[
8]. Note that the non-spinning Hubble constant
is a constant during the course of expansion, as the standard theories of cosmology assume. We can also measure the Hubble parameter
for the spinning Universe at photon decoupling and report it as the Hubble constant
[
9]. Since the spinning is invisible, we cannot directly measure the angular speed
.
To know the angular speed, we first calculate an equivalent angular speed:
and then use the Friedmann equation for the spinning Universe to convert it into
. Dividing by
, equation (8) provides the ratio:
Note that the ratio also depends on the angular speed. By rearranging, we have the angular speed:
Combining equations (12) and (4), we have:
Therefore, the observable Hubble constant
with respect to the size
of the Universe is:
Results
The Rotational Center of the Universe
For us (the observer) in the LS, the Rotational Center of the Universe is at the intersection of the rotational plain that is parallel to the equator of the Universe:
So the Rotational Center is at times the radius of the surface of last scattering away from the LS and at Galactic coordinates .
Angular Speed of the Universe
For the CMB,
. Since
and
, the angular speed of the Universe at photon decoupling is:
The Hubble Tension
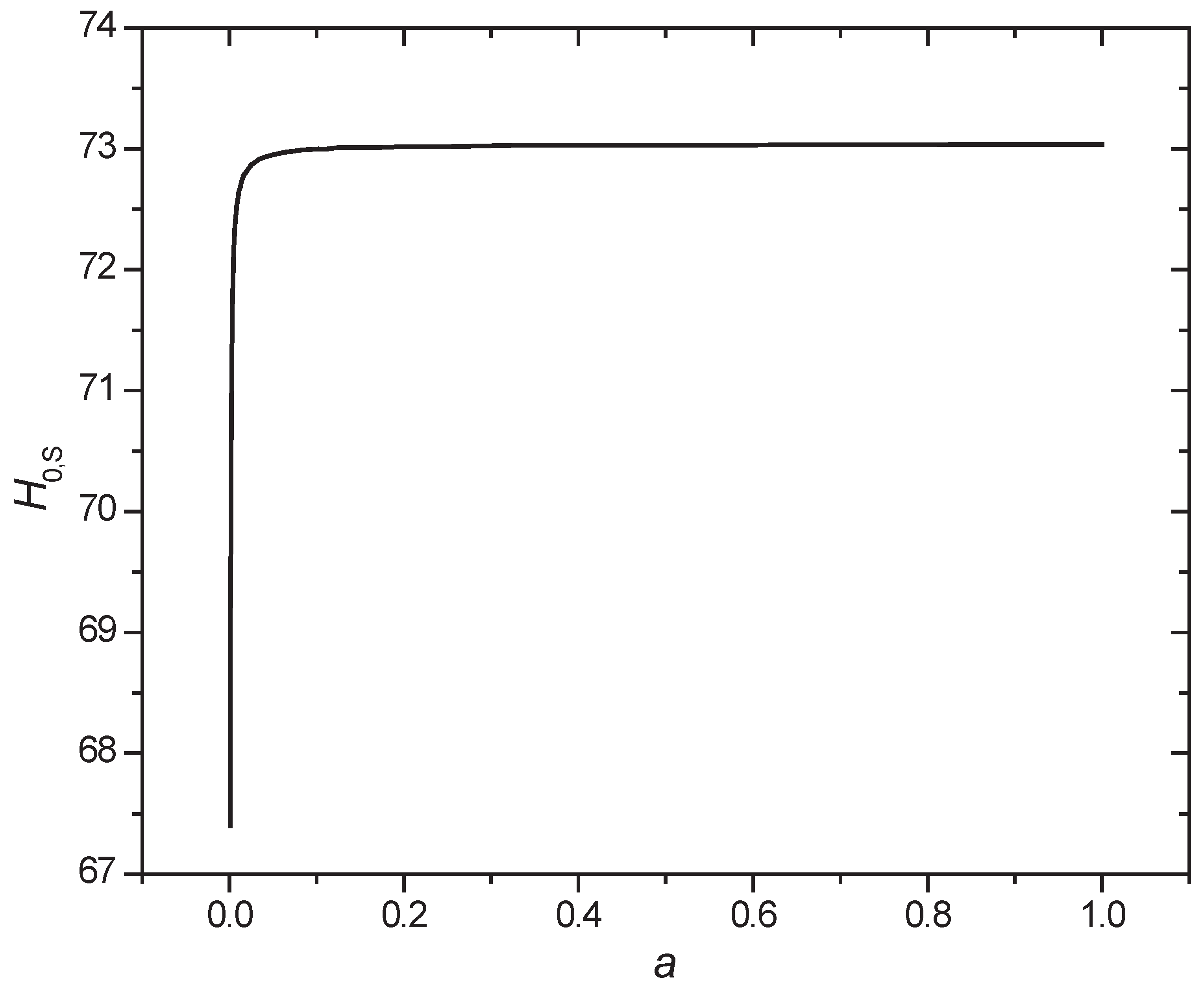
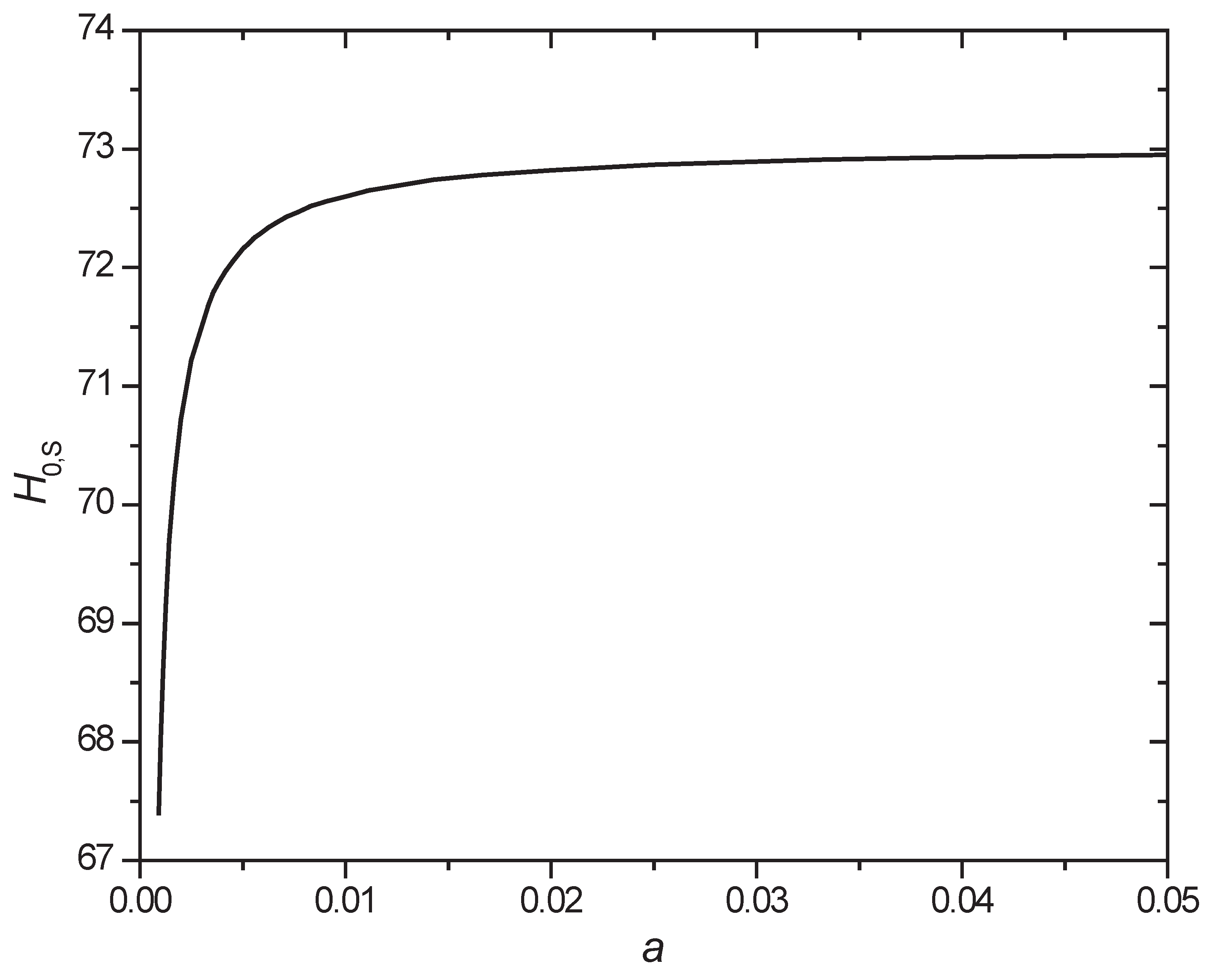
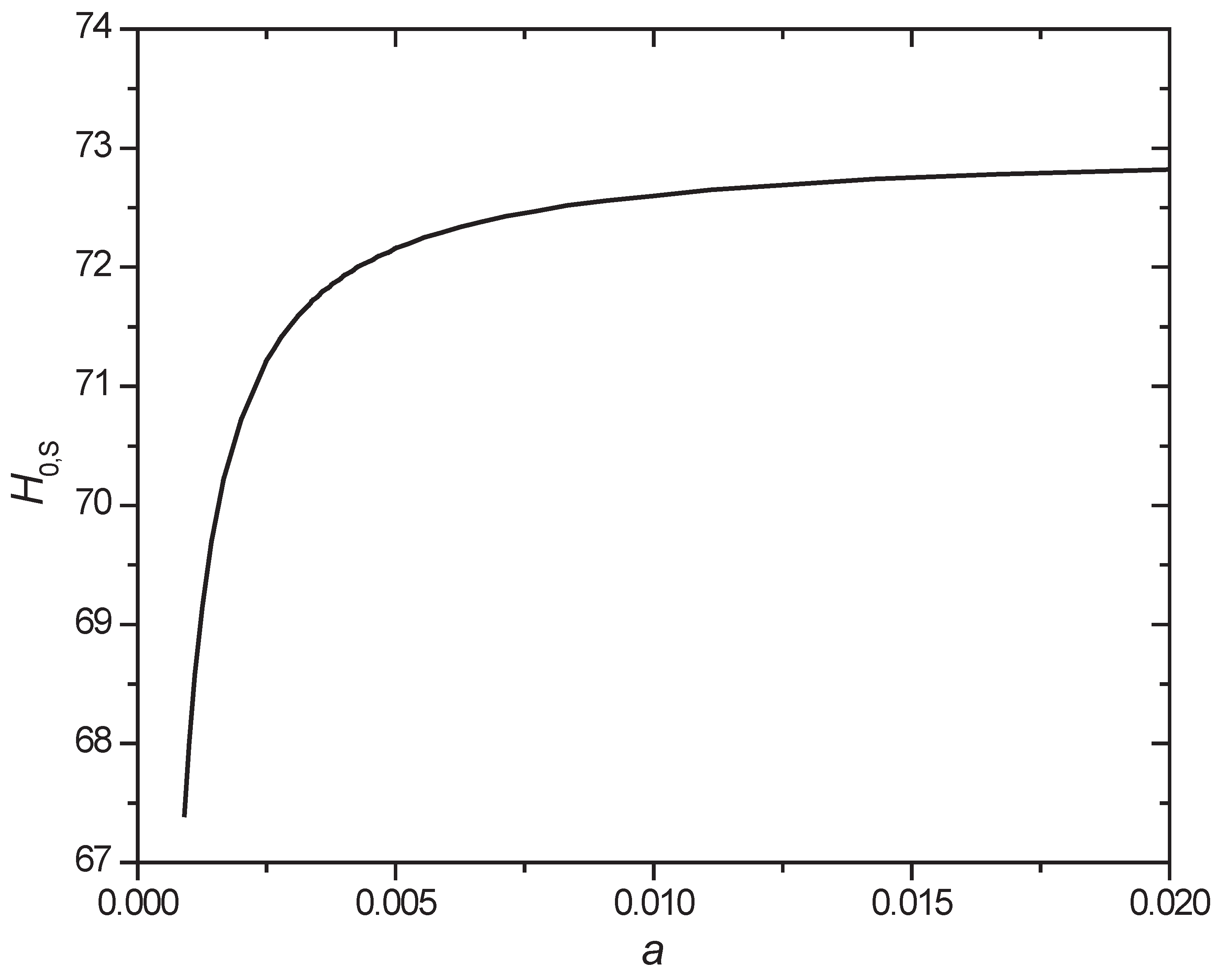
Based on equation (15), we plot the Hubble constant that we can observe at different sizes of the spinning Universe (
Figure 1,
Figure 2 and
Figure 3). The Hubble constant is quite stable as long as the scale factor
. The most significant change occurs when
.
The JWST can observe objects with redshifts up to
, corresponding to
,
,
, and
. Since the difference:
is much smaller than the error bar of
, the JWST confirms the Hubble constant measured locally [
10].
In conclusion, the Hubble tension [
8,
9] is caused by the invisible spinning of the Universe. With the spinning, the Universe is not perfectly isotropic and homogeneous.
The Angle that the Universe has Spun Since Photon Decoupling
Since photon decoupling, the Universe has experienced two eras. In the matter-dominated era, the Universe has expanded [
7]:
Therefore we can calculate the angle that the Universe has rotated:
In the cosmological-constant-dominated era, the Universe spins very slowly: at the matter-lambda equality,
; at present,
. Approximately,
In total, the angle that the Universe has spun since photon decoupling is:
By investigating region W in Gurzadyan and Penrose’s LVC map [
1,
2,
3,
6], which can be divided, roughly in the middle of the region, into one half with higher temperatures and the other half with lower temperatures. This characteristic pattern could only be seen when an observer was in the middle of LVC region W (i.e.
[
6]) at photon decoupling. Interestingly, we at present at
are able to observe it, meaning that the Universe has rotated an angle of
since photon decoupling. Thus we have a perfect match between the theoretical value and the observed value.
Acknowledgements
J.B.B. would like to thank Profs. Z. Shen, K. Yao, X. Jiang, F. Bo, Y. Cheng, S. Han, G. Chen, and Q. Yu at Zhejiang University for their inspiration. N.P.B. would like to dedicate this work to his grandparents in China.
References
- Gurzadyan, V. G. & Penrose, R. On CCC-predicted concentric low-variance circles in the CMB sky. Eur. Phys. J. Plus. 128, 22 (2013). [CrossRef]
- Gurzadyan, V. G. & Penrose, R. CCC and the Fermi paradox. Eur. Phys. J. Plus. 131, 11 (2016).
- Penrose, R. Black holes, cosmology and space-time singularities. Nobel Lecture, Dec. 8, 2020. https://www.nobelprize.org/uploads/2024/02/penrose-lecture.pdf.
- Planck Collaboration: Akrami, Y. et al. Planck 2018 results. VII. Isotropy and Statistics of the CMB. Astron. Astrophys. 641, A7 (2020). [CrossRef]
- Marcos-Caballero, A. The Cosmic Microwave Background radiation at large scales and the peak theory. Univ. Cantabria Thesis (2017).
- Bao, N. P. & Bao, J.-B. The Big Bang from the Collapse of the Densest Object in the Previous Aeon. Preprints 2024, 2024111842. [CrossRef]
- Ryden, B. Introduction to Cosmology. 2nd. ed. (Cambridge Univ. Press, Cambridge, 2017).
- Riess, A. G. et al. A comprehensive measurement of the local value of the Hubble constant with 1 km/s/Mpc uncertainty from the Hubble Space Telescope and the SH0ES team. Astrophys. J. Lett. 934, L7 (2022). [CrossRef]
- Planck Collaboration: Aghanim, N. et al. Planck 2018 results. VI. Cosmological parameters. Astro. Astrophys. 641, A6 (2020).
- Riess, A. G. et al. JWST Validates HST Distance Measurements: Selection of Supernova Subsample Explains Differences in JWST Estimates of Local H0. Astrophys. J. 977, 120 (2024). [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).