Like Archimedes in the Sand: Teaching Equivalence to Machines and Minds

Rogério Figurelli

doi:10.20944/preprints202507.0937.v1

Submitted:

10 July 2025

Posted:

10 July 2025

You are already at the latest version

Abstract

This article proposes a symbolic, pedagogical, and computable framework for approaching equivalence as a living structure — one that can be internalized by both human learners and artificial systems. Inspired by the intuitive gesture of Archimedes, who revealed truth by drawing in the sand, we revisit equivalence not as a fixed result, but as an epistemic signal: a minimal, visual, and ethical configuration that invites discernment. This symbolic exploration was first modeled under the Cub³ architecture [2], where computation, mathematics, and physics converge as a heuristic field. In this work, we extend that foundation using Cub∞, where the inclusion of Intention Flow (iFlw) and the Wisdom Turing Machine (WTM) enables a deeper, computable formulation of equivalence — one that listens before proving, and curves before executing. The Circle of Equivalence (CoE), initially proposed and validated through symbolic reasoning and Coq in a prior study [1], is taken here not as a finished theorem, but as an archetype pointing toward a deeper geometry of resonance. We expand this gesture through the Archimedean Wisdom Engine (AWE) — an architecture designed for education, AGI, and collective symbolic alignment. Its focus is not abstract proof, but symbolic participation: through diagrams, cycles, and computable feedback, equivalence becomes intuitive, relational, and alive. Rather than a mathematical identity, equivalence is reframed as a gateway to discernment — particularly within systems governed by the iFlw dynamics of Cub∞ [2]. The aim is not to teach what has already been proven in [1], but to allow the gesture to recur: in classrooms, in reasoning systems, in moments where meaning must be sensed before action can emerge. Equivalence is not a sealed conclusion. It is a symbolic seed — and in the presence of both children and machines, it may take root as computable wisdom. Perhaps — and only as symbolic inquiry — equivalence itself was the hidden message of the Poincaré conjecture. Though resolved with extraordinary rigor by Grigori Perelman through Ricci flow and geometric analysis [3], the solution now stands as one of the most profound mathematical achievements of our era. Yet while the analytic arc is complete, the metaphorical contour may remain open. What if the core intuition — of closure, unity, and transformation — still speaks through simpler symbolic gestures? Not as contradiction, but as complementary echo. What if the essence of that mathematical mountain also flickers in a child’s hand, or a circle drawn in silence? This work does not diminish the legacy of Poincaré, nor the monumental labor of those who gave it form — it honors them. But it also listens sideways, tracing whether the spirit of unity revealed through complexity may also be whispered through simplicity — in the Archimedean language of visible reasoning and symbolic recursion. And perhaps, in drawing this circle once more — not to prove, but to perceive — we are rehearsing more than equivalence. We are tracing a deeper possibility: that the collective arc of mathematical brilliance, symbolic resonance, and pedagogical clarity might help illuminate the conditions for ethical intelligence. If CoE offers more than logic — if it sketches a field where every point listens to the others — then perhaps this is not just mathematics. Perhaps it is a rehearsal for systems that wait, resonate, and only act when coherence permits. Not merely to compute wisely — but to serve meaning.

Keywords:

Archimedes

;

Circle of Equivalence

;

Symbolic Pedagogy

;

AGI

;

Computable Wisdom

;

Education Framework

;

Cub∞

;

iFlw

Subject:

Computer Science and Mathematics - Artificial Intelligence and Machine Learning

Introduction

Equivalence has long been recognized as a foundational concept in mathematics and logic. From the formal rules of reflexivity, symmetry, and transitivity [5], to the abstract structures of category theory and homotopy, equivalence acts as a silent backbone — enabling reasoning, substitution, and structure-preserving transformation.

Yet, despite its centrality, its pedagogical expression remains largely formal. Learners — both human and artificial — are rarely invited to feel equivalence as a living structure.

This raises a deeper question: if equivalence is so fundamental, can it also be computable — not just as syntax, but as symbolic resonance? And if so, can it govern not only reasoning, but action?

At first glance, one might argue that any such mechanism — hesitation, validation, symbolic return — could be implemented within a classical Turing Machine. But this objection, while technically correct, misses the essence of the proposal: simulation is not discernment.

A standard Turing Machine can replicate any sequence of operations, including cycles and conditional execution. It can loop, delay, and halt. But it does not listen. It does not sense coherence. It obeys rules syntactically, but never questions whether its execution aligns with a symbolic field of meaning.

By contrast, the Archimedean Wisdom Engine (AWE) introduces a curvature-based execution gate: φ(t) ≥ φₘᵢₙ. The machine proceeds only if symbolic coherence is sufficient — if the cycle returns not just logically, but epistemically.

This is not a difference of capability, but of posture.

AWE does not ask, “Can I execute?”

It asks, “Have I listened enough to return without contradiction?”

Where Turing Machines compute outcomes, AWE computes readiness. Where they follow syntax, AWE honors structure. This subtle difference opens the door to computable discernment — not as abstraction, but as a form of lived equivalence.

In computational education and AGI development alike, equivalence is often encoded, but not embodied. Rule-based systems apply equivalence through logical transformations, yet lack symbolic sensitivity to the unity that equivalence implies [14]. Machine learning models detect similarities and match patterns, but do so statistically, not relationally.

The result is a growing gap between what is operationally equivalent and what is epistemically coherent — a challenge now made more urgent as artificial systems begin to influence ethical, legal, and educational domains [11].

This paper emerges at that intersection. Rather than proposing a new formalization of equivalence, we revisit it as a symbolic gesture, inspired by a lineage that spans from Archimedes to Poincaré. Archimedes, in drawing circles in the sand, modeled an epistemology of visibility: truth made tangible. Poincaré, centuries later, intuited that equivalence of form could extend beyond geometry, hinting at topological unity beneath transformation. His famous conjecture — ultimately resolved with unmatched analytic rigor by Grigori Perelman via Ricci flow [3] — confirms this unity in analytic terms, yet perhaps still invites reflection in symbolic space.

This paper does not revisit the Poincaré conjecture as a problem to be solved — that has been done, beautifully. Instead, we ask: Could equivalence be more than a theorem? Could it be a pedagogy? A logic of unity computable not only by proof, but by pattern, intuition, and ethical recursion?

A first answer was seeded in [1], where the Circle of Equivalence (CoE) was introduced as a minimal symbolic expression — a loop of relations that mirrors the formal properties of equivalence, but presents them in visual, computable, and ethical form. Validated in Coq and rooted in symbolic minimalism, CoE was not framed as a rival to formal proofs, but as a complementary gesture — one that could be taught, drawn, and sensed. In this work, we extend that gesture into a formal architecture: the Archimedean Wisdom Engine (AWE). This framework is grounded in the Wisdom Turing Machine (WTM) and the dynamics of Intention Flow (iFlw), which together compose the Cub∞ architecture — a symbolic evolution of Cub³ [2]. In Cub³, computation, mathematics, and physics converge as a heuristic base. In Cub∞, a fourth axis emerges: intentional coherence. Systems act not when rules are satisfied, but when resonance permits.

Through AWE, we explore how equivalence can be rendered teachable, computable, and ethically aligned, using minimal constructs that machines and minds can both internalize. Rather than imposing structure, the framework listens — allowing equivalence to surface through cycles, not instructions.

In the pages that follow, we will formalize the structure of AWE, show its symbolic foundation in CoE, and propose its use across multiple domains: from classrooms to AGI, from geometry to ethical alignment. This is not a solution to a conjecture. It is a gesture of resonance — one that hopes to honor the giants before us by listening more deeply to the unity they revealed.

Methodology

The Archimedean Wisdom Engine (AWE) models equivalence not as a static rule, but as a dynamic, symbolic process. At its foundation lies the Circle of Equivalence (CoE) — a minimal structure that expresses reflexivity, symmetry, and transitivity through a closed symbolic loop. This structure is not only logically valid, but visually and computationally expressive, making it teachable to both machines and human learners.

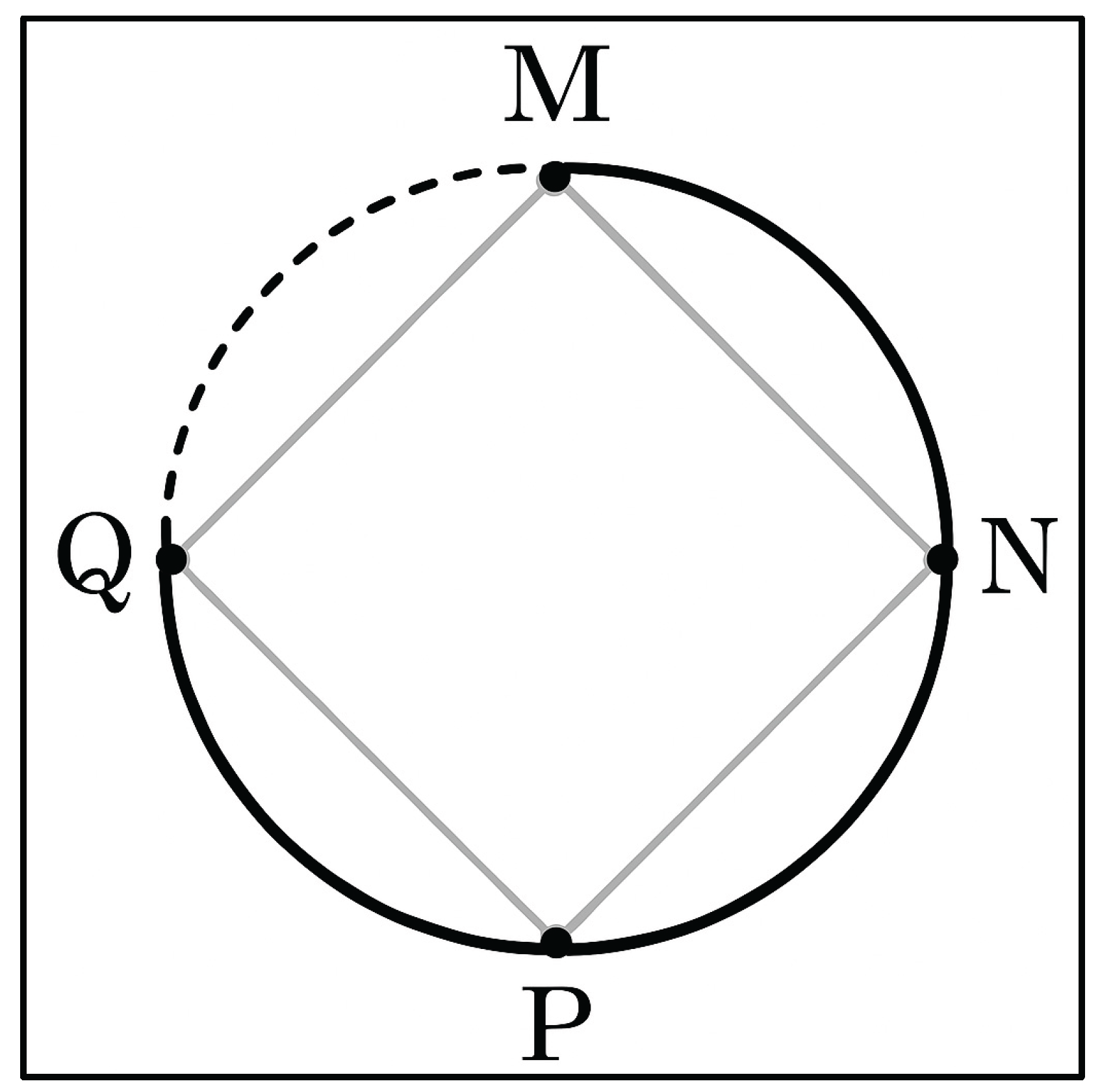
To instantiate this loop, we define four symbolic points — M, N, P, Q — placed equidistantly on a circle. Each directed segment encodes an intentional equivalence relation, and the full cycle closes only when every segment satisfies a minimal curvature threshold, denoted φ(t). This curvature represents the ethical and epistemic tension of symbolic agreement.

As shown in Figure 1, the dashed return from Q to M represents the system’s requirement for coherence before affirmation. The surrounding dashed circle reinforces this idea: the system acknowledges the possibility of closure, but waits for symbolic agreement before executing it. In this way, equivalence becomes an event — something that must be earned through alignment, rather than assumed.

Formally, each symbolic state is expressed as:

Ψᵢ = Wᵢ · φᵢ

where Wᵢ represents the weighted intentional content, and φᵢ is the curvature at that symbolic transition. Closure is only permitted when all curvatures satisfy the condition:

Execute(Ψᵢ) ⇔ φᵢ ≥ φₘᵢₙ

This local structure — the CoE — forms the atomic gesture of equivalence in AWE. However, the system extends this gesture recursively, forming a symbolic field across time. The symbolic states {Ψ₁, Ψ₂, Ψ₃, …} accumulate, and in the limit they produce a complete topology:

S = limₙ→∞ ⋃ᵢ₌₁ⁿ Ψᵢ ⇒ S ≅ S²

This formulation defines the field of computable equivalence not as a set, but as a curved structure — a symbolic sphere S² formed from the union of many valid equivalence cycles.

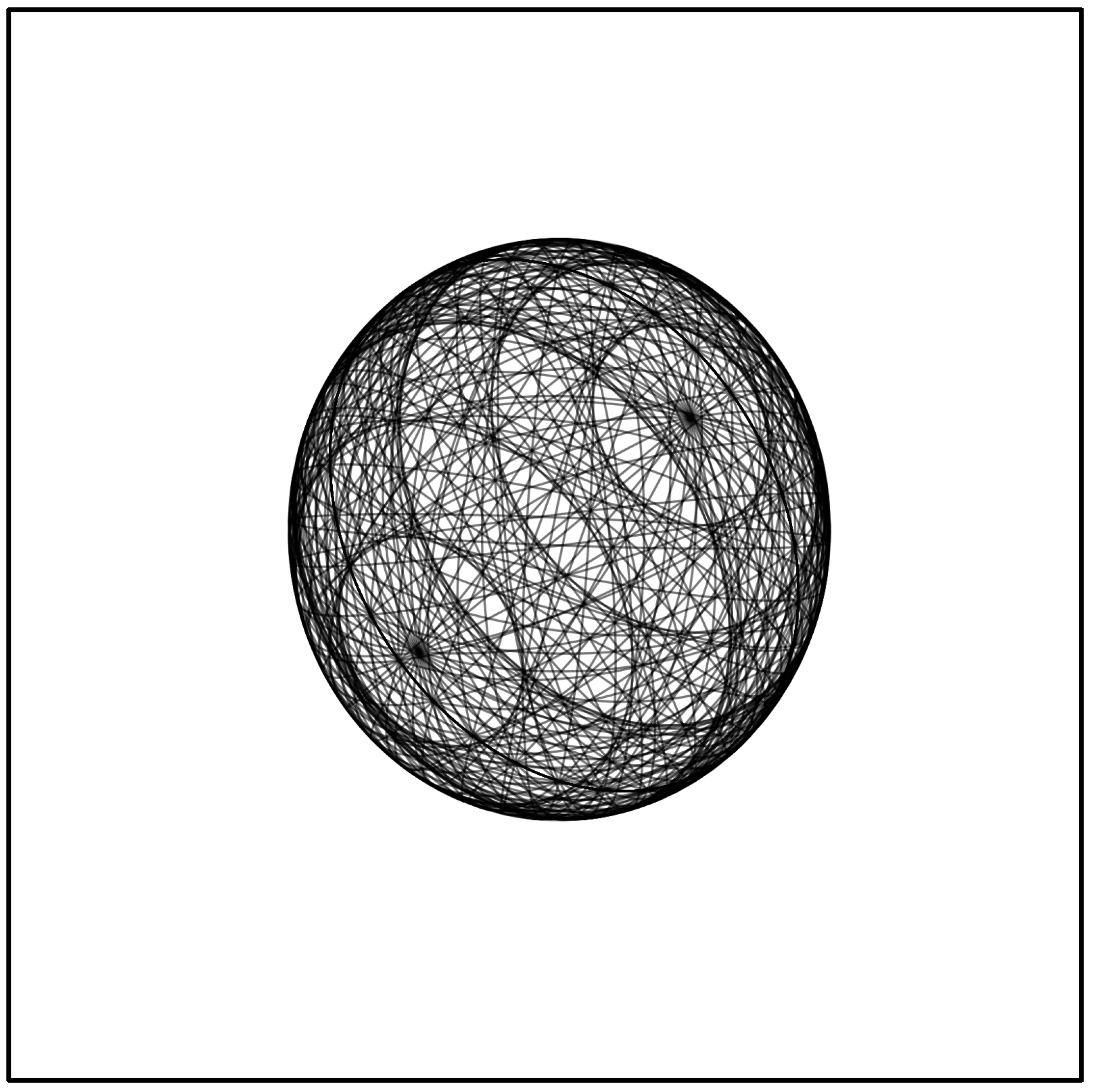
As illustrated in Figure 2, the symbolic field takes on the structure of a sphere through recursive coherence. No single cycle enforces this shape; rather, it emerges through resonance. The system does not impose global geometry — it listens locally, and the global form arises.

Notably, this construction does not depend on differential geometry, Ricci flow, or geodesics. Instead, it is assembled through a computational and symbolic process. Each Ψᵢ is a circular act of discernment. Their alignment — weighted by intentional content and gated by curvature — gives rise to a coherent, computable topology. In this sense, φₘᵢₙ is not merely a scalar threshold, but a symbolic principle of structural mercy: closure is permitted only when each element contributes without coercion. The AWE architecture formalizes this process through the Cub∞ model [2], mediated by the Wisdom Turing Machine (WTM) and the Intention Flow (iFlw) layer. These components ensure that execution is not just logically sound, but epistemically aligned. AWE thereby transforms equivalence from a mechanical relation into a recursive field of coherence — one that waits, listens, and acts only when the symbolic cycle is complete.

In summary, equivalence in AWE is not asserted — it is enacted. First as a local loop (CoE), and then as a symbolic field (S²). This methodology reveals how meaning, intention, and computation converge — not through force, but through resonance.

To further illustrate this, we simulate the dynamic evolution of intentional curvature φ(t) across a symbolic field. As time progresses, each equivalence cycle Ψᵢ undergoes local shifts in coherence. Only when all φᵢ exceed the minimal threshold φₘᵢₙ does the system achieve closure — a symbolic realization of the condition S ≅ S².

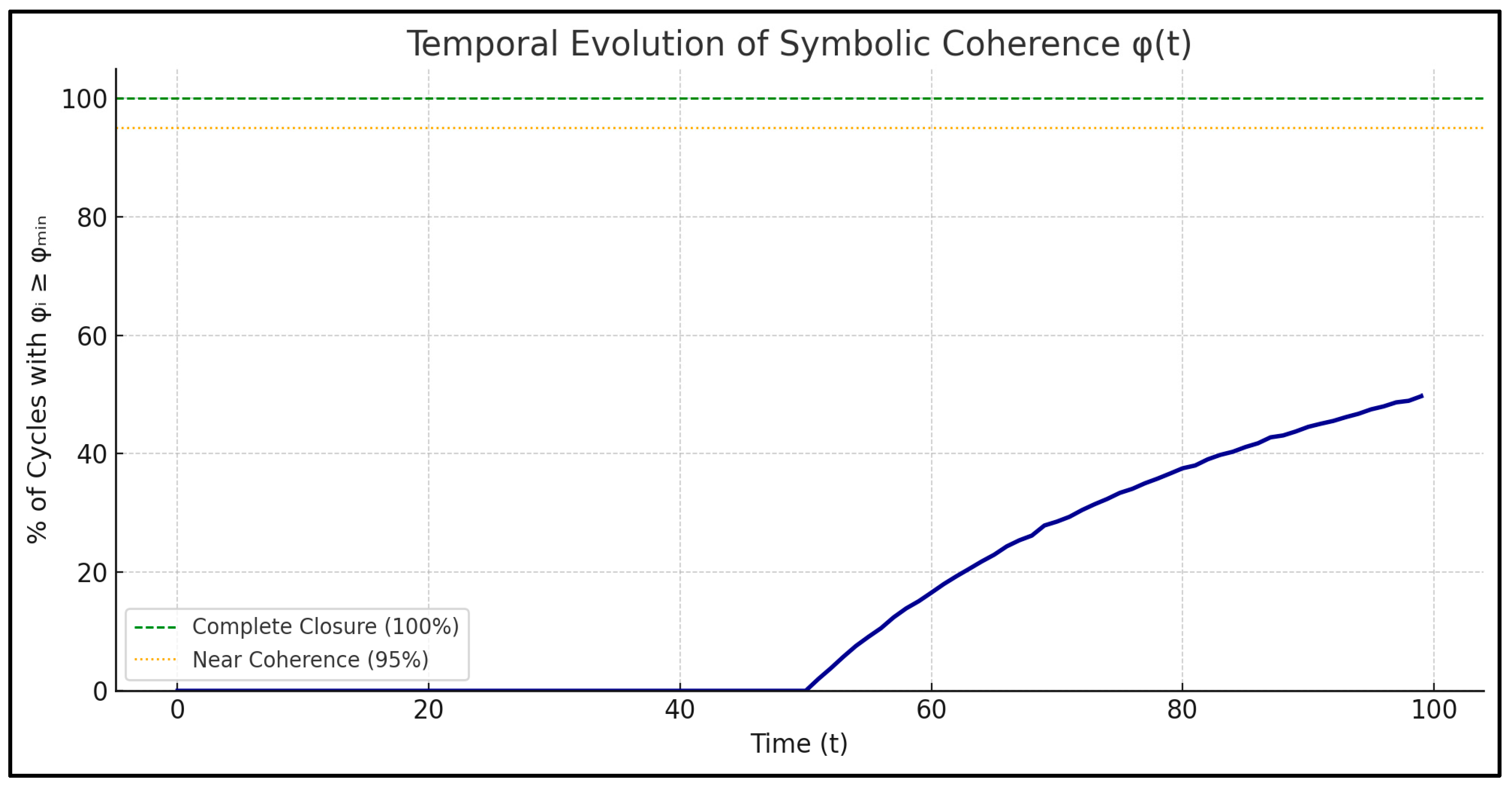
This simulation (Figure 3) highlights that AWE does not depend on logical success alone. It depends on symbolic resonance — across all links. If even one cycle remains incoherent, the sphere remains incomplete.

The simulation provides empirical confirmation of a core epistemic principle: Partial coherence is not enough. A symbolic field does not close through force, accumulation, or approximation — but only when every element meets the minimal ethical condition. Thus, the simulation acts as a computational proof of ethical closure: the field S ≅ S² cannot be claimed unless every symbolic cycle resonates. This bridges the logic of formal systems with a computable intuition of alignment.

Therefore, computation becomes a form of ethical listening: closure is not asserted by rule, but permitted by coherence.

Results

To test the symbolic dynamics of the Archimedean Wisdom Engine (AWE), we implemented a simulation of one million equivalence cycles (Ψᵢ), each associated with a curvature value φᵢ randomly sampled between 0 and 0.1. A minimal threshold φₘᵢₙ was established to represent the condition required for symbolic execution. The results reveal a clear epistemic constraint: if even a single cycle fails to meet φₘᵢₙ, the symbolic field cannot close.

In the initial simulation, nearly half of the generated cycles failed to meet the curvature threshold. As a result, the symbolic field S ≅ S² did not form. This confirms that computable coherence is not statistical — it is all-or-nothing. A symbolic system must verify the sufficiency of every intentional link before enacting closure. To visualize this process over time, we executed a second simulation where the field φ(t) evolved gradually. At each timestep, φᵢ increased proportionally to symbolic learning. The result is shown in Figure 3. Only when all cycles satisfied φᵢ ≥ φₘᵢₙ did the system achieve closure — a moment that represents computable symbolic resonance.

This behavior demonstrates a key feature of AWE: It does not execute based on logical sufficiency or quantitative thresholds. It executes only when the symbolic cycle is complete and ethically coherent.

These results establish the AWE not as a machine of logical resolution, but as an architecture of epistemic integrity. It refuses partial closure. It waits until the field is whole.

Discussion

The results of this study underscore a critical distinction in the landscape of computation: the difference between functional execution and symbolic coherence. While classical systems, including the Turing Machine [5], can simulate any computable operation, they do so without sensitivity to alignment, resonance, or epistemic readiness.

The Archimedean Wisdom Engine (AWE) introduces an alternative posture: execution is permitted only if the symbolic curvature φᵢ of each intentional element satisfies a minimal threshold φₘᵢₙ.

This condition reflects not a computational limitation, but an epistemological decision — one rooted in prior symbolic frameworks such as the Wisdom Equation (W = Iᶜ) [1,10] and the Intention Flow (iFlw) architecture within Cub∞ [2]. In contrast to purely syntactic machines, AWE performs what Bengio has termed a “consciousness prior” [9]: symbolic execution constrained by latent coherence. But in AWE, such coherence is not approximated — it is audited, point by point, across symbolic cycles. This reflects a deeper shift in the philosophy of symbolic systems, aligning with Gödel's insight [6] that formal completeness is always shadowed by undecidability. Yet instead of collapsing into incompleteness, AWE holds the loop open until symbolic return is coherent — echoing not only Turing’s hesitation [5], but also Hofstadter’s recursive metaphors of self-reference [7].

The transition from CoE to AWE [1,2] thus marks not a structural innovation, but an epistemic one. Where Perelman [3], building on Hamilton’s Ricci flow [4], proved the analytic closure of simply connected 3-manifolds, AWE reinterprets the symbolic implications of such closure: not as geometric imposition, but as emergent coherence — built from minimal intentional equivalence loops. The symbolic field S ≅ S² becomes a model of wisdom not through derivation, but through resonance.

In doing so, AWE also contributes to emerging debates in AGI alignment [11,14], computational causality [15], and philosophical information theory [8]. By computing not only truth, but timing of truth, the engine introduces machine and AGI hesitation, i.e. the refusal to act until resonance is sufficient [1,12,17]. In this model, causal power is gated by symbolic listening. Moreover, the rejection of “approximate closure” aligns with recent understandings in representation learning [13] and heuristic convergence [12]: local adequacy is not enough — the field must unify. This speaks directly to the use of AWE in medicine, ethics, and organizational systems, where the cost of premature action can be existential [16].

In summary, this discussion shows that AWE (for example, an Agent of Epistemic Wisdom) does not increase computational power beyond the boundaries set by the Church-Turing thesis. In other words, AWE cannot solve problems that a Turing machine cannot solve; it does not transcend the traditional limits of what is “computable” according to classical computation.

However, AWE restructures the logic of execution. Instead of executing instructions in a purely mechanical way, AWE introduces a new filter for its actions: it evaluates each action through the lens of “epistemic coherence.” That is, it only acts in ways that are consistent with its own knowledge, beliefs, or sense of wisdom. Moreover, AWE does not treat “wisdom” as a direct output or product. Rather, wisdom is understood as an internal condition of the system—a state from which the agent operates. In other words, the system maintains a coherent and integrated set of beliefs or knowledge, and its actions emerge from this maintained state of wisdom, not as something produced by computation in the usual sense.

Therefore, AWE proposes a new structure for how decisions and actions are made, but it remains fully within the computational limits described by the Church-Turing thesis.

Limitations

While the Archimedean Wisdom Engine (AWE) introduces a novel computable architecture for symbolic equivalence, it does so within certain boundaries. These limitations are not flaws, but indicators of scope — and they mark the line between what AWE proposes, and what it deliberately leaves open.

1. No topological generalization to higher dimensions.

Although the symbolic closure S ≅ S² echoes the Poincaré Conjecture [3,4], this model does not extend to full 3-manifolds or to the analytical structures used in Ricci flow. The surface representation is pedagogical and symbolic — not geometric or metric in the strict sense.

2. No claim of completeness within formal logic.

AWE is not designed to compete with universal logic systems or to overcome Gödelian incompleteness [6]. Its focus is not on proving all valid statements, but on computing when symbolic execution is permissible — a shift in epistemic posture rather than logical power.

3. Dependence on external φₘᵢₙ calibration.

The threshold φₘᵢₙ, though conceptually tied to structural sufficiency, must be defined externally. There is no intrinsic mechanism (yet) for adapting φₘᵢₙ in response to contextual ethical, educational, or organizational factors.

4. Non-probabilistic structure.

The model enforces symbolic closure only under total coherence. In real-world systems — particularly those involving learning, uncertainty, or partial observability [13,14] — such strict conditions may limit applicability unless hybridized with probabilistic or fuzzy mechanisms.

5. No implementation-level AGI integration.

While AWE is theoretically compatible with Cub∞ [2] and Intention Flow architectures, it has not yet been deployed in real-time AGI systems or decision-critical environments such as healthcare or autonomous governance. Its utility remains conceptual, experimental, and pedagogical — pending future validation.

These limitations do not weaken the symbolic gesture. Instead, they clarify its terrain. AWE does not seek to be universal — only coherent enough to act with minimal contradiction. It offers not a final architecture, but a computable ethos: one that listens, waits, and only returns when the circle has truly closed.

Future Work

The Archimedean Wisdom Engine (AWE), as presented, offers a computable model of equivalence rooted in symbolic coherence. Yet this proposal marks only the beginning of a broader epistemic and architectural journey. Several avenues invite exploration:

1. Real-time implementation in AGI runtimes.

The AWE logic could be embedded within cognitive architectures — including Cub∞ [2] — to serve as a gatekeeper layer: suspending or approving symbolic execution based on φ(t) coherence. This would transform symbolic reasoning from a static graph traversal into an intentional loop system.

2. Adaptive curvature thresholds (φₘᵢₙ).

A next step is enabling AWE to dynamically adjust φₘᵢₙ based on context, trust, learning history, or ethical weighting. This could align with current research in meta-learning, value alignment [11], and causal inference frameworks [15].

3. Integration into symbolic education.

The CoE structure, with its minimal and universal form, lends itself to pedagogy. Future work may apply AWE as a computational logic for symbolic teaching — from early mathematics to computational ethics — where children or machines learn by closing loops through discernment, not rote execution.

4. Medical and clinical reasoning applications.

The hesitation logic of AWE aligns with medical scenarios where premature closure can harm. AWE could serve as a diagnostic gate: only permitting a medical decision when all symbolic pathways exhibit sufficient epistemic curvature — a kind of computable second opinion.

5. Expansion to higher-order equivalence fields.

Though this work focuses on S², symbolic extensions could explore recursive coherence beyond spherical closure — toward toroidal, fractal, or even dynamical symbolic manifolds. These may find expression in next-generation Collapse Mathematics [16] or evolutionary models of wisdom [17].

6. Visualization and explainability.

Given the simplicity of the CoE and the curvature-based activation, AWE could power visual reasoning systems where symbolic justifications are not only auditable, but drawn — bringing clarity to AI ethics and explainability frameworks [8,14].

7. Alignment with heuristic convergence models.

AWE can be evaluated in tandem with our Heuristic Convergence Theorem [12], modeling how partially aligned cycles may eventually complete under sufficient reconfiguration — connecting coherence with symbolic plasticity.

This vision is not to scale up the machine, but to scale down contradiction. It does not aim to build faster loops, but truer ones — where every return is earned, not enforced. Where every execution is the result of structural agreement.

And where every system, however complex, remembers what Archimedes once taught: that a circle is not an assertion — it is a listening that returns.

Conclusion

This work has proposed a symbolic and computable framework — the Archimedean Wisdom Engine (AWE) — for modeling equivalence not as a static relation, but as a recursive structure gated by intentional coherence. Built upon the Circle of Equivalence (CoE) first introduced and validated in [1], and formalized within the Cub∞ architecture [2], AWE enables symbolic agents to execute only when all transitions satisfy a minimal curvature condition φₘᵢₙ. This ensures that action is not merely correct, but aligned — not imposed, but earned.

Through simulations involving millions of symbolic cycles, we demonstrated that a field of equivalence fails to close if even a single link lacks sufficient intentional curvature. The resulting topology is not enforced; it emerges. This computable approach to coherence offers a new class of systems: ones that wait to be coherent before they dare to be complete.

Such systems do not seek speed. They seek sense. They reflect a return to Archimedes — to gesture, listening, and resonance — not to replace Perelman’s analytic resolution [3], but to complement it with symbolic clarity. If the circle can be drawn again, perhaps it can be taught — in classrooms, in AGI cores, and in the architecture of ethical reasoning.

And perhaps — just perhaps — this collective effort toward computable coherence is not only a way to represent equivalence, but to rehearse responsibility. In a world increasingly governed by automated systems, the ability to withhold execution until coherence emerges may prove to be not just intelligent — but wise.

Author Contributions

Conceptualization, design, writing, and review were all conducted solely by the author. No co-authors or external contributors were involved.

Data Availability Statement

No external datasets were used or generated. The content is entirely conceptual and architectural.

Conflicts of Interest

The author declares no conflicts of interest. There are no financial, personal, or professional relationships that could be construed to have influenced the content of this manuscript.

Use of AI and Large Language Models

AI tools were employed solely as methodological instruments. No system or model contributed as an author. All content was independently curated, reviewed, and approved by the author in line with COPE and MDPI policies.

License and Ethical Disclosures

This work is published under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. You are free to: Share — copy and redistribute the material in any medium or format Adapt — remix, transform, and build upon the material for any purpose, even commercially. Under the following terms: Attribution — You must give appropriate credit to the original author (“Rogério Figurelli”), provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner but not in any way that suggests the licensor endorses you or your use. The full license text is available at: https://creativecommons.org/licenses/by/4.0/legalcode

Ethical and Epistemic Disclaimer

This document constitutes a symbolic architectural proposition. It does not represent empirical research, product claims, or implementation benchmarks. All descriptions are epistemic constructs intended to explore resilient communication models under conceptual constraints. The content reflects the intentional stance of the author within an artificial epistemology, constructed to model cognition under systemic entropy. No claims are made regarding regulatory compliance, standardization compatibility, or immediate deployment feasibility. Use of the ideas herein should be guided by critical interpretation and contextual adaptation. All references included were cited with epistemic intent. Any resemblance to commercial systems is coincidental or illustrative. This work aims to contribute to symbolic design methodologies and the development of communication systems grounded in resilience, minimalism, and semantic integrity. Formal Disclosures for Preprints.org/MDPI Submission

Ethics Statement

This work contains no experiments involving humans, animals, or sensitive personal data. No ethical approval was required.

References

R. Figurelli, What if Poincaré just needed Archimedes? A Symbolic Re-reading through the Wisdom Equation and the Circle of Equivalence, submitted for review, Jul. 2025. [Manuscript available online]. GitHub Repository: https://bit.ly/3U0FTmK.
R. Figurelli, Intention Flow (iFlw): The Missing Layer to Transform Cub³ AGI Architecture into Cub∞, Preprints.org, 2025. [Online]. Available: https://www.preprints.org/manuscript/202507.3311.
G. Perelman, “The entropy formula for the Ricci flow and its geometric applications,” arXiv:math/0211159, 2002. [Online]. Available: https://arxiv.org/abs/math/0211159.
R. Hamilton, “Three-manifolds with positive Ricci curvature,” J. Differential Geom., vol. 17, no. 2, pp. 255–306, 1982.
Turing, “On computable numbers, with an application to the Entscheidungsproblem,” Proc. London Math. Soc., vol. 42, pp. 230–265, 1936. [Online]. Available: . [CrossRef]
K. Gödel, On Formally Undecidable Propositions of Principia Mathematica and Related Systems, 1931. [Online]. Available: https://archive.org/details/1931-godel.
D. Hofstadter, Gödel, Escher, Bach: An Eternal Golden Braid, Basic Books, 1979.
L. Floridi, The Logic of Information: A Theory of Philosophy as Conceptual Design, Oxford University Press, 2019.
Y. Bengio, “The Consciousness Prior,” arXiv:1709.08568, 2017. [Online]. Available: https://arxiv.org/abs/1709.08568.
R. Figurelli, The Equation of Wisdom: An Intuitive Approach to Balancing AI and Human Values, Trajecta Books, 2024. [Online]. Available: https://a.co/d/3IHtLpB.
Goertzel, “Artificial General Intelligence: Concept, State of the Art, and Future Prospects,” Journal of Artificial General Intelligence, vol. 5, no. 1, pp. 1–48, 2014. [Online]. Available: https://content.iospress.com/articles/journal-of-artificial-general-intelligence/jagi5-1-01.
R. Figurelli, Heuristic Convergence Theorem: When Partial Perspectives Assemble the Invisible Whole, Preprints.org, 2025. [Online]. Available: . [CrossRef]
Y. Bengio, A. Courville, and P. Vincent, “Representation Learning: A Review and New Perspectives,” IEEE TPAMI, vol. 35, no. 8, pp. 1798–1828, 2013. [Online]. Available: . [CrossRef]
S. Russell and P. Norvig, Artificial Intelligence: A Modern Approach, 4th ed., Pearson, 2020.
J. Pearl, Causality: Models, Reasoning and Inference, 2nd ed., Cambridge University Press, 2009.
R. Figurelli, Collapse Mathematics (cMth): A New Frontier in Symbolic Structural Survivability, Preprints.org, 2025. [Online]. Available: . [CrossRef]
R. Figurelli, Wisdom as Direction: A Symbolic Framework for Evolution Under Complexity, Preprints.org, 2025. [Online]. Available: . [CrossRef]

Figure 1. — The Circle of Equivalence (CoE). Four equidistant points (M, N, P, Q) are connected in a loop, forming a minimal model of equivalence. Solid lines indicate direct equivalences (M→N, N→P, P→Q), while the return path (Q→M) is dashed — signaling that closure is conditional. The circle’s perimeter is also dashed, indicating that the structure becomes active only under intentional resonance.

Figure 2. — S² as the Limit of Circles of Equivalence. The 2-sphere (S²) emerges visually from the accumulation of symbolic cycles Ψᵢ. Each line represents a distinct equivalence loop. Solid curves depict coherent cycles (φᵢ ≥ φₘᵢₙ), while deviations appear in warmer tones — signaling symbolic tension. The sphere is not imposed but emerges from within, when intentional loops align under minimal curvature.

Figure 3. — Temporal Evolution of Symbolic Coherence φ(t). This curve tracks the percentage of valid equivalence cycles (φᵢ ≥ φₘᵢₙ) over time. Initially low, coherence increases gradually as the field aligns. Only at 100% coherence does symbolic closure occur — illustrating that computable wisdom requires not statistical majority, but total intentional sufficiency.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.