Submitted:
09 July 2025
Posted:
11 July 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
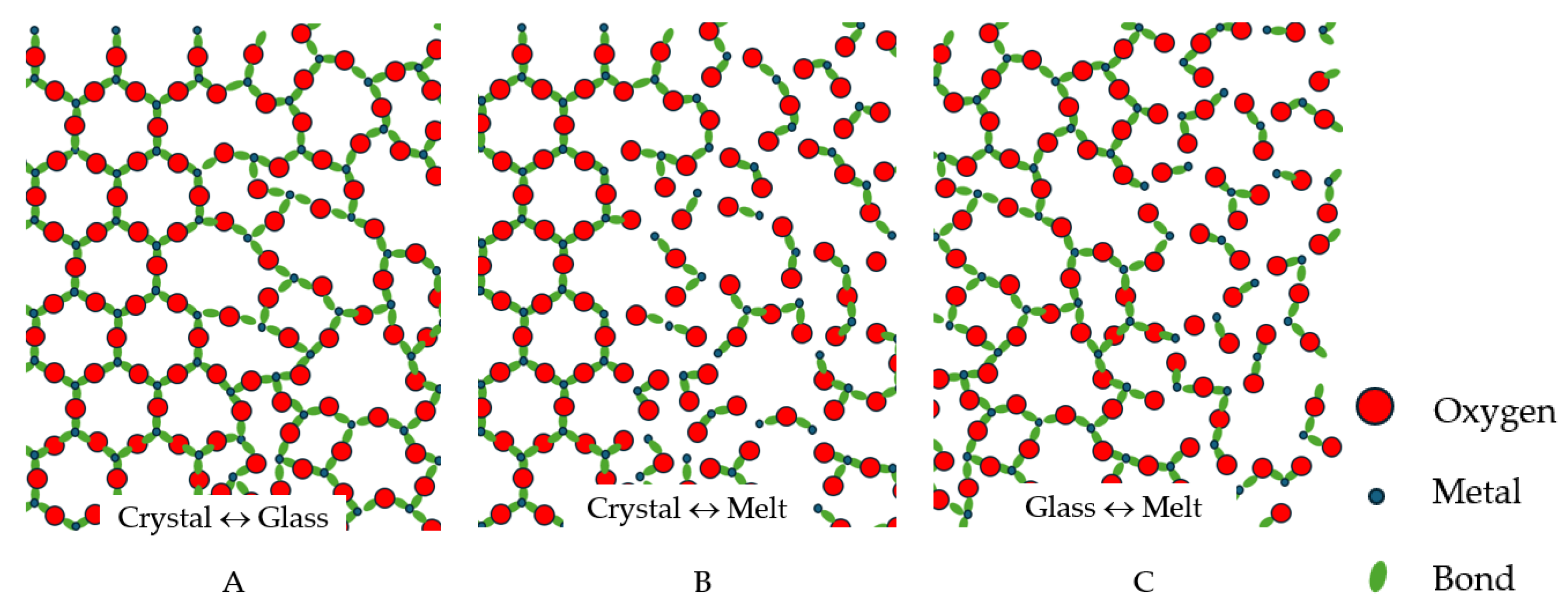
2. Structural Differences Between Glasses and Melts
3. Role of Configurons in the Phase Transformation
- Universality – all disordered systems should exhibit percolation-type transformations from solid-like at higher degrees of connectivity (e.g. lower temperatures) to liquid-like (plastic) at lower degrees of connectivity at higher temperatures.
- Singularities for derivative parameters – thermal expansion, heat capacity, shear modulus, and other properties of glasses show a relatively sudden change at the glass transition temperature. Derivative parameters of amorphous materials thus show typical features of second-order phase transformations e.g. theoretically they diverge at Tg.
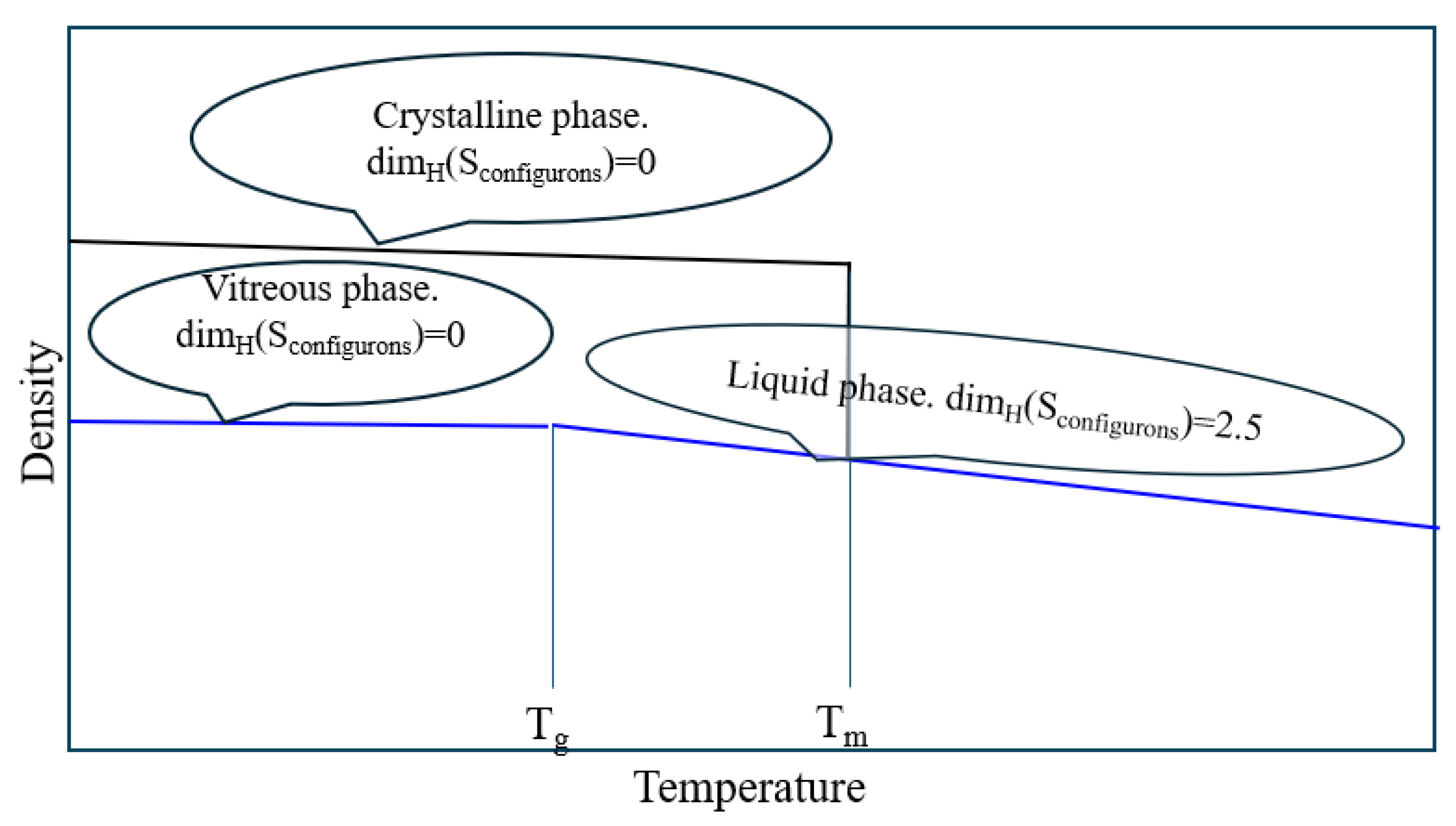
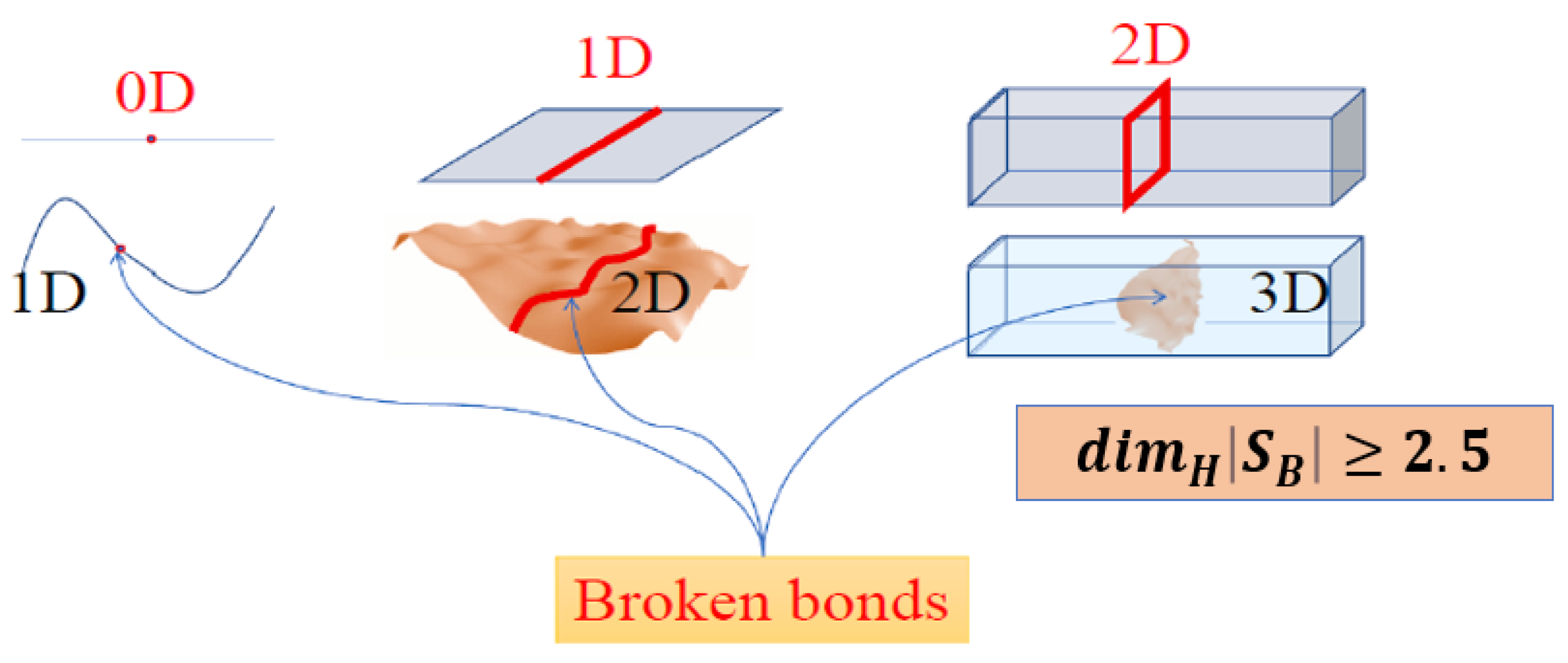
- Dimensionality change - the HB dimensionality of the system of configurons (broken bonds) changes at Tg from 0 in glasses to fractal DH ≈ 2.5 for melts.
- Dynamic (twinkling) fractals – The glass–liquid transition is accompanied by the formation of a percolation macroscopic cluster made up of broken bonds – configurons – which is dynamic in nature — similar to Wool's twinkling fractals [63,64,65]. The cluster is dynamical and changes with time due to configuron diffusion. Nonetheless, at any moment of time there, is a percolating cluster made of configurons above the Tg whereas no such macroscopic clusters can be seen in the glassy state e.g. below the Tg. The characteristic linear scale which describes the branch sizes of dynamic clusters formed by configurons is the correlation length ξ(T);
- Fractal medium range order – the higher cooling rate the larger remnant fractal cluster frozen at liquid–glass transition. Correlation length gives the average size of clusters made of broken bonds at T < Tg. At T > Tg it shows the average size of atomic clusters formed. Second-order phase transitions in ordered substances are typically associated with a change in the crystal lattice symmetry, and the symmetry is lower in the ordered phase than in the less ordered phase. In the spirit of Landau's ideas, the transition from a glass to a liquid spontaneously breaks the symmetry of bonds e.g. of the configuron system. At glass–liquid transition the amorphous material changes the group of isometries from the Euclidian to the fractal space group of isometries at length scales smaller than ξ(T).
- Two activation energies of viscosity – the viscous flow has a variable activation energy above the glass transition temperature Q(T) which is high for glasses and low at high temperatures (Table 2).
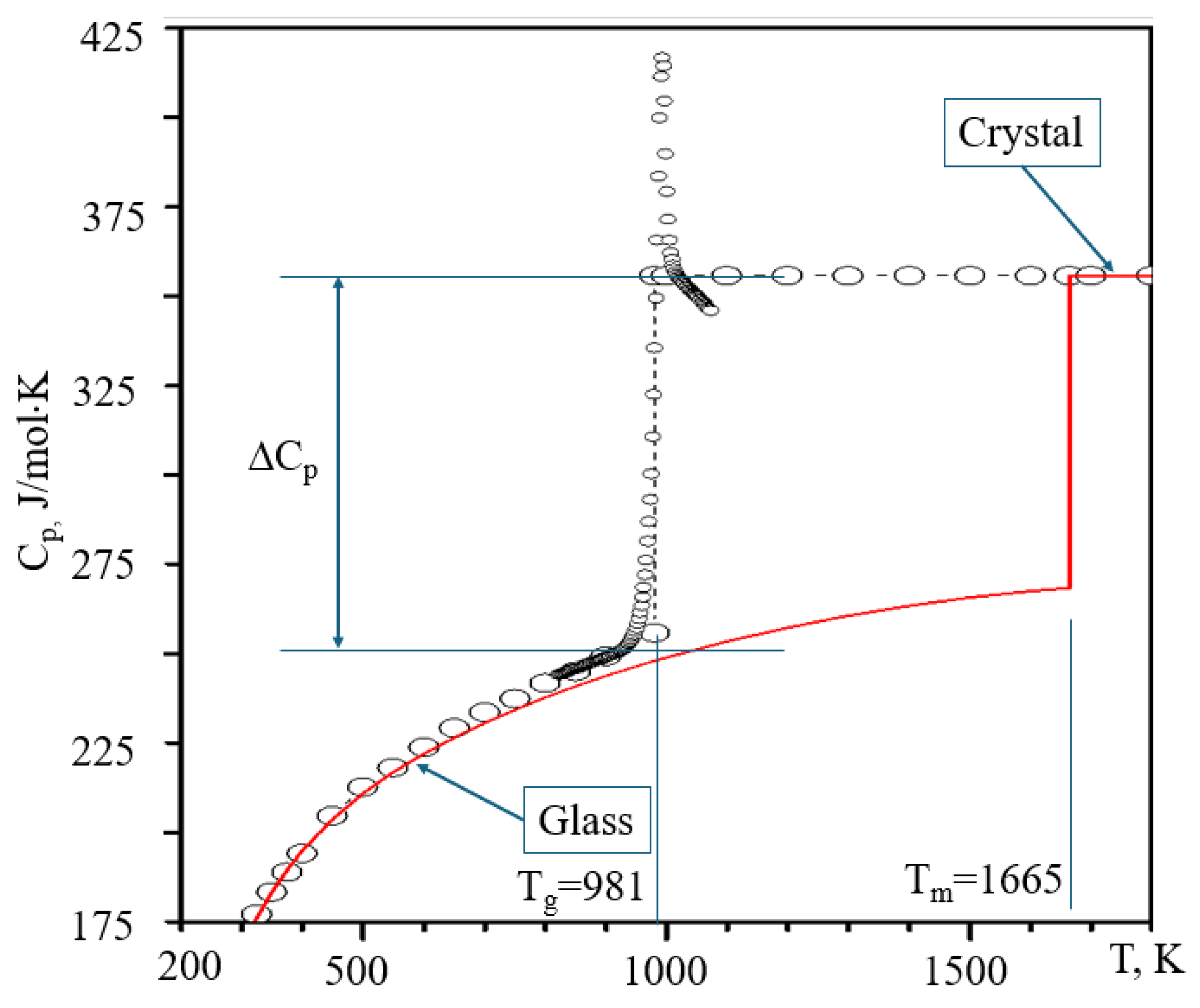
4. The Jump of Heat Capacity
5. Melting Criteria
6. Importance of Bonds Breakage
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CET | Coefficient of thermal expansion |
| CPT | Configuron percolation theory |
| DSC | Differential scanning calorimetry |
| HB | Hausdorff-Besicovitch dimensionality |
| MRO | medium-range order |
| SRO | short-range order |
References
- J.D. Musgraves, J. Hu, L. Calvez (Eds.), Springer Handbook of Glass, Springer Handbooks, Springer Nature Switzerland AG 2019, Cham. 2019, 1851 p. [CrossRef]
- D.S. Sanditov, M.I. Ojovan, M.V. Darmaev. Glass transition criterion and plastic deformation of glass. Physica B, 582, 411914, (2020). [CrossRef]
- J.W.P. Schmelzer, T.V. Tropin. Glass Transition, Crystallization of Glass-Forming Melts, and Entropy. Entropy 2018, 20, 103; [CrossRef]
- M.I. Ojovan, W.E. Lee. Connectivity and glass transition in disordered oxide systems. J. Non-Cryst. Solids, 356, 2534-2540 (2010). [CrossRef]
- M.G. Vasin. Glass transition as a topological phase transition. Phys. Rev E 106, 044124 (2022). [CrossRef]
- M. Gori, R. Franzosi, G. Pettini, M. Pettini. Topological Theory of Phase Transitions. J. Phys. A: Math. Theor. 55 (2022) 375002 (34pp). [CrossRef]
- Vesperini, R. Franzosi, M. Pettini. The Glass Transition: A Topological Perspective. (2024). [CrossRef]
- Z. Nussinov, N. B. Weingartner, F. S. Nogueira. The “glass transition” as a topological defect driven transition in a distribution of crystals and a prediction of a universal viscosity collapse. In: Topological Phase Transitions and New Developments. Eds. L. Brink, M. Gunn, J.V. José, J.M. Kosterlitz, K.K. Phua, World Scientific, pp. 61-79. (2018). [CrossRef]
- de Candia, A., Fierro, A., Coniglio, A. Scaling and universality in glass transition. Sci. Rep. 6, 26481; (2016). [CrossRef]
- M.I. Ojovan. Glass formation in amorphous SiO2 as a percolation phase transition in a system of network defects. J. Exp. Theor. Phys. Let., 79 (12) 632-634 (2004). [CrossRef]
- M.I. Ojovan, W.E. Lee. Topologically disordered systems at the glass transition. J. Phys.: Condensed Matter, 18, 11507-11520 (2006). [CrossRef]
- M.I. Ozhovan. Topological characteristics of bonds in SiO2 and GeO2 oxide systems at glass-liquid transition. J. Exp. Theor. Phys., 103 (5) 819-829 (2006). [CrossRef]
- M.I. Ojovan. Configurons: thermodynamic parameters and symmetry changes at glass transition. Entropy, 10, 334-364 (2008). [CrossRef]
- M. Ojovan. Glass formation.. Chapter 3.1 in P. Richet, R. Conradt, A. Takada, J. Dyon. Encyclopedia of Glass Science, Technology, History, and Culture. Wiley, Hoboken, NJ, 2021. 1568 p., pp. 249-259. [CrossRef]
- Ojovan, M.I., Tournier R.F. On structural rearrangements near the glass transition temperature in amorphous silica. Materials 2021, 14. 19 pp. [CrossRef]
- V. Županović, D. Žubrinić, Fractal Dimensions in Dynamics. J.-P. Françoise, G.L. Naber, T.S. Tsun, Encyclopedia of Mathematical Physics, Academic Press, 2006, 394-402, ISBN 9780125126663. [CrossRef]
- C.A. Angell, W. Sichina: Thermodynamics of the glass transition: Empirical aspects, Ann. N.Y. Acad. Sci. 279, 53–67 (1976). [CrossRef]
- C.A. Angell: Formation of glasses from liquids and biopolymers, Science 267, 1924–1935 (1995).
- Kittel, C. Introduction to solid state physics; J. Wiley and Sons Inc.: New York, 1996.
- Richert, R. Heterogeneous dynamics in liquids: fluctuations in space and time. J. Phys.: Condens. Matter 2002, 14, R703-R738. [CrossRef]
- J. Holubova, Z. Černošek, E. Cernoskova, M. Liska. Isothermal structural relaxation: temperature and time dependencies of relaxation parameters, J. Non-Cryst. Solids 326, 135–140 (2003). [CrossRef]
- J. Machacek, O. Gedeon, M. Liska. Group connectivity in binary silicate glasses, J. Non-Cryst. Solids 352, 2173–2179 (2006). [CrossRef]
- Fluegel: Glass viscosity calculation based on a global statistical modelling approach, Glass Technol. 48(1), 13–30 (2007).
- J.C. Mauro, Y. Yue, A.J. Ellison, P.K. Gupta, D.C. Allan. Viscosity of glass-forming liquids, Proc. Natl. Acad. Sci. 106(47), 19780–19784 (2009). [CrossRef]
- Q. Zheng, J.C. Mauro: Viscosity of glass forming systems, J. Am. Ceram. Soc. 100, 6–25 (2017).
- U. Fotheringham. Viscosity of glass and glass-forming melts. In: J.D. Musgraves, J. Hu, L. Calvez (Eds.), Springer Handbook of Glass, Springer Handbooks. (2019). [CrossRef]
- P. Richet, R. Conradt, A. Takada, J. Dyon. Encyclopedia of Glass Science, Technology, History, and Culture. Wiley, Hoboken, NJ, 2021. 1568 p. https://onlinelibrary.wiley.com/doi/book/10.1002/9781118801017.
- D.V. Louzguine-Luzgin, R. Belosludov, M. Saito, Y. Kawazoe, A. Inoue. Glass-transition behavior of Ni: Calculation, prediction, and experiment. J. Appl. Phys. 104, 123529 (2008). [CrossRef]
- J.C. Dyre. Colloquium: The glass transition and elastic models of glass-forming liquids. Rev. Mod. Phys. 78, 953–972 (2006). [CrossRef]
- R.F. Tournier, M.I. Ojovan. Undercooled phase behind the glass phase with superheated medium-range order above glass transition temperature. Physica B: Condensed Matter, 602, 412542, 17 pp.. (2021). [CrossRef]
- M.I. Ojovan. The Modified Random Network (MRN) Model within the Configuron Percolation Theory (CPT) of Glass Transition. Ceramics, 4 (2):121-134 (2021). [CrossRef]
- Tournier, R.F.; Ojovan, M.I. Prediction of Second Melting Temperatures Already Observed in Pure Elements by Molecular Dynamics Simulations. Materials, 2021, 14, 6509 (2021). [CrossRef]
- Tournier, R.F.; Ojovan, M.I. NiTi2, a New Liquid Glass. Materials 2023, 16, 6681. [CrossRef]
- D.S. Sanditov. M.I. Ojovan. On relaxation nature of glass transition in amorphous materials. Physica B, 523, 96–113. (2017). [CrossRef]
- D.S. Sanditov, M.I. Ojovan. Relaxation aspects of the liquid—glass transition. Physics Uspekhi 62 (2) 111 - 130 (2019). [CrossRef]
- Ojovan, M.I. On Viscous Flow in Glass-Forming Organic Liquids. Molecules 2020, 25 (17), 4029, 13 p. (2020). [CrossRef]
- Ojovan, M.I. The Flow of Glasses and Glass–Liquid Transition under Electron Irradiation. Int. J. Mol. Sci. 2023, 24, 12120. [CrossRef]
- Bruns, S., Durst, K., Local crack suppression and activation of plastic flow via electron irradiation in oxide glasses, Materials & Design (2025). [CrossRef]
- P.Y. Huang, S. Kurasch, A. Srivastava, V. Skakalova, J. Kotakoski, A.V. Krasheninnikov, R. Hovden, Q. Mao, J.C. Meyer, J. Smet, D.A. Muller, U. Kaiser. Direct Imaging of a Two-Dimensional Silica Glass on Graphene. Nano Letters, 12, 1081-1086 (2012). [CrossRef]
- Khouchaf, L., Boulahya, K., Das, P. P., Nicolopoulos, S., Kis, V. K., & Lábár, J. L. (2020). Study of the Microstructure of Amorphous Silica Nanostructures Using High-Resolution Electron Microscopy, Electron Energy Loss Spectroscopy, X-ray Powder Diffraction, and Electron Pair Distribution Function. Materials, 13 (19), 4393. [CrossRef]
- Wendt, H. H.; Abraham, F. F. Empirical Criterion for the Glass Transition Region Based on Monte Carlo Simulations. Phys. Rev. Lett. 1978, 41, 1244−1246. [CrossRef]
- M.I. Ojovan, D.V. Louzguine-Luzgin. Revealing Structural Changes at Glass Transition via Radial Distribution Functions. J. Phys. Chem. B, 124 (15), 3186-3194 (2020. [CrossRef]
- Scher, H.; Zallen, R. Critical Density in Percolation Processes. J. Chem. Phys. 1970, 53, 3759−3761. [CrossRef]
- Isichenko, M.B. Percolation, statistical topography, and transport in random media. Rev. Mod. Phys. 1992, 64, 961–1043. [CrossRef]
- N. Mattern, H. Hermann, S. Roth, J. Sakowski, M-P. Macht, P. Jovari, J. Jiang. Structural behavior of Pd40Cu30Ni10P20 bulk metallic glass below and above the glass transition. Appl. Phys. Lett., 82 (16) 2589-2591 (2003). [CrossRef]
- Egami, T. & Billinge, S. J. L. Underneath the Bragg Peaks: Structural Analysis of Complex Materials, Pergamon, 2003.
- T. Egami, C.W. Ryu. Origin of medium-range atomic correlation in simple liquids: Density wave theory. AIP Advances 13, 085308 (2023). [CrossRef]
- J. Du. Molecular Dynamics Simulations of Oxide Glasses. In: J.D. Musgraves, J. Hu, L. Calvez (Eds.), Springer Handbook of Glass, Springer Handbooks. https://doi.org/10.1007/978-3-319-93728-1_32. [CrossRef]
- Y. Yang, J. Zhou, F. Zhu, Y. Yuan, D.J. Chang, D.S. Kim, M. Pham, A. Rana, X. Tian, Y. Yao, S.J. Osher, A.K. Schmid, L. Hu, P. Ercius, J. Miao. Determining the three-dimensional atomic structure of an amorphous solid. Nature 592, 60 (2021. [CrossRef]
- P. Benigni. CALPHAD modeling of the glass transition for a pure substance, coupling thermodynamics and relaxation kinetics. CALPHAD: Computer Coupling of Phase Diagrams and Thermochemistry 72 (2021) 102238. [CrossRef]
- C.A. Becker, J. Ågren, M. Baricco, Q. Chen, S.A. Decterov, U.R. Kattner, J. H. Perepezko, G.R. Pottlacher, M. Selleby, Thermodynamic modelling of liquids: CALPHAD approaches and contributions from statistical physics, Phys. Status Solidi 52 (2014) 33–52. [CrossRef]
- J. Ågren, Thermodynamics of supercooled liquids and their glass transition, Phys. Chem. Liq. 18 (1988) 123–139. [CrossRef]
- P.B. Macedo, W. Capps, T.A. Litovitz, Two-state model for the free volume of vitreous B2O3, J. Chem. Phys. 44 (1966) 3357–3364. [CrossRef]
- S.A. Langer, A.T. Dorsey, J.P. Sethna, Entropy distribution of a two-level system: an asymptotic analysis, Phys. Rev. B 40 (1989) 345–352. [CrossRef]
- S.A. Langer, J.P. Sethna, E.R. Grannan, Nonequilibrium entropy and entropy distributions, Phys. Rev. B 41 (1990) 2261–2278. [CrossRef]
- V. Halpern, J. Bisquert, The effect of the cooling rate on the fictive temperature in some model glassy systems, J. Chem. Phys. 114 (2001) 9512–9517. [CrossRef]
- J. Bisquert, Master equation approach to the non-equilibrium negative specific heat at the glass transition, Am. J. Phys. 73 (2005) 735–741. [CrossRef]
- J. Bisquert, F. Henn, J.C. Giuntini, A simple model of entropy relaxation for explaining effective activation energy behavior below the glass transition temperature, J. Chem. Phys. 122 (2005) 1–9. [CrossRef]
- Takada, R. Conradt, P. Richet, Residual entropy and structural disorder in glass: a two-level model and a review of spatial and ensemble vs. temporal sampling, J. Non-Cryst. Solids 360 (2013) 13–20. [CrossRef]
- H. Jabraoui, S. Ouaskit, J. Richard, J.-L. Garden, Determination of the entropy production during glass transition: theory and experiment, J. Non-Cryst. Solids 533 (2020) 119907. [CrossRef]
- G. Adam, J. Gibbs: On the temperature dependence of cooperative relaxation properties in glass-forming liquids, J. Chem. Phys. 43, 139–146 (1965). [CrossRef]
- M.I. Ojovan. Ordering and structural changes at the glass-liquid transition. J. Non-Cryst. Solids, 382, 79-86 (2013). [CrossRef]
- R.P. Wool. Twinkling fractal theory of the glass transition. J. Polym. Sci. B Polym. Phys. 46 (2008) 2765–2778. [CrossRef]
- R.P. Wool, A. Campanella. Twinkling fractal theory of the glass transition: Rate dependence and time–temperature superposition. J. Polym. Sci. B Polym. Phys. 47 (2009) 2578–2589. [CrossRef]
- Stanzione, J. F., III; Strawhecker, K. E.; Wool, R. P. Observing the Twinkling Nature of the Glass Transition. J. Non-Cryst. Solids 2011, 357, 311−319.
- Hrma, P.; Ferkl, P.; Kruger, A.A. Arrhenian to non-Arrhenian crossover in glass melt viscosity. J. Non-Cryst. Solids 2023, 619, 122556.
- Ojovan, M.I.; Louzguine-Luzgin, D.V. On Crossover Temperatures of Viscous Flow Related to Structural Rearrangements in Liquids. Materials 2024, 17, 1261. [CrossRef]
- Ojovan, M.I.; Louzguine-Luzgin, D.V. The Minima of Viscosities. Materials 2024, 17, 1822. (12 p.). [CrossRef]
- J.J. Ludlam, S.N. Taraskin, S.R. Elliott, D.A. Drabold. Universal features of localized eigenstates in disordered systems. J. Phys.: Condens. Matter 17 (2005) L321–L327. [CrossRef]
- Lagendijk, B. van Tiggelen, D.S. Wiersma. Fifty years of Anderson localization. Physics Today 62 (8), 24–29 (2009). [CrossRef]
- A.D. Mirlin. Statistics of energy levels and eigenfunctions in disordered systems. Physics Reports 326 (2000) 259-382. [CrossRef]
- P.W. Anderson. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 109 (5) 1492-1505 (1958). [CrossRef]
- S.A. Dembovsky. Symmetry of a liquid and symmetry breaking at the glass transition. Physics Letters A 238 (1998) 315-321. [CrossRef]
- Salmon, P.S.: Order within disorder. Nature Materials 1(2), 87–88 (2002). [CrossRef]
- Zhou, Y., Xue, D., Tian, Y., et al.: Direct evidence for local symmetry breaking during a strain glass transition. Physical review letters 112(2), 025701 (2014). [CrossRef]
- Drozd-Rzoska, A., Rzoska, S.J., Starzonek, S.: New paradigm for configurational entropy in glass-forming systems. Scientific Reports 12(1), 1–9 (2022). [CrossRef]
- Albert, S.; Bauer, Th.; Michl, M.; Biroli, G.; Bouchaud, J.-P.; Loidl, A.; Lunkenheimer, P.; Tourbot, R.; Wiertel-Gasquet, C.; Ladieu, F. Fifth-order Susceptibility Unveils Growth of Thermodynamic Amorphous Order in Glass-formers. Science 2016, 352, 1308−1311. [CrossRef]
- Sanditov, D. S. Model of Delocalized Atoms in the Physics of the Vitreous State. J. Exp. Theor. Phys. 2012, 115, 112−124. [CrossRef]
- IUPAC. Compendium of Chemical Terminology; Royal Society of Chemistry: Cambridge. U.K., 1997; Vol. 66, p 583.
- Zheng, Q.; Zhang, Y.; Montazerian, M.; Gulbiten, O.; Mauro, J.C.; Zanotto, E.D.; Yue, Y. Understanding glass through differential scanning calorimetry. Chem. Rev. 2019, 119, 7848–7939. [CrossRef]
- J. Frenkel, Kinetic Theory of Liquids. Clarendon, Oxford, 1946.
- Frenkel, J. Über die Wärmebewegung in festen und flüssigen Körpern. Z. Physik, 1926, 35, 652–669 (1926). [CrossRef]
- D.C. Wallace. Statistical mechanics of monatomic liquids. Phys. Rev. E, 56 (4), 4179-4186 (1997). [CrossRef]
- D.C. Wallace. Liquid dynamics theory of high-temperature specific heat. Phys. Rev. E, 57 (2), 1717-1722 (1998). [CrossRef]
- H.B. Ke, P. Wen, W.H. Wang. The inquiry of liquids and glass transition by heat capacity. AIP Advances 2, 041404 (2012); [CrossRef]
- M.B. Tang, W.H. Wang, L. Xia, J.T. Zhao. Constant-volume heat capacity at glass transition. Journal of Alloys and Compounds 577 (2013) 299–302.
- C. Cockrell, R.W. Grimes. Crossover in atomic mobility underlying the glass transition in inorganic glasses. J. Phys.: Condens. Matter 37 (2025) 095402 (11pp). [CrossRef]
- K. Shirai, K. Watanabe, H. Momida, S. Hyun. First-principles study on the specific heat jump in the glass transition of silica glass and the Prigogine-Defay ratio. arXiv:2202.09088v1 [cond-mat.soft] 18 Feb 2022. 20 p. [CrossRef]
- Conradt, R. (2019). Thermodynamics and Kinetics of Glass. In: Musgraves, J.D., Hu, J., Calvez, L. (eds) Springer Handbook of Glass. Springer Handbooks. Springer, Cham. pp. 51-77. [CrossRef]
- R.A. Konchakov, A.S. Makarov, G.V. Afonin, J.C. Qiao, M.G. Vasin, N.P. Kobelev, V.A. Khonik. Critical behavior of the fluctuation heat capacity near the glass transition of metallic glasses. Journal of Non-Crystalline Solids 619 (2023) 122555. [CrossRef]
- I.S. Klein, C.A. Angell. Excess thermodynamic properties of glassforming liquids: The rational scaling of heat capacities, and the thermodynamic fragility dilemma resolved. J. Non-Cryst. Solids 451 (2016) 116–123. [CrossRef]
- D.V. Louzguine, S. Sobu, A. Inoue. The influence of scandium in effecting fragile to strong glass transition in aluminium-based alloys. Appl. Phys. Lett., 85 (17) 3758-3759 (2004). [CrossRef]
- M.M. Vopson, N. Rogers, I. Hepburn. The generalized Lindemann melting coefficient. Solid State Communications 318 (2020) 113977. [CrossRef]
- Melting. Encyclopaedia Britanica. https://www.britannica.com/science/melting (accessed 1.02.2025).
- F.A. Lindemann. Über die Berechnung molekularer Eigenfrequenzen. Physikalische Zeitschrift. 11 (14) 609–614 (1910).
- M. Born, Thermodynamics of Crystals and Melting. The Journal of Chemical Physics. 7 (8) 591–603 (1939). [CrossRef]
- M. Born, Proc. Cambridge Philos. Soc. 36, 160 (1940); M. Born, K. Huang, Dynamical Theory of Crystal Lattices. Clarendon, Oxford (1956).
- F.A. Lindemann, The calculation of molecular vibration frequencies, Phys. Z. 11 (1910) 609–614.
- J.J. Gilvarry, The Lindemann and grüneisen laws, Phys. Rev. 102 (2) (1956) 308–316.
- R. Guardiola, J. Navarro, On the Lindemann criterion for quantum clusters at very low temperature, J. Phys. Chem. 115 (2011) 6843–6850. [CrossRef]
- V. Lubchenko. A Universal Criterion of Melting. J. Phys. Chem. B 2006, 110, 18779-18786. [CrossRef]
- D.S. Sanditov. A criterion for the glass–liquid transition. Journal of Non-Crystalline Solids 385 (2014) 148–152. [CrossRef]
- R.F. Tournier. Lindemann’s rule applied to the melting of crystals and ultra-stable glasses. Chemical Physics Letters 651 (2016) 198–202. [CrossRef]
- Tournier, R.F.; Ojovan, M.I. Multiple Melting Temperatures in Glass-Forming Melts. Sustainability, 2022, 14, 2351. [CrossRef]
- S.A. Khrapak. Lindemann melting criterion in two dimensions. Phys. Rev. Res. 2, 012040(R) (2020). [CrossRef]
- J. Wang, J. Li, S. Yip, S. Phillpot, D. Wolf. Mechanical instabilities of homogeneous crystals. Phys. Rev. B, 52 (17) 12627-12635 (1995). [CrossRef]
- D.V. Louzguine-Luzgin, R.V. Belosludov, M.I. Ojovan. Room-temperature Pressure-induced Phase Separation in Glassy Alloys. Materials Today Communications, 2024, 109453. [CrossRef]
- Angell, C.A.; Rao, K.J. Configurational excitations in condensed matter, and “bond lattice” model for the liquid-glass transition. J. Chem. Phys. 1972, 57, 470-481.
- Bunde, S. Havlin, Fractals and Disordered Systems, Springer-Verlag, Berlin, Heidelberg, 1996.
- D. Stauffer, A. Aharony, Introduction to Percolation Theory, Taylor & Francis, London, 1994.
- K.J. Schrenk, N. Posé, J.J. Kranz, L.V.M. van Kessenich, N.A.M. Araújo, H.J. Herrmann, Percolation with long-range correlated disorder, Phys. Rev. E 88 (2013) 052102. [CrossRef]
- P. Richet, Y. Bottinga, L. Denielou, J.P. Petitet, C. Tequi, Thermodynamic properties of quartz, cristobalite and amorphous SiO2: drop calorimetry measurements between 1000 and 1800 K and a review from 0 to 2000 K, Geochimica et Cosmochimica Acta, 46, 12, 1982, 2639-2658. [CrossRef]
- G.J. Dienes. Frequency Factor and Activation Energy for the Volume Diffusion of Metals. J. Appl. Phys. 21 (1950) 1189-1192. [CrossRef]
- D.P. Almond, A.R. West. The activation entropy for transport in ionic conductors. Solid State Ionics 23 (1987) 27–35. [CrossRef]
- Bolmatov, D.; Brazhkin, V.; Trachenko, K. The phonon theory of liquid thermodynamics. Sci. Rep. 2012, 2, 421. [CrossRef]
- Bolmatov, D. The Phonon Theory of Liquids and Biological Fluids: Developments and Applications. J. Phys. Chem. Lett. 2022, 13, 7121–7129. [CrossRef]
- Trachenko, K. Theory of Liquids: From Excitations to Thermodynamics; Cambridge University Press: Cambridge, UK, 2023.
- Glova, M. Karttunen. Learning glass transition temperatures via dimensionality reduction with data from computer simulations: Polymers as the pilot case. J. Chem. Phys. 161, 184902 (2024. [CrossRef]
- E. Noether. Invariante Variations probleme. Nachr. v. d. Ges. d. Wiss. zu Göttingen 1918, pp 235-257.
- R. P. Feynman and S. Weinberg, Elementary particles and the laws of physics, Cambridge, University Press, 1999, ISBN 0 521 65862 4), p.73. [CrossRef]
- J. Hanc, S. Tuleja, M. Hancova. Symmetries and Conservation Laws: Consequences of Noether’s Theorem. Am. J. Phys. 72, 428–435 (2004). [CrossRef]
- Louzguine-Luzgin, D.V. Structural Changes in Metallic Glass-Forming Liquids on Cooling and Subsequent Vitrification in Relationship with Their Properties. Materials 2022, 15, 7285. [CrossRef]
- Louzguine-Luzgin, D.V. Crystallization of Metallic Glasses and Supercooled Liquids. Materials 2024, 17, 3573. [CrossRef]
- Kantor, Y.;Webman, I. Elastic properties of random percolating systems. Phys. Rev. Lett. 1984, 52, 1891–1894. [CrossRef]
- Stoch, P., Krakowiak, I. Thermal properties of Sr-containing iron-phosphate glasses experimental and theoretical approach. J Therm Anal Calorim (2025). [CrossRef]
- L. D. Landau and E. M. Lifshitz, Course of Theoretical Physics Volume 5: Statistical Physics Part 1, Elsevier, Amsterdam (2012).
- N. Goldenfeld, Lectures on Phase Transitions and the Renormalization Group, CRC Press, Boca Raton, FL (2018).
- M. Henkel and M. Pleimling, Non-Equilibrium Phase Transitions: Volume 2: Ageing and Dynamical Scaling Far from Equilibrium, Springer Science & Business Media, Dordrecht (2011).
- H. Haken, Synergetics: An Introduction: Nonequilibrium Phase Transitions and Self-organization in Physics, Chemistry and Biology, Springer, Berlin (2004).
- M. C. Cross and P. C. Hohenberg, Pattern formation outside of equilibrium, Rev. Mod. Phys. 65, 851 (1993).
- Wang J., Li R. Effects, methods and limits of the cryopreservation on mesenchymal stem cells. Stem Cell Research & Therapy (2024) 15:337. [CrossRef]
- Gallino, I., Busch, R. (2024). Thermodynamic and Kinetic Aspects of the Glass Transition. In: Physical Metallurgy of Bulk Metallic Glass-Forming Liquids. Springer Series in Materials Science, vol 341. Springer, Cham. [CrossRef]
- Zhang, HR., Yang, Q., Fang, ZL. et al. Size-dependent vitrification in hybrid glasses at micro-meter scale. Sci. China Phys. Mech. Astron. 68, 266103 (2025). [CrossRef]
- Stiehler, M.E., Georgarakis, K. From metallic liquids to metallic glasses: in-situ monitoring the atomic structure evolution by synchrotron X-ray diffraction, Critical Reviews in Solid State and Materials Sciences, 2025. [CrossRef]
- M.I. Ojovan. Vitreous materials for nuclear waste immobilisation. XXVII International Congress on Glass (ICG 2025), January 20-24, 2025. Biswa Bangla Convention Centre, Kolkata, India. Book of Abstracts. KT-S6-2. P.204. CSIR-Central Glass and Ceramic Research Institute, Kolkata - 700 032, India (2025). [CrossRef]
- M.I. Ojvan, D.V. Louzguine-Luzgin. Three crossover temperatures related to structural changes in glass forming systems. XXVII International Congress on Glass (ICG 2025), January 20-24, 2025. Biswa Bangla Convention Centre, Kolkata, India. Book of Abstracts. IT-S2-7. P. 79. CSIR-Central Glass and Ceramic Research Institute, Kolkata - 700 032, India (2025).
| Degree of Ordering | Degree of Connectivity | |
| Low | High | |
| High | Liquid crystals; Liquid quasi-crystals | Crystals; Quasi-crystals |
| Medium | Liquid glasses | Glass-crystalline materials |
| Low | Melts | Glass 1 |
| Table 1. |
Low (in the glass) T <Tg |
Intermediate (in the supercooled melt) Tg<T<TA |
High (in the melt) T>TA=(1.10±0.15)Tm |
Extremely High |
| Viscous flow type | Arrhenian with high activation energy QH |
Non-Arrhenian, apparent variable activation energy Q(T) |
Arrhenian with low activation energy QL |
Non-activated, growing with temperature rise |
| Universal viscosity equation 1 | ||||
| Alloy, compound | Tg, K | ΔCv, J/mol⋅K |
| La55Al25Ni20 | 465 | 12.31 |
| Zr65Al7.5Ni10Cu17.5 | 653 | 11.02 |
| Mg65Cu25Y10 | 380 | 10.06 |
| Zr41.2Ti13.8Cu12.5Ni10Be22.5 | 623 | 11.95 |
| Pd77.5Cu6Si16.5 | 625 | 10.33 |
| Pd40Cu30Ni10P20 | 525 | 10.89 |
| Pd40Ni40P20 | 551 | 11.02 |
| Zr55Al10Ni5Cu30 | 653 | 11.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





