The Relationship Between Cognitive Activation and Math Anxiety in Japan: Moderating Roles of Socioeconomic Status and Math Self-Efficacy

Yuno Shimizu

doi:10.20944/preprints202507.0675.v2

Submitted:

25 August 2025

Posted:

27 August 2025

You are already at the latest version

Abstract

Math anxiety undermines students’ motivation and achievement and is a pervasive challenge in mathematics education. Although prior studies have shown that cognitively demanding instruction can alleviate anxiety, the possibility of nonlinear effects and contextual moderators remains underexplored. Drawing on nationally representative data from 5,760 Japanese 15-year-olds in PISA 2022, this study examined the curvilinear relationship between cognitive activation and math anxiety, and the moderating roles of student SES, school SES, and math self-efficacy. Multilevel regression analysis revealed that mathematical-thinking activation was associated with reductions in math anxiety at lower to moderate levels, but its benefits plateaued beyond that point, whereas reasoning-focused activation showed negligible curvilinear effects. Student SES and school SES moderated these associations in complex ways, suggesting that cognitive activation can act as a compensatory resource in low-SES contexts. In contrast, math self-efficacy, although strongly predictive of anxiety as a main effect, did not moderate the relationship. These findings refine control-value and cognitive load theories by highlighting nonlinear and SES-dependent dynamics, and they underscore that instructional quality affects not only cognitive but also emotional outcomes. Practically, the results suggest the value of promoting mathematical-thinking activation in teacher training to reduce math anxiety, particularly among socioeconomically disadvantaged students.

Keywords:

cognitive activation

;

math anxiety

;

socio-economic status (SES)

;

math self-efficacy

;

multilevel analysis

Subject:

Social Sciences - Education

Introduction

It is a universal phenomenon in modern society that people feel negative emotions such as anxiety and fear toward mathematics. According to the results of the 2022 PISA (Programme for International Student Assessment) survey conducted by the Organisation for Economic Co-operation and Development (OECD), 59.8% of 15-year-olds in OECD member countries and 68.8% in Japan responded “completely agree” or “agree” to the statement “I often worry that it will be difficult for me in mathematics classes” (OECD, 2024a). Additionally, 64.9% of 15-year-olds in OECD member countries and 68.6% in Japan responded “completely agree” or “agree” to the statement “I worry that I will get poor marks in mathematics” (OECD, 2024a). These findings suggest that anxiety and fear toward mathematics are widespread and culturally pervasive. Such negative emotions have long been a central focus of affective research in mathematics, beginning with Gough’s (1954) study on “mathemaphobia” and Dreger & Aiken’s (1957) work on “number anxiety” (Batchelor et al., 2019). These constructs have since evolved into what is now widely recognized as math anxiety, a psychological phenomenon extensively studied in educational psychology.

Math anxiety is defined as feelings of tension and apprehension that interfere with the manipulation of numbers and the solving of mathematical problems in a wide variety of contexts, including daily life and academic settings (Ramirez et al., 2018). While math anxiety shares similarities with general anxiety and test anxiety, it is considered a distinct construct. This distinction is supported by research showing a relatively low contribution from shared genetic factors (approximately 9%) and non-shared environmental factors (approximately 4%) in comparison to other types of anxiety (Wang et al., 2014), as well as unique correlation patterns with external criterion variables (Hembree, 1990).

The negative association between math anxiety and math learning and performance is one of the most robust and well-replicated findings in the field. Meta-analyses have consistently shown that math anxiety is significantly negatively correlated with learning motivation (Li et al., 2021), the extent of high school math learning (Hembree, 1990), and math performance (Barroso et al., 2021). Furthermore, longitudinal and panel data studies have demonstrated that math anxiety negatively predicts math learning and performance over time (Ahmed et al., 2012; Gunderson et al., 2018). These findings underscore the importance of identifying instructional practices that can alleviate math anxiety, thereby promoting more positive learning outcomes.

One such instructional practice is cognitive activation by mathematics teachers, which has emerged as a significant factor in reducing math anxiety. Cognitive activation refers to instructional strategies that promote constructive, reflective, and higher-order thinking in learners (Baumert et al., 2010). In mathematics lessons, this often involves encouraging students to reflect on problem-solving processes and providing them with tasks that require extended reasoning (Burge et al., 2015). The core components of cognitive activation include: (1) activating prior knowledge and fostering conceptual understanding, (2) posing problems that engage learners in higher-order thinking, and (3) facilitating meaningful participation in classroom discourse (Lipowsky et al., 2009). These practices align with constructivist learning theories, such as Piaget’s and Vygotsky’s, and emphasize the active, constructive, and interactive modes of learning in the ICAP framework (Chi, 2009).

Empirical research has indicated that cognitive activation can reduce math anxiety. For example, Zuo et al. (2024) used structural equation modeling on data from 17,112 eighth-grade students in China and found that cognitive activation was negatively associated with math anxiety, both directly and indirectly via math self-efficacy. Similarly, Liu et al. (2022) conducted a multilevel analysis on 3,088 fourth-grade students and 57 teachers in China and found a direct negative relationship between cognitive activation and math anxiety. Burge et al. (2015), using PISA 2012 data from England, also reported that cognitive activation was negatively associated with math anxiety. However, given that instructional effectiveness often varies by cultural and national context (e.g., Liu et al., 2022), the extent to which these findings generalize to Japanese students remains unclear.

Notably, most previous studies have focused on linear associations between cognitive activation and math anxiety. However, some evidence suggests a curvilinear (inverted U-shaped) relationship in related outcomes such as mathematics performance, where moderate cognitive activation optimises performance while very low or very high levels impair it (Caro et al., 2016; Nachbauer, 2024). Given the strong link between mathematics performance and math anxiety, it is plausible that a similar non-linear mechanism may operate for anxiety. According to the control-value theory of achievement emotions (Pekrun, 2006; Pekrun & Stephens, 2010), anxiety arises when students perceive high value in academic tasks but low control over outcomes. Thus, cognitive activation may reduce anxiety when tasks are appropriately challenging, but may increase anxiety when demands exceed students’ competence. Complementarily, cognitive load theory (Sweller, 1988) suggests that when task demands overload students’ working memory, cognitive resources become depleted, leading to stress and heightened anxiety. Together, these perspectives indicate that the link between cognitive activation and math anxiety may follow a curvilinear pattern.

Empirical findings are consistent with this theoretical reasoning. For example, Frenzel et al. (2009) demonstrated that perceived teaching quality, including cognitive activation, was systematically related to students’ enjoyment and anxiety. Similarly, Fauth et al. (2014) and Goetz et al. (2013) found that challenging tasks foster interest and reduce boredom only when students can master them. These results suggest that moderate levels of cognitive activation can buffer negative emotions, whereas excessive activation may undermine perceived control and increase anxiety.

In addition, this relationship may be moderated by socioeconomic status (SES). SES reflects access to various resources—economic, social, cultural, and human—that affect educational outcomes (National Centre for Education Statistics, 2012). Burge et al. (2015) found that the negative relationship between cognitive activation and math anxiety was significant only among students with medium to high levels of economic, social, and cultural capital. Although their study focused on England, similar patterns have been observed in other outcomes. For example, Caro et al. (2016) found that cognitive activation had a greater positive impact on academic achievement for students with higher SES. These findings suggest that the effectiveness of cognitive activation may depend on students’ SES, with diminished effects among students with lower SES.

Moreover, it is important to consider both individual-level (Student SES) and contextual-level (School SES) factors. School SES reflects the average SES of the school’s student body and shapes the educational environment through access to material and human resources (Chiu & Khoo, 2005), teacher quality, peer effects (Van Ewijk & Sleegers, 2010), and classroom discipline (Willms, 2010). High-SES schools are generally better equipped to support academic achievement (Perry et al., 2022). In Japan, the school system further stratifies students into academically ranked high schools, often in line with socioeconomic background (Takashiro, 2024; Matsuoka, 2015). Thus, School SES may also moderate the link between cognitive activation and math anxiety, beyond the effects of Student SES alone.

Math self-efficacy—students’ belief in their ability to perform specific tasks—may be another moderating factor. According to Bandura’s (1986) social cognitive theory, math self-efficacy influences motivation, learning engagement, and emotional responses. Students with low math self-efficacy may be less responsive to cognitively demanding instruction, potentially limiting the anxiety-reducing benefits of cognitive activation (Shimizu, 2025). In contrast, students with high math self-efficacy are more likely to engage with cognitively activating tasks, which may reduce their math anxiety. Although prior studies have not directly tested this interaction, research on disciplinary climate in mathematics classrooms has shown that the positive effect of a structured environment on achievement is contingent on students’ level of math self-efficacy (Cheema & Kitsantas, 2014).

Based on this theoretical and empirical background, the present study aims to investigate: (1) the curvilinear effect of cognitive activation on math anxiety and (2) the moderating effects of Student SES, School SES, and Math Self-Efficacy on this relationship.

Hypothesis 1. Cognitive activation has a negative relationship with math anxiety.
Hypothesis 2. Cognitive activation has a negative curvilinear relationship with math anxiety.
Hypothesis 3. Student SES moderates the negative relationship between cognitive activation and math anxiety.
- 3-a. When Student SES is high, the negative relationship between cognitive activation and math anxiety becomes stronger.
- 3-b. When Student SES is low, the negative relationship between cognitive activation and math anxiety becomes weaker.
Hypothesis 4. School SES moderates the negative relationship between cognitive activation and math anxiety.
- 4-a. When School SES is high, the negative relationship between cognitive activation and math anxiety becomes stronger.
- 4-b. When School SES is low, the negative relationship between cognitive activation and math anxiety becomes weaker.
Hypothesis 5. Math self-efficacy moderates the negative relationship between cognitive activation and math anxiety.
- 5-a. When math self-efficacy is high, the negative relationship between cognitive activation and math anxiety becomes stronger.
- 5-b. When math self-efficacy is low, the negative relationship between cognitive activation and math anxiety becomes weaker.

Method

Data

In this study, I used the data from students in Japan (valid responses: 182 schools [departments], 5760 students) from the PISA 2022 dataset published by the OECD. This large-scale international survey, conducted every three years, targets 15-year-old learners to assess their proficiency in essential academic domains. Beyond the core evaluations in reading, mathematics, and science, PISA integrates multi-actor questionnaires involving students, caregivers, educators, and school administrators to explore how diverse con-textual and individual attributes relate to academic literacy outcomes (OECD, 2023). The 2022 iteration engaged nearly 690,000 participants, representing a global cohort of 15-year-olds.

Measures

Math Anxiety

Math anxiety was measured using the OECD’s ANXMAT score (OECD, 2023), based on six items (e.g., “I often worry that it will be difficult for me in math class.”). Items were rated on a four-point scale (1 = Strongly agree to 4 = Strongly disagree) and scaled with the Partial Credit Model (PCM) to ensure cross-cycle comparability. The score was standardised (M = 0, SD = 1 across OECD countries), with higher values indicating greater anxiety.

Cognitive Activation

Cognitive activation in mathematics lessons was measured using two scales developed by the OECD (2023): the Cognitive Activation for Fostering Reasoning (COGACRCO) and Cognitive Activation for Encouraging Mathematical Thinking (COGACMCO). These scores were calculated using IRT based on responses to 18 items designed to assess the extent to which students are exposed to cognitively demanding instructional practices.

The COGACRCO scale captures how frequently students are encouraged to articulate their thought processes and solve complex problems independently. Sample items include “The teacher asks us to decide on our own procedures for solving complex problems” and “The teacher asks us to explain how we solved a problem.”

The COGACMCO scale reflects how often students are prompted to reflect deeply on problems and engage in extended reasoning. Sample items include “The teacher asks questions that make us reflect on the problem” and “The teacher presents problems that require us to think for an extended time.”

Both scales used a four-point Likert scale ranging from Never or hardly ever (1) to In all or nearly all lessons (4). Responses were scaled using the PCM and standardised across OECD countries (M = 0, SD = 1). Higher scores indicate greater exposure to cognitively activating teaching practices.

In this study, cognitive activation was treated as a school-level variable by calculating the school-mean values of COGACRCO and COGACMCO, centered on the overall sample mean.

SES

Student SES was measured using the ESCS (Economic, Social, and Cultural Status) index, a composite of parental education, occupation, and household possessions. The index is standardised (M = 0, SD = 1) across OECD countries. School SES was calculated as the school average of student SES, centred on the sample mean.

Math Self-Efficacy

Math self-efficacy was measured with the OECD’s MATHEFF scale (nine items, e.g., “Calculating how much more expensive a computer would be after adding tax”), rated on a four-point scale (1 = Not at all confident to 4 = Very confident). Scores were scaled with PCM and standardised across OECD countries (M = 0, SD = 1). Higher values indicate greater self-efficacy.

Gender

Gender was included as a control (item ST004Q01: 1 = female, 2 = male). A dummy variable was created (0 = female, 1 = male).

Analysis Strategies

Analyses proceeded in two steps. First, descriptive statistics (means and SDs) were calculated. Second, to test curvilinear and moderating effects, multilevel regression models were estimated using student weights (W_FSTUWT) and school weights (W_SCHGRNRABWT). All models used random intercepts; random slopes for cognitive activation were tested but dropped due to zero/negative variance.

The following four models were estimated:

• Model 1 (Baseline Model): Included the male dummy variable (control), cognitive activation (linear and quadratic terms), student SES, school SES, and math self-efficacy as predictors, with math anxiety as the outcome.

• Model 2: Added interaction terms between student SES and both the linear and quadratic terms of cognitive activation.

• Model 3: Added interaction terms between school SES and both the linear and quadratic terms of cognitive activation.

• Model 4: Added interaction terms between math self-efficacy and both the linear and quadratic terms of cognitive activation.

Cognitive activation variables were mean-centred before creating quadratic terms. Following OECD guidelines for single-country analysis (OECD, 2024b), two-stage weights were applied. Given the cross-sectional design, results should be interpreted as associational, not causal.

Results

Descriptive Statistics

Table 1 presents the descriptive statistics for the variables used in this study. For student-level variables, the mean value for math anxiety was positive, and the mean value for math self-efficacy was negative. This indicates that, relative to the OECD average, 15-year-old students in Japan tend to experience higher math anxiety and lower math self-efficacy.

Regarding school-level variables, the mean value of cognitive activation for fostering reasoning was approximately zero, while the mean value of cognitive activation for encouraging mathematical thinking was negative. These results suggest that, on average, Japanese mathematics teachers implement cognitive activation strategies that foster reasoning at a level comparable to the OECD average, but make less frequent use of cognitive activation practices designed to promote extended mathematical thinking.

Relationship Between Cognitive Activation and Math Anxiety

Table 2 shows the results of Model 1. Math self-efficacy emerged as the strongest predictor: a one-SD increase in math self-efficacy was associated with a 0.37-SD decrease in math anxiety (p < .001). Gender also had a significant effect, with boys reporting on average 0.19 SD lower anxiety than girls. School SES was positively associated with math anxiety (B = 0.13, p < .001), indicating that students in higher-SES schools reported slightly higher levels of anxiety.

When controlling for these covariates, the squared term of cognitive activation for fostering reasoning was significantly negative in predicting math anxiety (B = −0.29, p < .001). Figure 1, which visualises the relationship over the 2.5th to 97.5th percentile range of cognitive activation for fostering reasoning, shows only a very slight negative quadratic pattern. Although statistically significant, the effect size was small and the curve appeared nearly flat, suggesting that math anxiety remained almost constant regardless of the level of cognitive activation for fostering reasoning.

In contrast, the squared term of cognitive activation for encouraging mathematical thinking was significantly positive (B = 0.19, p < .01). Figure 2 shows that math anxiety initially decreased as cognitive activation for encouraging mathematical thinking increased, but eventually plateaued. This indicates that increasing cognitive activation for encouraging mathematical thinking is beneficial for reducing anxiety up to a certain level, after which the benefit no longer increases.

Therefore, Hypotheses 1 and 2 were partially supported.

Moderating Effect of Student SES on the Relationship Between Cognitive Activation and Math Anxiety

The results of Model 2 in Table 2 show that the interaction between student SES and the squared term of cognitive activation for encouraging mathematical thinking was significantly negative (B = −0.39, p < .01). Figure 3 visualises this interaction. Among students with low SES, increases in cognitive activation for encouraging mathematical thinking initially reduced math anxiety but levelled off at higher levels. In contrast, among high-SES students, math anxiety remained relatively stable across levels of cognitive activation for encouraging mathematical thinking. This pattern suggests that cognitive activation for encouraging mathematical thinking serves as a compensatory resource for students with fewer socioeconomic advantages.

Therefore, Hypotheses 3-a and 3-b were not supported.

Moderating Effect of School SES on the Relationship Between Cognitive Activation and Math Anxiety

Model 3 results (Table 2) indicate that the interaction between school SES and the squared term of cognitive activation for fostering reasoning was significantly positive (B = 0.37, p < .05), while the interaction between school SES and cognitive activation for encouraging mathematical thinking was significantly negative (B = −0.16, p < .05). Figure 4 and Figure 5 depict these results.

Figure 4 shows that in low-SES schools, both low and high levels of cognitive activation for fostering reasoning were associated with lower math anxiety, whereas moderate levels were associated with higher anxiety. In high-SES schools, math anxiety remained largely stable regardless of activation level.

Figure 5 illustrates that in high-SES schools, increased cognitive activation for encouraging mathematical thinking was associated with lower math anxiety. In contrast, in low-SES schools, the decline in anxiety with increasing activation was less pronounced, narrowing the anxiety gap between high- and low-SES schools at higher levels of activation.

Therefore, Hypothesis 4-a was partially supported, while Hypothesis 4-b was not supported.

Moderating Effect of Math Self-Efficacy on the Relationship Between Cognitive Activation and Math Anxiety

The results of Model 4 in Table 2 indicate that math self-efficacy did not significantly moderate the relationship between either type of cognitive activation and math anxiety. Although self-efficacy strongly predicted lower math anxiety as a main effect, it did not alter the strength or shape of the relationship between cognitive activation and anxiety.

Therefore, Hypothesis 5 was not supported.

Discussion

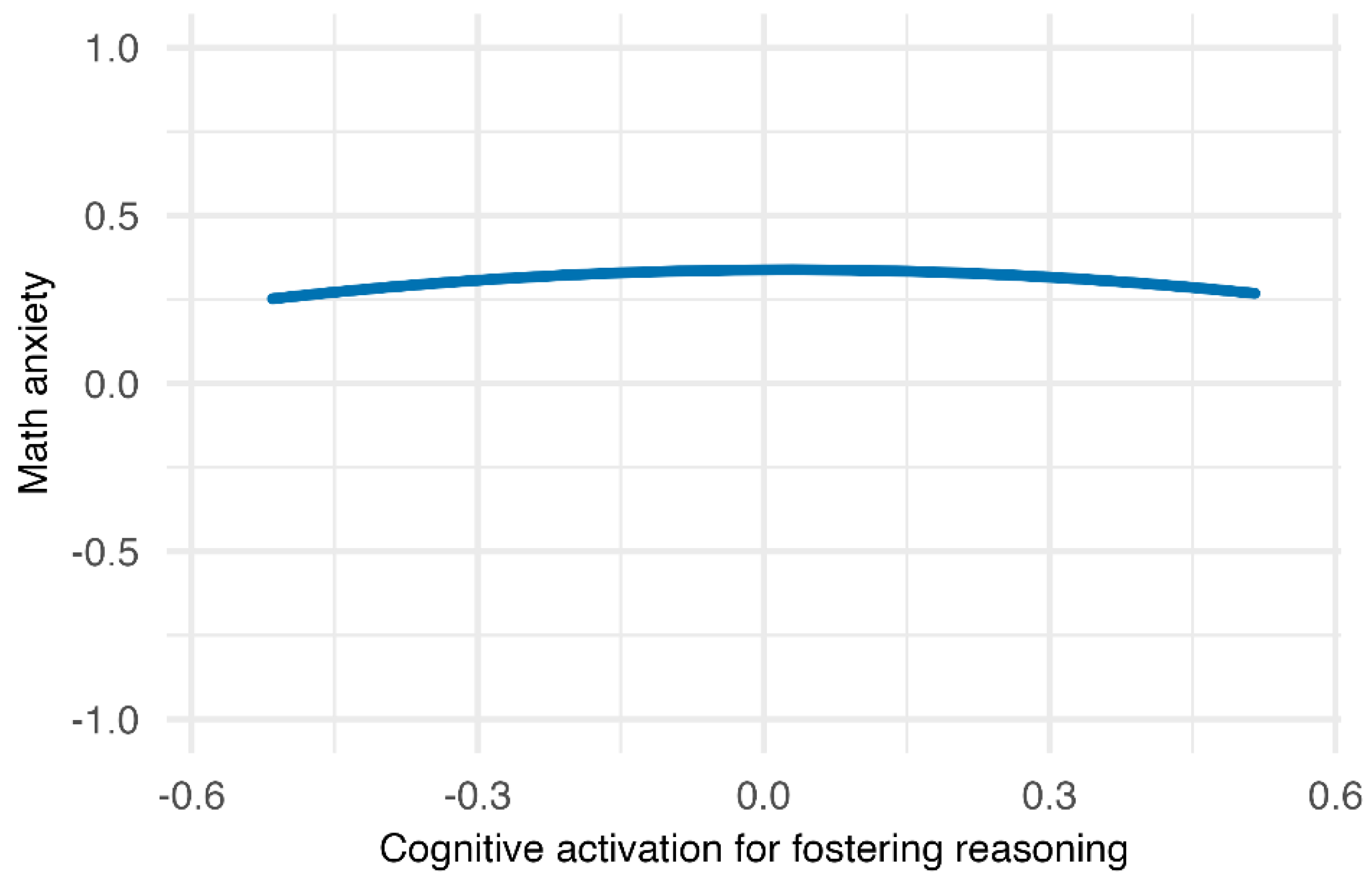
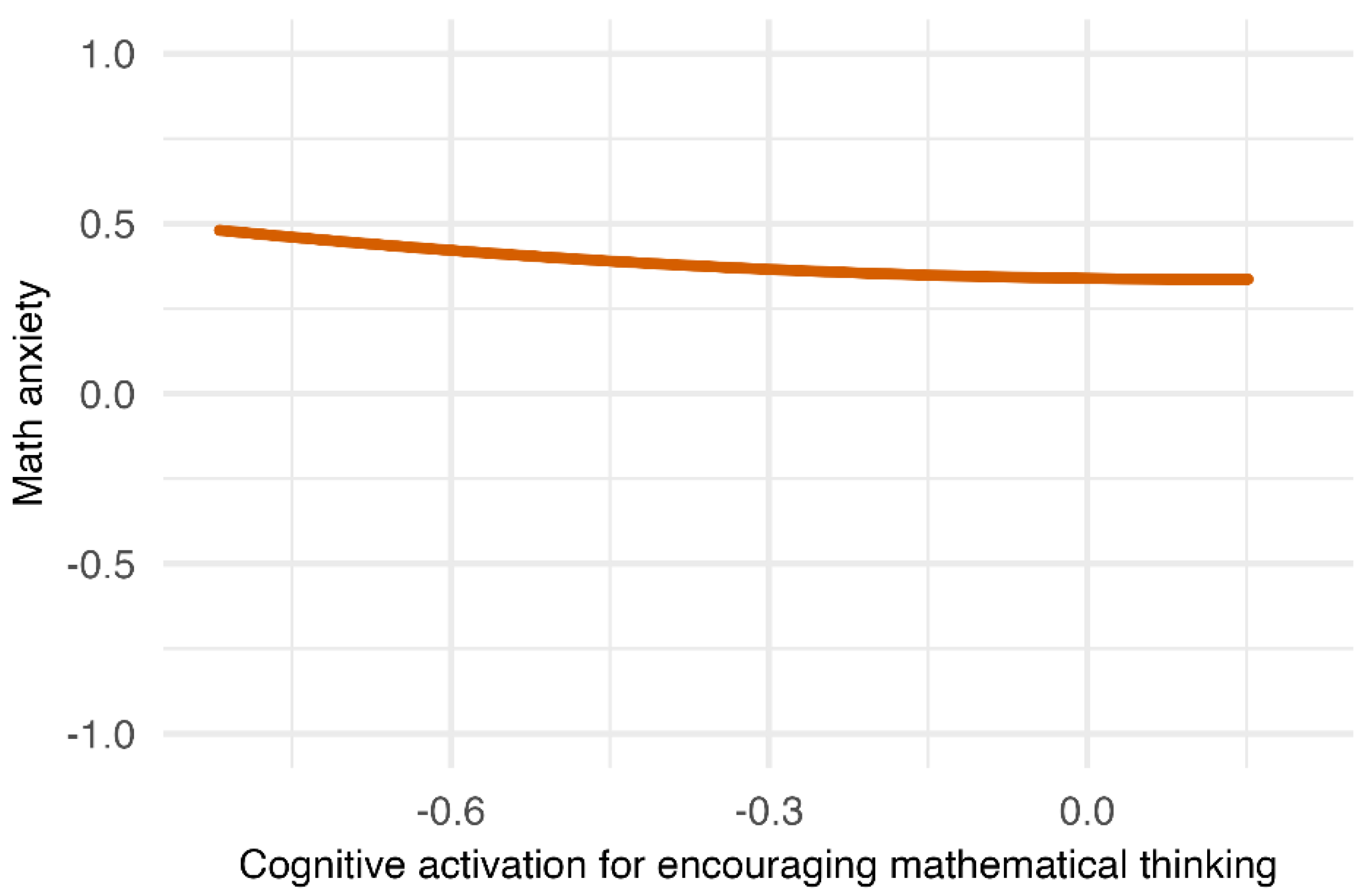
This study investigated the curvilinear effect of cognitive activation on math anxiety and the moderating effects of SES and math self-efficacy, using the Japanese dataset from PISA 2022 and multilevel regression analysis (Table 2, Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5). The results indicated that cognitive activation for fostering reasoning exhibited a negative curvilinear relationship with math anxiety; however, the magnitude of the effect was small, and the overall pattern was essentially flat. In contrast, cognitive activation for encouraging mathematical thinking was initially associated with a reduction in math anxiety, but this effect gradually plateaued. Therefore, Hypotheses 1 and 2 were partially supported.

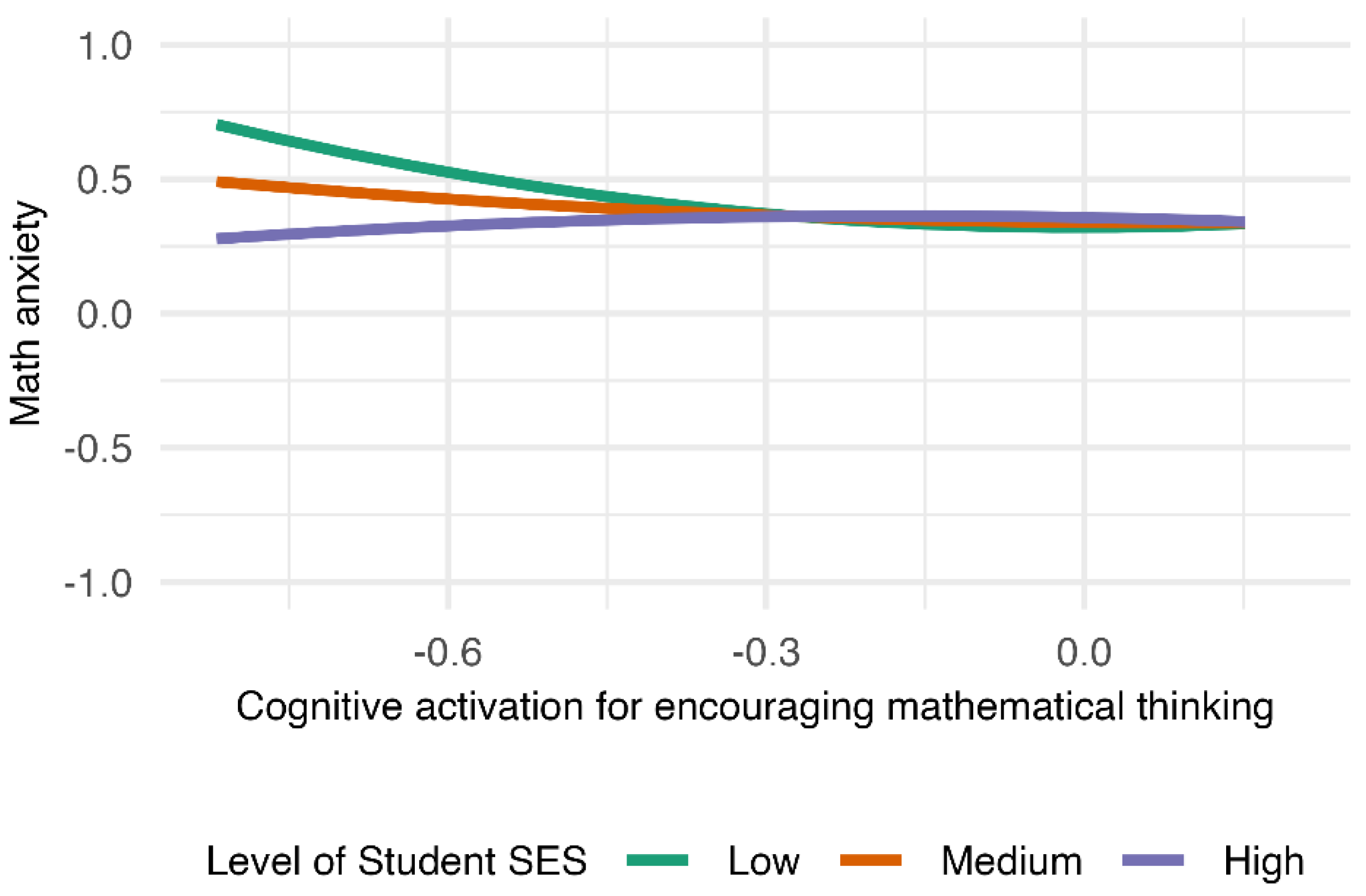
Student SES negatively moderated the relationship between cognitive activation for encouraging mathematical thinking and math anxiety. Specifically, when student SES was low, increased cognitive activation was initially associated with lower math anxiety, but the effect diminished over time. Consequently, Hypotheses 3-a and 3-b were not supported. However, this trend contributed to a narrowing of the math anxiety gap between high- and low-SES school groups.

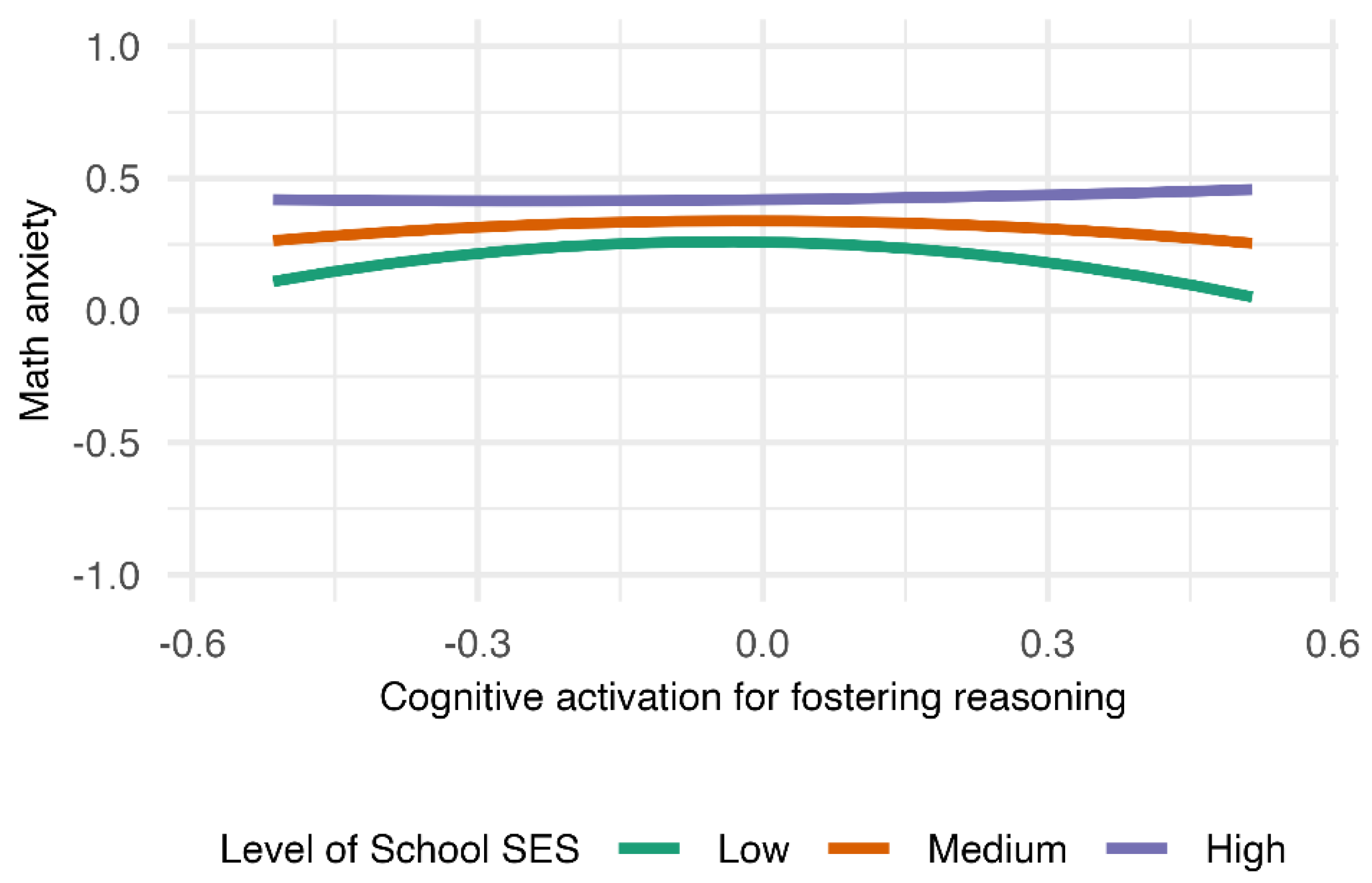
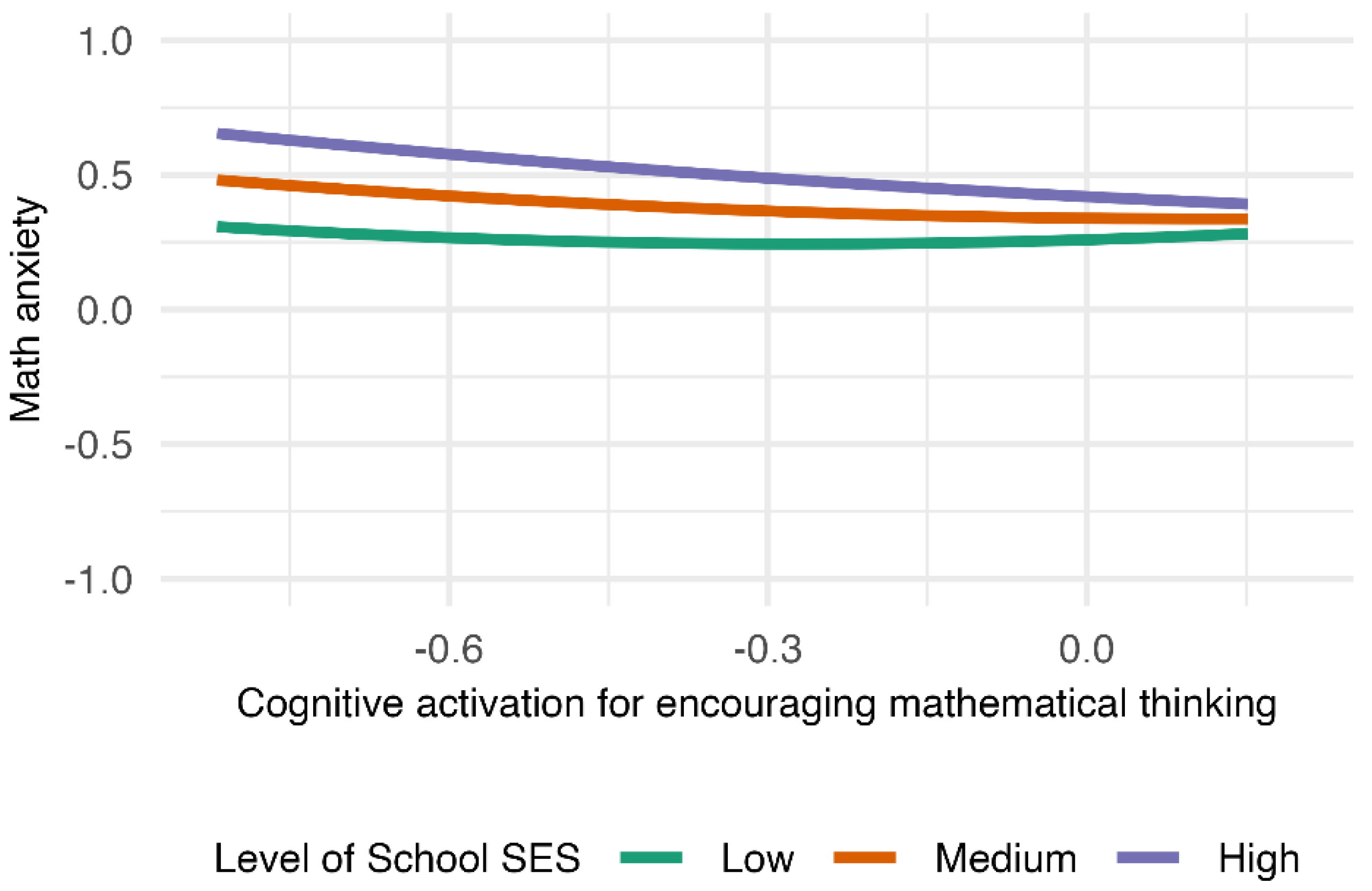
School SES moderated the relationship between cognitive activation and math anxiety. When school SES was low, both low and high frequencies of cognitive activation for fostering reasoning were associated with reduced math anxiety, whereas moderate levels were associated with higher anxiety. Conversely, in high-SES schools, increased cognitive activation for encouraging mathematical thinking was linked to reduced math anxiety, and the difference between high- and low-SES groups converged. Thus, Hypothesis 4-a was partially supported, while Hypothesis 4-b was not. Math self-efficacy did not significantly moderate the relationship between cognitive activation and math anxiety, and Hypothesis 5 was not supported.

The Relationship Between Cognitive Activation and Math Anxiety

The present findings extend prior research on the link between cognitively demanding instruction and students’ emotional responses in mathematics. While previous studies (e.g., Zuo et al., 2024; Liu et al., 2022) found a linear negative association between cognitive activation and math anxiety, the present study revealed a nonlinear (curvilinear) relationship.

Specifically, the results suggest that greater use of cognitive activation strategies that encourage mathematical thinking initially reduces math anxiety but eventually plateaus. This pattern is consistent with earlier studies that identified beneficial effects of cognitive activation (Zuo et al., 2024; Liu et al., 2022), while also highlighting that the benefits may not increase indefinitely.

One possible explanation is that increased mathematical-thinking–oriented activation promotes student engagement, thereby enhancing motivation and reducing anxiety. From a theoretical perspective, control-value theory (Pekrun, 2006) suggests that anxiety arises when students perceive low control over valued tasks, while cognitive load theory (Sweller, 1988) indicates that excessive task demands can overload working memory and increase stress. Together, these frameworks provide a rationale for why cognitive activation may reduce anxiety up to a point but yield diminishing returns at higher levels.

However, though statistically significant, the quadratic effect for reasoning-focused activation was practically negligible, and the curve was nearly flat. One plausible explanation is that, in the present dataset, the average level of reasoning-focused activation was relatively low, suggesting that Japanese mathematics teachers make limited use of such practices compared to international standards (see Table 1). As a result, the restricted range of this instructional practice may have reduced its potential to explain meaningful variation in students’ anxiety. In this context, even though the large sample size allowed the detection of a statistically significant quadratic effect, its educational significance appears limited.

The Moderating Effect of SES on the Relationship Between Cognitive Activation and Math Anxiety

Contrary to the original hypothesis, the results revealed that when student SES was low, increased cognitive activation for encouraging mathematical thinking initially reduced math anxiety, though the effect faded at higher activation levels. Interestingly, this pattern contributed to closing the gap in math anxiety between high- and low-SES students. This suggests cognitive activation may be a compensatory strategy for students with fewer educational resources outside school.

Theoretically, this pattern contrasts prior findings on achievement outcomes, where cognitively demanding instruction has been shown to benefit higher-SES students more strongly (Caro et al., 2016). Our results, by focusing on math anxiety rather than achievement, indicate a different distribution of benefits: mathematical-thinking–oriented activation appears to reduce math anxiety more for low-SES students at lower–to–moderate levels, with diminishing returns beyond that range. One interpretation is that such activation may initially raise perceived control among students with fewer out-of-school supports, thereby lowering anxiety, but once task demands exceed available scaffolding, additional activation no longer yields incremental reductions.

At the school level, in high-SES schools, frequent use of cognitive activation for encouraging mathematical thinking was consistently associated with reduced math anxiety. This is consistent with prior research (Perry et al., 2022) suggesting that high-SES schools often provide supportive environments and instructional resources that facilitate effective teaching. In Japan, teachers in high-SES schools also report higher instructional efficacy and job satisfaction (Matsuoka, 2015b), which may enable them to implement cognitively demanding practices more effectively.

In low-SES schools, an intriguing pattern emerged: math anxiety was lower when cognitive activation for fostering reasoning was infrequently or frequently used, but higher when used moderately. This non-monotonic pattern may reflect variability in implementation quality under resource constraints. At moderate levels, reasoning-oriented practices might be introduced without sufficient scaffolding, increasing cognitive load and anxiety; very low use may limit exposure to challenging demands; and very high use may occur mainly in classrooms where teachers can support such practices effectively. Additionally, as shown in Table 1, the average level of reasoning-focused activation in this sample was relatively low, suggesting range restriction that can attenuate its association with emotional outcomes. Together, these points underscore that the quality and support accompanying cognitively demanding instruction—not merely its frequency—are crucial for shaping students’ math anxiety.

The Moderating Effect of Math Self-Efficacy on the Relationship Between Cognitive Activation and Math Anxiety

Contrary to expectations, math self-efficacy did not significantly moderate the relationship between cognitive activation and math anxiety. This finding diverges from the moderating role predicted by social cognitive theory (Bandura, 1986) and the control-value theory of achievement emotions (Pekrun, 2006), which suggest that competence beliefs should buffer emotional reactions to cognitively demanding instruction.

However, the absence of a moderation effect does not necessarily contradict the control-value theory of achievement emotions. Instead, it may indicate that math self-efficacy functions primarily as a mediator rather than a moderator. According to the control-value theory of achievement emotions, students’ perceived control is a proximal determinant of achievement emotions, including anxiety. Cognitive activation may therefore reduce math anxiety indirectly by enhancing students’ perceived control (i.e., self-efficacy), which subsequently lowers their anxiety levels. This mediational pathway has been supported by previous studies (e.g., Zuo et al., 2024), showing that cognitively demanding instruction increases math self-efficacy, decreasing math anxiety.

Another possible explanation is that the measure of math self-efficacy (MATHEFF) used in this study may not fully capture the context-specific aspects of competence beliefs most relevant to classroom practices. There may be a misalignment between students’ general confidence in solving mathematical problems and their emotional responses to cognitively activating instruction, especially when such practices are inconsistently or poorly implemented. Future research should therefore test both moderation and mediation models, ideally with more context-specific measures of math self-efficacy, to clarify the precise role of competence beliefs in shaping students’ math anxiety.

Theoretical Contributions

This study makes several contributions to theory. First, by identifying a curvilinear association between mathematical-thinking activation and math anxiety, the findings extend previous research that assumed a strictly linear relationship. Integrating control-value theory (Pekrun, 2006) with cognitive load theory (Sweller, 1988), the results suggest that moderate levels of cognitive activation may enhance perceived control and reduce anxiety, whereas excessive levels may impose cognitive overload and diminish these benefits. This refinement highlights the value of considering nonlinear dynamics in research on instructional quality and students’ emotions.

Second, the moderation results regarding socioeconomic status contrast with prior findings on achievement outcomes. While Caro et al. (2016) reported that cognitively demanding instruction benefited high-SES students more strongly in terms of achievement, the present study shows that, for math anxiety, low-SES students appeared to gain more benefit at lower to moderate levels of activation. This indicates that the distribution of benefits depends on whether the outcome is cognitive (achievement) or affective (anxiety). The finding thus broadens theoretical perspectives by emphasising that instructional effects on learning and emotions may not align.

Third, the differentiation between reasoning-focused activation and mathematical-thinking activation revealed distinct associations with math anxiety. While reasoning-focused activation showed negligible emotional effects, mathematical-thinking activation exhibited a curvilinear pattern with practical significance. This underscores that not all sub-dimensions of cognitive activation are equally relevant to students’ affective experiences, suggesting that theoretical models of teaching quality (e.g., Klieme et al., 2009) may benefit from further differentiation among activation types.

Fourth, despite its strong main effect, the absence of a moderating effect of math self-efficacy suggests that self-efficacy may function primarily as a mediator rather than a moderator. This aligns with control-value theory, which posits that perceived control is a proximal determinant of achievement emotions. The findings, therefore, refine theoretical understanding of competence beliefs in the context of cognitively demanding instruction, highlighting the need for future research to test mediation models more explicitly.

Practical implications

The findings of this study offer important implications for mathematics education. First, the results suggest that prioritising mathematical-thinking activation may be more effective in reducing math anxiety than relying solely on reasoning-focused practices. This implies that practices that stimulate conceptual reflection and extended reasoning can play a central role in shaping students’ emotional outcomes, although their effectiveness appears to plateau at higher levels.

Second, the findings indicate that cognitive activation may serve as a compensatory resource for students from low-SES backgrounds. At lower to moderate levels, mathematical-thinking activation was associated with more substantial reductions in anxiety for disadvantaged students, suggesting its potential to help narrow socioeconomic disparities in emotional outcomes.

Third, results at the school level emphasise the importance of instructional quality. In low-SES schools, reasoning-focused activation was sometimes linked to higher anxiety when implemented inconsistently, underscoring the need for sufficient scaffolding and teacher capacity. This highlights that the frequency and quality of cognitively demanding practices matter for students’ emotional well-being.

Finally, Japanese mathematics teachers reported lower average use of cognitive activation compared to international peers. This finding points to the potential value of strengthening teacher training curricula to incorporate cognitive activation—particularly mathematical-thinking activation—to address Japan’s comparatively high levels of math anxiety.

Limitations

This study has several limitations that also point to promising directions for future research. First, the PISA 2022 dataset is cross-sectional, which precludes strong causal inference. Longitudinal or experimental designs would be valuable to establish the directionality of effects between cognitive activation, self-efficacy, and math anxiety.

Second, cognitive activation was analysed at the school-mean level rather than at the classroom level, due to data constraints. This aggregation may have masked within-school heterogeneity in teaching quality. Future studies could incorporate classroom-specific identifiers to better capture teacher–student interactions.

Third, the measures of cognitive activation relied on student self-reports, which may reflect perceptions rather than actual teaching practices. Future research could integrate self-reports with classroom observations and teacher reports to strengthen construct validity.

Finally, this study focused exclusively on 15-year-old students in Japan. The extent to which these findings generalise to other age groups or cultural contexts remains uncertain. Cross-national and developmental comparisons could provide valuable evidence on whether the observed plateauing effects and SES patterns are universal or culture specific.

Author Note

This study used secondary data from the PISA 2022 cycle. Ethical approval and informed consent were obtained by the OECD, and therefore no additional approval was required. The study adhered to the ethical principles of the Committee on Publication Ethics (COPE) and was conducted in accordance with the Declaration of Helsinki.

The PISA 2022 dataset analyzed in this study is publicly available on the OECD website: https://www.oecd.org/en/data/datasets/pisa-2022-database.html (accessed on June 26, 2025).

This article is a revised and expanded version of a paper originally published in Japanese as “数学教師の認知的活性化は数学不安を低減しうるか？” (“Can Cognitive Activation by Math Teachers Reduce Math Anxiety?”) in Shoto Kyoiku Ronshu: The Japanese Journal of Primary Education, Vol. 26, pp. 38–47, by The Primary Education Society, Kokushikan University.

I have no conflicts of interest to disclose.

References

Ahmed, W., Minnaert, A., Kuyper, H., & Van Der Werf, G. (2012). Reciprocal relationships between math self-concept and math anxiety. Learning and Individual Differences, 22(3), 385–389. [CrossRef]
Bandura, A. (1986). Social foundations of thought and action: A social cognitive theory. Prentice-Hall, Inc.
Barroso, C., Ganley, C. M., McGraw, A. L., Geer, E. A., Hart, S. A., & Daucourt, M. C. (2021). A meta-analysis of the relation be-tween math anxiety and math achievement. Psychological Bulletin, 147(2), 134–168. [CrossRef]
Batchelor, S., Torbeyns, J., & Verschaffel, L. (2019). Affect and mathematics in young children: An introduction. Educational Studies in Mathematics, 100(3), 201–209. [CrossRef]
Baumert, J., Kunter, M., Blum, W., Brunner, M., Voss, T., Jordan, A., Klusmann, U., Krauss, S., Neubrand, M., & Tsai, Y.-M. (2010). Teachers’ Mathematical Knowledge, Cognitive Activation in the Classroom, and Student Progress. American Educational Research Journal, 47(1), 133–180. [CrossRef]
Burge, B., Lenkeit, J., & Sizmur, J. (2015). PISA in practice. Cognitive activation in maths: How to use it in the classroom. National Foundation for Educational Research.
Caro, D. H., Lenkeit, J., & Kyriakides, L. (2016). Teaching strategies and differential effectiveness across learning contexts: Evidence from PISA 2012. Studies in Educational Evaluation, 49, 30–41. [CrossRef]
Cheema, J. R., & Kitsantas, A. (2014). Influences of disciplinary classroom climate on high school student self-efficacy and mathematics achievement: A look at gender and racial–ethnic differences. International Journal of Science and Mathematics Education, 12(5), 1261–1279. [CrossRef]
Chi, M. T. H. (2009). Active-Constructive-Interactive: A conceptual framework for differentiating learning activities. Topics in Cognitive Science, 1(1), 73–105. [CrossRef]
Chiu, M. M., & Khoo, L. (2005). Effects of resources, inequality, and privilege bias on achievement: Country, school, and student level analyses. American Educational Research Journal, 42(4), 575–603. [CrossRef]
Dreger, R. M., & Aiken, L. R. (1957). The identification of number anxiety in a college population. Journal of Educational Psychology, 48(6), 344–351. [CrossRef]
Fauth, B., Decristan, J., Rieser, S., Klieme, E., & Büttner, G. (2014). Student ratings of teaching quality in primary school: Dimensions and prediction of student outcomes. Learning and Instruction, 29, 1–9. [CrossRef]
Frenzel, A. C., Goetz, T., Lüdtke, O., Pekrun, R., & Sutton, R. E. (2009). Emotional transmission in the classroom: Exploring the relationship between teacher and student enjoyment. Journal of Educational Psychology, 101(3), 705–716. [CrossRef]
Goetz, T., Lüdtke, O., Nett, U. E., Keller, M. M., & Lipnevich, A. A. (2013). Characteristics of teaching and students’ emotions in the classroom: Investigating differences across domains. Contemporary Educational Psychology, 38(4), 383–394. [CrossRef]
Gough, M. F. (1954). Why failures in mathematics? Mathemaphobia: Causes and treatments. The Clearing House, 28(5), 290–294.
Gunderson, E. A., Park, D., Maloney, E. A., Beilock, S. L., & Levine, S. C. (2018). Reciprocal relations among motivational frameworks, math anxiety, and math achievement in early elementary school. Journal of Cognition and Development, 19(1), 21–46. [CrossRef]
Hembree, R. (1990). The nature, effects, and relief of mathematics anxiety. Journal for Research in Mathematics Education, 21(1), 33–46. [CrossRef]
Klieme, E., Pauli, C., & Reusser, K. (2009). The Pythagoras Study: Investigating effects of teaching and learning in Swiss and German mathematics classrooms. In T. Janík & T. Seidel (Eds.), The power of video studies in investigating teaching and learning in the classroom (pp. 137–160). Waxmann.
Li, Q., Cho, H., Cosso, J., & Maeda, Y. (2021). Relations between students’ mathematics anxiety and motivation to learn mathematics: A meta-analysis. Educational Psychology Review, 33(3), 1017–1049. [CrossRef]
Lipowsky, F., Rakoczy, K., Pauli, C., Drollinger-Vetter, B., Klieme, E., & Reusser, K. (2009). Quality of geometry instruction and its short-term impact on students’ understanding of the Pythagorean Theorem. Learning and Instruction, 19(6), 527–537. [CrossRef]
Liu, Y., Wang, C., Liu, J., & Liu, H. (2022). The role of cognitive activation in predicting mathematics self-efficacy and anxiety among internal migrant and local children. Educational Psychology, 42(1), 83–107. [CrossRef]
Matsuoka, R. (2015a). School socioeconomic compositional effect on shadow education participation: Evidence from Japan. British Journal of Sociology of Education, 36(2), 270–290. [CrossRef]
Matsuoka, R. (2015b). School socioeconomic context and teacher job satisfaction in Japanese compulsory education. Educational Studies in Japan, 9, 41–54. [CrossRef]
Nachbauer, M. (2024). How schools affect equity in education: Teaching factors and extended day programs associated with av-erage achievement and socioeconomic achievement gaps. Studies in Educational Evaluation, 82, 101367. [CrossRef]
National Center for Education Statistics. (2012). Improving the measurement of socioeconomic status for the national assessment of educational progress: A theoretical foundation. National Center for Education Statistics. https://nces.ed.gov/nationsreportcard/pdf/researchcenter/socioeconomic_factors.pdf.
OECD. (2023). PISA 2022 Results (Volume I): The state of learning and equity in education. OECD Publishing. [CrossRef]
OECD. (2024a). PISA 2022 Results (Volume V): Learning strategies and attitudes for life. OECD Publishing. [CrossRef]
OECD. (2024b). PISA 2022 Technical Report. OECD Publishing. [CrossRef]
Pekrun, R. (2006). The control-value theory of achievement emotions: Assumptions, corollaries, and implications for educational research and practice. Educational Psychology Review, 18, 315–341. [CrossRef]
Pekrun, R., & Stephens, E. J. (2010). Achievement emotions: A control-value approach. Social and Personality Psychology Compass, 4(4), 238–255. [CrossRef]
Perry, L. B., Saatcioglu, A., & Mickelson, R. A. (2022). Does school SES matter less for high-performing students than for their lower-performing peers? A quantile regression analysis of PISA 2018 Australia. Large-Scale Assessments in Education, 10(1), 17. [CrossRef]
Ramirez, G., Shaw, S. T., & Maloney, E. A. (2018). Math anxiety: Past research, promising interventions, and a new interpretation framework. Educational Psychologist, 53(3), 145–164. [CrossRef]
Shimizu, Y. (2025). Relation between mathematics self-efficacy, mathematics anxiety, behavioural engagement, and mathematics achievement in Japan. Psychology International, 7(2), 36. [CrossRef]
Sweller, J. (1988). Cognitive load during problem solving: Effects on learning. Cognitive Science, 12(2), 257–285. [CrossRef]
Takashiro, N. (2024). Educational inequality and low SES in Japan: A literature review. In The Palgrave Handbook of Global Social Problems (pp. 1–19). Springer International Publishing. [CrossRef]
Van Ewijk, R., & Sleegers, P. (2010). The effect of peer socioeconomic status on student achievement: A meta-analysis. Educational Research Review, 5(2), 134–150. [CrossRef]
Wang, Z., Hart, S. A., Kovas, Y., Lukowski, S., Soden, B., Thompson, L. A., Plomin, R., McLoughlin, G., Bartlett, C. W., Lyons, I. M., & Petrill, S. A. (2014). Who is afraid of math? Two sources of genetic variance for mathematical anxiety. Journal of Child Psychology and Psychiatry, 55(9), 1056–1064. [CrossRef]
Willms, J. D. (2010). School composition and contextual effects on student outcomes. Teachers College Record: The Voice of Scholarship in Education, 112(4), 1008–1037. [CrossRef]
Zuo, S., Huang, Q., & Qi, C. (2024). The relationship between cognitive activation and mathematics achievement: Mediating roles of self-efficacy and mathematics anxiety. Current Psychology, 43(39), 30794–30805. [CrossRef]

Figure 1. Relationship between cognitive activation for fostering reasoning and math anxiety. Note. The range of the x-axis is from 2.5 percentile to 97.5 percentile.

Figure 2. Relationship between cognitive activation for encouraging mathematical thinking and math anxiety. Note. The range of the x-axis is from 2.5 percentile to 97.5 percentile.

Figure 3. Student SES moderates the effects of cognitive activation for encouraging mathematical thinking on math anxiety. Note. The range of the x-axis is from 2.5 percentile to 97.5 percentile.

Figure 4. School SES moderates the effects of cognitive activation for fostering reasoning on math anxiety. Note. The range of the x-axis is from 2.5 percentile to 97.5 percentile.

Figure 5. School SES moderates the effects of cognitive activation for encouraging mathematical thinking on math anxiety. Note. The range of the x-axis is from 2.5 percentile to 97.5 percentile.

Table 1. Descriptive statistics.

Variable	M	SD
Student level
Male	0.50	0.50
Student SES	-0.01	0.71
Math self-efficacy	-0.49	1.23
Math anxiety	0.33	1.12
School level
School SES	-0.04	0.39
CAR	-0.01	0.29
CAM	-0.35	0.28

Note. Male, male dummy; CAR, cognitive activation for fostering reasoning; and CAM, cognitive activation for encouraging mathematical thinking.

Table 2. Predicting students’ math anxiety.

	Model 1		Model 2		Model 3		Model 4
	B	SEB	B	SEB	B	SEB	B	SEB
Intercept	0.34***	0.01	0.34***	0.01	0.34***	0.01	0.34***	0.01
Student level
Male	-0.19***	0.01	-0.19***	0.01	-0.19***	0.01	-0.19***	0.01
Student SES	0.00	0.01	0.02	0.02	0.00	0.01	0.00	0.01
Math self-efficacy	-0.37***	0.01	-0.37***	0.01	-0.37***	0.01	-0.37***	0.01
School level
School SES	0.13***	0.02	0.13***	0.02	0.08**	0.03	0.13***	0.02
CAR	0.02	0.03	0.01	0.03	-0.01	0.04	0.01	0.03
CAM	-0.03	0.03	-0.03	0.03	-0.04	0.03	-0.03	0.03
CAR2	-0.29***	0.06	-0.29***	0.06	-0.30***	0.07	-0.29***	0.06
CAM2	0.19**	0.07	0.19**	0.07	0.16*	0.07	0.19**	0.07
Interaction
Student SES*CAR	―	―	0.02	0.05	―	―	―	―
Student SES*CAM	―	―	-0.04	0.05	―	―	―	―
Student SES*CAR2	―	―	0.12	0.09	―	―	―	―
Student SES*CAM2	―	―	-0.39**	0.11	―	―	―	―
School SES*CAR	―	―	―	―	0.05	0.09	―	―
School SES*CAM	―	―	―	―	-0.16*	0.08	―	―
School SES*CAR2	―	―	―	―	0.37*	0.16	―	―
School SES*CAM2	―	―	―	―	-0.05	0.18	―	―
Self-efficacy*CAR	―	―	―	―	―	―	0.05	0.03
Self-efficacy*CAM	―	―	―	―	―	―	0.02	0.03
Self-efficacy*CAR2	―	―	―	―	―	―	-0.03	0.05
Self-efficacy*CAM2	―	―	―	―	―	―	0.02	0.06
Random effects
Between school variance	0.03		0.03		0.04		0.03
Within student variance	1.04		1.04		1.04		1.04

Note. CAR, cognitive activation for fostering reasoning; CAM, cognitive activation for encouraging mathematical thinking; CAR2, the square of cognitive activation for fostering reasoning; and CAM2, the square of cognitive activation for encouraging mathematical thinking. *** p < .001, ** p < .01, * p < .05

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.