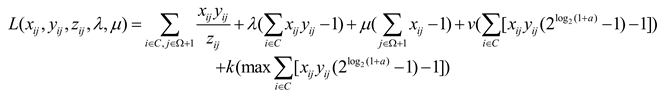Considering the Economy of Multimodal Energy in High-Power LTE Communications Electricity Usage Strategy

1. Introduction

With the massive increase in the number of mobile devices and the continuous rise in communication services, the demand for network traffic has also continued to rise [1]. Wireless communication is a high-energy-consuming industry, with 50 to 80 percent of its energy consumption on the base station side [2]. The current mainstream manufacturers' 5G (fifth generation mobile communication technology) base stations consume about 3.5 to 4 kilowatts of power at full load per system. According to statistics, the existing operating micro base stations consume an average of about 65 kilowatt-hours per day. If calculated at an electricity price of 1 yuan per kilowatt-hour, the annual electricity cost for 5G base stations alone in the country will reach 76.3 billion yuan. As of October 2023, the total number of 5G base stations in China reached 3.215 million [4], accounting for 28.1 percent of the total number of communication base stations in the country. According to China Tower data, the typical power consumption of 5G base stations is around 3,500 watts [27], and reducing the power consumption of base stations has become an urgent problem for operators [5]. When base station equipment operates in high energy consumption mode, it usually has higher temperatures and greater current pressure, accelerating the aging of base station equipment. Network data show that operating at room temperature can save more than 35 percent of electricity and reduce equipment failure rate by more than 30 percent compared to operating at high energy consumption and high temperature. A standard 5G communication base station can save about 11,200 yuan in electricity per year. There are currently about 114,500 5G base stations in Beijing, which can save about 1.279 billion yuan in electricity per year, with an estimated emission reduction of about 14,000 tons. The cost reduction will not only increase the funds for operation and maintenance such as energy storage, improve the reliability of the base stations, but also shorten the payback period, promote the full coverage of the base station network, increase the market penetration rate and facilitate digital transformation.

The current main methods of reducing power consumption for base stations include technological upgrades, sleep management, and hardware upgrades. But the potential problems of these methods are also obvious, including the possibility of reducing or delaying the response speed of communication services, affecting the user experience, and the uncertain burden of requiring a large amount of funds for research and development, installation, commissioning and maintenance in the case of large-scale deployment of base stations. These problems can be largely avoided through energy consumption modeling and optimization analysis methods. Therefore, this paper studies the optimization of communication energy consumption cost in LTE base station groups with high data transmission requirements and large-scale Internet of Things access scenarios: under the condition of ensuring normal communication among users in the base station group, considering D2D communication among users to construct the energy consumption structure model of the LTE base station group, seeking the existence of the minimum value and the main influencing factors of energy consumption cost; At the same time, multiple energy supply methods are considered to reduce the energy cost of the base station group. The main tasks are as follows.

1) In response to the issue of excessively high communication energy consumption in LTE base station clusters with high data transmission demands and large-scale Internet of Things access scenarios, a two-layer cellular base station network containing macro base stations and micro base stations is considered. Under the premise of ensuring the quality of user services, multi-energy power supply scenarios such as wind power, photovoltaic power generation, and grid power supply are taken into account, with the goal of minimizing the energy cost of base stations. Establish a physical model of energy consumption constraints based on the strategy of multi-energy supply and user-base association, and deduce the mathematical model.

2) Analyze the characteristics of the mathematical model and prove that the model is a convex optimization problem. Conduct the minimum value analysis of the energy minimization mathematical model based on convexity analysis and Weier-strass theorem, and prove the optimality, uniqueness and convergence analysis. Also, analyze the physical condition variables of the multi-energy power supply model when seeking the minimum value based on the mathematical model.

3) Simulation analysis of the built multi-energy supply base station group model of wind, solar and storage. To be practical, based on the Beijing summer time-of-use electricity price scheme, the model built will be compared with the power supply cost of conventional base stations to analyze and verify the economic feasibility of the proposed scheme; The optimization strategy of the key impact factor of base station cost was compared and simulated with other base station consumption reduction methods to verify that the proposed method can ensure that the base station achieves better economic rationality, that is, the minimum energy cost, under the reasonable allocation of user bandwidth.

The main content of this paper is structured as follows. Section 1 provides a brief summary of the relevant work. Section 2 establishes and introduces the energy consumption cost model of LTE base station groups in scenarios with high data transmission requirements and large-scale Internet of Things access. Section 3 converts the formula of the model. Section 4 presents the proof of the extreme values of the constraint function and the solution process. Section 5 presents performance simulation and analysis. Section 6 presents the conclusion of this paper. To achieve power supply optimization for base stations in multi-energy scenarios, reduce the amount of electricity purchased from the grid and thereby lower electricity charges; It can also play a role in peak shaving and valley filling, and can flexibly adjust energy supply based on real-time electricity prices, load demand and the output of renewable energy to further improve energy utilization efficiency.

2. Related Work

2.1. Research on Power Consumption Reduction Strategies for Base Station Communications

Compared with the first four generations of network communication technologies, large-scale and high-transmission demand base stations such as 5G have broad application prospects in new fields. One problem brought about by this is that the power consumption required for transmitting a large amount of communication data will also increase several times, leading to a significant increase in the operating costs of operators. How to reduce the total energy consumption of base stations through reasonable resource allocation without affecting users' normal network usage has become an important issue in current research. On the basis of considering the uncertainties of energy reduction and ensuring user correlation, optimizing the sum of the total transmission power of each base station to minimize the total energy cost of system base stations [6] can effectively control the energy allocation strategy of base stations to reduce energy consumption. Another approach is to model it as a coalition game with the aim of maximizing system throughput and ensuring the minimum threshold rate for users [8]. In response to this issue, literature [9] focused on analyzing the power consumption of large-scale, high-transmission demand base stations, studied the sources of power consumption of communication base stations, and proposed effective power consumption control strategies. Reference [10], considering that the high speed, large bandwidth, and low latency transmission characteristics of large-scale, high-transmission-demand base stations must be supported by sufficient energy, proposed the use of "smart operation" to achieve "energy conservation and emission reduction" to reduce electricity cost expenditure; At the same time, reference [11] designed an energy-saving power supply system for base stations and, from the perspective of control, proposed an automatic switching control strategy based on DC bus voltage information. Reference [12] conducted a comprehensive analysis and test analysis of the energy-saving effects of the three methods of energy conservation and emission reduction, completed the data comparison study of detailed parameters, and reached a complete set of data conclusions with practical operational value. In response to the problem that many base stations are idle during periods of low communication load, reference [13] studied the issue of multiple operators sharing base stations to achieve energy conservation and proposed a new game theory method for macro base stations.

2.2. Research on the Constraint Problem of Base Station Energy Consumption

The method of establishing mathematical constraint functions through actual physical models and using extremum optimization to optimize physical models has become one of the mainstream methods in current optimization research. Reference [14] proposed a capacity optimization configuration constraint model for base station photovoltaic energy storage systems to address the current problems of high power consumption and high cost for communication operators of large-scale, high-transmission-based base stations, considering the impact of different time-of-use electricity prices and energy storage costs on the economic benefits of base station photovoltaic energy storage systems; Some of the situations in wireless sensor networks are the same as those in base stations, with the goal of minimizing communication overhead, the communication overhead model and the mathematical method for solving the optimal threshold are also feasible;[15] Reference [16] developed a mathematical model based on minimum communication overhead for the problem of additional communication overhead generated by the dynamic load balancing process; Another study proposes a network benefit-maximization resource allocation problem that takes into account cache cost, benefit and communication energy efficiency on the basis of fog wireless access networks. There are also several studies on energy consumption balance that have transformed the constraint function and solved the extremum [17]. Reference [18] constructed a multi-dimensional utility function to alleviate the power consumption of base stations due to the increasing base station load, taking into account three factors: the accepted signal-dry-noise ratio of users, the utilization of renewable energy, and the base station load. By transforming the problem of minimizing the operating cost of multi-base station systems into the problem of maximizing the utility value of the multi-dimensional utility function; In other studies, there are also methods for balancing network energy consumption based on Measurement reports (MR); [19,20] A study of time slot reallocation schemes based on centralized clustering and time slot reallocation schemes based on distributed clustering was proposed.

In summary, in the above study, strategies such as optimizing transmission power, controlling base station energy allocation, and adopting smart operation were proposed to minimize energy cost, and multiple optimization models were proposed, such as resource allocation based on capacity optimization of photovoltaic storage systems, minimum communication overhead, and maximizing network benefits. However, the extreme value optimization method under the base station energy cost constraint model has not been used to identify the main cause of the high energy consumption of the base station, nor has the impact of multi-energy power supply mode on the overhead of the LTE base station group been considered. Therefore, in this paper, the main influencing factors of base station energy consumption are solved by establishing constraint problems, and the impact of multi-energy power supply on the energy consumption of LTE base station groups is studied. The energy consumption of LTE base station groups is optimized by combining the above two methods.

3. Base Station Energy Consumption Modeling

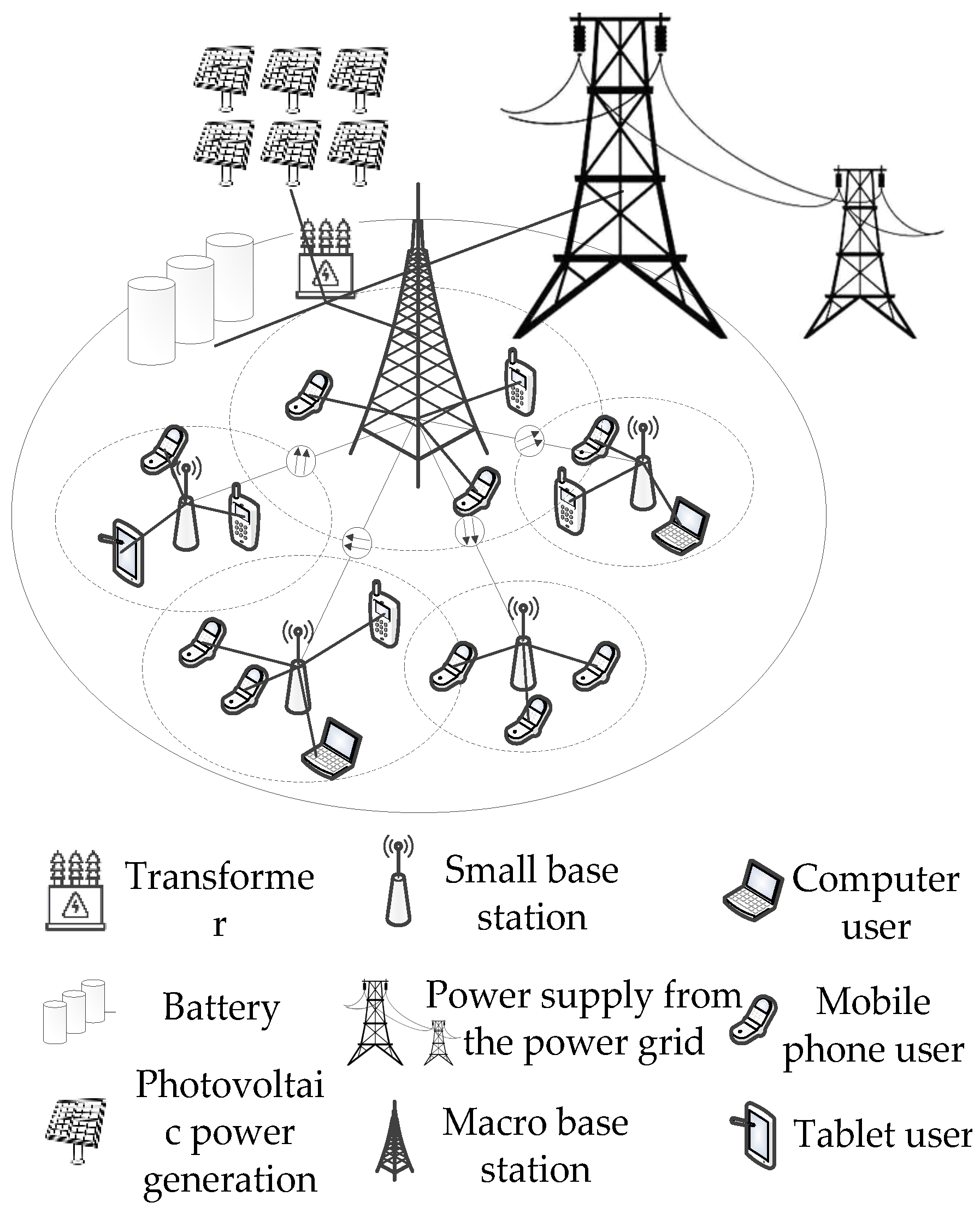
Base station types include macro base stations, micro base stations, pico base stations and flying base stations. Based on considering the power consumption model and social attributes in reference [6], and considering the multi-energy power supply scenarios of wind power generation, photovoltaic power generation and grid power supply, a multi-energy power supply base station model based on user interaction is constructed. As shown in Figure 1, there is a group of multi-energy power supply double-layer honeycomb network base stations located at the center in the system. It includes Macro Base stations (MBS) and Micro Base stations (MBS). Within the coverage area of the macro base stations, there are L(L$\in \Omega$) honeycomb-shaped distributed micro base stations and I randomly distributed users. Macro base stations and micro base stations are powered by multiple energy sources to ensure continuous communication within the coverage area. The base station cluster is equipped with a standard number of photovoltaic panels for self-supply of power to the base station. Eight 550Wp photovoltaic modules are installed on the roof of the base station [26], and it can also receive power from wind turbines at the same time. Only consider the association relationship and resource allocation within $\tau$ time interval of a. Suppose that within each time interval $\tau$, each communication user can only be associated with one base station, and any base station can only be powered by one type of energy within that time interval $\tau$.

3.1. Channel Model Construction

According to Shannon's formula, the actual data transmission rate of cellular users $R_i$ should be:

$$B{b}_{ij}{\log }_2(1+{\displaystyle \frac{p_{ij}{g}_{ij}}{{\sigma }^2+I_{ij}}})=R_i$$

(1)

In the formula: $b_{ij}$ (variable) represents the percentage of bandwidth allocated by the base station to the user (0-1), B is the total bandwidth (quantitative), ${\mathrm{p}}_{ij}$ and $g_{ij}$ are respectively the power and channel gain of communication between the user and the base station, $I_{ij}$ is the comprehensive interference received by the user from the base station and other users, and is set as ${\sigma }^2$ constant. $R_i$ is the noise constant. A represents the maximum information transmission rate in the channel with Gaussian white noise interference. The Ministry of Industry and Information Technology's second-quarter telecommunications service quality bulletin shows that the current downlink data transmission rate is approximately 131Mbps. Considering that the usage of some users is either too high or too low, for the convenience of calculation, this value is taken as the average (quantitative). Although the signal-to-dry ratio (SINR) cannot be calculated as a fixed value within a certain communication area, considering that the SINR can be stabilized within a certain small range through dynamic/closed-loop power control, AMC, frequency multiplexing and network optimization techniques, and this background is that the user group of urban base stations and the environmental interference is relatively stable, Therefore, the average value SINR (quantitative) is taken here as the calculation parameter.

Suppose that when users are associated with the base station and the base station allocates resources for the associated users, the channel remains stable. To simplify the noise calculation, it is assumed that the noise of cellular users connected to the micro base station is the maximum noise and is a constant [23]. Represent the association relationship within the time interval with the binary variable $x_{ij}$:

$$x_{ij}=\left\{\begin{array}{l}0\\ 1\end{array}\right.$$

(2)

In the formula: Take 1 when the user is associated with the base station; otherwise, take 0.

3.2. Power Consumption Model Construction

On the basis that the user has a fixed data transmission rate, the total transmission power of the full bandwidth of the base station can be obtained as:

$$P_{ij}=（2^{{\displaystyle \frac{R_{\mathrm{i}}}{B{b}_{ij}}}}-1）{\displaystyle \frac{{\sigma }^2+I_{ij}}{g_{ij}}}$$

(3)

Based on the user association, let the actual total transmission power of the base station be:

$$P_j={\displaystyle \sum _{i\in C}{x}_{ij}{P}_{ij}{b}_{ij}}$$

(4)

According to the user association strategy, the total power consumed by the base station can be obtained as:

$$P_j^{all}={\mu }_i{P}_j+P_j^s$$

(5)

In the formula: ${\mu }_j$ is the power factor consumed by the base station for data transmission, $P_j^s$ is the power consumed by the static circuit, and C is the user set.

3.3. Cost Model Construction

The cost model of the base station group is constructed based on the channel model and power consumption model, and only the correlation and resource allocation within one time interval are considered. During this time interval, the base station can only be powered by one type of energy. The energy consumption of the base station is expressed as:

$$E_j^c=P_j^{all}\tau +P_D$$

(6)

In the formula: A represents the static energy consumption of the base station [14], and is taken as the average value of the static energy consumption per unit time within a day. The renewable energy A stored in the base station during the period is:

$$G_{\mathrm{j}}={\eta }_{dis}\left[\min \{G+G_j^H-E_j^c,E_{\max }\}\right]-{\theta }_j$$

(7)

In the formula: A represents the supply/capture volume of renewable energy (including wind power and photovoltaic power) in the previous period. When the photovoltaic power generation of the base station is insufficient, wind power supply or grid supply is selected. G represents the renewable energy stored by the base station in the previous period. A indicates the low energy threshold, A is the upper limit of the maximum energy storage of the battery, and A is the discharge efficiency of the energy storage. That is, when it is lower than this point, data transmission cannot work.

The indicator function for setting the energy consumption type of the micro base station is:

$${\delta }_j=\left\{\begin{array}{c}0,G_j<E_j^c\\ 1,G_j\ge E_j^c\end{array}\right.$$

(8)

In the formula: When 0 is taken, grid energy is used; when 1 is taken, renewable energy is consumed. Define m as the unit price of grid energy and n as the unit price of renewable energy [22], and m>n>0;

Based on the channel model and power consumption model, combined with the multi-energy power supply setting, while considering that the energy consumption of base stations is related to the user connection relationship and resource allocation strategy, and taking the energy consumption and the unit price of energy as the main variables, the total energy cost price A of all base stations can be obtained. Transform this energy cost savings problem into a condition optimization problem and express it as follows:

$$\min W={\displaystyle \sum _{j\in \Omega +1}\mathrm{m}(1-{\delta }_j)E_j^c+n}{\delta }_j{E}_j^{c}s.t.\left\{\begin{array}{c}{C}_1\\ C_2\\ C_3\end{array}\begin{array}{c}0\le P_j\le P_j^{\max }，\\ {\displaystyle \sum _{i\in C}{x}_{ij}{b}_{ij}=1},\\ {\displaystyle \sum _{j\in \Omega +1}{x}_{ij}=1},{\displaystyle \sum _{d\in D}{x}_d^i=1},\end{array}\begin{array}{c}\forall \mathrm{j}\in \Omega +1\\ \forall \mathrm{j}\in \Omega +1\\ \forall \mathrm{i}\in C\end{array}\right.$$

(9)

In the formula: A represents the transmission power constraint of the base station, that is, the maximum transmission power limit; A indicates that the total proportion of bandwidth resources allocated by the base station to users is guaranteed to be 1; A indicates that a user can only be connected to one base station within a certain period of time and the downlink resources between users are multiplexed one-to-one. C is the set of the number of communication users.

4. Base Station Energy Consumption Overhead Model Transformation

The problem of minimizing the energy consumption of LTE base station groups in scenarios with high data transmission requirements and large-scale Internet of Things access is transformed into the corresponding mathematical model and simplified to study the existence of the minimum value. The key focus is on minimizing the energy consumption cost of base station equipment, while ensuring normal communication between users and the continuous power supply of base stations. Formalize and simplify the physical model (9) :

Let $G_j=x_{1\alpha }$$G=x_2=a_3$, $G_j^H=x_{3\alpha }=\mu$, $E_j^c=x_{4\alpha }$, ${\theta }_j=x_{5\alpha }=a_2$, $E_{\max }=d=a_4$, $\tau =e=b_2$, $P_j^{all}=x_{7\alpha }$, $E_j^c=x_{6\alpha }$, $n=b=b_1$, $m=a=b_7$, ${\mu }_j=j=b_4$, $P_j^s=g=b_3$, ${\sigma }^2=h=b_5$, $I_{ij}=i=b_6$, $b_{ij}=y_{ij}$, $p_{ij}={\eta }_{ij}$, $g_{ij}=z_{ij}$, $j\in \Omega +1$, $i\in C$.

On this basis, the constraint condition C₁ is simplified as:

$$x_{1\alpha }=\min \left\{x_2+x_{3\alpha }-x_{4\alpha },d\right\}-x_{5\alpha }<x_{6\alpha }=x_{7\alpha }e$$

(10)

At this point, the objective function is:

$$\min f={\displaystyle \sum _{j\in \Omega +1}{b}_7{x}_{7j}{b}_2}=b_7{b}_{2}c{b}_3+b_7{b}_2{b}_4(b_5+b_6)(2^{{\log }_2(1+a_1)}-1)[{\displaystyle \frac{{\mathrm{x}}_{11}{y}_{11}}{z_{11}}}+\dots +{\displaystyle \frac{x_{(\Omega +1)C}{y}_{(\Omega +1)C}}{z_{(\Omega +1)C}}}]$$

(11)

Therefore, the objective function is:

$$\min f=\left\{\begin{array}{l}{b}_1({\displaystyle \frac{x_{11}{y}_{11}}{z_{11}}}+\dots +{\displaystyle \frac{x_{(\Omega +1)C}{y}_{(\Omega +1)C}}{z_{(\Omega +1)C}}}),x_{1\alpha }\\ =\min \left\{a_3+\mu -b_2\{[b_4{x}_{ij}{y}_{ij}(2^{{\log }_2(1+a_1)}-1){\displaystyle \frac{b_5+b_6}{z_{ij}}}]+b_3\},a_4\right\}-a_2\\ \ge b_2\{[b_4{x}_{ij}{y}_{ij}(2^{{\log }_2(1+a_1)}-1){\displaystyle \frac{b_5+b_6}{z_{ij}}}]+b_3\}\\ b_7({\displaystyle \frac{{\mathrm{x}}_{11}{y}_{11}}{z_{11}}}+\dots +{\displaystyle \frac{x_{(\Omega +1)C}{y}_{(\Omega +1)C}}{z_{(\Omega +1)C}}}),x_{1\alpha }\\ =\min \left\{a_3+\mu -b_2\{[b_4{x}_{ij}{y}_{ij}(2^{{\log }_2(1+a_1)}-1){\displaystyle \frac{b_5+b_6}{z_{ij}}}]+b_3\},a_4\right\}-a_2\\ <b_2\{[b_4{x}_{ij}{y}_{ij}(2^{{\log }_2(1+a_1)}-1){\displaystyle \frac{b_5+b_6}{z_{ij}}}]+b_3\}\end{array}\right.$$

(12)

Obviously, formula (12) is in polynomial form. Considering that the original objective function is f piecewise function, except for the two constants $b_1$ and $b_7$, all other parts are the same, and the remaining constant parts do not contain negative values. Therefore, the constant part does not affect the value point of the minimum value of the function f. The final simplified mathematical model constraint function f for the communication overhead of LTE base station groups is:

$$\begin{gathered} \min f=b_7({\displaystyle \frac{{\mathrm{x}}_{11}{y}_{11}}{z_{11}}}+\dots +{\displaystyle \frac{x_{(\Omega +1)C}{y}_{(\Omega +1)C}}{z_{(\Omega +1)C}}})\begin{array}{l}\mathrm{s}.\mathrm{t}{.\mathrm{C}}_1:0\le {\displaystyle \sum _{i\in C}[x_{ij}{y}_{ij}(2^{{\log }_2(1+a_1)}-1)\frac{b_5+b_6}{z_{ij}}]}\\ \le \max {\displaystyle \sum _{i\in C}[x_{ij}{y}_{ij}(2^{{\log }_2(1+a_1)}-1)\frac{b_5+b_6}{z_{ij}}]}\end{array}{C}_2:{\displaystyle \sum _{i\in C}{\mathrm{x}}_{\mathrm{ij}}{\mathrm{y}}_{ij}}=1 \\ {C}_3:{\displaystyle \sum _{j\in \Omega +1}{x}_{ij}}=1 \\ {C}_4:{\displaystyle \sum _{j\in \Omega +1}{x}_{ij}}=1 \\ {C}_5:y_{ij}>0 \\ {C}_6:(d>)z_{ij}>0 \end{gathered}$$

(13)

Among them, $x_{ij},y_{ij},z_{ij}$ are all variables greater than 0, and $a,b$ is a constant. Since in practical applications $b_7>b_1>0$, it is obvious that when the condition (15) is satisfied, the local optimal solution of f is the global optimal solution:

$$\min \left\{a_3+\mu -b_2\{[b_4{x}_{ij}{y}_{ij}(2^{{\log }_2(1+a_1)}-1){\displaystyle \frac{b_5+b_6}{z_{ij}}}]+b_3\},a_4\right\}-a_2\ge b_2\{[b_4{x}_{ij}{y}_{ij}(2^{{\log }_2(1+a_1)}-1){\displaystyle \frac{b_5+b_6}{z_{ij}}}]+b_3\}$$

(14)

5. Optimization Analysis

According to the simplified mathematical model analysis in Section 3, under certain conditions such as electricity investment, operating and maintenance costs, signal-to-dry ratio, channel gain and noise power, without considering the power supply mode, the energy consumption of the base station is mainly related to the number of associated users, bandwidth allocation ratio and channel gain between the base station and users. The number of associated users is a variable that cannot be controlled; The Bandwidth allocation ratio is controllable, and the utilization of resources and the overall efficiency and performance of the network can be improved through Dynamically Bandwidth Assignment (DBA). According to the analysis, the quality of the channel gain is mainly determined by the hardware. When the channel gain is good, the signal transmission quality is often better, which may reduce the transmission power required by the base station to maintain the signal strength, thereby reducing energy consumption to a certain extent.

In this section, the minimum existence of the mathematical model in Section 3 is solved based on convexity analysis and the Weier-strass theorem, and optimality, uniqueness and the solution process are analyzed.

5.1. Analysis of the Model's Energy Consumption Optimality

This section analyzes and presents the existence of the minimum value of the communication energy consumption cost model of LTE base station groups in scenarios with high data transmission requirements and large-scale Internet of Things access from the theoretical and mathematical derivation perspectives. Thus, the corresponding certain conditions for the existence of the minimum value can be found through mathematical derivation. In practical applications, by constraining the corresponding conditions, the energy consumption cost of the base station group can be minimized to the greatest extent on the premise of ensuring the normal operation of the base station and the normal communication of users.

Based on the simplified model of the objective function obtained in the previous section, perform polynomial splitting of the objective function. According to the convexity theory of fractional functions and by proving the convexity of a single fractional term, it can be proved that the mathematical model of the objective function is a strictly convex function. By analyzing the continuity of the objective function under constraints and combining the Weier-strass extreme value theorem, it can be analyzed that the minimum value of the solution exists.

Theorem 1 - The energy consumption cost model of LTE base station groups in scenarios with high data transmission requirements and large-scale Internet of Things access has a convex constraint function structure under the given constraints: Assuming the user output transmission rate is constant, the static energy consumption of the base station is constant, the transmission consumption of the base station is constant and the noise constant is constant, then the structure of the communication energy consumption overhead function model of the double-layer cellular LTE base station is a convex function, and there exists a minimum value. Proof: See Appendix 1.

Based on the KKT conditions, Lagrange multipliers are introduced and Lagrange functions are defined to obtain the gradient conditions, original feasibility conditions, dual feasibility conditions and complementary relaxation conditions that need to be verified. According to the Slater condition, through example ${x^0}_{ij},{y^0}_{ij},{z^0}_{ij}$ and verification, it can be known that if the minimum value exists, then this value is the optimal solution.

Theorem 2 - Existence of the minimum optimal Solution of the constraint Function: The unique minimum value obtained by solving based on the model of Theorem 1 is also the optimal solution of the objective function. Proof: See Appendix 2.

Analysis shows that, on the premise of ensuring the quality of user services, during the communication process of multi-energy power supply base stations with dense deployment of micro base stations, there exists a minimum energy consumption, and this minimum value is the optimal minimum value. That is, in the process of energy consumption in base station communication, there exists a scheme that can minimize the overall energy consumption of the base station while ensuring that the communication quality is not affected. According to (11) and the power supply price, it can be known that when choosing energy sources and considering photovoltaic power supply > wind power supply > grid power supply, the overall energy consumption of the base station can be minimized.

To sum up, it can be proved that under the given base station energy consumption model and constraints, there exists an optimal solution, and the minimum energy consumption point is unique. The predictability of the system is of great significance. Under the base station energy consumption model shown in Figure 2, it is proved by 4.1 that the energy consumption surface is convex, that is, the energy minimization problem can be effectively solved through the convex optimization method, and the possibility of finding the global optimal solution is relatively large.

5.2. Solution of the Model's Minimum Energy Consumption

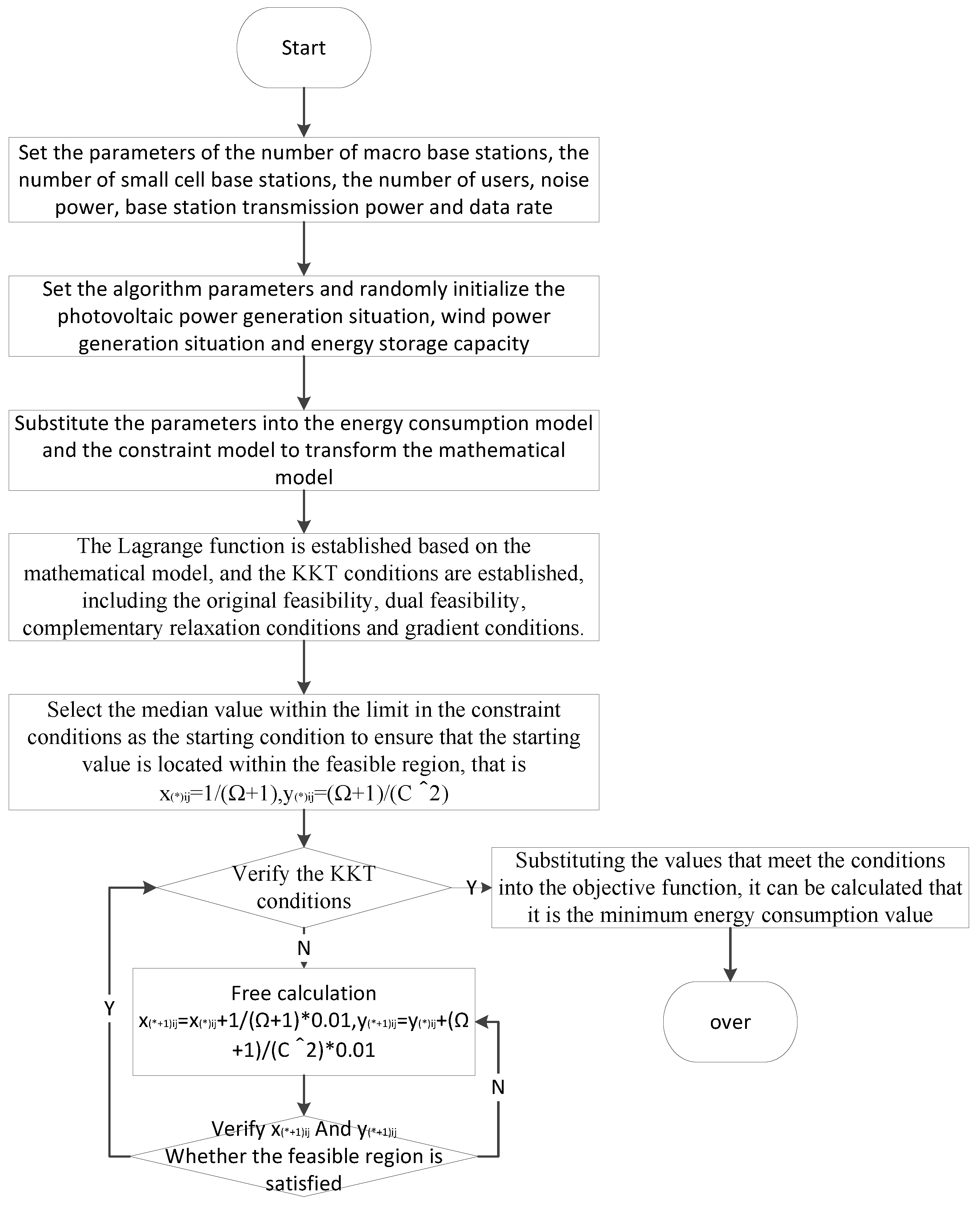
When solving the minimum value of the base station energy consumption constraint optimization problem, considering that this model is a convex optimization model, the solution process is shown in Figure 3. When transforming the problem into the form of a Lagrange function, the constraint conditions are paired with the set Lagrange multipliers to construct the Lagrange equation:

$$x_{1\alpha }=\min \left\{x_2+x_{3\alpha }-x_{4\alpha },d\right\}-x_{5\alpha }<x_{6\alpha }=x_{7\alpha }e$$

(16)

In the formula: i represents the number of inequality constraints, j represents the number of inequality constraints, and ${\lambda }_i$ and ${\mu }_j$ are the Lagrange multipliers of the corresponding constraints respectively.

The KKT conditions include:

(1) Original feasibility:

$$x_{1\alpha }=\min \left\{x_2+x_{3\alpha }-x_{4\alpha },d\right\}-x_{5\alpha }<x_{6\alpha }=x_{7\alpha }e$$

(17)

(2) Duality feasibility:

$$x_{1\alpha }=\min \left\{x_2+x_{3\alpha }-x_{4\alpha },d\right\}-x_{5\alpha }<x_{6\alpha }=x_{7\alpha }e$$

(18)

(3) Complementary relaxation conditions:

$$x_{1\alpha }=\min \left\{x_2+x_{3\alpha }-x_{4\alpha },d\right\}-x_{5\alpha }<x_{6\alpha }=x_{7\alpha }e$$

(19)

(4) Gradient conditions:

$$x_{1\alpha }=\min \left\{x_2+x_{3\alpha }-x_{4\alpha },d\right\}-x_{5\alpha }<x_{6\alpha }=x_{7\alpha }e$$

(20)

The process of approximating the minimum value through the interior point method. If the minimum value satisfies the KKT condition, the minimum base station energy consumption value can be obtained by substituting it into the original objective function for calculation. The solution process is shown in Figure 2.

6. Simulation Analysis

This section verifies the convergence of the minimum value solution and the superiority of the model method through MATLAB R2018a simulation, and simulates and evaluates the proposed multi-energy supply LTE base station group energy consumption overhead model. In order to be practical, based on the time-of-use electricity price and lighting conditions in Beijing during summer, compare the communication overhead of LTE base station groups under conventional high data transmission requirements and large-scale Internet of Things access scenarios and the communication overhead of LTE base stations under multi-energy power supply; According to Section 4, it is easy to know that this model has a minimum value under the three key cost influencing factors in Section 3, and the key cost influencing factors are analyzed in combination with multiple base station energy consumption optimization methods.

6.1. Solution of the Model's Minimum Energy Consumption

Suppose the macro base station in the system is located at the central position with a coverage radius of 500 meters, and around it are evenly distributed 7 micro base stations with a coverage radius of 300 meters powered by multiple energy sources. Set the total number of users to 700 and consider the random flow distribution of users. The expression for the total base station link loss is:

$$L(d)=128.1+37.6\log d$$

(21)

The path loss expression of the micro base station link is:

$$L(d)=140.7+36.7\log d$$

(22)

The expression for the link loss between users is:

$$L(d)=148+40\log d$$

(23)

The fixed data rate for users is 1Mb/s, and each base station is allocated a bandwidth of 10MHz. The number of system users is 20 to 100, the physical distance between users is 25m to 75m, and the noise power is -174σ/ (dBm/Hz). Based on the known objective function and constraint conditions, the convergence process is simulated and analyzed.

The convergence of the model's minimum value was verified through multiple convergence methods. As shown in Table 1, the model can converge to the minimum value within a relatively short period of time. The interior point method ultimately failed to converge to the target value, while the convergence speed of the gradient descent method was obviously better than that of the Newton method. Although the interior point method can rapidly narrow the search range by gradually approaching the constraint boundary, resulting in a fast convergence speed, considering the influence of the obstacle parameters in the early stage of iteration, the deviation is relatively large; However, the Newton method is slower than the gradient descent method because the Hessian matrix takes time to calculate in high dimensions. The gradient descent method performs better in this model when the step size is set appropriately. Therefore, the gradient descent method is selected when calculating the minimum value of the model.

6.2. Simulation Analysis

Regarding the base station and user data in the simulation, based on the parameter Settings in Section 5.1, the fixed data rate for users is set to 1Mb/s, and each base station is allocated a bandwidth of 10MHz. The number of system users is 20 to 100, the physical distance between users is 25m to 75m, and the noise power is -174σ/ (dBm/Hz). Suppose the base station has the conditions for photovoltaic power generation and wind energy supply.

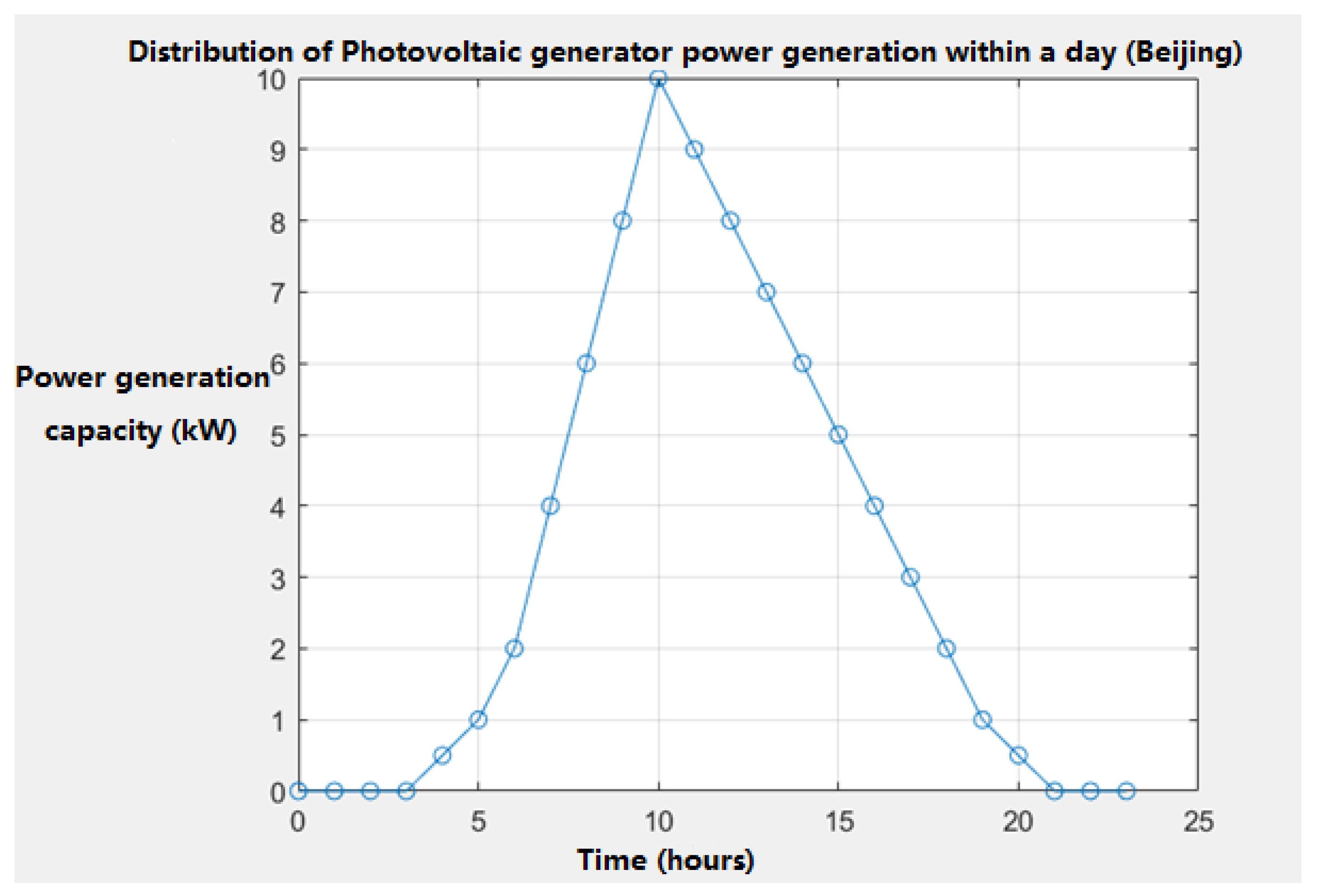
In the photovoltaic power generation data simulation of multi-energy power supply base stations, approximately 50 square meters of photovoltaic power generation panels are required for setting up 7 base stations. The photoelectric conversion efficiency is set at 0.2 for power generation simulation. To approach the real situation, the solar irradiation within one day in summer in Beijing was selected. The power generation simulation of photovoltaic panels within the base station cluster within one day is shown in Figure 3. Obviously, the peak power generation mainly occurs between 9 a.m. and 3 p.m., and the operation time is from 4 a.m. to 8 p.m. Even at night, base stations still need to purchase electricity from the power grid when they are in operation.

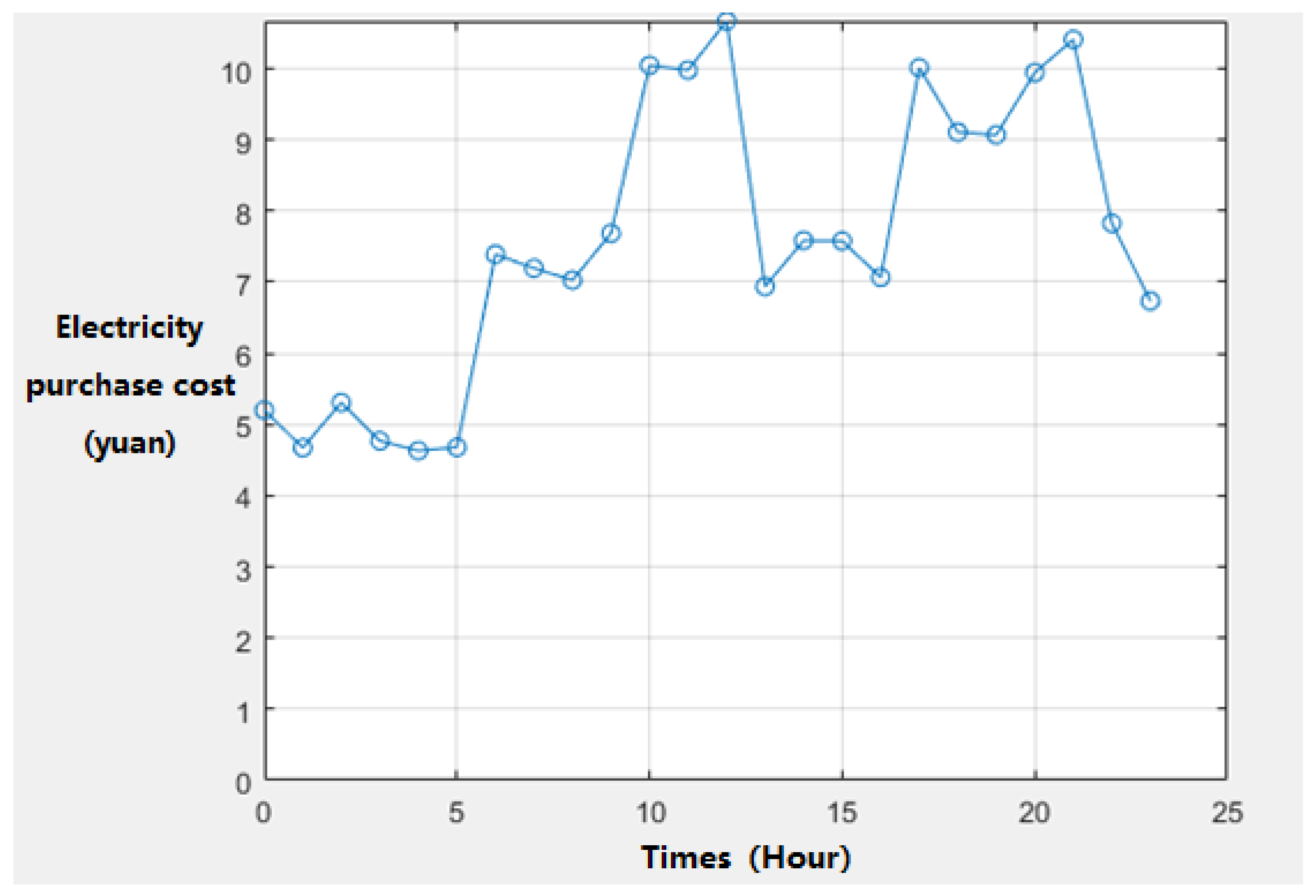
In order to make the simulation results closer to the communication energy consumption cost of the LTE base station group within one day in the scenarios of high data transmission requirements and large-scale Internet of Things access, the power purchase price of the base station when choosing grid power supply refers to the power purchase price in Beijing. The power consumption of the operator's base station belongs to the single or two-part time-of-use power consumption for industrial and commercial use. Considering that the power supply of the base station is at the voltage level of 1 to 10 kilovolts, the single power supply mode is selected. The specific prices are shown in Table 2. As can be seen from the table, the lowest electricity price period is from 11 p.m. to 7 a.m. the next day, which is a relatively small period for the operation of wind and solar power generation.

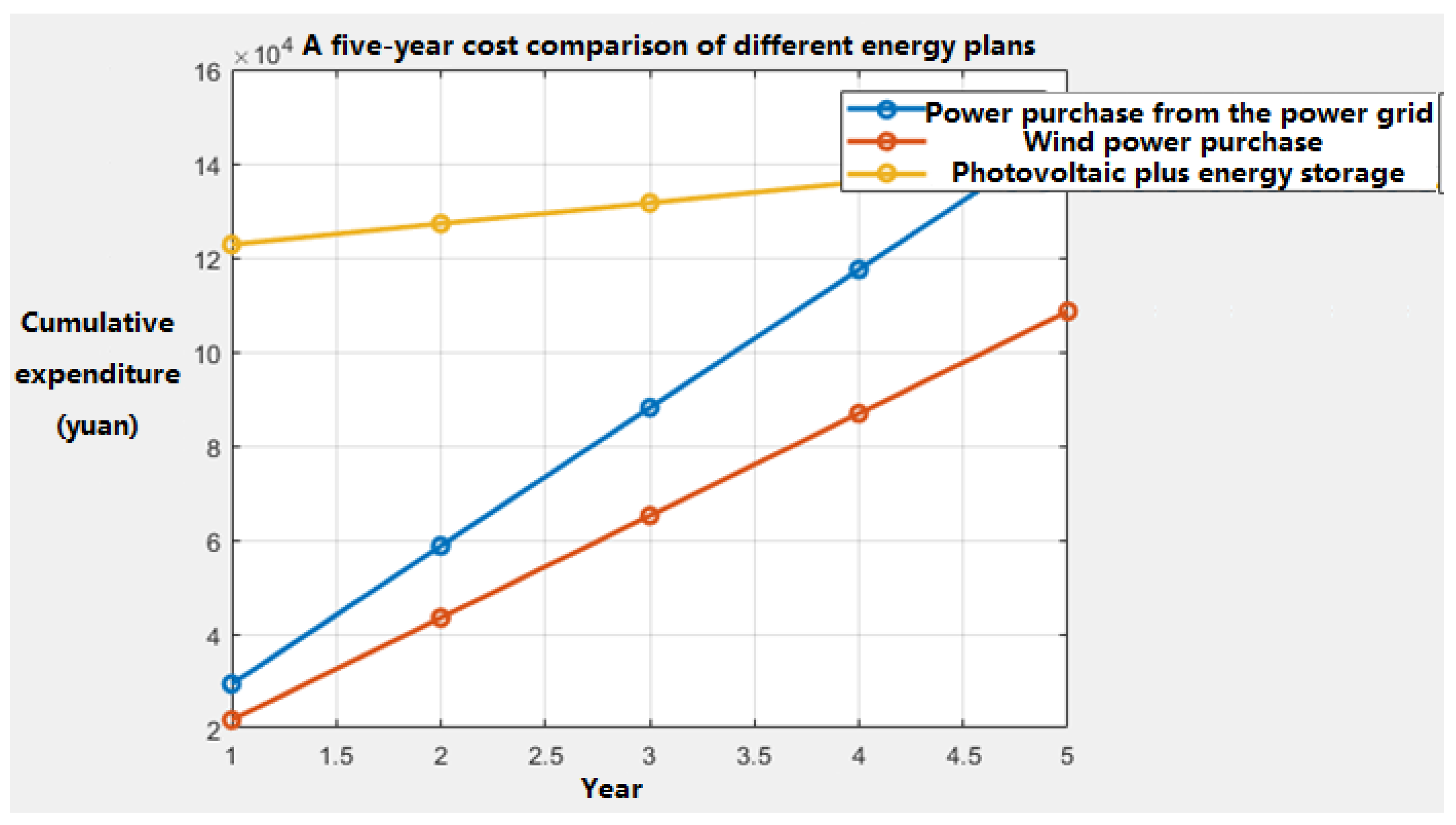
Based on the time-of-use electricity price for power purchase in the power grid, if the average power consumption of the base station per hour per day is 3.8 kilowatt-hours, then the average daily power purchase cost is 80.4526 yuan. If wind power is purchased, considering that Inner Mongolia and Xinjiang are Class I resource areas and the on-grid electricity price is 0.51 yuan /kWh, the line loss cost in the on-grid link is calculated by the on-grid electricity price × the verified line loss rate ÷ (1- verified line loss rate), and the line loss cost is 0.0157 yuan /kWh. Then the comprehensive electricity price is approximately 0.6757 yuan /kWh. The average daily electricity purchase expense is approximately 59.5 yuan. Suppose the maximum allowable installation capacity of photovoltaic power is 25kW, the construction cost of photovoltaic power generation is 3735 yuan /kW, the maximum power generation capacity of a single photovoltaic module is 400 W, the payback period is 15 years, the maintenance cost per unit output power is 0.21 yuan /kW, and the maximum allowable installation capacity of energy storage is 15 kW·h. The installation investment cost per unit capacity is 1,000 yuan /(kW·h), the annual operation and maintenance cost per unit capacity is 100 yuan /(kW·h), and the average daily attenuation rate is taken as 0.04%. Then, the photovoltaic construction cost is approximately 93,375 yuan, the annual operation and maintenance cost is approximately 5.25 yuan, the energy storage construction cost is approximately 25,000 yuan, and the operation and maintenance cost is approximately 2,500 yuan. The cost comparison of the three power supply schemes within five years is shown in the following figure:

Figure 4. shows the comparison of the annual cost of a single base station under three power supply schemes over five years.

Figure 4. shows the comparison of the annual cost of a single base station under three power supply schemes over five years.

Based on the time-of-use electricity price for industrial and commercial use in Beijing, when only the power supply from the power grid is used as the energy supply for the base station, referring to the load per hour of the base station within a day in reference [14], and taking into account the user activity level, the electricity consumption cost of the base station group within a day is simulated as shown in the following figure.

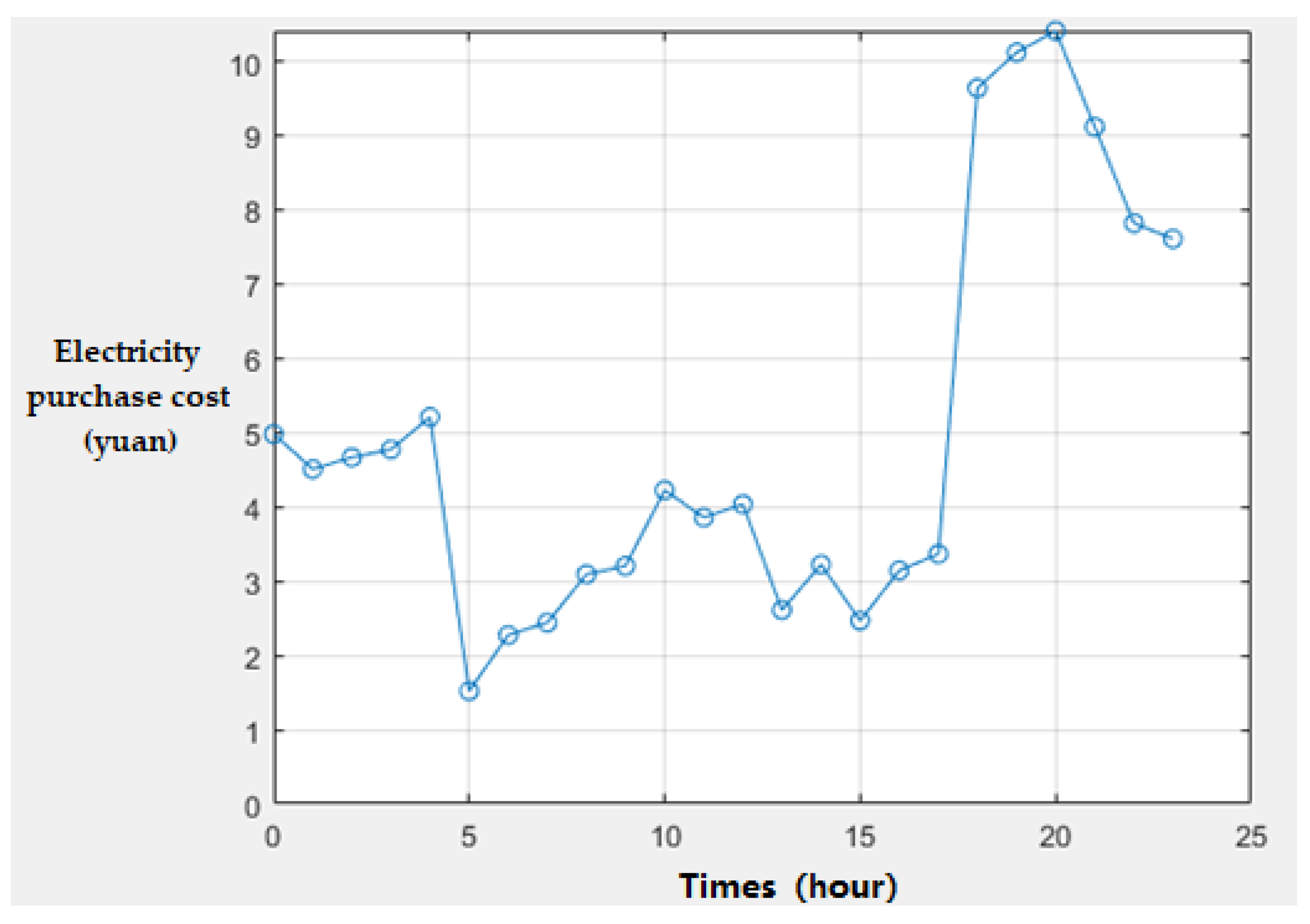
As can be seen from Figure 5, the daily communication energy consumption and power purchase cost of the base station group is approximately 181.95 yuan. The main time periods for power purchase cost are concentrated in the morning, evening and evening. It can be analyzed that it is related to the user activity level.

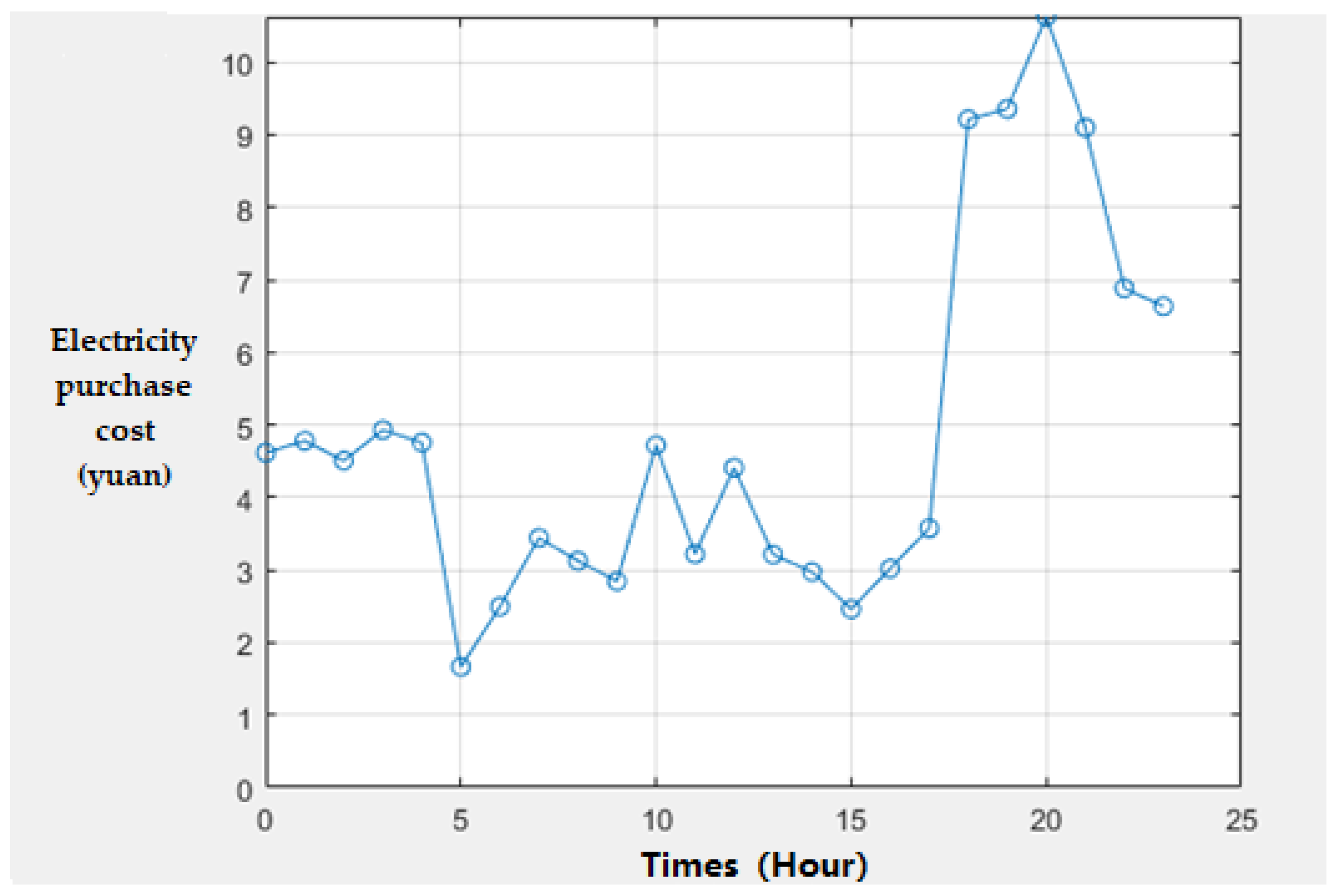
Based on time-of-use electricity prices, according to the construction of the minimum energy consumption model for multi-energy base station groups, the multi-energy power supply base station groups of wind and solar power are considered. Photovoltaic power generation is the supply for the base stations themselves. When the power supply is insufficient, wind power generation is selected. Secondly, the power supply from the power grid is considered. The simulated power consumption of the base station group within 24 hours is shown in Figure 6. And according to the optimal bandwidth allocation percentage in the case of user association obtained in the minimum energy consumption model, as shown in Figure 9. It can be known from Figure 6 that when considering the optimal bandwidth allocation simultaneously under this multi-energy power supply model, the total daily communication overhead of the base station group is 125.40 yuan. Obviously, when considering multi-energy power supply from wind power, during the midday and morning when sunlight is better, the amount of electricity that base stations need to purchase from the power grid is significantly reduced, and the cost of purchasing electricity within a day is saved by approximately 31.08%. It can be known from Figure 7 that when considering the optimal bandwidth allocation situation, the total daily power purchase cost of the base station is approximately 116.56 yuan, which is further reduced by 7.05% on the basis of Figure 8.

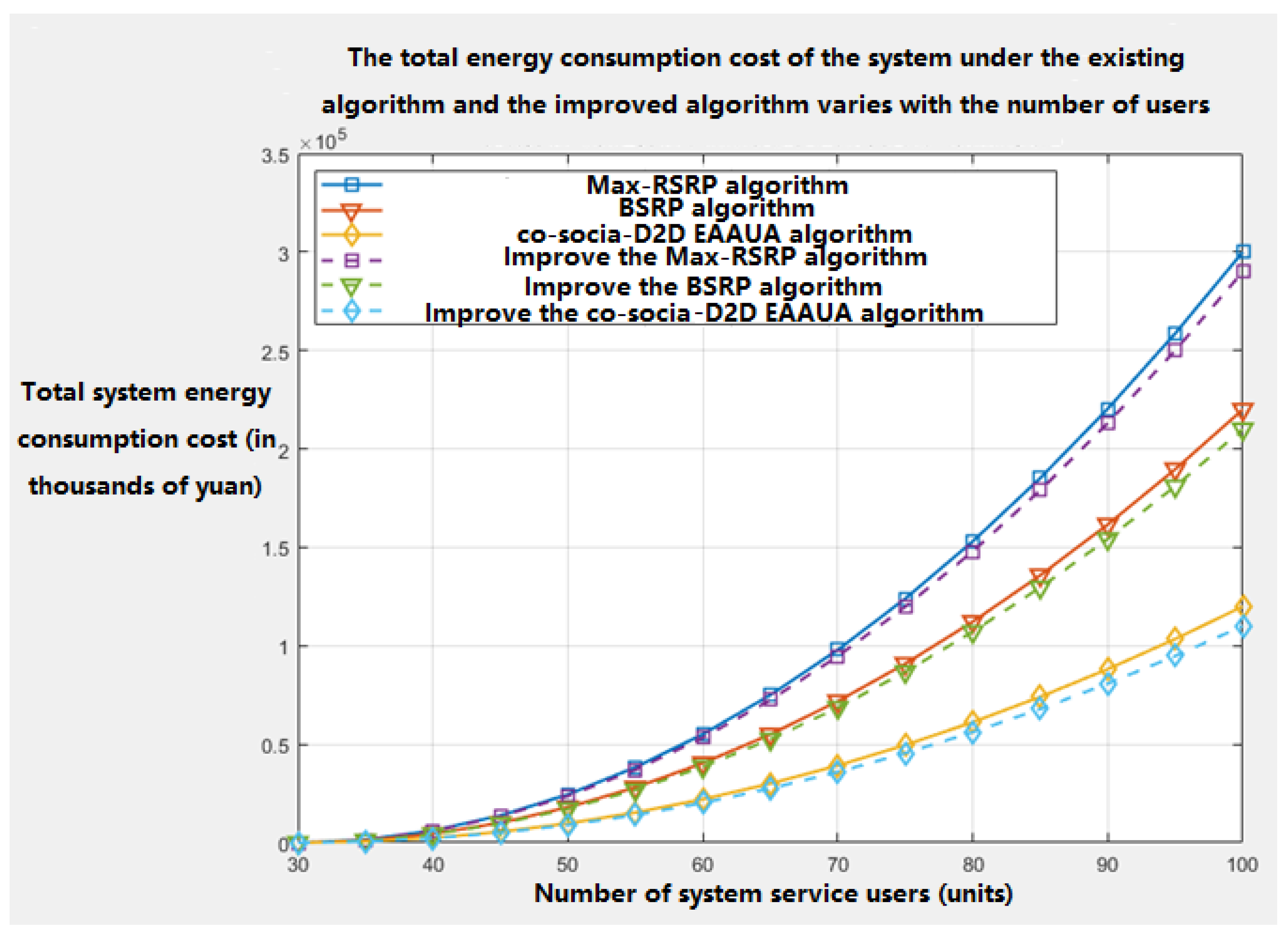
To verify the influence of the main influencing factors of the communication overhead of LTE base station groups analyzed in Section 4 on the actual communication energy consumption overhead of base station groups in scenarios with high data transmission requirements and large-scale Internet of Things access, The key factors of the adaptive sensing user-base station association algorithm Co-social-D2D EAAUA algorithm in reference [6], the maximum reference signal receiving power max-RSRP algorithm in reference [28], and the base station preference bias factor algorithm BSRP algorithm in reference [29] were optimized. And compare it with the overhead situation of the original algorithm when the number of users increases. The simulation results are shown in Figure 8. These three algorithms are the connection scheme algorithms between base stations and users. The algorithms are optimized by adjusting the percentage of user bandwidth based on the user connection scheme. It can be known from Figure 8 that the algorithm optimized for key factors has a slightly better overhead situation than the original algorithm when the number of users served by the base station increases.

When only grid power supply and photovoltaic power generation are considered, the power consumption strategy of base stations is shown in Table 3 as follows:

By comparing the results, it can be seen that the proposed model has better energy consumption performance and to some extent meets the demand for reducing the energy consumption of base station communication. According to the derivation process, in this context, when the base station group uses renewable energy as much as possible, the energy consumption of this base station group is the least, the best economic rationality and the highest rate of return can be achieved within the multi-energy supply base station, and the minimum energy consumption point can always be found according to the energy consumption curve of the base station.

7. Results

A study was conducted on minimizing the energy consumption of multi-power supply base stations based on user communication. Under the premise of ensuring normal user communication, direct connection communication is carried out, while considering the multi-energy power supply scenarios of wind power generation, photovoltaic power generation and grid power supply. Based on this, a physical model of base station energy consumption is established. According to the mathematical model, it is known that the optimal energy consumption is related to the user association and the percentage of bandwidth allocation. The Weier-strass theorem was used to solve the extreme value of the optimal energy consumption of the mathematical model. The existence of the most and least values was proved by the convex function theorem method and the Karush-Kuhn-Tucker condition. The result optimality and convergence speed of the algorithm were analyzed, and it was confirmed that the surface of the base station energy consumption problem is convex. The physical conditions required for the base station to reach the minimum energy consumption were mapped. The analysis found that the energy consumption of the base station was mainly related to the number of associated users, the bandwidth allocation ratio, and the channel gain between the base station and users. The simulation results show that the established model is analyzed by combining the spatio-temporal diversity of renewable energy. The experiment shows that compared with the traditional base station operation and power supply strategy, the model can reduce the economic cost of communication energy consumption by considering the multi-energy power supply of the base station and the dynamic bandwidth allocation of related users, and can reduce the economic cost by about 31.08% through the multi-energy power supply of wind and solar power. The key variable control obtained through the minimization method can reduce the economic cost by approximately 7.05%. Optimizing power supply for base stations in multi-energy scenarios can reduce the amount of electricity purchased from the grid, thereby lowering electricity charges; On the other hand, it has the function of peak shaving and valley filling. It can also flexibly adjust energy supply based on real-time electricity prices, load demand and the output of renewable energy, further improving energy utilization efficiency. Considering that the energy consumption adjusted for key control variables of base station communication is significantly lower than that of conventional communication, the proposed optimization method has better energy efficiency performance, and the given model has better performance in reducing the energy consumption of LTE base station groups in scenarios with high data transmission requirements and large-scale Internet of Things access. To a certain extent, increase the construction and maintenance funds for energy storage and other operations, improve the reliability of base stations, shorten the payback period, promote the full coverage construction of LTE base station networks, increase market penetration, and promote digital transformation.

Appendix A.1. The Model of Energy Consumption Cost of LTE Base Station Groups in Scenarios with High Data Transmission Requirements and Large-Scale Internet of Things Access Has a Convex Structure of the Constraint Function Under the Given Constraints

It is obvious that the objective function f is the sum of multiple fractions. According to the convexity theory of fraction functions: if the objective function f is the sum of multiple fractions and each fraction is convex, then the objective function is also convex. Therefore, it is only necessary to prove that each fraction ${\displaystyle \frac{x_{ij}{y}_{ij}}{z_{ij}}}$ is strictly convex in the positive number field to prove that the objective function is convex.

According to the convexity theory of fractional functions, if ${\displaystyle \frac{x_{ij}{y}_{ij}}{z_{ij}}}$ single fractional term function $f(x_{ij},y_{ij},z_{ij})$ satisfies the following conditions, then function A is a convex function:

1) $x_{ij}$,$y_{ij}$ is an affine function, that is, a polynomial function with a maximum degree of 1.

2) $z_{ij}$ is a positive affine function, that is, a polynomial function with a positive value of the highest degree of 1 and.

Constraint conditions $C_1$ and $C_2$ are affine constraint conditions, and constraint condition $C_3$ is A linear constraint condition. According to the definition of convex programming, it can be known that the constraint set defined by constraint conditions $C_1$, $C_2$, and $C_3$ is a convex set. Combining the constraint conditions $C_1$, $C_2$, $C_3$, $C_4$, $C_5$, $C_6$, the variables $x_{ij}$, $y_{ij}$, and $z_{ij}$ are restricted within a bounded closed range, it can be known that the constraint set is compact, that is, the objective function is convex.

According to the Weierstrass theorem, if the objective function is continuous and the set of constraints is compact, the function must have a minimum or minimum value on the set of constraints.

Since $x_{ij}$, $y_{ij}$, and $z_{ij}$ are all positive, according to the constraint conditions, the denominator is not zero. Therefore, each term of ${\displaystyle \frac{x_{ij}{y}_{ij}}{z_{ij}}}$ is continuous, and thus the objective function $\min f$ is also continuous. According to the constraints $C_2$, and $C_3$, it can be known that the variable A is all limited within the bounded range, and according to the constraints, it can be known that $x_{ij}$, $y_{ij}$ is a finite positive value. Moreover, the set defined by the constraint conditions is a closed set, that is, a closed set in a finite-dimensional space is defined.

According to the above two conditions, it can be known that, based on Weierstrass 'extremum theorem [24], the objective function has a minimum value on the constraint set.

According to the above proof of the convexity of the objective function, it can be known that since each fraction term $\min f$ of the objective function ${\displaystyle \frac{x_{ij}{y}_{ij}}{z_{ij}}}$ is strictly convex, according to the convex function determination theorem, the objective function is also strictly convex, that is, the objective function satisfies that for any $u\ne v$, there is:

$$f\left(\lambda u+(1-\lambda )\mathrm{v}\right)<\lambda f\left(u\right)+(1-\lambda )f\left(v\right)$$

(A1)

That is, the minimum value is unique.

Completed.

Appendix B.1. Existence of Minimum Optimal Solutions for Constrained Functions

Based on the objective function and constraint conditions, the Lagrange multiplier $\lambda ,\mu ,v,k$ is introduced, and the Lagrange function is defined as:

(B1)

From the above formula, take the partial derivatives of $x_{ij}$, $y_{ij}$, and $z_{ij}$ respectively and set them to 0 to obtain the gradient conditions:

$${\displaystyle \frac{\partial L}{\partial x_{ij}}}={\displaystyle \sum _{i\in C,j\in \Omega +1}\frac{y_{ij}}{z_{ij}}+\lambda {\displaystyle \sum _{i\in C}{y}_{ij}}+u(\Omega +1)+v({\displaystyle \sum _{i\in C}{y}_{ij}(2^{{\log }_2(1+a)}-1))}}=0$$

(B1)

$${\displaystyle \frac{\partial L}{\partial y_{ij}}}={\displaystyle \sum _{i\in C,j\in \Omega +1}\frac{x_{ij}}{z_{ij}}+\lambda {\displaystyle \sum _{i\in C}{x}_{ij}}+v({\displaystyle \sum _{i\in C}{x}_{ij}(2^{{\log }_2(1+a)}-1))}=0}$$

(B2)

$${\displaystyle \frac{\partial L}{\partial z_{ij}}}=-{\displaystyle \sum _{i\in C,j\in \Omega +1}\frac{x_{ij}{y}_{ij}}{{z^2}_{ij}}=0}$$

(B3)

The original feasibility conditions to be verified are:

$$\begin{gathered} 0\le {\displaystyle \sum _{i\in C}[x_{ij}{y}_{ij}(2^{{\log }_2(1+a_1)}-1)\frac{b_5+b_6}{z_{ij}}]}\le \max {\displaystyle \sum _{i\in C}[x_{ij}{y}_{ij}(2^{{\log }_2(1+a_1)}-1)\frac{b_5+b_6}{z_{ij}}]} \\ {\displaystyle \sum _{i\in C}{\mathrm{x}}_{\mathrm{ij}}{\mathrm{y}}_{ij}}=1 \\ {\displaystyle \sum _{j\in \Omega +1}{x}_{ij}}=1 \end{gathered}$$

(B4)

The dual feasibility condition to be verified is to ensure that the Lagrange multiplier is non-negative under the maximum and minimum values:

$$\lambda \ge 0,\mu \ge 0,v\ge 0,k\ge 0$$

(B5)

The complementary relaxation condition to be verified is that it is necessary to ensure that the Lagrange multiplier multiplied by the corresponding constraint function is zero under the maximum and minimum values:

$$\lambda ({\displaystyle \sum _{i\in C}{x}_{ij}{y}_{ij}-1})=0$$

(B6)

$$\mu ({\displaystyle \sum _{j\in \Omega +1}{x}_{ij}-1})=0$$

(B7)

$$v({\displaystyle \sum _{i\in C}[x_{ij}{y}_{ij}(2^{{\log }_2(1+a)}-1)-1]})=0$$

(B8)

$$k(\max {\displaystyle \sum _{i\in C}[x_{ij}{y}_{ij}(2^{{\log }_2(1+a)}-1)-1]})=0$$

(B9)

According to the Slater[25] condition, in convex optimization problems, if there exists a strictly feasible point (i.e., the point where all inequality constraints strictly hold), then the solution under the KKT condition exists.

Suppose there exists point $x_{ij}$, $y_{ij}$, and $z_{ij}$ as a strictly feasible point, which satisfies all the constraints under the KKT condition and the inequality constraints hold strictly. Location: ${x^0}_{ij}={\displaystyle \frac{1}{\left|C\right|(\Omega +1)}}$, ${y^0}_{ij}=\left|C\right|(\Omega +1)$, ${z^0}_{ij}=1$.

Substituting the constraint conditions and verifying the calculation, it can be obtained that:

$${\displaystyle \sum _{i\in C}{x^0}_{ij}{y^0}_{ij}}={\displaystyle \sum _{i\in C}\frac{1}{\left|C\right|(\Omega +1)}}\cdot \left|C\right|(\Omega +1)={\displaystyle \sum _{i\in C}1}=\left|C\right|$$

(B10)

$${\displaystyle \sum _{j\in \Omega +1}{x^0}_{ij}}={\displaystyle \sum _{j\in \Omega +1}\frac{1}{\left|C\right|(\Omega +1)}}=(\Omega +1)\cdot {\displaystyle \frac{1}{\left|C\right|(\Omega +1)}}={\displaystyle \frac{(\Omega +1)}{\left|C\right|(\Omega +1)}}={\displaystyle \frac{1}{\left|C\right|}}$$

(B11)

$$\begin{array}{l}{\displaystyle \sum _{i\in C}[{x^0}_{ij}{y^0}_{ij}}(2^{{\log }_2(1+a)}-1)-1]={\displaystyle \sum _{i\in C}[\frac{1}{\left|C\right|(\Omega +1)}}\cdot \left|C\right|(\Omega +1)(2^{{\log }_2(1+a)}-1)-1]\\ ={\displaystyle \sum _{i\in C}[(2^{{\log }_2(1+a)}-1)-1]}={\displaystyle \sum _{i\in C}[(1+a-1)-1]}={\displaystyle \sum _{i\in C}[a-1]}=\left|C\right|(a-1)\end{array}$$

(B12)

According to $a>0$, it can be known that $a-1<a$. Assigning the value $a$ such that $a$ satisfies $0\le \left|C\right|(a-1)$, that is, $a>1$ (which can be other positive values) or $C\ne 0$ can satisfy the original feasibility condition.

1)For $\lambda ({\displaystyle \sum _{i\in C}{x}_{ij}{y}_{ij}-1})=0$, since ${\displaystyle \sum _{i\in C}{x^0}_{ij}{y^0}_{ij}}=\left|C\right|$, it is obvious that $\lambda =0$ conforms.

2) For $\mu ({\displaystyle \sum _{j\in \Omega +1}{x}_{ij}-1})=0$, since ${\displaystyle \sum _{j\in \Omega +1}{x^0}_{ij}}={\displaystyle \frac{1}{\left|C\right|}}$, it is obvious that $\mu =0$ conforms.

3) For $v({\displaystyle \sum _{i\in C}[x_{ij}{y}_{ij}(2^{{\log }_2(1+a)}-1)-1]})=0$, since ${\displaystyle \sum _{i\in C}[{x^0}_{ij}{y^0}_{ij}}(2^{{\log }_2(1+a)}-1)-1]=\left|C\right|(a-1)$, it is obvious that $v=0$ conforms.

4) For $k(\max {\displaystyle \sum _{i\in C}[x_{ij}{y}_{ij}(2^{{\log }_2(1+a)}-1)-1]})=0$, since ${\displaystyle \sum _{i\in C}[{x^0}_{ij}{y^0}_{ij}}(2^{{\log }_2(1+a)}-1)-1]=\left|C\right|(a-1)$, where $a>1$ (can take other positive values) or $C\ne 0$, it is obvious that $k=0$ satisfies.

From the above derivation, it can be known that based on this objective function and constraint conditions, there exists a minimum value that satisfies the conditions, and this minimum value is the optimal solution.

Completed.