On Bekenstein and Hawking’s “Black Hole Thermodynamics”

1. Is the Area of the Event Horizon the Entropy of a Black Hole?

In 1971, Hawking put forward a theorem that the area of event horizon of a black hole (or the total area of some black holes) never decreases. Bekenstein immediately followed him saying that this non-decrease in the area of event horizon was similar to the non-decrease in entropy of a solitary system in thermodynamics. Based on such a “similarity”, Bekenstein claimed that the area of event horizon of a black hole should be the “black hole’s entropy.” [1,2,3,4].

The authors assert that the “similarity” Bekenstein spoke of is false. There is no any similarity between the non-decrease in the entropy of a solitary thermodynamic system and the non-decrease in the area of the event horizon of a black hole (or holes). And, there is also no any substantial physical connection between the two kinds of the processes of “something never decreases”.

As is well known, the increase in entropy of a solitary system is due to the irreversible processes that happen within the system, and it has nothing to do with the exterior environment.

Contrary, the increase in a black hole’s area is due to the import mass of matter or radiations from the exterior. How much mass enters into the black hole from the exterior, how much the area of the event horizon increases. If there is no mass input, no matter whatever happens in or out the black hole, its area of event horizon is impossible to increase.

Obviously, the physical mechanism and the geometric pattern of the two kinds of the processes of “increase of something” are totally different. Bekenstein blindly spoke of the “similarity” between the two kinds of something monotonically increase processes.

Let’s make some more detailed compare between the physical mechanisms of the two kinds of something increase processes.

The increase in entropy of a solitary system is due to, as mentioned above, some irreversible processes within the system. There are a variety of such irreversible processes, and all of them belong to the category of thermodynamics, showing strong thermodynamic characteristics. For examples: Work converts into heat through friction or collision, heat transmits spontaneously from high temperature to low temperature, non-uniform distribution of pressure (or of density) of gas changes automatically toward uniform（e.g., the air leakage of a car tire）, and so on. All these processes are in the direction from concentration to dispersion of energy and mass, from order to disorder. They are all consumption processes, as so called usually.

Quite differently, the increase in a black hole’s area is only determined by the import amount of the mass of matter or radiations from the exterior. The quantitative relation between the increase of the import mass and the increase of the area of the event horizon can be determined directly and easily by the formula of the area of event horizon. Let us take a Schwarzschild black hole as an example.

The radius of the event horizon of a Schwarzschild black hole is

$$R={\displaystyle \frac{2GM}{c^2}}$$

(1)

The area of the event horizon of the black hole is

$$A=4\pi R^2={\displaystyle \frac{16\pi G^2{M}^2}{c^4}}$$

(2)

And the increase of the area due to the import mass M is

$$\Delta A={\displaystyle \frac{32\pi G^{2}M}{c^4}}\Delta M.$$

(3)

These simple relations belong purely to the fundamental relativistic static mechanics, and absolutely have nothing to do with thermodynamics.

“Non-decrease in the area of a black hole” is actually non-decrease in the radius of the black hole, i.e., “non-decrease in the mass of a black hole”. Only the last description, “non-decrease in mass”, is significant: Black holes can only take in matter or radiations, never release them. Non-decrease in the radius of black hole, non-decrease in the area of event horizon, and so on, are all valid, but none of them has any special physical meaning.

The authors assert, the event horizon of a black hole is actually a “one way membrane” for matter and radiations. Matter and radiations can pass it from the exterior of a black hole into the interior, but they can never pass it from the interior to the exterior. Hence, contrary to the dissipating processes of all thermodynamic events, the increase of the mass of a black hole is a special and typical concentration process of matter and radiations. Black holes are Maxwell’s demons in the Nature.

The increase of the entropy of a solitary system and the increase of the area of black hole (or holes) are different in physical mechanisms, their fundamental tendencies are just opposite each other. Beikenstein alleged that the area of the black hole is just the entropy of the black hole is very superficial. He was seriously wrong.

As is well known, in the fundamental theory of thermodynamics, there are various forms of entropies, and all the entropies in different forms, or of different objects, may quantitatively equivalent to each other. In other words, entropy is an independent equivalent quantity in physics (similarly, energy is another equivalent quantity in physics). The equivalent relations between the entropies of different forms and of different objects are based on the reversible processes that can link up these different entropies: A certain quantity of entropy in one form or of one object can convert through a reversible process into a corresponding quantity of entropy in another form or of another object. Because of the process is reversible, the final entropy, of course, can convert back totally to the initial entropy, leaving no any other effect. The two entropies are thus equal to each other in quantity.

Actually, this criterion may be regarded as a theorem as follows.

The Theorem of Entropy Conservation: Entropy Is Conserved in All Reversible Process

The meaning of “reversible process” here is also well known: it must be a quasi-static process, without any friction or collision, without any heat transmission due to difference in temperature, and without any gas transfer due to difference in pressure (e.g., the leakage of air in a car tire) , and so on. And the final state of the system and the environment can convert back step by step to the initial state. Or, more generally, after the process, the system may convert back by any other longer or more complicated quasi-static process, with both the system and the environment eventually restore to their original states.

Hence, if someone who intends to introduce a new form of entropy into thermodynamics, he or she should find out a reversible process that can link up this new entropy with any of the traditional entropies, for examples, the heat-temperature-quotient entropy, volume expanding entropy, phase-change entropy, chemical entropy, etc., and determine the quantitative equivalent relation between the new entropy and the traditional ones.

Can we find any reversible process that can link up the area of the event horizon of a black hole with some traditional entropy?

The falling process of matter or radiations into a black hole is terribly violent, and we cannot control it in any way. Such a process itself is extremely not quasi-static, extremely irreversible, hence we cannot use it to establish a way of mutual conversion between the “area entropy” and any traditional entropy.

And, due to the peculiar properties of black holes, it seems very apparently that we cannot find any more complicated reversible process that can link up reversibly the area of the event horizon of a black hole with any traditional entropy, to say nothing of determining their quantitative equivalent relation. So, we come to the conclusion that a black hole’s area should not be introduced as a new member into the entropy family.

2. Hawking: The “Radiation”, “Temperature” and “Lifetime” of a BH

Fu & Fu: Hawking’s These Three “New Concepts” Are All Incorrect

According to Hawking and the followers, black holes have thermal radiation, that is due to the positive photon and negative photon produced in the quantum fluctuations of the vacuum at the event horizon of the black holes. Hawking claimed further that the event horizon has a “temperature” T_bh, that is proportional to the gravitational acceleration κ there, differing only a coefficient, $T_{bh}=\kappa /2\pi k$ [5].

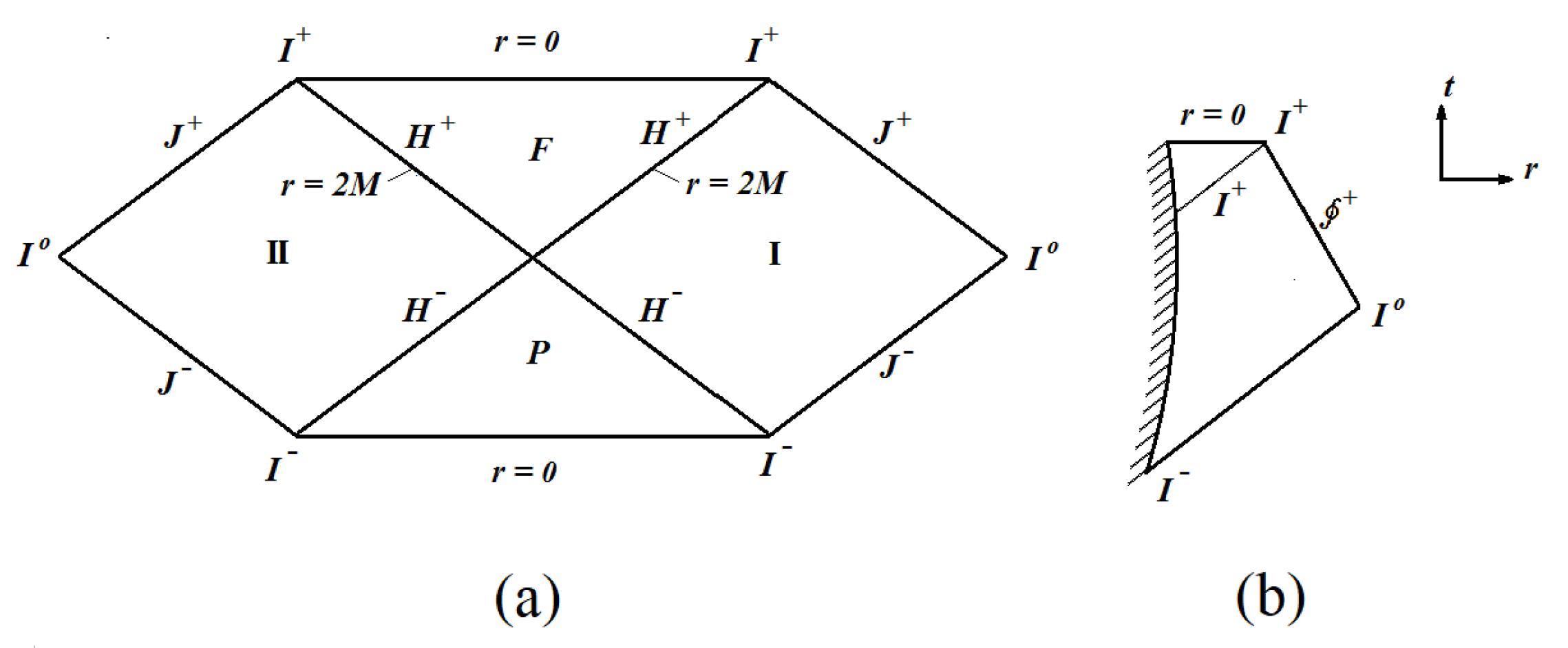
For collapsing black holes and stable black holes, the corresponding derivations of the “thermal radiation” were accomplished by Hawking et al. Hawking started his derivation from the Penrose diagram, as shown in Figure 1(a). The shaded part in Figure 1(b) represents the collapsing black hole.

The vacuum at the event horizon of a black hole fluctuates ceaselessly. Pairs of virtual positive photons and negative photons are frequently produced. Most of them annihilate each other immediately. A few pairs of them survive and become photons and anti-photons in the selection by the powerful gravitational field. They have the traveling wave functions as follows,

Figure 1. Derivation of Hawking’s thermal radiation.

Figure 1. Derivation of Hawking’s thermal radiation.

${\Psi }_{\omega }^{out}~r^{-1}{e}^{-i\omega (t-\Xi r\text{'})}{Y}_{lm}$ outward traveling wave (4)${\Psi }_{\omega }^{in}~r^{-1}{e}^{-i\omega (t+\Xi r\text{'})}{Y}_{lm}$ inward traveling wave (5)

Hawking claimed that expression (4) is the wave function of a positive photon moving outward, and expression (5) is the wave function of a negative photon moving inward. And he claimed that, the positive photon leaves the black hole, travels into the cosmic space (undergoing red shift), forming the so called “Hawking radiation”. The negative photon (having negative mass) enters the event horizon, and approaches to the central part of the black hole to combine with the main mass of the black hole, its negative mass reducing the black hole’s main mass slightly. In a word, the vacuum fluctuation results in a photon radiation to the cosmic space in the cost of a slight reduction of the main mass of the black hole [5].

The above derivation is adequate for both a collapsing black hole and a stable black hole.

Hawking also derived an intensity of the number of outward ejecting photons from the event horizon as a function of the frequency of the photons with an expression as follows,

$$N_{\omega }^2={\displaystyle \frac{1}{e^{\frac{2\pi (\omega -{\omega }_0)}{\kappa }}-1}}$$

(6)

Hawking claimed that equation (6) is the expression of “the spectrum of the black hole radiation” and it is consistent with the spectrum of the thermal radiation of a black body at a temperature T, as expressed by Planck’s formula, differing only in the exponent part in the denominator: The temperature T in Planck’s formula is replaced by the gravitational acceleration at the event horizon, $\kappa$.The two “temperature” differ only a constant coefficient

$$T_{bh}={\displaystyle \frac{\kappa }{2\pi k}}.$$

(7)

Hence, Hawking concluded that Hawking radiation is “thermal radiation”, i.e., the black body radiation; and the gravitational acceleration at the event horizon, $\kappa$, represents the temperature of the black hole.

The authors assert that, Hawking’s these derivations and astonishing conclusions are both incorrect. The reasons are as follows.

(A) Hawking’s“black hole radiation”, as described by his expressions (4) and (5), is a unidirectional radiation, along the direction of the radius of the black hole, perpendicular to the corresponding area element of the event horizon dA, where the quantum fluctuation happens.

However, the authors argue, black body radiation from any element area dA of a black body surface at a certain temperature T must be isotropic. That is different from Hawking’s unidirectional radiation from the area element dA of the event horizon of a black hole.

The equilibrium thermal radiation in a cavity at certain temperature T is a typical black body radiation, sometimes people call it equilibrium radiation. It is random and isotropic. At any point within the cavity, for any direction within the 4 solid angle, the radiation is identical in intensity as well as in spectrum. If the cavity has a small hole on its wall, the radiation that ejected out from the hole is a typical black body radiation, that is isotropic, not unidirectional.

The equilibrium thermal radiation in a cavity may be dealt with as a photon gas. The phase space of the photon gas is of 6 dimensions: x, y, z, p_x, p_y, p_z. According to Bose-Einstein statistics, in a cavity of volume V and at temperature T, for the frequency interval from $\omega$ to $\omega +d\omega$ (i.e., for the momentum interval from $p$ to $p+dp$, as $p={\displaystyle \frac{\epsilon }{c}}={\displaystyle \frac{\hslash \omega }{c}}$), the energy of the general single color thermal radiation is

$$U(\omega ,T)d\omega =Vu(\omega ,T)d\omega =V\times {\displaystyle \frac{2\times 4\pi P^{2}dP}{h^3}}{\displaystyle \frac{1}{e^{{}_{\frac{\hslash \omega }{kT}}}-1}}\hslash \omega d\omega ={\displaystyle \frac{V}{{\pi }^2{c}^3}}{\displaystyle \frac{\hslash {\omega }^3}{e^{\frac{\hslash \omega }{kT}}-1}}d\omega .$$

(8)

Where $V\times 2\times 4\pi p^{2}dp$ is the volume in the phase space of the photon gas in the cavity from frequency $\omega$ to $\omega +d\omega$. According to Heisenberg’s uncertainty principle, for the photon gas, the volume in the phase space of each quantum state is $h^3$. Hence, the number of quantum states of the photons in the cavity for the frequency interval from $\omega$ to $\omega +d\omega$ is ${\displaystyle \frac{V\times 2\times 4\pi p^{2}dp}{h^3}}={\displaystyle \frac{V}{{\pi }^2{c}^3}}{\omega }^{2}d\omega$. Factor 2 is due to the spin of the photons, which may be positive or negative in the direction of the momentum. Expression ${\displaystyle \frac{1}{(e^{\frac{\hslash \omega }{kT}}-1)}}$ is the Bose distribution factor, i.e., the average number of photons in each quantum state of energy level $\epsilon$. Take the product of the number of quantum states from $\omega$ to $\omega +d\omega$, the Bose distribution factor, and the energy of each photon $\hslash \omega$, one derived equation (8).

In (8), $u(\omega ,T)d\omega$ is the single color energy density, i.e., the energy of the thermal radiation per unit volume in the cavity and in the frequence interval from ω to ω+dω.

$$u(\omega ,T)d\omega ={\displaystyle \frac{2\times 4\pi p^{2}dp}{h^3}}={\displaystyle \frac{1}{(e{}_{\frac{\hslash \omega }{kT}}-1)}}\hslash \omega d\omega ={\displaystyle \frac{1}{{\pi }^2{c}^3}}{\displaystyle \frac{\hslash {\omega }^3}{(e^{\frac{\hslash \omega }{kT}}-1)}}d\omega$$

(9)

Thus, the corresponding single color emissivity of the surface of a black body at temperature T, i.e., the energy in the frequency interval from ω to ω+dω emitted per unit time from per unit area of the surface of a black body at temperature T, is

$$J(\omega ,T)d\omega ={\displaystyle \frac{1}{4}}cu(\omega ,T)d\omega ={\displaystyle \frac{1}{4{\pi }^2{c}^2}}{\displaystyle \frac{\hslash {\omega }^3}{(e^{\frac{\hslash \omega }{kT}}-1)}}d\omega 。$$

(10)

Equation (7) is the famous Planck’s formula for black body radiation

Integral (7) for all the we may derive

$$J={\displaystyle \frac{1}{4}}cu,$$

(11)

where J is the full color emissivity of the surface of a black body at temperature T, i.e., the energy emitted per unit time from per unit area of the surface of a black body at a temperature T, and u is the energy density of the equilibrium thermal radiation in the cavity. Relation (11) is also well known by most people.

In equation (8), expression $4\pi p^{2}dp$ represents a spherical layer in the photon gas momentum space, which demonstrates that the black body radiation is isotropic.

“Hawking radiation” is produced in vacuum fluctuation. It ejects from the area element dA on the event horizon, in the direction along the radius of the black hole. Equations (4) and (5) are both expressions of travelling waves along the radius of the black hole. So, Hawking radiation is obviously unidirectional, not an isotropic radiation. How can we regard it as a thermal radiation?

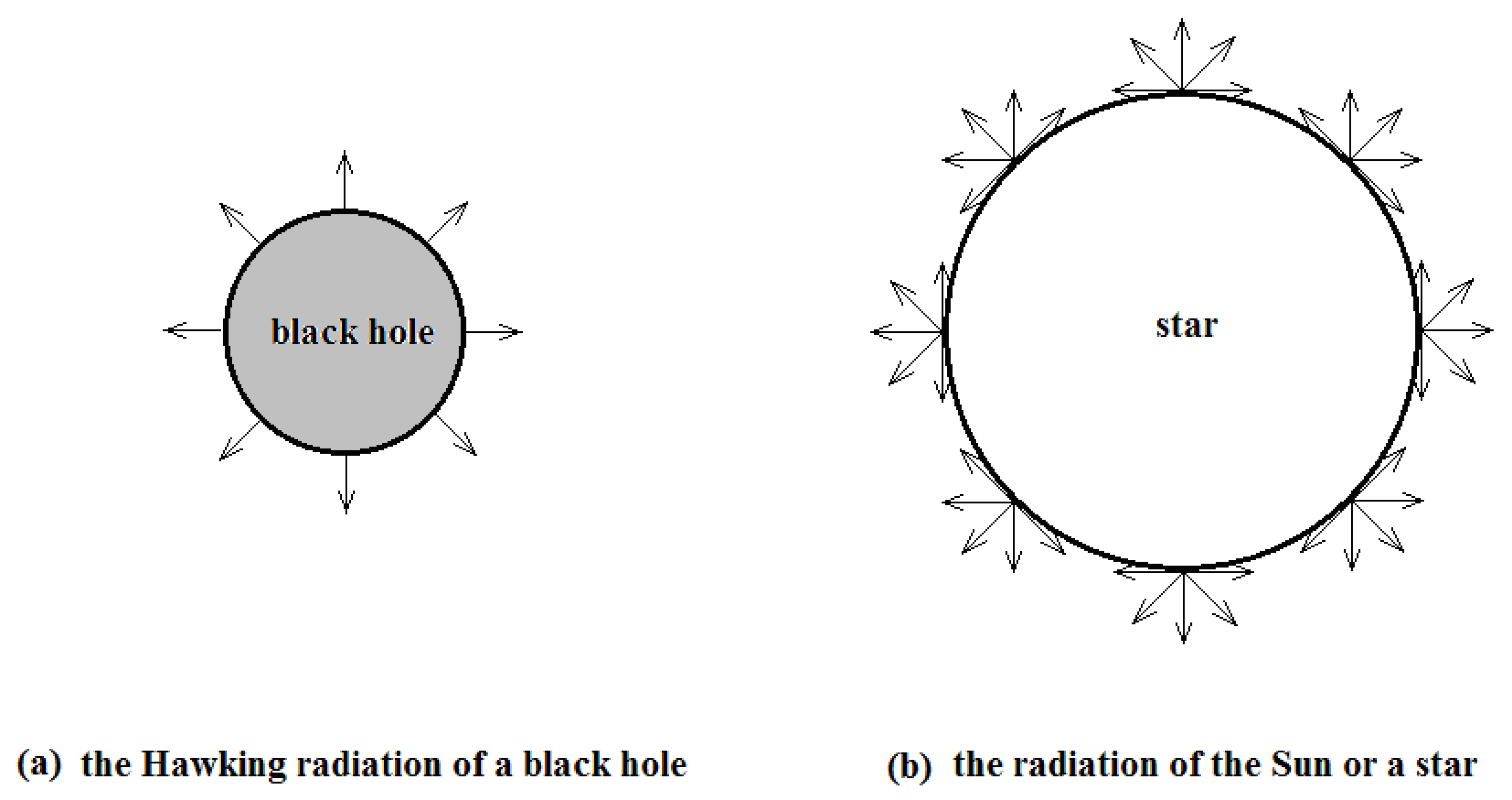
The surface of the sun or any other star is super incandescent, at very high temperatures. They are black bodies, as they take in any radiation falling on them. Their radiations are typical black body’s radiations. Of course, they are isotropic, with a spectrum of Equation (10).

The Hawking radiation emitted from the exterior of an area element dA of the event horizon is perpendicular to the area element and in the direction of the radius of the black hole. All the radiations from one area element dA are parallel each other. So, we say, Hawking radiation is unidirectional, not isotropic, as shown in Figure 1 (a).

The radiation emitted from the sun or any star is black body radiation.

Figure 1. The two kinds of radiations of a black hole and of a star are completely different. (a) The radiation emitted by any point at the exterior of the event horizon of a black hole is just along the radius of the black hole. It is unidirectional, not isotropic. (b) The radiation ejected by any point on the surface of the sun or a star is isotropic.

Figure 1. The two kinds of radiations of a black hole and of a star are completely different. (a) The radiation emitted by any point at the exterior of the event horizon of a black hole is just along the radius of the black hole. It is unidirectional, not isotropic. (b) The radiation ejected by any point on the surface of the sun or a star is isotropic.

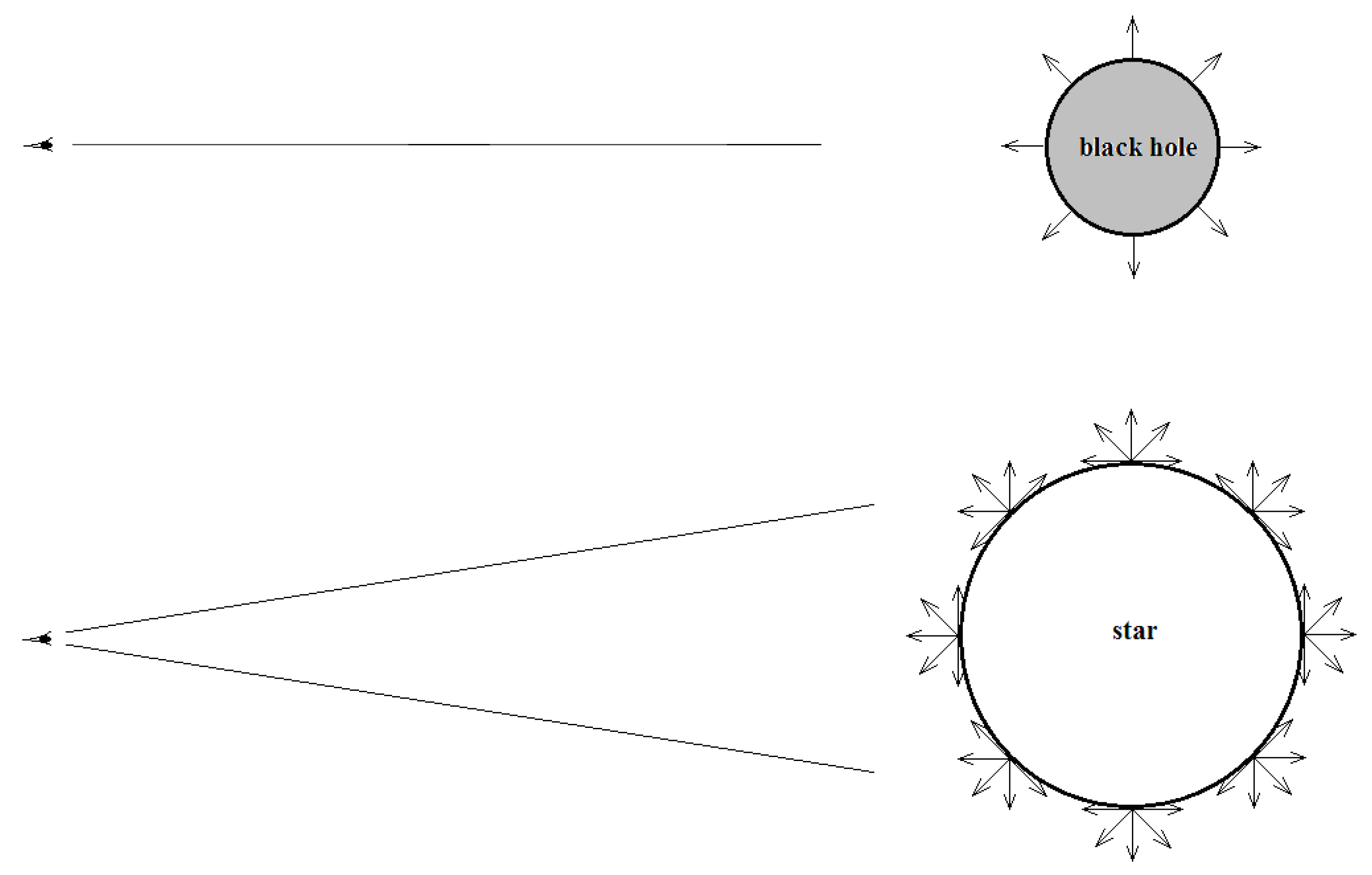
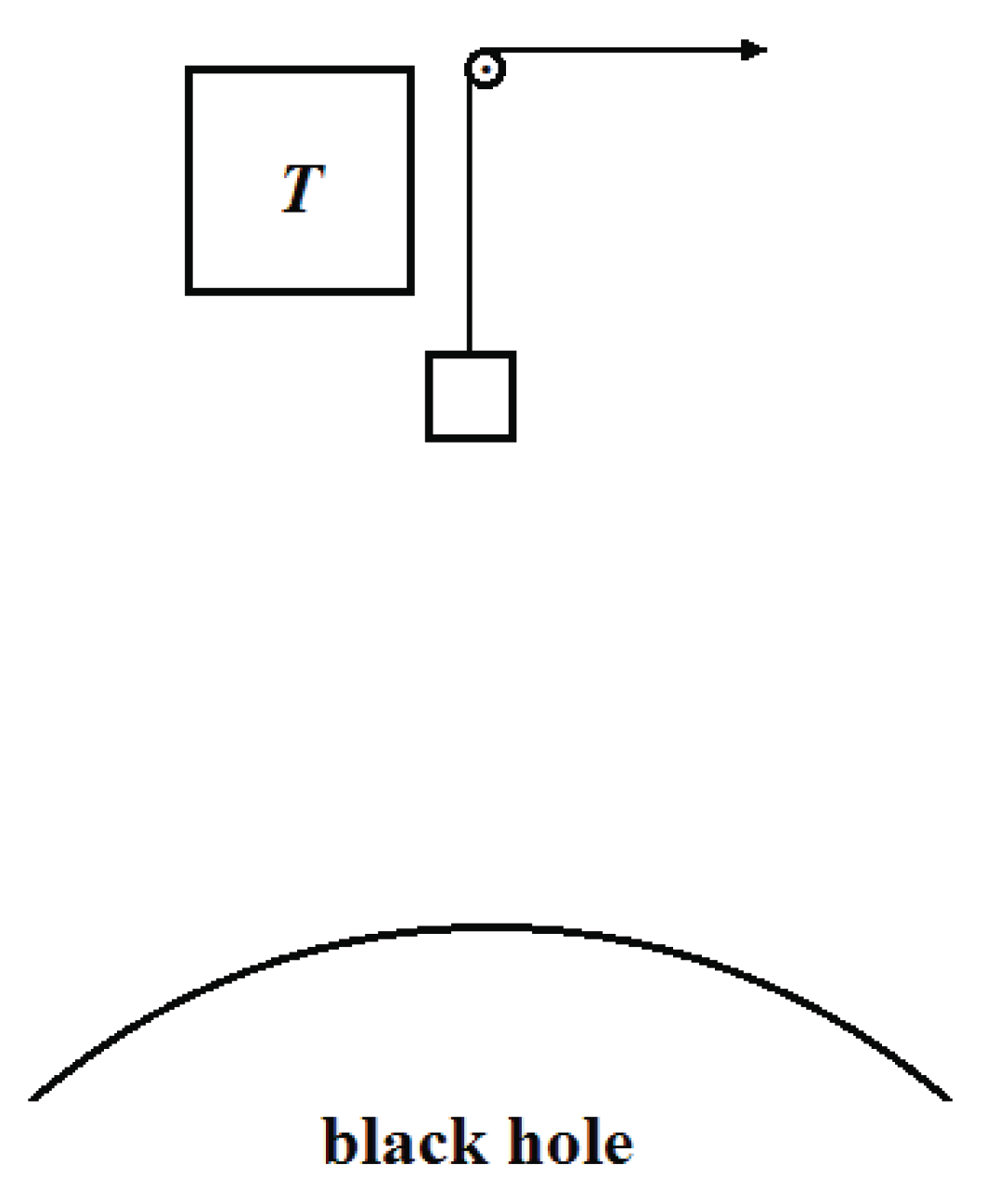
Figure 2. Two far-left observers.

Figure 2. Two far-left observers.

Above: The radiation ejected by a black hole is unidirectional, just along the radii of the black hole. The far-left observer can see only a point (or an extremely small spot) of the black hole.

Below: The radiation ejected by a star is isotropic. The far-left observer can see the whole left semi-sphere of the star.

It is isotropic, as shown in Figure 1 (b).

In (8), the expression $4\pi p^{2}dp$ represents a spherical layer in the momentum space. Hence, the black body radiation is certainly isotropic, as shown in Figure 1.

Black body radiation and black hole radiation are totally different from each other.

Hawking radiation is not a thermal radiation. Thus, the gravitational acceleration near the event horizon is certainly not the temperature of the black hole.

However, as Hawking was so confident that the “temperature” of a black hole is $T_{bh}={\displaystyle \frac{\kappa }{2\pi k}}$, he used it （he is too brave） to derive the Stefan-Boltzmann’s law for the event horizon of a black hole.

Stefan-Boltzmann law: The emissivity, i.e., the full-color emission of thermal radiation per unit time and from per unit area of the surface of a black body at a certain temperature T is directly proportional to the fourth power of the temperature,

$$J=J(T)={\displaystyle \frac{d^{2}E}{dAdt}}=\sigma T^4$$

(12)

This law can be derived from experiments directly, for example, the experiments with a current-carrying filament in a glass bulb. Experiments show that σ is a physical constant.

This law may also be derived by theory, with an integration of Planck’s formula (10) over all the $\omega$, from 0 to ∞. The result is

$$J={\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{1}{4{\pi }^2{c}^2}\frac{\hslash {\omega }^3}{e^{\frac{\hslash \omega }{kT}-1}}d\omega =\frac{{\pi }^2{k}^4}{60c^2{\hslash }^3}}{T}^4=\sigma T^4.$$

(13)

The theoretical value of σ is consistent excellently with the value derived from all the experiments and observations.

Equations (8) ~ (13) are all closely related to the isotropic property of the thermal radiation of a black body.

“Hawking radiation” of a black hole, as described by himself, is unidirectional, not isotropic. Hence，all of Hawking’s discussion about Stefan-Boltzmann law of the event horizon of a black hole is nonsense.

However, after his derivation from black hole’s temperature to black hole’s Stefan Boltzmann law, Hawking took another new brave step. He calculated the “life times” of the different black holes due to their “mass evaporation”. He found that, the less the mass of a black hole is, the stronger the gravitational acceleration at its event horizon is, and the higher the “temperature” there is, and according to Stefan-Boltzmann’s law, the faster the mass of the black hole should evaporate. Hawking calculated the “life time” of various black holes, and came to the conclusion that, for the black holes of the magnitude order of various stars, or of the magnitude order of various galaxy cores, their lifetimes are all extremely long, longer than the life time of the Universe. So, it is impossible for us to have the chance to observe their final disappear due to the evaporation by astronomic observation. Hawking then imagined a special kind of very small “primitive black holes”, which was probably formed in some initial stage of the big bang, relating to some unknown but extremely violent rush or squeezing processes of mass. These “primitive black holes” are very small, hence the gravitational accelerations and the “temperatures” near their event horizon are extremely high, and their mass evaporations are very fast. At last, the evaporation becomes faster and faster, and, every such small black hole will disappear extremely quickly like an explosion. Hawking predicted that, probably, today, we may still have the chance to see such explosions of some primitive small black holes by astronomic observations [6].

These ideas and discussions of Hawking are all rooted in peculiar imaginations, far away from common sense.

(B) Actually, the vacuum fluctuations at the event horizon of a black hole cannot produce any “Hawking radiation”

According to Hawking et al., the powerful gravitational field has a sifting effect on the virtual positive and negative photons produced in the vacuum fluctuation near the event horizon, resulting in the main mass of the black hole reduces by receiving negative photons ceaselessly, as shown by (5), and emits positive photons to the outer space, as shown by (4). This is the mechanism of the so called “Hawking radiation”.

Hawking’s above idea is wrong.

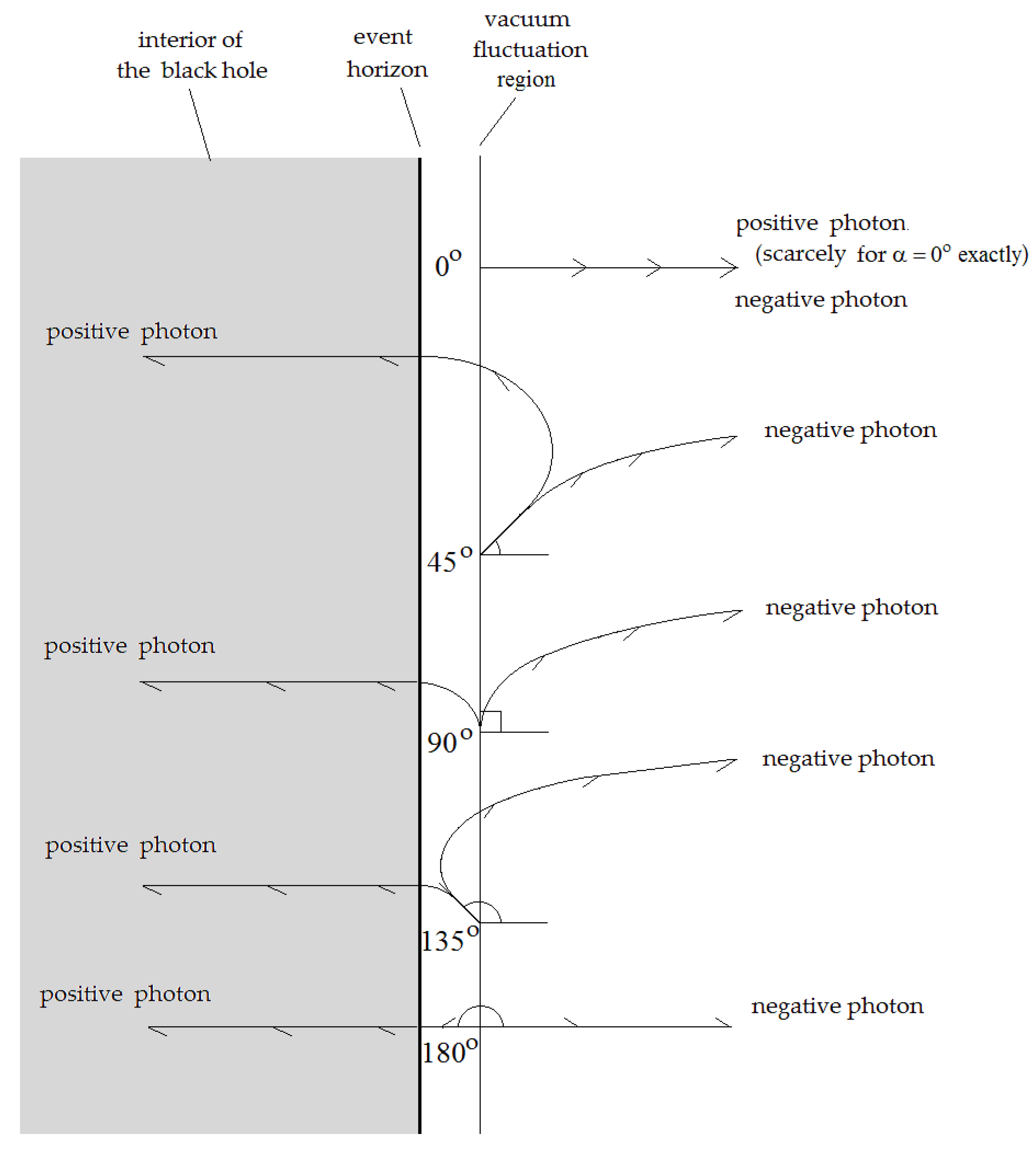
Let us begin with the vacuum fluctuation. It produces a virtual pair of positive and negative photons. They are actually matter and anti matter. According to the Principle of Energy Conservation, their energies, one is positive, and the other is negative, and equal in magnitude. According to the Principle of Momentum Conservation, their momenta, the one of the positive photon is in any direction in the 4 solid angle, and the other of the negative photon is equal in magnitude, but opposite in direction with the first one. However, as the mass of a negative photon is negative, its speed should be identical in direction with the speed of the positive photon. The initial positive momentum and the two velocities of the photon pair are all in the same direction, which is possible in any direction in the 4 solid angle due to the fluctuation. Only the momentum of the negative photon is in the opposite direction, as shown in Figure 4. Due to the extremely powerful gravitational field, their trajectories and final destination are different.

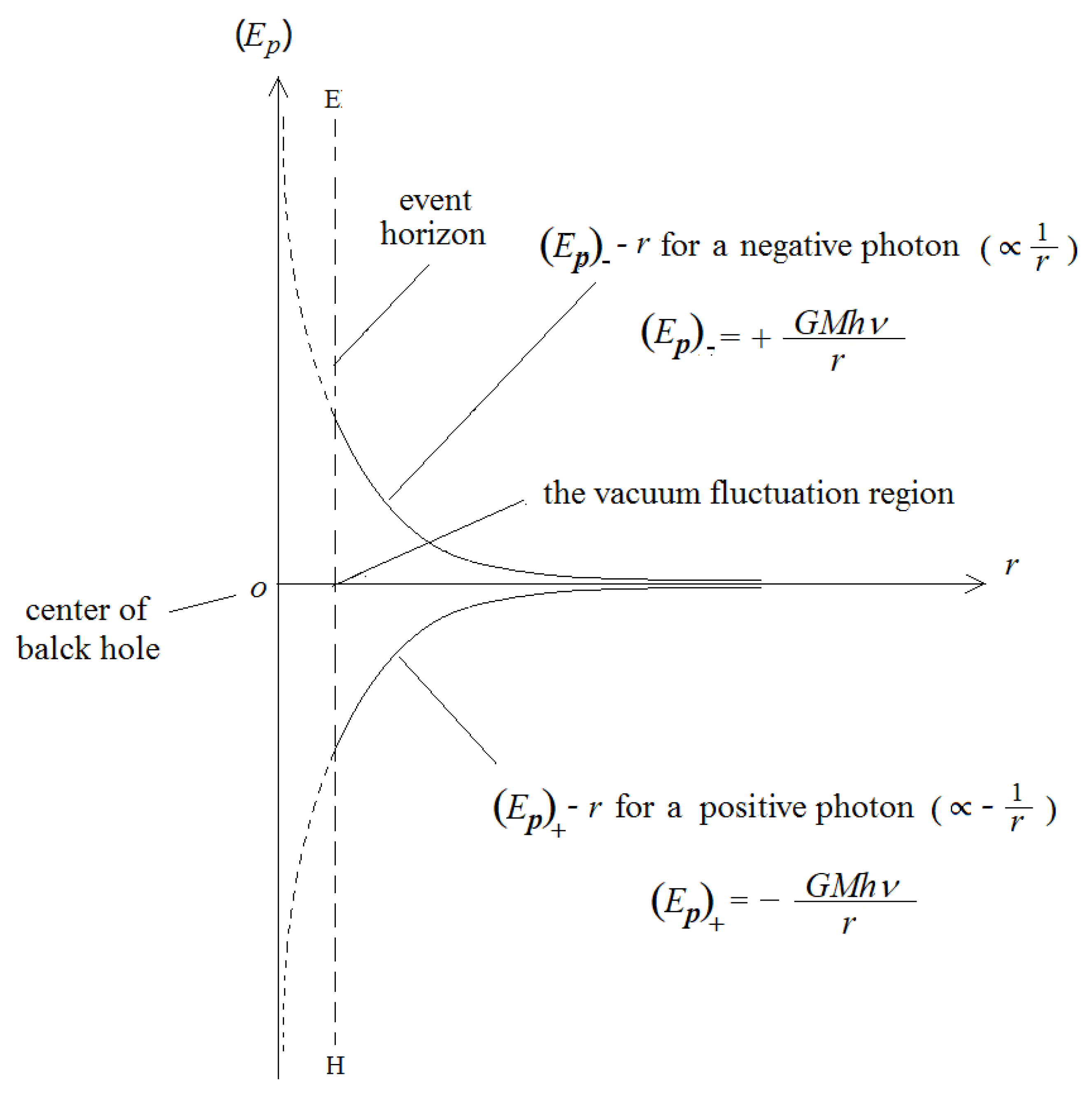
Figure 5 is the E_p – r curves for the photon and negative-photon, that is, the relations of the potential energies of the positive and negative photons with respect to the distance from the center of the black hole, respectively.

It is easy to find that almost all the positive photons will finally fall into the black hole and combine with the main mass of the black hole. And all the negative photons, due to their negative mass, will be ejected by the main mass of the black hole, finally fly off the black hole into the vast exterior space, and annihilate with the matched photons they encountered in their ways. Let us see some examples as shown in Figure 4.

Figure 5. The relations of the gravitational energy E_p of the positive or negative photon to the distance r from the photon to the center of the black hole.

Figure 5. The relations of the gravitational energy E_p of the positive or negative photon to the distance r from the photon to the center of the black hole.

Figure 6. The extremely powerful gravitational field near the event horizon promotes the virtual pairs of positive and negative particles to separate, going forward along different ways. All the positive photons enter the black hole and combine with the main mass of the black hole. All the negative photons are repelled to the cosmic space, annihilate with the matched photons they encountered in their ways.

Figure 6. The extremely powerful gravitational field near the event horizon promotes the virtual pairs of positive and negative particles to separate, going forward along different ways. All the positive photons enter the black hole and combine with the main mass of the black hole. All the negative photons are repelled to the cosmic space, annihilate with the matched photons they encountered in their ways.

The paths for α = - 45^o, - 90 ^o, -135^o, etc., are symmetric, omitted in the figure.

The first case, α = 0^o, the direction of the initial velocity of the pair of photons is outward. The two photons both fly outwards. The positive one undergoes red shift, and it can fly off the black hole far away. The negative photon undergoes blue shift slowly, it flies outward until it meets some matched positive photon in the space, and annihilates with it. Thus, the space has derived an outward flying positive photon, and lost a positive photon of itself by the annihilation with the outward flying negative photon. The derivation and lost cancel each other.

In the cases of α = 45^o，90^o，135^o, etc., as shown in the figure, all the positive photons are doomed to fall finally into the black hole, increasing the main mass of the black hole slightly. And all the negative photons are doomed to finally fly off the black hole to the vast cosmic space, and annihilate soon with the matched positive photons they meet. Thus, when the black hole receives a positive photon, increasing slightly the main mass of the black hole, the space receives a negative photon and then, due to an annihilation, loses a free positive photon. The process of the two parts corresponding to a single process of a positive photon comes from the far space and falls into the black hole.

Now let us see the case of α = 180^o, as shown in the lowest part of Figure 6. First, the pair of the positive and negative photons both fly into the event horizon. The positive photon flies straight forward to the center of the black hole and combines with the main mass of the black hole, increasing the main mass of the black hole slightly. The negative photon first flies inward, undergoes red shift seriously until all its kinetic energy is exhausted (changes to its potential energy), and return back to fly outward to the vast cosmic space, undergoing blue shift. When it meets a matched positive photon in its way in the space, they annihilate together. Thus, the space loses a free positive photon, and the black hole obtains a positive photon.

In a word, what Hawking said of “black hole radiation”, or “black hole evaporation”, is impossible to happen.

The black holes accept matter particles and radiations, never emit them. This is absolutely true. Otherwise, why we call them Black Holes?

A black hole takes in matter and radiation from the surrounding space ceaselessly. At least, it takes in the thermal radiation of the 3K microwave background radiation ceaselessly. The quantum fluctuation of vacuum is extremely weak, and its influence is extremely weak and negligible. It is not worth to consider it too much.

Hawking once had a well-known saying: From the big bang to black holes.

According to his words, it seems as if the matter and energy absorbed by the black holes would be buried in the black holes forever. Never will they be liberated again.

We may follow Hawking’s words and say: From the black holes to a new big bang. The rebirth of these buried matter and energy waits a new big bang to come. About this, we have another monograph to discuss [7,8,9].