The Hidden Mathematics to Promote Next- Generation Creative Writing Pedagogy for Professionals: The Algorithmic Muse

1. Introduction

Deconstructing the Art/Science Dichotomy

The romantic idea that a creative writer is little more than a channel for some sudden, unearthly inspiration has been entrenched into the Western literary tradition for several centuries (Wimsatt and Brooks, 2022). This view considers creativity as something spontaneous, mystical almost, and therefore diametrically opposed to the logical, rule-bound world of mathematics. Writing workshops under modern creative writing pedagogy generally prioritise subjective responses to voice, tone, and emotional effect over technical structure instruction (McGurl, 2011). This paper contends that this perceived chasm between art and logic is a false one. Structure is not the cage of creativity but its skeleton. From the rigid metrical constraints of a Shakespearean sonnet to the archetypal plot points of the hero’s journey, literature is replete with underlying patterns, symmetries, and algorithms (Stiemsma, 2024). The Russian Formalists were among the first to systematically analyze these mechanics, treating literature as a system of devices and structures rather than purely a medium for personal expression (de Vos, 2024). More recently, the rise of digital humanities and computational creativity has provided new language and tools to explore this intersection (Di Rosario, 2021; O’Sullivan et al., 2025).

The central theme of this paper is that by making these “hidden mathematics” visible and teachable, we can revolutionize creative writing pedagogy. This approach does not seek to reduce literature to a mere equation but rather to empower writers with a new set of analytical and generative tools. It aims to foster a “next-generation thinking” where writers are not just storytellers but also story architects, capable of manipulating complex systems of plot, character, and theme with intention and precision. This paper will explore the frameworks for this pedagogy, confront its inherent challenges, and map its prospects in an increasingly computational world.

2. Mathematical Frameworks for Literary Creation

Some main mathematical ideas are chosen and matched with the elements of literary creation to forge linkage between mathematical concepts and creative writing. This provides a new vocabulary that serves in the deconstruction of a text and the scaffolding for producing new ones.

2.1. Narrative as Algorithm

The cornerstone of a plot is, for instance, an algorithm: a finite sequence of instructions precisely laid down, which can be programmed onto a computer, if it so be. Perhaps the most famous literary algorithm is Campbell’s (2008), or the “Hero’s Journey,” which is a pattern comprising seventeen stages that lie at the core of innumerable myths and screenplays. More modern writing manuals such as Blake Snyder’s Save the Cat! (2005) took this even further, providing an almost frame-by-frame blueprint, setting out precise moments for inciting incidents to occur, the midpoint, and the final act. Often, critics frown upon such systems for encouraging unoriginal writing-with this very challenge taken up later-thereby these structures serve as an educational aid, not as rigid rules, but as proven algorithms for plotting tension and emotional catharsis (Jackson, 2022).

Tutoring students that the plot is an algorithm demystifies the process. They learn to flow chart their stories by identifying in “$if-then$” agency decision points for their characters and tracking their logical cause-and-effect progression. This computational way of looking at matters allows them to notice, with analytical clarity, that their plot has a sagging second act or an unearned climax (Batty and Taylor, 2021).The work of Propp (1968), who identified 31 sequential “functions” common to Russian folktales, provides a foundational academic model for this algorithmic view of narrative.

2.2. Poetics, Patterns, and Symmetries

Poetry is perhaps the most overtly mathematical literary form. Prosody has to do with patterns of stress and unstressed syllables, metrical feet, and rhyme schemes (Haskell, 2021). A sonnet is a very precise 14-line structure that is defined by its rhyme scheme (for instance, ABAB CDCD EFEF GG) and meter (usually iambic pentameter).A villanelle is a recursive algorithm, with its first and third lines repeating in a specific sequence throughout the poem (Lane, 2019).

Using these forms mathematically, students begin to appreciate their intricacies and the creative tension that emerges while imposing emotional content into a confining container (Pinsky, 1998). Symmetry and asymmetry hold great meaning for the narrative structure as well. A classic tragic arc is a symmetrical inversion of a heroic one (rise then fall, vs. fall then rise). Character foils are created through asymmetry, highlighting a protagonist’s qualities by contrasting them with another character’s opposite traits (Destrée et al., 2020). By teaching students to recognize and deploy these patterns, educators give them control over the aesthetic and emotional rhythm of their work (Tipper and Gilman, 2024).

2.3. Combinatorics and Generative Brainstorming

Combinatorics, the branch of mathematics dealing with combinations and permutations, is a powerful engine for creativity. Renowned for its inventive use of combinatorial constraints to produce fresh literary works, the French movement Oulipo (short for Ouvroir de littérature potentielle) uses ten sonnets with changeable lines to create an amazing ${10}^{14}$possible poems (Hutchison, 2020). Combinatorial thought is a great approach in the classroom to help one to get beyond writer’s block.

Teachers can give lists of character types, locations, genres, and main conflicts to inspire kids to come up with fresh narrative ideas. For instance: “A hard-boiled detective” + “in a zero-gravity space station” + “must solve a murder where the only witness is an AI” should be used. According to computational creativity experts, this strategy encourages authors to stray from their typical cognitive processes and explore fascinating new narrative possibilities (Sawyer and Henriksen, 2024; Cropley et al., 2023). By methodically examining the “space of the possible,” it uncovers linkages that might be overlooked by intuition alone (Montfort, 2021).

2.4. Fractals, Self-Similarity, and Thematic Cohesion

How would you describe a “fractal” in simple terms? The component’s smaller parts are roughly akin to the larger one on comparatively small scale (Mageed and Bhat, 2022; Mageed, 2023; Mageed, 2024 a-m, Mageed and Li, 2025; Mageed, 2025 a-c), and it is shaped like spheres with self-similarity.

This theory is a brilliant example of how themes and forms may interact in a long-form story. Consider this: the battle of one chapter, scene, or perhaps even the structure of a sentence can mirror the main conflict of a book—the big picture.

As in Jennifer Egan’s A Visit from the Goon Squad, a non-linear, fragmented plot structure may reflect a story that penetrates social fracture. This fractal pattern recurs in dialogue where people are continuously interrupting one another and in circumstances that seem abrupt (Eggers, 2023). Students who are taught to think fractally are more likely to create profoundly meaningful stories in which form, and content are inseparable (Bandia et al.,2024).

It moves beyond asking “What is your theme?” to “How is your theme mathematically represented at every level of the story’s structure?” (Mohseni et al., 2020; Mageed and Nazir, 2024).

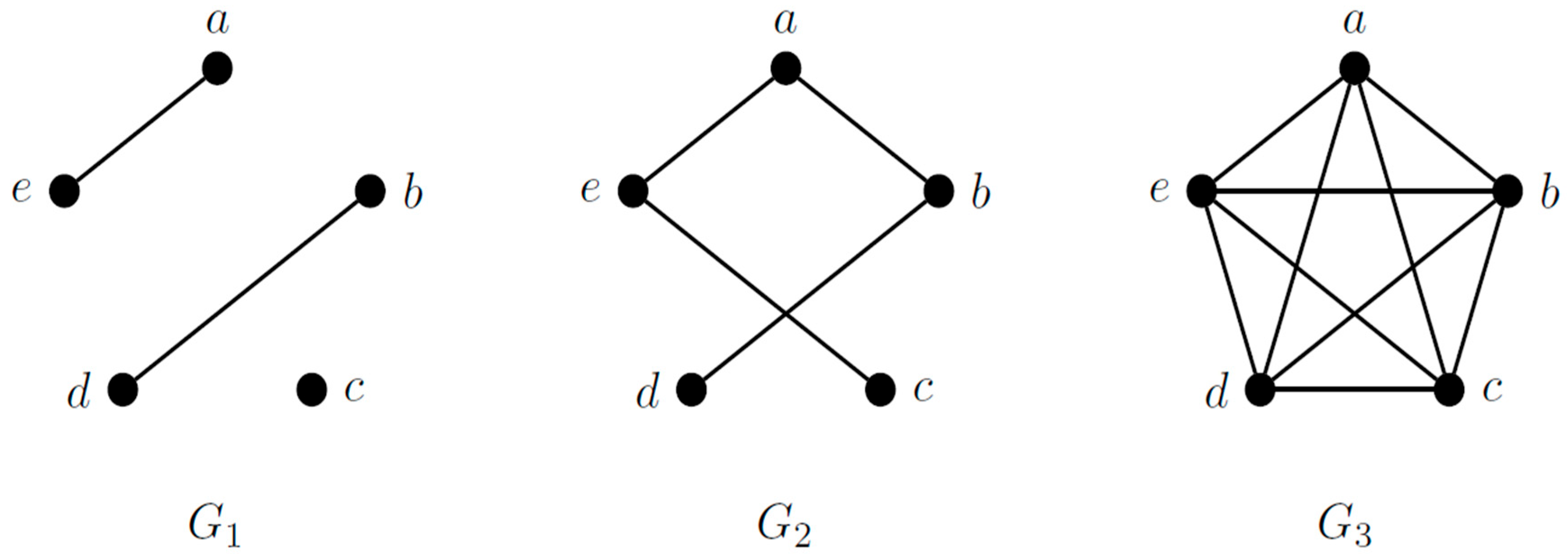
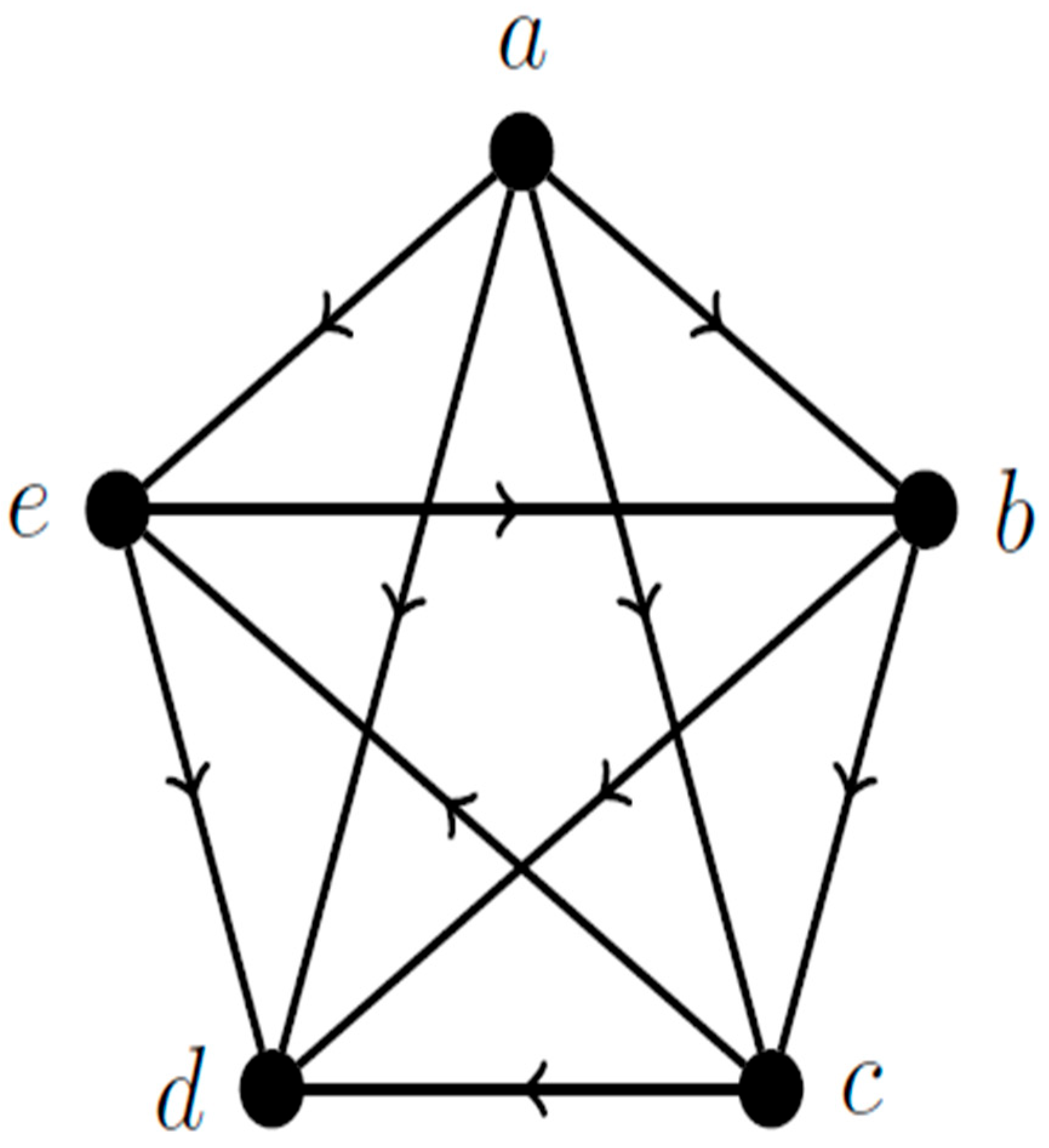
2.5. Graph Theory and Narrative Networks

Complex narratives can be thought of as intricate networks. In this structure, characters act as nodes, while their different relationships—be they familial, romantic, or antagonistic—serve as the edges linking them. Plot points also operate as nodes, linked together by lines of causality. Graph theory offers a unique visual and analytical tool to map out these systems (Saoub, 2021). Students can even design their stories as graphs, which helps them manage big groups of people, keep track of convoluted story lines, and maintain consistency in world-building (King, 2022). For a more descriptive of what graph theory can be linked to complex narratives.

Let’s think on the next things. Every one of the five teams in the Roanoke Soccer League’s end-of-season competition plays every other team once with no ties—a round-robin format. Graphs help us to study and see the structure of the competition; each team is shown as a vertex (a dot), and an edge (a line) connects two vertices if those teams have played against one another. Particularly as the competition advances, graphs G₁ and G₂ show how the games are scheduled and played among the teams; this graphical representation aids in better grasp of the connections and results of the tournaments as illustrated in Figure 1 (Saoub, 2021). Every vertex in these graphs stands for a team, and the edges denote the games that have taken place between them. Graph G₃ shows the complete tournament, in which every team has faced every other, hence offering a thorough overview of the results of the event.

The text explains how graph models can help a tournament director determine the number of games needed and the outcomes of those games. By counting the edges in graph G₃, we find that 10 games are required. To represent the results of the games, we can add arrows to the edges, creating a directed graph (digraph) that shows which teams won against others, as in Figure 2 (Saoub, 2021), such as the Aardvarks winning all their matches, while other teams have varying records.

This technique operates particularly well for genres like science fiction and fantasy, where extensive systems of magic or technology, family trees, and complicated political alignments are frequently included (Paulding, 2022). Authors can identify characters that may be feeling a little alone and require more integration into the story by imagining the story as a network. They can also see how a single incident affects the entire novel (Pósfai and Barabási, 2016). The author is transformed from a storyteller to a world architect by this “systems thinking” (Schmidt, 2021).

3. Open Challenges and Pedagogical Considerations

Integrating mathematics into the creative writing classroom holds great promise, but it also comes with its fair share of challenges that need to be tackled for it to truly thrive.

3.1. The Risk of Formulaic Writing

The most significant and valid criticism is that this approach will produce derivative, “paint-by-numbers” stories that slavishly follow a formula (Lee, 2023). If every student is taught the same algorithm (e.g., Save the Cat!), will all their stories become homogenous? This is a genuine risk if the frameworks are taught as prescriptive rules rather than descriptive tools. The pedagogical emphasis must be on understanding the algorithm to innovate upon it. The goal is to teach students the principles of narrative tension so they can invent their own structures, not just copy existing ones (Macdonald, 2023). The key is to present these mathematical structures as a classical education—one must first learn the rules before one can artfully break them (Uchkunovich, 2025).

3.2. Pedagogical and Ideological Resistance

Many creative writing instructors and students are drawn to the field precisely because it feels like a refuge from the quantitative, systematized thinking that dominates other disciplines (Barton and Leonard, 2021). Introducing mathematical language can feel like a colonization of a sacred humanistic space (Fish, 2021).

Overcoming this resistance requires a careful and empathetic pedagogical approach. Instructors must frame these tools as supplementary, not supplanting, and demonstrate their value through an analysis of beloved literary works, showing how authors like Shakespeare or Austen were masterful (if perhaps intuitive) mathematical architects (Underwood, 2019).

3.3. Assessment and Evaluation

In this new paradigm, how is a story graded? Conventional rubrics emphasise emotional resonance, literary style, and character depth (Smith, 2020). Criteria like structural integrity, thematic self-similarity, or creative application of a combinatorial constraint would need to be added by a mathematically-informed pedagogy.

This requires developing new, hybrid rubrics that can value both the architectural ingenuity and the ineffable “soul” of a piece (Culham, 2023). Balancing these quantitative and qualitative assessments without privileging one over the other will be a significant challenge for educators (Bazerman and Russell, 2020).

3.4. The Role of Digital Tools and the Digital Divide

With the advent of AI writing aids like GPT-4 and Sudowrite, this change in teaching approaches is truly taking off. Just like powerful creative engines, these devices can quickly generate new story concepts, evaluate data for pace, or suggest complex themes. This creates unique chances but also creates some problems, especially in access, digital literacy, and upholding academic integrity. Rather than letting these technologies replace the own critical thinking of the students, teachers have to assist them in using them as creative and analytic instruments. The key is to guarantee that these technologies are accessible to everyone on an equal basis.

4. Prospects for Next-Generation Thinking

Navigating these challenges successfully opens exciting prospects for the future of creative writing and its pedagogy

4.1. Fostering Computational and Systems Literacy

Writers develop a type of computational literacy that goes well beyond the written word when they begin to see stories as systems (Wing, 2006). They start to comprehend feedback loops, complex, dynamic interactions, and the appearance of novel features. Applying this systems-thinking approach to storytelling enables them to address the intricate, interrelated narratives that we encounter in the twenty-first century, whether in science, literature, or politics (Payne, 2022).

4.2. Empowering Neurodiverse Learners

For neurodiverse learners, particularly those on the autism spectrum who often thrive in logic, patterns and organized systems, a method of teaching that is based on mathematics can be an excellent starting point (Grandin, For children who find it difficult to interpret subtle social cues or display emotions in conventional means, the clear, rational framework of an algorithmic plot or a balanced character arc offers a safe and approachable way to explore creative expression (Bluhm, 2020). It presents a unique, equally valuable route to creativity.

4.3. Interdisciplinary Innovation

This approach inherently breaks down the institutional silos between the humanities and STEM fields (Gaukroger, 2020). It invites collaboration between creative writing departments, computer science programs, and mathematics departments. Future courses could be co-taught, exploring everything from procedural poetry generation to the use of data visualization in narrative design (Drucker, 2020). This interdisciplinary fusion could lead to entirely new literary forms and new ways of understanding the creative process itself (Berry, 2022).

4.4. A New Relationship with AI

Instead of viewing AI as a threat, a mathematically-literate writer can engage with it as a sophisticated creative partner (Piper, 2023). They can use AI to rapidly prototype combinatorial ideas, to model the network effects of a plot change, or to check for thematic consistency at a fractal level. The writer’s role shifts from pure originator to that of a discerning curator, a creative director guiding a powerful mathematical muse (Ryan, 2024). This human-AI collaboration may be the hallmark of the next generation of literary production.

Artificial Intelligence (AI) (Mageed and Nazir, 2024) has changed how we create art by introducing new methods for artistic expression. This paper examines how AI can transform poetry into visual art, specifically focusing on abstract expressionism, which emphasizes emotional and abstract qualities. By using a tool called Leonardo AI, the research shows that even simple poetic phrases can lead to meaningful and impactful artworks, highlighting the collaboration between human creativity and AI technology.

The Leonardo AI is a tool used in this study to create visual art based on the poetic work titled “Internal Monologues in Poetic Form” by Ismail A Mageed(Mageed and Nazir, 2024). The Mageed and Nazir (2024) explored how this AI can transform simple poetic phrases into unique visual interpretations, showcasing the connection between poetry and abstract art. It also highlights some unresolved questions and suggests future directions for research in this area.

In Figure 3 (Yildirim, 2023) created by Leonardo AI, green spaces, like parks and gardens, are primarily located at ground level, which is a common feature in urban design. The inclusion of bridges in these images suggests a focus on improving transportation and movement within the city. Additionally, the crowded skyline filled with tall buildings highlights the contrast between realistic-looking structures and those that are generated purely by computer algorithms, emphasizing the varying levels of detail and authenticity in the visualizations.

The “visual effect of poetic message” refers to how the arrangement and design of words in a poem can enhance its meaning and emotional impact (Mageed and Nazir, 2024). For example, in the work by Franz Mon, the shape and layout of the text create a visual representation that complements the poem’s themes, making the reading experience more engaging, as depicted in Figure 4 (Bajohr, 2024). This concept is important in visual poetry, where the interplay between text and images allows for a richer understanding of the artistic message being conveyed.

Leonardo AI effectively creates abstract expressionist images that capture the deeper meanings behind poetic themes of “Internal Monologues in Poetic Form” by Ismail A Mageed(Mageed and Nazir, 2024). The generated visuals use symbolism, such as hearts and water, to explore complex ideas like love, life, and change(Mageed and Nazir, 2024). For instance, a heart in water symbolizes both fragility and strength, while waterfalls represent the ongoing nature of life, reflecting the poem’s thoughtful and introspective tone(Mageed and Nazir, 2024), as portrayed by Figure 5, Figure 6 and Figure 7 (Mageed and Nazir, 2024).

5. Conclusion

The proposal to integrate mathematical thinking into creative writing pedagogy is not an attempt to mechanize art or to find a single equation for the perfect novel. It is a call to recognize and harness the powerful, elegant structures that have always underpinned our most enduring stories. By teaching the algorithms of plot, the symmetries of character, the combinatorics of invention, and the fractals of theme, we are not caging the muse; we are giving her a new language and a more robust architectural toolkit.

The challenges—of resisting formula, of overcoming ideological inertia, and of assessing a new kind of craft—are substantial. But the prospects are more compelling. This synthesis promises to create a new generation of writers who are both passionate artists and deliberate designers, capable of building narrative worlds of greater complexity, resonance, and innovation. They will be writers who understand that the shortest path between two emotional points is not always a straight line, but is often a beautifully constructed, mathematically sound, and profoundly human curve. By embracing the algorithmic muse, we can teach writers not just to tell stories, but to understand the very nature of story itself.